Dynamics of weak interactions in the ligand layer of meta-mercaptobenzoic acid protected gold nanoclusters Au₆₈(m-MBA)₃₂ and Au₁₄₄(m-MBA)₄₀

Abstract

Atomically precise metal nanoclusters, stabilized and functionalized by organic ligands, are emerging nanomaterials with potential applications in plasmonics, nano-electronics, bio-imaging, nanocatalysis, and as therapeutic agents or drug carriers in nanomedicine. The ligand layer has an important role in modifying the physico-chemical properties of the clusters and in defining the interactions between the clusters and the environment. While this role is well recognized from a great deal of experimental studies, there is very little theoretical information on dynamical processes within the layer itself. Here, we have performed extensive molecular dynamics simulations, with forces calculated from the density functional theory, to investigate thermal stability and dynamics of the ligand layer of the meta-mercaptobenzoic acid (m-MBA) protected Au₆₈ and Au₁₄₄ nanoclusters, which are the first two gold nanoclusters structurally solved to atomic precision by electron microscopy [Azubel et al., Science, 2014, 345, 909 and ACS Nano, 2017, 11, 11866]. We visualize and analyze dynamics of three distinct non-covalent interactions, viz., ligand–ligand hydrogen bonding, metal–ligand O=C–OH⋯Au interaction, and metal–ligand Ph(π)⋯Au interaction. We discuss their relevance for defining, at the same time, the dynamic stability and reactivity of the cluster. These interactions promote the possibility of ligand addition reactions for bio-functionalization or allow the protected cluster to act as a catalyst where active sites are dynamically accessible inside the ligand layer.

---

Monolayer protected clusters (MPCs) are atomically precise metal nanoparticles with well-defined mass and chemical composition. They have a hybrid structure consisting of a tightly packed core of diameter roughly 1–3 nm (from ten to few hundred metal atoms) that is stabilized by a covalently bound molecular layer consisting of ligand molecules. MPCs have an advantageous, stable, well-defined molecular structure and size compared to larger, colloidal metal nanoparticles, in which variations in diameter are typically of the order of 10% and neither the metal–ligand interface, nor the structure of the ligand surface are known in the molecular scale. Up to now, well over 100 different MPCs have been synthesized and characterized to molecular precision.^1,2 Many studies have confirmed their unique structural, optical, magnetic, and catalytic properties. These nanomaterials are expected to have applications in catalysis, sensing, plasmonics, bioimaging and nanomedicine, where the knowledge of the atom-precise structure of the MPCs gives a unique advantage to understand structure–property relationships and tune the structure for a desired function – an ultimate dream for researchers working with any nanomaterial.

A vast majority of the fundamental studies of the physico-chemical properties of MPCs have dealt with gold nanoclusters stabilized by organic thiols.¹ In general, it is now well-recognized that the ligand layer plays a very important role not only in the synthesis, forming the protective layer stopping the growth of the nucleating metal core, but also modifying the physico-chemical properties of the gold core and the whole MPC.³ First and foremost, the organic surface makes the MPC either hydrophilic or hydrophobic, defining the solubility of the MPC in its environment. Second, the ligand layer may affect crucially the electronic and optical properties of the metal core via charge-transfer and/or imposing chirality. Third, the ligand layer controls the accessibility of foreign molecules to metal sites at the metal–ligand interface, which has impact on the potential catalytic activity of the MPC or its affinity to bind bio-active molecules, sensing moieties or drugs, to name a few. It is thus clear that understanding of the interactions also within the ligand layer becomes crucial for controlling the MPCs’ properties for various applications.

Water-soluble gold nanoparticles are widely studied for potential biological and medical applications, and popular ligands include glutathione, cysteine, and various aromatic or aliphatic carboxylic acids.^3–5 Achieving atomic precision in the structural determination of water-soluble MPCs has proven to be challenging. Up to now, only two successful total-structure determinations from single crystal X-ray experiments have been reported: those of the para-mercaptobenzoic acid (p-MBA) stabilized Au₁₀₂ and Au₁₄₆ clusters,^6,7 in contrast to over 100 X-ray structures of hydrophobic MPCs. Furthermore, three distinct ambient stable sizes of meta-mercaptobenzoic acid (m-MBA) stabilized gold clusters were reported by Azubel and Kornberg.⁸ By using low-dose electron microscopy (EM) techniques and 3D image reconstruction, Azubel and collaborators were able to determine the 3D atomic structure of the gold core for two of those clusters, namely Au₆₈ ⁹ and Au₁₄₄.¹⁰

p-MBA and m-MBA ligands differ from each other only by the location of the carboxylic COOH group (carbon 4 or 3 position in the phenyl ring, respectively). Despite this minute difference in the ligand structure, they seem to induce rather different characteristics for the gold cluster. Clusters stabilized by p-MBA are functionalized for applications mainly by thiolate-to-thiolate ligand exchange or by using the COOH group to bind functional molecules on the ligand surface. Clusters functionalized by this strategy have been used, e.g., for imaging enteroviruses by EM^11,12 and for building small covalently linked cluster assemblies (“clusters of clusters”).¹³ Large disc-like and hollow capsid superstructures (hundreds of nm in size) of p-MBA stabilized clusters have been observed as well, as a result of spontaneous self-assembly in solution driven by weak interactions between the clusters’ organic surfaces.¹⁴

In contrast, m-MBA-stabilized gold clusters have been shown to be reactive towards biomolecules, such as thiol-modified DNA and proteins with an exposed cysteine group, via irreversible ligand addition reactions,⁸ and this propensity has been used successfully in designing cluster-marker hybrids for tracking proteins in live cells.¹⁵ This observation raised an intriguing question on how can the ligand layer keep the cluster size stable and at the same time enable irreversible chemical reactions between the cluster and foreign molecules? Our previous work¹⁶ using molecular dynamics modeling and density functional theory (DFT) calculations with computational models for Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)_40–53 clusters suggested that, in addition to an expected π–π ligand stacking possible for both m-MBA and p-MBA ligand layers, there are three other possible non-covalent interactions in the ligand layer, brought by the chemical structure of the m-MBA ligand, that are not expected in the p-MBA protected clusters. The location of the COOH group in position 3 of the phenyl ring allows for (i) COOH⋯COOH hydrogen bonding between two neighbouring ligands as well as (ii) hydrogen-bond-like O=C–OH⋯Au interaction at the ligand–gold interface. Furthermore, we found (iii) π⋯Au interactions when the ligand was lying “flat” on the gold core. We suggested that these interactions are crucial for dynamical stability, keeping the size of the metal core unchanged but allowing for irreversible ligand additions to gold sites protected by the O=C–OH⋯Au or π–Au interactions. IR data on m-MBA stabilized Au₆₈ and Au₁₄₄ clusters confirmed the O=C–OH⋯Au interaction by revealing an additional C=O stretch frequency at about 1730 cm⁻¹ not present in the reference cluster Au₁₀₂ (p-MBA)₄₄. This frequency corresponded to a prediction from DFT calculations.¹⁶ Later, a combination of experimental and computational work by Maran and collaborators suggested that hydrogen–gold interactions may be present also in gold clusters stabilized by short alkylthiolates.¹⁷

In this work we have employed massively parallel molecular dynamics simulations, with the interatomic forces calculated from DFT, to study the dynamics of the weak interactions in Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀ at elevated temperatures. We show that the average atomic structure of the gold core corresponds well to the 3D reconstruction from the EM data.^9,10 The ligands exhibit a wide range of dynamical behavior as characterised by their root-mean-square deviation (RMSD) values. Strengths of the O=C–OH⋯Au and π⋯Au interactions in Au₆₈ (m-MBA)₃₂ are estimated as 0.5 eV and 0.8 eV, respectively, and activation barriers for breaking those interactions and exposing gold atoms are of the order of 1 eV. Dynamical breaking of these interactions is observed in the molecular dynamics (at 300 K) extended up to 20 ps time scale. These results lay out a theoretical foundation to understand the dynamics of the ligand layer in m-MBA protected gold clusters which is crucial for further engineering of such materials for applications in biological imaging and nanomedicine.

1. Results

The structures of the Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀ clusters were determined experimentally with atomic precision using transmission electron microscopy (TEM) and confirmed by density functional theory (DFT) calculations.^9,10,16 In the earlier studies, DFT calculations on the 68-atom cluster were performed using a model system [Au₆₈ (SH)₃₂], while those for the 144-atom cluster were performed considering the true ligands, but with the Au atoms fixed to the experimental positions. The experiments gave information only on the positions of the Au atoms in the cluster, and the coordinates for the ligand layer were generated using an in-house algorithm.^16,18 The algorithm assigns positions for S atoms close to the Au atoms based on the knowledge of Au–S interfaces from a database of known experimental and computational model structures, using criteria such as nearest neighbor Au–S distances, Au–S coordination, and S–Au–S and Au–Au–S bond angles. The PhCOOH moieties were then added to the structure after the S positions were determined satisfactorily.

In this DFT study, we consider the two cluster systems with true ligands (m-MBA) and with all atoms free to move in order to optimize the structure. We present our results in four sections where we analyze the (i) optimized structure with respect to the experimental data, (ii) effects of temperature on fluxionality and stability of the cluster, (iii) weak but unique interactions in the m-MBA-protected cluster, and (iv) effects of temperature on these weak interactions.

1.1. Analyzing the structures of Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀

The two clusters, Au₆₈ and Au₁₄₄ have almost symmetrically arranged cores with truncated face-centered cubic (FCC) like packing as can be seen in Fig. 1(a) and (b). The Au₆₈ cluster consists of an Au atom at the center inside a 12 atom-cuboctahedron, surrounded by 24 atoms extending along the FCC-like framework with the rest of the 31 atoms deviating from the FCC packing. Similarly, the atoms in the Au₁₄₄ cluster also conform to FCC packing in the core of the cluster while deviating from FCC packing on the surface. Interestingly, both these clusters were found to have C₁ symmetry which is caused by the random arrangement of surface Au atoms. The atoms in Fig. 1(a) and (b) show the experimental structure, while the blue arrows show the deviation of each atom brought about by the DFT optimization. Though the figure shows only Au atoms, note that the DFT calculations were performed on the clusters with the m-MBA ligands. As can be seen, the atoms in the outer shell of the clusters deviate more from the experimental structure than those in the cluster core.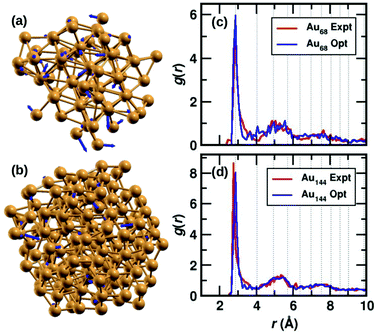

Fig. 1 The structures of (a) Au₆₈ and (b) Au₁₄₄ cores (without ligands) from ref. 9 and 10, respectively. The Au atoms are shown in golden color, the blue arrows indicate the deviation of the DFT-optimized structure with respect to the experimental structure. The tip of the arrows shows the position of the atom after optimization. Pair-correlation function g(r) of Au–Au pairs in the experimental (red) and optimized structures (blue) for the (c) 68- and (d) 144-atom clusters, respectively.

We also calculate the root-mean-square deviation (RMSD) to measure the difference between the experimental and optimized structures. When we consider only the Au atoms, excluding the m-MBA ligands, the RMSD values were calculated to be 1.24 Å and 0.80 Å for the Au₆₈ and Au₁₄₄ clusters, respectively. Previously as reported in ref. 9, we had optimized a simplified model for the cluster, viz., Au₆₈ (SH)₃₂. In that case, the RMSD for the Au atoms with respect to the experimental structure was calculated to be 0.72 Å.

In Fig. 1(c) and (d), we compare the pair-correlation function, g(r), of Au–Au interactions in the experimental (shown in red) and optimized structures (shown in blue) of Au₆₈ and Au₁₄₄, respectively. The pair-correlation function gives information about the probability of finding atoms at a distance from any given atom, or in other words, the distribution of atoms in the cluster. A sharp and intense peak is observed at Au–Au distance r ∼ 2.9 Å in all cases that indicate the nearest neighbor Au–Au bond length and confirms the excellent match between the experimental and our computational results in both systems. The pair-correlation peak positions for Au–Au pairs in bulk FCC Au are shown in dotted lines for comparison. At higher values of r, we see a tendency for a more uniform distribution which is in line with the understanding that only the cluster core has FCC-like packing. These results validate the stability of the experimentally determined structures for the two clusters.

1.2. Effects of temperature on the structure

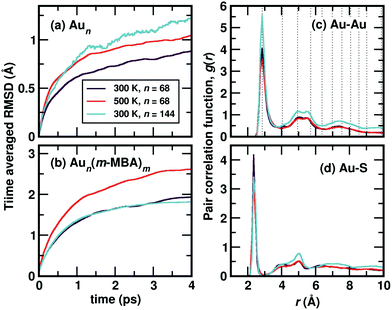
Starting from the optimized structures of Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀, we then performed ab initio molecular dynamics simulations. For the 68-atom cluster, we studied target temperatures of 300 K and 500 K, for a simulation time of around 20 ps and 15 ps, respectively and for the 144-atom cluster, we show our results at 300 K for a simulation time of 10 ps. The temperature increases from 0 K to the target temperature in the first ∼4 ps of the simulation.

The average root-mean-square deviations (RMSD) of the Au atoms in the clusters after thermal equilibration, with respect to the optimized structure were calculated to be 1.13 Å and 1.48 Å for Au₆₈ at 300 K and 500 K, respectively, and 1.65 Å for Au₁₄₄ at 300 K. This can be attributed to thermal effects due to the increase in temperature from 0 K to the respective target temperature. If all atoms in the clusters (Au and the ligands) were considered, the average RMSD with respect to the optimized structure were calculated to be 3.33 Å and 3.37 Å for Au₆₈ at 300 K and 500 K, respectively, and 2.90 Å for Au₁₄₄ at 300 K.

In Fig. 2(a), we plot time evolution of the RMSD of the Au atoms in the two clusters, at different temperatures for a time window of 4 ps, averaged over several time origins. In Fig. 2(b), we show the similar data, but now considering all atoms in the cluster. On comparing the data for the 68-atom cluster at 300 K (maroon) and 500 K (orange), we see higher values of RMSD for 500 K, which is as expected from thermal effects. As we compare the two sizes of clusters, viz., 68-atom cluster (maroon) and 144-atom cluster (turquoise), both at 300 K, we see an increase in the RMSD values of the Au atoms in the 144 cluster, which suggests that there are higher number of Au atoms that do not conform to FCC packing and are more mobile than atoms in the 68 cluster. However, upon considering all atoms, Au as well as the ligands, the two clusters behave approximately the same at 300 K.

Fig. 2 Time-averaged root-mean-square deviation (RMSD) of Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀ clusters as a function of simulation time after temperature equilibration, evaluated for (a) the gold core and (b) all atoms of the cluster. The pair-correlation function, g(r), of (c) Au–Au and (d) Au–S pairs, in the two clusters, the 68-atom cluster at 300 K and 500 K and 144-atom cluster at 300 K.

We show the calculated pair correlation function, g(r) after equilibration of temperature, of Au–Au and Au–S interactions in the cluster, in Fig. 2(c) and (d), respectively. For both pairs of interaction, we see sharp peaks at Au–Au distance r ∼ 2.9 Å and Au–S distance r ∼ 2.4 Å, indicating the first nearest neighbor distances of Au–Au and Au–S bonds, respectively. The peak corresponding to Au–Au bonds is broadened in width when compared to the peak observed in Fig. 1(b), which can be attributed to temperature effects. At higher values of r, the function seems to approach a continuous shape which suggests an amorphous nature in the cluster. These results suggest that both clusters with all Au–Au and Au–S bonds are structurally stable at room temperature. Earlier studies on differential scanning calorimetry of gold thiolate clusters have demonstrated the thermal stability of neutral clusters such as Au₂₅ (SR)₁₈ up to temperatures of ∼494 K.¹⁹ Our results of the 68-atom cluster at 500 K suggest that they are thermally stable however, we also keep in mind that the simulated timescale ∼15 ps may be very short to observe any large deviation or breaking of Au–S bonds.

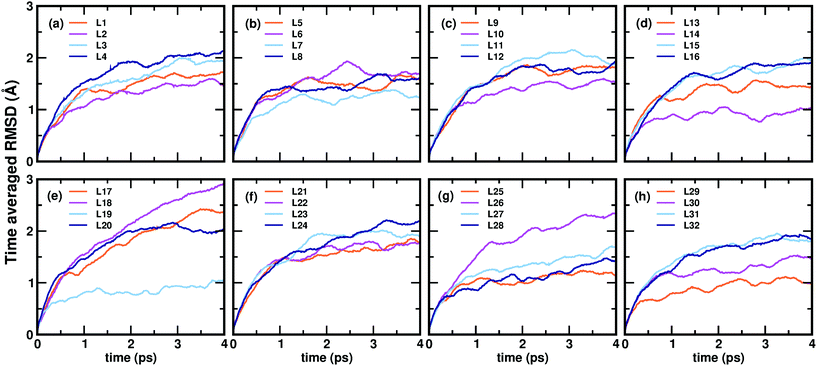
Now, we move on to examine the dynamics of the individual ligands in the clusters. In Fig. 3, we show the time-averaged RMSD of each of the 32 ligands in the Au₆₈ (m-MBA)₃₂ cluster at 300 K for a time window of 4 ps. We see that each ligand has unique dynamics, some ligands being more mobile than others. A similar graph showing the time-averaged RMSD values of the 40 ligands in Au₁₄₄ (m-MBA)₄₀ at 300 K is shown in the ESI (Fig. S1†). In Fig. 4(a) and (b), we plot the maximum value of RMSD of each ligand in the 68 and 144 clusters, respectively, observed in our simulations at 300 K, in ascending order. We also show snapshots of the clusters at 300 K, in different orientations. In the ESI,† we repeat Fig. 4 in Fig. S2† with zoomed-in images of the clusters Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀, in different orientations and each of their ligands labelled in Fig. S3 and S4,† respectively. Additional multimedia files (mpg) showing the molecular dynamics simulations of the systems considered here are also provided. These help to understand and assess the different degrees of mobility and orientation dynamics of every ligand in the cluster. We note here the large difference in ligand mobility within the given cluster: in Au₆₈, the most mobile ligand is about three times more mobile than the least mobile one, and in Au₁₄₄ the corresponding ratio is about 4 : 1. This result is similar to what we have seen previously while performing molecular dynamics simulations of the Au₁₀₂ (p-MBA)₄₄ cluster in water, using classical force fields.²⁰

Fig. 3 (a)–(h) Show the time-averaged root-mean-square deviation (RMSD) of every individual ligand in the Au₆₈ (m-MBA)₃₂ cluster, after temperature equilibration, as a function of simulation time evaluated at 300 K.

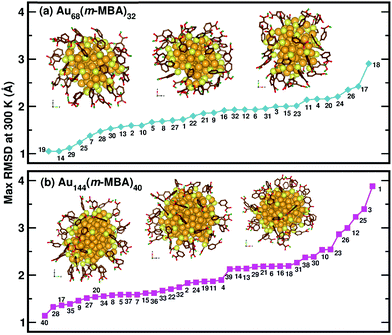Fig. 4 The maximum values of time-averaged RMSD of each ligand in the (a) 68-atom cluster and (b) 144-atom cluster, are plotted in ascending order. The snapshots from three different orientations of the Au₆₈ (m-MBA)₃₂ and Au₁₄₄ (m-MBA)₄₀ clusters at 15 ps and 8 ps, respectively are also shown. The numbering of the ligands is the same as in Fig. 3. Au, S, C, O, and carboxylic H atoms are shown in golden, pale yellow, brown, red, and green colors, respectively.

1.3. Unique interactions in a m-MBA-protected cluster

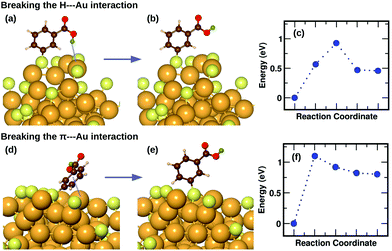
We have previously described,¹⁶ using a combination of experimental and computational methods, that the presence of the m-MBA ligands leads to very different properties in Au₆₈ (m-MBA)₃₂ from those in other thiolate-protected gold nanoclusters of similar size. The position of the acid group (C3 or meta position) in the aromatic ring creates a range of possibility for weak interactions that are absent in p-MBA protected clusters or organo-soluble thiolate-protected clusters. These weak interactions include H-bonds between ligands within the ligand layer as well as two new unexpected interactions at the ligand–Au interface: (i) H-bond-like COOH⋯Au interactions formed when the carboxylic H atom is directed toward the gold core and (ii) π⋯Au interactions formed when the aromatic ring lies flat on the gold core. Earlier,¹⁶ we had performed molecular dynamics simulations using classical force fields to describe thiol–gold interactions. Based on these simulations, we had reported the presence of close COOH⋯Au interactions with distances in the range of 2.3 to 2.7 Å and π⋯Au interactions with distances between the phenyl ring center and an Au atom, less than 2.8 Å.

In this section, we describe how we have used DFT and climbing-image nudged elastic band method²¹ to investigate in detail the stability and energy barriers involved in the breaking of the weak ligand⋯Au interactions in an Au₆₈ (m-MBA)₃₂ cluster. In the optimized structure, we find two cases of COOH⋯Au interactions, where the carboxylic hydrogen is pointed towards the Au core with d(H–Au), the distance between H and Au atoms, 3.67 Å and 3.68 Å. These correspond to ligands #7 and #1, respectively in Fig. 3 and 4(a). In Fig. 5(a), we show an zoomed-in image of the optimized structure of the cluster and highlight a single ligand that forms the weak COOH⋯Au bond [d(H–Au) = 3.67 Å]. We calculated the energy of the structure (keeping all atoms fixed except the ligand and interacting Au atoms) considering the same ligand with its carboxylic hydrogen pointed away from the Au core [d(H–Au) = 5.16 Å], as shown in Fig. 5(b). We define the energy difference between these two structures as the H⋯Au interaction energy and it was calculated to be 0.46 eV, which is the cost to break this interaction. The energy pathway to go from the structure in Fig. 5(a) and (b) is shown in Fig. 5(c); the barrier to break the H⋯Au interaction was calculated to be 0.93 eV. At the transition state, the value of d(H–Au) was found to be 4.08 Å.

Fig. 5 (a) The optimized structure of Au₆₈ (m-MBA)₃₂ highlighting a COOH⋯Au interaction. (b) The ligand in (a) is modified such that the carboxylic H is pointed away from the Au core breaking the interaction. (d) The optimized structure of Au₆₈ (m-MBA)₃₂ highlighting a π⋯Au interaction, (e) the structure with the ligand in (d) modified such that it stands upright breaking the interaction. (c) and (f) show the energy profiles as obtained from CI-NEB calculations for the minimum energy pathway from structure (a) to (b), and (d) to (e), respectively. Au, S, C, O, phenyl H and carboxylic H are shown in golden, pale yellow, brown, red, white and green colors, respectively. All the ligands were included in the calculation but the other ligands are not shown for clarity.

We also find two π⋯Au interactions with distances between the center of the phenyl ring and the closest Au atom, d(π–Au) = 3.01 Å (ligand #14) and d(π–Au) = 3.06 Å (ligand #22). In Fig. 5(d), we show the cluster highlighting the ligand with d(π–Au) = 3.01 Å, where the phenyl ring is facing and protecting an Au atom on the surface. In Fig. 5(e), we show the structure with the same ligand standing in an upright position with d(π–Au) = 4.89 Å. As in the case of the broken H⋯Au interaction, this structure was calculated keeping all atoms except the involved ligand and neighboring Au atoms fixed. The energy difference between the two structures was calculated to be 0.80 eV, which we estimate is the energy lost upon breaking the π⋯Au interaction. The energy profile for the minimum-energy pathway from the structure in Fig. 5(d) and (e) is shown in Fig. 5(f) and the barrier was calculated to be 1.10 eV. At the transition state, the distance between the center of the phenyl ring and the Au atom was found to be 3.97 Å. The angle made by the C atom in the para-position of the phenyl ring, S and Au atom changes from 51.8° in the initial state, to 81.5° in the transition state, to 118.3° in the final state.

The binding energy of an AuH molecule with covalent bonding has a value of around 3 eV.²² Weak interactions between H and Au atoms, similar to that observed in m-MBA clusters, have also been observed and reported for several gold complexes.²³ The H⋯Au weak H-bond-like interactions were first observed between neutral triangular gold clusters and formamide or formic acid, where the estimated the H⋯Au binding energies were found to be around 0.16 eV for Au⋯H–N and 0.22 eV for Au⋯H–O interactions.²⁴ The binding energy for the H-bond observed in [Au⋯H₂O]⁻, on the other hand, was calculated to be 0.45 eV.²⁵ These values are in the range of hydrogen bond strengths which is generally between 0.05 eV–0.50 eV in molecules containing N–H, O–H or F–H bonds.

1.4. Effects of temperature on the weak interactions

To understand the dynamics of the weak interactions that are present in m-MBA-protected clusters, we examine in detail the case of the Au₆₈ (m-MBA)₃₂ cluster at 300 K. We consider an interaction between (i) carboxylic H and O atoms of different ligands, (ii) carboxylic H and Au, and (iii) phenyl π-ring and Au, to be a weak bond if d(H–O), d(H–Au) or d(π–Au) is less than 4 Å. Here, d(X–Y) is the distance between atoms X and Y and d(π–Au) is the distance between the center of a phenyl ring and an Au atom.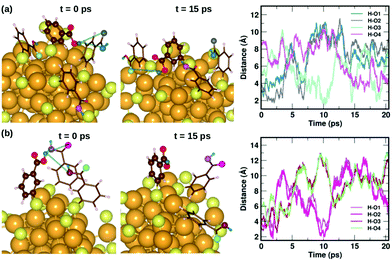

1.4.1. Inter-ligand COOH⋯COOH hydrogen bonding. In Fig. 6, we examine two examples of dynamic interactions between ligands in the ligand shell at 300 K, where hydrogen bonds are continuously formed and broken. We show snapshots of the cluster at 0 ps and 15 ps and how the distances between a particular carboxylic hydrogen atom and oxygen atoms in neighboring ligands change with time. Fig. 6(a) highlights the interaction of one ligand's (ligand #30) carboxylic hydrogen (green) with oxygen atoms (blue, grey, turquoise and violet) in neighboring ligands. At 0 ps, the green H atom may be weakly linked to blue and grey O atoms in the same ligand, as time progresses, it breaks these bonds and forms new H-bonds with O atoms (grey and turquoise) in two different ligands, and finally at 15 ps, it seems to form one H-bond with the turquoise O atom in one ligand. In the second example in Fig. 6(b), the green carboxylic hydrogen in ligand #16 forms H-bonds with two magenta and maroon colored O atoms at 0 ps and moves away from these interactions at 15 ps. This analysis helps to give us a clear visual understanding of how dynamic these ligands are and how easily they form and break these weak interactions between them.

Fig. 6 Two examples highlighting the dynamics of hydrogen bonds formed by COOH⋯COOH interactions. In (a) and (b), we show how carboxylic hydrogen atoms of ligands #30 and #16, respectively, interact with oxygen atoms in neighboring ligands. The color scheme for the atoms is the same as in Fig. 5. In (a), the carboxylic hydrogen (green) binds to O atoms colored blue, grey, turquoise and violet. In (b), the carboxylic hydrogen binds to O atoms colored violet, magenta, maroon and pale green.

1.4.2. Hydrogen-bond-like O=C–OH⋯Au interaction at the ligand–gold interface. Fig. 7 displays two examples of the hydrogen-bond-like H⋯Au interactions, and how they change as a function of simulation time. In the first panel Fig. 7(a) shows the interaction of the carboxylic hydrogen atom (green) in the highlighted ligand (ligand #7) with two Au and two S atoms on the cluster surface at t = 0 ps and 15 ps and how the distances between the H and Au/S atoms vary as a function of time. At t = 0 ps, the carboxylic hydrogen atom binds to an Au atom (lavender) and a S atom (pale blue). At t = 15 ps, the carboxylic hydrogen is still pointed towards the Au core, but has now changed its interactive neighbors. It now binds to another Au (purple) and S atom (blue).

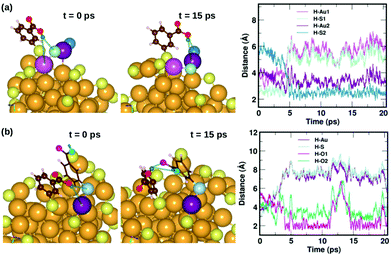Fig. 7 Two examples highlighting the dynamics of weak COOH⋯Au interactions. In (a), we show how the carboxylic hydrogen of ligand #7 binds to different Au and S atoms on the cluster surface as a function of time, while in (b), we show another case, where the carboxylic hydrogen of ligand #1 that initially binds to an Au and S on the surface moves away and forms H-bonds with O atoms in a neighboring ligand. The color scheme for the atoms is the same as in Fig. 5. In (a), the carboxylic hydrogen binds to Au atoms colored lavender and purple, and S atoms colored pale blue and blue. In (b), the carboxylic hydrogen binds to Au, S and O atoms colored purple, pale blue, turquoise and magenta, respectively.

In the second panel Fig. 7(b), we present the interaction between the carboxylic hydrogen in the highlighted ligand (ligand #1) with an Au, S and two O atoms in a neighboring ligand. At t = 0 ps, the H binds to an Au (purple) and S (pale blue) atom on the surface of the cluster. At t = 15 ps, we find that during the course of the molecular dynamics simulations, the H turns away from the Au core and makes hydrogen-bonds with O atoms (turquoise and magenta) in the carboxylic group of the neighboring ligand. The distances between the H atom and the Au/S/O atoms as a function of time are plotted and shown in Fig. 7(b). This is also interesting as we see that there may be a competition for favored interactions.

1.4.3. π⋯Au interactions at the ligand–gold interface. Similarly, in Fig. 8, we show the dynamics of two ligands that form weak π⋯Au interactions. At t = 0 ps, the ligands are aligned such that their phenyl rings lie above an Au atom on the cluster. However, at t = 15 ps, the ligands move away thereby leaving the Au atom unprotected. In panel (a), the ligand (ligand #14) binds to an Au atom that is colored lavender, while in panel (b), it (ligand #22) binds to an Au atom that is colored blue. We also show in both panels the distance between the center of the phenyl ring and the Au atom plotted as a function of the simulation time. This we believe may turn out to be the interaction with most potential to be exploited to facilitate a catalytic nature in these clusters. A low-coordinated Au atom that was protected by the π⋯Au interaction could be available as an active site for a catalytic reaction as the ligand moves away from the surface of the cluster.

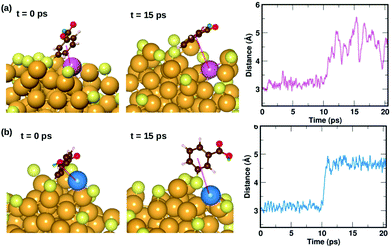Fig. 8 Two examples highlighting the dynamics of ligands that form weak π⋯Au interactions. The ligand that is initially lying flat on the cluster, protecting an Au atom at t = 0 ps, moves away from the atom at t = 10 ps. The distance between the center of the phenyl ring and the protected Au atom is plotted as a function of time. The color scheme for the atoms is the same as in Fig. 5. In (a), the ligand (#14) binds to an Au atom highlighted in lavender color, while in (b) the ligand (#22) binds to an Au atom in blue color.

2. Discussion

The current hypothesis is that atomically precise MPCs may be highly beneficial for catalysis, for several reasons.²⁶ First, they have unique geometric and electronic structure. Second, there is an abundance of low-coordination atomic sites on the surface of the clusters. Third, they have quantized energy levels which makes activation of reactant molecules viable.^1,27,28 Fourth, one can control their solubility in water by tuning the nature of the ligand thereby promoting green chemistry or enable use in biological applications.²⁹ Fifth, they are highly dynamic and flexible under reaction conditions that facilitates the exploration of novel catalytic routes. Finally, it is also possible to have control and structurally characterize them down to atomic level which allows for rational design of better catalysts. However, thorough investigations of their catalytic behavior are still in very early stages.

Computational studies have contributed to the understanding of MPC and their catalytic behavior. However, there are intrinsic challenges to studying such metal–ligand interfaces.³⁰ Most DFT studies on reaction mechanisms on MPCs have been carried out on ligand-decorated metal surface models due to the computational limitations in studying large number of atoms. Models with classical force fields would significantly speed up simulations, but the variety of bonds within the MPCs make fitting of parameters demanding and reliable modeling of chemistry (making and breaking bonds) with classical force fields is still largely an unsolved challenge. There also exists a lack of experimental knowledge of the structure and dynamics at the interface which makes first-principles calculations on these systems still rare,^31–34 but also highly attractive.

Several studies show Au MPCs to be effective for a variety of important reactions such as CO oxidation,³⁵ aerobic oxidation of alcohols,³⁶ α-hydroxylation of benzylic ketones,³⁷N-formylation of amines,³⁸ oxidation of organoboron compounds,³⁹ intramolecular addition of toluene sulfonamide⁴⁰ and intramolecular addition of primary amines,⁴¹ with experimental evidence and proposed reaction mechanisms suggesting that these clusters perform as catalysts without the removal of ligands.²⁶ There are also detailed studies carried out to show the effects of chain length of thiolate ligands on the accessibility, catalytic activity and selectivity of MPC catalysts.³ Recently, we have proposed, tested and confirmed the reaction mechanism involved in the hydrogenation of ketones to alcohols, using a combination of experiments and DFT calculations, catalysed by an atomically precise thiolate protected copper-hydride cluster.⁴² The reaction is shown to proceed without the removal of any ligands.

Some authors have also noted that these clusters may not necessarily be the actual catalyst, but instead the precatalysts, as these clusters often decompose or deform during chemical reactions. The removal of the ligands have also been shown to be important for several catalytic reactions.²⁶ However, the thermal treatment for the removal of surface ligands is found to be an aggressive method that sometimes lead to sintering of the Au nanoclusters even at low loading concentration.^43–45

These examples suggest that there exists different views on how the ligand affects the catalytic behavior of the MPC, however in all of them, the exact role of the ligands during a reaction remain vague. In addition to catalysis, MPCs can be used in sensing applications due to their luminescence properties² and in transistors, switches or electrometers due to their electrical and optical properties.⁴⁶ MPCs formed by the conjugation of oligonucleotides with Au nanoclusters can also be used in biosensors, disease diagnosis and gene expression.^47,48 It is certain that a quantitative and/or qualitative understanding of the behavior of ligands around a cluster will be of fundamental importance in the future research of MPCs in any of these applications. In this direction, we believe that the present study offers significant insight into comprehending, down to the atomic level, the dynamics and active role of ligands in an MPC.

The m-MBA protected Au clusters have already been shown to exhibit a higher reactivity towards thiol-modified DNA and proteins (with an exposed cysteine group) than other similar-sized thiolate protected Au clusters, which is attributed to the presence of the unique non-covalent metal–ligand interactions discussed in detail in this manuscript. It is evident that these highly mobile ligands are crucial in stabilizing and keeping the size of the cluster constant, while also allowing for ligand-additions or more interestingly perhaps reactants to adsorb at gold sites protected by the O=C–OH⋯Au or π⋯Au interactions. Our analysis of the barriers to break and dynamics of each of these interactions suggest that under the reaction conditions, it is possible to conclude that the ligands may leave Au sites on the cluster unprotected making them ideal for catalysis.

3. Conclusions

In this study, we have focused on m-MBA-protected Au_n clusters, that have been shown to be unique with a new range of interactions present at the Au–ligand interface that are absent in p-MBA- or other thiolate-protected Au clusters. These clusters present, in addition to the strong Au–S covalent bonding that links the ligands to the Au cluster, three unique interactions, viz., (i) inter-ligand H-bonding, (ii) H-bond-like H⋯Au bonding, and (iii) π⋯Au bonding. We have shown that these clusters are very stable at temperatures of 300 K up to 500 K. Each ligand is found to be unique in its orientation, and mobility around the ligand shell.

We have also described the dynamic interactions in the ligand shell and the ligand–Au interface by showing explicit examples of how they are continuously formed and broken at 300 K. We believe that these are important steps forward in the understanding of what exactly happens at a metal–ligand interface. We find the H⋯Au and π⋯Au interactions of particular consequence for applications such as catalysis. Interestingly, these ligands are highly mobile at room temperature, and the energy required to break these interactions were calculated to be 0.93 eV and 1.10 eV, respectively. These results in addition to the examples showing the dynamic nature of these ligands, help us to understand how easily these low-coordinated Au atoms on the surface, can be protected and/or made available as active sites for reactions.

4. Computational methods

We have performed density functional theory calculations as implemented in the GPAW package which uses the projector-augmented wave method.⁴⁹ We have used a real-space grid with grid spacing of 0.2 Å. The electron–electron interactions were treated within the generalized gradient approximation using the PBE (Perdew–Burke–Ernzerhof) functional.⁵⁰

The coordinates of the Au atoms in the Au₆₈ and Au₁₄₄ clusters were obtained from experimental transmission electron microscopy (TEM) data,^9,10 and were used as initial coordinates for DFT optimization. The initial structures for the ligand layers in both clusters were created using an in-house algorithm described previously.¹⁶ To construct the initial coordinates for the ligand S atoms, we rely on our knowledge of the bonding environment of gold–thiolate interfaces from known structures. The organic part of the ligand is then added to the selected Au–S interface positions in random order with preference to using the natural bonding direction (in which the ligand makes an angle ∼90° with respect to the nearest neighbor Au–S bonds). In cases of possible overlapping ligands, the orientation pointing directly away from the center of mass of the cluster were used. The final model structures were initialized using classical force field simulations by first turning on gradually the interactions between ligands to get rid of remaining overlaps and then finally optimizing the overall ligand layer arrangement. The final optimized structure from these classical MD simulations were used as initial geometries for the DFT calculations described in this work.

The clusters were simulated in a non-periodic cubic cell large enough to include ∼6 Å vacuum in all six directions around the clusters. All atoms were allowed to be free during structural optimization, until forces on the atoms were below 0.05 eV Å⁻¹. Fermi–Dirac smearing of width 0.05 eV was used for the occupation numbers to hasten convergence. The root-mean-square deviation measurements were done using the RMSD Tool plugin in the Visual Molecular Dynamics (VMD) software.⁵¹

Ab initio molecular dynamics simulations were performed using Langevin dynamics with target temperatures of 300 K and 500 K. In both cases, a friction parameter of 0.01 fs⁻¹, and time step of 2 fs were used. To enable the 2 fs time step with acceptable numerical accuracy, we increased the masses of all hydrogen atoms to that of deuterium atoms.⁵²

The barriers to break the H⋯Au and π⋯Au interactions were computed using the climbing-image nudged elastic band method.²¹ When performing these calculations, only the atoms in the involved ligand and the Au atoms that interact with the ligand were allowed to be free. The obtained transition states were validated upon analyzing their vibrational frequencies.

The results presented in this paper were obtained from massively parallel calculations (performed on MareNostrum in the Barcelona Supercomputing Center). Two examples illustrate the needed computer resources: the molecular dynamics simulation for Au₆₈ (m-MBA)₃₂ at 300 K was performed on 960 cores for approximately 1300 hours and the NEB calculation to determine the dissociation barrier for the H⋯Au interaction was performed on 2400 cores for approximately 250 hours. This is explained by the large size of the system both in terms of the real-space grid and number of occupied valence electron states: 2380 electrons for Au₆₈ (m-MBA)₃₂ and 3624 valence electrons for Au₁₄₄ (m-MBA)₄₀.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Academy of Finland (grants 292352, 294217 and 319208 to H. H. and 307623 to K. H.). The computations were made in the Barcelona Supercomputing Center as a PRACE project no. 2018194723.

References

1. Protected Metal Clusters: From Fundamentals to Applications, ed. T. Tsukuda and H. Häkkinen, Elsevier Ltd., 2015.
2. I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208.
3. R. R. Nasaruddin, T. Chen, N. Yan and J. Xie, Coord. Chem. Rev., 2018, 368, 60.
4. Y. Zhang, C. Zhang, C. Xu, X. Wang, C. Liu, G. I. Waterhouse, Y. Wang and H. Yin, Talanta, 2019, 200, 432–442.
5. D. M. Chevrier, A. Chatt and P. Zhang, J. Nanophotonics, 2012, 6, 064504.
6. P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430.
7. S. Vergara, D. A. Lukes, M. W. Martynowycz, U. Santiago, G. Plascencia-Villa, S. C. Weiss, M. J. de la Cruz, D. M. Black, M. M. Alvarez, X. Lopez-Lozano, C. O. Barnes, G. Lin, H. C. Weissker, R. L. Whetten, T. Gonen, M. J. Yacaman and G. Calero, J. Phys. Chem. Lett., 2017, 8, 5523.
8. M. Azubel and R. D. Kornberg, Nano Lett., 2016, 16, 3348.
9. M. Azubel, J. Koivisto, S. Malola, D. Bushnell, G. L. Hura, A. L. Koh, H. Tsunoyama, T. Tsukuda, M. Pettersson, H. Häkkinen and R. D. Kornberg, Science, 2014, 345, 909.
10. M. Azubel, A. L. Koh, K. Koyasu, T. Tsukuda and R. D. Kornberg, ACS Nano, 2017, 11, 11866.
11. V. Marjomäki, T. Lahtinen, M. Martikainen, J. Koivisto, S. Malola, K. Salorinne, M. Pettersson and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1277.
12. M. Martikainen, K. Salorinne, T. Lahtinen, S. Malola, P. Permi, H. Häkkinen and V. Marjomäki, Nanoscale, 2015, 7, 17457.
13. T. Lahtinen, E. Hulkko, K. Sokolowska, T.-R. Tero, V. Saarnio, J. Lindgren, M. Pettersson, H. Häkkinen and L. Lehtovaara, Nanoscale, 2016, 8, 18665.
14. N. Nonappa, T. Lahtinen, J. S. Haataja, T. Tero, H. Häkkinen and O. Ikkala, Angew. Chem., Int. Ed., 2017, 55, 16035.
15. M. Azubel, S. D. Carter, J. Weiszmann, J. Zhang, G. J. Jensen, Y. Li and R. D. Kornberg, eLife, 2019, 8, e43146.
16. T.-R. Tero, S. Malola, B. Koncz, E. Pohjolainen, S. Lautala, S. Mustalahti, P. Permi, G. Groenhof, M. Pettersson and H. Häkkinen, ACS Nano, 2017, 11, 11872.
17. T. Dainese, M. Agrachev, S. Antonello, D. Badocco, D. M. Black, A. Fortunelli, J. A. Gascón, M. Stener, A. Venzo, R. L. Whetten and F. Maran, Chem. Sci., 2018, 9, 8796.
18. S. Malola, P. Nieminen, A. Pihlajamäki, J. Hämäläinen, T. Kärkkäinen and H. Häkkinen, Nat. Commun., 2019, 10, 3793.
19. M. A. Tofanelli and C. J. Ackerson, J. Am. Chem. Soc., 2012, 134, 16937.
20. K. Salorinne, S. Malola, O. A. Wong, C. D. Rithner, X. Chen, C. J. Ackerson and H. Häkkinen, Nat. Commun., 2016, 7, 10401.
21. H. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901.
22. A. Kant and K. A. Moon, High Temp. Sci., 1979, 11, 55.
23. H. Schmidbaur, H. G. Raubenheimer and L. Dobrzańskad, Chem. Soc. Rev., 2014, 43, 345.
24. E. S. Kryachko and F. Remacle, Chem. Phys. Lett., 2005, 404, 142.
25. W. Zheng, X. Li, S. Eustis, A. Grubisic, O. Thomas, H. de Clercq and K. Bowen, Chem. Phys. Lett., 2007, 444, 232.
26. J. Fang, B. Zhang, Q. Yao, Y. Yang, J. Xie and N. Yan, Coord. Chem. Rev., 2016, 322, 1–29.
27. R. Jin, Nanoscale, 2015, 7, 1549.
28. O. Lopez-Acevedo, K. A. Kacprzak, J. Akola and H. Häkkinen, Nat. Chem., 2010, 2, 329.
29. C. J. Ackerson, P. D. Jadzinsky and R. D. Kornberg, J. Am. Chem. Soc., 2005, 127, 6550.
30. M. A. Ortuño and N. López, Catal.: Sci. Technol., 2019, 9, 5173.
31. Y. Pei, N. Shao, Y. Gao and X. C. Zeng, ACS Nano, 2010, 4, 2009.
32. N. Almora-Barrios, I. Cano, P. W. N. M. van Leeuwen and N. López, ACS Catal., 2017, 7, 3949.
33. D. R. Alfonso, D. Kauffman and C. Matranga, J. Chem. Phys., 2016, 144, 184705.
34. D. R. Kauffman, D. Alfonso, C. Matranga, P. Ohodnicki, X. Deng, R. C. Siva, C. Zeng and R. Jin, Chem. Sci., 2014, 5, 3151.
35. C. G. Long, J. D. Gilbertson, G. Vijayaraghavan, K. J. Stevenson, C. J. Pursell and B. D. Chandler, J. Am. Chem. Soc., 2008, 130, 10103.
36. H. Tsunoyama, N. Ichikuni, H. Sakurai and T. Tsukuda, J. Am. Chem. Soc., 2009, 131, 7086.
37. H. Sakurai, I. Kamiya, H. Kitahara, H. Tsunoyama and T. Tsukuda, Synlett, 2009, 245.
38. P. Patcharee, K. Hiroaki, C. Warinthorn and S. Hidehiro, Chem. Lett., 2010, 39, 1174.
39. H. Tsunoyama, H. Sakurai, N. Ichikuni, Y. Negishi and T. Tsukuda, Langmuir, 2004, 20, 11293.
40. H. Kitahara, I. Kamiya and H. Sakurai, Chem. Lett., 2009, 38, 908.
41. H. Kitahara and H. Sakurai, Chem. Lett., 2010, 39, 46.
42. C. Sun, N. Mammen, S. Kaappa, P. Yuan, G. Deng, C. Zhao, J. Yan, S. Malola, K. Honkala, H. Häkkinen, B. K. Teo and N. Zheng, ACS Nano, 2019, 13, 5975.
43. A. Longo, E. J. J. de Boed, N. Mammen, M. van der Linden, K. Honkala, H. Häkkinen, P. E. de Jongh and B. Donoeva, Chem. – Eur. J., 2020, 26, 7051.
44. B. Zhang, A. Sels, G. Salassa, S. Pollitt, V. Truttmann, C. Rameshan, J. Llorca, W. Olszewski, G. Rupprechter, T. Bürgi and N. Barrabés, ChemCatChem, 2018, 10, 5372.
45. S. Pollitt, V. Truttmann, T. Haunold, C. Garcia, W. Olszewski, J. Llorca, N. Barrabés and G. Rupprechter, ACS Catal., 2020, 10, 6144.
46. M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293.
47. X. Qian, X.-H. Peng, D. O. Ansari, Q. Yin-Goen, G. Z. Chen, D. M. Shin, L. Yang, A. N. Young, M. D. Wang and S. Nie, Nat. Biotechnol., 2008, 26, 83.
48. N. L. Rosi, D. A. Giljohann, C. S. Thaxton, A. K. R. Lytton-Jean, M. S. Han and C. A. Mirkin, Science, 2006, 312, 1027.
49. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dulak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez- Acevedo, P. G. Moses, J. Ojanen, T. Olsen and V. Petzold, et al. , J. Condens. Matter Phys., 2010, 22, 253202.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
51. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
52. K. A. Feenstra, B. Hess and H. Berendsen, J. Comput. Chem., 1999, 20, 786–798.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 shows the time-averaged RMSD of each of the 40 ligands in the Au₁₄₄ (m-MBA)₄₀ cluster at 300 K for a time window of 4 ps. Fig. S2 shows the maximum RMSD values of every ligand in the 68-atom and 144-atom clusters at 300 K. Fig. S3 and S4 show the structures of the two clusters at 300 K with S atoms labelled with the ligand numbers. In addition, we provide three multimedia files to show the MD simulation of (i) Au₆₈ (m-MBA)₃₂ at 300 K, (ii) Au₆₈ (m-MBA)₃₂ at 500 K and (iii) Au₁₄₄ (m-MBA)₄₀ at 300 K. See DOI: 10.1039/D0NR07366K

---