Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Key role of the meniscus shape in crystallization of organic semiconductors during meniscus-guided coating†
Ke
Zhang
a,
Zuyuan
Wang
a,
Tomasz
Marszalek
 ab,
Michal
Borkowski
b,
George
Fytas
a,
Paul W. M.
Blom
ab,
Michal
Borkowski
b,
George
Fytas
a,
Paul W. M.
Blom
 a and
Wojciech
Pisula
a and
Wojciech
Pisula
 *ab
*ab
aMax Planck Institute for Polymer Research, Ackermannweg 10, Mainz 55128, Germany. E-mail: pisula@mpip-mainz.mpg.de
bDepartment of Molecular Physics, Faculty of Chemistry, Lodz University of Technology, Zeromskiego 116, Lodz 90-924, Poland
First published on 3rd April 2020
Abstract
Solution processable organic semiconductors (OSCs) hold advantages for the fabrication of flexible and large-area electronic devices. Meniscus-guided coating (MGC) is one promising technique to tune the crystallization and thin film morphology of OSCs. In this work, we demonstrate the crucial role of the meniscus shape in the fluid flow and crystallization of OSCs during MGC. We demonstrate that angle-dependent dip-coating (ADDC) allows precise control of the meniscus shape. The use of a small meniscus angle during ADDC of 2,7-dioctyl[1]benzothieno[3,2-b][1]benzothiophene (C8-BTBT) enhances the crystallization and mass deposition of the OSC due to an increased upward fluid flow. The resulting aligned crystalline film with high surface coverage favors the charge carrier transport in C8-BTBT based field-effect transistors. This work provides comprehensive insight into the fundamental mechanism of OSC crystallization during MGC, which is important for the large-area deposition of OSCs for practical electronic applications.
New conceptsMeniscus-guided coating is an attractive technique to deposit thin films of organic semiconductors for electronic devices, but only little insight into the fundamental principles of the fluid mechanics for the crystal growth and film formation has been so far provided. In this work, angle-dependent dip-coating is demonstrated as a novel key concept to control the meniscus shape and to modulate the film growth and morphology of solution processable semiconductors in a convenient and efficient way. As the main conceptual approach, the shape of the meniscus is adjusted by tuning the deposition angle of the solution on the moving substrate. Comprehensive insights into the fluid dynamics during dip-coating are gained from the combination of experimental results and steady-state simulations. It is observed that at small meniscus angle the concentration gradient and mass deposition of the solute are increased, leading to improved film morphology and charge carrier transport in field-effect transistors. Angle-dependent meniscus-guided coating as a new concept for semiconductor materials and understanding the relation between film formation and fluid mechanics are important for scaling-up solution processing techniques for practical applications of electronic technologies. |
Introduction
Solution processable organic semiconductors (OSCs) are promising for large area, lightweight, and flexible electronics, such as organic field-effect transistors (OFETs).1–3 Control over the morphology and molecular packing of OSCs is crucial to realize excellent charge carrier transport in OFETs.4,5 Meniscus-guided coating (MGC),6 including dip-coating,7 zone-casting,8 blade-coating,9 and solution shearing,10 provides an efficient way to grow OSCs into highly crystalline thin films. Among various MGC techniques, dip-coating is an excellent approach to precisely control the film thickness with minimal solution waste.11 Homogeneous monolayers based on conjugated polymers have been fabricated for OFET applications through careful control of the withdrawal speed of the substrate and the concentration of the solution.12,13 In the case of small molecule OSCs, the dip-coated films are prone to structural defects, such as non-uniform morphology, void formation, and dendritic growth, due to the limited-mass-transport.14–16According to the relation between the coating speed and the resulting film thickness, MGC is classified into two deposition regimes, evaporation (or capillary) and Landau–Levich (or Landau–Levich–Derjaguin), with an additional transition region as the mixed regime.6 In addition, the evaporation rate (ν) and coating speed during MGC significantly influence the crystal growth of OSCs. For instance, fast evaporation of low boiling point solvents can improve the growth of crystalline acene films during dip-coating.17 A predictive model for the equilibrium coating speed for solvents of different boiling points and substrate temperatures is proposed.18 Furthermore, mixed solvents permit tuning the solubility, nucleation rate and crystallization of OSCs.15,19 The wettability and surface energy of the substrate also play a critical role in determining the nucleation and crystal growth of OSCs during MGC.20,21
Recently, a broad variety of MGC methods have been developed to more precisely control the nucleation and crystal growth of small molecule and polymer OSCs to further improve the charge carrier transport.4,22 Solution shearing using a micropillar-pattered blade enhances the mass transport during coating by re-directing the fluid flow. In this way, the dendritic crystal growth of 6,13-bis(triisopropylsilylethynyl)pentacene (TIPS-pentacene) was transformed into large domains of millimeter-size.10 Bi-phasic dip-coating allows depositing films from a small solution volume even at limited solubility of the OSC.23,24 Template-assisted blade-coating can reduce the free energy barrier for polymer crystallization to attain alignment.25 Channel-restricted meniscus self-assembly is attributed to micro-confinement and enables control over the meniscus width, leading to uniform growth of organic crystals.26 A comprehensive understanding of the crystallization and film growth mechanism of OSCs during MGC is essential for thin film deposition for electronic applications. A firm understanding of the alignment mechanism has been developed, but only little insight into the fundamental principles of the fluid mechanics for the crystal growth of OSCs has been so far provided. A comprehensive study of the relation between the meniscus shape, fluid mechanical process and OSC crystallization during MGC is still required.
In this work, angle-dependent dip-coating (ADDC) is applied for MGC to precisely control the meniscus shape.27 The advantage of dip-coating is its simplicity and accurate adjustment of the coating angle as already reported for inorganic sol–gel films. The control over the thickness and homogeneity of the films deposited in the Landau–Levich regime was significantly improved at large tilting angles α (Fig. 1a).28 The experimental results on ADDC of 2,7-dioctyl[1]benzothieno[3,2-b][1]benzothiophene (C8-BTBT) and two-dimensional fluid simulations reveal that the streamline stagnation point between the upward and recirculation flow is mainly affected by the meniscus shape. A narrow meniscus shape at small angle β elevates the evaporation rate (νm) and upward flow at the meniscus, leading to a larger concentration gradient near the contact line, favoring the crystal growth of the OSC during MGC. This fluid flow assisted crystallization is also favored by higher supersaturation caused by a lower solubility of the OSC. On the other hand, the crystallization is limited on substrates with low surface energy due to an increased nucleation barrier. This work gives a comprehensive insight into the OSC crystallization behavior during MGC taking into account fluid mechanical processes. These findings and conclusions are crucial for the deposition of homogenous and ordered thin films from solution and the up-scaling of the MGC process for practical applications.
Experimental section
Materials
C8-BTBT, polystyrene (400 kDa), hexamethyldisilazane (HMDS) and octadecyltrichlorosilane (OTS) are purchased from Sigma and used without further purification.Angle-dependent dip-coating
Silicon substrates with a 300 nm thick SiO2 layer were treated by oxygen plasma at 100 W for 3 min to increase the surface energy to around 62–67 mN m−1. In addition, the oxygen plasma treatment is beneficial for a high-quality modification of the SiO2 surface by the OTS and HMDS self-assembled monolayers. Angle-dependent dip-coating of C8-BTBT was performed from a CHCl3 or CHCl3:hexane solution at a concentration of 3 mg mL−1. The dip-coating speeds ranged from 10 μm s−1 to 1000 μm s−1, and the substrate tilt angles were tuned from 0° to 75° in an ambient atmosphere. The HMDS or OTS self-assembled monolayers were obtained by exposing the silicon wafers to the corresponding silane vapor at 150 °C for 6 h.Morphology characterization
The film morphology was characterized by a Leica POM and a Bruker Dimension Icon FS AFM in tapping mode. Contact angle measurements were performed with a contact angle meter, Data Physics, OCA35. GIWAXS was carried out by means of a solid anode X-ray tube (Siemens Kristalloflex X-ray source, copper anode X-ray tube operated at 35 kV and 40 mA), Osmic confocal MaxFlux optics, an X-ray beam with pinhole collimation and a MAR345 image plate detector. Film thickness measurements were performed using a KLA Tencor Profiler and a Bruker Dimension Icon FS AFM. The coverage ratio was characterized using ImageJ.COMSOL simulation
Steady-state simulations were conducted by using the COMSOL Multiphysics package. The flow and concentration distributions were captured by using the Creeping Flow and Transport of Dilute Species models. The model dimensions were determined based on the experimentally obtained shape of the meniscus during ADDC.Charge transport characterization
A bottom-gate and top-contact configuration was employed for OFET devices. Heavily doped n-type Si wafers were used as a gate electrode and a 300 nm thick SiO2 layer (capacitance of 11 nF cm−2) was adopted as a gate dielectric layer. Source and drain electrodes were deposited at a thickness of 50 nm by gold evaporation. The transistor channel length and width were 25 μm and 500 μm, respectively. A Keithley 4200-SCS was used for all standard electrical measurements in a glove-box under a nitrogen atmosphere.Results and discussion
Angle-dependent dip-coating of C8-BTBT
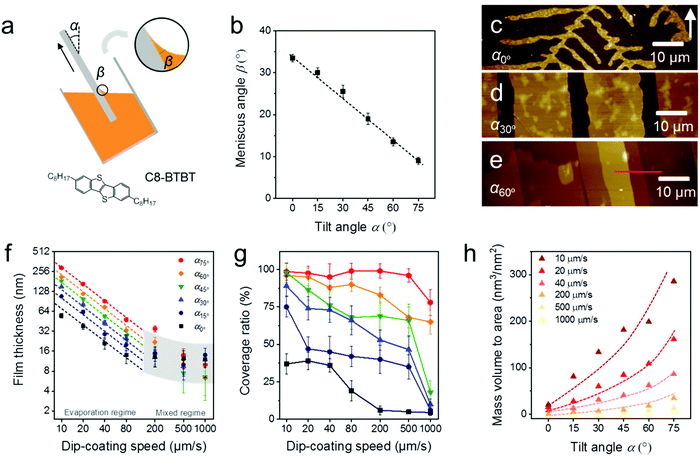
During MGC of OSCs, the meniscus refers to the liquid shape between the substrate and coating head or bulk solution, which is determined by a combination of surface tension and external forces (usually gravity).29 The meniscus shape is not only influenced by the surface energy of the substrate and the surface tension of the solution, but also depends on the substrate tilt angle (α) during dip-coating (Fig. 1a) or the distance of the coating head to the substrate during slot coating and zone-casting. When an oxygen plasma treated silicon substrate (Splasma) is immerged into CHCl3, a capillary action occurs at the interface between Splasma and the bulk solvent and a stable meniscus is achieved immediately. The meniscus angle of CHCl3 (βCHCl3) decreases from 33–34° to less than 10° when Splasma is tilted from α0° to α75° (Fig. 1b and Fig. S1, ESI†).The same meniscus angle is observed for the diluted solution and the pure solvent during dip-coating.30 In addition, the meniscus angle is independent of the coating speed in the evaporation regime (coating speed less than 100 μm s−1), but elongates for high coating speeds in the Landau–Levich regime (coating speed higher than 1000 μm s−1).31 To investigate the role of the meniscus shape in the OSC deposition, C8-BTBT coating was carried out in the evaporation regime by ADDC on Splasma from CHCl3. The molecular structure of C8-BTBT is shown in Fig. 1a. Dip-coating was chosen for MGC since it is a relatively facile coating technique and allows precise adjustment of the coating angle. During dip-coating of C8-BTBT at 20 μm s−1, βCHCl3 on Splasma was precisely controlled by solely varying α. At α0° dendritic crystals are grown due to the limited-mass-transport of C8-BTBT (Fig. 1c and 2).14,31 When the substrate is tilted to α30°, the growth of dendritic crystals is suppressed and the film turns into crystalline ribbons aligned in the coating direction (Fig. 1d and 2). This implies enhanced mass transport for the crystal growth caused by the substrate tilting. At further substrate tilting of α60°, a terrace-like crystalline morphology is formed (Fig. 1e and 2). The height plot along the red line in Fig. 1e exhibits a difference between single terrace steps of around 2.9 nm corresponding to the molecular length of C8-BTBT and its interlayer distance (Fig. S2a, ESI†).32
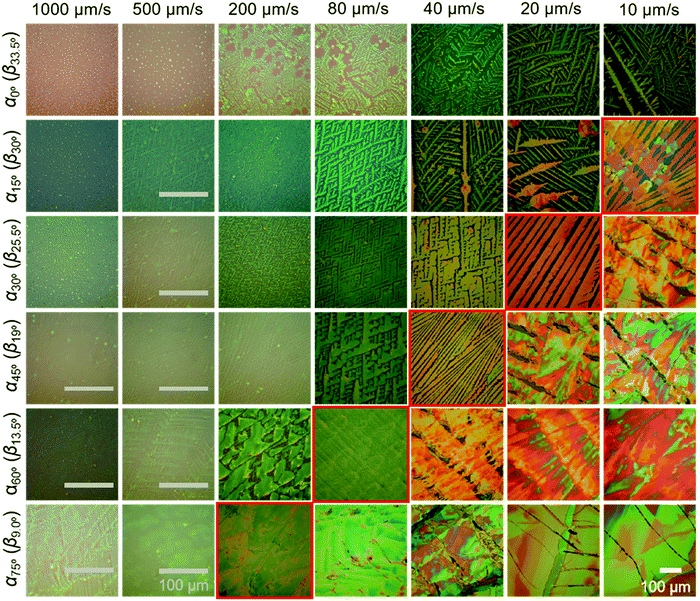
During ADDC of C8-BTBT in the speed range from 10 μm s−1 to 1000 μm s−1, the deposition regimes are characterized by the resulting film thickness. As shown in Fig. 1f, the evaporation regime is established for deposition speeds from 10 μm s−1 to 80 μm s−1, characterized by a power-law decrease (exponent −1) in film thickness corresponding to observations during blade coating of C8-BTBT,33 while the mixed regime is found between 200 μm s−1 and 1000 μm s−1.11 Interestingly, in the evaporation regime of ADDC, the film thickness is greatly influenced by α. For instance, for a dip-coating speed of 10 μm s−1, the film thickness is around 200 nm at α60° and 3.4 times higher than at α0° (Fig. 1f and Fig. S2, ESI†). In addition, the coverage of the crystalline C8-BTBT film also improves with larger α and small βCHCl3, as show in Fig. 1g and 2. For dip-coating speeds between 20 μm s−1 and 500 μm s−1, the coverage ratio is below 50% for α between 0° and 15°, and increases to above 75% for α between 60° and 75°. This behavior is in good agreement with observations for blade-coated nanoparticles.34 It was found that a moderately curved meniscus ensures also homogeneous particle film formation. The mass deposition (mass to area) of C8-BTBT for different dip-coating speeds derived from the thickness and coverage ratio implies that a large α enhances the mass transport for the film deposition (Fig. 1h). The improvement in mass deposition is especially large for small dip-coating speeds. As previously reported for blade-coating, the amount of molecules per unit volume supplied to the meniscus-line region can be also increased by the solute concentration.33
The crystalline C8-BTBT films obtained at different dip-coating speeds and α exhibit distinct morphologies, such as crystalline dots, dendrites, ribbons, and slip-stick structures (Fig. 2).14,35 Similar types of morphologies were observed for C8-BTBT by varying the boiling point of the solvent during blade coating.33 Aligned crystalline ribbons result from balanced-mass-transport at appropriate dip-coating speed and α, as highlighted by the red frame of the corresponding optical microscopy images in Fig. 2 and Fig. S2c (ESI†). Limited-mass-transport in the regimes of elevated dip-coating speed and low α leads to crystal-dots and dendritic growth. On the other hand, in regimes of low dip-coating speed and large α, the competition between pinning and depinning forces induces a “stick-slip” morphology with a certain spacing/stripe ratio.6,35 The reduced spacing at high α contributes to the raised coverage ratio. It implies that the formation of the stick-slip morphology is subject to the meniscus shape.
Since the thickness of the dip-coated films is proportional to the evaporation rate of the bulk solution (νbulk),11νbulk(α) was measured to clarify its influence on the film thickness at various α (Fig. S3, ESI†). During ADDC of C8-BTBT from a not completely solvent filled vial (15 mL), νbulk(75°) is around 2.3 times larger than νbulk(0°) at α0° (Fig. S4, ESI†), wherein this difference (varied νbulk(α)) is attributed to the change of the liquid level during tilting the vial (Fig. 1a). On the other hand, the film thickness at α75° is 4.5 times higher than at α0° (Fig. S4, ESI†), and thus different from the νbulk(75°)/νbulk(0°) ratio, indicating a substantial impact of the meniscus shape on the mass deposition during ADDC.
Fluid flow simulation
To better understand the role of the meniscus shape in the film formation during MGC, the fluid mechanical process at the meniscus has been explored. During ADDC, the fluid flows involve capillary flow induced by non-uniform solvent evaporation, Marangoni flow caused by a surface tension gradient, and Couette flow driven by substrate movement.29,36,37 A fundamental feature is the presence of a stagnation point, where the streamline is perpendicular to the solution surface, separating the fluid into the “upward flow region” and “recirculation flow region” (Fig. 3a).29 Modelling the fluid flow at the meniscus is challenging and includes various factors, such as the surface tension of the solution, surface energy of the substrate, and viscosity.30 Alternatively, we focus on the fundamental role of the meniscus shape in the fluid mechanical process and film growth. A two-dimensional fluid simulation was performed based on the Stokes flow, whereby the Marangoni effect is ignored (Fig. S5, ESI†). All fluid simulations were performed in the evaporation regime at a dip-coating speed of 20 μm s−1. The x-axis of the Cartesian coordinates represents the distance along the substrate from the contact line (x), while the y-axis is related to the height perpendicular to the substrate (Fig. 3a). The meniscus shapes for different β were derived from the optical images in Fig. S1b (ESI†). The plots in Fig. 3b demonstrate that the meniscus height and β decrease simultaneously, whereby for β < 15° the meniscus height is less than 0.25 mm at x < 1 mm (Fig. 3b).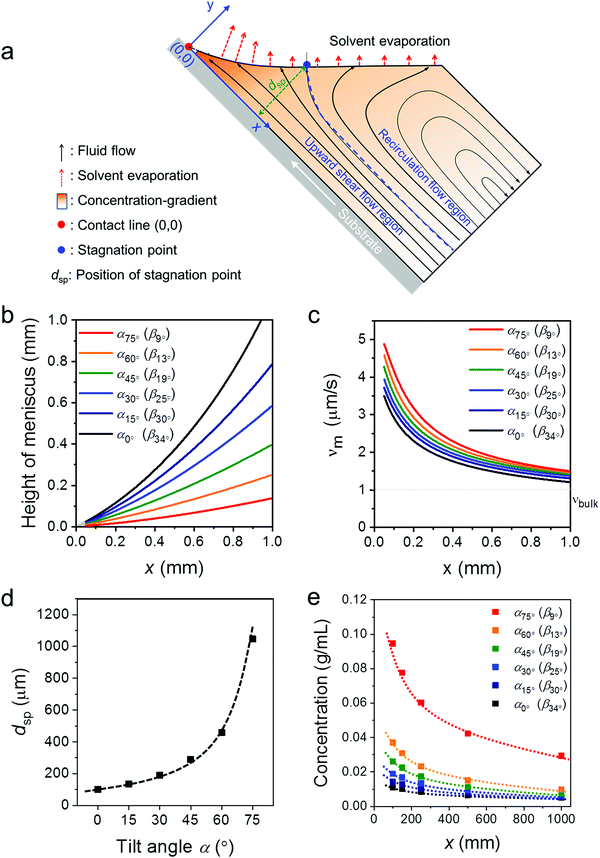 | ||
| Fig. 3 Fluid simulation for ADDC based on νbulk(0°). (a) Key parameters in the applied meniscus model. (b) Meniscus height for different β derived from the optical images in Fig. S1b (ESI†). (c) Evaporation rate (νm) as a function of x. (d) Position of the stagnation point (xsp) as a function of α. (e) Solute concentration at the meniscus (cm) as a function of α. | ||
The meniscus model for different geometries was established including the solvent evaporation, fluid flow, and concentration gradient (Fig. 3a). As the evaporation rate at the meniscus (νm) is influenced by νbulk and the meniscus shape,38,39 assuming νbulk(α) = νbulk(0°), νm for different β is calculated to reveal the role of the meniscus shape in evaporation. Fig. 3c demonstrates that νm increases with the decrease of x to a much higher extent than νbulk(0°). In additional, a sharp β leads to a high νm, resulting from a thin meniscus. At the same time, the distance of the stagnation point (dsp) shifts away from the substrate from 100 μm to 1000 μm when β declines from 33.5° to 9° (Fig. 3c and Fig. S6, ESI†). The shift of the stagnation point contributes to a wider upward flow region that transports more solute to the meniscus and contact line. This simulation demonstrates that a small β leads to a high νm and an upward flow and in this way induces a larger concentration gradient at the meniscus (Fig. 3d and Fig. S6, ESI†). For instance, at x = 0.1 mm, the solute concentration (cm) at β13° (α60°) is 2 and 3.5 times higher than at β25° (α30°) and β34° (α0°), respectively (Fig. 3e). Due to the raised cm caused by the small β, C8-BTBT is more prone to saturate and nucleate at the contact line.40
The fluid simulation for different α (and β) was also performed for varied νbulk(α) conditions to compare with the experimental data obtained for ADDC of C8-BTBT. As shown in Fig. S6 (ESI†), besides the contribution of small β, the gradually larger νbulk(α) additionally increases νm and intensifies the upward flow, contributing to a higher cm. For instance, at x = 0.1 mm, cm at β13° based on νbulk(α) is around 2 times that based on νbulk(0°) (Fig. S7, ESI†).
ADDC was also performed from a larger container (50 mL) completely filled by the solution to achieve the same νbulk, excluding the influence of varied νbulk under the experimental conditions (Fig. S8, ESI†). Due to extensive material consumption, these experiments were performed for two representative cases. C8-BTBT and polystyrene (400 kDa) were dip-coated at 200 μm s−1 and 80 μm s−1, respectively. Higher film thicknesses of C8-BTBT and polystyrene were obtained at greater α, where the increased mass deposition results solely from small β (Fig. S8b and c, ESI†). These results directly confirm the role of the meniscus shape in the mass deposition during MGC.
Impact of the substrate surface energy
The OSC crystallization during MGC is more complex, including not only the fluid flow, but also the supersaturated concentration as the driving force and barrier for crystal nucleation and growth. The crystallization behavior of OSCs greatly depends on the substrate roughness and surface energy of the substrate, concentration and solubility.21 For instance, the nucleation barrier for two-dimensional spherulite heterogeneous nucleation in solution deposited films, ΔGhet*, is determined by the concentration (c), solubility (δ), temperature (T), and surface energy between the solution and the crystals (γCL), as shown in eqn (1)41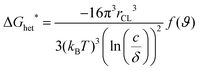 | (1) |
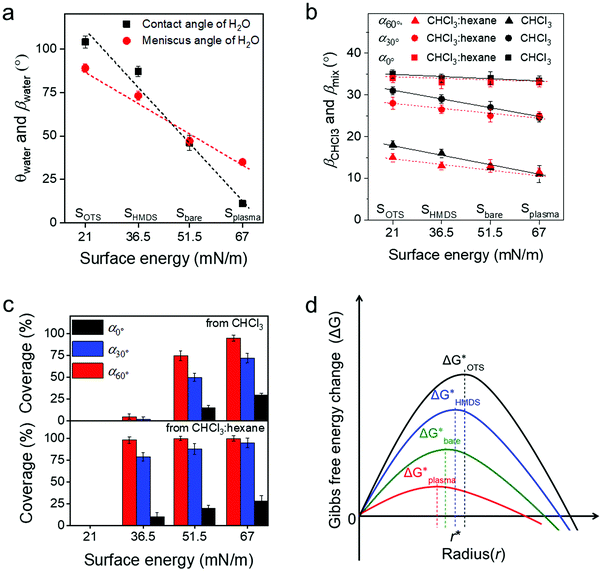
To deeper understand the role of the meniscus shape in OSC crystallization, the influence of the surface energy on film coating of C8-BTBT was studied. The modulation of the surface energy was achieved by plasma treatment and self-assembly monolayer modification of the substrate using hexamethyldisilazane (HMDS) and octadecyltrichlorosilane (OTS), whose surface energy can be estimated by combining the equation of state with the Young equation.21 Details on the contact angle measurements are shown in Table S1 (ESI†). As presented in Fig. 4a (ESI†), the surface energy for the bare SiO2 surface (Sbare) is around 51.5 mN m−1 and for Splasma it is 67 mN m−1. However, HMDS and OTS modifications (SHMDS and SOTS) decrease the surface energy to 36.5 and 21 mN m−1, respectively (Fig. 4a).21,42
The meniscus angle of water (βwater) at α0° increases from 31° to 88° when the surface energy declines from 67 to 21 mN m−1 (Fig. 4a and Fig. S9a, ESI†). This trend corresponds to the surface energy dependent contact angle of water (θwater). In contrast to βwater, βCHCl3 remains at around 33°–35.5° for the same surface energy range (Fig. 4b and Fig. S9b, ESI†). The surface energy independent behavior of βCHCl3 is due to the much lower surface tension of CHCl3 (26.7 mN m−1) compared to water (72.7 mN m−1). However, the coverage ratio and crystallization of C8-BTBT during coating at α0° and 20 μm s−1 significantly rely on the surface energy of the substrate. The coverage is reduced for small surface energy, which is also related to morphology changes in the film (Fig. 4c). For instance, at α0° the dendritic C8-BTBT crystals on Splasma are much wider than those on Sbare, but almost no nucleation occurs on SHMDS and SOTS (Fig. S10a, ESI†). For substrates with different surface energy, βCHCl3 shows a similar trend of decrease when α changes from 0° to 30° and 60° (Fig. 4b). The declined βCHCl3 leads to a higher coverage of C8-BTBT on Splasma and Sbare, but does not efficiently improve the crystallization on SHMDS and SOTS (Fig. 4c and Fig. S10b, ESI†). Therefore, in the case of a similar β during MGC, the crystallization of the OSC still significantly depends on the surface energy of the substrate. Differences in the crystallization behavior are attributed to the surface energy dependent nucleation barrier, which decreases in the order ΔGOTS* > ΔGHMDS* > ΔGbare* > ΔGplasma* (Fig. 4d).43,44 These results indicate that the fluid flow assisted crystallization on a substrate with low surface energy is weakened by the high nucleation barrier (Fig. 4d).43
To facilitate the fluid flow assisted crystallization on a low surface energy substrate, a mixed-solvent (CHCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane 4
hexane 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was introduced to reduce the solubility of C8-BTBT and thus to improve the supersaturation (Fig. S10c, ESI†). The meniscus angle of the mixed-solvent (βmix) is also independent of the surface energy of the substrate. At the same α, βmix is slightly lower than βCHCl3, resulting from the smaller surface tension of hexane (18.4 mN m−1), as shown in Fig. 4b and Fig. S9c (ESI†). When dip-coated at α0° and 20 μm s−1 from the mixed-solvent, C8-BTBT exhibits dendritic morphologies with low coverage on Splasma, Sbare, and SHMDS (Fig. S8b, ESI†). The coverage of C8-BTBT greatly enhances at larger α and reaches above 95% at α60° (Fig. 4c). This coverage improvement at large α (small β) is directly attributed to the increased upward flow and the reduced solubility, leading to higher supersaturation being necessary to overcome the nucleation barrier on SHMDS. This means that to some extent the fluid flow assisted crystallization is facilitated by the raised supersaturation (Fig. S10c, ESI†). However, even under the same deposition conditions no nucleation occurs on SOTS, which may require a much higher supersaturation of C8-BTBT for nucleation on this type of surface during dip-coating. Because of this reason, the substrate surface modification by self-assembled monolayers of moderate surface energy provides the appropriate requirements for excellent mobility OFETs through the improvement of the crystallization during MGC at small β and reduction of the trap density at the interface.
1) was introduced to reduce the solubility of C8-BTBT and thus to improve the supersaturation (Fig. S10c, ESI†). The meniscus angle of the mixed-solvent (βmix) is also independent of the surface energy of the substrate. At the same α, βmix is slightly lower than βCHCl3, resulting from the smaller surface tension of hexane (18.4 mN m−1), as shown in Fig. 4b and Fig. S9c (ESI†). When dip-coated at α0° and 20 μm s−1 from the mixed-solvent, C8-BTBT exhibits dendritic morphologies with low coverage on Splasma, Sbare, and SHMDS (Fig. S8b, ESI†). The coverage of C8-BTBT greatly enhances at larger α and reaches above 95% at α60° (Fig. 4c). This coverage improvement at large α (small β) is directly attributed to the increased upward flow and the reduced solubility, leading to higher supersaturation being necessary to overcome the nucleation barrier on SHMDS. This means that to some extent the fluid flow assisted crystallization is facilitated by the raised supersaturation (Fig. S10c, ESI†). However, even under the same deposition conditions no nucleation occurs on SOTS, which may require a much higher supersaturation of C8-BTBT for nucleation on this type of surface during dip-coating. Because of this reason, the substrate surface modification by self-assembled monolayers of moderate surface energy provides the appropriate requirements for excellent mobility OFETs through the improvement of the crystallization during MGC at small β and reduction of the trap density at the interface.
Molecular packing and charge carrier transport
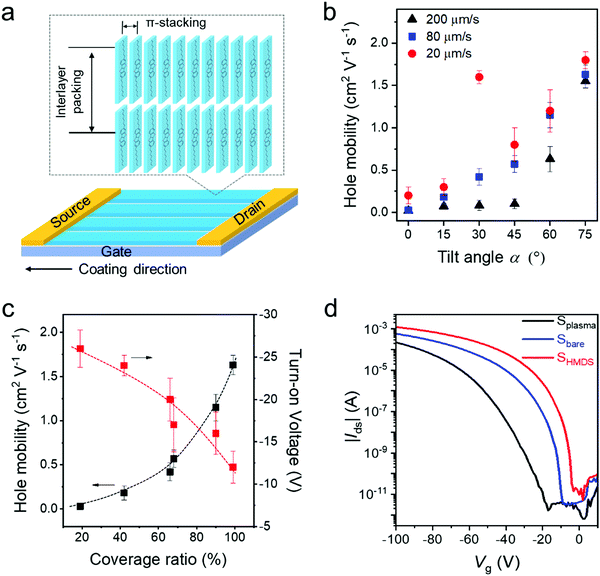
To study the packing of C8-BTBT in the dip-coated films, grazing incidence wide-angle X-ray scattering (GIWAXS) was performed. The GIWAXS patterns of dip-coated C8-BTBT films indicate identical molecular packing in films cast at 20 μm s−1 from CHCl3 at α0°, α30°, and α60° on Splasma (Fig. S11a–c, ESI†). The distinct out-of-plane scattering intensity at qz = 0.22 Å−1 for qxy = 0 Å−1 is assigned to an interlayer distance of 2.85 nm, corresponding to the step-height of the terrace-like morphology observed by AFM (Fig. 1e and Fig. S2a, ESI†). The in-plane reflection at qz = 0 Å−1 and qxy = 1.90 Å−1 is associated with a π-stacking distance of 0.33 nm, which is characteristic for preferential edge-on organization of the molecules towards the surface, where the long molecular axis is parallel to the out-of-plane direction (Fig. 5a).45 The higher reflection intensity at α60° is related to the greater film thickness, whereas the low intensity at α0° is attributed to the low surface coverage.To probe the charge carrier transport of C8-BTBT obtained by ADDC, bottom-gate and top-contact transistors were fabricated, where the channel length (25 μm) was parallel to the coating direction (Fig. 5a). The average charge carrier mobilities of crystalline C8-BTBT films dip-coated on Splasma increase with larger α for different dip-coating speeds (Fig. 5b). As derived from the transfer curves, the transistors show a pronounced Ion/Ioff ratio of around 107–108 (Fig. S11d–f, ESI†). When dip-coated at 200 μm s−1, dendritic crystals and a low coverage ratio of C8-BTBT lead to a mobility of less than 0.2 cm2 V−1 s−1 at α < 45°, which improves for α > 60° (Fig. 5b and Fig. S11d, ESI†). At a deposition speed of 80 μm s−1, the mobilities gradually rise from 0.03 cm2 V−1 s−1 to 1.5 cm2 V−1 s−1 with larger tilt angle α (Fig. 5b and Fig. S11e, ESI†). At the same time, the turn-on voltage is reduced from −25 V to around −15 V. At 20 μm s−1, the mobility also increases from 0.2 cm2 V−1 s−1 to 1.8 cm2 V−1 s−1 for α from 0° to 75°, except the extraordinary high upwards outlier of 1.6 cm2 V−1 s−1 at α30° (Fig. 5b and Fig. S11f, ESI†). This value, found only for α30° and 20 μm s−1, results from the well aligned crystalline structures (Fig. 2). This confirms the common knowledge that both high coverage ratio and pronounced alignment of crystalline films are important for the charge transport in OFETs.4 For instance, superior charge carrier mobilities were obtained for high coverage of C8-BTBT bar-coated from mixed solvents on a wettable surface.46Fig. 5c depicts the charge carrier mobility and turn-on voltage as a function of the coverage ratio for C8-BTBT films cast at 80 μm s−1. Thereby, the coverage ratio varies with α as discussed for Fig. 1g. Both transistor parameters improve for higher coverage ratios. The charge carrier mobility slightly increases by taking into account the coverage ratio in the calculation of the device parameters (Fig. S12, ESI†). The decrease in turn-on voltage with higher coverage ratio at larger α is attributed to a homogenous film morphology with less domain boundaries, which typically act as trapping sites for charge carriers.
Surface modification can also favor the charge carrier transport in OFETs.42 The transfer curves in Fig. 5d reveal that the average mobility rises from 1.5 cm2 V−1 s−1 for Splasma to 2.0 cm2 V−1 s−1 for Sbare and to 2.7 cm2 V−1 s−1 for SHMDS when C8-BTBT is dip-coated from a mixed-solvent at 20 μm s−1 and α60°. This improvement in device performance is attributed to the reduction of the surface trap density,47 and a slightly improved in-plane molecular order (Fig. S13, ESI†) due to the self-assembled monolayer applied at the interface. On all three types of surfaces the C8-BTBT molecules are edge-on arranged as evident from the in-plane (100) and (010) and out-of-plane (001) reflections in the GIWAXS pattern (Fig. S14, ESI†).32 The highest mobility of around 3.6 cm2 V−1 s−1 is obtained for SHMDS at 20 μm s−1 and α60° which corresponds to an average performance of C8-BTBT.48 Notably, the small β and low solubility of C8-BTBT in the mixed-solvent significantly favor the crystallization of the organic semiconductor during ADDC, improving the device performance. It is assumed that the charge carrier mobility of dip-coated C8-BTBT can be further improved by blending with thermoplastic polymers to optimize the film morphology.49,50
Conclusions
In this work, we have demonstrated the crucial role of the meniscus shape in the fluid flow and crystallization of a small molecule OSC during MGC. Through controlling the meniscus shape by ADDC, we found that the increased upward flow at small β enlarges the concentration gradient at the meniscus, yielding raised supersaturation and mass deposition of the OSC. On the other hand, at low surface energy of the substrate the fluid flow assisted crystallization at small β is suppressed by an elevated nucleation barrier. The resulting aligned film morphologies and higher surface coverage significantly enhance the charge carrier transport in the dip-coated C8-BTBT films. These results provide new insights into the crystallization mechanism of OSCs during MGC. The control of the meniscus shape is a convenient and efficient way to modulate the crystallization of OSCs for improving their film deposition by MGC. This is an important aspect since a variety of OSCs encounter enormous challenges in the deposition of well-ordered and homogeneous films. The understanding of the correlation between crystallization and fluid mechanics is also crucial for scaling-up the solution processing of OSCs towards practical applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. Zhang thanks the China Scholarship Council (CSC) for financial support. M. Borkowski and T. Marszalek acknowledge the Foundation for Polish Science financed by the European Union under the European Regional Development Fund (POIR.04.04.00-00-3ED8/17-01). W. Pisula acknowledges the National Science Centre, Poland, through the grant UMO-2015/18/E/ST3/00322. Z. Wang and G. Fytas acknowledge the financial support by ERC AdG SmartPhon (Grant No. 694977). Open Access funding provided by the Max Planck Society.Notes and references
- H. Dong, X. Fu, J. Liu, Z. Wang and W. Hu, Adv. Mater., 2013, 25, 6158–6183 CrossRef CAS PubMed.
- H. Sirringhaus, Adv. Mater., 2014, 26, 1319–1335 CrossRef CAS PubMed.
- S. Wang, J. Xu, W. Wang, G.-J. N. Wang, R. Rastak, F. Molina-Lopez, J. W. Chung, S. Niu, V. R. Feig, J. Lopez, T. Lei, S.-K. Kwon, Y. Kim, A. M. Foudeh, A. Ehrlich, A. Gasperini, Y. Yun, B. Murmann, J. B.-H. Tok and Z. Bao, Nature, 2018, 555, 83–88 CrossRef CAS PubMed.
- Y. Diao, L. Shaw, Z. Bao and S. C. B. Mannsfeld, Energy Environ. Sci., 2014, 7, 2145–2159 RSC.
- X. Zhang, J. Jie, W. Deng, Q. Shang, J. Wang, H. Wang, X. Chen and X. Zhang, Adv. Mater., 2016, 28, 2475–2503 CrossRef CAS PubMed.
- (a) X. Gu, L. Shaw, K. Gu, M. F. Toney and Z. Bao, Nat. Commun., 2018, 9, 534 CrossRef PubMed; (b) M. Richard, A. Al-Ajaji, S. Ren, A. Foti, J. Tran, M. Frigoli, B. Gusarov, Y. Bonnassieux, E. G. Caurel, P. Bulkin, R. Ossikovski and A. Yassar, Adv. Colloid Interface Sci., 2020, 275, 102080 CrossRef PubMed.
- S. Wang, W. Pisula and K. Müllen, J. Mater. Chem., 2012, 22, 24827–24831 RSC.
- W. Pisula, A. Menon, M. Stepputat, I. Lieberwirth, U. Kolb, A. Tracz, H. Sirringhaus, T. Pakula and K. Müllen, Adv. Mater., 2005, 17, 684–689 CrossRef CAS.
- M. R. Niazi, R. Li, E. Q. Li, A. R. Kirmani, M. Abdelsamie, Q. Wang, W. Pan, M. M. Payne, J. E. Anthony, D.-M. Smilgies, S. T. Thoroddsen, E. P. Giannelis and A. Amassian, Nat. Commun., 2015, 6, 8598 CrossRef CAS PubMed.
- Y. Diao, B. C.-K. Tee, G. Giri, J. Xu, D. H. Kim, H. A. Becerril, R. M. Stoltenberg, T. H. Lee, G. Xue, S. C. B. Mannsfeld and Z. Bao, Nat. Mater., 2013, 12, 665–671 CrossRef CAS PubMed.
- D. Grosso, J. Mater. Chem., 2011, 21, 17033–17038 RSC.
- M. Li, C. An, T. Marszalek, I. Lieberwirth, M. Baumgarten, K. Müllen and W. Pisula, Adv. Mater., 2016, 28, 2245–2252 CrossRef CAS PubMed.
- M. Li, D. K. Mangalore, J. B. Zhao, J. H. Carpenter, H. P. Yan, H. Ade, H. Yan, K. Müllen, P. W. M. Blom, W. Pisula, D. M. de Leeuw and K. Asadi, Nat. Commun., 2018, 9, 451 CrossRef PubMed.
- G. Qu, J. J. Kwok and Y. Diao, Acc. Chem. Res., 2016, 49, 2756–2764 CrossRef CAS PubMed.
- A. Tracz, T. Makowski, S. Masirek, W. Pisula and Y. H. Geerts, Nanotechnology, 2007, 8, 485303 CrossRef.
- J. Jang, S. Nam, K. Im, J. Hur, S. N. Cha, J. Kim, H. B. Son, H. Suh, M. A. Loth, J. E. Anthony, J.-J. Park, C. E. Park, J. M. Kim and K. Kim, Adv. Funct. Mater., 2012, 22, 1005–1014 CrossRef CAS.
- G. Giri, E. Verploegen, S. C. B. Mannsfeld, S. Atahan-Evrenk, D. H. Kim, S. Y. Lee, H. A. Becerril, A. Aspuru-Guzik, M. F. Toney and Z. Bao, Nature, 2011, 480, 504–508 CrossRef CAS PubMed.
- R. Janneck, F. Vercesi, P. Heremans, J. Genoe and C. Rolin, Adv. Mater., 2016, 28, 8007–8013 CrossRef CAS PubMed.
- J. Chang, C. Chi, J. Zhang and J. Wu, Adv. Mater., 2013, 25, 6442–6447 CrossRef CAS PubMed.
- S. Park, G. Giri, L. Shaw, G. Pitner, J. Ha, J. H. Koo, X. Gu, J. Park, T. H. Lee, J. H. Nam, Y. Hong and Z. Bao, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5561–5566 CrossRef CAS PubMed.
- F. Zhang, E. Mohammadi, X. Luo, J. Strzalka, J. Mei and Y. Diao, Langmuir, 2018, 34, 1109–1122 CrossRef CAS PubMed.
- G. De Luca, W. Pisula, D. Credgington, E. Treossi, O. Fenwick, G. M. Lazzerini, R. Dabirian, E. Orgiu, A. Liscio, V. Palermo, K. Müllen, F. Cacialli and P. Samori, Adv. Funct. Mater., 2011, 21, 1279–1295 CrossRef CAS.
- M. Li, C. An, W. Pisula and K. Müllen, Small, 2014, 10, 1926–1931 CrossRef CAS PubMed.
- D. R. Ceratti, B. Louis, X. Paquez, M. Faustini and D. Grosso, Adv. Mater., 2015, 27, 4958–4962 CrossRef CAS PubMed.
- E. Mohammadi, C. Zhao, Y. Meng, G. Qu, F. Zhang, X. Zhao, J. Mei, J.-M. Zuo, D. Shukla and Y. Diao, Nat. Commun., 2017, 8, 16070 CrossRef CAS PubMed.
- W. Deng, X. Zhang, H. Dong, J. Jie, X. Xu, J. Liu, L. He, L. Xu, W. Hu and X. Zhang, Mater. Today, 2019, 24, 17–25 CrossRef CAS.
- N. J. Arfsten, A. Eberle, J. Otto and A. Reich, J. Sol-Gel Sci. Technol., 1997, 8, 1099–1104 CAS.
- T. Bottein, J. Loizillon and D. Grosso, J. Phys. Chem. B, 2017, 121, 6220–6225 CrossRef CAS PubMed.
- A. Filali, L. Khezzar and E. Mitsoulis, Comput. Fluids, 2013, 82, 110–121 CrossRef.
- K. Zhang, T. Marszalek, P. Wucher, Z. Y. Wang, L. Veith, H. Lu, H. J. Räder, P. M. Beaujuge, P. W. M. Blom and W. Pisula, Adv. Funct. Mater., 2018, 28, 1805594 CrossRef.
- Z. Chai, S. A. Abbasi and A. A. Busnaina, ACS Appl. Mater. Interfaces, 2018, 10, 18123–18130 CrossRef CAS PubMed.
- S. Kwon, J. Kim, G. Kim, K. Yu, Y.-R. Jo, B.-J. Kim, J. Kim, H. Kang, B. Park and K. Lee, Adv. Mater., 2015, 27, 6870–6877 CrossRef CAS PubMed.
- M. Chen, B. Peng, S. Huang and P. K. L. Chan, Adv. Funct. Mater., 2020, 30, 1905963 CrossRef CAS.
- P. Born, S. Blum, A. Munoz and T. Kraus, Langmuir, 2011, 27, 8621–8633 CrossRef CAS PubMed.
- H. Bodiguel, F. Doumenc and B. Guerrier, Langmuir, 2010, 26, 10758–10763 CrossRef CAS PubMed.
- B. B. Patel and Y. Diao, Nanotechnology, 2018, 29, 044004 CrossRef PubMed.
- C. Hsueh, F. Doumenc and B. Guerrier, Eur. Phys. J.: Spec. Top., 2013, 219, 51–57 Search PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- R. D. Deegan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 475–485 CrossRef CAS PubMed.
- O. Goto, S. Tomiya, Y. Murakami, A. Shinozaki, A. Toda, J. Kasahara and D. Hobara, Adv. Mater., 2012, 24, 1117–1122 CrossRef CAS PubMed.
- N. T. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- S. C. Lim, S. H. Kim, J. H. Lee, M. K. Kim, D. J. Kim and T. Zyung, Synth. Met., 2005, 148, 75–79 CrossRef CAS.
- J. R. Ray, B. Lee, J. Baltrusaitis and Y. S. Jun, Environ. Sci. Technol., 2012, 46, 13167–13175 CrossRef CAS PubMed.
- Y. S. Jun, D. Kim and C. W. Neil, Acc. Chem. Res., 2016, 49, 1681–1690 CrossRef CAS PubMed.
- Y. D. Park, J. A. Lim, H. S. Lee and K. Cho, Mater. Today, 2007, 10, 46–54 CrossRef CAS.
- Z. Zhang, B. Peng, X. Ji, K. Pei and P. K. L. Chan, Adv. Funct. Mater., 2017, 27, 1703443 CrossRef.
- L. L. Chua, J. Zaumseil, J. F. Chang, E. C. W. Ou, P. K. H. Ho, H. Sirringhaus and R. H. Friend, Nature, 2005, 434, 194–199 CrossRef CAS PubMed.
- R. Wawrzinek, J. Sobus, M. U. Chaudhry, V. Ahmad, A. Grosjean, J. K. Clegg, E. B. Namdas and S.-C. Lo, ACS Appl. Mater. Interfaces, 2019, 11, 3271–3279 CrossRef CAS PubMed.
- Y. Yuan, G. Giri, A. L. Ayzner, A. P. Zoombelt, S. C. B. Mannsfeld, J. Chen, D. Nordlund, M. F. Toney, J. Huang and Z. Bao, Nat. Commun., 2014, 5, 3005 CrossRef PubMed.
- K. Haase, C. T. da Rocha, C. Hauenstein, Y. Zheng, M. Hambsch and S. C. B. Mannsfeld, Adv. Electron. Mater., 2018, 4, 1800076 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh00141d |
| This journal is © The Royal Society of Chemistry 2020 |