Preliminary chemical reduction for synthesizing a stable porous molecular conductor with neutral metal nodes†
Shohei
Koyama
a,
Tappei
Tanabe
a,
Shinya
Takaishi
 a,
Masahiro
Yamashita
ab and
Hiroaki
Iguchi
a,
Masahiro
Yamashita
ab and
Hiroaki
Iguchi
 *a
*a
aDepartment of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aramaki-Aza-Aoba, Aoba-ku, Sendai, Miyagi 980-8578, Japan. E-mail: h-iguchi@tohoku.ac.jp
bSchool of Materials Science and Engineering, Nankai University, Tianjin 300350, China
First published on 23rd September 2020
Abstract
Preliminary chemical reduction of naphthalenediimide (NDI)-based organic ligands was applied to the synthesis of a porous molecular conductor (PMC) with neutral metal nodes (cobalt(II) acetylacetonate). The obtained semiconductive PMC (PMC-2) was stable due to the neutral metal nodes, providing an advantage over electrochemical reduction.
Porous molecular conductors (PMCs) are new electrically conductive materials, which share features of both metal–organic frameworks (MOFs) and molecular conductors.1 Although electron-conductive MOFs2–10 have been extensively studied over the last decade, owing to their potential electronics applications,11–13 they are generally prepared using a “through-bond approach”2–11 with the aim of delocalizing electrons along the frameworks. On the other hand, the design of PMCs involves a “through-space approach”, in which charge transport pathways (e.g. π-stacking) among organic ligands are incorporated. This approach is advantageous due to the variety of useable ligands and the availability of single crystals.14–19 However, only a few MOFs possess sufficient amounts of conduction carriers in the through-space conduction pathways.20–22
Incorporating numerous conduction carriers was possible by applying an electrocrystallization method, which is typically used for the preparation of molecular conductors.23–25 The first PMC [Cd(OH2)4(NDI–py)](NO3)1.3±0.1·nDMA (PMC-1) was synthesized by electrochemically reducing N,N′-di(4-pyridyl)-1,4,5,8-naphthalenetetracarboxydiimide (NDI–py) in the presence of Cd(NO3)2 in an N,N-dimethylacetamide (DMA) solution.1PMC-1 has a large carrier density of 0.7 ± 0.1 e− per NDI core. However, the electrochemical method cannot be used with combinations of metal sources and organic linkers that react and precipitate immediately, because the generation of radical species is limited at the surface of the electrode and is slower than precipitation is. For instance, it is difficult to introduce neutral metal complexes as the metal nodes in PMCs because neutral non-conductive coordination polymers typically precipitate prior to electrochemical reaction. In addition, electrocrystallization is not suitable for large-scale synthesis. In order to overcome these difficulties, a new methodology to synthesize PMCs is necessary.
Herein, we present a new method for synthesizing PMCs involving chemical reduction of the ligands prior to the formation of the coordination network. To the best of our knowledge, a similar method was used to the synthesis of radical MOFs only once, whereas their conducting properties were not reported.26 To prove the validity of the method, [Co(acac)2] (acac = acetylacetonate) was chosen to act as the neutral metal node because it can form stable linear coordination polymers with pyridyl-based bridging ligands.27,28 As expected, upon mixing DMA solutions of [Co(acac)2(MeOH)2] and NDI–py, the linear coordination polymer [Co(acac)2(NDI–py)]·2DMA (2′) rapidly precipitated (Fig. S1 and Table S2, ESI†). There are no conduction carriers or π–π interactions between the NDI cores in 2′. Thus, through-space conduction does not occur. To employ the [Co(acac)2] complex in PMCs, we chemically reduced NDI–py using cobaltocene29,30 in advance, and then the DMA solution was layered onto a solution of [Co(acac)2(MeOH)2] with RbBPh4 for slow liquid–liquid diffusion. A new semiconducting coordination polymer with a neutral metal node, Rb0.5[Co(acac)2(NDI–py)]·2DMA (PMC-2), was obtained.
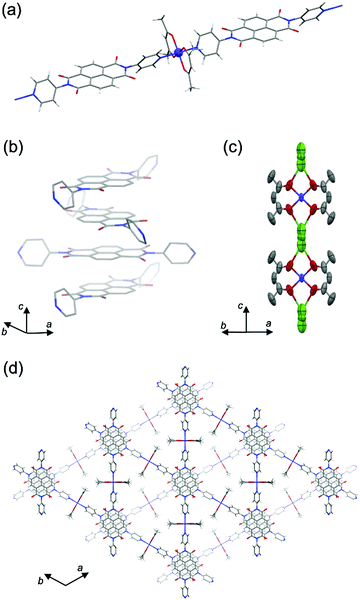
From single-crystal X-ray diffraction (SXRD) analysis, PMC-2 crystallized as conglomerates in the space groups P6422 and P6222 like PMC-1 did.1PMC-2 has a threefold infinite π-stacked columnar structure along the c axis constructed of linear coordination polymers of [Co(acac)2] and NDI–py (Fig. 1 and Fig. S2, S3 and Table S1, ESI†). The distance between π-conjugated planes of NDI–py was determined to be 3.186 Å, which is shorter than that of neutral NDI molecules (>3.3 Å),31 suggesting that there are attractive interactions between NDI cores enhanced by the presence of radicals. In fact, the results of calculations on the LUMO of NDI–py monomer and dimer extracted from the crystal structure (Fig. S4, ESI†) indicate that there is significant orbital overlap between the NDI–py molecules. Such an infinite π-stacked array of NDI cores in coordination polymers is still rare,1,17,32–38 even though vast numbers of coordination polymers with NDI-based ligands have been reported.39,40 The LUMO level of NDI–py in PMC-2 was calculated to be −4.17 eV from the first reduction potential in the solid-state cyclic voltammogram (Fig. S5, ESI†). This value is comparable to the LUMO level of NDI dimer in the DFT calculation.
Focusing on Co ion, the four coordination Co–O(acac) bonds are crystallographically equivalent. The coordination bond lengths for Co–O(acac) and Co–N(NDI–py) were determined to be 2.031(4) Å and 2.191(3) Å, respectively, and are consistent with the coordination environment for a high-spin Co2+ ion.27,28,41 Moreover, the electron configuration is supported by the magnetic properties (Fig. S6 and S7, ESI†), and thus, the charge of the [Co(acac)2] moiety is considered to be neutral.
The Rb+ ion is disordered in three different positions between two adjacent [Co(acac)2] moieties along the c axis (Fig. 1c). The total occupancy of the Rb+ ion was fixed to 50% to agree with the results of inductively coupled plasma (ICP) analysis (48.3%). Since the Rb+ ion compensates for the charge of the reduced NDI–py, we concluded that the mean charge of NDI–py was nearly −0.5. Thus, the charge of the NDI core is quantifiable via the number of countercations. This is one of the advantages of PMCs with neutral metal nodes. In the case of PMC-1, the cationic [Cd(OH2)4]2+ nodes require counteranions (NO3−) in the pores to compensate for the charge. However, the NO3− ions were difficult to quantify, and thus, there is a large uncertainty in the charge of NDI–py (−0.7 ± 0.1).
Four lattice DMA molecules coordinate to a Rb+ ion via the oxygen atoms (Fig. S2, ESI†), and their occupancy could be reasonably fixed to 50%, which is consistent with the total occupancy of Rb+ ion. As a result, there are two DMA molecules in the pore per [Co(acac)2(NDI–py)] moiety. From thermogravimetric analysis (TGA) of PMC-2, the 20% weight loss up to 200 °C (Fig. S8, ESI†) indicates the liberation of two DMA molecules (19.5% in theory). The lattice DMA molecules were fixed only when the crystal was slowly cooled (−2 K min−1) from room temperature. The residual electron density in the pores was too dispersed to establish the structure of DMA when the crystal was rapidly cooled to 120 K, suggesting that the DMA molecules fluctuate at room temperature.
From the viewpoint of crystal engineering, the Co2+ ions help to form linear coordination polymers as metal nodes and provide a platform for modifying the pore sizes and charge of counterions by replacing coordinating ligands. The moderate substitution inertness of Co2+ ions enables the formation of the coordination polymers in PMC-2 without exchanging the acac ligands for solvent molecules. No precipitate formed when more labile [Zn(acac)2] moieties were used likely due to the elimination of the acac ligands from the Zn2+ ion.
Solid-state absorption spectra of PMC-2 acquired in both air and inert gas (Ar) are shown in Fig. 2 along with the spectra of PMC-1 and NDI–py. According to previous research,1,42–46 broad bands around 2.0 and 2.7 eV were assigned to the intramolecular electron transition of NDI˙−. Weak broad bands in the near infrared region at 0.3 and 1.1 eV were assigned to charge transfer (CT) between NDI˙− and NDI0 cores (NDI˙− + NDI0 → NDI0 + NDI˙−) and the CT between two NDI˙− cores (NDI˙− + NDI˙− → NDI0 + NDI2−), respectively. The spectrum of PMC-2 is similar to that of PMC-1 under inert atmospheres. From DFT calculations on a NDI–py monomer (Fig. S4, ESI†), HOMO−2 and LUMO are mainly made of the π-orbitals of the NDI core. The energy of the (HOMO−2)–LUMO gap (3.44 eV) is consistent with the intense band around 3.3 eV observed in the absorption spectrum of the NDI–py ligand. Thus, the band is thought to be an intramolecular π–π* transition in a neutral NDI core. It is noteworthy that the π–π* transition band is almost negligible in the spectra of PMC-2, whereas it appears in the spectrum of PMC-1 measured in air, suggesting that PMC-2 is more resistant to air oxidation than PMC-1 is.
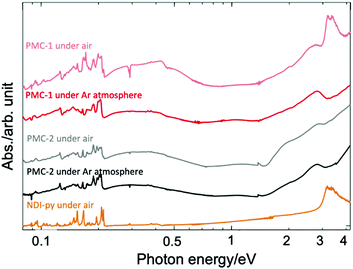 | ||
| Fig. 2 Solid-state absorption spectra of PMC-2 (black line), PMC-1 (red line), and NDI–py ligand (orange line) acquired as KBr pellets. | ||
The color of PMC-2 did not change even after it was exposed to ambient air for 120 hours in the dark, whereas the color of PMC-1 gradually faded. The powder XRD (PXRD) patterns of PMC-2 were also unchanged over 120 hours in ambient air (Fig. S10, ESI†). During TGA of PMC-2, no significant weight loss was observed in a nitrogen gas flow (100 mL min−1) over 10 hours at room temperature (Fig. S9, ESI†). Weight loss only occurred when the temperature was over 70 °C, whereas for PMC-1, it started at room temperature (Fig. S8, ESI†). These results indicate that the solvent molecules in the pores block oxygen molecules from entering and, thus, improve the oxidative resistance of PMC-2. In addition, the counterions in the pores may also improve the resistance to oxygen via the SOMO energy of the NDI˙− radical. The radical is stabilized by the Rb+ ions in the case of PMC-2 but destabilized by the NO3− anions in the case of PMC-1. The increased durability toward the elimination of solvent molecules is probably due to the following three reasons. (1) Pore size and volume are smaller due to the introduction of bulky [Co(acac)2] moieties as metal nodes in comparison with those of PMC-1 with compact [Cd(OH2)4]2+ nodes (Fig. S3, ESI†). (2) There are attractive interactions between the DMA molecules and the Rb+ ions. (3) [Co(acac)2] nodes are more stable than the [Cd(OH2)4]2+ nodes in PMC-1, which can release H2O molecules.
Direct current (DC) electrical conductivities (σ) of single crystals were measured along the c axis by using a two probe method. The temperature dependence of σ (Fig. 3) indicated that PMC-2 exhibited semiconducting behaviour with a low activation energy (Ea) of 82 meV, which was calculated by fitting the data with the Arrhenius equation in the range of 150–222 K (blue dotted line in Fig. S11, ESI†). The σ value of PMC-2 at 300 K (σ300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) was (1.2–1.6) × 10−6 S cm−1, which is much lower than that of PMC-1 (σ300
K) was (1.2–1.6) × 10−6 S cm−1, which is much lower than that of PMC-1 (σ300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = (1.0–3.3) × 10−3 S cm−1). Although the charge of NDI–py is a non-integer value, the relatively low conductivity and the semiconducting (not metallic) behaviour of PMC-2 suggest that the carriers are localized. In fact, in our previous work on PMC-1 with an average charge of NDI–py of −0.7 ± 0.1, we have observed a similar phenomenon probably because the randomly accommodated counterions (NO3−) induce a non-periodic charge localization. In the case of PMC-2, Rb+ ions locating near the conductive pathways are disordered with a 50% occupancy, and this would cause a random charge localization and decrease the electrical conductivity. The calculated transfer integral between adjacent LUMO orbitals (255.8 meV) is larger than those of NDI-based organic semiconductors47,48 and comparable to those of highly conducting molecular conductors.49 Thus, the π-stacked array of NDI cores has the potential to exhibit a higher intrinsic conductivity if a random charge localization does not occur. Moreover, despite the difference in the counterions, PMC-2 has almost the same π-stacked arrays of NDI cores as PMC-1 does. This feature is promising for studying intrinsic conduction properties of molecular conductors without a structural perturbation of the π-stacked arrays typically caused by surrounding counterions.
K = (1.0–3.3) × 10−3 S cm−1). Although the charge of NDI–py is a non-integer value, the relatively low conductivity and the semiconducting (not metallic) behaviour of PMC-2 suggest that the carriers are localized. In fact, in our previous work on PMC-1 with an average charge of NDI–py of −0.7 ± 0.1, we have observed a similar phenomenon probably because the randomly accommodated counterions (NO3−) induce a non-periodic charge localization. In the case of PMC-2, Rb+ ions locating near the conductive pathways are disordered with a 50% occupancy, and this would cause a random charge localization and decrease the electrical conductivity. The calculated transfer integral between adjacent LUMO orbitals (255.8 meV) is larger than those of NDI-based organic semiconductors47,48 and comparable to those of highly conducting molecular conductors.49 Thus, the π-stacked array of NDI cores has the potential to exhibit a higher intrinsic conductivity if a random charge localization does not occur. Moreover, despite the difference in the counterions, PMC-2 has almost the same π-stacked arrays of NDI cores as PMC-1 does. This feature is promising for studying intrinsic conduction properties of molecular conductors without a structural perturbation of the π-stacked arrays typically caused by surrounding counterions.
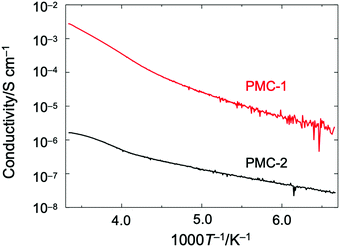 | ||
| Fig. 3 Temperature dependence of electrical conductivity of single crystalline PMC-2 (black) and PMC-1 (red) measured along the c axis (the direction of π-stacked columnar structure). | ||
In conclusion, the chemical reduction method could be used to synthesize PMC-2, which contains neutral metal nodes. NDI–py was reduced by cobaltocene prior to mixing with the neutral [Co(acac)2] via liquid–liquid slow diffusion. This method is more versatile than the previously used electrochemical method because it can be used with reactive combinations of metal sources and organic ligands. In addition, the introduction of neutral metal nodes improved PMC-2 as follows: (1) durability was increased. DMA molecules in the pore remained up to 70 °C, increasing the resistance to oxidation. (2) The charge of NDI core could be determined more precisely by counting the countercations (Rb+). Since various countercations and metal complexes can be used to prepare PMCs using our method, cation size and ligand bulkiness can be varied to modulate the electronic properties, thermal stability and porosity of PMCs. Finally, additional physical properties can be introduced by using neutral metal nodes, advancing the research on conductive soft crystals50 and functional framework materials.
We acknowledge Prof. Akutagawa and Dr. Hoshino at Tohoku University for acquiring the ESR spectrum. We also acknowledge Prof. B. K. Breedlove for language editing. This work was partly supported by JSPS KAKENHI Grant Numbers JP18H04498 (H. I.), JP18K14233 (H. I.), JP19H05631 (H. I., S. T. and M. Y.) and JP20J22404 (S. K.), by the CASIO Science Promotion Foundation (H. I.), by the Ogasawara Foundation for the Promotion of Science and Engineering (H. I.), by the Program for Interdisciplinary Research in Tohoku University Frontier Research Institute for Interdisciplinary Sciences (H. I.), and by the Toyota Riken Scholar Program (H. I.). M. Y. acknowledges the support by the 111 project (B18030) from China. Preliminary crystal structure analysis was performed under the approval of the Photon Factory Program Advisory Committee (Proposal No. 2018G083, beamline NW2A).
Conflicts of interest
There are no conflicts to declare.Notes and references
- L. Qu, H. Iguchi, S. Takaishi, F. Habib, C. F. Leong, D. M. D'Alessandro, T. Yoshida, H. Abe, E. Nishibori and M. Yamashita, J. Am. Chem. Soc., 2019, 141, 6802–6806 CrossRef CAS.
- S. Takaishi, M. Hosoda, T. Kajiwara, H. Miyasaka, M. Yamashita, Y. Nakanishi, Y. Kitagawa, K. Yamaguchi, A. Kobayashi and H. Kitagawa, Inorg. Chem., 2009, 48, 9048–9050 CrossRef CAS.
- H. Miyasaka, N. Motokawa, S. Matsunaga, M. Yamashita, K. Sugimoto, T. Mori, N. Toyota and K. R. Dunbar, J. Am. Chem. Soc., 2010, 132, 1532–1544 CrossRef CAS.
- T. Kambe, R. Sakamoto, K. Hoshiko, K. Takada, M. Miyachi, J.-H. Ryu, S. Sasaki, J. Kim, K. Nakazato, M. Takata and H. Nishihara, J. Am. Chem. Soc., 2013, 135, 2462–2465 CrossRef CAS.
- D. Sheberla, L. Sun, M. A. Blood-Forsythe, S. Er, C. R. Wade, C. K. Brozek, A. Aspuru-Guzik and M. Dincă, J. Am. Chem. Soc., 2014, 136, 8859–8862 CrossRef CAS.
- L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, J. Am. Chem. Soc., 2015, 137, 15703–15711 CrossRef CAS.
- N. Lahiri, N. Lotfizadeh, R. Tsuchikawa, V. V. Deshpande and J. Louie, J. Am. Chem. Soc., 2017, 139, 19–22 CrossRef CAS.
- L. S. Xie, L. Sun, R. Wan, S. S. Park, J. A. DeGayner, C. H. Hendon and M. Dincă, J. Am. Chem. Soc., 2018, 140, 7411–7414 CrossRef CAS.
- J. G. Park, M. L. Aubrey, J. Oktawiec, K. Chakarawet, L. E. Darago, F. Grandjean, G. J. Long and J. R. Long, J. Am. Chem. Soc., 2018, 140, 8526–8534 CrossRef CAS.
- M. Ko, L. Mendecki and K. A. Mirica, Chem. Commun., 2018, 54, 7873–7891 RSC.
- D. Sheberla, J. C. Bachman, J. S. Elias, C.-J. Sun, Y. Shao-Horn and M. Dincă, Nat. Mater., 2017, 16, 220–224 CrossRef CAS.
- L. Wang, Y. Han, X. Feng, J. Zhou, P. Qi and B. Wang, Coord. Chem. Rev., 2016, 307, 361–381 CrossRef CAS.
- D. M. D’Alessandro, Chem. Commun., 2016, 52, 8957–8971 RSC.
- T. C. Narayan, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2012, 134, 12932–12935 CrossRef CAS.
- S. S. Park, E. R. Hontz, L. Sun, C. H. Hendon, A. Walsh, T. V. Voorhis and M. Dincă, J. Am. Chem. Soc., 2015, 137, 1774–1777 CrossRef CAS.
- D. Chen, H. Xing, Z. Su and C. Wang, Chem. Commun., 2016, 52, 2019–2022 RSC.
- X. Kuang, S. Chen, L. Meng, J. Chen, X. Wu, G. Zhang, G. Zhong, T. Hu, Y. Li and C.-Z. Lu, Chem. Commun., 2019, 55, 1643–1646 RSC.
- D. Bechu, L. S. Xie, N. Le Breton, S. Choua, M. Dincă, M. W. Hosseini and S. A. Baudron, Chem. Commun., 2020, 56, 2407–2410 RSC.
- T. Murata, T. Koide, H. Nobukuni, R. Tsuji and Y. Morita, Int. J. Mol. Sci., 2020, 21, 4723 CrossRef.
- J. Y. Koo, Y. Yakiyama, G. R. Lee, J. Lee, H. C. Choi, Y. Morita and M. Kawano, J. Am. Chem. Soc., 2016, 138, 1776–1779 CrossRef CAS.
- G. Skorupskii, B. A. Trump, T. W. Kasel, C. M. Brown, C. H. Hendon and M. Dincă, Nat. Chem., 2020, 12, 131–136 CrossRef CAS.
- H. Wentz, G. Skorupskii, A. B. Bonfim, J. L. Mancuso, C. H. Hendon, E. H. Oriel, G. T. Sazama and M. G. Campbell, Chem. Sci., 2020, 11, 1342–1346 RSC.
- H. Anzai, J. M. Delrieu, S. Takasaki, S. Nakatsuji and J. Yamada, J. Cryst. Growth, 1995, 154, 145–150 CrossRef CAS.
- P. Batail, K. Boubekeur, M. Fourmigue and J.-C. P. Gabriel, Chem. Mater., 1998, 10, 3005–3015 CrossRef CAS.
- A. Mizuno, Y. Shuku, R. Suizu, M. M. Matsushita, M. Tsuchiizu, D. R. Manñeru, F. Illas, V. Robert and K. Awaga, J. Am. Chem. Soc., 2015, 137, 7612–7615 CrossRef CAS.
- S. Tang, H. Ruan, R. Feng, Y. Zhao, G. Tan, L. Zhang and X. Wang, Angew. Chem., Int. Ed., 2019, 58, 18224–18229 CrossRef CAS.
- B.-Q. Ma, S. Gao, T. Yi and G.-X. Xu, Polyhedron, 2001, 20, 1255–1261 CrossRef CAS.
- S. Koyama, H. Iguchi, S. Takaishi, G. Cosquer, S. Kumagai, J. Takeya, T. Okamoto and M. Yamashita, Chem. Lett., 2019, 48, 756–759 CrossRef CAS.
- Y. Wu, M. D. Krzyaniak, J. F. Stoddart and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 2948–2951 CrossRef CAS.
- G. Bélanger-Chabot, A. Ali and F. P. Gabbaï, Angew. Chem., Int. Ed., 2017, 56, 9958–9961 CrossRef.
- Y. Matsunaga, K. Goto, K. Kubono, K. Sako and T. Shinmyozu, Chem. – Eur. J., 2014, 20, 7309–7316 CrossRef CAS.
- L. Qin, W.-N. Zhao, G.-J. Yu, L.-P. Xu and L. Han, Inorg. Chem. Commun., 2013, 34, 47–50 CrossRef CAS.
- N. Kyratzis, W. Cao, E. I. Izgorodina and D. R. Turner, CrystEngComm, 2018, 20, 4115–4126 RSC.
- J. I. Lovitt, C. S. Hawes and T. Gunnlaugsson, CrystEngComm, 2019, 21, 207–217 RSC.
- X. Shang, I. Song, J. H. Lee, W. Choi, H. Ohtsu, G. Y. Jung, J. Ahn, M. Han, J. Y. Koo, M. Kawano, S. K. Kwak and J. H. Oh, ACS Appl. Mater. Interfaces, 2019, 11, 20174–20182 CrossRef CAS.
- J.-J. Liu, S.-B. Xia, D. Liu, J. Hou, H. Suo and F.-X. Cheng, Dyes Pigm., 2020, 177, 108269 CrossRef CAS.
- P. Hao, H. Zhu, Y. Pang, J. Shen and Y. Fu, CrystEngComm, 2020, 22, 3371–3377 RSC.
- K. Fuku, M. Miyata, S. Takaishi, T. Yoshida, M. Yamashita, N. Hoshino, T. Akutagawa, H. Ohtsu, M. Kawano and H. Iguchi, Chem. Commun., 2020, 56, 8619–8622 RSC.
- M. Pan, X.-M. Lin, G.-B. Li and C.-Y. Su, Coord. Chem. Rev., 2011, 255, 1921–1936 CrossRef CAS.
- A. Kuznetsova, V. Matveevskaya, D. Pavlov, A. Yakunenkov and A. Potapov, Materials, 2020, 13, 2699 CrossRef CAS.
- R. C. Elder, Inorg. Chem., 1968, 7, 1117–1123 CrossRef CAS.
- D. Gosztola, M. P. Niemczyk, W. Svec, A. S. Lukas and M. R. Wasielewski, J. Phys. Chem. A, 2000, 104, 6545–6551 CrossRef CAS.
- C. F. Leong, B. Chan, T. B. Faust and D. M. D’Alessandro, Chem. Sci., 2014, 5, 4724–4728 RSC.
- P. M. Usov, C. Fabian and D. M. D’Alessandro, Chem. Commun., 2012, 48, 3945–3947 RSC.
- A. Takai, T. Yasuda, T. Ishizuka, T. Kojima and M. Takeuchi, Angew. Chem., Int. Ed., 2013, 52, 9167–9171 CrossRef CAS.
- C. S. Jacobsen, in Semiconductors and Semimetals, ed. E. Conwell, Optical Properties, Academic Press, Boston, 1988, ch. 5, vol. 27, pp. 293–384 Search PubMed.
- T. Kakinuma, H. Kojima, M. Ashizawa, H. Matsumoto and T. Mori, J. Mater. Chem. C, 2013, 1, 5395–5401 RSC.
- A. Kawasaki, T. Takeda, N. Hoshino, W. Matsuda, S. Seki and T. Akutagawa, Cryst. Growth Des., 2020, 20, 1276–1284 CrossRef CAS.
- T. Mori, Bull. Chem. Soc. Jpn., 2016, 89, 973–986 CrossRef CAS.
- M. Kato, H. Ito, M. Hasegawa and K. Ishii, Chem. – Eur. J., 2019, 25, 5105–5112 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, crystallographic details, thermogravimetric analysis, PXRD patterns and magnetic susceptibility. CCDC 2004231 (2′) and 2004232 (PMC-2). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cc03541f |
| This journal is © The Royal Society of Chemistry 2020 |