Open Access Article
Open Access ArticleExperiment stands corrected: accurate prediction of the aqueous pKa values of sulfonamide drugs using equilibrium bond lengths†
Beth A.
Caine
ab,
Maddalena
Bronzato
c and
Paul L. A.
Popelier
 *ab
*ab
aManchester Institute of Biotechnology (MIB), 131 Princess Street, Manchester M1 7DN, UK. E-mail: pla@manchester.ac.uk
bSchool of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK
cSyngenta AG, Jealott's Hill, Warfield, Bracknell, RG42 6E7, UK
First published on 29th May 2019
Abstract
We show here for the first time that strongly correlated linear relationships exist between equilibrium bond lengths of the sulfonamide group and aqueous pKa values. Models are constructed for three variants of the SO2NHR group: primary benzene sulfonamide derivatives (e.g. diuretic drugs furosemide and hydrochlorothiazide), N-phenyl substituted 4-amino-N-phenylbenzenesulfonamide analogues (e.g. the sulfa antibiotic sulfadiazine) and phenylsulfonylureas (e.g. insulin secretagogue, glimepiride). In the context of these compounds, we present solutions to some of the more complex challenges in pKa prediction: (i) prediction for multiprotic compounds, (ii) predicting macroscopic values for compounds that tautomerize, and (iii) quantum chemical pKa prediction for compounds with more than 50 atoms. Using bond lengths as a powerful descriptor of ionization feasibility, we also identify that literature values for drug compounds celecoxib, glimepiride and glipizide are inaccurate. Our newly measured experimental values match our initial predictions to within 0.26 pKa units, whereas previous values were found to deviate by up to 1.68 pKa units. For glimepiride, our corrected value denotes a percentage of ionization at intracellular pH, which is only now in excellent agreement with its known therapeutic efficacy. We propose that linear relationships between bond lengths and pKa should emerge for any set of congeners, thus providing a powerful method of pKa prediction in instances where pKa data exist for close congeners, thereby obviating the need for thermodynamic cycles.
1. Introduction
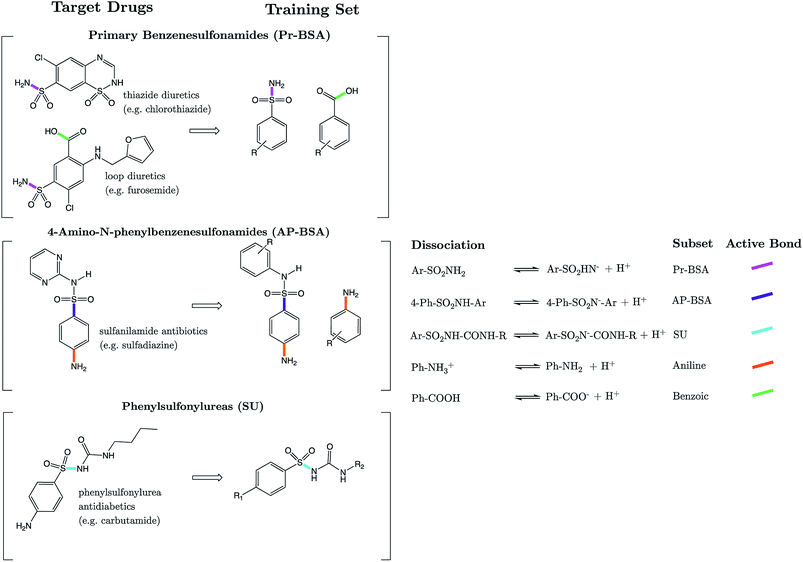
The sulfonamide group, SO2NHR, is an acidic moiety that features heavily in pharmaceutical and agrochemical compounds, yet is surprisingly uncommon in nature. ZINC, a database commonly used in virtual screening, listed 4781 commercially available derivatives of methylsulfonamide in 2016.1 There are ∼200 sulfonamide-containing drugs currently on the market.2 Examples include antibiotics, anti-glaucoma,3 diuretics, anticonvulsants, antidiabetics and anti-cancer agents.4–6 Due to the prevalence of this group in the design of modern bioactive compounds, research into optimized methods for their synthesis continues to be of relevance.7–9 Sulfonamide antibiotics (SAs) were the first widely used antibiotic agents, and arguably paved the way for the antibiotic revolution. Their antibacterial action stems from the competitive inhibition of p-aminobenzoic acid in the folic acid metabolism cycle, which prevents bacterial multiplication. It is estimated that after administration, 30–90% of SAs are excreted either as the parent compound, or as acetic acid conjugates.10 Recent reports suggest that the environmental pollution caused by such widespread historical usage of SAs and other antibiotics may pose harmful effects to aquatic organisms.11 Further risk to human health may also arise from their prevalence in the food chain via the soil environment.12The acid dissociation constant, Ka, defines the extent to which dissociation of a proton is thermodynamically feasible at a given pH. It provides a means to rationalize acid–base activity in aqueous conditions, an insight that is fundamental to numerous areas of chemistry and biochemistry. Approaches to pKa prediction may be classified as either “first principles” or “empirical”. Purely first-principles methods access the pKa value via the calculation of ΔG for dissociation, using the van't Hoff's isotherm to calculate the dissociation constant. The broad applicability of this approach makes it attractive, and it has been explored using many quantum mechanical approaches.13–18 However, the significant CPU-time that electronic structure calculations incur remains a detriment to the utility of this approach in larger scale screening studies. The program “Jaguar pKa” by Schrödinger is the only commercially available first-principles base pKa prediction package.19,20 The second widely explored approach is to construct an empirically derived model based on the relationships between various chemical descriptors and experimental pKa data. The programs Marvin21 (ChemAxon), Epik22 (Schrödinger), and “Classic” and “GALAS” of ACD Labs23 are just some examples of commercially available packages, all of which implement variants of an empirical-based workflow. Other recent empirical approaches have implemented machine learning methods such as artificial neural nets24 and support vector regression.25
Philipp et al. recently highlighted several issues that remain relevant to both first-principles and empirical-based communities.20 Firstly, the use of 2D molecular representations (e.g. SMILES or SMARTS strings), can lead to poor predictions for compounds with pKa values strongly influenced by geometric features. For example, steric effects, or stereospecific hydrogen bonding interactions, can affect the thermodynamic feasibility of dissociation. Whereas these effects must be explicitly parameterized using 2D structures, the problem becomes less pronounced in first-principles approaches due to the use of 3D geometries. Another problem highlighted by Phillipp et al. is the case of tautomerizable compounds. A theoretically rigorous quantum mechanical approach requires the generation of an ensemble of low-lying conformations for each tautomeric state. This increases computation times, a problem further enhanced in the case of multiprotic tautomerizable compounds. For empirical approaches the problem with tautomerism arises with the need to recognize the dominant tautomeric state, owing to the fact that different tautomers may have different pKa values. Experimental evidence in support of tautomeric preference is lacking for many species.26,27
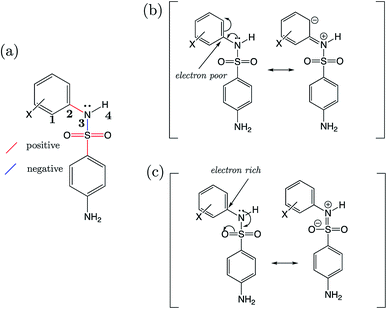
Strikingly well-defined linear relationships between bond lengths and pKa have now been shown to emerge for many functional groups.28–33 The bond length allows for the partitioning of chemical space into subsets of compounds, within which the site of ionization shares a specific local chemical environment. In the current work, we demonstrate for the first time that linear relationships exist between bond lengths of three variants of the sulfonamide group and their propensity to ionize in aqueous conditions. Fig. 1 shows the common skeletons of the training sets and their corresponding target drugs for the three classes of sulfonamides studied: primary benzene sulfonamide derivatives, 4-amino-N-phenylbenzenesulfonamides and phenylsulfonylureas. We then show how these relationships may be exploited to predict pKa values of sulfonamide groups on a number of pharmaceutically relevant compounds. We also pose solutions for the more complex issues in pKa prediction by demonstrating how to predict with excellent accuracy for (i) multiprotic compounds, (ii) compounds containing more than 50 atoms, and (iii) those compounds that tautomerize. Furthermore, we add credence to the notion that AIBL models (AIBL = Ab Initio Bond Lengths) providing accurate predictions may be established for any type of ionizable group, given that some experimental data are available for parameterization.
2. Computational methods
2.1 Conformational search
Geometries of all stationary points were optimized at B3LYP/6-311G(d,p) level using GAUSSIAN09 with tight convergence criteria, in both gas and solvent phase using CPCM. Vibrational analysis was then performed at the same level to confirm the nature of the stationary points. For primary benzene sulfonamides (Pr-BSA, Set 1 or S1), two input structures were generated for each compound of the training set (S1-1 to S1-22, listed in Tables S1–S4 in the (ESI†)): an anti-conformer and a syn-conformer, where the labels anti and syn denote the orientation of the nitrogen lone pair relative to the C–S bond of the sulfonamide fragment. For the 4-amino-N-phenylbenzenesulfonamide (AP-BSA, Set 2 or S2) training set (labelled S2-1 to S2-38, and listed in Tables S5 and S6 of the ESI†), the most stable conformation of 4-amino-N-phenylbenzenesulfonamide was identified from an ensemble of 15 optimized geometries by a comparison of total energies. This geometry was then used as the common 3D skeleton for the construction of the remaining 37 S2 analogues. The same method of generating low-lying conformations for the common fragment was used for the third and final series, the sulfonylureas set (SU, Set 3), which contains compounds SU-1 to SU-30, listed in Tables S7–S9.† For compounds with flexible substituent groups, several starting geometries were generated for all cases via manual rotation around bonds of the substituent group, whilst the sulfonamide group was left unchanged.For test set compounds TS1-1 to TS1-10 (listed in Results section and in Tables S10–S14†), a conformational search was performed via use of the “Conformers” plug-in within the MarvinSketch program (version 16.1.4.0) by ChemAxon.21 A total of 25 conformers were generated using the Dreiding force-field, with diversity threshold and time step set to default. Each conformer was optimized at the B3LYP/6-311G(d,p) level in the gas-phase using GAUSSIAN09 with tight convergence criteria. The most stable geometry of the compound, whilst keeping the syn conformation of the sulfonamide group, was then identified by a comparison of total energies. For compounds with more than one site of ionization, the proton at the most acidic site of ionization (–SO2N–H– for TS1-7 to TS1-11 and COO-H for TS1-12 to TS1-14) was removed and the anionic state was also optimized. Optimizations were performed with both the 6-311G(d,p) and 6-311+G(d,p) basis sets. The geometries of the N-heterocyclic arenesulfonamide (NHAS) test set compounds labelled TS2-1 to TS2-10 (listed later in the text and in Table S15†), were once again obtained via selection of the most stable from a conformational ensemble of 25, after optimization using GAUSSIAN09. For the sulfonylureas of the test set, denoted TSU, the compounds glibenclamide, glimepiride and glipizide (listed in Table S16†), the number of constituent atoms exceeds 50, and they have a number of rotatable bonds in the R1 and R2 groups. To identify the most stable geometry for each species, a conformational ensemble of 30 geometries was generated using Marvin for each TSU compound, once again followed by optimization using GAUSSIAN09. The above procedure was performed both in gas-phase and with the CPCM, in all cases.
2.2 Experimental data
Experimental data were procured from several different literature sources and are referenced throughout the text and in the ESI.† All pKa values correspond to measurements taken as close to standard conditions as possible, i.e. 298.15 K and 1 atm. The new values for celecoxib, glimepiride and glipizide were measured in this work using the SiriusT3 instrument, an automatic titration system incorporating in situ UV spectroscopy. More details of experimental measurements are given in Technical Section 1 of the ESI.†2.3 Model validation
Each of the three subgroups studied here consist of a series of closely related analogues of benzene sulfonamide (S1-1 to S1-22 and TS1-1 to TS1-14, a total of 22 + 14 = 36 compounds), 4-amino-N-phenylbenzenesulfonamides (S2-1 to S2-38 and TS2-1 to TS2-10, a total of 38 + 10 = 48 compounds) and phenylsulfonylurea (SU-1 to SU-30 and TSU-1 to TSU-6, a total of 30 + 6 = 36). Each of the three subsets was analyzed separately for the existence of linear relationships between bond lengths close to the site of ionization and pKa. Ordinary least-squares regression was performed and assessment goodness-of-fit of was performed using the squared correlation coefficient (r2) and the Root-Mean-Squared-Error of Estimation (RMSEE). Cross validation was performed by calculation of the leave-one-seventh-out q2 value using the program SIMCA-P,34 to give some estimation of model predictability. The equations defining these metrics can be found in Technical Section 2 of the ESI,† in addition to Mean Absolute Error (MAE)-based criteria that Roy has recommended35 for evaluation of QSAR/QSPR models.2.4 IQA calculations
In the Discussion section, the trend in bond length variation with pKa is analysed to derive a rationale for the origins of each relationship. The energy decomposition framework called Interacting Quantum Atoms (IQA)36 was used via the program AIMAll (version16.01.09) to derive quantities describing the extent of delocalization between atoms, and the electrostatic interaction between atoms, respectively. Details of this procedure can be found in Technical Section 3.3. Results
3.1 Models: primary benzene sulfonamides (Pr-BSAs)
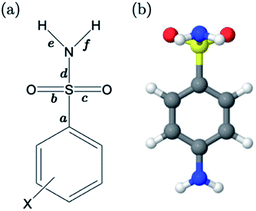
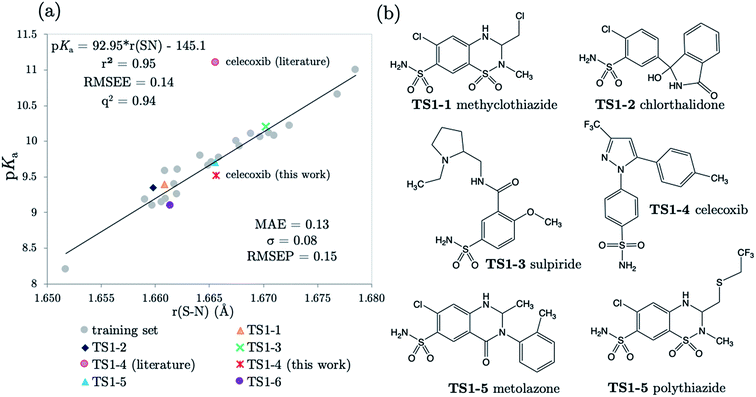
For primary benzene sulfonamides we wish to predict the thermodynamic feasibility of the dissociation SO2–NH2 → SO2–N−H + H+. The bond lengths of the sulfonamide group under investigation are shown in Fig. 2a, labelled a–f. Several studies concerning the gas-phase conformation of benzene sulfonamide and its derivatives have been performed.37–39 The general consensus is that two dominant conformations exist for the –SO2NH2 group, which can be labelled “syn” and “anti” denoting the orientation of the lone pair on the nitrogen atom relative to the C–S bond (shown in Fig. S1 of the ESI†). In this work we use a set of 22 substituted benzene sulfonamides (labelled S1-1 to S1-22 and shown in Tables S1–S4†) to construct bond length-pKa models. For each S1 compound, the syn and anti-conformers were located (shown in Fig. S1 of the ESI†). We find that, in the presence of the CPCM implicit solvation model, the anti-conformer (Fig. 2b) is on average ∼4 kJ mol−1 more stable than syn across the series.Results of linear regression of each bond length a–f of the CPCM-solvated structures against pKa reveal superior internal validation statistics for the S–N bonding distance (r2 = 0.95, q2 = 0.94 and RMSEE = 0.14). The full set of statistics for each bond length model can be found in Table S17.†
The proximity of an ortho-substituent to the sulfonamide group means that it can influence bond lengths of SO2NH2via steric effects and intramolecular hydrogen bonding interactions, depending on the type of substituent. If the ortho compounds are removed, strong (r2 > 0.8), positive correlations with pKa are observed for all bonds except C–S (a), which is negatively correlated. That is to say, shorter S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (b and c), S–N (d) and N–H (e and f) bond distances are indicative of a greater propensity to ionize, whilst the C–S bond becomes longer with increased acidity. These relationships are illustrated in the plots shown in Fig. S2.† We note that the nature of the variation in bonding distances a–f is the same for syn and anti-conformers in both gas and solvent phase. Therefore, the effect that a substituent has on the constituent bond lengths of the ionizable group is reflected in the relative propensity of the molecule to lose a proton. Overall, those compounds with substituents that make the phenyl group more electron-poor exhibit a lower pKa, and vice versa. In the next section, we make predictions for 14 drug molecules using the equation describing the linear line of best fit for the SN bond length model, i.e., pKa = 92.95 × r(S–N) − 145.10.
O (b and c), S–N (d) and N–H (e and f) bond distances are indicative of a greater propensity to ionize, whilst the C–S bond becomes longer with increased acidity. These relationships are illustrated in the plots shown in Fig. S2.† We note that the nature of the variation in bonding distances a–f is the same for syn and anti-conformers in both gas and solvent phase. Therefore, the effect that a substituent has on the constituent bond lengths of the ionizable group is reflected in the relative propensity of the molecule to lose a proton. Overall, those compounds with substituents that make the phenyl group more electron-poor exhibit a lower pKa, and vice versa. In the next section, we make predictions for 14 drug molecules using the equation describing the linear line of best fit for the SN bond length model, i.e., pKa = 92.95 × r(S–N) − 145.10.
3.2 Predictions: neutral Pr-BSAs
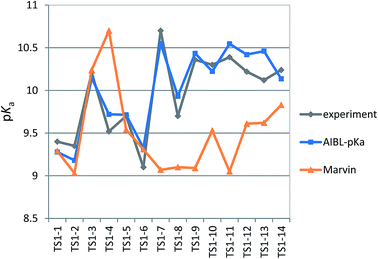
We chose six compounds for the first test set (TS1) which exhibit a pKa value corresponding to dissociation of the proton at the sulfonamide group, whilst the rest of the molecule is in a neutral state. These six compounds are methyclothiazide (TS1-1), chlorthalidone (TS1-2), sulpiride (TS1-3), celecoxib (TS1-4), metolazone (TS1-5) and polythiazide (TS1-6).Predictions made using the equation above for the S–N bond (d) solvated model are illustrated in Fig. 3, and listed in Table S18.† All compounds are predicted for to within 0.5 units from literature values aside from celecoxib. Our prediction of 9.72 for celecoxib shows an error of −1.38 with respect to the existing experimental value40 of 11.1. Due to the anomalously large error of our prediction, a new experimental measurement was taken using the UV-metric technique. As celecoxib is poorly soluble in water but readily dissolves in methanol, it was necessary to perform Yasuda-Shedlovsky extrapolation. This procedure delivers a pKa value for aqueous conditions from the relationship between pKa value and methanol concentration. Details of the experimental procedure are given in Technical Section 1 of the ESI.† This treatment returned a new experimental value of 9.525 as the average of four measurements, with a standard deviation of 0.06. This new value is now 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units from our predicted value of 9.72. This success shows that AIBL is able to correct for an erroneous experiment. As the precise conditions of the 11.1 value are unknown, we can only postulate that it was obtained in non-standard conditions. An increase in ∼1.5 units can most likely be ascribed to the response of the equilibrium to a lower temperature, the presence of another solvent or a higher ionic strength.
log units from our predicted value of 9.72. This success shows that AIBL is able to correct for an erroneous experiment. As the precise conditions of the 11.1 value are unknown, we can only postulate that it was obtained in non-standard conditions. An increase in ∼1.5 units can most likely be ascribed to the response of the equilibrium to a lower temperature, the presence of another solvent or a higher ionic strength.
The predictions made by the Marvin tool are also very accurate (MAE = 0.34, see Table S18†). This is likely due to the prevalence of benzene sulfonamide analogues and accompanying pKa data in the literature. However, it should be noted that the correction of the pKa value for celecoxib would not have been realized using the Marvin program, because at 10.7, Marvin's value lies closer to original literature value, and has an error of +1.18 when compared to the new value.
3.3 Predictions: anionic Pr-BSAs
The next 8 test compounds are shown in Fig. 4. Each compound of this set has at least two sites of ionization, one of which is a primary sulfonamide group. The thiazide drugs (TS1-7 to TS1-11) exhibit a pKa(1) value in the range 6 to 9,41 corresponding to dissociation from a tertiary sulfamoyl group in their secondary ring.42 Compounds TS1-12 to TS1-14, (bumetanide, furosemide and piretanide) all contain primary sulfonamide groups in addition to a more acidic carboxylic acid group (pKa(1) ∼ 3.5). Therefore, we optimized the anionic forms (carboxylate anion TS1-12 to TS1-14, and sulfonamide anion for TS1-7 to TS1-11), as well as the neutral states in order to assess the effect of protonation state on prediction accuracy. The results shown in Fig. 4 (and Table S19†) indicate that representation of each compound in the anionic microstate is necessary for accurate prediction of their pKa values. This assertion is illustrated by a marked decrease in MAE from 0.87 to 0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units for predictions made using the neutral species compared to the anionic state. This improvement (in going from the neutral to the anionic form) is evident even without the inclusion of diffuse functions for non-hydrogen atoms in the basis set. However, inclusion of diffuse functions (6-311+G(d,p)) provides further amelioration of prediction accuracy such that the MAE is reduced to just 0.20, using the SN bond in the anionic form. Allowing distribution of electronic charge over a larger spatial area, via the inclusion of diffuse functions, should provide a more accurate description of the diminished electron repulsion at the anion. Thus, we can expect to obtain a better representation of electron distribution near to the active bond site, more accurate bond lengths and greater prediction accuracy. To avoid the lack of consistency the whole training set could be re-optimized with 6-311+G(d,p), rather than just the set of anionic species. However, as the approach taken delivers excellent predictions, this was not deemed necessary.
log units for predictions made using the neutral species compared to the anionic state. This improvement (in going from the neutral to the anionic form) is evident even without the inclusion of diffuse functions for non-hydrogen atoms in the basis set. However, inclusion of diffuse functions (6-311+G(d,p)) provides further amelioration of prediction accuracy such that the MAE is reduced to just 0.20, using the SN bond in the anionic form. Allowing distribution of electronic charge over a larger spatial area, via the inclusion of diffuse functions, should provide a more accurate description of the diminished electron repulsion at the anion. Thus, we can expect to obtain a better representation of electron distribution near to the active bond site, more accurate bond lengths and greater prediction accuracy. To avoid the lack of consistency the whole training set could be re-optimized with 6-311+G(d,p), rather than just the set of anionic species. However, as the approach taken delivers excellent predictions, this was not deemed necessary.
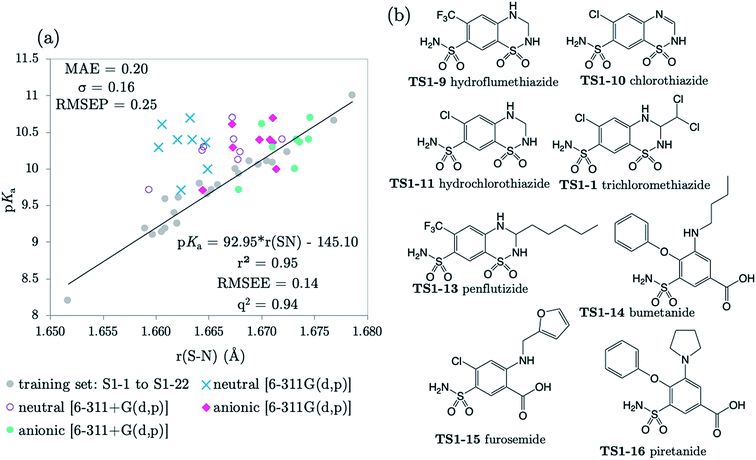 | ||
| Fig. 4 (a) The relationship between S–N equilibrium bond lengths calculated using CPCM and pKa values for the training set S1-1 to S1-22, (gray dots), and the test set, consisting of 8 drug diprotic drug compounds, labelled TS1-7 to TS1-14. SN bond lengths for the test set have been calculated for the neutral state using the 6-311G(d,p) basis set (blue crosses) and the 6-311+G(d,p) basis set (purple circles), the anionic form of each compound using 6-311G(d,p) (pink diamonds) and with the addition of one set of diffuse functions to this basis set [6-311+G(d,p)] (green dots). Bond length values can be found in Tables S11–S14 of the ESI.† (b) Structures of drug compounds TS1-7 to TS1-14. MAE, standard deviation (σ) and RMSEP shown correspond to the anionic B3LYP/6-311+G(d,p) predictions. | ||
The applicability radius of this primary sulfonamide model is wide: it covers ortho-, meta- and para-substitution and may be used to predict pKa values of sulfonamide groups on diprotic compounds. Whilst the performance of Marvin is still good, with an overall MAE of 0.65, a standard deviation of 0.41 and a RMSEP of 0.82, 4 out of the 16 predictions showed errors of more than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log unit and 4 others were between 0.5 and 1
log unit and 4 others were between 0.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log unit. Furthermore, for 3 out of 5 thiazides (TS1-7, TS1-9 and TS1-11), Marvin predicts that the primary sulfonamide group is more acidic than the tertiary sulfamoyl group. No AIBL-pKa errors exceeded 0.34
log unit. Furthermore, for 3 out of 5 thiazides (TS1-7, TS1-9 and TS1-11), Marvin predicts that the primary sulfonamide group is more acidic than the tertiary sulfamoyl group. No AIBL-pKa errors exceeded 0.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units, and the trend in pKa values across the series from TS1-7 to TS1-14 mirrors that of the experimental values remarkably well, as shown in Fig. 5 Technical Section 4 of the ESI† also details how the model passes Roy's MAE-based evaluation criteria.
log units, and the trend in pKa values across the series from TS1-7 to TS1-14 mirrors that of the experimental values remarkably well, as shown in Fig. 5 Technical Section 4 of the ESI† also details how the model passes Roy's MAE-based evaluation criteria.
Taking the ipso carbon as the atom bound to the carboxylic acid group, compounds TS1-12, TS1-13 and TS1-14 can be classed as meta- and para- (m/p) substituted benzoic acids. Previous work showed that the gas-phase C–O bond (in the COOH fragment) of m/p substituted benzoic acids is positively correlated to aqueous pKa (as is the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance, whilst the C–C and O–H distances instead show a negative correlation). Using the pKa data collated in our previous publication,28 41 compounds were re-optimized in the gas-phase at the B3LYP/6-311G(d,p) level of theory. The results previously obtained at the HF/6-31G(d) level were corroborated: the C–O bond length model has an r2 of 0.90 with pKa values. The equation describing this relationship (pKa = 144.97 × r(C–O) − 192.56) was used to predict the pKa values for the carboxylic acid group, modelled in its neutral form, using the most stable gas-phase conformers identified for TS1-12 to TS1-14. According to the literature, bumetanide, furosemide and piretanide exhibit pKa(1) values of 3.74,43 3.64
O bond distance, whilst the C–C and O–H distances instead show a negative correlation). Using the pKa data collated in our previous publication,28 41 compounds were re-optimized in the gas-phase at the B3LYP/6-311G(d,p) level of theory. The results previously obtained at the HF/6-31G(d) level were corroborated: the C–O bond length model has an r2 of 0.90 with pKa values. The equation describing this relationship (pKa = 144.97 × r(C–O) − 192.56) was used to predict the pKa values for the carboxylic acid group, modelled in its neutral form, using the most stable gas-phase conformers identified for TS1-12 to TS1-14. According to the literature, bumetanide, furosemide and piretanide exhibit pKa(1) values of 3.74,43 3.64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 and 4.00.45 Our model predicts values of 3.47, 3.33 and 4.23. Whilst it is true that the accurate prediction of pKa values for benzoic acid derivatives is no longer considered a challenge for existing methodologies, (although Marvin predicts values of 4.69, 4.26, 4.68), it is pleasing to note that we return an excellent level of accuracy. Furthermore, the relative order of acidity between compounds is predicted correctly by our model.
44 and 4.00.45 Our model predicts values of 3.47, 3.33 and 4.23. Whilst it is true that the accurate prediction of pKa values for benzoic acid derivatives is no longer considered a challenge for existing methodologies, (although Marvin predicts values of 4.69, 4.26, 4.68), it is pleasing to note that we return an excellent level of accuracy. Furthermore, the relative order of acidity between compounds is predicted correctly by our model.
3.4 Models: 4-amino-N-phenylbenzenesulfonamides (AP-BSA)
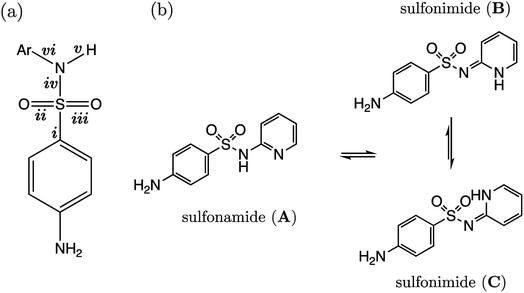
Several drugs have been identified by the derivatization of sulfanilamide with an aromatic group at the N1 position (denoted “Ar” in Fig. 6a). For such compounds, the influence of the electron-withdrawing arene group causes a general increase in acidity of the –SO2NH– proton relative to primary sulfonamides. This decrease in pKa value means that in aqueous conditions many of these drugs are ionized at physiological pH. One class of secondary sulfonamides which have found widespread usage as therapeutics are N-heterocyclic arenesulfonamides (NHAS). For these species, the aryl group contains a heteroatom at the 2-position, allowing them to exhibit sulfanilamide–sulfanilamide tautomerism (Fig. 6b). It is suggested that both tautomeric forms may be important for their therapeutic activity. A recent study46 by Chourasiya et al. has looked specifically at tautomeric polymorphism for a series of sulfanilamide drugs. By comparing gas-phase free energies of the amide and imide forms, they noted that compounds with an N1-2- or N1-4-pyridyl group preferred the amide state. Their calculations, carried out with an implicit model representing a DMSO environment, suggested that the stability of the imide form is heightened in the presence of a polar solvent. In this work we focus on the sulfonamide form of each S2 and TS2 species only because, based on previous work for guanidines,33 we expect optimal correlations to emerge using bond lengths of the most stable tautomeric form.The use of the CPCM implicit solvation model in our geometry optimization for compounds S2-1 to S2-38 provides a marginally superior goodness-of-fit over gas-phase geometries, as measured by r2 (see Table S20†). The C–S bond may be referred to as the most “active bond”, as it exhibits the highest r2 value, at 0.96. The cross-validation q2 value, which gives an estimate of model predictivity, is also impressively high for C–S at 0.95 and the RMSEE is respectable at 0.23 log units. For S2, the sign of the S–N (iv) slope is negative whilst bonds i, ii, iii, v and vi have a positive correlation. For this series, the most acidic compound is the 2-Br, 4-NO2 derivative (labelled S2-37, pKa = 5.7), whereas the least acidic species is the 4-NH2 derivative (labelled S2-9, pKa = 10.22). We therefore find that the most acidic species in the series has the longest S–N bond (iv), and the shortest C–N bond (vi).
The presence of the p-amino group on sulfanilamide means there is an additional microdissociation reaction NH3+ → NH2 + H+, which has a pKa value of ∼2. For the sulfonamide group dissociation, the relevant state is the neutral state of each compound. Therefore, the relevant microstate for the aniline group dissociation is the protonated state. However, here we use the neutral state of the compound in accordance with work by Harding et al., which illustrated how there is a linear relationship between r(C–N) and pKa values for aniline derivatives in the conjugate base form. The variation in C–N bonding distance with pKa across a congeneric series can be attributed to the varying extent of sp2 hybridization of the nitrogen atom, which is influenced by phenyl substituent groups. For example, in the work of Harding et al., the C–N, and both N–H bonds have a positive correlation with pKa, i.e., a shorter bond length (in the presence of ortho and para electron-withdrawing substituents) corresponds to a lower pKa. This bond-shortening effect, coupled with an increase in trigonal planarity, is indicative of a higher degree of sp2 character of the nitrogen atom as the phenyl ring becomes more electron-poor at the ipso carbon. Enhanced, substituent-induced nitrogen sp2 hybridization provides greater resonance stabilization of the neutral conjugate base form. However, a more electron-poor ipso carbon destabilizes the conjugate (cationic) acid, thereby favouring the dissociation of N+–H, and thus rationalizing the lower pKa measured for such species. In this work, 20 aniline derivatives were optimized at the same level of theory used throughout this work [B3LYP/6-311G(d,p)]. Because previous work by Harding et al. showed that gas-phase bond lengths exhibit a strong linear relationship with pKa, calculations were also carried out in vacuo to minimize CPU time. Predictions were made using gas-phase C–N bond lengths (of the amine group) of test set compounds TS2-1 to TS2-5 and TS2-9 using the equation pKa(aniline) = 141.57 × r(C–N) − 193.51, for which the r2 value for the line of best fit was 0.92.
3.5 Predictions: AP-BSA
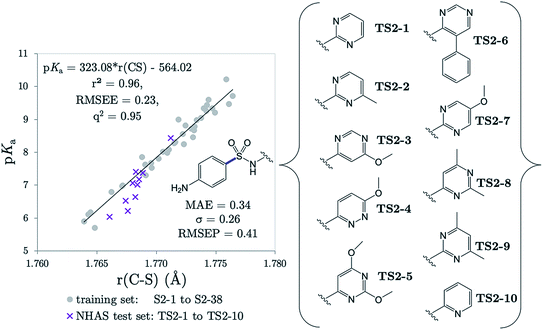
The r(C–S)/CPCM model (pKa = 323.08 × r(C–S) − 564.02) was tested in the case of 10 NHAS drug compounds, which are labelled TS2-1 to TS2-10, and shown in Fig. 7. Experimental aniline pKa values are available for compounds TS2-1 to TS2-5 and TS2-9. Our predictions showed an MAE of 0.34, a standard deviation of absolute errors of 0.26 and a RMSEP of 0.40. All predicted values can be found in Table S21.† Low errors (<0.5 pKa units) are observed for the sulfonamide group predictions for 6 compounds TS2-1, TS2-2, TS2-4, TS2-8, TS2-9 and TS2-10, indicating that this model can be applied to 2-pyridine NHAS compounds. However, in the case of compounds TS2-1 to TS2-5, there are multiple pKa values in the literature associated with the sulfonamide group, making it a difficult task to truly discern the accuracy of our model. Fig. 7 was produced by choosing the values that best match our predictions, yet there are still three prediction errors that exceed 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units: TS2-3 (−0.84), TS2-5 (−0.62) and TS2-7 (−0.63). Without additional re-measurement of experimental values, it cannot be confirmed whether the values we predict are indeed more accurate than the reported experimental values, such as in the case of celecoxib.
log units: TS2-3 (−0.84), TS2-5 (−0.62) and TS2-7 (−0.63). Without additional re-measurement of experimental values, it cannot be confirmed whether the values we predict are indeed more accurate than the reported experimental values, such as in the case of celecoxib.
Representation of each of the compounds TS2-1 to S2-10 as the higher energy sulfonimide tautomer reveals no relationship between bond length and pKa (i.e. r2 < 0.5 for all bonds). Yet, in the sulfonamide state the r2 value for the test set alone is 0.87. It may be asserted that, given our aqueous-phase experimental observable is related to a structural feature of the sulfonamide state, we provide further corroboration to the work of Chourasiya and co-workers, which suggests this state is dominant in aqueous conditions.
Using the same experimental values used to construct Fig. 7, the MAE value for Marvin's predictions is found to be 0.70 with a standard deviation of 0.67. Taking the values closest to Marvin's predictions these values become 0.66 and 0.70. However, the general performance of Marvin is good for this series, and the larger MAE value can be mainly attributed to larger errors for four compounds: TS2-3 (0.93), TS2-6 (0.97), TS2-8 (1.28) and TS2-10 (2.19). A plot showing the general trend across the series for experimental, AIBL-pKa values and Marvin predictions can be found in Fig. S3 of the SI.† Technical Section 5 also details how our model fares according to Roy's MAE-based evaluation criteria for the 14 compounds TS2-1 to TS1-10. The majority of training set data is taken from just one source, where the exact conditions (i.e. temperature, solvent) are not reported. It is feasible that the values given in that work were recorded at a temperature lower than 298 K, with a small percentage of another less polar solvent, or at a different ionic strength to the drug compounds. The amalgamation of the test and training set data points returns a linear fit with an r2 value of 0.95. It may be asserted that the use of this equation, in the case of future predictions may help towards reducing systematic error associated with deviation from standard conditions between test and training set.
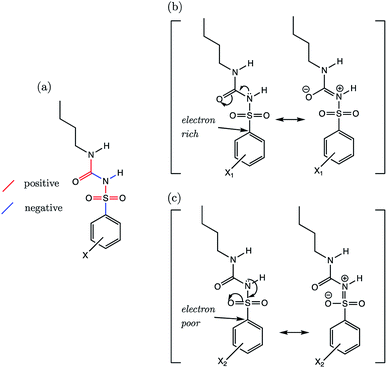
3.6 Models: sulfonylureas (SU)
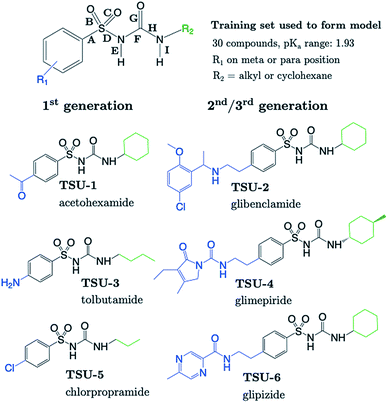
The sulfonylurea group is common to many compounds that have been recognized for their biological activities. These include antihypertensive,47 antineoplastic48 and antibacterial49 drugs, in addition to some compounds that exhibit herbicidal action.50 Notably, sulfonylurea (SU) drugs have been used extensively in the treatment of non-insulin dependent diabetes mellitus. Antidiabetic SU drugs may be broadly classified into first, second or third generation, where second and third generation SU drugs generally require smaller dosage, and provide a longer action than first generation analogues. First generation drugs contain a central phenylsulfonylurea fragment, with a small para-substituent on the phenyl ring. Second and third generation SU drugs have much larger R1 groups (see groups highlighted in blue in Fig. 8). Due to the influence of the carbonyl group, sulfonylureas are more acidic by 2–4 pKa units compared to the primary and secondary sulfonamides discussed in the previous sections.The most recent computational study of sulfonylurea type compounds was carried out by Kasetti et al. in 2010.51 In that work, the authors note that the global minimum conformation of the sulfonylurea fragment, in the gas-phase, contains an N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S hydrogen bond. The existence of this IHB is corroborated by analysis of bond critical point properties (a concept derived from Atoms in Molecules theory and carried out by the program AIM2000). The iminol tautomeric forms of sulfonylureas were also assessed for their stability relative to the amine form, and were found to be ∼21–25 kJ mol−1 higher in energy. Our working hypothesis is that an AIBL-pKa model should emerge from the bond lengths of the lowest energy conformations of the lowest energy tautomeric form of our compounds. Therefore, only the amine tautomer form is considered in the following discussion.
S hydrogen bond. The existence of this IHB is corroborated by analysis of bond critical point properties (a concept derived from Atoms in Molecules theory and carried out by the program AIM2000). The iminol tautomeric forms of sulfonylureas were also assessed for their stability relative to the amine form, and were found to be ∼21–25 kJ mol−1 higher in energy. Our working hypothesis is that an AIBL-pKa model should emerge from the bond lengths of the lowest energy conformations of the lowest energy tautomeric form of our compounds. Therefore, only the amine tautomer form is considered in the following discussion.
The most stable conformation of all 35 compounds of our dataset contain a phenylsulfonylurea fragment, the 3D geometry of which closely resembles that of the optimized structure reported by Kasetti et al. This structure is shown in Fig. S3.† In the following analysis, we use the 6 marketed drug compounds (shown in Fig. 8) as a test set. With the additional data procured from the literature making up the training set (30 compounds, SU-1 to SU-30 as shown in Table S7†), there is a 20/80 split of external test set to training set.
Phenylsulfonylureas are found to have the same active bond length as the Pr-BSA series (S–N), despite the differing chemical environment of the acidic proton (full set of statistics relating to each bond length vs. pKa model is shown in Table S22†). Although the r2 and q2 values for the S–N bond (D) model are only 0.93, the RMSEE is particularly low at 0.14. Notably, a relationship emerges here for the S–N bond lengths despite significant variation in the identity of both the R1 and R2 groups (see Table S7†).
3.7 Predictions: SU drugs
Table 1 shows that four out of six SU drugs were predicted to within 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units from literature experimental values. The largest prediction errors in Table 1 correspond to glipizide and glimepiride. Due to their size and conformational flexibility, a second conformer search (50 input conformers) was carried out to rule out the possibility that the poor prediction accuracy is due to identification of an incorrect global minimum. The most stable arrangement returned by this second conformer search was found to match that of the first. The low-lying geometries of glimepiride have been discussed a number of times in the literature. The general consensus is that in vacuo, a “U-shape” conformation is preferred. However, if hydrogen bonding interactions with a solvent environment were to be modelled explicitly, an “extended” conformation should be favoured. Here, we find that the most stable geometry in both gas and solvent phase (CPCM) is the U-shaped conformation, which at the B3LYP/6-311G(d,p) level, is ∼4 kJ mol−1 more stable than the extended geometry previously identified as most stable by Kasetti.51 Grbic and co-workers have reported52 the most recent experimental pKa value for glimepiride (7.26). In both conformations, the bond length predicts a greater ionization propensity than this value suggests (5.02 for the extended form and 5.58 for U-shaped).
log units from literature experimental values. The largest prediction errors in Table 1 correspond to glipizide and glimepiride. Due to their size and conformational flexibility, a second conformer search (50 input conformers) was carried out to rule out the possibility that the poor prediction accuracy is due to identification of an incorrect global minimum. The most stable arrangement returned by this second conformer search was found to match that of the first. The low-lying geometries of glimepiride have been discussed a number of times in the literature. The general consensus is that in vacuo, a “U-shape” conformation is preferred. However, if hydrogen bonding interactions with a solvent environment were to be modelled explicitly, an “extended” conformation should be favoured. Here, we find that the most stable geometry in both gas and solvent phase (CPCM) is the U-shaped conformation, which at the B3LYP/6-311G(d,p) level, is ∼4 kJ mol−1 more stable than the extended geometry previously identified as most stable by Kasetti.51 Grbic and co-workers have reported52 the most recent experimental pKa value for glimepiride (7.26). In both conformations, the bond length predicts a greater ionization propensity than this value suggests (5.02 for the extended form and 5.58 for U-shaped).
| ID | Drug | r(S–N) | Exp. pKa | AIBL-pKa | AE | Marvin | AE |
|---|---|---|---|---|---|---|---|
| a pKa value measured in this work. All bond lengths for compounds TSU-1 to TSU-6 are given in Table S16 in the ESI. | |||||||
| TSU-1 | Chlorpropamide | 1.68513 | 4.75 (ref. 53) | 4.69 | 0.06 | 4.31 | 0.44 |
| TSU-2 | Carbutamide | 1.69367 | 5.79 (ref. 54) | 5.75 | 0.04 | 4.35 | 1.44 |
| TSU-3 | Acetohexamide | 1.68266 | 4.31 (ref. 54) | 4.39 | 0.08 | 3.33 | 0.98 |
| TSU-4 | Glibenclamide | 1.68980 | 5.22 (ref. 55)/5.30 (ref.56)/6.80 (ref. 56) | 5.27 | 0.05/0.03/1.53 | 4.32 | 0.90/0.98/2.48 |
| TSU-5 | Glipizide | 1.68822 | 5.21a/5.90 (ref.57) | 5.07 | 0.14/0.83 | 4.32 | 0.89/1.58 |
| TSU-6 | Glimepiride | 1.69235 | 5.32a/7.26 (ref. 52)/8.03 (ref. 52) | 5.58 | 0.26/1.68/2.45 | 4.32 | 1.00/2.94/3.71 |
| MAE | 0.10 | 0.94 | |||||
| σ | 0.09 | 0.31 | |||||
| RMSEP | 0.13 | 0.98 | |||||
To investigate the cause of these large prediction errors, pKa values for glimepiride and glipizide were measured once more in this work using the UV-metric method. Measurements were taken in three different methanol concentrations, and pKa values in aqueous conditions were obtained via Yasuda-Shedlovsky extrapolation. The new value for glipizide of 5.21 matches our prediction (5.07) to within 0.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units and the new value for glimepiride matches our prediction to within 0.26
log units and the new value for glimepiride matches our prediction to within 0.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. Given that our prediction and the new measurement are similar, and given that these two values are also close to those of the structurally similar compounds, glipizide and glibenclamide, we are inclined to believe that 5.32 is the most accurate experimental value for glimepiride.
log units. Given that our prediction and the new measurement are similar, and given that these two values are also close to those of the structurally similar compounds, glipizide and glibenclamide, we are inclined to believe that 5.32 is the most accurate experimental value for glimepiride.
There is an important consequence of the substantial correction in pKa value established here. According to the Henderson–Hasselbalch equation, the new pKa value of 5.32 for glimepiride suggests that 99% of molecules are ionized at pH 7.4 (cell pH), whereas the previously reported value of 7.26 suggests that only 58% are ionized. The therapeutic activity of insulin secretagogues like glimepiride is known to stem from their ability to bind to a receptor on the ATP sensitive K+ channels of pancreatic β-cell membranes.58 It is thought that the anionic state of the molecule partakes in this binding activity.59 A higher percentage of molecules existing in their ionized state means that there is a higher percentage that can partake in binding with the receptor to block the channel, which should be linked to greater efficacy of the drug. As glimepiride is currently used in the treatment of diabetes, the lower value that we report is perhaps in better agreement with its known therapeutic effects.
Finally, we note that the use of the S–N bond length of the glimepiride conformer that is likely to be more stable in solution gives a marginally larger error than the most stable gas-phase/CPCM conformation, compared to the new value of 5.32. This perhaps goes against chemical intuition. However, it is pleasing to note that good estimations of pKa may be made without user knowledge of explicitly solvated conformational preference, as is almost always the case in practice.
Table 1 shows that the average prediction accuracy of the Marvin program is inferior to that of AIBL for the same compounds, with all but one of the predictions giving an error of more than 0.5 units. Moreover, the Marvin MAE is 0.94 whereas ours is 0.10. Note that Marvin and AIBL have been compared on an equal footing and allowing for their best performance because, for both, we took the experimental values closest to their respective predictions. The trend of experimental pKa variation across the test set series is compared to AIBL-pKa predictions and Marvin is shown in Fig. S5,† showing that AIBL performs very well in this respect. Roy's criteria for MAE evaluation cannot be applied here because the test set contains less than 10 compounds.
4. Discussion
4.1 Pr-BSA (S1 and TS1)
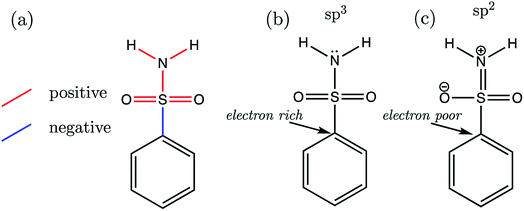
Now that we have presented the results of model construction and validation, we may take this opportunity to analyse the nature of the AIBL-pKa relationships derived here, starting with the Pr-BSA series we label “S1”. Breneman and Weber60 have previously studied the charge and energy redistribution of sulfonamide (HSO2NH2) and fluorosulfonamide (FSO2NH2) molecules as they undergo conformational change. At a modest level of theory [HF/6-31G(d)], the authors analyzed the charge and energy of the sulfur atom and amine group of these two species during rotation around each of their interlinking S–N bond. For fluorosulfonamide, the global minimum geometry is found to be analogous to the one that we label anti in this work (which is used in models and predictions), whereas sulfonamide prefers to adopt the syn conformer. This means that in fluorosulfonamide the lone pair on nitrogen sits adjacent to the S–F σ* antibonding orbital, whereas in sulfonamide the lone pair is syn to the S–H bond, but anti to the vector sum of the S–O bonds.We may build on the work of Breneman and Weber to begin to understand the patterns of bond length variation between our series of congeners. Significantly, the authors note that the S–N bond length of fluorosulfonamide is shorter than that of sulfonamide (at each increment of the rotation). The authors attribute this shortening effect to the increased sp2 character of the fluorosulfonamide amine group compared to that of sulfonamide, which instead has more sp3 character. The authors claim that as the N lone pair is donated towards the sulfur (and partially into the S–F σ* antibonding orbital), this in turn, enhances the electronegativity of the N atom. Subsequently, σ-withdrawal of electron density occurs from the sulfur atom towards the now more electronegative N atom. This hypothesis is in part evidenced by those authors' observation that, in the syn conformation of fluorosulfonamide, the nitrogen of the amino group is at its peak electron population, whereas sulfur is at its most depleted. In the parlance of the authors, the fluorine atom provides a better electron sink, stabilising the anti-conformation in fluorosulfonamide via delocalization of the lone pair on nitrogen into the S–F σ* antibonding orbital. In the absence of the F atom, the sulfonamide system favours the syn-conformation, due to the stabilization afforded by lone pair donation to the S–O σ* antibonding orbitals over the higher energy S–H σ* orbital.
Now we may consider the above rationale in the context of the S1 series, which are most stable in the anti-conformation. The most acidic compound of the set is S1-19 (the 2,3,4,5,6-F5 derivative). In addition to having the lowest pKa value, this compound is found to have the longest C–S (a) bond length and the shortest b–f bond length of the whole series. Fig. 9 illustrates the overall pattern of bond length variation with pKa in terms of positive or negative correlation (shown in red or blue in Fig. 9a and in Table S17†). One interpretation of this variation in bond distances is related to the fact that the ipso carbon of the phenyl group in S1-19 will be more electron-poor compared to the unsubstituted analogue S1-1. It follows that the C–S σ* antibonding orbital would be a better electron sink in S1-19 than in the unsubstituted species S1-1, making rehybridization of the N lone pair more favourable (Fig. 9b to c). Consequently, in line with the above rationale, the S–N bonding distance is shorter in species with more electron-withdrawing substituents due a relative increase in its s character. Greater s character of the sulfonamide N atom then in turn explains why compounds with shorter N–H (e and f) bonds have lower pKa values: enhanced s character suggests that the electrons of the anion lone pair are held closer to the nucleus, thus providing enhanced stabilization to the anionic state.
In accordance with the above hypothesis, the reduction in S–N bond length will be accompanied by an increase in the C–S bond length, as electron density is put into the σ* antibonding orbital, decreasing bond order. Indeed, the C–S bond length vs. pKa plot has a negative slope, showing that congeners with the highest pKa values have the longest CS distances (Fig. 9a).
To add further credence to the link between bond distances and pKa, an Interacting Quantum Atoms (IQA) analysis was performed on the wavefunctions of compounds S1-1, S1-4 and S1-9, representing the unsubstituted species, the most basic (4-NHCH3, pKa = 11.00) and one of the most acidic compounds. Due to the close proximity in space between an ortho substituent and the ionizable group, S1-9 was chosen as the more acidic species over S1-19 in order to restrict substituent effects to those transmitted through bonds of the aromatic ring. The inter-atomic Vcl(A,B) values derived from IQA analysis can be interpreted as a more negative value denoting a more favourable electrostatic interaction. For the three species, S1-1, S1-4 and S1-9, we find that the trend in the magnitude of Vcl(A,B) values mirrors that of the bond lengths, i.e. the lower the pKa, the shorter the bond and the more negative the Vcl(A,B) value is (values are listed in Table S23†). Similarly, the exchange-correlation energy terms Vxc(A,B), which represent the degree of electron delocalization (or covalency) of an interaction, also mirror the trends in bond lengths with pKa (a more negative Vxc(A,B) value corresponds to a shorter bond A–B), except in the case of both sets of Vxc(N,H) values. For both N–H bonds, the extent of electron delocalization decreases between N and H atoms with increased acidity (i.e. absolute value of Vxc(N,H) decreases from 334 kJ mol−1 in S1-4 to 329 kJ mol−1 in S1-9), whilst simultaneously, the electrostatic interaction between N and H atoms increases with acidity (i.e. the absolute value of Vcl(N,H) increases from 206 kJ mol−1 in S1-4 to 228 kJ mol−1 in S1-9). These observations suggest that, as the N atom gains s character in going from sp3 to sp2 hybridization (Fig. 9a and b), there is a decrease in electron delocalization between N and H atoms, which is in line with an increased propensity for N–H cleavage.
4.2 AP-BSA (S2 and TS2)
For the AP-BSA series we can rationalize the variation in bond lengths (shown in Fig. 10a) with pKa by considering the effect of substituent groups on the N-phenyl ring. Firstly, it can be asserted that each substituent will affect the relative propensity of π-donation from the sulfonamide nitrogen into the N-phenyl group, akin to that described earlier for aniline derivatives (Section 3.4). A substituent X causing a decrease in electron density at the ipso carbon of the N-phenyl group promotes conjugation of the sulfonamide nitrogen lone pair into the aromatic ring. This effect is illustrated in Fig. 10b. Therefore, a substituent group causing the ipso carbon of N-phenyl to become more electron-poor will result in a relatively larger contribution from a resonance canonical with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (bond vi in Fig. 6a) double bond character. Whilst the sulfonamide nitrogen lone pair is partaking in conjugation with the N-phenyl ring, there is a lesser contribution from a resonance structure with S
N (bond vi in Fig. 6a) double bond character. Whilst the sulfonamide nitrogen lone pair is partaking in conjugation with the N-phenyl ring, there is a lesser contribution from a resonance structure with S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (iv) bond character, because the lone pair is instead donated towards the SO2 moiety. Substituents on the N-phenyl ring causing the ipso carbon to be electron-rich cause the opposite effects on bonds C
N (iv) bond character, because the lone pair is instead donated towards the SO2 moiety. Substituents on the N-phenyl ring causing the ipso carbon to be electron-rich cause the opposite effects on bonds C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (vi) and S
N (vi) and S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (iv), which is illustrated in Fig. 10c.
N (iv), which is illustrated in Fig. 10c.
Support for the above rationale can be found in the observed increase in the C1–C2–N3–H4 dihedral angle towards 180° (i.e. co-planarity of the N–H moiety with the N-phenyl ring), the more strongly electron-withdrawing the substituents are and the lower the pKa. The variation in this torsional angle can be explained by an increase in sp2 character of the sulfonamide nitrogen as the lone pair is conjugated with the π-system, towards a quinoid-type resonance structure (Fig. 10b).
4.3 SU and TSU
By reducing the set to only the 18 n-butyl derivatives (SU-1 to SU-18), we can restrict the variation in substituent effects to the phenyl group. In doing so, r2 values of all AIBL-pKa models (except for N–H aka (I)) lie above 0.8, demonstrative of a good linear fit (shown in Table S24†). For the sulfonylurea group, the direction of variation of C–S (A), S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (B), S
O (B), S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (C), and S–N (D) bond distances (Fig. 11a) with aqueous pKa values mirrors that of the analogous bonds found in the primary benzene sulfonamide series S1 (Fig. 9a).
O (C), and S–N (D) bond distances (Fig. 11a) with aqueous pKa values mirrors that of the analogous bonds found in the primary benzene sulfonamide series S1 (Fig. 9a).
Using a similar rationale as for the benzene sulfonamides, we can assert that when the substituent X on the Ph group makes the ipso carbon electron-rich, the C–S σ* antibonding orbital a worse electron sink (Fig. 11b). When the X substituent on the Ph group causes the ipso carbon becomes electron-poor (Fig. 11c), it becomes more stabilising to put electron density into the C–S σ* antibonding orbital, and thus it is a better electron sink. In this latter case, the shortening effect on the S–N bond and the lengthening of the C–S bond would be enhanced. However, with a more electron-rich sulfur, the lone pair on nitrogen can instead be delocalized across the N–C (F) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (G) bonds of the urea fragment. This direction of delocalization being favoured would explain why in the most basic compound of the series (SU-5, 4-NMe2, pKa = 5.85), which contains a good π-electron donating group, the C–S (A) and N–C (F) bonds are also the shortest. The C
O (G) bonds of the urea fragment. This direction of delocalization being favoured would explain why in the most basic compound of the series (SU-5, 4-NMe2, pKa = 5.85), which contains a good π-electron donating group, the C–S (A) and N–C (F) bonds are also the shortest. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (G) of the urea moiety in SU-5 is also the longest, suggestive of a situation similar to that shown in Fig. 10b.
O bond (G) of the urea moiety in SU-5 is also the longest, suggestive of a situation similar to that shown in Fig. 10b.
5. Conclusions
We have demonstrated for the first time that highly correlated linear relationships exist between equilibrium bond lengths and aqueous pKa values for three pharmaceutically relevant variants of the sulfonamide group. For primary benzene sulfonamides, the active bond, i.e. the bonding distance that shows the strongest linear relationship with pKa, is the S–N bond (r2 = 0.95, q2 = 0.94 and RMSEE = 0.14), where N is the site of ionization. For the secondary sulfonamide groups of 4-amino-N-phenylbenzenesulfonamides, the C–S bond lengths can be used to predict the pKa (r2 = 0.96, q2 = 0.95 and RMSEE = 0.23). Finally, for phenylsulfonylureas, the S–N bond adjacent to the site of ionization is most highly correlated (r2 = 0.93, q2 = 0.93 and RMSEE = 0.14).For the first time in the context of the AIBL approach, we have also proposed rationales for bond length variation in the presence of substituent groups, and why this may be related to their propensity to ionize.
A significant feature of the work is that we have shown that the AIBL approach may be applied to predict pKa values of compounds with more than one ionizable group. This feat is achieved by optimization of the compound with the pKa(1) site in its dissociated, anionic state. Prediction accuracy is found to be optimized by adding diffuse functions to non-hydrogen atoms [6-311+G(d,p)]. In our workflow, quantum chemical calculations are performed on only the relevant microstate, yet the average absolute error on our predictions is 0.16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. The overall accuracy of the AIBL predictions presented here is found to be superior to that provided by Marvin for the same series of compounds.
log units. The overall accuracy of the AIBL predictions presented here is found to be superior to that provided by Marvin for the same series of compounds.
Finally, we have corrected the experimental aqueous pKa values of three drug compounds: celecoxib, glimepiride and glipizide. For celecoxib, our model predicted a value of 9.72 for the sulfonamide group, which is lower by 1.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units than the widely quoted literature value of 11.1. The pKa was measured once more in this work, which returned a value only 0.2 pH units away from our predicted value (9.52). Furthermore, our prediction of 5.58 for glimepiride was corroborated by a new experimental value of 5.32. Both of these new glimepiride pKa values suggest that a significantly higher proportion of molecules exist in their anionic state at pH 7.4 than is suggested by the previously reported value (7.26). The pKa value of glipizide was also re-measured, and the new value of 5.21 was found to be closer to our predicted value of 5.07 than the existing literature value (5.90). Moreover, glimepiride and glipizide both contain more than 50 atoms, which would invoke significant CPU time in a conventional first-principles workflow. However, we perform a quantum chemical calculation on only the neutral species, and arrive at accurate predictions despite the significant size and complexity of these compounds.
log units than the widely quoted literature value of 11.1. The pKa was measured once more in this work, which returned a value only 0.2 pH units away from our predicted value (9.52). Furthermore, our prediction of 5.58 for glimepiride was corroborated by a new experimental value of 5.32. Both of these new glimepiride pKa values suggest that a significantly higher proportion of molecules exist in their anionic state at pH 7.4 than is suggested by the previously reported value (7.26). The pKa value of glipizide was also re-measured, and the new value of 5.21 was found to be closer to our predicted value of 5.07 than the existing literature value (5.90). Moreover, glimepiride and glipizide both contain more than 50 atoms, which would invoke significant CPU time in a conventional first-principles workflow. However, we perform a quantum chemical calculation on only the neutral species, and arrive at accurate predictions despite the significant size and complexity of these compounds.
In the lead optimization process of drug discovery, we propose that AIBL can serve as a highly accurate estimator of pKa variation for various series of analogues generated for an active scaffold. Furthermore, the AIBL-pKa approach can be used to check the consistency of a group of pKa measurements, and can therefore serve as a rectifier for experimental outliers.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
P. L. A. P. thanks the EPSRC for Fellowship funding (EP/K005472) while P. L. A. P and B. A. C. thank the BBSRC for funding her PhD studentship under the “iCASE” award BB/L016788/1 (with a contribution from Syngenta Ltd) and for funding a subsequent postdoc with Impact Acceleration funding (IAA_105) (with a contribution of Lhasa Ltd).References
- E. Hansen, E. Limé, P.-O. Norrby and O. Wiest, J. Phys. Chem. A, 2016, 120, 3677–3682 CrossRef CAS PubMed.
- H.-X. Dai, A. F. Stepan, M. S. Plummer, Y.-H. Zhang and J.-Q. Yu, J. Am. Chem. Soc., 2011, 133, 7222–7228 CrossRef CAS PubMed.
- S. Z. Fisher, M. Aggarwal, A. Y. Kovalevsky, D. N. Silverman and R. McKenna, J. Am. Chem. Soc., 2012, 134, 14726–14729 CrossRef CAS PubMed.
- T. Saha, M. S. Hossain, D. Saha, M. Lahiri and P. Talukdar, J. Am. Chem. Soc., 2016, 138, 7558–7567 CrossRef CAS PubMed.
- T. Uehara, Y. Minoshima, K. Sagane, N. H. Sugi, K. O. Mitsuhashi, N. Yamamoto, H. Kamiyama, K. Takahashi, Y. Kotake, M. Uesugi, A. Yokoi, A. Inoue, T. Yoshida, M. Mabuchi, A. Tanaka and T. Owa, Nat. Chem. Biol., 2017, 13, 675–680 CrossRef CAS.
- P. Beck, M. Reboud-Ravaux and M. Groll, Angew. Chem., Int. Ed., 2015, 54, 11275–11278 CrossRef CAS PubMed.
- Y. Chen, P. R. D. Murray, A. T. Davies and M. C. Willis, J. Am. Chem. Soc., 2018, 140, 8781–8787 CrossRef CAS PubMed.
- J. R. DeBergh, N. Niljianskul and S. L. Buchwald, J. Am. Chem. Soc., 2013, 135, 10638–10641 CrossRef CAS PubMed.
- F. Shi, M. K. Tse, S. Zhou, M.-M. Pohl, J. Radnik, S. Hübner, K. Jähnisch, A. Brücker and M. Beller, J. Am. Chem. Soc., 2009, 131, 1775–1779 CrossRef CAS PubMed.
- A. B. A. Boxall, P. Blackwell, R. Cavallo, P. Kay and J. Tolls, Toxicol. Lett., 2002, 131, 19–28 CrossRef CAS.
- Y. Hu, X. Yan, Y. Shen, M. Di and J. Wang, Ecotoxicol. Environ. Saf., 2018, 157, 150–158 CrossRef CAS PubMed.
- X. Hu, Q. Zhou and Y. Luo, Environ. Pollut., 2010, 158, 2992–2998 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, M. Diedenhofen and M. E. Beck, J. Phys. Chem. A, 2003, 107, 9380–9386 CrossRef CAS.
- H. Lu, X. Chen and C. G. Zhan, J. Phys. Chem. B, 2007, 111, 10599–10605 CrossRef CAS PubMed.
- S. Zhang, J. Baker and P. Pulay, J. Phys. Chem. A, 2010, 114, 425–431 CrossRef CAS PubMed.
- F. Eckert, M. Diedenhofen and A. Klamt, Molecular Physics, 2010, 108, 229–241 CrossRef CAS.
- J. Ho and M. L. Coote, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 649–660 CAS.
- J. Jensen, C. J. Swain and L. Olsen, J. Phys. Chem. A, 2017, 121, 699–707 CrossRef CAS.
- A. D. Bochevarov, M. A. Watson and J. R. Greenwood, J. Chem. Theory Comput., 2016, 12, 6001–6019 CrossRef.
- D. M. Philipp, M. A. Watson, H. S. Yu, T. B. Steinbrecher and A. D. Bochevarov, Int. J. Quantum Chem., 2017, 118, 1–8 Search PubMed.
- MARVIN, http://www.chemaxon.com Search PubMed.
- Epik, http://www.schrodinger.com Search PubMed.
- ACD Labs, https://www.acdlabs.com Search PubMed.
- M. Li, H. Zhang, B. Chen, Y. Wu and L. Guan, Sci. Rep., 2018, 8, 3991 CrossRef PubMed.
- M. Goodarzi, M. P. Freitas, C. H. Wu and P. R. Duchowicz, Chemom. Intell. Lab. Syst., 2010, 101, 102–109 CrossRef CAS.
- Y. Connolly Martin, Drug Discovery Today: Technologies, 2018 Search PubMed.
- Y. Connolly Martin, J. Comput.-Aided Mol. Des., 2009, 23, 693–704 CrossRef PubMed.
- A. P. Harding and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2011, 13, 11264–11282 RSC.
- I. Alkorta, M. Z. Griffiths and P. L. A. Popelier, J. Phys. Org. Chem., 2013, 26, 791–796 CrossRef CAS.
- M. Z. Griffiths, I. Alkorta and P. L. A. Popelier, Mol. Inf., 2013, 32, 363–376 CrossRef CAS.
- C. Anstöter, B. A. Caine and P. L. A. Popelier, J. Chem. Inf. Model., 2016, 56, 471–483 CrossRef.
- C. Dardonville, B. A. Caine, M. N. de la Fuente, G. M. Herranz, B. C. Mariblanca and P. L. A. Popelier, New J. Chem., 2017, 41, 11016–11028 RSC.
- B. A. Caine, C. Dardonville and P. L. A. Popelier, ACS Omega, 2018, 3, 3835–3850 CrossRef CAS.
- SIMCA-P 10.0, UMETRICS, Umeå, Sweden, 2002 Search PubMed.
- K. Roy, R. N. Das, P. Ambure and R. B. Aher, Chemom. Intell. Lab. Syst., 2016, 152, 18–33 CrossRef CAS.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- M. Remko and C.-W. von der Lieth, Bioorg. Med. Chem., 2004, 12, 5395–5403 CrossRef CAS PubMed.
- M. Remko, J. Mol. Struct.: THEOCHEM, 2010, 944, 34–42 CrossRef CAS.
- V. Petrov, V. Petrova, G. V. Girichev, H. Oberhammer, N. I. Giricheva and S. Ivanov, J. Org. Chem., 2006, 71, 2952–2956 CrossRef CAS PubMed.
- S. K. Paulson, M. B. Vaughn, S. M. Jessen, Y. Lawal, C. J. Gresk, B. Yan, T. J. Maziasz, C. S. Cook and A. Karim, J. Pharmacol. Exp. Ther., 2001, 297, 638–645 CAS.
- S. Goto, Y. Odawara, M. Nakano and Y. Araki, Yakugaku Zasshi, 1978, 98, 236–241 CrossRef CAS.
- T. Takayangi, M. Isoda, D. Itoh and H. Mizuguchi, Bunseki Kagaku, 2017, 99, 509–514 CrossRef.
- B. Song, A. K. Galande, K. Kodukula, W. H. Moos and S. M. Miller, Drug Dev. Res., 2011, 72, 416–426 CrossRef CAS.
- H. Wan, A. G. Holman, Y. Wang, W. Lindberg, M. Englund, M. B. Nagard and R. A. Thompson, Rapid Commun. Mass Spectrom., 2003, 17, 2639–2648 CrossRef CAS PubMed.
- M. Manderscheid and T. Eichinger, J. Chromatogr. Sci., 2003, 41, 323–326 CAS.
- S. S. Chourasiya, D. R. Patel, C. M. Nagaraja, A. K. Chakraborti and P. V. Bharatam, New J. Chem., 2017, 41, 8118–8129 RSC.
- P. Deprez, B. Heckmann and A. Corbier, Bioorg. Med. Chem. Lett., 1995, 5, 2605–2610 CrossRef CAS.
- F. Mohamadi, M. M. Spees and G. B. Grindey, J. Med. Chem., 1992, 35, 3012–3016 CrossRef CAS.
- J. Wang, Y. Xiao, Y. Li, Y. Ma and Z. Li, Bioorg. Med. Chem., 2007, 15, 374–380 CrossRef CAS PubMed.
- R. A. LaRossa and J. V. Schloss, J. Biol. Chem., 1984, 259, 8753–8757 CAS.
- Y. Kasetti, N. K. Patel, S. Sundriyal and P. V. Bharatam, J. Phys. Chem. B, 2010, 114, 11603–11611 CrossRef CAS PubMed.
- S. Grbic, J. Parojcic, A. Malenovic, Z. Djuric and M. Maksimovic, J. Chem. Eng. Data, 2010, 55, 1368–1371 CrossRef CAS.
- S. Asada, R. Fujita and Y. Shirakura, Yakugaku Zasshi, 1974, 94, 80–87 CrossRef CAS.
- S. Asada, T. Nakasato and S. Takino, Yakugaku Zasshi, 1973, 93, 1647–1654 CrossRef CAS.
- H. Wan, A. G. Holman, Y. Wang, W. Lindberg, M. Englund, M. B. Nagard and R. A. Thompson, Rapid Commun. Mass Spectrom., 2003, 17, 2639–2648 CrossRef CAS PubMed.
- P. Hadju, K. F. Kohler, F. H. Schmidt and H. Spingler, Arzneim. Forsch., 1969, 19, 1381–1386 Search PubMed.
- R. J. Prankerd, in Profiles of Drug Substances, Excipients, and Related Methodology, ed. H. Brittain, Elsevier, 2007, vol. 33 Search PubMed.
- M. Schwanstecher, C. Schwanstecher, C. Dickel, F. Chudziak, A. Moshiri and U. Panten, Br. J. Pharmacol., 1994, 113, 903–911 CrossRef CAS.
- U. Quast, D. Stephan, S. Bieger and U. Russ, Diabetes, 2004, 53(suppl 3), S156–S164 CrossRef CAS PubMed.
- C. M. Breneman and L. W. Weber, Can. J. Chem., 1996, 74, 1271–1282 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01818b |
| This journal is © The Royal Society of Chemistry 2019 |