Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A d10 Ag(I) amine–borane σ-complex and comparison with a d8 Rh(I) analogue: structures on the η1 to η2:η2 continuum†
Alice
Johnson
 a,
Antonio J.
Martínez-Martínez
a,
Antonio J.
Martínez-Martínez
 a,
Stuart A.
Macgregor
a,
Stuart A.
Macgregor
 *b and
Andrew S.
Weller
*b and
Andrew S.
Weller
 *a
*a
aChemistry Research Laboratories, Department of Chemistry, University of Oxford, Oxford, OX1 3TA, UK. E-mail: andrew.weller@chem.ox.ac.uk
bInstitute of Chemical Sciences, Heriot Watt University, Edinburgh EH14 4AS, UK. E-mail: S.A.Macgregor@hw.ac.uk
First published on 23rd April 2019
Abstract
H3B·NMe3 σ-complexes of d8 [(L1)Rh][BArF4] and d10 [(L1)Ag][BArF4] (where L1 = 2,6-bis-[1-(2,6-diisopropylphenylimino)ethyl]pyridine) have been prepared and structurally characterised. Analysis of the molecular and electronic structures reveal important but subtle differences in the nature of the bonding in these σ-complexes, which differ only by the identity of the metal centre and the d-electron count. With Rh the amine–borane binds in an η2:η2 fashion, whereas at Ag the unsymmetrical {Ag⋯H3B·NMe3} unit suggests a structure lying between the η2:η2 and η1 extremes.
Introduction
Transition metal σ-complexes, in which an E–H bond (e.g., E = H, B, C, Si) binds with a metal centre through a 3-centre 2-electron interaction, are of fundamental interest due to their central role in E–H activation.1 For example, amine–borane σ-complexes,2 exemplified by [M]⋯H3B·NRH2 (Fig. 1), are key intermediates in the catalytic dehydropolymerisation of amine–boranes that leads to the formation of B–N polymeric materials,3–5 B–B coupling6 or hydroboration reactions.7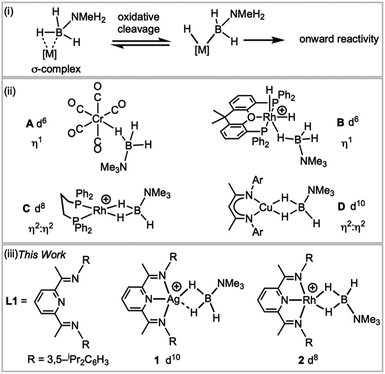 | ||
| Fig. 1 (i) H–B activation; (ii) examples of σ-amine–borane complexes, (iii) complexes reported in this work. [BArF4]− anions are not shown. | ||
H3B·NMe3 is often used as a model substrate for such processes as it provides insight into the initial binding step of the amine–borane, there being no protic N–H available for onward reaction. Transition metal σ-complexes of H3B·NMe3 have been reported across the transition metal series,5e.g. for group 6 (A),2 7,8 8 (ref. 9) and 9 (B, C).6,10 Both η1 and η2:η2 binding modes of H3B·NMe3 have been observed, depending on the steric and electronic demands of the metal, Fig. 1(ii), and the principal bonding interaction can be described by σ-donation from the B–H bond into an empty metal d orbital.2 Recently the isolation of the first H3B·NMe3 σ-complex of a group 11 metal was reported, the d10 Cu(I) complex D, with a η2:η2-bound H3B·NMe3. Analysis of the bonding showed that the bent {CuL2} fragment presents a LUMO largely of 4s character that receives electron density from the B–H bonds, while back bonding was negligible.11,12 This is a relatively rare example a coinage metal13–17 that shows close interactions with E–H bonds.
We report here a straightforward route to a H3B·NMe3 σ-complex of the coinage metal Ag(I), complex 1Fig. 1(iii), that is supported by the pincer ligand 2,6-bis-[1-(2,6-diisopropylphenylimino)-ethyl]pyridine, L1. Such highly tuneable ligands have been used, for example, with Fe and Co centres in olefin polymerisation catalysis.18,19 They also support the generation of latent low coordinate Ag(I) complexes, e.g. (L)AgOTf (OTf = triflate), that coordinate arenes;20,21 while (L)RhCl have been used as precursors for nanoparticle dehalogenation catalysts22 (L = 2,6-bis-[1-(2,6-R-phenylimino)ethyl]pyridine). The synthesis of a directly analogous σ-complex of Rh(I), 2, is also reported here. This offers a rare opportunity to directly compare the structures, bonding and NMR spectroscopic reporters for mono-cationic d8 and d10 σ-complexes in systems where only the identity of the metal is changed.
Results and discussion
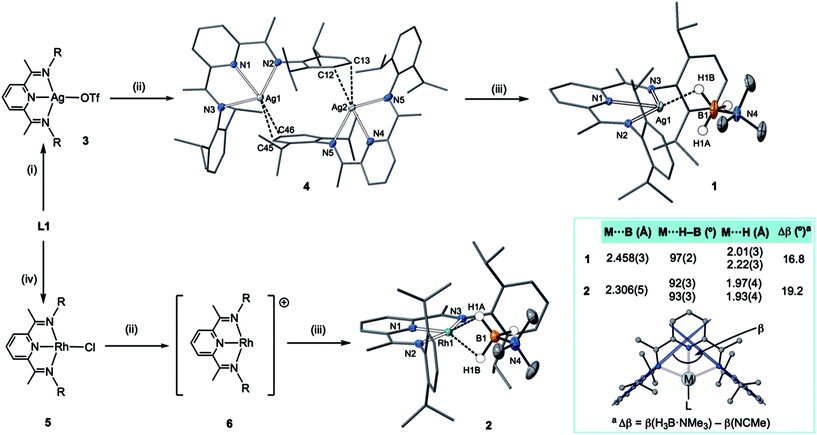
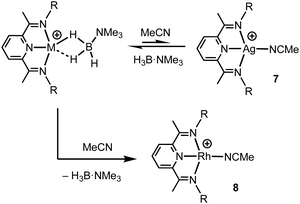
An appropriate operationally unsaturated precursor for the synthesis of a H3B·NMe3 adduct of Ag(I) is the arene-bridged dimeric complex [(L1)Ag]2[BArF4]2, 4 (Scheme 1), which comes from addition of Na[BArF4] to (L1)AgOTf, 3, itself prepared by addition of Ag[OTf] to free L1. The synthesis and structure of monomeric complex 3 is detailed in the ESI.†In the solid-state complex 4 is a solvent-free, weakly associated dimer, which approaches coordinative saturation through η2 interactions with the aryl groups on a neighbouring ligand. There is no crystallographically imposed symmetry. The Ag⋯arene distances suggest a weak interaction [Ag⋯C 2.439(6)–2.623(6) Å]. They are comparable, but generally longer, than distances found in a Ag(I)–N-heterocyclic carbene arene-bridged dimer [2.444(4), 2.348(4) Å],23 or [(L)Ag(η2-toluene)][OTf] [2.464(7) Å].20 The appearance of a very simple 1H NMR spectrum for 4 as signalled by a single iPr-environment even at 183 K (CD2Cl2), suggests these weak silver–arene interactions are not retained in solution, or at the very least the molecule is highly fluxional, as the solid-state structure (even allowing for time-averaged C2 symmetry) would be expected to show 4 different iPr groups. DOSY (Diffusion-Ordered Spectroscopy) experiments determined the diffusion coefficients for complexes 3 and 4 in CD2Cl2 to be very similar (1.166 ± 0.014 × 10−9 m2 s−1 for 3 and 1.126 ± 0.013 × 10−9 m2 s−1 for 4), suggesting 4 is a monomer in solution, likely a CD2Cl2 adduct similar to that observed for a Ag(I)–N-heterocyclic carbene complex reported by Rivard and co-workers.23 Consistent with this latent coordinative unsaturation, addition of one equivalent (per Ag) of H3B·NMe3 to 4 gave the air- and light-stable, bright yellow σ-complex [(L1)Ag(H3B·NMe3)][BArF4], 1, isolated in 98% yield. Similarly, addition of one equivalent of Na[BArF4]24 to (L1)RhCl 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 in CH2Cl2 affords the known latent-coordinatively unsaturated 6,26 which also likely exists as an adduct in CH2Cl2 solution,27 that forms a σ-complex [(L1)Rh(H3B·NMe3)][BArF4] 2 with H3B·NMe3, which can be isolated as a dark green solid (79% yield).
25 in CH2Cl2 affords the known latent-coordinatively unsaturated 6,26 which also likely exists as an adduct in CH2Cl2 solution,27 that forms a σ-complex [(L1)Rh(H3B·NMe3)][BArF4] 2 with H3B·NMe3, which can be isolated as a dark green solid (79% yield).
The molecular structures of 1 and 2 were determined by single crystal X-ray diffraction (Scheme 1). For both, the high quality of the data allowed for the BH3 hydrogens to be located and freely refined. The different electron configurations of the d8 Rh(I) and d10 Ag(I) centres lead to subtle differences in the coordination geometry about each metal centre. In both cases a κ3-binding of L1 is observed, albeit with considerably longer Ag–N distances [2.3737(13)–2.4306(13) Å] than Rh–N [1.910(2)–2.061(2) Å], even taking into account the small difference in covalent radii (Rh, 1.42; Ag, 1.45 Å). This may simply reflect a weaker binding of Ag compared to Rh.
Turning to the interaction of the borane with the metal centre, in complex 1 the Ag⋯B distance [2.458(3) Å] is comparable to other Ag⋯H–B interactions, e.g. Ag(PPh3)(CB11H12) [2.504(3) Å].28 One B–H is closer to Ag (H1B), but the other (H1A) is not much further removed [2.01(2) and 2.22(3) Å respectively], while the M⋯H(1B)–B angle is rather open [97(2)°]. The bonding in 1 therefore appears to approach η2:η2, i.e. the limiting structure found for D, as η1 coordination of the B–H bond would be expected to give a much wider angle and longer M⋯B distance.13 For complex 2 the H3B·NMe3 ligand clearly adopts a more symmetrical η2:η2 binding mode, with a corresponding shorter Rh⋯B distance [2.306(5) Å], equivalent M⋯H–B angles, and M⋯H distances that are the same. While the Rh⋯B distance is long compared to other amine–borane σ-complexes of Rh(I) that show η2:η2 binding, e.g.C [2.199(3) Å], it is shorter than found for η1 binding, e.g.B [2.759(6) Å].6 This lengthening may be due to the steric effects with flanking {iPr2C6H3} groups. To measure such effects, in a self-consistent manner, we have prepared and structurally characterised (ESI†) the corresponding MeCN adducts (Scheme 2), [(L1)Ag(NCMe)][BArF4], 7, and [(L1)Rh(NCMe)][BArF4], 8, by addition of 100 equivalents or one equivalent of MeCN respectively to the corresponding amine–borane complexes.29 The linear nitrile offers a minimal steric profile and thus baselines the metal–ligand geometry, and in particular the angle formed between the two planes that the aryl rings define (β), Scheme 1 inset. Coordination of the amine–borane results in the aryl groups moving apart, and this is measured as Δβ between the two structures. That this is slightly larger for complex 2 compared with 1 [19.2° versus 16.8°] confirms the greater steric pressure in the more strongly bound Rh-complex. Interestingly, the local coordination environment around Rh, with the σ-amine–borane {H2B} motif sitting orthogonal to the ligand plane is reminiscent of the bonding mode calculated for the closely related, but much less stable, σ-methane complex [Rh(PONOP)(H2CH2)][BArF4] [PONOP = κ3-2,6-(tBu2PO)2C5H3N],30 although in this case an η2-structure is slightly favoured over the symmetric η2:η2 motif.
These subtle structural differences are carried over into the solution NMR data. For 1 the BH3 group is observed as a singlet at δ 1.82 in the 298 K 1H{11B} NMR spectrum (CD2Cl2), shifted slightly downfield compared to the free ligand [δ 1.64] (Scheme 3). At 183 K this separates into a broad doublet due to coupling to 107/109Ag [J(AgH) = 41 Hz], confirmed by measurement at two different spectrometer frequencies, alongside a temperature-induced chemical shift. This signal did not resolve into terminal and coordinated B–H resonances, suggesting a low energy exchange, even at 183 K. The loss of coupling at higher temperature suggests an exchange process that involves rapid and reversible H3B·NMe3 decoordination. In the 11B NMR spectrum the amine–borane is observed as a broad quartet at δ −16.3, shifted upfield compared to free H3B·NMe3 in CD2Cl2 [δ −8.3, Δδ –8]. The NMR data for complex 2 are subtly different. The BH3 group is observed as a doublet at δ −1.37 [J(RhH) = 15.1 Hz] in the 298 K 1H{11B} NMR spectrum. This coupling constant does not change upon lowering the temperature to 183 K, indicative of both fast exchange and a process that retains the borane bound with the metal centre. We propose a hemilabile η2:η2–η1–η2:η2 fluxional process, as has been calculated31 in related systems. The 11B NMR signal for complex 2 shows a broad singlet at δ −4.2, now shifted downfield compared to free H3B·NMe3, Δδ +4.1.
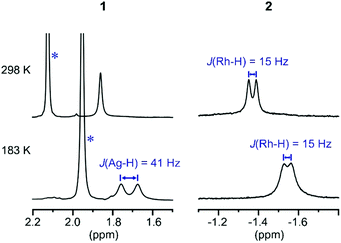 | ||
| Scheme 3 1H{11B} NMR spectra of the H3B·NMe3 region of complexes 1 and 2 at 298 K and 183 K (CD2Cl2). * Mark signals due to NMe3 groups. | ||
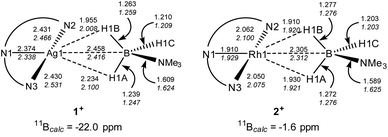
DFT calculations32 have been employed to assess the different M⋯H3B·NMe3 interactions in 1+ and 2+, the cations of 1 and 2 respectively. Optimised geometries (Scheme 4) reproduce the more symmetric structure of 2+ compared to the Ag⋯H3B·NMe3 moiety in 1+. The calculations also highlight subtle changes in the B–H bond distances, in particular a lengthening of the B1–H1A and B1–H1B bonds in 2+ (both 1.276 Å) relative to the shorter distance computed for the non-interacting B1–H1C bond (1.203 Å). In 1+ the B–H distances follow the trend B1–H1B (1.263 Å) > B1–H1A (1.239 Å) > B1–H1C (1.210 Å) suggesting that B1–H1B and B1–H1A both interact with the Ag centre, albeit to a different extent. 11B chemical shifts of δ−22.0 and δ−1.6 were computed for 1+ and 2+ respectively, and compare with δ−11.7 calculated for free H3B·NMe3 [Δδ –10.3 and +10.1 respectively]. Thus the experimental trend is reproduced, although the shifts relative to H3B·NMe3 are over-estimated in the calculations.
The fully optimised structures provided generally good agreement with the experimentally-determined metrics, but do over-estimate the M⋯B1 and M–N distances. One of us33 and others34 have shown that geometries computed for isolated molecular species can deviate significantly from experimental structures derived from X-ray crystallography, especially where weak intramolecular interactions are at play in defining the observed geometry. Therefore, electronic structure analyses were based on geometries in which the heavy atoms were fixed in the positions determined experimentally with only the H atom positions being optimised. These structures (data in plain text, Scheme 4) show the same geometric trends for the B–H and M⋯H distances as the fully optimised structures, although the Ag⋯H3B·NMe3 unit is somewhat more symmetrical than before. These structures were then analysed with Quantum Theory of Atoms in Molecules (QTAIM),35 Natural Bond Orbital (NBO)36 and Non-Covalent Interaction Plots (NCIPlots).37
Details of the QTAIM molecular graphs for 1+ and 2+ are shown in Scheme 5. The asymmetry of 1+ is highlighted by the appearance of the single Ag1–H1B bond path. Accordingly, the B1–H1B Bond Critical Point (BCP) shows a reduced electron density, ρ(r), indicative of donation to the Ag centre. However, ρ(r) for the B1–H1A BCP is also lower than that for B1–H1C and this, along with the rather flat electron density topology between Ag1 and H1A, suggests a weak interaction may be present. For 2+ the symmetrical Rh⋯H3B·NMe3 interaction is reflected in two similar bond paths, Rh1–H1B and Rh1–H1A, which encircle a Ring Critical Point (RCP). ρ(r) values for the associated BCPs are similar to the Ag1–H1B BCP in 1+, although the higher values of ρ(r) associated with the Rh system suggest a stronger M⋯H3B·NMe3 interaction in that case.
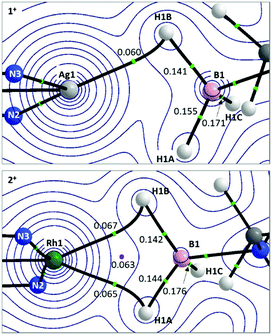 | ||
| Scheme 5 Details from the QTAIM molecular graphs for 1+ (top) and 2+ (bottom), focussing on the M⋯H3B·NMe3 regions. Contours are plotted in the M–H1B–H1A plane with selected atoms, bond paths and critical points lying above or below this plane being cloaked for clarity. Values of ρ(r), the electron densities at selected BCPs (green circles) and RCPs (pink circles) are shown e Å−3. Full molecular graphs and Laplacian contour plots are available in the ESI.† | ||
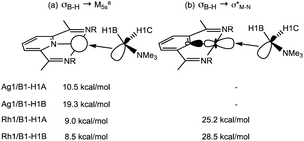
NBO calculations on 1+ highlight the Ag 5s orbital as the key acceptor in the Ag⋯H3B·NMe3 interaction, with donation from both σ-orbitals associated with B1–H1A and B1–H1B (Scheme 6). Quantifying these through the 2nd order perturbation analysis confirms the latter donates more strongly (ΔE(2) = 19.3 kcal mol−1) but that donation from B1–H1A is also significant (ΔE(2) = 10.5 kcal mol−1). For 2+ the d8 electron count means a second low-lying acceptor becomes available in the form of the Rh1–N1 σ* orbital, whereas the equivalent orbital for the d10 Ag+ complex is filled. Donation into the Rh1–N1 σ* orbital now dominates in 2+ and occurs to a similar extent (ca. 27 kcal mol−1) from both B1–H1A and B1–H1B. These interactions are reinforced by weaker donation into the predominantly Rh 5s acceptor orbital (ca. 9 kcal mol−1). The total donation is therefore approximately twice that computed for the Ag ← H1B–B1 interaction. In neither cation is there evidence for any significant M → H3B·NMe3 back donation, as noted previously.2
Scheme 7 shows two views of the NCIPlots for both 1+ and 2+. These plots highlight regions of weak interactions and are colour-coded from blue (most stabilising) through green (weakly stabilising) to red (most destabilising). Considering the Rh cation first, the broad blue region between Rh1 and the H3B·NMe3 ligand indicates an area of significant stabilisation that runs approximately parallel to the H1A–B1–H1B bonds. When viewed down the B1⋯Rh1 axis (Scheme 7(iv)) a strong blue-red alternation is seen. Red regions flag up areas of destabilising charge depletion that are often associated with ring critical points (for example the red disks within the three rings of the L1Rh moiety). In this case the QTAIM study revealed a single RCP between Rh1 and B1 (Scheme 5), however, we have previously argued that the alternating blue–red-blue pattern indicates a stabilising interaction between a metal centre (here Rh1) and both centres of a σ-bond (here B1–H1A and B1–H1B).38 This pattern is therefore consistent with the H3B·NMe3 adopting an η2:η2 binding mode in 2+.
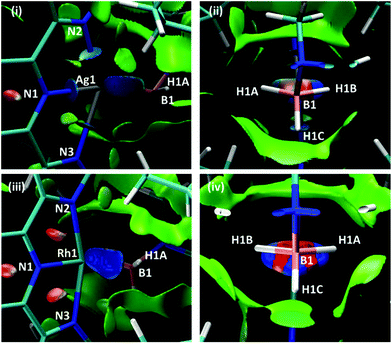 | ||
| Scheme 7 NCIPlots for 1+ and 2+ viewed from (i)/(iii) above the pyridine ring and (ii)/(iv) down the B1⋯M1 axis; isosurfaces are generated for s = 0.3 au and −0.07 < ρ < 0.07 au. | ||
For 1+ the NCIPlot displays a similarly shaped region between the Ag centre and the H3B·NMe3 ligand and the blue–red–blue alternation in Scheme 7(ii) suggests a similar Ag ← H1B–B1 interaction to those seen above with Rh. More asymmetry is again seen for the Ag⋯H3B·NMe3 interaction, especially in the lighter turquoise region between Ag1 and H1A and the less intense red associated with the B1–H1A bond when viewed down the Ag⋯B1 axis (Scheme 7(ii)). Thus, the Ag⋯H3B·NMe3 interaction is intermediate between the η2:η2 geometry seen for 2+ and the η1 geometry proposed for species of type A and B in Fig. 1. This study also highlights the nuanced interpretation of the electron density topology that is available through the NCIPlot approach.39,40 The NCIPlot outcomes are also entirely consistent with the continuum of bond interactions that emerge from the NBO analyses.
Conclusions
By selecting a ligand framework, L1, that supports latent low coordinate complexes of Rh and Ag, the structures of, and bonding in, d8 and d10 σ-amine borane complexes can be directly compared empirically and using computational methods. The d8-Rh(I) metal centre, which has access to an additional d-based unoccupied orbital compared with Ag(I), binds H3B·NMe3 more strongly, as evidenced by: (i) a more definitive η2:η2 M⋯H2B coordination motif, (ii) a significantly shorter M⋯B distance, (iii) a non-dissociative process for H3B·NMe3 fluxionality, (iv) stronger M⋯H3B interactions as measured by QTAIM and NBO analysis and (v) NCIPlots that highlight the more symmetric and stronger σ-bonding in the Rh-analogue. The coherence of all of these experimental and computational observations underscores the importance of deploying multiple analytical methodologies when studying this important class of complex.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EPSRC EP/M024210/1 and SCG Chemicals Co. Ltd. Dr Nicholas Rees for DOSY experiments.Notes and references
- R. N. Perutz and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2007, 46, 2578–2592 CrossRef CAS PubMed.
- M. Shimoi, S.-i. Nagai, M. Ichikawa, Y. Kawano, K. Katoh, M. Uruichi and H. Ogino, J. Am. Chem. Soc., 1999, 121, 11704–11712 CrossRef CAS.
- E. M. Leitao, T. Jurca and I. Manners, Nat. Chem., 2013, 5, 817 CrossRef CAS PubMed.
- A. L. Colebatch and A. S. Weller, Chem. – Eur. J., 2019, 25, 1379–1390 CrossRef CAS PubMed.
- D. Han, F. Anke, M. Trose and T. Beweries, Coord. Chem. Rev., 2019, 380, 260–286 CrossRef CAS.
- H. C. Johnson, C. L. McMullin, S. D. Pike, S. A. Macgregor and A. S. Weller, Angew. Chem., Int. Ed., 2013, 52, 9776–9780 CrossRef CAS PubMed.
- H. C. Johnson, R. Torry-Harris, L. Ortega, R. Theron, J. S. McIndoe and A. S. Weller, Catal. Sci. Technol., 2014, 4, 3486–3494 RSC.
- T. Kakizawa, Y. Kawano and M. Shimoi, Organometallics, 2001, 20, 3211–3213 CrossRef CAS.
- Y. Kawano, M. Hashiva and M. Shimoi, Organometallics, 2006, 25, 4420–4426 CrossRef CAS.
- R. Dallanegra, A. P. M. Robertson, A. B. Chaplin, I. Manners and A. S. Weller, Chem. Commun., 2011, 47, 3763–3765 RSC.
- A. E. Nako, A. J. P. White and M. R. Crimmin, Dalton Trans., 2015, 44, 12530–12534 RSC.
- A. Hicken, A. J. P. White and M. R. Crimmin, Inorg. Chem., 2017, 56, 8669–8682 CrossRef CAS PubMed.
- E. A. Romero, P. M. Olsen, R. Jazzar, M. Soleilhavoup, M. Gembicky and G. Bertrand, Angew. Chem., Int. Ed., 2017, 56, 4024–4027 CrossRef CAS PubMed.
- F. Rekhroukh, L. Estévez, C. Bijani, K. Miqueu, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2016, 55, 3414–3418 CrossRef CAS PubMed.
- M. Joost, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, Organometallics, 2013, 32, 898–902 CrossRef CAS.
- A. Ilie, C. I. Raţ, S. Scheutzow, C. Kiske, K. Lux, T. M. Klapötke, C. Silvestru and K. Karaghiosoff, Inorg. Chem., 2011, 50, 2675–2684 CrossRef CAS PubMed.
- A. J. Clarke, M. J. Ingleson, G. Kociok-Köhn, M. F. Mahon, N. J. Patmore, J. P. Rourke, G. D. Ruggiero and A. S. Weller, J. Am. Chem. Soc., 2004, 126, 1503–1517 CrossRef CAS PubMed.
- V. C. Gibson, C. Redshaw and G. A. Solan, Chem. Rev., 2007, 107, 1745–1776 CrossRef CAS PubMed.
- S. D. Ittel, L. K. Johnson and M. Brookhart, Chem. Rev., 2000, 100, 1169–1204 CrossRef CAS PubMed.
- T. Jurca, S. I. Gorelsky, I. Korobkov and D. S. Richeson, Dalton Trans., 2011, 40, 4394–4396 RSC.
- T. Jurca, S. Ouanounou, S. I. Gorelsky, I. Korobkov and D. S. Richeson, Dalton Trans., 2012, 41, 4765–4771 RSC.
- M. L. Buil, M. A. Esteruelas, S. Niembro, M. Oliván, L. Orzechowski, C. Pelayo and A. Vallribera, Organometallics, 2010, 29, 4375–4383 CrossRef CAS.
- M. M. D. Roy, M. J. Ferguson, R. McDonald and E. Rivard, Chem. Commun., 2018, 54, 483–486 RSC.
- A. J. Martínez-Martínez and A. S. Weller, Dalton Trans., 2019, 48, 3551–3554 RSC.
- E. L. Dias, M. Brookhart and P. S. White, Organometallics, 2000, 19, 4995–5004 CrossRef CAS.
- E. L. Dias, M. Brookhart and P. S. White, Chem. Commun., 2001, 423–424 RSC.
- G. M. Adams, F. M. Chadwick, S. D. Pike and A. S. Weller, Dalton Trans., 2015, 44, 6340–6342 RSC.
- N. J. Patmore, C. Hague, J. H. Cotgreave, M. F. Mahon, C. G. Frost and A. S. Weller, Chem. – Eur. J., 2002, 8, 2088–2098 CrossRef CAS.
- Addition of only 1 equivalent of MeCN to 1 causes broadening, but no significant chemical shift change, of the H3B·NMe3 signal that suggests a rapid ligand exchange is occurring, that favours the amine–borane adduct.
- W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Science, 2009, 326, 553 CrossRef CAS PubMed.
- A. G. Algarra, L. J. Sewell, H. C. Johnson, S. A. Macgregor and A. S. Weller, Dalton Trans., 2014, 43, 11118–11128 RSC.
- DFT calculations were perfomed with Gaussian 09 with optimisations using the BP86 functional with SDD basis sets and pseudopotentials on Rh and Ag and 6-31G** basis sets on all other atoms. 11B chemical shifts were computed with the B3LYP functional with 6-311++g** basis sets on C, N, B and H atons and included a correction of dichloromethane solvation (PCM approach). See ESI† for full details and references.
- L. R. Collins, N. A. Rajabi, S. A. Macgregor, M. F. Mahon and M. K. Whittlesey, Angew. Chem., Int. Ed., 2016, 55, 15539–15543 CrossRef CAS PubMed.
- J. Moellmann and S. Grimme, Organometallics, 2013, 32, 3784–3787 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1994 Search PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, A. J. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI., 2013 Search PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- A. J. Martínez-Martínez, B. E. Tegner, A. I. McKay, A. J. Bukvic, N. H. Rees, G. J. Tizzard, S. J. Coles, M. R. Warren, S. A. Macgregor and A. S. Weller, J. Am. Chem. Soc., 2018, 140, 14958–14970 CrossRef PubMed.
- C. Narth, Z. Maroun, R. A. Boto, R. Chaudret, M.-L. Bonnet, J.-P. Piquemal and J. Contreras-García, in Applications of Topological Methods in Molecular Chemistry, ed. R. Chauvin, C. Lepetit, B. Silvi and E. Alikhani, Springer International Publishing, Cham, 2016 Search PubMed.
- J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis, characterisation data, structures of 3, 7 and 8, computational details. CCDC 1895514–1895519. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9dt00971j |
| This journal is © The Royal Society of Chemistry 2019 |