Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The critical role of hydrogen on the stability of oxy-hydroxyl defect clusters in uranium oxide†
Joseph M.
Flitcroft
 a,
Marco
Molinari
a,
Marco
Molinari
 *ab,
Nicholas A.
Brincat
c,
Nicholas R.
Williams
c,
Mark T.
Storr
c,
Geoffrey C.
Allen
d and
Stephen C.
Parker
*ab,
Nicholas A.
Brincat
c,
Nicholas R.
Williams
c,
Mark T.
Storr
c,
Geoffrey C.
Allen
d and
Stephen C.
Parker
 *a
*a
aDepartment of Chemistry, University of Bath, Bath, BA2 7AY, UK. E-mail: s.c.parker@bath.ac.uk
bDepartment of Chemistry, University of Huddersfield, Queensgate, Huddersfield, HD1 3DH, UK. E-mail: m.molinari@hud.ac.uk
cAWE plc, Aldermaston, Reading, Berkshire, RG7 4PR, UK
dInterface Analysis Centre, University of Bristol, Bristol, BS2 8BS, UK
First published on 4th June 2018
Abstract
Despite considerable work applying ab initio techniques to model the role of defects on mechanical, structural and electronic properties of oxides, there has been little on the role of trapped hydrogen, despite it being virtually always present. We propose a framework for identifying reversible and irreversible hydrogen traps. We demonstrate that the thermodynamic stability of oxy-hydroxyl defects is defined by an interplay of formation and binding energies. This framework is applicable to all oxides and is essential for describing the solubility and diffusivity of hydrogen at the macroscopic level. For the most important actinide oxide in nuclear energy, uranium oxide, hydrogen significantly impacts the stability of oxygen defect clusters, and with increased local hydrogen concentration it forms irreversible traps. Crucially, hydrogen stabilises isolated Willis clusters, named after their discoverer and originally reported in 1963, which all subsequent ab initio calculations have predicted to be unstable, but of course, none considered hydrogen.
Introduction
The presence of hydrogen in oxide materials is often overlooked despite its significant impact on materials properties,1–4 including mechanical resistivity,5 conductivity,6 (photo-)catalysis,7–9 gate materials,10 insulator to metal transition11 and chemo- and photo-chromism.12 Perhaps one of the most compelling arguments, for investigating hydrogen defects, is that control over these materials properties would only be gained when a complete survey of the chemistry and atom-level structures of complex defects is compiled.Hydrogen is of primary concern in metals and uranium is no exception, with its legacy from the first generation of nuclear reactors. As a metal, uranium is susceptible to oxidation in the presence of water vapour and oxygen forming a thin uranium oxide coating layer that provides a protective physical barrier that quenches corrosion of the metal. In common with other metals,5 the aqueous corrosion of uranium generates hydrogen species that permeate through the oxide layer13–15 and react with the metal to form hydride species.16 However, uranium hydride is pyrophoric and thus it is a major concern in the design of long-term storage facilities. To prevent formation of the hydride, trapping of hydrogen within the oxide coating layer is required, and this can be best achieved by identifying and controlling the defects that efficiently trap hydrogen.
In the case of uranium oxide, experimental data on solubility and diffusivity of hydrogen is limited,17–19 and the nature of the diffusing hydrogen species is still undetermined, with both molecular17 and atomic18,19 hydrogen proposed. The latter, in particular, is essential for predicting any diffusivity and trapping. Evidence of hydrogen trapping was first reported by Sherman and Olander,19 who saw the release of hydrogen from samples at high temperatures (800–1450 °C). Wheeler suggested that this hydrogen may be in the form of strongly bound species (i.e. hydroxyl groups) that are effectively trapped.17
There is also evidence that oxygen deficiency increases hydrogen solubility compared to oxygen-rich conditions.19 In the latter, the excess oxygen is incorporated as isolated oxygen interstitials at low oxygen partial pressure, which cluster at higher oxygen concentration.20–28 This leads to a variety of potential hydrogen traps. A further level of complexity is then due to the microstructure of polycrystalline oxide materials, which has an impact on the diffusivity of hydrogen,17–19 as it does for the diffusivity of oxygen in fluorite oxides.29–32
Glascott proposed a comprehensive mathematical model for hydriding initiation in uranium metal, which included hydrogen diffusivity in the oxide coating layer.33,34 However, such macroscopic modelling is unable to provide insight into the structural features that interact directly with hydrogen in the material. This can only be realised through atomistic modelling that can identify the geometry of hydrogen trapping sites.
Recently, ab initio studies have begun to characterise the nature of hydrogen species, and have found that both hydroxyl groups and hydride species may form, with the latter identified as more favourable.35,36 Other theoretical work has focussed on the adsorption, desorption and dissociation of water on uranium oxide surfaces,37,38 which is one of the routes that hydrogen can be incorporated into the uranium oxide lattice and before reaching the metal. Whereas there is data suggesting the existence of hydrogen traps in oxygen-rich uranium oxide, there are no atom-level models to support this proposition. The present work applies ab initio modelling techniques to examine the dependence of hydrogen trapping on oxygen defect clusters under oxygen-rich conditions.
Methodology
First principle calculations
A cubic unit cell comprised of 32 UO2 units was generated by a 2 × 2 × 2 expansion of the fluorite 4 UO2 unit cell. All calculations were performed using the VASP code,39 with PAW pseudo-potentials and the GGA PBE functional.40 The Dudarev41 approach was used for the implementation of the onsite Hubbard U parameter, with U = 4.5 eV and J = 0.54 eV.42 The plane-wave cut-off energy was set at 400 eV and a Γ-centred 2 × 2 × 2 Monkhorst–Pack k-point grid was used for all calculations, in line with previous work22,25,43 and convergence criteria for the electronic and ionic relaxations were 1 × 10−6 eV per atom and 1 × 10−2 eV A−1, respectively. All calculations were performed at constant pressure with collinear 1k antiferromagnetic ordering. This is considered an appropriate approximation for the experimentally observed 3k non-collinear antiferromagnetic ordering,29,44 and is line with previous work.22,25,26,28 VASP accounts for relativistic effects through scalar relativistic methods45,46 and spin orbit coupling (SOC). In our previous work,35 we examined the effect of SOC on hydrogen defects in UO2. The produced a consistent shift in the energies, which is in line with previous work for UO2.47,48 SOC does not remove the tetragonal distortion caused by the antiferromagnetic ordering, which can only be removed using the experimentally observed 3k non-collinear ordering.44 The effect of SOC has also been shown to be negligible on structure, relative stability and electronic properties of other actinide oxides.49 For all these reasons and as the inclusion of SOC vastly increases the computational expense, it has not been included in here. All structural models were generated using the METADISE50 code and all structural figures were created using VESTA.51Results and discussion
UO2+x structural models
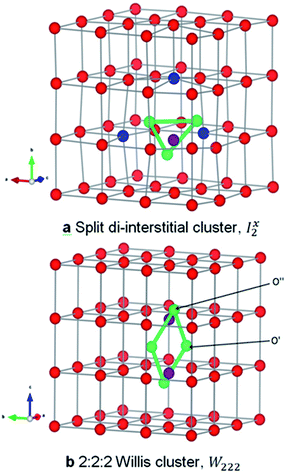
The two smallest oxygen clusters proposed in uranium oxide are the split di-interstitial (I2x) and the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Willis cluster (W222), shown in Fig. 1. We use the nomenclature common in the literature for the split interstitial clusters (I2x)22 and have adapted this to also refer to the Willis clusters (W222). Upon the incorporation of excess oxygen the UO2 lattice is oxidised, such that for every additional oxygen, two uranium atoms are oxidised from U4+ to U5+. The Kroger–Vink notation is commonly used in the literature for defects in solids22,26 and we use this to describe the point defects used as reference states.
2 Willis cluster (W222), shown in Fig. 1. We use the nomenclature common in the literature for the split interstitial clusters (I2x)22 and have adapted this to also refer to the Willis clusters (W222). Upon the incorporation of excess oxygen the UO2 lattice is oxidised, such that for every additional oxygen, two uranium atoms are oxidised from U4+ to U5+. The Kroger–Vink notation is commonly used in the literature for defects in solids22,26 and we use this to describe the point defects used as reference states.
A I2x cluster (Fig. 1a) has a central oxygen vacancy 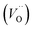 surrounded by three oxygen interstitials
surrounded by three oxygen interstitials 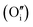 located approximately 1.6 Å away in 〈111〉 directions. This causes the displacement of three lattice oxygen by approximately 0.3 Å from their lattice sites, highlighted in blue in Fig. 1a. In the models presented here the excess oxygen changes the stoichiometry from UO2.00 to UO2.06, and leads to the oxidation of four nearest neighbour uranium ions to the cluster from U4+ to U5+. A I2x cluster is found to have a formation energy of −123 kJ mol−1 in agreement with previously reported literature values.22,23
located approximately 1.6 Å away in 〈111〉 directions. This causes the displacement of three lattice oxygen by approximately 0.3 Å from their lattice sites, highlighted in blue in Fig. 1a. In the models presented here the excess oxygen changes the stoichiometry from UO2.00 to UO2.06, and leads to the oxidation of four nearest neighbour uranium ions to the cluster from U4+ to U5+. A I2x cluster is found to have a formation energy of −123 kJ mol−1 in agreement with previously reported literature values.22,23
A W222 (Fig. 1b) consists of two 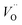 and four
and four 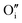 each located approximately 1 Å from an octahedral interstitial site; two
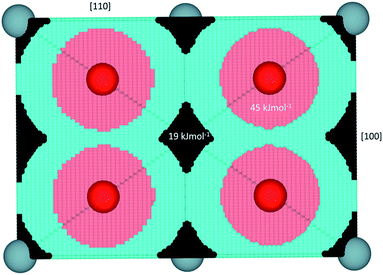
each located approximately 1 Å from an octahedral interstitial site; two 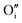 are found in 〈110〉 directions (O′) and two in 〈111〉 directions (O′′). The W222 cluster was the first defect cluster proposed to rationalise the UO2+x structure,20 and was initially predicted to be stable using interatomic potential model calculations.21 However, the advent of DFT has demonstrated single, isolated W222 clusters are unstable with respect to I2x clusters.23 Recently, DFT calculations have found that edge-sharing W222 clusters are stable in UO2+x, but only in a narrow composition range (0.125 < x < 0.25),25 becoming unstable by x = 0.33,26 emphasising how sensitive UO2 defect chemistry is to oxygen partial pressure.
are found in 〈110〉 directions (O′) and two in 〈111〉 directions (O′′). The W222 cluster was the first defect cluster proposed to rationalise the UO2+x structure,20 and was initially predicted to be stable using interatomic potential model calculations.21 However, the advent of DFT has demonstrated single, isolated W222 clusters are unstable with respect to I2x clusters.23 Recently, DFT calculations have found that edge-sharing W222 clusters are stable in UO2+x, but only in a narrow composition range (0.125 < x < 0.25),25 becoming unstable by x = 0.33,26 emphasising how sensitive UO2 defect chemistry is to oxygen partial pressure.
UO2+xHy structural models
Hydrogen was added to the UO2.06 models of W222 (Willis cluster, Fig. 1b) and I2x (split di-interstitial cluster, Fig. 1a) clusters and the local hydrogen concentration was varied from 117 to 467 μg H/g UO2, which is equivalent to y in UO2+xHy varying from around 0.03 to 0.12. This is achieved by the addition of 1 to 4 hydrogen species to the oxygen clusters in simulation cell of U32O62+2. The addition of hydrogen to the oxygen clusters resulted in the formation of hydroxyl species within the cluster. As the defect clusters are made of oxygen and hydroxyl species these defect clusters will now collectively be referred to as oxy-hydroxyl clusters. The chosen configurations were selected to maximise the interactions between the oxygen and hydrogen species; details in the ESI.† The formation of each hydroxyl group within the oxygen defect split di-interstitial and Willis clusters (each containing 4U5+) results in the reduction of a U5+ to U4+. The concentration of U5+ in each oxy-hydroxyl cluster is reported in ESI.†It is important to note that, hydrogen can interact with oxygen clusters in different ways, and as we discuss later this drastically impacts the stability of the oxy-hydroxyl cluster. The newly formed hydroxyl group can hydrogen bond to lattice oxygen ions (L) or defect oxygen ions belonging to the cluster (D). This makes only two different conformations for each local hydrogen concentration in a I2x (LI2x and DI2x), as it is composed of three equivalent 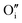 (Fig. 1a). The lower symmetry of the Willis cluster (arising from the two symmetrically inequivalent
(Fig. 1a). The lower symmetry of the Willis cluster (arising from the two symmetrically inequivalent 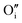 ) is responsible for the greater number of possible distinct configurations; e.g.
) is responsible for the greater number of possible distinct configurations; e.g.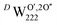 denotes three hydrogen atoms, one at a O′ interstitial site and one at each of the two O′′ sites, and all three species are hydrogen bonded oxygen species of the defect cluster (D).
denotes three hydrogen atoms, one at a O′ interstitial site and one at each of the two O′′ sites, and all three species are hydrogen bonded oxygen species of the defect cluster (D).
Energetics of hydrogen in UO2+x
In order to define irreversible and reversible hydrogen traps it is necessary to introduce two energy terms, the formation and the binding energies of oxy-hydroxyl clusters.The formation of the oxy-hydroxyl clusters is considered as the energy of dissolving hydrogen and oxygen gas into a UO2 matrix according to eqn (1).
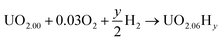 | (1) |
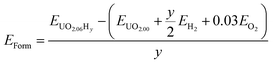 | (2) |
In order to assess whether the oxy-hydroxyl clusters are more energetically favourable than isolated point defects, eqn (3) is considered, where the most stable isolated hydrogen defect is 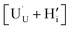 comprising of a hole on the uranium as U5+
comprising of a hole on the uranium as U5+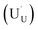 compensating the hydride ion
compensating the hydride ion  . The charge state of the hydrogen interstitial is dependent on the location in the lattice (Fig. 2), where the hydride is more stable than the protonic form by 26 kJ mol−1. The isolated oxygen interstitial compensated by two U5+ is given by
. The charge state of the hydrogen interstitial is dependent on the location in the lattice (Fig. 2), where the hydride is more stable than the protonic form by 26 kJ mol−1. The isolated oxygen interstitial compensated by two U5+ is given by 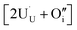 . These interstitial defects come together to form the oxy-hydroxyl defect cluster [cluster], either based on the split di-interstitial, I2x,
. These interstitial defects come together to form the oxy-hydroxyl defect cluster [cluster], either based on the split di-interstitial, I2x, 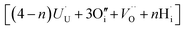 or the 2
or the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Willis cluster, W222,
2 Willis cluster, W222, 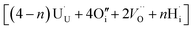 , in the presence of hydrogen. In every case, hydrogen now forms protonic defects and so reduces the U5+ associated with the hydride to U4+ and reduces an additional U5+ associated with the
, in the presence of hydrogen. In every case, hydrogen now forms protonic defects and so reduces the U5+ associated with the hydride to U4+ and reduces an additional U5+ associated with the 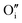 , leading to the formation of the cluster in a simulation cell with a stoichiometry of UO2.06Hy.
, leading to the formation of the cluster in a simulation cell with a stoichiometry of UO2.06Hy.
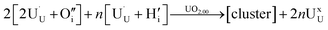 | (3) |
 | ||
| Fig. 2 Representation of hydrogen behavior in UO2 projected in a [110] direction. Black represents regions where hydride is predicted to be energetically most stable, light blue the H˙ radical, pink protonic behavior (i.e. forms a hydroxyl), red the lattice oxygen and blue are the uranium ions. The energies of formation for a hydride or hydroxyl defect by dissolving H2 gas into UO2 are shown on the respective regions. Values taken from ref. 35. | ||
The preference for formation of oxy-hydroxyl clusters over isolated point defects (i.e. separated oxygen interstitial 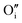 and hydride) is expressed using the binding energy (EBind) of the oxy-hydroxyl cluster per hydrogen atom in the simulation cell, n,
and hydride) is expressed using the binding energy (EBind) of the oxy-hydroxyl cluster per hydrogen atom in the simulation cell, n,
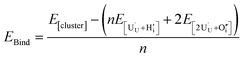 | (4) |
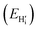 this is a hydride (EForm = 19 kJ mol−1),35 and an
this is a hydride (EForm = 19 kJ mol−1),35 and an 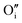 in stoichiometric UO2
in stoichiometric UO2 for oxygen, with a formation energy calculated to be −119 kJ mol−1 in agreement with previous literature.27 The reference energy for uranium oxide is the energy of stoichiometric UO2. A negative value of binding energy indicates an energetic preference for the interstitial species to cluster in an oxy-hydroxyl defect cluster rather than form isolated point defects within the UO2 lattice, i.e. hydride and
for oxygen, with a formation energy calculated to be −119 kJ mol−1 in agreement with previous literature.27 The reference energy for uranium oxide is the energy of stoichiometric UO2. A negative value of binding energy indicates an energetic preference for the interstitial species to cluster in an oxy-hydroxyl defect cluster rather than form isolated point defects within the UO2 lattice, i.e. hydride and 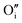 . We follow the procedure of Minervini et al.52 for calculating the binding energy.
. We follow the procedure of Minervini et al.52 for calculating the binding energy.
The most stable oxy-hydroxyl UO2+xHy clusters
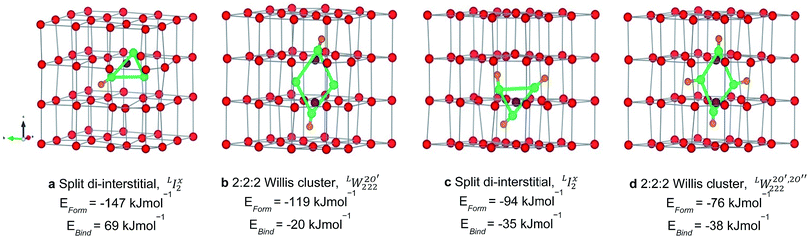
The structures of the most stable configurations at each local hydrogen clusters at each local hydrogen concentration, 117 to 467 μg H/g UO2, are presented in Fig. 3 along with their formation and binding energies. Data for all other configurations along with their energetics is presented in the ESI.† The most stable cluster is based on a I2x (split di-interstitial) geometry at local concentrations of 117 and 351 μg H/g UO2, which correspond to 1 and 3 hydrogen species added to the oxygen cluster (−146 and −95 kJ mol−1/H). This results in the reduction of 1U5+ to 1U4+ and 3U5+ to 3U4+ within the UO2 lattice respectively, as the oxidised UO2+x including a split di-interstitial cluster contains 4U5+. Whereas the most stable W222 (Willis) cluster is found at local concentrations of 234 μg H/g UO2 and 467 μg H/g UO2, which correspond to 2 and 4 hydrogen species added to the oxygen cluster (−119 and −76 kJ mol−1/H), this is balanced by the reduction of 2U5+ at 234 μg H/g UO2 and complete reduction of all U5+ at 467 μg H/g UO2. In these clusters there is a strong interaction between the hydroxyl groups and lattice oxygen atoms. There seems to be an odd–even relationship for the most stable oxy-hydroxyl clusters. Oxygen clusters with odd numbers of interstitials oxygen atoms, the I2x, are stabilized by an odd number of hydrogen species, whereas oxygen clusters with even numbers of oxygen interstitials (W222) are stabilized by an even number of hydrogen species.Energetics of oxy-hydroxyl UO2+xHy clusters as a function of cluster geometry
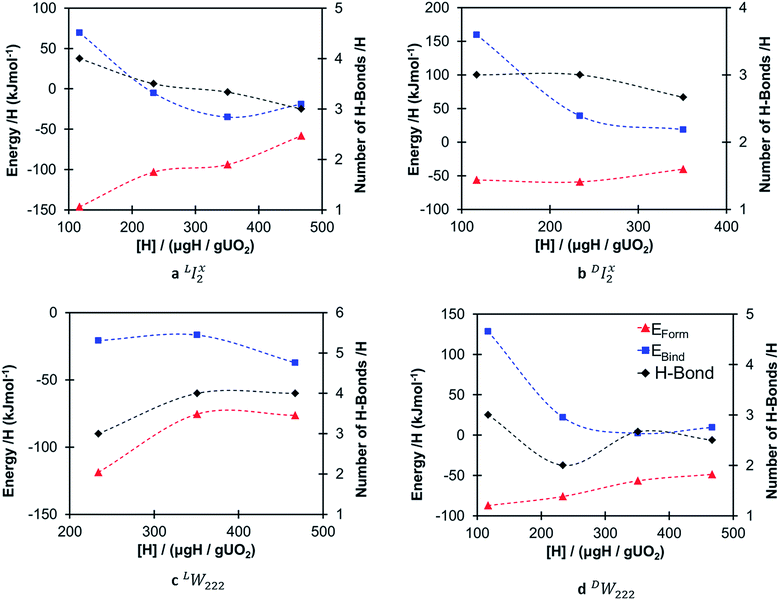
Fig. 4 shows the formation (eqn (2)) and binding (eqn (4)) energies (in kJ mol−1) per hydrogen species as a function of local hydrogen concentration ([H] in μg H/g UO2) for the most stable configurations of the oxy-hydroxyl clusters. We provide separate figures depending on the nature of the oxygen cluster either split di-interstitial (I2x) or Willis (W222) clusters, and whether the newly formed hydroxyl group hydrogen bonds to lattice oxygen ions (L) or defect oxygen ions belonging to the cluster (D). This gives four different combinations LI2x, DI2x, LW222 and DW222. In each case addition of hydrogen to the oxygen defect cluster resulted in favourable formation energies, however these become less favourable with increasing hydrogen concentration and the effect is less pronounced for DW222 (Fig. 4d). Additionally, oxy-hydroxyl clusters where a hydrogen bonding network is formed with lattice oxygen atoms (Fig. 4a and c) are always favoured compared to those with a hydrogen bonding network formed within the oxygen of the defect cluster (Fig. 4b and 3d). This shows a preference for the hydroxyl groups in the cluster to be arranged such that they hydrogen bond with oxygen of the lattice (L) rather than oxygen of the defect (D).The preference for defect clusters over isolated point defects is expressed by the binding energy. This is generally unfavourable (i.e. isolated point defects dominate) at low hydrogen concentrations (117–234 μg H/g UO2) and becomes increasingly favourable (i.e. defect clusters dominate) at higher concentrations (351–467 μg H/g UO2). At the highest concentration (467 μg H/g UO2) all clusters with favourable formation energies also have favourable binding energies (Fig. 4). There is no straightforward correlation between stability of the clusters and the total number of hydrogen bonds (Fig. 4). It appears that as the hydrogen concentration increases the number of hydrogen bonds per hydrogen decreases with the exception of LW222 clusters (Fig. 4c).
We have investigated hydrogen interaction with two types of oxygen defect cluster (split di-interstitial (I2x) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Willis (W222) clusters) in uranium oxide. We found that the stability and geometry of these clusters radically change as a function of local hydrogen concentration. These oxygen defect clusters act as hydrogen traps and thus will macroscopically affect the material in terms of mechanical properties and hydrogen solubility and diffusion. This will significantly impact long term storage and disposal of uranium metal as hydrogen diffusion through the protective oxide layer forms pyrophoric hydride at the interfaces.
2 Willis (W222) clusters) in uranium oxide. We found that the stability and geometry of these clusters radically change as a function of local hydrogen concentration. These oxygen defect clusters act as hydrogen traps and thus will macroscopically affect the material in terms of mechanical properties and hydrogen solubility and diffusion. This will significantly impact long term storage and disposal of uranium metal as hydrogen diffusion through the protective oxide layer forms pyrophoric hydride at the interfaces.
We found that, remarkably, the presence of hydrogen stabilises the Willis cluster when an appropriate hydrogen bonding network is established, suggesting that trapped hydrogen may have been present when these clusters were originally reported in uranium oxide.20 Although the Willis cluster is stabilized by hydrogen, it is only the most stable defect at 234 and 467 μg H/g UO2, with the split di-interstitial the most stable at 117 and 351 μg H/g UO2. This indicates that oxygen defect chemistry in UO2 is not only strongly dependent on oxygen stoichiometry,25,26 but also on hydrogen partial pressure. This opens key chemical challenges to determine whether other oxy-hydroxyl clusters will be directly stabilised, to what extent these clusters will appear in other materials, and whether the properties of oxide materials will be affected.
For all clusters, with one exception (ESI Table 4†), addition of hydrogen resulted in the formation of hydroxyl groups, which are essential for the formation of a hydrogen bonding network capable of stabilising oxy-hydroxyl clusters. Although there is little experimental work on the interaction of hydrogen with UO2, hydroxyl groups were suggested as potential traps for hydrogen species by Wheeler17 at concentrations of up to 10%. Sherman and Olander19 also acknowledged the presence of hydrogen bound to a variety of defects (rather than simply dissolved as interstitial species) and proposed that oxygen vacancies may be a stable location for hydrogen defects. Indeed, our data shows that the Willis cluster can only be stabilized by forming a hydrogen bonding network that prevents an interstitial oxygen (O′′) from moving to the vacant oxygen site (Fig. 1b) and thus relaxing to a I2x cluster. In some of the defect configurations, generally the least stable ones, we observe hydrogen species positioned at oxygen vacancy sites but still bound to an oxygen interstitial, which is in line with the proposition put forward by Sherman and Olander.19
Based on the formation energies (which define the thermodynamic stability) and binding energies (which define the preference of having oxy-hydroxyl) we can identify, from a thermodynamic viewpoint, reversible and irreversible hydrogen traps in uranium oxide. This provides atom-level parameters that could be implemented in mathematical models to determine hydrogen transport in uranium oxide,17,19,33,34 and each different hydrogen trap now may be considered explicitly. We suggest that oxy-hydroxyl clusters with favourable formation (i.e. negative) and binding energies (i.e. negative) correspond to irreversible traps, as they will form and will not dissociate into isolated defects. Clusters with a favourable formation energy and an unfavourable binding energy (0 < EBind < 80 kJ mol−1) represent reversible hydrogen traps. These correspond to metastable intermediates that are reversible in nature, as the clusters can form but they are not the most stable defect configurations however they do not have sufficient energy for the hydroxyl bond to dissociate.35 Whereas traps with a binding energy greater than the threshold of 80 kJ mol−1 are still metastable intermediates but are less likely to exist, as there is sufficient energy to convert the hydroxyl groups into hydride defects. This threshold for the binding energy of reversible traps (80 kJ mol−1) corresponds to the energy barrier to form an isolated hydride group from a stable isolated hydroxyl species.35
Using our definition for the irreversible and reversible nature of hydrogen traps in UO2, we have made an assessment of the probability of these oxy-hydroxyl clusters to be present within the lattice. This helps rationalise the experimentally observed reversible and irreversible hydrogen traps in UO2, by providing atom level insights into the nature of defect clusters within UO2. However, our calculations do not attempt to determine the absolute concentration of traps as this would require the calculation of free energy terms and is beyond the scope of this work, but represents a key area of future development. Furthermore, while the formation and binding energies allow us to define the nature of traps as reversible or irreversible, simply being an irreversible trap does not guarantee a high concentration of that trap. As in order for the cluster to have a greater concentration than the isolated point defects, its binding energy should be lower than the formation energy of the individual components.53 Thus, a trap can be irreversible in nature and have a low concentration. Within the cluster configurations studied in this work, the only case where the binding energy is greater than the formation energies of the individual point defects is the 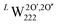 cluster (Fig. 3d), which suggests that this might be the dominant irreversible trap for hydrogen in UO2.
cluster (Fig. 3d), which suggests that this might be the dominant irreversible trap for hydrogen in UO2.
We have generated thermodynamic distributions of irreversible and reversible hydrogen traps as a function of temperature, by calculating the probability of different clusters based on their formation energy. Eqn (5) displays the calculation of free energy, where the ΔGi is the free energy for the oxy-hydroxyl cluster i, Ω is the degeneracy of the oxy-hydroxyl cluster (we report the degeneracy of a cluster in ESI†), EForm,i is the formation energy calculated in eqn (2) and we rescale them so that this value to zero for the most stable defect cluster, R is the gas constant and T is the temperature.
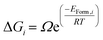 | (5) |
The probability is then given by
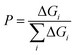 | (6) |
While this approach does not explicitly include the effect of temperature on the defect clusters, as the comparison is between defects all in the solid phase the cohesive energy term will be dominant and entropy terms are unlikely to reverse the conclusions. This again represents key areas for future research, both for the explicit inclusion of temperature and configurational entropy on the stability of defect clusters.
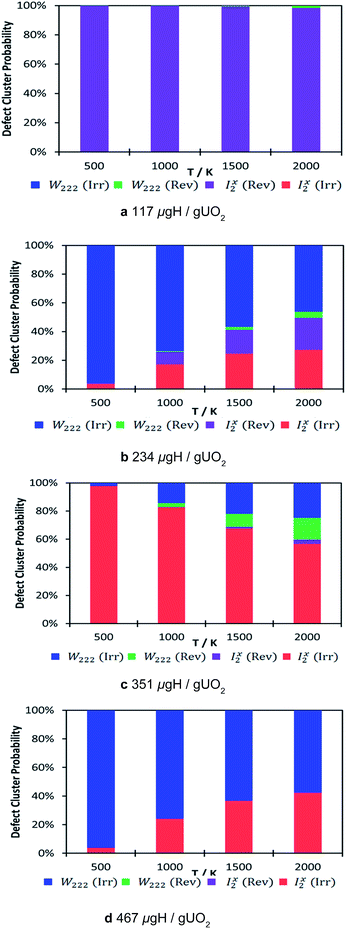
The thermodynamic distribution of all the clusters at each hydrogen concentration is presented in Fig. 5. The calculated probabilities show the predicted nature of the oxy-hydroxyl clusters based on the oxygen defect geometry (i.e. Willis or split di-interstitial) and trap nature (i.e. reversible or irreversible). As the concentration of hydrogen increases, there is a clear shift from reversible trapping, which dominates at the lowest concentration 117 μg H/g UO2, to irreversible trapping, independent of cluster type (Fig. 5). Although we cannot compare our data directly with experimental de-trapping data,17,19 as this accounts for kinetic parameters, it is intriguing that experimental data suggests that hydrogen dissolved in uranium oxide is not released by a diffusion controlled process. Examining the desorption curve for uranium oxide single crystal shows a first desorption peak at approximately 1100 K and a second and more discernible desorption peak at approximately 1700 K, associated with energies of 80 and 210 kJ mol−1 respectively.19 This precludes hydrogen diffusion via interstitial sites in the UO2 lattice and supports the idea that hydrogen is bound to discrete sites, as we see in our ab initio model structures. These hydrogen traps will be characterised by a binding energy and a rate constant of release.
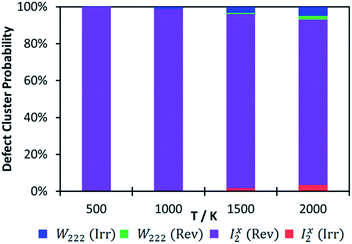
While we calculated the binding energies for oxy-hydroxyl defect clusters in uranium oxide, we have no information on the rate constants for hydrogen release, which depend on temperature. When considering a thermodynamic distribution that accounts for all hydrogen traps at all local hydrogen concentrations (Fig. 6), irreversible trapping (i.e. negative binding energy) appears at temperatures higher than 900 K and is slightly more likely to be based on the Willis geometry (1.3% at 1000 K and 5% at 2000 K) compared to the split di-interstitial (0.3% at 1000 K and 3.5% at 2000 K). Up to 10% of irreversible hydrogen traps appear at 2000 K, whereas the majority (up to 90%) of hydrogen traps will still metastable intermediates (i.e. reversible traps) based on the I2x cluster (Fig. 6). As the irreversible traps are stabilised by a more complex hydrogen bonding network, they are more stable at higher local hydrogen concentrations and thus their thermodynamic distribution increases with temperature, contrary to the metastable (reversible) traps that are mainly oxy-hydroxyl clusters with low local hydrogen concentration and a weaker hydrogen bonding network.
Conclusions
To conclude, we found that hydrogen strongly affects the structure and energetics of oxygen defect clusters in uranium oxide, as has been shown for many other oxides.1–5 Our analysis defines a thermodynamic route to determine reversible (metastable) and irreversible hydrogen traps, and show that there are stable local oxygen-rich regions (i.e. oxygen defect clusters) that can trap and sustain high local hydrogen concentrations despite low overall concentration in the sample. Our ab initio approach allows for quantitative measurement of the population of hydrogen traps, which changes as a function of local hydrogen concentration and temperature. This shows that we need atom-level models and insight if we are to predict macroscopic properties such as the dynamics of hydrogen defects and microstructural changes under non-equilibrium conditions that can arise in service due to the presence of extreme environments (e.g. radiation, temperature). Thus this work demonstrates when investigating defect clusters in oxides that the inclusion of hydrogen as part of these studies is overdue.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank J. Glascott for useful discussions on hydrogen in actinides. This work made use of ARCHER, the UKs national HPC facility funded by EPSRC (EP/L000202) through the Material Chemistry Consortium, and Balena, the University of Bath HPC platform. We thank AWE, the University of Bath, the University of Huddersfield, and EPSRC (EP/P007821/1, EP/K016288/1, EP/R010366/1) for funding. © British Crown Owned Copyright 2018/MOD. Published with permission of the controller of Her Britannic Majesty's Stationary Office.References
- T. Norby, M. Widerøe, R. Glockner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- T. Norby, Nature, 2001, 410, 877878 CrossRef PubMed.
- T. Norby and Y. Larring, Curr. Opin. Solid State Mater. Sci., 1997, 2, 593–599 CrossRef.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Phys. Chem. C, 2017, 121, 12817–12825 Search PubMed.
- L. Meng, X. De-Gang, M. Evan, L. Ju, Z. Xi-Xiang and S. Zhi-Wei, Nat. Commun., 2016, 8, 14564 Search PubMed.
- C. G. Van de Walle, Phys. Rev. Lett., 2012, 85, 10121015 Search PubMed.
- S. K. Cushing, F. Meng, J. Zhang, B. Ding, C. Chen, L. Ru-Shi, A. D. Bristow, J. Bright, P. Zheng and N. Wu, ACS Catal., 2017, 7, 1742–1748 CrossRef.
- W. Xin-Ping and G. Xue-Qing, Phys. Rev. Lett., 2016, 116, 086102 CrossRef PubMed.
- H. Malerød-Fjeld, D. Clark, I. Yuste-Tirados, R. Zanon, D. Catalan-Martinez, D. Beeaff, S. H. Morejudo, P. K. Vestre, T. Norby, R. Haugsrud, J. M. Serra and C. Kjølseth, Nat. Energy, 2017, 2, 923–931 CrossRef.
- E. L. Silva, A. G. Marinopoulos, R. B. L. Vieira, R. C. Valao, H. V. Alberto, J. M. Gil, R. L. Lichti, P. W. Mengyan and B. B. Baker, Phys. Rev. B, 2016, 94, 014104 CrossRef.
- X. Leng, J. Pereiro, J. Strle, G. Dubuis, A. T. Bollinger, A. Gozer, J. Wu, N. Litombe, C. Pangopoulos and C. I. BoZovi, npj Quantum Materials, 2017, 2, 1–7 CrossRef.
- A. Borgschulte, O. Sambalova, R. Delmelle, S. Jenatsch, R. Hany and F. Nuesch, Sci. Rep., 2017, 7, 40761 CrossRef PubMed.
- C. A. Colmenares, Prog. Solid State Chem., 1984, 15, 257–364 CrossRef.
- A. G. Ritchie, J. Less-Common Met., 1984, 98, 193–214 CrossRef.
- J. M. Haschke, T. H. Allen and L. A. Morales, J. Alloys Compd., 2001, 314, 78–91 CrossRef.
- C. A. Stitt, N. J. Harker, K. R. Hallam, C. Paraskevoulakpos, A. Banos, S. Rennie, J. Jowset and T. B. Scott, PLoS One, 2015, 10, 1–13 Search PubMed.
- V. J. Wheeler, J. Nucl. Mater., 1971, 40, 189–194 CrossRef.
- D. R. Olander, D. Sherman and M. Balooch, J. Nucl. Mater., 1982, 107, 31–45 CrossRef.
- D. F. Sherman and D. R. Olander, Hydrogen dissolution in and release form nonmetals I uranium dioxide, J. Nucl. Mater., 1989, 166, 307–320 CrossRef.
- B. T. M. Willis, Nature, 1963, 197, 755–756 CrossRef.
- C. R. A. Catlow, Proc. R. Soc. London, 1977, 353, 533–561 CrossRef.
- D. A. Andersson, J. Lezama, B. P. Uberuaga, C. Deo and S. D. Conradson, Phys. Rev. B, 2009, 79, 024110 CrossRef.
- H. Geng, Y. Chen, Y. Kaneta, M. Iwasawa, T. Ohnuma and M. Kinoshita, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104120 CrossRef.
- J. Wang, R. C. Ewing and U. Becker, Sci. Rep., 2014, 4, 4216 CrossRef PubMed.
- N. A. Brincat, M. Molinari, S. C. Parker, G. C. Allen and M. T. Storr, J. Nucl. Mater., 2015, 456, 329–333 CrossRef.
- N. A. Brincat, M. Molinari, G. C. Allen, M. T. Storr and S. C. Parker, J. Nucl. Mater., 2015, 467, 724–729 CrossRef.
- F. Gupta, G. Brillant and A. Pasturel, Philos. Mag., 2007, 87, 2561–2569 CrossRef.
- L. Desgranges, G. Baldinozzi, D. Simeone and H. E. Fischer, Inorg. Chem., 2016, 55, 7485–7491 CrossRef PubMed.
- B. Dorado, G. Jomard, M. Freyss and M. Bertolus, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035114 CrossRef.
- S. T. Murphy, E. E. Jay and R. W. Grimes, J. Nucl. Mater., 2014, 447, 143–149 CrossRef.
- N. R. Williams, M. Molinari, S. C. Parker and M. T. Storr, J. Nucl. Mater., 2015, 458, 45–55 CrossRef.
- L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294 CrossRef PubMed.
- J. Glascott, Philos. Mag., 2014, 94, 221–241 CrossRef.
- J. Glascott, Philos. Mag., 2014, 94, 1393–1413 CrossRef.
- J. M. Flitcroft, N. A. Brincat, M. Molinari, S. C. Parker and M. T. Storr, Chem. Commun., 2015, 51, 16209 RSC.
- A. Bingyun, Q. Ruizhi, L. Haiyan and C. Piheng, J. Phys. Chem. C, 2016, 120, 18445–18451 Search PubMed.
- T. Bo, J. Lan, Y. Zhao, C. He, Z. Chai and W. Shi, J. Nucl. Mater., 2014, 54, 446–454 CrossRef.
- B. E. Tegner, M. Molinari, A. Kerridge, S. C. Parker and N. Kaltsoyannis, J. Phys. Chem. C, 2016, 121, 1675–1682 Search PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- M. R. Castell, S. L. Dudarev, C. Muggelberg, A. P. Sutton, G. A. A. D. Briggs and D. T. Goddard, J. Vac. Sci. Technol., 1998, 16, 1055 CrossRef.
- T. Yamazaki and A. Kotani, J. Phys. Soc. Jpn., 1991, 60, 49–52 CrossRef.
- N. A. Brincat, S. C. Parker, M. Molinari, G. C. Allen and M. T. Storr, Inorg. Chem., 2014, 53, 12253–12264 CrossRef PubMed.
- R. Laskowski, G. K. H. Madsen, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 140408 CrossRef.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 2631 Search PubMed.
- A. H. MacDonald, W. E. Pickett and D. D. Koelling, J. Phys. Chem. C, 1980, 13, 2675–2683 Search PubMed.
- F. Bottin, G. Geneste and G. Jomard, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 115438 CrossRef.
- P. Santini, R. Lemanski and P. Edros, Adv. Phys., 1999, 48, 537–653 CrossRef.
- X. D. Wen, R. L. Martin, L. E. Roy, G. E. Scuseria, S. P. Rudin, E. R. Batista, T. M. McCleskey, B. L. Scott, B. Bauer, J. J. Joyce and T. Durakiewicz, J. Chem. Phys., 2012, 137, 154707 CrossRef PubMed.
- G. W. Watson, E. T. Kelsey, N. H. deLeeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef.
- L. Minervini, M. O. Zacate and R. W. Frimes, Solid State Ionics, 1999, 116, 339–349 CrossRef.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 91, 3851–3879 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta02817f |
| This journal is © The Royal Society of Chemistry 2018 |