Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Acidity and basicity interplay in amide and imide self-association†
Wilmer E.
Vallejo Narváez
 ,
Eddy I.
Jiménez
,
Eddy I.
Jiménez
 ,
Eduardo
Romero-Montalvo‡
,
Eduardo
Romero-Montalvo‡
 ,
Arturo
Sauza-de la Vega
,
Arturo
Sauza-de la Vega
 ,
Beatriz
Quiroz-García
,
Marcos
Hernández-Rodríguez
,
Beatriz
Quiroz-García
,
Marcos
Hernández-Rodríguez
 * and
Tomás
Rocha-Rinza
* and
Tomás
Rocha-Rinza
 *
*
Institute of Chemistry, National Autonomous University of Mexico, Ciudad Universitaria, Circuito Exterior, Del. Coyoacán, Mexico City, 04510, Mexico. E-mail: marcoshr@unam.mx; tomasrocharinza@gmail.com
First published on 5th April 2018
Abstract
Amides dimerise more strongly than imides despite their lower acidity. Such an unexpected result has been rationalised in terms of the Jorgensen Secondary Interactions Hypothesis (JSIH) that involves the spectator (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OS) and H-bonded (C
OS) and H-bonded (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OHB) carbonyl groups in imides. Notwithstanding the considerable body of experimental and theoretical evidence supporting the JSIH, there are some computational studies which suggest that there might be other relevant intermolecular interactions than those considered in this model. We conjectured that the spectator carbonyl moieties could disrupt the resonance-assisted hydrogen bonds in imide dimers, but our results showed that this was not the case. Intrigued by this phenomenon, we studied the self-association of a set of amides and imides via1H-NMR, 1H-DOSY experiments, DFT calculations, QTAIM topological analyses of the electron density and IQA partitions of the electronic energy. These analyses revealed that there are indeed repulsions of the type OS⋯OHB in accordance with the JSIH but our data also indicate that the C
OHB) carbonyl groups in imides. Notwithstanding the considerable body of experimental and theoretical evidence supporting the JSIH, there are some computational studies which suggest that there might be other relevant intermolecular interactions than those considered in this model. We conjectured that the spectator carbonyl moieties could disrupt the resonance-assisted hydrogen bonds in imide dimers, but our results showed that this was not the case. Intrigued by this phenomenon, we studied the self-association of a set of amides and imides via1H-NMR, 1H-DOSY experiments, DFT calculations, QTAIM topological analyses of the electron density and IQA partitions of the electronic energy. These analyses revealed that there are indeed repulsions of the type OS⋯OHB in accordance with the JSIH but our data also indicate that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OS group has an overall attraction with the interacting molecule. Instead, we found correlations between self-association strength and simple Brønsted–Lowry acid/base properties, namely, N–H acidities and C
OS group has an overall attraction with the interacting molecule. Instead, we found correlations between self-association strength and simple Brønsted–Lowry acid/base properties, namely, N–H acidities and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O basicities. The results in CDCl3 and CCl4 indicate that imides dimerise less strongly than structurally related amides because of the lower basicity of their carbonyl fragments, a frequently overlooked aspect in the study of H-bonding. Overall, the model proposed herein could provide important insights in diverse areas of supramolecular chemistry such as the study of multiple hydrogen-bonded adducts which involve amide or imide functional groups.
O basicities. The results in CDCl3 and CCl4 indicate that imides dimerise less strongly than structurally related amides because of the lower basicity of their carbonyl fragments, a frequently overlooked aspect in the study of H-bonding. Overall, the model proposed herein could provide important insights in diverse areas of supramolecular chemistry such as the study of multiple hydrogen-bonded adducts which involve amide or imide functional groups.
Introduction
Hydrogen bonds (HBs) in amides and imides are ubiquitous directional forces in nature. HBs in these functional groups are responsible for the secondary interactions, along with other interactions of the tertiary and quaternary structures of proteins.1,2 Other molecules in which hydrogen bonding is relevant are nucleic acids. The recognition among nitrogenous bases such as uracil and thymine is crucial in the DNA, RNA and other related systems.3 Besides HBs, base stacking, steric and electrostatic effects can be important in the stabilisation of nucleic acids.4 Additionally, the dimerisation of amides and imides is of interest in several fields such as supramolecular chemistry in which the self-recognition of these functional groups is relevant.5,6The formation of amide and imide dimers is frequently studied by NMR or IR spectroscopy to determine self-association constants in solution.7,8 Rebek and co-workers9 examined the intramolecular imide–imide and amide–amide association through NMR measurements. The corresponding results indicate that despite their lower acidity, amides exhibit stronger self-associations than imides. Electronic structure calculations made by Jorgensen and co-workers are consistent with these unexpected experimental observations.10 We consider herein a rationalisation of the surprising stronger self-association of amides as compared with imides based on three different criteria.
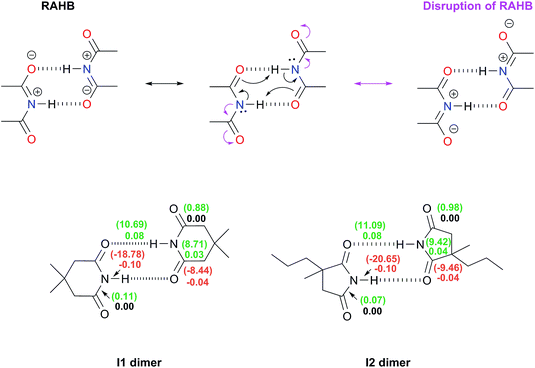
(i) Repulsions involving the spectator carbonyls of imides
The Jorgensen Secondary Interactions Hypothesis (JSIH),11 is usually invoked to explain the larger Kdimer of amides as compared to imides in spite of their lower acidic character.9,10 The JSIH considers that amides and imides have a similar kind of primary (hydrogen-bonded) interactions, namely OHB⋯H contacts as shown in Fig. 1-i. On the other hand, secondary electrostatic interactions (attractions or repulsions between 2.3 and 3.7 Å)11 among atoms in the neighbourhoods of HBs are different in amide and imide dimers. In both cases the molecular clusters present secondary repulsive interactions of the carbonyl oxygens (OHB⋯OHB) and hydrogens (H⋯H) involved in HBs between the monomers (black double arrows in the above-mentioned figure). Nevertheless, the imide dimers present two additional repulsive interactions OHB⋯OS (green arrows), wherein OS denotes the oxygen atom in a spectator carbonyl group. The repulsions OHB⋯OS are also consistent with the notion of two nearly parallel repulsive C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O electric dipoles in the imide dimers (purple arrows). There is a considerable body of theoretical and experimental work which is concordant with the JSIH. For example, crystallographic data of some imides such as maleimide, trans-3,4-diphenylsuccinimide, and 1-methyl-hydantoin show that the separation between OS and OHB is very long (>4 Å)12 in agreement with the proposed repulsive character of the interaction of these atoms. Additionally, the JSIH has also been successfully used to study tetrapeptide analogues,13 stabilisation of base-pairs (A–T and G–C),14 and triply hydrogen bonded complexes.15
O electric dipoles in the imide dimers (purple arrows). There is a considerable body of theoretical and experimental work which is concordant with the JSIH. For example, crystallographic data of some imides such as maleimide, trans-3,4-diphenylsuccinimide, and 1-methyl-hydantoin show that the separation between OS and OHB is very long (>4 Å)12 in agreement with the proposed repulsive character of the interaction of these atoms. Additionally, the JSIH has also been successfully used to study tetrapeptide analogues,13 stabilisation of base-pairs (A–T and G–C),14 and triply hydrogen bonded complexes.15
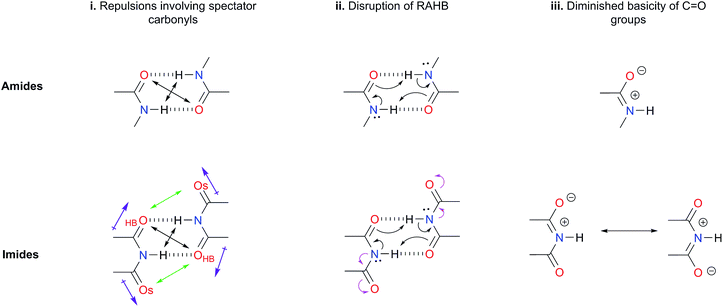 | ||
| Fig. 1 Hypotheses (i)–(iii) considered in this work to explain the larger self-association of amides as compared with that of imides. | ||
(ii) Disruption of the resonance-assisted hydrogen bond (RAHB) in imide dimers
As schematised by the black arrows in Fig. 1-ii, the hydrogen bonds in both amide and imide dimers can be regarded as resonance-assisted hydrogen bonds. Electron withdrawing groups adjacent to these RAHBs16,17 could impair the electron flux across these interactions (magenta arrows shown at the bottom of Fig. 1-ii).(iii) Intrinsic acid/base properties of amides and imides
An analysis of the inductive and resonance effects in these compounds suggests not only a higher acidity of the protons in imides but also a smaller basicity of their oxygens, because of the distribution of the negative charge of the zwitterionic structure across two carbonyl groups as illustrated in Fig. 1-iii. The hydrogen bond strength relates to the acid/base properties of the hydrogen donor and the acceptor groups involved in the interaction. Nonetheless, the basicity of the carbonyl is often overlooked when addressing HBs involving this moiety. We conjectured that the acidity of the N–H fragment together with the basicity of the carbonyl group could be responsible for the differences in the self-association of imides and amides.Given this background, we performed a combined experimental and theoretical study to elucidate the factors governing the self-association of amides and imides. We analysed hypotheses (i)–(iii) through 1H-NMR titrations, 1H-DOSY experiments, electronic structure calculations as well as quantum chemical topology tools, namely, the Quantum Theory of Atoms in Molecules (QTAIM)18 and the Interacting Quantum Atoms (IQA) energy partition.19 Our results indicate the existence of repulsions between OHB and OS, but these interactions are more than compensated by other intermolecular attractions. Moreover, we found that criterion (iii) is the most suitable to explain the experimental tendencies of the self-association of imides and amides through an interplay of the respective basicity and acidity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–H groups. In other words, a weak HB acceptor carbonyl (as it is the case in many of the examined imides) can significantly weaken the investigated self-association processes despite a strong acidity of the imidic hydrogen and vice versa. Our results not only explain the studied phenomenon but also provide a model which could be exploited in diverse areas of supramolecular chemistry, such as the study of multiple hydrogen-bonding complexes which entail the amide and imide functional groups.
O and N–H groups. In other words, a weak HB acceptor carbonyl (as it is the case in many of the examined imides) can significantly weaken the investigated self-association processes despite a strong acidity of the imidic hydrogen and vice versa. Our results not only explain the studied phenomenon but also provide a model which could be exploited in diverse areas of supramolecular chemistry, such as the study of multiple hydrogen-bonding complexes which entail the amide and imide functional groups.
Results and discussion
Self-association of amides and imides: 1H-NMR and 1H-DOSY
First, we studied the dimerisation of 2-pyrrolidone (A1), an archetype for the study of the self-association of the functional groups concerned in this investigation,7b,20 in different deuterated solvents such as chloroform-d, acetonitrile-d3 and DMSO-d6, and also considered the reported value in CCl4 in order to select the most suitable solvent for this research. Another feature of 2-pyrrolidone which makes it particularly suitable for this purpose is the fact that it is liquid at room temperature and thereby its self-association is easier to study in deuterated solvents which cover a broad range of polarity. As expected, Kdimer diminishes with the polarity of the medium (Table 1), to the point that it is very complicated to reliably determine the self-association constant of A1 in solvents as polar as DMSO. Additionally, common imides are usually found as crystalline solids and therefore they are rather insoluble in apolar environments. Hence, we decided to carry out the measurements of Kdimer in chloroform-d due to its optimal compromise between the solubility of the investigated systems and the possibility to accurately determine their self-association constants. The attainment of this compromise prevented the analysis of a larger collection of amides and imides than that considered in this paper.Next, we employed 1H-DOSY experiments to evaluate if imide and amide dimers are indeed the predominant supramolecular aggregates in CDCl3. This circumstance is particularly relevant in the case of imides for which it has been suggested that larger clusters might be formed in solution21 while polymeric structures can occur in the solid state.22 More specifically, we used this technique to determine the hydrodynamic radii (rH) of the studied amide and imide dimers as reported in Table 2 (the structures of the referred compounds are displayed in Table 3). In addition, we also computed the theoretical hydrodynamic radii from electronic structure calculations (rcalc). As expected, structurally similar compounds have close values for rH and rcalc, e.g., the radii of amides A1, A2 and imide I4 are alike because all of them are unsubstituted five-membered rings. A4, A5 and I1 are likewise six-membered heterocycles with closely related structures as reflected in their values of rcalc and rH. Nevertheless, the cyclic chains in the uracil derivatives I5 and I8 and the benzo-derivatives A6, A7 and I3 introduce discrepancies between rH and rcalc. This condition occurs because the spherical particle model employed in the estimation of rH does not represent the oblate spheroid character of these dimers. Despite these differences, the experimental rH values are always smaller than the computed rcalc data (apart from I8 for which rcalc and rH are similar). These results indicate that the investigated amides and imides do not form trimers or larger clusters to an appreciable extent.
| Key | Structure | K dimer (M−1) | pKa | Key | Structure | K dimer (M−1) | pKa | Key | Structure | K dimer (M−1) | pKa |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The values of Kdimer were determined with errors lower than 2% (see Fig. S2–S13 in the ESI). b Statistical factor applied to imides with equivalent (or nearly equivalent) carbonyls and value of the corresponding corrected self-association constant (Kcorr). c pKa of the compound without alkyl substituents. d pKa of the species without alcohol protecting groups. e Data for molecules with a methyl instead of a cyclohexyl substituent. | |||||||||||
| A1 |
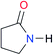
|
2.7 | [24.2]24 | I1 |
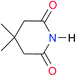
|
1.4, Kcorr: 0.4b | (11.4)c,25 | I8 |
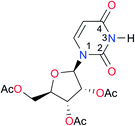
|
8.6 | (9.0)d,26 |
| A2 |
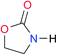
|
8.3 | [20.8]27 | I2 |
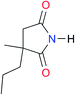
|
3.3, Kcorr: 0.8b | [14.7]c,33 (9.6)c,28 | I9 |
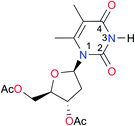
|
12.7 (ref. 29) | (9.3)d,29 |
| A3 |
|
1.0 (ref. 30) | I3 |
|
2.1, Kcorr: 0.5b | [13.4]c,31 (10.2)c,32 | I10 |
|
3.1 (ref. 29) | (8.2)d,29 | |
| A4 |
|
740.0 | [17.0]33, (11.7)34 | I4 |
|
1.2, Kcorr: 0.3b | (4.4)35 | I11 |
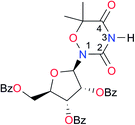
|
5.3 (ref. 29) | (8.7)d,29 |
| A5 |
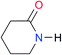
|
1.8 | [26.6]24 | I5 |
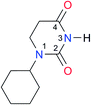
|
2.6 | (9.7)e,36 | I12 |
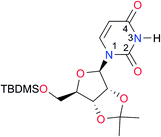
|
8.0 (ref. 37) | (9.0)d,26 |
| A6 |
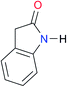
|
8.0 | [18.5]27 | I6 |
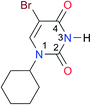
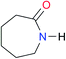
|
4.1 (ref. 8) | I13 |
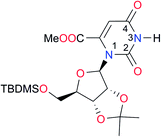
|
5.0 (ref. 37) | (7.9)d,38 | |
| A7 |
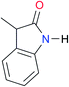
|
7.6 | I7 |
|
2.7 (ref. 8) | (8.4)e,39 | |||||
Once we chose a suitable solvent and verified that the dimeric species are indeed predominantly formed in solution, we consider now the compounds shown in Table 3. This collection of systems contains a good variety of structures and even some previously reported derivatives of nitrogenous bases found in RNA.3 In agreement with previous studies,9 the self-association of amides is stronger than that of imides for molecules with the same ring size and unsaturation patterns, e.g., A5vs.I1, A1vs.I2, A6vs.I3 and A4vs.I6–I13. These results point out that an increase in acidity does not necessarily lead to a stronger self-association. For example, the decreasing orders of acidity of the structurally related imides (I7–I11) are I7 ≈ I10 > I11 > I8 > I9, while those of dimerisation are backwards. We found, however, also exceptions to this behaviour, for instance A5vs.A4 and I5vs.I8 in which acidity and self-association increase in the same direction. Based on the above experimental results, now we proceed to examine the three considered hypotheses concerning the comparison of the self-association between amides and imides.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OHB and C
OHB and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OS dipoles also present a slight repulsive interaction between them (1.1 kcal mol−1 in each case).
OS dipoles also present a slight repulsive interaction between them (1.1 kcal mol−1 in each case).
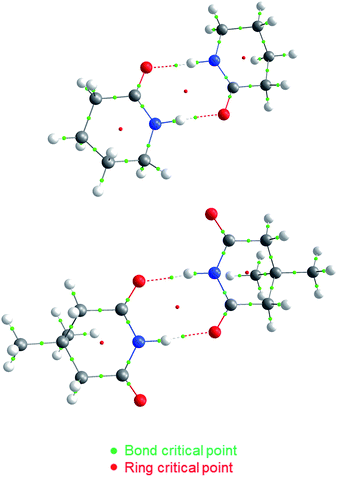 | ||
| Fig. 2 QTAIM molecular graphs for dimers of A5 (top) and I1 (bottom). The bond and ring critical points are indicated. | ||
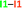 .a The data are reported in kcal mol−1. The full set of IQA interaction energies can be found in Table S3 in the ESI
.a The data are reported in kcal mol−1. The full set of IQA interaction energies can be found in Table S3 in the ESI
| a The IQA deformation energies of the interacting monomers are 16.4 and 20.0 kcal mol−1, therefore the IQA formation energy of the molecular cluster is Eform = (16.4 + 20.0 − 46.8) kcal mol−1 = −10.4 kcal mol−1. |
|---|
|
The same analysis can also be carried out for every atom in one monomer (say those diplayed in green in Table 4, with the corresponding results shown in the right of the same chart) to obtain the complete IQA interaction energy of the system. The results indicate that not only the atoms considered in the JSIH contribute significantly to the formation of the molecular cluster. In particular, the carbon of the spectator carbonyl group (C1) shows an attraction to the adjacent molecule. The attractive interaction of C1 towards the contiguous monomer more than compensates the repulsion of O13 (−12.5 kcal mol−1 + 10.7 kcal mol−1 = −1.8 kcal mol−1). We computed the same value for the other spectator carbonyl group. This attraction between the spectator carbonyl moiety and the whole interacting molecule evidences the numerous relevant intermolecular atomic pairwise interactions in the system.
The importance of the intermolecular interactions not considered by the JSIH in hydrogen-bonded dimers had already been pointed out by Popelier and Joubert.41 Their results were not in accordance with the JSIH in a detailed examination of the relative energetic stability of 27 naturally occurring H-bonded nitrogen base pairs in the gas phase. These researchers considered multipolar expansions of the electrostatic energy (i.e., charge–charge, charge–dipole etc. contacts) which included up to terms which depend on R−6 (e.g. dipole–hexadecapole and quadrupole–octupole interactions), R being the distance between two multipoles. One of the main conclusions of this study concerns the difficulty to explain the relative stability of H-bonded clusters by only considering a subset of atomic pairs located in the boundaries between the interacting monomers as opposed to taking into account the whole set of intermolecular pairs of atoms in the system.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds as schematised in Fig. 1-ii. The DIs, which decrease because of self-association, describe interactions whose covalent character diminishes because of the intermolecular HBs. Conversely, a positive value for ΔDI evidences a chemical bond with an increased covalent character following the formation of the dimer. The same trend analysis can be applied to the change in the magnitude of the IQA exchange–correlation contribution Δ|VXC| of these bonds. The results shown in the bottom of Fig. 3 indicate that there is no such disruption of the RAHB in imide dimers due to these spectator carbonyl groups. The lengths (Table S10 in the ESI†) along with the Δ|VXC| values and the ΔDIs for the C–N and C
O bonds as schematised in Fig. 1-ii. The DIs, which decrease because of self-association, describe interactions whose covalent character diminishes because of the intermolecular HBs. Conversely, a positive value for ΔDI evidences a chemical bond with an increased covalent character following the formation of the dimer. The same trend analysis can be applied to the change in the magnitude of the IQA exchange–correlation contribution Δ|VXC| of these bonds. The results shown in the bottom of Fig. 3 indicate that there is no such disruption of the RAHB in imide dimers due to these spectator carbonyl groups. The lengths (Table S10 in the ESI†) along with the Δ|VXC| values and the ΔDIs for the C–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os bonds are barely affected. Moreover, in most cases the ΔDI of the spectator C
Os bonds are barely affected. Moreover, in most cases the ΔDI of the spectator C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the absolute value of VXC increase slightly because of the formation of the RAHB in imide dimers as opposed to the flux of electrons suggested at the top of Fig. 3.
O and the absolute value of VXC increase slightly because of the formation of the RAHB in imide dimers as opposed to the flux of electrons suggested at the top of Fig. 3.
Additionally, the changes in the DIs and distances of the bonds involved in this RAHB are substantially larger than those of the neighbouring C–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Os interactions. These data point out that the disruption of the RAHB in imides is not the factor which explains the larger self-association of amides with respect to imides, a condition consistent with the observation that electron delocalisation is not the most stabilizing effect in resonance-assisted hydrogen bonds.44
Os interactions. These data point out that the disruption of the RAHB in imides is not the factor which explains the larger self-association of amides with respect to imides, a condition consistent with the observation that electron delocalisation is not the most stabilizing effect in resonance-assisted hydrogen bonds.44
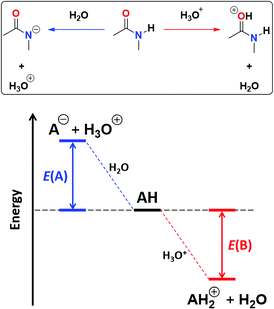
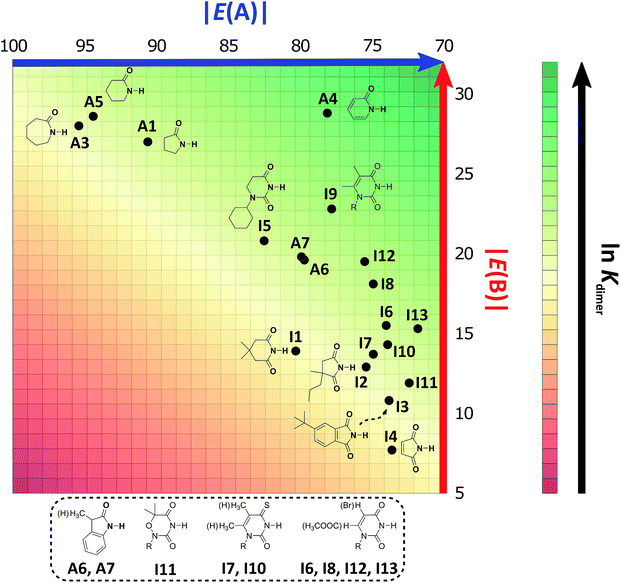
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O protonation, E(B), as shown in Fig. 4.45 The acidity of the N–H proton is reduced with the magnitude of |E(A)| while a high value of |E(B)| indicates a strong basicity of the oxygen in the carbonyl group. The deprotonation energies for a wide variety of species which include imides, amides, (thio)ureas,46 squaramides47 and carboxylic acids48 correlate very well with the corresponding experimental pKa values, ditto for |E(B)| and pKBH+, which indicates the pKa of the conjugate acid of the species under consideration (see Tables S7, S8 and Fig. S29, S30 in the ESI† for the data of the complete set of compounds). Subsequently, we calculated |E(A)| and |E(B)| for compounds A1–A7 and I1–I13 (Table 5).
O protonation, E(B), as shown in Fig. 4.45 The acidity of the N–H proton is reduced with the magnitude of |E(A)| while a high value of |E(B)| indicates a strong basicity of the oxygen in the carbonyl group. The deprotonation energies for a wide variety of species which include imides, amides, (thio)ureas,46 squaramides47 and carboxylic acids48 correlate very well with the corresponding experimental pKa values, ditto for |E(B)| and pKBH+, which indicates the pKa of the conjugate acid of the species under consideration (see Tables S7, S8 and Fig. S29, S30 in the ESI† for the data of the complete set of compounds). Subsequently, we calculated |E(A)| and |E(B)| for compounds A1–A7 and I1–I13 (Table 5).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer of the compounds shown in Table 3. The |E(B)| and |E(A)| values were computed with the SMD-(CHCl3)-M06-2x/6-311++G(2d,2p) approximation
Kdimer of the compounds shown in Table 3. The |E(B)| and |E(A)| values were computed with the SMD-(CHCl3)-M06-2x/6-311++G(2d,2p) approximation
| Compound | |E(A)| (kcal mol−1) | |E(B)| (kcal mol−1) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer Kdimer |
|---|---|---|---|
a |E(B)| value of the most basic oxygen atom within the molecule.43 (e.g. in I5, |E(B)| for the other carbonyl group equals 16.1 kcal mol−1).
b ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer after the consideration of the statistical factor.
c Data for the compound without methyl groups. Kdimer after the consideration of the statistical factor.
c Data for the compound without methyl groups.
|
|||
| A1 | 90.6 | 27.0 | 0.97 |
| A2 | 84.5 | 17.6 | 2.11 |
| A3 | 95.4 | 28.0 | 0.01 |
| A4 | 78.1 | 28.8 | 6.61 |
| A5 | 94.4 | 28.6 | 0.59 |
| A6 | 79.7 | 19.6 | 2.07 |
| A7 | 79.9 | 19.8 | 2.03 |
| I1 | 80.3 | 13.9 | −1.08b |
| I2 | 75.4 | 12.9a | −0.18b |
| I3 | 73.8 | 10.8a | −0.63b |
| I4 | 73.6 | 7.7 | −1.21b |
| I5 | 82.5 | 20.8a | 0.96 |
| I6 | 74.0 | 15.5 | 1.41 |
| I7 | 74.9 | 13.7 | 0.99 |
| I8 | 74.9 | 18.1a | 2.15 |
| I9 | 77.8 | 22.8a | 2.54 |
| I10 | 73.9 | 14.3a | 1.13 |
| I11 | 72.4c | 11.9c | 1.67 |
| I12 | 75.5 | 19.5a | 2.08 |
| I13 | 71.7 | 15.3 | 1.61 |
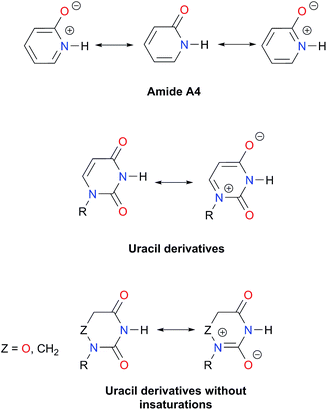
As expected, imides are more acidic and less basic than amides as suggested by the resonance structures in Fig. 1-iii. The change in Brønsted–Lowry acidity or basicity can substantially modify the self-association constants of hydrogen-bonded systems.21,52 We found a good correlation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer as a function of |E(A)| and |E(B)| whose distribution of points adjusts to a first-degree polynomial model. The species A2 was not contemplated in the correlation because it is a cyclic carbamate that can form bifurcated hydrogen bonds with CHCl3 as indicated by DFT geometry optimisations and schematised in Fig. S31 in the ESI.† We conjectured that this feature can substantially affect the self-association of A2 in comparison with the rest of the studied compounds. Indeed, the exclusion of A2 improved the value of r2 in Fig. 5 considerably. We note that the coefficients multiplying |E(B)| and |E(A)| (C|E(B)| and C|E(A)|) are positive and negative respectively. These conditions support the model that self-association increases with the acidity of the N–H moiety and the basicity of the C
Kdimer as a function of |E(A)| and |E(B)| whose distribution of points adjusts to a first-degree polynomial model. The species A2 was not contemplated in the correlation because it is a cyclic carbamate that can form bifurcated hydrogen bonds with CHCl3 as indicated by DFT geometry optimisations and schematised in Fig. S31 in the ESI.† We conjectured that this feature can substantially affect the self-association of A2 in comparison with the rest of the studied compounds. Indeed, the exclusion of A2 improved the value of r2 in Fig. 5 considerably. We note that the coefficients multiplying |E(B)| and |E(A)| (C|E(B)| and C|E(A)|) are positive and negative respectively. These conditions support the model that self-association increases with the acidity of the N–H moiety and the basicity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. Besides, |C|E(B)|| > |C|E(A)||, and hence the dimerisation processes of the examined compounds are more sensitive to changes in the basicity of the carbonyl group than to modifications of the acidity of the amidic or imidic hydrogen. In general, this model points out that a high acidity or basicity by itself does not ensure a large association constant since there must be a balance between these properties to observe a substantial value of Kdimer. In other words, very poor acceptor or donor features of a system can substantially hinder its self-association process as it is the case for imides and basic amides A3 and A5 respectively. This analysis indicates that the low basicity of the carbonyl groups in imides allows us to explain why these compounds dimerise less strongly than amides notwithstanding their larger acidic character. The model in Fig. 5 allows us to interpret a series of experimental observations in CDCl3. For example, the lowest value of the dimerisation constant corresponds to maleimide I4, a compound with high acidity but the one with the smallest basicity among the analysed systems. On the other hand, A4 undergoes the strongest self-association among the molecules of interest. It has the highest basicity and an acidic character similar to the examined imides. These results point out that the occurrence of an aromatic sextet (top of Fig. 6) might favor zwitterionic structures that lead to a high self-association constant.49 The relevance of the basicity of the C
O group. Besides, |C|E(B)|| > |C|E(A)||, and hence the dimerisation processes of the examined compounds are more sensitive to changes in the basicity of the carbonyl group than to modifications of the acidity of the amidic or imidic hydrogen. In general, this model points out that a high acidity or basicity by itself does not ensure a large association constant since there must be a balance between these properties to observe a substantial value of Kdimer. In other words, very poor acceptor or donor features of a system can substantially hinder its self-association process as it is the case for imides and basic amides A3 and A5 respectively. This analysis indicates that the low basicity of the carbonyl groups in imides allows us to explain why these compounds dimerise less strongly than amides notwithstanding their larger acidic character. The model in Fig. 5 allows us to interpret a series of experimental observations in CDCl3. For example, the lowest value of the dimerisation constant corresponds to maleimide I4, a compound with high acidity but the one with the smallest basicity among the analysed systems. On the other hand, A4 undergoes the strongest self-association among the molecules of interest. It has the highest basicity and an acidic character similar to the examined imides. These results point out that the occurrence of an aromatic sextet (top of Fig. 6) might favor zwitterionic structures that lead to a high self-association constant.49 The relevance of the basicity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragments in the self-association of amides and imides is also observed for the uracil analogues I6–I13. These imides are more basic than other compounds with the same functional group and hence dimerise more strongly. Furthermore, the consideration of the basicity of the C
O fragments in the self-association of amides and imides is also observed for the uracil analogues I6–I13. These imides are more basic than other compounds with the same functional group and hence dimerise more strongly. Furthermore, the consideration of the basicity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups is also useful to rationalise which fragments are involved in the dimerisation. For example, it is well known that uracil derivatives (I6, I8, I9, I12 and I13) form hydrogen bonds with the oxygen at C-4 rather than the one at C-2.29 This finding is consistent with our results which indicate that the carbonyl at position four is more basic than its counterpart at position two. The larger basicity of the oxygen bonded to C-4 is associated with the condition that the corresponding carbonyl is conjugated with N-1 via a C-5, C-6 double bond. When this is no longer the case, e.g.I5 and I11, the most basic carbonyl is the one at C-2 as illustrated in the middle and bottom of Fig. 6 (uracil derivatives with and without unsaturations). These observations are supported by the model proposed herein, 2D-NOE analyses29 and proton affinity calculations for I5 (Table 5).
O groups is also useful to rationalise which fragments are involved in the dimerisation. For example, it is well known that uracil derivatives (I6, I8, I9, I12 and I13) form hydrogen bonds with the oxygen at C-4 rather than the one at C-2.29 This finding is consistent with our results which indicate that the carbonyl at position four is more basic than its counterpart at position two. The larger basicity of the oxygen bonded to C-4 is associated with the condition that the corresponding carbonyl is conjugated with N-1 via a C-5, C-6 double bond. When this is no longer the case, e.g.I5 and I11, the most basic carbonyl is the one at C-2 as illustrated in the middle and bottom of Fig. 6 (uracil derivatives with and without unsaturations). These observations are supported by the model proposed herein, 2D-NOE analyses29 and proton affinity calculations for I5 (Table 5).
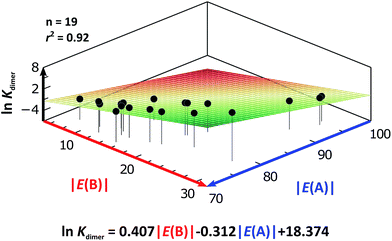 | ||
Fig. 5 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer as a function of |E(A)| and |E(B)| (given in kcal mol−1) for the compounds shown in Table 3 and the first-degree model adjusted for the distribution of points. Kdimer as a function of |E(A)| and |E(B)| (given in kcal mol−1) for the compounds shown in Table 3 and the first-degree model adjusted for the distribution of points. | ||
Following the same arguments concerning the relative importance of basicity and acidity of the examined compounds, we can explain why among the studied five-membered heterocycles, amide A1 associates more strongly than imides I2 and I4. Six-membered rings also follow this trend, as observed when comparing A4vs.I5–I13. The same occurs with derivatives of benzene A6, A7vs.I3 as shown in Fig. 7. On the other hand, when two species have a comparable acceptor capacity, the factor which establishes the stronger self-association is the N–H acidity. In this way, we can explain the differences in self-association between compounds of the same family, such as amides A3, A5 and A1 or imides I2vs.I1. Another appealing feature of this model is that it explains the unexpected result that the uracil-containing species dimerise more strongly than amides A5 or A3. Given that all these uracil derivatives have similar acidities, the dimerisation strength is, in this case, based on the variation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O basicities. In addition, there is a good correlation between the experimental values of ln
O basicities. In addition, there is a good correlation between the experimental values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer with those predicted in the model of Fig. 5 as shown in Fig. S32 in the ESI.† Thus, the consideration of the proton acceptor and donor capacities described in this research is a reasonable alternative approach to interpret the differences in the self-association of amides and imides.
Kdimer with those predicted in the model of Fig. 5 as shown in Fig. S32 in the ESI.† Thus, the consideration of the proton acceptor and donor capacities described in this research is a reasonable alternative approach to interpret the differences in the self-association of amides and imides.
Self-association in CCl4
We considered amide and imide dimerisation constants reported in CCl4 as well.21,50 As discussed above, the apolar nature of carbon tetrachloride results in larger dimerisation constants than those obtained in CDCl3 (ref. 51) (Fig. 8). The set of examined compounds comprises a variety of systems with electron donor and acceptor fragments and hence it allows us to consider the effect of these functional groups on ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer. Similar to the previous discussion of the results in chloroform, there is a correlation between (i) ln
Kdimer. Similar to the previous discussion of the results in chloroform, there is a correlation between (i) ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer and (ii) the basicity of the carbonyl group together with the acidity of the N–H moiety as shown in Fig. 9. The models of Fig. 5 and 9 are qualitatively similar. In particular, C|E(B)| > 0, C|E(A)| < 0 and |C|E(B)|| > |C|E(A)||. The last-mentioned condition indicates once again that the dimerisation constant of amides and imides is more sensitive to the basicity of the carbonyl group than to the acidity of the N–H moiety, hence the larger association of amides in comparison to imides.
Kdimer and (ii) the basicity of the carbonyl group together with the acidity of the N–H moiety as shown in Fig. 9. The models of Fig. 5 and 9 are qualitatively similar. In particular, C|E(B)| > 0, C|E(A)| < 0 and |C|E(B)|| > |C|E(A)||. The last-mentioned condition indicates once again that the dimerisation constant of amides and imides is more sensitive to the basicity of the carbonyl group than to the acidity of the N–H moiety, hence the larger association of amides in comparison to imides.
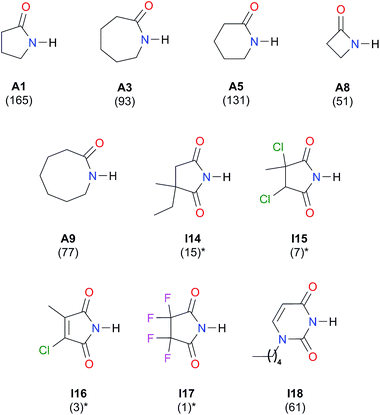 | ||
| Fig. 8 Self-association constants (M−1) reported in CCl4 by IR spectroscopy.21,50 *The values were corrected by a statistical factor of four. | ||
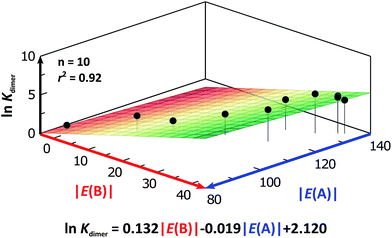 | ||
Fig. 9 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kdimer as a function of |E(A)| and |E(B)| (given in kcal mol−1) of the molecules shown in Fig. 8 and studied in CCl4. The resulting first-degree model adjusted for the distribution of points is reported as well. The corresponding data are reported in Table S9 in the ESI.† Kdimer as a function of |E(A)| and |E(B)| (given in kcal mol−1) of the molecules shown in Fig. 8 and studied in CCl4. The resulting first-degree model adjusted for the distribution of points is reported as well. The corresponding data are reported in Table S9 in the ESI.† | ||
Analysis of heterodimers
The examination of heterodimers gives further insights about the dimerisation of amides and imides. The determination of Kheter indicates that hetero-association between A5 and I1 is stronger than in each homodimer as illustrated in Fig. 10. To rationalise this observation, we consider the relative strength of the individual HBs involved in the heterodimerisation and compared them with those in the homodimers. First, we took into account 1H-NMR spectroscopy results. The change in the N–H chemical shift due to complexation, ΔδN–H, is reported to increase with the strength of the association.52,53 The change in chemical shift of the imidic hydrogen within the A5–I1 adduct (HB-1 in Fig. 10) is larger than that in the A5 homodimer. Furthermore, the value of ΔδN–H in the amidic hydrogen (HB-2 in the same figure) involved in the heterodimer is smaller than the corresponding value for the HB in the imide homodimer. Fig. S15† shows similar results obtained for A1 and I2 heterodimers. The measurement of Kheter was performed with a constant total amount of amide A1 while imide I2 was added to the system. The value of δN–H diminished through the titration, a condition indicative of a weakening of the HB entailing the amidic hydrogen. In the opposite experiment (having a constant total amount of I2 and titrating with A1) the value of δN–H for the imidic proton increased more than in the corresponding homodimers, evidencing the strengthening of the hydrogen bond of the heterodimer which involves this proton. The last-mentioned effect is also observed in the A5–I1 molecular cluster.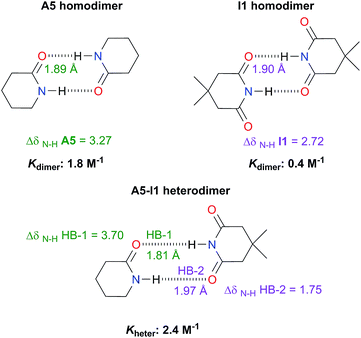 | ||
| Fig. 10 Association constants (considering the statistical factor correction) and changes in chemical shift ΔδN–H (in ppm) of the imidic and amidic protons within the A5, I1, hetero- and homodimers at infinite dilution (complete information in Fig. S14 in the ESI†). We also show the hydrogen bond lengths calculated at the SMD-(CHCl3)-M06-2x/6-311++G(2d,2p) approximation. | ||
Concerning the A5–I1 and A1–I2 heterodimers, the strongest HB-1 is formed between the most acidic proton (the one in the imide) and the most basic carbonyl (found within the amide). On the other hand, the weakest HB takes place in the interaction of the less acidic proton, i.e. N–H of amides A5 and the less basic carbonyl (the one in the imide). The strengths of the HBs in the amide and imide homodimers are between these two extremes. These results along with those of DFT geometry optimisations of the A5–I1 heterodimer show the following trend of descending HB strength:
HB-1 > HB in A5 homodimer > HB in I1 homodimer > HB-2
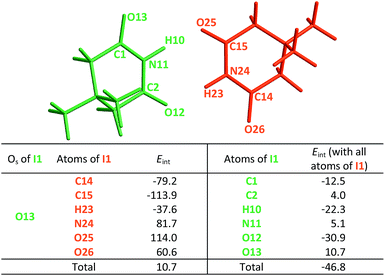
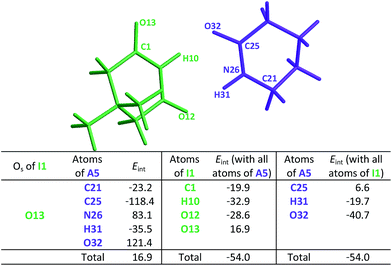
This order is similar to that found by Jorgensen10 and Leszczynski54 who studied computationally the hetero- and homodimers of 2-pyrrolidone and succinimide. According to the JSIH, we should expect the hydrogen bond lengths within the heterodimer to be located somewhere between those of the homodimers. Moreover, the shortest hydrogen bond HB-1 is observed next to a presumed electrostatic or dipole–dipole repulsion involving the spectator carbonyl of A5 as opposed to HB-2 which does not present this effect. Despite the aforementioned agreement of the JSIH with structural data, this hypothesis is not completely consistent with the H-bond strength and distance patterns found in the heterodimers. In contrast, the consideration of the acidity and the basicity of the N–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragments explains the observed association constants, hydrogen bond distances and chemical shift patterns in these systems. The QTAIM and IQA analysis of the intermolecular interactions within the heterodimers A5–I1 (Table 6) and A1–I2 (Tables S5 and S6 in the ESI†) is consistent with the previous discussion. The oxygen of the spectator C
O fragments explains the observed association constants, hydrogen bond distances and chemical shift patterns in these systems. The QTAIM and IQA analysis of the intermolecular interactions within the heterodimers A5–I1 (Table 6) and A1–I2 (Tables S5 and S6 in the ESI†) is consistent with the previous discussion. The oxygen of the spectator C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in the imide presents a strong repulsion with the oxygen of the neighbouring carbonyl involved in the HB and with the rest of the molecules of the amide. These repulsions are even stronger than in the case of the I1 homodimer. Still, the hydrogen bond closest to the OS atom in the A5–I1 heterodimer is the strongest of the system. The relative strength of these HBs is revealed by their lengths as previously discussed and other indices used in the study of hydrogen bonds which include (i) Espinosa's empirical formula55 (Fig. S28 in the ESI†) and (ii) the IQA intermolecular attractions with the interacting molecule (H10 along with O32 on one hand and H31 together with O12 on the other) as reported in the middle and right of Table 6. Despite the repulsion of the oxygen in the spectator carbonyl, this C
O in the imide presents a strong repulsion with the oxygen of the neighbouring carbonyl involved in the HB and with the rest of the molecules of the amide. These repulsions are even stronger than in the case of the I1 homodimer. Still, the hydrogen bond closest to the OS atom in the A5–I1 heterodimer is the strongest of the system. The relative strength of these HBs is revealed by their lengths as previously discussed and other indices used in the study of hydrogen bonds which include (i) Espinosa's empirical formula55 (Fig. S28 in the ESI†) and (ii) the IQA intermolecular attractions with the interacting molecule (H10 along with O32 on one hand and H31 together with O12 on the other) as reported in the middle and right of Table 6. Despite the repulsion of the oxygen in the spectator carbonyl, this C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group has an overall attractive interaction with the neighbouring imide or amide in a similar fashion to the corresponding homodimers. These IQA homo- and heterodimer results point out that the OHB⋯OS repulsions or those between the corresponding dipole carbonyls are not the decisive factor for the energetics of the amide and imide dimerisation.
O group has an overall attractive interaction with the neighbouring imide or amide in a similar fashion to the corresponding homodimers. These IQA homo- and heterodimer results point out that the OHB⋯OS repulsions or those between the corresponding dipole carbonyls are not the decisive factor for the energetics of the amide and imide dimerisation.
 heterodimer. The data are reported in kcal mol−1. The full set of IQA interaction energies can be found in Table S4 in the ESIa
heterodimer. The data are reported in kcal mol−1. The full set of IQA interaction energies can be found in Table S4 in the ESIa
| a The IQA deformation energies of the amide and imide are 20.9 and 21.7 kcal mol−1, so that the IQA formation energy of the molecular cluster is Eform = (20.9 + 21.7 − 54.0) = −11.4 kcal mol−1. |
|---|
|
Significance in the field of molecular recognition
Our investigation provides an alternative model to the JSIH to rationalise experimental observations concerning the homo- and heterodimerisation of amides and imides, for example, the hydrogen bond distance pattern in amide/imide heterodimers and the relative magnitude of Kdimer for these systems. The interplay of acidity and basicity allows us to explain other baffling results e.g. the fact that 2-ethyl-2-methylsuccinimide self-associates much more strongly (by a factor of 15) than tetrafluorosuccinimide.21 Based on the common consideration of the N–H acidity alone, it is expected that the last-mentioned compound would have a larger Kdimer. Likewise and according to the JSIH, the fluorinated compound should dimerise to a larger extent because the charges in the carbonyl oxygens are less negative than those in the alkylated succinimide. The alternative explanation that we offer is that the fluorine atoms reduce substantially the basicity of the carbonyls, thereby impairing the self-association of this compound.Additionally, our results can be useful in understanding why amides are much more used in many technologies such as crystal engineering, development of materials and pharmaceuticals than imides.56 The analysis presented herein indicates that self-association of these functional groups is more sensitive to the basicity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety than it is to the acidity of the N–H group. Hence, the modification of the basicity of this carbonyl represents a good opportunity in the modulation of the strength of the non-covalent interactions established by these groups. For example, the change of a carbonyl in a crucial amide for a more basic imino fragment in vancomycin enhances the association properties with the cell wall of bacteria immune to this antibiotic.57 This increase of association restores antimicrobial activity and represents a strategy to address vancomycin-resistant infections.
O moiety than it is to the acidity of the N–H group. Hence, the modification of the basicity of this carbonyl represents a good opportunity in the modulation of the strength of the non-covalent interactions established by these groups. For example, the change of a carbonyl in a crucial amide for a more basic imino fragment in vancomycin enhances the association properties with the cell wall of bacteria immune to this antibiotic.57 This increase of association restores antimicrobial activity and represents a strategy to address vancomycin-resistant infections.
Finally, the results of our investigation suggest a different approach for the analysis of the stability of multiple hydrogen-bonded systems such as uracil–diamino purine, cytosine–guanine and ADA–DAD systems.58,59 Generally, these systems are examined by considering only the acidity and basicity of the intermediate hydrogen bond and the JSIH. It would be nevertheless desirable to examine the Brønsted–Lowry acid/base properties for every HB in the system which could lead to valuable insights about the molecular recognition of hydrogen-bonded homo- and heterodimers.
Experimental
General experimental and computational details are given in the ESI.†Conclusions
We investigated the reasons underlying the stronger self-association of amides as compared to imides. Our results indicate that the spectator carbonyl presents indeed repulsions with the oxygens involved in the HB but these repulsive interactions are not the key factor in the energetics of the H-bonded systems examined herein. This statement is based on the relevance of the pairwise interactions which are not accounted for by the JSIH and the experimental and theoretical examination of amide–imide homo- and heterodimers. Our results also reveal that the spectator carbonyl groups in imides do not interfere with the resonance-assisted hydrogen bonds in the dimers of these species. Then, we consider the Brønsted–Lowry acid/base properties of the HB donors and acceptors involved in the interaction within these molecular aggregates. The examination of the basicity of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, the acidity of the N–H moiety and Kdimer resulted in a first-degree model suggesting that the proton acceptor capacity of the carbonyl group is more important than the acidity of the amidic or imidic hydrogens for the self-association of the investigated compounds. This model also indicates that there must be a balance between the respective acidity and basicity of the N–H and C
O group, the acidity of the N–H moiety and Kdimer resulted in a first-degree model suggesting that the proton acceptor capacity of the carbonyl group is more important than the acidity of the amidic or imidic hydrogens for the self-association of the investigated compounds. This model also indicates that there must be a balance between the respective acidity and basicity of the N–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragments to observe a substantial self-association of these systems. Particularly, amides exhibit larger self-association constants because of their higher basicities in comparison with imides. Similar conclusions were drawn from systems investigated in CCl4. Our results also explain the hydrogen bond distance patterns found in amide and imide homo- and heterodimers. The acidity/basicity balance in the dimerisation of amides and imides is an alternative approach to the JSIH in order to explain this phenomenon. Overall, we expect that the application of the insights presented herein will prove valuable to understand and modulate hydrogen bonds between the investigated functional groups which are present in a wide variety of supramolecular systems throughout biology and chemistry.
O fragments to observe a substantial self-association of these systems. Particularly, amides exhibit larger self-association constants because of their higher basicities in comparison with imides. Similar conclusions were drawn from systems investigated in CCl4. Our results also explain the hydrogen bond distance patterns found in amide and imide homo- and heterodimers. The acidity/basicity balance in the dimerisation of amides and imides is an alternative approach to the JSIH in order to explain this phenomenon. Overall, we expect that the application of the insights presented herein will prove valuable to understand and modulate hydrogen bonds between the investigated functional groups which are present in a wide variety of supramolecular systems throughout biology and chemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge computer time from DGTIC/UNAM (projects LANCAD-UNAM-DGTIC-250 and 252), financial support from DGAPA-UNAM (grant IN207318), CONACyT/México (grants 254014 and 253776) and the Ph.D. scholarships No. 273438 and 336875 to W. E. V. N and E. I. J respectively. This study benefits from resources at LURMN in IQ-UNAM, financed by CONACYT Mexico (Project: 0224747) and UNAM. We are indebted to Prof. Anatoli Iatsimirski for performing the calculations of the heterodimerisation constants and for his important contributions to this work. We also thank M. Sc. E. Hernández-Huerta for support in the search for information from the literature and Dr V. Duarte-Alaniz for his assistance on data graphing. In addition, we are grateful to F. J. Pérez, L. Velasco, and M. C. García for mass analysis, and M. A. Peña, E. Huerta, H. Ríos and R. Gaviño for recording NMR experiments, as well as M. Aguilar-Araiza, D. Vázquez-Cuevas and G. Cortés-Romero for technical support.Notes and references
- L. Pauling, R. B. Corey and H. R. Branson, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 205–211 CrossRef CAS.
- A. E. García and K. Y. Sanbonmatsu, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 2782–2787 CrossRef PubMed.
- R. Dahm, Hum. Genet., 2008, 122, 565–581 CrossRef CAS PubMed.
- (a) E. T. Kool, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 1–22 CrossRef CAS PubMed; (b) K. M. Guckian, B. A. Schweitzer, R. X.-F. Ren, C. J. Sheils, D. C. Tahmassebi and E. T. Kool, J. Am. Chem. Soc., 2000, 122, 2213–2222 CrossRef CAS PubMed.
- (a) A. Diez-Martinez, E. K. Kim and R. Krishnamurthy, J. Org. Chem., 2015, 80, 7066–7075 CrossRef CAS PubMed; (b) W. Jiang, K. Tiefenbacher, D. Ajami and J. Rebek, Chem. Sci., 2012, 3, 3022–3025 RSC.
- (a) J. R. Quinn and S. C. Zimmerman, Org. Lett., 2004, 6, 1649–1652 CrossRef CAS PubMed; (b) B. Askew, P. Ballester, C. Buhr, K. S. Jeong, S. Jones, K. Parris, K. Williams and J. Rebek, J. Am. Chem. Soc., 1989, 111, 1082–1090 CrossRef CAS; (c) E. I. Jiménez, W. E. Vallejo Narváez, C. A. Román-Chavarría, J. Vazquez-Chavez, T. Rocha-Rinza and M. Hernández-Rodríguez, J. Org. Chem., 2016, 81, 7419–7431 CrossRef PubMed.
- (a) J. M. Purcell, H. Susi and J. R. Cavanaugh, Can. J. Chem., 1969, 47, 3655–3660 CrossRef CAS; (b) W. Luo, C. Lin, J. Lin, Dah-YuKao and J. Chen, J. Chin. Chem. Soc., 2000, 47, 1177–1183 CrossRef CAS.
- (a) Y. Kyogoku, R. C. Lord and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1967, 57, 250–257 CrossRef CAS PubMed; (b) T. Hupp, C. Sturm, E. M. Basílio Janke, M. P. Cabre, K. Weisz and B. Engels, J. Phys. Chem. A, 2005, 109, 1703–1712 CrossRef CAS PubMed.
- K. S. Jeong, T. Tjivikua and J. Rebek, J. Am. Chem. Soc., 1990, 112, 3215–3217 CrossRef CAS.
- W. L. Jorgensen and D. L. Severance, J. Am. Chem. Soc., 1991, 113, 209–216 CrossRef CAS.
- W. L. Jorgensen and J. Pranata, J. Am. Chem. Soc., 1990, 112, 2008–2010 CrossRef CAS.
- (a) P. J. Cox and S. F. Parker, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 2578–2580 CrossRef; (b) S. Hachiya, Y. Kasashima, F. Yagishita, T. Mino, H. Masu and M. Sakamoto, Chem. Commun., 2013, 49, 4776–4778 RSC; (c) M. Puszyńska-Tuszkanow, M. Daszkiewicz, G. Maciejewska, Z. Staszak, J. Wietrzyk, B. Filip and M. Cieślak-Golonka, Polyhedron, 2011, 30, 2016–2025 CrossRef.
- R. R. Gardner and S. H. Gellman, J. Am. Chem. Soc., 1995, 117, 10411–10412 CrossRef CAS.
- J. R. Quinn, S. C. Zimmerman, J. E. Del Bene and I. Shavitt, J. Am. Chem. Soc., 2007, 129, 934–941 CrossRef CAS PubMed.
- T. J. Murray and S. C. Zimmerman, J. Am. Chem. Soc., 1992, 114, 4010–4011 CrossRef CAS.
- D. Rusinska-Roszak, J. Phys. Chem. A, 2015, 119, 3674–3687 CrossRef CAS PubMed.
- J. Ho, C. J. Easton and M. L. Coote, J. Am. Chem. Soc., 2010, 132, 5515–5521 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules; A quantum theory, 1994 Search PubMed.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- A. E. Shchavlev, A. N. Pankratov, V. B. Borodulin and O. A. Chaplygina, J. Phys. Chem. A, 2005, 109, 10982–10996 CrossRef CAS PubMed.
- J. Hine, S. Hahn and J. Hwang, J. Org. Chem., 1988, 53, 884–887 CrossRef CAS.
- A. V. Galanti, J. Appl. Polym. Sci., 1984, 29, 1611–1616 CrossRef CAS.
- E. J. Cabrita and S. Berger, Magn. Reson. Chem., 2001, 39, S142–S148 CrossRef CAS.
- F. G. Bordwell and H. E. Fried, J. Org. Chem., 1991, 56, 4218–4223 CrossRef CAS.
- G. Schwarzenbach and K. Lutz, Helv. Chim. Acta, 1940, 23, 1139–1146 CrossRef CAS.
- M. Aljahdali, A. A. El-Sherif, M. M. Shoukry and S. E. Mohamed, J. Solution Chem., 2013, 42, 1028–1050 CrossRef CAS.
- F. G. Bordwell, J. E. Bartmess and J. A. Hautala, J. Org. Chem., 1978, 43, 3095–3101 CrossRef CAS.
- H. F. Walton and A. A. Schilt, J. Am. Chem. Soc., 1952, 74, 4995–4996 CrossRef CAS.
- A. Dunger, H. H. Limbach and K. Weisz, Chem.–Eur. J., 1998, 4, 621–628 CrossRef CAS.
- J. Chen, J. Chem. Soc., Faraday Trans., 1994, 90, 717–720 RSC.
- I. Koppel, J. Koppel, F. Degerbeck, L. Grehn and U. Ragnarsson, J. Org. Chem., 1991, 56, 7172–7174 CrossRef CAS.
- R. A. Mcclelland, N. E. Seaman, J. M. Duff and R. E. Branston, Can. J. Chem., 1985, 63, 121–128 CrossRef CAS.
- F. G. Bordwell, Acc. Chem. Res., 1988, 21, 456–463 CrossRef CAS.
- J. W. Bunting, A. Toth, C. K. M. Heo and R. G. Moors, J. Am. Chem. Soc., 1990, 112, 8878–8885 CrossRef CAS.
- J. Von Sonntag, W. Knolle, S. Naumov and R. Mehnert, Chem.–Eur. J., 2002, 8, 4199–4209 CrossRef CAS.
- H. S. Levene, P. A. Bass and L. W. Simms, J. Biol. Chem., 1926, 70, 229–241 Search PubMed.
- A. Diez-Martinez, E. K. Kim and R. Krishnamurthy, J. Org. Chem., 2015, 80, 7066–7075 CrossRef CAS PubMed.
- J. Jonas and J. Gut, Collect. Czech. Chem. Commun., 1962, 27, 716–723 CrossRef CAS.
- A. Psoda, Z. Kazimierczuk and D. Shugar, J. Am. Chem. Soc., 1974, 96, 6832–6839 CrossRef CAS PubMed.
- J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
- P. L. A. Popelier and L. Joubert, J. Am. Chem. Soc., 2002, 124, 8725–8729 CrossRef CAS PubMed.
- (a) The delocalisation indices represent a measure of the degree of covalency of a given pairwise interaction in a molecule or molecular cluster according to ref. 18; (b) M. García-Revilla, P. L. A. Popelier, E. Francisco and Á. Martín Pendás, J. Chem. Theory Comput., 2011, 7, 1704–1711 CrossRef PubMed; (c) X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- The carbonyl in position 4 of uracil derivatives participates to a greater extent in H-bonding than that in position 2, as shown by NMR experiments (ref. 29). The same reference also shows that for I10 and I11, the C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in position 2 participates more in the self-association than that in position 4. The proton affinity calculations of I5 show that the most basic carbonyl for this compound is in position 2 (see Table 5).
O in position 2 participates more in the self-association than that in position 4. The proton affinity calculations of I5 show that the most basic carbonyl for this compound is in position 2 (see Table 5). - J. M. Guevara-Vela, E. Romero-Montalvo, A. Costales, Á. M. Pendás and T. Rocha-Rinza, Phys. Chem. Chem. Phys., 2016, 18, 26383–26390 RSC.
- Z. B. Maksić, B. Kovačević and R. Vianello, Chem. Rev., 2012, 112, 5240–5270 CrossRef PubMed.
- G. Jakab, C. Tancon, Z. Zhang, K. M. Lippert and P. R. Schreiner, Org. Lett., 2012, 14, 1724–1727 CrossRef CAS PubMed.
- X. Ni, X. Li, Z. Wang and J. P. Cheng, Org. Lett., 2014, 16, 1786–1789 CrossRef CAS PubMed.
- F. G. Bordwell and D. Algrim, J. Org. Chem., 1976, 41, 2507–2508 CrossRef CAS.
- J. I. Wu, J. E. Jackson and P. V. R. Schleyer, J. Am. Chem. Soc., 2014, 136, 13526–13529 CrossRef CAS PubMed.
- N. A. Prokopenko, I. A. Bethea, C. J. Clemens IV, A. Klimek, K. Wargo, C. Spivey, K. Waziri and A. Grushow, Phys. Chem. Chem. Phys., 2002, 4, 490–495 RSC.
- D. M. Porter and W. S. Brey, J. Phys. Chem., 1967, 71, 3779–3783 CrossRef CAS PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- For example, amide A4, has the highest value of ΔδN–H (5.69 ppm) and of the self-association constant as well (Table 3). The same trend can be observed for A5 and I1 (Fig. 10) and another structurally-related amide–imides pairs (Fig. S2 and S13 in the ESI†).
- O. Lukin and J. Leszczynski, J. Phys. Chem. A, 2002, 106, 6775–6782 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- N. Qiao, M. Li, W. Schlindwein, N. Malek, A. Davies and G. Trappitt, Int. J. Pharm., 2011, 419, 1–11 CrossRef CAS PubMed.
- J. Xie, J. G. Pierce, R. C. James, A. Okano and D. L. Boger, J. Am. Chem. Soc., 2011, 133, 13946–13949 CrossRef CAS PubMed.
- B. A. Blight, C. A. Hunter, D. A. Leigh, H. McNab and P. I. T. Thomson, Nat. Chem., 2011, 3, 244–248 CrossRef CAS PubMed.
- M. K. Tiwari and K. Vanka, Chem. Sci., 2017, 8, 1378–1390 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational details. Protocol for the recording of 1H-DOSY and 1H-NMR titrations (A1, A2, A4–A7, I1–I5 and I8). Correlations of the computed acidity and basicity with experimental data. Molecular graphs of the monomers and dimers of amides and imides computed with SMD-M06-2x/6-311++G(2d,2p) electron densities. Characterisation of selected HBs in terms of the topological properties of ρ(r) such as delocalisation index and the Interacting Quantum Atoms energy partition. XYZ coordinates and electronic energies of all species addressed in the paper. See DOI: 10.1039/c8sc01020j |
| ‡ Present address: Department of Chemistry, University of British Columbia, Okanagan, 3247 University Way, Kelowna, British Columbia, Canada V1V 1V7. |
| This journal is © The Royal Society of Chemistry 2018 |