Rational design of patchy colloids via landscape engineering
Andrew W.
Long
a and
Andrew L.
Ferguson
 *abc
*abc
aDepartment of Materials Science and Engineering, University of Illinois at Urbana-Champaign, 1304 West Green Street, Urbana, IL 61801, USA. E-mail: alf@illinois.edu; Fax: +1 217 333 2736; Tel: +1 217 300 2354
bDepartment of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, 600 South Mathews Avenue, Urbana, IL 61801, USA
cDepartment of Physics, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, IL 61801, USA
First published on 17th October 2017
Abstract
We present a new data-driven inverse design platform for self-assembling materials that we term “landscape engineering”. The essence of the approach is to sculpt the self-assembly free energy landscape to favor the formation of target aggregates by rational manipulation of building block properties. The approach integrates nonlinear manifold learning with hybrid Monte Carlo techniques to efficiently recover self-assembly landscapes, which we subsequently optimize using the covariance matrix adaptation evolutionary strategy (CMA-ES). We demonstrate the effectiveness of this technique in the design of anisotropic patchy colloids to form hollow polyhedral capsids. In the case of icosahedral capsids, our approach discovers a building block possessing a 76% improvement in the assembly rate over an initial expert-designed building block. In the case of octahedral clusters, our platform produces a building block with a 60% yield despite being challenged with a poor initial building block design incapable of forming stable octahedra.
Design, System, ApplicationBuilding block self-assembly is an important process in the fabrication of many biological and functional materials systems. We propose a novel data-driven inverse design platform capable of designing self-assembling building blocks to form desired target aggregates by rational engineering of the underlying self-assembly free energy landscape. This method employs the diffusion map nonlinear dimensionality reduction technique to infer the low-dimensional manifold containing the important collective modes of the self-assembly dynamics and hybrid Monte Carlo sampling to efficiently construct free energy landscapes in this low-dimensional space. By virtue of the interpretability of the diffusion map coordinates as the slow dynamical modes of the assembly process, the resultant self-assembly landscapes encapsulate both the thermodynamic (what will form?) and mechanistic (how will it form?) aspects of assembly within a dynamically interpretable low-dimensional parameterization. Using a directed evolutionary strategy, we optimize building block architectures to form a desired target aggregate by sculpting the features of the underlying self-assembly landscape to favor the production of the target structure. We apply this design framework to a class of anisotropic patchy colloids to systematically design building blocks capable of robust assembly of desired hollow polyhedral capsids. These results demonstrate the efficacy of this landscape engineering approach in both improving upon expert-designed architectures, and in discovering optimal designs from poor initial guesses. |
1 Introduction
Self-assembly, the spontaneous organization of building blocks into hierarchical structures, is a prominent formation mechanism for biological systems, driving the growth of lipid membranes,1,2 viral capsids,3,4 fibrils,5 and potentially even the precursors of RNA.6 The spontaneous nature of self-assembly allows for the fabrication of these structures, using the intrinsic geometric and chemical properties of the building blocks to guide the assembly of complex aggregates with a high degree of specificity. This specificity in self-assembly has made it a valuable fabrication technique for the “bottom-up” synthesis of novel materials.7–9 Self-assembly has been used extensively across materials applications, from honeycomb nanoscale superstructures formed from unlike covalently-linked organo-functionalized inorganic clusters,10 biomimetic vesicles for targeted drug delivery11,12 and cell penetrating peptides,13–15 to sensing with protein reactive dye nanoparticles16 and hierarchical ZnO nanostructures,17 and optoelectronic devices such as organic solar cells18,19 and photonic crystals.20 This diversity of applications has led to an intense interest in understanding the microscopic mechanisms guiding the self-assembly process, and in developing design rules and frameworks to rationally engineer self-assembling building blocks capable of forming desired target aggregates.A variety of design paradigms have been developed for the problem of robust self-assembly of a target structure, including the use of DNA-hybridization,21,22 geometric templating,23,24 geometrical manifolds,25 implicit parameter evolution,26,27 local bond rules28 Markov state models,29,30 partition functions,31,32 and integrated molecular simulation and experimental synthesis.33,34 While these techniques have proven successful in manipulating the chemistry and geometry of building blocks to possess a desired thermodynamic ground state structure, the dynamics of assembly can play an important role in dictating the accessibility and kinetic stability of the various aggregate structures.35 Path-based design techniques simultaneously engage the thermodynamics and dynamical pathways of assembly by defining and manipulating the structural pathways along which aggregates form.36 These “pathway engineering” techniques,31 seek to engineer building blocks and assembly conditions to direct assembly along desired assembly routes and away from trapping states.
Self-assembly of rigid building blocks such as patchy colloids proceeds in a 6N-dimensional phase space describing the Cartesian coordinates and orientation of each of the N constituent building blocks. The dimensionality of this space is even higher for “floppy” building blocks such as peptides possessing internal degrees of freedom. The high dimensionality of configurational phase space can make it challenging to identify and enumerate all accessible assembly pathways.37 It is generically true, however, that interactions between building block degrees of freedom give rise to a small number of emergent collective modes governing the important long-time assembly dynamics and to which the remaining degrees of freedom are effectively slaved.37,38 Accordingly, the self-assembly dynamics admit low-dimensional parameterizations in a small number of collective order parameters. Such low-dimensional descriptions can prove exceedingly valuable in identifying and discriminating the important metastable aggregation states and the low-free energy pathways by which they are connected.
Dimensionality reduction techniques are a class of machine learning approaches that can furnish collective order parameters in which to construct self-assembly free energy landscapes by identifying low-dimensional surfaces lying latent within high-dimensional data sets. Linear dimensionality reduction techniques, such as principal components analysis (PCA), determine a linear projection of a high-dimensional data set onto a low-dimensional hyperplane preserving the bulk of the variance in the data.39 PCA is poorly suited to the analysis of self-assembly processes for two main reasons. First, it requires the representation of the self-assembling aggregates within a common basis set, which is challenging for aggregates that are both freely translating and rotating through space and which can possess varying numbers of building blocks. Second, the low-dimensional assembly landscapes emerge from complex multi-body interactions that are expected to yield complex and convoluted manifolds that are inadequately described by hyperplane approximations. Nonlinear dimensionality reduction techniques, such as Isomap,40 Laplacian eigenmaps,41 and diffusion maps,42,43 integrate information on pairwise distances between samples in a dataset to identify and extract a representation of the low-dimensional intrinsic manifold that preserves the intrinsic geometry and topology of the data. Diffusion maps, in particular, furnish collective variables that are coincident with the slowest dynamical modes of the self-assembly process, and have shown great promise in defining low-dimensional manifolds for colloidal and Janus particle self-assembly.37,38
Having defined the collective variables in which to parameterize the self-assembly free energy landscape, the landscape itself can be estimated by projecting simulation data into these variables. For systems containing high free energy barriers unbiased sampling is typically unable to comprehensively and efficiently explore the accessible configurational space. Accordingly, enhanced sampling techniques are generally employed to accelerate landscape exploration and recovery. A number of techniques may be employed to this end, including umbrella sampling,44 metadynamics,45,46 and adaptive biasing force,47 but difficulties may arise from the absence of explicit expressions for the collective variables in terms of the particle coordinates. The recently developed diffusion-map-directed molecular dynamics (DM-d-MD)48,49 and intrinsic map dynamics (iMapD)50 approaches ameliorate these difficulties by enabling accelerated exploration to be performed directly in diffusion map coordinates. In this work, we propose a biased hybrid Monte Carlo scheme51–53 to perform sampling directly in the diffusion map coordinate space to achieve rapid sampling and exploration of the configurational phase space of cluster aggregation.
With the self-assembly free energy landscape parameterized by dynamically meaningful collective coordinates in hand, we perform inverse building block design by manipulating the building block properties to sculpt the free energy landscape to favor the assembly of a desired target aggregate. We cast this landscape engineering procedure as an optimization problem that seeks to maximize an objective function defined over the landscape. In this work, we adopt the simplest objective function corresponding to minimization of the free energy of the target aggregate. Although this choice would appear to be exclusively thermodynamic in nature, we show that its optimization implicitly captures aspects of the kinetic assembly mechanisms by funneling the dynamical assembly routes that emerge as low-free energy pathways within the dynamically meaningful low-dimensional parameterization towards this desired minimum. More sophisticated choices of objective function that more explicitly incorporate dynamical aspects of assembly are possible, for example minimization of the action along the minimum free energy path.54,55 The optimization problem may be tackled using any number of optimization techniques, including gradient descent,56 swarm approaches,57 and genetic algorithms.58 In this study we employ the covariance matrix adaptation evolutionary strategy (CMA-ES) as a state-of-the-art technique59,60 that has previously been used in the design of substrates to direct the assembly of lamella patterned block copolymers.27,61
We demonstrate our inverse design procedure in the self-assembly of a class of double annular ring patchy colloids that serve as a flexible model of experimentally-realizable anisotropic colloidal building blocks.9 This model provides a minimal representation of long-ranged attractive and short-ranged excluded volume interactions by employing rigid groups of soft spheres possessing isotropic pair potentials. Specificity in interactions between different particle is a coarse-grained mimic of experimentally-demonstrated surface functionalization techniques such as complementary DNA oligonucleotides or antibody/antigen pairs.9,62–65 This model is amenable to efficient simulation wherein interaction anisotropy is encoded and tuned by the particle architecture rather than through modifications of the underlying force field. Nevertheless, our inverse design approach is agnostic to the particular choice of model, and we could have equally well chosen to employ a popular Kern–Frenkel-type model of patchy particles in which interaction anisotropy is treated through radially and orientationally dependent interaction potentials.3,66–69 We employ landscape engineering to optimize the polar angles controlling the placement of the annular rings to maximally favor the assembly of icosahedral and octahedral hollow capsids. In both cases, we show that the technique rapidly converges towards an optimal building block design. We validate the designed building blocks in unbiased simulations of assembly to quantify the improvements in assembly rate and yield. Our approach is directly extensible to more complex self-assembling systems and arbitrary objective functions, opening the door to automated data-driven design of self-assembling materials.
2 Materials and methods
2.1 Patchy colloid model
In this work, we consider self-assembly of the double ring patchy colloid model proposed by Zhang and Glotzer,9 and which we have previously studied using diffusion maps.37 A similar patchy particle model was employed by Guo et al. in simulations of the self-assembly of tunable supracolloidal helices.70 In this model, the surface of a spherical colloidal particle (type A) is decorated with two annular rings of smaller spheres (types B and C), as portrayed in Fig. 1. The diameter of these three species is chosen as σA = 5σ, σB = σC = σ. For a given polar angle ϕ, we generate a ring as the maximal non-overlapping arrangement of patch spheres over the central sphere. After generating rings at ϕB, ϕC, we rotate the C-ring around it's central axis to minimize the overlap between patch particles in the B- and C-rings. These rings are then rigidly constrained to the surface of the central A-sphere, neglecting all intraparticle interactions.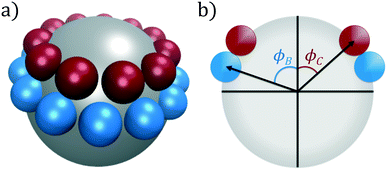 | ||
| Fig. 1 Double annular ring patchy colloid model used in this study. (a) A central particle of type A (silver) is decorated with two rings of types B (blue) and C (red), visualized in VMD.71 (b) The location of these coaxial rings are determined by the polar angles (ϕB, ϕC). For each ring, we compute the maximal number of non-overlapping patch particles for this given height and evenly distribute these patches around the surface of the central particle. | ||
Colloidal interactions are determined by the patchy rings, enabling a rich diversity of interactions built up from spherically symmetric potentials.9,72 Type-specific interactions between B–B and C–C patches are given by the Lennard-Jones potential
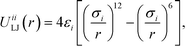 | (1) |
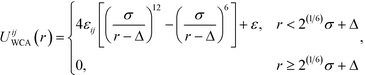 | (2) |
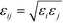 is defined by the Berthelot mixing rule,74 and Δij = (σi + σj)/2 − σ shifts the potential to act between particle surfaces.75
is defined by the Berthelot mixing rule,74 and Δij = (σi + σj)/2 − σ shifts the potential to act between particle surfaces.75
For this study, colloid structure is optimized to stabilize a target self-assembled aggregate by tuning the polar angles, (ϕB, ϕC). Previous studies of this patchy colloid model have shown that manipulation of the polar angles induces self-assembly of a variety of different polyhedral architectures.9,37 Since the number of particles Ni in a ring may change with varying ϕi due to geometric constraints on how many particles can occupy an annular ring, we redistribute the sum of the particle Lennard-Jones εi parameters such that the total interaction strength Ei = Niεi is conserved for each particle type i = {B,C}.
Following ref. 37, simulations are performed in dimension less units, with σ = σB = σC = 1, σA = 5, ε = εA = 1, EB = NBεB = 14 and EC = NCεC = 11, and m = mA = mB = mC = 1. For these parameters, ΔAA = 4, ΔAB = ΔAC = 2, and ΔBC = 0, such that A overlaps are effectively forbidden and the particles interact primarily by specific surface interactions between the B and C rings. We use the dimensionless mapping previously defined in ref. 37 to map our dimensionless simulations to real units. We consider particles of size σA = 5σ = 1 μm, with the density ρA = 1 g cm−3, and an energy scale of ε = 1kBT at T = 298 K. The real temperature is given as T = εT*/kB and real time is given by 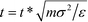 . Our simulations are run at T* = 0.8, giving a real temperature of 238.4 K, with a time step of dt* = 5 × 10−3 which yields a real unit time step of dt = 0.36 μs.
. Our simulations are run at T* = 0.8, giving a real temperature of 238.4 K, with a time step of dt* = 5 × 10−3 which yields a real unit time step of dt = 0.36 μs.
2.2 Landscape engineering for patchy colloid design
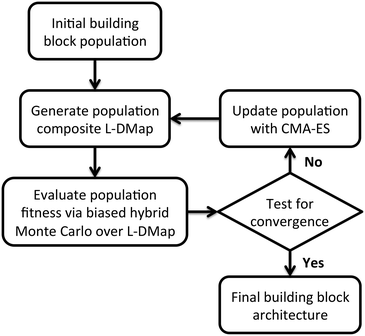
We employ an evolutionary strategy for building block design by iterative sculpting of the self-assembly free energy landscape by directed manipulation of the patchy particle polar angles. A schematic flowchart of the iterative procedure is presented in Fig. 2. Given an initial ensemble of building block designs, we conduct Langevin dynamics simulations of the self-assembly of each particle design and apply diffusion maps to construct a low-dimensional parameterization of the accessible configurational space.37,76 We then perform enhanced sampling over the low-dimensional landscape to determine the self-assembly free energy landscape for each particle design, compute the relative stability of the target self-assembled aggregate, and assign a fitness to each design. We then analyze the relative fitnesses of the swarm of initial particle designs using CMA-ES to predictively design a new generation of particle designs predicted to possess higher fitness. We loop through this process – unbiased sampling, composite diffusion map analysis, enhanced sampling in the low-dimensional space, CMA-ES update of the particle design – until the CMA-ES approach converges to a stable optimal building block design. We now proceed to describe each step in detail.After this initialization procedure, we run Langevin dynamics simulations using the potentials described in section 2.1 at T* = 0.8 for 2.5 × 10−6 time steps with dt* = 5 × 10−3, with diameter-scaled dampening coefficients γi = λσi, where we select in our dimensionless units λ = 1. We sample configurations every 250 time steps, yielding 104 snapshots per trajectory. For each of the P building blocks we perform three independent runs to provide a representative sample of the accessible structures of a given building block over which to build a set of low-dimensional descriptors using diffusion maps. In this work we employ P = 9–10 as a balance between good exploration of the building block design space and the computational burden associated with the simulation and analysis of each generation of the optimization loop.
Diffusion maps. Nonlinear dimensionality reduction using diffusion maps has been used extensively in the study of single-molecule folding,81–83 self-assembly,37,38,84 and colloidal crystallization85,86 to define low-dimensional parameterizations of the dynamical evolution of the system. The primary requirement to apply diffusion maps to the problem of assembly is a measure of similarity between cluster aggregates. An appropriate measure of configurational similarity must eliminate the invariances associated with translation, rotation, and the identical nature of the self-assembling building blocks. We previously proposed a graph-based distance metric that represents each self-assembled cluster as an interaction graph in which nodes represent building blocks and edges pairwise interactions determined according to some geometric or energetic criterion.37,38,76,86 This graph abstraction of each aggregate mods out the symmetries associated with translation, rotation, and particle fungibility, and admits natural and efficient measures of similarity based on graph matching. Specifically, we define the distance dij between two aggregates xi and xj with corresponding interaction graphs Gi and Gj as,
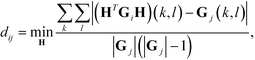 | (3) |
Having computed the N × N matrix of graph-based pairwise distances d between an ensemble of aggregates {xi}Ni=1 observed in our simulation trajectories, the diffusion map approach proceeds by constructing a fictitious random walk over this high-dimensional point cloud. Importantly, we lump together into this ensemble clusters observed within the Langevin dynamics simulations conducted for each of the candidate building blocks within the population at a particular iteration of the design loop. Generating a single composite diffusion map space allows us to assess the impact of building block architecture upon the self-assembly landscape within a unified basis set.
To construct the random walk, we first convolve the distances matrix with a Gaussian kernel to produce the matrix A,
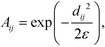 | (4) |
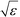 defines the characteristic step size of the random walk, and Aij may be considered a relative (unnormalized) hopping probability. Systematic procedures exist to define appropriate values of
defines the characteristic step size of the random walk, and Aij may be considered a relative (unnormalized) hopping probability. Systematic procedures exist to define appropriate values of 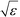 by analysis of the A matrix. Row normalization of A yields a right-stochastic Markov transition matrix M = D−1A, where D is a diagonal matrix of row sums,
by analysis of the A matrix. Row normalization of A yields a right-stochastic Markov transition matrix M = D−1A, where D is a diagonal matrix of row sums, 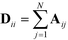 . Spectral decomposition of M yields a set of eigenvalues {λi}Ni=1 in non-ascending order with corresponding eigenvectors
. Spectral decomposition of M yields a set of eigenvalues {λi}Ni=1 in non-ascending order with corresponding eigenvectors 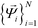 , including the top trivial pair
, including the top trivial pair 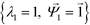 .
.
These eigenvectors are discrete approximations to the eigenfunctions of the backwards Fokker–Planck operator describing diffusion over the data. The eigenvalues correspond to the implied time scales of these relaxation modes, and identification of a gap in the eigenvalue spectrum after λk+1 reveals a separation of relaxation timescales between the slow relaxation modes (i.e. large eigenvalues) and fast modes (i.e. small eigenvalues). This motivates the construction of the k-dimensional diffusion mapping in the top k non-trivial modes,
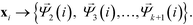 | (5) |
In this work, we utilize the L-method89 to identify gaps in eigenvalue spectra. In all cases we identify a gap after λ3, prompting the construction of two-dimensional embeddings in (![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) 2,
2, ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) 3).
3).
Landmark acceleration. Due to the computational complexity of graph matching as a distance measure, we utilize the recently developed landmark diffusion map (L-dMap) algorithm as a computationally efficient and highly accurate approximation for the standard diffusion map technique described above to realize massive accelerations of our runtime performance.80 Here we provide the key methodological details for L-dMaps, the full details of this method are presented in ref. 80.
Given the samples {xi}Ni=1 and pairwise distance matrix d, we identify a subset of M ≪ N aggregates, {zj}Mj=1 ⊆ {xi}Ni=1, to serve as landmark points via k-medoids clustering,90 with corresponding landmark multiplicities {cj}Mj=1 given by the number of points x within the Voronoi volume surrounding each landmark {zj}Mj=1. We use these M landmarks to compute an inexpensive diffusion map embedding that we subsequently use to efficiently project the remaining (N–M) non-landmark points.
We compute the unnormalized hopping probability Ãij between landmarks zi and zj as,
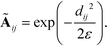 | (6) |
Defining the diagonal multiplicity matrix ![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) = diag (ci), the normalized Markov matrix for the reduced problem is given by
= diag (ci), the normalized Markov matrix for the reduced problem is given by ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) =
= ![[D with combining tilde]](https://www.rsc.org/images/entities/b_char_0044_0303.gif) −1Ã where
−1Ã where ![[D with combining tilde]](https://www.rsc.org/images/entities/b_char_0044_0303.gif) is the diagonal matrix,
is the diagonal matrix,
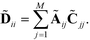 | (7) |
Incorporating the C matrix into the normalization accounts for the local density of points around each landmark, and assures that the resulting M × M random walk possesses the same eigenvectors as those which would be recovered from the N × N random walk in which each landmark point is replicated Cii times as a representative of the Cii points residing within its Voronoi volume.80,91
The collective variables spanning the low-dimensional intrinsic manifold are then given by the solution of the eigenvalue problem, ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif)
![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif)
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) =
= ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif)
![[capital Lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1ed.gif) , enforcing the normalization condition
, enforcing the normalization condition 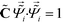 . We have shown that the
. We have shown that the 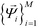 serve as close approximations to the full diffusion map but are computable at a fraction of the cost.80
serve as close approximations to the full diffusion map but are computable at a fraction of the cost.80
The remaining (N–M) non-landmark points are embedded landmark diffusion map manifold via the Nyström extension.92–94 For an out-of-sample point xnew, we compute the distance to all landmarks {zj}Mj=1 to construct the kernel vector 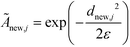 . We normalize this kernel vector and concatenate it onto our
. We normalize this kernel vector and concatenate it onto our ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) matrix as an additional row with elements
matrix as an additional row with elements 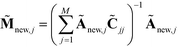 . The coordinates of this new point in the k-dimensional diffusion map space defined by the top l = 2, …,(k + 1) non-trivial eigenvectors of
. The coordinates of this new point in the k-dimensional diffusion map space defined by the top l = 2, …,(k + 1) non-trivial eigenvectors of ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) is given as
is given as
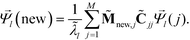 | (8) |
The computational speedup of landmark diffusion maps is realized by the reduction in cost of the calculation of the diffusion map embedding from ∼![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2) to ∼
(N2) to ∼![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (M2 + NM).80 In this work, N ∼ 105 and M ∼ 102, so the computational savings are substantial. C++ and Python implementations of our graph alignment and landmark diffusion map approaches are available at https://github.com/awlong/DiffusionMap.
(M2 + NM).80 In this work, N ∼ 105 and M ∼ 102, so the computational savings are substantial. C++ and Python implementations of our graph alignment and landmark diffusion map approaches are available at https://github.com/awlong/DiffusionMap.
![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) } providing a low-dimensional parameterization of the configurational space containing the important assembly dynamics, we wish to recover the self-assembly free energy landscape supported by this parameterization. Theoretically we can estimate the free energy landscape from a prolonged unbiased simulation, approximating the probability density function P(
} providing a low-dimensional parameterization of the configurational space containing the important assembly dynamics, we wish to recover the self-assembly free energy landscape supported by this parameterization. Theoretically we can estimate the free energy landscape from a prolonged unbiased simulation, approximating the probability density function P(![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) ) and free energies as βF(
) and free energies as βF(![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) ) = −ln
) = −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(
P(![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) ) + C, where we use F to denote the Helmholtz free energy,
) + C, where we use F to denote the Helmholtz free energy, 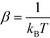 , and C is an arbitrary additive constant. However, this process suffers from poor sampling of rugged landscapes due to kinetic trapping behind high free energy barriers. Instead, we efficiently compute the landscape by performing accelerated sampling directly in the diffusion map collective coordinates.
, and C is an arbitrary additive constant. However, this process suffers from poor sampling of rugged landscapes due to kinetic trapping behind high free energy barriers. Instead, we efficiently compute the landscape by performing accelerated sampling directly in the diffusion map collective coordinates.
Efficient sampling along reaction coordinates is a problem of intense interest in the molecular simulation community, with a variety of developments in recent years. For systems where the reaction coordinates are constructed as analytical functions of the particle coordinates, biasing forces can be derived to localize systems in particular regions of the reaction coordinate space within molecular or Langevin dynamics simulations.95–98 It is a well known deficiency of diffusion maps, and nonlinear manifold learning techniques in general, that they do not furnish explicit mappings between particle coordinates and the low-dimensional projections.99 We circumvent this difficulty by performing Monte Carlo sampling, whereby we can localize sampling within particular regions of the low-dimensional embedding by accepting or rejecting trial moves under the action of a biasing potential formulated in the collective variables. Kevrekidis and co-workers proposed an approach using lifting and restricting operators to translate between the low and high-dimensional spaces,100 but this approach did not apply any bias to localize the dynamical evolution of the system. We observe that a small number of techniques have very recently been proposed to compute biasing forces within low-dimensional projections lacking an explicit functional mapping and thereby enabling biased molecular dynamics calculations,101–104 but these approaches employ nearest-neighbor embeddings or basis function expansions to furnish only approximate biasing forces.
Our Monte-Carlo accelerated sampling procedure proceeds by defining a collection of harmonic umbrella potentials44α in the low-dimensional collective coordinates,
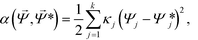 | (9) |
![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) * is a k-dimensional harmonic center, and κj is the strength of the harmonic constraint in the jth dimension. At the beginning of our simulation, we tag a single colloid for which the aggregation state is tracked to identify the cluster's location in diffusion map space,
* is a k-dimensional harmonic center, and κj is the strength of the harmonic constraint in the jth dimension. At the beginning of our simulation, we tag a single colloid for which the aggregation state is tracked to identify the cluster's location in diffusion map space, ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) . In this way, we are biasing the self-assembly of a particular aggregate in a sea of colloids evolving according to the unbiased system Hamiltonian.
. In this way, we are biasing the self-assembly of a particular aggregate in a sea of colloids evolving according to the unbiased system Hamiltonian.
Trial moves are proposed using a hybrid Monte Carlo (HMC) approach,51 where moves are generated using a short molecular dynamics simulation in the microcanonical ensemble. As the particles studied are strongly attractive, single-particle Metropolis Monte Carlo strategies will yield a critical slowing phenomena as aggregation occurs that produces extremely poor acceptance probabilities due to an exponential dependence on the change in potential energy when moving a single particle.105 For each HMC step, translational and rotational velocities are randomly sampled from the Maxwell–Boltzmann distribution with scaling to impose zero net momentum. Particle positions are evolved in the microcanonical ensemble using an NVE integrator implemented using the Velocity-Verlet algorithm.79 The use of an NVE integrator ensures that the proposed move is reversible. Upon completing a series of NVE integration steps, the system energy is given by the Hamiltonian H(q,p) = U(q) + K(p), where U(q) is the potential energy for the system with particles at locations q, and K(p) is the kinetic energy of the system with momenta p. Acceptance of this HMC step from the initial state (qi, pi, ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) i) to the trial state (qi+1, pi+1,
i) to the trial state (qi+1, pi+1, ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) i+1) in the presence of an umbrella restraining potential centered on
i+1) in the presence of an umbrella restraining potential centered on ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) * is determined by a Metropolis criterion,
* is determined by a Metropolis criterion,
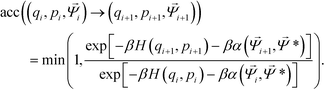 | (10) |
The benefits of HMC sampling are that it is able to rapidly sample system configurations, avoiding the low acceptance ratios of non-cluster based moves, and it is easily implemented within molecular dynamics simulation packages. We note that traditional Monte Carlo techniques involving cluster moves could also be employed for these types of simulations,105,106 however for these cases a multiple time-stepping method might prove best to limit the number of calls to the expensive biasing potential.107
We place umbrella restraining potentials over the low-dimensional diffusion map embedding in (Ψ2, Ψ3) space using Lloyd's algorithm108 to evenly partition the convex hull encompassing the projection of our unbiased simulation data. For our initial sampling pass, we generate 80 centers inside the convex hull. Since our landscapes are typically not convex, we exclude centers outside of a skin depth of our landscape, which we define to be δ = 0.005. We bin the points of the convex hull onto a 50 × 50 grid, adding each filled grid location to our set of biasing centers to effectively smooth the hull boundary shape and remove noise from the boundary due to sampling. This set of centers defines an initial series of umbrella sampling windows. Subsequent runs are performed as needed to improve coverage of under sampled regions of the manifold.
We initialize each umbrella sampling run from the previously collected simulation snapshot located closest to the umbrella window in (Ψ2, Ψ3) space. We freeze the configuration of the cluster attached to the tagged particle and disassociate the remaining particles in the box using the fast inertial relaxation engine (FIRE) algorithm109 with purely WCA interactions between particles and a time step of dt* = 10−5 until the system energy has stabilized within a tolerance of 0.1 kBT. After this initialization, we unfreeze the tagged cluster and allow the system to evolve using the hybrid Monte Carlo approach as described above. For each Monte Carlo step, we log the starting location in the diffusion map space, as well as the system kinetic and potential energies. Trial moves are proposed via short molecular dynamics runs at T* = 0.8 for 250 steps at dt* = 5 × 10−3. Upon completing this step, we calculate the diffusion map coordinates for the tagged cluster. We use the harmonic spring constants of κ = κΨ2 = κΨ3 = 1250 kBT, resulting in acceptance probabilities of approximately 30–40%. We perform 1.6 × 104 Monte Carlo steps in this fashion, allowing for equilibration to these biasing conditions by running first for 8 × 103 steps, followed by data collection for the remaining 8 × 103 steps.
Having conducted the ensemble of biased umbrella sampling runs over the manifold, we patch together the biased probability distributions to estimate the maximum likelihood unbiased free energy landscape βF(![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) ) using the BayesWHAM algorithm presented in ref. 110. This approach is a Bayesian implementation of the weighted histogram analysis method (WHAM)111 that recovers a statistically optimal estimation of the self-assembly free energy landscape equipped with uncertainty estimates furnished by sampling of the Bayes posterior. This landscape allows us to determine the fitness of each building block design within the generation, and deploy the optimization strategy described in the next section to rationally sculpt the landscape to favor the target aggregate.
) using the BayesWHAM algorithm presented in ref. 110. This approach is a Bayesian implementation of the weighted histogram analysis method (WHAM)111 that recovers a statistically optimal estimation of the self-assembly free energy landscape equipped with uncertainty estimates furnished by sampling of the Bayes posterior. This landscape allows us to determine the fitness of each building block design within the generation, and deploy the optimization strategy described in the next section to rationally sculpt the landscape to favor the target aggregate.
Having defined the fitness metric associated with any particular landscape, we now seek to optimize this property of the landscape by directed manipulation of the building block design, in this case the polar angles (ϕB, ϕC) of the two rings. Many possible optimization techniques exist, from gradient descent techniques56 to swarm techniques115 to evolutionary strategies.59 Here we use the covariance matrix adaptation evolutionary strategy (CMA-ES),59,60 Within each generation of the optimization loop, CMA-ES selects the top μ samples within the population of P candidate building blocks and uses their locations in feature space to update the estimate of the covariance matrix C and the step size σ in the design space of the two polar angles. Full details of this adaptation procedure for the covariance matrix and step size are given in ref. 60. Having updated C and σ within iteration i, we compute a new population of P building block designs in iteration (i + 1) as,
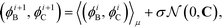 | (11) |
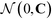 is the multi-dimensional normal distribution with mean 0 and covariance C. Given this new generation of building blocks, we check for convergence on the distribution of samples in the polar angle feature space, cutting off when the standard deviation within the generation is <1° in both ϕB and ϕC. If unconverged, we pass back through the iterative loop (Fig. 2), performing unbiased Langevin dynamics simulations for the new generation, applying landmark diffusion maps, conducting umbrella sampling to determine free energy surfaces, and conducting another round of CMA-ES. In this way, we devise a data-driven optimization framework capable of iteratively converging to a desired building block architecture with minimal user intervention. Since this inverse design approach proceeds by modifying the building block properties to engineer desired features of the underlying free energy landscape, we term this approach “landscape engineering”.
is the multi-dimensional normal distribution with mean 0 and covariance C. Given this new generation of building blocks, we check for convergence on the distribution of samples in the polar angle feature space, cutting off when the standard deviation within the generation is <1° in both ϕB and ϕC. If unconverged, we pass back through the iterative loop (Fig. 2), performing unbiased Langevin dynamics simulations for the new generation, applying landmark diffusion maps, conducting umbrella sampling to determine free energy surfaces, and conducting another round of CMA-ES. In this way, we devise a data-driven optimization framework capable of iteratively converging to a desired building block architecture with minimal user intervention. Since this inverse design approach proceeds by modifying the building block properties to engineer desired features of the underlying free energy landscape, we term this approach “landscape engineering”.
3 Results and discussion
3.1 Expert-directed optimization of hollow icosahedral formation
From previous studies of the patchy particles described in section 2.1,9,37 it is known that double-ring patchy colloid with polar angles (ϕ0B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0C) = (70.6°, 49.0°) robustly form hollow icosahedral aggregates. As a first test of our data-driven inverse design platform, we wished to determine whether the procedure could improve over this expert-designed building block architecture with polar rings placed to maximize contact between the sticky patches within an idealized icosahedral aggregate.
ϕ0C) = (70.6°, 49.0°) robustly form hollow icosahedral aggregates. As a first test of our data-driven inverse design platform, we wished to determine whether the procedure could improve over this expert-designed building block architecture with polar rings placed to maximize contact between the sticky patches within an idealized icosahedral aggregate.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0C) building block, with spacing ±5° in each dimension. Accordingly, our first generation comprises the P = 9 building block designs {(ϕ1B,
ϕ0C) building block, with spacing ±5° in each dimension. Accordingly, our first generation comprises the P = 9 building block designs {(ϕ1B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1C)} = {(ϕ0B,
ϕ1C)} = {(ϕ0B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0C),
ϕ0C),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ϕ0B ± 5°,
(ϕ0B ± 5°,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0C ± 5°)}. For each architecture, we run three unbiased simulations with differing random seeds to sample the variety of aggregate structures that can be formed. We perform a two-stage landmarking procedure to identify representative cluster topologies. First, for each architecture we generate K = 400 landmarks from data accumulated from these three unbiased simulations. Next, we aggregate these landmark points across all architectures and perform another round of landmark selection, resulting in a set of K = 400 composite landmarks spanning the aggregates sampled by all nine architectures.
ϕ0C ± 5°)}. For each architecture, we run three unbiased simulations with differing random seeds to sample the variety of aggregate structures that can be formed. We perform a two-stage landmarking procedure to identify representative cluster topologies. First, for each architecture we generate K = 400 landmarks from data accumulated from these three unbiased simulations. Next, we aggregate these landmark points across all architectures and perform another round of landmark selection, resulting in a set of K = 400 composite landmarks spanning the aggregates sampled by all nine architectures.
We utilize these K = 400 composite landmarks to generate the composite L-dMap embedding representing the low-dimensional manifold containing the important configurational assembly dynamics. In each case, a gap in the eigenvalue spectrum informs a two-dimensional embedding into the leading eigenvectors (Ψ2, Ψ3). We observe that these eigenvectors emerge from an application of diffusion maps to the ensemble of structures explored in the unbiased simulation runs, and so the precise order parameters identified by the approach differ between generations. Using the hybrid Monte Carlo approach discussed in section 2.2.3, we perform umbrella sampling for each colloid architecture to sample over this landscape, and reconstruct an estimate of the unbiased self-assembly free energy landscape using BayesWHAM.110 Finally, we compute the inherent structures over the free energy landscape for each colloid to find free energy wells representing the locally stable cluster structures. We compute the fitness of each landscape as the difference between our desired icosahedral structure and the free energy well of the most stable competing aggregate, Δ(βF) = βFicos − βFmin≠icos.
Employing Δ(βF) as a measure of the fitness of each colloidal architecture, we pass these fitness values to the CMA-ES algorithm, which selects the top μ = ⌊P/2⌋ candidates over which to perform data-driven predictive design of the next generation of candidate architectures. We start the optimization procedure with covariance matrix C = I, step size σ = 5° and evolution paths 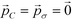 .60 The CMA-ES algorithm updates the covariance matrix and evolution paths, providing the distribution from which to draw new colloid architectures. We impose no restrictions on the range of allowable polar angles for either ring, allowing for overlap or reordering of the top and bottom rings. Using eqn (11), we draw P = 10 samples from this distribution to construct the second generation of colloidal architectures {(ϕ2B,
.60 The CMA-ES algorithm updates the covariance matrix and evolution paths, providing the distribution from which to draw new colloid architectures. We impose no restrictions on the range of allowable polar angles for either ring, allowing for overlap or reordering of the top and bottom rings. Using eqn (11), we draw P = 10 samples from this distribution to construct the second generation of colloidal architectures {(ϕ2B,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ2C)} predicted by CMA-ES to have improved fitness (i.e., enhanced stability of the target icosahedral aggregate). We continue iterating until the distribution of new configurations is sufficiently small – less than 1° in {(ϕnB,
ϕ2C)} predicted by CMA-ES to have improved fitness (i.e., enhanced stability of the target icosahedral aggregate). We continue iterating until the distribution of new configurations is sufficiently small – less than 1° in {(ϕnB,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕnC)} – at which point we declare the optimization procedure to have converged. The fittest candidate within this terminal generation represents the optimal design produced by our procedure.
ϕnC)} – at which point we declare the optimization procedure to have converged. The fittest candidate within this terminal generation represents the optimal design produced by our procedure.
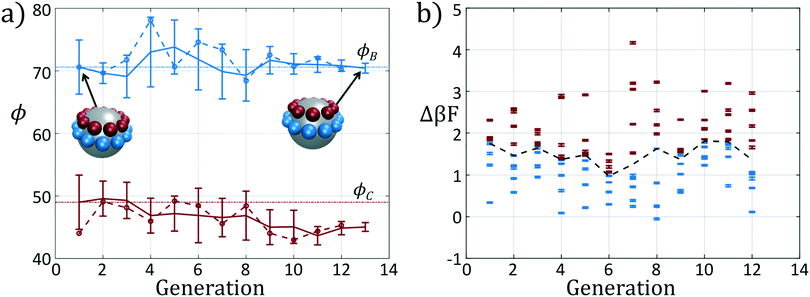
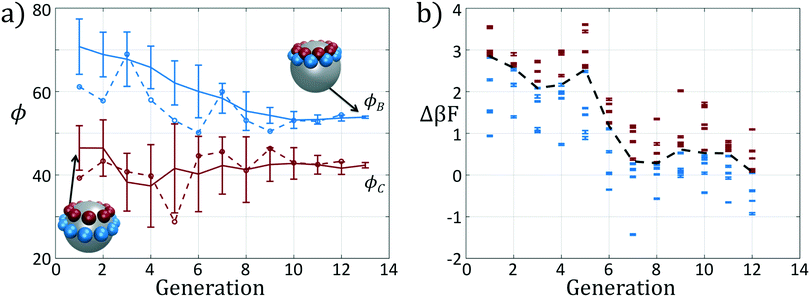
We present the sample paths of our data-driven optimization procedure in Fig. 3. From the distribution of polar angles as a function of optimization generation shown in Fig. 3a, we observe that the optimization procedure fluctuates around the expert-derived polar angles for several generations, but after four generations the interior polar angle ϕC (red) deviates from our expert-derived value by moving closer to the particle zenith. The optimization procedure converges within 12 generations, and we arrive at a final population with a standard deviation of less than 1° around the mean of (ϕB, ϕC) = (70.7°, 45.0°). The landscape engineering procedure converged upon an optimal building block design with the same outer polar angle ϕB (blue) as the expert-designed building block, but a smaller inner polar angle ϕC (red) shifted 4° towards the zenith.
In Fig. 3b we show the fitnesses of each candidate in each generation. In the early stages of the optimization procedure, the fitness metric Δ(βF) cannot be directly compared between generations since the underlying free energy surface is parameterized by different collective variables {Ψ2, Ψ3}. However, the CMA-ES procedure acts within a single generation, and so identifies the top candidates and proposes a predictive optimization step within a unified fitness basis. In the latter stages of the optimization as the particle designs converge, the fitness metrics do become comparable since the particle designs converge and the basis vectors stabilize between generations.
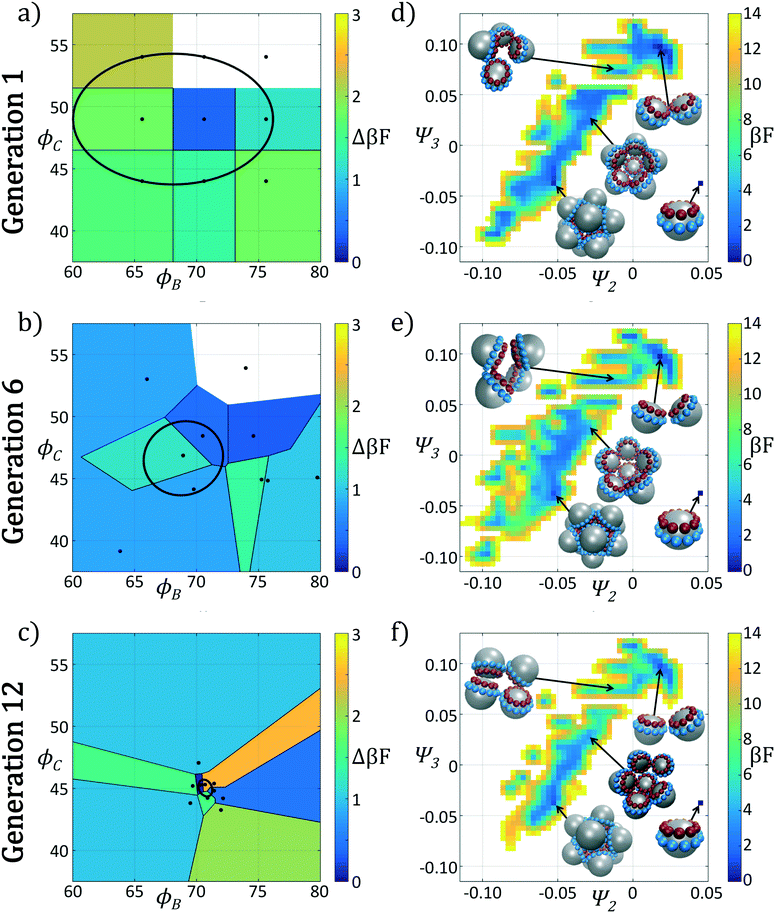
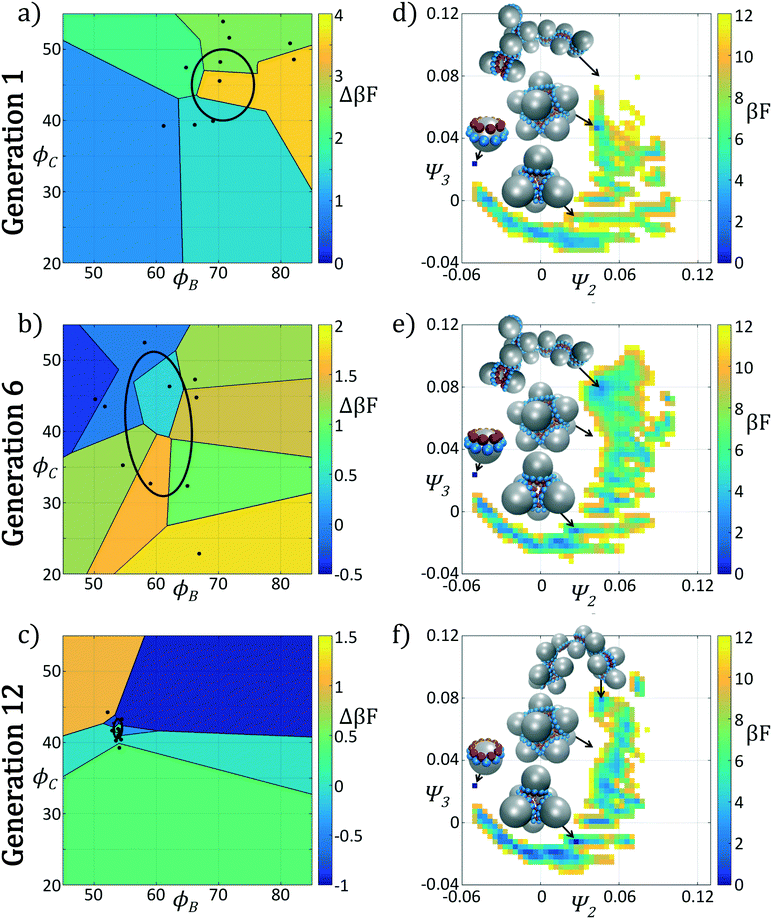
In Fig. 4 we show the ensemble of colloidal architectures in generations 1, 6, and 12 of the optimization process (panels a–c), and free energy surfaces showing the stability of the various competing self-assembled aggregates for the fittest candidate in each generation (d–f). Fig. 4a–c show that the fitness landscape in the design space of the two polar angles is quite rugged. Nevertheless, the CMA-ES is able to ably handle this rugged topography and the covariance matrix shrinks and converges to the optimum design over the course of the 12 generations. This reduction in the search space eventually leads to a converged particle geometry of (ϕB, ϕC) = (70.7°, 45.0°). Fig. 4d–f show the modulation of the underlying free energy landscape imposed by CMA-ES optimization of the polar angles. Using the fittest colloid structure for each generation from the CMA-ES optimizer, we construct a single composite diffusion map to enable inter-generational landscape comparison. We utilize the same landmarking strategy described above to allow for computationally efficient embedding of points in the diffusion map space, and free energy landscapes for each generation's building block are constructed using the procedure described in section 2.2.3.
The first generation in Fig. 4d shows that the primary mechanism for icosahedral formation is through a single energy valley from (Ψ2, Ψ3) = (−0.025, 0.050) → (−0.055, 0.040) with ΔF ≈ −1 kBT along this pathway, connecting small assembled aggregates to the icosahedron. This assembly pathway has been previously described in ref. 37, 116 and 117, as the monomeric addition pathway describing the sequential locking of new colloids into the aggregate structure. The icosahedron resides in a shallow free energy well, serving as a metastable state for the assembly process at free energy of Ficos = 0.4 kBT with respect to the monomer free energy. The assembly of larger aggregates proceeds via attachment to the icosahedral surface, or via formation of a misassembled icosahedron, as observed by the low-free energy pathway leading to large aggregates at (Ψ2, Ψ3) = (−0.100, −0.100).
The optimization procedure leads to structural shifts in the free energy landscape across generations. By generation 6 the stability of small sized clusters is reduced, leading to a widening and flattening of the free energy valley observed in the first generation. The volume of configuration space marking the transition between small and large cluster regimes, located at (Ψ2, Ψ3) ≈ (−0.025, −0.060), is expanded, making the formation of these larger clusters easier. The formation of aggregates larger than the icosahedron is disfavored, as illustrated by elevation of the free energy of the pathway towards (Ψ2, Ψ3) = (−0.043, −0.075). Interestingly, the free energy of the target icosahedron relative to the monomer has actually increased relative to generation 1, raised slightly to Ficos = 1.2 kBT, corresponding to an increase of 0.8 kBT. This initial decrease in fitness is due to exploration of the design space by CMA-ES with a rather large covariance matrix prior to tightening of this distribution and convergence to an optimal design in the latter stages of the process.
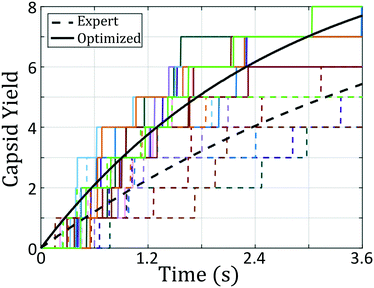
Continuing the optimization procedure through generation 12, we observe a marked improvement in landscape features. The monomeric-assembly valley has narrowed from generation 6 and the landscape has been further tilted to drive assembly from small clusters to the icosahedron, reaching Ficos = 1.1 kBT. Upon transitioning over the small cluster barrier regime, assembly occurs downhill to the icosahedral sink state that serves as a local minimum, competing with the dimer state existing at Fdimer = 0 kBT, which has increased in energy by 0.6 kBT from generation 6 to 12. Dynamic simulations also reveal that the icosahedra are strongly kinetically stabilized (section 3.1.2), wherein once formed we never observe dissociation on the time scale of our simulations. Furthermore, large aggregates populating the lower left corner of the intrinsic manifold have been destabilized, leading to fewer misassembled massive clusters. Moreover, the smooth character of the free energy surface around the icosahedron means that those defective aggregates that do form can easily tumble down into the icosahedral minimum, providing this target structure with a large basin of attraction in configurational space.
In sum, using only the simple fitness measure of relative stability for the desired icosahedral configuration, our data-driven design strategy has effected drastic changes to the landscape. As illustrated in Fig. 3a, ϕB remains unchanged from the initial architecture, and by decreasing ϕC by only 4°, our optimal design has destabilized the formation of large aggregates by disfavoring promiscuous bonding between particles and enlarged the basin of attraction for the icosahedral target structure.
3.2 Optimization of octahedral formation from a poor starting configuration
Having shown the effectiveness of this technique in improving the design of icosahedral forming building blocks around an expert-guided starting configuration, we sought to validate this method by considering the optimization of a target aggregate from a poor initial design. In this case, we use the optimal icosahedral building block with (ϕB, ϕC) = (70.7°, 45.0°) as a starting point for the optimization of building blocks to assemble into octahedral aggregates. This new structure shares a similar hollow structure to the icosahedron, but previous studies have shown that the polar angles required to stabilize octahedra are quite different, with (ϕB, ϕC) = (50.7°, 39.3°) corresponding to the values leading to optimal geometric alignment of the sticky patches in an idealized octahedron.9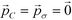 ,60 and use these parameters to generate a set of P = 10 candidate building blocks around the starting structure using eqn (11). We use the same update, landmarking, and sampling procedures as described in section 3.1, modifying the fitness measure now to be for the relative octahedral free energy, Δ(βF) = βFoct − βFmin≠oct. In this case, our initial candidate architecture is such a poor guess that it does not form any target octahedra over the course of our unbiased or biased calculations. As such, we demonstrate the capability of our inverse design technique to favor the assembly of a physically realizable but initially unstable aggregate that was not even observed in the simulations of our initial particle design. Despite this lack of direct sampling, the landscape engineering approach readily predicts the location of the octahedral structure by Nyström extension (eqn (8)) of the idealized octahedron onto the diffusion map manifold, providing a means of approximating the free energy of the octahedral aggregate with which we measure building block fitness. Within 13 generations, the optimization procedure produces an narrowly distributed ensemble of building block designs with a standard deviation of <1° in both polar angles, prompting us to declare the optimization converged.
,60 and use these parameters to generate a set of P = 10 candidate building blocks around the starting structure using eqn (11). We use the same update, landmarking, and sampling procedures as described in section 3.1, modifying the fitness measure now to be for the relative octahedral free energy, Δ(βF) = βFoct − βFmin≠oct. In this case, our initial candidate architecture is such a poor guess that it does not form any target octahedra over the course of our unbiased or biased calculations. As such, we demonstrate the capability of our inverse design technique to favor the assembly of a physically realizable but initially unstable aggregate that was not even observed in the simulations of our initial particle design. Despite this lack of direct sampling, the landscape engineering approach readily predicts the location of the octahedral structure by Nyström extension (eqn (8)) of the idealized octahedron onto the diffusion map manifold, providing a means of approximating the free energy of the octahedral aggregate with which we measure building block fitness. Within 13 generations, the optimization procedure produces an narrowly distributed ensemble of building block designs with a standard deviation of <1° in both polar angles, prompting us to declare the optimization converged.
We present the results of this optimization of polar angles for octahedral forming patchy colloids in Fig. 6. We see a steady decline in the exterior ring angle ϕB (blue) through 8 generations of this optimization scheme, eventually converging to ϕB = 53.7°. Meanwhile the interior polar angle ϕC (red) stays roughly constant, oscillating around it's starting position until stabilizing at ϕC = 42.0° during the final iteration. We can see that this procedure only takes 13 completed generations to fully converge, having only attempted 130 unique building block architectures in this 2D feature space to yield a finalized design. The optimized colloid qualitatively conforms to our expectations, since the polar angles must decrease from their icosahedral values in order to achieve the 90° angle between the vertices of the octahedral cluster.
We observe a marked improvement in the free energy profile over generations compared to the expert-direct optimization from the previous section. As illustrated in Fig. 6b the fitness of the first five generations remains rather flat, before the relative stability of the desired octahedron improves precipitously between generations 5 and 7 by ∼3 kT. The fitness then remains approximately stable for the remainder of the optimization.
The trends in fitness over the course of the optimization are explained by the behavior of the CMA-ES algorithm in each generation. We show in Fig. 7a–c an initial large increase in the covariance matrix as the optimization algorithm expands its search area of the rugged design space between generations 1 and 6, followed by shrinking and convergence to the optimum design by generation 12. The structure of the free energy landscape changes quite dramatically over this optimization procedure as illustrated in Fig. 7d–f. For the initial configuration in generation 1 (Fig. 7d), we observe a free energy well in this low-dimensional landscape around the icosahedral configuration at (Ψ2, Ψ3) ≈ (0.042, 0.045), with a valley in the free energy landscape connecting monomers to pentamer and hexamer configurations. There exists a barrier to nucleation of structures above this hexameric regime, which when crossed leads to a valley of connected states driving towards the icosahedral configuration.
By generation 6, shown in Fig. 7e, the shape of the landscape has adapted to reduce icosahedral stability. The location of the icosahedral cluster now exists as a high-energy state on the boundary of the landscape. This reduction in icosahedral stability comes with an increase in stability for the newly formed octahedral free energy well around (Ψ2, Ψ3) ≈ (0.025, 0.012), with the free energy with respect to the monomer state decreasing from Foct = 6.2 kBT → 2.1 kBT. Due to the decrease in polar angles of the inner ring, shifting from ϕC = 45.0° → 41.1°, we observe a greater stability of the dimer state due to face-to-face interactions between particle C rings. This dimer stability enables the formation of dimer chains, with dimers interlocking at 90° angles mediated by the exterior particle B rings, which we observe as an opening up of the landscape in the Ψ3 > 0.04 region.
Continued optimization leads to a reduction of the dimer stability, and a subsequent reduction in chain formation by generation 12 (Fig. 7f). By increasing the interior angle slightly to ϕC = 42°, the face-to-face interaction is now less stable due to an increased protrusion of the central particle surface through the patch ring. The shifting landscape now has completely destabilized the icosahedral configuration, evidenced by a noticeable gap at the icosahedral location. Meanwhile the well around the octahedral state becomes deeper as compared to previous generations, reaching below the monomer free energy at Foct = −0.01 kBT, while the pentamer state also becomes markedly more stable as a pivotal transition state for octahedral formation. Using only a simple measure of relative structural stability as fitness, this optimization procedure is able to sculpt the structure of the free energy landscape structure, filling in the sinks and troughs around undesirable aggregation states and deepening and widening the basin of attraction of the desired configuration.
4 Conclusions
We have demonstrated a novel building block design framework by engineering the free energy landscape for self-assembly of a desired aggregate, and have tested its efficacy in the design of patchy colloids to form hollow capsid structures. Many-body landmark diffusion maps enable the reconstruction of the low-dimensional intrinsic manifold for self-assembly, providing a reduced set of collective order parameters containing the important self-assembly dynamics. Hybrid Monte Carlo is employed to perform enhanced sampling directly in the low-dimensional diffusion map embedding and recover estimates of the unbiased self-assembly free energy surface supported by the diffusion map collective variables. By determining the free energy landscape for a variety of different building blocks, we develop a map between building block design and fitness of the landscape measured according to an appropriate thermodynamic, kinetic, or hybrid metric. By applying state-of-the-art optimization algorithms, we then perform data-driven inverse design to sculpt the free energy landscape to favor particular target aggregates and identify promising building block structures capable of robust self-assembly of the desired aggregate.We test this design platform in the formation of icosahedral and octahedral clusters from a double ring patchy colloid model. The design process, having started with the expert-defined colloid configuration, proposed a new patchy colloid that showed an 76% improvement in aggregation rate. By marrying expert knowledge with building block design engines, we believe this technique will offer a useful methodology in the continued development of novel materials systems formed via bottom-up self-assembly. In an instance where expert-knowledge is lacking this technique can still suggest building blocks capable of reliably forming into a desired terminal aggregate. We start the optimization of octahedral-forming patchy colloids from our icosahedral-forming colloid, a scenario where the octahedron is highly unstable. Through continued iteration of the free energy landscape, our technique dissolves the free energy pathway leading to formation of icosahedra, and develops a new energy well around the octahedral configuration. The converged building block architecture proposed by this landscape engineering platform is capable of reaching 60% yield in tests of octahedral capsid formation.
We foresee the integration of machine learning, statistical thermodynamics, and optimization engines to play an important role in the design and development of next generation self-assembled materials. Machine-learned order parameters have been widely used to improve our understanding of molecular folding and materials assembly, and here we propose a novel means of performing accelerated sampling and optimization directly in the low-dimensional embeddings to efficiently recover and engineer the underlying free energy surface to favor a particular target aggregate. While the systems studied here were simulated, we have previously demonstrated the application of diffusion maps directly to particle tracking experiments of Janus colloid self-assembly.38 We envision that analogous landscape-based optimization frameworks to those described herein may be deployed on data collected from experiment rather than simulation to direct experimentation towards promising candidates and guide and direct self-assembling materials design.118,119 Moving beyond colloidal assembly, we believe this same framework can also be employed in the study of molecular self-assembly, as illustrated in a recent application of many-body diffusion maps in the study of asphaltene aggregation, a primary foulant in crude oil extraction.84 Accordingly, we propose that our landscape engineering framework can be of use in the engineering of a variety of self-assembling materials of scientific and technological importance, including organic electronics,19,96 tissue scaffolds,120 and cell-penetrating peptides for antimicrobial therapies.13,14
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This material is based upon work supported by a National Science Foundation CAREER Award to A. L. F. (Grant No. DMR-1350008).References
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774 CrossRef CAS PubMed.
- K. Ariga, J. P. Hill, M. V. Lee, A. Vinu, R. Charvet and S. Acharya, Sci. Technol. Adv. Mater., 2008, 9, 014109 CrossRef PubMed.
- M. F. Hagan and D. Chandler, Biophys. J., 2006, 91, 42–54 CrossRef CAS PubMed.
- A. T. Da Poian, A. C. Oliveira and J. L. Silva, Biochemistry, 1995, 34, 2672–2677 CrossRef CAS PubMed.
- E. Gazit, Rev. Geophys., 2005, 272, 5971–5978 CAS.
- M. C. Chen, B. J. Cafferty, I. Mamajanov, I. Gállego, J. Khanam, R. Krishnamurthy and N. V. Hud, J. Am. Chem. Soc., 2014, 136, 5640–5646 CrossRef CAS PubMed.
- J. B. Matson, R. H. Zha and S. I. Stupp, Curr. Opin. Solid State Mater. Sci., 2011, 15, 225–235 CrossRef CAS PubMed.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- C. Ma, H. Wu, Z.-H. Huang, R.-H. Guo, M.-B. Hu, C. Kübel, L.-T. Yan and W. Wang, Angew. Chem., Int. Ed., 2015, 54, 15699–15704 CrossRef CAS PubMed.
- N. Steinmetz, T. Lin, G. Lomonossoff and J. Johnson, Viruses and Nanotechnology, Springer, Berlin Heidelberg, 2009, vol. 327, pp. 23–58 Search PubMed.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168 CrossRef CAS PubMed.
- C. Chen, J. Hu, S. Zhang, P. Zhou, X. Zhao, H. Xu, X. Zhao, M. Yaseen and J. R. Lu, Biomaterials, 2012, 33, 592–603 CrossRef CAS PubMed.
- C. Chen, F. Pan, S. Zhang, J. Hu, M. Cao, J. Wang, H. Xu, X. Zhao and J. R. Lu, Biomacromolecules, 2010, 11, 402–411 CrossRef CAS PubMed.
- X. Zhao, F. Pan, H. Xu, M. Yaseen, H. Shan, C. A. E. Hauser, S. Zhang and J. R. Lu, Chem. Soc. Rev., 2010, 39, 3480–3498 RSC.
- P. Anees, S. Sreejith and A. Ajayaghosh, J. Am. Chem. Soc., 2014, 136, 13233–13239 CrossRef CAS PubMed.
- H. Zhang, R. Wu, Z. Chen, G. Liu, Z. Zhang and Z. Jiao, CrystEngComm, 2012, 14, 1775–1782 RSC.
- L. Bian, E. Zhu, J. Tang, W. Tang and F. Zhang, Prog. Polym. Sci., 2012, 37, 1292–1331 CrossRef CAS.
- X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- H. Ning, A. Mihi, J. B. Geddes, M. Miyake and P. V. Braun, Adv. Mater., 2012, 24, OP153–OP158 CAS.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Phys. Rev. Lett., 2005, 94, 058302 CrossRef PubMed.
- H. Yan, S. H. Park, G. Finkelstein, J. H. Reif and T. H. LaBean, Science, 2003, 301, 1882–1884 CrossRef CAS PubMed.
- Y. Yin, Y. Lu, B. Gates and Y. Xia, J. Am. Chem. Soc., 2001, 123, 8718–8729 CrossRef CAS PubMed.
- J. Y. Cheng, A. M. Mayes and C. A. Ross, Nat. Mater., 2004, 3, 823–828 CrossRef CAS PubMed.
- M. Holmes-Cerfon, S. J. Gortler and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E5–E14 CrossRef CAS PubMed.
- M. Z. Miskin, G. Khaira, J. J. de Pablo and H. M. Jaeger, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 34–39 CrossRef CAS PubMed.
- J. Qin, G. S. Khaira, Y. Su, G. P. Garner, M. Miskin, H. M. Jaeger and J. J. de Pablo, Soft Matter, 2013, 9, 11467–11472 RSC.
- S. Hormoz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5193–5198 CrossRef CAS PubMed.
- X. Tang, M. A. Bevan and M. A. Grover, Mol. Syst. Des. Eng., 2017, 2, 78–88 CAS.
- V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed.
- E. Jankowski and S. C. Glotzer, Soft Matter, 2012, 8, 2852–2859 RSC.
- E. Jankowski and S. C. Glotzer, J. Phys. Chem. B, 2011, 115, 14321–14326 CrossRef CAS PubMed.
- O.-S. Lee, S. I. Stupp and G. C. Schatz, J. Am. Chem. Soc., 2011, 133, 3677–3683 CrossRef CAS PubMed.
- J. B. Matson and S. I. Stupp, Chem. Commun., 2012, 48, 26–33 RSC.
- M. F. Hagan, O. M. Elrad and R. L. Jack, J. Chem. Phys., 2011, 135, 104115 CrossRef PubMed.
- H. M. Jaeger and J. J. de Pablo, APL Mater., 2016, 4, 053209 CrossRef.
- A. W. Long and A. L. Ferguson, J. Phys. Chem. B, 2014, 118, 4228–4244 CrossRef CAS PubMed.
- A. W. Long, J. Zhang, S. Granick and A. L. Ferguson, Soft Matter, 2015, 11, 8141–8153 RSC.
- I. T. Jolliffe, Principal Component Analysis, Springer, New York, 2nd edn, 2002 Search PubMed.
- V. de Silva and J. B. Tenenbaum, Adv. Neural Inf. Process. Syst., 2003, 15, 721–728 Search PubMed.
- M. Belkin and P. Niyogi, Neural Comput., 2003, 15, 1373–1396 CrossRef.
- R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner and S. W. Zucker, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7426–7431 CrossRef CAS PubMed.
- R. R. Coifman and S. Lafon, Appl. Comput. Harmon. Anal., 2006, 21, 5–30 CrossRef.
- G. Torrie and J. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- E. Darve, D. Rodríguez-Gómez and A. Pohorille, J. Chem. Phys., 2008, 128, 144120 CrossRef PubMed.
- W. Zheng, M. A. Rohrdanz and C. Clementi, J. Phys. Chem. B, 2013, 117, 12769–12776 CrossRef CAS PubMed.
- J. Preto and C. Clementi, Phys. Chem. Chem. Phys., 2014, 16, 19181–19191 RSC.
- E. Chiavazzo, R. Covino, R. R. Coifman, C. W. Gear, A. S. Georgiou, G. Hummer and I. G. Kevrekidis, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5494–E5503 CrossRef CAS PubMed.
- S. Duane, A. Kennedy, B. J. Pendleton and D. Roweth, Phys. Lett. B, 1987, 195, 216–222 CrossRef CAS.
- R. M. Neal, Handbook of Markov Chain Monte Carlo, Chapman & Hall/CRC Press, 2011, ch. 5, pp. 113–162 Search PubMed.
- M. A. Gonzalez, E. Sanz, C. McBride, J. L. F. Abascal, C. Vega and C. Valeriani, Phys. Chem. Chem. Phys., 2014, 16, 24913–24919 RSC.
- D. Branduardi and J. D. Faraldo-Gómez, J. Chem. Theory Comput., 2013, 9, 4140–4154 CrossRef CAS PubMed.
- L. Maragliano, A. Fischer, E. Vanden-Eijnden and G. Ciccotti, J. Chem. Phys., 2006, 125, 024106 CrossRef PubMed.
- S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004 Search PubMed.
- M. Dorigo, M. Birattari and T. Stutzle, IEEE Comput. Intell. Mag., 2006, 1, 28–39 CrossRef.
- M. Mitchell, An Introduction to Genetic Algorithms, MIT Press, 1998 Search PubMed.
- N. Hansen and A. Ostermeier, Evol. Comput., 2001, 9, 159–195 CrossRef CAS PubMed.
- N. Hansen, S. D. Müller and P. Koumoutsakos, Evol. Comput., 2003, 11, 1–18 CrossRef PubMed.
- G. S. Khaira, J. Qin, G. P. Garner, S. Xiong, L. Wan, R. Ruiz, H. M. Jaeger, P. F. Nealey and J. J. de Pablo, ACS Macro Lett., 2014, 3, 747–752 CrossRef CAS.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609 CrossRef CAS PubMed.
- W. J. Parak, T. Pellegrino, C. M. Micheel, D. Gerion, S. C. Williams and A. P. Alivisatos, Nano Lett., 2003, 3, 33–36 CrossRef CAS.
- I. A. Banerjee, L. Yu and H. Matsui, Nano Lett., 2003, 3, 283–287 CrossRef CAS.
- A. V. Tkachenko, Phys. Rev. Lett., 2002, 89, 148303 CrossRef PubMed.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS.
- R. P. Sear, J. Chem. Phys., 1999, 111, 4800–4806 CrossRef CAS.
- D. Ghonasgi and W. G. Chapman, Mol. Phys., 1993, 79, 291–311 CrossRef CAS.
- A. Šarić, Y. C. Chebaro, T. P. Knowles and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17869–17874 CrossRef PubMed.
- R. Guo, J. Mao, X.-M. Xie and L.-T. Yan, Sci. Rep., 2014, 4, 7021 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- S. C. Glotzer, M. J. Solomon and N. A. Kotov, AIChE J., 2004, 50, 2978–2985 CrossRef CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1857–1858 Search PubMed.
- Glotzer Group, Shifted Lennard Jones Potential, http://hoomd-blue.readthedocs.io/en/stable/module-md-pair.htmlhoomd.md.pair.slj Search PubMed.
- A. W. Long, C. L. Phillips, E. Jankowksi and A. L. Ferguson, Soft Matter, 2016, 12, 7119–7135 RSC.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- T. D. Nguyen, C. L. Phillips, J. A. Anderson and S. C. Glotzer, Comput. Phys. Commun., 2011, 182, 2307–2313 CrossRef CAS.
- A. W. Long and A. L. Ferguson, Appl. Comput. Harmon. Anal., 2017 DOI:10.1016/j.acha.2017.08.004.
- R. A. Mansbach and A. L. Ferguson, J. Chem. Phys., 2015, 142, 105101 CrossRef PubMed.
- A. L. Ferguson, A. Z. Panagiotopoulos, P. G. Debenedetti and I. G. Kevrekidis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13597–13602 CrossRef CAS PubMed.
- M. A. Rohrdanz, W. Zheng, M. Maggioni and C. Clementi, J. Chem. Phys., 2011, 134, 124116 CrossRef PubMed.
- J. Wang, M. A. Gayatri and A. L. Ferguson, J. Phys. Chem. B, 2017, 121, 4923–4944 CrossRef CAS PubMed.
- D. J. Beltran-Villegas, R. M. Sehgal, D. Maroudas, D. M. Ford and M. A. Bevan, J. Chem. Phys., 2012, 137, 134901 CrossRef PubMed.
- W. F. Reinhart, A. W. Long, M. P. Howard, A. L. Ferguson and A. Z. Panagiotopoulos, Soft Matter, 2017, 13, 4733–4745 RSC.
- M. Zaslavskiy, F. Bach and J.-P. Vert, Bioinformatics, 2009, 25, 1259–1267 CrossRef PubMed.
- R. Singh, J. Xu and B. Berger, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12763–12768 CrossRef CAS PubMed.
- S. Salvador and P. Chan, 16th IEEE International Conference on Tools with Artificial Intelligence, 2004, pp. 576–584 Search PubMed.
- H.-S. Park and C.-H. Jun, Expert. Syst. Appl., 2009, 36, 3336–3341 CrossRef.
- A. L. Ferguson, A. Z. Panagiotopoulos, P. G. Debenedetti and I. G. Kevrekidis, J. Chem. Phys., 2011, 134, 135103 CrossRef PubMed.
- C. Fowlkes, S. Belongie, F. Chung and J. Malik, IEEE Trans. Pattern Anal. Mach. Intell., 2004, 26, 214–225 CrossRef PubMed.
- C. T. H. Baker, The Numerical Treatment of Integral Equations, Clarendon Press, Oxford, 1977, vol. 13 Search PubMed.
- Y. Bengio, J.-F. Paiement, P. Vincent, O. Delalleau, N. Le Roux and M. Ouimet, Adv. Neural Inf. Process. Syst., 2004, 16, 177–184 Search PubMed.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, 2nd edn, 2002 Search PubMed.
- B. A. Thurston, J. D. Tovar and A. L. Ferguson, Mol. Simul., 2016, 42, 955–975 CrossRef CAS.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- F. Marinelli, F. Pietrucci, A. Laio and S. Piana, PLoS Comput. Biol., 2009, 5, 1–18 Search PubMed.
- A. L. Ferguson, A. Z. Panagiotopoulos, I. G. Kevrekidis and P. G. Debenedetti, Chem. Phys. Lett., 2011, 509, 1–11 CrossRef CAS.
- C. R. Laing, T. A. Frewen and I. G. Kevrekidis, Nonlinearity, 2007, 20, 2127 CrossRef.
- B. Hashemian, D. Millán and M. Arroyo, J. Chem. Phys., 2013, 139, 214101 CrossRef PubMed.
- C.-G. Li, J. Guo, G. Chen, X.-F. Nie and Z. Yang, 2006 International Conference on Machine Learning and Cybernetics, 2006, pp. 3201–3206 Search PubMed.
- V. Spiwok and B. Králová, J. Chem. Phys., 2011, 135, 224504 CrossRef PubMed.
- D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103 CrossRef PubMed.
- S. Whitelam and P. L. Geissler, J. Chem. Phys., 2007, 127, 154101 CrossRef PubMed.
- J. Liu and E. Luijten, Phys. Rev. Lett., 2004, 92, 035504 CrossRef PubMed.
- B. Hetényi, K. Bernacki and B. J. Berne, J. Chem. Phys., 2002, 117, 8203–8207 CrossRef.
- S. Lloyd, IEEE Trans. Inf. Theory, 1982, 28, 129–137 CrossRef.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- A. L. Ferguson, J. Comput. Chem., 2017, 38, 1583–1605 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- J. D. Schmit, K. Ghosh and K. Dill, Biophys. J., 2010, 100, 450–458 CrossRef PubMed.
- N. Nakagawa and M. Peyrard, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 5279–5284 CrossRef CAS PubMed.
- R. Tarjan, SIAM J. Comput., 1972, 1, 146–160 CrossRef.
- J. Kennedy and R. Eberhart, IEEE International Conference on Neural Networks, 1995, pp. 1942–1948 Search PubMed.
- A. W. Wilber, J. P. K. Doye, A. A. Louis, E. G. Noya, M. A. Miller and P. Wong, J. Chem. Phys., 2007, 127, 085106 CrossRef PubMed.
- A. W. Wilber, J. P. K. Doye, A. A. Louis and A. C. F. Lewis, J. Chem. Phys., 2009, 131, 175102 CrossRef PubMed.
- T. Lookman, P. V. Balachandran, D. Xue, J. Hogden and J. Theiler, Curr. Opin. Solid State Mater. Sci., 2017, 21, 121–128 CrossRef CAS.
- D. Xue, P. V. Balachandran, J. Hogden, J. Theiler, D. Xue and T. Lookman, Nat. Commun., 2016, 7, 11241 CrossRef CAS PubMed.
- S. Zhang, F. Gelain and X. Zhao, Semin. Cancer Biol., 2005, 15, 413–420 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |