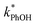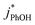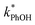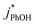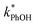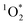Concentrations of a triplet excited state are enhanced in illuminated ice†
Zeyuan
Chen
ab and
Cort
Anastasio
 *ab
*ab
aDepartment of Land, Air and Water Resources, University of California, Davis, 1 Shields Ave., Davis, CA 95616, USA. E-mail: canastasio@ucdavis.edu; Fax: +1-530-752-1552; Tel: +1-530-754-6095
bAtmospheric Science Graduate Group, University of California, Davis, 1 Shields Ave., Davis, CA, USA
First published on 9th December 2016
Abstract
Photochemical reactions influence the fates and lifetimes of organic compounds in snow and ice, both through direct photoreactions and via photoproduced transient species such as hydroxyl radical (˙OH) and, perhaps, triplet excited states of organic compounds (i.e., triplets). While triplets can be important oxidants in atmospheric drops and surface waters, little is known of this class of oxidants in frozen samples. To investigate this, we examined the photoreaction of phenol with the triplet state of 3,4-dimethoxybenzaldehyde (3DMB*), a product from biomass combustion, in illuminated laboratory ices. Our results show that the rate of phenol loss due to 3DMB* is, on average, increased by a factor of 95 ± 50 in ice compared to the equivalent liquid sample. We find that this experimentally measured freeze concentration factor, FEXP, is independent of total solute concentration and temperature, in contrast to what is expected from a liquid-like region whose composition follows freezing point depression. We also find that FEXP for triplets is independent of pH, although the rates of phenol loss increase with decreasing pH in both solution and ice. The enhancement in the rate of phenol loss in/on ice indicates that concentrations of triplet excited states are enhanced in ice relative to solution and suggests that this class of oxidants might be a significant sink for organics in snow and ice.
Environmental impactSnowpacks are an important reservoir and reactor for pollutants deposited from the atmosphere. Organic pollutants in snow can be destroyed and transformed via photochemical reactions, but relatively little is known of these pathways. This work studies the ice reactivity of the triplet excited state of 3,4-dimethoxybenzaldehyde, which can react with a variety of electron-rich toxic organics such as phenols and phenyl urea pesticides. Here we show that concentrations of the DMB triplet in/on ice are enhanced by nearly a factor of 100 relative to the same sample studied as a liquid, suggesting triplet excited states might be important oxidants for organic pollutants in environmental snowpacks. This triplet enhancement in/on ice is intermediate between previously reported results for hydroxyl radical (no enhancement) and singlet molecular oxygen (with an enhancement on the order of 104), showing the diversity of reactive species behavior in illuminated ice. |
1. Introduction
Photochemical reactions in snow and ice can play major roles in the processing and cycling of organic compounds between snowpack, surface water, and the atmosphere.1,2 These reactions are initiated by both direct photochemical reactions and a variety of photooxidants, including hydroxyl radical (˙OH), singlet molecular oxygen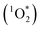 , and, perhaps, triplet excited states of organic compounds (3C*).1,3,4 Of these oxidants, ˙OH has been relatively well studied because it reacts rapidly with most organic compounds and is ubiquitous within illuminated snow.5–10 While
, and, perhaps, triplet excited states of organic compounds (3C*).1,3,4 Of these oxidants, ˙OH has been relatively well studied because it reacts rapidly with most organic compounds and is ubiquitous within illuminated snow.5–10 While 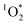 is more selective (i.e., overall less reactive) than ˙OH, Bower and Anastasio found that the
is more selective (i.e., overall less reactive) than ˙OH, Bower and Anastasio found that the  concentration increases by a factor of approximately 10
concentration increases by a factor of approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in/on illuminated ice compared to the same sample studied as solution.3,11 In contrast to ˙OH and
000 in/on illuminated ice compared to the same sample studied as solution.3,11 In contrast to ˙OH and 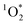 , very little is known about 3C* in ice or snow, although this class of oxidants can be an important sink for phenols and other organics in atmospheric drops and lake waters.12–18 Triplets might also be important as oxidants for halides, forming reactive halogen species that can alter atmospheric chemistry.19,20
, very little is known about 3C* in ice or snow, although this class of oxidants can be an important sink for phenols and other organics in atmospheric drops and lake waters.12–18 Triplets might also be important as oxidants for halides, forming reactive halogen species that can alter atmospheric chemistry.19,20
Triplet excited states are formed when a chromophoric organic compound absorbs a photon.13,21 This absorption leads first to a short-lived singlet excited state of the organic chromophore (1C*), which can either decay back to the ground state or undergo intersystem crossing (ISC) to reach the lowest excited triplet state:
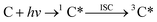 | (1) |
Once formed, 3C* can react with organic compounds, or be physically quenched, but its primary fate is generally reaction with dissolved oxygen to form 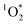 . This pathway is the dominant source of
. This pathway is the dominant source of 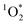 in natural waters:21
in natural waters:21
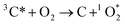 | (2) |
Given the large enhancements in 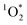 concentrations in/on illuminated ice observed by Bower and Anastasio,3,11 we expect that C* concentrations are also significantly enhanced in ice.
concentrations in/on illuminated ice observed by Bower and Anastasio,3,11 we expect that C* concentrations are also significantly enhanced in ice.
To examine this question, here we use illuminated ice and liquid samples to study the loss of a chemical probe, phenol (PhOH), via reaction with the triplet excited state of 3,4-dimethoxybenzaldehyde (3DMB*), a surrogate for environmental triplet states. Based on past work, solutes in many laboratory ices appear to be concentrated in liquid-like regions (LLRs),22,23 where they exhibit kinetics similar to those in solution.3,11 Using this approach, here we examine how 3DMB* reactivity depends on total solute concentration, temperature, and pH in ice and liquid. We also use our data to calculate the experimental freeze concentration factor11 (i.e., FEXP, the factor by which the 3DMB* concentration increases in LLRs) and compare it to the theoretical freeze concentration factor (FFPD) calculated from the freezing point depression model.22
2. Materials and methods
2.1. Materials
All reagents were used as received. Phenol (PhOH; 99%), 3,4-dimethoxybenzaldehyde (DMB; 99%), sodium chloride (NaCl; 99%), and hydrochloric acid (HCl; 99%) were obtained from Sigma-Aldrich. Solutions were made with purified water (Milli-Q) from a Milli-Q Plus system (Millipore; ≥18.2 MΩ cm) with an upstream Barnstead B-Pure cartridge to remove organics. We made the stock solutions gravimetrically and verified the concentrations using ultraviolet-visible spectroscopy. All solutions were air saturated.2.2. Sample preparation, illumination, and chemical analysis
In our illumination experiments we followed the loss of phenol to quantify the triplet excited state of DMB, which reacts rapidly with PhOH in solution.14,24,25 Our standard sample composition was 100 nM PhOH, 100 nM DMB, 100 μM HCl (to achieve pH 4.0 ± 0.2), and 900 μM NaCl (to control the total solute concentration at 2.0 mM). To examine the impact of each of these parameters on ice and liquid reactivity, we carried out a series of experiments where we varied one of the parameters while keeping the remaining ones at the standard condition. For every condition we prepared a blank with the same composition as the sample, but without DMB.We made ice samples and blanks by pipetting 1 mL aliquots of each solution into 2 mL glass HPLC autosampler vials (12 mm diameter, 32 mm height), sealing them with a PTFE-faced silicone septum and screw cap, and placing them vertically in a temperature-controlled freeze chamber at −10 °C, above the eutectic temperature for NaCl (Teu = −21.5 °C).26 Once frozen, we transferred the vials to a temperature-controlled illumination chamber (purged with dry air to prevent water vapor condensation on the exterior of the vial) coupled to a monochromatic illumination system (MIS).3 Samples were illuminated vertically in the 1 cm L × 1 cm W × 4 cm H sample holder of the illumination chamber. Liquid samples and blanks were made and illuminated in the same way as ice samples and blanks except that they were cooled and illuminated at 5 °C. Prior to illumination, all samples were allowed a minimum of 5 minutes to equilibrate to the chamber temperature.
Samples and blanks were illuminated at 313 nm, a wavelength where DMB absorbs strongly (εDMB,313 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 ± 290 M−1 cm−1),14 for sequentially increasing amounts of time. For each experiment we also deployed dark controls, which had the same composition as the samples, but were not illuminated. Ice samples, blanks, and dark controls were melted in the dark at room temperature before placing the vials in an autosampler and analyzing with HPLC.
290 ± 290 M−1 cm−1),14 for sequentially increasing amounts of time. For each experiment we also deployed dark controls, which had the same composition as the samples, but were not illuminated. Ice samples, blanks, and dark controls were melted in the dark at room temperature before placing the vials in an autosampler and analyzing with HPLC.
We measured PhOH and DMB concentrations using an isocratic HPLC system consisting of: a Shimadzu SPD-20A UV-Vis detector and LC-20A pump; ThermoScientific BetaBasic-18 column, 250 × 3 mm, 5 μm bead; degassed eluent of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 acetonitrile/Milli-Q; flow rate of 0.6 mL min−1; injection volume of 500 μL (into a 2 mL loop); 269 nm detection wavelength. The limit of quantification for both PhOH and DMB was 5 nM.
80 acetonitrile/Milli-Q; flow rate of 0.6 mL min−1; injection volume of 500 μL (into a 2 mL loop); 269 nm detection wavelength. The limit of quantification for both PhOH and DMB was 5 nM.
2.3. Kinetic analysis
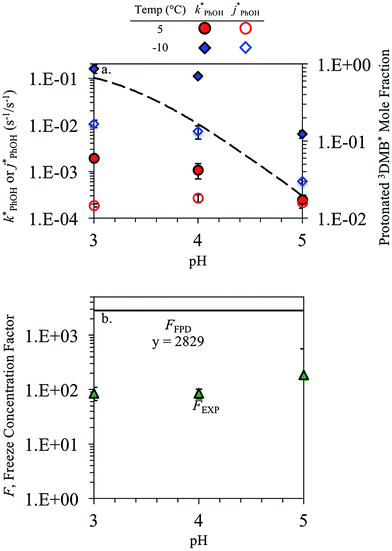
In each illumination experiment the decay of PhOH followed (pseudo) first-order kinetics, i.e., plots of ln([PhOH]/[PhOH]0) versus time were linear, where [PhOH] and [PhOH]0 are concentrations at times t and zero, respectively. In each illuminated solution containing DMB we determined the pseudo-first-order rate constant for PhOH loss due to 3DMB* (i.e., k′PhOH) from the slope of the ln([PhOH]/[PhOH]0) plot. We performed the same experiment for each corresponding blank, which did not contain DMB; the pseudo-first-order rate constant in this experiment (jPhOH) accounts for phenol loss from direct photodegradation as well as any other background reaction pathways in the absence of DMB. The measured value of k′PhOH is the sum of all PhOH pathways in the experiment, i.e., the pseudo-first-order rate constant due to triplet reaction (equivalent to kPhOH+3DMB*[3DMB*]) and the contribution from reactions not involving the DMB triplet (which is measured by jPhOH):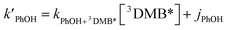 | (3) |
While it is possible that other oxidants, such as  and ˙OH, might also contribute to PhOH loss in our experiments with DMB, these appear to be minor since: (1) we see the opposite of the pH dependence that would occur for
and ˙OH, might also contribute to PhOH loss in our experiments with DMB, these appear to be minor since: (1) we see the opposite of the pH dependence that would occur for 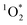 , as discussed below, and (2) we see an enhancement in PhOH loss in ice compared to in solution, while previous work found no ˙OH enhancement in ice.10 In addition, we form very little HOOH, and therefore expect very little ˙OH, in our experiments.14 We also expect that the singlet excited state of DMB is a minor sink for PhOH. Although singlet excited states are very reactive, they are also very short lived and thus have low steady-state concentrations;27 since 3DMB* reacts very rapidly with PhOH,25 a somewhat more reactive – but much less abundant – 1DMB* state should make only a small contribution to PhOH loss.
, as discussed below, and (2) we see an enhancement in PhOH loss in ice compared to in solution, while previous work found no ˙OH enhancement in ice.10 In addition, we form very little HOOH, and therefore expect very little ˙OH, in our experiments.14 We also expect that the singlet excited state of DMB is a minor sink for PhOH. Although singlet excited states are very reactive, they are also very short lived and thus have low steady-state concentrations;27 since 3DMB* reacts very rapidly with PhOH,25 a somewhat more reactive – but much less abundant – 1DMB* state should make only a small contribution to PhOH loss.
We corrected for small variations in photon flux between experiments by first measuring the photolysis rate constant of 10 μM 2-nitrobenzaldehyde (2NB)28 illuminated as ice or liquid (to match the sample phase) in the same 2 mL capped vials. The first-order rate constant for 2NB loss (j2NB) was determined in the same manner as k′PhOH and jPhOH. Then PhOH loss rate constants were normalized to photon flux by dividing k′PhOH and jPhOH by the measured j2NB for that day:
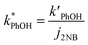 | (4) |
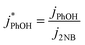 | (5) |
2.4. Freeze concentration factors
The freeze-concentration factor predicted from freezing-point depression, FFPD, is the ratio of the concentration of a solute in liquid-like regions (assuming no precipitation, reaction, or evaporation during freezing) to the concentration of the solute in solution prior to freezing: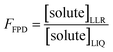 | (6) |
As predicted by freezing point depression, the freeze-concentration factor is inversely proportional to 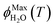 , the fraction of H2O molecules in the original aqueous sample that are present in LLRs in the frozen sample,22 where
, the fraction of H2O molecules in the original aqueous sample that are present in LLRs in the frozen sample,22 where 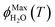 is determined by the total solute concentration in the unfrozen solution ([TS]LIQ), the temperature of the frozen sample (T), the freezing point of the solvent (Tf), and the cryoscopic constant (Ef (or kF) = 1.86 K kg mol−1 for water).22 Written in terms of FFPD, this relationship is:
is determined by the total solute concentration in the unfrozen solution ([TS]LIQ), the temperature of the frozen sample (T), the freezing point of the solvent (Tf), and the cryoscopic constant (Ef (or kF) = 1.86 K kg mol−1 for water).22 Written in terms of FFPD, this relationship is:
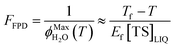 | (7) |
Thus FFPD in ice is determined by two factors: the temperature of the ice and the total solute concentration in the unfrozen solution. Note that our substitution into eqn (8) of Cho et al.22 to yield our eqn (7) gives a slightly different expression for Ef, with a term Tf × T in the numerator rather than the standard Tf2. For our current work the effect of this difference is very small, causing less than a 4% change in calculated values of FFPD for our standard temperature of −10 °C.
Following the general approach of Bower and Anastasio,11 we determined the experimentally measured freeze-concentration factor (FEXP) using our PhOH loss measurements. Following the solute definition for FFPD in eqn (6), we determined FEXP from the ratio of the concentrations of 3DMB* in the LLRs and initial liquid solution:
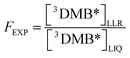 | (8) |
Thus our experimentally determined freeze-concentration factor in this work is specific for the DMB triplet excited state. As described in ESI Section S2,† the triplet concentration, and thus FEXP, will be affected by any differences in dissolved O2 or ϕISC between solution and ice.
In both ice and liquid samples the concentration of 3DMB* is determined from the measured loss of PhOH, as shown by re-arranging eqn (2), taking into account the normalization with j2NB:
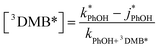 | (9) |
Combining eqn (8) and (9) gives
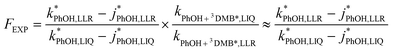 | (10) |
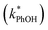 and without
and without 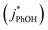 DMB in ice and solution experiments, respectively. The ratio kPhOH+3DMB*,LIQ/kPhOH+3DMB*,LLR in eqn (10) is approximately unity based on previous work,14 which showed that the pseudo first-order rate constant for PhOH loss via3DMB* (essentially
DMB in ice and solution experiments, respectively. The ratio kPhOH+3DMB*,LIQ/kPhOH+3DMB*,LLR in eqn (10) is approximately unity based on previous work,14 which showed that the pseudo first-order rate constant for PhOH loss via3DMB* (essentially  ) is independent of temperature between 5 and 20 °C. Since
) is independent of temperature between 5 and 20 °C. Since 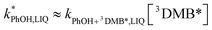 , this indicates that the second-order rate constant for PhOH + 3DMB* is essentially independent of temperature.
, this indicates that the second-order rate constant for PhOH + 3DMB* is essentially independent of temperature.
2.5. Uncertainties
Uncertainties for k′PhOH and jPhOH are determined from the standard error of the linear regression of the slope of ln([PhOH]/[PhOH]0) versus illumination time. The analogous procedure is used to determine the error in j2NB. These uncertainties are propagated to determine standard errors for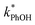 ,
, 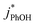 , and FEXP. Error bars on plots represent ±1 standard error; some error bars are smaller than their corresponding symbols.
, and FEXP. Error bars on plots represent ±1 standard error; some error bars are smaller than their corresponding symbols.
3. Results and discussion
3.1. Effects of DMB and PhOH concentrations
Because the freeze-concentration effect greatly increases the concentrations of solutes in LLRs compared to in the unfrozen initial solution, we were initially concerned that DMB might aggregate or precipitate in our ice LLRs, which might decrease the formation rate and steady-state concentration of 3DMB*. However, as shown in Fig. 1,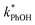 is linearly related to DMB concentration in both solution and ice, suggesting there is no aggregation or precipitation of DMB in our ice samples. As described in ESI Section S1,† we can model our reaction system using a series of kinetic equations that describe the formation and destruction of the DMB triplet state. The equation describing the steady-state concentration of 3DMB* in ice and solution (eqn (S4)†) predicts that
is linearly related to DMB concentration in both solution and ice, suggesting there is no aggregation or precipitation of DMB in our ice samples. As described in ESI Section S1,† we can model our reaction system using a series of kinetic equations that describe the formation and destruction of the DMB triplet state. The equation describing the steady-state concentration of 3DMB* in ice and solution (eqn (S4)†) predicts that 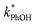 will linearly depend on [DMB], which is consistent with Fig. 1. Fig. 1 also shows that at concentrations below 50 nM DMB,
will linearly depend on [DMB], which is consistent with Fig. 1. Fig. 1 also shows that at concentrations below 50 nM DMB, 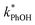 is, at most, 3 times higher than the background rate constant in the absence of DMB (i.e.,
is, at most, 3 times higher than the background rate constant in the absence of DMB (i.e., 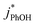 , the y-intercept in Fig. 1). Therefore, we used 100 nM DMB for subsequent liquid and ice experiments in order to obtain a good signal for
, the y-intercept in Fig. 1). Therefore, we used 100 nM DMB for subsequent liquid and ice experiments in order to obtain a good signal for 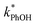 .
.
Fig. 1 also shows that the slope for the ice line is 40 times greater than the solution line, indicating there is greater reactivity in ice compared to in solution. Since 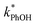 can be approximated by the photon-flux-normalized product of [3DMB*] times the second-order rate constant kPhOH+3DMB*, where kPhOH+3DMB* has been shown to have no significant dependence on temperature,14 our interpretation of Fig. 1 is that [3DMB*] is greater in ice compared to in the equivalent solution. As described in Section S2,† the ratio of the slopes from Fig. 1 is approximately equal to the freeze-concentration factor, with modification for any differences in the efficiency of intersystem crossing to the triplet state, and in the concentration of dissolved oxygen, between solution and ice (eqn (S15)†).
can be approximated by the photon-flux-normalized product of [3DMB*] times the second-order rate constant kPhOH+3DMB*, where kPhOH+3DMB* has been shown to have no significant dependence on temperature,14 our interpretation of Fig. 1 is that [3DMB*] is greater in ice compared to in the equivalent solution. As described in Section S2,† the ratio of the slopes from Fig. 1 is approximately equal to the freeze-concentration factor, with modification for any differences in the efficiency of intersystem crossing to the triplet state, and in the concentration of dissolved oxygen, between solution and ice (eqn (S15)†).
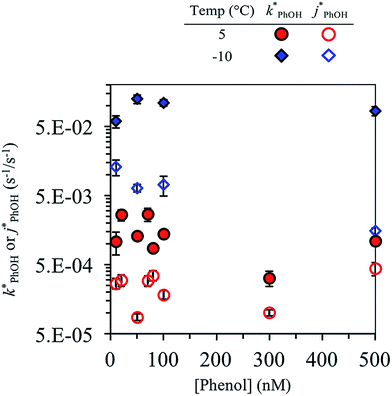
Fig. 2 shows the analogous experiments where we kept DMB constant at 100 nM but varied the concentration of PhOH. Values of 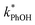 are within experimental error of each other across our range (10–500 nM), i.e., the corrected rate constant for phenol loss is independent of phenol concentration. As described by eqn (S5),† this indicates that PhOH is a minor sink for the triplets in our experiments, consistent with the idea that O2 is the dominant sink, which is generally the case in natural waters as well.21,29 Since
are within experimental error of each other across our range (10–500 nM), i.e., the corrected rate constant for phenol loss is independent of phenol concentration. As described by eqn (S5),† this indicates that PhOH is a minor sink for the triplets in our experiments, consistent with the idea that O2 is the dominant sink, which is generally the case in natural waters as well.21,29 Since 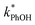 and
and 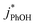 are independent of PhOH concentration (Fig. 2), we used 100 nM PhOH for subsequent ice and liquid experiments since this low concentration still gives good PhOH signals on the HPLC.
are independent of PhOH concentration (Fig. 2), we used 100 nM PhOH for subsequent ice and liquid experiments since this low concentration still gives good PhOH signals on the HPLC.
3.2. Dependence on total solute
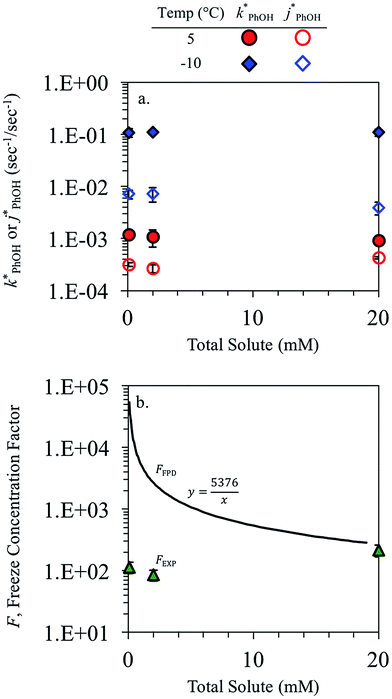
The total solute (TS) concentration in solution is one of two environmental variables that determine the freeze-concentration factor (FFPD) in the freezing-point depression model. TS concentrations in natural snows and ices range from tens of micromolar in remote continental regions up to a few molar in coastal areas.30,31 As shown in eqn (7), FFPD is inversely proportional to the TS concentration. In contrast to this expectation, we find that TS has no significant effect on our experimentally measured freeze-concentration factor, FEXP (Fig. 3b). As shown by the solid line in Fig. 3b, the model FFPD decreases from about 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 270 as TS increases from 0.1 to 20 mM. However, the measured FEXP based on the DMB triplet shows no statistically significant (95% CI) change over this range of total solute, ranging from 85 ± 17 to 210 ± 46 (Fig. 3b and ESI Table S1†). This is because the rate constants for phenol loss in the presence
000 to 270 as TS increases from 0.1 to 20 mM. However, the measured FEXP based on the DMB triplet shows no statistically significant (95% CI) change over this range of total solute, ranging from 85 ± 17 to 210 ± 46 (Fig. 3b and ESI Table S1†). This is because the rate constants for phenol loss in the presence 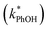 and absence of DMB
and absence of DMB 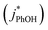 are independent of TS both in the ice samples and in the liquid samples (Fig. 3a). Consistent with our results in Fig. 1 and 2, we also see an enhancement of triplet concentrations in ice, with
are independent of TS both in the ice samples and in the liquid samples (Fig. 3a). Consistent with our results in Fig. 1 and 2, we also see an enhancement of triplet concentrations in ice, with 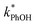 approximately 100 times larger in frozen samples than in aqueous samples. We see a similar, though smaller, enhancement in reactivity for samples that do not contain DMB:
approximately 100 times larger in frozen samples than in aqueous samples. We see a similar, though smaller, enhancement in reactivity for samples that do not contain DMB: 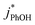 on ice is 20 times larger than in solution. This background reactivity represents oxidants other than 3DMB* and likely includes singlet molecular oxygen
on ice is 20 times larger than in solution. This background reactivity represents oxidants other than 3DMB* and likely includes singlet molecular oxygen 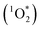 , other triplet states, hydroxyl radical, and direct photodegradation. The factor of 20 enhancement in ice likely indicates that the background concentrations of 3C* and
, other triplet states, hydroxyl radical, and direct photodegradation. The factor of 20 enhancement in ice likely indicates that the background concentrations of 3C* and 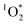 are larger in ice compared to solution, consistent with what we have seen with furfuryl alcohol as a probe for
are larger in ice compared to solution, consistent with what we have seen with furfuryl alcohol as a probe for 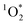 .3
.3
While we have plotted the ice data in Fig. 3 using the TS concentration in the initial solution, based on freezing point depression we expect [TS] in the LLRs is 5.4 M at −10 °C, independent of the starting solute concentration (eqn (7)). To examine whether this very high TS concentration affects 3DMB*–phenol chemistry, we also ran a liquid test (5 °C) with a total solute concentration of 5.4 M, mostly from NaCl. The resulting value of 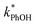 is four times higher than the average of the liquid values between 0.1 and 20 mM total solute concentrations (Table S1†). One possible explanation for this enhancement may be that the additional chloride (and trace amounts of bromide in the NaCl) increases the efficiency of phenol transformation, as found for triplet-mediated reactions in surface waters.32,33 As hypothesized previously,32,34,35 the high chloride concentration might switch the major sink for the triplet excited state from dissolved oxygen to chloride. Thus, instead of producing singlet molecular oxygen (a minor sink for phenol in our system) the triplet excited state would produce chloride radicals,32,34,35 which are more reactive and can contribute to PhOH loss.36,37 Regardless of the reason for the higher reactivity in the 5.4 M TS solution experiment, the resulting value of
is four times higher than the average of the liquid values between 0.1 and 20 mM total solute concentrations (Table S1†). One possible explanation for this enhancement may be that the additional chloride (and trace amounts of bromide in the NaCl) increases the efficiency of phenol transformation, as found for triplet-mediated reactions in surface waters.32,33 As hypothesized previously,32,34,35 the high chloride concentration might switch the major sink for the triplet excited state from dissolved oxygen to chloride. Thus, instead of producing singlet molecular oxygen (a minor sink for phenol in our system) the triplet excited state would produce chloride radicals,32,34,35 which are more reactive and can contribute to PhOH loss.36,37 Regardless of the reason for the higher reactivity in the 5.4 M TS solution experiment, the resulting value of 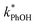 is still a small fraction of the value in ice, suggesting that the freeze concentration of DMB is the dominant factor explaining the increase in
is still a small fraction of the value in ice, suggesting that the freeze concentration of DMB is the dominant factor explaining the increase in 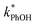 in ice compared to in solution.
in ice compared to in solution.
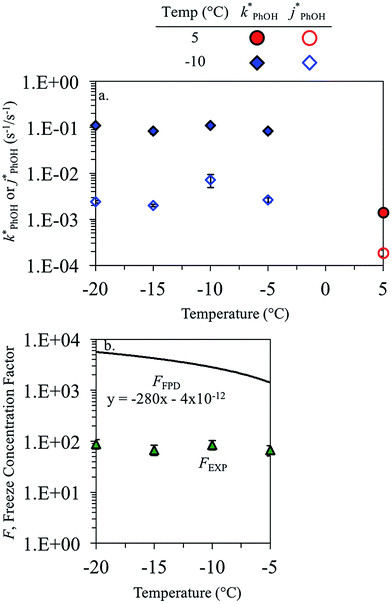
3.3. Temperature dependence
As shown in eqn (7), temperature is the other environmental variable influencing FFPD, with this freeze-concentration factor decreasing with increasing temperature. We saw very good agreement between FFPD and FEXP across the temperature range of −35 to −5 °C in our previous work with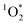 as a probe for LLRs,11 as did Cho et al. in their NMR work.22 In contrast, as shown in Fig. 4a, here we see no statistically significant differences in
as a probe for LLRs,11 as did Cho et al. in their NMR work.22 In contrast, as shown in Fig. 4a, here we see no statistically significant differences in 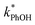 between −20 and −5 °C; we also see roughly no change in
between −20 and −5 °C; we also see roughly no change in 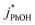 over this range, although it is much lower than
over this range, although it is much lower than 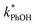 . For all of the ice temperatures, the experimentally determined values of FEXP determined from triplet reactivity are 20 to 60 times lower than the corresponding theoretical freeze concentration factors calculated from freezing-point depression (Fig. 4b). While values of FFPD range from 1400 at −5 °C to 5700 at −20 °C, our average (±1σ) value for FEXP is 77 ± 11. The only temperature-related difference in kinetics is between the ice and solution results, where
. For all of the ice temperatures, the experimentally determined values of FEXP determined from triplet reactivity are 20 to 60 times lower than the corresponding theoretical freeze concentration factors calculated from freezing-point depression (Fig. 4b). While values of FFPD range from 1400 at −5 °C to 5700 at −20 °C, our average (±1σ) value for FEXP is 77 ± 11. The only temperature-related difference in kinetics is between the ice and solution results, where 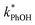 for ice is approximately 100 times faster than the liquid value, similar to the difference between ice and solution seen above.
for ice is approximately 100 times faster than the liquid value, similar to the difference between ice and solution seen above.
One possible explanation for the temperature independence of our experimental results is that the range of temperature used is too small to experimentally see variations in 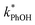 . However, as described above, FFPD increases by a factor of 4 between −5 and −20 °C, a difference that would be easily observed experimentally; in contrast, measured FEXP values vary by 11% or less from the average value. Another possible explanation may be that PhOH becomes a competing sink for 3DMB*, thereby suppressing the triplet concentration, in the highly concentrated liquid-like regions of ice. If we assume that the concentration of each solute (including PhOH) increases by a factor of FFPD when a solution is frozen, then the PhOH concentration in LLRs will be 280 μM for our standard condition, approximately half of the calculated O2 concentration in LLRs (520 μM) assuming Henry's law and an ambient O2 amount. As shown in Section S3,† under these conditions O2 is the dominant sink but PhOH is also important, with calculated pseudo-first-order rate constants for 3DMB* loss of 1.0 × 106 s−1 (triplet lifetime of 1 μs) for O2 and 1.8 × 105 s−1 (triplet lifetime of 6 μs) for PhOH. In this case, PhOH would only suppress the 3DMB* concentration (and thus k′PhOH) by approximately 20%. If we use the smaller, measured value of FEXP, [PhOH]LLR is only 7.7 μM and phenol is a negligible sink, accounting for less than 1% of 3DMB* loss in the ice. Thus, PhOH becoming an important sink for 3DMB* cannot explain the lack of a temperature dependence in FEXP. While we cannot explain this odd behavior, it might be connected to a temperature-dependent variation in dissolved O2 concentrations in the LLRs, a topic we explore in Section 3.5.
. However, as described above, FFPD increases by a factor of 4 between −5 and −20 °C, a difference that would be easily observed experimentally; in contrast, measured FEXP values vary by 11% or less from the average value. Another possible explanation may be that PhOH becomes a competing sink for 3DMB*, thereby suppressing the triplet concentration, in the highly concentrated liquid-like regions of ice. If we assume that the concentration of each solute (including PhOH) increases by a factor of FFPD when a solution is frozen, then the PhOH concentration in LLRs will be 280 μM for our standard condition, approximately half of the calculated O2 concentration in LLRs (520 μM) assuming Henry's law and an ambient O2 amount. As shown in Section S3,† under these conditions O2 is the dominant sink but PhOH is also important, with calculated pseudo-first-order rate constants for 3DMB* loss of 1.0 × 106 s−1 (triplet lifetime of 1 μs) for O2 and 1.8 × 105 s−1 (triplet lifetime of 6 μs) for PhOH. In this case, PhOH would only suppress the 3DMB* concentration (and thus k′PhOH) by approximately 20%. If we use the smaller, measured value of FEXP, [PhOH]LLR is only 7.7 μM and phenol is a negligible sink, accounting for less than 1% of 3DMB* loss in the ice. Thus, PhOH becoming an important sink for 3DMB* cannot explain the lack of a temperature dependence in FEXP. While we cannot explain this odd behavior, it might be connected to a temperature-dependent variation in dissolved O2 concentrations in the LLRs, a topic we explore in Section 3.5.
3.4. pH dependence
To examine whether pH affects the concentration of 3DMB* within LLRs, we supplemented our standard condition of pH 4 with additional samples at pH 3 and 5, keeping TS constant at 2.0 mM. Smith et al.14 found that kPhOH+3DMB* is strongly dependent upon pH in solution, increasing by a factor of nearly 20 between pH 6 and 2. Their results indicated that the protonated DMB triplet has a pKa of 3.3 ± 0.2 and is more reactive than the neutral form.14 As shown in Fig. 5a, we also find that the reactivity increases at lower pH in solution, where the ratio of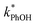 is 9
is 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for pH 3, 4, and 5, respectively. This suggests that 3DMB* is the primary oxidant reacting with PhOH and that
1 for pH 3, 4, and 5, respectively. This suggests that 3DMB* is the primary oxidant reacting with PhOH and that 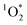 is not an important sink for PhOH; since
is not an important sink for PhOH; since 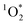 reacts more rapidly with the deprotonated phenolate ion compared to the neutral phenol,13,38 it should exhibit a pH dependence that is opposite of what we observe in Fig. 5. The increase in solution reactivity with decreasing pH mirrors the mole fraction of 3DMB* that is protonated in the solutions, as shown by the dashed line in Fig. 5a. The ratio of the protonated 3DMB* mole fraction is 34
reacts more rapidly with the deprotonated phenolate ion compared to the neutral phenol,13,38 it should exhibit a pH dependence that is opposite of what we observe in Fig. 5. The increase in solution reactivity with decreasing pH mirrors the mole fraction of 3DMB* that is protonated in the solutions, as shown by the dashed line in Fig. 5a. The ratio of the protonated 3DMB* mole fraction is 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at pH 3, 4, and 5, respectively, roughly comparable with the reactivity ratio. In contrast,
1 at pH 3, 4, and 5, respectively, roughly comparable with the reactivity ratio. In contrast, 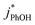 in liquid is independent of pH (Fig. 5a).
in liquid is independent of pH (Fig. 5a).
In the ice samples 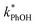 also increases with decreasing pH, although the behavior differs from that in solution, with a ratio of 25
also increases with decreasing pH, although the behavior differs from that in solution, with a ratio of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for ice at pH 3, 4, and 5, respectively (Fig. 5a). This change in the relative reactivities suggests that the pKa might be different in ice compared to in solution. However, the situation is complicated since the pH values listed here are those of the solution prior to freezing and the acidities in the ice LLRs will be different. We find that
1 for ice at pH 3, 4, and 5, respectively (Fig. 5a). This change in the relative reactivities suggests that the pKa might be different in ice compared to in solution. However, the situation is complicated since the pH values listed here are those of the solution prior to freezing and the acidities in the ice LLRs will be different. We find that 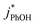 in ice has a pH dependence similar to that of
in ice has a pH dependence similar to that of 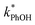 , with a ratio of 17
, with a ratio of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for pH 3, 4, and 5, respectively. This large increase suggests the background oxidants might be triplet excited states with pKa's similar to DMB, since the reactivities with
1 for pH 3, 4, and 5, respectively. This large increase suggests the background oxidants might be triplet excited states with pKa's similar to DMB, since the reactivities with 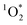 , direct photodegradation, and ˙OH reaction are insensitive to pH in this range.39 The absence of a pH dependence for
, direct photodegradation, and ˙OH reaction are insensitive to pH in this range.39 The absence of a pH dependence for 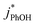 in solution suggests that a different set of reaction pathways controls the background reactivities in ice and solution.
in solution suggests that a different set of reaction pathways controls the background reactivities in ice and solution.
As shown in Fig. 5b, when we translate our results to freeze-concentration factors, FEXP for 3DMB* at pH 3 and 4 is essentially the same (86 ± 1), approximately 30 times less than predicted by FFPD. Since we kept TS constant in our experiments, FFPD is independent of pH. FEXP at pH 5 is larger than the values in more acidic solutions, but the pH 5 value has a very large propagated error because of the small difference in 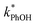 and
and 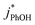 for the solution experiment.
for the solution experiment.
3.5. Discussion and uncertainties
In past research, Cho et al. used Nuclear Magnetic Resonance (NMR) to show that experimental freeze-concentration factors, FEXP, matched values calculated from freezing-point depression (i.e., FFPD).22 Later work by Bower and Anastasio, using Rose Bengal as a sensitizer for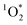 and furfuryl alcohol as a probe, showed there was good agreement between FEXP and FFPD for
and furfuryl alcohol as a probe, showed there was good agreement between FEXP and FFPD for 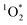 in NaCl ice samples with total solute concentrations of 1 mM and above.11 Since the Rose Bengal triplet state is the precursor for
in NaCl ice samples with total solute concentrations of 1 mM and above.11 Since the Rose Bengal triplet state is the precursor for 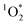 , we expected that 3DMB* would behave similar to
, we expected that 3DMB* would behave similar to 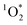 in LLRs. While FEXP for 3DMB* is greater than 1, showing an enhancement in ice, the factor is significantly lower than predicted (except at 20 mM total solute). Furthermore, FEXP for 3DMB* is essentially independent of temperature and total solute concentration, in contrast to our expectation that these variables should control F, as in Bower and Anastasio.11
in LLRs. While FEXP for 3DMB* is greater than 1, showing an enhancement in ice, the factor is significantly lower than predicted (except at 20 mM total solute). Furthermore, FEXP for 3DMB* is essentially independent of temperature and total solute concentration, in contrast to our expectation that these variables should control F, as in Bower and Anastasio.11
While the steady-state concentration of reactive DMB triplet is only modestly enhanced in LLRs compared to the initial solution, we expect that unreactive solutes (e.g., NaCl) are enhanced by a factor of FFPD in the LLRs. To address the modest enhancement in triplet concentration, we first look at the kinetic relationship between 3DMB* and 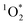 . The primary sink for 3DMB* in solution is O2, forming
. The primary sink for 3DMB* in solution is O2, forming 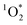 , whose major sink is water.3 As derived in Section S4,† under conditions when O2 is the major sink for 3DMB*, the singlet oxygen concentration is independent of the dissolved O2 level (eqn (S21)†), but the triplet excited state concentration decreases with increasing O2 (eqn (S2)†). Thus an enhancement of dissolved O2 in our LLRs (relative to the initial solution) would suppress the 3DMB* concentration (eqn (S2)†) and lead to lower values of FEXP. In contrast to past work by Bower and Anastasio,11 who prepared ice from solution in Teflon molds that were open to the air, in this work we prepared ice from solution in sealed glass vials; it is unclear if the sealed containers lead to an increase of dissolved O2 concentration in LLRs. Measuring O2 levels in ice is, at least for us, essentially impossible because the LLR sizes are very small (sub-millimeter) and they are located within the ice samples.23 However, measurements of O2 levels in LLRs would be very helpful in evaluating whether dissolved O2 is enhanced in liquid-like regions in ice samples made in closed containers.
, whose major sink is water.3 As derived in Section S4,† under conditions when O2 is the major sink for 3DMB*, the singlet oxygen concentration is independent of the dissolved O2 level (eqn (S21)†), but the triplet excited state concentration decreases with increasing O2 (eqn (S2)†). Thus an enhancement of dissolved O2 in our LLRs (relative to the initial solution) would suppress the 3DMB* concentration (eqn (S2)†) and lead to lower values of FEXP. In contrast to past work by Bower and Anastasio,11 who prepared ice from solution in Teflon molds that were open to the air, in this work we prepared ice from solution in sealed glass vials; it is unclear if the sealed containers lead to an increase of dissolved O2 concentration in LLRs. Measuring O2 levels in ice is, at least for us, essentially impossible because the LLR sizes are very small (sub-millimeter) and they are located within the ice samples.23 However, measurements of O2 levels in LLRs would be very helpful in evaluating whether dissolved O2 is enhanced in liquid-like regions in ice samples made in closed containers.
Another possible reason why FEXP based on triplet reactivity is lower than predicted values is shown by eqn (S15):†FEXP depends on the quantum yield for intersystem crossing (ϕISC), which might vary between solution and ice for DMB. In contrast, based on the good agreement between FEXP and FFPD in the work by Bower and Anastasio,11 it appears that ϕISC for Rose Bengal is similar in ice and solution. While we cannot identify a specific reason for the lower-than-expected enhancement in 3DMB* concentrations in ice, we suggest that future work simultaneously measure both 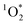 and 3C* in the same illuminated ice and solution samples to better constrain the system.
and 3C* in the same illuminated ice and solution samples to better constrain the system.
As a final uncertainty, it is possible that oxidants other than 3DMB* might be contributing to the loss of PhOH in our experiments and thus confounding our determination of the triplet state enhancement. However, there are several lines of evidence for 3DMB* as the main oxidant for PhOH in our samples: (1) illumination of DMB efficiently forms its triplet state, which rapidly reacts with PhOH,14,25 (2) the observed pH dependence of PhOH loss (Fig. 5) is consistent with the acid–base behavior of the 3DMB* reaction with phenols in solution,14,24 and (3) there is previous evidence for an enhancement in triplet state concentrations in ice, based on 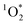 measurements using Rose Bengal as the triplet precursor.11 As discussed in Section 2.3, we also have evidence that ˙OH,
measurements using Rose Bengal as the triplet precursor.11 As discussed in Section 2.3, we also have evidence that ˙OH, 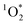 , and the singlet excited state of DMB are minor sinks for PhOH in our samples. Another possible PhOH sink is the group of poorly characterized “long-lived photooxidants” (LLPOs), which are significant sinks for another triplet probe, 2,4,6-trimethyl phenol (TMP), during illumination of surface waters and solutions of colored dissolved organic matter (CDOM).40,41 The evidence for LLPOs in this past aqueous work was that the rate constant for TMP loss increased with decreasing TMP concentration at low concentrations. In contrast, as shown in Fig. 2, we see no change in
, and the singlet excited state of DMB are minor sinks for PhOH in our samples. Another possible PhOH sink is the group of poorly characterized “long-lived photooxidants” (LLPOs), which are significant sinks for another triplet probe, 2,4,6-trimethyl phenol (TMP), during illumination of surface waters and solutions of colored dissolved organic matter (CDOM).40,41 The evidence for LLPOs in this past aqueous work was that the rate constant for TMP loss increased with decreasing TMP concentration at low concentrations. In contrast, as shown in Fig. 2, we see no change in 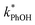 with decreasing PhOH concentration, in either ice or solution, indicating no significant role for LLPOs. This is consistent with past results with 4-methylphenol (4 MP), which is more difficult to oxidize than TMP, showing no evidence of reacting with LLPOs in solution.42 Since PhOH is more difficult to oxidize than 4 MP,21 it is not surprising that LLPOs appear insignificant in our work. However, despite our evidence for 3DMB* and against other reactive intermediates as the oxidant for PhOH, since this probe is not specific to 3DMB* it is possible that other oxidants might be contributing to PhOH oxidation.
with decreasing PhOH concentration, in either ice or solution, indicating no significant role for LLPOs. This is consistent with past results with 4-methylphenol (4 MP), which is more difficult to oxidize than TMP, showing no evidence of reacting with LLPOs in solution.42 Since PhOH is more difficult to oxidize than 4 MP,21 it is not surprising that LLPOs appear insignificant in our work. However, despite our evidence for 3DMB* and against other reactive intermediates as the oxidant for PhOH, since this probe is not specific to 3DMB* it is possible that other oxidants might be contributing to PhOH oxidation.
4. Conclusions and implications
On average, the 3DMB* concentration in LLRs of illuminated ice is increased by a factor of near 100 relative to in solution, but is independent of temperature and total solute, which are the variables that should govern the freeze-concentration factor. Under our standard conditions, our experimentally determined FEXP based on triplet concentrations is roughly 30 times lower than the predicted FFPD from freezing-point depression. Previously, Bower et al. found using furfuryl alcohol and Rose Bengal that the enhancement of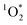 within LLRs is well described by freezing-point depression.11 However, using bisphenol A (BPA) as the probe for
within LLRs is well described by freezing-point depression.11 However, using bisphenol A (BPA) as the probe for 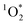 gave experimental freeze-concentration factors that were much lower than FFPD43 and that did not vary with total solute concentration, as we see for [3DMB*] here. It is unclear why reactive species in these two systems do not follow a freezing-point depression model and whether they do so for similar reasons. Based on past evidence that concentrations of unreactive solutes in LLRs follow freezing-point depression,11,22 we suspect that the weaker enhancement of 3DMB* in the current work is a result of secondary chemistry such as suppression of the triplet state by enhanced O2 concentrations in LLRs.
gave experimental freeze-concentration factors that were much lower than FFPD43 and that did not vary with total solute concentration, as we see for [3DMB*] here. It is unclear why reactive species in these two systems do not follow a freezing-point depression model and whether they do so for similar reasons. Based on past evidence that concentrations of unreactive solutes in LLRs follow freezing-point depression,11,22 we suspect that the weaker enhancement of 3DMB* in the current work is a result of secondary chemistry such as suppression of the triplet state by enhanced O2 concentrations in LLRs.
The three oxidants we have studied to date – ˙OH, 3C*, and 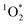 – show a wide range of enhancements in/on ice, a result of differences in enhancements in oxidant sources and sinks. As shown in Table 1,
– show a wide range of enhancements in/on ice, a result of differences in enhancements in oxidant sources and sinks. As shown in Table 1,  in LLRs is enhanced by a factor of approximately FFPD, at least under many conditions, a consequence of its source (e.g., Rose Bengal) being enhanced in LLRs compared to solution but its sink (H2O) being essentially constant.3,11 In contrast, the ˙OH concentration in LLRs is essentially the same as in the equivalent solution, which we believe is a consequence of the concentrations of both sources and sinks being similarly increased in LLRs.10 The DMB triplet represents an intermediate case, with an enhancement in ice (nearly a factor of 100), but not to the extent expected from freezing-point depression. This suggests that the source of triplets (here DMB) is enhanced in LLRs compared to solution, but either not to the extent predicted by FFPD or in combination with an increase in the triplet sink, O2.
in LLRs is enhanced by a factor of approximately FFPD, at least under many conditions, a consequence of its source (e.g., Rose Bengal) being enhanced in LLRs compared to solution but its sink (H2O) being essentially constant.3,11 In contrast, the ˙OH concentration in LLRs is essentially the same as in the equivalent solution, which we believe is a consequence of the concentrations of both sources and sinks being similarly increased in LLRs.10 The DMB triplet represents an intermediate case, with an enhancement in ice (nearly a factor of 100), but not to the extent expected from freezing-point depression. This suggests that the source of triplets (here DMB) is enhanced in LLRs compared to solution, but either not to the extent predicted by FFPD or in combination with an increase in the triplet sink, O2.
While the enhancement in triplet excited state concentrations in laboratory ice is smaller than predicted from freezing-point depression, it is still significant. This enhancement suggests that triplets might be important sinks for certain organic species and for halides in natural snow and ice. Characterizing this potential sink in the cryosphere will require characterizing triplet concentrations in environmental samples and assessing whether the corresponding ice kinetics of triplets can be modeled using freezing-point depression.11,43–45
Acknowledgements
This work is dedicated to the memory of Roland von Glasow, who explored the chemistry and physics of the polar and marine boundary layers with enthusiasm and wonder; he is sorely missed. We thank the National Science Foundation for funding (Grant CHE-1214121), Jon Bower for assistance with initial experiments, Ted Hullar for editorial assistance on early drafts, and the anonymous reviewers for very constructive comments.References
- A. M. Grannas, A. E. Jones, J. Dibb, M. Ammann, C. Anastasio, H. J. Beine, M. Bergin, J. Bottenheim, C. S. Boxe, G. Carver, G. Chen, J. H. Crawford, F. Domine, M. M. Frey, M. I. Guzman, D. E. Heard, D. Helmig, M. R. Hoffmann, R. E. Honrath, L. G. Huey, M. Hutterli, H. W. Jacobi, P. Klan, B. Lefer, J. McConnell, J. Plane, R. Sander, J. Savarino, P. B. Shepson, W. R. Simpson, J. R. Sodeau, R. von Glasow, R. Weller, E. W. Wolff and T. Zhu, An overview of snow photochemistry: evidence, mechanisms and impacts, Atmos. Chem. Phys., 2007, 7(16), 4329–4373 CrossRef CAS.
- J. Klanova, P. Klan, J. Nosek and I. Holoubek, Environmental ice photochemistry: monochlorophenols, Environ. Sci. Technol., 2003, 37(8), 1568–1574 CrossRef CAS PubMed.
- J. P. Bower and C. Anastasio, Measuring a 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-fold enhancement of singlet molecular oxygen (1O2*) concentration on illuminated ice relative to the corresponding liquid solution, Atmos. Environ., 2013, 75, 188–195 CrossRef CAS.
000-fold enhancement of singlet molecular oxygen (1O2*) concentration on illuminated ice relative to the corresponding liquid solution, Atmos. Environ., 2013, 75, 188–195 CrossRef CAS. - V. F. McNeill, A. M. Grannas, J. P. D. Abbatt, M. Ammann, P. Ariya, T. Bartels-Rausch, F. Domine, D. J. Donaldson, M. I. Guzman, D. Heger, T. F. Kahan, P. Klan, S. Masclin, C. Toubin and D. Voisin, Organics in environmental ices: sources, chemistry, and impacts, Atmos. Chem. Phys., 2012, 12(20), 9653–9678 CrossRef CAS.
- C. Anastasio, E. S. Galbavy, M. A. Hutterli, J. F. Burkhart and D. K. Friel, Photoformation of hydroxyl radical on snow grains at Summit, Greenland, Atmos. Environ., 2007, 41(24), 5110–5121 CrossRef CAS.
- C. Anastasio and A. L. Jordan, Photoformation of hydroxyl radical and hydrogen peroxide in aerosol particles from Alert, Nunavut: implications for aerosol and snowpack chemistry in the Arctic, Atmos. Environ., 2004, 38(8), 1153–1166 CrossRef CAS.
- A. J. Beyersdorf, N. J. Blake, A. L. Swanson, S. Meinardi, J. E. Dibb, S. Sjostedt, G. Huey, B. Lefer, F. S. Rowland and D. R. Blake, Hydroxyl concentration estimates in the sunlit snowpack at Summit, Greenland, Atmos. Environ., 2007, 41(24), 5101–5109 CrossRef CAS.
- J. L. France, M. D. King and J. Lee-Taylor, Hydroxyl (OH) radical production rates in snowpacks from photolysis of hydrogen peroxide (H2O2) and nitrate (NO3−), Atmos. Environ., 2007, 41(26), 5502–5509 CrossRef CAS.
- A. Fede and A. M. Grannas, Photochemical production of singlet oxygen from dissolved organic matter in ice, Environ. Sci. Technol., 2015, 49(21), 12808–12815 CrossRef CAS PubMed.
- Z. Chen, L. Chu, E. S. Galbavy, K. Ram and C. Anastasio, Hydroxyl radical in/on illuminated polar snow: formation rates, lifetimes, and steady-state concentrations, Atmos. Chem. Phys., 2016, 16(15), 9579–9590 CAS.
- J. P. Bower and C. Anastasio, Using singlet molecular oxygen to probe the solute and temperature dependence of liquid-like regions in/on ice, J. Phys. Chem. A, 2013, 117(30), 6612–6621 CrossRef CAS PubMed.
- D. Vione, V. Maurino, C. Minero, E. Pelizzetti, M. A. J. Harrison, R. I. Olariu and C. Arsene, Photochemical reactions in the tropospheric aqueous phase and on particulate matter, Chem. Soc. Rev., 2006, 35(5), 441–453 CAS.
- S. Canonica, U. Jans, K. Stemmler and J. Hoigne, Transformation kinetics of phenols in water – photosensitization by dissolved natural organic material and aromatic ketones, Environ. Sci. Technol., 1995, 29(7), 1822–1831 CrossRef CAS PubMed.
- J. D. Smith, V. Sio, L. Yu, Q. Zhang and C. Anastasio, Secondary organic aerosol production from aqueous reactions of atmospheric phenols with an organic triplet excited state, Environ. Sci. Technol., 2014, 48(2), 1049–1057 CrossRef CAS PubMed.
- N. K. Richards-Henderson, A. T. Pham, B. B. Kirk and C. Anastasio, Secondary organic aerosol from aqueous reactions of green leaf volatiles with organic triplet excited states and singlet molecular oxygen, Environ. Sci. Technol., 2015, 49(1), 268–276 CrossRef CAS PubMed.
- T. Zeng and W. A. Arnold, Pesticide photolysis in prairie potholes: probing photosensitized processes, Environ. Sci. Technol., 2013, 47(13), 6735–6745 CrossRef CAS PubMed.
- S. W. Yan and W. H. Song, Photo-transformation of pharmaceutically active compounds in the aqueous environment: a review, Environ. Sci.: Processes Impacts, 2014, 16(4), 697–720 CAS.
- C. K. Remucal, The role of indirect photochemical degradation in the environmental fate of pesticides: a review, Environ. Sci.: Processes Impacts, 2014, 16(4), 628–653 CAS.
- I. Loeff, J. Rabani, A. Treinin and H. Linschitz, Charge-transfer and reactivity of n–pi* and pi–pi* organic triplets, including anthraquinonesulfonates, in interactions with inorganic anions – a comparative-study based on classical Marcus theory, J. Am. Chem. Soc., 1993, 115(20), 8933–8942 CrossRef CAS.
- A. Jammoul, S. Dumas, B. D'Anna and C. George, Photoinduced oxidation of sea salt halides by aromatic ketones: a source of halogenated radicals, Atmos. Chem. Phys., 2009, 9(13), 4229–4237 CrossRef CAS.
- S. Canonica, B. Hellrung and J. Wirz, Oxidation of phenols by triplet aromatic ketones in aqueous solution, J. Phys. Chem. A, 2000, 104(6), 1226–1232 CrossRef CAS.
- H. Cho, P. B. Shepson, L. A. Barrie, J. P. Cowin and R. Zaveri, NMR investigation of the quasi-brine layer in ice/brine mixtures, J. Phys. Chem. B, 2002, 106(43), 11226–11232 CrossRef CAS.
- T. Hullar and C. Anastasio, Direct visualization of solute locations in laboratory ice samples, Cryosphere, 2016, 10(5), 2057–2068 Search PubMed.
- C. Anastasio, B. C. Faust and C. J. Rao, Aromatic carbonyl compounds as aqueous-phase photochemical sources of hydrogen peroxide in acidic sulfate aerosols, fogs, and clouds. 1. Non-phenolic methoxybenzaldehydes and methoxyacetophenones with reductants (phenols), Environ. Sci. Technol., 1997, 31(1), 218–232 CrossRef CAS.
- J. D. Smith, H. Kinney and C. Anastasio, Aqueous benzene-diols react with an organic triplet excited state and hydroxyl radical to form secondary organic aerosol, Phys. Chem. Chem. Phys., 2015, 17(15), 10227–10237 RSC.
- G. M. Marion and S. A. Grant, FREZCHEM: a chemical thermodynamic model for aqueous solutions at subzero temperatures, Hanover, NH, 1994 Search PubMed.
- K. McNeill and S. Canonica, Triplet state dissolved organic matter in aquatic photochemistry: reaction mechanisms, substrate scope, and photophysical properties, Environ. Sci.: Processes Impacts, 2016, 18, 1381–1399 CAS.
- E. S. Galbavy, K. Ram and C. Anastasio, 2-Nitrobenzaldehyde as a chemical actinometer for solution and ice photochemistry, J. Photochem. Photobiol., A, 2010, 209(2–3), 186–192 CrossRef CAS.
- S. Halladja, A. Ter Halle, J. P. Aguer, A. Boulkamh and C. Richard, Inhibition of humic substances mediated photooxygenation of furfuryl alcohol by 2,4,6-trimethylphenol. Evidence for reactivity of the phenol with humic triplet excited states, Environ. Sci. Technol., 2007, 41(17), 6066–6073 CrossRef CAS PubMed.
- H. Beine, C. Anastasio, F. Domine, T. Douglas, M. Barret, J. France, M. King, S. Hall and K. Ullmann, Soluble chromophores in marine snow, seawater, sea ice and frost flowers near Barrow, Alaska, J. Geophys. Res., 2012, 117, D00R15 CrossRef.
- J. E. Dibb, L. D. Ziemba, J. Luxford and P. Beckman, Bromide and other ions in the snow, firn air, and atmospheric boundary layer at Summit during GSHOX, Atmos. Chem. Phys., 2010, 10, 9931–9942 CrossRef CAS.
- P. Calza, D. Vione and C. Minero, The role of humic and fulvic acids in the phototransformation of phenolic compounds in seawater, Sci. Total Environ., 2014, 493, 411–418 CrossRef CAS PubMed.
- K. S. Golanoski, S. Fang, R. Del Vecchio and N. V. Blough, Investigating the mechanism of phenol photooxidation by humic substances, Environ. Sci. Technol., 2012, 46(7), 3912–3920 CrossRef CAS PubMed.
- K. M. Parker, J. J. Pignatello and W. A. Mitch, Influence of ionic strength on triplet-state natural organic matter loss by energy transfer and electron transfer pathways, Environ. Sci. Technol., 2013, 47(19), 10987–10994 CrossRef CAS PubMed.
- M. Brigante, M. Minella, G. Mailhot, V. Maurino, C. Minero and D. Vione, Formation and reactivity of the dichloride radical (Cl2−) in surface waters: a modelling approach, Chemosphere, 2014, 95, 464–469 CrossRef CAS PubMed.
- F. Wilkinson and J. G. Brummer, Rate constants for the decay and reactions of the lowest electronically excited singlet state of molecular oxygen in solution, J. Phys. Chem. Ref. Data, 1981, 10(4), 809–1000 CrossRef CAS.
- P. Neta, R. E. Huie and A. B. Ross, Rate constants for reactions of inorganic radicals in aqueous solution, J. Phys. Chem. Ref. Data, 1988, 17(3), 1027–1284 CrossRef CAS.
- P. G. Tratnyek and J. Hoigné, Oxidation of substituted phenols in the environment – a QSAR analysis of rate constants for reaction with singlet oxygen, Environ. Sci. Technol., 1991, 25(9), 1596–1604 CrossRef CAS.
- M. Rinke and C. Zetzsch, Rate constants for the reactions of OH radicals with aromatics – benzene, phenol, aniline, and 1,2,4-trichlorobenzene, Ber. Bunsen-Ges. Phys. Chem., 1984, 88(1), 55–62 CrossRef CAS.
- H. Kawaguchi, Rates of sensitized photooxidation of 2,4,6-trimethylphenol by humic acid, Chemosphere, 1993, 27(11), 2177–2182 CrossRef CAS.
- S. Canonica and J. Hoigne, Enhanced oxidation of methoxy phenols at micromolar concentration photosensitized by dissolved natural organic material, Chemosphere, 1995, 30(12), 2365–2374 CrossRef CAS.
- S. Canonica and M. Freiburghaus, Electron-rich phenols for probing the photochemical reactivity of freshwaters, Environ. Sci. Technol., 2001, 35(4), 690–695 CrossRef CAS PubMed.
- J. P. Bower and C. Anastasio, Degradation of organic pollutants in/on snow and ice by singlet molecular oxygen (1O2*) and an organic triplet excited state, Environ. Sci.: Processes Impacts, 2014, 16(4), 748–756 CAS.
- F. Domine, J. Bock, D. Voisin and D. J. Donaldson, Can we model snow photochemistry? Problems with the current approaches, J. Phys. Chem. A, 2013, 117(23), 4733–4749 CrossRef CAS PubMed.
- J. L. Thomas, J. Stutz, B. Lefer, L. G. Huey, K. Toyota, J. E. Dibb and R. von Glasow, Modeling chemistry in and above snow at Summit, Greenland – part 1: model description and results, Atmos. Chem. Phys., 2011, 11(10), 4899–4914 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6em00534a |
| This journal is © The Royal Society of Chemistry 2017 |