Superstructural diversity in two dimensions: crystal engineering of laminated solids
Michael J. Zaworotko
Department of Chemistry, University of South Florida, 4202 E. Fowler Avenue, SCA 400, Tampa, Florida 33620, USA.. E-mail: zaworo@chuma1.cas.usf.edu
First published on 13th December 2000
Abstract
The application of supramolecular concepts such as self-assembly to the solid state offers an approach to crystal design and crystal engineering, namely supramolecular synthesis of solids, that is based upon the design of infinite networks. Self-assembly of more than one molecular component, modular self-assembly, is particularly attractive since it can be accomplished in one-pot reactions with existing molecular components and allows for facile fine-tuning of structural and functional features. The challenges and opportunities that face crystal engineering are illustrated by concentrating on the superstructural diversity that has been exhibited in 2D network structures. Despite the observed superstructural diversity, which can manifest itself in the form of supramolecular isomerism, and the range of molecular components that have been utilized, these structures have in common an inherent ability to mimic clays by intercalation of guest molecules.
Michael John Zaworotko was born in South Wales in 1956 and attended Bedwellty Grammar School and Imperial College, where he received a B.Sc. in 1977. His doctoral research was conducted at the University of Alabama under the supervision of Prof. Jerry L. Atwood and the Ph.D. was granted in 1982. This was followed by post-doctoral research in structural and organometallic chemistry with Prof. S. R. Stobart at University of Victoria, Canada. He joined the faculty at Saint Mary’s University, Halifax, Canada in 1985, where he remained until 1998. His interest in crystal engineering was developed during a sabbatical leave at the Frank J. Seiler Research Laboratory at the United States Air Force Academy in Colorado Springs, USA. He moved to the University of Winnipeg, Canada in 1998, where he served as Dean of Arts and Science and to the University of South Florida, Tampa, USA in September 1999, where he currently serves as Chairperson of the Department of Chemistry. His current interests focus upon expanding the field of crystal engineering further into the nanoscale by concentrating upon biological and synthetic supermolecules. |
From molecules to crystal engineering and design
That the physical and chemical properties of crystalline solids are as critically dependent upon the distribution of molecular components within the crystal lattice as the properties of its individual molecular components has provided impetus for research into crystal design and engineering. In such a context, it is probably more than coincidental that the late 1980s represents a watershed for research in this area. A provocative statement by Maddox1 highlighted the issue as follows: ‘One of the continuing scandals in the physical sciences is that it remains in general impossible to predict the structure of even the simplest crystalline solids from a knowledge of their chemical composition’. It is reasonable to assert that Maddox’s statement still holds true, especially for organic solids. Nevertheless, it has not precluded a seemingly exponential growth in research activity devoted to the subjects of crystal design and crystal engineering. This should be unsurprising since the implications of crystal engineering go beyond materials science. Indeed, the term crystal engineering was first coined in a contribution by G. M. J. Schmidt concerning the subject of organic solid-state photochemistry.2 An important consequence of Schmidt’s research into solid-state reactions is that it is implicit by use of the term crystal engineering that crystals can be thought of as the sum of a series of molecular recognition events, self-assembly, rather than the result of the need to ‘avoid a vacuum’. In other words, crystal engineering uses the concepts of supramolecular chemistry. It is now evident that supramolecular chemistry, defined by Lehn as chemistry beyond the molecule,3 and ‘supramolecular assemblies’ are inherently linked to the concepts of crystal engineering. Therefore, crystal engineering has implications that extend into areas as diverse as pharmaceutical development and synthetic chemistry. In the context of the former, there are important processes and intellectual property implications related to polymorphism.4,5 In the context of synthetic chemistry, solid-phase organic synthesis can be solvent free and offer significant yield and regioselectivity advantages over solution phase reactions,6 including some that cannot be effected in solution.7–9The field of crystal engineering developed further in the 1980s thanks to a series of papers and monographs by Desiraju10,11 and Etter12 that concentrated upon applying the Cambridge Structural Database for analysis, interpretation and design of noncovalent bonding patterns in organic solids. In this contribution, we focus upon how these supramolecular concepts have been exploited to rationally generate laminated architectures in the solid state. Particular emphasis is placed upon supramolecular isomerism and how it affords superstructural diversity in two classes of compound: coordination polymers and organic networks.
Coordination polymers: networks from first principles
Coordination polymers exemplify how crystal engineering has become a paradigm for the design of new supramolecular architectures. In this context, the work of Wells13,14 serves as an excellent reference point. Wells defined crystal structures in terms of their topology by reducing them to a series of points (nodes) of a certain geometry (tetrahedral, trigonal planar, etc.) that are connected to a fixed number of other points. The resulting structures, which can also be calculated mathematically, can be either discreet (zero-dimensional) polyhedra or infinite (one-, two-, and three-dimensional) periodic nets. It is perhaps surprising that it was not until the 1990s that the approach of Wells began to bear fruit in the laboratory. Discrete coordination compounds that are based upon Platonic or Archimedean polyhedra have attracted considerable interest in recent years15–17 and are conceptually related to the ‘Wellsian’ approach. However, we shall focus upon infinite architectures, for which Robson and coworkers18 delineated principles that facilitated rapid development of the field of coordination polymers. In effect, Robson extrapolated Wells’ work on inorganic network structures into the realm of metal–organic compounds and coordination polymers. In this context, the ‘node and spacer’ approach has been remarkably successful at producing predictable network architectures. Scheme 1 illustrates some of the simplest architectures that can be generated by using commonly available metal moieties and linking them with linear ‘spacer’ ligands.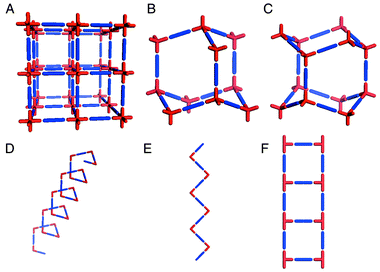 | ||
| Scheme 1 A schematic representation of some of the simple 3D and 1D network architectures that have been structurally characterized for metal–organic polymers: A. octahedral; B. cubic diamondoid; C. hexagonal diamondoid; D. helix; E. zigzag chain; F. molecular ladder. | ||
These network structures are salient from a design perspective as follows:• Each of the networks illustrated in Scheme 1 is based upon at least two components (i.e. the metal node and the ligand spacer) and the components can be pre-selected for their inherent ability to self-assemble. These network structures can therefore be regarded as blueprints for the construction of networks that, in principle, can be generated from a diverse range of chemical components, i.e. they are prototypal examples of modular frameworks. It should be noted that the construction of networks from single component systems also represents an important area of activity but that there are conceptual differences between the two approaches.• The architecture alone often affords information that allows the chemist to predict some of the bulk properties. For example, most of the structures in Scheme 1 inherently generate cavities that are based upon the size and length of the spacer ligand. The 3D architectures A–C represent in some ways the ultimate challenge in terms of crystal engineering since they lead directly to crystal structure prediction. It should therefore be unsurprising that diamondoid19 and octahedral20–22 frameworks have attracted considerable attention. In general, for 3D architectures one would expect rigidity to be coupled with porosity, i.e. analogies to zeolites may be drawn. In the case of 1D structures one would normally expect close-packing variability in the context of how adjacent networks pack with respect to one another.• We have coined the term ‘supramolecular isomerism’23 to define the existence of more than one superstructure for a given set of molecular components. This concept is illustrated by structures B and C, which represent cubic and hexagonal diamondoid structures, respectively, and structures D and E, which are also supramolecular isomers of one another. It is important to note that, although supramolecular isomerism affords superstructural diversity, it also limits the number of possible architectures to those that can be generated rationally from the molecular components that are present in a network.
The diversity of network structures that can result from supramolecular isomerism is the focus of this article. In the case of 2D architectures, one would anticipate that networks would possess an inherent ability to intercalate guest molecules, i.e. clay-like properties will be expected. As revealed herein, this is indeed the case for many of the 2D networks that have been studied by us and other groups. We also highlight the surprising degree of diversity that can exist in 2D structures.
Square-grid coordination polymers
Square-grid networks exemplify a particularly simple and commonly reported example of a predictable 2D metal–organic network. Square grid coordination polymers are based upon 1∶2 metal:ligand complexes with linear bifunctional spacer ligands. They were first reported using cyano ligands24–26 and have recently been expanded in terms of chemical type and cavity size to include pyrazines,27–30 4,4′-bipyridine(bipy)30–35 and longer analogues of bipy.23,36 These compounds can indeed be regarded as being analogues of clay minerals since they also have an ability to intercalate guest molecules. However, they have added features that are not likely to be present in clays and they are complementary to ‘organoclays’,37 which are chemically modified inorganic clays or calixarene ‘organic clay mimics’,38,39 that are based upon calix[4]arenesulfonate salts that form alternating hydrophobic and hydrophilic layers. For example, cavities lie within the plane of the structure and they are suitable for either interpenetration or enclathration of a wide range of organic guest molecules. Furthermore, since they are designed from first principles, it is possible to design the cavities to be inherently hydrophobic or hydrophilic and to tune their dimensions, although interpenetration can mitigate against the existence of frameworks with very large cavities.40 Finally, it should be noted that the metal sites can possess chemical as well as structural properties. Indeed, catalytically active sites have been incorporated into square-grid structures.32Square-grid networks generated with bipy spacer ligands were first reported by Fujita et al.32 Fujita’s compounds are based on Cd(II) and related structures were subsequently reported for other transition metals, including Co(II) and Ni(II) and Zn(II). Although these 2D coordination networks are isostructural within the coordination grid (effective dimensions of the diagonals are ca. 1.3 × 1.3 nm), the crystal structures of compounds can differ in the manner in which the networks stack with respect to each other. In particular, interlayer separations can lie in the range 0.6–0.8 nm and the quantity of guest molecule can vary. [M(bipy)2(NO3)2]·guest (M = Co, Ni)41–43 exhibits three basic packing modes (Fig. 1). These packing modes are similar in that the square-grid networks are parallel to one another but they differ in the manner in which the square grids pack with respect to one another and the relative proportion of guest molecule that is present. Type A compounds exhibit 2∶1 guest∶host stoichiometry and interplanar separations of ca. 0.6 nm, type B compounds generally crystallize with 2.5 guest molecules per metal center and interlayer separations are ca. 0.8 nm. Type C compounds have interlayer separations that are similar to those seen for type B compounds and have 3∶1 stoichiometry.
![Perspective views of the stacking of square-grid network architectures
of formula [M(bipy)2(NO3)2]:(a)
A type grids; (b) B type grids; (c) C type grids. The square grid is
represented schematically.](/image/article/2001/CC/b007127g/b007127g-f1.gif) | ||
| Fig. 1 Perspective views of the stacking of square-grid network architectures of formula [M(bipy)2(NO3)2]:(a) A type grids; (b) B type grids; (c) C type grids. The square grid is represented schematically. | ||
In all of these compounds the proportion of the crystal that is occupied by guest molecules is ca. 50% by volume. In such a situation it becomes reasonable to question whether interactions between the guest molecules determine the cavity shape and crystal packing of the square grid polymers rather than vice versa. Careful examination of the crystal packing in {[Ni- (bipy)2(NO3)2]·2pyrene }n reveals that the pyrene molecules form an independent noncovalent network that is complementary from a topological perspective with the square-grid coordination polymer. Indeed, the resulting crystal represents what is to our knowledge the first compound in which it has been revealed that two very different types of 2D net interpenetrate. The square-grid coordination networks [Fig. 2(a)] possess inner cavities of ca. 0.8 × 0.8 nm and stack in such a manner that they lie parallel to one another with an interlayer separation of ca. 0.79 nm.
![Space-filling illustrations of the two independent networks in
[M(bipy)2(NO3)2]·2pyrene: (a) the
metal–organic coordination polymer square-grid, and (b) the
noncovalent (4,4) net of pyrene molecules.](/image/article/2001/CC/b007127g/b007127g-f2.gif) | ||
| Fig. 2 Space-filling illustrations of the two independent networks in [M(bipy)2(NO3)2]·2pyrene: (a) the metal–organic coordination polymer square-grid, and (b) the noncovalent (4,4) net of pyrene molecules. | ||
The pyrene nets [Fig. 2(b)] are sustained by edge-to-face interactions and contain cavities of dimensions ca. 0.65 × 0.35 nm. The planes of the neighboring molecules intersect at an angle of ca. 60° and there are no face-to-face stacking interactions between the molecules. The pyrene nets can be regarded as distorted (4,4) nets (if the node is the point in space at which the vectors of the four pyrene planes intersect) or as a distorted brick wall form of a (6,3) net (if the nodes exist at the point of the edge-to-face interactions). It is important to note that, as revealed by Scheme 2, a (6,3) planar net is also complementary from a topological sense with the (4,4) coordination polymer net and that the coordination polymer nets must pack in a staggered manner if they are to fit with the noncovalent net.
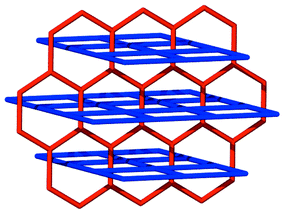 | ||
| Scheme 2 A schematic diagram that illustrates how honeycomb (6,3) and square (4,4) nets can interpenetrate. | ||
That the crystal structure can be viewed as coexistence of interpenetrating covalent and noncovalent nets is potentially important in the context of understanding the structure and stoichiometry of other compounds that are based upon interpenetrated covalent and noncovalent nets. It also illustrates how polarity in crystals can be generated from subtle packing of achiral components, since the pyrene molecules form chiral nets.
This mode of packing is not unique to {[Ni(bipy)2- (NO3)2]·2pyrene}n . Indeed, its naphthalene analogue, {[Ni(bipy)2(NO3)2]·3 C10H8}n,43 can be interpreted as being the result of interpenetration of hexagonal and square nets and a study of a series of related compounds has revealed the presence of noncovalent nets in every compound.44 The noncovalent hexagonal nets formed by naphthalene and veratrole are illustrated in Fig. 3.
![Space-filling illustrations of the hexagonal (6,3) networks formed by
(a) veratrole, and (b) naphthalene in the intepentrated structures [Ni-
(bipy)2(NO3)2]·3aromatic.](/image/article/2001/CC/b007127g/b007127g-f3.gif) | ||
| Fig. 3 Space-filling illustrations of the hexagonal (6,3) networks formed by (a) veratrole, and (b) naphthalene in the intepentrated structures [Ni- (bipy)2(NO3)2]·3aromatic. | ||
Coordination polymers in which identical (4,4) planar networks interpenetrate have been observed to exhibit two types of interpenetration, both of which are examples of inclined interpenetration.40 The most commonly encountered form might be described as diagonal/diagonal inclined interpenetration and was observed in the prototypal [M(bipy)2X2]n compound [Zn(bipy)2(H2O)2]SiF6.32 The other mode of interpenetration might be described as parallel/parallel inclined interpenetration and to our knowledge has only been reported for two compounds.45,46 These types of interpenetration are illustrated in Scheme 3(a) and 3(b), respectively, and differ in how the networks orient and cut through each other.
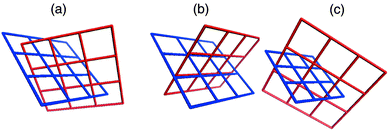 | ||
| Scheme 3 A schematic that illustrates the three modes of inclined interpenetration that have been observed for square-grid networks: (a) diagonal/diagonal, (b) parallel/parallel, and (c) parallel/diagonal. | ||
Parallel refers to a structure in which a ‘spacer’ ligand from one network threads through the cavity of the other, diagonal refers to a structure in which a ‘node’ from one network (e.g. the metal moiety) is within the cavity of the other. One would anticipate that the structure that is adapted by a particular compound would be influenced by several geometric factors: the relative size of the cavity; the distance between adjacent nodes within a network; the thickness of the layers and how this limits the interlayer separation of adjacent networks; the steric bulk of the node. In this context, it is important to note that, with all other things being equal, the diagonal/diagonal mode of interpenetration facilitates an interlayer separation that is 41.4% greater than that of the parallel/parallel mode. Furthermore, the diagonal/diagonal mode ensures a staggered orientation of parallel layers whereas an eclipsed orientation is necessary if the parallel/parallel structure is present. Therefore, in terms of steric considerations, it would be expected that the diagonal/diagonal mode would be most favored. However, circumstances where the interlayer separation would ideally be shorter, or where the metal atoms in adjacent layers would be eclipsed (e.g. to maximize interlayer interactions) could favor the parallel/parallel mode.
The structures we have studied that are based upon complementary covalent and noncovalent networks exhibit a third mode of inclined interpenetration that is a hybrid of the modes described above: parallel/diagonal inclined interpenetration. The noncovalent (4,4) arene networks exhibit parallel inclined interpenetration with respect to the (4,4) metal–organic coordination networks, whereas the covalent coordination networks demonstrate diagonal inclined interpenetration with respect to the arene networks [Scheme 3(c)]. This structural feature means that the nitrate groups of adjacent parallel coordination polymer grids are staggered and that the interlayer separation is a consequence of the size of the arene network. It should therefore be unsurprising that Type A grids result when templated by the smallest arenes (benzene and derivatives) as they exhibit smaller interlayer separations than type B and C packing. Grid types B and C occur in the presence of larger or more arenes.
A question that cannot yet be answered with certainty concerns whether or not the noncovalent networks of aromatic molecules can exist in the absence of the coordination polymers. In this context, the existence of a 1∶1 binary compound between ferrocene and pyrene45 represents an important prototype since pairs of ferrocene molecules are stacked inside a pyrene 2D network that is sustained by noncovalent C–H⋯π interactions (Fig. 4). This pyrene network is a slightly distorted version of that observed in {[Ni(bipy)2(NO3)2]·2 pyrene}n.
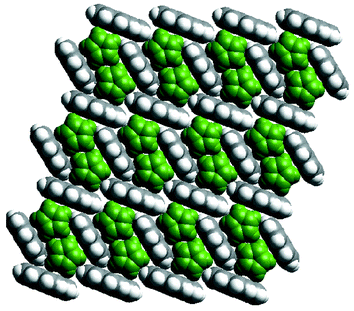 | ||
| Fig. 4 A space-filling illustration of the crystal structure of the cocrystal formed by ferrocene (green) and pyrene. | ||
From the above it should be clear that even for the relatively narrow class of compounds of formula [M(bipy)2X2]n, there are many permutations of metal, anion and guest. It should be noted that grids in which there are two types of spacer ligand, rectangular grids, have also been reported.29,30 It therefore seems likely that square and rectangular grids will represent a generic class of synthetic clay mimic.
Other 2D architectures
The existence of supramolecular isomerism is well exemplified by the diverse range of architectures that can be generated by self-assembly of T-shaped nodes. In the context of coordination polymers, this effectively means linking of mer-substituted octahedral metal moieties or trisubstituted square-planar metal centers. In such a situation the stoichiometry is based upon a 1∶1.5 metal : spacer ligand ratio. The T-shape node has thus far produced examples of 1D, 2D and 3D networks. There are three distinct 2D supramolecular isomers: brick wall,45,48–55 herringbone,51,56–58 and bilayer.59–61 Schematic illustrations of these structures are presented in Scheme 4(a)–(c), respectively. It is interesting to note that, if one calculates the possible 2D networks that are possible for T-shaped nodes (Scheme 4), three of the five possibilities have already been realized.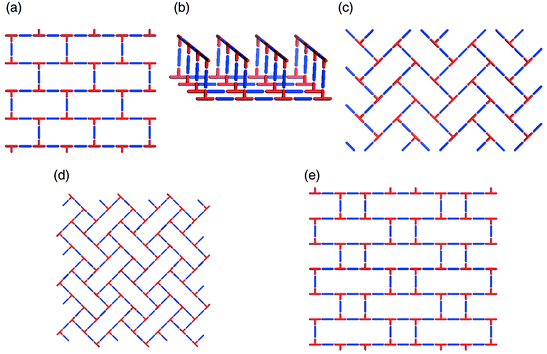 | ||
| Scheme 4 A schematic illustration of 2D nets that can be generated for T-shape building blocks: that have been characterized or might be expected to occur: (a) brick wall; (b) bilayer; (c) herringbone; (d) long-and-short brick; (e) basket weave; (d) and (e) are yet to be realized. | ||
The brick architecture was first observed as the product of the reaction between heptacoordinate Cd(II) and 1,4-bis[(4-pyridyl)methyl]-2,3,5,6-tetrafluorophenylene.35 The T-shape geometry is the result of two nitrate ligands chelating in a bidentate manner, thereby occupying four of the seven coordination sites. The structure is triply interpenetrated and, as such, does not have channels or cavities. Interestingly, in a similar system using the non-fluorinated pyridyl-based ligand, a 1D ladder structure was observed. In several of the compounds that exhibit the herringbone or ‘parquet floor’ architecture the coordination sphere is similar to that of the brick architectures: heptacoordinate Cd(II) or Co(II), with two terminal bidentate nitrate ligands and coordination to one end of three 4,4′-azopyridine bridging ligands; an isostructural example has also been reported with 1,2-bis(4-pyridyl)ethyne as the bridging ligand.60
The bilayer architecture has been observed in at least three compounds.59–63 Interestingly, it has been observed as the product from the reaction of Co(NO3)2 and bipy, which also generates ladder, square-grid and herringbone architectures. The bilayer form of [Co(bipy)1.5(NO3)2] is observed if crystallization occurs in the presence of CS259 or H2O.61,63 The bilayers pack by partial interdigitation (Scheme 5), which allows 1D channels to run through the structure. This structure is somewhat relevant since it represents one of the first reported examples of a synthetic compound that might be regarded as a metal–organic zeolite, i.e. the structure is porous and stable to loss of guest.63 The bilayer architecture has also been reported for systems using 1,2-bis(4-pyridyl)ethane.64
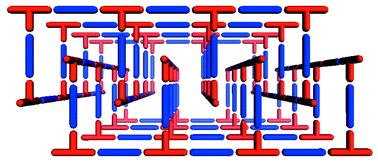 | ||
| Scheme 5 A schematic that illustrates how porosity can be generated by partial interdigitation of bilayer networks. | ||
The number of supramolecular isomers already observed in the Co(NO3)2/bipy system indicates the importance of template and crystallization conditions. It seems reasonable to assert that it is only a matter of time and effort before the weave and long-and-short brick motifs, Scheme 4(d) and 4(e), respectively, will also be realized.
In terms of topology, it should be noted that brick and herringbone motifs are both examples of (6,3) nets and can therefore be regarded as being closely related to honeycomb (6,3) nets. Honeycomb networks are quite common in organic structures because of the availability of trigonal nodes (i.e. 1,3,5-trisubstituted benzenes such as trimesic acid and species such as the guanadinium cation) but they seldom occur in the context of metal–organic polymers because trigonal and trigonal-bipyramidal coordination geometries are relatively rare. However, [Cu(pyrazine)1.5]BF465 is based upon trigonal Cu(I) and it should therefore be unsurprising that it crystallizes as a honeycomb (6,3) net. That there now exist a number of ligands with trigonal geometry means that it is likely that a wider range of honeycomb structures will be generated in the near future.
3D structures via 2D structures
Manipulation of 2D structures represents a possible entry into the generation of 3D architectures. In such a context, there are two relatively simple strategies: cross-linking of 2D structures and interpenetration of identical or different 2D networks.Cross-linking becomes feasible if one selects an appropriate 2D structure that has functionality in the axial direction. Such an approach has been widely used by clay chemists and hence the term ‘pillaring’ might be applied to describe such a process. [M(bipy)2(SiF6)] could be used as a prototype in the context of coordination polymers since it can be regarded as having been generated from square-grid coordination polymers that are cross-linked by μ-SiF6 anions.20,22
Interpenetration is a widely encountered phenomenon40 that can mitigate against the existence of frameworks with very large cavities. However, Scheme 6 reveals that there are situations in which interpenetration can occur, generate porosity and afford 3D structures. Square-grid polymers that are based upon longer spacer ligands such as 1,2-bis(4-pyridyl)ethane (bipy-eta) or 1,2-bis(4-pyridyl)ethylene (bipy-ete) can interpenetrate in such a fashion.40,41
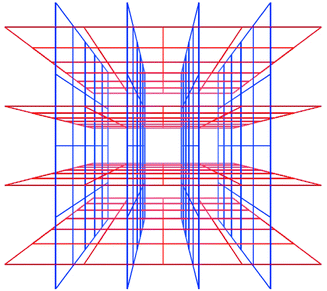 | ||
| Scheme 6 A schematic diagram that illustrates how square-grids can interpenetrate and generate channels. | ||
Organic networks–molecular and ionic structures involving trimesic acid
It is possible in both principle and practice to draw a number of analogies between organic networks and coordination polymers. In particular, the ‘node and spacer’ approach can be employed equally well with noncovalent interactions as with coordinate covalent bonds. This is especially true for hydrogen bonds, for which the donor (i.e. a protic hydrogen atom) and the acceptor (i.e. a region of electron density) can be compared with metal atoms and ligands, respectively. Furthermore, as noted by Etter,12 in cases where there are multiple hydrogen bonding sites, there is a fair degree of predictability concerning which donors and acceptors will engage. In this context, networks that involve NH⋯O and/or OH⋯O hydrogen bonds, including those that exploit the carboxylic dimer or its deprotonated form, represent a wide range of reliable and ubiquitous supramolecular synthons that already have been applied in a broad range of systems.Molecular networks sustained by trimesic acid
Hydrogen-bonded 2D networks are well exemplified the well known structure of trimesic acid (1,3,5-benzene tricarboxylic acid, H3TMA), a polyfunctional carboxylic acid that is inexpensive and chemically robust. It possesses trigonal exodentate functionality that facilitates self-assembly into two dimensions. Fig. 5 illustrates how the hydrogen-bonding pattern in 2D networks formed by H3TMA generates cavities of predictable size (ca. 1.4 nm diameter). In pure H3TMA66 the honeycomb grid is puckered and the cavities are filled by self-inclusion, or interpenetration, of other networks. However, subsequent reports revealed that there are methods for preparing the non-interpenetrated or open framework form of H3TMA.67,68 If crystallized in the presence of alkanes, H3TMA forms open-framework honeycomb layers that align in such a manner that adjacent sheets are almost eclipsed with respect to each other [Fig. 5(b)]. The resulting architecture observed in the crystal structure is essentially identical to that depicted in Fig. 5(a).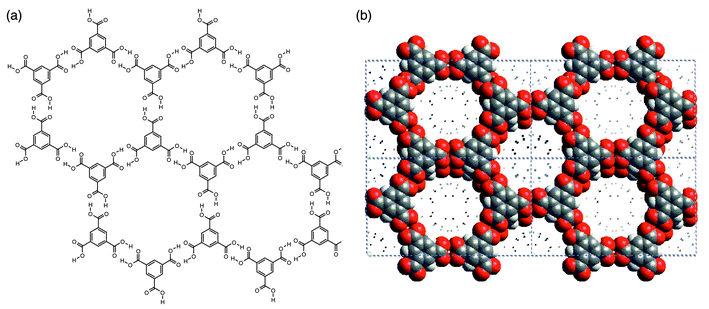 | ||
| Fig. 5 Schematic (a) and space-filling (b) views of the open-framework phase of trimesic acid. | ||
H3TMA represents an example of a self-assembled motif. However, this limits options in terms of supramolecular synthesis, especially when compared to modular systems. The H3TMA network can be modified in several ways if modular approaches are employed. For example, [H3TMA][bipy]1.5 would be expected to exist as an expanded form of H3TMA since the pyridine–carboxylic acid supramolecular synthon appears to be more stable than the carboxylic acid dimer itself.69 As depicted in Fig. 6, the anticipated expanded honeycomb structure indeed occurs and the cavities are large (ca. 2.6 × 3.5 nm). However, the cavities are filled by the interpenetration of three independent networks [Fig. 6(b)], thereby affording a close-packed structure with no cavities. This type of interpenetration, parallel interpenetration, resembles weaving, is facilitated by puckering of the pseudohexagons that form the network. Indeed, the hexagons resemble the chair conformation of cyclohexane.
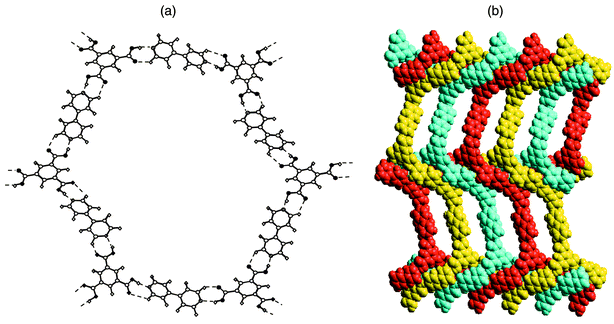 | ||
| Fig. 6 The cocrystal formed by trimesic acid and 4,4′-bipyridine: (a) a single ‘expanded trimesic acid’ honeycomb network and (b) a space-filling view of how the puckered honeycomb networks interpenetrate. | ||
Rao and coworkers recently reported a related structure that is based upon modular self-assembly:70 an organic network formed by trithiocyanuric acid (TCA) and bipy. Adjacent layers are aligned parallel to each other and there is no interpenetration.
Networks sustained by anions of trimesic acid
Anionic forms of H3TMA also represent an appropriate node for generation of 2D superstructures. Ammonium salts of the deprotonated forms of H3TMA offer a simple entry into such systems.71–73Scheme 7 illustrates two motifs that demonstrate how the ammonium moiety might extend anionic forms of H3TMA into honeycomb networks.![The two supramolecular isomers that have been seen for self-assembly of
carboxylate and ammonium moieties in
[NH2(c-C6H11)2]3
[TMA].](/image/article/2001/CC/b007127g/b007127g-s7.gif) | ||
| Scheme 7 The two supramolecular isomers that have been seen for self-assembly of carboxylate and ammonium moieties in [NH2(c-C6H11)2]3 [TMA]. | ||
In the case of TMA3− and the dicyclohexylammonium cation, supramolecular isomers A74 and B75 have both been observed to generate laminated structures. The generation of A or B appears to be solvent dependent. It has also been shown that self-assembly of the lamellar structure can occur on surfaces.74 An important feature of architectures that are sustained by A and B is that some of their components and features can be fine-tuned without destroying the basic architecture. For example, the ammonium cation substituents can be changed without influencing the basic molecular recognition properties in the context of motifs A and B. For secondary amines, organic substituents would extend above and below the network, and in appropriate circumstances would preclude interpenetration.
If alkyl substituents are present on the ammonium cation and the stoichiometry is 1∶2 then the typical result is a laminated material with poor ability to adsorb molecules because of interdigitation of the alkyl substituents.72 However, use of dibenzylamine mitigates against interdigitation and promotes reversible incorporation of aromatic guest molecules.73 The resulting compounds are structurally related to clays, but they are inherently hydrophobic and have generic affinity for a wide range of aromatic guests over alcohols or water. In a series of host–guest compounds, the stoichiometry remains constant, [NH2(CH2Ph)2]2[HTMA], but there is variation in the geometry of the hydrogen bond layer and in the manner in which guest molecules are incorporated. In general, the benzyl groups form a plethora of aromatic C–H⋯π interactions to the surrounding guest molecules. The unit cell lengths are typically multiples of ca. 1.2 × 1.7 × 2.1 nm (stacking axis, short axis and long axis, respectively). The length of the stacking axis represents the interlayer separation and a doubling of the length of the stacking axis occurs when adjacent layers are not related by translation. Multiples of short and long axes also occur because of differences in the arrangement of guest molecules between benzyl groups. In effect, guest molecules and/or benzyl groups do not necessarily repeat with the asymmetric unit of the H-bonded layer. The crystal structures might be classified based upon the stacking axis as being of one of two types: (a) identical packing of adjacent layers (i.e. related by translation); (b) adjacent layers which are different from each other. The hydrogen bonded sheets can be either flat or corrugated. In effect, the host matrix is a flexible, generic host material for aromatic molecules. A representative series of structures is illustrated in Fig. 7 and, as should be clear, there is no interdigitation of benzyl groups.
![The crystal structures of four ‘organic clays’ sustained by
[(trimesate){NH2(CH2Ph)2}2
]. The benzyl moieties preclude interdigitation and facilitate
reversible sorption of aromatic molecule: (a) pyrene; (b) naphthalene; (c)
nitrobenzene; (d) veratrole.](/image/article/2001/CC/b007127g/b007127g-f7.gif) | ||
| Fig. 7 The crystal structures of four ‘organic clays’ sustained by [(trimesate){NH2(CH2Ph)2}2 ]. The benzyl moieties preclude interdigitation and facilitate reversible sorption of aromatic molecule: (a) pyrene; (b) naphthalene; (c) nitrobenzene; (d) veratrole. | ||
A series of related structures that is based upon two-dimensional layers resulting from hydrogen bonding of the trigonal guanidinium cation, C(NH2)3+, and organic sulfonate ions RSO3− has been extensively studied by the Ward group.76 Interdigitation of the organic substituent of the sulfonate ions on adjacent layers and ionic hydrogen bonding predictably leads to a series of laminar architectures.
Summary and conclusions
The fundamental precept of crystal engineering is that all information necessary for design of extended 1D, 2D and 3D structures is already present at the molecular level in existing chemical species. However, crystal engineering does not address the important issues of crystal structure prediction, crystal growth and crystal nucleation. In the case of growth and nucleation, the role of kinetic factors and inhibitors in controlling morphology, polymorphs and supramolecular isomers is critical. Crystal engineering does not yet address control of such factors, rather it afford ‘recipes’. Based upon this understanding and the results described herein one can make several assertions:Prediction vs. design
It is important to stress the significant conceptual difference between crystal engineering and crystal structure prediction. They are not synonymous. In short, crystal structure prediction is precise (i.e. space group and exact details of packing are defined) and deals primarily with known molecules, many of which are not disposed to predictable self-assembly.77,78 Crystal engineering is far less restrictive from a conceptual perspective since it focuses more broadly upon the design of new and existing network architectures. In effect, the principles of design are based upon a blueprint, in many cases a blueprint that is first recognized via a serendipitous discovery, and they allow the designer to select components in a judicious manner. Therefore, a desired network structure or blueprint can be limited to chemical moieties, in many cases commercially available moieties, that are predisposed to a successful outcome. In short, crystal engineering represents a paradigm for supramolecular synthesis of new solid phases and there are no real limits in terms of chemical moieties that can be involved.What does self-assembly mean in this context of crystal engineering?
That one can exploit self-assembly principles to design new solid phases has important implications. First and foremost, all the information necessary to build networks is already stored in known molecules. In the context of the results reported herein, all structures are air- and water-stable and were generated in one-pot reactions using commercially available reagents. Second, if one uses a modular self-assembly approach then fine-tuning of structures is both facile and can be effected broadly. It should be intuitive that most molecules are not self-complementary, i.e. their molecular recognition sites cannot be fully satisfied by self-assembly. It therefore follows that modular structures, i.e. those based upon more than one component, are often going to be both more diverse and more controllable than single component phases.Relevance to 0D structures
The principles of self-assembly have also been applied towards the design and isolation of discrete molecular structures. Such structures are exemplified by molecular squares79–81 and, more recently, by striking examples of new high molecular weight compounds that can be described as spheroid organic82,83 or coordination architectures.15–17,84 The design principles behind the isolation and development of these new classes of compound are based upon applying the concept of self-assembly in the context of geometric considerations found in regular (Platonic) and semi-regular (Archimedean) solids.82 Interestingly, such structures are also known in zeolites (e.g. Linde A, which is based upon an edge-skeleton generated by fused, truncated octahedra85) and in biological self-assembled systems such as mammalian picornaoviruses.86–89It is reasonable to expect a great deal of synergy between these two areas of research. In the context of how self-assembly of discrete structures will influence crystal engineering, it is reasonable to assert that a wide range of nanosized molecular species will become available for self-assembly of synthetic clay-like and zeolite-like architectures. Such structures would be unprecedented and offer nanoscale channels and cavities in addition to novel functionality. The hierarchy of such systems, which is inherently a consequence of self-assembly approaches, and the interesting possibilities that exist for use of such ‘secondary building units’ in materials science have already been highlighted by others.90,91
Acknowledgements
I gratefully acknowledge the generous financial support of the NSERC during 1986–99 and Saint Mary’s University. I am also indebted for the contributions to this work by a group of talented, hard-working students and coworkers, many of who were undergraduates when they were active in my group. Thanks to them I never need to be reminded that the primary benefit of research is that it is for people and by people. I will only accept a small part of the blame for the contributions that these individuals are now making to science and society.Notes and references
- J. Maddox, Nature, 1988, 335, 201 CrossRef.
- G. M. J. Schmidt, Pure Appl. Chem., 1971, 27, 647 CAS.
- J. M. Lehn, Supramolecular Chemistry: Concepts and Perspectives, VCH, Weinheim, 1995. Search PubMed.
- J. Bernstein, R. J. Davey and J. O. Henck, Angew. Chem., Int. Ed., 1999, 38, 3441 CrossRef.
- J. D. Dunitz and J. Bernstein, Acc. Chem. Res., 1995, 28, 193 CrossRef CAS.
- K. Tanaka and F. Toda, Chem. Rev., 2000, 100, 1025 CrossRef CAS.
- L. R. Macgillivray, J. L. Reid and J. A. Ripmeester, J. Am. Chem. Soc., 2000, 122, 7817 CrossRef CAS.
- J. Xiao, M. Yang, J. W. Lauher and F. W. Fowler, Angew. Chem., Int. Ed., 2000, 39, 2132 CrossRef CAS.
- J. J. Kane, R. F. Liao, J. W. Lauher and F. W. Fowler, J. Am. Chem. Soc., 1995, 117, 12 003 CrossRef CAS.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311 CrossRef CAS.
- G. R. Desiraju, Crystal Engineering: the Design of Organic Solids, Elsevier, Amsterdam, 1989. Search PubMed.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120 CrossRef CAS.
- A. F. Wells, Three-Dimensional Nets and Polyhedra, Wiley, New York, 1977. Search PubMed.
- A. F. Wells, Structural Inorganic Chemistry, Oxford University Press, Oxford, 1975. Search PubMed.
- B. Olenyuk, J. A. Whiteford, A. Fechtenkotter and P. J. Stang, Nature, 1999, 398, 796 CrossRef CAS.
- N. Takeda, K. Umemoto, K. Yamaguchi and M. Fujita, Nature, 1999, 398, 794 CrossRef CAS.
- A. Muller, E. Krickemeyer, H. Bogge, M. Schmidtmann and F. Peters, Angew. Chem., Int. Ed., 1998, 37, 3360 CAS.
- B. F. Abrahams, B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1991, 113, 3606 CrossRef CAS.
- M. J. Zaworotko, Chem. Soc. Rev., 1994, 23, 283 RSC.
- S. Subramanian and M. J. Zaworotko, Angew. Chem., Int. Ed. Engl., 1995, 34, 2127 CrossRef CAS.
- H. Li, M. Eddaoudi, M. O’Keeffe and O. M. Yaghi, Nature, 1999, 402, 276 CrossRef CAS.
- S. Noro, S. Kitagawa, M. Kondo and K. Seki, Angew. Chem., Int. Ed., 2000, 39, 2081 CrossRef.
- T. L. Hennigar, D. C. Macquarrie, P. Losier, R. D. Rogers and M. J. Zaworotko, Angew. Chem., Int. Ed. Engl., 1997, 36, 972 CrossRef CAS.
- S. Nishikiori and T. Iwamoto, Inorg. Chem., 1986, 25, 788 CrossRef CAS.
- S. Nishikiori and T. Iwamoto, J. Inclusion Phenom., 1984, 2, 341 CrossRef CAS.
- S. Nishikiori and T. Iwamoto, Bull. Chem. Soc. Jpn., 1983, 56, 3246 CAS.
- T. Miyoshi, T. Iwamoto and Y. Sasaki, Inorg. Chim. Acta, 1972, 6, 59 CrossRef CAS.
- S. R. Batten, B. F. Hoskins and R. Robson, New J. Chem., 1998, 22, 173 RSC.
- B. F. Abrahams, M. J. Hardie, B. F. Hoskins, R. Robson and E. E. Sutherland, J. Chem. Soc., Chem. Commun., 1994, 1049 RSC.
- L. R. Macgillivray, R. H. Groeneman and J. L. Atwood, J. Am. Chem. Soc., 1998, 120, 2676 CrossRef CAS.
- M. Aoyagi, K. Biradha and M. Fujita, Bull. Chem. Soc. Jpn., 2000, 73, 1369 CrossRef CAS.
- M. Fujita, Y. J. Kwon, S. Washizu and K. Ogura, J. Am. Chem. Soc., 1994, 116, 1151 CrossRef CAS.
- R. W. Gable, B. F. Hoskins and R. Robson, J. Chem. Soc., Chem. Commun., 1990, 1677 RSC.
- D. Hagrman, R. P. Hammond, R. Haushalter and J. Zubieta, Chem. Mater., 1998, 10, 2091 CrossRef CAS.
- J. Lu, T. Paliwala, S. C. Lim, C. Yu, T. Y. Niu and A. J. Jacobson, Inorg. Chem., 1997, 36, 923 CrossRef CAS.
- S. H. Park, K. M. Kim, S. Lee and O. S. Jung, Bull. Korean Chem. Soc., 1998, 19, 79 Search PubMed.
- M. S. Wang and T. J. Pinnavaia, Chem. Mater., 1994, 6, 468 CrossRef CAS.
- A. W. Coleman, S. G. Bott, S. D. Morley, C. M. Means, K. D. Robinson and J. L. Atwood, Angew. Chem., Int. Ed. Engl., 1988, 27, 1361 CrossRef.
- J. L. Atwood, G. W. Orr, N. C. Means, F. Hamada, H. Zhang, S. G. Bott and K. D. Robinson, Inorg. Chem., 1992, 31, 603 CrossRef CAS.
- S. R. Batten and R. Robson, Angew. Chem., Int. Ed., 1998, 37, 1461 CrossRef.
- K. Biradha, D. Dennis, V. A. MacKinnon, C. Seward and M. J. Zaworotko, Current Challenges on Large Supramolecular Assemblies, ed. G. Tsoucaris, Kluwer, Dordrecht, 1999, pp. 115–132. Search PubMed.
- K. Biradha, K. V. Domasevitch, B. Moulton, C. Seward and M. J. Zaworotko, Chem. Commun., 1999, 1327 RSC.
- K. Biradha, K. V. Domasevitch, C. Hogg, B. Moulton, K. N. Power and M. J. Zaworotko, Cryst. Eng., 1999, 2, 37 CrossRef CAS.
- K. Biradha, A. Mondal, B. Moulton and M. J. Zaworotko, J. Chem. Soc., Dalton Trans., 2000, 3837 RSC.
- L. Carlucci, G. Ciani and D. M. Proserpio, New J. Chem., 1998, 22, 1319 RSC.
- T. Soma and T. Iwamoto, Acta Crystallogr., Sect. C, 1996, 52, 1200 CrossRef.
- R. Atencio, K. V. Domasevitch and M. J. Zaworotko, Cryst. Eng., 2000, 3, 63 CrossRef CAS.
- L. Carlucci, G. Ciani and D. M. Proserpio, J. Chem. Soc., Dalton Trans., 1999, 1799 RSC.
- M. Kondo, M. Shimamura, S. Noro, S. Minakoshi, A. Asami, K. Seki and S. Kitagawa, Chem. Mater., 2000, 12, 1288 CrossRef CAS.
- M. Kondo, A. Asami, K. Fujimoto, S. Noro, S. Kitagawa, T. Ishii and H. Matsuzaka, Int. J. Inorg. Mater., 1999, 1, 73 CrossRef CAS.
- M. Fujita, Y. J. Kwon, O. Sasaki, K. Yamaguchi and K. Ogura, J. Am. Chem. Soc., 1995, 117, 7287 CrossRef CAS.
- Y. B. Dong, M. D. Smith, R. C. Layland and H. C. Zur Loye, Chem. Mater., 2000, 12, 1156 CrossRef CAS.
- Y. B. Dong, M. D. Smith, R. C. Layland and H. C. Zur Loye, J. Chem. Soc., Dalton Trans., 2000, 775 RSC.
- C. V. K. Sharma and R. D. Rogers, Cryst. Eng., 1998, 1, 19 Search PubMed.
- H. J. Choi and M. P. Suh, J. Am. Chem. Soc., 1998, 120, 10 622 CrossRef CAS.
- R. Masse, J. F. Nicoud, M. Bagieu-Beucher and C. Bourgogne, Chem. Phys., 1999, 245, 365 CrossRef CAS.
- M. A. Withersby, A. J. Blake, N. R. Champness, P. A. Cooke, P. Hubberstey and M. Schroder, New J. Chem., 1999, 23, 573 RSC.
- Y. B. Dong, R. C. Layland, N. G. Pschirer, M. D. Smith, U. H. F. Bunz and H. C. Zur Loye, Chem. Mater., 1999, 11, 1413 CrossRef CAS.
- K. N. Power, T. L. Hennigar and M. J. Zaworotko, New J. Chem., 1998, 22, 177 RSC.
- A. Rujiwatra, C. J. Kepert and M. J. Rosseinsky, Chem. Commun., 1999, 2307 RSC.
- S. Kitagawa and M. Kondo, Bull. Chem. Soc. Jpn., 1998, 71, 1739 CAS.
- C. J. Kepert and M. J. Rosseinsky, Chem. Commun., 1999, 375 RSC.
- M. Kondo, T. Yoshitomi, K. Seki, H. Matsuzaka and S. Kitagawa, Angew. Chem., Int. Ed. Engl., 1997, 36, 1725 CrossRef CAS.
- R. Atencio, K. Biradha, T. L. Hennigar, K. M. Poirier, K. N. Power, C. M. Seward, N. S. White and M. J. Zaworotko, Cryst. Eng., 1998, 1, 203 Search PubMed.
- L. R. Macgillivray, S. Subramanian and M. J. Zaworotko, Chem. Commun., 1994, 1325 RSC.
- D. J. Duchamp and R. E. Marsh, Acta Crystallogr., Sect. B, 1969, 25, 5 CrossRef CAS.
- F. H. Herbstein, M. Kapon and G. M. Reisner, J. Inclusion Phenom., 1987, 5, 211 CrossRef CAS.
- F. H. Herbstein, Top. Curr. Chem., 1987, 140, 107 Search PubMed.
- C. V. K. Sharma and M. J. Zaworotko, Chem. Commun., 1996, 2655 RSC.
- A. Ranganathan, V. R. Pedireddi, G. Sanjayan, K. N. Ganesh and C. N. R. Rao, J. Mol. Struct., 2000, 522, 87 CrossRef CAS.
- K. Biradha, D. Dennis, V. A. Mackinnon, C. V. K. Sharma and M. J. Zaworotko, J. Am. Chem. Soc., 1998, 120, 11 894 CrossRef CAS.
- C. V. K. Sharma, C. B. Bauer, R. D. Rogers and M. J. Zaworotko, Chem. Commun., 1997, 1559 RSC.
- R. E. Melendez and M. J. Zaworotko, Supramol. Chem., 1997, 8, 157 Search PubMed.
- R. E. Melendez, C. V. K. Sharma, M. J. Zaworotko, C. Bauer and R. D. Rogers, Angew. Chem., Int. Ed. Engl., 1996, 35, 2213 CrossRef CAS.
- D. J. Plaut, K. M. Lund and M. D. Ward, Chem. Commun., 2000, 769 RSC.
- K. T. Holman and M. D. Ward, Angew. Chem., Int. Ed., 2000, 39, 1653 CrossRef CAS.
- P. Ball, Nature, 1996, 381, 648 CrossRef CAS.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309 CrossRef CAS.
- S. Belanger, M. H. Keefe, J. L. Welch and J. T. Hupp, Coord. Chem. Rev., 1999, 192, 29 CrossRef.
- P. J. Stang and B. Olenyuk, Acc. Chem. Res., 1997, 30, 502 CrossRef CAS.
- M. Fujita and G. Ogura, J. Am. Chem. Soc., 1990, 112, 5645 CrossRef CAS.
- L. R. MacGillivray and J. L. Atwood, Nature, 1997, 389, 469 CrossRef CAS.
- M. M. Conn and J. Rebek, Chem. Rev., 1997, 97, 1647 CrossRef CAS.
- D. L. Caulder and K. N. Raymond, Acc. Chem. Res., 1999, 32, 975 CrossRef CAS.
- W. M. Meier and D. H. Olson, Atlas of Zeolite Structure Types, Butterworth-Heinemann, Boston, MA, 1992. Search PubMed.
- S. Kim, T. J. Smith, M. S. Chapman, M. G. Rossmann, D. C. Pevear, F. J. Dutko, P. J. Felock, G. D. Diana and M. A. Mckinlay, J. Mol. Biol., 1989, 210, 91 CrossRef CAS.
- R. Acharya, E. Fry, D. Stuart, G. Fox, D. Rowlands and F. Brown, Nature, 1989, 337, 709 CrossRef CAS.
- M. Luo, G. Vriend, G. Kamer, I. Minor, E. Arnold, M. G. Rossmann, U. Boege, D. G. Scraba, G. M. Duke and A. C. Palmenberg, Science, 1987, 235, 182 CAS.
- J. M. Hogle, M. Chow and D. J. Filman, Science, 1985, 229, 1358 CAS.
- M. Eddaoudi, H. L. Li and O. M. Yaghi, J. Am. Chem. Soc., 2000, 122, 1391 CrossRef CAS.
- G. A. Ozin, Chem. Commun., 2000, 419 RSC.
| This journal is © The Royal Society of Chemistry 2001 |
