Open Access Article
Open Access ArticleNMR methods for the analysis of mixtures
Jean-Nicolas
Dumez

Nantes Université, CNRS, CEISAM UMR6230, F-44000 Nantes, France. E-mail: jean-nicolas.dumez@cnrs.fr
First published on 2nd December 2022
Abstract
NMR spectroscopy is a powerful approach for the analysis of mixtures. Its usefulness arises in large part from the vast landscape of methods, and corresponding pulse sequences, that have been and are being designed to tackle the specific properties of mixtures of small molecules. This feature article describes a selection of methods that aim to address the complexity, the low concentrations, and the changing nature that mixtures can display. These notably include pure-shift and diffusion NMR methods, hyperpolarisation methods, and fast 2D NMR methods such as ultrafast 2D NMR and non-uniform sampling. Examples or applications are also described, in fields such as reaction monitoring and metabolomics, to illustrate the relevance and limitations of different methods.
1. Introduction
Mixtures of molecules in solution are ubiquitous in chemical science. Samples of biological, environmental and agricultural origins are frequently found or handled in the form of mixtures. In chemical synthesis, samples usually involve a mixture of reactants, products, and side or by products. Analytical sciences strive to provide a characterisation of mixtures that is as complete as possible. Ideally, the identity and concentration of all the components in a mixture should be accessed. In the case of samples that are out of equilibrium, this information is sought after as a function of time.Nuclear magnetic resonance (NMR) spectroscopy is a powerful approach for the analysis of mixtures.1,2 The most common NMR experiment has several essential features that are highly favourable for mixture analysis. It relies on a “pulse-acquire” pulse sequence, carried out at thermal spin equilibrium, to yield 1D spectra, most commonly for 1H spins. This experiment is simple to implement, it can be fast, and it already yields a wealth of structural information, which is useful to identify components. It is also non-invasive and non-destructive, meaning that the sample can be retrieved after analysis for storage or other analyses, and also, in the case of monitoring applications, that experiments can be repeated multiple times on the same sample as a function of time. 1D 1H NMR also provides straightforward access to quantitative information on concentrations.
The power of NMR spectroscopy also results from the vast space of possible experiments that can be carried out, with a given instrument and a given sample, through the use of different pulse sequences. This makes it possible, through the controlled manipulations of nuclear spins, to access chemical information that would otherwise remain invisible or inaccessible. The process of developing NMR pulse sequences has sometimes been referred to as “spin choreography” or “spin alchemy”.3
In the case of mixture analysis, classic 1D experiments carried out at thermal spin equilibrium may turn out to be insufficient for a variety of reasons. One of them is the complexity of the sample, and of the resulting spectroscopic data. The superimposed information available in 1D spectra may be difficult to disentangle. As a result, signals that are detected cannot always be analysed. Another possible reason is the concentration of the components, in light of the modest sensitivity of NMR spectroscopy. NMR is sometimes referred to as a “universal” detector, since there are virtually no criteria other than concentration for a small molecule to be detectable by NMR. However, the limits of detection for NMR experiments are very unfavourable compared to other analytical methods, and this, together with issues of dynamic range, sets a limit on the range of samples that may be analysed. A third limitation concerns the analysis of samples that change over time. While classic 1D experiments are relatively fast, the methods available to address the complexity of mixtures usually require more time, thus limiting the throughput of the analysis and making them incompatible with real-time analyses on short time scales. These three types of obstacles are met in many uses of NMR spectroscopy, such as the high-throughput analysis of mixtures for metabolomics applications, or the real-time monitoring of reactions in chemical synthesis. This provides a motivation for “spin alchemists” to design NMR methods that address the challenges of mixture analysis, and make them available to the broad chemical science community.
This feature article describes a selection of NMR methods that are designed and used for the analysis of mixtures. It is organised in three main sections, corresponding to methods to address the complexity, concentrations, and changing nature of mixtures, as illustrated in Fig. 1. An additional section briefly describes opportunities to access broader operating conditions through the use of flow NMR. For each of the methods, the type of information that can be accessed is highlighted. The underlying NMR concepts are also sketched, with minimal technical details. In practice, NMR solutions are rarely universal, and they usually come with a trade-off such as, for example, resolution or speed at the expense of sensitivity. This is also why there is a large variety of them. This article also aims at helping the interested reader to navigate the landscape of NMR methods for the analysis of mixtures. Note that this necessarily limited overview only covers homogeneous solutions, and focuses on small molecules.
2. Complexity
The most commonly used NMR experiment for mixture analysis is the 1D 1H pulse-acquire experiment. Protons have a spin I = 1/2, over 99% natural abundance, and the largest gyromagnetic ratio among stable nuclei, resulting in favourable sensitivity from an NMR point of view. However, the chemical-shift dispersion in 1H spectra is limited to 10–15 ppm. In addition, the large abundance of 1H nuclei result in the ubiquitous presence of 1H–1H couplings, that yield diverse multiplet structures and broaden NMR signals. Overall, the spectra of all but the simplest mixtures are usually complex.The complexity of the NMR spectra for mixtures has several origins. First, similar compounds have similar spectra and as a result the spectrum of a mixture may be complex even with a moderate number of detectable compounds. Second, the number of compounds can be very large. This is for example the case in biofluids or extracts of biological samples. In the spectra of mixtures, signal overlap prevents the reliable identification and accurate quantification of signals. The assignment of each signal in the spectrum to a specific compound, even resolved one, is also not trivial. Note that samples such as natural organic matter, which comprise tens of thousands of compounds that are mostly unknown, and call for the use dedicated methods, are outside the scope of the review.4
An array of methods is available to address overlap and assignment issues in NMR spectra.5–10 These methods may aim at simplification, meaning that the number of peaks in the spectrum is reduced, separation, meaning that the spectra of different components in the mixture are separated, or dispersion/correlation, meaning that the signals are distributed in additional dimensions, as well as combinations of these three features. Classic 2D experiments such as COSY, TOCSY and HSQC are dispersion/correlation methods. By spreading signals along two dimensions rather than one, they make it possible to resolve signals that overlap in 1D 1H spectra.10 In addition, since they correlate two signals or more from the same components, they can help to assign these signals to a known compounds with more confidence. In this section we describe other methods that were specifically developed to address the complexity of mixtures, and can complement or replace the use of 2D NMR.
2.1. Pure-shift NMR
Signal overlap in 1D 1H NMR spectra is due in part to the effect of 1H–1H J couplings, because of which signals appear as multiplets with a total width that is given by the number and sizes of the J couplings, rather than the natural linewidth of a peak. Broadband homonuclear decoupling, which refers to the complete suppression of the effects of J couplings in 1D 1H spectra, has been a long-standing goal of NMR spectroscopists. One of the earliest methods to achieve broadband decoupling consists of taking the 45° projection of a J-resolved 2D spectrum.11 While this approach has found some applications in metabolomics,12 it requires magnitude processing of the data, resulting in unfavourable lineshapes that defeat in part the purpose of homonuclear decoupling.More recently, several strategies have been described to select a subset of nuclear spins, the active spins, and decouple them from their coupling partners, the passive spins. Two of these methods were actually first described several decades ago. In the BIRD approach, the active spins are all the protons that are bound to a carbon-13, while the passive spins are all the other protons.13 In the Zangger–Sterk (ZS) method,14 the 1D 1H spectrum is mapped onto the spatial length of the tube, such that for each signal, there exists a thin slice in the sample in which only the spins contributing to the signal are active. These methods were revived, updated and expanded in the 2010s.15–18
The most recent method for broadband homonuclear decoupling is the pure shift yielded by chirp excitation (PSYCHE) method.19 With PSYCHE, the separation between active and passive spins is based on the application of two consecutive pulses with a small tip angle β, as in the anti-z COSY pulse sequence.20 The active spins are the statistical fraction of the spins that are refocused by the pair of pulses. Their contribution of decoupled spins to the signal (for small angles) scales as β2, while that of undecoupled spins scales as β4.
Homonuclear broadband decoupling methods can give excellent resolution for 1D 1H spectra. For this reason, they can help to distinguish peaks that overlap in an undecoupled 1D 1H spectrum.17 The BIRD, ZS and PSYCHE broadband decoupling methods all come with a sensitivity penalty. For BIRD, since only 13C-bound protons contribute to the signal, the penalty is almost 100-fold. For the ZS methods, there exists a compromise between sensitivity losses and the minimum frequency difference between decoupled spins, and it results in a sensitivity loss of 10 to 50-fold. For PSYCHE, there is a trade-off between sensitivity and the size of decoupling artefacts, which is controlled through the flip angle of the frequency-swept pulses. A sensitivity loss of about a factor of 5 to 10-fold is typically reported.
Homonuclear decoupling is also possible for 2D experiments. BIRD-based decoupling can notably be incorporated into 2D HSQC experiments, with no sensitivity penalty for experiments at natural 13C abundance.18 This was exploited for the quantitative analysis of biological mixtures.21,22
Another feature of these pure-shift methods is that the data are most often not acquired in a single scan, but rather a series of chunks that are concatenated before Fourier transformation. This is because J refocusing is only exact at a single time point, and approximately valid over a surrounding chunk. The consequences are two-fold. First, the sensitivity per square root of measurement time is reduced if only one chunk is acquired with each scan. Methods to alleviate this limitation have been described.15,23,24 Second, chunking artefacts appear in the decoupled spectrum, mostly because of J evolution during the chunk time. These artefacts reduce the range of concentrations that can be simultaneously characterised with a pure-shift spectrum. Moutzouri et al. have reported a multi-scan implementation of a pure-shift pulse sequence in which chunking artefacts are suppressed by cycling their phase across multiple scans.25 This makes it possible to restore the dynamic range for mixture analysis. This is illustrated in Fig. 2, where the use of pure-shift NMR with sideband suppression makes it possible to detect unambiguously a minor component in a mixture, with a concentration that is 3% of that of the major component. The relevance of 1D pure-shift NMR methods for the analysis of biological complex mixtures is also being evaluated.26,27 it was notably found that the reduced overlap of PSYCHE spectra helped to identify metabolites, such as glutamine, that could not be reliably identified from conventional 1D 1H spectra.27
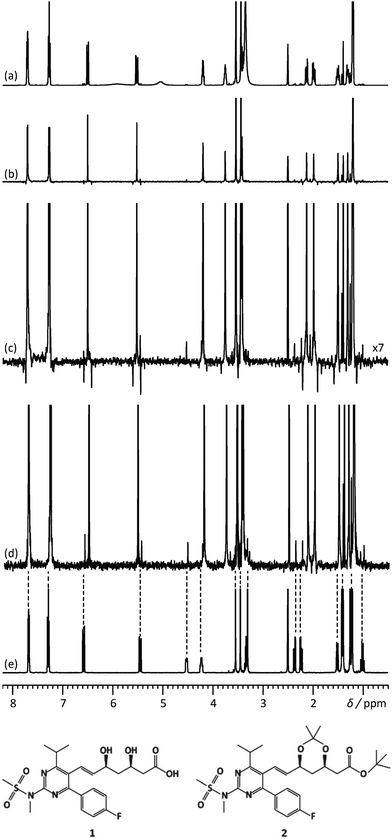 | ||
| Fig. 2 500 MHz (a) 1D 1H spectrum, (b) 1H pure shift spectrum recorded using the unmodified Zangger–Sterk pulse sequence, (c) vertical expansion of the spectrum (b and d) 1H pure shift spectrum acquired with the pulse sequence modified to remove sidebands, for a mixture containing rosuvastatin (1) and 2.8% of its precursor BEM (2). (e) 1D 1H spectrum of BEM. Spectra c and d were acquired in approximately 9 h with an sw1 of 39.0625 Hz and 16 chunks using an RSNOB spatially selective spin inversion element with a peak RF amplitude of 47 Hz. Reproduced from ref. 25 with permission from the Royal Society of Chemistry. | ||
An efficient alternative to broadband homonuclear decoupling is the use of band-selective decoupling.5,6 In this approach, the active spins are those within a selected frequency region of the spectrum, and the passive spins are all those outside that region. The main advantage of band-selective decoupling methods is that they have virtually no sensitivity penalty, in contrast to other pure-shift methods. Also, they are more straightforward to implement in a single scan. When the properties of the mixture of interest allow it, they are a method of choice to resolve the signals of structurally similar compounds. Band-selective pure-shift NMR was for example used, in 2D spectra, to distinguish diastereoisomers with near-identical 1H and 13C spectra,28 or enantiomers in chiral solvating agents.29
The pure-shift NMR methodology has recently been extended to suppress also the effect of heteronuclear couplings. This is particularly important in the case of compounds that contain fluorine atoms, such as many pharmaceutical compounds.30
2.2. Diffusion-ordered spectroscopy
Diffusion-ordered NMR spectroscopy, or DOSY, aims to separate the spectra of components in a mixture, without physical separation of the components themselves.7 In DOSY experiments, the separation is made according to the translational diffusion coefficients of the molecules. A pair of pulsed-field gradients (PFGs) separated by a delay is used to induce a diffusion-dependent attenuation of the peaks in the spectrum,31,32 and the resulting diffusion weighted signal is analysed to extract both the component spectra and the diffusion coefficients. The concept of “size-resolved NMR spectrometry” was introduced as early as 1981 by Stilbs.33 It was popularised by Johnson and co-workers who introduced the DOSY representation of the data, which consists of a 2D graphical display of the estimated diffusion coefficients for selected peaks or region in the spectrum.34 Conceptually, the 1D spectrum of each component can be found by simply drawing a line at the corresponding diffusion coefficient in the 2D DOSY display.PFG NMR and DOSY have found numerous applications to the analysis of mixtures.35 Note that while the term DOSY originally refers to a specific data processing and display method, it can refer nowadays also to the experiment itself. One class of applications consists of studying interactions in solution, for aggregates and oligomers formed by, e.g., organometallic species.36 DOSY is also largely used in supramolecular chemistry, to characterise the size and shape of supramolecular objects.37 Virtual separation by DOSY NMR has been assessed for different classes of samples, such as dietary supplements and pharmaceuticals, as a tool to detect counterfeit products.38
The virtual separation of NMR spectra with standard DOSY methods, however, is limited by the difficulty to resolve overlapping signals. The most common method for data analysis consists of a non-linear least square fit of the data with one or several exponential functions. When mono-exponential fitting is used, the resulting peak in the DOSY display appears at an intermediate value, that cannot be immediately assigned to one component. Multi-exponential fitting can resolve overlapping peaks,39 but only with excellent SNR and a sufficient difference in diffusion coefficients between the two compounds. As a result, standard DOSY methods are useful for assignment and identification, but they do not increase signal dispersion.
A possible approach to improve the separation of overlapping spectra is to use multivariate processing methods. They consist of algorithmically solving the problem:
| x = CPT, | (1) |
Another approach to address overlap issues it to use broadband homonuclear decoupling methods, so that fewer peaks, if any, overlap in the 1D 1H spectrum. Virtual separation with DOSY can then work very well. This was illustrated for a variety of pure-shift methods.46,47
A third possibility to improve spectral separation is to use the DOSY method to separate the 2D spectra of components in a mixture, with the so-called 3D DOSY family of methods (2 spectral dimensions and 1 diffusion dimension).34,48–50 Since signal dispersion is improved in 2D spectra, 3D DOSY can help to address the overlap issues of 2D DOSY. In addition, with 3D DOSY structural information is obtained for all the separated components. This is illustrated in Fig. 3, with the separation of HSQC spectra of five B vitamins. Importantly, in this case the 1H spectra could not be separated by regular 2D DOSY because of peak overlap.51 Conveniently, a large variety of methods to analyse PFG NMR data have been implemented in the open-source GNAT package.52
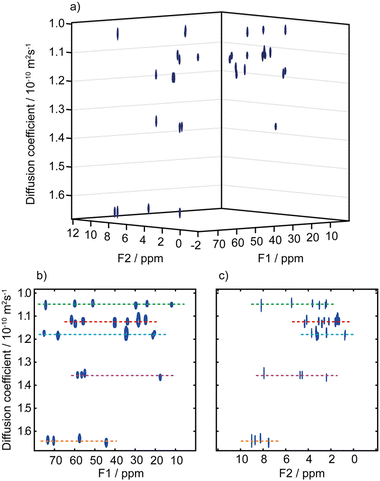 | ||
| Fig. 3 (a) Pseudo-3D DOSY plot of the Oneshot–HSQC spectrum of mixture of five B vitamins (biotin, B7; pyridoxine hydrochloride, B6; pantothenic acid calcium complex, B5; niacin, B3; and thiamine hydrochloride, B1) in DMSO-d6. (b) 2D projection along F2, and (c) 2D projection along F1. F1 and F2 are the 13C and 1H dimensions, respectively. Dashed lines are used to aid visualization and indicate the peaks of biotin, B7 (red); pyridoxine hydrochloride, B6 (purple); pantothenic acid, B5 (blue); niacin, B3 (orange); and thiamine hydrochloride, B1 (green). The spectra from the five components are easily distinguished, with diffusion coefficients of (1.05, 1.12, 1.18, 1.36, and 1.64) × 10−10 m2 s−1 for vitamins B1, B7, B5, B6, and B3, respectively. Data acquisition took 45 h, but a much shorter acquisition would have sufficed. Reproduced with permission from ref. 51, © 2018 American Chemical Society. | ||
The separation power of diffusion NMR can be increased by adding macromolecules that have different exchange or binding properties with the different analytes. Using such “matrix-assisted DOSY” approach, spectra that could not be separated without the matrix can become well resolved in the diffusion dimension.53,54 When solid matrices are used for that purpose, high-resolution magic-angle spinning (HRMAS) is employed to remove magnetic susceptibility broadening. This approach was coined “NMR chromatography”.55,56 Interestingly, when small molecules are bound to nanoparticles, they can be distinguished from unbound small molecules with a diffusion filter. This forms the basis of a chemosensing strategy that was developed by Rastrelli and co-workers, and applied to the detection and, together with NMR chromatography, the identification of small organic molecules.57–59
2.3. Maximum-quantum NMR
Maximum quantum (MaxQ) NMR refers to the use of a series of 2D multiple-quantum/single-quantum correlation spectra to analyse complex mixtures of small molecules. MaxQ NMR was described by Reddy and Caldarelli in 2010.8,60 It is based on the observations that (i) a spin system comprising N spins can form only one N-quantum coherence (N is named the maxQ order) and (ii) in an NQ/1Q 2D correlation experiments, that coherence will result in a series of peaks that are uncoupled in the indirect dimension, and that correspond to the 1D spectrum for the spin system in the direct dimension. NQ/1Q 2D correlation experiments can thus provide increased dispersion and spectral separation.In the MaxQ approach, a series of nQ/SQ correlation spectra is acquired, with n ranging from 1 to 5. The spectra are then analysed in decreasing order of the coherence order, with 1D spectra of molecular fragments obtained by taking traces in the 2D spectra, at positions that corresponds to singlets in the indirect dimension. The knowledge of the chemical shifts for the compounds identified on the pQ/SQ spectrum helps to identify the corresponding signals in the (p − 1)Q/SQ spectrum, and thus focus on the compounds for which (p − 1) is the maxQ value. With this method, Reddy and Caldarelli were able to separate the spectra of 16 polycyclic aromatic compounds identified as primary pollutants.61 Maximum quantum NMR was also combined with DOSY NMR to benefit from the separation power of the two methods simultaneously.62,63
2.4. Polarisation transfer experiments
Polarisation transfer experiment make it possible to simultaneously address the overlap and assignment issues of mixture analyses by NMR. The most popular polarisation transfer scheme for such applications is the TOCSY (total correlation spectroscopy) block, which drives polarisation transfer among all the spins that belong to the same spin system. In 2D TOCSY spectra, the spectrum of molecular fragment can be extracted from the data, provided that a peak is well resolved for at least one chemical site in the corresponding spin system. This strategy was used by Brüschweiler and co-workers, together with a database of fragment spectra, to help identify compounds in complex metabolic mixtures.64,65Since the TOCSY block only correlates nuclear spins within the same spin systems, it cannot in general reveal the entire 1D spectrum of a mixture component. This can be achieved using the NOESY (nuclear Overhauser effect spectroscopy) experiment in a viscous solvent. Because the nuclear Overhauser effect is a through space transfer, polarisation can propagate across all the 1H spins in a molecule, provided that it tumbles sufficiently slowly (the NOE for fast-tumbling molecules does not result in efficient spin diffusion). This concept was first demonstrated by Simpson and co-workers, who showed that the 1D 1H spectra of component mixtures could be extracted from a 2D NOESY spectrum acquired in an oil–chloroform mixture, for a three-component mixture.66 This approach requires a resolved 1H resonance for each compound. Interestingly, when sufficient time and sensitivity are available to record a 2D HSQC NOESY spectrum, the 1D spectrum of a compound can be extracted with the less stringent requirement of having a well resolved 13C signal. This approach has been generalised by Lameiras and co-workers, who dubbed it ViscY, for mixture analysis in viscous solvent by NMR spin diffusion spectroscopy.67–69 They have described several solvents (such as glycerol and glycerol carbonate) and solvent mixtures (such as blends of dimethylsulfoxide with glycerol or water), as well as band-selective 2D experiments, that make it possible to separate the 1D spectra of structurally similar compounds.
Polarisation transfer blocks are also useful in selective 1D experiment.70–72 In this approach, the signal of a chemical site is selectively excited, and a polarisation transfer block is used such that the resulting spectrum contains also, and exclusively, the signals from correlated chemical sites. Selective 1D experiments may be advantageous compared to 2D experiments when only a subset of compounds is of interest, and when achieving the resolution needed in the indirect dimension of a 2D experiments would require a prohibitive experiment duration. They are also useful to address dynamic range issues.
This was illustrated, for example, by Sandusky et al., who showed that selective TOCSY experiments could be used for the quantitative analysis of compounds that were 1000 times less concentrated than the most abundant compounds in the mixture.70 Selective experiments were also used by Lameiras and co-workers for ViscY experiments. Fig. 4 shows an example of ViscY experiments, in which the spectra of four phosphorus-based compounds are separated, using selective 1D NOESY experiments in a sulfolane/DMSO-d6 mixture.69
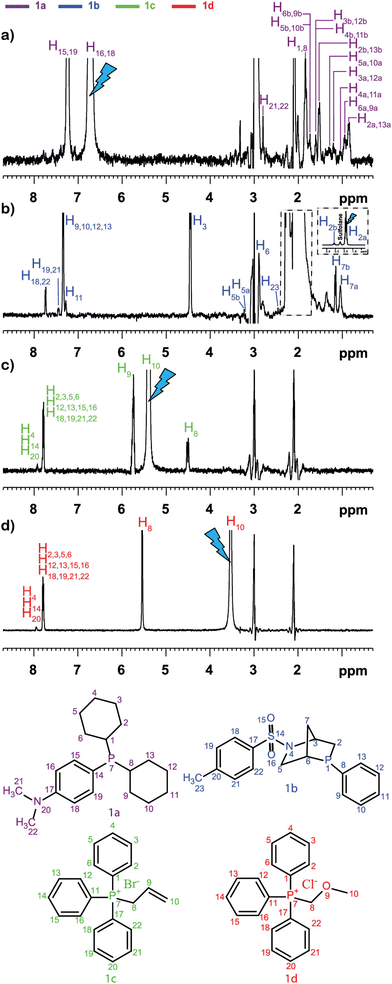 | ||
Fig. 4 Multiplet selective excitation 1D 1H NOESY spectra of a phosphorus-based compound test mixture (20 mM) dissolved in sulfolane/DMSO-d6 (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 v/v) (a–d), tm = 1 s, at 258 K, at 500 MHz (1H). The initial selective inversion pulses excite: (a) H16,18(1a), (b) H2a(1b), (c) H10(1c), and (d) H10(1d) proton resonances. Reproduced with permission from ref. 69, © 2020 American Chemical Society. 3 v/v) (a–d), tm = 1 s, at 258 K, at 500 MHz (1H). The initial selective inversion pulses excite: (a) H16,18(1a), (b) H2a(1b), (c) H10(1c), and (d) H10(1d) proton resonances. Reproduced with permission from ref. 69, © 2020 American Chemical Society. | ||
Selective experiment can also be combined with broadband homonuclear decoupling, to yield pure-shift spectra of selected components in mixtures. One advantage of this approach is that the spectra of the minor components are not contaminated by the decoupling artefacts of the major components.71
A limitation of standard selective experiments is that they rely on a well-resolved signal for the component(s) of interest. This may not always be available, especially for mixtures of stereoisomers or mixtures with a high number of components. Several methods have been developed, that make it possible to select a single 1H multiplet, even when it overlaps with other signals.73–78 Conceptually, these pulse sequences rely on a pure-shift evolution for the spectral selection block. The chemical-shift selective filter (CSSF) described by Hall and Norwood is a multi-scan implementation of such type of selective experiment, which relies on an incremented delay to eliminate off-resonance signals.77,78 An improved CSSF method, was used by Robinson et al. together with a TOCSY block to separate the 1D 1H spectra of a trisaccharide and its unknown degradation product.73 The GEMSTONE approach, recently described by Adams et al., replaces the incremented delay of the original CSSF by a spatial parallelisation method.75 It makes it possible to collect selective TOCSY for overlapped multiplets in a single scan.76
In the case of compounds that contain fluorine atom, another possible approach for polarisation transfer experiment is to select a signal of interest in the 19F spectrum, which usually has good resolution, followed by polarisation transfer to a neighbouring proton, and TOCSY-type transfer within the targeted 1H spin system.79
3. Concentrations
Despite its many advantages for mixture analysis, NMR spectroscopy is often limited in terms of applications by its modest sensitivity. Limits of detection and quantification may be usefully improved by increasing the magnetic field, or using a cryogenically cooled probe, but they remain orders of magnitude less favourable than with, e.g., mass spectrometry, even for 1D 1H experiments, that are the most sensitive. For experiments involving low-abundant heteronuclei such as carbon-13, the required duration to have enough SNR is often prohibitive for time-resolved or high-throughput studies. The limited sensitivity of NMR spectroscopy originates from the low population differences between nuclear spin energy levels at natural abundance, expressed as the polarisation level (with 1 corresponding to fully polarised spins). At a magnetic field of 11.7 T and a temperature of 298 K, the polarisation level for 1H is only 0.004%.Hyperpolarisation methods make it possible to increase the polarisation levels of nuclear spins by several orders of magnitude,80–85 approaching full polarisation in some cases. Several hyperpolarisation methods are now well established for applications in solution-state NMR spectroscopy, and are being assessed for mixture analysis applications. These are based on dynamic nuclear polarisation (DNP), and parahydrogen (pH2). These methods rely on very different physical principles and instrumentation, and they have very different features in terms of molecules and nuclei that can be polarised, polarisation levels that can be reached, and types of NMR experiments that can be recorded. In this section we describe how DNP and pH2 can help to lower the concentrations that can be accessed with NMR. Note that for mass-limited samples, sensitivity can also be increased by using tailored coils and probes (e.g., ref. 86), that will not be covered in this article.
3.1. Dynamic nuclear polarisation
Dissolution dynamic nuclear polarisation (D-DNP) consists of polarising a sample in the solid state, dissolving it with a hot solvent, and transferring it to a spectrometer to acquire NMR data with enhanced sensitivity.80,87 The polarisation step is typically carried out in a cryostat at a temperature of 1.2 to 4 K and a magnetic field of 3.4 to 10 T, by microwave irradiation of a sample doped with molecules that bear unpaired electrons. At such temperature and magnetic field, electron spins have almost unity polarisation, and the microwave irradiation results in polarisation transfer from the spins of unpaired electrons to nuclear spins. Polarisation levels in excess of 50% can be achieved in the solid state for a variety of nuclei, with carbon-13 being by far the most used. The high relevance of D-DNP for solution-state NMR stems from the fact that the nuclear spin polarisation can be preserved to a certain extent through the dissolution and transfer process. As a result, signal enhancements of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 or more can be routinely obtained for 13C NMR in solution.
000 or more can be routinely obtained for 13C NMR in solution.
One of the key features of D-DNP is that it is a single-shot method, because the dissolution step is irreversible. In addition, once the sample is dissolved, the nuclear spin polarisation decays irreversibly on a time scale given by the longitudinal relaxation times of the polarised nuclei. In many systems, the dissolution, transfer and stabilisation times add up to more than 10 s.87 This is why most applications of D-DNP rely on the hyperpolarisation of quaternary carbons, which have relaxation time constants that can be larger than 20 s. Several groups have also reported instrumentation developments that make is possible to reduce the delay between dissolution and detection to less than 5 seconds.88–91 With such devices, a broader range of chemical sites can be observed.
D-DNP is used extensively for kinetic studies based on the injection of hyperpolarised compounds in a mixture containing other reactants and/or catalysts, or in cell cultures.92–101 In such applications, hyperpolarisation methods make it possible to acquire 13C NMR spectra with a time resolution of a few seconds, which would be impossible to achieve at thermal equilibrium. They also make it possible to observe intermediate species that would be invisible with conventional NMR methods. For example, Hilty and co-workers have described a series of studies of polymerisation reactions using DNP-hyperpolarised monomers.93,95,97 They used time-series of 1D 13C NMR spectra at natural abundance to measure and compare reaction rates for different monomers, and also observe polymer products and side products, during a time of 10 to 30 s after the start of the reaction. Lerche, Meier and co-workers have used DNP-hyperpolarised 13C-labelled substrates to track the metabolic fate of molecules such as glucose and fructose in biological systems such as cancer cell or yeast cultures.98,100 Time-series of 1D 13C NMR spectra were used to track intermediates in metabolic pathways.
D-DNP is also investigated as a method to increase sensitivity in NMR metabolomics.91,102–105 Lerche and co-workers have used D-DNP for sensitivity enhanced stable-isotope resolved analysis (SIRA).91,103 In this approach, a biological system is fed with 13C-labelled sugars for a period of time, before undergoing metabolic quenching and extraction. DNP-enhanced 13C-NMR spectra of the extracts are then quantitatively analysed to classify sample types and identify potential biomarkers. Giraudeau and co-workers have shown that D-DNP can also be used to for hyperpolarised 13C NMR of complex metabolic extracts at natural abundance.102 This involved the use of polarisation method in the solid state that consists of first polarising 1H spins by DNP, and then transferring their polarisation to 13C spins by cross-polarisation (CP).106 This CP-based approach gives high 13C polarisation levels even for natural-abundance samples, as illustrated in Fig. 5 in the case of a tomato extract. Importantly, it was also shown that D-DNP experiments can have a repeatability of better than 4% for the relative area of peaks above the limit of quantification (SNR ≥ 10).104 This paved the way to the first implementation of hyperpolarised 13C NMR in an untargeted metabolomics workflow.105 Interestingly, the expected limit of detection for of hyperpolarised 13C NMR using D-DNP is not significantly higher than that of 1H NMR at thermal equilibrium. The goal is instead to benefit from the significantly higher dispersion of 13C 1D NMR spectra compared to 1D 1H NMR, with realistic experiment durations.
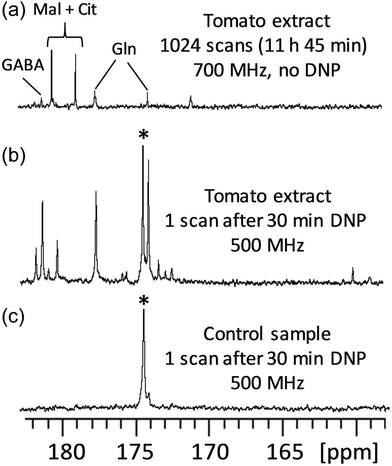 | ||
Fig. 5
13C NMR spectra (quaternary region) of mature green tomato fruit pericarp extracts. (a) Conventional (non-hyperpolarised) spectrum of 20 mg extract (prepared from 20 mg lyophilized grounded tissue) dissolved in 700 μL D2O, recorded with 1024 scans (11 h 45 min) at 700 MHz with a cryogenic probe. (b) Spectrum of an identical extract recorded with D-DNP combined with CP. The extract was first dissolved in a 200 μL mixture of H2O/D2O/glycerol-d8 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) doped with 25 mM TEMPOL, then polarized for 30 min at 1.2 K and 6.7 T, and finally dissolved with 5 mL of hot D2O and transferred in about 10 seconds to a 500 MHz spectrometer equipped with a cryogenic probe. (c) Same as (b), but the tomato extract was replaced by a control sample prepared under strictly identical conditions without any biological material. The hyperpolarized spectra result from the sum of six consecutive acquisitions using 30° pulses spaced by 7.7 s. *Indicates the signal of a 13C-labeled pyruvate impurity from the D-DNP setting. Cit: citrate; GABA: γ-aminobutyrate; Gln: glutamine; Mal: malate. Reproduced from ref. 102 with permission from the Royal Society of Chemistry. 5) doped with 25 mM TEMPOL, then polarized for 30 min at 1.2 K and 6.7 T, and finally dissolved with 5 mL of hot D2O and transferred in about 10 seconds to a 500 MHz spectrometer equipped with a cryogenic probe. (c) Same as (b), but the tomato extract was replaced by a control sample prepared under strictly identical conditions without any biological material. The hyperpolarized spectra result from the sum of six consecutive acquisitions using 30° pulses spaced by 7.7 s. *Indicates the signal of a 13C-labeled pyruvate impurity from the D-DNP setting. Cit: citrate; GABA: γ-aminobutyrate; Gln: glutamine; Mal: malate. Reproduced from ref. 102 with permission from the Royal Society of Chemistry. | ||
Overall, the main advantage of D-DNP for mixture analysis is that it is a broadband method, that can yield high polarisation levels for virtually arbitrary molecules and chemical sites. The single-shot nature of the method however limits the type of NMR experiments that can be recorded, while the fast-decaying nature of the spin polarisation restricts the chemical site that can actually observed. Fast-injection systems, and fast 2D NMR experiments described in Section 4, have the potential to increase the information content of DNP-enhanced spectra for mixture analysis.
Several hyperpolarisation methods based on dynamic nuclear polarisation make it possible to perform multi-shot experiments. This is for example the case of Overhauser DNP,84,85 which was recently shown to provide enhancements of up to 1000 for 13C NMR at high field85 and which can also be implemented with flow,107 and rapid-melt DNP.108 These and related methods do not yet provide high-resolution spectra, that would be suitable for mixture analysis, but they have the potential to become analytical methods that are both broadband in terms of compounds that can be observed, and versatile in terms of spectra that can be acquired. Intriguing possibilities are also opened by the injection of highly polarised molecules prepared with DNP or pH2, followed by intermolecular cross-relaxation, which may become relevant for mixture analysis.109,110 Interestingly, such broadband hyperpolarisation methods will raise important dynamic range questions, as actual limits of detection will only be improved if dilute components can be detected in the presence of much more concentrated compounds.
3.2. Parahydrogen-based hyperpolarisation
Signal amplification by reversible exchange (SABRE) is a hyperpolarisation method that relies on a reversible interaction between a substrate, a metal centre, and dissolved dihydrogen enriched in its para form.81 In SABRE, the source of polarisation is parahydrogen. Dihydrogen exists in the form of two spin isomers, named ortho and para, that correspond to different spin and rotational states of the molecule. The equilibrium distribution between the two forms at room temperature is 75% ortho and 25% para. Dihydrogen gas can be enriched in its para form simply by cooling it in the presence of a metal oxide, reaching 50% parahydrogen at 77 K (liquid nitrogen temperature) and close to 100% at 20 K. The gas enriched in its para form can be stored for extended periods of time, as the two forms interconvert very slowly in the absence of a catalyst. Para-hydrogen is thus a reservoir of spin order. In SABRE, that reservoir is exploited through: (i) the addition of parahydrogen to a metal centre, often in an iridium complex; (ii) a transfer of polarisation from the hydride protons to nuclear spins in the substrates bound to the metal centre.SABRE was initially demonstrated with a single substrate of interest.81 Shortly afterwards, the potential of SABRE-based hyperpolarisation for analytical applications was illustrated by Lloyds et al.111 A key feature of SABRE is the reversible nature of the hyperpolarisation process, which can occur multiple times for a given substrate. As a result, an array of classic 2D NMR experiments can be used with little modifications to record spectra with enhanced sensitivity. Experimental complications, however, result from the fact that the polarisation transfer occurs spontaneously only at low magnetic field (in the milliTesla range of 1H and in the microTesla range for 15N). The sample thus has to be moved between a polarisation region and the NMR spectrometer. The most used methods consist of dropping the sample in the magnet after shaking, or using a flow system to shuttle the sample between a polarisation region (where parahydrogen gas is bubbled) and the detection region.112
The potential of SABRE for mixture analysis has been explored by Tessari and co-workers, who showed that the method can be applied to complex mixtures of molecules with concentrations in the micromolar range, provided that an appropriate co-substrate is also added to the mixture.113,114 They also showed that the signal intensity changes linearly with concentration in that regime. With a standard-addition method, they were able to quantify several analytes in an artificial mixture.115 Also working with a co-substrate, they recorded 2D DOSY data with a flow shuttle.116 The transfer of polarisation between the hydride ligands, which results from pH2 addition to a metal centre, to the substrate, can also be performed with pulse sequences. This is exploited in several pulse sequences developed by Tessari and co-workers, who designed 2D experiments that correlate hydride signals with signals from, e.g., the ortho proton of a heterocycle in the target substrate.117 The resulting 2D spectre provide excellent signal dispersion, and can also be used for quantitative analysis by standard addition.
One key feature of SABRE hyperpolarisation is that it is a selective method, in the sense that not all molecules, and not all the spins within these molecules, can be polarised. This can be seen as a limitation in the perspective of fully untargeted analyses. It can also be turned into an advantage for the analysis of selected classes of compounds. This was demonstrated with the development of a “chemosensing” strategy based on SABRE, which was used to analyse coffee extracts after methanol extraction,118 and urine samples after solid-phase extraction (SPE).119,120 Using zero-quantum/single quantum correlation experiments, Sellies et al. were able to detect and quantify analytes in urine.120 Reimets et al. further showed that quantification of metabolites in urine using SABRE and a standard addition process was also possible without SPE, using 2D spectra such as the one shown in Fig. 6.121 One of the challenges of this approach is the identification of the observed compounds.
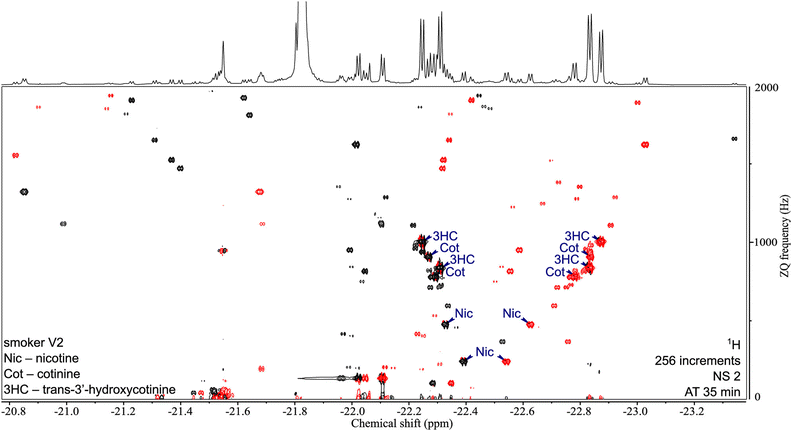 | ||
| Fig. 6 2D ZQ pH2 HP spectrum of a urine extract in CDCl3. Each complex of an analyte and the active catalyst [Ir(H2)(IMes)(mtz)3] gives rise to two opposite phase doublets at the same ZQ frequency. Chiral analytes (i.e., Nic, Cot, and 3HC) can combine with the catalyst in two ways due to the stereogenic center on iridium in the complex, forming two diastereomers with different physical properties. Signals were assigned by internal standard addition during method development. Upper 1D trace recorded separately with the 1D SEPP sequence. Reproduced with permission from ref. 121, © 2021 American Chemical Society. | ||
The scope of molecules that can be polarised with SABRE keeps on expanding through the development of new chemical systems and pulse sequences.122–125 Duckett and co-workers have for example introduced a relay strategy that can be used to polarise molecules with exchangeable protons.122 They for example used benzylamine, that both binds to the metal centre and has exchangeable protons.124 Using this approach, they were able to polarise different sugar molecules, with a response that varies linearly with concentration if the sample is sufficiently dilute.
SABRE is also being used for reaction monitoring applications.126–128 This was illustrated by Halse, Duckett and co-workers, who monitored the activation of the SABRE catalyst and proton-deuterium exchange in a SABRE hyperpolarised substrate.126 This was achieved with single-shot measurement of hyperpolarisation lifetimes for several protons in the substrates, which reflect both the extent of catalyst activation and the degree of substrate deuteration. SABRE was also used to produce hyperpolarised substrates for reaction monitoring. In a different approach, Norcott has combined SABRE hyperpolarisation with selective experiments to analyse the reaction mixtures produced by the methanolysis of an amide, at different stages of the reactions.129
The spin order of parahydrogen can also be released by hydrogenation of the target substrate, using a metal catalyst. This concept, named para-hydrogen induced polarisation (PHIP), was first described by Bowers and Weitekamp in 1986, and reported experimentally a year later.82,83 PHIP requires the presence of an unsaturation that can be hydrogenated in the target molecule, or the use of a cleavable side-arm. It has been used to produce hyperpolarised substrates, that are subsequently injected in either an enzymatic solution or cell culture.130–132 In order to extend the hyperpolarisation lifetime, and benefit from higher signal dispersion, the spin order is transfer to a neighbouring carbon-13 that has a long longitudinal relaxation time. As in the D-DNP case, the enhanced polarisation makes it possible to monitor (bio)chemical reactions with high time resolution, but with much more accessible instrumentation.
4. Change
Multidimensional experiments are essential for many applications of NMR, and mixture analysis is no exception. For mixture analysis, 2D experiments are the most frequently used multidimensional experiments, and higher-dimensional spectra are seldom recorded. The increased signal dispersion and correlation information provided by 2D spectra are essential to address overlap issues, assign signals, and obtain structural information. The duration of 2D experiments, however, is in many cases a limitation. While 1D spectra can be acquired in less than 1 second, conventional 2D experiments typically last 10 minutes at least, sometimes much more, even when sensitivity is not a limitation. This is an obstacle for the time-resolved analysis of samples that evolve in time, found in reaction monitoring applications, as well as for applications that require a high sample throughput, such as metabolomics, in which one is interested in changes in concentration over large sets of samples. Conventional 2D experiments are also not generally compatible with single-shot hyperpolarisation methods such as dissolution DNP, and this restricts the information content of the sensitivity enhanced spectra.Several complementary concepts have been introduced to accelerate multidimensional experiments.133–140 The duration of conventional 2D experiments originates from the point-by-point sampling of the additional dimension, which requires the consecutive acquisition of multiple scans with an incremented parameter. This is compounded by the inter-scan delays required for magnetisation recovery. Experiments may notably be accelerated by reducing the number of data points required to reconstruct the indirect dimension,134,135 by reducing the delay that separates consecutive scans,137–140 and by spatial parallelisation.133,136 These three types of methods have been tailored for mixture analysis and exploited for a variety of applications. This section describes examples of fast 2D methods used for the analysis of mixtures.
4.1. Ultrafast 2D NMR
Ultrafast (UF) 2D NMR is the fastest method to collect 2D NMR data. In UF 2D NMR, the scan-to-scan incrementation of a parameter value found in classic 2D NMR (e.g., of the t1 evolution time) is replaced by a spatial parallelisation approach, in which the parameter value varies as a function of position in the sample.141,142 This is achieved with the combined application of a frequency-swept pulse and a magnetic field gradient. Together with magnetic-resonance imaging methods that make it possible to effectively collect separate free-induction decay (FID) signal per sample slice, such spatial encoding provides a full 2D data set in a single scan of less than 1 second. This corresponds to an acceleration by up to three orders of magnitude. UF 2D NMR was first introduced for 2D spectroscopy in 2002,133 and related concepts were concurrently described for the acceleration of 2D DOSY experiments.136The potential of UF 2D NMR for mixture analysis was recognised early on, with the use of UF implementations of 2D correlation experiments such as TOCSY.143,144 Examples were reported of reaction monitoring, including the detection of a short-lived intermediates,145 and of the in-line acquisition of 2D spectra for a liquid chromatography type setup.143 A series of examples of reaction monitoring applications were then described by Herrera and co-workers who, for example, obtained mechanistic insights into the synthesis of pyrimidines.144,146–149 They notably made use of a rapid-injection device, to capture intermediate species with a half-life of a few minutes.
Interestingly, the relevance of UF 2D NMR for mixture analysis is not limited to single-scan implementations. In fact, UF 2D NMR spectra acquired in a single scan have limitations in terms of spectral width, resolution and sensitivity. These limitations can be alleviated through the acquisition of a few (typically 2 to 8) scans, that makes it possible to increase the accessible spectral width and/or the sensitivity.150 Such hybrid UF 2D NMR experiments have proven particularly useful for quantitative analyses of complex mixtures for, e.g., metabolomics applications.151–155 UF 2D NMR spectra are virtually free of t1 noise, and this was found to improve the limit of quantification of signal-averaged UF 2D spectra compared to conventional 2D spectra.151
Some of the 2D methods specifically designed for mixture analysis, described in Section 2, have also been implemented in an ultrafast fashion. This is notably the case of multiple-quantum/single quantum correlation experiments.156–158 Le Guennec et al. showed that the spatial encoding process used in UF 2D NMR is applicable to multiple-quantum coherences, and this made it possible to collect double-quantum spectroscopy (DQS) experiments in one or a few scans.156 Compared to COSY spectra, DQS results have the advantage of not displaying “diagonal” peaks, which helps to address overlap issues, as illustrated in Fig. 7. UF DQS spectra were then shown to be useful for quantification,157 as well as for experiments performed in magic-angle spinning conditions.159 The method was further extended by Concilio et al., who demonstrated the spatial encoding of multiple-quantum coherences of order up to 5, and used the resulting approach for a maximum-quantum analysis of a mixture of aromatic compounds.158
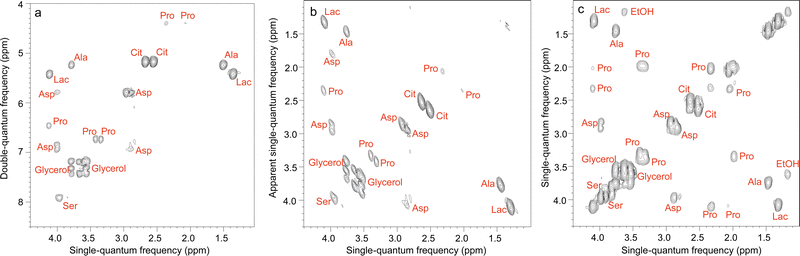 | ||
| Fig. 7 Ultrafast NMR spectra of a mixture of 7 metabolites in H2O/D2O (90/10): (a) DQS (c) COSY. All spectra were recorded in four interleaved scans to increase the observable spectral width, and four dummy scans resulting in an acquisition time of 41 s, using a double-quantum build-up delay τ = 25 ms. Spectrum (b) was obtained from spectrum (a) by a shearing transformation at a processing stage. All spectra were recorded with a 600 MHz spectrometer equipped with a cryogenic probe. Reproduced from ref. 156 with permission from the Royal Society of Chemistry. | ||
Diffusion NMR experiments can also be accelerated by spatial parallelisation. In this case, different slices in the sample undergo magnetic-field gradient pulses of different effective duration.136,160,161 This was first demonstrated by Thrippleton et al.,136 and later revisited by Shrot et al.,160 who used a more general detection scheme. More recently, Guduff et al. showed that UF (also called spatially encoded or SPEN) DOSY NMR can be extended to higher dimensional experiments, in order to acquire 3D DOSY data set (as described in Section 2.2) in a few minutes instead of a few hours.161Fig. 8 shows the result of the separation of 2D COSY spectra for a mixture of three short-chain alcohols and one amino acid, based on data that was acquired in 12 min. This approach relies on one spatially encoded diffusion dimension and one conventional chemical shift dimension. The reverse, one conventional diffusion dimension and one spatially encoded chemical shift dimension is also possible, and provides a different trade-off between acceleration and sensitivity.162 Like their conventional counterparts, UF DOSY experiments can be made more robust against convection effects, and this has proven useful for experiments carried out in organic solvents, notably for reaction monitoring applications.163 Multivariate processing algorithms may also be exploited to improve the separation of component spectra achieved with UF DOSY experiments. For DECRA, this required the design of alternative frequency swept pulses, and resulted in a duration of just a few second for both the acquisition and the processing/analysis steps.164
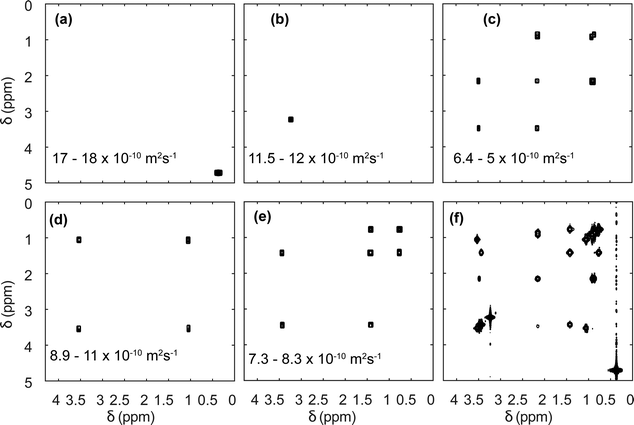 | ||
| Fig. 8 SPEN 3D DOSY of a mixture of 3 alcohols (methanol, ethanol, propanol) and an amino-acid (L-valine), at a concentration of ∼100 mM in D2O. (a–e) COSY-type spectra obtained as slabs of the 3D (D, δdirect, δindirect) dataset resulting from DOSY processing. The selected range in D is shown in each panel. The slice of the (z, δdirect, δindirect) dataset with the lowest diffusion gradient area is shown in (f). The experiment was carried out with a 600 MHz spectrometer equipped with a triple-axis gradient high-resolution probe, and lasted 12 min. Adapted from ref. 161 with permission from the Royal Society of Chemistry. | ||
The combination of UF 2D NMR and single-shot hyperpolarisation methods is particularly promising for mixture analysis.102,165–169 This is notably the case for dissolution DNP, which provides high polarisation levels for a broad range of molecules, but which is also not generally compatible with multi-scan pulse sequences. For example, the mixing step of a COSY pulse sequence would completely deplete the enhanced polarisation. Interestingly, even for experiments that may be recorded in multiple-scans with dissolution-DNP, the sensitivity of the UF implementation may be more favourable. Frydman and Blazina first reported the acquisition of UF 2D spectra for DNP-hyperpolarised substrates, using heteronuclear 2D correlation pulse sequences.170 These experiments were later adapted for a variety of substrates.102,165,171 Provided that the delay between dissolution and detection can be made sufficiently short, homonuclear 2D spectra can also be recorded in a single scan with 1H hyperpolarisation.169,172 This combination is not limited to 2D spectroscopy, and Guduff et al. have shown that reliable 2D DOSY spectra can also be recorded in a single-scan from DNP-hyperpolarised substrates.167
4.2. Non-uniform sampling
Multidimensional NMR experiments classically rely on the discrete Fourier transform to go from time-domain to frequency-domain representations. For the indirect dimension of 2D spectra, N1 time points are collected on a regular time grid with spacing Δt1, and this provides N1 spectral points with a spectral width of 1/Δt1 after FT. While this is very robust and general, it is also unnecessarily inefficient in most cases. Non uniform sampling (NUS) refers to a family of methods that consist of (i) collecting only a fraction of the points from those that would form a regular grid, (ii) using an algorithm that depart from the classic Fourier transform to reconstruct the spectrum.134,135,173 These methods rely on the assumption that multidimensional spectra are sparse. This means that among all the possible spectra that would be compatible with the collected data, the algorithm reconstructs the one that is the sparsest. The degree of undersampling is usually expressed as the NUS level, defined as the number of acquired points divided by the number of points that would be needed to achieve the same spectral width and digital resolution with uniform sampling.NUS has proven useful for the 2D experiments that are typically used for mixture analysis.153,174–176 The number of points used to obtain a 2D spectrum with NUS cannot be taken arbitrarily low. Empirically, it was found that at least 64 points were needed in the case of HSQC and DQF-COSY experiments applied on an artificial mixture of 30 metabolites, designed to mimic the composition of human serum.153 In this example, the resulting durations were of about 30 min for each experiment. This corresponds to an acceleration by a factor of 2 to 3 compared to the conditions that would typically have been used for such experiments. The quantitative information required for the subsequent statistical analysis was found to be preserved at such NUS levels, which makes them a relevant option for metabolomics applications.153,176,177
Interestingly, a given number of t1 points can be distributed over a time grid that spans a much larger range of values than that of the corresponding uniformly sampled experiments. In other words, from a practical point of view NUS is also very useful to increase the resolution of 2D spectra of complex mixtures. This was illustrated by Le Guennec et al., with the acquisition of HSQC and TOCSY spectra of an artificial mixture of metabolites.178 They found that, using 256 points in the HSQC case and 512 in the TOCSY case (corresponding to experiment duration of 2 h and 1 h), resolution could be increased by a factor of up to 8 using non uniform sampling. Importantly, they also showed that successful reconstruction for such NUS levels was not successful with the so-called “exponential sampling” strategy, which consists of selecting the acquired t1 points with an exponentially weighted probability (short t1 values are more likely to be acquired). They used instead “Poisson-gap” sampling,179 which is designed to avoid large gaps in sampling schedule, and was found to give reduced artefact levels.
Non-uniform sampling is also relevant for the analysis of mixtures that evolve in time.173,180–183 In this case, it can be implemented in a so-called “time-resolved” fashion by: (i) acquiring a long series of t1 points, with repetition time TR, according to a randomised non-uniform sampling schedule, and (ii) using a sliding-window processing, that consists of taking Nw consecutive points to reconstruct a spectrum, then moving the range of selected points by one or several units to reconstruct the next spectrum. While each spectrum is effectively acquired over a duration of Nw × TR, and represents an average sample composition over that duration, the time resolution is improved compared to the processing of non-overlapping data sets. TR-NUS was used by Dass et al. to monitor the fermentation of wheat flour.180 They collected a series of points of 2D HSQC experiments, randomly sampled from a full grid of 200 points. From this data, a times series of 2D HSQC spectra was obtained, and analysed by integration of selected peaks to track the concentration of ethanol and glycerol during fermentation, as illustrated in Fig. 9. The use of TR-NUS was recently made easier by the release of a software package for data processing and analysis.181
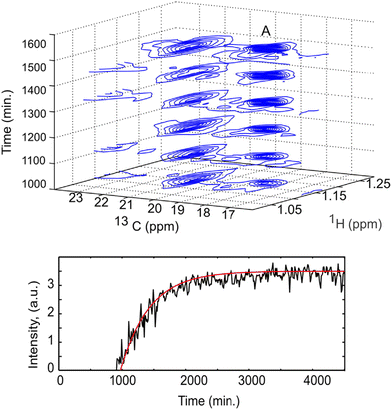 | ||
| Fig. 9 Fermentation of milk monitored using a TR-NUS 13C HSQC experiment. The top panel shows a stack of reconstructed 13C HSQC spectra that correspond to different time points in the fermentation process. The extra 13C dimension separates the ethanol cross peak (A), enabling simple determination of fermentation kinetics. The reaction rate, assuming first-order kinetics (fitted red line), was calculated from the change in ethanol cross peak intensity with (bottom panel). Reprinted with permission from ref. 180, © 2015 American Chemical Society. | ||
The “time-resolved” approach is also applicable to diffusion NMR/DOSY experiments.184–186 In this case a randomised list of gradient amplitudes is generated, and used to collect a time series of diffusion-attenuated spectra. As in the TR-NUS case, Nw consecutive spectra are analysed to estimate diffusion coefficients, and the window of processed spectra can then be moved by one or a few units. In contrast to TR-NUS, TR-DOSY does not necessarily require specific reconstruction algorithms, because the non-linear least-square fit used in conventional DOSY experiments can be applied to arbitrary grids of gradient values. For both TR-NUS and TR-DOSY, the window size for the processing can be chosen and adjusted after the data is acquired. Its value governs a trade-off between time resolution on the one hand, and SNR and artefact levels on the other hand.
Several time-resolved 2D experiments can be acquired simultaneously, by acquiring points for different 2D experiments in an interleaved fashion. This was recently used by Urbańczyk and co-workers to monitor a photo-polymerisation reaction in situ, with a combination of TR-NUS, to obtain a series of 2D HSQC spectra, and TR-DOSY.187
4.3. Fast-pulsing and concatenated experiments
A third possible route to accelerate 2D NMR experiments consists of reducing the time TR that separates two consecutive scans.137–140 In most conventional 2D experiments, the majority of this delay is dedicated to the return of longitudinal magnetisation from nearly zero to its equilibrium value, through nuclear spin relaxation. In order to reduce the repetition time without sacrificing too much sensitivity, some magnetisation has to be preserved along the longitudinal axis, or the recovery of longitudinal magnetisation has to be accelerated. A combination of the two approaches is also possible.The classic implementation of the HSQC pulse sequence entirely depletes the 1H longitudinal magnetisation at each scan. Its modified “ALSOFAST” version, however, can return a controlled fraction of the magnetisation along the z axis at the end of each scan.188,189 This makes it possible to operate in a “fast-pulsing” regime, in which short repetition times and small-angle excitation are combined to obtain 2D spectra in a few seconds with good sensitivity (measured as the signal to noise ration per square root of total experiment time). The ALSOFAST HSQC pulse sequence was used by Schaetlein et al. for metabolomics and fluxomics studies on a 13C-enriched cancer cell model.189 The authors showed that the experiment could be used to obtain “low-resolution” 2D spectra in 2 seconds, that were suitable to statistical analysis, or “high-resolution” spectra in one minute, that could be used for fluxomics analysis. For samples at natural abundance, the sensitivity of this fast HSQC experiment can be increased by replacing the relaxation delay by a spin-lock, that distributes the polarisation of 12C-bound protons to 13C-bound protons.137 The resulting ASAP (acceleration by sharing adjacent polarisation) was also shown to be compatible with the statistical analyses for series of spectra from complex samples.190
The concepts of NMR supersequences and no relaxation delay NMR spectroscopy (NORD) make it possible to reduce the total time required to collect multiple 2D spectra for a given sample.139,191 The corresponding pulse sequences are concatenated, such that each block taps into a different pool of magnetisation. A single recovery delay can then be used for the combined pulse sequence. Promising results were notably obtained by Hansen et al. for the analysis of complex mixtures with NOAH supersequences. They obtained HSQC, HSQC-TOCSY and TOCSY spectra of mouse urine with an acceleration by a factor of 2.192
5. Conditions of operation
Virtually all of the methods described so far in this feature article were developed and applied with samples placed in a classic NMR tube of 5 mm outer diameter. While this is a powerful approach, as attested by the breadth and depth of chemical information obtained with these experiments, it can also be a limitation for mixture analysis. Sometimes the experimental conditions of interest cannot be replicated faithfully in a high-field NMR spectrometer. This is particularly true for reaction monitoring applications.193 Flow NMR is a powerful approach to benefit from the information content of NMR spectra while analysing, in real time, a system in its usual operating conditions.194 Flow NMR is becoming widespread notably through the use of benchtop NMR spectrometers. These have been reviewed recently195 and will not be covered here. In parallel, the development of devices for flow NMR at high field has provided access to experimental conditions that could previously be probed only in a more indirect manner, while keeping the resolution and sensitivity offered by high-field magnets.196–198 This also raises challenges in terms of pulse sequence development, as some important pulse sequences that address the limitations of 1D NMR experiments are not compatible with continuous flow conditions.As outlined in Section 2, diffusion-ordered NMR spectroscopy (DOSY) is a particularly powerful approach for mixture analysis. It is based on the measurement of translational diffusion coefficients, using pulsed magnetic-field gradients. Since typical diffusion lengths in DOSY NMR experiments on small molecules are of 10 μm or less, DOSY NMR may appear to be incompatible with measurements carried out on a sample that undergoes a bulk displacement over an average length of more than 100 μm during the “diffusion” delay. Indeed, when classic DOSY pulse sequences are used, with diffusion encoding along the main direction of the flow, the estimated diffusion coefficients are highly inaccurate. Marchand et al. recently showed that, using a convection compensated pulse sequences, and a diffusion-encoding axis that is orthogonal to the main direction of the flow, accurate diffusion coefficients can be measured for samples flowing at up to 3 mL min−1.199 In addition, they showed that the use of multiple orthogonal axes in convection-compensated diffusion NMR pulse sequences also made it possible to reduce the number of scans to just one per value of the diffusion-encoding gradient. This “one-shot” implementation makes it possible to collect a complete data set in less than 90 s, thus giving a useful tool for reaction monitoring application, as illustrated in Fig. 10. Concurrently to this work, Thomlinson et al. showed that, using a low pulsation pump, or an empirical correction for flow effects, consistent values of diffusion coefficients could also be obtained with a single-axis gradient probe.200
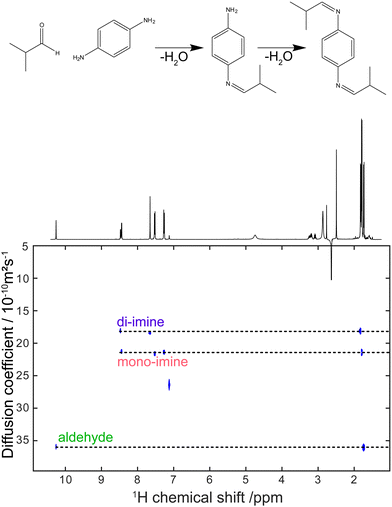 | ||
| Fig. 10 DOSY spectrum obtained during a di-imination reaction monitored by online NMR at a flow rate of 3 mL min−1. The experiment duration was 80 s. Adapted with permission from ref. 199. © 2022 Wiley-VCH GmbH. | ||
Ultrafast 2D NMR experiments are also built on specific assumptions on molecular positions, that may appear not to be verified in continuous flow conditions. When the spatial encoding axis is parallel to the main direction of the flow, interferences between spatial encoding and bulk sample motion result in significant signal attenuation. This can be compounded by the pulsatile nature of the flow, that results in non-repeatable values of the peak volume, thus preventing the use of UF 2D NMR for reaction monitoring in continuous flow.201 These issues can be addressed with the use of a spatial encoding axis that is orthogonal to the main direction of the flow. This was probably key to the success of UF 2D NMR experiments in continuous flow on a benchtop spectrometer, for which the field gradient was transverse.202 At high field, Jacquemmoz et al. recently showed that a transverse axis of a triple-axis gradient probe had to be used for spatial encoding, in order to obtain good-quality UF 2D NMR. In both cases, the resulting peak volumes can be used for accurate reaction monitoring.
6. Outlook
The development and applications of NMR methods for the analysis of mixtures forms a dynamic area of research. Methods are being developed, updated or refined to tackle the challenges of reaching the resolution, sensitivity and speed that are required for specific applications. It is striking to note that, while a paper entitled “Mixture analysis by NMR spectroscopy” was published more than 25 years ago,203 powerful methods are still reported today, for which the novelty lies in the way in which nuclear spins are handled. In fact, some of the most recent developments in the field might have been implemented on hardware available at the time, but the corresponding ideas were not mature yet.From a user's point of view, NMR pulse sequences usually become available relatively fast as updates to commercial vendor software, or through online libraries. This also means that there is a wealth of options to choose from. When faced with a resolution or assignment problem, should one go for a pure-shift experiment, a selective experiment, a 2D experiment. The answer is usually problem dependent, and can often be a combination of several methods, tailored for a specific sample. Similarly, for an application that requires fast multidimensional experiments, should one choose spatial parallelisation or non-uniform sampling? And should it be combined with fast-pulsing methods? In some cases, the timescale or interest or the available sensitivity will answer the question. In cases were all the options are available, careful comparisons are needed to establish the relative merits of each approach. Tutorials are for example available, that compare the features of several fast methods.174 The uptake of new NMR methods beyond a circle of experts also depends on the ease with which these methods can be implemented. Efforts to distribute implementation guides are clearly helping in this respect. Most methods can likely have impact only if they become usable as a “black box”. One can expect that, within a few years, this will become true of approaches such as ultrafast 2D NMR and time-resolved non-uniform sampling.
Several of the methods described here require the installation of new hardware. This is especially true for the hyperpolarisation methods described in Section 3. At this stage, these approaches are more exploratory, and it remains to be seen whether they will become widely used. Many striking examples were reported for applications of D-DNP to reaction monitoring, and more recent results on the use of hyperpolarised NMR for the analysis of “static” complex mixtures are very promising. The increasing availability of commercial instrumentation for these methods will also probably help to reveal the usefulness of hyperpolarised NMR for mixture analysis. Interestingly, improved limits of detection automatically result in increased complexity of the spectra, and this exacerbates the need for NMR methods that address this complexity. Similarly, the short-lived nature of the enhanced spin polarisation produced with single-shot hyperpolarisation calls for the development of fast 2D NMR methods.
An increasing number of development and applications is also observed in the emerging and fast-growing area of benchtop NMR, which was not covered in this article. Compact instruments provide access to previously inaccessible samples. This is the case for profiling application, which in principle are possible also at high field, but in practice are precluded by cost and availability reasons. This is also true for monitoring applications, which can now be implemented in the fume hood, on in industrial plants. Flow NMR at low and high field also significantly broaden the scope or reactions and processes that can be analysed.
Overall, NMR methods for the analysis of mixtures are expected to keep on growing, through the introduction of novel concepts and hardware. An increasing role of digital chemistry concepts can also be expected, which will blend with current spin dynamics concept to further increase the information content of NMR experiments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I am very grateful to the many colleagues with whom I have add the chance to work on these topics. I would particularly like to thank Patrick Giraudeau for useful critical feedback on the manuscript. This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreements no 801774/DINAMIX) the Region Pays de la Loire (Connect Talent HPNMR), the Agence Nationale de la Recherche (ANR-21-CE07-0056-02), and the I-SITE NExT (iChem4.0). The NExT initiative is supported by Nantes Université, the Région des Pays de la Loire and Nantes Métropole in the frame of the Programme d’Investissement d’Avenir (PIA). The author also acknowledges the French National Infrastructure for Metabolomics and Fluxomics MetaboHUB-ANR-11-INBS-0010 (http://www.metabohub.fr) and the Corsaire metabolomics core facility (Biogenouest).Notes and references
- J. V. Duynhoven, E. V. Velzen and D. M. Jacobs, Annu. Rep. NMR Spectrosc., 2013, 80, 181 CrossRef.
- R. Novoa-Carballal, E. Fernandez-Megia, C. Jimenez and R. Riguera, Nat. Prod. Rep., 2011, 28, 78 RSC.
- R. Freeman, Spin Choreography: Basic Steps in High Resolution NMR, Oxford University Press, 1998 Search PubMed.
- N. G. Bell, L. Murray, M. C. Graham and D. Uhrin, Chem. Commun., 2014, 50, 1694 RSC.
- L. Castanar and T. Parella, Magn. Reson. Chem., 2015, 53, 399 CrossRef CAS PubMed.
- L. Castanar, Magn. Reson. Chem., 2017, 55, 47 CrossRef CAS PubMed.
- G. A. Morris, eMagRes, 2009 DOI:10.1002/9780470034590.emrstm0119.pub2.
- G. N. M. Reddy and S. Caldarelli, Chem. Commun., 2011, 47, 4297 RSC.
- P. Lameiras and J. M. Nuzillard, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 123, 1 CrossRef CAS PubMed.
- P. Giraudeau, Magn. Reson. Chem., 2014, 52, 259 CrossRef CAS PubMed.
- W. P. Aue, J. Karhan and R. R. Ernst, J. Chem. Phys., 1976, 64, 4226 CrossRef CAS.
- C. Ludwig and M. R. Viant, Phytochem. Anal., 2010, 21, 22 CrossRef CAS PubMed.
- J. R. Garbow, D. P. Weitekamp and A. Pines, Chem. Phys. Lett., 1982, 93, 504 CrossRef CAS.
- K. Zangger and H. Sterk, J. Magn. Reson., 1997, 124, 486 CrossRef CAS.
- N. H. Meyer and K. Zangger, Angew. Chem., Int. Ed., 2013, 52, 7143 CrossRef CAS PubMed.
- N. H. Meyer and K. Zangger, Chem. Phys. Chem., 2014, 15, 49 CrossRef CAS PubMed.
- J. A. Aguilar, S. Faulkner, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2010, 49, 3901 CrossRef CAS PubMed.
- L. Paudel, R. W. Adams, P. Kiraly, J. A. Aguilar, M. Foroozandeh, M. J. Cliff, M. Nilsson, P. Sandor, J. P. Waltho and G. A. Morris, Angew. Chem., Int. Ed., 2013, 52, 11616 CrossRef CAS PubMed.
- M. Foroozandeh, R. W. Adams, N. J. Meharry, D. Jeannerat, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2014, 53, 6990 CrossRef CAS PubMed.
- A. J. Pell, R. A. Edden and J. Keeler, Magn. Reson. Chem., 2007, 45, 296 CrossRef CAS PubMed.
- I. Timari, C. Wang, A. L. Hansen, G. Costa Dos Santos, S. O. Yoon, L. Bruschweiler-Li and R. Bruschweiler, Anal. Chem., 2019, 91, 2304 CrossRef CAS PubMed.
- J. Farjon, C. Milande, E. Martineau, S. Akoka and P. Giraudeau, Anal. Chem., 2018, 90, 1845 CrossRef CAS PubMed.
- P. Sakhaii, B. Haase, W. Bermel, R. Kerssebaum, G. E. Wagner and K. Zangger, J. Magn. Reson., 2013, 233, 92 CrossRef CAS PubMed.
- J. Mauhart, S. Glanzer, P. Sakhaii, W. Bermel and K. Zangger, J. Magn. Reson., 2015, 259, 207 CrossRef CAS PubMed.
- P. Moutzouri, Y. Chen, M. Foroozandeh, P. Kiraly, A. R. Phillips, S. R. Coombes, M. Nilsson and G. A. Morris, Chem. Commun., 2017, 53, 10188 RSC.
- G. Bertho, L. Lordello, X. Chen, C. Lucas-Torres, I. E. Oumezziane, C. Caradeuc, M. Baudin, S. Nuan-Aliman, C. Thieblemont, V. Baud and N. Giraud, J. Proteome Res., 2022, 21, 1041 CrossRef CAS PubMed.
- J. M. Lopez, R. Cabrera and H. Maruenda, Sci. Rep., 2019, 9, 6900 CrossRef PubMed.
- L. Castanar, R. Roldan, P. Clapes, A. Virgili and T. Parella, Chemistry, 2015, 21, 7682 CrossRef CAS PubMed.
- L. Castanar, M. Perez-Trujillo, P. Nolis, E. Monteagudo, A. Virgili and T. Parella, Chem. Phys. Chem., 2014, 15, 854 CrossRef CAS PubMed.
- C. Mycroft, M. Nilsson, G. A. Morris and L. Castanar, Chem. Phys. Chem., 2022 DOI:10.1002/cphc.202200495.
- D. Sinnaeve, eMagRes, 2016, 967–980 CAS.
- W. S. Price, Concepts Magn. Reson., 1997, 9, 299 CrossRef CAS.
- P. Stilbs, Anal. Chem., 2002, 53, 2135 CrossRef.
- C. S. Johnson, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203 CrossRef CAS.
- G. Pagès, V. Gilard, R. Martino and M. Malet-Martino, Analyst, 2017, 142, 3771 RSC.
- D. Li, I. Keresztes, R. Hopson and P. G. Williard, Acc. Chem. Res., 2009, 42, 270 CrossRef CAS PubMed.
- L. Avram and Y. Cohen, Chem. Soc. Rev., 2015, 44, 586 RSC.
- S. Balayssac, S. Trefi, V. Gilard, M. Malet-Martino, R. Martino and M. A. Delsuc, J. Pharm. Biomed. Anal., 2009, 50, 602 CrossRef CAS PubMed.
- M. Nilsson, M. A. Connell, A. L. Davis and G. A. Morris, Anal. Chem., 2006, 78, 3040 CrossRef CAS PubMed.
- P. Stilbs and K. Paulsen, Rev. Sci. Instrum., 1996, 67, 4380 CrossRef CAS.
- M. Nilsson and G. A. Morris, Anal. Chem., 2008, 80, 3777 CrossRef CAS PubMed.
- B. Antalek and W. Windig, J. Am. Chem. Soc., 1996, 118, 10331 CrossRef CAS.
- W. Windig and B. Antalek, Chemom. Intell. Lab. Syst., 1997, 37, 241 CrossRef CAS.
- I. Toumi, B. Torrésani and S. Caldarelli, Anal. Chem., 2013, 85, 11344 CrossRef CAS PubMed.
- G. Dal Poggetto, L. Castanar, R. W. Adams, G. A. Morris and M. Nilsson, J. Am. Chem. Soc., 2019, 141, 5766 CrossRef CAS PubMed.
- S. Glanzer and K. Zangger, Chemistry, 2014, 20, 11171 CrossRef CAS PubMed.
- M. Nilsson and G. A. Morris, Chem. Commun., 2007, 933 RSC.
- S. Viel and S. Caldarelli, Chem. Commun., 2008, 2013 RSC.
- M. Nilsson, A. M. Gil, I. Delgadillo and G. A. Morris, Chem. Commun., 2005, 1737 RSC.
- J. M. Newman and A. Jerschow, Anal. Chem., 2007, 79, 2957 CrossRef CAS PubMed.
- G. Dal Poggetto, L. Castanar, M. Foroozandeh, P. Kiraly, R. W. Adams, G. A. Morris and M. Nilsson, Anal. Chem., 2018, 90, 13695 CrossRef CAS PubMed.
- L. Castañar, G. D. Poggetto, A. A. Colbourne, G. A. Morris and M. Nilsson, Magn. Reson. Chem., 2018, 56, 546 CrossRef PubMed.
- J. Cassani, M. Nilsson and G. A. Morris, J. Nat. Prod., 2012, 75, 131 CrossRef CAS PubMed.
- N. V. Gramosa, N. Ricardo, R. W. Adams, G. A. Morris and M. Nilsson, Magn. Reson. Chem., 2016, 54, 815 CrossRef PubMed.
- T. Gonzalez-Garcia, T. Margola, A. Silvagni, F. Mancin and F. Rastrelli, Angew. Chem., Int. Ed., 2016, 55, 2733 CrossRef CAS PubMed.
- G. Pages, C. Delaurent and S. Caldarelli, Angew. Chem., Int. Ed., 2006, 45, 5950 CrossRef CAS PubMed.
- M. V. Salvia, F. Ramadori, S. Springhetti, M. Diez-Castellnou, B. Perrone, F. Rastrelli and F. Mancin, J. Am. Chem. Soc., 2015, 137, 886 CrossRef CAS PubMed.
- M. Diez-Castellnou, M. V. Salvia, S. Springhetti, F. Rastrelli and F. Mancin, Chemistry, 2016, 22, 16957 CrossRef CAS PubMed.
- F. De Biasi, F. Mancin and F. Rastrelli, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 117, 70 CrossRef CAS PubMed.
- G. N. Manjunatha Reddy and S. Caldarelli, Anal. Chem., 2010, 82, 3266 CrossRef CAS PubMed.
- G. N. Reddy and S. Caldarelli, Analyst, 2012, 137, 741 RSC.
- G. N. Manjunatha Reddy, M. Yemloul and S. Caldarelli, Magn. Reson. Chem., 2017, 55, 492 CrossRef CAS PubMed.
- E. Piersanti, C. Righetti, D. Ribeaucourt, A. J. Simaan, Y. Mekmouche, M. Lafond, J. G. Berrin, T. Tron and M. Yemloul, Analyst, 2022, 147, 2515 RSC.
- F. Zhang and R. Brüschweiler, Angew. Chem., Int. Ed., 2007, 46, 2639 CrossRef CAS PubMed.
- F. Zhang, S. L. Robinette, L. Bruschweiler-Li and R. Bruschweiler, Magn. Reson. Chem., 2009, 47(suppl 1), S118 CrossRef CAS PubMed.
- A. J. Simpson, G. Woods and O. Mehrzad, Anal. Chem., 2008, 80, 186 CrossRef CAS PubMed.
- P. Lameiras and J. M. Nuzillard, Anal. Chem., 2016, 88, 4508 CrossRef CAS PubMed.
- P. Lameiras, S. Patis, J. Jakhlal, S. Castex, P. Clivio and J. M. Nuzillard, Chemistry, 2017, 23, 4923 CrossRef CAS PubMed.
- F. Pedinielli, J. M. Nuzillard and P. Lameiras, Anal. Chem., 2020, 92, 5191 CrossRef CAS PubMed.
- P. Sandusky and D. Raftery, Anal. Chem., 2005, 77, 2455 CrossRef CAS PubMed.
- G. Dal Poggetto, L. Castañar, G. A. Morris and M. Nilsson, RSC Adv., 2016, 6, 100063 RSC.
- N. MacKinnon, P. T. While and J. G. Korvink, J. Magn. Reson., 2016, 272, 147 CrossRef CAS PubMed.
- P. T. Robinson, T. N. Pham and D. Uhrin, J. Magn. Reson., 2004, 170, 97 CrossRef CAS PubMed.
- S. J. Duncan, R. Lewis, M. A. Bernstein and P. Sandor, Magn. Reson. Chem., 2007, 45, 283 CrossRef CAS PubMed.
- P. Kiraly, N. Kern, M. P. Plesniak, M. Nilsson, D. J. Procter, G. A. Morris and R. W. Adams, Angew. Chem., Int. Ed., 2021, 60, 666 CrossRef CAS PubMed.
- P. Kiraly, M. Nilsson, G. A. Morris and R. W. Adams, Chem. Commun., 2021, 57, 2368 RSC.
- L. D. Hall and T. J. Norwood, J. Magn. Reson., 1988, 78, 582 CAS.
- L. D. Laurance and T. J. Norwood, J. Magn. Reson., 1988, 76, 548 Search PubMed.
- L. Castanar, P. Moutzouri, T. M. Barbosa, C. F. Tormena, R. Rittner, A. R. Phillips, S. R. Coombes, M. Nilsson and G. A. Morris, Anal. Chem., 2018, 90, 5445 CrossRef CAS PubMed.
- J. H. Ardenkjaer-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acd. Sci. U. S. A., 2003, 100, 10158 CrossRef CAS PubMed.
- R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, I. G. Khazal, J. Lopez-Serrano and D. C. Williamson, Science, 2009, 323, 1708 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541 CrossRef CAS.
- D. Dai, X. Wang, Y. Liu, X. L. Yang, C. Glaubitz, V. Denysenkov, X. He, T. Prisner and J. Mao, Nat. Commun., 2021, 12, 6880 CrossRef CAS PubMed.
- G. Liu, M. Levien, N. Karschin, G. Parigi, C. Luchinat and M. Bennati, Nat. Chem., 2017, 9, 676 CrossRef CAS PubMed.
- J. N. Thomas, V. Ramaswamy, I. M. Litvak, T. L. Johnston, A. S. Edison and W. W. Brey, IEEE Trans. Appl. Supercond., 2021, 31, 20210222 Search PubMed.
- S. J. Elliott, Q. Stern, M. Ceillier, T. El Daraï, S. F. Cousin, O. Cala and S. Jannin, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 59 CrossRef CAS PubMed.
- H.-Y. Chen and C. Hilty, Chem. Phys. Chem., 2015, 16, 2646 CrossRef CAS PubMed.
- M. Ceillier, O. Cala, T. El Daraï, S. F. Cousin, Q. Stern, S. Guibert, S. J. Elliott, A. Bornet, B. Vuichoud, J. Milani, C. Pages, D. Eshchenko, J. G. Kempf, C. Jose, S. A. Lambert and S. Jannin, Journal of Magnetic Resonance Open, 2021, 8–9, 100017 CrossRef.
- S. Katsikis, I. Marin-Montesinos, M. Pons, C. Ludwig and U. L. Günther, Appl. Magn. Reson., 2015, 46, 723 CrossRef CAS.
- A. B. Frahm, D. Hill, S. Katsikis, T. Andreassen, J. H. Ardenkjaer-Larsen, T. F. Bathen, S. A. Moestue, P. R. Jensen and M. H. Lerche, Talanta, 2021, 235, 122812 CrossRef CAS PubMed.
- S. Bowen and C. Hilty, Angew. Chem., Int. Ed., 2008, 47, 5235 CrossRef CAS PubMed.
- Y. Lee, G. S. Heo, H. Zeng, K. L. Wooley and C. Hilty, J. Am. Chem. Soc., 2013, 135, 4636 CrossRef CAS PubMed.
- C. H. Chen, W. C. Shih and C. Hilty, J. Am. Chem. Soc., 2015, 137, 6965 CrossRef CAS PubMed.
- Y. Kim, C. H. Chen and C. Hilty, Chem. Commun., 2018, 54, 4333 RSC.
- J. Kim, Y. Kim, Q. S. Luu, J. Kim, C. Qi, C. Hilty and Y. Lee, Chem. Commun., 2020, 56, 15000 RSC.
- Y. Kim, H. Samouei and C. Hilty, Chem. Sci., 2021, 12, 2823 RSC.
- P. R. Jensen, S. Meier, J. H. Ardenkjaer-Larsen, J. O. Duus, M. Karlsson and M. H. Lerche, Chem. Commun., 2009, 5168 RSC.
- P. R. Jensen and S. Meier, Chem. Commun., 2020, 56, 6245 RSC.
- P. R. Jensen, F. Sannelli, L. T. Stauning and S. Meier, Chem. Commun., 2021, 57, 10572 RSC.
- C. Kjeldsen, J. H. Ardenkjaer-Larsen and J. O. Duus, J. Am. Chem. Soc., 2018, 140, 3030 CrossRef CAS PubMed.
- J.-N. Dumez, J. Milani, B. Vuichoud, A. Bornet, J. Lalande-Martin, I. Tea, M. Yon, M. Maucourt, C. Deborde, A. Moing, L. Frydman, G. Bodenhausen, S. Jannin and P. Giraudeau, Analyst, 2015, 140, 5860 RSC.
- M. H. Lerche, D. Yigit, A. B. Frahm, J. H. Ardenkjaer-Larsen, R. M. Malinowski and P. R. Jensen, Anal. Chem., 2018, 90, 674 CrossRef CAS PubMed.
- A. Bornet, M. Maucourt, C. Deborde, D. Jacob, J. Milani, B. Vuichoud, X. Ji, J. N. Dumez, A. Moing, G. Bodenhausen, S. Jannin and P. Giraudeau, Anal. Chem., 2016, 88, 6179 CrossRef CAS PubMed.
- A. Dey, B. Charrier, E. Martineau, C. Deborde, E. Gandriau, A. Moing, D. Jacob, D. Eshchenko, M. Schnell, R. Melzi, D. Kurzbach, M. Ceillier, Q. Chappuis, S. F. Cousin, J. G. Kempf, S. Jannin, J.-N. Dumez and P. Giraudeau, Anal. Chem., 2020, 92, 14867 CrossRef CAS PubMed.
- A. Bornet, R. Melzi, A. J. Perez Linde, P. Hautle, B. van den Brandt, S. Jannin and G. Bodenhausen, J. Phys. Chem. Lett., 2013, 4, 111 CrossRef CAS PubMed.
- R. Kircher, H. Hasse and K. Munnemann, Anal. Chem., 2021, 93, 8897 CrossRef CAS PubMed.
- M. Sharma, G. Janssen, J. Leggett, A. P. Kentgens and P. J. van Bentum, J. Magn. Reson., 2015, 258, 40 CrossRef CAS PubMed.
- T. R. Eichhorn, A. J. Parker, F. Josten, C. Muller, J. Scheuer, J. M. Steiner, M. Gierse, J. Handwerker, M. Keim, S. Lucas, M. U. Qureshi, A. Marshall, A. Salhov, Y. Quan, J. Binder, K. D. Jahnke, P. Neumann, S. Knecht, J. W. Blanchard, M. B. Plenio, F. Jelezko, L. Emsley, C. C. Vassiliou, P. Hautle and I. Schwartz, J. Am. Chem. Soc., 2022, 144, 2511 CrossRef CAS PubMed.
- S. Korchak, L. Kaltschnee, R. Dervisoglu, L. Andreas, C. Griesinger and S. Gloggler, Angew. Chem., Int. Ed., 2021, 60, 20984 CrossRef CAS PubMed.
- L. S. Lloyd, R. W. Adams, M. Bernstein, S. Coombes, S. B. Duckett, G. G. Green, R. J. Lewis, R. E. Mewis and C. J. Sleigh, J. Am. Chem. Soc., 2012, 134, 12904 CrossRef CAS PubMed.
- R. E. Mewis, K. D. Atkinson, M. J. Cowley, S. B. Duckett, G. G. Green, R. A. Green, L. A. Highton, D. Kilgour, L. S. Lloyd, J. A. Lohman and D. C. Williamson, Magn. Reson. Chem., 2014, 52, 358 CrossRef CAS PubMed.
- N. Eshuis, N. Hermkens, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, J. Am. Chem. Soc., 2014, 136, 2695 CrossRef CAS PubMed.
- R. Fraser, F. Rutjes, M. C. Feiters and M. Tessari, Acc. Chem. Res., 2022, 55, 1832 CrossRef CAS PubMed.
- N. Eshuis, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 1481 CrossRef CAS PubMed.
- I. Reile, R. Aspers, J. M. Tyburn, J. G. Kempf, M. C. Feiters, F. Rutjes and M. Tessari, Angew. Chem., Int. Ed., 2017, 56, 9174 CrossRef CAS PubMed.
- N. Eshuis, R. L. E. G. Aspers, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 14527 CrossRef CAS PubMed.
- N. K. Hermkens, N. Eshuis, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, Anal. Chem., 2016, 88, 3406 CrossRef CAS PubMed.
- I. Reile, N. Eshuis, N. K. Hermkens, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes and M. Tessari, Analyst, 2016, 141, 4001 RSC.
- L. Sellies, I. Reile, R. Aspers, M. C. Feiters, F. Rutjes and M. Tessari, Chem. Commun., 2019, 55, 7235 RSC.
- N. Reimets, K. Ausmees, S. Vija and I. Reile, Anal. Chem., 2021, 93, 9480 CrossRef PubMed.
- W. Iali, P. J. Rayner and S. B. Duckett, Sci. Adv., 2018, 4, eaao6250 CrossRef PubMed.
- P. M. Richardson, R. O. John, A. J. Parrott, P. J. Rayner, W. Iali, A. Nordon, M. E. Halse and S. B. Duckett, Phys. Chem. Chem. Phys., 2018, 20, 26362 RSC.
- P. M. Richardson, W. Iali, S. S. Roy, P. J. Rayner, M. E. Halse and S. B. Duckett, Chem. Sci., 2019, 10, 10607 RSC.
- L. Sellies, R. Aspers, M. C. Feiters, F. Rutjes and M. Tessari, Angew. Chem., Int. Ed., 2021, 60, 26954 CrossRef CAS PubMed.
- O. Semenova, P. M. Richardson, A. J. Parrott, A. Nordon, M. E. Halse and S. B. Duckett, Anal. Chem., 2019, 91, 6695 CrossRef CAS PubMed.
- B. J. Tickner, P. J. Rayner and S. B. Duckett, Anal. Chem., 2020, 92, 9095 CrossRef CAS PubMed.
- P. J. Rayner, M. Fekete, C. A. Gater, F. Ahwal, N. Turner, A. J. Kennerley and S. B. Duckett, J. Am. Chem. Soc., 2022, 144, 8756 CrossRef CAS PubMed.
- P. L. Norcott, Phys. Chem. Chem. Phys., 2022, 24, 13527 RSC.
- E. Cavallari, C. Carrera, S. Aime and F. Reineri, Chemistry, 2017, 23, 1200 CrossRef CAS PubMed.
- J. Eills, E. Cavallari, C. Carrera, D. Budker, S. Aime and F. Reineri, J. Am. Chem. Soc., 2019, 141, 20209 CrossRef CAS PubMed.
- Y. Ding, S. Korchak, S. Mamone, A. P. Jagtap, G. Stevanato, S. Sternkopf, D. Moll, H. Schroeder, S. Becker, A. Fischer, E. Gerhardt, T. F. Outeiro, F. Opazo, C. Griesinger and S. Glöggler, Chem.: Methods, 2022, 2, e202200023 CAS.
- L. Frydman, T. Scherf and A. Lupulescu, Proc. Natl. Acd. Sci. U. S. A., 2002, 99, 15858 CrossRef CAS PubMed.
- K. Kazimierczuk and V. Y. Orekhov, Angew. Chem., Int. Ed., 2011, 50, 5556 CrossRef CAS PubMed.
- D. J. Holland, M. J. Bostock, L. F. Gladden and D. Nietlispach, Angew. Chem., Int. Ed., 2011, 50, 6548 CrossRef CAS PubMed.
- M. J. Thrippleton, N. M. Loening and J. Keeler, Magn. Reson. Chem., 2003, 41, 441 CrossRef CAS.
- D. Schulze-Sunninghausen, J. Becker and B. Luy, J. Am. Chem. Soc., 2014, 136, 1242 CrossRef PubMed.
- E. Kupce and R. Freeman, Magn. Reson. Chem., 2007, 45, 2 CrossRef CAS PubMed.
- E. Kupce and T. D. W. Claridge, Angew. Chem., Int. Ed., 2017, 56, 11779 CrossRef CAS PubMed.
- K. Motiram-Corral, M. Perez-Trujillo, P. Nolis and T. Parella, Chem. Commun., 2018, 54, 13507 RSC.
- J. N. Dumez, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 101 CrossRef CAS PubMed.
- C. Lhoste, B. Lorandel, C. Praud, A. Marchand, R. Mishra, A. Dey, A. Bernard, J.-N. Dumez and P. Giraudeau, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 130–131, 1 CrossRef CAS PubMed.
- B. Shapira, A. Karton, D. Aronzon and L. Frydman, J. Am. Chem. Soc., 2004, 126, 1262 CrossRef CAS PubMed.
- A. Herrera, E. Fernandez-Valle, E. M. Gutierrez, R. Martinez-Alvarez, D. Molero, Z. D. Pardo and E. Saez, Org. Lett., 2010, 12, 144 CrossRef CAS PubMed.
- M. Gal, M. Mishkovsky and L. Frydman, J. Am. Chem. Soc., 2006, 128, 951 CrossRef CAS PubMed.
- A. Herrera, E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero, Z. D. Pardo, E. Saez and M. Gal, Angew. Chem., Int. Ed., 2009, 48, 6274 CrossRef CAS PubMed.
- Z. D. Pardo, G. L. Olsen, M. E. Fernandez-Valle, L. Frydman, R. Martinez-Alvarez and A. Herrera, J. Am. Chem. Soc., 2012, 134, 2706 CrossRef CAS PubMed.
- I. Fernandez, M. E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero-Vilchez, Z. D. Pardo, E. Saez-Barajas, A. Sanchez and A. Herrera, J. Org. Chem., 2014, 79, 8086 CrossRef CAS PubMed.
- M. E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero-Vilchez, Z. D. Pardo, E. Saez-Barajas and A. Herrera, J. Org. Chem., 2015, 80, 799 CrossRef CAS PubMed.
- L. Frydman, A. Lupulescu and T. Scherf, J. Am. Chem. Soc., 2003, 125, 9204 CrossRef CAS PubMed.
- M. Pathan, S. Akoka, I. Tea, B. Charrier and P. Giraudeau, Analyst, 2011, 136, 3157 RSC.
- A. Le Guennec, I. Tea, I. Antheaume, E. Martineau, B. Charrier, M. Pathan, S. Akoka and P. Giraudeau, Anal. Chem., 2012, 84, 10831 CrossRef CAS PubMed.
- A. L. Guennec, P. Giraudeau and S. Caldarelli, Anal. Chem., 2014, 86, 5946 CrossRef CAS PubMed.
- T. Jézéquel, C. Deborde, M. Maucourt, V. Zhendre, A. Moing and P. Giraudeau, Metabolomics, 2015, 11, 1231 CrossRef.
- J. Marchand, E. Martineau, Y. Guitton, B. Le Bizec, G. Dervilly-Pinel and P. Giraudeau, Metabolomics, 2018, 14, 60 CrossRef PubMed.
- A. Le Guennec, P. Giraudeau, S. Caldarelli and J.-N. Dumez, Chem. Commun., 2015, 51, 354 RSC.
- L. Rouger, B. Gouilleux, M. Pourchet-Gellez, J. N. Dumez and P. Giraudeau, Analyst, 2016, 141, 1686 RSC.
- M. G. Concilio, C. Jacquemmoz, D. Boyarskaya, G. Masson and J. N. Dumez, Chem. Phys. Chem., 2018, 19, 3310 CrossRef CAS PubMed.
- M. Andre, M. Piotto, S. Caldarelli and J. N. Dumez, Analyst, 2015, 140, 3942 RSC.
- Y. Shrot and L. Frydman, J. Magn. Reson., 2008, 195, 226 CrossRef CAS PubMed.
- L. Guduff, I. Kuprov, C. Van Heijenoort and J. N. Dumez, Chem. Commun., 2017, 53, 701 RSC.
- C. Jacquemmoz and J. N. Dumez, Chem. Phys. Chem., 2018, 19, 3204 CrossRef CAS PubMed.
- G. Hamdoun, L. Guduff, C. van Heijenoort, C. Bour, V. Gandon and J.-N. Dumez, Analyst, 2018, 143, 3458 RSC.
- R. Mishra, A. Marchand, C. Jacquemmoz and J.-N. Dumez, Chem. Commun., 2021, 57, 2384 RSC.
- P. Giraudeau, Y. Shrot and L. Frydman, J. Am. Chem. Soc., 2009, 131, 13902 CrossRef CAS PubMed.
- V. Daniele, F.-X. Legrand, P. Berthault, J.-N. Dumez and G. Huber, Chem. Phys. Chem., 2015, 16, 3413 CrossRef CAS PubMed.
- L. Guduff, D. Kurzbach, C. van Heijenoort, D. Abergel and J.-N. Dumez, Chem. – Eur. J., 2017, 23, 16722 CrossRef CAS PubMed.
- L. Guduff, P. Berthault, C. van Heijenoort, J.-N. Dumez and G. Huber, Chem. Phys. Chem., 2019, 20, 392 CrossRef CAS PubMed.
- K. Singh, C. Jacquemmoz, P. Giraudeau, L. Frydman and J. N. Dumez, Chem. Commun., 2021, 57, 8035 RSC.
- L. Frydman and D. Blazina, Nat. Phys., 2007, 3, 415 Search PubMed.
- M. Mishkovsky and L. Frydman, Chem. Phys. Chem., 2008, 9, 2340 CrossRef CAS PubMed.
- R. Panek, J. Granwehr, J. Leggett and W. Köckenberger, Phys. Chem. Chem. Phys., 2010, 12, 5771 RSC.
- D. Golowicz, P. Kasprzak, V. Orekhov and K. Kazimierczuk, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 116, 40 CrossRef CAS PubMed.
- E. Martineau, J. N. Dumez and P. Giraudeau, Magn. Reson. Chem., 2020, 58, 390 CrossRef CAS PubMed.
- E. Martineau, S. Akoka, R. Boisseau, B. Delanoue and P. Giraudeau, Anal. Chem., 2013, 85, 4777 CrossRef CAS PubMed.
- T. V. Schlippenbach, P. J. Oefner and W. Gronwald, Sci. Rep., 2018, 8, 4249 CrossRef PubMed.
- P. N. Reardon, C. L. Marean-Reardon, M. A. Bukovec, B. E. Coggins and N. G. Isern, Anal. Chem., 2016, 88, 2825 CrossRef CAS PubMed.
- A. Le Guennec, J. N. Dumez, P. Giraudeau and S. Caldarelli, Magn. Reson. Chem., 2015, 53, 913 CrossRef CAS PubMed.
- P. C. Aoto, R. B. Fenwick, G. J. Kroon and P. E. Wright, J. Magn. Reson., 2014, 246, 31 CrossRef CAS PubMed.
- R. Dass, W. Kozminski and K. Kazimierczuk, Anal. Chem., 2015, 87, 1337 CrossRef CAS PubMed.
- M. Urbanczyk, A. Shchukina, D. Golowicz and K. Kazimierczuk, Magn. Reson. Chem., 2019, 57, 4 CrossRef CAS PubMed.
- D. Golowicz, M. Kazmierczak and K. Kazimierczuk, Magn. Reson. Chem., 2021, 59, 213 CrossRef CAS PubMed.
- Y. Wu, C. D'Agostino, D. J. Holland and L. F. Gladden, Chem. Commun., 2014, 50, 14137 RSC.
- M. Urbanczyk, D. Bernin, A. Czuron and K. Kazimierczuk, Analyst, 2016, 141, 1745 RSC.
- T. S. C. MacDonald, W. S. Price and J. E. Beves, Chem. Phys. Chem., 2019, 20, 926 CrossRef CAS PubMed.
- L. L. Fillbrook, M. D. Nothling, M. H. Stenzel, W. S. Price and J. E. Beves, ACS Macro Lett., 2022, 11, 166 CrossRef CAS PubMed.
- K. Kristinaityte, A. Mames, M. Pietrzak, F. F. Westermair, W. Silva, R. M. Gschwind, T. Ratajczyk and M. Urbańczyk, J. Am. Chem. Soc., 2022, 144, 13945 CrossRef PubMed.
- D. Schulze-Sunninghausen, J. Becker, M. R. M. Koos and B. Luy, J. Magn. Reson., 2017, 281, 151 CrossRef PubMed.
- M. P. Schatzlein, J. Becker, D. Schulze-Sunninghausen, A. Pineda-Lucena, J. R. Herance and B. Luy, Anal. Bioanal. Chem., 2018, 410, 2793 CrossRef PubMed.
- R. Sharma, N. Gogna, H. Singh and K. Dorai, RSC Adv., 2017, 7, 29860 RSC.
- T. M. Nagy, K. E. Kover and O. W. Sorensen, Angew. Chem., Int. Ed., 2021, 60, 13587 CrossRef CAS PubMed.
- A. L. Hansen, E. R. Kupce, D. W. Li, L. Bruschweiler-Li, C. Wang and R. Bruschweiler, Anal. Chem., 2021, 93, 6112 CrossRef CAS PubMed.
- Y. Ben-Tal, P. J. Boaler, H. J. A. Dale, R. E. Dooley, N. A. Fohn, Y. Gao, A. Garcia-Dominguez, K. M. Grant, A. M. R. Hall, H. L. D. Hayes, M. M. Kucharski, R. Wei and G. C. Lloyd-Jones, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 129, 28 CrossRef CAS PubMed.
- A. M. R. Hall, J. C. Chouler, A. Codina, P. T. Gierth, J. P. Lowe and U. Hintermair, Catal. Sci. Technol., 2016, 6, 8406 RSC.
- T. Castaing-Cordier, D. Bouillaud, J. Farjon and P. Giraudeau, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Academic Press, 2021, pp. 191–258 Search PubMed.
- A. M. R. Hall, R. Broomfield-Tagg, M. Camilleri, D. R. Carbery, A. Codina, D. T. E. Whittaker, S. Coombes, J. P. Lowe and U. Hintermair, Chem. Commun., 2017, 54, 30 RSC.
- A. M. R. Hall, P. Dong, A. Codina, J. P. Lowe and U. Hintermair, ACS Catal., 2019, 9, 2079 CrossRef CAS.
- A. S. H. Ryder, W. B. Cunningham, G. Ballantyne, T. Mules, A. G. Kinsella, J. Turner-Dore, C. M. Alder, L. J. Edwards, B. S. J. McKay, M. N. Grayson and A. J. Cresswell, Angew. Chem., Int. Ed., 2020, 59, 14986 CrossRef CAS PubMed.
- A. Marchand, R. Mishra, A. Bernard and J. N. Dumez, Chemistry, 2022, e202201175 CAS.
- I. A. Thomlinson, M. G. Davidson, C. L. Lyall, J. P. Lowe and U. Hintermair, Chem. Commun., 2022, 58, 8242 RSC.
- C. Jacquemmoz, F. Giraud and J.-N. Dumez, Analyst, 2020, 145, 478 RSC.
- B. Gouilleux, B. Charrier, S. Akoka, F.-X. Felpin, M. Rodriguez-Zubiri and P. Giraudeau, TrAC, Trends Anal. Chem., 2016, 83, 65 CrossRef CAS.
- M. Lin and M. J. Shapiro, Anal. Chem., 1997, 69, 4731 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |