DOI:
10.1039/D4YA00057A
(Review Article)
Energy Adv., 2024,
3, 689-711
A comprehensive review of entropy engineered GeTe: an antidote to phase transformation
Received
29th January 2024
, Accepted 20th February 2024
First published on 21st February 2024
Abstract
Driven by the burgeoning demand for high performance eco-friendly thermoelectric materials in the mid-temperature range (573–773 K), we herein focus on GeTe based alloys that exhibit a high thermoelectric figure-of-merit >2.0 owing to their promising band structure with a conversion efficiency of ∼13.3% for the segmented module and ∼14% for the single leg device. However, the drawback is the phase transition at ∼700 K, which is inevitable, and the irony is that practical application of thermoelectrics has no space for phase transition, as it can be detrimental owing to the unexpected change resulting in deterioration of the devices under operation, thus limiting their mass-market applications either as power generators or as refrigerators. Nevertheless, a comprehensive review is needed for finding ways to cease or abase the phase transformation in the operating temperature regime. In this regard, the most recently developed GeTe-based thermoelectric materials are reviewed coupled with the blooming paradigm, i.e., entropy engineering. The review article thus summarizes the concept of entropy engineering owing to its contribution to boosting thermoelectric performance by increasing the configurational entropy of the system and cites several case studies. Towards the end, future scope and directions were proposed to use entropy tailored GeTe based alloys for the development of high efficiency power generators.

Ranita Basu
| Dr Ranita Basu is a Research Scientist in the Physics Group of Bhabha Atomic Research Centre (BARC) and an Assistant Professor in Homi Bhabha National Institute, Mumbai. She joined the prestigious BARC Training School after the completion of her MSc in Chemistry in 2007 at the University of Calcutta. She received her PhD degree in Chemical Sciences in 2015 from Homi Bhabha National Institute, Mumbai for her research topic on “Studies on thermoelectric properties of heavily doped semiconducting alloys for the development of power generators”. Her current research interest includes materials for energy harvesting especially thermoelectric materials for taping waste heat energy, which include chalcogenides such as bismuth-telluride, lead telluride, tin telluride, silicon–germanium alloys, etc. Her research interest also includes fabrication of power generators with enhanced efficiency using new contact materials. She has published more than 50 peer reviewed journal papers with review articles on thermoelectric materials and device fabrication in high impact journals. She is a recipient of Emerging Women in Material Science Award sponsored by Wiley. |

Ajay Singh
| Dr Ajay Singh is presently working as Scientific Officer (H) at the Technical Physics Division of Bhabha Atomic Research Centre (BARC) Mumbai. He joined BARC in 1999 after graduating from the 42nd Batch of Training School. He completed his MSc (Physics) at HNB Garhwal University in 1997 and PhD at Mumbai University in 2004. He is a recipient of the Humboldt Post-doctoral fellowship (2005–2007), the DAE Young Scientist Award for excellence in the Science and Technology – 2007, the National Academy of Sciences India (NASI) Young Scientist Platinum Jubilee Award – 2010, the DAE Solid State Physics Symposium Young Achiever Award (DAE SSPS YAA) – 2010, the Indian National Science Academy (INSA) Young Scientist Medal – 2012, the DAE Science & Technical Excellence Award – 2015 and the MRSI Medal – 2022. He is a fellow of the Maharashtra Academy of Sciences. His present research interests include design and development of high performance thermoelectric materials, thermoelectric power generators and essential interfacial electronics required for applications of thermoelectric generators. He has published 150 peer reviewed journal papers and has been granted 1 US patent. |
1. Introduction
Power generation using the concept of thermoelectricity has proven its reliability in planetary explorations owing to its ability to directly transform heat into electricity. Nonetheless, the doomed efficiency impedes its broad application.1,2 Innovative research conducted by the thermoelectric community in the last decade has improved the performance of thermoelectric devices significantly, which led to energy harvesting from natural and waste heat and thus provided an alternative solution to mitigate the energy crisis.3–10 The conversion efficiency of a TE device is defined by the figure of merit (ZT) of the thermoelectric alloy given by 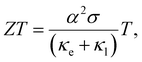 where α implies the Seebeck coefficient, σ implies the electrical conductivity, and κe and κl are the electronic and lattice thermal conductivities, respectively, at temperature T.11,12
where α implies the Seebeck coefficient, σ implies the electrical conductivity, and κe and κl are the electronic and lattice thermal conductivities, respectively, at temperature T.11,12
Various strategies were adapted in the past to enhance the ZT, which include optimization of carrier concentration (n) and point defect scattering, causing the peak ZT to hover around 1. However, the recent concepts and approaches proposed by the thermoelectric materials researchers, which include the design of new alloys proposed by Slack, i.e. phonon glass electron crystals,13 wherein different properties can be exploited synergistically, have revolutionized the field.14–18 It is worth mentioning that, in the field of thermoelectricity, it is essentially the inter-coupling of electrons (or holes) and the phonon flow mediated by defects that determines the performance of thermoelectric materials. Thus, defect engineering via two fundamental strategies, i.e. band engineering and phonon engineering, is frequently considered to tailor thermoelectric properties (as shown in Fig. 1). Using different dopants in the main matrix, the power factor is improved by altering the band structure and simultaneously the lattice thermal conductivity is reduced using microstructure engineering.15–17 Needless to mention, the oldest and extensively studied thermoelectric alloy, which evoked gusto in the domain of thermoelectrics and led to evolution of new concepts to harvest waste heat energy, is the PbTe system.19–44 However, Pb toxicity impedes its application, leading to the adoption of eco-friendly modalities. In this regard, the scientific community's attention has now shifted to Pb-free alternatives and one of the analogues is GeTe.45–50
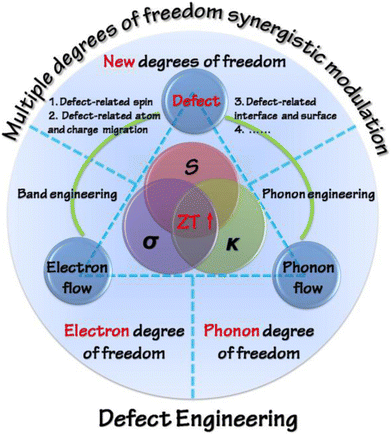 |
| | Fig. 1 Schematic representation displaying the strategies meant for optimization of ZT on the basis of defect engineering with the perception of synergistically modulating multiple degrees of freedom. Reproduced with permission from Copyright © 2016, American Chemical Society.18 | |
However, the challenge with GeTe (as shown in Fig. 2(a)) is that it undergoes phase transformation from the rhombohedral structure (α-GeTe, space group R3m) at ambient temperature to β-GeTe (cubic), space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, at 700 K, designated as the critical temperature. Intrinsically, GeTe is a degenerate p-type semiconductor with high hole strength. This can be attributed to the fact that during synthesis, plenty of Ge vacancies arise, which cause high carrier concentration, thus conflicting with the generally accepted optimal range.45–55 To quench the high carrier concentration, group III, IV and V elements are added at the Ge site and Se can be added at the Te site.49,56–60
m, at 700 K, designated as the critical temperature. Intrinsically, GeTe is a degenerate p-type semiconductor with high hole strength. This can be attributed to the fact that during synthesis, plenty of Ge vacancies arise, which cause high carrier concentration, thus conflicting with the generally accepted optimal range.45–55 To quench the high carrier concentration, group III, IV and V elements are added at the Ge site and Se can be added at the Te site.49,56–60
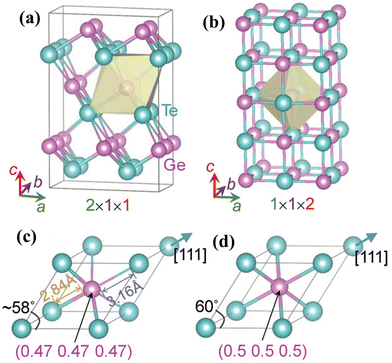 |
| | Fig. 2 Characteristics of the GeTe alloy as a thermoelectric material. Crystal structures of (a) rhombohedral GeTe and (b) cubic GeTe along with the respective primitive cells of (c) rhombohedral GeTe and (d) cubic-GeTe. Reproduced with permission from © 2019 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.51 | |
A recent breakthrough in the field of materials science is the preparation of single and multi-phasic high entropy alloys (entropy engineering) with significantly improved mechanical properties. In-depth understanding of the concept of phase engineering accordingly may lead to development of desired crystal structures depending on the applications (Fig. 3(a)). Moreover, to suppress the phase transition, the concept of high entropy or entropy engineering is an emerging paradigm, which focusses on the center of the multicomponent phase diagram instead of the edges in the case of conventional alloys (Fig. 3(b)).61–68 This perception enables the development of thermoelectric materials with enhanced performance along with long range ordering and simultaneously imposing disorder at short range, which decrease thermal transport and improve electrical transport.
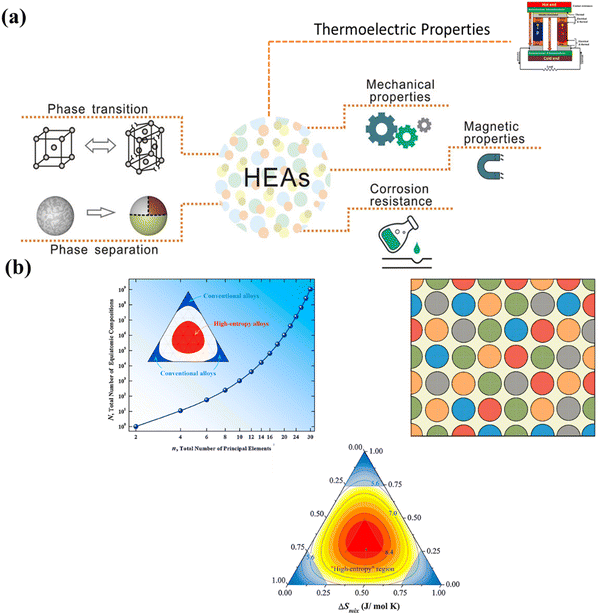 |
| | Fig. 3 (a) Schematic illustration depicting phase engineering in high entropy alloys, which governs their mechanical properties and accordingly decides their applications and (b) demonstration of the change in the equiatomic compositions as the principal element varies. The diagram also depicts how the phase space enhances for the high entropy alloys in comparison to the conventional alloys. Reproduced and adapted from ref. 69 and 70. Copyright © 2020 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Copyright © 2016 Elsevier Ltd, respectively, and under the terms of the Creative Commons CC-BY-NC-ND license.62 | |
Entropy engineering, thus, embraces introduction of multiple dopants for desired properties to fill the atomic position in the matrix, enhances the configurational entropy and thus subsequently enhances the structural symmetry or overpowers the structural phase transformation.69 This causes the increase in the Seebeck coefficient by augmenting the effective mass. In addition, incessant increase of entropy via introduction of several elements as dopants intensifies the phonon scattering and thus diminishes the lattice thermal conductivity largely. This high entropy concept has been efficaciously executed in some of the thermoelectric materials, viz. Ag9GaSe6,72–74 (Cu7PSe6)72,74,75 and Cu2S with inferior symmetry.72,73,76
Hu et al. in one of his articles explicitly explained the entropy engineering in SnTe and illustrated how the high entropy effect differs from multi-elemental doping.71 He explained that high entropy alloying is a subset of multi-principal element alloying and is associated with four core effects (Fig. 4(a)–(c)). In view of this fact, the paradigm can be effective for achieving high thermoelectric performance although with a compromise in the carrier mobility (Fig. 4(d)).
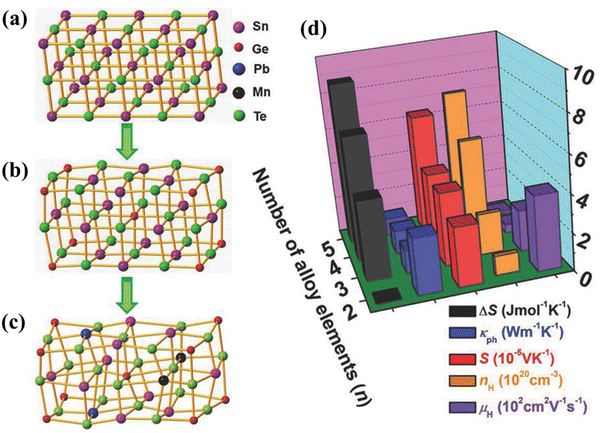 |
| | Fig. 4 (a)–(c) Schematic illustration depicting the change in lattice distortion with the increase in the addition of dopants in symmetric IV–VI chalcogenides. (d) Representation to demonstrate the nature of change in properties: (i) entropy of mixing ΔS; (ii) lattice thermal conductivity κph; (iii) Seebeck coefficient S; (iv) carrier concentration nH; and (v) carrier mobility μH at 300 K for highly symmetric IV–VI chalcogenides. Reproduced with permission from ref. 71. Copyright © 2018 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | |
GeTe, being one of the low symmetry thermoelectric materials in the low temperature regime (≤700 K), was re-envisioned as a matrix where the hypothesis of high entropy can be realized in order to suppress the phase transition followed by optimization of carrier strength and reduction of thermal conductivity as the performance of pristine GeTe is at the mercy of the high hole concentration and high thermal conductivity.45–55,77 As illustrated in Fig. 5, GeTe, which remained unexplored for a prolonged period owing to its phase transition in the operating temperature regime and limited knowledge on the tailoring of electronic band structure, has regained attention. This is attributed to the better understanding of the electronic band structure via density functional theory and validation with the experimental findings.47,77
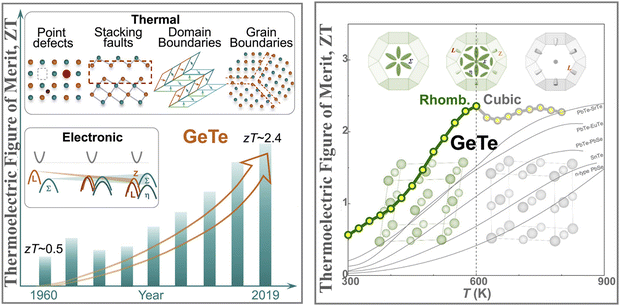 |
| | Fig. 5 Schematic representation demonstrating electronic and thermal contribution to the high thermoelectric performance of GeTe over the years. Detailed investigation revealed that slight symmetry reduction is beneficial over high symmetry GeTe based alloys for thermoelectric applications. Reproduced and adapted from ref. 47 and 77 under the terms of the Creative Commons CC-BY-NC-ND license. | |
Initially, chemical doping with single elements (such as In, Pb, Bi and Sb) was accomplished to optimize the carrier concentration,78,79 but the results showed that dual doping is preferred to obtain ZTs exceeding 2.0,79–83 such as for Ge1−x−ySbxZnyTe,84 Ge1−x−ySbxInyTe,54 and Ge1−x−yBixCdyTe.85,86 As illustrated in Fig. 6, the vast list of elements in the periodic table has promoted the progress of GeTe thermoelectrics. The highlighted elements in the periodic table, viz. Ti, V and Cr, were doped to boost the ZT of GeTe by reducing the charge carrier scattering or refining the band structure and thus aiding in enhancing electron transport properties. La and Nd were also beneficial for tailoring the band structure; aliovalent dopants such as Bi and Sb or other elements of group 15 were utilized to optimize the charge carriers along with halogens (I); Sn introduces Rashba splitting; and In introduces resonant levels. Doping at the anionic site is advantageous to introduce point defect scattering of phonons and thus reduces the lattice thermal conductivity. However, the problem is that phase transition still persists, which is detrimental to thermoelectric devices,87 as it leads to stress due to mismatch in the thermal expansion coefficient in different phases, with the concentration of charge carriers (holes for GeTe) deviating from the optimized value. Evidently, one of the key issues with GeTe based alloys is to reduce the phase transition towards the lower temperature so that the applications of high symmetrical structures can be extended over a wide temperature regime. Although considerable headway has been made with the high entropy materials towards designing novel alloys for thermoelectric applications, in this review our aim is to solve the fundamental problem pertaining to phase transition in GeTe and suppressing it to ambient temperature from 700 K via entropy engineering so that the alloys with superior band structures can be utilized for the fabrication of thermoelectric devices.87–93
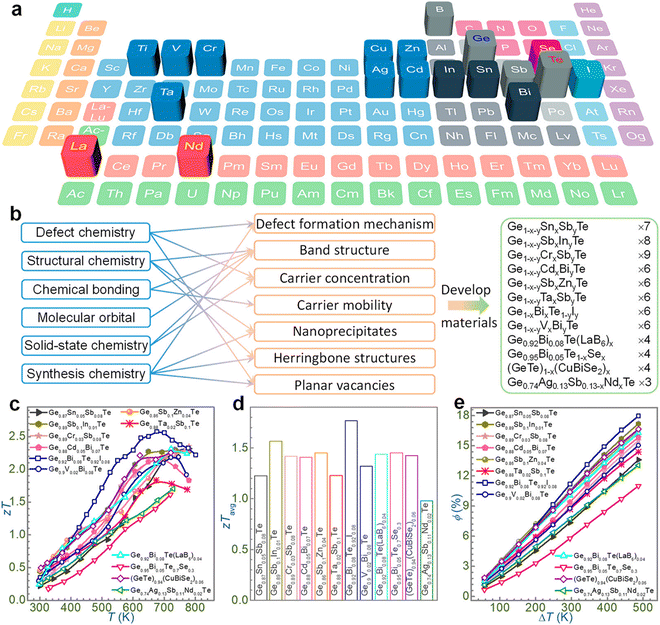 |
| | Fig. 6 Outline of the recent outcomes of GeTe thermoelectrics in terms of chemical principles. (a) Elements in the periodic table (highlighted) employed to tailor the GeTe thermoelectrics; (b) strategies utilized to enhance the thermoelectric performance on the basis of chemical disciplines and the GeTe derivatives developed so far; (c)–(e) summary of the results on GeTe thermoelectrics obtained by different groups. Reproduced and adapted from ref. 79, Copyright © 2022, American Chemical Society. | |
2. Genesis of entropy engineering
The term “entropy” was defined and developed in 1870 by the famous scientist Ludwig Boltzmann by probing the statistical behavior of the microscopic constituents of a system.94,95 The hypothesis proposed by Boltzmann states that there lies a correlation between the entropy or randomness of a system in a predefined state and the possibility of the presence of a given state:| | S = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω, ω, | (1) |
where S defines the contribution of disorder or entropy of the system for the predefined state, kB is the Boltzmann constant and is given by 1.38 × 10−23 J K−1, and ω is the probability of distribution of the constituents in the system.
For an alloy system, the Gibbs energy of mixing is given by:
| | | ΔGmix = ΔHmix − TΔSmix, | (2) |
where Δ
Gmix, Δ
Hmix and Δ
Smix are the free energy, enthalpy and entropy of mixing respectively.
Eqn (2) shows that at constant Δ
Hmix enhanced entropy of mixing will lead to lowering of Δ
Gmix and thus will result in an alloy system with high stability. Thus, increasing the entropy of mixing has a remarkable impact on the microstructure of the material and subsequently on its macroscopic properties. In this regard, the aim is to maximize the Δ
Smix. In thermodynamics, the configurational entropy of mixing for
n components to have random solid solution is given by:
| | 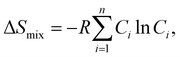 | (3) |
where
Ci is defined as the molar concentration of the
ith constituent and
R is the universal gas constant.
Eqn (3) indicates that Δ
Smix of an alloy can be maximized by designing the alloy with an equimolar ratio of multiple principal elements, which can be defined as
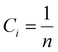
and upon substitution in
eqn (3) gives:
| | 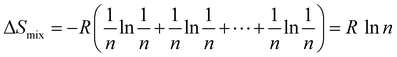 | (4) |
From
eqn (4), it can be concluded that for a ternary alloy system, Δ
Sconf is 1.10
R and accordingly it increases with the increase in the number of elements in the alloy system. Unlike the philosophy of traditional alloy design, the entropy maximization concept emphasizes the entropic contribution instead of the contribution of the cohesive energy to the free energy. This influences the thermodynamic stability of the alloy system at finite temperature and favours the solid-solution formation with high symmetrical crystal structure. The thermoelectric researchers worldwide are now inclined towards the novel philosophy of entropy engineering by adding multiple elements for designing advanced alloys with symmetric crystal structures to boost the Seebeck coefficient and decrease the phonon conduction simultaneously. This enhances the thermoelectric performance unlike the earlier trend of designing complex crystal structures for reducing the lattice thermal conductivity alone.
87–93
3. GeTe as a thermoelectric material
The entire essence of thermoelectricity is having a high ZT thermoelectric material for the fabrication of efficient devices.9,62 This involves development either of high temperature power generators or near room temperature refrigerators. The widely used materials for this niche application include silicides,96–98 chalcogenides,19–44,99–101 half-Heusler,102,103 Zintls,104,105etc. Among chalcogenides, Pb–X, Ge–X, and Sn–X, where X = S, Se and Te, are widely used for power generators in the mid-temperature regime i.e. 500 K ≤ T ≤ 800 K,106,107 whereas Bi2Te3108–110 and Ag2Se111–116 are for near room temperature applications.
In mid-temperature applications, IV–VI chalcogenides are well-known thermoelectrics owing to their remarkable band structures19–55 and pioneering bonding technique, which is termed as “metavalent bonding”.117–122 Among them PbTe based alloys stand out. This is because PbTe based alloys possess optimized carrier concentration and so the proven strategies, which guarantee high ZT, can be realized efficiently. Fig. 7(a) demonstrates the bonding mechanism involved in various compounds. The x-axis depicts the electrons transferred, which is more prominent in the case of ionic compounds and the y-axis demonstrates the electrons shared, which is more pronounced in covalent compounds. An emerging bonding technique known as metavalent bonding is mapped in the plot. These alloys with metavalent bonding show exceptional thermoelectric performance (illustrated in Fig. 7(b)) owing to their electronic band structure with high band degeneracy and significant band anisotropy to empower the coupled power factor. The bonding mechanism also illustrates soft chemical bonds along with high anharmonicity, which subdues the lattice thermal conductivity. The bonding mechanism thus interwove the outstanding thermoelectric performance of octahedrally coordinated chaclogenides. To avoid Pb-toxicity, the hunt for alternatives123–126 has led to the detailed investigation of GeTe based alloys from the thermoelectric point of view, as they have been known since the 1960s. They remained unexplored due to phase transition at ∼700 K as discussed earlier.127–129
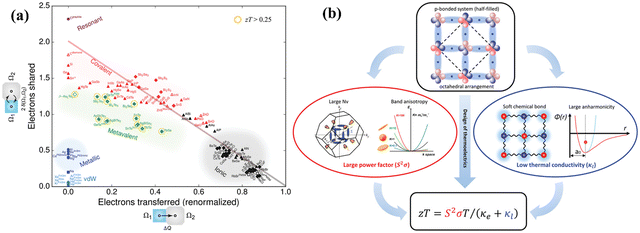 |
| | Fig. 7 (a) A 2-dimensional map to showcase the electron transfer and bonding in materials. x-Axis denotes the number of relative electrons transferred and y-axis denotes the sharing of electrons among neighboring basins via the quantum topological method. Octahedrally coordinated chalcogenides with unusual properties (high values of ε∞, large anharmonicities, an intermediate electrical conductivity, pronounced electron–phonon coupling, and an effective coordination number mismatch with ordinary covalent bonding) are depicted in green and have been termed as metavalent bonding compounds. Reproduced and reprinted from ref. 117, © 2019 RWTH Aachen University. Published by Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (b) Schematic representation depicting the exceptional thermoelectric performance of octahedral chalcogenides having metavalent bonding. Reproduced and reprinted from ref. 119, © 2019 The Authors. Published by Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | |
The slight distortion of high symmetric cubic rock-salt structure along the [111] direction with an interaxial angle of α = 88.2° at 300 K is approximated as rhombohedral GeTe with three longer and three shorter bonds in octahedral geometry.127–129 However, with increase in temperature, known as the critical temperature, ∼700 K, which may change depending on the carrier concentration to (650 ± 100 K)128 as illustrated in Fig. 8(a), the rhombohedral transits to cubic lattice displaying symmetrical variation to its average. This structural transition is suspended and the cubic rock-salt structure stabilizes prominently as the cation–anion pair changes to a heavier cation i.e. Ge → Sn → Pb. This is attributed to the differences in hybridization of orbitals and bonding ionicity. For GeTe, the structural deformation to low symmetric rhombohedral from the symmetrical cubic phase is predominantly due to the stereochemical activity of the lone pair electrons on the s-orbital of Ge and is related to the intense hybridization between the s-orbital of the cation and the p-orbital of the anion. This provokes a remarkable deformation in the allocation of electrons, which in due course causes the decline in the structural symmetry. From the viewpoint of transport of charge, an enhancement of either s–p hybridization or ionicity of the bond augments the isotropic nature of the light valence band (L-band), which eventually decreases its 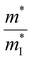 and thus makes it superior among group IV–VI chalcogenides.129–135Fig. 8(b) demonstrates that although the cubic structure (at elevated temperature) has high symmetry in comparison to the rhombohedral structure at low temperature, as far as thermoelectricity is concerned, slight symmetry breaking is preferred as it leads to high band degeneracy. In addition, the doping at the cationic site displaces Ge from the off-center and therefore the energy difference between the light (L) and heavy (Σ) valence bands reduces and subsequently aids in valence band convergence (illustrated in Fig. 8(c)). The doping at the cationic site (Fig. 8(d)) also increases the interaxial angle, the density-of-state effective mass and consequently the Seebeck coefficient.
and thus makes it superior among group IV–VI chalcogenides.129–135Fig. 8(b) demonstrates that although the cubic structure (at elevated temperature) has high symmetry in comparison to the rhombohedral structure at low temperature, as far as thermoelectricity is concerned, slight symmetry breaking is preferred as it leads to high band degeneracy. In addition, the doping at the cationic site displaces Ge from the off-center and therefore the energy difference between the light (L) and heavy (Σ) valence bands reduces and subsequently aids in valence band convergence (illustrated in Fig. 8(c)). The doping at the cationic site (Fig. 8(d)) also increases the interaxial angle, the density-of-state effective mass and consequently the Seebeck coefficient.
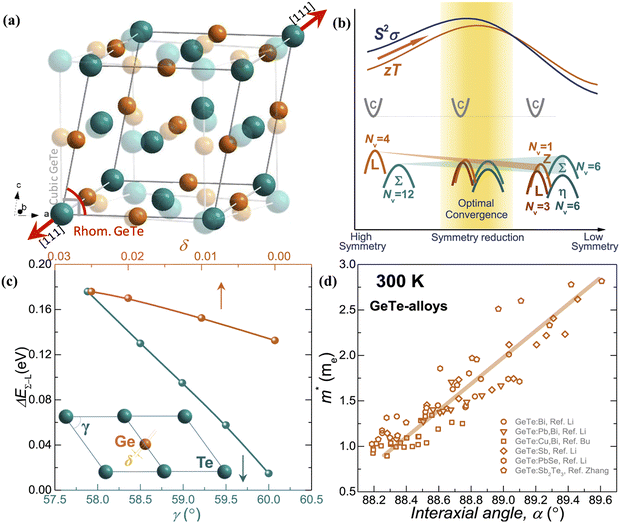 |
| | Fig. 8 Schematic details of the electronic basis of GeTe: (a) crystal structures depicting both rhombohedral (coloured) and cubic (transparent) phases of GeTe; (b) schematic representation illustrating that slight symmetry breaking is beneficial for enhanced band convergence leading to high band degeneracy; and (c) depiction demonstrating the change in the energy offset, i.e., the difference in the L- and Σ valence bands with the variation in the rhombohedral angle (γ in the primitive cell) and displacement from the off-center (δ) (the inset displays the primitive cell, γ < 60° and γ = 60° for r-GeTe and c-GeTe respectively); (d) change in the density-of-state effective mass (m*) with the variation in the rhombohedral angle (α) at 300 K. for GeTe-alloys. Reproduced and adapted from ref. 47 under the terms of the Creative Commons CC-BY-NC-ND license. | |
3.1. Electronic properties of GeTe
The band diagram of cubic-GeTe is analogous to those of PbTe and SnTe, where the maxima of the valence band and minima of the conduction band lie at the L-point of the Brillouin zone (Nv = 4) and thus lead to the direct band gap. However, the secondary valence band, which is located in the Σ direction, is energetically lower than the L band with a high band degeneracy of Nv = 12 and an energy offset ΔEL−Σ ∼ 64 meV, as depicted in Fig. 9.45,47 The low energy offset value indicates that the two valence bands are strategically placed for convergence at elevated temperature in comparison to PbTe (ΔEL−Σ ∼ 100 meV)31 and SnTe (ΔEL−Σ ∼ 300 meV).15 This implies a favorable pathway for transportation of charge carriers and is self-explanatory for realization of enhanced ZT in the symmetric GeTe phase at elevated temperature.
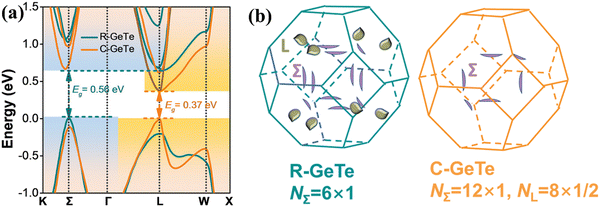 |
| | Fig. 9 (a) Calculated electronic band structure of GeTe featuring both R-GeTe (rhombohedral GeTe) and C-GeTe (cubic GeTe) respectively; (b) calculated Fermi surfaces for both R-GeTe and C-GeTe considering spin–orbit coupling. Reproduced and reprinted from ref. 45, © 2020 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | |
Nevertheless, the location of the L and Σ bands at different Brillouin zones shows different responses when lattice distortion occurs along the [111] direction, i.e. the L-point of the Brillouin zone. Thus, directional lattice distortion was explicitly employed to manipulate the energy of the bands. This causes a substantial decrease of L-band energy and thus the maximum of the valence band is the Σ band in the rhombohedral GeTe. Moreover, the reduction in symmetry or symmetry breaking in the crystal structure separates the L-band with 4 carrier pockets into 3 L and 1 Z. Simultaneously, the 12 carrier pockets in the Σ band splits into 6 Σ and 6η (illustrated in Fig. 8(b)).45,47,77,136 This creates a hindrance in the rhombohedral phase to attain optimum band convergence and thus makes it an inferior candidate as a thermoelectric material in comparison to the usual cubic analogue.136 However, the increased degree of freedom augments the tuning of band energies and is adequate to converge all the bands. This mode of crystal structure engineering, which facilitates the band structure manipulation, opens an avenue such that slight symmetry deviation is electronically favorable towards enhanced thermoelectric performance.77,136
3.2. Entropy stabilized GeTe
The noteworthy feature of the high entropy concept in thermoelectrics is ultralow lattice thermal conductivity. This is because of the fact that the extremely distorted lattices obtained in high-entropy alloys induce high strain, which eventually causes effective phonon scattering and minimizes the lattice thermal conductivity to an extent that it resembles the unique phonon glass performance. Nonetheless, the ideal thermoelectric alloy with enhanced behavior should exhibit “phonon-glass-electron-crystal” behavior.13 In high-entropy alloys, attaining electron-crystal properties is the bottleneck.137
As discussed earlier, the “high-entropy alloy” concept, which eschews the traditional paradigm of “base element” concept, involves designing alloys by shifting the focus from the vertices to the central part of the phase diagram (Fig. 2(b)). This radical deviation, which involves multiple elements (contradicting the rule of Parsimony by Pauling138) causing complexity and disorder in the unit cell, enlarges the chemical space. This is due to the reason that addition of multiple elements instigates disorder and complexity in the lattice, amplifies the chemical space and thus unearths the design of new thermoelectric alloys. On a lighter note, it is noteworthy to mention that any material that qualifies for technological applications, although widely known for exquisite purity, essentially needs a finite level of substitutional disorder for its extensive use. The burgeoning demand for high entropy thermoelectric alloys takes advantage of these emerging properties essential for diminishing the lattice thermal conductivity without compromising the charge transport. Moreover, the increase in the compositional space with the addition of new elements leads to entropy driven structural stabilization, which eventually leads to a highly symmetrical cubic structure possessing a high Seebeck coefficient and band degeneracy and thus enhanced thermoelectric performance.137,139–141Fig. 10(a) demonstrates the different levels of entropy and the change in the configurational entropy of the system with the increase in the number of components. As the configurational entropy increases, the thermal conductivity reduces as desired in thermoelectrics (Fig. 10(b)).
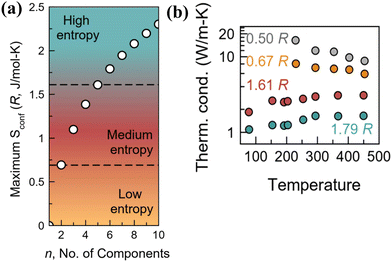 |
| | Fig. 10 (a) Schematic representing the variation in categories in configurational entropy with the increase in the number of components; the plot shows that high entropy can be attained when the number of constituent elements is at least 5, which share a similar crystallographic site. (b) Plot demonstrating the lowering of thermal conductivity with the increase in the configurational entropy. Reproduced and adapted from ref. 137. Copyright © 2023, American Chemical Society. | |
However, the topic of high entropy faces linguistic problems and the terminology has evolved continually with time. This is because canonically multiple elements sharing a common crystallographic site are termed as solid solutions. Thus, to distinguish solid solutions from high entropy alloys, a further criterion was essential and this is where unanimous consensus was lacking.137,139 Thus, to have a model for the expansion of enhanced performance thermoelectric materials, a suitable design of the composition of the materials and temperature of operation is essential. For high-entropy GeTe based alloys, analysis of the properties in different temperature regimes and at different chemical compositions was carried out by Li et al. using an interpretable machine learning workflow. The methodology involves constructing the dataset from experiments based on preceding research on thermoelectrics and subsequently descriptors are established depending on the atomic features.131 To choose pertinent features, some of the feature selection mechanisms, viz., Pearson correlation, exhaustive and univariate feature selection, are considered. The elected features are then utilized in the ZT value, which is a target variable for exercise and testing. Global interpretability, which includes examination of the contribution of the interactive parameters to ZT (target variable), local interpretability approaches, choice of materials and optimization of performances, reveals that the ZT values of the thermoelectric alloys are primarily controlled by the temperature with little impact of molar volume and electronegativity. By applying interpretable machine learning tools, the prediction and optimization of the performance of the thermoelectric alloys can be assessed for samples with prior knowledge. This enables a thorough approach towards designing workflow apart from assessment and forecast of the thermoelectric properties of alloys. This methodology was used to select and develop high entropy GeTe-based alloys with enhanced performance.
3.3. Futuristic GeTe based alloys via entropy engineering
GeTe and its derivatives, being non-toxic among group IV–VI elements, have the proficiency to replace the widely studied PbTe alloys because of their high toxic load. However, due to low symmetry rhombohedral structure, which is responsible for the generation of the ferroelectric domain, abundant microstructures are available to optimize for the enhancement of thermoelectric performance. Recent advancements in the solid-state physics and the techniques involved in the synthesis provide an efficient means of enhancing the thermoelectric performance.
One of the difficulties associated with GeTe is high carrier concentration (∼1021 cm−3) due to the intrinsic Ge vacancies, which has a negative impact on thermoelectricity (depicted in Fig. 11(a)–(c)).140 Moreover, these intrinsic vacancies restrict the carrier transport and thus deteriorate the mobility of the charge carriers. Here, lies the role of chemical principles for the enhancement of thermoelectric properties. To obtain optimized properties, the dopants are screened, which is generally directed by the chemical valencies and defect chemistry.79 In addition, dopants are also added to improve the electronic transport properties based on the intense understanding of the molecular orbital theory and to reduce the lattice thermal conductivity by strengthening the phonon scattering with the introduction of imperfections. Thus, chemistry essentially benefits the GeTe thermoelectrics as multiple elements are added simultaneously. The result is that the presence of multiple elements enhances the chemical space, increases the configurational entropy and ultimately provides benefit towards high thermoelectric performance.
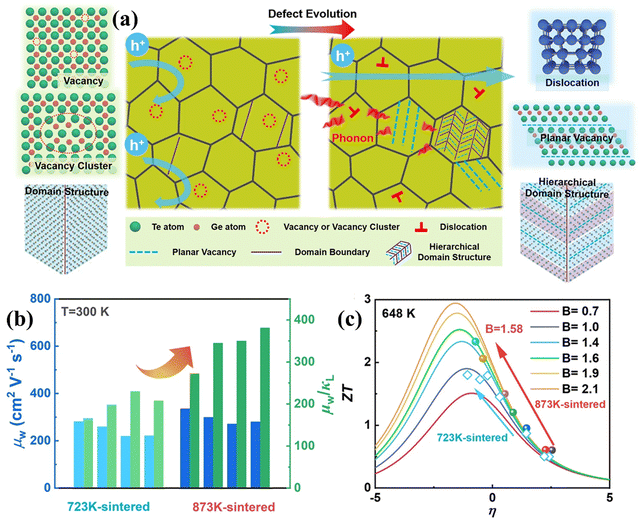 |
| | Fig. 11 (a) Schematic demonstrating the nature of carriers and phonons in the GeTe-derivatives with hierarchical architecturing; (b) plot displaying μw (weighted mobility) and μw/κL, for Ge-deficient samples at 300 K (sintered at 873![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K), with respect to the samples sintered at 723 K), with respect to the samples sintered at 723![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, and (c) ZT value with respect to the reduced Fermi potential having different quality factors at 648 K, and (c) ZT value with respect to the reduced Fermi potential having different quality factors at 648![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. Reproduced and adapted from ref. 140 under the terms of the Creative Commons CC-BY-NC-ND license. K. Reproduced and adapted from ref. 140 under the terms of the Creative Commons CC-BY-NC-ND license. | |
3.3.1. (GeTe)1−x(LiSbTe2)x.
In Fig. 12, Liu et al. alloyed LiSbTe2 with GeTe, with an aim to stabilize the cubic structure in the range of 300–773 K. The material provided a superior ZTavg of ∼1.38 in the aforesaid temperature range and can be used for the fabrication of thermoelectric devices.142 This can be attributed to the fact that in LiSbTe2, the formal charges on Li, Sb and Te are +1, +3 and −2 respectively. This implies that Li has no lone pair, whereas Sb loses the three-5p electrons in the outermost orbital, leaving two electrons in the 5s orbital as the lone pair. However, the 5s2 lone pair on Sb is more stable than the 4s2 lone pair on Ge as the stability of the lone pair increases on descending the group, and so the Sb lone pair is more stable than the Ge lone pair.143 When alloying with LiSbTe2, where Li and Sb occupy the Ge site partially in both cubic and rhombohedral phases, the average stereochemical activity of the lone pair on the cation is remarkably impeded, causing suppression in the phase-transition temperature. This stabilizes the cubic structure, which promotes the convergence of multiple bands along with phonon scattering. Thus, with the addition of multiple elements the phase transition was averted and the conversion efficiency was raised to 17%, being one of the highest values among those of polycrystalline p-type alloys.
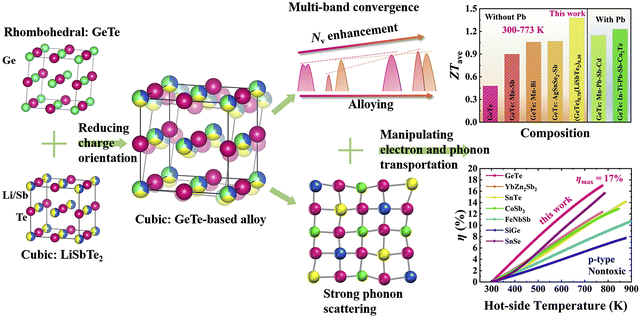 |
| | Fig. 12 Schematic demonstration of the origin of crystal structure and the factors responsible for enhanced thermoelectric performance of the GeTe-derivatives. Reproduced and adapted from ref. 142, under the Creative Commons CC-BY-NC-ND license. | |
3.3.2. Ge1−w−x−yInwPbxSbyTe1−zIz.
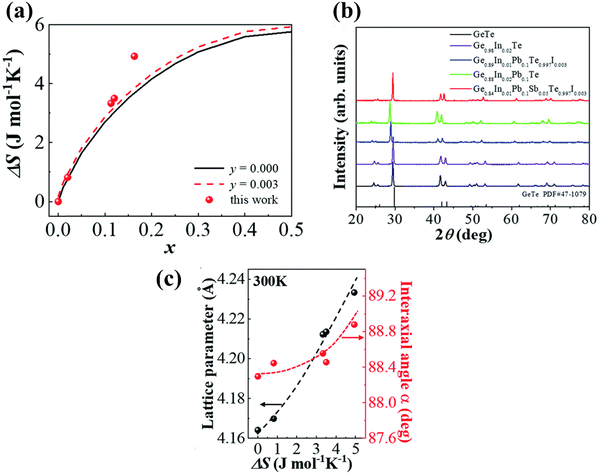
In harmony with the beneficial effect of entropy engineering to suppress the phase transition in GeTe, Qui et al. consecutively added multiple dopants continuously. Thermodynamically, the configurational entropy (ΔS) was calculated for multiple species using the equation 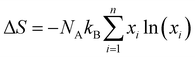 and is plotted as shown in Fig. 13(a). The addition of the species shows the increase in the ΔS value as x increases. The powder XRD pattern confirms the formation of more symmetrical crystal structures with the increased number of elements followed by the analysis (Fig. 13(b)), which reveals increase in the lattice parameter along the α-axis due to the larger atoms at the Ge site as well as the opening of the interaxial angle (Fig. 13(c)).
and is plotted as shown in Fig. 13(a). The addition of the species shows the increase in the ΔS value as x increases. The powder XRD pattern confirms the formation of more symmetrical crystal structures with the increased number of elements followed by the analysis (Fig. 13(b)), which reveals increase in the lattice parameter along the α-axis due to the larger atoms at the Ge site as well as the opening of the interaxial angle (Fig. 13(c)).
 |
| | Fig. 13 (a) Plot showing the increase in the configurational entropy with the increase in the constituents of the alloy; (b) powder XRD patterns of GeTe and its derivatives at room temperature. The room temperature GeTe phase resembles the rhombohedral crystal structure and no appreciable secondary phase was seen with the addition of dopant elements; (c) change in the lattice parameters along the direction of a-axis and so the variation in the interaxial angles with the increase in ΔS. Reproduced and reprinted from ref. 144 with permission from the Royal Society of Chemistry. | |
Moreover, he demonstrated that the addition of the dopants increases the symmetry and brings down the phase transition temperature through DSC measurement as shown in Fig. 14(a)–(c).144
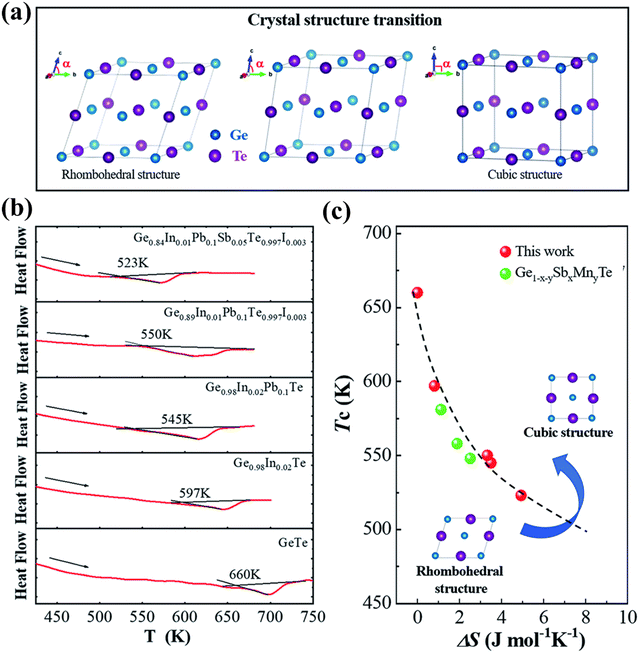 |
| | Fig. 14 (a) Schematic displaying the transition from the rhombohedral to cubic crystal structure in GeTe; (b) DSC plots with the endothermic peaks of pristine GeTe and its derivatives showcasing that with the addition of dopants at the cationic and anionic sites the phase transition temperature (Tc) shifts towards lower temperature; (c) plot of phase transition temperature vs. ΔS, depicting the shift towards low Tc. For comparison, Ge1−x−ySbxMnyTe was plotted. Reproduced from ref. 144 with permission from the Royal Society of Chemistry. | |
Measurement of transport properties (Fig. 15(a)–(c)) validates the finding that an increase in the number of elements increases the Seebeck coefficient, as the entropy engineering promotes band convergence leading to high effective mass, which eventually increases the power factor. Apart from the obvious enhancement in the electronic transport behaviour, the thermal transport properties also show improved behaviour owing to the fact that increase in the dopant introduces point defects (short range disorder) along with long range ordering. Thus, the sites for the scattering of phonons increase leading to diminished lattice thermal conductivity.
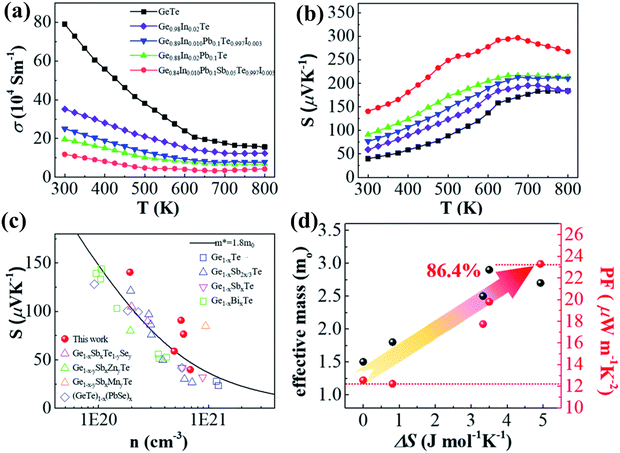 |
| | Fig. 15 Electronic transport properties of pristine GeTe and its derivatives vs. temperature: (a) electrical conductivity; (b) Seebeck coefficient; (c) Pisaranko plot for the Seebeck coefficient with respect to the carrier concentration and (d) change in effective mass and power factor with the increase in the configurational entropy. The plot shows the effect of entropy engineering towards high thermoelectric performance. Data from several other groups were also plotted for comparison. Reproduced from ref. 144 with permission from the Royal Society of Chemistry. | |
Fig. 16(a)–(d) show that the superior entropy alloy is Ge0.84In0.01Pb0.1Sb0.05Te0.997I0.003 with a ZTpeak of ∼2.1 at 800 K. If the ferroelectric phase transition can be pulled down at 300 K appropriately, then GeTe based alloys can be efficiently used as power generators for harvesting low-grade heat. Thus, attempts to research novel methods to augment transportation of electrons with damping propagation of phonons if probable, in chorus, will be able to raise the thermoelectric performance.144
 |
| | Fig. 16 (a) ZT values vs. T for both pristine and GeTe based alloys studied by Qiu et al.; (b) highest ZT values as a function of T for the high entropy sample studied by Qiu et al. and other groups; (c) ZTavg of the GeTe samples and GeTe based alloys studied by Qiu et al. and other groups in the temperature regime of 300–523 K; (d) variation of ZT vs. configurational entropy. Reproduced from ref. 144 with permission from the Royal Society of Chemistry. | |
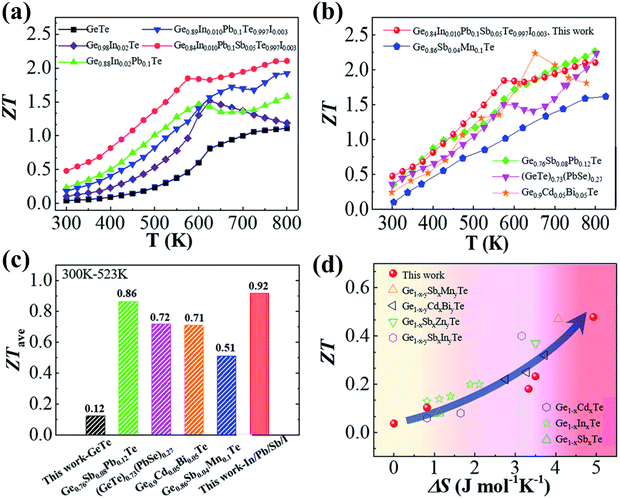
3.3.3. Ge1−2x−yPbxSnxSbyTe.
Recently, Das et al. in his study mentioned that doping GeTe with 2.5 mol% Pb and Sn each (Ge0.95Pb0.025Sn0.025Te) enriches the configurational entropy in contrast to the pseudoternary systems such as PbTe1−2xSexSx, SnTe1−2xSexSx and GeTe1−2xSexSx.145 This is because in the case of pseudo-ternary systems, enthalpy surpasses the entropy and eventually phase separation occurs. The borderline, which separates the secondary phases from the main matrix, scatters the majority charge carriers and the phonons of similar dimensions and hence manifests a negative impact on the thermoelectric properties. However, in 11 mol% Sb-doped Ge1−2xPbxSnxTe, addition of multiple elements enhances the entropy propelled structural stability in conjunction with an increase in solid solubility limits and hence, the methodology diminishes the phonon conduction (κL) from 2.8 W m−1 K−1 for pristine GeTe to 1.9 W m−1 K−1 for Ge0.95Pb0.025Sn0.025Te samples. The addition of Sb optimizes the carrier concentration by quenching it along with enhancement of the Seebeck coefficient by converging the valence band. Consequently, the ball-milled followed by spark plasma sintered Ge0.84Pb0.025Sn0.025Sb0.11Te displays a much reduced κL of ∼1.1 W m−1 K−1 and a ZTpeak of 2.3 at 723 K with a ZTavg of 1.3 in the 300–723 K range. Provoked by the raised ZT, a two-leg device was demonstrated with Ge0.84Pb0.025Sn0.025Sb0.11Te (p-type) and I and In doped PbTe (n-type) legs, which exhibits a high output power density of ∼590 mW cm−2 at ΔT = 448 K as shown in Fig. 17(a)–(d).85
 |
| | Fig. 17 (a) ZT of ball-milled followed by spark plasma sintered high entropy GeTe based Ge0.84Pb0.025Sn0.025Sb0.11Te vs. T. The plot depicts no hysteresis upon thermal cycling. Besides, the data are highly reproducible; (b) demonstration of a two leg thermoelectric module with the Ge0.84Pb0.025Sn0.025Sb0.11Te (p-type) leg and the Pb0.997In0.003Te0.996I0.004 (n-type) leg. Inset displays the actual image of the device; (c) output power density vs. measured current at different ΔT; and (d) maximum output power density vs. ΔT for a two-leg device. Reproduced and adapted from ref. 145. | |
3.3.4. Ge1−w−x−y−zAgwSbxPbyBizTe.
In a similar experiment conducted by Jiang et al., multiple elements viz. Ag, Sb and Pb were alloyed with GeTe due to their enhanced solubility limits.135 The study reveals the presence of an impurity phase by X-ray diffraction analysis (Fig. 18(a)), when the number of components is three. However, the secondary phase disappears for the alloy with five components due to entropy driven structural stabilization. The single phase was further stabilized by the presence of Cd, Mn and Sn. Transport property measurement shows strong scattering of phonons due to alloying along with Anderson localization,146–149 which is actually inevitable in disordered systems and is deleterious for electrons. However, Jiang et al., in his experiment, maintained the Te sublattice ordered by not adding any constituents at the Te site.135 Addition of multiple elements at the Ge site causes disorder and eventually Anderson localization. Nevertheless, since the valence band has more contribution from the 5p orbitals of Te, the impact due to the disordered Ge site on the electron transport properties of p-type GeTe is less. To corroborate the diminished influence of multiple elements in entropy engineered GeTe, the atomic structure was studied for both pristine GeTe and high entropy GeTe based alloys using high-angle annular dark field (HAADF) imaging (Z-contrast nature) in the STEM mode. The study reveals more intense spots for high entropy alloys in comparison to the pristine GeTe. Moreover, the Ge atom deviates from the geometric centre of the rhombus created by Te atoms in the GeTe alloy, causing a polarized electric field, the basis of ferroelectricity. The parameter, δ, in Fig. 18(b)(C and F) defines the deviation of the Ge atom from the geometric centre. The calculations of atomic resolution HAADF images of GeTe based samples reveal that the δ value reduces with the rise in the elemental species and is in concurrence with the XRD results. This indicates the gradual shift from the less symmetric rhombohedral structure to the high symmetry cubic crystal structure for the high entropy alloy and subsequently the faded ferroelectricity.150,151 This eventually leads to redistribution and delocalization of the electrons. Moreover, all the Ge–Te bond lengths were dissimilar: three shorter bonds due to electron localization and three longer bonds. On the contrary, for the high entropy alloys wherein there are more alloying elements, the localized electrons undergo transfer of electrons from the shorter to the longer bonds and thus aid in delocalization of electrons. The delocalized electrons thus reduce the energy-offset values amid valence bands and illustrate the raised equivalent degenerated valleys. This ultimately explains the high power factors of entropy-engineered GeTe alloys.
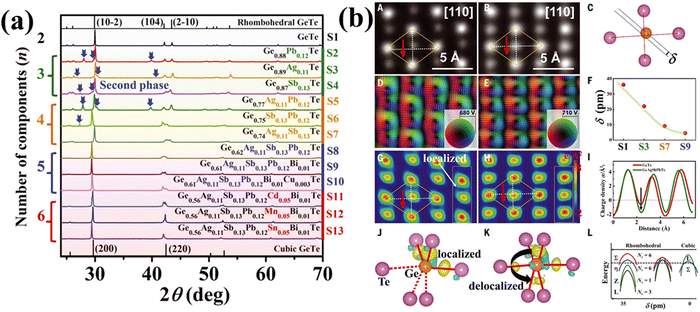 |
| | Fig. 18 (a) XRD patterns of GeTe based high entropy materials at room temperature. Secondary phases as indicated by the blue arrow were seen for samples with less components; (b) (A)–(L) images depict the delocalization of the electrons and off-centering of Ge in the high entropy GeTe alloys. Reproduced and adapted from ref. 135. Copyright © 2022, The American Association for the Advancement of Science. | |
Transport property measurement of the series of samples reveals that electronic conduction is compromised in alloys with multiple elements, while the Seebeck coefficient follows the reverse trend. Consequently, the power factor seems to be low in the low temperature range for the low-entropy alloys via scattering of the charge carriers by the multiple phases. The power factor was also low for pure GeTe in the low temperature range owing to the low Seebeck coefficient (Fig. 19(a)). Lattice thermal conductivity (Fig. 19(b)), as expected, shows an ultra-low value in the entire temperature regime, signifying temperature independent behaviour. With all the optimized values, the ZT value of Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te was calculated to be 0.6 at 300 K and 2.7 at 750 K (Fig. 19(c)). Thus, the entropy enhancement by multiple element alloying, in contrast to strong alloy scattering and Anderson localisation of the charge carriers, boosts the delocalisation of electrons resulting in improved electrical properties and band convergence. In addition, the high entropy system dampens the conduction of phonons and thus reduces lattice thermal conductivity. Because of the high ZT values of the high entropy GeTe alloy, along with average ZT values higher than those of usual p-type thermoelectric alloys, the thermoelectric module was realized with high experimental conversion efficiency. The module developed using n-type Pb0.997In0.003Te0.996I0.004 and p-type Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te with a leg length of 11 mm demonstrates a conversion efficiency of 10.5%. However, efforts were also made to demonstrate the segmented module with low temperature legs using commercially available p-type Bi0.5Sb1.5Te3 and Bi2Te2.7Se0.3 as n-type with different (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 8
3, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 9
3 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) ratios. The 8
3) ratios. The 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 segmented module displays a significantly high conversion ratio of 13.3% at ΔT = 506 K. The high conversion efficiency is attributed to the fact of having optimized ZT in the entire range of operation (Fig. 19(e) and (f)).
3 segmented module displays a significantly high conversion ratio of 13.3% at ΔT = 506 K. The high conversion efficiency is attributed to the fact of having optimized ZT in the entire range of operation (Fig. 19(e) and (f)).
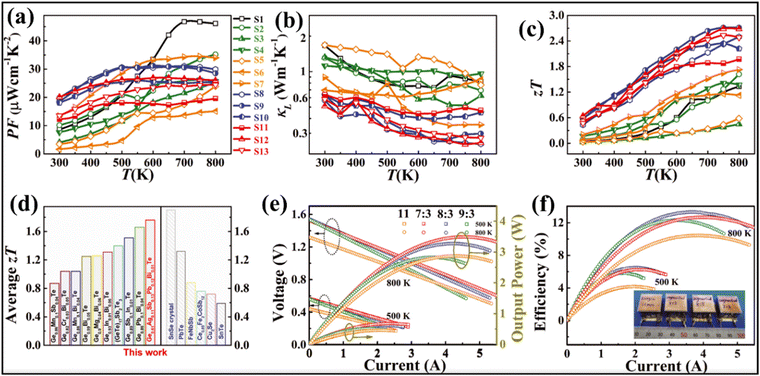 |
| | Fig. 19 (a) Power factor; (b) lattice thermal conductivity; (c) ZT vs. T of the GeTe based alloys studied by Jiang et al.; (d) plot to compare the ZTavg of the GeTe alloys studied by Jiang et al. and by other groups and also to compare some of the high ZT materials, viz. SnSe crystals, PbTe, half-Heusler (FeNbSb), skutterudite (Ce0.85Fe3CoSb12), ionic liquid (Cu2Se) and SnTe; (e) output voltage and output power vs. T; and (f) maximum conversion efficiencies vs. I for the engineered 11, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 8 3, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 9 3 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 devices. Reproduced and adapted from ref. 135. Copyright © 2022, The American Association for the Advancement of Science. 3 devices. Reproduced and adapted from ref. 135. Copyright © 2022, The American Association for the Advancement of Science. | |
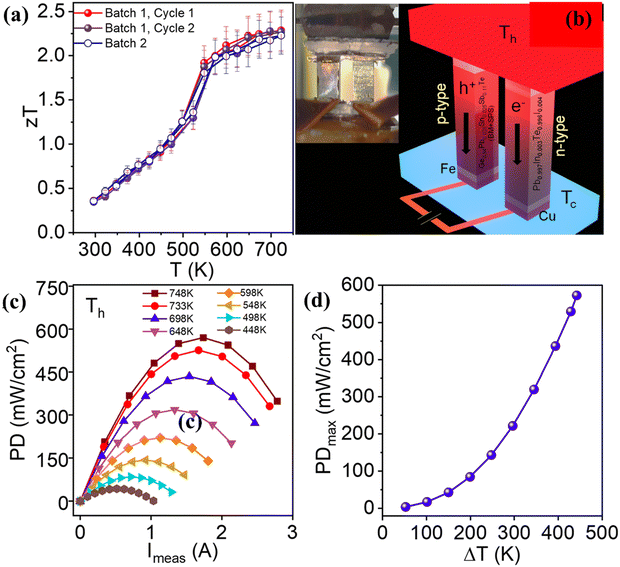
3.3.5. [(GeTe)1−x(Cu2Te)x]1−y(PbSe)y.
In a different experiment conducted by Bu et al., the single leg thermoelectric device constructed using high entropy GeTe–Cu2Te–PbSe ((Ge1−xCu2xTe)1−y(PbSe)y) alloys displays a conversion efficiency of 14% at ΔT = 440 K. The enhanced performance of the alloy was attributed to the optimization of the simultaneous electronic and thermal properties in terms of charge carrier concentration and intensified phonon scattering respectively. Initially, the methodologies adapted to quench the excess carrier concentration had an adverse effect on the carrier mobility. Nonetheless, alloying 1.5%Cu2Te was found to be beneficial, as it seemed to reduce hole concentration by one order of magnitude i.e. ∼1021 cm−3 to 1020 cm−3 without deteriorating the mobility. Moreover, alloying of PbSe suppresses the lattice thermal conductivity along with suppression of formation of Ge vacancies. Within the temperature of operation, the alloy displays a peak ZT of > 2.5 and a ZTavg of 1.8 and the characteristics of the material and the device are depicted in (Fig. 20(a) and (b)).152 The output characteristics of the device are shown in (Fig. 20(c)–(e)). The remarkable conversion efficiency of the GeTe based alloy is compared with the reported values of TAGS, half-Heusler, and skutterudites as depicted in Fig. 20(f).
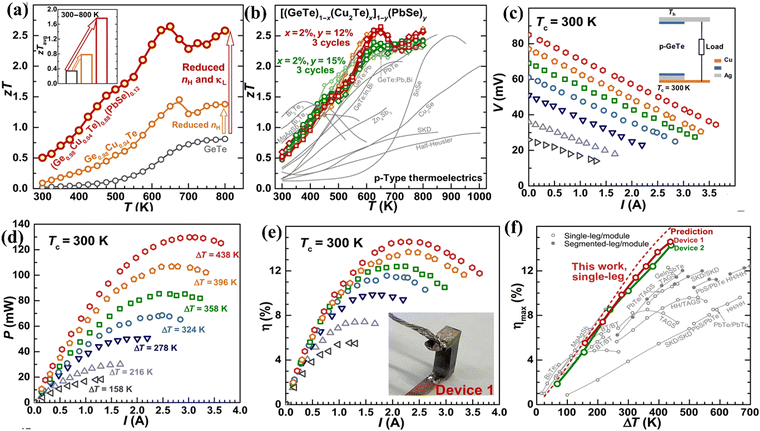 |
| | Fig. 20 (a) Change in ZT and ZTavgvs. T; (b) repeated data acquisition of the high entropy GeTe ((Ge0.98Cu0.04Te)1−y(PbSe)y) alloys studied by Bu et al. to validate the reproducibility and their comparison with the other reported high-performance p-type thermoelectric alloys; (c) module characteristics; (d) power output; (e) efficiency as a function of current; and (f) maximum efficiency that can be attained for a single leg entropically enriched GeTe alloy as a function of ΔT and its comparison with the reported values of TAGS, half-Heusler, and skutterudites and prediction. Reproduced and adapted from ref. 152. Copyright © 2021 under a Creative Commons Attribution Non-Commercial License 4.0 (CC BY-NC). | |
3.3.6. Ge1−w−x−y−zMnwPbxSbyCdzTe.
Although in the genome of functional materials, configurational entropy is a blooming descriptor,153 Zhi et al. in his study (Fig. 21) explicitly mentioned that due to the adverse effect on carrier mobility in high-entropy alloying, where the principal elements are present with the atomic percentage ranging from 5–35% to accomplish ΔS > 1.5R, there is a setback. Instead, he mentioned that medium entropy alloys, 1R < ΔS < 1.5R, are beneficial as they are capable of balancing the lattice thermal conductivity to attain a glass-like limit in addition to stabilizing the high symmetry cubic crystal structure near room temperature.154 According to Zhi et al., it is the judicious selection of the alloying species based on the previous reports, to consider, that can aid in realizing high ZT. Most importantly, the prerequisite condition for an alloying species is that it should have high solid solubility, >5 mol% in the main matrix, i.e. GeTe. Based on the requirement, Mn, Sb, Pb and Cd were shortlisted to be added at the Ge site. These elements have unique properties: Mn and Cd can aid in band convergence of the valence bands and Pb and Sb quench the high hole concentration of GeTe by raising the ΔG of the Ge vacancies. These elements were established as sole dopants and as dual dopants in GeTe; however, their participation in co-alloying GeTe to form a medium entropy alloy was not known. In this regard, the atomic percentages of the elements were adjusted in a way that ΔS was increased to 1.14 for Ge0.63Mn0.15Pb0.1Sb0.06Cd0.06Te (Fig. 21(a)). Based on the X-ray diffraction pattern, the lattice parameter and interaxial angle were calculated with the increase in the number of alloying elements (Fig. 21(b) and (c)). Differential scanning calorimetry analysis was performed to identify the evolution of phase transition temperature with the enhancement of ΔS (Fig. 21(d)). Surprisingly, this medium entropy alloy was capable of suppressing the phase transition temperature at 655 K for GeTe to 300 K and the XRD pattern further confirms the cubic GeTe with the increase of ΔS.
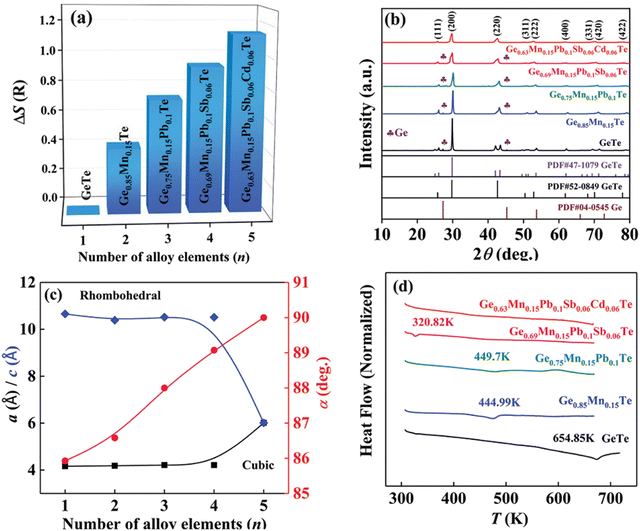 |
| | Fig. 21 (a) Configurational entropy ΔS, (b) powder XRD patterns, (c) lattice parameter a/c and interaxial angle, α, at 300 K, of GeTe-based alloys, and (d) DSC curves showing the lowering of the phase transition temperature of medium entropy GeTe-based alloys. Reproduced and adapted from ref. 154 © 2021 The Authors. Advanced Science published by Wiley-VCH GmbH under the terms of the Creative Commons CC BY license. | |
The result is that the medium entropy alloy composition Ge0.63Mn0.15Pb0.1Sb0.06Cd0.06Te could enhance the Seebeck coefficient and reduce lattice thermal conductivity simultaneously without compromising the carrier mobility (Fig. 22). The entropy engineered alloy displayed a ZTpeak of 2.1 (873 K) and ZTavg of 1.3 (300 and 873 K). The results were compared with the data reported in the literature for low- and high-entropy GeTe alloys (Fig. 23), and Table 1 shows the configurational entropies of all the samples reviewed in this article.
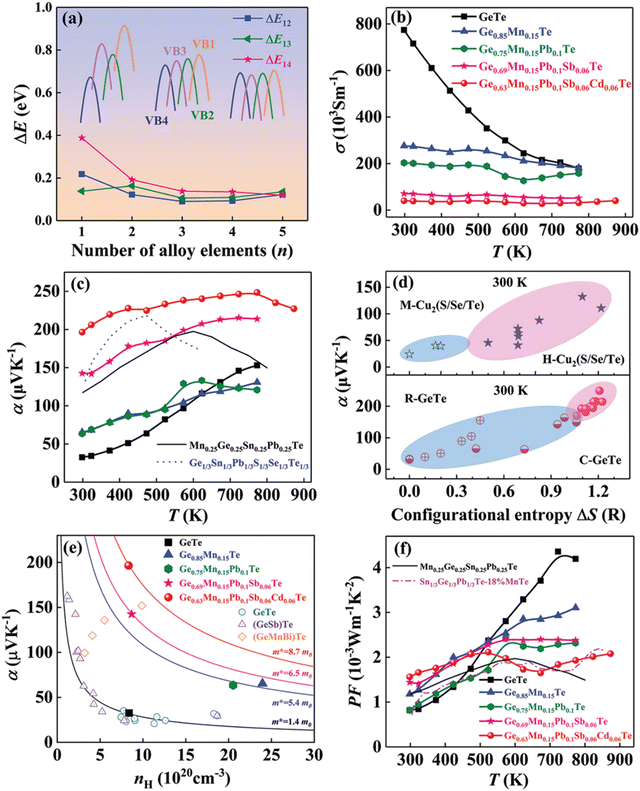 |
| | Fig. 22 (a) Change in the energy offset value, ΔE, with the increase in the alloy elements of four valence bands in GeTe-based alloys; (b) electrical conductivity, (c) Seebeck coefficient, and (f) power factor vs. T of GeTe-based alloys.11,54 (d) Variation of α vs. ΔS for pristine GeTe alloys in both rhombohedral and cubic crystal structures as well as for medium and high entropy GeTe-based alloys and their comparison with literature data. (e) Pisarenko plot α vs. nH for medium entropy GeTe-based alloys and their comparison with the literature data. Reproduced and adapted from ref. 154 © 2021 The Authors. Advanced Science published by Wiley-VCH GmbH under the terms of the Creative Commons CC BY license. | |
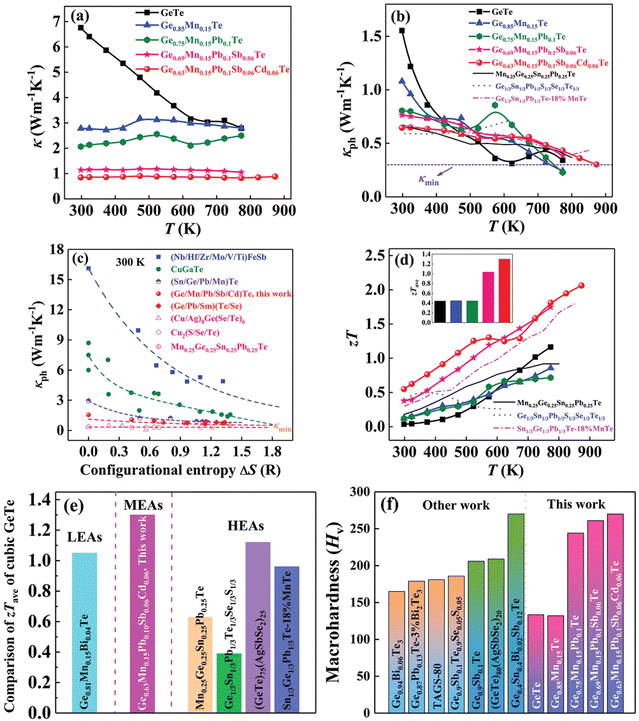 |
| | Fig. 23 (a) Total thermal conductivity, (b) lattice thermal conductivity, and (d) zT vs. T for medium entropy GeTe-based alloys. Inset (d) displays the zTavg values in the operating temperature regime; (c) lattice thermal conductivity vs. ΔS for GeTe-based alloys in comparison with literature data. The dashed lines are guides to the eyes. (e) Comparison of zTave of cubic GeTe with different compositions.11,40,41,44,54 (f) Vickers hardness Hv of GeTe-based alloys at 300 K compared with literature data. Reproduced and adapted from ref. 154 © 2021 The Authors. Advanced Science published by Wiley-VCH GmbH under the terms of the Creative Commons CC BY license. | |
Table 1 Configurational entropies of the samples reviewed in this article
| Compound |
Configurational entropy (ΔS) in J mol−1 K−1 |
| GeTe |
5.76 |
| (GeTe)0.7(LiSbTe2)0.3 |
9.946 |
| Ge0.84In0.01Pb0.1Sb0.05Te0.997I0.03 |
8.672 |
| Ge0.84Pb0.025Sn0.025Sb0.11Te |
8.144 |
| Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te |
11.169 |
| (Ge0.98Cu0.04Te)0.88(PbSe)0.12 |
9.416 |
| Ge0.63Mn0.15Pb0.1Sb0.06Cd0.06Te |
10.513 |
The hardness measurement by the Vickers hardness method shows that the mechanical properties of the medium entropy alloy samples are significantly enhanced for practical applications.
4. Summary and perspectives
As far as thermoelectricity is concerned, it is always challenging to optimize ZT due to the inherently intertwined parameters and so various strategies were put forward to decouple and adjust the quasi-independent parameters to enhance the ZT value. In this review, the concept of entropy engineering was enlightened with its beneficial effect on GeTe thermoelectrics. It is certainly a difficult task to attain a delicate balance among several prevailing mechanisms to reach the sweet spot of high ZT by simultaneously reducing the lattice thermal conductivity and without compromising much of the electrical conductivity. Thus, innovative physical mechanisms are always required to push thermoelectrics to a new level of performance, which can be competitive enough with other technologies available for energy conversion and suitable for widespread usage as thermoelectric power generators and coolers.155
In the mid temperature range, GeTe based alloys are widely studied eco-friendly thermoelectric materials owing to their excellent thermoelectric performance. Unfortunately, these alloys undergo phase transition at ∼700 K, and real thermoelectric applications have no space for such phase transitions. However, the result is that it has a low symmetry phase (rhombohedral crystal structure) at low temperature and a high symmetry phase (cubic crystal structure) at high temperature. The high symmetry structure is advantageous for thermoelectrics as it gives high band degeneracy, whereas low symmetry is beneficial because of low phonon conduction. Thus, effort should be put into breaking the symmetry in such a way that both effects can be accomplished simultaneously.
The blooming entropy engineering concept thus applies the idea of adding multiple elements in GeTe for alloying, preferably at the concentration of 5–35 at%. In addition, aliovalent doping at the Ge site also optimizes the carrier concentration, which is otherwise a persistent problem in GeTe and hence it was unexplored for a prolonged period. The alloys thus obtained were high entropy alloys with high configurational entropies, no phase segregation, high symmetry, reduced phase transition temperature, improved power factors and low lattice thermal conductivity but at the cost of reduced mobility. In order to avert this, medium entropy was preferred, where the elements for doping should be such that 1R < ΔS < 1.5R (Table 1). In this scenario, the carrier mobility is not compromised and high ZT is obtained.156,157 The systematic investigation of IV–VI chalcogenides with the thermodynamic landscape of (Ge,Sn,Pb)(S,Se,Te) (as shown in Fig. 24) reveals that a Ge-poor composition at the cationic site and S-poor composition at the anionic site are stable with low phase transition temperature and easy to synthesize.50,158–161
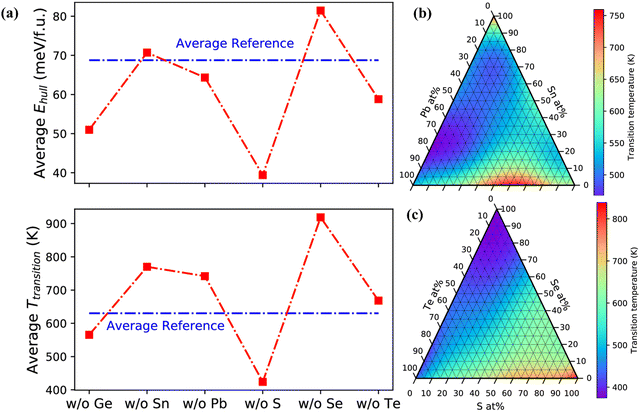 |
| | Fig. 24 (a) Average energy and average phase transition temperature above the convex hull (Ehull) and for alloy compositions respectively that lack one of the constituent elements; (b) and (c) phase-transition temperature vs. work functions of cation and anion compositions. Reproduced with permission from ref. 159 Copyright 2020, American Chemical Society. | |
The novel theories mentioned above should be executed experimentally with new elements at the cationic and the anionic site to enhance the thermoelectric performance of GeTe based alloys with industrial production at the macroscale. This will enable the macro-fabrication process and real thermoelectric power generator applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to acknowledge the members of Thin Film Devices Section for constant support.
Notes and references
-
D. M. Rowe, CRC Handbook of Thermoelectrics, CRC, Boca Raton, FL, 1st edn, 1995 Search PubMed
 .
.
- H. J. Goldsmid and A. W. Penn, Phys. Lett., 1968, 27A, 523 CrossRef
 .
.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466 RSC
 .
.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8619 CrossRef CAS PubMed
 .
.
- S. Zohreh, Z. Stamatis, C. Boris, S. Sally and C. Yuanlong, Sustainable Energy Technol. Assess., 2020, 37, 100604 CrossRef
 .
.
- C. J. Vineis, A. Shakouri, A. Majumdar and M. G. Kanatzidis, Adv. Mater., 2010, 22, 3970–3980 CrossRef CAS PubMed
 .
.
- W. Sun, R. Sui, G. Yuan, H. Zheng, Z. Zeng, P. Xie, L. Yuan, Z. Ren, F. Cai and Q. Zhang, Mater. Today Phys., 2021, 18, 100391 CrossRef CAS
 .
.
- X. L. Shi, J. Zou and Z. G. Chen, Chem. Rev., 2020, 120(15), 7399–7515 CrossRef CAS PubMed
 .
.
- R. Basu, ChemNanoMat, 2023, 9, e202200551 CrossRef CAS
 .
.
- M. Zebarjadi and G. Chen, APL Mater., 2016, 4, 104401 CrossRef
 .
.
- E. Altenkirch, Phys. Zeitschrift, 1911, 12, 920–924 Search PubMed
 .
.
-
A. F. Ioffe, Semiconductor Thermoelements, and Thermoelectric Cooling, Infosearch, London, 1957 Search PubMed
 .
.
-
G. S. Nolas, G. A. Slack, J. L. Cohn and S. B. Schujman, The next generation of thermoelectric materials, Seventeenth International Conference on Thermoelectrics. Proceedings ICT98 (Cat. No. 98TH8365), Nagoya, Japan, 1998, pp. 294–297 DOI:10.1109/ICT.1998.740376.
- L.-D. Zhao, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2014, 7, 251–268 RSC
 .
.
- S. Mandava, R. Basu, B. Khasimsaheb, S. Bathula, A. Singh and S. Neeleshwar, Mater. Adv., 2021, 2, 4352–4361 RSC
 .
.
- S. Ahmad, A. Singh, S. Bhattacharya, M. Navaneethan, R. Basu, R. Bhatt, P. Sarkar, K. N. Meshram, A. K. Debnath, K. P. Muthe and D. K. Aswal, Band Convergence and Phonon Scattering Mediated Improved Thermoelectric Performance of SnTe–PbTe Nanocomposites, ACS Appl. Energy Mater., 2020, 3, 8882–8891 CrossRef CAS
 .
.
- S. Ahmad, A. Singh, S. Bhattacharya, M. Navaneethan, R. Basu, R. Bhatt, P. Sarkar, K. N. Meshram, K. P. Muthe, S. Vitta and D. K. Aswal, ACS Appl. Energy Mater., 2020, 3, 7113–7120 CrossRef CAS
 .
.
- Z. Li, C. Xiao, H. Zhu and Y. Xie, J. Am. Chem. Soc., 2016, 138, 14810–14819 CrossRef CAS PubMed
 .
.
- A. D. LaLonde, Y. Pei, H. Wang and G. J. Snyder, Mater. Today, 2011, 14, 526–532 CrossRef CAS
 .
.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed
 .
.
- Y. Xiao and L. D. Zhao, npj Quantum. Mater., 2018, 3, 55 CrossRef
 .
.
- O. Delaire, J. Ma and K. Marty, Nat. Mater., 2011, 10, 614–619 CrossRef CAS PubMed
 .
.
- Y. Pei, A. LaLonde, S. Iwanaga and G. J. Snyder, Energy Environ. Sci., 2011, 4, 2085–2089 RSC
 .
.
- K. Biswas, J. He, G. Wang, S.-H. Lo, C. Uher, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2011, 4, 4675 RSC
 .
.
- H. J. Wu, L. D. Zhao, F. S. Zheng, D. Wu, Y. L. Pei, X. Tong, M. G. Kanatzidis and J. Q. He, Nat. Commun., 2014, 5, 4515 CrossRef CAS PubMed
 .
.
- K. Ahn, K. Biswas, J. He, I. Chung, V. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2013, 6, 1529–1537 RSC
 .
.
- Y. Wu, P. Nan, Z. Chen, Z. Zeng, R. Liu, H. Dong, L. Xie, Y. Xiao, Z. Chen, H. Gu, W. Li, Y. Chen, B. Ge and Y. Pei, Adv. Sci., 2020, 7, 1902628 CrossRef CAS PubMed
 .
.
- Y. Pei, A. F. May and G. J. Snyder, Adv. Energy Mater., 2011, 1, 291–296 CrossRef CAS
 .
.
- Y. Pei, A. D. LaLonde, H. Wang and G. J. Snyder, Energy Environ. Sci., 2012, 5, 7963 RSC
 .
.
- Z. Wang, G. Wang, R. Wang, X. Zhou, Z. Chen, C. Yin, M. Tang, Q. Hu, J. Tang and R. Ang, ACS Appl. Mater. Interfaces, 2018, 10, 22401–22407 CrossRef CAS PubMed
 .
.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed
 .
.
- H. Liu, Z. Chen, C. Yin, B. Zhou, B. Liu and R. Ang, Appl. Phys. A: Mater. Sci. Process., 2019, 125, 225 CrossRef
 .
.
- P. Jood, M. Ohta, M. Kunii, X. Hu, H. Nishiate, A. Yamamoto and M. G. Kanatzidis, J. Mater. Chem. C, 2015, 3, 10401 RSC
 .
.
- A. D. LaLonde, Y. Pei and G. Jeffrey Snyder, Energy Environ. Sci., 2011, 4, 2090 RSC
 .
.
- Q. Zhang, E. K. Chere, Y. Wang, H. S. Kim, R. He, F. Cao, K. Dahal, D. Broido, G. Chen and Z. Ren, Nano Energy, 2016, 22, 572–582 CrossRef CAS
 .
.
- D. Wang, Y. Qin, S. Wang, Y. Qiu, D. Ren, Y. Xiao and L.-D. Zhao, Ann. Phys., 2019, 1900421 Search PubMed
 .
.
- G. Tan, C. C. Stoumpos, S. Wang, T. P. Bailey, L.-D. Zhao, C. Uher and M. G. Kanatzidis, Adv. Energy Mater., 2017, 7, 1700099 CrossRef
 .
.
- J. Zhang, D. Wu, D. He, D. Feng, M. Yin, X. Qin and J. He, Adv. Mater., 2017, 29, 1703148 CrossRef PubMed
 .
.
- K. Ahn, M.-K. Han, J. He, J. Androulakis, S. Ballikaya, C. Uher, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2010, 132, 5227–5235 CrossRef CAS PubMed
 .
.
- K. F. Hsu, S. Loo and F. Guo, Science, 2004, 303, 818–821 CrossRef CAS PubMed
 .
.
- Y. Zhong, J. Tang, H. Liu, Z. Chen, L. Lin, D. Ren, B. Liu and R. Ang, ACS Appl. Mater. Interfaces, 2020, 12, 49323–49334 CrossRef CAS PubMed
 .
.
- J. Androulakis, C.-H. Lin, H.-J. Kong, C. Uher, C.-I. Wu, T. Hogan, B. A. Cook, T. Caillat, K. M. Paraskevopoulos and M. G. Kanatzidis, J. Am. Chem. Soc., 2007, 129, 9780 CrossRef CAS PubMed
 .
.
- M. H. Lee, J. H. Yun, G. Kim, J. E. Lee, S.-D. Park, H. Reith, G. Schierning, K. Nielsch, W. Ko, A.-P. Li and J.-S. Rhyee, ACS Nano, 2019, 13, 3806–3815 CrossRef CAS PubMed
 .
.
- Y. Pei, N. A. Heinz, A. LaLonde and G. J. Snyder, Energy Environ. Sci., 2011, 4, 3640–3645 RSC
 .
.
- W.-D. Liu, D.-Z. Wang, Q. Liu, W. Zhou, Z. Shao and Z.-G. Chen, Adv. Energy Mater., 2020, 10, 2000367 CrossRef CAS
 .
.
- J. Li, X. Zhang, X. Wang, Z. Bu, L. Zheng, B. Zhou, F. Xiong, Y. Chen and Y. Pei, J. Am. Chem. Soc., 2018, 140, 16190–16197 CrossRef CAS PubMed
 .
.
- X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, Joule, 2020, 4, 986–1003 CrossRef CAS
 .
.
- S. Perumal, S. Roychowdhury and K. Biswas, J. Mater. Chem. C, 2016, 4, 7520–7536 RSC
 .
.
- E. Hazan, N. Madar, M. Parag, V. Casian, O. Ben-Yehuda and Y. Gelbstein, Effective Electronic Mechanisms for Optimizing the Thermoelectric Properties of GeTe-Rich Alloys, Adv. Electron. Mater., 2015, 1, 1500228 CrossRef
 .
.
- M. Hong, M. Li, Y. Wang, X.-L. Shi and Z.-G. Chen, Adv. Mater., 2023, 35, 2208272 CrossRef CAS PubMed
 .
.
- M. Hong, J. Zou and Z.-G. Chen, Thermoelectric GeTe with Diverse Degrees of Freedom Having Secured Superhigh Performance, Adv. Mater., 2019, 31, 1807071 CrossRef PubMed
 .
.
- T. Chatterji, C. M. N. Kumar and U. D. Wdowik, Phys. Rev. B, 2015, 91, 054110 CrossRef
 .
.
- U. V. Waghmare, N. A. Spaldin, H. C. Kandpal and R. Seshadri, Phys. Rev. B, 2003, 67, 125111 CrossRef
 .
.
- M. Hong, Z.-G. Chen, L. Yang, Y.-C. Zou, M. S. Dargusch, H. Wang and J. Zou, Adv. Mater., 2018, 30, 1705942 CrossRef PubMed
 .
.
- P. Gorai, P. Parilla, E. S. Toberer and V. Stevanović, Chem. Mater., 2015, 27, 6213–6221 CrossRef CAS
 .
.
- J. Li, Z. Chen, X. Zhang, H. Yu, Z. Wu, H. Xie, Y. Chen and Y. Pei, Adv. Sci., 2017, 4, 1700341 CrossRef PubMed
 .
.
- X. Wang, W. Xue, Z. Zhang, X. Li, L. Yin, C. Chen, B. Yu, J. Sui, F. Cao, X. Liu, J. Mao, Y. Wang, X. Lin and Q. Zhang, Stabilizing the Optimal Carrier Concentration
in Al/Sb-Codoped GeTe for High Thermoelectric Performance, ACS Appl. Mater. Interfaces, 2021, 13, 45717–45725 CrossRef CAS PubMed
 .
.
- L. Xu, G. Wu, R. Wang, Z. Yan, J. Cai, J. Yang, X. Wang, J. Luo, X. Tan, G. Liu and J. Jiang, ACS Appl. Mater. Interfaces, 2022, 14, 14359–14366 CrossRef CAS PubMed
 .
.
- A. Suwardi, J. Cao, Y. Zhao, J. Wu, S. W. Chien, X. Y. Tan, L. Hu, X. Wang, W. Wang, D. Li, Y. Yin, W.-X. Zhou, D. V. M. Repaka, J. Chen, Y. Zheng, Q. Yan, G. Zhang and J. Xu, Mater. Today Phys., 2020, 14, 100239 CrossRef
 .
.
- Y. Jin, Y. Xiao, D. Wang, Z. Huang, Y. Qiu and L.-D. Zhao, ACS Appl. Energy Mater., 2019, 2, 7594–7601 CrossRef CAS
 .
.
- J. Dong, J. Gao and Q. Yan, Mater. Lab., 2023, 2, 230001 Search PubMed
 .
.
- Y. F. Ye, Q. Wang, J. Lu, C. T. Liu and Y. Yang, Mater. Today, 2016, 19, 349–362 CrossRef CAS
 .
.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS
 .
.
- Y. Zhang, T. T. Zuo, Z. Tang, M. C. Gao, K. A. Dahmen, P. K. Liaw and Z. P. Lu, Prog. Mater. Sci., 2014, 61, 1–93 CrossRef CAS
 .
.
- D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448–511 CrossRef CAS
 .
.
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS
 .
.
-
B. S. Murty, J. W. Yeh and S. Ranganathan, High-Entropy Alloys, Butterworth-Heinemann, London, 2014 Search PubMed
 .
.
- B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213 CrossRef
 .
.
- X. Chang, M. Zeng, K. Liu and L. Fu, Adv. Mater., 2020, 32, 1907226 CrossRef CAS PubMed
 .
.
- D. K. Aswal, R. Basu and A. Singh, Energy Convers. Manage., 2016, 114, 50–67 CrossRef
 .
.
- L. Hu, Y. Zhang, H. Wu, J. Li, Y. Li, M. Mckenna, J. He, F. Liu, S. J. Pennycook and X. Zeng, Adv. Energy Mater., 2018, 8, 1802116 CrossRef
 .
.
- M. A. Buckingham, B. Ward-O’Brien, W. Xiao, Y. Li, J. Qu and D. J. Lewis, Chem. Commun., 2022, 58, 8025–8037 RSC
 .
.
- R. Z. Zhang, F. Gucci, H. Zhu, K. Chen and M. J. Reece, Inorg. Chem., 2018, 57, 13027–13033 CrossRef CAS PubMed
 .
.
- J.-Y. Liu, L. Chen and L.-M. Wu, Nat. Commun., 2022, 13, 2966 CrossRef CAS PubMed
 .
.
- R. Chen, P. Qiu, B. Jiang, P. Hu, Y. Zhang, J. Yang, R. X. Shi and L. Chen, J. Mater. Chem. A, 2018, 6, 6493–6502 RSC
 .
.
- C. R. McCormick and R. E. Schaak, J. Am. Chem. Soc., 2021, 143, 1017–1023 CrossRef CAS PubMed
 .
.
- J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 2, 976–987 CrossRef CAS
 .
.
- M. Hong, K. Zheng, W. Lyv, M. Li, X. Qu, Q. Sun, S. Xu, J. Zou and Z.-G. Chen, Energy Environ. Sci., 2020, 13, 1856–1864 RSC
 .
.
- M. Hong and Z.-G. Chen, Acc. Chem. Res., 2022, 55, 3178–3190 CrossRef CAS PubMed
 .
.
- N. Man, J. Cai, Z. Guo, G. Liu, P. Sun, H. Wang, Q. Zhang, X. Tan, Y. Yin and J. Jiang, ACS Appl. Energy Mater., 2021, 4, 4242–4247 CrossRef CAS
 .
.
- Z. Liu, J. Sun, J. Mao, H. Zhu, W. Ren, J. Zhou, Z. Wang, D. J. Singh, J. Sui, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5332 CrossRef CAS PubMed
 .
.
- S. Perumal, M. Samanta, T. Ghosh, U. S. Shenoy, A. K. Bohra, S. Bhattacharya, A. Singh, U. V. Waghmare and K. Biswas, Joule, 2019, 3, 2565–2580 CrossRef CAS
 .
.
- Y. Jin, D. Wang, Y. Qiu and L.-D. Zhao, J. Mater. Chem. C, 2021, 9, 6484–6490 RSC
 .
.
- M. Hong, Y. Wang, T. Feng, Q. Sun, S. Xu, S. Matsumura, S. T. Pantelides, J. Zou and Z.-G. Chen, J. Am. Chem. Soc., 2019, 141, 1742–1748 CrossRef CAS PubMed
 .
.
- E. Nshimyimana, S. Hao, X. Su, C. Zhang, W. Liu, Y. Yan, C. Uher, C. Wolverton, M. G. Kanatzidis and X. Tang, J. Mater. Chem. A, 2020, 8, 1193–1204 RSC
 .
.
- M. Hong, Y. Wang, W. Liu, S. Matsumura, H. Wang, J. Zou and Z.-G. Chen, Adv. Energy Mater., 2018, 8, 1801837 CrossRef
 .
.
- A. Suwardi, J. Cao, L. Hu, F. Wei, J. Wu, Y. Zhao, S. H. Lim, L. Yang, X. Y. Tan, S. W. Chien, Y. Yin, W.-X. Zhou, W. L. M. Nancy, X. Wang, S. H. Lim, X. Ni, D. Li, Q. Yan, Y. Zheng, G. Zhang and J. Xu, J. Mater. Chem. A, 2020, 8, 18880–18890 RSC
 .
.
- A.-C. Yeh, S. Gorsse, V. Keppens and D. A. Gilbert, APL Mater., 2023, 11, 030402 CrossRef CAS
 .
.
- X. Wang, W. Guo and Y. Fu, J. Mater. Chem. A, 2021, 9, 663–701 RSC
 .
.
- R. Chen, Y. Yan, W. Zhang, F. Liu, H. Kang, E. Guo, Z. Chen and T. Wang, Chem. Mater., 2023, 35, 2202–2212 CrossRef CAS
 .
.
- Z. Lei, X. Liu, H. Wang, Y. Wu, S. Jiang and Z. Lu, Scr. Mater., 2019, 165, 164–169 CrossRef CAS
 .
.
- Y. Zhang, Y. J. Zhou, J. P. Lin, G. L. Chen and P. K. Liaw, Adv. Eng. Mater., 2008, 10, 534–538 CrossRef CAS
 .
.
- B. Jiang, Y. Yu, H. Chen, J. Cui, X. Liu, L. Xie and J. He, Nat. Commun., 2021, 12, 3234 CrossRef CAS PubMed
 .
.
- A. Ruffa, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 5895 CrossRef CAS
 .
.
- C. A. Gearhart, Am. J. Phys., 1990, 58, 468–480 CrossRef
 .
.
- R. Basu, S. Bhattacharya, R. Bhatt, M. Roy, S. Ahmad, A. Singh, M. Navaneethan, Y. Hayakawa, D. K. Aswal and S. K. Gupta, J. Mater. Chem. A, 2014, 2, 6922–6930 RSC
 .
.
- R. Basu and A. Singh, Mater. Today Phys., 2021, 21, 100468 CrossRef CAS
 .
.
- S. Ahmad, R. Basu, P. Sarkar, A. Singh, A. Bohra, S. Bhattacharya, R. Bhatt, K. N. Meshram, S. Samanta, P. Bhatt, M. Navaneethan, Y. Hayakawa, A. K. Debnath, S. K. Gupta, D. K. Aswal, K. P. Muthe and S. C. Gadkari, Materialia, 2018, 4, 147–156 CrossRef CAS
 .
.
- A. K. Bohra, R. Bhatt, A. Singh, S. Bhattacharya, R. Basu, P. Bhatt, M. Navaneethan, S. K. Sarkar, S. Anwar, K. P. Muthe and D. K. Aswal, Phys. Status Solidi RRL, 2020, 14, 2000102 CrossRef CAS
 .
.
- S. Bhattacharya, R. Basu, R. Bhatt, S. Pitale, A. Singh, D. K. Aswal, S. K. Gupta, M. Navaneethan and Y. Hayakawa, J. Mater. Chem. A, 2013, 1, 11289–11294 RSC
 .
.
- S. Bhattacharya, A. Bohra, R. Basu, R. Bhatt, S. Ahmad, K. N. Meshram, A. K. Debnath, A. Singh, S. K. Sarkar, M. Navneethan, Y. Hayakawa, D. K. Aswal and S. K. Gupta, J. Mater. Chem. A, 2014, 2, 17122–17129 RSC
 .
.
- Z. Dong, J. Luo, C. Wang, Y. Jiang, S. Tan, Y. Zhang, Y. Grin, Z. Yu, K. Guo, J. Zhang and W. Zhang, Nat. Commun., 2022, 13, 35 CrossRef PubMed
 .
.
- H. Zhu, W. Li, A. Nozariasbmarz, N. Liu, Y. Zhang, S. Priya and B. Poudel, Nat. Commun., 2023, 14, 3300 CrossRef CAS PubMed
 .
.
- S. M. Kauzlarich, S. R. Brown and G. J. Snyder, Dalton Trans., 2007, 2099–2107 RSC
 .
.
- J. Shuai, J. Mao, S. Song, Q. Zhang, G. Chen and Z. Ren, Mater. Today Phys., 2017, 1, 74–95 CrossRef
 .
.
- Y. Xing, R. Liu, J. Liao, C. Wang, Q. Zhang, Q. Song, X. Xia, T. Zhu, S. Bai and L. Chen, Joule, 2020, 4, 2475–2483 CrossRef CAS
 .
.
- S. K. Sahu, A. K. Bohra, P. G. Abichandani, A. Singh, S. Bhattacharya, R. Bhatt, R. Basu, P. Sarkar, S. K. Gupta, K. P. Muthe and S. C. Gadkari, Design and development of DC to DC voltage booster to integrate with PbTe/TAGS-85 based thermoelectric power generators, Mater, Sci. Energy Tech., 2019, 2, 429–433 Search PubMed
 .
.
- B. Zhu, X. Liu, Q. Wang, Y. Qiu, Z. Shu, Z. Guo, Y. Tong, J. Cui, M. Guc and J. He, Energy Environ. Sci., 2020, 13, 2106 RSC
 .
.
- Y. Sun, F. Guo, Y. Feng, C. Li, Y. Zou, J. Cheng, X. Dong, H. Wu, Q. Zhang, W. Liu, Z. Liu, W. Cai, Z. Ren and J. Sui, Nat. Commun., 2023, 14, 8085 CrossRef CAS PubMed
 .
.
- Q. Shi, J. Li, X. Zhao, Y. Chen, F. Zhang, Y. Zhong and R. Ang, ACS Appl. Mater. Interfaces, 2022, 14, 49425–49445 CrossRef CAS PubMed
 .
.
- S. Y. Tee, D. Ponsford, C. L. Lay, X. Wang, X. Wang, D. C. J. Neo, T. Wu, W. Thitsartarn, J. C. C. Yeo, G. Guan, T.-C. Lee and M.-Y. Han, Adv. Sci., 2022, 9, 2204624 CrossRef CAS PubMed
 .
.
- H. Wu, X.-L. Shi, J. Duan, Q. Liu and Z.-G. Chen, Energy Environ. Sci., 2023, 16, 1870–1906 RSC
 .
.
- S. Huang, T.-R. Wei, H. Chen, J. Xiao, M. Zhu, K. Zhao and X. Shi, ACS Appl. Mater. Interfaces, 2021, 13, 60192–60199 CrossRef CAS PubMed
 .
.
- N. Jakhar, D. K. Kedia, A. Kumar, K. Saurabh and S. Singh, Appl. Phys. Lett., 2023, 122, 163901 CrossRef CAS
 .
.
- J. Zhang, M. Nisar, H. Xu, F. Li, Z. Zheng, G. Liang, P. Fan and Y.-X. Chen, ACS Appl. Mater. Interfaces, 2023, 15, 47158–47167 CrossRef CAS PubMed
 .
.
- T.-R. Wei, P. Qiu, K. Zhao, X. Shi and L. Chen, Adv. Mater., 2023, 35, 2110236 CrossRef CAS PubMed
 .
.
- J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2019, 31, 1806280 CrossRef PubMed
 .
.
- M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777 CrossRef PubMed
 .
.
- Y. Yu, M. Cagnoni, O. Cojocaru-Mirédin and M. Wuttig, Adv. Funct. Mater., 2020, 30, 1904862 CrossRef CAS
 .
.
- I. Maria, R. Arora, M. Dutta, S. Roychowdhury, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2023, 145, 9292–9303 CrossRef CAS PubMed
 .
.
- R. Basu, C. Nayak, R. Kumar, D. Bhattacharyya, S. N. Jha and A. Singh, ACS Appl. Energy Mater., 2023, 6(5), 2981–2988 CrossRef CAS
 .
.
- W. Zhang, H. Zhang, S. Sun, X. Wang, Z. Lu, X. Wang, J.-J. Wang, C. Jia, C.-F. Schön, R. Mazzarello, E. Ma and M. Wuttig, Adv. Sci., 2023, 10, 2300901 CrossRef CAS PubMed
 .
.
- S. Li, X. Li, Z. Ren and Q. Zhang, J. Mater. Chem. A, 2018, 6, 2432–2448 RSC
 .
.
- M. Zhou, G. J. Snyder, L. Li and L.-D. Zhao, Inorg. Chem. Front., 2016, 3, 1449–1463 RSC
 .
.
- A. Banik, S. Roychowdhury and K. Biswas, Chem. Commun., 2018, 54, 6573–6590 RSC
 .
.
- M. K. Brod, M. Y. Toriyama and G. J. Snyder, Chem. Mater., 2020, 32, 9771–9779 CrossRef CAS
 .
.
- S. Roychowdhury, M. Samanta, S. Perumal and K. Biswas, Chem. Mater., 2018, 30, 5799–5813 CrossRef CAS
 .
.
- C. Wang, Z. Zeng, Y. Chen, J. Wu, J. Ma, J. Embs, Y. Pei and Y. Chen, npj Comput. Mater., 2021, 7, 118 CrossRef CAS
 .
.
- M. Li, M. Hong, X. Tang, Q. Sun, W.-Y. Lyu, S.-D. Xu, L.-Z. Kou, M. Dargusch, J. Zou and Z.-G. Chen, Nano Energy, 2020, 73, 104740 CrossRef CAS
 .
.
- A. Suwardi, D. Bash, H. K. Ng, J. R. Gomez, D. V. M. Repaka, P. Kumara and K. Hippalgaonkar, J. Mater. Chem. A, 2019, 7, 23762–23769 RSC
 .
.
- W. Li and M. Liu, ACS Appl. Electron. Mater., 2023, 5, 4523–4533 CrossRef CAS
 .
.
- A. Li, C. Hu, B. He, M. Yao, C. Fu, Y. Wang, X. Zhao, C. Felser and T. Zhu, Nat. Commun., 2021, 12, 5408 CrossRef CAS PubMed
 .
.
- N. Wang, M. Li, H. Xiao, Z. Gao, Z. Liu, X. Zu, S. Li and L. Qiao, npj Comput. Mater., 2021, 7, 18 CrossRef CAS
 .
.
- H. Namiki, M. Kobayashi, K. Nagata, Y. Saito, N. Tachibana and Y. Ota, Mater. Today Sustainable, 2022, 18, 100116 CrossRef
 .
.
- B. Jiang, W. Wang, S. Liu, Y. Wang, C. Wang, Y. Chen, L. Xie, M. Huang and J. He, Science, 2022, 377, 208–213 CrossRef CAS PubMed
 .
.
- S. Roychowdhury and K. Biswas, Slight Symmetry Reduction in Thermoelectrics, Chem, 2018, 4, 939–942 CAS
 .
.
- S. S. Aamlid, M. Oudah, J. Rottler and A. M. Hallas, J. Am. Chem. Soc., 2023, 145, 5991–6006 CrossRef CAS PubMed
 .
.
- R. Basu, S. Mandava, U. S. Shenoy, D. K. Bhat, B. Khasimsaheb, A. K. Debnath, A. Singh and S. Neeleshwar, Mater. Adv., 2021, 2, 7891–7906 RSC
 .
.
- W.-Y. Ching, S. San, J. Brechtl, R. Sakidja, M. Zhang and P. K. Liaw, npj Comput. Mater., 2020, 6, 45 CrossRef CAS
 .
.
- Y. Jiang, J. Dong, H.-L. Zhuang, J. Yu, B. Su, H. Li, J. Pei, F.-H. Sun, M. Zhou, H. Hu, J.-W. Li, Z. Han, B.-P. Zhang, T. Mori and J.-F. Li, Nat. Commun., 2022, 13, 6087 CrossRef CAS PubMed
 .
.
- B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371, 830–834 CrossRef CAS PubMed
 .
.
- M. Liu, J. Zhu, B. Cui, F. Guo, Z. Liu, Y. Zhu, M. Guo, Y. Sun, Q. Zhang, Y. Zhang, W. Cai and J. Sui, Cell Rep. Phys. Sci., 2022, 3, 100902 CrossRef CAS
 .
.
- M. J. Smiles, J. M. Skelton, H. Shiel, L. A. H. Jones, J. E. N. Swallow, H. J. Edwards, P. A. E. Murgatroyd, T. J. Featherstone, P. K. Thakur, T.-L. Lee, V. R. Dhanak and T. D. Veal, J. Mater. Chem. A, 2021, 9, 22440–22452 RSC
 .
.
- Y. Qiu, Y. Jin, D. Wang, M. Guan, W. He, S. Peng, R. Liu, X. Gao and L.-D. Zhao, J. Mater. Chem. A, 2019, 7, 26393–26401 RSC
 .
.
- A. Das, P. Acharyya, S. Das and K. Biswas, J. Mater. Chem. A, 2023, 11, 12793–12801 RSC
 .
.
- Z. Tian, ACS Nano, 2019, 13, 3750–3753 CrossRef CAS PubMed
 .
.
- S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Science, 2021, 371, 722–727 CrossRef CAS PubMed
 .
.
- M. T. Agne, F. R. L. Lange, J. P. Male, K. S. Siegert, H. Volker,C. Poltorak, A. Poitz, T. Siegrist, S. Maier, G. J. Snyder and M. Wuttig, Matter, 2021, 4, 2970–2984 CrossRef CAS
 .
.
- K. Yamamoto, A. Aharony, O. Entin-Wohlman and N. Hatano, Phys. Rev. B, 2017, 96, 155201 CrossRef
 .
.
- E. M. Levin, M. F. Besser and R. Hanus, J. Appl. Phys., 2013, 114, 083713 CrossRef
 .
.
- D. Di Sante, P. Barone, R. Bertacco and S. Picozzi, Adv. Mater., 2013, 25, 509–513 CrossRef CAS PubMed
 .
.
- Z. Bu, X. Zhang, B. Shan, J. Tang, H. Liu, Z. Chen, S. Lin, W. Li and Y. Pei, Sci. Adv., 2021, 7, 2738 CrossRef PubMed
 .
.
- R. H. Liu, H. Y. Chen, K. P. Zhao, Y. T. Qin, B. B. Jiang, T. S. Zhang, G. Sha, X. Shi, C. Uher, W. Q. Zhang and L. D. Chen, Adv. Mater., 2017, 29, 1702712 CrossRef PubMed
 .
.
- S. Zhi, J. Li, L. Hu, J. Li, N. Li, H. Wu, F. Liu, C. Zhang, W. Ao, H. Xie, X. Zhao, S. J. Pennycook and T. Zhu, Adv. Sci., 2021, 8, 2100220 CrossRef CAS PubMed
 .
.
- C. Xu, Z. Liang, W. Ren, S. Song, F. Zhang and Z. Ren, Adv. Energy Mater., 2022, 12, 2202392 CrossRef CAS
 .
.
- M. Zhang, Z. Gao, Q. Lou, Q. Zhu, J. Wang, Z. Han, C. Fu and T. Zhu, Adv. Funct. Mater., 2023, 2307864 Search PubMed
 .
.
- D.-Z. Wang, W.-D. Liu, M. Li, K. Zheng, H. Hu, L.-C. Yin, Y. Wang, H. Zhu, X.-L. Shi, X. Yang, Q. Liu and Z.-G. Chen, Adv. Funct. Mater., 2023, 33, 2213040 CrossRef CAS
 .
.
- S. Roychowdhury, T. Ghosh, R. Arora, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2018, 57, 15167 CrossRef CAS PubMed
 .
.
- Z. H. Deng, A. Olvera, J. Casamento, J. S. Lopez, L. Williams, R. Lu, G. S. Shi, P. F. P. Poudeu and E. Kioupakis, Chem. Mater., 2020, 32, 6070 CrossRef CAS
 .
.
- C. X. Zhang, C. Y. Wang, Y. C. Xie, B. Chen and C. H. Zhang, Mater. Des., 2018, 157, 394 CrossRef CAS
 .
.
- J. Tang, Z. Yao, Y. Wu, S. Lin, F. Xiong, W. Li, Y. Chen, T. Zhu and Y. Pei, Mater. Today Phys., 2020, 15, 100247 CrossRef
 .
.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab and
Ajay
Singh
ab
*ab and
Ajay
Singh
ab
 where α implies the Seebeck coefficient, σ implies the electrical conductivity, and κe and κl are the electronic and lattice thermal conductivities, respectively, at temperature T.11,12
where α implies the Seebeck coefficient, σ implies the electrical conductivity, and κe and κl are the electronic and lattice thermal conductivities, respectively, at temperature T.11,12

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, at 700 K, designated as the critical temperature. Intrinsically, GeTe is a degenerate p-type semiconductor with high hole strength. This can be attributed to the fact that during synthesis, plenty of Ge vacancies arise, which cause high carrier concentration, thus conflicting with the generally accepted optimal range.45–55 To quench the high carrier concentration, group III, IV and V elements are added at the Ge site and Se can be added at the Te site.49,56–60
m, at 700 K, designated as the critical temperature. Intrinsically, GeTe is a degenerate p-type semiconductor with high hole strength. This can be attributed to the fact that during synthesis, plenty of Ge vacancies arise, which cause high carrier concentration, thus conflicting with the generally accepted optimal range.45–55 To quench the high carrier concentration, group III, IV and V elements are added at the Ge site and Se can be added at the Te site.49,56–60




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω,
ω,
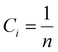 and upon substitution in eqn (3) gives:
and upon substitution in eqn (3) gives: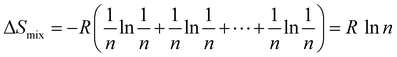

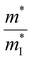 and thus makes it superior among group IV–VI chalcogenides.129–135Fig. 8(b) demonstrates that although the cubic structure (at elevated temperature) has high symmetry in comparison to the rhombohedral structure at low temperature, as far as thermoelectricity is concerned, slight symmetry breaking is preferred as it leads to high band degeneracy. In addition, the doping at the cationic site displaces Ge from the off-center and therefore the energy difference between the light (L) and heavy (Σ) valence bands reduces and subsequently aids in valence band convergence (illustrated in Fig. 8(c)). The doping at the cationic site (Fig. 8(d)) also increases the interaxial angle, the density-of-state effective mass and consequently the Seebeck coefficient.
and thus makes it superior among group IV–VI chalcogenides.129–135Fig. 8(b) demonstrates that although the cubic structure (at elevated temperature) has high symmetry in comparison to the rhombohedral structure at low temperature, as far as thermoelectricity is concerned, slight symmetry breaking is preferred as it leads to high band degeneracy. In addition, the doping at the cationic site displaces Ge from the off-center and therefore the energy difference between the light (L) and heavy (Σ) valence bands reduces and subsequently aids in valence band convergence (illustrated in Fig. 8(c)). The doping at the cationic site (Fig. 8(d)) also increases the interaxial angle, the density-of-state effective mass and consequently the Seebeck coefficient.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K), with respect to the samples sintered at 723
K), with respect to the samples sintered at 723![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, and (c) ZT value with respect to the reduced Fermi potential having different quality factors at 648
K, and (c) ZT value with respect to the reduced Fermi potential having different quality factors at 648![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. Reproduced and adapted from ref. 140 under the terms of the Creative Commons CC-BY-NC-ND license.
K. Reproduced and adapted from ref. 140 under the terms of the Creative Commons CC-BY-NC-ND license.
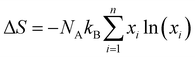 and is plotted as shown in Fig. 13(a). The addition of the species shows the increase in the ΔS value as x increases. The powder XRD pattern confirms the formation of more symmetrical crystal structures with the increased number of elements followed by the analysis (Fig. 13(b)), which reveals increase in the lattice parameter along the α-axis due to the larger atoms at the Ge site as well as the opening of the interaxial angle (Fig. 13(c)).
and is plotted as shown in Fig. 13(a). The addition of the species shows the increase in the ΔS value as x increases. The powder XRD pattern confirms the formation of more symmetrical crystal structures with the increased number of elements followed by the analysis (Fig. 13(b)), which reveals increase in the lattice parameter along the α-axis due to the larger atoms at the Ge site as well as the opening of the interaxial angle (Fig. 13(c)).






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 8
3, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 9
3 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) ratios. The 8
3) ratios. The 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 segmented module displays a significantly high conversion ratio of 13.3% at ΔT = 506 K. The high conversion efficiency is attributed to the fact of having optimized ZT in the entire range of operation (Fig. 19(e) and (f)).
3 segmented module displays a significantly high conversion ratio of 13.3% at ΔT = 506 K. The high conversion efficiency is attributed to the fact of having optimized ZT in the entire range of operation (Fig. 19(e) and (f)).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 8
3, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 9
3 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 devices. Reproduced and adapted from ref. 135. Copyright © 2022, The American Association for the Advancement of Science.
3 devices. Reproduced and adapted from ref. 135. Copyright © 2022, The American Association for the Advancement of Science.




.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


