Possibilities and limitations of convolutional neural network machine learning architectures in the characterisation of achiral orthogonal smectic liquid crystals

Abstract

Machine learning is becoming a valuable tool in the characterisation and property prediction of liquid crystals. It is thus worthwhile to be aware of the possibilities but also the limitations of current machine learning algorithms. In this study we investigated a phase sequence of isotropic – fluid smecticA – hexatic smectic B – soft crystal CrE – crystalline. This is a sequence of transitions between orthogonal phases, which are expected to be difficult to distinguish, because of only minute changes in order. As expected, strong first order transitions such as the liquid to liquid crystal transition and the crystallisation can be distinguished with high accuracy. It is shown that also the hexatic SmB to soft crystal CrE transition is clearly characterised, which represents the transition from short- to long-range order. Limitations of convolutional neural networks can be observed for the fluid to hexatic SmA to SmB transition, where both phases exhibit short-range ordering.

---

1. Introduction

Artificial neural networks, first proposed in 1943, began as an information processing model based on neurons firing in the brain.¹ The idea was first implemented in 1958 as the perceptron, an algorithm for binary classification of images.² Since then, neural networks have improved significantly, particularly due to the introduction of back-propagation and increased computing power.¹ Convolutional neural networks (CNNs) were developed specifically for image analysis or other grid-based data and have been applied successfully to automating otherwise time-intensive tasks with examples as diverse as classifying land use from satellite images³ or classifying benign and malignant masses for breast cancer diagnosis.⁴

In recent years, machine learning has shown to be quite successful in many areas of science. In physics⁵ particularly in the fields of particle physics and cosmology,⁶ but also in astronomy^7–9 or photonics.¹⁰ Another wide field of applicability of machine learning lies in various aspects of material science.¹¹ In chemistry, machine learning algorithms are employed in the computer-aided planning of synthetic work¹² and the discovery of novel drugs.¹³ In biology the techniques are used in the development of biosensors,¹⁴ and particular success of machine learning is found in various medical imaging techniques^15–17 and the image interpretation in cancer research.^18–20

With the successful implementation of machine learning in solid state physics and material science, it is not surprising that efforts have also been expanded into the fields of liquid crystals (LCs) and soft matter in general.^21–23 Naturally, the prediction of liquid crystalline behaviour and phase transitions, particularly that from the isotropic liquid to the nematic liquid crystal phase were of paramount importance in the beginning of the use of machine learning methodologies in liquid crystals.^24–27 At this stage investigations were often carried out on thermotropic LCs with computer generated Schlieren textures, but sometimes also with experimental textures. This work is to a large extent connected to the identification of topological defects in experimental²⁸ and simulated nematic textures,²⁹ thus related to object recognition.³⁰ Closely relating to this is an investigation of machine learning detection of bubbles and islands in free-standing smectic films,³¹ and work on active nematics relating to hydrodynamics.³²

Further machine learning studies were connected to theoretical predictions of the molecular ordering of binary mixtures of molecules with different length,³³ the self-assembled nanostructures of lyotropic liquid crystals,³⁴ and the local structure of liquid crystalline polymers.³⁵ An aspect which is now gaining momentum is the use of machine learning in the prediction of physical properties. This has for example been demonstrated for the dielectric properties of a nematic LC through a comparison of the experimental and predicted values.³⁶ Another example is the prediction of elastic constants in relation to experimental and simulated curves.³⁷ Also melting temperatures have been shown to be predictable,³⁸ as has structural colour, i.e. selective reflection in formulation space,³⁹ or minimisation of threshold voltages in ZnO doped liquid crystals.⁴⁰

In terms of applications, where machine learning is used as a methodology for readout, one needs to mention various sensors, which were first introduced by the group of Abbott.^41,42 The readout mechanism is based on texture transitions when a liquid crystal responds to molecules changing the orientation from homeotropic to planar or vice versa. The concept was applied to biochemical sensors, detecting endotoxins from different bacterial species,⁴³ or SARS-CoV-2.⁴⁴ Similarly, gases⁴⁵ and gas mixtures⁴⁶ can be detected. A recent review of biochemical sensors on the basis of liquid crystals can be found in ref. 47.

In recent years we have demonstrated that not only binary classification tasks between two individual liquid crystal phases can be predicted with very high accuracy close to 100%,⁴⁸ but that also more complicated multiphase tasks such as distinguishing between isotropic, orientationally ordered, fluid smectic, hexatic smectic and soft crystal phases can be achieved.⁴⁸ This includes the characterisation of phase transitions⁴⁹ and also the distinction between different smectic subphases; ferroelectric, ferrielectric and antiferroelectric phases by their textures.⁵⁰

2. Methodology

At this point we do not want to repeat the basic formalism of machine learning and refer to some previous papers^48–50 where this is discussed in detail, together with a publication where different supervised machine learning architectures are tested with respect to regularization, training epochs, overfitting, and number of layers.⁵¹

2.1. Convolution

Convolutional layers are an effective way of reducing the number of parameters required in the network when the input data is large and grid-based. A tensor (kernel) of chosen width and height (smaller than the input), where the values are trainable parameters, is moved over the whole image with a chosen step size (stride). At each step, the aligned kernel and grid values are multiplied and summed, resulting in a feature map showing where in the input image areas similar to the kernel can be found. At each layer, multiple feature maps are output, increasing the number of channels from the input layer (which has only one channel for a greyscale image). The kernel for each subsequent layer then has a depth equal to the number of channels input to that layer.

Generally, each convolutional layer is followed by a pooling layer which reduces the height and width (but not the number of channels) of the input. Again, a kernel is passed over all the data but, rather than having trainable parameters, it outputs either the average (average pooling) or maximum value (max pooling) of the area of the grid it covers.

2.2. Regularization

A common problem in training neural networks is overfitting, where the network exactly fits to training data, learning features that cannot be generalised to new unseen examples. One way to prevent this is by increasing the size of the training sample. This is not always possible, so that other methods must be used.

Reducing the number of parameters in the model can prevent the network from having the capacity to overfit. However, if reduced too much, this can lead to underfitting (meaning the model is inaccurate when evaluated on both the training and unseen data). Dropout regularization involves randomly removing nodes from the network with a given probability (the dropout rate), to prevent the network from relying on any one input or feature.⁵² The model will require more epochs to train. This method is generally applied to fully connected layers, but not convolutional layers. Data augmentation is a method of artificially increasing the size of the training set. For images, this can involve rotations, translations, shears, flips, or changes to brightness or contrast. The final method used is batch normalization. This prevents overfitting⁵³ as well as accelerating training.⁵⁴

2.3. Architectures

Two types of convolutional neural network (CNN) models were employed, based on their performance in classifying LC phases. The ReLU activation function is applied in all layers except the output, where the softmax activation function is used. All convolutional layers have a stride of 1 × 1. Categorical cross-entropy is used as the loss function and Adam as the optimization algorithm.

The sequential model consists of several convolutional layers, each implementing the convolution operation described above, with a kernel size of 3 × 3 and a max pooling operation with kernel size 2 × 2. These are followed by global average pooling (where the pool size is equal to the input size) followed by several dense (fully connected) layers. Each convolutional layer has batch normalization applied and the number of channels is doubled at each layer. Dropout is applied after each dense layer and the number of nodes is halved at each layer. L2 regularization with λ = 0.001 is applied to all convolutional and dense layers. An example sequential CNN architecture is shown in Fig. 1. In each case, the number of channels in the final convolutional layer is equal to the number of nodes in the first dense layer.

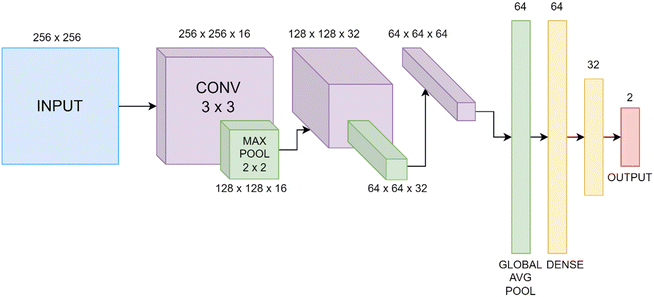Fig. 1 Example sequential CNN architecture, including layer output dimensions. “CONV” represents a 3 × 3 convolutional layer and “MAX POOL” and “GLOBAL AVG POOL” maximum and global average pooling.

The inception model was introduced to decrease the computational cost of a CNN, by running several convolutions in parallel. The InceptionV3 network has 2.39 × 10⁷ trainable parameters, making it too large for the dataset used here, hence likely to overfit.⁵⁵ Therefore, a simplified version is used, using the stem (first section of the network), shown in Fig. 2(a), and a number of inception modules, shown in Fig. 2(b). Each of these inception modules consist of an arrangement of parallel convolution and max pooling layers, using kernel sizes of 1 × 1, 3 × 3 and 5 × 5. These are followed by a global average pooling layer, then several dense layers, with the number of nodes halving at each one (similarly to the sequential model). Again, batch normalization is applied after each convolutional layer and dropout is applied after each dense layer. L2 regularization is applied to all convolutional and dense layers with λ = 0.001.

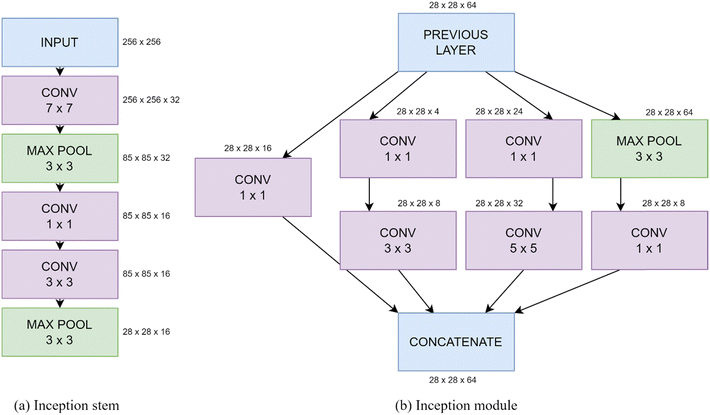Fig. 2 Schematics of an example (a) inception stem and (b) module showing the kernel sizes of each convolutional and pooling layer.

2.4. Tuning hyperparameters

The models were built, trained, and tested using Keras and Tensorflow libraries with GPUs provided by Google Colaboratory. Each model was adjusted in order to achieve the highest validation accuracy, which was then tested on the test dataset. In each case, the number of convolutional layers (or inception modules), dense layers, channels, learning rate, batch size, and dropout rate were varied. These variables are known as hyperparameters. The models were monitored during training by plotting the accuracy and loss of both the training and validation datasets at each epoch. For a successful model, both the training and validation curves should be similar with the accuracy reaching a plateau when its maximum is achieved. The number of epochs each model ran for was chosen to be slightly above when this plateau was reached. The model was then saved at the epoch with the highest validation accuracy and tested.

In order to find the optimum hyperparameter values, the number of layers and channels was first set to low values, then increased incrementally until overfitting was seen (diagnosed by a large gap between the test and validation curves). Batch size and learning rate were varied to find the combination giving the highest validation and test accuracy. Each model was trained and tested three times to find the mean and standard deviation of the test set accuracy. The uncertainty due to the finite size of the test dataset is negligible.

3. Experimental

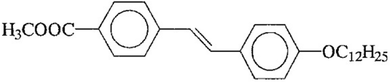
The mesogen used in this study, 4-dodecyloxy-4′-carboxymethyl-trans-stilbene, is abbreviated as 12 Me:
and has a phase sequence of: Cryst 132 CrE 154 SmB 161 SmA 166 Iso.⁵⁶ Temperatures are given in degrees Celsius.

The material was observed in self-constructed sandwich cells of thickness d = 10 μm made from glass substrates which were cleaned with acetone but otherwise left untreated, thus without ITO or alignment layers applied. The cells were placed in a hot stage (Linkam LTSE350) with temperature control (Linkam TP94) of relative temperatures to 0.1 K accuracy. The cell was filled by capillary action in the isotropic phase and texture transitions followed via video recording during phase transitions in a polarizing microscope (Leica Optipol) between crossed polarisers at a frame rate of 10 fps at a resolution of 2048 × 1088 pixels (UI-3360CP-C-HQ, uEye Gigabit Ethernet).

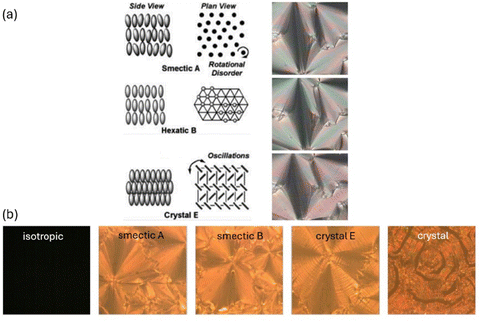
The thermotropic achiral liquid crystal phases investigated can be placed broadly into three categories, the fluid smectic SmA phase, the hexatic smectic SmB phase and the soft crystal CrE (SmE) phase (Fig. 3(a)). These are framed at elevated temperatures by the disordered isotropic liquid and at low temperatures by the three dimensionally ordered crystal (Fig. 3(b)).

Fig. 3 (a) Structures of the liquid crystal phases investigated. Staring from elevated temperatures the fluid SmA phase exhibits free rotational freedom of the long axis and isotropic order when looked onto a smectic layer. In contrast, the hexatic SmB phase locally exhibits hexatic bond orientational order, while the soft crystal SmE (CrE) phase is three dimensionally ordered. (b) Illustrates textures of the five phases investigated by machine learning.

All of the liquid crystal phases belong to the orthogonal type, thus with the molecular long axis on average being parallel to the smectic layer normal. The fluid SmA as well as the hexatic SmB phase exhibit fan-shaped textures which appear very similar to each other and can hardly be distinguished in polarizing microscopy. The soft crystal SmE phase in contrast exhibits a typical striation across the fans, while in the crystalline phase cracks appear in the structure.

Individual images of the videos were frame grabbed at each phase transition using VLC media player. Each video was taken over a known temperature range, across a transition where textures clearly changed, allowing them to be labelled with their phase based on whether they occurred before or after the transition. Videos of 30 heating and 30 cooling cycles were taken, each over the same temperature range at the same rate of temperature change. Training, validation and testing datasets were created with an approximate ratio of 70 : 15 : 15, with the validation data set being used to monitor underfitting and overfitting during training.

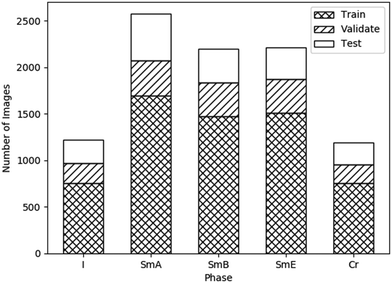
Data leakage is a problem whereby the accuracy of the model is overestimated due to overly similar data in the testing and training sets. In order to prevent this, the videos were split between datasets (rather than the images) so that images from the same video were not split between datasets. Each image initially had a size of 2048 × 1088 pixels. These were split into 6 images each, cropped and scaled to a resolution of 256 × 256 pixels, and converted to greyscale, such that each pixel had a value between 0 and 1. The dataset was augmented by flipping each image vertically and horizontally. Fig. 4 shows the number of images of each phase in each dataset.

Fig. 4 Number of available images, after augmentation, for the disordered isotropic, fluid SmA, hexatic SmB, soft crystal SmE and crystalline phase. Also indicated are the ratios of these images used for training, validation and testing, roughly 70%: 15%: 15%, respectively.

4. Results

4.1. Augmentations

Before applying the models, various data augmentations were tested. These augmentations were tested on the SmB to SmE transition using the sequential model. All images in the datasets were flipped horizontally and vertically in order to provide large enough dataset sizes to train the networks. However, further augmentations can also be applied to reduce overfitting. These augmentations are applied randomly to images during the training of each batch, implying that the dataset size does not increase. The following augmentations were tested.

The brightness of each image was adjusted by a random value between −0.2 and +0.2, with this value being added to each pixel value. The contrast of each image was adjusted by a random contrast factor, γ, between −0.2 and 0.2. For a pixel value x in an image with a mean pixel value μ, this adjusts the pixel value to x → (x − μ) γ − μ. Finally, each image was rotated by a random angle between −0.2π and +0.2π rad. Areas outside the regions filled by the input through reflecting the image across the boundary. Each augmentation was tested on two models, both of which used a learning rate of 10⁻⁴, a batch size of 16, and a dropout rate of 0.5. The remaining hyperparameters are specified in Table 1.

Table 1 Details of the architecture of the two models employed to test the influence of augmentations on the test accuracy

Hyperparameter	Model 1	Model 2
Convolutional layers	4	5
Starting channels	8	16
Dense layers	2	3

---

The test accuracies of each of these models, with each augmentation applied, are displayed in Fig. 5. The rotation augmentation clearly decreased the accuracy significantly. The training accuracy reached 96.2% and 97.6% for each model respectively, showing severe overfitting. This is likely due to the image being reflected into the unfilled regions. As the augmentations are only applied to the training set, the network may have then been unable to generalise the learned features to the unseen images without any reflections.

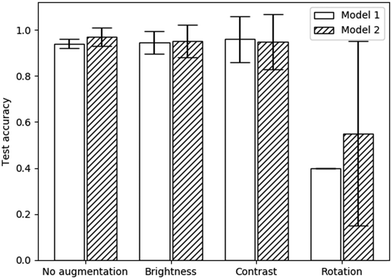Fig. 5 Test accuracies with various augmentations applied to each model specified in Table 1. Error bars represent 95% confidence intervals.

Both the brightness and contrast augmentations produced no significant change in the test accuracy when compared to a lack of augmentations. Brightness and contrast augmentations also resulted in higher uncertainties as well as requiring more epochs to train (25 rather than 20). Therefore, no augmentations were used (except for the previously applied flips) in any subsequent models. Although these augmentations were only tested on two model architectures, the results are likely generalisable to other models as well because the augmentations are applied before each batch is trained. It can also be assumed that these results would be applicable to the other phase transitions used in this study due to the similarity in the structures of each texture (see Fig. 3).

4.2. Binary classifiers

4.2.1. Isotropic to SmA transition. The first binary classification task is to differentiate between the Isotropic and the SmA phase, which, due to the simplicity of the isotropic texture can be expected to be achieved at extremely high accuracy. The hyperparameters and results for the sequential and inception model are given in Table 2 and the confusion matrices of Fig. 6(a) and (b), respectively.

Table 2 Architecture details and test accuracies for the sequential and the inception model, optimised for the Iso to SmA transition datasets

I to SmA	Sequential model	Inception model
Convolutional layers	1	NA
Inception modules	NA	1
Starting channels	16	4
Dense layers	2	2
Batch size	16	16
Learning rate	1 × 10^−4	5 × 10^−5
Dropout rate	0.5	0.5
Trainable parameters	650	2402
Test accuracy	1 ± 0	1 ± 0

---

Fig. 6 Confusion matrices for (a) the sequential and (b) the inception model, displaying the probability of a sample from each true phase being assigned a particular predicted phase. The error is calculated as the standard error over three runs of the model.

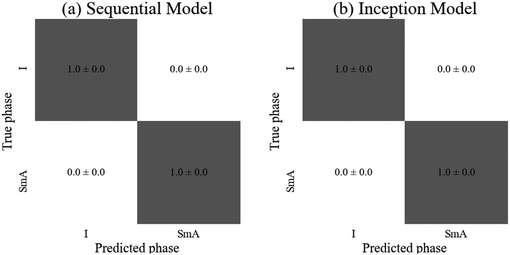
Both models achieved (100 ± 0)% accuracy. As presented in Fig. 4, there are approximately twice as many images in the SmA dataset than in the Iso dataset which could have introduced bias in the network, with Iso images being incorrectly classified as SmA. However, this was clearly not the case, due to the uniformity of the texture of the isotropic phase. This implies that there were no features of the Iso phase to be learned by the network, so convolutional layers may have been unnecessary. Although both models resulted in the same accuracy and uncertainty, the sequential model required only 650 parameters (in comparison to 2402 for the inception model), suggesting it is the most suitable model for a classification task of this simple type, requiring the least time and computing power to train. For applications such as the above introduced (bio)sensors, a sequential CNN will thus be absolutely sufficient to obtain close to 100% accuracy in the readout.

4.2.2. SmA to SmB transition. As can already be seen from the texture examples shown, the SmA to SmB transition is extremely subtle, possibly displaying a slightly smoother texture in the SmB phase. This behaviour is particularly the case for the transition from fluid to hexagonal of the orthogonal liquid crystal phases. The situation is much different for transitions between orthogonal and tilted phases, for example SmA to SmC, which are quite easy to distinguish. Despite the fact that both are fluid smectic phases and the transition is continuous, high accuracies with small errors are obtained.⁴⁸ Minute changes in textures can be observed for transitions between tilted phases, such as fluid SmC to hexatic SmI or hexatic SmI to hexatic SmF, and in these cases accuracies are relatively low and errors quite large too.⁴⁸ It will therefore not be surprising to also observe low accuracies for the case of the orthogonal SmA to SmB transition. The hyperparameters, test accuracies, and confusion matrices are displayed in Table 3.

Table 3 Architecture details and test accuracies for the sequential and the inception model, optimised for the SmA to SmB transition datasets

SmA to SmB	Sequential model	Inception model
Convolutional layers	4	NA
Inception modules	NA	1
Starting channels	8	16
Dense layers	2	2
Batch size	16	16
Learning rate	1 × 10^−4	1 × 10^−4
Dropout rate	0.5	0.5
Trainable parameters	30 930	31 298
Test accuracy	0.56 ± 0.07	0.6 ± 0.1

---

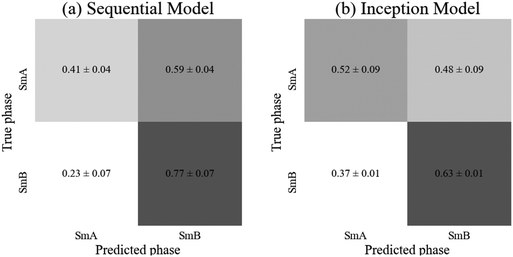
Neither model achieved an accuracy significantly above 50%, hence was no more accurate than randomly assigning each test image arbitrarily to a phase. Both models appear to show a bias towards the SmB phase, with (59 ± 9)% and (48 ± 17)% of SmA images being classified as SmB by the sequential and inception models respectively (Fig. 7). The SmA dataset contains approximately 400 more image samples than the SmB dataset, so this imbalance is not the cause of the bias. The validation accuracy reached 71% and 68% in each of the sequential and inception models, suggesting there are some meaningful differences between the validation and test datasets which is possibly responsible for the bias. However, the validation accuracy showed significant fluctuations during training, so taking the epoch with the highest validation accuracy would likely not generalise to high accuracy on new, unseen data. Neither model appears suitable for this classification task, however, it is possible that a larger dataset combined with a larger network capacity would be capable of identifying the features of this subtle transition. Alternatively, a different mesogen may produce more visible texture changes during this transition, displaying differing features that these networks are capable of learning.

Fig. 7 Confusion matrices for (a) the sequential and (b) the inception model, displaying the probability of a sample from each true phase being assigned a particular predicted phase. The error is calculated as the standard error over three runs of the model.

At this point it is worthwhile to mention the recent results of Osiecka-Drewniak et al.,⁵⁷ who studied a very similar transition between two orthogonal phases, fluid SmA to soft crystal SmB (also called CrB). In this case higher accuracies of 80–90% were reported, which can be attributed to the clear differences in textures between the smooth SmA fans and the striated CrB fans. This striation can often be observed for soft crystal phases, as will be demonstrated below for the hexatic SmB to the soft crystal SmE (CrE) phase, both of which being orthogonal. Yet, both phases are clearly distinguishable due to the striations which allow for high identification accuracies, in our case close to 100%.

4.2.3. SmB to soft crystal E (CrE) transition. As just mentioned, the SmB to SmE transition is more easily discernible than SmA to SmB, distinguished by striation lines appearing across the fan-shaped textures. The optimised hyperparameters, results, and confusion matrices are displayed in Table 4 and Fig. 8.

Table 4 Architecture details and test accuracies for the sequential and the inception model, optimised for the hexatic SmB to soft crystal SmE transition datasets

SmB to SmE	Sequential model	Inception model
Convolutional layers	4	NA
Inception modules	NA	1
Starting channels	16	16
Dense layers	3	2
Batch size	32	16
Learning rate	1 × 10^−4	5 × 10^−5
Dropout rate	0.6	0.6
Trainable parameters	108 530	31 298
Test accuracy	0.99 ± 0.01	0.99 ± 0.01

---

Fig. 8 Confusion matrices for (a) the sequential and (b) the inception model, displaying the probability of a sample from each true phase being assigned a particular predicted phase. The error is calculated as the standard error over three runs of the model.

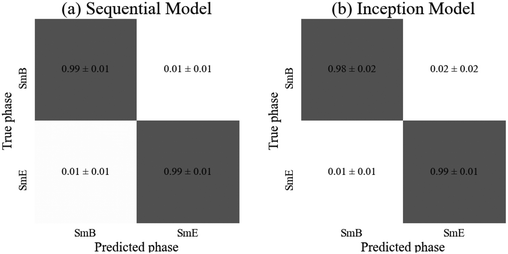
Both models achieved high accuracies of (99 ± 1)% so either could be appropriately employed for identification of the transitions into the soft crystal phases. However, the sequential model required around three times as many parameters in order to achieve this accuracy, so the inception model is faster to train (although it required 40 epochs rather than the 30 required for the sequential model). The slight improvement in accuracy for the SmA phase by the sequential model (shown in the confusion matrices of Fig. 8) is statistically insignificant so the inception model is quicker to train for this particular classification task than the sequential model, while both are very suitable to distinguish the hexatic from the soft crystal phase.

4.2.4. Soft crystal E to crystalline transition. The final binary classifier we investigated is the transition from the soft crystal E (CrE) to the crystalline (Cr) phase. These two phases show significant texture differences, due to formation of cracks during crystallization, thus suggesting that a high accuracy will be achievable. Model hyperparameters, results, and confusion matrices are displayed in Table 5 and Fig. 9.

Table 5 Architecture details and test accuracies for the sequential and the inception model, optimised for the soft crystal SmE to crystalline transition datasets

SmE to Cr	Sequential model	Inception model
Convolutional layers	3	NA
Inception modules	NA	1
Starting channels	16	16
Dense layers	3	2
Batch size	16	16
Learning rate	1 × 10^−4	5 × 10^−5
Dropout rate	0.5	0.5
Trainable parameters	30 322	31 298
Test accuracy	0.989 ± 0.001	0.99 ± 0.01

---

Fig. 9 Confusion matrices for (a) the sequential and (b) the inception model, displaying the probability of a sample from each true phase being assigned a particular predicted phase. The error is calculated as the standard error over three runs of the model.

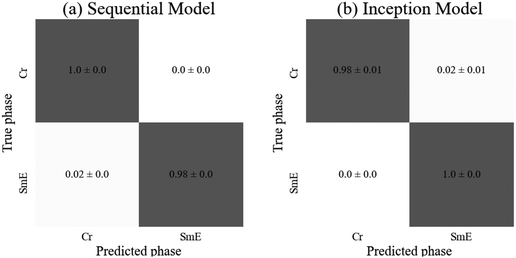
As anticipated, both models achieved similar accuracies, with the inception model resulting in a significantly higher standard deviation. The sequential model achieved 100% test accuracy on all three training instances for the crystalline phase, and the inception model achieved the same on the SmE phase (Fig. 9). Despite the SmE dataset containing approximately double the number of images compared to the Crystal dataset, there is no evidence of bias in either network. The sequential model required slightly fewer parameters as well as ten fewer epochs to train, yet both architectures are well suited to predict the phases involved.

4.3. Multiphase classifier

Due the difficulties of distinguishing between the fluid SmA and the hexatic SmB phases, these two datasets were combined to form a new dataset named SmAB, which consists of the orthogonal smectic phases. To prevent bias towards this new, significantly larger category, half of the images were removed at random. The multiphase classifier thus investigates the sequence: disordered isotropic – the smectic orthogonal liquid crystal – the soft crystal–crystalline. The optimised hyperparameters and test accuracies are given in Table 6.

Table 6 Architecture details and test accuracies for the sequential and the inception model, optimised for the multiphase classifier isotropic-orthogonal smectic-soft crystal–crystal transition datasets

Multiphase	Sequential model	Inception model
Convolutional layers	6	NA
Inception modules	NA	1
Starting channels	16	16
Dense layers	4	2
Batch size	16	16
Learning rate	1 × 10^−4	5 × 10^−5
Dropout rate	0.5	0.5
Trainable parameters	1 648 206	31 298
Test accuracy	0.99 ± 0.01	0.984 ± 0.006

---

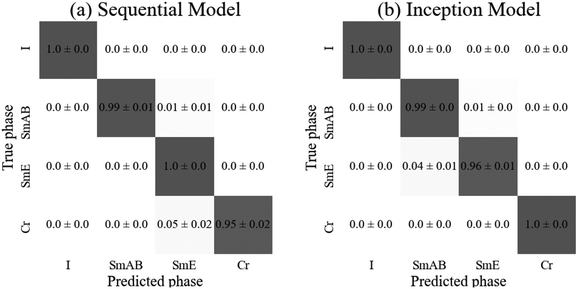
There is no statistical difference between the test accuracies of each model. As expected, both consistently identified the isotropic phase correctly. All other phases were generally correctly identified with the exceptions being the sequential model mislabeling (5 ± 3)% of the crystal images as smectic and the inception model mislabeling (4 ± 2)% of soft crystal E images as orthogonal smectic liquid crystal (SmAB). These three phases all show significant similarity, with some shared features so some confusion is to be expected. Overall, both models achieved high accuracy, however, the sequential model required fifty times the number of parameters compared to the inception model. Therefore, the inception model appears to be better suited to the more complicated, high capacity classification tasks of multiphase classifiers, also requiring only 50 rather than 100 epochs to train. The confusion matrices for both models are depicted in Fig. 10.

Fig. 10 Confusion matrices for (a) the sequential and (b) the inception model, displaying the probability of a sample from each true phase being assigned a particular predicted phase. The error is calculated as the standard error over three runs of the model.

5. Discussion

As demonstrated in several publications,^48–50,57 liquid crystal phases and their transitions including whole phase sequences, can be characterized from textures via machine learning architectures. The simplest characterization is that of the clearing point, which describes the transition from the disordered isotropic phase to the ordered, birefringent liquid crystal. This transition can be localized with extremely high accuracy of practically 100%, independent of the machine learning architecture employed.⁴⁹ It represents basically a “black/bright” or “yes/no” decision when textures are viewed between crossed polarisers. This is practically equivalent to the situation where gases, chemicals or biomolecules initiate a homeotropic to planar transition, which makes it tremendously useful for the application in sensors.^41,42 It should be pointed out though that the actual transition from isotropic to the homeotropic nematic (or orthogonal SmA) liquid crystal phase is significantly harder to characterize by machine learning.⁴⁹

Other transitions, like nematic to SmA, or the fluid orthogonal SmA to fluid tilted SmC phase can also be verified with high accuracy.^48–51 In general, orthogonal to tilted transitions are identified with high accuracy, as are transitions from liquid crystal to soft crystal, independent if orthogonal phases are involved (SmA–CrB,⁵⁷ SmB–CrE (this work)) or not. On the contrary, transitions between orthogonal liquid crystals (fluid SmA–hexatic SmB (this work)) or tilted liquid crystals (fluid SmC–hexatic SmI⁴⁸) represent some limitations for conventional machine learning architectures such as sequential CNNs or inception models. This is in part shown in the present study, as can be seen in Fig. 11.

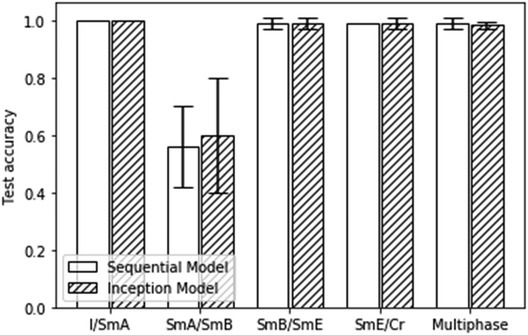Fig. 11 Test accuracies for all of the presented binary and multiphase classification scenarios. Errors represent 95% confident intervals.

A similar result as depicted in Fig. 11 was obtained for the machine learning test accuracies of a homologous series of materials with predominantly tilted mesophases.⁴⁸ In summary, transitions between orthogonal and tilted phases, as well as those between liquid crystal and soft crystal phases can very well be characterized by machine learning. Limitations are found for the characterization of transitions between orthogonal fluid to hexatic phases (SmA–SmB) and for tilted fluid to hexatic phases (SmC–SmI).

6. Conclusions

In this investigation we have studied the possibilities and limitations of sequential and parallel convolutional neural networks for the characterization of orthogonal liquid crystal and soft crystal phases. It was demonstrated that this task can readily be performed, with the exception of the fluid SmA to hexatic SmB transition, the reason being the lack of identifiable features that distinguish both phases in their texture appearance. Possibly a larger dataset would be required to allow larger networks to be trained without risking overfitting, such as ResNet⁵⁸ and EfficientNet.⁵⁹

In general the inception models required fewer trainable parameters to achieve the same accuracy as the sequential models disregarding the isotropic to SmA transition. The reason being likely the possibility that both models could have used less complex and lower capacity architectures, with no convolutional layers. This general behaviour is expected as the 1 × 1 convolutions utilized in the inception module are used to reduce the number of channels, hence reducing the number of feature maps at each layer, reducing the number of trainable parameters required.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Dr J. Schacht for the provision of the investigated compound 12 Me.

References

1. Y.-C. Wu and J.-W. Feng, Wirel. Pers. Commun., 2018, 102(2), 1645–1656,  DOI:10.1007/s11277-017-5224-x.
2. H. D. Block, Rev. Mod. Phys., 1962, 34(1), 123–135.
3. C. Yang, F. Rottensteiner and C. Heipke, ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci., 2018, IV–3, 251–258.
4. R. Rasti, M. Teshnehlab and S. L. Phung, Pattern Recogn., 2017, 72, 381–390.
5. G. Carleo, I. Cirac, K. Cranmer, L. Laudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborova, Rev. Mod. Phys., 2019, 91, 045002.
6. A. Radovic, M. Williams, D. Rousseau, M. Kagan, D. Bonacorsi, A. Himmel, A. Aurisano, K. Terao and T. Wongjirad, Nature, 2018, 560, 41–48.
7. N. M. Ball and R. J. Brunner, Int. J. Mod. Phys. D, 2010, 19, 1049–1106.
8. S. Sen, S. Agarwal, P. Chakraborty and K. P. Singh, Exp. Astron., 2022, 53, 1–43.
9. S. K. Meher and G. Panda, Eur. Phys. J.: Spec. Top., 2021, 230, 2285–2317.
10. S. So, T. Badloe, J. Noh, J. Bravo-Abad and J. Rho, Nanophotonics, 2020, 9, 1041–1057.
11. L. Zhang and S. Shao, J. Appl. Phys., 2022, 132, 100701.
12. C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 1281–1289.
13. H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, Drug Discovery Today, 2018, 23, 1241–1250.
14. F. Cui, Y. Yue, Y. Zhang, Z. Zhang and H. S. Zhou, ACS Sens., 2020, 5, 3346–3364.
15. A. Maier, C. Syben, T. Lasser and C. Riess, Z. Med. Phys., 2019, 29, 86–101.
16. J.-G. Lee, S. Jun, Y.-W. Cho, H. Lee, G. B. Kim, J. B. Seo and N. Kim, Korean J. Radiol., 2017, 18, 570–584.
17. M. Shehab, L. Abualigah, Q. Shambour, M. A. Abu-Hashem, M. K. Y. Shambour, A. I. Alsalibi and A. H. Gandomi, Comput. Biol. Med., 2022, 145, 105458.
18. S. L. Goldenberg, G. Nir and S. E. Salcudean, Nat. Rev. Urol., 2019, 16, 391–403.
19. A. Hosny, C. Parmar, J. Quackenbush, L. H. Schwartz and H. J. W. L. Aerts, Nat. Rev. Cancer, 2018, 18, 501–510.
20. D. C. Cires, A. Giusti, L. M. Gambardella and J. Schmidhuber, Medical Image Computing and Computer-Assisted Intervention – MICCAI, Springer, Berlin, 2013, pp. 411–418.
21. P. S. Clegg, Soft Matter, 2021, 17, 3991–4005.
22. A. L. Ferguson, J. Phys.: Condens. Matter, 2018, 30, 043002.
23. T. Orlova, A. Piven, D. Darmoroz, T. Aliev, T. Mahmoud, T. Abdel Razik, A. Boitsev, N. Grafeeva and E. Skorb, Digital Discovery, 2023, 2, 298–315.
24. H. Y. D. Sigaki, R. F. de Souza, R. T. de Souza, R. S. Zola and H. V. Ribeiro, Phys. Rev. E, 2019, 99, 013311.
25. H. Y. D. Sigaki, E. K. Lenzi, R. S. Zola, M. Perc and H. V. Ribeiro, Sci. Rep., 2020, 10, 7664.
26. A. A. B. Pessa, R. S. Zola, M. Perc and H. V. Ribeiro, Chaos, Solitons Fractals, 2022, 154, 111607.
27. C.-H. Chen, K. Tanaka and K. Funatsu, Mol. Inf., 2019, 38, 1800095.
28. E. N. Minor, S. D. Howard, A. A. S. Green, M. A. Glaser, C. S. Park and N. A. Clark, Soft Matter, 2020, 16, 1751–1759.
29. M. Walters, Q. Wei and J. Z. Y. Chen, Phys. Rev. E, 2019, 99, 062701.
30. A. Dhillon and G. K. Verma, Prog. Artif. Intell., 2020, 9, 85–112.
31. E. Hedlund, K. Hedlund, A. Green, R. Chowdhury, C. S. Park, J. E. Maclennan and N. A. Clark, Phys. Fluids, 2022, 34, 103608.
32. J. Colen, M. Han, R. Zhang, S. A. Redford, L. M. Lemma, L. Morgan, P. V. Ruijgrok, R. Adkins, Z. Bryant, Z. Dogic, M. L. Gardel, J. J. de Pablo and V. Vitelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2016708118.
33. T. Inokuchi, R. Okamoto and N. Arai, Liq. Cryst., 2020, 47, 438–448.
34. T. C. Le and N. Tran, ACS Appl. Nano Mater., 2019, 2, 1637–1647.
35. H. Doi, K. Z. Takahashi, K. Tagashira, J.-I. Fukuda and T. Aoyagi, Sci. Rep., 2019, 9, 16370.
36. P. Y. Taser, G. Onsal and O. Ugurlu, Bull. Mater. Sci., 2023, 46, 1.
37. J. Zaplotnik, J. Pišljar, M. Škarabot and M. Ravnik, Sci. Rep., 2023, 13, 6028.
38. A. Soyemi, S. K. Pandey, S. A. Vaara and T. Szilvási, Liq. Cryst., 2023 DOI:10.1080/02678292.2023.2275293.
39. A. T. Nguyen, H. M. Childs, W. M. Salter, A. V. Filippas, B. T. McInnes, K. Senecal, T. J. Lawton, P. A. D’Angelo, W. Zukas, T. E. Alexander, V. Ayotte, H. Zhao and C. Tang, Liquids, 2023, 3, 440–455.
40. G. Önsal, O. Uğurlu, Ü. H. Kaynar and D. Türsel Eliiyi, Sci. Rep., 2023, 13, 12802.
41. K. Nayani, Y. Yang, H. Yu, P. Jani, M. Mavrikakis and N. Abbott, Liq. Cryst. Today, 2020, 29, 24–35.
42. Y. Cao, H. Yu, N. L. Abbott and V. M. Zavala, ACS Sens., 2018, 3, 2237–2245.
43. S. Jiang, J.-H. Noh, C. Park, A. D. Smith, N. L. Abbott and V. M. Zavala, Analyst, 2021, 146, 1224–1233.
44. Y. Xu, A. M. Rather, S. Song, J.-C. Fang, R. L. Dupont, U. I. Kara, Y. Chang, J. A. Paulson, R. Qin, X. Bao and X. Wang, Cell Rep. Phys. Sci., 2020, 1, 100276.
45. E. Ramou, S. I. C. J. Palma and A. C. A. Roque, ACS Appl. Mater. Interfaces, 2022, 14, 6261–6273.
46. N. Bao, S. Jiang, A. Smith, J. J. Schauer, M. Mavrikakis, R. C. Van Lehn, V. M. Zavala and N. L. Abbott, ACS Sens., 2022, 7, 2545–2555.
47. X. Zhan, Y. Liu, K.-L. Yang and D. Luo, Biosensors, 2022, 12, 577.
48. I. Dierking, J. Dominguez, J. Harbon and J. Heaton, Liq. Cryst., 2023, 50, 1526–1540.
49. I. Dierking, J. Dominguez, J. Harbon and J. Heaton, Front. Soft. Matter, 2023, 3, 1114551.
50. R. Betts and I. Dierking, Soft Matter, 2023, 19, 7502–7512.
51. I. Dierking, J. Dominguez, J. Harbon and J. Heaton, Liq. Cryst., 2023, 50, 1461–1477.
52. S. Wager, S. Wang and P. S. Liang, in Dropout training as adaptive regularization, Advances in Neural Information Processing Systems, 26, 2013 DOI:10.48550/arXiv.1307.1493.
53. P. Luo, X. Wang, W. Shao and Z. Peng, Towards Understanding regularization in batch normalization, arXiv, 2018, preprint, arXiv:1809.00846,  DOI:10.48550/arXiv.1809.00846.
54. S. Ioffe and C. Szegedy, Batch normalization: Accelerating deep network training by reducing internal covariate shift, Proceedings of the 32nd International Conference on Machine Learning, arXiv, 2015, preprint, arXiv:1502.03167 DOI:10.48550/arXiv.1502.03167.
55. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke and A. Rabinovich, Going deeper with convolutions, arXiv, 2014, preprint, arXiv:1409.4842 DOI:10.48550/arXiv.1409.4842.
56. J. Schacht, M. Buivydas, F. Gouda, L. Komitov, B. Stebler, S. T. Lagerwall, P. Zugenmaier and F. Horii, Liq. Cryst., 1999, 26, 835–847.
57. N. Osiecka-Drewniak, Z. Galewski and E. Juszynska-Gałazka, Crystals, 2023, 13, 1187.
58. K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, 2016, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770–778 DOI:10.48550/arXiv.1512.03385.
59. M. Tan and Q. V. Le, EfficientNet: Rethinking model scaling for convolutional neural networks, International Conference on Machine Learning, arXiv, 2019, preprint, arXiv:1905.11946v5 DOI:10.48550/arXiv.1905.11946.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00295d

---