First-principles evaluation of MnO₂ polymorphs as cathode material in lithium-ion batteries

Abstract

Polymorphic materials, e.g. manganese dioxide (MnO₂) exhibit promise in energy storage applications, such as serving as cathode material for Li-ion batteries (LIBs). The flexibility to arrange the polyhedral building blocks within their lattice structures allows tunable properties for enhanced performance. In this work, we carried out first-principles simulations to scrutinize the structural, thermodynamic and kinetic properties of polymorphic MnO₂ during Li-ion intercalation. We explored polymorph-specific metrics in dictating its overall performance as cathode material in LIBs, such as thermal and mechanical stability during reversible Li-ion intercalation, achievable energy density, volumetric storage capacity, and Li-ion mobility. Our comprehensive analyses reveal that there are inherent trade-offs among the evaluated properties for optimal performance. For instance, tunneled polymorphs such as α and β phases of MnO₂ allow fast Li-ion diffusion, yet suffer from limited capacity and strain-induced structural vulnerabilities. On the other hand, the spinel (λ) phase of MnO₂ offers a higher voltage window but shows significantly more sluggish Li-ion transport behavior. Overall, the findings and insights presented in this study will provide practical guidelines for materials selection and structural engineering of MnO₂ polymorphs for advanced battery applications.

---

1 Introduction

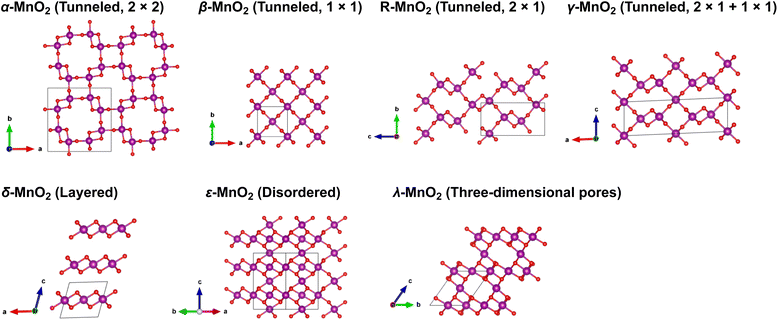
Manganese oxides (MnO₂) with a variety of tunable polymorphic phases have been broadly used in energy production and storage applications, such as batteries, supercapacitors and catalysis, thanks to their earth-abundant, environmentally friendly nature and low manufacturing cost. Their initial application in energy storage can be traced back to the Leclanche' cell in the 1860s, and later advanced to the widely used 1.5 V Zn/MnO₂ alkaline primary cells.^1,2 Over the past decades, driven by high demands of sustainable energy storage technologies to reduce carbon emission, extensive efforts have been invested to employ MnO₂ in large-scale electrical energy storage devices such as supercapacitors and rechargeable batteries.^2,3 As shown in Fig. 1, The crystalline phases of MnO₂, although all comprised of interlinked MnO₆ octahedra, present diverse local structural features and can be roughly categorized into three categories: (i) polymorphs with one-dimensional tunnels, including α-MnO₂ (hollandite), β-MnO₂ (pyrolusite), R-MnO₂ (ramsdellite) and γ-MnO₂ (intergrowth) that features 2 × 2, 1 × 1, 2 × 1, and mixed 1 × 1 and 2 × 1 tunnels, respectively; (ii) two-dimensional layered structure as seen in δ-MnO₂ (birnessite); (iii) structure exhibiting three-dimensional pores, such as λ-MnO₂ (spinel). The distinct crystallographic features and local bonding characteristics of MnO₂ polymorphs effectively lead to variations in their structural, thermodynamic and kinetic properties when deployed as cathode material in lithium-ion batteries (LIBs).^4,5 A comprehensive understanding of the unique attributes of various phases, along with possible trade-offs between them, is prerequisite for rational design and engineering of MnO₂ to achieve its optimal performance.

Fig. 1 Crystal structures of MnO₂ polymorphs investigated in this work.

Among all the polymorphic phases of MnO₂, α-MnO₂ is perhaps the most studied phase as a cation host. For example, both Ling⁶ and Tompsett⁷ have predicted from first-principles simulations that the open channels in α-MnO₂ would allow reversible Li-ion intercalation with relatively fast kinetics.^6–9 Larger cations, such as K⁺, and NH₄⁺ have also been successfully introduced into the α-MnO₂ lattice, which induces additional stabilizing effects as discussed by Yuan et al.¹⁰ and Kempaiah et al.¹¹ In contrast, early studies raised concerns regarding the viability of β-MnO₂ as an efficient ion conductor, speculating that its compact structure may limit the number of available atomic sites for Li-ion insertion and its narrow 1 × 1 tunnels would hinder Li-ion transport, thereby affecting both the storage and rate capacities of LIBs when used as active cathode material.^12,13 However, subsequent studies revealed good cycling performance of β-MnO₂.^14–16 This was later rationalized by density functional theory (DFT) simulations performed by Wang et al.,¹⁷ which showed even lower activation energies of Li-ion diffusion along the β-MnO₂ tunnels as compared to α-MnO₂. Numerous studies have been conducted to investigate the electrochemical properties of metastable γ-,^18,19 λ-,^20–22 and δ-MnO₂ (ref. 23 and 24) that were prepared using different synthetic approaches. Although promising electrochemical performances have been demonstrated, a fundamental understanding of the correlations between local structure, chemistry, and the electrochemical response of these different MnO₂ polymorphs remains lacking. Compared to other polymorphic phases, R-MnO₂ is considerably less studied due to the synthesis challenges of producing unavoidable inter-grown β-MnO₂, which eventually leads to the formation of γ-MnO₂. Nevertheless, recently Gupta et al.²⁵ were able to conduct a thorough evaluation of the structural, electronic and electrochemical properties of R-MnO₂ using a combination of experimental and theoretical methods. A significant voltage decay is observed with increased lithiation, which is attributed to specific local Li-ion coordination environments in the R-MnO₂ lattice. In this regard, γ-MnO₂, which presents a complex intergrowth of MnO₆ octahedra, combining structural features of both β- and R-phases, may offer unique design opportunities by manipulating the arrangements of its local structural motifs for optimal performance. Indeed, Gupta et al.²⁶ have demonstrated successful creation of γ-MnO₂ microstructures that incorporate the benefits of both β- and R-phases of MnO₂ through synthetic control of their phase evolution kinetics.

Unlocking the full potential of highly tunable MnO₂ polymorphs requires a comprehensive understanding of their individual physicochemical properties as well as their associated advantages/disadvantages when used in practical applications. To this end, a number of previous attempts, either from experiments²⁷ or simulations,^28–30 have been made to compare some of the distinct properties offered by different MnO₂ polymorphs. However, these investigations were often limited to specific material aspects such as crystal structure and thermodynamic stability. Here instead, we aim for a comprehensive assessment of the structural, thermodynamic and kinetic properties of all seven distinct MnO₂ polymorphic phases, including α-, β-, R, γ-, δ-, ε-, and λ-phases, to be used as cathode material in LIBs. Our results offer valuable insights into materials selection and rational design of complex microstructures for optimal performance, especially when considering various trade-offs among their fundamental physicochemical properties, such as energy density, Li-ion mobility and large-scale processability.

2 Methods

Spin-polarized DFT calculations were performed using the Vienna Ab intio Simulation Package (VASP)^31,32 with the projector-augmented-wave (PAW) pseudopotentials³³ that are truncated at 600 eV. Two different exchange-correlation approximations were considered and compared, i.e. the Perdew–Burke–Erzenhof (PBE) type generalized gradient approximation (GGA)³⁴ with a Hubbard U correction of 3.9 eV applied to Mn 3d electrons^35,36 and the meta-GGA Strongly Constrained and Appropriately Normed (SCAN) approximation.³⁷ A benchmark study performed by Kitchaev et al.²⁸ highlights the capability of SCAN functional to accurately predict the formation energies, band gaps, magnetic and lattice structures of all MnO₂ polymorphs. In this work, we also found that the SCAN functional, in comparison to PBE + U, can better reproduce cell parameters of all MnO₂ polymorphic phases and predict their thermodynamic and electronic properties. Here in the main text, we present the results calculated by the SCAN functional and discuss potential discrepancies that may arise when using the PBE + U approach. Detailed results of the PBE + U calculations are provided in the ESI (ESI).† All structural optimizations with no symmetry constraints were performed with a Γ-centered k-point grid of sampling densities exceeding 30/a × 30/b × 30/c in the first Brillouin zone, and the energies and forces were converged to 10⁻⁶ eV and 10 meV Å⁻¹, respectively. For the magnetic properties, a number of experimental^38–41 and theoretical²⁸ studies suggest that all polymorphs, except for β-MnO₂, exhibit antiferromagnetic (AFM) ordering in their ground states. However, during lithiation, the ground-state AFM ordering of Li_xMnO₂ may be disrupted due to broken symmetry or local variation in Mn oxidation states. The interplay between the magnetic ordering of MnO₆ and partial occupancy of Li-ions, especially for low symmetry MnO₂ polymorphs, further complicates the calculation of voltage profile and Li-ion diffusion barriers. To allow systematic comparison across different polymorphs, in this work, we constrain the magnetic ordering of all MnO₂ phases to the FM states. To evaluate the kinetic properties of MnO₂, the Climbing Image Nudged Elastic Band (CI-NEB)⁴² method was used to determine the transition states during Li-ion migration and to extract the energy barriers. Supercell structures with cell parameters of around 1–1.5 nm in each dimension were used to avoid spurious interactions between the migrating Li-ion and its periodically repeated images. For all CI-NEB calculations, single Γ point k-point was used to sample the first Brillouin zone and the energy and force convergence thresholds were set to 10⁻⁵ eV and 5 × 10⁻² eV Å⁻¹, respectively.

3 Results and discussion

3.1 Atomic structures of Li_xMnO₂

Table 1 summarizes the lattice parameters and cell volumes of different MnO₂ polymorphs predicted by SCAN and PBE + U (U = 3.9 eV) functionals in comparison with available experimental values. We note here that relatively large uncertainties may exist in the experimentally determined cell parameters of δ- and ε-MnO₂ due to contamination, such as insertion of undesired guest species for the case of δ-MnO₂ (ref. 28) or disordering caused by thermally activated rearrangements of MnO₆ octahedra as seen in ε-MnO₂.⁴³ The ε phase of MnO₂ generally adopts a NiAs-type lattice structure with Mn⁴⁺ and vacancies randomly occupying 50% of all available octahedral sites. For simplicity, in this work we consider a relatively ordered structure of ε-MnO₂ by removing 1/4 and 3/4 Mn atoms from two adjacent MnO layers along the c-axis, as suggested by Jiang et al.⁴⁴ As shown in Table 1, the SCAN functional can accurately reproduce the lattice parameters of all MnO₂ polymorphic phases compared to experiments, while PBE + U tends to overestimate. Among all MnO₂ polymorphic phases considered here, α-MnO₂ exhibits the largest cell volume due to the presence of 2 × 2 open tunnels whereas β-MnO₂ is the most compact structure with 1 × 1 narrow tunnels (see structure representations provided in Fig. 1). Comparing the band structures calculated using SCAN and PBE + U functional (Fig. S1 and S2†), PBE + U (U = 3.9 eV) predicts a metallic structure of β-MnO₂ whereas SCAN resolves the semiconducting nature as has been observed in the experiment. This further verifies that improved predictability can be obtained using the SCAN functional.

Table 1 Predicted lattice parameters and cell volumes of MnO₂ polymorphs using SCAN and PBE + U (U = 3.9 eV) (in italic font) functionals in comparison with experimental values (in parenthesis)

	Lattice constant (Å)	Number of formula units	Volume (Å^3 f.u.^−1)
α	a = b = 9.71/9.91 (9.80), c = 2.85/2.93 (2.85)	8	33.54/35.88 (34.2)
β	a = b = 4.40/4.47 (4.39), c = 2.85/2.95 (2.86)	4	27.68/29.45 (27.8)
R	a = 2.84/2.92 (2.86), b = 4.62/4.59 (4.49), c = 9.02/9.45 (9.29)	4	29.69/31.72 (29.8)
γ	a = 13.68/13.91 (13.7), b = 2.85/2.93 (2.86), c = 4.46/4.55 (4.46)	6	8.95/30.68 (29.2)
δ	a = b = 2.85/2.93 (2.83), c = 4.74/5.27 (uncertain)	4	32.99/37.49
ε	a = b = 5.54/5.70, c = 8.35/8.54	8	27.78/30.03
λ	a = b = c = 5.68/5.82 (5.67)	4	32.41/34.89 (32.3)

---

Upon lithiation, the MnO₂ lattices tend to expand and the degree of expansion correlates to their mechanical stability during reversible Li-ion intercalation, especially for polycrystalline samples where considerable amount of stress can build-up at the grain boundaries leading to delamination, cracking or breakdown of the entire cathode particles. Here we track the volume change of MnO₂ polymorphs at different stages of lithiation and plot the results in Fig. 2. As expected, cell expansions are generally observed in all MnO₂ polymorphs during lithiation, among which β-MnO₂ experiences the largest volume change (over 30%) due to its compact crystal structure in the pristine phase. The δ and λ phases of MnO₂ exhibit reasonable volume change (within 10%), signifying improved stability and resistance to mechanical fatigue during extended cycling. It is worth mentioning here that the volume of each MnO₂ polymorphic phase does not necessarily increase linearly with respect to Li-ion content, which is likely due to variations in the preferred Li-ion intercalation sites at different Li-ion concentrations as will be discussed below.

The distinct crystal structures of MnO₂ polymorphs offer a variety of Li-ion intercalation sites. Here we surveyed different atomic sites to accommodate Li-ions (see Fig. S3†), and compared their relative formation energies as shown in Table S1.† Jahn–Teller distortion is generally observed, as indicated by the formation of asymmetrical Li–O bonds at different Li-ion intercalation sites (see Table S1†). Overall, α-MnO₂ presents the most diverse local environments to accommodate Li-ions owing to its open 2 × 2 tunnel structure. For example, it has been observed previously that a Li-ion can occupy any of the 8h, 8h′, 2a and 2b atomic sites within the 2 × 2 tunnel.^6,7,9,10 In this work, we explored additional Li-ion intercalation sites in the 1 × 1 tunnel at the center of four 2 × 2 tunnels (see Fig. S4†), and found that Li insertion into the 1 × 1 tunnel is energetically unfavored. Based on full cell relaxation, our results confirm that the 8h atomic site within the 2 × 2 tunnel is the lowest energy site to accommodate Li, as also shown in previous studies.^6,7

In other polymorphs, two types of lithiation sites are identified, i.e. the tetrahedral (four oxygen-coordinated Li) and octahedral (six oxygen-coordinated Li) sites, which either share the corners or the edges of the MnO₆ octahedra. In addition, two energetically inequivalent octahedral sites (Oct-(a) and Oct-(b) in β-MnO₂, Oct-(d) and Oct-(e) in γ-MnO₂, see Fig. S3†), with an energy difference of >100 meV, are also identified in the 1 × 1 tunnels of β- and γ-MnO₂ due to variations in local geometry and the electrostatic interactions between the intercalated Li-ions and surrounding ions. Among all these available atomic sites for Li-ions intercalation (as summarized in Fig. S3 and Table S1†), their preferred occupancy varies in different MnO₂ polymorphs. For example, in the β-, ε-, and R-phases, the octahedral sites are energetically more favorable for single Li-ion intercalation whereas in the λ-phase, the tetrahedral sites are preferred. Interestingly, for the cases of γ- and δ-phases, the tetrahedral sites become thermodynamically unstable, and Li-ions are found to always reside at the octahedral sites, as shown in Table S1.†

It is further observed that the energy landscape for Li-ions to occupy these distinct atomic sites varied strongly with respect to local strain and/or Li-ion concentration. In α-MnO₂, the 8h octahedra sites are always preferred for Li-ion occupancy. Below the Li : Mn ratio of 0.5 (i.e. x < 0.5 of Li_xMnO₂), up to two Li-ions occupy the 8h octahedra sites that are far apart within the 2 × 2 tunnel structure. This atomic arrangement, as depicted in Fig. S4,† effectively draws two corner-sharing MnO₆ octahedra closer in one dimension (either along the a or b-axis), which induces a volume contraction that cannot be compensated by expansions in other dimensions. However, at x > 0.5, more than two Li-ions need to be accommodated in the 2 × 2 tunnel, causing lattice expansion in both a and b directions and therefore a significant increase in cell volume is observed as shown in Fig. 2. For other polymorphs, the octahedral sites are generally favored in the fully lithiated state, and the tetrahedral sites may become favorable at lower Li-ion concentrations, such as for the cases of ε- and λ-MnO₂. Due to the preferences of these site occupancies, various degrees of lattice distortion and cell volume change are observed. For example, in ε-Li_xMnO₂, Li-ions all reside at the tetrahedral sites in the 1/4 Mn + 3/4 vac. layers at x < 0.5, which stretches the cell in the c direction, leading to significant volume expansion. At x > 0.5, Li-ions predominantly occupy the higher symmetry octahedral sites (see Oct-(a) and Oct-(b) sites for ε-MnO₂ in Fig. S3 and S4†), which stabilize the MnO₂ lattice as evidenced by slower evolution of the cell volume (see Fig. 2) at these high Li-ion concentrations. For the case of λ-Li_xMnO₂, the tetrahedral sites are also energetically preferred at x < 0.5, and with increased Li-ion contents, the octahedral sites become increasingly favorable. Unlike these relatively compact MnO₂ phases, polymorphs presenting three-dimensional pore structures can offer sufficient space for Li-ion intercalation and thus experience less lattice distortion and cell volume change. As shown in Fig. 1, both R- and γ-MnO₂ feature the 2 × 1 tunnel structure. At low Li-ion content, each Li-ion occupies a single atomic site within the 2 × 1 tunnel. Beyond certain thresholds, i.e. 1/2 and 1/3 for R- and γ-phase, respectively, at least two Li-ions must be accommodated within the same 2 × 1 tunnel. In particular, for the γ phase, Li-ions will begin to occupy the octahedral sites within the 1 × 1 tunnel once all available sites in the 2 × 1 tunnels are fully occupied, which occurs at x = 2/3, and this will lead to significant volume expansion as shown in Fig. 2.

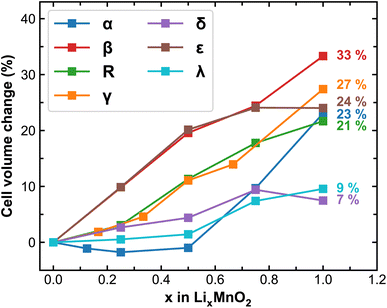Fig. 2 Predicted cell volume change (in %) of MnO₂ polymorphs during lithiation. The numbers in the plot represent the volume at full lithiation relative to the pristine MnO₂.

The cell volume change of MnO₂ during lithiation effectively defines its theoretical volumetric capacity. In Table 2, we compare the calculated volumetric capacity of all MnO₂ polymorphs. Except for α-LiMnO₂, most polymorphs possess a theoretical capacity of 1200–1300 mA h cm⁻³. The considerably lower volumetric capacity of α polymorph is due to incomplete occupancy of all available atomic sites in its spacious 2 × 2 and 1 × 1 tunnels at the stoichiometry of LiMnO₂. If all octahedral sites within the 1 × 1 tunnel are fully occupied (reaching a stoichiometry of Li_1.25MnO₂), its theoretical capacity can increase to 1434.1 mA h cm⁻³, although constraints apply from the electronic structure perspective.

Table 2 Predicted theoretical volumetric capacity (mAh cm⁻³) of all MnO₂ polymorphs when used as cathode materials in LIBs

α	β	R	γ	δ	ε	λ
1078.1	1205.6	1232.0	1208.2	1294.4	1291.7	1253.3

---

3.2 Thermodynamic stability and cell voltage

Fig. 3 compares the ab initio energies per formula unit of all MnO₂ and LiMnO₂ polymorphs predicted by the SCAN functional. The comparison with the PBE + U calculations is provided in Fig. S4.† It is found that SCAN and PBE + U in fact predict different lowest-energy structures of MnO₂ polymorphs (β- and α-phase by SCAN and PBE + U, respectively). Comparing to existing literature, in which Hatakeyama et al.²⁷ reports the lowest-energy structure to be β-MnO₂, we believe the SCAN functional is more reliable to predict the energetics of different MnO₂ phases and therefore for the remainder discussion of their thermodynamic and kinetic properties, we again focus on the results obtained using the SCAN functional. As shown in Fig. 3, lithiation changes the relative thermal stability among polymorphs. For pristine MnO₂, the β- and α-phases show high stability while the λ-phase is meta-stable. However, upon full lithiation, the λ-phase exhibits enhanced stability surpassing that of the β- and α-phases. The R-phase shows high stability in both charged and discharged states. As detailed in the method section, we opted to constrain all studied Li_xMnO₂ structures to the FM electronic states to allow systematic comparison of the different MnO₂ polymorphic phases. To address the potential implications of this assumption, we compare the electronic properties obtained for MnO₂ and LiMnO₂ polymorphs under the FM and AFM configurations. As shown in Fig. S6,† the AFM ordering can lead to lower formation energy, up to 0.2 eV f.u.⁻¹ compared to their FM counterparts. The relative stability remains consistent among MnO₂ polymorphs with both FM and AFM orderings. The R- and λ-phases of LiMnO₂ are found as the most energetically stable among FM and AFM configurations, respectively.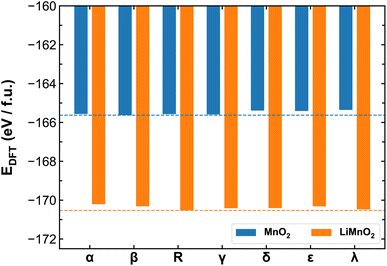

Fig. 3 Ab initio energies of different MnO₂ and LiMnO₂ polymorphs calculated using the SCAN functional. The dash lines mark the lowest energies obtained for β-MnO₂ and R-LiMnO₂.

It is worth noting that Li–Mn intermixing (interchange) can be common in Li-rich LMO cathode materials due to synthesis environments and migration of cations during charge/discharge cycles.^45–47 To assess the likelihood of Li–Mn mixing, we calculate and compare the defect formation energy of Li–Mn exchange in all seven polymorphic phases of LiMnO₂. An exchanged Li–Mn pair within 3 Å distance is placed in the supercells of LiMnO₂ and the results are summarized in Fig. S7 in the ESI.† It is found that by introducing a Li–Mn exchange defect, the lattice structure of δ-LiMnO₂ can be further stabilized, which suggests the alternating layer of Li and Mn presented in δ-LiMnO₂ are prone to cation mixing, thus making it more susceptible to irreversible phase transformation during charge/discharge cycles. All other polymorphs are found to remain stable in their pristine phases as compared to the defected phases. It is worth noting that the ε-phase, which is already disordered, shows the strongest resistance to further cation mixing. The cation mixing can also readily occur in the λ-LiMnO₂ phase, but energetically less favored in the tunneled phases (α-, β-, R-, and γ-LiMnO₂). Although we expect the stability of such Li–Mn exchange defects and their population can be modulated by local Li content, our current simulation results imply that the intrinsically more disordered ε-LiMnO₂ can be more tolerable for further structural degradation.

The open circuit voltage (OCV) profile of each polymorphic phase is derived from the DFT energies obtained for the most stable configurations of Li_xMnO₂ (0 < x < 1) (see structures in Fig. S1†). The lowest-energy end-point configurations of MnO₂ and LiMnO₂ are taken as references to compute the formation energies (at 0 K) of all intermediate phases using the following equation:

E_f(Li_xMnO₂) = E(Li_xMnO₂) − xE(LiMnO₂) − (1 − x)E(MnO₂) (1)

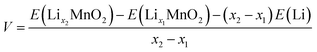where E is the total energies computed by DFT. By plotting the formation energies of Li_xMnO₂ as a function of Li-ion content, x, a convex hull can be constructed to understand the relative stability of all intermediate phases. The OCVs can also be predicted from these thermodynamic data using the following equation:⁴⁸

Fig. 4 renders the calculated formation energy convex hull and voltage profiles of different Li_xMnO₂ polymorphic phases. We note that because the simulations are performed using the cells containing different numbers of formula units, as specified in Table 1, the sampled lithiation ratios (x) vary among different polymorphs. For the four tunneled structures, i.e. α-, β-, γ- and R-MnO₂, the predicted OCV commences at approximately 3 V, which gradually decreases with increasing Li-ion content. Among them, α-Li_xMnO₂ exhibits the largest OCV sweep, over 1 V and R-Li_xMnO₂ shows the most stable voltage output (2.5–3 V) over the entire range of lithiation, which would be beneficial for achieving an overall higher energy density. Although our current simulations do not encompass a comprehensive sampling of all possible atomic arrangements of Li, especially at high Li-ion concentrations, the results adequately capture the experimentally observed trend of voltage decay in α-, β-, and R-phases of MnO₂. More specifically, both β and R-phase show higher discharge capacities than the α-phase owing to their flatter OCV curves, as documented in.^49,50 Noticeable drops in the voltage profile of ε- and λ-phases are observed at x = 0.75 and 0.5, respectively, due to the switch of preferred lithiation sites (from tetrahedral to octahedral as previously discussed), which is accompanied by significant energy penalties. Interestingly, the voltage of λ-phase is predicted to recover at x > 0.75 owing to the redistribution of Li occupancy in the lattice structure. For instance, at x = 0.75, one-third of Li-ions occupy the octahedral sites while the other two-thirds reside at the tetrahedral sites, leading to a lower symmetry structure with stronger electrostatic repulsion. This effectively destabilizes the lattice structure and results in a noticeable drop in the voltage. Upon further lithiation to LiMnO₂, Li-ions start to migrate to all octahedral sites, transforming the lattice to a high-symmetry structure with reduced electrostatic repulsion, which gives rise to the recovered voltage as shown in Fig. 4.

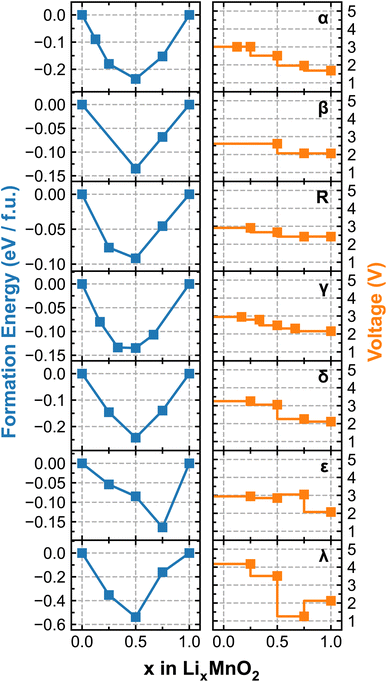Fig. 4 Calculated formation energy convex hull (left) and voltage profile (right) of each Li_xMnO₂ polymorphic phase.

3.3 Li-ion mobility

In addition to the structural and thermodynamic properties, the kinetic properties of MnO₂ are also pivotal for its performance as cathode material in LIBs. Here we evaluate Li-ion migration barriers in different phases of Li_xMnO₂, at both Li- and vacancy-diluted limits, using the DFT CI-NEB method.⁴² Based on specific crystallographic symmetries, distinct Li-ion diffusion pathways are identified between local minima and the corresponding energy profiles are extracted from the NEB calculations. A continuous Li-ion diffusion network can thus be obtained by connecting segments of these diffusion pathways. Various distinct Li-ion diffusion pathway segments are surveyed and compared to identify the energetically most favorable ones. A close visualization of all these distinct Li-ion diffusion pathways can be found in Fig. 5–11, along with the corresponding energy barriers calculated at both Li- and vacancy-diluted limits for different Li_xMnO₂ polymorphs. The relatively open structures, featuring either the 2 × 2 or 2 × 1 tunnel, generally offer a higher degree of freedom for Li-ion diffusion due to the presence of multiple open channels along the tunnel or in the planes nonparallel to the tunnel direction.

As illustrated in Fig. 5, Li-ion diffusion in α-MnO₂ can occur along the tunnel direction (path 1) or in the plane perpendicular to it (path 2). At lithium-diluted limit (Li_0.0625MnO₂), the 8h′ site is found energetically more stable than the 8h site by 79.5 meV, at fixed supercell dimension during the DFT relaxation. We note here that the relative energies obtained here with fixed cell dimension are different from the results obtained upon full cell relaxation where the 8h site is found more favorable. Although both the 8h′ and 8h are off-centered sites within the 2 × 2 tunnel structure, they provide unique coordination environments for Li-ions (2-fold vs. 5-fold for the 8h′ and 8h site, respectively) and due to the low symmetry elements presented at these Li-ion intercalation sites, their relative stability is very sensitive to local strain and consequently the simulation protocols, e.g. supercell size and relaxation scheme. Here for all CI-NEB calculations, we consider fixed cell dimensions and compare the activation energies for single Li-ion or vacancy diffusion. We admit that the predicted energy barriers may be slightly different if using a larger simulation cell or by explicitly relaxing the local strain induced during Li/vacancy migration, however, we expect such variation would be small. In this work, we aim to obtain a comparative understanding of how the morphological features of MnO₂ would affect Li-ion mobility and what design strategies can be used to selectively enhance Li-ion diffusivity in the three dimensional structure. As shown in Fig. 5, based on fixed cell relaxation, the activation energy for Li-ion hopping between the two neighboring 8h′ sites in α-MnO₂ is about 73 meV along the tunnel direction (calculated using the SCAN functional), which agrees well with a previous study performed using the GGA + U functional,⁷ and 12 meV along the in-plane direction. On the other hand, Li-ion migration through the 8h sites requires an activation energy of 65.7 meV (Fig. 5(b2)). At vacancy-diluted limit (Li_0.9375MnO₂), a single Li-ion is removed from LiMnO₂ to create a vacancy, allowing the lattice to relax into a more stable configuration with all surrounding Li-ion displaced from the original 8h site to a new tetrahedral site that is similar to the 8h′ site as identified at the Li-diluted limit (see Fig. 5(c)), but with shorter Li–O bonds formed within the tetrahedron. It is found that Li-ions migration through the two adjacent tetrahedral sites involves passing through a lower-energy meta-stable 8h site. An energy barrier of 41.3 meV is required for a Li-ion to escape from this local minimum, which is substantially lower than the value of 0.55 eV for Li-ion diffusion along the c-axis among the 8h′ sites, as reported by Tompsett et al.⁷ for a Li_0.75MnO₂ composition. The in-plane diffusion of Li-ion between two neighboring 8h sites is predicted to be extremely sluggish, due to the high activation energy required (∼516 meV). This implies that Li-ions will predominantly diffuse within the 2 × 2 tunnel structure at the vacancy-diluted limit. Overall, we expect sufficient 1-dimensional Li-ion transport in α-MnO₂ along the tunnel direction at both Li- and vacancy-diluted limits. At lower Li-ion concentrations, a spiral-type diffusion pattern, involving simultaneous diffusion along the tunnel and in-plane directions, may occur within the spacious 2 × 2 tunnels.

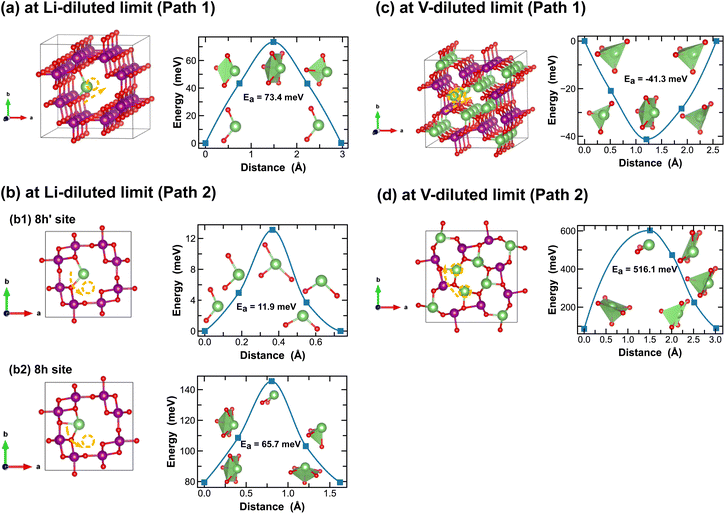Fig. 5 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in α-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

In contrast, Li-ion diffusion in β-MnO₂ is mostly restricted within the narrow 1 × 1 tunnel structure along the c-axis, as shown in Fig. 6. At the Li-diluted limit (Li_0.014MnO₂), Li-ion hopping from one stable octahedral site to the next involves passing through a meta-stable octahedral site, as shown in Fig. 6(a). The energy barrier to move a Li-ion from the most stable octahedral site to a meta-stable one is about 49.5 meV, which is defined by the energy of Li-ion at the tetrahedrally coordinated transition state. At the vacancy-diluted limit, no meta-stable site is observed along the Li-ion diffusion pathway, and the energy barrier is found substantially higher than that at the Li-diluted limit. The formation of meta-stable Li-ion intercalation sites at lower lithium concentrations is likely due to the higher degree of freedom for stretching or rotating that the lattice can offer to accommodate Li-ion migration. Nevertheless, our results imply that although the narrow 1 × 1 tunnel in β-MnO₂ would allow rapid Li-ion diffusion at the highly charged states, the increased energy barrier for Li-ion migration at the discharged states will negatively impact its overall rate capacity and cyclability.

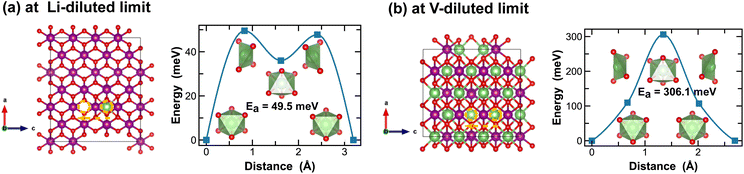Fig. 6 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in β-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

Both R- and γ-MnO₂ feature a 2 × 1 tunnel structure, presenting a variety of distinct Li-ion diffusion pathways that are different from those identified in α- and β-MnO₂, as shown in Fig. 7 and 8. At Li-diluted limits (Li_0.0208MnO₂), a Li-ion prefers to occupy the octahedral site in R-MnO₂ and tetrahedral site in γ-MnO₂ within the 2 × 1 tunnel structure. When moving between these most stable sites, γ-MnO₂ shows lower activation energies (100.2 meV vs. 317.9 meV as found in R-MnO₂). Upon reaching the vacancy-diluted limit, Li-ion diffusion occurs between the two octahedral sites within the 2 × 1 tunnels in both phases, and the energy barriers are much higher than those at the Li-diluted limit (505.2 meV and 464.9 meV in R- and γ-LiMnO₂, respectively). The energy barriers calculated for Li-ion diffusion along the 2 × 1 tunnel in R-phase, at both Li- and vacancy-diluted limits, agree well with the values previously reported by Gupta et al.²⁵ Similar to the case of α-LiMnO₂, possible Li-ion diffusion pathways nonparallel to the tunnel direction are also explored (see Fig. 7(b, d) and 8(b, d)). In general, these pathways show higher activation energies for Li-ion diffusion and thus are less favorable compared to pathways along the 2 × 1 tunnel direction in both γ- and R-phases. Since γ-phase also presents the 1 × 1 tunnels, Li-ion diffusion along the 1 × 1 tunnel direction are also examined, which involves hopping between two octahedral sites as shown in Fig. 8(c and e). At the Li-diluted limit, sites within the 1 × 1 tunnel are significantly less favorable to occupy than those in the larger 2 × 1 tunnels, with an energy difference exceeding 1 eV. Although these sites offer less energy penalty (162.4 meV) for Li-ions to move between them, they are less likely to be the dominant Li-ion diffusion channels. In contrast, at the vacancy-diluted limit, a single vacancy is found energetically more favorable to reside within the 1 × 1 tunnel than the 2 × 1 tunnel by 410 meV, and it requires less energy to migrate (313.6 meV vs. 464.9 meV).

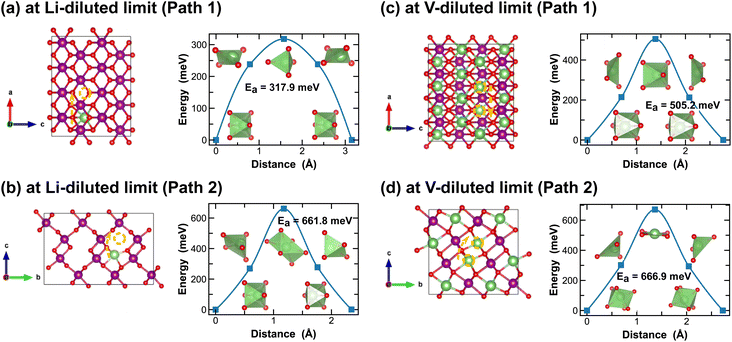Fig. 7 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in R-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

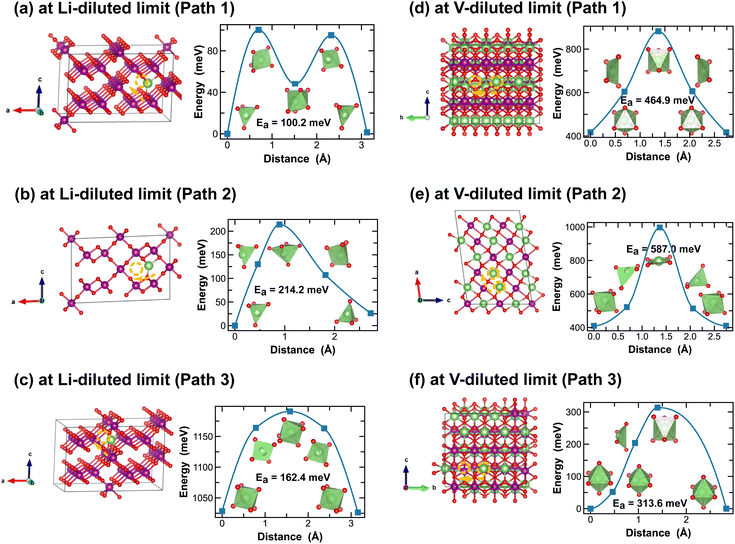Fig. 8 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in γ-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

Overall, although both R and γ-phases of LiMnO₂ possess the 2 × 1 tunnel structure, the γ-phase offers better Li-ion transport kinetics, especially at the vacancy-diluted limit, which is attributed to the additional diffusion pathway presented along the 1 × 1 tunnel direction in γ-LiMnO₂.

For the layered LiMnO₂ structures, such as the δ- and ε-phases, Li-ion diffusion predominantly occurs at the inter-layers. As shown in Fig. 9 and 10, Li-ion diffusion in δ- and ε-LiMnO₂ involves moving from one octahedral site to another, but with distinct local coordination environment experienced at the transition sites, which ultimately define the energy penalty for migration. For instance, in δ-MnO₂, the transition state shows a distorted square planar geometry along the single Li-ion diffusion pathway (Fig. 9(a)) and a well-defined octahedral geometry for single vacancy diffusion (Fig. 9(b)). The associated energy barriers are 713.3 meV and 657.3 meV, respectively.

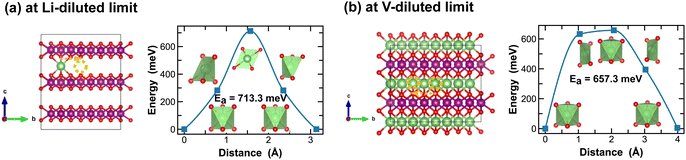Fig. 9 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in δ-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

Fig. 10 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in ε-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

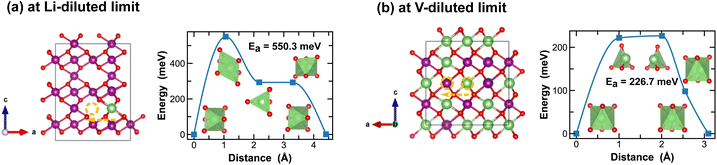
On the other hand, ε-MnO₂ exhibits a higher degree of disorders due to partial (1/2) occupancy of Mn⁴⁺ at the cation sites of the NiAs prototype structure. Here we adopt a high-symmetry structure as discussed previously and evaluate the kinetics for Li-ion migration. At the Li-diluted limit, multiple vacant octahedral sites are identified between the alternating layers of ε-Li_0.021MnO₂. Inter/Cross-layer diffusion is found challenging due to the presence of densely packed MnO₆ octahedra across the layers. An energetically feasible pathway for Li-ion diffusion is to pass through two octahedral sites within the 1/4 Mn + 3/4 vac. layers, which offer more space, as shown in Fig. 10(a). Along this pathway, a Li-ion moves through a distorted octahedral transition state and a meta-stable tetrahedral site, with an energy barrier of 550.3 meV. At the vacancy-diluted limit, a single vacancy also diffuses between the 1/4 Mn + 3/4 Li layers, with a reduced activation energy of 226.7 meV. Overall, the δ and ε-phases of MnO₂ show slower Li-ion diffusion due to the relatively high energy barriers observed. However, the Li-ion transport kinetics are found less dependent on local Li-ion concentration, as compared to other polymorphs, especially in δ-MnO₂, which is likely due to its unique layered structure that experiences less three-dimensional distortion during lithiation/delithiation.

The spinel λ-phase of MnO₂ has long been considered as a promising cathode material for LIBs, given its high voltage and mechanical robustness. However, it suffers from sluggish Li-ion transport kinetics. As shown in Fig. 11(a), at the Li-diluted limit, Li-ions primarily diffuse through the tetrahedral sites that are connected by the meta-stable octahedral sites within the three-dimensional pore structure. The associated energy barrier, approximately 500 meV, is significantly higher than those observed in the tunnel structures of other polymorphic phases discussed above. Moreover, this energy barrier escalates to 743.1 meV at the vacancy-diluted limit due to the closure of open channels presented in the original three-dimensional pore structure (see structure representation in Fig. 11(b)).

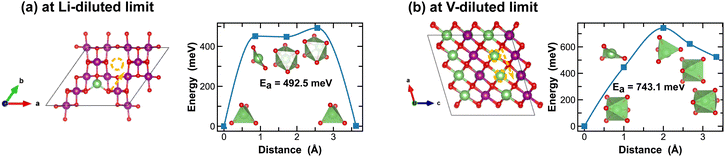Fig. 11 Li-ion diffusion pathways identified at lithium- and vacancy diluted limits (in λ-MnO₂ and LiMnO₂, respectively), with the predicted energy barriers, E_a, in meV.

We acknowledge the limitations of our current NBE calculations, such as the lack of sampling all possible Li diffusion pathways, especially at intermediate Li concentrations, and the neglect of temperature effects. To resolve these limitations, we are developing a machine-learning force field to model Li-ion transport in Li_xMnO₂ phases and extract Li-ion diffusivity at various temperatures. The results and insights obtained from these calculations will be shared with the community in a follow-up manuscript.

3.4 Performance metrics

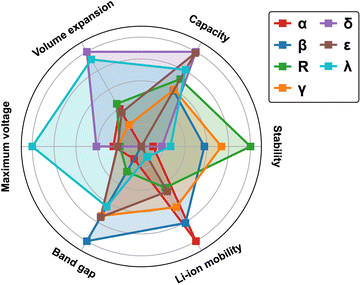
To provide a comparative overview of various MnO₂ polymorphs for LIB cathode applications, we present a radar plot in Fig. 12 based on simulation results discussed in the previous sections. All metrics are normalized to a scale of 0 to 1, with 0 indicating the least desirable and 1 representing the optimal. For instance, a smaller bandgap (normalized to 1) correlates to improved electronic conductivity (results from detailed band structure calculations can be found in Fig. S3 in ESI†), while a larger volume expansion (normalized to 0) during lithiation signifies deteriorated mechanical robustness. The metrics for measuring thermodynamic stability and Li-ion mobility are based on the average values derived from MnO₂ and its fully lithiated version, i.e. LiMnO₂. Inherent correlations are found between the structural features and materials properties:

Fig. 12 Radar plot comparing performance matrices for all MnO₂ and LiMnO₂ polymorphic phases.

The α-phase, recognized by its open 2 × 2 tunnel structure, allows rapid Li-ion transport but at reduced (volumetric) capacity. In addition, lithiation to the low-symmetry sites induce local distortion in the tunnel structure, compromising its structural stability during reversible Li-ion intercalation.

The compact β-phase stands out for its good thermal stability and electronic conductivity. Surprisingly, the narrow 1 × 1 tunnels are found sufficient for Li-ion transport, however, large volume expansion is expected upon lithiation, which makes it susceptible to mechanical failure during operation.

Both R-and γ-phases are featured by the 2 × 1 tunnels in their crystal structures and possess similar material properties. For example, they both show relatively balanced attributes across most metrics, with the R-phase being particularly stable at both charged and discharged states.

The layered δ-phase undergoes the least volume change upon full lithiation, indicating its enhanced mechanical stability. It also offers the highest Li-ion storage capacity. However, it suffers greatly from low thermodynamic stability, electronic conductivity and sluggish Li-ion transport kinetics.

The ε-phase provides high volumetric capacity, but falls short on thermal stability. It is possible that our current simulation based on a high-symmetry representation of its crystal structure underestimates its formation energy. During operation, more disordered structures may emerge with improved stability due to increased entropy contributions.

The spinel λ-phase, featured by the three-dimensional pore structure, shows the most balanced properties across all matrices investigated. It has an exceptionally high cell voltage compared to other MnO₂ polymorphs, however, its practical application is limited by the sluggish Li-ion transport kinetics.

In summary, trade-offs observed among various metrics can be largely attributed to the structural characteristics of different polymorphs, specifically, the distribution of Mn and Li within their lattices, which give rise to local variations in Mn–O hybridization and the resulting electronic response during Li-ion insertion/extraction. The tunneled structures (α, β, R, and γ-phases) generally allow rapid Li-ion transport, although their mechanical robustness and storage capacities vary. For example, the α-phase is structurally more flexible due to the presence of open tunnels, yet suffers from limited volumetric capacity to store Li-ions. In contrast, the compact beta-phase can achieve higher storage capacity but is subject to significant lithiation-induced volume expansion. The λ-phase, distinguished by its three-dimensional pore structure, enables a more uniform distribution of Li- and Mn- ions, with minimized electrostatic repulsion upon lithiation and thus can deliver balanced performance matrices, including voltage, capacity, and mechanical stability. However, once the pores are gradually filled, sluggish Li-ion transport kinetics can be expected due to the blocking effects.

4 Conclusions

In this work, we carried out a series of first-principles calculation to compare the fundamental physicochemical properties of various MnO₂ polymorphic phases for LIB cathode applications. While various trade-offs are apparent across the metrics of all polymorphs, no single polymorph is found optimal to achieve the desired performance. For example, the α polymorph potentially offers great rate capacity given its open structure to facilitate Li-ion transport, however, it under-performs in all other metrics, such as stability and the energy density that it can achieve. Conversely, the λ-phase excels in several aspects including cell voltage, mechanical stability, volumetric storage capacity, and electronic properties. Yet, it faces challenges with thermal stability and presents less-than-ideal Li-ion transport kinetics for practical applications. Both γ- and R-polymorphs, with the presence of 2 × 1 tunnels, demonstrate relatively balanced performance across the assessed metrics. Overall, if one can combine features of λ- and β-phases through structural engineering, enhanced performance may be achieved.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was performed under the auspices of the U. S. DOE by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 and supported by Laboratory Directed Research and Development Grant 23-SI-002.

References

1. Y. Chabre and J. Pannetier, Prog. Solid State Chem., 1995, 23, 1–130.
2. T. Brousse, D. Bélanger, K. Chiba, M. Egashira, F. Favier, J. Long, J. R. Miller, M. Morita, K. Naoi, P. Simonet al., Springer Handbook of Electrochemical Energy, 2017, pp. 495–561.
3. J. Shin, J. K. Seo, R. Yaylian, A. Huang and Y. S. Meng, Int. Mater. Rev., 2020, 65, 356–387.
4. S. Devaraj and N. Munichandraiah, J. Phys. Chem. C, 2008, 112, 4406–4417.
5. C. Sun, Y. Zhang, S. Song and D. Xue, J. Appl. Crystallogr., 2013, 46, 1128–1135.
6. C. Ling and F. Mizuno, Chem. Mater., 2012, 24, 3943–3951.
7. D. A. Tompsett and M. S. Islam, Chem. Mater., 2013, 25, 2515–2526.
8. C. Ling, R. Zhang, T. S. Arthur and F. Mizuno, Chem. Mater., 2015, 27, 5799–5807.
9. M. H. Alfaruqi, S. Islam, J. Lee, J. Jo, V. Mathew and J. Kim, J. Mater. Chem. A, 2019, 7, 26966–26974.
10. Y. Yuan, A. Nie, G. M. Odegard, R. Xu, D. Zhou, S. Santhanagopalan, K. He, H. Asayesh-Ardakani, D. D. Meng and R. F. Klie, et al. , Nano Lett., 2015, 15, 2998–3007.
11. R. Kempaiah, H. Chan, S. Srinivasan, S. K. Sankaranarayanan, B. Narayanan and A. Subramanian, ACS Appl. Energy Mater., 2021, 4, 12099–12111.
12. S. Turner and P. R. Buseck, Science, 1981, 212, 1024–1027.
13. D. Murphy, F. Di Salvo, J. Carides and J. Waszczak, Mater. Res. Bull., 1978, 13, 1395–1402.
14. D. Su, H.-J. Ahn and G. Wang, NPG Asia Mater., 2013, 5, e70.
15. F. Jiao and P. G. Bruce, Adv. Mater., 2007, 19, 657–660.
16. J.-Y. Luo, J.-J. Zhang and Y.-Y. Xia, Chem. Mater., 2006, 18, 5618–5623.
17. D. Wang, L.-M. Liu, S.-J. Zhao, B.-H. Li, H. Liu and X.-F. Lang, Phys. Chem. Chem. Phys., 2013, 15, 9075–9083.
18. W. I. Jung, M. Nagao, C. Pitteloud, K. Itoh, A. Yamada and R. Kanno, J. Mater. Chem., 2009, 19, 800–806.
19. C. Wang, Y. Zeng, X. Xiao, S. Wu, G. Zhong, K. Xu, Z. Wei, W. Su and X. Lu, J. Energy Chem., 2020, 43, 182–187.
20. C. Yuan, Y. Zhang, Y. Pan, X. Liu, G. Wang and D. Cao, Electrochim. Acta, 2014, 116, 404–412.
21. H. Kim, N. Venugopal, J. Yoon and W.-S. Yoon, J. Alloys Compd., 2019, 778, 37–46.
22. S. Kim, J. S. Kang, H. Joo, Y.-E. Sung and J. Yoon, Environ. Sci. Technol., 2020, 54, 9044–9051.
23. M. H. Alfaruqi, J. Gim, S. Kim, J. Song, D. T. Pham, J. Jo, Z. Xiu, V. Mathew and J. Kim, Electrochem. Commun., 2015, 60, 121–125.
24. Q. Xie, G. Cheng, T. Xue, L. Huang, S. Chen, Y. Sun, M. Sun, H. Wang and L. Yu, Mater. Today Energy, 2022, 24, 100934.
25. P. K. Gupta, A. Bhandari, J. Bhattacharya and R. G. S. Pala, J. Phys. Chem. C, 2018, 122, 11689–11700.
26. P. K. Gupta, A. Bhandari, J. Bhattacharya and R. G. S. Pala, J. Power Sources, 2020, 450, 227619.
27. T. Hatakeyama, N. L. Okamoto and T. Ichitsubo, J. Solid State Chem., 2022, 305, 122683.
28. D. A. Kitchaev, H. Peng, Y. Liu, J. Sun, J. P. Perdew and G. Ceder, Phys. Rev. B, 2016, 93, 045132.
29. D. A. Kitchaev, S. T. Dacek, W. Sun and G. Ceder, J. Am. Chem. Soc., 2017, 139, 2672–2681.
30. S. Ma, X. Ye, X. Jiang, W. Cen, W. Jiang and H. Wang, J. Alloys Compd., 2021, 852, 157007.
31. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
36. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al. , APL Mater., 2013, 1, 011002Mn.
37. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
38. N. Yamamoto, T. Endo, M. Shimada and T. Takada, Jpn. J. Appl. Phys., 1974, 13, 723–724.
39. J. E. Greedan, N. Raju, A. Wills, C. Morin, S. Shaw and J. Reimers, Chem. Mater., 1998, 10, 3058–3067.
40. L. Guo, D. Peng, H. Makino, T. Hanada, S. Hong, K. Sumiyama, T. Yao and K. Inaba, J. Appl. Phys., 2001, 90, 351–354.
41. H. Zhu, J. Luo, H. Yang, J. Liang, G. Rao, J. Li and Z. Du, J. Phys. Chem. C, 2008, 112, 17089–17094.
42. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
43. C.-H. Kim, Z. Akase, L. Zhang, A. H. Heuer, A. E. Newman and P. J. Hughes, J. Solid State Chem., 2006, 179, 753–774.
44. Y. Jiang, L. Yuan, X. Wang, W. Zhang, J. Liu, X. Wu, K. Huang, Y. Li, Z. Liu and S. Feng, Angew. Chem., 2020, 132, 22848–22855.
45. A. Boulineau, L. Croguennec, C. Delmas and F. Weill, Solid State Ionics, 2010, 180, 1652–1659.
46. T. Matsunaga, H. Komatsu, K. Shimoda, T. Minato, M. Yonemura, T. Kamiyama, S. Kobayashi, T. Kato, T. Hirayama and Y. Ikuhara, et al. , Chem. Mater., 2016, 28, 4143–4150.
47. S. Zhang, J. Wang, L. Sun, F. Dang, Y. Du, H. J. Seifert and T. Lei, Phys. Rev. Mater., 2022, 6, 055404.
48. I. A. Courtney, J. Tse, O. Mao, J. Hafner and J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 15583.
49. C. Julien, A. Mauger, A. Vijh, K. Zaghib, C. Julien, A. Mauger, A. Vijh and K. Zaghib, Lithium Batteries, Springer, 2016.
50. C. M. Julien and A. Mauger, Nanomaterials, 2017, 7, 396.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4se00279b

---