Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Equivalent circuit models for predicting electrical and gas output characteristics of CO2 electrolysis cells†
Yuki
Kudo
 *,
Akihiko
Ono
,
Satoshi
Mikoshiba
and
Ryota
Kitagawa
*,
Akihiko
Ono
,
Satoshi
Mikoshiba
and
Ryota
Kitagawa
Corporate Research & Development Center, Toshiba Corporation, Kawasaki, Kanagawa 212-8582, Japan. E-mail: yuki.kudo@toshiba.co.jp
First published on 14th May 2024
Abstract
This paper proposes an equivalent circuit model that simulates the current–voltage characteristics, faradaic efficiency, and gas flow rates output from the cathode and anode channels for a CO2 to CO producing electrolysis cell. Considering that the CO2 flow rate introduced into the cathode channel limits the CO partial current density, this model can predict the output of CO, H2, and CO2 flow rates from the cathode channel. Furthermore, the model also enables the prediction of CO2 flow rate output from the anode channel by assuming that both the carbonate and hydrogen carbonate ions transfer from the cathode side to the anode side. These simulations are validated using experimental results of the dependence of the electrical and gas output characteristics on the CO2 flow rate. Our results show that the proposed model based on electrochemical kinetics and ion transfer phenomena can contribute to efficient power supply controllers and auxiliary equipment designs for CO2 electrolysis systems.
Introduction
Global warming has become an urgent issue, and the development of technologies for recycling carbon dioxide (CO2), which is a greenhouse gas, has become increasingly important.1 CO2 electrolysis technology, which electrochemically converts CO2 into raw materials for fuels and chemical products using renewable energy sources such as wind and solar power, is a promising technology for promoting the spread of renewable energy and reducing CO2.2–4 Since various chemical compounds including carbon monoxide (CO), formic acid (HCOOH), methane (CH4), and ethylene (C2H4) have been obtained through improved catalyst materials, there has been research into new catalysts from the viewpoint of improving catalytic activity and selectivity.5–7 In particular, CO has been a major focus of research as it can be used as a chemical raw material and reducing agent, and a selectivity of more than 95% has been achieved.8–14 In contrast, the low solubility and diffusivity of CO2 in liquid electrolytes limit the current density of CO2 electrolysis to a few tens of milliamperes per square centimeter, which is challenging from an economic point of view. By employing a gas diffusion electrode (GDE) that can supply CO2 close to the catalyst, the current density can be increased to a practical value of more than 1 A cm−2.15–18 Such technological developments for high current density have enabled high-throughput CO2 processing in smaller CO2 electrolysis cells (ECs). In addition, membrane electrode assemblies (MEAs), which are zero gap-type cells with a short distance between electrodes, are being developed to reduce ohmic loss.19–24In order to further improve the performance of CO2 ECs, it is crucial to optimize the structure of the GDE and cell operating conditions. Since various physical phenomena such as electrochemical reactions, chemical equilibrium reactions, mass transport, and heat transport co-occur in CO2 ECs, several researchers have been studying models based on multiphysics simulations that take into account multiple physical phenomena and their interactions, and guidelines for designing good CO2 ECs have been proposed.25–28 In multiphysics simulations, it is vital that the many parameters are set correctly. However, it is difficult to individually determine with high accuracy the physical properties and nanostructural parameters of each component of the CO2 EC as well as the behaviors of chemical species such as gases and ions inside the cell to translate these into the many parameters. In addition, the longer time required for precise calculation by multiphysics models may be unsuitable for predicting the performance of scaled-up cells and designing control and operating systems for CO2 ECs. Therefore, for the design of a pilot-scale CO2 electrolyzer, Edwards et al. proposed a semi-empirical model and demonstrated its ability to accurately predict the performance of the electrolyzer.29
In electrochemical devices such as lithium-ion batteries, fuel cells, and water ECs, equivalent circuit models that represent functional descriptions by circuit elements have been constructed and are used to predict device performance.30–37 This paper proposes a simple equivalent circuit model representing a CO2 EC producing CO as circuit elements based on mathematical equations derived from electrochemical kinetics and ion transfer phenomena as a simulation technique that can predict cell performance with fewer parameters in a shorter calculation time. Furthermore, providing electrical and gas input/output terminals on the circuit elements is expected to enable the prediction of the electrical and gas output characteristics of the cell in response to electric power and CO2 flow input.
Equivalent circuit model for CO2 EC producing CO
In this section, we describe the operating principles, a mass balance model, and an electrical characteristics model of a CO2 EC that produces mainly CO along with a small amount of hydrogen (H2), and then propose an equivalent circuit model.Principle of operation
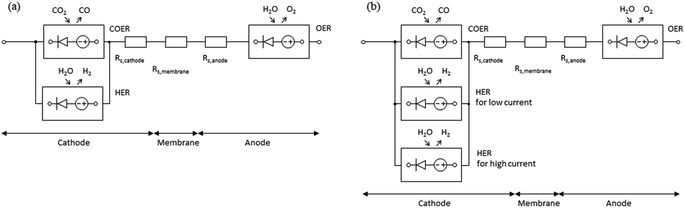
As shown in Fig. 1a, in a zero-gap type CO2 EC, electrolysis reactions occur at both electrodes when a voltage is applied between the cathode and anode (i.e., when an electric current flows). At the cathode, the primary and side electrolysis reactions produce CO from CO2 and H2 from H2O, while at the anode, oxygen (O2) is produced. In addition, as described below, carbonate ions (CO32−) and hydrogen carbonate ions (HCO3−) move from the cathode to the anode and react with H+ to produce CO2 at the anode.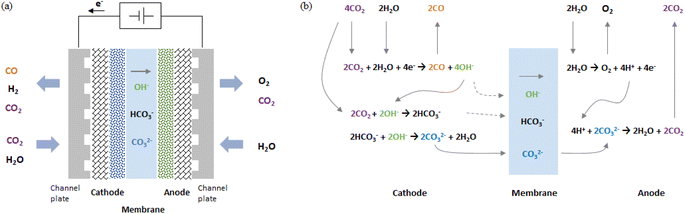 | ||
| Fig. 1 Schematic drawing of (a) configuration of zero-gap type CO2 EC producing CO and (b) electrochemical and chemical equilibrium reaction steps. | ||
Fig. 1b schematically illustrates the steps of the CO2 electrolytic reaction. First, CO2 and H2O introduced into the cathode receive electrons and are decomposed into CO and OH−.
Cathode:
| CO2 + H2O + 2e− → CO + 2OH− | (1) |
OH− reacts with CO2 to produce a hydrogen carbonate ion, which further reacts with OH− to produce carbonate ions. The details of the chemical equilibrium reactions are described in the literature.25,26
| CO2 + OH− ↔ HCO3− | (2) |
| HCO3− + OH− ↔ CO32− + H2O | (3) |
CO32− and HCO3− move to the anode through the membrane by drift and diffusion. The solid gray line in Fig. 1b shows an example of the case in which many CO32− move.
At the anode, H2O is decomposed into O2, H+, and electrons (for acidic oxygen evolution reactions).
Anode:
| 2H2O → O2 + 4H+ + 4e− | (4) |
H+ reacts with CO32− or HCO3− transferred from the cathode and is converted to H2O and CO2.
| 2H+ + CO32− ↔ H2O + CO2 | (5) |
| H+ + HCO3− ↔ H2O + CO2 | (6) |
Summarizing eqn (1) through (6), the overall reaction of the CO2 EC is the CO evolution reaction (COER) and O2 evolution reaction (OER).
Overall reaction:
| 2CO2 → 2CO + O2 | (7) |
In a CO2 EC using an anion exchange membrane, COER proceeds by transferring anions such as CO32− or HCO3− from the cathode to the anode. In this kind of anion transfer type cell, some of the CO2 input into the cathode is output from the anode (as shown in eqn (5) and (6)).27,38
When the CO2 input flow rate is sufficiently high, the CO2 reduction reaction shown in eqn (1) is the main reaction. However, when the CO2 input flow rate is low or when little CO2 reaches the catalyst because flooding (in which the pores of the gas diffusion layer and catalyst layer become filled with water), the H2 evolution reaction (HER) can occur as a side reaction.
Mass balance model
We describe a model for estimating the gas output from the cathode and anode based on the operating principles of the CO2 EC.The CO and H2 molar flow rates output from the cathode are expressed in terms of the partial current density used for COER and HER.
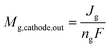 | (8) |
In anion transfer type cells, some CO2 input to the cathode becomes CO32− or HCO3−, which moves to the anode by drift and diffusion and is converted to CO2 again. Therefore, the unreacted CO2 output from the cathode is the CO2 input to the cathode minus the CO2 used for COER and the CO2 output from the anode.
| MCO2,cathode,out = MCO2,cathode,in − MCO,cathode,out − MCO2,anode,out | (9) |
In this model, we assume that unreacted CO2 is quickly discharged. Because CO2 and CO are equimolar reactions, as shown in eqn (1), the second term on the right side of eqn (9) is expressed using the CO flow rate produced by CO2 reduction. Since the charges of CO32− and HCO3− differ by a factor of two, as shown in eqn (5) and (6), the CO2 (per reaction electron number) output from the anode depends on the ion species. Several papers have reported that the anions migrating across the membrane in CO2 ECs with AEM are CO32−.21,38,39 However, as discussed later in the Results section, our measured CO2 EC's characteristics can be explained by considering both CO32− and HCO3− migration. Therefore, we propose a model that considers CO32− and HCO3− migration by expressing the fraction of CO32− that transfers from the cathode to the anode as G (the fraction of HCO3− = 1 − G). Using G, the CO2 output from the anode can be expressed as
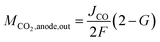 | (10) |
As in eqn (8), the O2 output from the anode can be expressed using the current JO2 produced by OER. Moreover, if only OER occurs in the anode, JO2 is equal to the total current density (Jtotal) and thus can also be expressed as
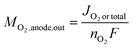 | (11) |
A more generalized mass balance model for the case in which the CO2 reduction reaction produces CxHyOz is described in the ESI.†
Electrical characteristic model and equivalent circuit model
We consider a model that represents the steady-state current–voltage characteristics of the CO2 EC using the fewest possible parameters. Combined with the mass balance model above, we then propose a simple equivalent circuit model that can predict electrical and gas output characteristics.First, the Tafel equation can describe the electrode kinetics equation because the error between the Butler–Volmer equation as the general formula of the electrode kinetics and the Tafel equation is small in the region of high overpotentials (approximately 0.2 V or more). The current due to OER at the anode and the current due to HER in the side reaction at the cathode can be expressed as follows.
OER at anode:
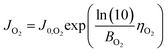 | (12) |
HER at cathode:
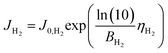 | (13) |
However, since COER does not occur if the CO2 input flow rate is zero, the effect of the CO2 input flow rate needs to be considered for COER such that COER depends on the amount of CO2 reaching the catalyst, and an equation incorporating the diffusion limit of CO2 is applied to the Tafel equation.40 Using the CO limiting current density (JCO, L), which is the maximum current density where COER occurs, the partial current density of COER (JCO) can be expressed as follows.
COER at cathode:
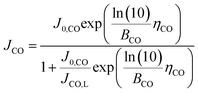 | (14) |
The maximum flow rate of CO2 available for COER is the amount of CO2 input from the cathode minus the CO2 that moves to the anode. In other words, JCO, L is limited by the maximum flow rate of CO2 available for COER. Using G, the fraction of CO32− that transfers from the cathode to the anode, the relationship between JCO, L and the CO2 flow rate input to the cathode can be expressed as
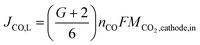 | (15) |
In the case of JCO, L, the CO2 flow rate output from the anode can be expressed as
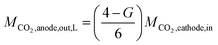 | (16) |
A more generalized equation for the case in which the CO2 reduction reaction produces CxHyOz is described in the ESI.†
Based on COER of the main reaction, the cell voltage (Vcell) can be expressed as the sum of the theoretical voltage (the standard electrode potential of OER minus that of COER), the cathode overpotential ηCO for COER, the anode overpotential ηO2 for OER, and ohmic drops (IR drops).
| Vcell = UO2 − UCO + ηCO + ηO2 + JtotalA(Rs,cathode + Rs,anode + Rs,membrane) | (17) |
| Vcell = UO2 − UH2 + ηH2 + ηO2 + JtotalA(Rs,cathode + Rs,anode + Rs,membrane) | (18) |
Based on the mass balance and electrical characteristics models described above, the equivalent circuit models are shown in Fig. 2. Since eqn (12)–(14) include an exp function and have characteristics similar to those of a diode, these are represented by the symbol for a diode with gas inputs and outputs. The DC power supply imitates the potential shift due to standard electrode potential and pH. In the cathode, when COER (the main reaction) and HER (the side reaction) co-occur, the potentials of COER and HER for the reference electrode are equal. Therefore, they can be represented by a parallel circuit of COER and HER elements, as shown in Fig. 2a. As described later in the Results section, HERs in the low and high current density regions behave differently in the measured CO2 EC characteristics. In such cases, we propose a model with two HER elements with different characteristics connected in parallel, as shown in Fig. 2b.
Experimental
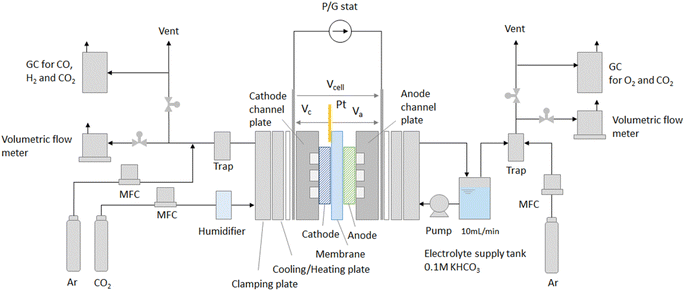
We measured the electrical and gas output characteristics versus CO2 flow rate in the CO2 EC to estimate the equivalent circuit parameters and for model validation.A schematic drawing of the experimental setup is shown in Fig. 3. An MEA composed of cathode/membrane/anode is sandwiched between titanium flow channel plates. The potentials were measured by touching a Pt pseudo-reference electrode to the membrane on the cathode side. The cell temperature was set to 50 °C, and CO2 was supplied to the cathode inlet at flow rates of 2.5, 5, 7.5, and 10 sccm cm−2 per electrode area. CO2 was humidified to suppress precipitation of the anode electrolyte as salts at the cathode. The anode flow channel was fed with 0.1 M KHCO3 at a flow rate of 10 ml min−1. The electrode area (cathode and anode) was 16 cm2 (=4 cm × 4 cm), which was a medium-sized area that could be evaluated on a laboratory scale. Au/C was used as the cathode catalyst.24 The gas diffusion layer (GDL) was commercially available carbon paper with a microporous layer. The electrode area, thickness, and CO2 flow rate, which are important parameters affecting cell performance, are described in detail in the ESI.†
After diluting the gas output from the cathode and anode sides with Ar, the flow rate was measured using a volumetric flow meter. Since the mixed gas is output from the cell, highly accurate flow measurement using a volumetric flowmeter is essential. The gas concentration output from the cell was analyzed by gas chromatography.
The cathode potential and anode potential relative to the Pt pseudo-reference electrode (Vc and Va) and the cell voltage (Vcell) were measured for a constant current flow between the cathode and anode. Note that Va here includes the IR drop at the membrane. The IR drops were removed from the measured potentials, and the overpotentials ηCO, ηH2, and ηO2 were calculated. The output gas flow rate, the partial current densities, and the faradaic efficiencies of each gas were also calculated. Tafel plots were performed in COER, HER, and OER to estimate the Tafel slopes and the exchange current densities. Details of the experimental methods and calculation formulae are described in the ESI.†
Results, simulation, and discussion
First, we estimated equivalent circuit parameters, and then examined the model validity by comparing the experimental and simulated data.Estimation of equivalent circuit parameters
The following procedure was used to estimate the equivalent circuit parameters.Step 1. Estimate the CO32− transfer fraction G, a key parameter in our model.
Step 2. Estimate the parameters of the Tafel equation from the measured overpotentials.
Step 3. Using the parameters estimated in Step 2 as initial values, re-estimate the parameters by fitting an equivalent circuit model considering the effect of CO2 flow rate.
Step 1.
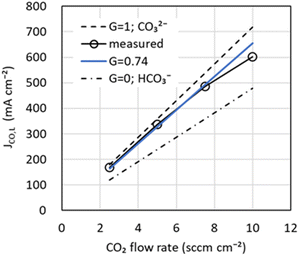
As shown in eqn (10) and (15), the originality of our model is that the fraction of CO32− moving from the cathode to the anode is used to represent the CO2 flow rate output from the anode and the CO limiting current density JCO, L. Fig. 4 shows JCO, Lversus CO2 flow rate. Note that JCO, L was obtained from the total current density dependence (Jtotal) of JCO at varying CO2 flow rates (see Fig. S3 in the ESI†). In Fig. 4, the theoretical values of JCO, L for CO32− (G = 1) and HCO3− (G = 0) using eqn (15) are shown as dotted and dotted-dashed lines, respectively. The measured JCO, L is slightly lower than the theoretical value of CO32−, suggesting that CO32− and HCO3− have moved. In addition, JCO, L exhibited a nonlinear change with respect to the CO2 flow rate. Several researchers reported a phenomenon in which salts of electrolyte precipitate inside the cathode in the high current density region and inhibit CO2 diffusion to the catalyst.41–43 Since this salt precipitation phenomenon accelerates with increasing current density, CO2 diffusion may be inhibited in the high current density region, resulting in lower JCO, L. In our model, nonlinear dependence in JCO, L is disregarded, and G is obtained by the least-squares method using data from 2.5 to 7.5 sccm cm−2. G was estimated to be 0.74, making the percentages of CO32− and HCO3− migration about 74% and 26%, respectively. The blue line in Fig. 4, shows the calculated value of JCO, L using the estimated G. Note the difference between the model and the actual measurement in the high current density region. In the future, we intend to investigate a model of salt precipitation for the non-linearity of JCO, L.
Step 2.
Fig. 5 shows Tafel plots (calculated using eqn (S1)–(S6)† with IR correction from JCO and JH2versus the cathode potential and JO2versus the anode potential at a CO2 flow rate of 5 sccm cm−2 and temperature of 50 °C). In Fig. 5a, the slope of ηCO gradually increases as log (JCO) increases. This suggests that the increase in JCO, or the increase in CO2 consumption, decreases the CO2 available for COER, thereby increasing ηco. Therefore, the Tafel slope (B) and the exchange current density (J0) were estimated using the data in the low current density region, where CO2 consumption is small (Table 1). The calculated values are shown by solid lines in Fig. 5a, where the Tafel slope for COER (BCO) is 136 mV decade−1, which is close to the reported case of COER with a Au catalyst5,8,44,45, suggesting that the COER reported here has a similar reaction mechanism in which the CO2 absorption process is the rate-limiting step.
 | ||
| Fig. 5 Tafel plots at a CO2 flow rate of 5 sccm cm−2 and cell temperature of 50 °C. (a) CO evolution reaction (COER). (b) H2 evolution reaction (HER). (c) O2 evolution reaction (OER). | ||
| Parameter | Value | Unit |
|---|---|---|
| B CO | 136 | mV decade−1 |
| J 0,CO | 3.81 × 10−3 | mA cm−2 |
| B H2 (high current density) | 54.4 | mV decade−1 |
| J 0,H2 (high current density) | 1.16 × 10−16 | mA cm−2 |
| B H2 (low current density) | 977 | mV decade−1 |
| J 0,H2 (low current density) | 7.34 × 10−1 | mA cm−2 |
| B O2 | 154 | mV decade−1 |
| J 0,O2 | 1.66 × 10−1 | mA cm−2 |
The overpotential of HER shown in Fig. 5b shows two regions with different slopes in the low and high current density regions. This indicates that two reaction mechanisms exist in the HER, and the Tafel parameters were therefore estimated separately for the two regions (Table 1). The Tafel slope (BH2) in the high current density region was 54 mV decade−1, which is close to the Tafel slope of 60 mV decade−1 of polycrystalline gold.46 However, the Tafel slope in the low-current region was 977 mv decade−1, which is much larger compared with the 60–120 mv decade−1 reported for single or polycrystalline gold.46–48 This reaction mechanism is unknown and will be the subject of future work. To describe the behavior of these two HERs, the equivalent circuit model for the simulation described below employs two HER elements with different characteristics (low current density region and high current density region) connected in parallel, as shown in Fig. 2b.
At the OER overpotential ηO2 shown in Fig. 5c, the Tafel slope (BO2) estimated using data in the low current density region is 154 mv decade−1, which is larger than the value of 40–70 mV decade−1 reported for Ir-based catalysts.49–52 Nonlinear behavior is also exhibited where the slope increases with increasing current density, indicating that modeling by the Tafel equation is somewhat inappropriate. This behavior can be attributed to the difference in OH− concentration between the cathode and anode sides, that is, the effect of the potential difference due to the pH difference. Furthermore, the Pt pseudo-reference electrode is in tight contact with the cathode side of the membrane because the emphasis is on measuring the electrical properties of the cathode. Therefore, the measured anode potential includes the OER overpotential and potential change due to the pH difference between the cathode and anode side. If the pH difference increases with increasing current density, resulting in an increased potential difference between the cathode and anode, the BO2 may be slightly overestimated. Because it is not easy to measure the pH inside the cell, we have adopted an approximate model where pH is a constant value. It should be noted that the OER parameters in our equivalent circuit model include the effect of the pH difference and the activity of the anode catalyst.
Step 3.
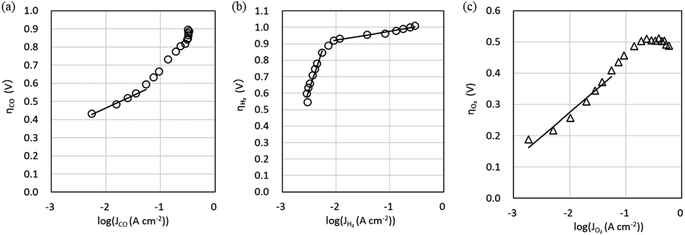
The characteristics of the COER element are described by eqn (14) and (15), which take into account the effect of CO2 flow rate, and the Tafel parameters were re-estimated by fitting using the equivalent circuit model in Fig. 2b. Simscape Electrical and Simulink (MathWorks®) were used as the circuit simulator and parameter estimator. The values from Step 2 (Table 1) were used as the initial values for the fitting. Fig. 6 shows the relationship between the cathode potential Vc and JCO and JH2 and the relationship between the anode potential Va and JO2. Both Vc and Va include the IR drops. Theoretical values such as the standard electrode potential of COER and the reference electrode potentials for the standard hydrogen electrode and pH approximated by constant values were excluded from the fitting parameters as fixed values (Table 2). Parameters were estimated by the least-squares method so that the difference between the experimental data indicated by the markers and the simulated data, indicated by the dotted lines in Fig. 6, would be small (Table 2).
 | ||
| Fig. 6 Measured cathode potential Vc and anode potential Va relative to the Pt pseudo-reference electrode and simulation using the equivalent circuit model in Fig. 2b. (a) CO evolution reaction (COER). (b) H2 evolution reaction (HER). (c) O2 evolution reaction (OER). | ||
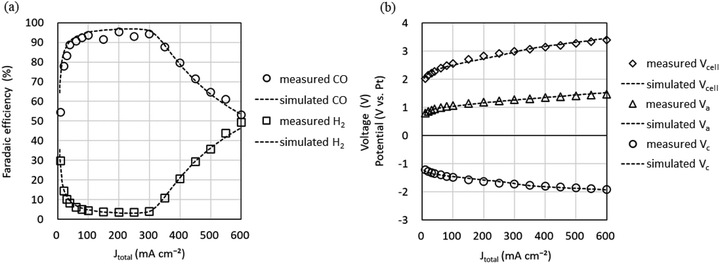
Fig. 7 shows the experimental data (markers) for the Jtotal dependence of faradaic efficiency (FE) and Vcell, Vc, and Va and the simulation data (dotted lines) using the parameters in Tables 2 and 3. It can be seen that the simulation reproduces well the shape of the Jtotal dependence of FE in the experiment. However, there is a slight difference between the experimental and simulated data in Vcell, which may be because constant values approximate pH and series resistances (Rss) in our model. Since measuring the current dependence of pH and each RS separately is difficult, we improve the equivalent circuit model based on multiphysics analysis.
| Parameter | Value | Unit |
|---|---|---|
| B CO | 132 | mV decade−1 |
| J 0,CO | 1.84 × 10−3 | mA cm−2 |
| B H2 (high current density) | 51.2 | mV decade−1 |
| J 0,H2 (high current density) | 6,13 × 10−19 | mA cm−2 |
| B H2 (low current density) | 587 | mV decade−1 |
| J 0,H2 (low current density) | 2.16 × 10−1 | mA cm−2 |
| B O2 | 138 | mV decade−1 |
| J 0,O2 | 8.06 × 10−2 | mA cm−2 |
Simulation using equivalent circuit model
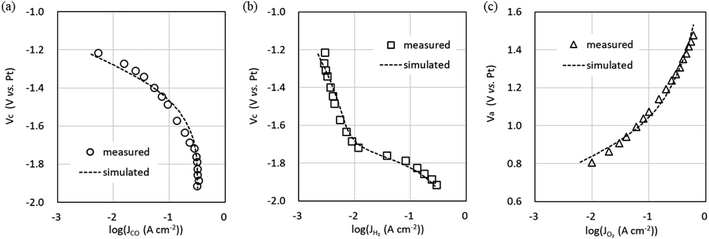
The CO output from the CO2 EC is intended to be used as feedstock for the chemical synthesis process at the latter stage of the CO2 EC. Since the composition of the feedstock gases is helpful information in the chemical synthesis process, predicting the gas composition output from the CO2 EC, that is, the flow rate of each gas, is vital in the system design. The equivalent circuit simulations were performed by varying the CO2 flow rate to predict the flow rate of each gas output from the CO2 EC.Fig. 8 shows the Jtotal dependence of gas flow rate output from the cathode for four CO2 input flow conditions. The values listed in Tables 2 and 3(determined from the experimental data at a CO2 flow rate of 5 sccm cm−2) and G = 0.74 were used for the simulation. It can be seen that the CO2 output flow rate decreases (Fig. 8a) and the CO flow rate increases with increasing Jtotal (Fig. 8b). It can also be seen that the CO flow rate saturates and the H2 flow rate of the sub-reaction starts (Fig. 8c) when the CO2 is used up. In addition, the simulation reproduces well this behavior of the experiment. The simulation of the CO2 flow rate output from the anode reproduces the shape of the experiment well, as shown in Fig. 8d. The simulations of faradaic efficiency and cell voltage at 2.5, 7.5, and 10 sccm cm−2 using parameter values determined at a CO2 flow rate of 5 sccm cm−2 also reproduced the shape of the experimental data well (Fig. S5 in the ESI†). The computation time for these equivalent circuit simulations was short, requiring only a few minutes. Thus, the equivalent circuit model can be used to predict each gas flow rate output from the cathode and anode and the electrical characteristics of the CO2 EC in a short time when the CO2 flow rate input to the cathode is varied. Therefore, the equivalent circuit model can be used to predict the output characteristics of the CO2 EC.
 | ||
| Fig. 8 Gas flow rate output from the cathode and anode channels versus total current density (Jtotal) for four CO2 input flow conditions. (a) CO2, (b) CO, and (c) H2 are output from the cathode channel. (d) O2 is output from the anode channel. Experimental data are shown as markers and simulation data using the values listed in Tables 2 and 3 and G = 0.74 as dotted lines. | ||
Conclusions
We proposed an equivalent circuit model for predicting the electrical and gas output characteristics of CO2 electrolysis cells (ECs). In this model, an element representing CO evolution reaction (COER) that takes into account the CO limiting current density (the maximum CO partial current density where COER occurs) and an element representing H2 evolution reaction (HER) are connected in parallel based on formulae derived from the electrode kinetics and ion transfer phenomenon, and this parallel circuit is connected in series with an element representing O2 evolution reaction (OER) and the series resistances of the cathode, anode, and membrane. We confirmed that simulations using our equivalent circuit model reproduce well the experimental results. Auxiliary equipment such as an electric power supply system, gas and liquid supply system, chemical product storage system, and cooling system are needed to operate the CO2 EC. The proposed model is highly compatible with the equivalent circuit models of the electrical, mass transport, and thermal systems of auxiliary equipment, and is useful for designing the auxiliary equipment.However, in our model, the pH difference between the cathode and anode side and the phenomenon whereby the membrane resistance depends on current density are imposed on the OER characteristics of the anode, which simplifies the behavior inside the cell. A multiphysics simulation is suitable for predicting this kind of cell internal behavior. It is desirable to improve the accuracy of the formulae of the equivalent circuit model based on the multiphysics model and build a model that more correctly represents cell behavior. The development of components such as electrocatalysts, electrodes, and membranes, understanding of cell behavior by the multiphysics model, and rapid system design by the equivalent circuit model are expected to contribute to faster practical application of CO2 electrolysis systems.
Author contributions
Y. Kudo conducted the modeling and performed the experiments. A. Ono assisted in the design of the automatic measuring equipment and the flow channel. S. Mikoshiba provided input on chemical equilibrium reactions. Y. Kudo wrote the manuscript with contributions and revisions from R. Kitagawa. All authors have read and agreed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Part of this work was commissioned by Ministry of the Environment, Government of Japan.References
- IPCC, IPCC Fifth Assessment Synthesis Report, Cambridge University Press, Cambridge, UK New York, NY, USA, 2014 Search PubMed.
- M. Jouny, W. Luc and F. Jiao, Ind. Eng. Chem. Res., 2018, 57, 2165–2177 CrossRef CAS.
- C. Chen, J. F. Khosrowabadi Kotyk and S. W. Sheehan, Chem, 2018, 4, 2571–2586 CAS.
- M. G. Kibria, J. P. Edwards, C. M. Gabardo, C.-T. Dinh, A. Seifitokaldani, D. Sinton and E. H. Sargent, Adv. Mater., 2019, 31, e1807166 CrossRef PubMed.
- Y. Hori, in Modern Aspects of Electrochemistry, ed. C. G. Vayenas, R. E. White and M. E. Gamboa-Aldeco, Springer New York, New York, NY, 2008, pp. 89–189 Search PubMed.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- G. Wang, J. Chen, Y. Ding, P. Cai, L. Yi, Y. Li, C. Tu, Y. Hou, Z. Wen and L. Dai, Chem. Soc. Rev., 2021, 50, 4993–5061 RSC.
- Y. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972 CrossRef CAS PubMed.
- C. Costentin, S. Drouet, M. Robert and J.-M. Savéant, Science, 2012, 338, 90–94 CrossRef CAS PubMed.
- C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 7231–7234 CrossRef CAS PubMed.
- J. Qiao, Y. Liu, F. Hong and J. Zhang, Chem. Soc. Rev., 2014, 43, 631–675 RSC.
- M. B. Ross, P. De Luna, Y. Li, C.-T. Dinh, D. Kim, P. Yang and E. H. Sargent, Nat. Catal., 2019, 2, 648–658 CrossRef CAS.
- R. Shi, J. Guo, X. Zhang, G. I. N. Waterhouse, Z. Han, Y. Zhao, L. Shang, C. Zhou, L. Jiang and T. Zhang, Nat. Commun., 2020, 11, 3028 CrossRef CAS PubMed.
- S. Jin, Z. Hao, K. Zhang, Z. Yan and J. Chen, Angew. Chem., 2021, 133, 20795–20816 CrossRef.
- K. Ogura, R. Oohara and Y. Kudo, J. Electrochem. Soc., 2005, 152, D213 CrossRef CAS.
- S. Verma, X. Lu, S. Ma, R. I. Masel and P. J. A. Kenis, Phys. Chem. Chem. Phys., 2016, 18, 7075–7084 RSC.
- C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. G. De Arquer, A. Kiani, J. P. Edwards, P. D. Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787 CrossRef CAS PubMed.
- F. P. García de Arquer, C.-T. Dinh, A. Ozden, J. Wicks, C. Mccallum, A. R. Kirmani, D.-H. Nam, C. Gabardo, A. Seifitokaldani, X. Wang, Y. C. Li, F. Li, J. Edwards, L. J. Richter, S. J. Thorpe, D. Sinton and E. H. Sargent, Science, 2020, 367, 661–666 CrossRef PubMed.
- R. B. Kutz, Q. Chen, H. Yang, S. D. Sajjad, Z. Liu and I. R. Masel, Energy Technol., 2017, 5, 929–936 CrossRef CAS.
- C. M. Gabardo, C. P. O'Brien, J. P. Edwards, C. Mccallum, Y. Xu, C.-T. Dinh, J. Li, E. H. Sargent and D. Sinton, Joule, 2019, 3, 2777–2791 CrossRef CAS.
- B. Endrődi, E. Kecsenovity, A. Samu, T. Halmágyi, S. Rojas-Carbonell, L. Wang, Y. Yan and C. Janáky, Energy Environ. Sci., 2020, 13, 4098–4105 RSC.
- H.-Y. Jeong, M. Balamurugan, V. S. K. Choutipalli, E.-S. Jeong, V. Subramanian, U. Sim and K. T. Nam, J. Mater. Chem. A, 2019, 7, 10651–10661 RSC.
- W. H. Lee, C. Lim, S. Y. Lee, K. H. Chae, C. H. Choi, U. Lee, B. K. Min, Y. J. Hwang and H.-S. Oh, Nano Energy, 2021, 84, 105859 CrossRef CAS.
- Y. Kofuji, A. Ono, Y. Sugano, A. Motoshige, Y. Kudo, M. Yamagiwa, J. Tamura, S. Mikoshiba and R. Kitagawa, Chem. Lett., 2021, 50, 482–484 CrossRef CAS.
- N. Gupta, M. Gattrell and B. Macdougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef CAS.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Phys. Chem. Chem. Phys., 2018, 20, 16973–16984 RSC.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Energy Environ. Sci., 2019, 12, 1950–1968 RSC.
- J. W. Blake, J. T. Padding and J. W. Haverkort, Electrochim. Acta, 2021, 393, 138987 CrossRef CAS.
- J. P. Edwards, T. Alerte, C. P. O'Brien, C. M. Gabardo, S. Liu, J. Wicks, A. Gaona, J. Abed, Y. C. Xiao, D. Young, A. Sedighian Rasouli, A. Sarkar, S. A. Jaffer, H. L. Maclean, E. H. Sargent and D. Sinton, ACS Energy Lett., 2023, 8, 2576–2584 CrossRef CAS.
- B. Yann Liaw, G. Nagasubramanian, R. G. Jungst and D. H. Doughty, Solid State Ionics, 2004, 175, 835–839 CrossRef.
- C. Wang, M. H. Nehrir and S. R. Shaw, IEEE Trans. Energy Convers., 2005, 20, 442–451 CrossRef.
- M. T. Winkler, C. R. Cox, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci., 2013, 110, E1076–E1082 CAS.
- O. Atlam and M. Kolhe, Energy Convers. Manage., 2011, 52, 2952–2957 CrossRef CAS.
- J. Milewski, G. Guandalini and S. Campanari, J. Power Sources, 2014, 269, 203–211 CrossRef CAS.
- A. Grimm, A. Sainte-Marie, G. J. Kramer and M. Gazzani, Int. J. Hydrogen Energy, 2022, 47, 11764–11777 CrossRef CAS.
- Y. Uchino, T. Kobayashi, S. Hasegawa, I. Nagashima, Y. Sunada, A. Manabe, Y. Nishiki and S. Mitsushima, Electrochemistry, 2018, 86, 138–144 CrossRef CAS.
- A. Abdel Haleem, J. Huyan, K. Nagasawa, Y. Kuroda, Y. Nishiki, A. Kato, T. Nakai, T. Araki and S. Mitsushima, J. Power Sources, 2022, 535, 231454 CrossRef CAS.
- G. O. Larrazábal, P. Strøm-Hansen, J. P. Heli, K. Zeiter, K. T. Therkildsen, I. Chorkendorff and B. Seger, ACS Appl. Mater. Interfaces, 2019, 11, 41281–41288 CrossRef PubMed.
- P. Mardle, S. Cassegrain, F. Habibzadeh, Z. Shi and S. Holdcroft, J. Phys. Chem. C, 2021, 125, 25446–25454 CrossRef CAS.
- L. I. Antropov, Theoretical Electrochemistry, Mir, New York, 1972 Search PubMed.
- E. R. Cofell, U. O. Nwabara, S. S. Bhargava, D. E. Henckel and P. J. A. Kenis, ACS Appl. Mater. Interfaces, 2021, 13, 15132–15142 CrossRef CAS PubMed.
- A. B. Moss, S. Garg, M. Mirolo, C. A. G. Rodriguez and R. Ilvonen, Joule, 2023, 7, 350–365 CrossRef CAS.
- S. Garg, Q. Xu, A. B. Moss, M. Mirolo, W. Deng, I. Chorkendorff, J. Drnec and B. Seger, Energy Environ. Sci., 2023, 16, 1631–1643 RSC.
- Y. Hori, A. Murata, K. Kikuchi and S. Suzuki, J. Chem. Soc. Chem. Commun., 1987, 728–729 RSC.
- S. Ringe, C. G. Morales-Guio, L. D. Chen, M. Fields, T. F. Jaramillo, C. Hahn and K. Chan, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- B. E. Conway and L. Bai, Electrochim. Acta, 1986, 31, 1013–1024 CrossRef CAS.
- A. Hamelin and M. J. Weaver, J. Electroanal. Chem. Interfacial Electrochem., 1987, 223, 171–184 CrossRef CAS.
- J. Perez, E. R. Gonzalez and H. M. Villullas, J. Phys. Chem. B, 1998, 102, 10931–10935 CrossRef CAS.
- Y. Matsumoto and E. Sato, Mater. Chem. Phys., 1986, 14, 397–426 CrossRef CAS.
- M. Bernt, A. Siebel and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, F305 CrossRef CAS.
- U. Babic, E. Nilsson, A. Patru, T. J. Schmidt and L. Gubler, J. Electrochem. Soc., 2019, 166, F214–F220 CrossRef CAS.
- Z. Taie, X. Peng, D. Kulkarni, I. V. Zenyuk, A. Z. Weber, C. Hagen and N. Danilovic, ACS Appl. Mater. Interfaces, 2020, 12, 52701–52712 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3se01709e |
| This journal is © The Royal Society of Chemistry 2024 |