Plasmon-enhanced second harmonic generation of metal nanostructures

Abstract

As the most common nonlinear optical process, second harmonic generation (SHG) has important application value in the field of nanophotonics. With the rapid development of metal nanomaterial processing and chemical preparation technology, various structures based on metal nanoparticles have been used to achieve the enhancement and modulation of SHG. In the field of nonlinear optics, plasmonic metal nanostructures have become potential candidates for nonlinear optoelectronic devices because of their highly adjustable physical characteristics. In this article, first, the basic optical principles of SHG and the source of surface symmetry breaking in metal nanoparticles are briefly introduced. Next, the related reports on SHG in metal nanostructures are reviewed from three aspects: the enhancement of SHG efficiency by double resonance structures, the SHG effect based on magnetic resonance and the harmonic energy transfer. Then, the applications of SHG in the sensing, imaging and in situ monitoring of metal nanostructures are summarized. Future opportunities for SHG in composite systems composed of metal nanostructures and two-dimensional materials are also proposed.

---

Cong-Cong Zhang

Cong-Cong Zhang received her bachelor's degree from Hebei Normal University in 2020. After that, she received her master's degree from Capital Normal University in 2023. She is pursuing her PhD degree in the School of Mathematics and Physics at China University of Geosciences (Wuhan) under the supervision of Prof. Si-Jing Ding. Her current research interests include second-order nonlinear signal enhancement and the coupling regulation of plasmons and excitons based on metal nanostructures.

Si-Jing Ding

Si-Jing Ding received her PhD degree from Wuhan University under the supervision of Prof. Qu-Quan Wang in 2016. She went on to work as a postdoc at Wuhan University from 2016 to 2018. She was a visiting scholar at the Chinese University of Hong Kong under the supervision of Prof. Jian-Fang Wang from 2017 to 2018. Currently, she is a full professor in the School of Mathematics and Physics at China University of Geosciences (Wuhan). She is mainly devoted to the study of plasmonic nanophotonics and nonlinear optics.

1. Introduction

Shortly after the invention of the ruby laser in 1961, Franken et al. used a ruby laser with an output wavelength of 694 nm to produce ultraviolet light at a wavelength of 347 nm when passed through a quartz crystal. This was the first observation of the optical second harmonic generation (SHG) phenomenon and also the first experimental discovery of a nonlinear optical process, marking the birth of nonlinear optics.^1,2 Many theoretical and experimental studies have been carried out on nonlinear optics.^3,4 Nonlinear optics plays a crucial role in the development and application of optical technology. Nonlinear optics can accomplish many unique functions, such as optical phase conjugation,⁵ laser source creation,⁶ signal transmission and conversion in optical fibers,⁷ and photoelectric signal modulation.⁸ A nonlinear optical effect is produced by the interaction between light and the medium, which itself is very weak.^9,10 Therefore, the enhancement of nonlinear signals has become an important aspect of nonlinear optics.

Metal nanostructures have attracted much attention because of their unique electromagnetic plasmon resonance characteristics, which are closely related to their size and shape. Metal nanomaterials have been widely used in many fields, such as surface-enhanced Raman scattering,^11–13 biochemical sensing,^14–16 chemical catalysis,¹⁷ medicine,^18,19 and nanophotonics.^20,21 In recent years, the nonlinear effects of metal nanostructures at the subwavelength scale have received extensive attention.^22,23 When light irradiates a metal nanostructure, the conduction electrons in the metal nanostructure will oscillate collectively to form surface plasmon resonance and generate a strong local electromagnetic field,²⁴ which can enhance the weak nonlinear signal.²⁵ By meticulously designing plasmonic metal nanostructures, we can also experimentally achieve the enhancement of SHG signals. Early SHG enhancement experiments with surface plasmons were carried out on an electrolytically roughened surface of bulk silver and the SHG enhancement was four orders of magnitude stronger than the SHG signal generated on a smooth silver surface.²⁶ Moreover, small changes in the geometry of metal nanostructures also have a great impact on surface plasmons, and this sensitivity produces the SHG signals of metal nanostructures with good tunability.^27–29 With further developments, researchers are constantly pursuing the lightness and portability of tools, and integrated optical circuits and integrated optical chips have become an urgent need.³⁰ Because the size of traditional materials is mostly greater than 10 nm, the preparation of integrated nonlinear optical devices is difficult.³¹ The emergence of metal nanostructures effectively solves this problem and their extremely small size creates good conditions for designing devices with extremely small volumes. Therefore, studying nonlinear optical properties based on metal nanostructures is highly important for designing nonlinear optical devices. These advantages have led to widely studied and wide-ranging nonlinear optical effects on metal nanostructures.

This mini-review focuses on the research on SHG in metal nanostructures. First, the basic optical principles of SHG in metal nanostructures are briefly described. Second, the enhancement and modulation of second harmonic signals in metal nanostructures are reviewed from three aspects: double-resonance-enhanced SHG, magnetic-resonance-enhanced SHG and harmonic energy transfer-enhanced SHG. Third, the applications of SHG based on the metal nanostructure in sensing, imaging and in situ monitoring are discussed. Finally, future developments in the field of SHG are proposed.

2. Basic principle of the second harmonic generation of metal nanostructures

SHG, also known as frequency doubling, is a nonlinear optical process in which two photons with the same frequency interact with a nonlinear medium to generate a new photon with twice the energy of the initial photon (frequency doubled and wavelength halved) (see Fig. 1a). SHG involves only the virtual energy transition process and the energy of two incident photons with frequency ω is equal to the energy of one emitted photon with frequency 2ω.³² According to the law of conservation of energy, the energy and momentum of the excited sample itself will not change; thus, the excited sample will not absorb energy during this process.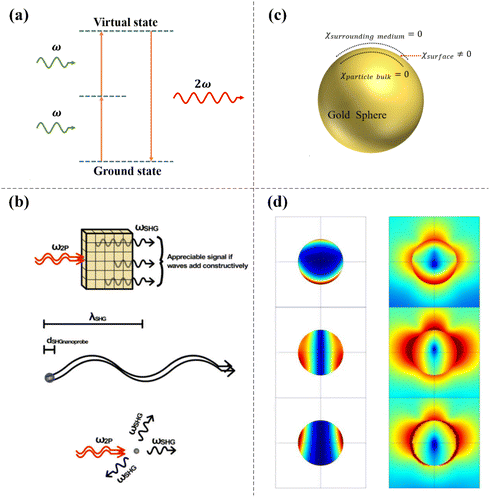

Fig. 1 The mechanism of SHG and surface symmetry breaking in metal nanostructures. (a) Energy-level diagram describing SHG. (b) Comparison of SHG in bulk materials and nanoparticles. Adapted with permission from ref. 35. Copyright 2012 John Wiley & Sons, Inc. (c) Schematic diagram of symmetry breaking-induced nonlinear response on the surface of a gold sphere. (d) Calculation of the spatial distribution of nonlinear current and the near-field map of the corresponding harmonic field amplitude of a 150 nm gold nanoparticle. Adapted with permission from ref. 42. Copyright 2010 The American Physical Society.

The optical response of a nonlinear medium can be determined by the electric polarization intensity P and the incident radiation field intensity E, and the total polarization intensity is usually expressed as follows:³³

P = ε₀[χ⁽¹⁾E + χ⁽²⁾E² + χ⁽³⁾E³ + …]

where ε₀ is the vacuum dielectric constant, χ⁽ⁿ⁾ is the nth-order susceptibility of the dielectric material, χ⁽¹⁾ is the linear susceptibility, χ⁽²⁾ is the second-order susceptibility and χ⁽³⁾ is the third-order susceptibility. The first term ε₀χ⁽¹⁾E corresponds to the absorption, scattering and reflection of light in the linear optical response. The second term ε₀χ⁽²⁾E² reflects second-order nonlinear optical effects such as SHG. The third term ε₀χ⁽³⁾E³ describes third-order nonlinear optical effects, such as third harmonic generation, stimulated Raman processes, coherent anti-Stokes Raman scattering and two-photon absorption. In linear optics, the field strength is moderate; thus, the higher-order terms in the equation can be neglected. In this case, the outgoing light has the same frequency and wavelength as the incident light. In nonlinear optics, the field strength is extremely large and higher-order terms can no longer be neglected. In this case, in addition to the linear response, light twice the incident frequency is produced and the process is SHG. Thus, SHG not only is related to the strength of the photoelectric field but is also correlated with the second-order susceptibility χ⁽²⁾ of the dielectric material.

Next, we explain the differences in the SHG signals between bulk materials and nanoparticles (see Fig. 1b). In bulk materials, appreciable SHG signals only appear when the generated SHG signals move through the material at the same speed as the incident photons, resulting in constructive interference.³⁴ The constructive interference is a consequence of the phase-matching conditions of SHG. In contrast, due to the small diameter of nanoparticles relative to the wavelength of the incident light and the wavelength of the SHG signal, strict phase-matching conditions are not required to obtain a significant SHG signal.³⁵ Due to their small size, the SHG signals generated anywhere in the material will always be in approximately the same phase, thus allowing scattering in multiple directions.^36,37

Under the electric dipole approximation, there is no second-order nonlinear effect in a centrosymmetric medium. The atomic arrangement of common metals (for example, gold, silver, and copper) is centrosymmetric; thus, SHG will not exist under the electric dipole approximation. However, this statement is not consistent with the experimental results, especially when surface plasmon resonance occurs in metal nanostructures, and the SHG signal is clearly observed.³⁸ This phenomenon actually occurs because the central symmetry at the interface of two centrally symmetric media is disrupted, resulting in the generation of a second harmonic signal in the interface layer.^39,40 Using spherical gold nanoparticles in solution as an example, the nonlinear susceptibility χ_{surrounding medium} in the solution environment is zero and the nonlinear susceptibility χ_{particle bulk} inside the gold sphere is also zero; therefore, symmetry breaking occurs on the surface of the gold sphere, the nonlinear susceptibility χ_surface on the surface of the gold sphere is no longer zero, and the SHG response can then be observed experimentally (see Fig. 1c). Wang et al. prepared rectangular subwavelength hole arrays with different shapes on a gold film on a glass substrate. Due to symmetry breaking, the atoms on the gold film surface have a nonzero second-order nonlinear susceptibility and the SHG signal could be observed under the excitation of an incident femtosecond pulsed laser. In contrast, the bulk atoms inside the gold film have no SHG response due to their central inversion symmetry.⁴¹ Their experimental results were consistent with those of other international research groups. With the finite element method, the spatial distributions of nonlinear currents on the surface and inside the bulk of 150 nm gold nanoparticles and the near-field distributions of the corresponding harmonic field amplitudes were theoretically simulated. The results also showed that the second harmonic signal on the surface of metal nanoparticles was much larger than the nonlinear signal caused by the field gradient inside the particles (see Fig. 1d).⁴² For plasmonic metal nanostructures, the component perpendicular to the surface has the largest proportion of surface nonlinear susceptibility; therefore, when exploring the surface nonlinear effect of metal nanostructures, only the nonlinear effect perpendicular to the surface was usually studied.^43,44

In general, the signals of second-order nonlinear processes are not obvious in the centrosymmetric structures. The research results of Kauranen et al. confirmed that the key to improve SHG conversion efficiency lies in the non-centrosymmetric local field distributions caused by the asymmetric morphology of metal nanostructures.⁴⁵ Therefore, researchers have designed various asymmetric metal nanostructures to obtain controllable local field distributions.⁴⁶ These different metal nanostructures have different effects on the SHG enhancement. A few examples are given here. The SHG signal of a T-shaped dimer nanostructure composed of gold nanoparticles is generated by the asymmetric distribution of the local fundamental field. When the fundamental field is asymmetrically distributed around the perimeter of the nanodimer, the local surface susceptibility of the particle will generate a strong SHG signal.⁴⁷ For G-shaped chiral nanostructures, structures with different orientations can produce different intensities of SHG for left and right circularly polarized light.⁴⁸ A metamaterial consisting of a U-shaped split-ring resonator breaks the original symmetry of the array, thus allowing the nanostructure to generate SHG enhancement.⁴⁹ The non-centrosymmetric effect caused by a subwavelength-size triangular nanoaperture on a metal thin film makes it exhibit a better SHG enhancement effect than a circular nanoaperture.⁵⁰ The second harmonic response of a sharp metal tip is the strongest for incident light polarized along the tip axis, due to the lower symmetry of tip-shaped structures relative to spherical structures.⁵¹ Moreover, Chen et al. proposed a method to quantify the influence of local field effects on second-order nonlinear susceptibility using white-light supercontinuum signals, and quantitatively extracted the contribution of non-centrosymmetry in a cross-shaped Ag nanohole to second-order nonlinear susceptibility through the experimental data. The results show that the second-order nonlinear susceptibility increases with an increase in the asymmetry of local field distribution in metal nanostructures.⁵² The studies listed above point out new directions for improving the nonlinear conversion efficiency of metal nanostructures.

Different plasmonic metal nanostructures have different abilities to enhance SHG signals due to their different asymmetries. Here, the effective second-order nonlinear susceptibility and the nonlinear conversion efficiency achieved using several representative metal nanostructures in the process of enhancing the SHG effect have been summarized, which can provide a reference for relevant researchers. For the nanocup formed using a metal-capped hemispherical nanoparticle, its maximum conversion efficiency is 1.8 × 10⁻⁹ during the enhanced SHG process and its effective second-order susceptibility is 3.2 pm V⁻¹.⁵³ A multiresonant log-periodic nanostructure composed of polarization-independent three-arm trapezoidal silver nanoantennas can realize the SHG effect with a conversion efficiency of 1.25 × 10⁻⁹ and a maximum second-order susceptibility of 1.9 pm V⁻¹.⁵⁴ A plasmonic metal nanostructure with sub-5 nm “double gaps” formed by placing gold nanoparticles in the trenches of gold thin films can effectively enhance SHG emission. The conversion efficiency of this system is 1.8 × 10⁻⁷ and its effective second-order susceptibility is 6.1 pm V⁻¹.⁵⁵ A metal–dielectric–metal nanostructure assembled using gold nanoparticles and a porous anodic alumina template has superior nonlinear conversion performance and its second harmonic conversion efficiency and effective second-order nonlinear susceptibility are 3.84 × 10⁻⁹ and 140 pm V⁻¹, respectively.⁵⁶ A planar 4π Archimedean nanospiral array structure with subwavelength dimensions can generate second harmonic light from any polarization state due to its inherent lack of symmetry. The maximum SHG conversion efficiency and effective second-order nonlinear susceptibility of this nanostructure are 1.3 × 10⁻⁸ and 15.3 pm V⁻¹, respectively.⁵⁷ The second-order susceptibility of different nanostructures listed above is in the same order of magnitude as that provided by widely used nonlinear crystals, which proves that these metal nanostructures can enhance SHG signals well.

3. Enhancement and modulation of SHG in plasmonic metal nanostructures

3.1 Double-resonance-enhanced SHG

Based on the inherent characteristics and advantages of SHG, such as its stable signal characteristics, ultrafast signal response and inherent polarization sensitivity, high-efficiency SHG conversion is necessary. To improve the low conversion efficiency of SHG, researchers have adopted many methods to enhance and modulate the nonlinear conversion efficiency. In traditional nonlinear optics, phase matching conditions,^58,59 enhanced incident light intensity⁶⁰ or natural materials with high nonlinear coefficients^61,62 are generally used to enhance SHG. However, these conditions are harsh and difficult to achieve, which greatly limits the SHG enhancement.

For metal nanostructures, when light is incident on the metal surface, it will lead to an interaction between free electrons on the metal surface and the incident electromagnetic field, which will produce a clear field enhancement on the metal surface and lead to the surface plasmon resonance phenomenon.^63,64 In the early study of classical nonlinear optical and hydrodynamic models, the SHG signal of the sample was nonlinearly enhanced with an increase in the amplitude of the fundamental frequency electric field. Therefore, excitation of the surface plasmon resonance in the metal nanostructures can improve the efficiency of SHG conversion;^65–67 this is a simple way to enhance the nonlinear response strength of SHG. The advantage of enhancing nonlinear optics by the surface plasmon resonance effect of metal nanostructures is that the resonance size of the sample is small and consequently the phase matching conditions can be disregarded. This approach relies mainly on the unique electromagnetic resonance characteristics of surface plasmon resonance to enhance the nonlinear effect.⁶⁸ Metzger et al. focused a pulsed laser on an aluminum nanoantenna array to excite the surface plasmon resonance of a structure and achieved more than an order of magnitude enhancement in the SHG conversion efficiency.⁶⁹ The increase in the intensity of SHG due to this regulation method was very limited. In this study, the enhancement of the fundamental frequency field is only used to improve the SHG conversion efficiency. If the resonance enhancement of the fundamental frequency and doubled frequency fields can be excited at the same time in double resonance mode,⁷⁰ the SHG conversion efficiency will be further enhanced. The principle of double resonance matching to enhance SHG is that the fundamental frequency mode increases the electric field intensity to amplify the SHG signal and then the amplified SHG signal is efficiently radiated outwards in frequency-doubling mode. Martin et al. designed an aluminum nanoantenna composed of three arms to achieve double resonance at the fundamental frequency and second harmonic frequency. They combined the surface integral equation (SIE) method with sensitive nonlinear optical experiments to verify that when quadrupole and dipole modes were coupled at the second harmonic wavelength; the SHG signal strength of the double resonance structure was greatly enhanced compared with that of a simple dipolar nanoantenna, which only supported the fundamental wavelength resonance. This detailed study on the enhancement mechanism of SHG in double resonance plasmonic nanoantennas has important guiding significance for the design of different nanostructures to enhance the strength of SHG (see Fig. 2a).⁷¹ Li et al. prepared Au nanodumbbells (NDs) with enlarged ends by a wet-chemical method and Au NDs were prepared with homogeneous and tunable end sizes. The transverse surface plasmon resonance and near-field enhancement were greatly improved at both ends of the end-enlarged Au NDs. When the end size of the Au NDs was adjusted to a certain size, the near-field enhancement of the fundamental and double frequencies could reach the maximum at the same time and then the Au NDs exhibited a double resonantly enhanced SHG signal, which was 10.3 times greater than the SHG signal of the Au nanorods (NRs) (see Fig. 2b).⁷² Ai et al. coated an Au nano-bipyramid grown by the seed-mediated method on the surface of an optical fiber and then adjusted the diameter of the optical fiber by flame heating to achieve the highest quality factor (Q ≈ 160). When the high-order fiber cavity mode resonated with the second harmonic wavelength, the fundamental wave light and the second harmonic light will propagated coherently in the fiber cavity dozens of times. Therefore, this doubly resonant plasmon-fiber system could achieve an ultrahigh SHG conversion efficiency. This work has improved the practical application value of plasmon-enhanced SHG nonlinear optical devices based on metal nanostructures (see Fig. 2c).⁷³ Wu et al. prepared large-area arrays of ball-in-bowl plasmonic nanostructures by assembling gold nanoparticles with porous anodic alumina templates using a solution-processing approach, which supported two resonance modes in the visible and near-infrared regions. The gap geometry of the ball-in-bowl nanostructures enlarged the size of the gap cavity and achieved a wide-angle response to polarization-independent SHG radiation (see Fig. 2d).⁵⁶ Park et al. designed metal bowtie nano-apertures (BNAs) as a 4 × 4 square periodic array by ion beam etching. The plasmonic resonance of this array structure at the fundamental wave could cause local field enhancement and its Fabry–Pérot resonance could promote the efficient transmission of the second harmonic signal. An SHG conversion efficiency of 1.4 × 10⁻⁸ was achieved in the experiment. Combined with the finite-difference time-domain (FDTD) simulation, the SHG response enhancement of the doubly resonant structure was one order of magnitude greater than that without second harmonic resonance (see Fig. 2e).⁷⁴

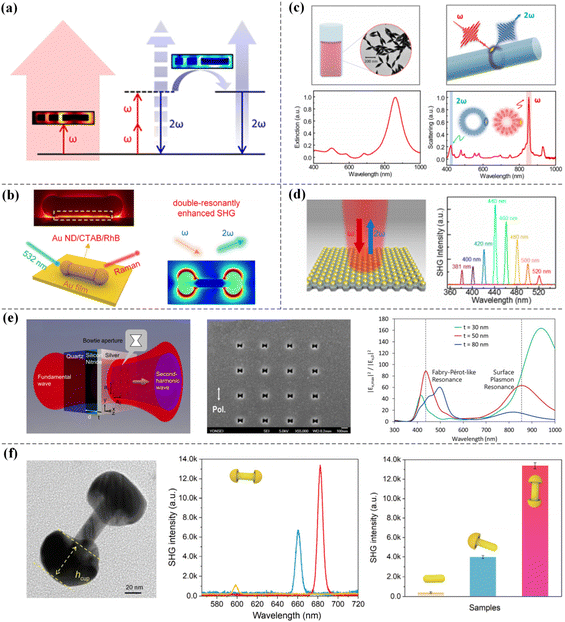Fig. 2 SHG enhancement based on a double resonance structure. (a) Aluminum double resonant nanoantenna composed of three arms and its second harmonic signal enhancement principle. Adapted with permission from ref. 71. Copyright 2017 American Chemical Society. (b) Double resonance structure of Au NDs with enlarged ends. Adapted with permission from ref. 72. Copyright 2022 American Chemical Society. (c) Double resonant system of a single Au nano-bipyramid coupled to a fiber cavity. Adapted with permission from ref. 73. Copyright 2021 American Chemical Society. (d) Large area arrays of ball-in-bowl plasmonic nanostructures by assembling gold nanoparticles with porous anodic alumina templates. Adapted with permission from ref. 56. Copyright 2020 American Chemical Society. (e) Metal BNAs in the form of 4 × 4 square periodic arrays. Adapted with permission from ref. 74. Copyright 2012 Optical Society of America. (f) Au rod-cup NCs and Au NRs prepared by a controllable wet-chemical method and their experimental SHG strength comparison. Adapted with permission from ref. 75. Copyright 2022 Springer Nature.

Kang et al. synthesized Au rod-cup nanocrystals (NCs). This nanostructure has several plasmon modes, including transverse dipole (TED), longitudinal electric dipole (LED), magnetic dipole (MD) and toroidal dipole (TD)-modulated LED resonances (anapole state). They found that the SHG intensity of the Au rod-cup NCs was dozens of times greater than that of Au NRs. When the TD and LED modes of the Au rod-cup NCs were in phase oscillation, the sample has a large extinction cross section, allowing efficient capture of light energy in the fundamental frequency mode. Moreover, the LED, TED-based plasmon coupling and MD modes enabled the Au rod-cup NCs to have extremely high scattering efficiency and powerful enhanced near-field effects in frequency-doubled mode (see Fig. 2f).⁷⁵

3.2 Magnetic-resonance-enhanced SHG

There are many intrinsic modes in plasmonic nanostructures; these modes include electric dipoles, magnetic dipoles, electric quadrupoles, and magnetic quadrupoles.⁷⁶ When the excitation conditions of the intrinsic mode are met, resonance occurs in the plasmonic nanostructure. If suitable plasmonic nanostructures can be designed, the SHG signal is also expected to increase. In addition to the nonlinear signal enhancement caused by the common electric dipole resonance, the magnetic dipole resonance generated in some metal nanostructures can also greatly enhance the intensity of the SHG signal. In addition to the metal nanostructures prepared by micro–nano processing technology, the strong magnetic plasmon resonance of metal nanoparticles prepared by chemical synthesis can also greatly enhance the SHG signal.

Ding et al. used a simple chemical method to synthesize Au nanocups and Au–Ag heteronanocups with controllable asymmetric geometries. The magnetic plasmons of these colloidal nanoparticles have excellent nonlinear optical responses. The maximum SHG signal of the bare Au nanocups was produced by the synergistic effect of the optimized magnetic plasmon resonance and the “lightning-rod effect”. Among other aspects, they demonstrated for the first time that Au–Ag heteronanocups with overgrown Ag nanoparticles were nonlinearly enhanced by synergistic magnetic and electric plasmon resonance and that the hybrid nanostructure has a double resonance mode, which was 21.8 times stronger than the SHG signal of bare Au nanocups (see Fig. 3a).⁷⁷ Razdolski et al. grew BTIG with a thickness of 4 μm on a gallium gadolinium garnet (GGG) substrate and then deposited a 100 × 100 μm thick (120 nm) Au fringe array on it to prepare an Au/(Bi,Tm) iron garnet (IG) structure. The enhanced magnetization of surface plasmon resonances (SPRs) in this kind of magnetic plasmonic crystal induced an enhancement of SHG and the sensitivity of SHG to SPR at the buried Au/garnet interface was also demonstrated by SHG magnetic contrasts (see Fig. 3b).⁷⁸ In recent years, the magnetic properties of nonlinear optical phenomena such as SHG in metamaterials have been extensively studied. Kruk et al. experimentally prepared a regular array composed of metal–dielectric–metal nanodisks. This optical metasurface structure has both electrical resonance and magnetic resonance. The experimental results showed that the intensity of the second harmonic signal greatly increased near the magnetic resonance of the metasurface. The numerical results further confirmed that the enhancement in the SHG signal originated from the superposition of the magnetic dipole and electric quadrupole of the metasurface structure (see Fig. 3c).⁷⁹ Although the study of second harmonic radiation is very complex, researchers have been attempting to achieve directional radiation. Zhang et al. designed metal nanocups with variable orientations using a simple and efficient nanomanufacturing technique. This three-dimensional (3D) plasmonic nanostructure has a magnetic dipole resonance that could greatly enhance the local field.^80,81 They experimentally found that adjusting the relative direction of the nanocup and incident light could change the second harmonic radiation direction; in addition, when the excitation power P(ω) was fixed, as the nanocup angle increased, the conversion efficiency of SHG, η_SH = P(2ω)/P(ω), also constantly improved. The finite element method was used to numerically study the nanocup with the same parameters as those used in the experiment. The results showed that the second harmonic light scattered by the nanocup was influenced by the orientation of the nanocup, which was essentially due to the magnetic dipole mode of the nanocup enhancing the SHG intensity; moreover, the magnetic dipole scattered the SHG around the nanocup into a circular profile along its orientation (see Fig. 3d).⁵³ Zhou et al. used chemical synthesis to prepare pointed nanocaps, open nanoshells and hollow nanostars by adjusting the morphology of Au nanoshells using six-pointed PbS nanostars as templates. Since the amount of chloroauric acid was continuously adjusted during the synthesis process, the plasmon resonance peak of the sample also redshifted and broadened due to the synergistic effect of the electric and magnetic plasmon modes. When the opening size of the nanoparticles was appropriate, two maximum SHG intensities could be experimentally observed; these intensities were caused by symmetry breaking and were essentially due to the electromagnetic field enhancement caused by the rich morphology of the nanoparticles (see Fig. 3e).⁸²

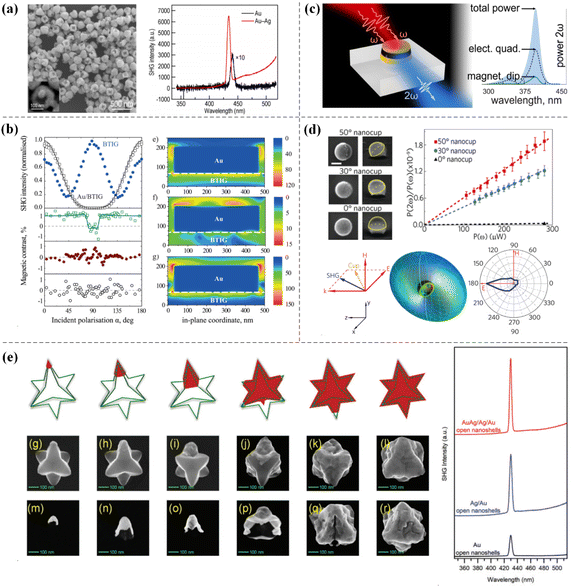Fig. 3 SHG enhancement based on magnetic dipole resonance. (a) Au nanocups and the nonlinear dual-resonance antennas of Au–Ag heteronanocups. Adapted with permission from ref. 77. Copyright 2019 American Chemical Society. (b) Au/(Bi, Tm) iron garnet (IG) perforated magnetic plasma crystals. Adapted with permission from ref. 78. Copyright 2015 American Chemical Society. (c) Metal–dielectric–metal nanodisk optical metasurface structure. Adapted with permission from ref. 79. Copyright 2015 Optica Publishing Group. (d) The orientation of the 3D nanocup affects the direction of second harmonic radiation. Adapted with permission from ref. 53. Copyright 2011 American Chemical Society. (e) Pointed nanocaps, open nanoshells, and hollow nanostars. Adapted with permission from ref. 82. Copyright 2021 Royal Society of Chemistry.

3.3 Harmonic energy transfer-enhanced SHG

In addition to the common methods of enhancing SHG, which are summarized in the above two sections, enhancing SHG based on regulating the energy transfer of the harmonic field also provides an effective way to enhance nonlinear effects and is more conducive to the design of efficient and compact nanodevices and their application in light field control engineering. Therefore, we introduce related research on harmonic energy transfer in metal nanostructures. Qiu et al. used chemical methods to synthesize hollow Au stars by a three-step method. These Au stars had a broadband response covering fundamental, second-harmonic (SH) and third-harmonic (TH) frequencies; in addition, based on the experimental observation, the greatly enhanced SH radiation was caused by the excitation of three resonances at the fundamental, SH and TH frequencies. Through experimental measurements, harmonic resonance energy transfer (HRET) from TH excitation to linear receptors mediated by χ⁽³⁾ → χ⁽¹⁾ cooperation was observed in the Au star antennas. χ⁽³⁾ → χ⁽²⁾ collaboration was also observed and electric field-induced harmonic energy transfer (E-HET) from TH excitation to the SH field occurred.⁸³ This research result has great guiding significance for practical applications. The THG intensity is very strong in gold bowtie antennas^84,85 and if such nanostructures need to be used in biotechnology applications, energy transfer from TH excitation to the SH field is highly needed (see Fig. 4a). Similarly, Feng et al. used a mild chemical method to prepare a series of Au/PbS/Au nanostars with adjustable tip lengths by changing the amount of chloroauric acid. Due to the asymmetry and local field enhancement, long spine Au/PbS/Au nanostars were finally experimentally obtained with the largest SHG intensity. In this study, the harmonic energy transfer method was also used to enhance the SHG intensity by suppressing the TH field energy (see Fig. 4b).⁸⁶ These results optimized the plasmon-enhanced SHG strength of metal nanostructures.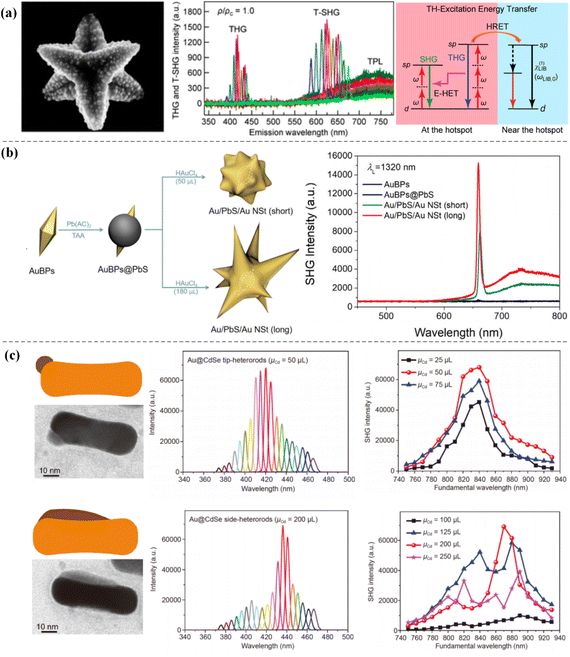

Fig. 4 The energy transfer of the harmonic field is regulated to enhance SHG. (a) TH excitation energy transfer of hollow Au stars. Adapted with permission from ref. 83. Copyright 2020 American Chemical Society. (b) Au/PbS/Au nanostars with multiple tips. Adapted with permission from ref. 86. Copyright 2022 Royal Society of Chemistry. (c) Au NRs, Au–Ag NRs, and asymmetric Au@CdSe heterorods. Adapted with permission from ref. 87. Copyright 2020, Science China Press and Springer-Verlag GmbH Germany, part of Springer Nature.

Wu et al. experimentally compared the plasmon-enhanced SHG of Au NRs, Au–Ag NRs and asymmetric Au@CdSe heterorods. Due to the asymmetric nanostructure and local field enhancement, the SHG of the asymmetric Au@CdSe heterorods was 617.7 times stronger than that of the Au NRs. Moreover, excitation wavelength-dependent SHG measurements of Au NRs and Au@CdSe side-heterorods also confirmed that the local interband transition of Au caused the harmonic energy transfer (see Fig. 4c).⁸⁷

In addition to the three aspects introduced above, relevant researchers have also used some other methods to enhance and regulate the nonlinear conversion efficiency in metal nanostructures. These methods include utilizing electric field Fano resonance,^88,89 magnetic field Fano resonance,^90,91 coupling of metal nanostructures with a nonlinear medium,^56,92 lattice resonance,^93,94 and so on. In recent years, Fano resonance has gradually become a research hotspot to improve the nonlinear conversion efficiency of SHG. Fano resonance at the fundamental frequency can bind the incident light energy to the surface of metal nanostructures, thus amplifying the surface nonlinear current and enhancing the second harmonic radiation. Zhang et al. experimentally observed fundamental Fano resonance and enhanced SHG signals using gold split nanodisks with narrow split gaps. The local electric field intensity in the near field of the structure is more than 70 times higher than that without Fano resonance and its energy conversion efficiency is also more than 10⁻¹¹ orders of magnitude.⁸⁹ Moreover, Yang et al. used three gold nanodisks of different sizes to construct a plasmonic metamolecule. The electromagnetic mode coupling of the metal nanostructure generated magnetic field Fano resonance, thereby enhancing the SHG signal.⁹⁰ Barium titanate is a kind of nonlinear medium, which can be combined with a gold shell to construct a core–shell nanocavity with an adjustable wavelength of plasmon resonance. When the excitation wavelength is located at the plasmon resonance peak of the composite nanostructure, the light field intensity inside barium titanate at the fundamental frequency is greatly enhanced and the second harmonic intensity is also exponentially enhanced.⁵⁶ Michaeli et al. experimentally found that the second harmonic efficiency generated by the split-ring resonator arrays under oblique incidence was 30 times greater than that under normal incidence. Through the coupled dipole approximation, it is proved that surface lattice resonance occurs at the second harmonic frequency when the nonlinear Rayleigh–Wood anomaly condition was satisfied, which led to an enhancement of SHG.⁹³

4. Practical application of SHG

4.1 Nonlinear imaging based on SHG

With the rapid development of nonlinear optics research, various nonlinear effects have been widely used in modern optics, such as coherent light sources,^95,96 all-optical switches,^97–99 nonlinear imaging,^100–103 and nanoprobes.¹⁰⁴ SHG has received extensive attention as a new optical imaging technique developed in recent years. In this section, we will focus on the study of nonlinear microscopic imaging of SHG in metal nanostructures. Sahu et al. reported an ultrasensitive collective plasmon-enhanced SHG microscopy approach in which simultaneous visualization and 3D directional imaging of individual R6G molecules were achieved via the electromagnetic field enhancement of surface hotspots on the arrays of plasmonic silver nanoholes. This discovery caused single molecule detection and molecular directed imaging based on SHG to be possible (see Fig. 5a).¹⁰⁵ When studying the optical properties of nanoparticles in solution, systematic measurements do not provide accurate and in-depth results due to the inhomogeneity of particle shape and size. Therefore, SHG measurements using a single metal nanoparticle that is sensitive to centrosymmetric breaking of the shape are necessary, which facilitates a new direction in the study of the nonlinear optical properties of metal nanoparticles. This approach also enables more comprehensive detection of the optical properties of the metal nanostructures (see Fig. 5b).¹⁰⁶ Chemically synthesized asymmetric colloidal Au-core/Ag-shell nanorods with high-efficiency SHG have great application potential in biomedical imaging. By comparing SHG and the TPL images of cells using Au–Ag nanorods, SHG images were found to show stronger intracellular signals, indicating that Au–Ag nanorods show excellent performance in monitoring morphological evolution and changes in living cells (see Fig. 5c).¹⁰⁷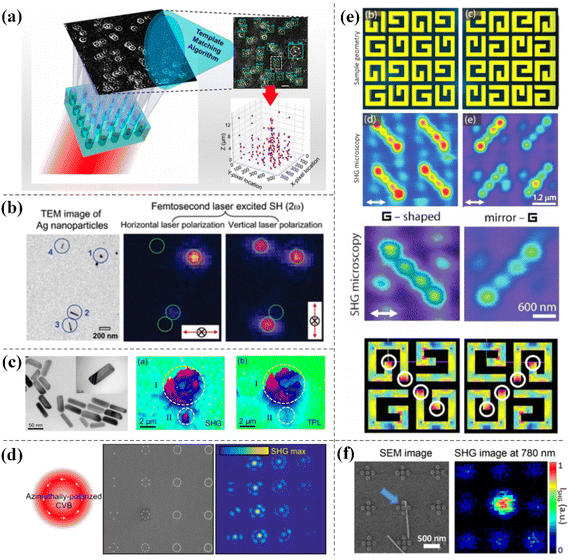

Fig. 5 The application of SHG in the imaging field. (a) Arrays of plasmonic silver nanoholes. Adapted with permission from ref. 105. Copyright 2019 American Chemical Society. (b) Symmetry breaking in single nanoparticles. Adapted with permission from ref. 106. Copyright 2005 American Chemical Society. (c) Colloidal Au-core/Ag-shell nanorods. Adapted with permission from ref. 107. Copyright 2018 Springer Nature. (d) Plasmonic oligomers with different symmetries. Adapted with permission from ref. 108. Copyright 2018 American Chemical Society. (e) G-shaped gold nanostructure arrays. Adapted with permission from ref. 109. Copyright 2012 American Chemical Society. (f) Plasmonic-semiconductor hybrid nanosystem consisting of a ZnO nanowire coupled to a gold pentamer oligomer. Adapted with permission from ref. 110. Copyright 2014 American Chemical Society.

Bautista et al. used SHG microscopy with cylindrical vector beams (CVBs) to study the collective effects of plasmonic oligomers composed of Au NRs with different spatial symmetries and observed that their SHG efficiency strongly dependent on the polarization of the incident CVBs and on interparticle effects; this study provided a new way of investigating coupling effects in the complex arrangements of nano-objects (see Fig. 5d).¹⁰⁸ High-intensity second harmonic sources within each unit cell are shown in the SHG microscopy images of G-shaped gold nanostructure arrays and this study demonstrated that plasma hotspots could be accurately mapped in conjunction with SHG microscopy (see Fig. 5e).¹⁰⁹ Grinblat et al. placed a single ZnO nanowire in the hotspot of a plasmonic oligomer, enabling a precise quantity of SH efficiency and field enhancement by observing the second harmonic light emitted from the mixed sample using a confocal microscope (see Fig. 5f).¹¹⁰

4.2 Sensing applications based on SHG

The second-order nonlinear effect has wide application value. In practical applications, the sensing function of SHG in the field of nonlinear optics is more sensitive than that in the field of linear optics; therefore, SHG has been widely used in sensing detection. Metzger et al. obtained measurements of the near-field distribution of polarization-resolved SHG from a gold dipole nanoantenna using a directional and polarization-sensitive aluminium nanoantenna as a local sensor. Using resonant plasmonic nanoantennas as local sensors, this novel and highly sensitive method can be used to study the nonlinear near-field distributions of more complex structures and may also be widely used in nonlinear nanoimaging in the future (see Fig. 6a).¹¹¹ In 2020, Verma et al. proposed a nonlinear plasmonic sensing method based on Au NRs for fast, sensitive and label-free detection of mercury in solution. The SHG of Au NRs as a function of mercury concentration was detected by two-photon Rayleigh scattering (TPRS). The method successfully increased the detection limit of mercury by 2–3 orders of magnitude compared to commonly used linear localized surface plasmon resonance (LSPR) sensing (see Fig. 6b).¹¹² Lan et al. achieved electronically controlled harmonic light generated using plasmonic crystals in electrolytic solutions. The electrical tunability of the SHG signal in this hybrid plasmonic–electrolyte system was sensitive to both the ion concentration and electrolyte type; thus, this work further demonstrates that combining electrical signals with nonlinear optical interactions has the potential to be used for sensing charged substances in any aqueous solution (see Fig. 6c).¹¹³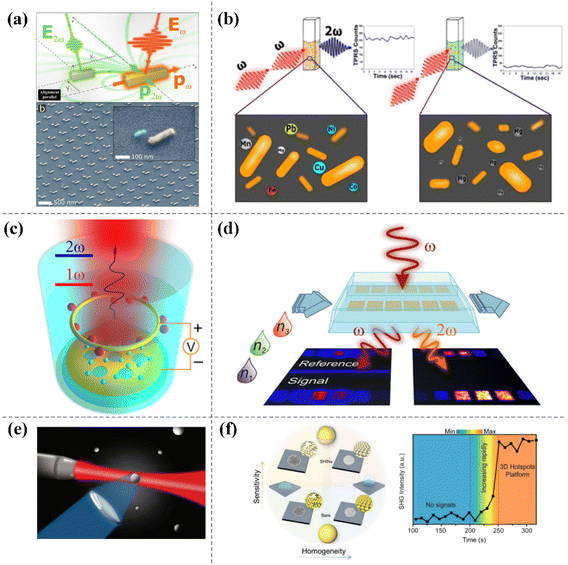

Fig. 6 The application of SHG in the sensing field. (a) Second harmonic resonant aluminum nanoantennas. Adapted with permission from ref. 111. Copyright 2017 American Chemical Society. (b) Au NRs as a plasmonic transducer. Adapted with permission from ref. 112. Copyright 2020 American Chemical Society. (c) Optical sensing device for generating SHG by electric control in electrolytic solution. Adapted with permission from ref. 113. Copyright 2016 American Chemical Society. (d) A sensing device based on an array of non-centrosymmetric plasmonic nanoantennas integrated into a microfluidic chip. Adapted with permission from ref. 114. Copyright 2018 American Chemical Society. (e) Silver metal nanoparticles producing multipolar SHG. Adapted with permission from ref. 115. Copyright 2012 American Chemical Society. (f) 3D metal SHIN substrates. Adapted with permission from ref. 116. Copyright 2019 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.

Studies related to sensing devices integrated into microfluidic chips based on non-centrosymmetric plasmonic nanoantenna arrays with enhanced SHG have also been reported. The experimental results were evaluated and found to be at least three times more sensitive in the nonlinear state than in the linear state (see Fig. 6d).¹¹⁴ Furthermore, Butet et al. theoretically calculated the SHG response of silver nanospheres to refractive index changes using Mie theory and the multipolar expansion of the electromagnetic field to demonstrate that sensing using multipolar surface plasmon resonance was more sensitive than sensing in the linear optical regime. This report provided theoretical support for further development of nonlinear spectral technology based on SHG (see Fig. 6e).¹¹⁵ Yang et al. invented a 3D hotspot platform for quantity detection of plasmon-enhanced SHG. They placed a drop of a solution of active nanoparticles coated with a silica layer on a hydrophobic silicon wafer and it was directly evaporated. During the evaporation process, as the distance between nanoparticles continued to shrink, the number of 3D hot spots generated also continued to increase, resulting in a sharp increase in the SHG signal. The 3D metal shell-isolated nanoparticle (SHIN) substrates exhibited more stable plasmon-enhanced SHG signals due to the protective SiO₂ shells; therefore, 3D hotspot platforms have great potential for plasmon-enhanced nonlinear spectroscopy as well as practical sensor applications (see Fig. 6f).¹¹⁶

4.3 In situ monitoring based on SHG

SHG is also widely used in in situ monitoring of various chemical reactions. Xue et al. performed photocatalytic redox experiments on silver on the surface of colloidal Ag nanoparticles (Ag NPs) and observed that photocatalytic oxidation of the Ag NP surface was the main reaction under lower-power femtosecond laser irradiation. The formation of silver oxides such as Ag₂O on the surface resulted in a decrease in the SHG signal. The photo-induced reduction was also observed under relatively high laser energy irradiation, which was reflected in the recovery of the SHG signal. Subtle structural changes on the surface of metal nanoparticles led to significant changes in their SHG emission signals, indicating that SHG was a sensitive probe for studying the surface structure of noble metal nanoparticles (see Fig. 7a).¹¹⁷ Sauerbeck et al. carried out simultaneous in situ second harmonic scattering (SHS) measurements during the growth of high quality Au nanoshells on colloidal silica particles. During shell growth, the SHS intensity reached a maximum in the middle stage of the reaction and dramatically decreased when the shell was completely closed. This in situ nonlinear optical characterization method allowed the repetitive synthesis of nanoshells with high optical quality (see Fig. 7b).¹¹⁸ Time-dependent SHG measurements were used to study the photocleavage dynamics of colloidal micro-RNA-functionalized nanoparticles under UV irradiation. By comparing the intensities of the measured SHG signals, the photocleaving efficiency of silver nanoparticles was 6 times greater than that of the corresponding polystyrene nanoparticles. These results demonstrated that SHG was a very sensitive nonlinear optical technique (see Fig. 7c).¹¹⁹ During the growth of nanoparticles, the corresponding plasmon hotspots were formed depending on the degree of roughness and surface inhomogeneity and different degrees of SHG signal enhancement were observed at different stages of growth. Based on this feature, the in situ growth dynamics of colloidal silver–gold core–shell (Ag@Au CS) nanoparticles in water were monitored by a stepwise synthesis method using the time-dependent SHG technique, which provided a detailed basis for studying complex colloidal nanoparticle growth mechanisms (see Fig. 7d).¹²⁰ Surface-sensitive time-dependent SHG spectroscopy was also used to study the photothermal cleavage and release of micro-RNA (miRNA) mimics or small interfering RNAs (siRNAs) from novel gold–silver–gold core–shell–shell (CSS) nanoparticles under near-infrared (NIR) irradiation, indicating that SHG-based nonlinear spectroscopy measurements could be a powerful strategy for probing biological and nanotechnological phenomena (see Fig. 7e).¹²¹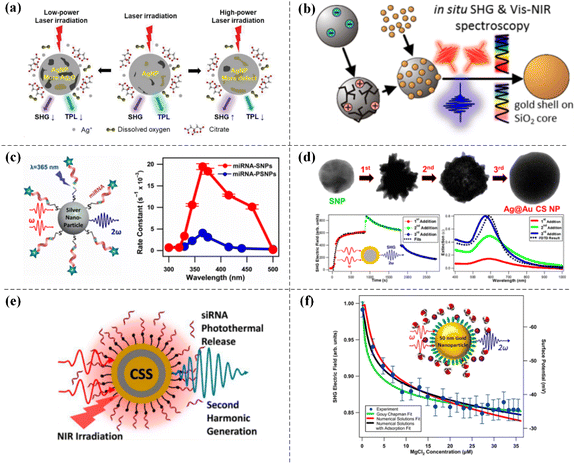

Fig. 7 The application of SHG in the field of in situ monitoring. (a) Photocatalytic redox on the surface of colloidal Ag NPs. Adapted with permission from ref. 117. Copyright 2021 Royal Society of Chemistry. (b) In situ nonlinear SHS of the seeded growth of Au nanoshells on silica core particles. Adapted with permission from ref. 118. Copyright 2014 American Chemical Society. (c) Colloidal miRNA-functionalized nanoparticles. Adapted with permission from ref. 119. Copyright 2016 American Chemical Society. (d) Colloidal Ag@Au CS nanoparticles. Adapted with permission from ref. 120. Copyright 2021 American Chemical Society. (e) Novel CSS nanoparticles. Adapted with permission from ref. 121. Copyright 2018 American Chemical Society. (f) Colloidal Au nanoparticles of 50 nm in water. Adapted with permission from ref. 122. Copyright 2015 American Chemical Society.

As a powerful and noninvasive surface-sensitive technique, SHG can also be used to study the surface charge density of colloidal nanoparticles. For example, Kumal et al. determined the surface charge density of 50 nm Au nanoparticles functionalized with mercaptosuccinic acid (MSA) in water by fitting the experimental SHG measurement results to a function and a theoretical model for increasing the electrolyte concentration. This SHG χ⁽³⁾ method is also known as the electric field induced second harmonic (EFISH) technique. The results of this study significantly contributed to further understanding the surface chemistry of colloidal nanoparticles in water (see Fig. 7f).¹²²

5. Conclusions and perspectives

Nonlinear optics is a very important research direction in the field of optics, and the development of nonlinear optics plays a tremendous role in promoting the technological progress of modern society. The rise of plasmonic nonlinear optics based on metal nanomaterials has led to an upsurge in research on SHG. This article summarizes related work on plasmonic SHG based on metal nanostructures from the perspective of principle to application. First, the basic principle of SHG and the origin of SHG on the surface of metal nanoparticles are introduced in the section Basic principle of the second harmonic generation of metal nanostructures. Then, different SHG enhancements and regulations via double resonance, magnetic resonance, and harmonic energy transfer are discussed. Finally, the application of SHG in the fields of nonlinear microscopic imaging, sensors and in situ monitoring is summarized. When the frequency of the incident light matches the surface plasmon resonance frequency, the light is strongly confined within the metal nanostructure, resulting in a substantial increase in the field intensity. This strong field strength promotes nonlinear interactions between light and materials, leading to the generation of second harmonic light. However, the SHG process in metal nanostructures is not always efficient and various factors, such as the shape, size, and nanostructure of the material, can affect the SHG efficiency. Therefore, further research is needed to optimize the design of metal nanostructures for enhanced SHG efficiency. With the continuous improvement of nanofabrication technology, many nanoparticles with complex geometric structures can be developed from theory to reality through top-down etching preparation methods, bottom-up growth methods, or chemical synthesis methods. We can expect additional research on new metal nanostructures for use in the innovative design and application of SHG in the future, which is highly important for revealing the basic process of interaction between light and matter at the nanoscale.

With the coordinated development of theory and technology in the field of nanophotonics, plasmon-enhanced SHG based on metal nanostructures has ushered in new development opportunities. By combining emerging two-dimensional (2D) materials with plasmonic metal nanostructures in recent years, the nonlinear effect of SHG has been enhanced to varying degrees. 2D materials have many advantages, such as atomic thickness, good structural stability and a strong nonlinear optical response. The nonlinear optical response of 2D materials is also adjustable and can be enhanced by exciton resonance and other methods. This approach also provides a new degree of freedom in energy valleys, which can lead to new possibilities for the construction of nonlinear optical devices.^123–127 Therefore, the composite structure formed with 2D materials and metal nanostructures may be used to develop nonlinear optical devices with high integration and high conversion efficiency. In recent years, relevant SHG research results have also been obtained. In 2020, Han et al. used nanoparticles on a mirror model to construct a surface plasmon nanocavity, controlling its surface plasmon resonance to match the second harmonic emission wavelength of monolayer WS₂, greatly increasing the incident electric field intensity, and ultimately achieving more than 300-fold SHG enhancement.¹²⁸ Zhang et al. constructed a nonlinear plasmon–exciton coupling system with adjustable second-order susceptibility. The SHG conversion efficiency of this system was three orders of magnitude greater than that of bare exciton materials on a film. This work provided a new powerful method to enhance SHG.¹²⁹ In summary, introducing 2D materials into plasmon SHG systems based on metal nanostructures is highly beneficial for increasing the control of SHG and enhancing the intensity of SHG signals. These characteristics indicate that the combination of SHG based on plasmonic metal nanostructures and 2D materials will further promote the application of these materials in the field of optical information.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (12274379, 12374288 and 12074296), the Ministry of Science and Technology of the People's Republic of China (2020YFA0211303), and the Knowledge Innovation Program of Wuhan-Shuguang Project (2023020201020329 and 2023010201020439).

References

1. T. H. Maiman, Nature, 1960, 187, 493–494.
2. P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118.
3. C. F. Li, Nonlinear Optics, Principles and Applications, 2017.
4. Y. R. Shen, Wiley Series in Pure and Applied Optics, in Principles of Nonlinear Optics, 2009.
5. R. W. Boyd, Nonlinear Optics, 3rd ed, Academic Press, San Diego, 2008.
6. J. A. Giordmaine and R. C. Miller, Phys. Rev. Lett., 1965, 14, 973–976.
7. K. Inoue, J. Lightwave Technol., 1992, 10, 1553–1561.
8. N. Imoto, H. A. Haus and Y. Yamamoto, Phys. Rev. A, 1985, 32, 2287.
9. A. V. Zayats, I. I. Smolyaninov and A. A. Maradudin, Phys. Rep., 2005, 408, 131–314.
10. M. I. Stockman, Opt. Express, 2011, 19, 22029–22106.
11. C. E. Talley, J. B. Jackson, C. Oubre, N. K. Grady, C. W. Hollars, S. M. Lane, T. R. Huser, P. Nordlander and N. J. Halas, Nano Lett., 2005, 5, 1569–1574.
12. J. F. Li, Y. F. Huang, Y. Ding, Z. L. Yang, S. B. Li, X. S. Zhou, F. R. Fan, W. Zhang, Z. Y. Zhou, D. Y. Wu, B. Ren, Z. L. Wang and Z. Q. Tian, Nature, 2010, 464, 392–395.
13. J. M. McLellan, Z. Y. Li, A. R. Siekkinen and Y. Xia, Nano Lett., 2007, 7, 1013–1017.
14. N. Liu, M. L. Tang, M. Hentschel, H. Giessen and A. P. Alivisatos, Nat. Mater., 2011, 10, 631–636.
15. K. M. Mayer and J. H. Hafner, Chem. Rev., 2011, 111, 3828–3857.
16. M. D. Malinsky, K. L. Kelly, G. C. Schatz and R. P. Van Duyne, J. Am. Chem. Soc., 2001, 123, 1471–1482.
17. M. C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346.
18. C. J. Murphy, A. M. Gole, J. W. Stone, P. N. Sisco, A. M. Alkilany, E. C. Goldsmith and S. C. Baxter, Acc. Chem. Res., 2008, 41, 1721–1730.
19. X. Huang, I. H. El-Sayed, W. Qian and M. A. El-Sayed, J. Am. Chem. Soc., 2006, 128, 2115–2120.
20. Y. Sakurai, M. Itou, B. Barbiellini, P. E. Mijnarends, R. S. Markiewicz, S. Kaprzyk, J. M. Gillet, S. Wakimoto, M. Fujita, S. Basak, Y. J. Wang, W. Al-Sawai, H. Lin, A. Bansil and K. Yamada, Science, 2011, 332, 698–702.
21. M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev, E. E. Narimanov, S. Stout, E. Herz, T. Suteewong and U. Wiesner, Nature, 2009, 460, 1110–1112.
22. J. Li, G. Hu, L. Shi, N. He, D. Li, Q. Shang, Q. Zhang, H. Fu, L. Zhou, W. Xiong, J. Guan, J. Wang, S. He and L. Chen, Nat. Commun., 2021, 12, 6425.
23. T. Y. Ning, Y. Y. Huo, S. Z. Jiang, J. Li and B. Y. Man, Plasmonics, 2016, 11, 1629–1636.
24. M. Danckwerts and L. Novotny, Phys. Rev. Lett., 2007, 98, 026104.
25. S. Kim, J. Jin, Y. J. Kim, I. Y. Park, Y. Kim and S. W. Kim, Nature, 2008, 453, 757–760.
26. C. K. Chen, A. R. B. de Castro and Y. R. Shen, Phys. Rev. Lett., 1981, 46, 145–148.
27. V. K. Valev, A. V. Silhanek, N. Verellen, W. Gillijns, P. Van Dorpe, O. A. Aktsipetrov, G. A. E. Vandenbosch, V. V. Moshchalkov and T. Verbiest, Phys. Rev. Lett., 2010, 104, 127401.
28. H. Husu, R. Siikanen, J. Makitalo, J. Lehtolahti, J. Laukkanen, M. Kuittinen and M. Kauranen, Nano Lett., 2012, 12, 673–677.
29. R. Czaplicki, H. Husu, R. Siikanen, J. Makitalo and M. Kauranen, Phys. Rev. Lett., 2013, 110, 093902.
30. A. Stone, H. Jain, V. Dierolf, M. Sakakura, Y. Shimotsuma, K. Miura, K. Hirao, J. Lapointe and R. Kashyap, Sci. Rep., 2015, 5, 10391.
31. M. Schumann, T. Buckmann, N. Gruhler, M. Wegener and W. Pernice, Light: Sci. Appl., 2014, 3, e175.
32. P. Pantazis, J. Maloney, D. Wu and S. E. Fraser, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14535–14540.
33. M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748.
34. R. W. Boyd, Nonlinear Optics, 2rd ed, Academic Press, San Diego, 2003.
35. W. P. Dempsey, S. E. Fraser and P. Pantazis, BioEssays, 2012, 34, 351–360.
36. Y. Pavlyukh and W. Hübner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245434.
37. J. Shan, J. I. Dadap, I. Stiopkin, G. A. Reider and T. F. Heinz, Phys. Rev. A, 2006, 73, 023819.
38. N. C. Panoiu, W. E. I. Sha, D. Y. Lei and G. C. Li, J. Opt., 2018, 20, 083001.
39. R. W. Terhune, P. D. Maker and C. M. Savage, Phys. Rev. Lett., 1962, 8, 40441.
40. F. Brown and M. Matsuoka, Phys. Rev., 1969, 185, 985–987.
41. B. L. Wang, R. Wang, R. J. Liu, X. H. Lu, J. Zhao and Z. Y. Li, Sci. Rep., 2013, 3, 2358.
42. G. Bachelier, J. Butet, I. Russier-Antoine, C. Jonin, E. Benichou and P. F. Brevet, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235403.
43. G. Bachelier, I. Russier-Antoine, E. Benichou, C. Jonin and P. F. Brevet, J. Opt. Soc. Am. B, 2008, 25, 955–960.
44. F. X. Wang, F. J. Rodríguez, W. M. Albers, R. Ahorinta, J. E. Sipe and M. Kauranen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233402.
45. R. Czaplicki, J. Mäkitalo, R. Siikanen, H. Husu, J. Lehtolahti, M. Kuittinen and M. Kauranen, Nano Lett., 2015, 15, 530–534.
46. J. Butet, P. F. Brevet and O. J. Martin, ACS Nano, 2015, 9, 10545–10562.
47. B. K. Canfield, H. Husu, J. Laukkanen, B. Bai, M. Kuittinen, J. Turunen and M. Kauranen, Nano Lett., 2007, 7, 1251–1255.
48. V. K. Valev, N. Smisdom, A. Silhanek, B. De Clercq, W. Gillijns, M. Ameloot, V. Moshchalkov and T. Verbiest, Nano Lett., 2009, 9, 3945–3948.
49. G. E. Hinton and R. R. Salakhutdinov, Science, 2006, 313, 504–507.
50. P. Schön, N. Bonod, E. Devaux, J. Wenger, H. Rigneault, T. W. Ebbesen and S. Brasselet, Opt. Lett., 2010, 35, 4063–4065.
51. A. Bouhelier, M. Beversluis, A. Hartschuh and L. Novotny, Phys. Rev. Lett., 2003, 90, 013903.
52. J. W. Chen, K. Wang, H. Long, H. B. Hu, X. B. Han, B. Wang and P. X. Lu, Opt. Express, 2017, 25, 1296–1307.
53. Y. Zhang, N. K. Grady, C. Ayala-Orozco and N. J. Halas, Nano Lett., 2011, 11, 5519–5523.
54. H. Aouani, M. Navarro-Cia, M. Rahmani, T. P. Sidiropoulos, M. Hong, R. F. Oulton and S. A. Maier, Nano Lett., 2012, 12, 4997–5002.
55. Z. Dong, M. Asbahi, J. Lin, D. Zhu, Y. M. Wang, K. Hippalgaonkar, H. S. Chu, W. P. Goh, F. Wang and Z. Huang, Nano Lett., 2015, 15, 5976–5981.
56. X. X. Wu, W. Y. Jiang, X. F. Wang, L. Y. Zhao, J. Shi, S. Zhang, X. Sui, Z. X. Chen, W. N. Du, J. W. Shi, Q. Liu, Q. Zhang, Y. Zhang and X. F. Liu, ACS Nano, 2020, 15, 1291–1300.
57. R. B. Davidson II, J. I. Ziegler, G. Vargas, S. M. Avanesyan, Y. Gong, W. Hess and R. F. Haglund Jr., Nanophotonics, 2015, 4, 108–113.
58. B. F. Levine, C. G. Bethea and R. A. Logan, Appl. Phys. Lett., 1975, 26, 375–377.
59. M. S. Piltch, C. D. Cantrell and R. C. Sze, J. Appl. Phys., 1976, 47, 3514–3517.
60. R. Sarma, D. Ceglia, N. Nookala, M. A. Vincenti, S. Campione, O. Wolf, M. Scalora, M. B. Sinclair, M. A. Belkin and I. Brener, ACS Photonics, 2019, 6, 1458–1465.
61. E. Barakat, M. P. Bernal and F. I. Baida, J. Opt. Soc. Am. B, 2013, 30, 1975–1980.
62. F. Dutto, M. Heiss, A. Lovera, O. López-Sánchez, A. F. Morral and A. Radenovic, Nano Lett., 2013, 13, 6048–6054.
63. W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830.
64. G. S. Agarwal and S. S. Jha, Solid State Commun., 1982, 41, 499–501.
65. X. Vidal, A. Fedyanin, A. Molinos-Gómez, S. Rao, J. Martorell and D. Petrov, Opt. Lett., 2008, 33, 699–701.
66. Y. Pu, R. Grange, C. L. Hsieh and D. Psaltis, Phys. Rev. Lett., 2010, 104, 207402.
67. J. Butet, J. Duboisset, G. Bachelier, I. Russier-Antoine, E. Benichou, C. Jonin and P. F. Brevet, Nano Lett., 2010, 10, 1717–1721.
68. M. Lapine, I. V. Shadrivov and Y. S. Kivshar, Rev. Mod. Phys., 2014, 86, 1093–1123.
69. B. Metzger, L. Gui, J. Fuchs, D. Floess, M. Hentschel and H. Giessen, Nano Lett., 2015, 15, 3917–3922.
70. M. Celebrano, X. F. Wu, M. Baselli, S. Grossmann, P. Biagioni, A. Locatelli, C. De Angelis, G. Cerullo, R. Osellame, B. Hecht, L. Dud, F. Ciccacci and M. Finazzi, Nat. Nanotechnol., 2015, 10, 412–417.
71. K. Y. Yang, J. Butet, C. Yan, G. D. Bernasconi and O. J. Martin, ACS Photonics, 2017, 4, 1522–1530.
72. Z. D. Li, H. S. Kang, M. Y. Long, J. C. Liu, T. Zhou, D. Zhu, L. Ma, S. J. Ding and L. Zhou, J. Phys. Chem. C, 2022, 126, 12129–12135.
73. Q. Ai, F. Sterl, H. Zhang, J. F. Wang and H. Giessen, ACS Nano, 2021, 15, 19409–19417.
74. S. Park, J. W. Hahn and J. Y. Lee, Opt. Express, 2012, 20, 4856–4870.
75. H. S. Kang, W. Q. Zhao, T. Zhou, L. Ma, D. J. Yang, X. B. Chen, S. J. Ding and Q. Q. Wang, Nano Res., 2022, 15, 9461–9469.
76. S. Kruk and Y. Kivshar, ACS Photonics, 2012, 4, 2638–2649.
77. S. J. Ding, H. Zhang, D. J. Yang, Y. H. F. Nan, Z. J. Yang, J. F. Wang, Q. Q. Wang and H. Q. Lin, Nano Lett., 2019, 19, 2005–2011.
78. I. Razdolski, S. Parchenko, A. Stupakiewicz, S. Semin, A. Stognij, A. Maziewski, A. Kirilyuk and T. Rasing, ACS Photonics, 2015, 2, 20–26.
79. S. Kruk, M. Weismann, A. Yu. Bykov, E. A. Mamonov, I. A. Kolmychek, T. Murzina, N. C. Panoiu, D. N. Neshev and Y. S. Kivshar, ACS Photonics, 2015, 2, 1007–1012.
80. M. Cortie and M. Ford, Nanotechnology, 2007, 18, 235704.
81. J. Ye, P. Van Dorpe, W. Van Roy, K. Lodewijks, I. De Vlaminck, G. Maes and G. Borghs, J. Phys. Chem. C, 2009, 113, 3110–3115.
82. T. Zhou, S. J. Ding, Z. Y. Wu, D. J. Yang, L. N. Zhou, Z. R. Zhao, L. Ma, W. Wang, S. Ma, S. M. Wang, J. N. Zou, L. Zhou and Q. Q. Wang, Nanoscale, 2021, 13, 19527–19536.
83. Y. H. Qiu, S. J. Ding, Y. J. Lin, K. Chen, D. J. Yang, S. Ma, X. G. Li, H. Q. Lin, J. F. Wang and Q. Q. Wang, ACS Nano, 2019, 14, 736–745.
84. T. Hanke, G. Krauss, D. Traütlein, B. Wild, R. Bratschitsch and A. Leitenstorfer, Phys. Rev. Lett., 2009, 103, 257404.
85. V. Knittel, M. P. Fischer, M. Vennekel, T. Rybka, A. Leitenstorfer and D. Brida, Phys. Rev. B, 2017, 96, 125428.
86. J. R. Feng, Z. R. Zhao, Z. L. Xiong, H. S. Kang, S. J. Ding, L. Ma and L. Zhou, Nanoscale, 2022, 14, 17633–17640.
87. B. Wu, P. F. Wang, Y. H. Qiu, S. Liang, Z. Y. Wu, L. Zhou and Q. Q. Wang, Sci. China Mater., 2020, 63, 1472–1479.
88. S. D. Liu, E. S. P. Leong, G. C. Li, Y. Hou, J. Deng, J. H. Teng, H. C. Ong and D. Y. Lei, ACS Nano, 2016, 10, 1442–1453.
89. S. Zhang, G. C. Li, Y. Q. Chen, X. P. Zhu, S. D. Liu, D. Y. Lei and H. G. Duan, ACS Nano, 2016, 10, 11105–11114.
90. D. J. Yang, S. J. Im, G. M. Pan, S. J. Ding, Z. J. Yang, Z. H. Hao, L. Zhou and Q. Q. Wang, Nanoscale, 2017, 9, 6068–6075.
91. K. Guo, C. Qian, Y. L. Zhang and K. H. Fung, Adv. Opt. Mater., 2018, 6, 1701154.
92. J. K. Hyun, T. Kang, H. Baek, H. Oh, D. S. Kim and G. C. Yi, ACS Photonics, 2015, 2, 1314–1319.
93. L. Michaeli, S. Keren-Zur, O. Avayu, H. Suchowski and T. Ellenbogen, Phys. Rev. Lett., 2017, 118, 243904.
94. R. Czaplicki, A. Kiviniemi, J. Laukkanen, J. Lehtolahti, M. Kuittinen and M. Kauranen, Opt. Lett., 2016, 41, 2684–2687.
95. E. J. Lim, M. M. Fejer and R. L. Byer, Electron. Lett., 1989, 25, 174–175.
96. K. L. Vodopyanov, M. M. Fejer, X. Yu, J. S. Harris, Y. S. Lee, W. C. Hurlbut, V. G. Kozlov, D. Bliss and C. Lynch, Appl. Phys. Lett., 2006, 89, 141119.
97. J. E. Heebner and R. W. Boyd, Opt. Lett., 1999, 24, 847–849.
98. M. Asobe, Opt. Fiber Technol., 1997, 3, 142–148.
99. S. R. Friberg, Y. Silberberg, M. K. Oliver, M. J. Andrejco, M. A. Saifi and P. W. Smith, Appl. Phys. Lett., 1987, 51, 1135–1137.
100. W. T. Wang, Z. H. Chen, G. Yang, D. Y. Guan, G. Z. Yang, Y. L. Zhou and H. B. Lu, Appl. Phys. Lett., 2003, 83, 1983–1985.
101. L. L. Li, T. J. Cui, W. Ji, S. Liu, J. Ding, X. Wan, Y. B. Li, M. H. Jiang, C. W. Qiu and S. Zhang, Nat. Commun., 2017, 8, 197.
102. J. W. Chen, K. Wang, H. Long, X. B. Han, H. B. Hu, W. W. Liu, B. Wang and P. X. Lu, Nano Lett., 2018, 18, 1344–1350.
103. P. J. Campagnola and L. M. Loew, Nat. Biotechnol., 2003, 21, 1356–1360.
104. G. C. Li, D. Lei, M. Qiu, W. Jin, S. Lan and A. V. Zayats, Nat. Commun., 2021, 12, 4326.
105. S. P. Sahu, A. Mahigir, B. Chidester, G. Veronis and M. R. Gartia, Nano Lett., 2019, 19, 6192–6202.
106. R. Jin, J. E. Jureller, H. Y. Kim and N. F. Scherer, J. Am. Chem. Soc., 2005, 127, 12482–12483.
107. S. J. Ding, D. J. Yang, X. L. Liu, F. Nan, Z. Q. Cheng, S. J. Im, L. Zhou, J. F. Wang and Q. Q. Wang, Nano Res., 2018, 11, 686–695.
108. G. Bautista, C. Dreser, X. Zang, D. Kern, M. Kauranen and M. Fleischer, Nano Lett., 2018, 18, 2571–2580.
109. V. K. Valev, Langmuir, 2012, 28, 15454–15471.
110. G. Grinblat, M. Rahmani, E. Cortés, M. Caldarola, D. Comedi, S. A. Maier and A. V. Bragas, Nano Lett., 2014, 14, 6660–6665.
111. B. Metzger, M. Hentschel and H. Giessen, Nano Lett., 2017, 17, 1931–1937.
112. M. S. Verma and M. Chandra, ACS Sens., 2020, 5, 645–649.
113. S. F. Lan, S. Rodrigues, Y. H. Cui, L. Kang and W. S. Cai, Nano Lett., 2016, 16, 5074–5079.
114. L. Ghirardini, A. L. Baudrion, M. Monticelli, D. Petti, P. Biagioni, L. Duò, G. Pellegrini, P. M. Adam, M. Finazzi and M. Celebrano, J. Phys. Chem. C, 2018, 122, 11475–11481.
115. J. Butet, I. Russier-Antoine, C. Jonin, N. Lascoux, E. Benichou and P. F. Brevet, Nano Lett., 2012, 12, 1697–1701.
116. Z. W. Yang, L. Y. Meng, J. S. Lin, W. M. Yang, P. Radjenovic, S. X. Shen, Q. C. Xu, Z. L. Yang, Z. Q. Tian and J. F. Li, Adv. Opt. Mater., 2019, 7, 1901010.
117. S. Xue, S. L. Chen, Q. Ling, Q. H. Yuan and W. Gan, Phys. Chem., 2021, 23, 19752–19759.
118. C. Sauerbeck, M. Haderlein, B. Schürer, B. Braunschweig, W. Peukert and R. N. K. Taylor, ACS Nano, 2014, 8, 3088–3096.
119. R. R. Kumal, M. Abu-Laban, C. R. Landry, B. Kruger, Z. Zhang, D. J. Hayes and L. H. Haber, Langmuir, 2016, 32, 10394–10401.
120. A. S. Dikkumbura, P. Hamal, M. Chen, D. A. Babayode, J. C. Ranasinghe, K. Lopata and L. H. Haber, J. Phys. Chem. C, 2021, 125, 25615–25623.
121. R. R. Kumal, M. Abu-Laban, P. Hamal, B. Kruger, H. T. Smith, D. J. Hayes and L. H. Haber, J. Phys. Chem. C, 2018, 122, 19699–19704.
122. R. R. Kumal, T. E. Karam and L. H. Haber, J. Phys. Chem. C, 2015, 119, 16200–16207.
123. X. P. Fan, Z. R. Ji, R. X. Fei, W. H. Zheng, W. J. Liu, X. L. Zhu, S. L. Chen, L. Yang, H. J. Liu, A. L. Pan and R. Agarwal, Nano Lett., 2020, 20, 2667–2673.
124. Y. Zhang, F. Wang, X. Feng, Z. D. Sun, J. W. Su, M. Zhao, S. Z. Wang, X. Z. Hu and T. Y. Zhai, Nano Res., 2021, 15, 2391–2398.
125. Y. W. Shan, Y. G. Li, D. Huang, Q. J. Tong, W. Yao, W. T. Liu and S. W. Wu, Sci. Adv., 2018, 4, eaat0074.
126. L. Karvonen, A. Säynätjoki, M. J. Huttunen, A. Autere, B. Amirsolaimani, S. Li, R. A. Norwood, N. Peyghambarian, H. Lipsanen, G. Eda, K. Kieu and Z. P. Sun, Nat. Commun., 2017, 8, 15714.
127. X. T. He, J. W. Liu, F. L. Shi, K. Shen, W. J. Chen, X. D. Chen and J. W. Dong, Sci. China: Phys., Mech. Astron., 2022, 65, 284212.
128. X. B. Han, K. Wang, P. D. Persaud, X. Y. Xing, W. W. Liu, H. Long, F. Li, B. Wang, M. R. Singh and P. X. Lu, ACS Photonics, 2020, 7, 562–568.
129. T. Z. Zhang, Q. B. Guo, Z. F. Shi, S. P. Zhang and H. X. Xu, ACS Photonics, 2023, 10, 1529–1537.

---