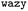Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sequence determinants of protein phase separation and recognition by protein phase-separated condensates through molecular dynamics and active learning†
Arya Changiarath a,
Aayush Aryaa,
Vasileios A. Xenidis
a,
Aayush Aryaa,
Vasileios A. Xenidis b,
Jan Padekenc and
Lukas S. Stelzl
b,
Jan Padekenc and
Lukas S. Stelzl *cde
*cde
aInstitute of Physics, Johannes Gutenberg University (JGU) Mainz, Germany
bDepartment of Biology, Aristotle University of Thessaloniki, Greece
cInstitute of Molecular Biology (IMB) Mainz, Germany
dInstitute of Molecular Physiology, Johannes Gutenberg University (JGU) Mainz, Germany. E-mail: lstelzl@uni-mainz.de
eKOMET1, Institute of Physics, Johannes Gutenberg University (JGU) Mainz, Germany
First published on 3rd August 2024
Abstract
Elucidating how protein sequence determines the properties of disordered proteins and their phase-separated condensates is a great challenge in computational chemistry, biology, and biophysics. Quantitative molecular dynamics simulations and derived free energy values can in principle capture how a sequence encodes the chemical and biological properties of a protein. These calculations are, however, computationally demanding, even after reducing the representation by coarse-graining; exploring the large spaces of potentially relevant sequences remains a formidable task. We employ an “active learning” scheme introduced by Yang et al. (bioRxiv, 2022, https://doi.org/10.1101/2022.08.05.502972) to reduce the number of labelled examples needed from simulations, where a neural network-based model suggests the most useful examples for the next training cycle. Applying this Bayesian optimisation framework, we determine properties of protein sequences with coarse-grained molecular dynamics, which enables the network to establish sequence–property relationships for disordered proteins and their self-interactions and their interactions in phase-separated condensates. We show how iterative training with second virial coefficients derived from the simulations of disordered protein sequences leads to a rapid improvement in predicting peptide self-interactions. We employ this Bayesian approach to efficiently search for new sequences that bind to condensates of the disordered C-terminal domain (CTD) of RNA Polymerase II, by simulating molecular recognition of peptides to phase-separated condensates in coarse-grained molecular dynamics. By searching for protein sequences which prefer to self-interact rather than interact with another protein sequence we are able to shape the morphology of protein condensates and design multiphasic protein condensates.
1 Introduction
Proteins and other biomolecules within cells can phase separate to form liquid-like droplets.1 Such phase-separated droplet regions provide a unique microenvironment essential for several important cellular processes and thus are an important way of regulating biological function. The human proteome has a very rich diversity in terms of composition.2 A predictive insight into which protein sequences could undergo phase-separation would improve understanding of the pathogenesis of several neurodegenerative diseases including Alzheimer’s disease,3,4 where protein phase separation and the formation of toxic aggregates of these proteins have been linked to pathogenesis. Different condensates or condensates with multiple distinct phases provide a way for biological processes to be regulated in time and space.5–7 Spatially separating different biochemical reactions is also a promising blueprint for biotechnological applications.8 This necessitates efficient strategies to design novel phase separating condensates and to develop molecules, such as artificial proteins, to bind selectively to phase-separated condensates. However, in other contexts such as designing protein interaction modules for synthetic biology,9 one might specifically want to reduce the propensity of proteins to interact and form condensates.Molecular dynamics (MD) simulations have played a major role in our understanding of protein–protein interactions and protein phase separation.1,10–12 The development of state-of-the-art molecular force fields has enabled accurate representation of molecular interactions, allowing these simulation models to successfully predict phase separation propensities of diverse protein sequences.11,13 Atomistic molecular dynamics simulations can provide essential insights into molecular driving forces by simplifying the description. However, building an exact quantitative understanding of a protein sequence–property relationship, to be able to predict the behaviour of a sequence without the necessity of a simulation or an experiment, has remained difficult to achieve. This is in part due to the large space of possible biological sequences, and also how sequence context will change the interaction characteristics of the amino acids.
One way to model such complicated relationships is via machine learning, and recently, important progress has been made in learning such relationships and also applying this progress to the interactions and phase behaviour of flexible and disordered proteins.14–17 A very successful strategy has been to combine physics-based simulations with machine learning and artificial intelligence.16,18,19 Ginell et al. have trained a neural network with a physics-based simulation model to predict how different disordered proteins will interact.14 With a physics-based simulation model von Bülow et al. have successfully trained a neural network to predict the phase separation propensities of proteins.15 In recent years, protein language models have been shown to organise protein sequences in biologically meaningful ways.20–23 Language models also seem to encode useful physical and chemical information, which makes it imperative to see how we can leverage the information encoded in such models to predict protein behaviour. Language models have been used in iterative design24 and for proposing entirely novel proteins.23 However, a key difficulty in mapping sequence–property relationships is the limited availability of “labelled” data needed for training. The property of interest may require experimental input or computationally expensive simulations. One must also note that not all labelled data is equally useful, and some specific examples may be more beneficial for training than others.
Active learning27 is a machine learning paradigm meant to address exactly this issue, where the model interacts with the human to suggest which labelled examples should be provided for training. Within such a framework, Bayesian Optimisation (BO) can be invoked to rank the most useful sequences in terms of their potential utility to the model and thus can be used to judiciously direct one’s resources. These approaches can be utilised to understand how chemical structure and biological sequences give rise to chemical28 and biological properties. Recently, An et al.29 used active learning to discover strongly interacting proteins that tend to phase-separate, while optimising the trade-off between thermodynamic stability and transport properties. In another context, it was demonstrated that active learning helps to design molecules selectively interacting with one phase of a lipid membrane over another phase of this membrane30 and to find small molecules binding to a protein.31 Chemical structure and biological sequences have to be inputted in a way that is amenable to machine learning. One possibility is to combine various metrics. Deep learning provides a way of achieving this and promising results based on autoencoder have been obtained.30 For biological sequences, language models may be a natural way of representing sequences and recent advances make it possible to use pre-trained language models for featurisation.24,25 Language models show a lot of promise for BO, as exemplified by a recent study by Hoffbauer and Strodel,17 where the authors showed that the biochemical knowledge encoded in an advanced pre-trained language model enables efficient active learning even when only limited data is available. Yang et al. have developed a very promising workflow based on a pre-trained language model25 and deep ensembles to express the learned relationships. Here we investigated three related questions: (1) Can we identify the sequence determinants which lead to protein self interactions and phase separation? (2) Can we understand and design new sequences which selectively bind to phase-separated protein condensates? (3) Can we design multiphasic condensates? To address these important questions in biophysics and physical chemistry we utilize the BO approach by Yang et al.25 (Fig. 1).
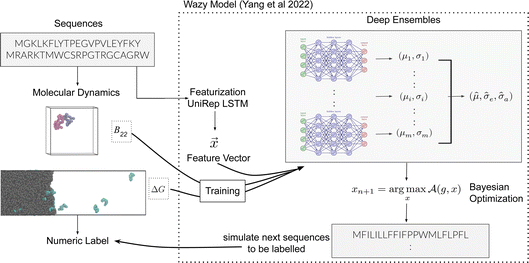 | ||
Fig. 1 Schematic overview of the active learning framework for predicting peptides using Bayesian Optimisation (BO) and Molecular Dynamics (MD) simulations: (A) MD simulations of protein chains to compute second virial coefficient (B22) and partition free energy (ΔG) for model training. This initial sample is fed to the  BO package,25 which utilises UniRep LSTM,24,26 to parse the protein sequence into a feature vector BO package,25 which utilises UniRep LSTM,24,26 to parse the protein sequence into a feature vector 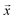 . Deep ensemble training on feature vectors and computed properties to establish sequence–property relationships. To choose which sequences the model would benefit the most from, an acquisition function . Deep ensemble training on feature vectors and computed properties to establish sequence–property relationships. To choose which sequences the model would benefit the most from, an acquisition function 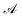 is used to rank and suggest the next set of sequences. The suggested sequences are simulated again, generating new data for subsequent training cycles. This iterative process helps the model learn the sequence–property relationship with fewer examples and simultaneously explore sequence space regions that contain proteins with the most extreme values of the property we studied. is used to rank and suggest the next set of sequences. The suggested sequences are simulated again, generating new data for subsequent training cycles. This iterative process helps the model learn the sequence–property relationship with fewer examples and simultaneously explore sequence space regions that contain proteins with the most extreme values of the property we studied. | ||
2 Methods
We study the mapping of a protein sequence to one of its properties, as represented by a numeric quantity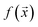 . As we shall describe later, f(x) could be the second virial coefficient B22, or another quantity that provides an estimate of the affinity of a sequence to bind to a condensate. Our scientific problem thus reduces to training a model to learn the mapping between
. As we shall describe later, f(x) could be the second virial coefficient B22, or another quantity that provides an estimate of the affinity of a sequence to bind to a condensate. Our scientific problem thus reduces to training a model to learn the mapping between 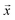 and
and 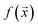 , while simultaneously exploring the protein sequence space to maximise this label. We utilize the
, while simultaneously exploring the protein sequence space to maximise this label. We utilize the 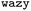 package25 which provides the framework for performing such optimisation tasks implemented here.
package25 which provides the framework for performing such optimisation tasks implemented here.
Fig. 1 illustrates our workflow: We begin with an initial set of protein sequences and conduct coarse-grained molecular dynamics simulations to extract for instance, B22 or ΔG values. We initialize a surrogate model within the protein sequence Bayesian Optimisation (BO) package 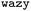 25 and provide it with an initial set of sequences and labels to calibrate the initial sequence–property mapping. During that,
25 and provide it with an initial set of sequences and labels to calibrate the initial sequence–property mapping. During that, 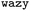 uses UniRep—a multiplicative Long-Short Term Memory (mLSTM) model24,26 for parsing the amino acid sequence into a feature vector x that contains the essential protein features in a fixed-length numeric vector.
uses UniRep—a multiplicative Long-Short Term Memory (mLSTM) model24,26 for parsing the amino acid sequence into a feature vector x that contains the essential protein features in a fixed-length numeric vector.
UniRep, trained on 24 million primary amino acid sequences in the UniRef50 database, has shown the ability to accurately partition structurally and evolutionarily similar proteins, even when they share little sequence identity.24 The resulting feature vectors, combined with the computed labels, serve as input for training the surrogate models, which in the context of 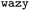 are ensembles of multi-layer perceptrons (MLPs). Such deep ensembles are appropriate for uncertainty quantification and offer greater expressive power compared to the Gaussian processes (GPs) that are otherwise typically chosen as surrogates.
are ensembles of multi-layer perceptrons (MLPs). Such deep ensembles are appropriate for uncertainty quantification and offer greater expressive power compared to the Gaussian processes (GPs) that are otherwise typically chosen as surrogates.
Following this initial calibration of sequence–property mapping, the Bayesian optimiser uses an acquisition function to rank which proteins would serve as the most useful examples for further training. This process simultaneously explores the sequence space, in search of regions with proteins that possess the highest values of the property we are studying. A batch of sequences is drawn from this for the next cycle of training. Coarse-grained simulations of these sequences are again performed, and the entire process is repeated for several iterations. In the subsequent sections, we provide a detailed account of the training and optimisation methodology.
2.1 Model description and optimisation
As mentioned before, the surrogate model in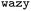 is an ensemble of feedforward neural networks (called a deep ensemble32). In such a model, the quantity of interest f(x) is independently predicted by not one but an ensemble of neural network models, which in this case is a Multi-Layer Perceptron (MLP). In the configuration used here, the ensemble comprises of 5 MLPs. UniRep24 parses an input sequence into a fixed-length feature vector of dimension N = 1900. Therefore, each individual MLP takes an input of dimension 1900, followed by three layers having 128, 32, and 2 neurons each. The last layer outputs two numbers: a mean
is an ensemble of feedforward neural networks (called a deep ensemble32). In such a model, the quantity of interest f(x) is independently predicted by not one but an ensemble of neural network models, which in this case is a Multi-Layer Perceptron (MLP). In the configuration used here, the ensemble comprises of 5 MLPs. UniRep24 parses an input sequence into a fixed-length feature vector of dimension N = 1900. Therefore, each individual MLP takes an input of dimension 1900, followed by three layers having 128, 32, and 2 neurons each. The last layer outputs two numbers: a mean ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) and a standard deviation
and a standard deviation ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) that characterise a normal distribution
that characterise a normal distribution 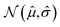 . The dispersion in the mean values
. The dispersion in the mean values ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) predicted by the individual models, and the sum of the variances
predicted by the individual models, and the sum of the variances ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) 2 of this
2 of this 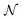 by the different models, together give a total uncertainty estimate. All networks layer but the last one is followed with the SiLU (also known as Swish) activation function. In addition, standard techniques such as dropout and weight decay are utilised to reduce overfitting. For further technical description about
by the different models, together give a total uncertainty estimate. All networks layer but the last one is followed with the SiLU (also known as Swish) activation function. In addition, standard techniques such as dropout and weight decay are utilised to reduce overfitting. For further technical description about 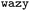 , we refer the reader to Yang et al., who designed it.25
, we refer the reader to Yang et al., who designed it.25
The advantage of deep ensembles is that neural networks possess more expressive power than Gaussian processes, while providing a way of uncertainty quantification. Bayesian optimisation works via ranking sequences using an acquisition function 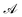 . Unless stated otherwise, for most of the work presented here, we chose the “upper confidence bound” (UCB) acquisition function33 which balances both exploitation of the known maximas and exploration of the parameter space:
. Unless stated otherwise, for most of the work presented here, we chose the “upper confidence bound” (UCB) acquisition function33 which balances both exploitation of the known maximas and exploration of the parameter space:
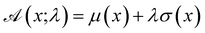 | (1) |
Another commonly used acquisition function is Expected Improvement (EI). The fundamental principle behind EI is to select the next point to evaluate based on the current best result. The choice of the acquisition function sensitively affects which regions of sequence space get explored for, and thus the arrival at, an optimal solution. Later, in Section 3.1, we will show the impact of this choice as observed in our study.
2.2 Training and validation
Optimisation of the surrogate model—by asking it to suggest sequences to be measured in a lab or simulated—requires an initial calibration. For most of the tasks studied here, an initial set of sequences was drawn from ProtGPT2,23 a protein language model constructed for de novo protein design. Quantities f(x), either B22 or ΔG values, were computed from coarse-grained molecular dynamics. This computed value was treated as the true or expected value of the property of interest. The length of all sequences used for training was chosen to be 21 amino acids.While training, to track the learning of the model, we set aside two sets of sequences for validation of the model’s predictive ability, which were never used for training. The first set was drawn the same way as the training data itself, with 42 21-amino acid length sequences drawn from the ProtGPT2 language model,23 spanning a wide range of B22 values. To track how well the approach captures strongly interacting peptides which are likely only a small fraction of natural protein sequences, we generated a second set of validation data. We took 22 21-amino acid sequences with very negative B22 values from the study of An et al. (2024)29 (see their ESI Tables). The true values of B22 for these validation sequences were computed in exactly the same way, from coarse-grained simulations. The coarse-grained simulations for calculating B22 were conducted for 10 μs.
For designing peptides that bind to condensates, an initial calibration set of 70 21-mer peptides was selected from An et al. (2024). For validation, 30 peptides were chosen from ProtGPT2. The simulations involving the condensate and peptides were performed for 0.6 μs.
Similar to Yang et al.,25 we will refer to an “optimisation step” as being the usage of one sequence-label pair after which the model is updated. Subsequent to each optimisation step, we predicted the numeric label for the validation set sequences and tracked the mean squared error from the residual between true (computed from simulations) and values predicted by the model. The exact size of the calibration and validation sets were chosen separately for the different tasks studied here (described in their respective subsections). In all that follows, we shall refer to the initial calibration as iteration 0.
2.3 Specifications of the coarse-grained molecular dynamics simulations
Residue-level coarse-grained simulations with the HPS model34 were run in HOOMD-blue v. 2.9.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 extended with azplugins (v. 2.9.2). Simulations were also conducted with the more recent CALVADOS2 simulation model.13 The second virial coefficient (B22) was calculated from the simulations of two 21-amino acid peptide sequences in a cubic box of dimension 8 nm × 8 nm × 8 nm. To determine the partition free energy, condensate simulations were conducted in a slab geometry of dimension 15 × 15 × 250 nm. The condensate was simulated with 300 chains of 140-amino acid CTD of RNA Polymerase II, and 30 chains of 21-amino acid peptides were added to the preformed condensate.
35 extended with azplugins (v. 2.9.2). Simulations were also conducted with the more recent CALVADOS2 simulation model.13 The second virial coefficient (B22) was calculated from the simulations of two 21-amino acid peptide sequences in a cubic box of dimension 8 nm × 8 nm × 8 nm. To determine the partition free energy, condensate simulations were conducted in a slab geometry of dimension 15 × 15 × 250 nm. The condensate was simulated with 300 chains of 140-amino acid CTD of RNA Polymerase II, and 30 chains of 21-amino acid peptides were added to the preformed condensate.
2.4 Computing the second virial coefficient from coarse-grained simulations
The second virial coefficient B22 is used as a measure of protein self interactions. This is well-reasoned, as B22 is an estimate of the intermolecular forces between two molecules in dilute solutions.34 It is well established that a negative B22 correlates strongly with the tendency to phase separate, an idea that led An et al.29 to similarly use B22 as a proxy label. We compute it using equilibrium molecular dynamics simulations with durations of 10 μs. The second virial coefficient is defined as:
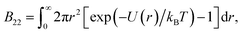 | (2) |
We compute B22 from the radial distribution function g(r)
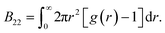 | (3) |
2.5 Designing binders to a specific condensate
In our simulations, we investigate sequence-specific binding to condensate formed by the intrinsically disordered C-terminal domain (CTD) of RNA Polymerase II. Here we consider two types of CTD condensates: one composed of ideal 140-mer CTD sequences (each containing 20 ideal YSPTSPS heptad repeats), and another representing the CTD of human RNA Polymerase II.To quantify the binding affinity of the designed peptides for the condensed phase, we calculated the partition free energy (ΔG) from the equilibrium densities in the coexisting dilute and dense phases. We calculated the partition free energy of the peptides to the condensate using the expression,36 ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ρdense/(ρdilute + ε)), which became the numeric label f(x) we wanted to train for. Here ΔG is the binding free energy, R is the gas constant, T is the temperature, ρdense is the density of the peptide in the dense condensate phase, and ρdilute is the density of the peptide in the dilute phase. ε is a small constant (=10−5) added to the denominator to prevent the divergence of ΔG when peptides strongly bind to the condensate.
log(ρdense/(ρdilute + ε)), which became the numeric label f(x) we wanted to train for. Here ΔG is the binding free energy, R is the gas constant, T is the temperature, ρdense is the density of the peptide in the dense condensate phase, and ρdilute is the density of the peptide in the dilute phase. ε is a small constant (=10−5) added to the denominator to prevent the divergence of ΔG when peptides strongly bind to the condensate.
2.6 Protein sequence descriptors
In addition to predictability of B22 or ΔG by the model, we kept track of the amino acid diversity, sequence properties such as mean hydropathy, fraction of residues that contribute to disorder or chain expansion, the number of charged residues, etc. For this, the amino acid compositions and relevant descriptors were estimated with the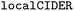 Python library from Holehouse et al.37
Python library from Holehouse et al.37
3 Results
As mentioned previously, we trained the model for several different tasks. In the following, we demonstrate the performance on each of these. Note that for each task, the model was trained independently from scratch. In Section 3.1, we show how the model successfully learnt to predict strongly self-interacting proteins, and suggest sequences that are likely to phase separate. In Section 3.3, utilising a different property—namely ΔG, which gives the binding affinity—we trained to find peptides that like to bind with pre-formed condensates, using CTD of the RNA Polymerase II as a test case. The method can be extended to multi-phasic condensates by defining a suitable fitness function to shape the morphologies of multi-phasic condensates. The success of the model on its ability to perform on these very different tasks with limited training data shows the generalised applicability of the method.3.1 Sequence-determinants of protein self-interaction from active learning
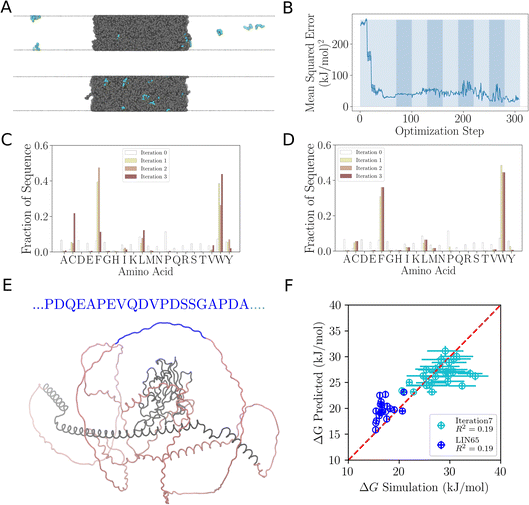
As the training progresses, the deep ensemble (Fig. 1) quickly learns the relationship between protein sequences and the second virial coefficient B22, quantifying a protein’s tendency to interact with another chain with identical sequence. In Fig. 2A, we see a rapid decline in the mean squared error (MSE) in its predictions for B22, on validation sequences the model has never seen during training, with the MSE dropping from more than 25 to just above 5. The alternating shaded regions mark the different iterations in the active learning process. Note that in Fig. 2, each optimisation step represents the training and update of the deep ensemble using one sequence and its corresponding label. The validation set used in Fig. 2A features sequences which follow the rules of natural protein sequences as encapsulated by ProteinGPT2.23 Note that while improvement against this set begins to stagnate at around 50 steps, we find a continued improvement with the second validation set of 21 mer sequences designed by An et al.29 (Fig. 2B). This is because, after the first 50 steps when the model is interrogated for suggestion, it already picks up chains with the most negative B22 values (Fig. 3A). Continued training on those sequences therefore does not improve the predictability of the average sequence, but improvement is seen against the An et al.29 sequences, which are enriched with more strongly interacting proteins. The MSE decreases from values above 200 to values below 100. After seeing more than 150 sequences, the MSE rises again, which could hint at overfitting. In addition, the decrease in the uncertainty estimate after 150 sequences in Fig. 2A may also be due to overfitting, as this suggests all models within the ensemble are predicting values closer to each other’s, while not improving in accuracy. Note that mean-squared error alone is not a complete indicator of progress during training.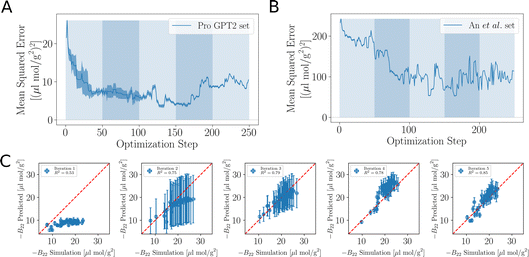 | ||
| Fig. 2 Accuracy of the learned relationship between protein sequence and B22. (A) Feedback between ML model and simulations. The shaded areas highlight the transitions between the sequences 0–50, 50–100, 100–150 and 150–200 in the first, second, and third iterations of the active learn procedure. The validation set is generated with ProtGPT2. (B) The same but with a validation set which includes more strongly interacting sequences from An et al. (C) Predicted B22 from the active learning and computed from coarse-grained molecular dynamics. After the network was trained with N = 50 sequences. At the second iteration with a total of N = 100. Third iteration with N = 150 sequences (Fig. S1†). | ||
When the model is interrogated for suggesting training examples, we also ask it to predict B22 values for these sequences. After coarse-grained molecular dynamics simulations of these suggested sequences were performed, we compared how well those forecasts matched with the true values (Fig. 2C). This improvement is quantitatively reflected in the coefficient of determination (R2), which indicates how well the model predictions match the observed data. Initially, there is poor agreement between predicted and true estimates, indicated by R2 = 0.53. The correlation between predicted and expected values continued to improve in the subsequent iterations as evidenced by the increasing R2 values. By the fourth iteration, the R2 value had risen to 0.85.
Note that a significantly longer calibration (e.g. 200 sequences instead of 50) in the initial training does not improve the overall outcome (see Fig. S1 in the ESI†). We tentatively conclude that results from the suggested sequences in active learning are more important, or that there is not much new information in these additional initial sequences.
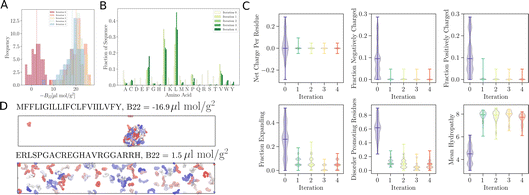
As remarked previously, after just 50 such steps, when the model was interrogated to suggest the next batch of sequences to train with, it already picked up sequences with very negative B22 values. When coarse-grained molecular dynamics simulations of these sequences were run, we found that the distribution of B22 values had clearly shifted from a mean value of −2.3 μL mol−1 g−2 to −18.7 μL mol−1 g−2 (see iteration 1 in Fig. 3A). Subsequent iterations of training with examples requested by the model led to a further shift to even further negative values.
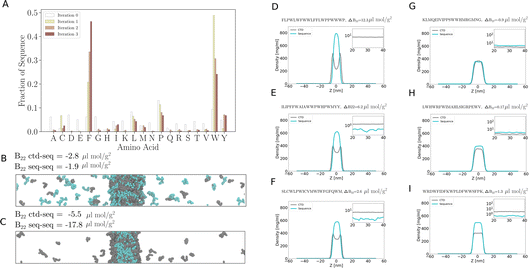
In addition to these quantitative metrics around B22 values, in Fig. 3B we show that even the amino acid composition of the suggested sequences changed in biologically meaningful ways. The sequences get enriched with hydrophobic amino acids such as Ile, Leu, and Val. Charged residues are already lost in the first stage of learning. Impressively, all of these biologically and chemically sensible changes emerged without explicit input regarding information about the charge or hydrophobicity of the residues during training. We attribute this to the featurisation with the UniRep LSTM, and it illustrates the remarkable ability of the model to learn and capture relevant physicochemical properties from the sequence data alone. Many of the sequences we provided initially feature charged residues (Fig. 3C). While these sequences are not highly charged, with a net charge per residue close to 0, some sequences are enriched in positively or negatively charged residues. The model seems to learn from the input sequences that a simple way to enhance protein–protein chain interactions is to eliminate charged residues. It is important to note that complementary patches of positively and negatively charged residues can give rise to strong interactions and protein condensation via complex coacervation.7,38 The input sequence set includes sequences which feature a third or half of the residues favouring expanded conformations. As the training progresses, the number of disorder promoting residues decreases strongly with iteration. At the same time the mean hydrophobicity of the suggested sequences increases.
We expect that sequences with large negative values of B22 interact strongly and phase separate, which we verified by simulating multiple chains for a sequence from iteration 3 (Fig. 3D). Multiple chains of this peptide form a condensate as expected given its favourable inter-chain interactions. Conversely, for sequences with a positive B22 we expect that the chains are not interacting with each other and that the chains prefer to stay separate from each other and do not phase separate as shown for a sequence from the validation data set (Fig. 3D). We note that the HPS model which underestimates interactions of Arg residues likely underestimates the self interactions of this peptide.
 | ||
Fig. 4 Optimisation by maximising −B22 values, where the simulations are conducted using the CALVADOS force field.13 (A) The distribution of B22 values for 5 iterations of optimisation. The observed distribution shifts towards increasingly negative values compared with the HPS model, indicating a trend towards sequences with stronger interactions. (B) The plot illustrates the fraction of amino acids present in the sequences suggested by  during each iteration of optimisation. Notably, there is a noticeable increase in the fraction of isoleucine (I), leucine (L), valine (V), and phenylalanine (F) over successive iterations. (C) Analysis of the amino acid compositions of the sequences suggested by the model after each iteration. during each iteration of optimisation. Notably, there is a noticeable increase in the fraction of isoleucine (I), leucine (L), valine (V), and phenylalanine (F) over successive iterations. (C) Analysis of the amino acid compositions of the sequences suggested by the model after each iteration. | ||
Therefore, to potentially identify alternative solutions while exploring the sequence space, we independently trained the model using sequences ranked best by the Expected Improvement (EI) acquisition function. The mean squared error (MSE) between the predicted and expected −B22 of the ProteinGPT2 validation set, decreased with each training step (Fig. 5A), similar to what we observed in the UCB-based model. The model suggests sequences with diverse amino acid compositions (Fig. 5B). Examining the suggested sequences, we found that the EI-based optimisation found less strong interactors (smaller −B22 values) compared to the model trained using the Upper Confidence Bound (UCB) acquisition function (Fig. S2†). The UCB-based optimisation predominantly predicted sequences with high negative B22 values, while the EI-based model predicted a wider range of sequences, mostly with negative B22 values and a small fraction with positive B22 values.
 | ||
Fig. 5 Optimisation using Expected Improvement (EI) acquisition function to find the optimal value of −B22. (A) Evolution of mean squared error (MSE) between the predicted and expected −B22 of the ProteinGPT2 validation set. (B) Fraction of amino acids in the sequences suggested by  after each iteration. (C) Snapshot of the simulations of sequences suggested by after each iteration. (C) Snapshot of the simulations of sequences suggested by  at the 4th iteration. (D) The sequences with more negative B22 showed clear phase separation (Fig. S2B†). at the 4th iteration. (D) The sequences with more negative B22 showed clear phase separation (Fig. S2B†). | ||
When we simulated the sequences suggested by the model in the 4th iteration, those with negative B22 values in particularly exhibited clear phase separation—forming dense, condensed phases (see Fig. 5C and D). The phase-separating sequence not only features aromatic residues such as Trp and Phe and hydrophobic residues such as Val, but also negatively charged Asp and positively charged Arg at its C-terminal end. Interactions of positively and negatively charged amino acids can also contribute to phase separation,38,41 provided the net charge of the sequence is low to moderate.38 Overall the optimisation using UCB led to the identification of sequences with stronger interactions than EI. However, we note that, in the search for an optimal solution, UCB had led to less diverse sequence structures. On the other hand, the sequences ranked by EI were more diverse in amino acid composition but this came at the cost of not touching the sequence space of the most negative B22 chains. These differences are evident in the distributions shown in Fig. S2.†
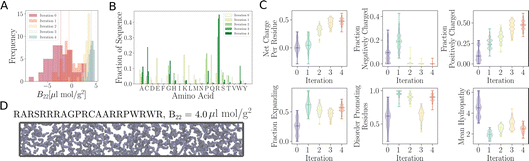
3.2 Designing peptides that do not interact
Employing the same approach, we can design peptides which do not interact with copies of themselves. For many biotechnological applications, one would want to minimise the interactions between proteins, e.g., to reduce the aggregation of therapeutic antibodies.42 Non-interacting sequences can be useful building blocks in protein design,9 for example when combining protein domains with different functionalities. To decrease the propensity for protein self-interaction, we maximise B22 rather than −B22, as previously done for promoting interactions.As the BO proceeds, suggested sequences tend to have more positive B22 values (Fig. 6A) than the initial set of sequences we have used to start the BO (referred to as “Iteration 0”). Interestingly, at the first iteration, the proposed sequences feature a combination of negatively charged amino acids, such as glutamic acid (Glu) and some aspartic acid (Asp) residues, as well as positively charged amino acids, including lysine (Lys) and arginine (Arg) (Fig. 6B and C). In the subsequent second, third and fourth iterations, Arg residues become highly enriched (Fig. 6B). Note that the enrichment in Arg residues may be partially due to the specific choices made in the parameterisation of the coarse-grained simulation model we employ. While Arg is positively charged and increasing the net positive or negative charge of a peptide can prevent phase separation,38 Arg residues have a very low tendency to interact with other protein residues in the version of residue-level coarse-grained HPS model34 we employ here. Tesei et al., have shown that a higher interaction strength of Arg for other amino acids leads to a better overall description of disorder proteins, their phase behaviour and properties.13,39 The net charge per residue increases as the training progresses (Fig. 6C). Residues tend to favour extended rather than collapsed conformations. The fraction of negatively charged amino acids in the selected sequences becomes negligible after the first iteration (Fig. 6C). Concurrently, the fraction of amino acids associated with favouring extended rather than collapsed conformations increases compared to the initially input sequences. Analogously, the fraction of disorder promoting residues increases with each iteration. However, in the third iteration, there is a temporary drop in the fraction of disorder promoting residues, but this trend is reversed in the fourth iteration, where a high level of disorder-promoting residues is observed once again. Conversely, the mean hydrophobicity decreases as there are almost no aromatic residues (Phe, Tyr, and Trp) present in the sequences suggested by the active learning process.
To test whether these sequences actually interact with each other or not, we observed their behaviour in our CG simulations. In Fig. 6D, we show a snapshot of such a simulation of protein with B22 = 4.0 μL mol g−2. Clearly, the suggested sequence remains uniformly distributed throughout the simulation box, preferring to not interact with its identical chains and therefore not showing any sign of phase separation.
3.3 Designing peptides binding to phase-separated condensates
To investigate the ability of peptides to interact with pre-formed condensates, we initiated 70 simulations with peptides and a pre-formed condensate of the C-terminal domain of RNA Polymerase II (CTD).7By optimising the peptide sequences to maximise the magnitude of the negative partition free energy (−ΔG), our active learning approach effectively identifies peptides with an enhanced propensity to interact with the condensed phase. Just like for the B22 task, the performance of the model was evaluated using the mean squared error (MSE) calculated for a validation set of peptides. Remarkably, the MSE showed a significant decrease after just 50 training steps—similar to other tasks studied here—with MSE dropping from above 200 to less than 50 indicating that the model could effectively capture the underlying patterns and characteristics of the peptide-CTD condensate interactions. In the second iteration hydrophobic residues such as Cys, Phe, Leu, and Trp residues are very prominently enriched (Fig. 7C, S4A and B†). After four iterations of the Bayesian optimisation cycle, peptides are highly enriched in Trp residues. At this stage, peptides are uniformly distributed in the dense condensate phase. At the same time sampling the dilute concentration of the peptides becomes very challenging and long simulations are required for proper equilibration of the peptides between the dilute and condensate phases. Once the peptides are interacting strongly with the condensates and the dilute concentration becomes difficult to sample further, so enhancing the interactions of the peptides with the condensates becomes difficult. However, at this stage, the design task has in some sense been successfully completed as strongly interacting protein sequences have been found. We note that the lack of sequence diversity means that these peptides are likely too hydrophobic to be useful for biochemical and biotechnological applications, but our investigation shows that it is possible to quickly identify sequences which bind to condensates given a coarse-grained simulation model.
We also performed iterative optimisation to identify sequences that bind effectively to human CTD condensates.43 The human CTD (hCTD) sequence deviates from the ideal CTD sequence, which consists of a consensus repeat of heptad motifs. During the training process with  ,25 the algorithm suggested peptide sequences with a similar composition to the sequences found in the previous case, but featuring a higher fraction of the following amino acid residues: Trp, Phe, Leu, and Cys (Fig. 7D, S4C and D).†
,25 the algorithm suggested peptide sequences with a similar composition to the sequences found in the previous case, but featuring a higher fraction of the following amino acid residues: Trp, Phe, Leu, and Cys (Fig. 7D, S4C and D).†
Once trained, such a model can quickly evaluate many novel sequences for their potential to interact with specific condensates without requiring time-consuming simulations for each sequence. It can generalize from learned patterns to predict the interaction propensity of sequences different from those in the training set. For instance, we used the trained model to investigate interactions between LIN-65 and RNA Polymerase II (Pol II). In C. elegans, LIN-65 (Fig. 7E) is an important regulator of chromatin organisation by supporting the formation of heterochromatin which represses the transcription of genes. Given that the CTD of RNA Pol II is critical for transcription, but LIN-65 is associated with the repression of transcription, we surmised that disordered sequences in the LIN-65 disordered regions may be disfavoured from binding to CTD condensates and this preference encoded in the sequence of LIN-65 could contribute to its specificity in separating transcribed genes from heterochromatin. Since the model is trained on 20-mer sequences, we divided the intrinsically disordered region of LIN-65 into 20-mer fragments (Fig. 7E, pin and blue regions). We then predicted the propensity of LIN-65 fragments to be recruited to CTD condensates using the trained model. The correlation plots shown in Fig. 7F, indicate that the recruitment propensity of LIN-65 fragments is lower than that of sequences suggested by  after the seventh iteration, as the ΔG is lower for LIN-65 fragments compared to the sequences
after the seventh iteration, as the ΔG is lower for LIN-65 fragments compared to the sequences 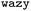 suggested (Fig. S4E and F†). This predictive ability without new simulations showcases the powerful application of machine learning in studying protein–condensate interactions.
suggested (Fig. S4E and F†). This predictive ability without new simulations showcases the powerful application of machine learning in studying protein–condensate interactions.
3.4 Design of multiphasic condensates
To explore the nature of sequences that can be recruited to CTD condensates while forming multiphasic structures, we employed a strategy based on the second virial coefficient (B22). We calculated B22 for a given sequence interacting with itself and with a 21-mer CTD sequence. The residue-level coarse-grained HPS force field we employ for these simulations captures the interactions of 21-mer CTD sequences well, as established through comparisons to all-atom simulations with explicit solvent.7 The fitness function, ΔB22 = −B22[seq–seq] + B22[seq–ctd], was optimised using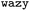 , aiming to identify sequences that interact more strongly with sequences of the same type than with CTD. Through this optimisation process,
, aiming to identify sequences that interact more strongly with sequences of the same type than with CTD. Through this optimisation process, 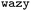 suggested highly hydrophobic sequences that exhibited stronger interactions with themselves compared to their interactions with the CTD sequence (Fig. 8 and S3).† To validate the formation of multiphasic condensates, we conducted simulations with a system comprising 300 chains of the 21-mer CTD sequence and 300 chains of the highly hydrophobic sequences suggested by
suggested highly hydrophobic sequences that exhibited stronger interactions with themselves compared to their interactions with the CTD sequence (Fig. 8 and S3).† To validate the formation of multiphasic condensates, we conducted simulations with a system comprising 300 chains of the 21-mer CTD sequence and 300 chains of the highly hydrophobic sequences suggested by 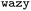 (Fig. 8B and C). Analysis of the density profiles from these simulations revealed a distinct phase separation, where the highly hydrophobic sequences formed the core of the condensate, while the comparatively less hydrophobic CTD sequences formed a surrounding shell (Fig. 8C–F). For lower ΔB22 values, the density profile shows a mixed condensate(Fig. 8G–I). This observation suggests that the highly hydrophobic sequences identified through the optimisation process have the propensity to be recruited to CTD condensates while maintaining a distinct phase separation, leading to the formation of a multiphasic condensate structure with a hydrophobic core and a CTD-rich shell.
(Fig. 8B and C). Analysis of the density profiles from these simulations revealed a distinct phase separation, where the highly hydrophobic sequences formed the core of the condensate, while the comparatively less hydrophobic CTD sequences formed a surrounding shell (Fig. 8C–F). For lower ΔB22 values, the density profile shows a mixed condensate(Fig. 8G–I). This observation suggests that the highly hydrophobic sequences identified through the optimisation process have the propensity to be recruited to CTD condensates while maintaining a distinct phase separation, leading to the formation of a multiphasic condensate structure with a hydrophobic core and a CTD-rich shell.
4 Conclusions
While modelling sequence–property relationships remains a difficult challenge, here we showed it is possible to train neural network models with molecular dynamics simulations to design disordered proteins to: (1) self-interact and phase separate and (2) to bind to phase separated condensates and (3) even shape the morphologies of phase-separated condensates. For this we employed the approach developed by Yang et al.25 that utilises appropriate featurisation from pre-trained sequence models,24,25,44 and Bayesian Optimisation (BO) for sampling the candidates most useful for training and protein design (Fig. 1). For these design tasks a limited number of sequences, with numeric labels from molecular dynamics, are sufficient, e.g., 50–100 sequences with labels are enough to predict B22 with reasonable accuracy (Fig. 2C). Even when no explicit information about the hydrophobicity and charge of individual amino acids is given,20 approaches based on pre-trained language models are able to learn biologically and chemically relevant information from the sequence data alone.Active learning provides a significant advantage when individual computations are expensive and an efficient way of traversing a large parameter space is needed. While training and optimising for certain fitness criteria, one must appropriately tune the balance between exploration and exploitation. The improvement using CALVADOS force-field13,39 highlighted the importance of the availability of state-of-the-art molecular force fields. The sequences identified from the coarse-grained simulations could be further explored with atomistic resolution along with explicit solvent, to include the role of water, ions and secondary structure formation and provide further insight into the molecular driving forces.30
A key limitation of the present work is that many of the peptides we suggest here may be too hydrophobic to be realised in a laboratory experiment. Recent work shows that one could explicitly consider the synthesizability of peptides in a neural network.45 As pointed out by An et al.,29 optimising interaction strength comes with a trade-off in terms of transport properties of the material and considering this in multi-parameter optimisation will yield protein sequences that are more balanced with regards to hydrophobic and non-hydrophobic residues. While we have not attempted to perform multi-parameter optimisation, for future practical applications to inform the design of novel materials underpinned by protein phase separation, multi-parameter optimisation is likely beneficial.
Data availability
All codes and datasets related to this study can be accessed at the following GitHub repository: https://github.com/cartilage-ftw/active-learning.Author contributions
A. C. S. designed and ran most of the HOOMD simulations. A. A. implemented the active learning workflow with the MD simulations. V. X. provided the protein sequences used for training. A. C. S., A. A., J. P. and L. S. conceived the study and interpreted the data. L. S. oversaw the study. A. C. S., A. A. and L. S. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. S. and L. S. S. thank M3ODEL for support. L. S. S. acknowledges support by ReALity (Resilience, Adaptation and Longevity) and Forschungsinitiative des Landes Rheinland-Pfalz. This project was funded by SFB 1551 Project No. 464588647 of the DFG (Deutsche Forschungsgemeinschaft). We acknowledge a mini grant from the Emergent AI (EAI) Center of Carl Zeiss Foundation. L. S. S. and A. A. thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 233630050 – TRR 146 for support. We gratefully acknowledge the advisory services offered and the computing time granted on the supercomputers Mogon II at Johannes Gutenberg University Mainz, which is a member of the AHRP (Alliance for High Performance Computing in Rhineland Palatinate) and the Gauss Alliance e.V. We thank Dr Noelia Ferruz, Prof. Dr Susanne Gerber, Yehor Tuchkov, Prof. Dr Heinz Koeppl, Dr Sören von Bülow and Prof. Dr Shikha Dhiman for inspiring discussions.Notes and references
- E. W. Martin, A. S. Holehouse, I. Peran, M. Farag, J. J. Incicco, A. Bremer, C. R. Grace, A. Soranno, R. V. Pappu and T. Mittag, Science, 2020, 367, 694–699 CrossRef CAS PubMed.
- B. Tsang, I. Pritišanac, S. W. Scherer, A. M. Moses and J. D. Forman-Kay, Cell, 2020, 183, 1742–1756 CrossRef CAS PubMed.
- A. Zbinden, M. Pérez-Berlanga, P. De Rossi and M. Polymenidou, Dev. Cell, 2020, 55, 45–68 CrossRef CAS PubMed.
- L. A. Gruijs da Silva, F. Simonetti, S. Hutten, H. Riemenschneider, E. L. Sternburg, L. M. Pietrek, J. Gebel, V. Dötsch, D. Edbauer, G. Hummer, L. S. Stelzl and D. Dormann, EMBO J., 2022, 41, e108443 CrossRef CAS PubMed.
- R. M. Welles, K. A. Sojitra, M. V. Garabedian, B. Xia, W. Wang, M. Guan, R. M. Regy, E. R. Gallagher, D. A. Hammer, J. Mittal and M. C. Good, Nat. Chem., 2024, 16, 1062–1072 CrossRef CAS PubMed.
- M. Farag, W. M. Borcherds, A. Bremer, T. Mittag and R. V. Pappu, Nat. Commun., 2023, 14, 5527 CrossRef CAS PubMed.
- A. Changiarath, J. J. Michels, R. H. Rodriguez, S. M. Hanson, F. Schmid, J. Padeken and L. S. Stelzl, bioRxiv, 2024, preprint, DOI:10.1101/2024.03.16.585180.
- M. Dzuricky, B. A. Rogers, A. Shahid, P. S. Cremer and A. Chilkoti, Nat. Chem., 2020, 12, 814–825 CrossRef CAS PubMed.
- A. Gräwe, M. Merkx and V. Stein, Bioconjugate Chem., 2022, 33, 1415–1421 CrossRef PubMed.
- S. Rekhi, C. G. Garcia, M. Barai, A. Rizuan, B. S. Schuster, K. L. Kiick and J. Mittal, Nat. Chem., 2024, 16, 1113–1124 CrossRef CAS PubMed.
- J. A. Joseph, A. Reinhardt, A. Aguirre, P. Y. Chew, K. O. Russell, J. R. Espinosa, A. Garaizar and R. Collepardo-Guevara, Nat. Comput. Sci., 2021, 1, 732–743 CrossRef PubMed.
- W. M. Jacobs, J. Chem. Theory Comput., 2023, 19, 3429–3445 CrossRef CAS PubMed.
- G. Tesei and K. Lindorff-Larsen, Open Research Europe, 2023, 2, 94 Search PubMed.
- G. M. Ginell, R. J. Emenecker, J. M. Lotthammer, E. T. Usher and A. S. Holehouse, bioRxiv, 2024, preprint, DOI:10.1101/2024.06.03.597104.
- S. von Bülow, G. Tesei and K. Lindorff-Larsen, bioRxiv, 2024, preprint, DOI:10.1101/2024.06.03.597109.
- F. Pesce, A. Bremer, G. Tesei, J. B. Hopkins, C. R. Grace, T. Mittag and K. Lindorff-Larsen, Sci. Adv., 2024, 10(35), eadm9926, DOI:10.1126/sciadv.adm9926.
- T. Hoffbauer and B. Strodel, bioRxiv, 2024, preprint, DOI:10.1101/2024.01.12.575432.
- X. Zeng, C. Liu, M. J. Fossat, P. Ren, A. Chilkoti and R. V. Pappu, APL Mater., 2021, 9, 021119 CrossRef CAS PubMed.
- P. Y. Chew, J. A. Joseph, R. Collepardo-Guevara and A. Reinhardt, Chem. Sci., 2023, 14, 1820–1836 RSC.
- A. Elnaggar, M. Heinzinger, C. Dallago, G. Rehawi, Y. Wang, L. Jones, T. Gibbs, T. Feher, C. Angerer, M. Steinegger, D. Bhowmik and B. Rost, IEEE Trans. Pattern Anal. Mach. Intell., 2022, 44, 7112–7127 Search PubMed.
- N. Brandes, D. Ofer, Y. Peleg, N. Rappoport and M. Linial, Bioinformatics, 2022, 38, 2102–2110 CrossRef CAS PubMed.
- R. Verkuil, O. Kabeli, Y. Du, B. I. M. Wicky, L. F. Milles, J. Dauparas, D. Baker, S. Ovchinnikov, T. Sercu and A. Rives, bioRxiv, 2022, preprint, DOI:10.1101/2022.12.21.521521.
- N. Ferruz, S. Schmidt and B. Höcker, Nat. Commun., 2022, 13, 4348 CrossRef CAS PubMed.
- E. C. Alley, G. Khimulya, S. Biswas, M. AlQuraishi and G. M. Church, Nat. Methods, 2019, 16, 1315–1322 CrossRef CAS PubMed.
- Z. Yang, K. A. Milas and A. D. White, bioRxiv, 2022, preprint, https://doi.org/10.1101/2022.08.05.502972 Search PubMed.
- E. J. Ma and A. Kummer, bioRxiv, 2020, preprint, DOI:10.1101/2020.05.11.088344.
- M. Aldeghi and C. W. Coley, Chem. Sci., 2022, 13, 8221–8223 RSC.
- K. Shmilovich, S. S. Panda, A. Stouffer, J. D. Tovar and A. L. Ferguson, Digital Discovery, 2022, 1, 448–462 RSC.
- Y. An, M. A. Webb and W. M. Jacobs, Sci. Adv., 2024, 10, eadj2448 CrossRef PubMed.
- B. Mohr, K. Shmilovich, I. S. Kleinwächter, D. Schneider, A. L. Ferguson and T. Bereau, Chem. Sci., 2022, 13, 4498–4511 RSC.
- Y. Khalak, G. Tresadern, D. F. Hahn, B. L. de Groot and V. Gapsys, J. Chem. Theory Comput., 2022, 18, 6259–6270 CrossRef CAS PubMed.
- B. Lakshminarayanan, A. Pritzel and C. Blundell, in NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2017, pp. 6405–6416 Search PubMed.
- P. I. Frazier, arXiv, preprint, arXiv:1807.02811, 2018, DOI:10.48550/arXiv.1807.02811.
- G. L. Dignon, W. Zheng, Y. C. Kim, R. B. Best and J. Mittal, PLoS Comput. Biol., 2018, 14, e1005941–23 CrossRef PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- J. A. Riback, L. Zhu, M. C. Ferrolino, M. Tolbert, D. M. Mitrea, D. W. Sanders, M.-T. Wei, R. W. Kriwacki and C. P. Brangwynne, Nature, 2020, 581, 209–214 CrossRef CAS PubMed.
- A. S. Holehouse, R. K. Das, J. N. Ahad, M. O. G. Richardson and R. V. Pappu, Biophys. J., 2017, 112, 16–21 CrossRef CAS PubMed.
- A. Bremer, M. Farag, W. M. Borcherds, I. Peran, E. W. Martin, R. V. Pappu and T. Mittag, Nat. Chem., 2022, 14, 196–207 CrossRef CAS PubMed.
- G. Tesei, T. K. Schulze, R. Crehuet and K. Lindorff-Larsen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(44), e2111696118 CrossRef CAS PubMed.
- J. Kyte and R. F. Doolittle, J. Mol. Biol., 1982, 157, 105–132 CrossRef CAS PubMed.
- D. J. Bauer, L. S. Stelzl and A. Nikoubashman, J. Chem. Phys., 2022, 157, 154903 CrossRef CAS PubMed.
- T. M. Prass, P. Garidel, M. Blech and L. V. Schäfer, J. Chem. Inf. Model., 2023, 63, 6129–6140 CrossRef CAS PubMed.
- D. Flores-Solis, I. P. Lushpinskaia, A. A. Polyansky, A. Changiarath, M. Boehning, M. Mirkovic, J. Walshe, L. M. Pietrek, P. Cramer, L. S. Stelzl, B. Zagrovic and M. Zweckstetter, Nat. Commun., 2023, 14, 5979 CrossRef CAS PubMed.
- Z. Lin, H. Akin, R. Rao, B. Hie, Z. Zhu, W. Lu, N. Smetanin, R. Verkuil, O. Kabeli, Y. Shmueli, A. dos Santos Costa, M. Fazel-Zarandi, T. Sercu, S. Candido and A. Rives, Science, 2023, 379, 1123–1130 CrossRef CAS PubMed.
- R. Zhang, H. Wu, Y. Xiu, K. Li, N. Chen, Y. Wang, Y. Wang, X. Gao and F. Zhou, arXiv, preprint, arXiv:1807.02811, 2023, DOI:10.48550/arXiv.1807.02811.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00099d |
| This journal is © The Royal Society of Chemistry 2024 |