Open Access Article
Open Access ArticlePredicting the rates of photocatalytic hydrogen evolution over cocatalyst-deposited TiO2 using machine learning with active photon flux as a unifying feature†
Yousof
Haghshenas
a,
Wei Ping
Wong
 b,
Denny
Gunawan
b,
Denny
Gunawan
 a,
Alireza
Khataee
c,
Ramazan
Keyikoğlu
c,
Amir
Razmjou
d,
Priyank Vijaya
Kumar
a,
Alireza
Khataee
c,
Ramazan
Keyikoğlu
c,
Amir
Razmjou
d,
Priyank Vijaya
Kumar
 a,
Cui Ying
Toe
a,
Cui Ying
Toe
 ae,
Hassan
Masood
a,
Rose
Amal
ae,
Hassan
Masood
a,
Rose
Amal
 a,
Vidhyasaharan
Sethu
f and
Wey Yang
Teoh
a,
Vidhyasaharan
Sethu
f and
Wey Yang
Teoh
 *ab
*ab
aSchool of Chemical Engineering, The University of New South Wales, NSW 2052, Australia. E-mail: wy.teoh@um.edu.my
bDepartment of Chemical Engineering, Sustainable Process Engineering Centre (SPEC), Universiti Malaya, 50603 Kuala Lumpur, Malaysia
cDepartment of Environmental Engineering, Gebze Technical University, 41400 Gebze, Turkey
dMineral Recovery Research Center (MRRC), School of Engineering, Edith Cowan University, Joondalup, Perth, WA 6027, Australia
eSchool of Engineering, The University of Newcastle, Callaghan, New South Wales 2038, Australia
fSchool of Electrical Engineering and Telecommunications, The University of New South Wales, NSW 2052, Australia
First published on 28th November 2023
Abstract
An accurate model for predicting TiO2 photocatalytic hydrogen evolution reaction (HER) rates is hereby presented. The model was constructed from a database of 971 entries extracted predominantly from the open literature. A key step that enabled high accuracy lies in the use of active photon flux (AcP, photons with energy equal to and greater than the bandgap energy of the photocatalyst) as the input feature describing the irradiation. The quantification of AcP, besides being a more direct feature describing the photocatalyst excitation, circumvents the use of lamp power ratings and light intensities as ambiguous inputs as they encompass varying degrees of AcP depending on the irradiation spectra. The AcP unifies four other key performing features (out of 46 initially screened), i.e., cocatalyst work functions, loadings of cocatalyst, alcohol type and concentrations, to afford a physically-intuitive model that can be generalized to a wide range of experimental conditions. The inclusion of AcP as an input to the machine learning model for HER prediction leads to a mean absolute error of 7 μmol h, which is a 90% reduction when compared to a model that does not use AcP. Verification of untested conditions with high HER rates, identified through Bayesian optimization, saw less than 9% deviation from the physically-measured kinetics, thus confirming the validity of the model.
Broader contextThe use of machine learning (ML) is gaining attraction in various areas of heterogeneous catalysis, offering the potential for accelerated discovery of advanced catalysts. However, the accuracy of ML models is often contingent on the availability and size of datasets, typically necessitating thousands, if not millions, of data points. Some areas, such as zeolite and metal–organic framework syntheses, single-atom catalyst design, electrocatalytic water splitting, and CO2 reduction, are making significant progress by benefiting either from the abundant physical data or the ability to generate high-throughput simulated data. In contrast, photocatalysis faces a unique challenge due to the substantial variability in operating conditions (and hence physical data) thus preventing their efficient use in ML model development. By using the hydrogen evolution reaction (HER) as the reaction of interest, we developed the first ML model that solves the heterogeneity of physical data in photocatalysis, thereby unlocking the wealth of literature data. Importantly, our model not only delivers accurate and generalizable predictions but also offers a rational basis for its conclusions. The ML framework serves as a legacy base model, where transfer learning can be performed to study other photocatalysts and photocatalytic reactions, requiring a smaller dataset with each transfer learning. |
1. Introduction
Hydrogen is quickly being established as a medium for decarbonization across various energy-intensive industries.1 The aim is to ultimately displace the use of fossil fuels for small- and large-scale power generation, land and sea transportation, as well as chemicals and fertilizers production.1 The effort is in large part driven by pledges made by almost 200 countries during the Intergovernmental Panel on Climate Change's Conference of Copenhagen (COP-21) to reduce carbon emission, where more than one-third of the parties committed to reducing at least 30% of emissions by 2030.2 With the deadline looming, industries are now scrambling for solutions to reduce the overall carbon footprints of their processes, and the utilization of green hydrogen and renewable electricity is central to many of the decarbonization strategies.Photocatalytic water splitting is a potential low-cost and long-term solution to green hydrogen production.3 A large-scale 100 m2 solar water splitting system using SrTiO3: Al photocatalysts with a peak production of 3.6–3.7 L min−1 of hydrogen has been demonstrated. Despite being in the early stages of development, the landmark demonstration recorded a solar-to-hydrogen efficiency of 0.76%, which remains far below the 10% mark required for commercialization. The process is limited by the sluggish 4-electron water oxidation reaction being an uphill reaction (ΔG° = +59 kJ mol−1). To overcome the limitation, opportunities arise from the addition of renewable or waste biomass as sacrificial hole scavengers in what is known as the photocatalytic hydrogen evolution reaction (HER) or reforming, reversing what is otherwise an uphill to a net downhill reaction (ΔG° < 0).4,5 Conveniently, the process permits the direct utilization of organics-laden wastewater discharge from industrial processes, for example, ethylene glycol and glycerol-containing wastewater from the anaerobic digestion of lignocellulose, or methanol from biodiesel production.6,7 An enhancement of HER rates of up to 25 times is not unusual for HER relative to that of pure water splitting.8 While the HER rate is dependent on the rates of hole transfer, which is in turn dependent on the surface adsorption and concentration of the hole scavenger as well as the mechanism of oxidation,9 it is at the same time dependent among others on the absorbance and quantum efficiency of the photocatalysts, with and without cocatalysts.10,11 Solving this multidimensional problem is a paramount challenge, at least at this point in time, due to the incomplete fundamental and quantitative understanding of the overall photocatalytic reaction at the atomistic level.
Attempts have been made to establish the dependency of HER rates as a function of experimental parameters using the 2k factorial design,12 but this method requires strict standardization of the experimental setup, e.g., reactor configuration, stirring mechanism, light source and intensity, and hence is not suitable for comparisons of published data reported by others using different setups. A more robust method is required, especially one that harnesses the abundance of differently collected literature data. The advent of machine learning in recent years has seen powerful methods being developed to not only statistically establish complex interactions between multi-parameters,13 but also allow high generalizability of datasets.14 The setback, however, is the need for a large dataset (often in the order of 104 entries or more for models of higher complexity),15 which for experiments related to reaction kinetics are especially expensive and laborious to generate.16 The integration of domain knowledge incorporates an established physical relationship between features into the modelling framework and it can potentially offset some of the need for an extremely large dataset by imposing model constraints that leverage theoretical insights, avoiding the need for the model to explicitly ‘relearn’ these insights from training data.11
In one of the earlier machine learning studies on photocatalysis, Can and Yildirim collected 540 kinetics data on water splitting over perovskite (ABX3, X = oxygen, halogen, sulfur) photocatalysts from 151 publications. Direct relationships between reported activities and the features of interest were somewhat difficult to establish due to, amongst the reasons, the non-standardized testing conditions of collected data and qualitative definition of light sources (defined as UV or visible light).17 Later attempts were made to parameterize lamp power and light sources,18 but the rated lamp power merely provides information on the electricity consumption and is not directly related to the light arriving at the reaction. Presuming the electrical-to-light efficiency is known for the light source, the effective power or irradiation intensity, I, decays rapidly with distance, d, between the light source and reaction volume (I being proportional to d−2),19 and such information on d is rarely available. An increasing number of papers are reporting the irradiation intensity at the front of the photocatalytic reactor, which provides a more direct account of the light available to the reaction. However, this does not readily relate to reaction kinetics especially when using different irradiation spectra. Without establishing a reliable feature to take into account the available light for the photocatalytic reaction, only superficial statistical generalizations of light sources can be achieved in describing the apparent activities of photocatalytic reactions.
In this paper, we develop a machine learning model to predict the HER rate on cocatalyst-deposited TiO2 by considering the precise physical role of light and its interaction with other reaction parameters. To do so, we transpose LI to photon fluxes, and more precisely to sum up photons with energy equal to greater than the bandgap energy of the photocatalyst (hv ≥ Eg). In this way, only the active photons are considered as a more direct feature of photocatalytic reactions. Doing so not only gives rise to an accurate and physically intuitive model that is consistent with experimental observations but also makes it generalizable to a wider range of reaction parameters. To put it simply, the multiparametric interactions affecting the reaction kinetics were appropriately incorporated into the machine learning model. To the best of our knowledge, this is the first time that active photon flux is considered in enabling the machine-learning of photocatalytic HER and in the process produces the most generalizable experimental database on this reaction. By using TiO2 and some of the most common cocatalysts (i.e., Pt, Au, Ni, Cu, Pd, NiO, Ag, Ir, Rh, Co and Cr), in view of their data abundance, and hence accuracy, the far-reaching goal is to establish the most accurate legacy model for subsequent transfer learning applications, specifically tailored to individual photocatalysts (including cocatalysts) and a diverse array of photocatalytic reactions.
2. Experimental
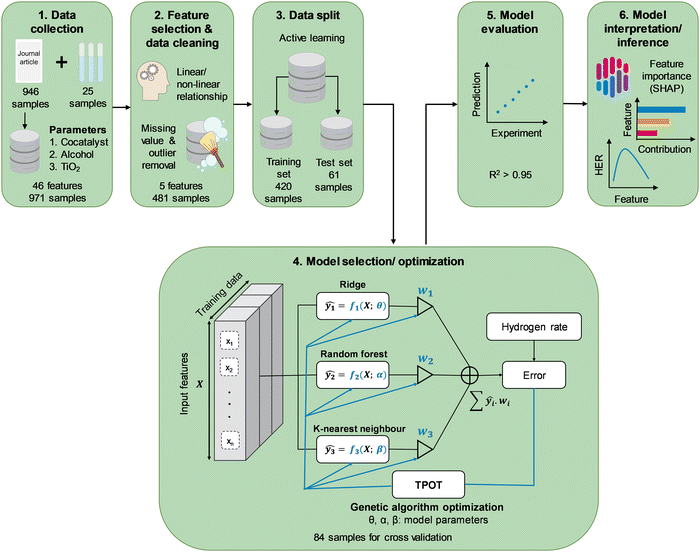
To develop an HER rate model using machine learning, data from experiments, including photocatalyst properties such as photocatalyst bandgap energy as well as reaction parameters such as type and concentration of organic substrate, are required. Characteristics of light sources, namely, type of irradiation source and intensity, were converted to active photon flux by means of photon counting, as outlined in detail in the ESI.† Briefly, the specific light spectrum was identified from the reported type of irradiation and scaled accordingly to the reported light intensity. The discretized spectral irradiance was converted to spectral photon flux by dividing by the photon energy at every wavelength, Eλ = hc/λ, where h is Planck's constant, c is the speed of light, and λ is the wavelength of interest. Integration of the spectral photon flux over the entire spectrum gives the apparent photon flux, while that at a wavelength below the absorption threshold, i.e., energy equal to greater than the bandgap energy, gives the active photon flux. Besides literature data, additional reaction kinetics were carried out to complement the literature data. In a typical experiment, 50 mg of TiO2 (Aeroxide® P25) was dispersed in 50 mL of predetermined concentration of alcohol solution (ChemSupply) and metal salt precursor. The selection of precursors includes chloroplatinic acid hexahydrate (H2PtCl6·6H2O, Aldrich), palladium(II) chloride (PdCl2, Aldrich), gold(III) chloride (AuCl3, Aldrich), silver nitrate (AgNO3, Aldrich), nickel(II) chloride hexahydrate (NiCl2·6H2O, Aldrich), and copper(II) nitrate trihydrate (Cu(NO3)2·3H2O, Aldrich). The suspension in a cylindrical-shaped Pyrex reactor was sonicated for 15 min, followed by purging with N2 for 15 min. A photocatalytic reaction was initiated through top irradiation (300 W Xe arc lamp, Oriel) via a quartz window. Evolved H2 was monitored by periodic sampling of the gas headspace and analysed using a gas chromatogram (Shimadzu GC-8A, HayeSep DB column). The actual light intensity irradiating on the photocatalytic suspension was measured offline by placing a calibrated thermopile sensor (Newport 919P-030-18) within the empty reactor but at the same height as the surface of the aqueous suspension.Gathering all the contributive parameters in the HER reaction provides an extensive dataset, but not all of its features are useful for a machine learning model. Therefore, the data were processed to extract the most relevant information to the HER rate (Scheme 1). This process includes selecting the best features using statistical relationships and physical understanding of the problem. Features with the highest linear and non-linear relationship with the HER rate were chosen among all features through a sequential step by step feature selection process. Whilst random data splitting is commonly used in selecting training/test sets,17 in this study an active learning approach was adopted in splitting the available data into training and test sets.20 Random Forest regressor and Gaussian process regressor were used as proxy models for the HER rate prediction. The latter was used because of its capability to visualize individual explainable trees and control the process of data splitting, while the Gaussian process regression is capable of finding samples with valuable information for further model training processes. The models in active learning are initially trained through 5-fold cross-validation using 10 randomly selected samples from the dataset. After training, the models were used to make predictions of the rest of the dataset. The random forest model was visualized to check the range of features at each level of tree and the Gaussian process was plotted with a range of uncertainty (standard deviation) of predictions. The samples with the highest prediction error using both models were selected as the new training samples for the random forest model, while the new training samples were selected from regions with the highest standard deviation for the Gaussian process model. Training of both models was restarted by adding new training samples to complete one epoch. The iterative process was repeated multiple times to avoid random fluctuations and continues until 80 percent of the dataset is selected for the training process. Both models were evaluated during active learning to monitor the accuracy of the model by adding new data. Subsequently, the selected training/test sets from this process were used for developing a completely new and final HER rate model. Due to the limited size of the dataset, this approach ensures that the most informative data was used for further training processes. To prevent any occurrence of data-leakage, the final HER rate model training was separated from the data splitting process.
Tree-based Pipeline Optimization Tool (TPOT) was used for the selection and optimization of the machine learning model.21 TPOT applies a genetic algorithm during the model training to choose the best model with optimized hyperparameters among a population of models including decision trees, support vector machine, k-nearest neighbours, AdaBoost, XGBoost, and artificial neural networks, Ridge/Lasso, and Random Forests. The TPOT optimization employed 100 times of model training for each combination of hyperparameters to avoid any random fluctuation through 10-fold repeated cross-validation within the training dataset in each iteration. This process involves 10 repetitions of 10-fold cross-validation with the training partition differently randomised for each repetition with different random seeding. Validation of the finally optimized model using TPOT was achieved through errors analysis on multiple sets of held-out data (test dataset) which was not seen by the model during the training process. Given that the HER rate is a continuous variable, the coefficient of determination (R2, eqn (1)) and MAE were reported as measures of strength of regression fit and model prediction accuracy, respectively. Additionally, we reported the RMSE to compare the proposed model with those reported in the literature where only the RMSE has been provided.
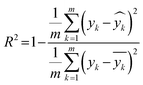 | (1) |
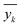 and
and 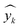 denote the true, mean, and predicted HER rates, respectively.
denote the true, mean, and predicted HER rates, respectively.
Due to the complexity of the optimized model with TPOT, it is highly desirable to understand how each input feature contributes to the model predictions. This can help determine if the developed model is consistent with domain knowledge about photocatalytic reactions. This study can be carried out by altering input feature values (one at a time as well as various combinations) and analysing the resultant changes in the distributions of the model predictions (std. mean, median, and range). These analyses can in turn reveal the joint effects of groups of input features on the predicted HER rates and allow for comparisons with domain knowledge. SHAP (Shapley Additive exPlanation) analyses were used to estimate the global and local influences of every input feature on the predicted HER rate by calculating its marginal contribution.22 The SHAP value, ϕi(x), shows the additive influence of each feature, i, on every model prediction for the input, x⊆X:
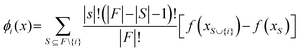 | (2) |
3. Results and discussion
3.1 Database construction and features engineering
A total of 946 entries of TiO2-based photocatalytic HER experiments were manually extracted from the literature and indexed into a database. The database comprises a wide range of cocatalysts: Pt, Pd, Cu, Au, Ir, Ag, Ni, NiO, Rh, Co, and Cr, and cocatalyst loadings; as well as organic substrates: methanol, ethanol, 1-propanol, 2-propanol, 1-butanol, tert-butanol, ethylene glycol, propane-1,3-diol, glycerol, propylene glycol, triethanolamine (TEOA), and the concentrations (Fig. 1). It is well-noted that more than 50% of the extracted data include Au and Pt as cocatalysts, while methanol and ethanol are among the most studied organic substrates in the literature (accounting for more than 70% of the data). However, this study aims to develop an HER rate prediction model using machine learning that can cover a wide range of cocatalysts and organic substrates. Consequently, its accuracy and performance reflect the distribution of training data, which in turn reflects the popularity of the studied cocatalyst and organic substrate in the literature. Therefore, it is expected that the final trained model would have different accuracies for different cocatalysts and organic substrates. This negative effect is somewhat offset by the use of active learning to determine the training partition, since the active learning algorithm chose at least one example involving each cocatalyst and organic substrate for the training partition. This led to a machine learning model that showed reasonably high accuracy for any cocatalyst or organic substrate.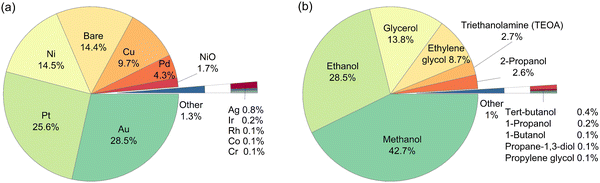 | ||
| Fig. 1 Breakdown on the type of (a) cocatalysts, and (b) organic substrates among the 946 entries of the literature-extracted dataset. | ||
To identify the most important yet independent features (among 46, see Table S1, ESI† for the complete list of features) for predicting the HER rate (Rate), features imparting the strongest influence (linear or nonlinear) on the Rate whilst at the same time exhibiting the lowest correlation with other features were shortlisted (see Table S1 for ranking of all features and Fig. S7, ESI†). The process involves initial longlisting of 12 features with a Gini index above 0.5, ranked in the decreasing order of AC > SSA > CL > AMW > Eg > CAN > CEN > AcP > CWF > drutile > Tcalcination > Xrutile (see Table S1, ESI†). On the contrary to AcP, LI with a low Gini index (0.33) did not make the selection due to its poor correlation with Rate, despite both being characteristics of the irradiation sources. This shall be further elaborated later in this subsection. Following the longlisting, the features were further ranked based on their covariances with Rate, revealing a revised order: CEN > CWF > CAN > AcP > CL > AMW > AC > Tcalcination > Eg > SSA > Xrutile > drutile (Fig. S5 and S6, ESI†). Because CEN, CWF and CAN refer to the same identity of the cocatalyst and hence redundant, CWF was selected as a representative feature due to its high covariance with the other two, as well as its quantitative implication on the photocatalytic charge separation process as elaborated below. As a TiO2 synthesis parameter, Tcalcination is strongly correlated with the crystallite properties, Xrutile and drutile, that in turn determines the Eg23 as well as SSA. As such, Eg and SSA were selected as representative features based on their high covariances with the other three features.
The loadings of TiO2 were excluded since in most cases, if not all, the photocatalyst concentrations are in excess relative to the incident irradiation. For example, when carrying out reactions under standard solar irradiance (A.M. 1.5 G, 1 sun), most of the active photons (hv ≥ Eg) are fully absorbed within the first few centimeters of the reaction depth (see the ESI† for the active photon flux calculations), whereas the typical photocatalytic suspension depth is of one magnitude higher. After recursive selection analysis, SSA was removed from the list of features. This is consistent with the general observation that photocatalysis, unlike thermal catalysis, rarely scales with SSA as a result of increased defects with increasing SSA that retard photocatalytic activities.24–26
Cocatalysts are essential in photocatalysis through (1) the formation of a Schottky barrier that enhances charge separation, and (2) enhancing surface charge transfer.27 In the HER, most efforts are concerned with the use of cocatalyst for surface electron transfer given the limited driving force (the potential difference between the TiO2 conduction band and that of proton reduction) ∼0.2 eV, while the rate of hole transfer is adequately accelerated through the oxidation of organic substrates. The fact that the features relating to cocatalyst identity, i.e., CEN, CWF and CAN, occupy the highest ranks in terms of covariance with Rate as a testament of the importance. As a feature, CWF has a direct effect on the Rate by dictating the extent of band bending on the TiO2 subsurface as well as the Schottky barrier at the cocatalyst-semiconductor interface.28 On the contrary, CEN and CAN cannot provide additional information, and hence CWF was retained as a descriptor of the type of cocatalysts. The quantitative loading of the cocatalysts is readily represented as CL in the database.
While AC is readily quantifiable, the identity of organic substrates is harder to quantify as there is a plethora of related properties that may affect the Rate, for example, the number of alpha-H, number of H, number of OH groups, polarity, and molecular weight.29 These relationships are not generalizable separately, e.g., the molecular weight cannot distinguish isomers. Therefore, a complex structure-representative single vector feature, hereby termed as ATI, was designed. It is a computed feature based on the structure–property relationship derived from principal component analysis (PCA). The inputs include AMW, the number of hydrogen atoms, the number of alpha hydrogens, the number of the hydroxyl group (–OH), polarity, and the distance of the closest hydrogen to the centre of mass of the molecule. To capture the number of electrons around every hydrogen atom as a representative of the electrostatic field in the space surrounding the hydrogen atom, the minimum number of valence electrons within the radius of 2 Å of each hydrogen atom, and the maximum number of valence electron within the radius of 3 Å of each hydrogen atom were considered as well. This practice was taken from well-known molecular structure representation approaches including, Sine matrix, Smooth Overlap of Atomic Positions (SOAP), Many-body Tensor Representation (MBTR), and Local Many-body Tensor Representation (LMBTR), as provided in the DScribe package.30,31
Being the driver of photocatalytic reactions, the characteristic of irradiation is an indispensable input in constructing a sensible model. This has been by far the most restrictive feature during the data mining process, where the bulk of published data would report the type of the light sources and their electrical power ratings, but without or with ambiguous information on the intensities irradiating the reaction volume. Most of the data admitted to the current database consists of information on the type of light source and LIs. When LI (in W m−2) was included as an input feature as is, the established database showed a rather low variability in Rate as a function of LI. Although LI is widely used as a metric, this can be rather misleading even when correctly measured in front of the reaction volume, since LI does not provide information on the spectrum. For example, a green light-emitting diode (LED) and blacklight of the same LI would yield contrasting results, with only the latter showing activity since the irradiating photons are of sufficiently high energy (hv ≥ Eg) to photoexcite the TiO2. In the most conservative scenario, each absorbed photon results in a single photoexcitation. In other words, the photon flux rather than LI would be a more meaningful feature describing photocatalytic events. The former requires quantitative spectral information from which the photon flux at each specific wavelength can be calculated (see the ESI†). When integrated over the entire spectrum this gives the ApP, but when integrated over the range of wavelengths with the equivalent photon energy equal to and greater than Eg it yields the AcP. The latter is chosen as the most direct feature describing the rate of photoactivation, which in turn is a direct function of the Rate. Since Eg is readily incorporated as part of the AcP calculation, the former can be made redundant.
Upon selecting the most influential features, i.e., CWF, CL, ATI, AC and AcP (Table 1), samples with missing features were omitted to maintain consistency throughout the database. Moreover, to reduce outlier destructive effects, samples with Rate outside of the range of 1.5 × IQR (IQR = Q3 − Q1, Qi: i-quantile) were removed. Considering that most literature data were obtained under low LI (≤158 mW cm−2), additional physical experiments were required to widen the range of LI and its effects on the Rate. Latin Hypercube Sampling (LHS) with three degrees of freedom for LI, CL, and CWF, was applied to design the 25 experiments with higher values of LI (see the list of additional experiments in the GitHub repository). These experiments were conducted in-house using a commercial P25 TiO2 photocatalyst and suspended in aqueous methanol aqueous solution (AC = 10 vol%) and irradiated under a Xe arc lamp. The LI (ranging from 204 to 697 mW cm−2) were converted to AcP as described above. The range of cocatalysts used range from Ag, Au, NiO, Pt, Pd, to Cu, and with loadings from 0.1 to 4.8 wt%. The newly designed experimental dataset was used in combination with the extracted data from the literature for training the machine learning model to predict the HER rate.
| Feature | Min | Max | Mean | Std dev. |
|---|---|---|---|---|
| Photocatalytic hydrogen evolution rate, Rate (μmol h−1) | 2.6 | 1 540 | 167 | 272 |
| Cocatalyst work function, CWF (eV) | 0 | 5.54 | 4.82 | 0.98 |
| Cocatalyst loading, CL (wt%) | 0 | 10.0 | 1.21 | 1.05 |
| Alcohol type indicator, ATI (−) | −2.15 | 0.96 | −0.23 | 1.06 |
| Alcohol concentration, AC (vol%) | 1.0 | 100 | 34.7 | 32.9 |
| Active photon flux, AcP (1017, photon cm−2 s−1) | 0.49 | 10.5 | 1.14 | 1.67 |
3.2 Prediction of photocatalytic hydrogen evolution rate and model robustness
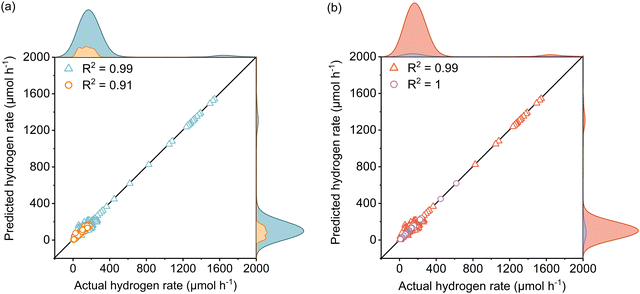
The active learning process were employed by the selected features to predict the Rate and resulted in 420 samples for the training dataset including 25 newly designed experiments. The rest of the data was kept away as an unseen test dataset which was not used during active learning and TPOT model optimization. The results showed in each iteration of active learning that the RMSE of the model on the test dataset decreases, and new information was fed into the model. Based on the active learning, AcP and CL returned the highest contributions thus showing their significance toward Rate (Fig. S10 and S11, ESI†). Further model optimization through TPOT using 420 samples in the training dataset selected a stacking model consisting of a 100 random forest, 3 ridge, and K-nearest neighbours with K = 8 regressors (Scheme 1 and Table S2, ESI†).Fig. 2(a) shows the predicted Rate against the actual Rate for cross-validation of training and unseen test dataset during the model training process. An R2 of 0.99, RMSE of 19.79 μmol h−1, and MAE of 7.25 μmol h−1 were measured for the training dataset, while R2 of 0.91, the RMSE of 15.93 μmol h−1, and MAE of 11.37 μmol h−1 were measured for the unseen test dataset. The model prediction represents less than 2% error compared with the physical Rate. Moreover, the normal distribution for predictions shows that the developed model does not overestimate nor underestimate the Rate. This is a vital characteristic of the model that ensures it does not bias the majority of Rate values in the training dataset (Fig. S12, ESI†).
Since the variation of Rate in the newly designed experimental dataset was mainly affected by light intensity, the reliability of the developed model to predict the Rate was examined separately for data extracted from theliterature and the newly designed experiments depicted in Fig. 2(b). The R2 of 0.99, RMSE of 19.87 μmol h−1, and MAE of 8.20 μmol h−1 for the literature dataset and the R2 of 1, RMSE and MAE of 0 μmol h−1 for the designed experiments dataset were measured for both datasets. Since both the literature dataset and newly designed experiment dataset hold transparent information of photoreforming on the cocatalyst deposited TiO2, as expected a similar R2 was measured during the model training process. The zero error on the experimental dataset suggests that the model is accurate over a large range of LI. Importantly, the model is also able to predict the Rate for a wide range of experimental setups with different light sources in the literature dataset (high generalizability of the model).
To assess the robustness of the model, especially on its susceptibility to random fluctuations, we performed a series of analyses. For repeatability analysis, a Bland–Altman32 value of 0.25 was measured, inferring that the accuracy of prediction is not significantly affected repeating the training process with different initialization. The y-scrambling method was employed with 100 times of random training/predictions showing values of 0.048 and 0.007 for the mean and standard deviation of the correlation of coefficients, respectively. If random (false) values of HER rate were given, the model was unable to make rational predictions. Finally, when the entire TPOT training/validation/optimization process was repeated 100 times with different random seeding, a mean value of 0.96 was found for the correlation of coefficient for all trained models with a standard deviation of 0.02. All the metrices above provide sufficient confidence that the model is not prone to random fluctuations.
Lastly, to verify that the active learning process did not cause any data-leakages, extra precaution was adopted. The test dataset was hidden from the training process and the models used during the TPOT process were in turn entirely isolated from the models in the active learning process. This ensures none of the samples in the training dataset were spotted in the test dataset. Multiple validations were conducted using different datasets unseen to the entire model development and training process. Four new datasets that were completely independent from one another were initially extracted from the literature, namely, DS1,33 DS2,34 DS3,35 and DS4.36 Predictions were performed returning RMSE values of 8.98, 6.88, 6.66, and 4.7 μmol h−1, respectively (Table 2). The consistently low RMSE for these new unseen datasets gave enough confidence that no data leakages or random fluctuations had taken place during the model training process.
| Dataset | RMSE (μmol h−1) | MAE (μmol h−1) | R 2 |
|---|---|---|---|
| Cross validation (training/validation) | 19.79 | 7.25 | 0.99 |
| Unseen test | 15.93 | 11.37 | 0.91 |
| Literature training | 19.87 | 8.20 | 0.99 |
| Newly designed experiments | 0 | 0 | 1 |
| Unseen DS1 | 8.98 | 6.77 | 0.89 |
| Unseen DS2 | 6.88 | 5.5 | 0.99 |
| Unseen DS3 | 6.66 | 6.06 | 0.99 |
| Unseen DS4 | 4.70 | 3.9 | 0.95 |
3.3 Features analysis and model insights (global and local model interpretation)
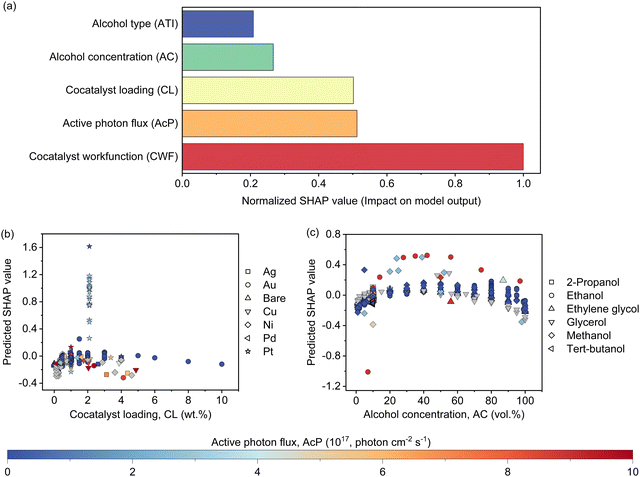
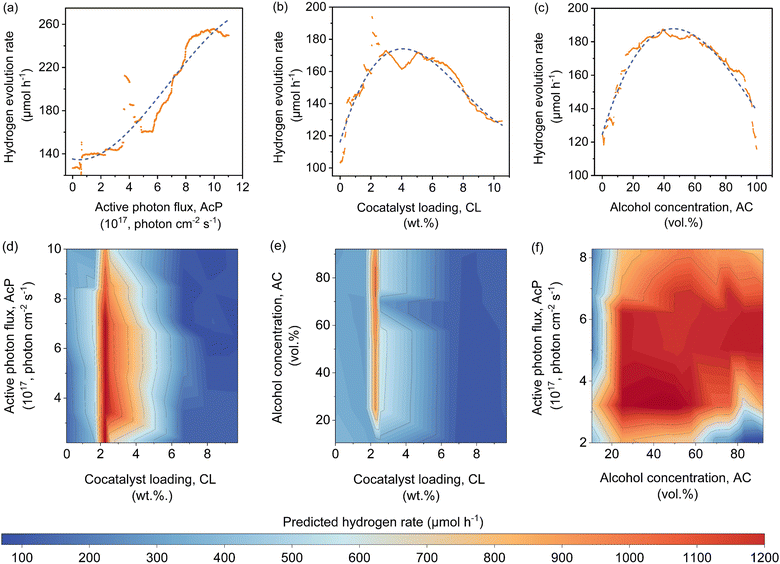
The features contribution based on SHAP analysis is shown in Fig. 3(a), measuring the influence of each feature in the global model. The contribution of features decreases in the order of CWF > AcP > CL > AC > ATI. Despite the CWF (i.e., the type of cocatalyst) exerting the largest influence on the model prediction, it does not in any way preclude the essential role of other features. In fact, it requires the ensemble of all other features to work in an inter-relatable fashion, albeit, with various degrees of influence on the output of the machine learning model. If one of the features such as CL (Fig. 3(b)) or AC (Fig. 3(c)) exceeds its optimum region, it can adversely affect the Rate and reduces the positive effect of other features that might be in their optimum regions. The negative SHAP value for very low or high CL in Fig. 3(b) is an indicator of the detrimental effect of CL on the Rate for all types of cocatalysts in this region regardless of the AcP value. The same trend can be captured for AC in Fig. 3(c). After all, the multidimensional nature of the photocatalytic HER demands all features to be at their optimal range to achieve a high Rate.To gain insights into the exact relationship of each continuous feature, at least as interpretable by the machine learning model, we randomly generated the predicted Rate as a function of AcP, CL (using Pt as the cocatalyst) and AC (using methanol as the organic substrate), while keeping other parameters constant. This is an important verification exercise to ascertain the consistency of the model outputs with the general understanding of the physical behaviour. As can be seen from Fig. 4(a), there is a general increase in the Rate for all samples (up to ∼255 μmol h−1) with increasing AcP. The upper limit of the former is probably due to the extensive scattering of photons that limited deeper penetration into the reaction volume, as well as the kinetic limitation of the redox reaction. We rule out the limitation of TiO2 loadings since the typical amount of loading is in excess relative to the available AcP (see the ESI†). As shown in Fig. 4(b), an optimum Rate was observed at CL of ca. 2 wt%, which concurs with the range commonly reported in the literature.23,37–39 As a feature, the CL is sensitive and requires only a small amount to achieve optimum Schottky barrier-enhanced charge separation and catalytic electron transfer. At higher loading amounts, the cocatalyst may act as charge recombination centres, thereby reducing the overall photocatalytic activity.40,41 With some knowledge of cocatalyst size as a function of CL, it is possible to compute the turnover frequencies of these electron transfer active sites from the predicted Rates (Fig. S17, ESI†). Like CL, an optimum Rate was also observed for AC = 40–60 vol%, which corresponds to 22–40 mol% of methanol in an aqueous solution (Fig. 4(c)). This optimum concentration can be envisioned since the photocatalytic HER involves both water and methanol as the reactants. Fig. 4(d)–(f) shows a higher-level illustration involving the coeffects of two variables. With the CWF and ATI fixed for that of Pt and methanol, respectively, the dominant effects of AcP, AC and CL as continuous variables can be captured from the contour plots.
To experimentally verify the predictions from the machine learning model, we used a Bayesian optimization package42,43 in Python to find the set of the parametric conditions (i.e., AcP, CL, and AC for a given CWF and ATI) that yield high predicted Rates. The package was used unchanged except to use a Gaussian Process prior modelled on the same training set as our prediction model instead of an uninformative prior. Specifically, this process was carried out for two less frequent conditions of CWF and ATI: Cond. 1 and 2, and two conditions of CWF and ATI that yield to superior hydrogen production: Cond. 3 and 4. The predicted HER rates showed a higher Rate than the samples with the same conditions of CWF and ATI in the training dataset. Additionally, the optimized conditions were predicted with the highest Rate in comparison with all candidates in the search space during Bayesian optimization (Tables S3 and S4, ESI†). Fig. 5 shows the experimental HER kinetics carried out under these four conditions, from which the corresponding Rates of 65.2, 82.6, 493.5, and 484.9 μmol h−1 were respectively measured. This shows that the predictions are within a commendable 9% deviation from the experimentally measured values.
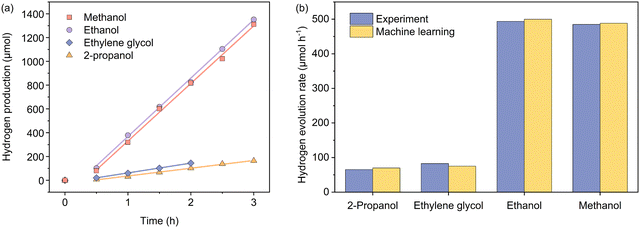 | ||
| Fig. 5 (a) Kinetics of photocatalytic hydrogen evolution carried out independently under four experimental conditions as suggested by the machine learning model, involving 2-propanol (Cond. 1), ethylene glycol (Cond. 2), ethanol (Cond. 3), and methanol (Cond. 4). Please refer to Table 3 for specific experimental parameters associated with each condition. (b) Comparisons between the actual and predicted hydrogen evolution rates under the four named conditions. | ||
| Cond. 1 | Cond. 2 | Cond. 3 | Cond. 4 | |
|---|---|---|---|---|
| a Irradiation was provided by Xe arc lamp irradiation with the intensity adjusted to give the appropriate active photon fluxes. | ||||
| CWF (−) | Pt | Pt | Pt | Pt |
| CL (wt%) | 1.5 | 2.1 | 2.2 | 2.6 |
| ATI (−) | 2-Propanol | Ethylene glycol | Ethanol | Methanol |
| AC (vol%) | 40.0 | 38.2 | 47.4 | 46.9 |
| AcPa (1016, photon cm−2 s−1) | 8.45 | 34.6 | 38.8 | 36.9 |
| Experimental Rate (μmol h−1) | 65.2 | 82.6 | 493.5 | 484.9 |
| Predicted Rate (μmol h−1) | 70.9 | 85.4 | 500.6 | 487. 7 |
| Absolute error (%) | 8.7 | 3.4 | 1.4 | 0.6 |
3.4 Effect of light characteristic inputs
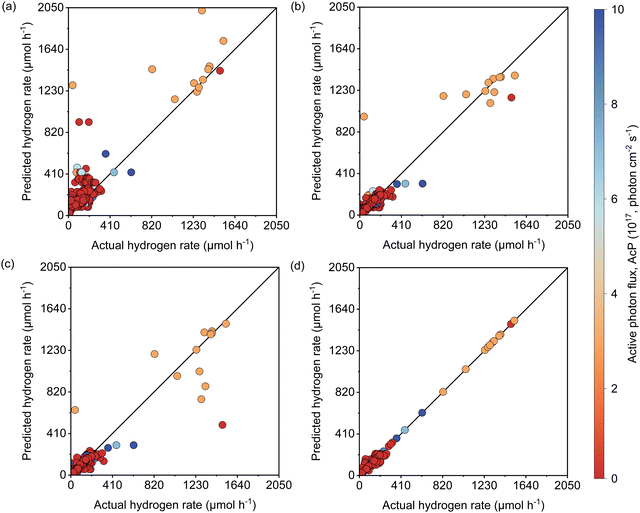
As described earlier, LI does not readily reflect the number of photons and may in fact skew the actual photon flux at longer wavelengths, where low spectral irradiance corresponds to an abundance of low energy photons. As a base comparison, Fig. 6(a) shows the model prediction without any form of input of light characteristics. Significant scattering between the prediction and actual HER rates can be seen with MAE of 74 μmol h−1. Without any input of light characteristics, the contribution of features decreases in the order AC > CL > ATI > CWF, which is significantly different from Fig. 3 and is incompatible with the knowledge domain (Fig. S16, ESI†).The inclusion of LI reduces the MAE to 30 μmol h−1 (Fig. 6(b)), while the conversion to ApP (photon flux over the entire spectrum) recorded an MAE of 31 μmol h−1 (Fig. 6(c)). In both cases, the light intensities at wavelengths longer than the photocatalyst absorption threshold, or in other words sub-bandgap photons, account for the deviations, especially during the training stage of the model. Broadband light sources such as the simulated solar and Xe arc lamp, with a significant portion of the intensities and photons in the visible and infrared range account for the largest deviations. A similar observation was made by Liu et al.44 (R2 = 0.82) when a single wavelength is used as a descriptor for broad spectrum irradiance. Lower errors can be expected if all data were derived from a common light source of the same intensity,45 but in this case, the input of light characteristic as a feature is unnecessary since there is no variability in the light source, albeit being a restricted model.46 As a generalized model, our data comprises of various light sources, from simulated solar lamps, Xe arc lamps, high- and mid-pressure Hg arc lamps, and blacklight, to LEDs (Fig. S15, ESI†). To cull the sub-bandgap photons, only photons with an energy equal to and above the reported bandgap for every sample are taken into account in calculating the AcP. This resulted in an impressive, reduced MAE of 7 μmol h−1 with strong alignment of data on the parity plot (Fig. 6(d)). To this end, we have identified and rationalized the selection of the most influential features describing the photocatalytic HER activity over cocatalyst-loaded TiO2. The use of AcP, as opposed to other more direct descriptors of light sources, is instrumental in unifying the other features, i.e., ATI, AC, CWF, and CL (Fig. S16, ESI†). Perhaps importantly, the choice of AcP is driven by fundamental rationalization of the photocatalytic event. The result is the most accurate and generalizable machine learning model, at least to the best of our knowledge, for predicting photocatalytic HER rates.
4. Conclusions
A highly accurate and intuitive machine learning model was developed to predict the HER rate of TiO2 photocatalysts using ATI, AC, CWF, CL and AcP as the input features (correlation coefficient of 0.91). The model was made possible by extracting 946 entries from the literature and complemented by 25 supplementary experiments to bridge any missing data within the range of interest. A key enabling step is the conversion of LI to AcP that corrected the discrepancies in the different light sources used in the literature and being a direct measure of TiO2 photoexcitation. The result is a prediction model with a significantly low MAE of 7 μmol h−1.Although the current machine learning model is limited to TiO2 (and necessarily so) being the most abundant source of data available in the literature, it nevertheless serves as a quintessential legacy platform for further transfer learning to predict the activities of other photocatalysts, cocatalysts, or reactions. Since the current model has learned the major patterns between photocatalyst properties and reaction conditions, a relatively small dataset will be sufficient to adapt the model for the new conditions and fine-tuning the prediction magnitudes. With a considerable number of photocatalysts being trained on its backbone and combining with the parallel effort in the crystal graph convolution neural network (CGCNN) on semiconductor materials,15 it can ultimately pave the way as a route for new photocatalyst discovery for various reactions. As a disclaimer, we do not envision the model to be adaptable to non-photocatalytic reactions such as electrocatalysis since they work in a relatively different domain.
Acronyms
| AC | Alcohol concentration |
| AcP | Active photons flux |
| ApP | Apparent photon flux |
| AMW | Alcohol molecular weight |
| AT | Alcohol type |
| ATI | Alcohol type indicator |
| CAN | Cocatalyst atomic number |
| CEN | Cocatalyst electronegativity |
| CL | The amount of cocatalyst loading |
| CWF | Cocatalyst work function |
| d rutile | Size of anatase crystal |
| E g | Bandgap |
| LI | Light intensity |
| MAE | Mean absolute error |
| Rate | Hydrogen evolution rate |
| RMSE | Root mean squared error |
| SSA | Specific surface area |
| T calcination | Calcination temperature |
| X rutile | Fraction of rutile phase |
Author contributions
W. Y. T., V. S. and R. A. procured the fundings, conceived and designed the project. Y. H. and H. M. developed the machine learning model. A. K., R. K. and A. R. performed the preliminary data collection. Y. H., W. P. W. and D. G. performed further data collection, carried out physical experiments and analyzed the collected data. P. K. and C. Y. T. contributed to the supervision of the project. Y. H., V. S. and W. Y. T. prepared the manuscript. All authors reviewed and contributed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is supported by the Ministry of Higher Education Malaysia via the Fundamental Research Grant Scheme (FRGS/1/2022/TK08/UM/02/43) and the Australian Research Council via the Discovery Project (DP200102121). W. Y. T. acknowledges the support of the Southeast Asia-European Joint Funding Scheme (JFS21-123 HYPERMIS), EPRO Adv Tech (IF044-2021), and UM Matching Grant (MG002-2022).References
- S. van Renssen, Nat. Clim. Change, 2020, 10, 799–801 CrossRef.
- C. Brief, Paris 2015: Tracking country climate pledges, https://www.carbonbrief.org/.
- H. Nishiyama, T. Yamada, M. Nakabayashi, Y. Maehara, M. Yamaguchi, Y. Kuromiya, Y. Nagatsuma, H. Tokudome, S. Akiyama, T. Watanabe, R. Narushima, S. Okunaka, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Nature, 2021, 598, 304–307 CrossRef PubMed.
- T. Kawai and T. Sakata, Nature, 1980, 286, 474–476 CrossRef.
- S. Naveenan and W. Y. Teoh, Curr. Opin. Chem. Eng., 2021, 34, 100740 CrossRef.
- X. C. Lv, C. Y. Hu, J. Shang, P. H. L. Sit, F. L. Y. Lam and W. Y. Teoh, Catal. Today, 2019, 335, 468–476 CrossRef.
- W. Y. Teoh, A. Urakawa, Y. H. Ng and P. Sit, Heterogeneous Catalysts: Advanced Design, Characterization, and Applications, John Wiley & Sons, 2021, vol. 2 Search PubMed.
- W. T. Chen, Y. S. Dong, P. Yadav, R. D. Aughterson, D. Sun-Waterhouse and G. I. N. Waterhouse, Appl. Catal., A, 2020, 602, 117703 CrossRef.
- C. Hu, D. Kelm, M. Schreiner, T. Wollborn, L. Madler and W. Y. Teoh, ChemSusChem, 2015, 8, 4005–4015 CrossRef PubMed.
- K. Takanabe, ACS Catal., 2017, 7, 8006–8022 CrossRef.
- H. Masood, C. Y. Toe, W. Y. Teoh, V. Sethu and R. Amal, ACS Catal., 2019, 9, 11774–11787 CrossRef.
- O. Fontelles-Carceller, M. J. Munoz-Batista, J. C. Conesa, M. Fernandez-Garcia and A. Kubacka, Appl. Catal., B, 2017, 216, 133–145 CrossRef.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. F. Wang and L. Yang, Nat. Rev. Phys., 2021, 3, 422–440 CrossRef.
- S. Y. Lee, S. Byeon, H. S. Kim, H. Jin and S. Lee, Mater. Des., 2021, 197, 109260 CrossRef.
- H. Masood, T. Sirojan, C. Y. Toe, P. V. Kumar, Y. Haghshenas, P. H. L. Sit, R. Amal, V. Sethu and W. Y. Teoh, Cell Rep. Phys. Sci., 2023, 4, 101555 CrossRef.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K.-I. Shimizu, ACS Catal., 2019, 10, 2260–2297 CrossRef.
- E. Can and R. Yildirim, Appl. Catal., B, 2019, 242, 267–283 CrossRef CAS.
- Q. L. Tao, T. Lu, Y. Sheng, L. Li, W. C. Lu and M. J. Li, J. Energy Chem., 2021, 60, 351–359 CrossRef CAS.
- N. Serpone, J. Photochem. Photobiol., A, 1997, 104, 1–12 CrossRef CAS.
- K. Tran and Z. W. Ulissi, Nat. Catal., 2018, 1, 696–703 CrossRef CAS.
- T. T. Le, W. Fu and J. H. Moore, J. Bioinform., 2020, 36, 250–256 CrossRef CAS PubMed.
- S. M. Lundberg and S. I. Lee, arXiv, 2017, preprint DOI:10.48550/arXiv:1705.07874v2.
- Y. K. Kho, A. Iwase, W. Y. Teoh, L. Mädler, A. Kudo and R. Amal, J. Phys. Chem. C, 2010, 114, 2821–2829 CrossRef CAS.
- W. Y. Teoh, L. Madler, D. Beydoun, S. E. Pratsinis and R. Amal, Chem. Eng. Sci., 2005, 60, 5852–5861 CrossRef CAS.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- Y. K. Kho, W. Y. Teoh, A. Iwase, L. Madler, A. Kudo and R. Amal, ACS Appl. Mater. Interfaces, 2011, 3, 1997–2004 CrossRef CAS PubMed.
- W. Y. Teoh, J. A. Scott and R. Amal, J. Phys. Chem. Lett., 2012, 3, 629–639 CrossRef CAS PubMed.
- Z. Zhang and J. T. Yates, Jr., Chem. Rev., 2012, 112, 5520–5551 CrossRef CAS PubMed.
- A. G. Dosado, W. T. Chen, A. Chan, D. Sun-Waterhouse and G. I. N. Waterhouse, J. Catal., 2015, 330, 238–254 CrossRef CAS.
- L. Himanen, M. O. J. Jager, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. J. Jager, M. Todorovic and P. Rinke, J. Chem. Phys., 2023, 158, 234802, DOI:10.1063/5.0151031.
- J. M. Bland and D. G. Altman, Lancet, 1986, 1, 307–310 CrossRef CAS.
- C. Marchal, A. Piquet, M. Behr, T. Cottineau, V. Papaefthimiou, V. Keller and V. Caps, J. Catal., 2017, 352, 22–34 CrossRef CAS.
- G. L. Chiarello, M. H. Aguirre and E. Selli, J. Catal., 2010, 273, 182–190 CrossRef CAS.
- G. L. Chiarello, M. V. Dozzi, M. Scavini, J.-D. Grunwaldt and E. Selli, Appl. Catal., B, 2014, 160–161, 144–151 CrossRef CAS.
- Y.-H. Chung, K. Han, C.-Y. Lin, D. O’Neill, G. Mul, B. Mei and C.-M. Yang, Catal. Today, 2020, 356, 95–100 CrossRef CAS.
- S. Kohtani, K. Yoshida, T. Maekawa, A. Iwase, A. Kudo, H. Miyabe and R. Nakagaki, Phys. Chem. Chem. Phys., 2008, 10, 2986–2992 RSC.
- W. Kurashige, R. Kumazawa, D. Ishii, R. Hayashi, Y. Niihori, S. Hossain, L. V. Nair, T. Takayama, A. Iwase, S. Yamazoe, T. Tsukuda, A. Kudo and Y. Negishi, J. Phys. Chem. C, 2018, 122, 13669–13681 CrossRef CAS.
- W. Kurashige, R. Hayashi, K. Wakamatsu, Y. Kataoka, S. Hossain, A. Iwase, A. Kudo, S. Yamazoe and Y. Negishi, ACS Appl. Energy Mater., 2019, 2, 4175–4187 CrossRef CAS.
- J. Disdier, J. M. Herrmann and P. Pichat, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 651–660 RSC.
- G. R. Bamwenda, S. Tsubota, T. Nakamura and M. Haruta, J. Photochem. Photobiol., A, 1995, 89, 177–189 CrossRef CAS.
- F. Nogueira, Bayesian Optimization: Open source constrained global optimization tool for Python, https://github.com/fmfn/BayesianOptimization.
- R. Garnett, Bayesian Optimization, Cambridge University Press, 2023 Search PubMed.
- Q. Liu, K. Pan, L. Zhu, Y. Zhou, Y. Lu, S. Wang, Z. Ding, W. Du and Y. Zhou, Green Chem., 2023, 25, 8778–8790 RSC.
- M. R. K. Estahbanati, M. Feilizadeh and M. C. Iliuta, Appl. Catal., B, 2017, 209, 483–492 CrossRef CAS.
- N. S. Ibrahim, W. L. Leaw, D. Mohamad, S. H. Alias and H. Nur, Int. J. Hydrogen Energy, 2020, 45, 28553–28565 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00246b |
| This journal is © The Royal Society of Chemistry 2024 |