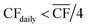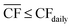Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Managing intermittency of renewable power in sustainable production of methanol, coupled with direct air capture†
George J.
Fulham
 *,
Paula V.
Mendoza-Moreno
and
Ewa J.
Marek
*,
Paula V.
Mendoza-Moreno
and
Ewa J.
Marek
 *
*
Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge CB3 0AS, Cambridgeshire, UK. E-mail: gf325@cam.ac.uk; ejm94@cam.ac.uk; pvm21@cam.ac.uk
First published on 4th June 2024
Abstract
Coupling direct air capture (DAC) with methanol production is a technically attainable opportunity for CO2 capture and utilisation (CCU). The process, known as power-to-methanol (PtM), consumes large amounts of renewable electricity for water electrolysis and DAC. However, the time-variability of renewable power remains a major challenge. Here, we consider erecting a wind farm as part of a PtM facility and propose using four parallel reactors to adjust the methanol production according to daily wind power generation, which we model for 90 onshore and offshore locations with real-world data. Batteries and reserve storage of compressed H2 and CO2 allow methanol production during near-zero availability of wind power. We investigate different operation strategies, aiming to either minimise the reserve storage or maximise production, ultimately finding minimised storage as more cost-effective. The resulting selling price of methanol from a plant powered by an onshore wind farm is $1400 per tonne, rising to $2200 for offshore wind power because of higher farm installation costs. However, with a well-located wind farm, coupled with improvements to DAC, electrolysis, and catalysts, the selling price falls as low as $300 per tonne of methanol, reaching parity with fossil fuel-derived methanol. Purchasing stable grid power for PtM avoids issues of intermittency, and results in a lower methanol selling price of $960 per tonne, falling to $340 with process improvements. However, life cycle assessment (LCA) shows the global warming potential (GWP) of the grid-based cases is no better than producing methanol from natural gas; whereas, wind-powered DAC-PtM delivers net-negative GWP between −760 and −1240 kgCO2eq. per tMeOH, demonstrating successful CCU.
Broader contextInterfacing renewable power with chemical production, known as power-to-X, is a promising way to replace fossil fuels. However, the steady operation of chemical processes is incompatible with the time-variability of renewable power sources such as wind or solar. The treatment of the interconnected grid as delivering wholly renewable power with 100% availability is unrealistic, and so intermittency must be addressed. Herein, we present a framework for dynamic plant operation to handle renewable power intermittency, developed for the example of power-to-methanol (PtM) sourcing atmospheric CO2 from direct air capture (DAC) and H2 from water electrolysis. The work underlines that new process configurations and operation regimes are required to adequately address the challenges presented by electrified chemical production. |
Introduction
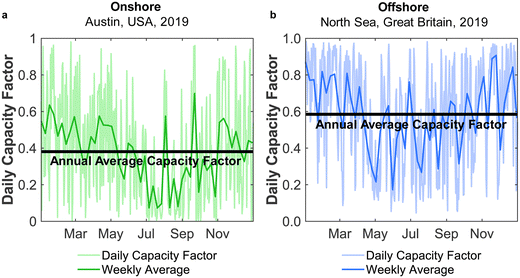
Direct air capture (DAC) of atmospheric CO2 has a prominent place in strategies for reducing and controlling carbon emissions.1,2 While DAC progresses towards commercialisation,3,4 the handling of DAC-captured CO2 remains an open question, with sequestration requiring a CO2 distribution infrastructure and access to sequestration sites.5 An appealing solution is to couple DAC with chemical production,6 as a form of CO2 capture and utilisation (CCU). DAC-CCU would realise the postulates of a circular carbon economy with CO2 as the carbon-source for manufacturing commodity chemicals – one of the simplest being methanol (MeOH). The storage and transport of methanol is far easier than CO2, given its liquid state at ambient conditions. Moreover, the production of acetic acid and formaldehyde from methanol7,8 opens a wide range of uses, enabling long-term CO2 removal in suitable products. Methanol will also act as a vital building block in the future chemical industry through the methanol-to-olefins (MtO) and methanol-to-gasoline (MtG) pathways, allowing the synthesis of value-added chemicals (e.g. aviation fuel) without fossil fuels.9 Additionally, methanol has been proposed as a promising future fuel for use in maritime transport.10 Given the large, and growing, global reliance on methanol – 80 Mt in 201811 up to 110 Mt in 202212 – the decarbonisation of its production is an essential task.Various methods have been proposed for upgrading CO2 to renewable methanol, although by far the most mature is to react CO2 with green H2, typically from water electrolysis.13 The process consumes a large amount of electricity, and so is referred to as power-to-methanol (PtM).9,14 Carbon dioxide could be captured from industrial point sources,15,16 but here, we focus on coupling DAC with PtM (DAC-PtM) for carbon circularity. To deliver an environmental benefit, DAC-PtM must avoid carbon-intensive electricity and use only renewable power,17,18 for which intermittency remains an unavoidable but easily overlooked challenge. In the example of wind power, the power generation fluctuates daily and seasonally, as shown in Fig. 1 for two exemplary locations, one onshore and the other offshore.
The effect of intermittency is often quantified using a capacity factor, which compares the true power generation of a site versus its nominal (max. achievable) capacity. Averaging the capacity factor across a year aids in the sizing of installations for power generation – i.e. if 100 MW of power is required on average, but a wind farm has a capacity factor of 0.50, then the actual installed capacity should be 200 MW. Yet, the suitable sizing of renewable power only partially addresses the problem of intermittency when interfacing renewable power with chemical production plants, which have historically been designed on the assumption of steady operation. Interconnected electricity grid networks could help obviate variability over time.19,20 However, the treatment of the grid as a “black box”, from which renewable electricity can be taken with 100% availability, is unrealistic. Steep growth is expected in consumer-side electricity demand;21–23 any substantial increase in electricity consumption coming from the chemical sector would certainly overburden the grid. A more feasible solution is for electrified chemical plants to generate their own renewable power, e.g. using wind or solar farms. Therefore, we must consider building and operating renewable power sources as part of a future electrified chemical industry, and confront the attendant challenges of intermittency.
The dynamic operation of power-to-methanol has begun recently to attract research attention,19,20,24–26 and the concept of dynamic operation is being implemented industrially for electrified chemical production of ammonia.27 In Section S1 of the ESI,† we outline salient prior studies investigating dynamic operation of power-to-methanol alongside power-to-X processes, as well as work examining off-grid and renewably powered direct air capture (DAC).
In the case of dynamically operated PtM, prior studies have primarily focused on optimisation of plant operation routines (e.g. the reliance on batteries or the purchase of grid electricity to supplement intermittent renewable power) subject to electricity price or availability.19,20,24 In some instances19 the treatment of operating and capital costs was simplified to aid computation, and often only a single candidate location has been considered for the renewable power generation; hence the effect of renewable power variation between sites is elided. A prior study by Chen et al.24 considered PtM at two candidate sites in the US and Germany for wind- and solar-powered PtM, with a mixture of reserve hydrogen storage and purchased grid electricity to enable continuous operation at full throughput. Their work ultimately found a wide divergence between the most economical solution at each site, confirming the need to consider many locations in yielding findings of wide applicability. Recently, Van Antwerpen et al.25 costed the production of MeOH across numerous sites in Australia, when reliant solely on wind and solar power, in which a single reactor was operated at steady state with the aid of reserve storage or held idle during very low power availability. The methanol selling price was found to be highly sensitive to the siting, and installation costs, of renewable power, and they also underlined the cost advantage of minimising the size of reserve storage – in particular batteries.
Here, we propose and investigate the use of multiple reactors in parallel for a DAC-PtM plant directly interfaced with a wind farm. The multi-reactor configuration allows methanol production to be scaled according to power availability – difficult to achieve with a single reactor25 – and avoids the immense reserve storage required for continuous operation of a single, large reactor. We support our analysis by combining real-world wind farm data for 90 candidate locations with a full process model for DAC-PtM to investigate the cost of DAC-PtM using the multi-reactor configuration, which we also compare against operating a single, large reactor with either wind power or electricity purchased from the grid. The analysis incorporates different strategies for dynamic operation, appraising the cost-effectiveness of maximising methanol production against reducing the plant reliance on reserve storage. Through life cycle analysis we then investigate the potential of renewably powered DAC-PtM to achieve net CO2 capture, contrasted against DAC-PtM with grid electricity. Finally, we extend our findings to consider directions for further optimisation of DAC-PtM at two specific wind farm sites.
Power-to-methanol plant
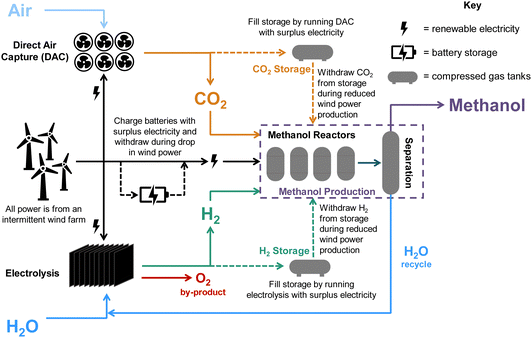
We consider a renewably-powered DAC-PtM plant, sourcing CO2 from low-temperature direct air capture (LT-DAC) with solid sorbents and H2 from water electrolysis using proton-membrane exchange (PEM) electrolysers. The annual production was set as 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes of methanol, with all sub-processes in the DAC-PtM entirely powered by either an onshore or offshore wind farm. The potential for power generation of such farms was assessed by taking real-world wind data from 90 worldwide locations. To allow the DAC-PtM plant to operate during periods of low wind, we consider reserve storage of compressed CO2 and H2 in tanks and electricity in batteries to enable uninterrupted production of methanol. The modular nature LT-DAC (i.e. multiple solid sorbent units in parallel28) and the fast start-up of PEM electrolyser stacks9 both allow the production of CO2 and H2 to be scaled according to the available wind power. We then propose an additional solution to handle power variability: multiple parallel reactors for methanol synthesis. By taking some reactors on- or off-line, the plant throughput and electricity demand are adjustable, matching the available wind power and alleviating the need for reserve storage. We then compare against solutions using only a single, large reactor instead, with appropriately adjusted sizes for electricity and CO2/H2 storage. A simplified schematic of the plant is given in Fig. 2. In the investigation, we vary the performance of wind farms and analyse the outputs from the DAC-PtM plant, and the cost-effectiveness of the plant under three cases – base, optimistic, pessimistic – differentiated according to changes in wind power performance and obtainable technological improvements across the whole DAC-PtM process.
000 tonnes of methanol, with all sub-processes in the DAC-PtM entirely powered by either an onshore or offshore wind farm. The potential for power generation of such farms was assessed by taking real-world wind data from 90 worldwide locations. To allow the DAC-PtM plant to operate during periods of low wind, we consider reserve storage of compressed CO2 and H2 in tanks and electricity in batteries to enable uninterrupted production of methanol. The modular nature LT-DAC (i.e. multiple solid sorbent units in parallel28) and the fast start-up of PEM electrolyser stacks9 both allow the production of CO2 and H2 to be scaled according to the available wind power. We then propose an additional solution to handle power variability: multiple parallel reactors for methanol synthesis. By taking some reactors on- or off-line, the plant throughput and electricity demand are adjustable, matching the available wind power and alleviating the need for reserve storage. We then compare against solutions using only a single, large reactor instead, with appropriately adjusted sizes for electricity and CO2/H2 storage. A simplified schematic of the plant is given in Fig. 2. In the investigation, we vary the performance of wind farms and analyse the outputs from the DAC-PtM plant, and the cost-effectiveness of the plant under three cases – base, optimistic, pessimistic – differentiated according to changes in wind power performance and obtainable technological improvements across the whole DAC-PtM process.
Methodology
Wind power intermittency
Electricity generation was considered at potential locations for wind farms worldwide. The chosen locations, listed in Table S1 in the ESI,† were split evenly between 30 onshore sites located in-land (taken here to mean greater than 20 km from the sea), 30 onshore coastal sites (i.e. less than 20 km from the sea), and 30 offshore locations. Wind speed data from the Global Wind Atlas29 were used in selecting suitable candidate locations for the wind farms.At each location, expected power generation data for the years 2016 to 2020 were extracted from the Renewables Ninja web application using a Python application programming interface (API).30,31 The API utilises the NASA Merra-2 global weather data set32 for the calculation of predicted wind or solar power generation, at any selected location over a given year. The analysis here employed Vestas V80 2000 turbines, with a hub height of 100 m, and a nominal nameplate farm capacity of 100 MW.33 The data, obtained in hourly intervals, were then processed to find the daily average power output, Pdaily. By comparing the daily power output against the nameplate capacity of the wind farm, Pnameplate, the daily capacity factor, CFdaily, was calculated for each location across a given year, with example results shown in Fig. 1. An annual average capacity factor, 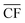 , was then determined. In total, daily and yearly power outputs and capacity factors were analysed for all 90 wind farms worldwide. Further methodological detail and results are provided in Section S2 of the ESI.†
, was then determined. In total, daily and yearly power outputs and capacity factors were analysed for all 90 wind farms worldwide. Further methodological detail and results are provided in Section S2 of the ESI.†
Since considered locations vary in the achievable power output, the size of the wind farm needed to run the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes per annum DAC-PtM plant also needs to differ. Thus, for each site, the required nameplate wind farm capacity, Pnameplate, was determined using eqn (1).
000 tonnes per annum DAC-PtM plant also needs to differ. Thus, for each site, the required nameplate wind farm capacity, Pnameplate, was determined using eqn (1).
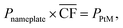 | (1) |
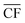 is the annual wind farm capacity factor and PPtM is the power demand to run DAC-PtM at full capacity – the same methodology was applied by Chen et al.24 in sizing wind and solar farms for PtM. The obtained nameplate capacity of the wind farm translates to the number of required wind turbines, and hence the cost of the wind farm at a given location.
is the annual wind farm capacity factor and PPtM is the power demand to run DAC-PtM at full capacity – the same methodology was applied by Chen et al.24 in sizing wind and solar farms for PtM. The obtained nameplate capacity of the wind farm translates to the number of required wind turbines, and hence the cost of the wind farm at a given location.
Dynamic plant operation and reserve storage strategies
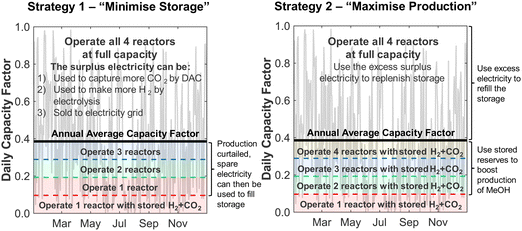
Although the nameplate wind farm capacity is matched to the annual energy requirements of the DAC-PtM plant, the daily fluctuations in the wind power, Pdaily, will regularly push the power generation below the annual average power, Paverage, as already expected from Fig. 1. During such periods, we reduce methanol production – and therefore reduce the plant power demand – by decreasing the number of operational synthesis reactors, alongside the production of CO2 and H2, according to the daily power availability. We chose here to use four parallel reactors; a discussion on using different numbers of reactors is provided in Section S10 of the ESI.† The capacity of reserve storage of H2, CO2, and electricity was then considered such that the DAC-PtM plant could continue to operate at reduced capacity during periods with very little or no wind power generation. We choose to primarily store reserve capacity as compressed H2 and CO2, rather than solely as electricity in batteries. Utility-scale batteries, as would be required for balancing intermittency for a wind-powered chemical plant, are discussed in the literature as providing a maximum of 10 h duration of discharging output,34 with a duration of 4 h commonly viewed as more practicable.35 Therefore, storage of electricity in batteries alone would greatly struggle to smooth out low wind power availability over 5 to 10 consecutive days range as found in analysis of the wind generation data (Section S2 of the ESI†). Secondly, the storage of compressed gases is more cost-effective than battery-based storage, as demonstrated in Section S5 of the ESI† and discussed in ref. 25.To operate the DAC-PtM plant at full capacity all-year round, using one large reactor, requires a huge reserve storage capacity equivalent to the throughput across ca. 90 days of operation (Section S6 of the ESI†). Such large storage is cost prohibitive and impractical. Dynamic operation of the plant is required, for which the configuration of multiple reactors is well-suited and forms the basis of the study here. We considered two alternative strategies for the dynamic operation of multiple reactors and usage of reserve storage:
• In Strategy 1, the number of operational reactors was curtailed to reduce the plant power consumption below the available wind power, with the plant only ever consuming stored reserves when the available power was insufficient to run even one of the four synthesis reactors. Otherwise, the plant operated with a small surplus of electricity during curtailed production which was used to refill the reserve storage; any electricity generated when the storage was full was treated as surplus. Given likely difficulties of aligning periods of surplus wind generation with grid-side electricity demand (e.g. because of concomitant strong performance of grid-integrated renewables), we used an additional pack of batteries to store the surplus electricity prior to sale.
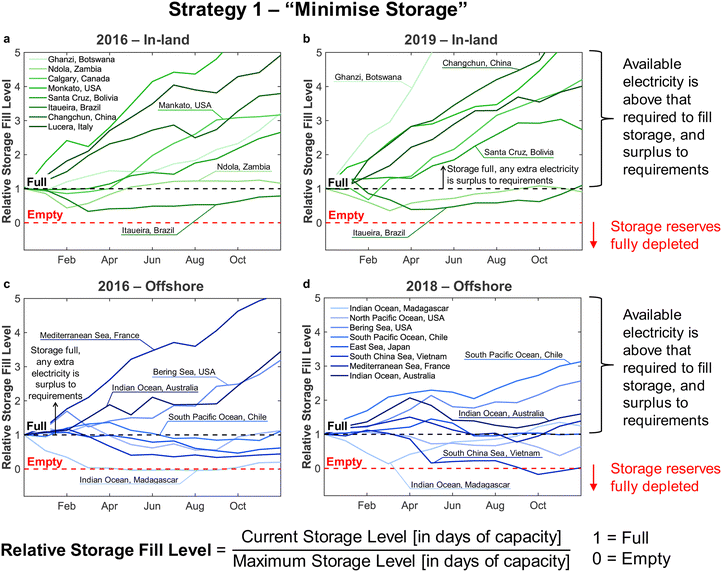
• In Strategy 2, reserve storage was used to ‘round up’ the number of operational reactors on a given day – e.g. if the wind power on a given day was equivalent to the power consumption when using 2.5 reactors, reserve storage was used to allow for the full operation of 3 reactors. Any surplus electricity was then used to replenish the stored reserves.
Strategy 1 focuses on reducing dependence upon, and size of, reserve storage (i.e. “minimise storage”) by attempting to operate the plant within the constraints of available power generation. Whereas, Strategy 2 aims to maximise throughput production by relying more upon storage (i.e. “maximise production”).
The two strategies are shown schematically in Fig. 3 and compared in Table 1. The storage capacity was treated in terms of the number of operational days it allowed a single reactor to be operated – i.e. a capacity of 15 days would allow the DAC-PtM plant to run with one of the four smaller reactors using reserve storage for 15 days without refilling.
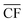 refers to the annual average capacity factor – i.e. annual average power generation as a fraction of the nameplate (max.) power. The daily capacity factor is denoted by CFdaily
refers to the annual average capacity factor – i.e. annual average power generation as a fraction of the nameplate (max.) power. The daily capacity factor is denoted by CFdaily
The required storage capacity was determined for each specific location as follows:
• For Strategy 1 (“minimise storage”), the storage capacity was calculated by considering the maximum number of days, in a two-month period, for which the daily power generation was below 1/4 of the power requirement for DAC-PtM at full throughput, PPtM (i.e. when 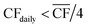 ). The 1/4 arises because the proposed plant layout uses four reactors, and so if ever the daily wind power fell below 1/4PPtM, the plant must consume CO2, H2, and electricity from the reserve storage to operate one small reactor.
). The 1/4 arises because the proposed plant layout uses four reactors, and so if ever the daily wind power fell below 1/4PPtM, the plant must consume CO2, H2, and electricity from the reserve storage to operate one small reactor.
• For Strategy 2 (“maximise production”), the storage capacity was calculated corresponding to the maximum number of days within a two-month period for which the plant relied upon the use of stored reserves, equivalent to when 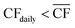 (Table 1).
(Table 1).
The appropriate sizing of reserve storage depends not only upon how frequently the plant consumes stored reserves, but also how often the reserve storage can be refilled. The storage tanks were filled by using the excess electricity (such as during curtailed production for Strategy 1, or when 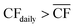 for Strategy 2) to perform extra DAC, electrolysis and compression for reserve storage of CO2 and H2, as well as charging of batteries. Hence, a model was developed to track the level of stored reserves across the year, when operating under each strategy, outlined fully in Section S8 of the ESI.† Obtained results are summarised in Fig. 4 and 5, which confirm the storage sizing as sufficient to allow continuous methanol production, with the storage only emptying on rare occurrences for one or two sites. In Fig. 4 and 5, results are shown for relative storage level, defined according to eqn (2), demonstrating the changes in the fill level specific to each location.
for Strategy 2) to perform extra DAC, electrolysis and compression for reserve storage of CO2 and H2, as well as charging of batteries. Hence, a model was developed to track the level of stored reserves across the year, when operating under each strategy, outlined fully in Section S8 of the ESI.† Obtained results are summarised in Fig. 4 and 5, which confirm the storage sizing as sufficient to allow continuous methanol production, with the storage only emptying on rare occurrences for one or two sites. In Fig. 4 and 5, results are shown for relative storage level, defined according to eqn (2), demonstrating the changes in the fill level specific to each location.
 | (2) |
At sites for which the relative storage level is above 1, the availability of excess electricity to fill storage is greater than the energy demand to consume storage; hence, the extra electricity is effectively a further surplus. At sites for which the storage level never comes close to zero, the methodology for sizing storage can be further optimised, reducing the planned storage without compromising continuous plant operation.
Although the methodology for sizing storage (i.e. the maximum number of days for which storage is needed during a two-month period) ensures continuous operation under both Strategies 1 and 2, the results differ noticeably. First, Strategy 2 (“maximise production”) requires much larger storage capacity, on average, than Strategy 1 (“minimise storage”), i.e. 50 to 60 days vs. 10 to 20 days, as Strategy 2 depends on storage far more often than Strategy 1 (Table 1). Second, operation under Strategy 2 (“maximise production”) is such that some sites draw very heavily upon storage, nearly emptying the reserves, before generating a large surplus later in the year (e.g. the site at in the South Pacific Ocean, Peru). Such seasonal patterns are not as pronounced under Strategy 1. The reason lies in Strategy 2 requiring storage whenever electricity generation falls below the yearly average (Table 1), causing higher sensitivity to seasonal variation in wind power generation than Strategy 1.
The disparity in storage levels between the start and end of the year – i.e. when the storage level finishes the year in December below its level at the start of the year in January – would need to be addressed in practice to ensure cyclic annual operation, potentially with deliberate diversions of electricity to re-fill the storage at an appropriate time of year.
Although the DAC-PtM plant with 4 reactors can operate continuously, the output production consequently changes across the year. To quantify the effective annual methanol production, we defined a separate capacity factor for the DAC-PtM plant itself, CFplant, in eqn (3).
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes of methanol. The resulting CFplant translates to the methanol production and revenue.
000 tonnes of methanol. The resulting CFplant translates to the methanol production and revenue.
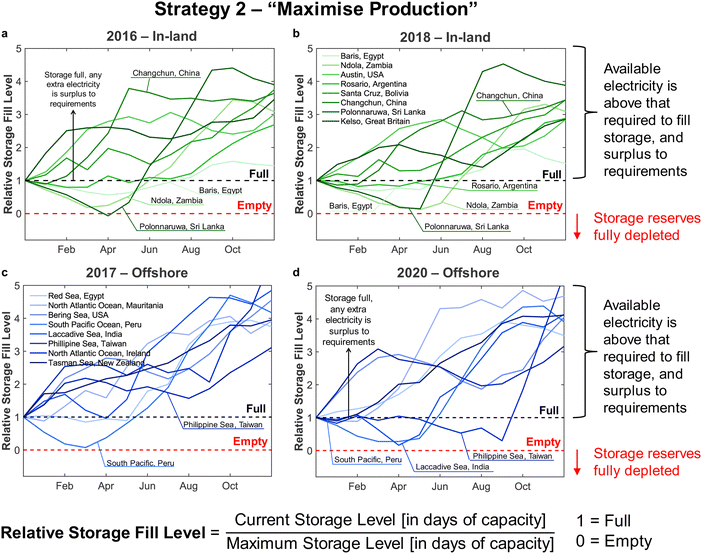
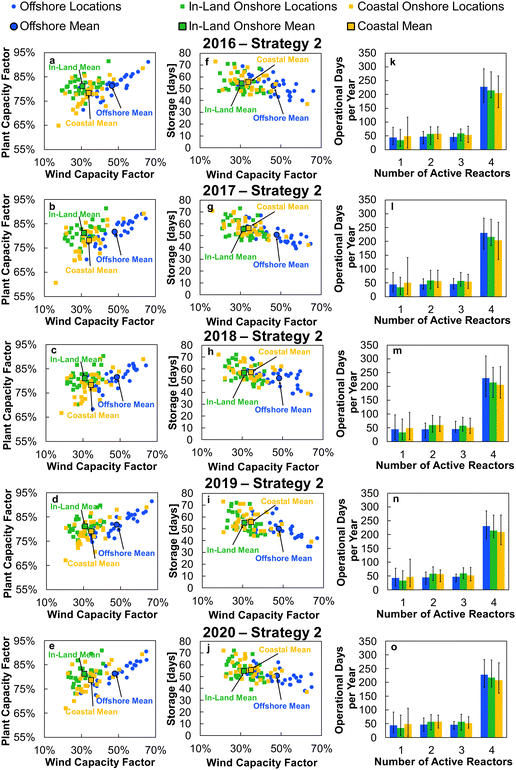
Applying the outlined methodology for Strategy 1 (“minimise storage”) in processing the wind power generation data yielded the results in Fig. 6 for plant capacity factor, storage requirements, and operational days of the PtM reactors. The results when operating wind-powered DAC-PtM under Strategy 2 (“maximise production”) are shown in Fig. 7. Comparing the results between years reveals that the plant capacity factors are consistent from year to year under both strategies, demonstrating that reliable prediction of wind-powered DAC-PtM performance is achievable. In general, increasing the wind farm 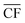 improves CFplant, and the offshore wind farm locations have higher average capacity factors than those situated onshore (Fig. 6 and 7a–e). Comparing both strategies shows Strategy 2 (“maximise production”) as achieving substantially higher plant capacity factors for the same underlying wind power performance – ca. 80% against 70% on average. For comparison, operating a single large reactor intermittently gives a much lower plant capacity factor of around 45 to 55% depending upon wind farm site (Section S7 in the ESI†).
improves CFplant, and the offshore wind farm locations have higher average capacity factors than those situated onshore (Fig. 6 and 7a–e). Comparing both strategies shows Strategy 2 (“maximise production”) as achieving substantially higher plant capacity factors for the same underlying wind power performance – ca. 80% against 70% on average. For comparison, operating a single large reactor intermittently gives a much lower plant capacity factor of around 45 to 55% depending upon wind farm site (Section S7 in the ESI†).
Comparison of the required storage capacities when operating under Strategies 1 and 2 shows that, on average, Strategy 2 (“maximise production”) requires approximately 3 times more storage than Strategy 1 (“minimise storage”) (cf.Fig. 6 and 7f–j). Inspecting the breakdowns of operational days (Fig. 6 and 7k–o) shows that under Strategy 1, in which production is always reduced to bring power demand below availability, the DAC-PtM operates far more often with only 1 reactor than under Strategy 2, which uses storage to avoid curtailment of production. The number of days spent using 2 or 3 reactors is roughly equivalent between the two strategies, but Strategy 2 spends a far greater proportion of the year using all 4 reactors – hence the plant capacity factor improvement.
Two clear bands of data points appear for the in-land onshore and offshore locations across Fig. 6 and 7. The coastal locations unsurprisingly yield results which lie between the offshore and in-land data sets, with drastic fluctuations similar to offshore locations, but without the very high offshore wind speeds.32 Coastal locations may therefore present suitable compromise sites for DAC-PtM (i.e. relatively high wind speeds without costly foundations in the ocean); however, in aiming to capture the worldwide spread of wind power, we focus the rest of our analysis on the in-land onshore and offshore sites. In Table S5 in the ESI,† we list the ten offshore and onshore locations with the highest CFplant values under both Strategies 1 and 2. The ranking shows that some locations (e.g. the Caribbean Sea to the coast of Venezuela or Baris in Egypt) deliver very high CFplant under both Strategies 1 and 2. However, some locations are much higher in the ranking for a specific strategy – e.g. Viborg in Denmark has the fifth highest CFplant under Strategy 2, but appears outside the top ten under Strategy 1 (Table S5 in the ESI†).
A five-year average of the values in Fig. 6 and 7 was applied in further modelling of wind-powered DAC-PtM for each strategy, considering the offshore and in-land wind farms. Using the five-year average, and spread across the locations, we extracted values representative of wind-powered DAC-PtM under three optimism cases: (1) base, (2) optimistic, and (3) pessimistic. The optimistic and pessimistic cases represent extreme values found from the 30 onshore and offshore sites, while the base case uses the mean values from all 30 locations. Given the inherent variability of wind power, the use of fixed values for parameters such as capacity factor would give a misleadingly narrow set of results when appraising wind-powered DAC-PtM. The use of varying optimism allowed the range of wind power performance, and the subsequent effect on DAC-PtM, to be captured. The key parameters are summarised in Table 2 for Strategies 1 and 2.
| Parameter | Base | Optimistic | Pessimistic | |||
|---|---|---|---|---|---|---|
| Offshore | Onshore | Offshore | Onshore | Offshore | Onshore | |
| Wind farm capacity factor, | 48% | 31% | 67% | 42% | 32% | 21% |
| Strategy 1 – “Minimise storage” Surplus [MW hsurp/MW hgen] Number of days per year with: | 0.25 | 0.26 | 0.13 | 0.25 | 0.37 | 0.34 |
| 4 operational reactors | 182 | 161 | 226 | 192 | 140 | 136 |
| 3 operational reactors | 47 | 54 | 72 | 86 | 30 | 30 |
| 2 operational reactors | 46 | 58 | 30 | 49 | 49 | 59 |
| 1 operational reactor | 90 | 92 | 37 | 38 | 146 | 140 |
| Plant capacity factor, CFplant | 72% | 70% | 83% | 80% | 61% | 61% |
| Number of days storage capacity | 17 | 14 | 6 | 4 | 39 | 36 |
| Strategy 2 – “Maximise production” Surplus [MW hsurp/MW hgen] Number of days per year with: | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 operational reactors | 229 | 215 | 291 | 277 | 175 | 181 |
| 3 operational reactors | 46 | 58 | 39 | 52 | 44 | 35 |
| 2 operational reactors | 46 | 58 | 21 | 28 | 66 | 74 |
| 1 operational reactor | 44 | 34 | 14 | 8 | 80 | 75 |
| Plant capacity factor, CFplant | 82% | 81% | 92% | 91% | 72% | 72% |
| Number of days storage capacity | 51 | 55 | 38 | 44 | 67 | 72 |
Process and techno-economic modelling
The production of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes per annum of methanol via direct air capture power-to-methanol (DAC-PtM) was modelled according to the process flowsheet outlined in Fig. S6 (ESI†), and schematised in Fig. 2. An equations-based approach was taken in modelling, outlined in detail in Section S11.2 of the ESI,† and summarised here.
000 tonnes per annum of methanol via direct air capture power-to-methanol (DAC-PtM) was modelled according to the process flowsheet outlined in Fig. S6 (ESI†), and schematised in Fig. 2. An equations-based approach was taken in modelling, outlined in detail in Section S11.2 of the ESI,† and summarised here.
In the considered DAC-PtM plant, all CO2 and H2 are produced by low-temperature direct air capture (LT-DAC) and polymer electrolyte membrane (PEM) electrolysis of water, respectively, with electricity sourced only from the wind farm. The production of CO2 and H2 is scaled according to the available wind power, thereby also adjusting the total flow of feed gas to the dynamically operated reactors. During periods of available wind power, the two gases undergo multi-stage compression, with inter-cooling by water, up to between 50 and 100 bar, i.e. the operating pressure for methanol synthesis which we varied between different modelling cases. Periods with excess electricity, as defined under each of the operation strategies (Table 1), are used to perform extra LT-DAC and PEM electrolysis. When operating at full capacity, about 80% of the two CO2 and H2 streams leaving the initial compression are mixed and supplied to the PtM reactors, while the remaining 20% of unmixed H2 and CO2 streams are further compressed to 300 and 150 bar, respectively, for storage within tanks. Given that the excess power available to fill the storage will be time-variant, the actual flowrates of H2 and CO2 entering storage will vary over time. However, for sizing the equipment within the storage loops (e.g. heat exchangers and turbomachinery), we used the aforementioned 80%/20% split of H2 and CO2 streams to the reactors and storage, respectively – equivalent to running all four reactors and filling the storage at a flowrate equal to the throughput of one reactor. Any excess electricity then also charges batteries. When withdrawing gases from storage, we considered the use of turboexpanders to draw down the pressure of the stored gases to the operating pressure in the methanol reactors (50 to 100 bar), allowing for electricity recovery during periods when the availability of wind power is low.
The production of methanol within the PtM reactors and the by-production of carbon monoxide and water were modelled using the Bussche and Froment kinetic model36 for a reactor operated at 250 °C and 50 to 100 bar over copper–zinc oxide catalysts. The PtM reactors evolve heat (ca. 0.6 MWth); here, the heat was removed by raising medium-pressure steam, which pre-heats the feed H2 and CO2.
The gas leaving the PtM reactors contains a mixture of MeOH, CO, and H2O, and unreacted H2 and CO2. The MeOH and H2O are separated from the rest of components by flash separation at 25 °C and 1 bar; the gas stream leaving the flash, consisting of mostly CO, CO2, and H2, is recycled back to the reactor. The Rachford–Rice equation was applied to describe the streams leaving the flash, using a two-constant activity coefficient model for methanol and water,37 and Henry's law for the dissolution of CO, CO2, and H2.38 To perform the flash separation, the reactor outlet gas must be cooled from 250 °C down to 25 °C; the majority of the cooling duty (ca. 75%) was heat-integrated with the recycle stream pre-heating. Cooling water was used for the remaining cooling duty down to 25 °C.
The MeOH and H2O mixture leaving the flash (with some dissolved CO, CO2, and H2) passes to a distillation column operating at ambient pressure, yielding 99.9 mol% purity MeOH in the tops. The distillation was approximated via short-cut methods: Fenske's equation for the minimum reflux ratio and Underwood's equations for the minimum number of stages. Binary VLE behaviour between methanol and water was assumed, again using a two-constant activity coefficient model.37 Dissolved gas within the MeOH and H2O, primarily CO2, leaves via venting at the condenser. The water leaving the column bottoms is recycled back to the initial water electrolysis stage, which fulfils approximately 2/3 of the total fresh water demand for the DAC-PtM. The remaining requirement for water for DAC-PtM is supplied using purified water from a reverse osmosis facility.
Compressor duties, for all gases other than pure H2, were calculated by first using the ideal gas law to determine the work required for isentropic compression, before using an isentropic efficiency to account for irreversibilities. For pure H2, the Soave–Redlich–Kwong equation of state was applied.39 All requisite heat capacity values (for heat capacity ratios and determining heat exchanger duties) were estimated using Shomate equations in the NIST WebBook.40
In addition to parallel reactors, the dynamic operation system also requires considering auxiliary process equipment and plant sub-systems. Heat exchangers and compressors typically operate within operational constraints on flowrates. Hence, for each reactor, we duplicate the heat exchangers for the feed and recycle loop pre-heat, compressors for the H2 and CO2 feed streams, and the recycle loop itself, as shown within the full schematic presented in Fig. S6 (ESI†). The dynamic operation of downstream separation (flash and distillation) is also accounted for by introducing a separate flash drum for each reactor outlet, from which crude MeOH product is sent to a balance tank. The balance tank then feeds into the distillation tower – assumed capable of operating under varied conditions. Such an assumption follows the work of Robinson and Luyben,41 who investigated control systems for dynamically operated distillation columns that achieve high turndown (∼50% of rated throughput) over time periods of ∼24 h. It remains possible, however, that two distillation columns could be required in parallel to fully realise dynamic operation of the DAC-PtM.
The cost of methanol production via DAC-PtM was considered through the capital expenditure (CAPEX) of erecting the facility, and the operating expenditure (OPEX) of daily DAC-PtM operation. The dominant source of expenditure for the plant results from electricity consumption, given the high reliance on electricity for fans in LT-DAC, electrolysis, and compressors. In other analyses of power-to-X processes, the translation of electricity usage to OPEX is based on a purchased cost of grid electricity, i.e. electrical OPEX [$ per kg] = electricity usage [MW h kg−1] × purchased price [$ per MW h]. If DAC-PtM uses only grid electricity, the capital cost of electricity generation does not contribute to the plant CAPEX; the assessments then rely on one value for cost of grid-integrated renewable electricity, obfuscating the results and making them liable to underpredictions. The modelling presented here considered the provision of electricity as part of the DAC-PtM facility, for which the notion of a purchased electricity price ceases to be applicable. Hence, we decomposed the cost of electricity into the two components: (i) wind farm OPEX (e.g. for maintenance of the turbines and wind farm infrastructure) and (ii) wind farm CAPEX (i.e. from building the wind farm).
The capital cost of installing the wind farm was calculated using eqn (4), which assumes a linear scaling of installed wind farm capital cost according to the nameplate capacity, as observed for real-world projects above 50 MW in size;42 the required wind farm sizes for all our DAC-PtM variants range from 50 to 90 MW.
| Wind farm cost [$] = Pnameplate [kW] × unit cost [$ per kW]. | (4) |
The capital cost for installation of offshore wind turbines differs versus onshore turbines.43 In 2018, the global average installed cost (turbines, supporting infrastructure, and installation) of an onshore wind farm was $1500 per kW, down from $1900 per kW in 2010; most projects had costs in the range $1100 up to $2500 per kW.44 Over the same time period, the average installed cost of offshore wind farms remained steady at between $4300 and $4500 per kW44 with many projects experiencing cost overruns.45 By 2030, the installed cost of onshore wind is forecast to fall to $800–1350 per kW, while offshore wind to $1700–3200.44,46
Offshore wind farms also incur higher operational and maintenance (O&M) costs than typical onshore farms,43,45 although the exact values are subject to uncertainty. The operational cost of an offshore wind farm was recently estimated as $22 per MW h,47 with another study estimating $31 per MW h.48 However, other work by Ederer49 gives much lower O&M costs for offshore farms, also finding the costs to be largely invariant with wind farm size above 60 MW but depending more on the distance from shore. They found that O&M costs rose from $35 per kW year (equivalent to $4 per MW h) to $57 per kW year (equivalent to $6.50 per MW h) when the distance from shore rose from 5 to 20 km. Wiser & Bolinger,42 in a survey of real-world onshore wind farm projects from 2000 to 2018, found O&M costs broadly in the range $30 to $50 per kW year ($1.50 to $5.75 per MW h), and have subsequently forecast very little future decrease.50
In modelling the installed cost of the wind farms, we took the middle-range 2030 values42 for a base case scenario, with the lower-bound of the 2030 predicted values taken as an optimistic case. The upper-bound of current project costs42,45 were taken as a pessimistic case. Realistically, the installed and operational costs of wind farms show a substantial geographical variation,43 although the globally-averaged cost values, used here, are appropriate given that we also average wind power performance across the worldwide locations.
The capital costs of the PEM and LT-DAC units were also assumed to scale linearly with size, given the modular nature of their construction.51,52 The range of potential costs of the LT-DAC system was taken from a recent review,52 in which the installation cost was estimated as $800 per tonne of CO2 captured annually, with an upper cost of $1350. Reduction to capital costs of ca. $300 per tonne of CO2 captured per annum have been suggested.53 The installation cost of the PEM electrolyser stack was scaled according to the input electrical power requirement. Recent reviews51,54 give costs from $360 to $840 per kWinput for PEM systems in 2030, with current costs of $1000 to $1200 per kWinput. Other authors9 have suggested higher current installation costs of $1500–2200 per kWinput.
The fully developed model of the DAC-PtM plant was varied to consider three optimism cases: (1) base case, (2) optimistic case, and (3) pessimistic case. The three cases differ in the performance of onshore and offshore wind farms, the cost of erecting and operating them, as well as changes to the DAC-PtM process, such as: (1) reductions in the energy requirements and installation costs of LT-DAC and PEM electrolysis; (2) improvements in catalyst selectivity towards methanol, methanol yield, and longevity; (3) changes in operating pressures and the performance of compressors and turboexpanders (e.g. isentropic efficiency). A summary of the key differences between the three optimism cases is given in Table 3. A full overview of all model assumptions is provided in Section S11.2 of the ESI;† all parameters used to calculate the OPEX and CAPEX for the whole DAC-PtM plant are given in the Tables S8 and S9 (ESI†), respectively.
| Parameter | Base | Optimistic | Pessimistic | Ref. |
|---|---|---|---|---|
| a Selectivity to MeOH for the base and pessimistic cases is estimated using the Bussche and Froment kinetic model36 (Section S11.1 in the ESI) whereas the optimistic case represents a potential state-of-the-art catalyst.55 b The optimistic case assumes that the required heat duty can be performed by some waste heat source; whereas the base and pessimistic cases require that the heat is provided within the DAC-PtM plant by electrical heating. | ||||
| Onshore wind farm | ||||
| Onshore wind farm OPEX [$ MW he−1] | 3.5 ± 2 | 1.5 ± 0.5 | 7 ± 4 | 43 and 50 |
| Installation cost of onshore wind farm [$ kWe−1] | 1100 ± 250 | 800 ± 100 | 2100 ± 400 | 45 and 50 |
| Offshore wind farm | ||||
| Offshore wind farm OPEX [$ MW he−1] | 22 ± 5 | 5 ± 2 | 31 ± 5 | 47–49 |
| Installation cost of offshore wind farm [$ kWe−1] | 2500 ± 500 | 1700 ± 200 | 4200 ± 500 | 44 and 45 |
| PEM electrolysis | ||||
| PEM electrical req. [kW he kgH2−1] | 52.5 ± 2.5 | 43.8 ± 2.0 | 62.7 ± 2.5 | 9 and 56 |
| Installation cost of PEM system [$ kWe−1] | 600 ± 200 | 360 ± 40 | 1800 ± 400 | 9 and 54 |
| Lifetime of PEM system [years] | 6 | 15 | 2 | 14 |
| LT-DAC | ||||
| LT-DAC electrical req. [kW he kgCO2−1] | 0.25 ± 0.07 | 0.15 ± 0.02 | 0.40 ± 0.05 | 52 and 57 |
| LT-DAC heat req.b [kW hth kgCO2−1] | 1.4 ± 0.25 | 1.0 ± 0.20b | 2.0 ± 0.35 | 52 and 57 |
| Installation cost of LT-DAC system [$ tnCO2−1 p.a.] | 800 ± 150 | 300 ± 200 | 1300 ± 250 | 52 and 53 |
| Reserve storage | ||||
| Battery storage [$ kW he−1] | 210 ± 90 | 130 ± 40 | 250 ± 100 | 35 |
| H2 storage tank [$ kgH2−1] | 560 ± 30 | 400 ± 70 | 730 ± 150 | 58 and 59 |
| CO2 storage tank [$ kgCO2−1] | 18 ± 3 | 14 ± 2 | 26 ± 4 | 60 |
| Other process parameters | ||||
| Isentropic efficiency, η | 85% | 90% | 70% | 61 |
| Operating pressure for methanol synthesis [bar] | 75 | 50 | 100 | 9 |
| CO2 conversion, X | 15 ± 2% | 40 ± 5% | 10 ± 1% | 62 |
| MeOH selectivity, Sa | 65 ± 3% | 99 ± 0.5% | 60 ± 5% | 36 and 55 |
| MeOH yield, Y [molMeOH kgcat−1 h−1] | 16 ± 3 | 40 ± 5 | 8 ± 1 | 55 |
Owing to the dynamic plant operation, the day-to-day plant OPEX varied according to the number of operational reactors each day. Consequently, the plant OPEX was determined for each operational state (i.e. 1, 2, 3, or 4 reactors), and then summed over an entire year according to the number of operational reactors each day. Further detail is provided in the Section S11.3 (ESI†).
Determination of methanol selling price
The minimum selling price of methanol was determined via a net present value (NPV) calculation, as shown in eqn (5), where the selling price ensures a specified rate of return on capital investment, r, over an economic lifetime of 15 years, such that the NPV became zero.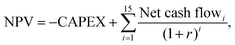 | (5) |
The incoming revenue for DAC-PtM also included the potential sale of CO2 or H2 produced, or the direct sale of surplus electricity to the grid. The latter was the primary consideration, for which we assumed that the surplus electricity was stored in batteries for later sale to the grid at a pre-agreed price. The use of battery storage was motivated by the fact that the periods of electricity surplus (e.g. windy days) may not correspond with times of high demand from the grid. In the base case, electricity was sold at $50 per MW h, and in the optimistic and pessimistic cases at $60 and $25 per MW h, respectively. Additionally, in the pessimistic case we assumed that only 50% of the surplus electricity can be sold due to insufficient demand from the grid (e.g. if the plant's wind-farm electricity were less attractive than other grid-integrated renewables).
The rate of return, r, was set as the weighted average cost of capital (WACC), which considers the breakdown of project financing – e.g. the cost of debt and equity. The WACC was adjusted between the three cases – 5% for base case, 4% for the optimistic case, and 7% for the pessimistic case – representing a typical spread of values of chemical production and renewable energy projects.63,64 Reduction of the WACC – which could be achieved by increased financing via state-backed loans rather than equity63 – acts to reduce the burden of capital cost within the methanol selling price. Further information on the NPV calculation is given in Section S12 of the ESI.†
As a benchmark, we also consider the selling price of methanol if produced from grid electricity rather than wind power, obviating any intermittency issues. Grid electricity decreases the plant CAPEX, given that the wind farm is no longer included as part of the DAC-PtM facility. However, the OPEX contribution increases as now electricity is purchased at the wholesale price (which we take as $50, 35, and 65 per MW h for the base, optimistic, and pessimistic cases, respectively.65,66
Life cycle assessment and the effective cost of net CO2 capture
An environmental impact assessment was performed over the cradle-to-gate life cycle for 1 tonne of MeOH. Similar to the techno-economic analysis, the base, optimistic, and pessimistic cases were assessed for both onshore and offshore wind under Strategies 1 and 2, then compared against the grid electricity scenario (with no intermittency). The assessment translated the material and energy inputs from the process model into the environmental impact score, global warming potential (GWP), by means of emission factors at the midpoint level via the ReCiPe 2016 method67 using the life cycle assessment standards (ISO 14040 and 14044 series).68 All emission factors of the life cycle inventory for each case, including raw materials and electricity generation, are summarised in Table S12 in the ESI.† The responsibility for GWP arising from the process was assigned solely to the methanol, not the oxygen by-product, and all remaining environmental impact categories of the ReCiPe method are excluded from this work for simplicity.For the wind-powered DAC-PtM scenarios, the life cycle emissions associated with onshore and offshore wind were incorporated in the analysis. In considering the emission intensity of grid electricity provision, three potential grid mixes were applied in the LCA: (1) a European average grid mix, comprising approximately 35% grid-integrated wind, solar, and hydro power but still with a strong (ca. 40%) reliance upon fossil fuels;69,70 (2) a Brazilian grid mix, in which around 69% of electricity generation is hydroelectric and 11% is from wind and solar power;70,71 (3) a Chinese grid mix, for which 64% of electricity generation is from coal power but with approximately one quarter of the mix being wind, solar and hydro power.70,72
The system boundary of the LCA includes the acquisition of all raw materials and the electricity requirements of the DAC-PtM process until the MeOH product arrives at the factory “gate” before final use. The common raw materials across all cases are copper and zinc oxide on alumina support as the catalyst, and water for electrolysis (see Table S12 in the ESI†). A once-through cooling system is assumed for the process, i.e. the warmed-up cooling water is discharged to a nearby body of water after use and no emissions are associated with the acquisition of cooling water or its re-cooling. The CO2 uptake by DAC was treated as a sink of carbon (i.e. negative CO2,eq. emissions); however, the analysis only assigned credit for the carbon content in the final methanol product, constrained by reaction stoichiometry as 1374 kgCO2eq. per tMeOH for all investigated cases.
Finally, we combined the findings of our LCA and techno-economic analysis to determine the effective cost of net carbon uptake by DAC-PtM according to eqn (6).
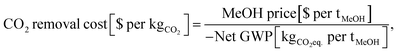 | (6) |
Results
Power-to-methanol production
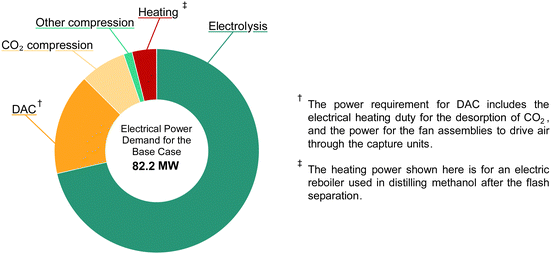
The total electrical power demand of the DAC-PtM facility, at full capacity and under the base case, is given in Fig. 8. The demand of 82.2 MWe, compared against the annual production capacity of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes of methanol (equivalent to 31.6 MWth in methanol on a lower heating value basis) gives an overall power-to-methanol efficiency, ηPtM, of approximately 40%, in agreement with previous studies.14 The electrolysis of water to produce H2 is the dominant electricity requirement, ranging from 70 to 85% of the total power across the three cases. Therefore, reducing the energy requirement of water electrolysis in the optimistic case (Table 3) drastically improves the DAC-PtM efficiency. Low-temperature direct air capture (LT-DAC) of CO2, considered here, has the second highest power demand after electrolysis. The large fan assemblies, to pull in sufficient air, represent a substantial electricity demand (1 to 4 MWe). However, the regeneration of the solid sorbent, by heating to 100 °C for desorption of CO2, dominates the operational duty for LT-DAC (10 and 20 MWth of thermal power). Waste heat usage is often discussed for LT-DAC;2,52 however, assuming universally available – and readily usable – waste heat is generous, particularly if locating DAC-PtM away from pre-existing process facilities. For the base and pessimistic cases, we provide the regenerative heat for LT-DAC via electrical heating; whereas, the optimistic case assumes that waste heat is available. Similarly, the reboiler was heated electrically for the distillation of methanol from water under the base and pessimistic cases; on-site steam was assumed as available in the optimistic case instead.
000 tonnes of methanol (equivalent to 31.6 MWth in methanol on a lower heating value basis) gives an overall power-to-methanol efficiency, ηPtM, of approximately 40%, in agreement with previous studies.14 The electrolysis of water to produce H2 is the dominant electricity requirement, ranging from 70 to 85% of the total power across the three cases. Therefore, reducing the energy requirement of water electrolysis in the optimistic case (Table 3) drastically improves the DAC-PtM efficiency. Low-temperature direct air capture (LT-DAC) of CO2, considered here, has the second highest power demand after electrolysis. The large fan assemblies, to pull in sufficient air, represent a substantial electricity demand (1 to 4 MWe). However, the regeneration of the solid sorbent, by heating to 100 °C for desorption of CO2, dominates the operational duty for LT-DAC (10 and 20 MWth of thermal power). Waste heat usage is often discussed for LT-DAC;2,52 however, assuming universally available – and readily usable – waste heat is generous, particularly if locating DAC-PtM away from pre-existing process facilities. For the base and pessimistic cases, we provide the regenerative heat for LT-DAC via electrical heating; whereas, the optimistic case assumes that waste heat is available. Similarly, the reboiler was heated electrically for the distillation of methanol from water under the base and pessimistic cases; on-site steam was assumed as available in the optimistic case instead.
Taking all differences across the DAC-PtM cases (outlined in Section S11, ESI†), the power demand changes from 82.2 MWe (ηPtM = 38%) in the base case to 55.7 MWe (ηPtM = 57%) and 101.7 MWe (ηPtM = 31%) in the optimistic and pessimistic cases, respectively, driven largely by changes in the electricity demand of PEM electrolysis and LT-DAC. Full breakdowns of power consumption are provided in Table S10 in the ESI,† for each of three cases at full methanol production capacity.
Methanol production costs for dynamic operation of multiple reactors
The OPEX and CAPEX values are shown for the dynamic operation of DAC-PtM under Strategy 1 (“minimise storage”) in Fig. 9 and for Strategy 2 (“maximise production”) in Fig. 10. The OPEX contributions correspond almost exactly to the power breakdown in Fig. 8, illustrating the heavy reliance of DAC-PtM upon electricity. The operating and capital expenditures are higher for the offshore than for the onshore wind farms (cf.Fig. 9 and 10a, c), as was also found by Choe et al.73 in a comparative study on power-to-fuel production. The installed cost of the wind farm is the largest capital cost in all instances, at anywhere between 30 and 60% of the total. Larger installed costs of offshore against onshore farms (Table 3) primarily drive the higher CAPEX for DAC-PtM reliant on offshore instead of onshore wind power (Fig. 9b and d and 10b and d). Reserve storage (batteries and compressed gases) contributes around 10 to 20% of the CAPEX under Strategy 1 (“minimise storage”), rising to 30 to 50% for the more storage-dependent Strategy 2 (“maximise production”). Changes in the reserve storage requirement for offshore versus onshore sites (Table 2) also have a small effect (ca. 2 to 4%) on CAPEX.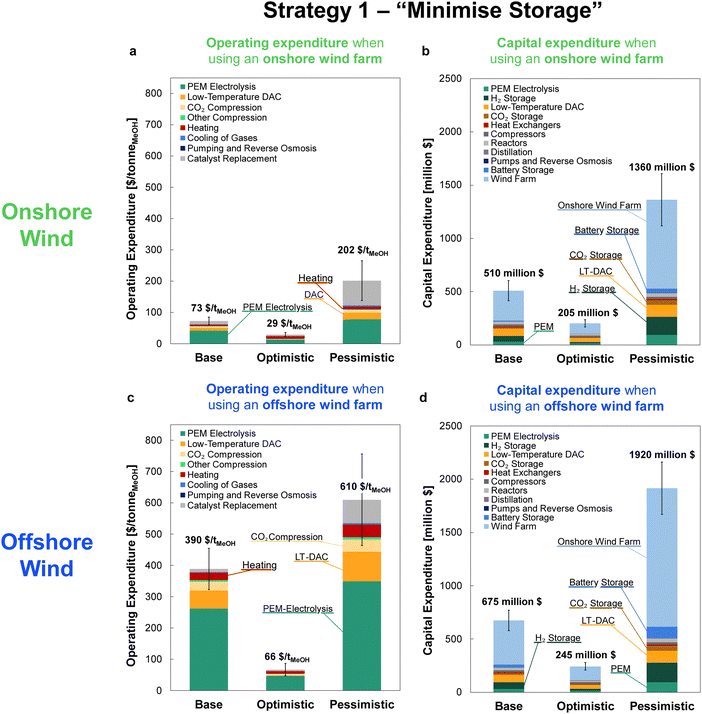 | ||
| Fig. 9 The costs of methanol production via DAC-PtM, operating under Strategy 1 (“minimise storage”) for the three optimism cases: base, optimistic, and pessimistic. (a) The operating expenditure (OPEX) with an onshore wind farm. (b) The capital costs (CAPEX) when reliant on an onshore wind. (c) The OPEX with an offshore wind farm. (d) The CAPEX with an offshore wind farm. The contributions are stacked as ordered in the legend, starting with PEM electrolysis at the base. Significant contributions are also labelled on the graphs. Error bars are provided, according to the estimated uncertainty in model parameters, detailed in Section S11 (ESI†). | ||
 | ||
| Fig. 10 The costs of methanol production via DAC-PtM when operating under Strategy 2 (“maximise production”) for the three optimism cases: base, optimistic, and pessimistic. (a) The operating expenditure (OPEX) with an onshore wind farm. (b) The capital costs (CAPEX) for the DAC-PtM facility when reliant on an onshore wind. (c) The OPEX with an offshore wind farm. (d) The CAPEX for the DAC-PtM facility with an offshore wind farm. The contributions are stacked as ordered in the legend, starting with PEM electrolysis at the base of the bars. Significant contributions are also labelled on the graphs. Error bars are provided for the OPEX and CAPEX, according to the estimated uncertainty in model parameters, detailed in Section S11 (ESI†). | ||
The values of OPEX are lower for Strategy 2 than Strategy 1 under comparable modelling cases – e.g. $390 vs. $264 per tonne of MeOH for the base case with offshore wind under Strategies 1 and 2, respectively. Operation under Strategy 2 leads to the process regularly withdrawing CO2 and H2 from storage, which in itself does not incur any operational costs, in order to maximise the production of methanol; hence, the operational costs per unit methanol produced become lower, on average, than under Strategy 1.
Comparing across the three optimism cases underlines the interplay of process modelling assumptions and wind power performance in determining the costs of DAC-PtM. The decrease in PEM electrolysis demand taken in the optimistic case (from the base value of 52.5 down to 43.8 kW he kgH2−1) primarily drove the reduction in DAC-PtM power demand. When coupled with more optimistic installation costs for the wind farms, the DAC-PtM CAPEX fell by around 2.5 times between the base and optimistic cases. The availability of waste heat further reduced the DAC-PtM electricity demand, evidenced by the lower share of LT-DAC in the OPEX for the optimistic cases in Fig. 9a and c and 10a and c. Conversely, the pessimistic cases show the potential for drastic increases in CAPEX (2.5–3 times) if sub-optimal process performance (e.g. lower PEM efficiency, increased DAC electricity demand, and reduced turbomachinery efficiency) becomes compounded by an expensive wind farm with low power stability.
Changes to the catalysts for methanol synthesis were also included across the optimism cases. The incumbent catalysts, copper and zinc oxide on an alumina support, remain the best available choice for methanol synthesis, but were designed for converting syngas (predominantly CO and H2) to methanol.9 The methanol yield is inferior with the CO2 and H2 feed-stock used in DAC-PtM;11 deactivation by sintering also remains a problem when current copper-catalysts support methanol synthesis from CO2.74 Research into alternative catalysts is ongoing.14,75 Here, the catalyst performance and lifetime were varied between the three cases. The base case applied the pre-existing Bussche and Froment rate model for methanol synthesis over Cu–ZnO catalysts,36 and current estimates for catalyst lifetime and cost;9 the pessimistic case considered faster catalyst deactivation (see Table S8 in the ESI†). The optimistic case assumed a new catalyst able to deliver equivalent methanol synthesis performance to that observed when using syngas over Cu–ZnO catalysts – namely high selectivity to methanol (ca. 99%), meaning less CO by-product to handle, and resistance to deactivation.
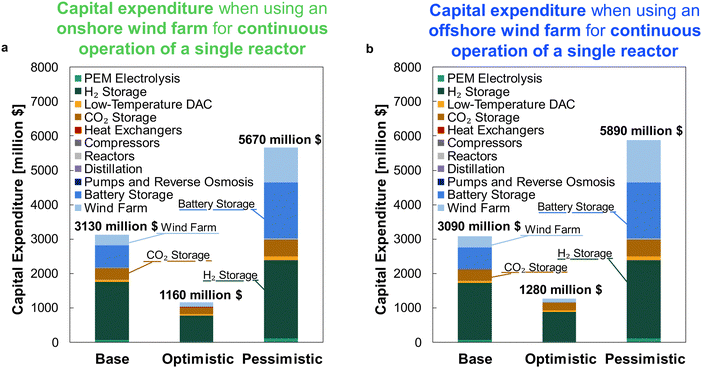
For comparison against the dynamic operation of multiple reactors, Fig. 11 shows the CAPEX for continuously operating wind-powered DAC-PtM with one large reactor. Reserve storage becomes the dominant source of capital expenditure – approximately $2500 ± 1500 million across the optimism cases – owing to the much larger consumption of stored reserves to operate the large reactor continuously (Section S6 in the ESI†). The dynamic operation of multiple reactors therefore drastically reduces the capital costs incurred by DAC-PtM, by approximately 3 to 4 times.
Methanol selling price
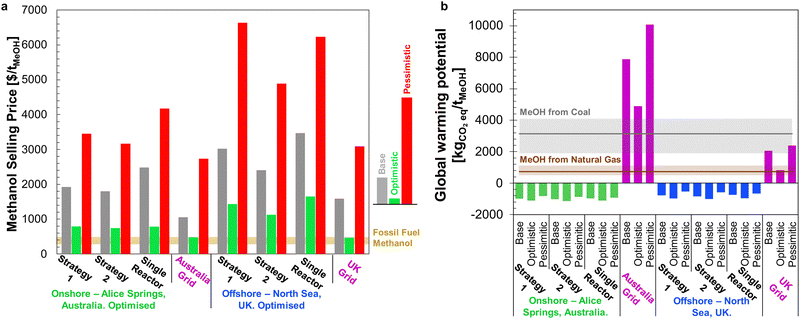
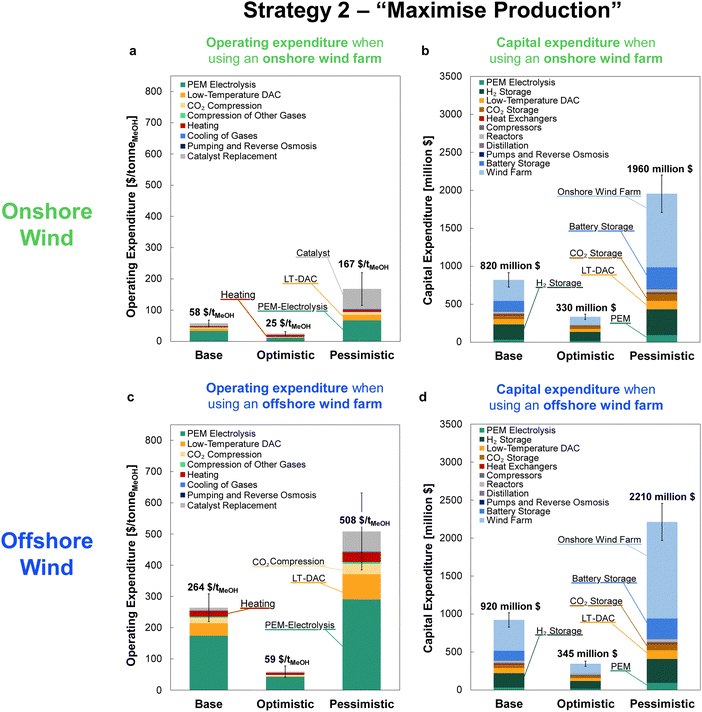
The minimum selling prices of methanol are shown in Fig. 12 under all investigated scenarios for the three optimism cases, using either onshore or offshore wind power. Comparison of the four-reactor DAC-PtM against a single, large reactor underlines the benefits of dynamic operation for managing intermittency. The huge storage requirement to operate a single, large reactor continuously renders DAC-PtM wholly infeasible even under optimistic assumptions (Fig. 12). The removal of all storage, thereby trading a ca. 3/4 reduction in capital cost for a CFplant of order just 50% (Section S7 in the ESI†), does reduce the selling price substantially – to around $1700 per tMeOH under the base case – but is still out-performed by the four-reactor DAC-PtM with onshore wind. Moreover, complete shut-down of the DAC-PtM plant during low wind power availability, as necessitated by removing all storage and operating without grid power, also poses numerous operational challenges (e.g. distillation column shut-down and start-up) which the multi-reactor dynamic operation framework avoids.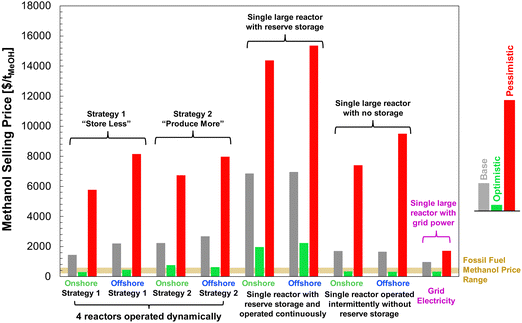 | ||
| Fig. 12 The methanol selling price from DAC-PtM under all investigated scenarios and optimism cases. For each scenario, moving left to right, the bars are ordered: base, optimistic, pessimistic. The range of methanol price, when derived from fossil fuel, is also shown for comparison.76,77 | ||
Across all scenarios of wind-powered DAC-PtM, the cost of capital dominates between 85 and 95% of the methanol selling price. Hence, the reduction of CAPEX, namely through a smaller wind farm with high CF and a stable power output to minimise storage, has a drastic effect in reducing methanol selling price – evidenced by the 3 to 5-fold decrease between base and optimistic cases. Strategy 1 (“minimise storage”) produces methanol at lower cost than Strategy 2 (“maximise production”), because the increased annual production of methanol (i.e. higher CFplant) under Strategy 2 does not outweigh the capital cost of storage required to achieve the boosted production versus Strategy 1.
Despite superior wind farm capacity factors, offshore wind yields methanol at greater cost than onshore wind. For the optimistic case, the selling price of methanol from onshore wind falls to $310 per tMeOH under Strategy 1, which outperforms the grid-derived methanol price of $340 per tMeOH – both reach parity with the typical fossil fuel-derived methanol price of ca. $300–500 per tonne.76,77 Offshore wind-powered DAC-PtM is also appealing under optimistic assumptions (selling price of $450 per tMeOH under Strategy 1).
Selling the oxygen by-product from electrolysis (ca. 1.5 kg of O2 per kg of MeOH) yields only $60 per tMeOH under the base case or $80 per tMeOH in the optimistic case, assuming a direct over-the-fence sale of the O2 at 20 bar, taking wholesale O2 prices.78 Prior work79 has reported O2 from electrolysis as having a purity comparable to cryogenic O2, with suitability for medical applications which could attract a higher selling price. A recent study80 has also suggested only a marginal additional cost of O2 post-processing (e.g. liquefaction) relative to the cost of electrolysis. Nevertheless, research examining the applications of O2 derived from electrolysis remains nascent and further work is required to appreciate the necessary distribution and intermediate storage infrastructure for integrating DAC-PtM with O2 consumers.
Life cycle assessment and the effective cost of carbon capture
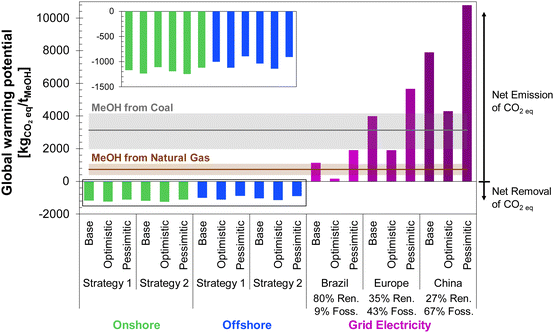
The global warming potential (GWP) for each DAC-PtM scenario investigated is shown in Fig. 13, alongside literature results for MeOH produced from syngas, either from natural gas13,81–84 or coal81,83–85 (see Table S11, ESI†). All emission factors used in the LCA are summarised in Table S12 (ESI†). A breakdown of all the contributions to the overall GWP of wind-powered DAC-PtM is provided in Tables S13 and S14 (ESI†) for grid-powered DAC-PtM.The results in Fig. 13 demonstrate that all wind-powered cases achieve a net-negative carbon intensity, with a GWP between −760 and −1240 kgCO2eq. per tMeOH. The substantial net uptake of CO2 is attributable to drawdown by DAC of atmospheric CO2 to produce methanol (1374 kgCO2 per tMeOH, according to reaction stoichiometry), coupled with the low carbon intensity of wind power. However, the lower embedded emissions of erecting an onshore wind farm (11 kgCO2eq. per MW h) lead to 8 to 18% larger net CO2 drawdown compared to offshore wind, despite the higher CF of the offshore sites, owing to the substantial foundational works at sea with embedded emissions of 25 kgCO2eq. per MW h.
Employing grid-power for DAC-PtM switches the process from a net-negative GHG intensity (CO2 drawdown) to a net CO2 emission across all investigated circumstances. The magnitude of the emissions depends on the energy mix of the electricity grid; the European and Chinese grids both remain heavily dependent on fossil fuels (39% and 67%, respectively), leading to DAC-PtM emissions comparable to, or exceeding, those of MeOH from natural gas or coal. In contrast, a DAC-PtM plant located in Brazil, with an 80% share of renewables in the electricity mix, results in a GWP comparable to or lower than GWP of MeOH produced directly from natural gas, although only for the base and optimistic cases. While the carbon intensity of the Brazilian grid is taken here as 155 kgCO2eq. per MW h, another study reported 130 kgCO2eq. per MW h, which would give a net-negative GWP of −105 kgCO2 per tMeOH for the optimistic case. Therefore, grid-powered DAC-PtM can offer the potential for net-negative carbon intensity, free of intermittency constraints, but only if the grid portfolio is dominated by renewable power sources.
Combining the LCA with the estimated costs in Fig. 13, the effective costs of net CO2 capture were determined according to eqn (6) and are summarised in Table 4, alongside the estimated methanol selling prices for the onshore and offshore wind-powered DAC-PtM. In utilising offshore wind power for DAC-PtM, the increased installation costs and embedded emissions compound one another, leading to markedly higher effective costs of net CO2 capture compared to onshore wind-powered DAC-PtM. When the achievable net CO2 drawdown (assessed with LCA) is below 1 tCO2eq. per tMeOH (∼70% of the 1.374 tCO2eq. per tMeOH molar ratio from reaction stoichiometry) – as in the base case offshore wind-powered DAC-PtM under Strategy 2 (see Table S13, ESI†) – the cost of net CO2 capture (eqn (6)) becomes higher than the selling price of MeOH, underlining that successful CCU must balance minimising the cost of DAC-PtM and maximising the CO2 drawdown.
| Cost of net CO2 capture [$ per tCO2] | Selling price of MeOH [$ per tMeOH] | |||||
|---|---|---|---|---|---|---|
| Base | Optimistic | Pessimistic | Base | Optimistic | Pessimistic | |
| Onshore Strategy 1 | 1268 | 248 | 5929 | 1440 | 305 | 5778 |
| Onshore Strategy 2 | 2301 | 675 | 8886 | 2231 | 753 | 6743 |
| Offshore Strategy 1 | 1985 | 361 | 7896 | 2202 | 447 | 8148 |
| Offshore Strategy 2 | 2778 | 551 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
2678 | 625 | 7978 |
With regards to the cost of solely performing DAC, independent of methanol synthesis, a recent study by Gutsch and Leker86 examined DAC with carbon sequestration (DACCS) when operating dynamically with off-grid solar PV power, estimating an optimised net CO2 removal cost of $877 per tCO2, falling to $216 per tCO2 with technology improvement and favourable project financing. Standalone DACCS, therefore, does capture CO2 at a lower net cost than DAC-PtM (Table 4), although the cost range reported by Gutsch and Leker remains far above even the highest current CO2 prices of ca. $100 per tCO2.87 Hence, the implementation of DACCS alone may prove challenging, especially if encumbered by limited access to suitable sequestration sites. Therefore, DAC-PtM can assist in the implementation and refinement of DAC at scale, also yielding a methanol product with numerous uses, both pre-established and developing.
Site-specific optimisation of plant design
The findings summarised in Fig. 12 and 13 demonstrate the utilisation of multiple reactors as an effective solution to mitigate the effects of intermittency upon renewably powered DAC-PtM, while delivering a substantial net capture of CO2. To fairly investigate our proposal for dynamic operation, the earlier analysis (results shown in Fig. 4–13) considers the global spread in wind power performance and installation costs, demonstrating a general approach, open for further optimisation. For example, Fig. 4 and 5 reveal that, for some locations, the storage level remained nearly full across a year, thus resizing would be the next step in the second-pass design.Here, we exemplify a further optimisation of the dynamic DAC-PtM process, accounting for the wind power performance and costs, taking one offshore and one onshore location. The considered offshore location in the North Sea, approximately 300 km Northeast from Teeside in the UK, achieved one of the highest plant capacity factors among offshore farms (Table S5 in the ESI†); similarly, the location at Alice Springs, near the centre of Australia, was the among the best performing onshore locations under Strategies 1 and 2 (Table S5 in the ESI†). Given the high quality of cost information and life cycle inventory data for wind power at these two locations (discussed further in Sections S15.3 and S15.4 of the ESI†), we were able to refine our calculations, to reach site-specific conclusions. The full methodology is outlined in Section S15.1 of the ESI;† the key aspects are as follows:
(1) The storage is resized to the minimum capacity needed for continuous operation and wind conditions across 2016–2020 – i.e. the storage was as a small as possible without the level falling below 1% of capacity across the 5-year period.
(2) The tolerance of operability of reactors for methanol synthesis was relaxed, allowing operations down to 80% of the nominal capacity before requiring shut-down or the utilisation of reserve storage. Prior work has suggested tolerance of such reactors to 20% perturbations in operating throughput.88
(3) The battery sizing was adjusted to storing only the reserve electricity required to operate the DAC-PtM, thus, removing the intermediate storage of surplus electricity for selling to the grid. Given the marginal contribution of electricity surplus sales to overall process viability, the extra cost of battery storage was deemed an unnecessary expenditure.
The outcomes of the optimisation procedure are summarised in Table 5, listing the revised storage sizes, available electricity surpluses, and the resultant plant capacity factors under Strategies 1 and 2, also re-considering a single reactor operated continuously. In Fig. S7 in the ESI,† we show daily storage levels tracked continuously across 2016 to 2020 at both locations, illustrating the optimality of the new storage sizing. After optimisation, the required size of reserve storage for Strategies 1 and 2 becomes comparable, aided by allowing the reactors to operate down to 80% load. The storage requirement to operate a single reactor is also reduced, substantially so for the Alice Springs site (23 days vs. 70 days prior to optimisation); however, continuous operation of the single reactor still requires markedly more reserve storage than the multi-reactor configuration (3–6 days).
| Alice Springs, Australia | North Sea, United Kingdom | |||||
|---|---|---|---|---|---|---|
| Strategy 1 | Strategy 2 | Single reactor | Strategy 1 | Strategy 2 | Single reactor | |
| a Under the base case modelling assumptions. The reserve electricity requirement of the DAC-PtM is sensitive to the assumed performance of sub-systems such as compressors, and so varies according to modelling optimism, see Section S11 in the ESI. | ||||||
| Reactor wind farm capacity factor | 36.5% | 36.5% | 36.5% | 58.6% | 58.6% | 58.6% |
| PtM plant capacity factor | 79.5% | 87.2% | 91.4% | 76.6% | 82.9% | 92.1% |
| Max. reactor standby duration [days] | 8 | 7 | 0 | 19 | 10 | 0 |
| Storage required [days equivalent] | 3.2 | 5.5 | 22.7 | 3.3 | 4.5 | 62.7 |
| CO2 storage required [tonnes] | 168 | 393 | 1,190 | 173 | 236 | 3287 |
| H2 storage required [tonnes] | 24 | 42 | 171 | 25 | 34 | 472 |
| Battery size [MW h]a | 23 | 40 | 164 | 24 | 33 | 453 |
| Surplus elec. [MW hsurp/MW hgen] | 0.219 | 0.174 | 0.087 | 0.213 | 0.176 | 0.079 |
Estimates of the maximum period for which a reactor could be held in a standby mode (i.e. not producing MeOH) are also shown in Table 5. Operation under Strategy 1, whereby the number of operational reactors is deliberately curtailed to hold the plant power demand at or below the available wind power, results in longer idle periods for reactors than Strategy 2. In the case of the single reactor, operated continuously at variable throughput with the support of reserve storage, no standby days arise from a lack of available wind power; however, reactor downtime would still be required for maintenance. Such operations could instead be performed during the idle periods inherent to operation under Strategies 1 and 2, although the need to depressurise and purge any equipment (to make ingress safe for engineers) would complicate the downtime procedure. Prolonged standby of reactors could also cause catalyst deactivation, however a dynamic nature multi-reactor configuration facilitates toggling between operational reactors to avoid long periods of inactivity in a given reactor.
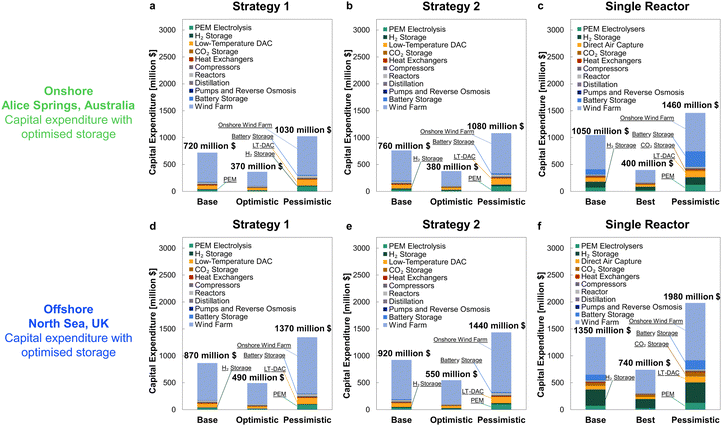
After applying the optimised outcomes from Table 5 and location-specific costs of wind farm installation, the revised capital expenditures are given in Fig. 14. The contribution of reserve storage is drastically reduced following the optimisation, particularly so for Strategies 1 and 2, for which the capital costs become overall comparable (cf.Fig. 9, 10 and 14). Even after optimisation, the cost of storage required to sustain continuous operation of a single, large reactor outstripped the multi-reactor configuration for both sites, but without drastically improving the resulting plant capacity factor (Table 5).
Comparing both locations, the considerably higher capacity factor within the North Sea – 58.6% vs. 36.5% for Alice Springs, which allows for a ∼40% smaller wind farm – still gives substantially higher installation costs across all scenarios. Expensive installation of offshore wind farms is particularly pronounced in the North Sea89 because of the long distance from shore and the need for extensive foundations in such deep waters.
Taking the estimated capital costs in Fig. 14, combined with operating costs for the optimised plant configurations and plant capacity factors, the selling prices of MeOH at each site are compared against operating DAC-PtM powered by local UK or Australian electricity grids in Fig. 15a. As for the global analysis (Fig. 12), dynamic operation of multiple reactors remains more cost-effective than operating DAC-PtM with a single, large reactor, even after optimisation. The optimisation does reveal, however, that Strategy 2 can achieve a lower selling price than Strategy 1 – as shown here for the Alice Springs onshore wind farm location across all three optimism cases. Owing to the comparatively high installation costs of wind farms in highly developed economies, such as the UK or Australia, the resulting methanol selling prices are above the globally averaged prices in Fig. 12.
Performing an LCA for the two locations (Sections S15.3 and S15.4 of the ESI†) yielded the GWP values shown in Fig. 15b. As in the global analysis (Fig. 13), wind-powered DAC-PtM again has a negative carbon intensity in all cases, although with a lower net CO2 capture for the offshore North Sea site than the Alice Springs location (between −1032 and −557 kgCO2eq. per tMeOH for the North Sea vs. −1158 to −862 kgCO2eq. per tMeOH for Alice Springs). For grid-powered cases, because the carbon intensity of the Australian grid is over three times higher than that of the UK (600 against 180 kgCO2eq. per MW h, respectively90,91), the grid-powered DAC-PtM at Alice Springs leads to CO2 emissions of 4900–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 kgCO2eq. per tMeOH, markedly worse than MeOH production from coal. The site-specific analysis presented here underlines the vast disparity in environmental impact between renewably powered and grid-reliant DAC-PtM; even the comparatively low carbon-intensity UK grid leads to a strongly positive net GWP of between 820–2400 kgCO2eq. per tMeOH.
100 kgCO2eq. per tMeOH, markedly worse than MeOH production from coal. The site-specific analysis presented here underlines the vast disparity in environmental impact between renewably powered and grid-reliant DAC-PtM; even the comparatively low carbon-intensity UK grid leads to a strongly positive net GWP of between 820–2400 kgCO2eq. per tMeOH.
Finally, combining the site-specific costs and LCA, we determined the cost of net CO2 capture for DAC-PtM under each wind-powered scenario (Table S19 in the ESI†), finding an optimised cost of $1760 per tCO2eq. at Alice Springs under the base case, falling to $655 per tCO2eq. under the optimistic modelling case; however, for the North Sea offshore wind farm, with higher production costs and larger embedded emissions, the effective cost rises starkly to around $3000 per tCO2eq. under the base case, only falling to a minimum of $1100 per tCO2eq. under the optimistic case.
Discussion
The prospect of DAC-PtM for carbon capture and utilisation
Methanol synthesis from CO2 has been investigated widely for the utilisation of captured carbon; however, most prior work has excluded the full costs and environmental impact of CO2 capture from their analysis, instead considering a pure stream of CO2 entering at their system boundary,13,92,93 focusing on performing capture from industrial point sources of CO2,93–96 or upgrading CO2 and H2 from biogas to MeOH.93,97 The combination of DAC with PtM has received less attention, with Bos et al.98 and Van Antwerpen et al.25 being two prominent exceptions.In Table 6, we summarise costs for PtM reported in published studies, drawing attention to the assumptions for sourcing power and CO2. We again emphasise that a clear distinction should be drawn between DAC and CO2 captured from industry – the utilisation of industrial point sources will, at best, serve to only abate further emissions, whereas DAC actively draws CO2 down from the atmosphere. Given the higher CO2 concentration in industrial flue gases, which makes capture less costly than DAC, the lower methanol costs for industrially coupled PtM shown in Table 6 are unsurprising. In the studies of Pérez-Fortes et al.92 and Nyari et al.,94 the low production costs also arise from their assumption of substantial carbon credits being paid (∼$300 per tonne of CO2) coupled with a ∼3-fold reduction in the price of on-demand green H2. The assumed source and price of electricity also add to the variation of methanol prices in Table 6. Notably, Bos et al.98 assumed access to grid-integrated wind power with 100% availability, thereby allowing continuous DAC-PtM at full capacity, leading to their very low selling prices. Daggash et al.76 also investigated DAC-PtM but using only the curtailed power from grid-integrated renewables (estimated as at most 2.5% of capacity), finding a selling price comparable to our base case for grid-powered DAC-PtM (Table 6). Van Antwerpen et al.,25 who accounted for the intermittency of wind and solar power erected for DAC-PtM, give estimates similar to our prices. The carbon credit (up to $100 per tCO2) incorporated by Van Antwerpen et al.25 helps explain their lower median cost estimates, and the increased range we report arises from our utilisation of data for worldwide selection of wind farm sites, both onshore and offshore, whereas Van Antwerpen et al.25 constrained their study to only onshore locations in Australia.
| Authors | CO2 source | Power source | Methanol cost [$ per tMeOH] |
|---|---|---|---|
| Pérez-Fortes et al. (2016)92 | Pure CO2 | Coal | 820 |
| Hank et al. (2018)93 | Biogas | Grid or wind | 680–1620 |
| Daggash et al. (2018)76 | DAC | Curtailed wind and solar | 960 |
| Harris et al. (2020)99 | Pure CO2 | Grid | 430–1610 |
| Nyari et al. (2020)94 | Flue gas | Grid | 760–922 |
| Adnan and Kibria (2020)13 | Pure CO2 | Grid | 430–1000 |
| Bos et al. (2020)98 | DAC | Grid-integrated wind | 325–870 |
| Chen et al. (2021)24 | Flue gas | Solar PV and wind | 1460–1490 |
| Kim et al. (2022)95 | Flue gas | Grid | 3690 |
| Moioli and Schildhauer (2022)97 | Biogas | Grid | 1300–1900 |
| Sollai et al. (2023)96 | Flue gas | Grid | 1040 |
| Van Antwerpen et al. (2023)25 | Flue gas | Solar PV or wind | 900–1300 |
| Van Antwerpen et al. (2023)25 | DAC | Solar PV or wind | 1140–1570 |
| This Study | |||
| 4 reactors, base case | DAC | Wind | 1440–2680 |
| 4 reactors, optimistic case | DAC | Wind | 310–750 |
| Single reactor, base case | DAC | Grid | 960 |
| Single reactor, optimistic case | DAC | Grid | 340 |
The sourcing of electrical power also determines whether PtM can deliver a net-negative carbon intensity, as our study underlines. Whilst purchasing grid power allows for continuous operation of DAC-PtM, the deleterious environmental consequences of doing so (Fig. 13) should eliminate grid-powered PtM as a viable option, for any CO2 source, unless the grid portfolio is almost entirely dominated by renewable energy. Otherwise, the methanol production must be directly integrated with renewable power, such as wind, for which our cradle-to-gate LCA shows a substantial net-negative GWP between −890 and −1250 kgCO2eq. per tMeOH for DAC-PtM. Our LCA is corroborated with Van Antwerpen et al.25 finding a carbon footprint of −873 kgCO2eq. per tMeOH. Adnan and Kibria13 found negative carbon intensity of around −570 kgCO2eq. per tMeOH for wind-powered PtM when excluding the capture stage from their system boundary, also estimating substantial positive net-emissions between 1200 and 1600 kgCO2eq. per tMeOH for PtM powered from the grid at a carbon intensity of 150 kgCO2eq. (roughly comparable to the UK grid considered in Fig. 15b).
In assessing DAC-PtM for CCU, however, the overall cradle-to-grave life cycle emissions of the methanol product are highly sensitive to the end-use, which we consider outside of our system boundary (cradle-to-gate), and therefore uncertain. The conversion of methanol to durable products (e.g. building and insulation materials, or paints and coatings) can achieve removal of atmospheric CO2 across the product lifetime, or longer with appropriate end-of-life handling, although the lifetimes of such products are poorly defined, ranging from a few years to multiple decades.100,101 Meanwhile, the utilisation of DAC-derived MeOH as a fuel or fuel additive can only approach carbon circularity (i.e. net-zero). Consequently, any comparisons of DAC-PtM against DAC with carbon sequestration (DACCS) must be cognisant of the varying timescales and permanence of carbon removal.
Operating challenges for dynamic DAC-PtM
The dynamic operation of multiple reactors provides a cost-effective and environmentally beneficial solution for implementing wind-powered DAC-PtM. But dynamic operation at industrial scale can present numerous challenges, especially around the frequent start-up and shut-down of methanol reactors. Our analysis suggests that across a year, the number of operational reactors will change on average 180 times if using onshore and 160 times for offshore wind power. Additionally, we estimate that an individual reactor may be held idle for 7 to 19 days (Table 5). Therefore, the reactors would spend approximately half of the year in a transitional or idle state.The reactor design employed in our analysis is based on the Lurgi reactor – commonly used for methanol synthesis, in which temperature is controlled by raising medium-pressure steam in a shell around tubes packed with a catalyst.102,103 The water-cooled configuration is superior for dynamic operation versus the alternative of gas-cooling, wherein the pre-heating of feed gas is directly heat-integrated with the reactor cooling. The raising of steam in the Lurgi design ensures continued cooling driven by thermosyphon convection of water104 even after the cessation of feed gas flow, as schematised by Fig. S8 in the ESI.† Varela et al.88 investigated the dynamic performance of the Lurgi reactor, finding attainment of steady state within 1.5 minutes of a 20% step change in hydrogen feed to the reactor. Information regarding the precise reactor start-up times is limited in the literature, although industrial reports describe entire methanol plant start-up from cold within three days with Lurgi reactors.105 Van Antwerpen et al.25 also report that idling synthesis reactors for ∼24 h is achievable with recirculation of the recycle loop. The available evidence suggests, therefore, good potential for dynamic operation of reactors over daily timescales, for which we propose the following operational program:
(1) Begin reactor shut-down by ceasing the feed of fresh CO2.
(2) Continue to circulate the recycle during the shut-down. The recycle ratio varies between 2 and 12 according to modelling optimism (i.e. the variation of MeOH single-pass yield), and so a substantial quantity of reactant gas is available in the recycle stream to sustain methanol synthesis after the cessation of fresh CO2 flow to the reactor.
(3) As CO2 and recycled CO diminish over time, the exothermic methanol synthesis reaction will slow down, and the reactor temperature begin to decrease.
(4) The reactor may then be flushed with H2, or inert ballast gas such as N2, and the outlet gas purged. The flow of fresh H2 to the reactor is then stopped, and the reactor held in a standby mode under H2 or the ballast gas. If using a ballast gas such as N2, an additional separation step, for example, with a pressure swing adsorption (PSA), might be necessary to provide an on-demand supply of N2, not currently included in our plant costings.
(5) To effect start-up, apply electrical heating to raise reactor temperature, and begin feeding fresh CO2 and H2.
In realising such a scheme of dynamic operation, catalyst stability is a key consideration. Experimental studies have shown progressive deterioration of the incumbent Cu–ZnO catalysts during daily start-up and shut-down conditions,106,107 whereas, the combination of Cu with ZrO2 remained stable under the same dynamic conditions (including exposure to H2 while being held in standby). Additionally, ZrO2-based catalysts improved the achieved selectivity towards methanol.107 At the scale of industrial reactors, modelling undertaken by Rezaie et al.108 estimated a ∼15% deterioration in MeOH production across 3 years of Cu–ZnO operation within a Lurgi reactor, which was supported by measured data for an industrial scale plant subjected to daily changes in operating load of ∼10%. Recent work by Masoudi et al.109 predicted similar deterioration of Cu–ZnO catalysts across three years under a CO2-rich synthesis gas (volumetric ratio CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO
CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 ≈ 1
H2 ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85
0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.5). However, further research is required to interrogate the dynamic operations at industrial scale and assess the potential for improved stability of new catalyst formulations (e.g. Cu–ZrO2).
6.5). However, further research is required to interrogate the dynamic operations at industrial scale and assess the potential for improved stability of new catalyst formulations (e.g. Cu–ZrO2).
Further optimisation and technology improvements for renewably powered DAC-PtM
At present, the cost of MeOH produced from wind-powered DAC-PtM is substantially higher than MeOH derived from fossil fuels, only approaching parity under our global optimistic cases (Fig. 12). The assumptions of our optimistic case – namely, favourable wind farm siting, catalyst optimisation, and progress in the electrolysis and DAC sub-systems, coupled with reduced capital costs in the project financing (Tables S8 and S9 and Section S12 in the ESI†) – are reasonable and attainable. Hence, we consider the favourable costs of DAC-PtM under the optimistic cases as feasible, noting also the significant environmental (and potentially monetary) value of the process having a net-negative CO2 intensity. In contrast to DAC-PtM, methanol production from fossil fuels is a mature process, the price of which will not decrease further below DAC-PtM (excepting an unlikely long-term fall in the price of fossil fuels) and may, in fact, increase if taxed in accordance with the substantial process emissions (Fig. 13).Our analysis demonstrates that in handling the challenge of intermittency attendant to wind-powered DAC-PtM, the utilisation of multiple parallel reactors produces methanol at lower costs than attempting to operate a single, large reactor. Moreover, our study points towards a regime of minimising storage requirement as more cost-effective than attempting to maximise production through increased reliance on reserve storage (cf. Strategies 1 and 2 in Fig. 12), although site-specific optimisation reveals the potential for Strategy 2 (more storage) to become marginally cheaper than Strategy 1 (less storage) if allowing increased tolerance in the operability limits of the reactors (Fig. 15a).
In conducting the optimisation at the specific North Sea and Alice Springs sites, our findings also suggest directions for future optimisation work. For example, when the installation costs of wind farms are very high compared to the global average (e.g. the North Sea), the cost-effectiveness of DAC-PtM would likely benefit from deliberately under-sizing the wind farm, thereby reducing the capital cost, in exchange for diminished plant capacity factor and a larger reserve storage requirement. More granular optimisation can also look to refine the DAC-PtM plant further by considering in detail the siting of wind farms at candidate locations – e.g. moving an offshore wind farm to shallower waters to reduce the installation costs but sacrificing the farms performance. However, these optima will be highly sensitive to local geographical, meteorological, and economic factors, necessitating specific and high-quality data to facilitate such sophisticated analyses.
Further technological innovations may also allow for reduction in the costs of renewably powered DAC-PtM. At present, our analysis considers the storage of pressurised H2 in tanks, which contributes as a substantial cost (Fig. 9–11), but certain locations may offer the potential for cheaper storage of H2 in geological formations. The applicability of storage in caverns, however, is commonly considered for hundreds or thousands of tonnes of H2,110 much larger than required here for DAC-PtM (∼20–40 tonnes of H2 under optimised Strategies 1 and 2, Table 5). Further cost-optimisation may thus involve identifying sites that are suitable for co-location of renewable power and geological H2 storage, and co-industry that would benefit from shared H2 storage.
Improvements in the energy efficiency of DAC-PtM are possible through the substitution of direct electrical heating in low-temperature DAC with heat pumps as considered in other work,86,98 for which heat at ∼100 °C is required – towards the upper-end of temperatures currently delivered by state-of-the-art heat pumps, sacrificing their coefficient of performance.111,112 In decreasing the plant energy requirement, heat pumps would serve to reduce the required size of a wind farm for electricity provision. However, the capital cost of erecting heat pumps at the scale required for DAC-PtM (ca. 10 MWe) remains significant. A recent publication112 has suggested installation costs of between $1 and 3 million for heat pumps of approximately 1 MWe size, although their analysis also suggests steep growth in costs if pushing to increase the heat pump supply temperature and capacity. Some authors113 mention integrating the heat evolved from the methanol synthesis with sorbent regeneration in LT-DAC. In contrast, we use the medium-grade heat from the reaction for pre-heating the feed and recycle loops (Section S11.1 in the ESI†). The heat evolved in the distillation condenser is at too low a temperature to be of use (∼65 °C), although our optimistic case already accounts for the potential of other low-grade waste heat streams in providing the LT-DAC regeneration duty in place of electrical heating. For example, the generation of H2 through solid acid electrolysis cells (SAEC) presents the possibility of integrating the rejected heat (at ∼200 °C) with the sorbent regeneration for LT-DAC; however, such technology remains nascent114 and may be unsuitable for during dynamic operation, unlike PEM electrolysers.
Conclusions
To deliver environmental benefits, electrification of the chemical industry necessitates designing plants to handle the intermittency and time-variability of renewable power. Taking the example of wind-powered DAC-PtM, our work has proposed and demonstrated that using multiple reactors is more cost-effective than operating DAC-PtM with a single, large reactor. A multi-reactor plant readily allows the production of methanol to be curtailed according to the available wind power, which drastically reduces the cost burden of reserve storage and plant operation.Using multiple reactors, and considering wind generation data for a selection of worldwide locations, the estimated methanol selling price lies between $1400 and $2700 per tonne, with effective costs of net CO2 capture in the range of $1250 to $2800 per tonne of CO2 when integrating the cost analysis with life cycle assessment. With a well-sited wind farm, coupled with realistic improvements to process technologies, the price of wind-powered DAC-PtM falls as low as $310 per tonne of methanol, or $250 per tonne of net CO2 capture – competitive with current DACCS approaches, where CO2 is stored rather than utilised. Our results clearly demonstrate that the cost-effectiveness of DAC-PtM depends primarily upon: (1) the selection of candidate wind farm locations, which optimise the balance between stable power generation and the cost of installation, and (2) the size of reserve storage, which benefits from designs optimised to account for plant location.
Purchasing grid power allows for the continuous operation of DAC-PtM without adopting the multi-reactor configuration. However, life cycle assessment has illustrated that grid-powered DAC-PtM carries a greater global warming potential than methanol produced from fossil fuels. In the absence of substantially decarbonised grid systems (>80% integrated renewables), only the direct provision of renewable power – in our study from wind – achieves net-negative CO2 emissions by DAC-PtM, between −1250 and −760 kgCO2eq. per tMeOH. Our results underline that successful carbon capture and utilisation (CCU) must not only minimise the cost of the product, in this case methanol, but also maximise the CO2 drawdown for the process. Unlike DAC with sequestration, converting DAC-derived CO2 to methanol yields a product with inherent value through downstream uses – although the lifetimes and emissions associated with any products derived from methanol should be borne in mind. This study has established a novel framework for interfacing renewable power with chemical production, supported by extensive real-world data (90 locations), aiming to provide an impetus for further work on DAC-PtM and new CCU opportunities.
Data availability
All the data used to support the findings of this study can be made available by the corresponding authors upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. J. Fulham acknowledges the financial support of the Harding Scholarship through the Cambridge Trust. P. V. Mendoza-Moreno acknowledges that this work was supported in part by the Bill & Melinda Gates Foundation [OPP1444]. Under the grant conditions of the Foundation, a Creative Commons Attribution 4.0 Generic License has already been assigned to the Author Accepted Manuscript version that might arise from the submission.References
- H. de Coninck et al., Strengthening and implementing the global response, Global warming of 1.5 °C: Summary for policy makers, 2018, pp. 313–443 (IPCC) Search PubMed.
- N. McQueen, et al., A review of direct air capture (DAC): scaling up commercial technologies and innovating for the future, Prog. Energy, 2021, 3(3), 032001, DOI:10.1088/2516-1083/abf1ce.
- L. Joppa et al. Microsoft's million-tonne CO2-removal pur chase—lessons for net zero, 2021, URL https://nature.com/articles/d41586-021-02606-3, Accessed September 10, 2022.
- M. Ozkan, S. P. Nayak, A. D. Ruiz and W. Jiang, Current status and pillars of direct air capture technologies, iScience, 2022, 103990, DOI:10.1016/j.isci.2022.103990.
- N. McQueen, et al., Cost analysis of direct air capture and sequestration coupled to low-carbon thermal energy in the united states, Environ. Sci. Technol., 2020, 54(12), 7542–7551, DOI:10.1021/acs.est.0c00476.
- M. Marchese, G. Buffo, M. Santarelli and A. Lanzini, CO2 from direct air capture as carbon feedstock for Fischer-Tropsch chemicals and fuels: Energy and economic analysis, J. CO2 Util., 2021, 46, 101487, DOI:10.1016/j.jcou.2021.101487.
- H. Cheung, R. S. Tanke and G. P. Torrence, Acetic Acid, Ullmann's Encyclopedia of Industrial Chemistry, John Wiley Sons, Ltd, 2000 Search PubMed.
- A. W. Franz et al. , Ullmann's Encyclopedia of Industrial Chemistry, Ch. Formaldehyde, John Wiley Sons, Ltd, 2016 Search PubMed.
- V. Dieterich, A. Buttler, A. Hanel, H. Spliethoff and S. Fendt, Power to-liquid via synthesis of methanol, DME or Fischer–Tropsch-fuels: a review, Energy Environ. Sci., 2020, 13, 3207–3252, 10.1039/D0EE01187H.
- M. Svanberg, J. Ellis, J. Lundgren and I. Landälv, Renewable methanol as a fuel for the shipping industry, Renewable Sustainable Energy Rev., 2018, 94, 1217–1228, DOI:10.1016/j.rser.2018.06.1180058.
- J. Sehested, Industrial and scientific directions of methanol catalyst development, J. Catal., 2019, 371, 368–375, DOI:10.1016/j.jcat.2019.02.002.
- T. J. Deka, A. I. Osman, D. C. Baruah and D. W. Rooney, Methanol fuel production, utilization, and techno-economy: A review, Environ. Chem. Lett., 2022, 20(6), 3525–3554, DOI:10.1007/s10311-022-01485-y.
- M. A. Adnan and M. G. Kibria, Comparative techno-economic and life-cycle assessment of power-to-methanol synthesis pathways, Appl. Energy, 2020, 278, 115614, DOI:10.1016/j.apenergy.2020.115614.
- S. Mbatha, et al., Power-to-methanol process: a review of electrolysis, methanol catalysts, kinetics, reactor designs and modelling, process integration, optimisation, and techno-economics, Sustainable Energy Fuels, 2021, 5(14), 3490–3569, 10.1039/D1SE00635E.
- G. Zang, P. Sun, A. Elgowainy and M. Wang, Technoeconomic and life cycle analysis of synthetic methanol production from hydrogen and industrial byproduct CO2, Environ. Sci. Technol., 2021, 55(8), 5248–5257, DOI:10.1021/acs.est.0c08237.
- F. Ausfelder and S. Baltac Special report on carbon capture utilisation and storage CCUS in clean energy transitions, 2020, URL https://iea.org/reports/ccus-in-clean-energy-transitions. Accessed 2 July, 2022.
- K. Bareiß, C. de la Rua, M. Möckl and T. Hamacher, Life cycle assessment of hydrogen from proton exchange membrane water electrolysis in future energy systems, Appl. Energy, 2019, 237, 862–872, DOI:10.1016/j.apenergy.2019.01.001.
- A. Sternberg, C. M. Jens and A. Bardow, Life cycle assessment of CO2-based C1-chemicals, Green Chem., 2017, 19(9), 2244–2259, 10.1039/C6GC02852G.
- S. Mucci, A. Mitsos and D. Bongartz, Cost-optimal power-to-methanol: Flexible operation or intermediate storage?, J. Energy Storage, 2023, 72, 108614, DOI:10.1016/j.est.2023.108614.
- A. Maggi, J. Bremer and K. Sundmacher, Multi-period optimization for the design and operation of a flexible power-to-methanol process, Chem. Eng. Sci., 2023, 119202, DOI:10.1016/j.ces.2023.119202.
- D. J. Hostick et al. Projecting electricity demand in 2050. Tech. Rep., Pacific Northwest National Laboratory (PNNL), 2014.
- A. Colmenar-Santos, A.-M. Mũnoz-Gomez, E. Rosales-Asensio and A. Lopez-Rey, Electric vehicle charging strategy to support renewable energy sources in europe 2050 low-carbon scenario, Energy, 2019, 183, 61–74, DOI:10.1016/j.energy.2019.06.118.
- G. Luderer, et al., Impact of declining renewable energy costs on electrification in low-emission scenarios, Nat. Energy, 2022, 7(1), 32–42, DOI:10.1038/s41560-021-00937-z.
- C. Chen and A. Yang, Power-to-methanol: The role of process flexibility in the integration of variable renewable energy into chemical production, Energy Convers. Manage., 2021, 228, 113673, DOI:10.1016/j.enconman.2020.113673.
- J. Van Antwerpen, et al., A model for assessing pathways to integrate intermittent renewable energy for e-methanol production, Int. J. Hydrogen Energy, 2023, 48(78), 30221–30237, DOI:10.1016/j.ijhydene.2023.04.177.
- N. Zheng, H. Zhu, G. Xiao, M. Ni and H. Xu, Dynamic-cycle simulation of power-to-methanol-to-power system with reversible solid oxide cells: Multi-physics and techno-economic analysis, Energy Convers. Manage., 2023, 294, 117573, DOI:10.1016/j.enconman.2023.117573.
- Green ammonia by Haldor Topsoe, Tech. Rep., U.S. Depertment of Energy, URL https://www.energy.gov/sites/default/files/2021-08/4-green-ammonia-haldor-topsoe.pdf.
- C. Beuttler, L. Charles and J. Wurzbacher, The role of direct air capture in mitigation of anthropogenic greenhouse gas emissions, Front. Clim., 2019, 1, 10, DOI:10.3389/fclim.2019.00010.
- Technical University of Denmark (DTU), Global wind atlas 3.0, URL https://globalwindatlas.info/, Accessed 10 July, 2022.
- S. Pfenninger and I. Staffell, Long-term patterns of european pv output using 30 years of validated hourly reanalysis and satellite data, Energy, 2016, 114, 1251–1265, DOI:10.1016/j.energy.2016.08.060.
- I. Staffell and S. Pfenninger, Using bias-corrected reanalysis to simulate current and future wind power output, Energy, 2016, 114, 1224–1239, DOI:10.1016/j.energy.2016.08.068.
- M. M. Rienecker, et al., MERRA: NASA's modern-era retrospective analysis for research and applications, J. Clim., 2011, 24(14), 3624–3648, DOI:10.1175/JCLI-D-11-00015.1.
- M. M. Alam, S. Rehman, J. P. Meyer and L. M. Al-Hadhrami, Review of 600–2500 kW sized wind turbines and optimization of hub height for maximum wind energy yield realization, Renewable Sustainable Energy Rev., 2011, 15(8), 3839–3849, DOI:10.1016/j.rser.2011.07.004.
- A. W. Frazier, W. Cole, P. Denholm, D. Greer and P. Gagnon, Assessing the potential of battery storage as a peaking capacity resource in the united states, Appl. Energy, 2020, 275, 115385, DOI:10.1016/j.apenergy.2020.115385.
- W. J. Cole and A. Frazier, Cost projections for utility-scale battery storageNREL/TP-6A20, National Renewable Energy Laboratory (NREL), 2019, p. 79236 Search PubMed.
- K. Bussche and G. Froment, A steady-state kinetic model for methanol synthesis and the water gas shift reaction on a commercial Cu/ZnO/Al2O3 catalyst, J. Catal., 1996, 161(1), 1–10, DOI:10.1006/jcat.1996.0156.
- N. Hendren and R. Baumann, McCabe-Thiele method for methanol/water separation, 2016, URL https://demonstrations.wolfram.com/McCabeThieleMethodForMethanolWaterSeparation/. Accessed March 29, 2022.
- R. Sander, “Henry’s Law Constants” in National Institute of Standards and Technology (NIST), chemistry webbook: NIST standard reference database number 69, ed. P. Linstrom and W. Mallard DOI:10.18434/T4D303. Accessed March 29, 2022.
- T. Matsoukas, Fundamentals of Chemical Engineering Thermodynamics, Pearson, 2012 Search PubMed.
- D. R. Burgess, “Thermochemical Data” in National Institute of Standards and Technology (NIST) chemistry webbook: NIST standard reference database number 69, ed. P. Linstrom and W. Mallard DOI:10.18434/T4D303. Accessed April 2, 2022.
- P. J. Robinson and W. L. Luyben, Turndown control structures for distillation columns, Ind. Eng. Chem. Res., 2010, 49(24), 12548–12559, DOI:10.1021/ie101945x.
- R. H. Wiser and M. Bolinger, 2018 Wind technologies market report, Tech. Rep., U.S. Department of Energy, 2019, DOE/GO-102019-51918130.
- International Renewable Energy Agency (IRENA), Renewable energy technologies: Cost analysis series: Wind power, 2012.
- Future of wind: Deployment, investment, technology, grid integration, and socio-economic aspects. Tech. Rep., International Renewable Energy Agency (IRENA), 2019.
- B. K. Sovacool, P. Enevoldsen, C. Koch and R. J. Barthelmie, Cost performance and risk in the construction of offshore and onshore wind farms, Wind Energy, 2017, 20(5), 891–908, DOI:10.1002/we.2069.
- G. Rubio-Domingo and P. Linares, The future investment costs of offshore wind: An estimation based on auction results, Renewable Sustainable Energy Rev., 2021, 148, 111324, DOI:10.1016/j.rser.13032021.111324.
- M. Shafiee, F. Brennan and I. A. Espinosa, A parametric whole life cost model for offshore wind farms, Int. J. Life Cycle Assess., 2016, 21, 961–975, DOI:10.1007/s11367-016-1075-z.
- F. Judge, et al., A lifecycle financial analysis model for offshore wind farms, Renewable Sustainable Energy Rev., 2019, 103, 370–383, DOI:10.1016/j.rser.2018.12.045.
- N. Ederer, Evaluating capital and operating cost efficiency of offshore wind farms: A dea approach, Renewable Sustainable Energy Rev., 2015, 42, 1034–1046, DOI:10.1016/j.rser.2014.10.071.
- R. Wiser, M. Bolinger and E. Lantz, Assessing wind power operating costs in the united states: Results from a survey of wind industry experts, Renewable Energy Focus, 2019, 30, 46–57, DOI:10.1016/j.ref.2019.05.003.
- S. Krishnan, et al., Present and future cost of alkaline and PEM electrolyser stacks, Int. J. Hydrogen Energy, 2023, 48(83), 32313–32330, DOI:10.1016/j.ijhydene.2023.05.031.
- M. Fasihi, O. Efimova and C. Breyer, Techno-economic assessment of CO2 direct air capture plants, J. Cleaner Prod., 2019, 224, 957–980, DOI:10.1016/j.jclepro.2019.03.086.
- M. Broehm, J. Strefler and N. Bauer, Techno-economic review of direct air capture systems for large scale mitigation of atmospheric CO2, Tech. Rep., Potsdam Institute for Climate Impact Research, 2015 Search PubMed.
- S. M. Saba, M. Müller, M. Robinius and D. Stolten, The investment costs of electrolysis–a comparison of cost studies from the past 30 years, Int. J. Hydrogen Energy, 2018, 43(3), 1209–1223, DOI:10.1016/j.ijhydene.2017.11.115.
- S. Sarp, S. G. Hernandez, C. Chen and S. W. Sheehan, Alcohol production from carbon dioxide: methanol as a fuel and chemical feedstock, Joule, 2021, 5(1), 59–76, DOI:10.1016/j.joule.2020.11.005.
- S. S. Kumar and V. Himabindu, Hydrogen production by PEM water electrolysis–a review, Mater. Sci. Energy Technol., 2019, 2(3), 442–454, DOI:10.1016/j.mset.2019.03.002.
- F. Sabatino, et al., A comparative energy and costs assessment and optimization for direct air capture technologies, Joule, 2021, 5(8), 2047–2076, DOI:10.1016/j.joule.2021.05.023.
- D. Baldwin, Development of high pressure hydrogen storage tank for storage and gaseous truck delivery, Tech. Rep., Hexagon Lincoln LLC, Lincoln, 2017.
- P. G. Panah, X. Cui, M. Bornapour, R.-A. Hooshmand and J. M. Guerrero, Marketability analysis of green hydrogen production in Denmark: Scale-up effects on grid-connected electrolysis, Int. J. Hydrogen Energy, 2022, 47(25), 12443–12455, DOI:10.1016/j.ijhydene.2022.01.254.
- Z. Liu, X. Yang, W. Jia, H. Li and X. Yang, Justification of CO2 as the working fluid for a compressed gas energy storage system, J. Energy Storage, 2020, 27, 101132, DOI:10.1016/j.est.2019.101132.
- M. Rahman, T. K. Ibrahim and A. N. Abdalla, Thermodynamic performance analysis of gas-turbine power-plant, Int. J. Phys. Sci., 2011, 6(14), 3539–3550, DOI:10.5897/IJPS11.272.
- A. de Klerk, Transport fuel: Biomass-, coal-, gas-and waste-to-liquids processes, Future Energy, Elsevier, 2020, pp. 199–226 Search PubMed.
- T. Helms, S. Salm and R. Wüstenhagen, et al., Investor-specific cost of capital and renewable energy investment decisions, Renewable Energy Finance, 2020, 111, 85, DOI:10.1142/97817832677740003.
- P. Hunt, The weighted average cost of capital for electricity and gas networks. Tech. Rep., Competition and Markets Authority, 2014 Search PubMed.
- B. Moreno and G. Dıaz, The impact of virtual power plant technology composition on wholesale electricity prices: A comparative study of some European Union electricity markets, Renewable Sustainable Energy Rev., 2019, 99, 100–108, DOI:10.1016/j.rser.2018.09.028.
- Z. Csereklyei, S. Qu and T. Ancev, The effect of wind and solar power generation on wholesale electricity prices in australia, Energy Policy, 2019, 131, 358–369, DOI:10.1016/j.enpol.2019.04.007.
- M. A. Huijbregts, et al., Recipe2016: a harmonised life cycle impact assessment method at midpoint and endpoint level, Int. J. Life Cycle Assess., 2017, 22(2), 138–147, DOI:10.1007/s11367-016-1246-y.
- ISO14040: 2006 Environmental management-Life cycle assessmentPrinciples and framework, Standard, International Organization for Standardization (ISO), Geneva, CH, 2006.
- European Council, How is EU electricity produced and sold?, 2022, URL https://www.consilium.europa.eu/en/infographics/how-is-eu-electricity-produced-and-sold/, Accessed 05/09/2023.
- International Energy Agency (IEA), World energy statistics and balances, 2022, URL https://www.iea.org/data-and-statistics/data-product/world-energy-statistics-and-balances, All rights reserved, Accessed 05/09/2023.
- M. V. Barros, C. M. Piekarski and A. C. De Francisco, Carbon footprint of electricity generation in Brazil: An analysis of the 2016–2026 period, Energies, 2018, 11(6), 1412, DOI:10.3390/en11061412.
- Z. Zhuo, et al., Cost increase in the electricity supply to achieve carbon neutrality in China, Nat. Commun., 2022, 13(1), 3172, DOI:10.1038/s41467-022-30747-0.
- C. Choe, S. Cheon, J. Gu and H. Lim, Critical aspect of renewable syn gas production for power-to-fuel via solid oxide electrolysis: Integrative assessment for potential renewable energy source, Renewable Sustainable Energy Rev., 2022, 161, 112398, DOI:10.1016/j.rser.2022.112398.
- A. Prasnikar, A. Pavlisic, F. Ruiz-Zepeda, J. Kovac and B. Likozar, Mechanisms of copper-based catalyst deactivation during CO2 reduction to methanol, Ind. Eng. Chem. Res., 2019, 58(29), 13021–13029, DOI:10.1021/acs.iecr.9b01898.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Recent advances in carbon dioxide hydrogenation to methanol via heterogeneous catalysis, Chem. Rev., 2020, 120(15), 7984–8034, DOI:10.1021/acs.chemrev.9b00723.
- H. A. Daggash, et al., Closing the carbon cycle to maximise climate change mitigation: power-to-methanol vs. power-to-direct air capture, Sustainable Energy Fuels, 2018, 2(6), 1153–1169, 10.1039/C8SE00061A.
- T. Blumberg, G. Tsatsaronis and T. Morosuk, On the economics of methanol production from natural gas, Fuel, 2019, 256, 115824, DOI:10.1016/j.fuel.2019.115824.
- C. C. Dorris, E. Lu, S. Park and F. H. Toro, High-purity oxygen production using mixed ionic-electronic conducting sorbents, Tech. Rep.,University of Pennsylvannia, LP Amina, 2016.
- G. Maggio, G. Squadrito and A. Nicita, Hydrogen and medical oxygen by renewable energy based electrolysis: A green and economically viable route, Appl. Energy, 2022, 306, 117993, DOI:10.1016/j.apenergy.2021.117993.
- C. Campbell-Stanway, V. Becerra, S. Prabhu and J. Bull, Investigating the role of byproduct oxygen in uk-based future scenario models for green hydrogen electrolysis, Energies, 2024, 17(2), 281, DOI:10.3390/en17020281.
- J. Li, X. Ma, H. Liu and X. Zhang, Life cycle assessment and economic analysis of methanol production from coke oven gas compared with coal and natural gas routes, J. Cleaner Prod., 2018, 185, 299–308, DOI:10.1016/j.jclepro.2018.02.100.
- A. Lerner, M. J. Brear, J. S. Lacey, R. L. Gordon and P. A. Webley, Life cycle analysis (LCA) of low emission methanol and di-methyl ether (DME) derived from natural gas, Fuel, 2018, 220, 871–878, DOI:10.1016/j.fuel.2018.02.066.
- R. Kajaste, M. Hurme and P. Oinas, Methanol-managing greenhouse gas emissions in the production chain by optimizing the resource base, Aims Energy, 2018, 6(6), 1074–1102, DOI:10.3934/energy.2018.6.1074.
- Carbon footprint of methanol, Tech. Rep., Methanol institute, 2022.
- Y. Liu, et al., Comprehensive analysis of environmental impacts and energy consumption of biomass-to-methanol and coal-to-methanol via life cycle assessment, Energy, 2020, 204, 117961, DOI:10.1016/j.energy.2020.117961.
- M. Gutsch and J. Leker, Co-assessment of costs and environmental impacts for off-grid direct air carbon capture and storage systems, Commun. Eng., 2024, 3(1), 14, DOI:10.1038/s44172-023-00152-6.
- J. F. Green, Does carbon pricing reduce emissions? A review of expost analyses, Environ. Res. Lett., 2021, 16(4), 043004, DOI:10.1088/1748-9326/abdae9.
- C. Varela, M. Mostafa, E. Ahmetovic and E. Zondervan, Agile operation of renewable methanol synthesis under fluctuating power inputs, Comput.-Aided Chem. Eng., 2020, 48, 1381–1386, DOI:10.1016/B978-0-12-823377-1.50231-7.
- V. Mytilinou and A. J. Kolios, Techno-economic optimisation of offshore wind farms based on life cycle cost analysis on the uk, Renewable Energy, 2019, 132, 439–454, DOI:10.1016/j.renene.2018.07.146.
- Department for Energy Security and Net Zero, UK Government, Green book supplementary guidance: Valuation of energy use and greenhouse gas emissions for appraisal, 2023.
- Department of Climate Change, Energy, the Environment and Water, Australian Government, Australia's emissions projections 2023, 2023.
- M. Perez-Fortes, J. C. Schöneberger, A. Boulamanti and E. Tzimas, Methanol synthesis using captured CO2 as raw material: Technoeconomic and environmental assessment, Appl. Energy, 2016, 161, 718–732, DOI:10.1016/j.apenergy.2015.07.067.
- C. Hank, et al., Economics & carbon dioxide avoidance cost of methanol production based on renewable hydrogen and recycled carbon dioxide–power-to-methanol, Sustainable Energy Fuels, 2018, 2(6), 1244–1261, 10.1039/C8SE00032H.
- J. Nyari, M. Magdeldin, M. Larmi, M. Järvinen and A. Santasalo-Aarnio, Techno-economic barriers of an industrial-scale methanol CCU-plant, J. CO2 Util., 2020, 39, 101166, DOI:10.1016/j.jcou.2020.101166.
- H. Kim, M. Byun, B. Lee and H. Lim, Carbon-neutral methanol synthesis as carbon dioxide utilization at different scales: Economic and environmental perspectives, Energy Convers. Manage., 2022, 252, 115119, DOI:10.1016/j.enconman.2021.115119.
- S. Sollai, A. Porcu, V. Tola, F. Ferrara and A. Pettinau, Renewable methanol production from green hydrogen and captured CO2: A technoeconomic assessment, J. CO2 Util., 2023, 68, 102345, DOI:10.1016/j.jcou.2022.102345.
- E. Moioli and T. Schildhauer, Eco-techno-economic analysis of methanol production from biogas and Power-to-X, Ind. Eng. Chem. Res., 2022, 61(21), 7335–7348, DOI:10.1021/acs.iecr.1c04682.
- M. Bos, S. Kersten and D. Brilman, Wind power to methanol: Renewable methanol production using electricity, electrolysis of water and CO2 air capture, Appl. Energy, 2020, 264, 114672, DOI:10.1016/j.apenergy.2020.114672.
- K. Harris, R. G. Grim, Z. Huang and L. Tao, A comparative technoeconomic analysis of renewable methanol synthesis from biomass and CO2: Opportunities and barriers to commercialization, Appl. Energy, 2021, 303, 117637, DOI:10.1016/j.apenergy.2021.117637.
- M. C. Heller, M. H. Mazor and G. A. Keoleian, Plastics in the us: toward a material flow characterization of production, markets and end of life, Environ. Res. Lett., 2020, 15(9), 094034, DOI:10.1088/1748-9326/ab9e1e.
- J. Di, B. K. Reck, A. Miatto and T. E. Graedel, United states plastics: Large flows, short lifetimes, and negligible recycling, Resour., Conserv. Recycl., 2021, 167, 105440, DOI:10.1016/j.resconrec.2021.105440.
- G. Bozzano and F. Manenti, Efficient methanol synthesis: Perspectives, technologies and optimization strategies, Prog. Energy Combust. Sci., 2016, 56, 71–105, DOI:10.1016/j.pecs.2016.06.001.
- V. Palma, E. Meloni, C. Ruocco, M. Martino and A. Ricca, State of the art of conventional reactors for methanol production, Methanol, Elsevier, 2018, pp. 29–51 Search PubMed.
- T. Wurzel, Lurgi MegaMethanol technology. Delivering the building blocks for the future fuel and monomer demand, Tech. Rep., Lurgi, 2006 Search PubMed.
- A. Gedde-Dahl, K. J. Kristiansen, H. Holm-Larsen and H. Topsøe, The 2,400 MTPD methanol plant at Tjeldbergodden, 1998.
- U. Ash-Kurlander, et al., Impact of daily startup–shutdown conditions on the production of solar methanol over a commercial Cu–ZnO–Al2O3 catalyst, Energy Technol., 2016, 4(5), 565–572, DOI:10.1002/ente.201600022.
- G. J. Fulham, X. Wu, W. Liu and E. J. Marek, Mechanistic insights into the role of zinc oxide, zirconia and ceria supports in Cu-based catalysts for CO2 hydrogenation to methanol, Chem. Eng. J., 2024, 480, 147732, DOI:10.1016/j.cej.2023.147732.
- N. Rezaie, A. Jahanmiri, B. Moghtaderi and M. Rahimpour, A comparison of homogeneous and heterogeneous dynamic models for industrial methanol reactors in the presence of catalyst deactivation, Chem. Eng. Process., 2005, 44(8), 911–921, DOI:10.1016/j.cep.2004.10.004.
- S. Masoudi, M. Farsi and M. R. Rahimpour, Dynamic optimization of methanol synthesis section in the dual type configuration to increase methanol production, Oil & Gas Science and Technology–Revue d’IFP Energies nouvelles, 74, 90, 2019 DOI:10.2516/ogst/2019062.
- D. D. Papadias and R. K. Ahluwalia, Bulk storage of hydrogen, Int. J. Hydrogen Energy, 2021, 46(70), 34527–34541, DOI:10.1016/j.ijhydene.2021.08.028.
- B. Zühlsdorf, F. Bühler, M. Bantle and B. Elmegaard, Analysis of technologies and potentials for heat pump-based process heat supply above 150 °C, Energy Convers. Manage., 2019, 2, 100011, DOI:10.1016/j.ecmx.2019.100011.
- A. Vannoni, A. Sorce, A. Traverso and A. F. Massardo, Large size heat pumps advanced cost functions introducing the impact of design COP on capital costs, Energy, 2023, 284, 129204, DOI:10.1016/j.energy.2023.129204.
- E. Prats-Salvado, N. Monnerie and C. Sattler, Synergies between direct air capture technologies and solar thermochemical cycles in the production of methanol, Energies, 2021, 14(16), 4818 CrossRef CAS.
- N. Fujiwara, H. Nagase, S. Tada and R. Kikuchi, Hydrogen production by steam electrolysis in solid acid electrolysis cells, ChemSusChem, 2021, 14(1), 417–427, DOI:10.1002/cssc.202002281.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee00933a |
| This journal is © The Royal Society of Chemistry 2024 |