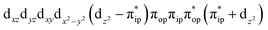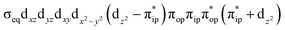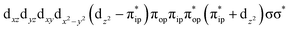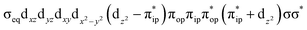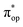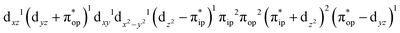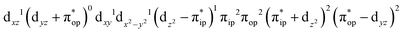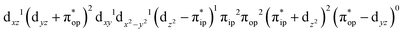Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into dioxygen binding on metal centers: an ab initio multireference electronic structure analysis†
Peng
Zhang
 ab,
Way-Zen
Lee
ab,
Way-Zen
Lee
 cd and
Shengfa
Ye
cd and
Shengfa
Ye
 *a
*a
aState Key Laboratory of Catalysis, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cDepartment of Chemistry, National Taiwan Normal University, Taipei 11677, Taiwan
dDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 807, Taiwan
First published on 22nd August 2024
Abstract
Why does binding of dioxygen (O2) to metal centers, the initial step of O2 storage, transportation, and activation, almost inevitably induce metal-to-O2 single-electron transfer and generate superoxo (O2−˙) species, instead of genuine O02 adducts? To address this question, this study describes highly correlated wavefunction-based ab initio calculations using CASSCF/NEVPT2 (CASSCF = complete active space self-consistent field, and NEVPT2 = N-electron valence state second-order perturbation theory) approaches to explore the electronic-structure evolution of O2 association on Fe(II)(BDPP) (H2BDPP = 2,6-bis((2-(S)-diphenylhydroxylmethyl-1-pyrrolidinyl)methyl)pyridine) and Co(II)(BDPP) to produce S = 3 Fe(III)(BDPP)(O2−˙) (1) and 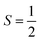 Co(III)(BDPP)(O2−˙) (2). CASSCF/NEVPT2 calculations suggest that the processes furnishing 1 and 2 feature an avoided crossing resulting from interactions of two diabatic curves, of which one is characterized as Co(II) and Fe(II) centers interacting with a triplet O2 ligand and the other as Co(III) and Fe(III) centers bound to a superoxo ligand. In both cases, the avoided crossing induces a one-electron transfer from the divalent metal center to the incoming O2 ligand and leads to formation of trivalent metal–O2−˙ complexes. To facilitate the interpretation of complicated multireference wavefunctions, we formulated two-fragment spin eigenfunctions utilizing Clebsch–Gordan coefficients (CGCs) to rationalize computed spin populations on the metal centers and the O2 ligand and compared these results with usual valence bonding (VB) analyses. It turns out that both methods give the same results and are complementary to each other. Finally, the limitation of DFT approaches in describing complex electronic structures involving metal–ligand magnetic couplings is delineated.
Co(III)(BDPP)(O2−˙) (2). CASSCF/NEVPT2 calculations suggest that the processes furnishing 1 and 2 feature an avoided crossing resulting from interactions of two diabatic curves, of which one is characterized as Co(II) and Fe(II) centers interacting with a triplet O2 ligand and the other as Co(III) and Fe(III) centers bound to a superoxo ligand. In both cases, the avoided crossing induces a one-electron transfer from the divalent metal center to the incoming O2 ligand and leads to formation of trivalent metal–O2−˙ complexes. To facilitate the interpretation of complicated multireference wavefunctions, we formulated two-fragment spin eigenfunctions utilizing Clebsch–Gordan coefficients (CGCs) to rationalize computed spin populations on the metal centers and the O2 ligand and compared these results with usual valence bonding (VB) analyses. It turns out that both methods give the same results and are complementary to each other. Finally, the limitation of DFT approaches in describing complex electronic structures involving metal–ligand magnetic couplings is delineated.
Introduction
Binding of dioxygen (O2) on metal cofactors of metalloproteins initiates a diverse array of physiologically pivotal processes, including O2 storage, transportation, and activation for substrate functionalization.1–6 Myoglobin, a heme enzyme containing a high spin ferrous center, reacts with O2 yielding a singlet O2 complex,7–9 while for nonheme enzymes isopenicillin N synthase (IPNS)10–12 and a variant of homoprotocatechuate 2,3-dioxygenase (Fe-HPCD) with the active site His200 mutated to Asn, labelled as 4-NC,13 and utilizing an alternative substrate 4-nitrocatechol, O2 addition results in a quintet O2 adduct that is best described as a high spin ferric center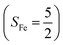 antiferromagnetically coupled to a superoxo ligand (O2−˙)
antiferromagnetically coupled to a superoxo ligand (O2−˙) 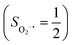 yielding an overall St = 2 ground state. To mimic enzymatic O2 binding, numerous model complexes have been synthesized and characterized.14,15 The reactions of O2 with a range of ferrous complexes, such as Fe(II)(BNPAMe2S)(Br) (BNPAMe2SH = (bis((6-(neopentylamino)pyridinyl)methyl)amino)-2-methylpropane-2-thiol,16 (LAdH)Fe (LAdH = tris(phosphinimine) ligand),17 Fe(S2Me2N3(Pr,Pr))18 and Fe(ttppc) (ttppc3− = 5,10,15-tris((2,4,6-triphenyl)phenyl)corrolate),19 all yield similar quintet Fe–O2 adducts. In contrast to the examples discussed above, treatment of O2 with a high spin Fe(II) precursor (SFe = 2), Fe(II)(BDPP) (H2BDPP = 2,6-bis((2-(S)-diphenylhydroxylmethyl-1-pyrrolidinyl)methyl)pyridine), at 193 K generates St = 3, instead of St = 2, Fe(III)(BDPP)(O2−˙) (1) attained by a ferromagnetic coupling of Fe(III) center
yielding an overall St = 2 ground state. To mimic enzymatic O2 binding, numerous model complexes have been synthesized and characterized.14,15 The reactions of O2 with a range of ferrous complexes, such as Fe(II)(BNPAMe2S)(Br) (BNPAMe2SH = (bis((6-(neopentylamino)pyridinyl)methyl)amino)-2-methylpropane-2-thiol,16 (LAdH)Fe (LAdH = tris(phosphinimine) ligand),17 Fe(S2Me2N3(Pr,Pr))18 and Fe(ttppc) (ttppc3− = 5,10,15-tris((2,4,6-triphenyl)phenyl)corrolate),19 all yield similar quintet Fe–O2 adducts. In contrast to the examples discussed above, treatment of O2 with a high spin Fe(II) precursor (SFe = 2), Fe(II)(BDPP) (H2BDPP = 2,6-bis((2-(S)-diphenylhydroxylmethyl-1-pyrrolidinyl)methyl)pyridine), at 193 K generates St = 3, instead of St = 2, Fe(III)(BDPP)(O2−˙) (1) attained by a ferromagnetic coupling of Fe(III) center 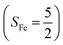 and a O2−˙ ligand
and a O2−˙ ligand 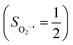 .20 While the corresponding reaction with high spin Co(II)(BDPP)21
.20 While the corresponding reaction with high spin Co(II)(BDPP)21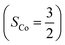 at 193 K furnishes a doublet Co(III)–O2−˙ species, Co(III)(BDPP)(O2−˙) (2), which has been characterized as consisting of a low spin Co(III) center (SCo = 0) interacting with a superoxo ligand
at 193 K furnishes a doublet Co(III)–O2−˙ species, Co(III)(BDPP)(O2−˙) (2), which has been characterized as consisting of a low spin Co(III) center (SCo = 0) interacting with a superoxo ligand 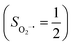 .22 Furthermore, the same product was also found for O2 addition to Co-HPCD,23 the Co derivative of Fe-HPCD, and a plethora of high spin or low spin Co(II) complexes, including Co-TPP (TPP2− = tetraphenylporphyrinate),24 Co(Me3TACN)(S2SiMe2) (Me3TACN = 1,4,7-trimethyl-1,4,7-triazacyclononane),25 Co(TpMe2)(tBu2APH) (TpMe2 = hydrotris(3,5-dimethylpyrazolyl)borate,26tBu2APH = 2-amino-4,6-di-tert-butylphenol), Co(salen)27 and Co(Por) (Por = porphyrin).28 Over-decade intensive investigations revealed that O2 association on divalent nonheme metal centers almost inevitably entails a metal-to-O2 electron transfer and thus produces a trivalent metal–O2−˙ complex.29,30 To the best of our knowledge, there is only one exception; O2 binding on a variant of Fe-HPCD labelled as Y257F-HPCA was proposed to form an Fe(II)–O2 intermediate, instead of Fe(III)–O2−˙.31–35 An intriguing question thus arises about whether it is viable to generate such an authenticated O2 adduct from O2 association on metal centers.
.22 Furthermore, the same product was also found for O2 addition to Co-HPCD,23 the Co derivative of Fe-HPCD, and a plethora of high spin or low spin Co(II) complexes, including Co-TPP (TPP2− = tetraphenylporphyrinate),24 Co(Me3TACN)(S2SiMe2) (Me3TACN = 1,4,7-trimethyl-1,4,7-triazacyclononane),25 Co(TpMe2)(tBu2APH) (TpMe2 = hydrotris(3,5-dimethylpyrazolyl)borate,26tBu2APH = 2-amino-4,6-di-tert-butylphenol), Co(salen)27 and Co(Por) (Por = porphyrin).28 Over-decade intensive investigations revealed that O2 association on divalent nonheme metal centers almost inevitably entails a metal-to-O2 electron transfer and thus produces a trivalent metal–O2−˙ complex.29,30 To the best of our knowledge, there is only one exception; O2 binding on a variant of Fe-HPCD labelled as Y257F-HPCA was proposed to form an Fe(II)–O2 intermediate, instead of Fe(III)–O2−˙.31–35 An intriguing question thus arises about whether it is viable to generate such an authenticated O2 adduct from O2 association on metal centers.
In parallel to intensive experimental research, a great deal of computational studies have been devoted to probing electronic structures of O2 adducts and evaluating electronic-structure evolution over the course of O2 binding processes.36–44 In this regard, density functional theory (DFT) calculations usually cannot yield satisfactory results, especially for those systems featuring antiferromagnetic coupling of two fragments. In principle, such a complicated electronic structure cannot be appropriately described by a single Slater determinant. Consequently, broken symmetry formalism has to be invoked, because of the inherent single determinant restriction of DFT approaches.45 The Kohn–Sham solution thus obtained is no longer the eigenfunction of Ŝ2; consequently, the resulting spin density is not correct, and the subsequent spin population analysis is physically unjustified. To obtain more accurate electronic structures, one has to resort to highly correlated wavefunction-based multireference approaches.36–38,42,44 To date, these methods have been successfully applied to O2 adducts of heme systems, but hardly to nonheme ones.30 To the best of our knowledge, only one ab initio study has been reported thus far where potential energy curves of varying spin states were computed for O2 association on a heme center.46 This work does not focus on the elucidation of electronic-structure changes occurring during this process but on the quintet-to-singlet spin crossover; hence, it does not provide sufficient information to address the aforementioned question.
In the present work, we describe a detailed multireference analysis of the electronic-structure evolution as O2 steadily approaches the Fe(II) and Co(II) centers in Fe(II)(BDPP) and Co(II)(BDPP) affording 1 and 2, respectively. Specifically, highly correlated wavefunction-based complete active space self-consistent field (CASSCF)47/N-electron valence state second-order perturbation theory (NEVPT2)48,49 computations were carried out on a series of geometric structures on the reaction trajectory generated by DFT computations. To interpret complicated multireference wavefunctions of O2 adducts, we constructed two-fragment spin eigenfunctions using Clebsch–Gordan coefficients (CGCs)50 to rationalize computed spin populations. CASSCF/NEVPT2 calculations suggest that the O2 binding processes furnishing 1 and 2 feature an avoided crossing of two diabatic curves that represent the limiting valence structures of Fe(II)/Co(II)–O02 and Fe(III)/Co(III)–O2−˙. Their interaction induces a spontaneous single-electron transfer from the divalent metal center to the incoming O2 ligand, thereby leading to the formation of trivalent metal–O2−˙ complexes as the final product for the O2 binding processes.
Computation setup
To obtain the reaction trajectory for the formation of complexes 1 and 2, the M–O2 distance steadily varied from 1.75 to 4.50 Å in an S = 3 and an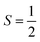 state, respectively, in relaxed surface scans conducted by using the B3LYP functional51,52 in conjunction with the def2-TZVP basis set53–55 for N, O, Fe, and Co, and the def2-SVP basis set56,57 for the other atoms (C and H atoms). Moreover, RIJCOSX approximations58 were employed in combination with the def2/J auxiliary basis set59,60 to speed up DFT computations. To take solvation effects into consideration, the CPCM model61 with THF as the solvent was applied, and D3BJ corrections62,63 were used to account for dispersion corrections. Frequency analysis on a given optimized geometry structure was performed to compute its zero point energy (ZPE) and thermal corrections. To compute reliable electronic structures, CASSCF calculations using the def2-TZVP basis set for all atoms were carried out at each geometric structure of the reaction trajectory. As verified below, the appropriate active spaces of complexes 1 and 2 were chosen to distribute 12 and 13 electrons, respectively, into 9 orbitals including five metal 3d-based orbitals (five spherical 3d orbitals are used here), two O2 π bonding (πip and πop) and the corresponding π* antibonding
state, respectively, in relaxed surface scans conducted by using the B3LYP functional51,52 in conjunction with the def2-TZVP basis set53–55 for N, O, Fe, and Co, and the def2-SVP basis set56,57 for the other atoms (C and H atoms). Moreover, RIJCOSX approximations58 were employed in combination with the def2/J auxiliary basis set59,60 to speed up DFT computations. To take solvation effects into consideration, the CPCM model61 with THF as the solvent was applied, and D3BJ corrections62,63 were used to account for dispersion corrections. Frequency analysis on a given optimized geometry structure was performed to compute its zero point energy (ZPE) and thermal corrections. To compute reliable electronic structures, CASSCF calculations using the def2-TZVP basis set for all atoms were carried out at each geometric structure of the reaction trajectory. As verified below, the appropriate active spaces of complexes 1 and 2 were chosen to distribute 12 and 13 electrons, respectively, into 9 orbitals including five metal 3d-based orbitals (five spherical 3d orbitals are used here), two O2 π bonding (πip and πop) and the corresponding π* antibonding 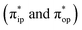 orbitals. For complex 1, CASSCF calculations averaged a triplet, a quintet, and a septet state, and for complex 2, a doublet, a quartet, and a sextet state were considered. Based on the converged state-average CASSCF wavefunction, complete active space configuration interaction (CASCI) calculations were employed to calculate spin density and spin populations of a specific spin state. On top of CASSCF wavefunctions, NEVPT2 computations were undertaken to obtain more precise electronic energies. To accelerate ab initio computations, RIJK approximations64 in conjunction with the def2/JK auxiliary basis set65 were used. Thus, the final potential energy surface was constructed by using the electronic energy derived from CASSCF/NEVPT2 calculations combined with the ZPE contribution and thermal corrections. All computations were performed using the ORCA-5.0.3 program package.66
orbitals. For complex 1, CASSCF calculations averaged a triplet, a quintet, and a septet state, and for complex 2, a doublet, a quartet, and a sextet state were considered. Based on the converged state-average CASSCF wavefunction, complete active space configuration interaction (CASCI) calculations were employed to calculate spin density and spin populations of a specific spin state. On top of CASSCF wavefunctions, NEVPT2 computations were undertaken to obtain more precise electronic energies. To accelerate ab initio computations, RIJK approximations64 in conjunction with the def2/JK auxiliary basis set65 were used. Thus, the final potential energy surface was constructed by using the electronic energy derived from CASSCF/NEVPT2 calculations combined with the ZPE contribution and thermal corrections. All computations were performed using the ORCA-5.0.3 program package.66
Results and discussion
Choice of active spaces
Unlike DFT, CASSCF is not a black box method. As the first step to initiate CASSCF calculations, one should prudently select a proper active space,67 for which some preliminary understanding is required of the electronic structure of the system under investigation. To ensure that the chosen active space is sufficient to provide reliable electronic structures, further calculations are often necessary with enlarged and/or truncated active spaces. Critically, CASSCF computations with suitable active spaces not only yield precise electronic structures but also result in fast convergence. Usually, because d and f orbitals of transition metal compounds are nearly degenerate which leads to strong multiconfiguration character, these orbitals should be included in the active space. Equally important is that to properly describe a metal–ligand covalent bond, the active space ought to contain its bonding and antibonding molecular orbitals (MOs). Otherwise, the CASSCF computations with an unbalanced active space would result in an incorrect electronic structure. Both criteria were used to choose a suitable active space for our CASSCF calculations.In the present case, in addition to 5 metal 3d-based orbitals, two π bonding (πip and πop) and two π* antibonding 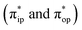 orbitals of the O2 ligand should be included in the active space. As elaborated below, this active space can properly describe the metal–O2 covalent bonding built from the metal 3d and O2 π* fragment orbitals of appropriate symmetry. Therefore, the active spaces of complexes 1 and 2 were chosen to distribute 12 and 13 electrons, respectively, in 9 orbitals. Depicted in Fig. 1 is the active space of complex 2 obtained by the CASSCF(13,9) computation at the Co–O2 bond length of 2.50 Å. An analogous active space was employed for complex 1.
orbitals of the O2 ligand should be included in the active space. As elaborated below, this active space can properly describe the metal–O2 covalent bonding built from the metal 3d and O2 π* fragment orbitals of appropriate symmetry. Therefore, the active spaces of complexes 1 and 2 were chosen to distribute 12 and 13 electrons, respectively, in 9 orbitals. Depicted in Fig. 1 is the active space of complex 2 obtained by the CASSCF(13,9) computation at the Co–O2 bond length of 2.50 Å. An analogous active space was employed for complex 1.
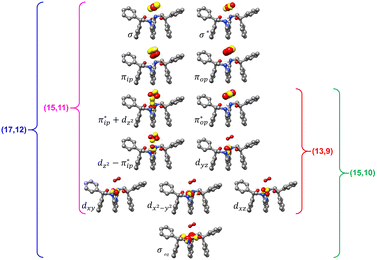 | ||
| Fig. 1 Different choices of active spaces (m,n) (m electrons in n orbitals) for complex 2 at the Co–O2 bond length of 2.50 Å. For clarity, hydrogen atoms are omitted for clarity. | ||
To test the appropriateness of the selected active space, we took complex 2 at the Co–O2 bond length of 2.50 Å as an example and performed a series of CASSCF computations with different active spaces. First, we added BDPP2− O and N 2p donor based σeq into the active space that is the σ bonding counterpart with respect to dx2−y2. Accordingly, two more electrons ought to be added into the active space, thereby resulting in an active space of CAS(15,10). Second, we constructed an active space of CAS(15,11) that includes O2 σ and σ* orbitals to take the entire 2p shells of the O2 moiety into consideration. Third, an even larger active space of CAS(17,12) was built up to encompass all the aforementioned effects. As summarized in Table 1, the occupation numbers of σeq are invariably 2 for all key electron configurations of each spin state derived from CASSCF(15,10) calculations. Similarly, the occupation numbers of O2 σ and σ* remain constants at 2 and 0, respectively, for all important electron configurations predicted by CASSCF(15,11) computations. Both findings hold true for the CASSCF(17,12) results. As such, for a given spin state, all CASSCF computations give qualitatively the same electronic structures as evidenced by almost identical percentage of each dominant electron configuration and hence spin populations on the Co center and the O2 moiety. Moreover, we have also performed CASSCF calculations with these three distinct active spaces on complex 2 at a longer (4.50 Å) and a shorter (1.91 Å) Co–O2 bond length, and again the calculations produced analogous results, as shown in Fig. S1 and S2 (ESI†). In addition, we have also carried out CASSCF(13,9) calculations using different basis sets, such as def2-SV, def2-SVP, def2-TZVP and def2-TZVPP, and the same electronic structures were obtained as listed in Tables S1–S3 (ESI†). In summary, the active space of CAS(13,9) combined with the def2-TZVP basis set is sufficient to yield reliable electronic structures and bonding features for complex 2 at varying Co–O2 bond distances. Likewise, CASSCF(12,9) with the def2-TZVP basis set should produce satisfactory results for the O2 association process affording complex 1 as well.
O2 binding on Fe(II)(BDPP) affording complex 1
Depicted in Fig. 2 is the St = 3 potential energy surface of O2 bonding to high spin Fe(II)(BDPP) calculated using CASSCF(12,9)/NEVPT2 computations. As expected, starting point 7A with a Fe–O2 bond length of 4.00 Å is best interpreted as a high spin Fe(II) ion (SFe = 2) ferromagnetically coupled with a triplet O2 ligand (SO2 = 1) yielding an overall septet state. Consistent with this assignment, ab initio calculations indicate that this state is distinguished by a leading electron configuration of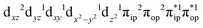 (95%). As shown in Fig. 2, the computed spin density and spin populations (Löwdin analysis, 3.86 for Fe and 2.00 for O2; Mulliken analysis, 3.91 for Fe and 2.00 for O2) further corroborate this electronic-structure formulation. Of note, because spin populations estimated by Löwdin and Mulliken analyses are essentially the same, in the following section, we only discuss the former but list the latter in Fig. 2. As the O2 ligand steadily approaches the Fe center, the energy of this valence structure invariably rises as shown by the corresponding diabatic potential curve (magenta line). During this process, the nature of the Fe–O2 bonding remains essentially the same as indicated by the unchanged spin populations on the Fe(II) center and the O2 ligand, for instance, complex 7B. However, starting from the Fe–O2 distance of 2.30 Å, CASSCF(12,9) calculations could converge to another solution as exemplified by complex 71. It features a sole electron configuration of
(95%). As shown in Fig. 2, the computed spin density and spin populations (Löwdin analysis, 3.86 for Fe and 2.00 for O2; Mulliken analysis, 3.91 for Fe and 2.00 for O2) further corroborate this electronic-structure formulation. Of note, because spin populations estimated by Löwdin and Mulliken analyses are essentially the same, in the following section, we only discuss the former but list the latter in Fig. 2. As the O2 ligand steadily approaches the Fe center, the energy of this valence structure invariably rises as shown by the corresponding diabatic potential curve (magenta line). During this process, the nature of the Fe–O2 bonding remains essentially the same as indicated by the unchanged spin populations on the Fe(II) center and the O2 ligand, for instance, complex 7B. However, starting from the Fe–O2 distance of 2.30 Å, CASSCF(12,9) calculations could converge to another solution as exemplified by complex 71. It features a sole electron configuration of 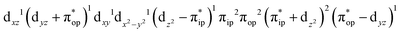 (100%) and is best described as a high spin Fe(III) center
(100%) and is best described as a high spin Fe(III) center 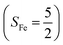 ferromagnetically coupled with a superoxo ligand
ferromagnetically coupled with a superoxo ligand 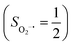 as suggested by the computed spin density and spin populations (4.74 for Fe and 1.03 for O2). Its energy first descends for the Fe–O2 distance lowering from 2.30 Å to 2.06 Å and then ascends as the Fe–O2 distance further decreases; thus, its diabatic potential curve (crimson curve) displays a local minimal (71) at a Fe–O2 distance of ∼2.00 Å.
as suggested by the computed spin density and spin populations (4.74 for Fe and 1.03 for O2). Its energy first descends for the Fe–O2 distance lowering from 2.30 Å to 2.06 Å and then ascends as the Fe–O2 distance further decreases; thus, its diabatic potential curve (crimson curve) displays a local minimal (71) at a Fe–O2 distance of ∼2.00 Å.
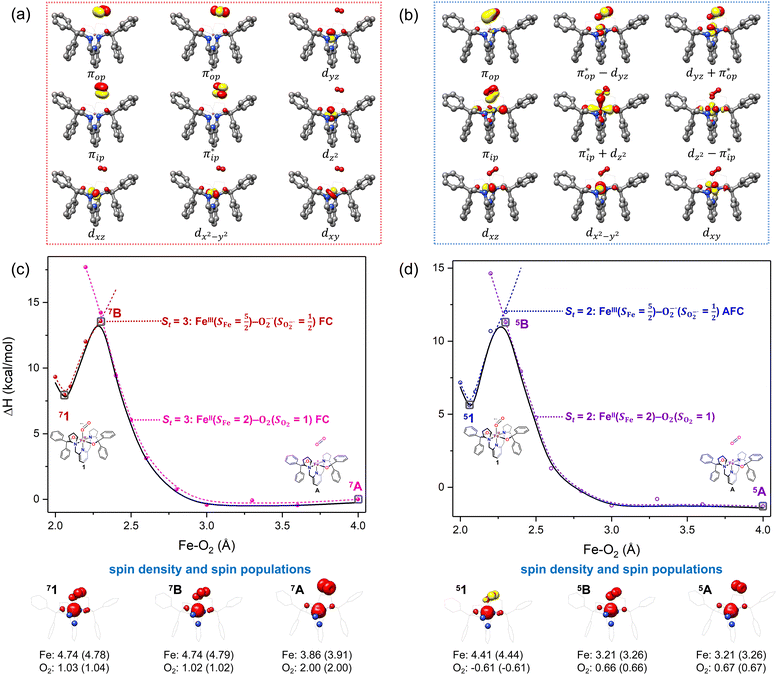 | ||
Fig. 2 Active spaces of complexes A (a) and 1 (b); septet potential energy surface for the reaction of Fe(II)(BDPP) with O2 as a function of the Fe–O2 bond distance obtained from CASSCF(12,9)/NEVPT2 computations; dot lines denote diabatic potential curves (magenta line denotes an St = 3 FeII–O2 complex consisting of as an SFe = 2 FeII center ferromagnetically coupled (FC) with an SO2 = 1 O2 ligand; the crimson line denotes an St = 3 FeIII–O2−˙ complex consisting of an 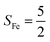 FeIII center ferromagnetically coupled (FC) with an FeIII center ferromagnetically coupled (FC) with an 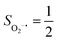 O2−˙ ligand) and the black line denotes an adiabatic curve for the reaction on the S = 3 potential surface; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Fe center and the O2 unit calculated for complexes 7A (Fe(II)(BDPP) + O2), 7B, and 71 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (c); the quintet potential energy surface for the reaction of Fe(II)(BDPP) with O2 as a function of the Fe–O2 bond distance obtained from CASSCF(12,9)/NEVPT2 computations; the dot lines denote diabatic potential curves (violet line denotes a quintet state FeII–O2 complex, interpreted as an SFe = 2 FeII compound magnetically coupled with an SO2 = 1 O2 ligand; the blue line denotes a quintet state FeIII–O2−˙ complex, interpreted as an O2−˙ ligand) and the black line denotes an adiabatic curve for the reaction on the S = 3 potential surface; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Fe center and the O2 unit calculated for complexes 7A (Fe(II)(BDPP) + O2), 7B, and 71 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (c); the quintet potential energy surface for the reaction of Fe(II)(BDPP) with O2 as a function of the Fe–O2 bond distance obtained from CASSCF(12,9)/NEVPT2 computations; the dot lines denote diabatic potential curves (violet line denotes a quintet state FeII–O2 complex, interpreted as an SFe = 2 FeII compound magnetically coupled with an SO2 = 1 O2 ligand; the blue line denotes a quintet state FeIII–O2−˙ complex, interpreted as an 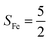 FeIII center antiferromagnetically coupled (AFC) with an FeIII center antiferromagnetically coupled (AFC) with an 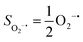 ligand) and the black lines denote adiabatic curves for the reaction on the S = 2 potential surface; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Fe center and O2 unit calculated for complexes 5A (Fe(II)(BDPP) + O2), 5B, and 51 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (d); hydrogen atoms are omitted for clarity. ligand) and the black lines denote adiabatic curves for the reaction on the S = 2 potential surface; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Fe center and O2 unit calculated for complexes 5A (Fe(II)(BDPP) + O2), 5B, and 51 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (d); hydrogen atoms are omitted for clarity. | ||
The interaction of the aforementioned two diabatic potential curves results in an avoided crossing near the Fe–O2 bond length of 2.30 Å and a barrier of 13.6 kcal mol−1. Moreover, the entire process is moderately endothermic with a driving force of 8.0 kcal mol−1. This value should be somewhat overestimated by our computations, because experimentally 71 is stable at low temperatures (<193 K) but releases O2 affording Fe(II)(BDPP) upon raising the temperature. The overestimation of the binding barrier can be ascribed to the fact that the active space employed does not suffice to capture escalating electron correlations at the transition state where two diabatic surfaces strongly interact. Nevertheless, the entire process can be interpreted as shifting one β electron from the Fe dxz orbital to the O2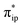 orbital, thus leading to the formation of 71. As indicated by the septet potential surface, because in the avoided crossing region an energetically favorable electron transfer from the Fe(II) center to the O2 ligand takes place, which allows the system to ultimately convert into 71, it is unlikely to trap the proposed Fe(II)–O2 complex during this O2 binding process. In line with this prediction, UV-vis measurements at 193 K showed that no intervening intermediate could be detected en route to 71.20
orbital, thus leading to the formation of 71. As indicated by the septet potential surface, because in the avoided crossing region an energetically favorable electron transfer from the Fe(II) center to the O2 ligand takes place, which allows the system to ultimately convert into 71, it is unlikely to trap the proposed Fe(II)–O2 complex during this O2 binding process. In line with this prediction, UV-vis measurements at 193 K showed that no intervening intermediate could be detected en route to 71.20
Experimentally, the O2 adducts of IPNS10–12 and the 4-NC variant of Fe-HPCD13 have been spectroscopically identified to be quintet Fe(III)-superoxo species. However, our CASSCF(12,9)/NEVPT2 computations could not allow to determine the exact ground state of complex 1 because the estimated septet–quintet energy gap of 2.4 kcal mol−1 falls within the range of uncertainty for ab initio calculations. Thus, we also investigated the reaction of Fe(II)(BDPP) with O2 in an St = 2 state. As shown in Fig. 2, the quintet potential energy surface computed for the O2 binding process is essentially parallel to the septet one in the sense that there exists an analogous avoided crossing around the Fe–O2 distance of 2.30 Å derived from interactions of two diabatic potential curves, yielding a barrier of 11.3 kcal mol−1. Furthermore, the quintet reaction also entails a comparable driving force of 5.6 kcal mol−1. As elaborated below, the diabatic potential curve starting with complex 5A describes the energy variation of an St = 2 state attained by a magnetic coupling of a high spin Fe(II) center (SFe = 2) and a triplet O2 ligand (SO2 = 1) as a function of the Fe–O2 distance; the other one represents a high spin Fe(III) center 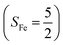 antiferromagnetically coupled with a doublet superoxo ligand
antiferromagnetically coupled with a doublet superoxo ligand 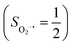 .
.
Ab initio calculations reveal that complex 5A is isoenergetic to 7A and, importantly, the leading electron configuration 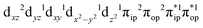 (94%) of the former species is also the same as that of the latter. This can be traced back to the large Fe–O2 separation that prevents any non-negligible metal–ligand interactions from occurring. Following this line of reasoning, 5A should contain a quintet Fe(II) center (SFe = 2) that is exchange coupled to a triplet O2 ligand (SO2 = 1). However, the spin populations calculated for the Fe center (3.21) and the O2 ligand (0.67) differ significantly from those expected for non-interacting SFe = 2 Fe(II) and SO2 = 1 O2 fragments. To solve this problem, the vector coupling model was invoked to construct the spin eigenfunction with a well-defined total spin S of the resulting state derived from the magnetic coupling of a high spin Fe(II) center and a triplet O2 ligand using CGCs. In the present case, the former entity can be characterized by spin eigenfunction |S1,M1〉 = |2,M1〉 (M1 = ±2, ±1, 0), and the latter by |S2,M2〉 = |1,M2〉 (M2 = ±1, 0). The quintet state originating from the interaction of these two fragments should be distinguished by spin eigenfunction |S,M〉 = |2,M〉 (M = ±2, ±1, 0), and its standard component reads
(94%) of the former species is also the same as that of the latter. This can be traced back to the large Fe–O2 separation that prevents any non-negligible metal–ligand interactions from occurring. Following this line of reasoning, 5A should contain a quintet Fe(II) center (SFe = 2) that is exchange coupled to a triplet O2 ligand (SO2 = 1). However, the spin populations calculated for the Fe center (3.21) and the O2 ligand (0.67) differ significantly from those expected for non-interacting SFe = 2 Fe(II) and SO2 = 1 O2 fragments. To solve this problem, the vector coupling model was invoked to construct the spin eigenfunction with a well-defined total spin S of the resulting state derived from the magnetic coupling of a high spin Fe(II) center and a triplet O2 ligand using CGCs. In the present case, the former entity can be characterized by spin eigenfunction |S1,M1〉 = |2,M1〉 (M1 = ±2, ±1, 0), and the latter by |S2,M2〉 = |1,M2〉 (M2 = ±1, 0). The quintet state originating from the interaction of these two fragments should be distinguished by spin eigenfunction |S,M〉 = |2,M〉 (M = ±2, ±1, 0), and its standard component reads 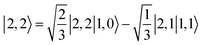 , where the functions on the right hand of the equal sign are written as |S1,M1|S2,M2〉. This spin eigenfunction features Ŝz expectation values (the spin projection along the z axis) of
, where the functions on the right hand of the equal sign are written as |S1,M1|S2,M2〉. This spin eigenfunction features Ŝz expectation values (the spin projection along the z axis) of 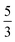 and
and 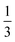 for the Fe(II) center and the O2 unit, respectively. Indeed, both values are in line with the computed spin populations (3.21 for Fe and 0.67 for O2), because ideally spin populations are twice the Ŝz expectation values, thus affirming the proposed electronic-structure assignment.
for the Fe(II) center and the O2 unit, respectively. Indeed, both values are in line with the computed spin populations (3.21 for Fe and 0.67 for O2), because ideally spin populations are twice the Ŝz expectation values, thus affirming the proposed electronic-structure assignment.
Regarding the O2 binding process furnishing 51, as the Fe–O2 distance decreases from 4.00 Å to 2.30 Å (violet curve), the wavefunction steadily acquires multireference character having three dominant electron configurations of 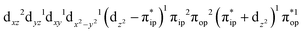 ,
, 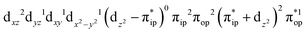 , and
, and 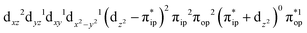 . These three electron configurations differ in their varying occupation numbers in
. These three electron configurations differ in their varying occupation numbers in 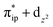 and
and 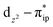 orbitals, both of which, in fact, describe the covalent interaction between the Fe(II) center and the O2 ligand (Fig. 1). During this process, the weight of the first one plummets from 94% to 57%, while those of the last two rise from 0% to 21% and 12%, respectively, likely suggesting the progressively strengthened covalent Fe–O2 interaction. However, the spin density and spin populations computed for 5B are analogous to those for 5A. This finding demonstrates that the electronic structure of 5B is nearly the same as that of 5A, indicative of weak covalent Fe–O2 interaction of 5B. As the Fe–O2 bond length further declines, one electron is shifted from the Fe(II) center to the O2 ligand near the avoided crossing region accompanied by a rapid adjustment of the electronic structure of the nascent Fe(III) center to afford 51 in the end.
orbitals, both of which, in fact, describe the covalent interaction between the Fe(II) center and the O2 ligand (Fig. 1). During this process, the weight of the first one plummets from 94% to 57%, while those of the last two rise from 0% to 21% and 12%, respectively, likely suggesting the progressively strengthened covalent Fe–O2 interaction. However, the spin density and spin populations computed for 5B are analogous to those for 5A. This finding demonstrates that the electronic structure of 5B is nearly the same as that of 5A, indicative of weak covalent Fe–O2 interaction of 5B. As the Fe–O2 bond length further declines, one electron is shifted from the Fe(II) center to the O2 ligand near the avoided crossing region accompanied by a rapid adjustment of the electronic structure of the nascent Fe(III) center to afford 51 in the end.
CASSCF(12,9) calculations reveal that the quintet state of complex 51 features strong multireference character and consists of three key electron configurations of 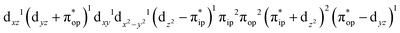 (39%),
(39%), 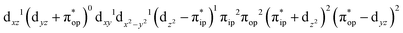 (30%), and
(30%), and 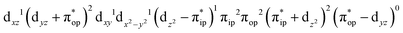 (27%). Apparently, this wavefunction is too complex to extract any chemically sensible bonding information from its predominant electron configurations. Specifically, the first one could be interpreted as a high spin Fe(III) center
(27%). Apparently, this wavefunction is too complex to extract any chemically sensible bonding information from its predominant electron configurations. Specifically, the first one could be interpreted as a high spin Fe(III) center 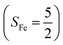 antiferromagnetically coupled to a doublet superoxo ligand
antiferromagnetically coupled to a doublet superoxo ligand 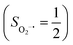 , the second one as a quintet Fe(IV) center (SFe = 2) bound to a singlet peroxo ligand (SO22− = 0), and the last one as a high spin Fe(II) center (SFe = 2) coordinated by a singlet O2 ligand (SO2 = 0). However, as demonstrated in Fig. 2, the spin density calculated for complex 51 exhibits a spherical shape for the Fe center, reminiscent of the high spin Fe(III) center
, the second one as a quintet Fe(IV) center (SFe = 2) bound to a singlet peroxo ligand (SO22− = 0), and the last one as a high spin Fe(II) center (SFe = 2) coordinated by a singlet O2 ligand (SO2 = 0). However, as demonstrated in Fig. 2, the spin density calculated for complex 51 exhibits a spherical shape for the Fe center, reminiscent of the high spin Fe(III) center 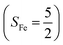 in complexes 7B and 71, but different from the high spin Fe(II) center (SFe = 2) in complexes 7A and 5A. Moreover, the spin density reveals substantial negative spin primarily populating the O2
in complexes 7B and 71, but different from the high spin Fe(II) center (SFe = 2) in complexes 7A and 5A. Moreover, the spin density reveals substantial negative spin primarily populating the O2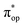 orbital, thereby signaling that the O2 ligand is best described as a doublet superoxo ligand
orbital, thereby signaling that the O2 ligand is best described as a doublet superoxo ligand 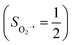 . Based on these findings, we surmised that complex 51 is best described as a high spin Fe(III) center
. Based on these findings, we surmised that complex 51 is best described as a high spin Fe(III) center 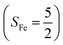 antiferromagnetically coupled with a superoxo ligand
antiferromagnetically coupled with a superoxo ligand 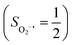 affording an overall St = 2 state. Following the route used to interpret the electronic structure of 5A, such a bonding situation should be described by
affording an overall St = 2 state. Following the route used to interpret the electronic structure of 5A, such a bonding situation should be described by 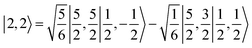 . This spin eigenfunction furnishes Ŝz expectation values of
. This spin eigenfunction furnishes Ŝz expectation values of 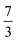 and
and 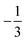 for the Fe center and the O2 ligand, respectively, congruent with the computed spin populations (4.41 for Fe and −0.61 for O2), affirming the bonding interpretation.
for the Fe center and the O2 ligand, respectively, congruent with the computed spin populations (4.41 for Fe and −0.61 for O2), affirming the bonding interpretation.
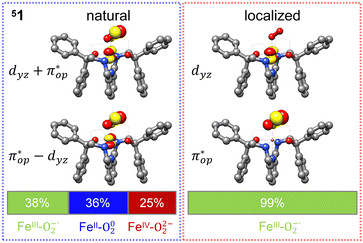
Alternatively, to interpret the multireference wavefunction computed for complex 51, valence bonding (VB) reading68–71 was also employed as exemplified by the VB analysis of the electronic structure of the myoglobin O2 adduct reported by Sason and coworkers.72 As shown in Fig. 3, upon localization of 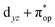 and
and 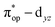 , representing bonding and antibonding interactions of dyz and
, representing bonding and antibonding interactions of dyz and 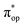 , the ground state wavefunction re-expressed in the basis of the localized orbitals (dyz and
, the ground state wavefunction re-expressed in the basis of the localized orbitals (dyz and 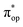 ) contains merely one electron configuration of
) contains merely one electron configuration of 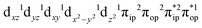 (99%), whereas the original one in the basis of the natural orbitals exhibits strong multireference character having three dominant electron configurations as discussed above. It should be pointed out that both wavefunctions are equivalent because they are related by a unitary transformation of orbitals in the active space. Moreover, the computed spin density and spin populations reveal that the majority spin is located on the Fe center and the minority one of the opposite sign on the O2 ligand. As such, the spin-up and spin-down electrons, which are spin paired, are located in the dyz and
(99%), whereas the original one in the basis of the natural orbitals exhibits strong multireference character having three dominant electron configurations as discussed above. It should be pointed out that both wavefunctions are equivalent because they are related by a unitary transformation of orbitals in the active space. Moreover, the computed spin density and spin populations reveal that the majority spin is located on the Fe center and the minority one of the opposite sign on the O2 ligand. As such, the spin-up and spin-down electrons, which are spin paired, are located in the dyz and 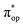 MOs, respectively. Both findings therefore approve of the electronic-structure assignment presented above.
MOs, respectively. Both findings therefore approve of the electronic-structure assignment presented above.
Clearly, in the case of complex 51, VB analyses is as efficient as constructing two-fragment spin eigenfunction in interpreting its multireference wavefunction. However, this approach is not applicable to complex 5A where the absence of any covalent interactions between the Fe center and the O2 ligand renders localization fruitless. It follows that VB analysis cannot be used to characterize multireference wavefunctions without strong electron correlations. In this respect, our simple approach does not have such a limitation.
The reaction of Fe(II)(BDPP) with O2 in an St = 1 state also features two diabatic potential curves, one denotes a high spin Fe(II) center (SFe = 2) antiferromagnetically coupled with a triplet O2 ligand (SO2 = 1), and the other describes an intermediate spin Fe(III) center 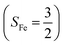 antiferromagnetically coupled with a doublet superoxo ligand
antiferromagnetically coupled with a doublet superoxo ligand 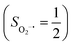 . Although the triplet transformation is barrierless, it is highly endothermic by 30.2 kcal mol−1. (See the ESI† for more details) and cannot contribute to the actual reaction. Taken together, O2 association on a high spin ferrous center proceeds either on a septet or on a quintet surface, in line with the experimental findings.20
. Although the triplet transformation is barrierless, it is highly endothermic by 30.2 kcal mol−1. (See the ESI† for more details) and cannot contribute to the actual reaction. Taken together, O2 association on a high spin ferrous center proceeds either on a septet or on a quintet surface, in line with the experimental findings.20
O2 binding on Co(II)(BDPP) affording complex 2
As shown in Fig. 4, starting from 2C at a Co–O2 distance of 4.50 Å, the diabatic potential curve (magenta line) of the doublet state arising from an antiferromagnetic coupling of a high spin Co(II) center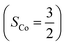 and a triplet O2 ligand (SO2 = 1) is constantly uphill as the Co–O2 bond length decreases. Furthermore, starting from the Co–O2 distance of 2.50 Å, we could find another diabatic potential curve (crimson line) that is best described as a low spin Co(III) ion (SCo = 0) interacting with a doublet superoxide radical
and a triplet O2 ligand (SO2 = 1) is constantly uphill as the Co–O2 bond length decreases. Furthermore, starting from the Co–O2 distance of 2.50 Å, we could find another diabatic potential curve (crimson line) that is best described as a low spin Co(III) ion (SCo = 0) interacting with a doublet superoxide radical 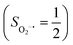 . Its energy first decreases for the Co–O2 distance descending from 2.50 Å to 1.90 Å and then increases for the even shorter Co–O2 distances; hence, a local minimal (22) is located at the Co–O2 length of ∼1.90 Å. Two diabatic potential curves interact in the vicinity of the Co–O2 distance being 2.40 Å and generate an avoided crossing with a barrier of 24.7 kcal mol−1 for the O2 binding reaction affording complex 22. Moreover, the entire process is slightly endothermic by 8.4 kcal mol−1. In analogy to the O2 association yielding 71, our ab initio computations likely overestimate the barrier and the driving force, because experimentally complex 22 is stable at low temperatures (<193 K) but releases O2 upon elevating the temperature.22
. Its energy first decreases for the Co–O2 distance descending from 2.50 Å to 1.90 Å and then increases for the even shorter Co–O2 distances; hence, a local minimal (22) is located at the Co–O2 length of ∼1.90 Å. Two diabatic potential curves interact in the vicinity of the Co–O2 distance being 2.40 Å and generate an avoided crossing with a barrier of 24.7 kcal mol−1 for the O2 binding reaction affording complex 22. Moreover, the entire process is slightly endothermic by 8.4 kcal mol−1. In analogy to the O2 association yielding 71, our ab initio computations likely overestimate the barrier and the driving force, because experimentally complex 22 is stable at low temperatures (<193 K) but releases O2 upon elevating the temperature.22
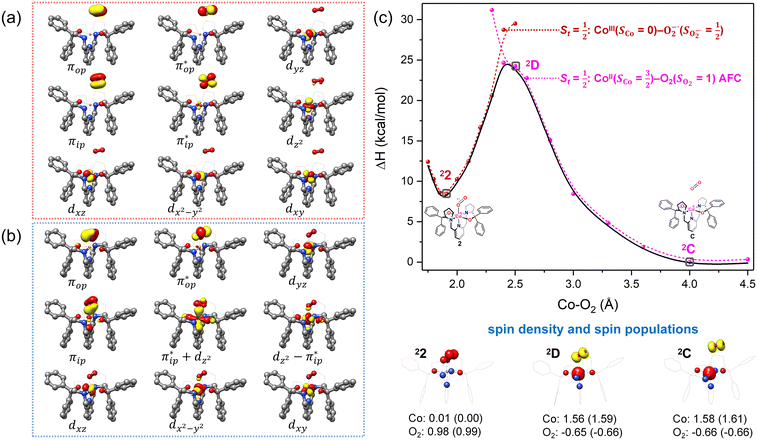 | ||
Fig. 4 Active spaces of complexes C (a) and 2 (b); the doublet potential energy surface for the reaction of Co(II)(BDPP) with O2 as a function of the Co–O2 bond distance obtained by CASSCF(13,9)/NEVPT2 computations. The dot lines denote diabatic potential curves, namely, the magenta line denotes a doublet CoII–O2 complex, interpreted as an 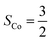 CoII center antiferromagnetically coupled (FC) with a triplet O2 ligand (SO2 = 1); the crimson line denotes a doublet CoIII–O2−˙ complex, interpreted as an SCo = 0 CoIII ion interacting with a doublet O2−˙ ligand CoII center antiferromagnetically coupled (FC) with a triplet O2 ligand (SO2 = 1); the crimson line denotes a doublet CoIII–O2−˙ complex, interpreted as an SCo = 0 CoIII ion interacting with a doublet O2−˙ ligand 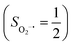 ; the black line denotes the ; the black line denotes the 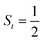 adiabatic curve; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Co center and the O2 ligand calculated for complexes 2C (Co(II)(BDPP) + O2), 2D and 22 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (c); hydrogen atoms are omitted for clarity. adiabatic curve; spin density and Löwdin and Mulliken (in parentheses) spin populations on the Co center and the O2 ligand calculated for complexes 2C (Co(II)(BDPP) + O2), 2D and 22 on the reaction trajectory are shown at the bottom, yellow and red denote negative and positive spin density, respectively, and local spin populations are also listed in the ESI† (c); hydrogen atoms are omitted for clarity. | ||
CASSCF(13,9) calculations of complex 2C produce a predominant electron configuration of 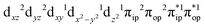 accounting for 80% of the wavefunction. As demonstrated in Fig. 4, the computed spin density plot exhibits a double-layer donut shape of the O2 ligand, which implies that unpaired electrons equally populate its
accounting for 80% of the wavefunction. As demonstrated in Fig. 4, the computed spin density plot exhibits a double-layer donut shape of the O2 ligand, which implies that unpaired electrons equally populate its 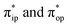 orbitals. Therefore, both findings suggest that complex 2C is best interpreted as a high spin Co(II) center
orbitals. Therefore, both findings suggest that complex 2C is best interpreted as a high spin Co(II) center 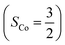 antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1) yielding an overall
antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1) yielding an overall 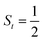 ground state. Again, we constituted two-fragment spin eigenfunctions using CGCs to interpret this wavefunction and it reads
ground state. Again, we constituted two-fragment spin eigenfunctions using CGCs to interpret this wavefunction and it reads 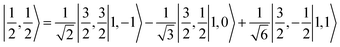 . This spin eigenfunction gives Ŝz expectation values of
. This spin eigenfunction gives Ŝz expectation values of 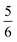 and
and 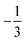 for the Co(II) center and the O2 ligand, respectively. Indeed, both values are in line with the computed spin populations, which confirms the proposed electronic-structure assignment.
for the Co(II) center and the O2 ligand, respectively. Indeed, both values are in line with the computed spin populations, which confirms the proposed electronic-structure assignment.
On the other hand, ab initio calculations suggest that complex 22 features a leading configuration of 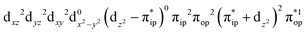 (95%). Clearly, its electronic structure is best described as a low spin Co(III) center (SCo = 0) bound to a doublet superoxo ligand
(95%). Clearly, its electronic structure is best described as a low spin Co(III) center (SCo = 0) bound to a doublet superoxo ligand 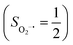 , congruent with the computed spin density and spin populations of 0.01 for the Co center and of 0.98 for the O2 moiety as demonstrated in Fig. 4.
, congruent with the computed spin density and spin populations of 0.01 for the Co center and of 0.98 for the O2 moiety as demonstrated in Fig. 4.
Regarding the O2 binding process furnishing 22, as the Co–O2 distance decreases from 4.50 Å to 2.30 Å (magenta curve), the wavefunction steadily acquires multireference character with three dominant electron configurations of 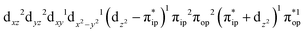 ,
, 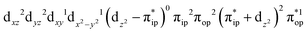 , and
, and 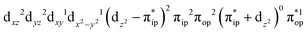 . These three electron configurations differ in their varying occupation numbers in
. These three electron configurations differ in their varying occupation numbers in 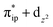 and
and 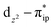 orbitals that describe the covalent interaction between the Co(II) center and O2 ligand as depicted in Fig. 1. During this process, the weights of the last two terms rise from 0% to 34% and 17%, respectively, which comes at the price of the percentage of the first one that lowers from 80% to 22%, perhaps signaling the increased Co–O2 bonding strength. However, the electronic structure of 2D is similar to that of 2C as evidenced by the comparable spin density and spin populations computed for both species, which suggests that the Co–O2 covalent interaction is rather weak. As the Co–O2 distance further declines, a one-electron transfer from the Co(II) center to the O2 ligand occurs around the avoided crossing region concurrent with a rapid adjustment of the electronic structure of the Co(III) center furnishing complex 22.
orbitals that describe the covalent interaction between the Co(II) center and O2 ligand as depicted in Fig. 1. During this process, the weights of the last two terms rise from 0% to 34% and 17%, respectively, which comes at the price of the percentage of the first one that lowers from 80% to 22%, perhaps signaling the increased Co–O2 bonding strength. However, the electronic structure of 2D is similar to that of 2C as evidenced by the comparable spin density and spin populations computed for both species, which suggests that the Co–O2 covalent interaction is rather weak. As the Co–O2 distance further declines, a one-electron transfer from the Co(II) center to the O2 ligand occurs around the avoided crossing region concurrent with a rapid adjustment of the electronic structure of the Co(III) center furnishing complex 22.
The doublet potential energy surface of the O2 association process yielding 22 is also constructed by two diabatic potential curves, one represents the reactant complex containing a high spin Co(II) center 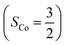 antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1) yielding an overall
antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1) yielding an overall 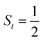 ground state, and the other describes the product complex consisting of a low spin Co(III) ion (SCo = 0) interacting with a doublet superoxide radical
ground state, and the other describes the product complex consisting of a low spin Co(III) ion (SCo = 0) interacting with a doublet superoxide radical 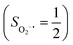 . For the reaction of Co(II)(BDPP) with O2, the emergence of the avoided crossing region suggests that no intermediate other than 22 can be observed and that the Co(II)–O2 adduct does not exist, consistent with the experimental findings.22
. For the reaction of Co(II)(BDPP) with O2, the emergence of the avoided crossing region suggests that no intermediate other than 22 can be observed and that the Co(II)–O2 adduct does not exist, consistent with the experimental findings.22
For O2 binding on Fe(II)(BDPP) and Co(II)(BDPP), our ab initio calculations show that the former process has a lower barrier of 13.6 kcal mol−1 to 71 than the latter (24.7 kcal mol−1) to 22. This theoretical prediction is congruent with the experimental observation that the generation of 71 is much faster than that of 22.20,22 Furthermore, both transformations feature an avoided crossing that realizes one-electron transfer from a divalent metal center to O2 and furnishes a trivalent metal center and a superoxo ligand as the final product; consequently, the divalent–O2 adduct cannot be formed.
As elaborated in the section of Introduction, except one case, reactions of O2 with a wide variety of Fe(II) and Co(II) precursors reported thus far all generate Fe(III) or Co(III) superoxo products, which intimates that the avoided crossing found for the O2 addition processes on Fe(II)(BDPP) and Co(II)(BDPP) occurs in those transformations as well. In fact, the O2 association to related Mn(II)(BDPP) also produces a Mn(III)–O2−˙ complex, instead of Mn(II)–O2.29 Likewise, the treatment of a series of Cu(I) species including [Cu(NH2-TMPA)]+ (TMPA = tris-methyl pyridine amine),73 [Cu(TMG3tren)]+ (TMG3tren = tris(tetramethylguanidino)tren)74 and [Cu(Ar3-TMPA)]+ (Ar = tpb, dpb and dtbpb)75 with O2 invariably affords Cu(II)–O2−˙, whereas the authenticated O2 adduct, Cu(I)–O2, is yet to be disclosed. For more reactions of O2 and metal complexes affording superoxo adducts, readers may refer to review articles.76–80 However, the reaction of O2 with Y257F-HPCA was proposed to furnish Fe(II)–O2 rather than Fe(III)–O2−˙. This proposition was solely based on 57Fe Mössbauer measurements that give an unambiguous assignment of the Fe oxidation state, but the detailed information about the exact valence state of the O2 ligand remains lacking. Therefore, thorough experimental research is required to verify the advocated electronic-structure assignment and disprove and/or substantiate our theoretical prediction.
Comments on DFT computations
For a given state distinguished by a total spin of S, Ms, its spin projection along the z axis, possesses 2S + 1 values (−S, −S + 1, …, S − 1, S) and constitutes 2S + 1 microstate labelled as |S,Ms〉. Among them, only |S,S〉 and |S, −S〉 could be represented by a single Slater determinant, whereas others have to be constructed as a linear combination of a series of Slater determinants, all having the same eigenvalue of Ms with respect to Ŝz, in order to be the eigenfunctions of Ŝ2. Therefore, single-Slater-determinant approaches such as DFT could only deal with |S,S〉 and |S, −S〉. Both are equivalent except for the different eigenvalue for Ŝz; hence, typically merely |S,S〉 called the standard component is computed. A representative example is complex 22 in Fig. 5, for which the spin populations of Co and O2 from B3LYP calculations with 〈Ŝ2〉 = 0.76 are −0.02 and 1.00, respectively, congruent with the anticipated spin eigenfunction of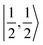 .
.
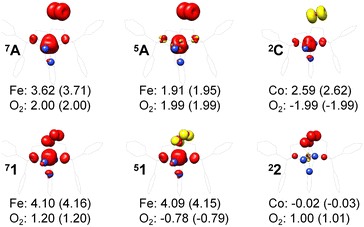 | ||
| Fig. 5 Spin density and Löwdin and Mulliken (in parentheses) spin populations for the metal center and the O2 ligand from DFT calculations; ligand atoms are omitted for clarity. | ||
For systems featuring magnetic couplings of two fragments with their respective spins of S1 and S2, the resulting state may possess a total spin St = S1 − S2, S1 − S2 + 1, …, S1 + S2, (S1 > S2) according to the well-established rule of angular momentum addition. As elaborated above, the spin wavefunction, |S,M〉, could be built up by the spin eigenfunctions of two constituent fragments, |S1,M1〉 and |S2,M2〉. Of note, as required by the symmetry of CGCs, M = M1 + M2. Geometrically, this means that the z component of the vector sum of two angular momenta is equal to the algebraic sum of their z components. For ferromagnetic coupling with St = S1 + S2, the spin eigenfunction of its standard component, |S1 + S2, S1 + S2〉, could also be represented by a single Slater determinant constructed by the combination of two single Slater determinants distinguished by |S1,S1〉 and |S2,S2〉 for the two components into one. Thus, such systems can be properly treated with DFT, for instance, the septet reaction of O2 with Fe(II)(BDPP). As demonstrated in Fig. 5, the spin populations on the Fe center and O2 ligand estimated by B3LYP computations for 7A (3.62 for Fe(II) and 1.99 for O2) and 71 (4.10 for Fe(III) and 1.20 for O2−˙) are all in line with those (3.86 for Fe(II) and 2.00 for O2 in 7A, 4.74 for Fe(III) and 1.03 for O2−˙ in 71) derived from CASSCF(12,9) calculations. Moreover, the computed Ŝ2 expectation values of 〈Ŝ2〉 = 12.00 for 7A and 〈Ŝ2〉 = 12.00 for 71 indicate that both B3LYP solutions are devoid of considerable spin contamination and are eigenfunctions of Ŝ2 having well-defined energies.
The situation is distinctly different for systems involving antiferromagnetic couplings where the resulting state has a total spin of St < S1 + S2, and the wavefunction of its standard component, |St,St〉, cannot be represented as a single determinant but has to be constructed as a linear combination of a range of Slater determinants with the eigenvalue of Ŝz being St to fulfill the requirement of spin symmetry. Therefore, in principle, DFT cannot be used to compute the electronic structures of such systems.
For one particular case with St = S1 − S2, its standard component |S1 − S2, S1 − S2〉 again should be built up as a linear combination of |S1,S1|S2, −S2〉, |S1,S1 − 1|S2, −S2 + 1〉, …, all featuring the same the Ŝz eigenvalue of S1 − S2. Importantly, the first one could be described as a single Slater determinant formed by the combination of two single Slater determinants characterized by |S1,S1〉 and |S2, −S2〉 for the two constituent fragments into one. Broken symmetry formalism exploits this feature and approximate |S1 − S2,S1 − S2〉 as |S1,S1|S2, −S2〉, which means just choosing the first component from the above series. Consequently, the resulting solution is no longer the eigenfunction of Ŝ2 and spin density and spin populations derived from broken symmetry calculations are not correct. Generally speaking, nonnegligible spin contamination should be regarded as a characteristic of broken symmetry solutions that can be used to differentiate it from usual “spin-pure” solution discussed above. A case in point is complex 2C where spin populations of 2.59 for Co(II) and −1.99 for O2 provided by broken symmetry B3LYP calculations are in line with the expected values for 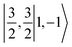 (Fig. 5). These erroneous values differ significantly from those (1.58 for Co(II) and −0.66 for O2) derived from CASCSF(13,9) calculations, but nevertheless indicate that the local spins of the Co(II) center and the O2 ligand are
(Fig. 5). These erroneous values differ significantly from those (1.58 for Co(II) and −0.66 for O2) derived from CASCSF(13,9) calculations, but nevertheless indicate that the local spins of the Co(II) center and the O2 ligand are 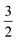 and 1, respectively, thus yielding a qualitatively correct bonding description of complex 2C. However, this DFT solution suffers from unacceptable spin contamination with 〈Ŝ2〉 = 2.77. As a consequence, its energy is not reliable because it is not the eigenfunction of the Hamiltonian operator, Ĥ, either. As shown in Fig. 5, complex 51 also belongs to this category.
and 1, respectively, thus yielding a qualitatively correct bonding description of complex 2C. However, this DFT solution suffers from unacceptable spin contamination with 〈Ŝ2〉 = 2.77. As a consequence, its energy is not reliable because it is not the eigenfunction of the Hamiltonian operator, Ĥ, either. As shown in Fig. 5, complex 51 also belongs to this category.
While for other resulting state with S1 − S2 < St < S1 + S2, its standard component cannot be approximately by a single Slater determinant any more. For example, for St = S1 + S2 − 1, the standard component characterized by |S1 + S2 − 1,S1 + S2 − 1〉 should be constructed as a linear combination of the wavefunction distinguished by |S1,S1 − 1|S2,S2〉 and |S1,S1|S2,S2 − 1〉. As elaborated above, both |S1,S1 − 1〉 and |S2,S2 − 1〉 cannot be represented by a single Slater determinant; hence, neither can |S1,S1 − 1|S2,S2〉 nor |S1,S1|S2,S2 − 1〉. Thus, DFT completely fails for this kind of systems as exemplified by complex 5A. As depicted in Fig. 5, spin populations on Fe(II) of 1.90 and O2 of 1.99 for O2 erroneously predicted by DFT calculations indicate that the converged B3LYP solution is best interpreted as a triplet Fe(II) center (SFe = 1) ferromagnetically coupled to a triplet O2 ligand (SO2 = 1); therefore, the local spins of Fe and O2 are qualitatively wrong.
In summary, only systems possessing two ferromagnetically coupled fragments, DFT calculations can be used to compute their electronic structures and spin density and spin populations and give reliable energies; otherwise, DFT computations in principle produce incorrect electronic structures and spin density and spin populations. For states with St = S1 − S2, the electronic structure can be approximately computed by invoking broken symmetry formalism in the framework of DFT calculations. But interpreting the resulting spin density and populations requires particular caution. In particular, for open-shell singlets, the artificial spin density obtained from broken symmetry calculations is qualitatively incorrect, because there does not exist any spin density everywhere for diamagnetic systems irrespective of being closed-shell or open-shell singlets. For comparison, the potential energy surfaces computed by DFT are summarized in the ESI.†
Conclusions
CASSCF/NEVPT2 calculations were employed to explore the electronic-structure evolution over the course of O2 binding on Co(II) and Fe(II) precursors affording Fe(III)–O2−˙ (1) and Co(III)–O2−˙ (2) complexes. For the former reaction on the septet and quintet potential surfaces, starting complex 7,5A is best formulated as a high spin Fe(II) center (SFe = 2) ferromagnetically or magnetically coupled with a triplet O2 ligand (SO2 = 1), while product 7,51 consists of a high spin Fe(III) center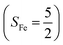 ferromagnetically or antiferromagnetically coupled a superoxo ligand
ferromagnetically or antiferromagnetically coupled a superoxo ligand 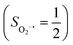 . Regarding the latter reaction in an
. Regarding the latter reaction in an 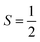 state, initial complex 2C could be best characterized as a high spin Co(II) center
state, initial complex 2C could be best characterized as a high spin Co(II) center 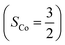 antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1), while O2 adduct 22 contains a low spin Co(III) center (SCo = 0) interacting with a superoxo ligand
antiferromagnetically coupled to a triplet O2 ligand (SO2 = 1), while O2 adduct 22 contains a low spin Co(III) center (SCo = 0) interacting with a superoxo ligand 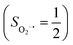 . As O2 steadily approaches the divalent metal center, the diabatic energy curve of M(II)–O2 constantly rises in energy and interacts with that of M(III)–O2−˙ at a M–O2 distance of around ∼2.40 Å. This interaction generates an avoided crossing that effects a spontaneous single-electron transfer from the divalent metal center to the incoming O2 ligand, thereby leading to M(III)–O2−˙ as the final product and ruling out the possibility of formation of a bona fide M(II)–O2 complex. This view has been used to explain the reaction outcomes of related O2 association processes.
. As O2 steadily approaches the divalent metal center, the diabatic energy curve of M(II)–O2 constantly rises in energy and interacts with that of M(III)–O2−˙ at a M–O2 distance of around ∼2.40 Å. This interaction generates an avoided crossing that effects a spontaneous single-electron transfer from the divalent metal center to the incoming O2 ligand, thereby leading to M(III)–O2−˙ as the final product and ruling out the possibility of formation of a bona fide M(II)–O2 complex. This view has been used to explain the reaction outcomes of related O2 association processes.
To extract electronic-structure information from complicated multireference wavefunctions, we constructed two-fragment spin eigenfunctions with CGCs to rationalize computed spin density and fragment spin populations on metal centers and O2 moieties and deduced corrected electronic-structure formulations. This approach is complementary to usual VB analyses as demonstrated by applications of both methods to analyze the electronic-structure of O2 adduct 51. This species features antiferromagnetic coupling of a high spin Fe(III) center 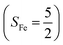 and a superoxo ligand
and a superoxo ligand 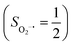 ; however, directly reading out electron configurations of the resulting authenticated multireference wavefunctions hardly gains any chemically sensible bonding information.
; however, directly reading out electron configurations of the resulting authenticated multireference wavefunctions hardly gains any chemically sensible bonding information.
For systems involving metal–ligand or metal–metal antiferromagnetic couplings with St = S1 − S2, DFT calculations, despite giving a qualitatively right electronic structure, invariably suffer from spin contamination. Consequently, the resulting spin density and spin populations are not reliable. Furthermore, DFT fails completely for systems with S1 − S2 < St < S1 − S2 in predicting qualitatively correct electronic structures. Only for ferromagnetically coupled systems with St = S1 + S2, DFT is able to give exact electronic structures and energies.
Author contributions
S. Y. conceived the presented idea. P. Z. performed the computations and wrote the original draft. S. Y. and W. L. reviewed and edited the final draft. All authors discussed the results and contributed to the final manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work conducted in Dalian was supported by the National Key R&D Program of China (No. 2021YFA1502803), the National Natural Science Foundation of China (92161204) and the DaIian Institute of Chemical Physics, Chinese Academy of Sciences (Grant: DICP I202312). W. L. is grateful for the financial support from the Ministry of Science and Technology of Taiwan (MOST 111-2113-M-003-008-MY3 to W.-Z. L.). We are indebted to Mr Haowei Chen for his helpful discussions.Notes and references
- M. Costas, M. P. Mehn, M. P. Jensen and L. Que Jr, Chem. Rev., 2004, 104, 939 CrossRef CAS PubMed.
- E. G. Kovaleva and J. D. Lipscomb, Nat. Chem. Biol., 2008, 4, 186 CrossRef CAS PubMed.
- E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659 CrossRef CAS PubMed.
- C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Chem. Rev., 2017, 117, 2059 CrossRef CAS PubMed.
- X. Huang and J. T. Groves, Chem. Rev., 2017, 118, 2491 CrossRef PubMed.
- A. J. Jasniewski and L. Que, Jr., Chem. Rev., 2018, 118, 2554 CrossRef CAS PubMed.
- L. Pauling and C. D. Coryell, Proc. Natl. Acad. Sci. U. S. A., 1936, 22, 210 CrossRef CAS PubMed.
- B. A. Springer, S. G. Sligar, J. S. Olson and G. N. Phillips Jr., Chem. Rev., 1994, 94, 699 CrossRef CAS.
- K. Shikama, Chem. Rev., 1998, 98, 1357 CrossRef CAS PubMed.
- J. E. Baldwin and M. Bradley, Chem. Rev., 1990, 90, 1079 CrossRef CAS.
- P. L. Roach, I. J. Clifton, V. Fülöp, K. Harlos, G. J. Barton, J. Hajdu, I. Andersson, C. J. Schofield and J. E. Baldwin, Nature, 1995, 375, 700 CrossRef CAS PubMed.
- P. L. Roach, I. J. Clifton, C. M. H. Hensgens, N. Shibata, C. J. Schofield, J. Hajdu and J. E. Baldwin, Nature, 1997, 387, 827 CrossRef CAS PubMed.
- M. M. Mbughuni, M. Chakrabarti, J. A. Hayden, E. L. Bominaar, M. P. Hendrich, E. Münck and J. D. Lipscomb, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16788 CrossRef CAS PubMed.
- L. Que Jr. and R. Y. N. Ho, Chem. Rev., 1996, 96, 2607 CrossRef PubMed.
- E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y. Yang and J. Zhou, Chem. Rev., 2000, 100, 235 CrossRef CAS PubMed.
- R. A. Baglia, J. P. T. Zaragoza and D. P. Goldberg, Chem. Rev., 2017, 117, 13320 CrossRef CAS PubMed.
- S. Yadav, V. Yadav, M. A. Siegler, P. Moënne-Loccoz, G. N. L. Jameson and D. P. Goldberg, J. Am. Chem. Soc., 2024, 146(12), 7915 CrossRef CAS PubMed.
- C. Winslow, H. Lee, M. J. Field, S. J. Teat and J. Rittle, J. Am. Chem. Soc., 2021, 143(34), 13686 CrossRef CAS PubMed.
- M. N. Blakely, M. A. Dedushko, P. C. Y. Poon, G. Villar-Acevedo and J. A. Kovacs, J. Am. Chem. Soc., 2019, 141(5), 1867 CrossRef CAS PubMed.
- J. Sacramento, T. Albert, M. Siegler, P. Moënne-Loccoz and D. P. Goldberg, Angew. Chem., Int. Ed., 2022, 61, e202111492 CrossRef CAS PubMed.
- C. Chiang, S. T. Kleespies, H. D. Stout, K. K. Meier, P. Li, E. L. Bominaar, L. Que Jr., E. Münck and W. Lee, J. Am. Chem. Soc., 2014, 136, 10846 CrossRef CAS PubMed.
- P. Zhang, Y. Tian, Z. Wang, W. Lee and S. Ye, Chem. – Eur. J., 2024, 30, e202400336 CrossRef CAS PubMed.
- C. Wang, H. Chang, Y. Lai, H. Fang, C. Li, H. Hsu, Z. Li, T. Lin, T. Kuo, F. Neese, S. Ye, Y. Chiang, M. Tsai, W. Liaw and W. Lee, J. Am. Chem. Soc., 2016, 138, 14186 CrossRef CAS PubMed.
- A. J. Fielding, J. D. Lipscomb and L. Que Jr., J. Am. Chem. Soc., 2012, 134, 796 CrossRef CAS PubMed.
- F. A. Walker and J. Bowen, J. Am. Chem. Soc., 1985, 107, 7632 CrossRef CAS.
- J. B. Gordon, A. C. Vilbert, M. A. Siegler, K. M. Lancaster, P. Moënne-Loccoz and D. P. Goldberg, J. Am. Chem. Soc., 2019, 141(5), 3641 CrossRef CAS PubMed.
- P. Kumar, S. V. Lindeman and A. T. Fiedler, J. Am. Chem. Soc., 2019, 141, 10984 CrossRef CAS PubMed.
- A. Huber, L. Müller, H. Elias, R. Klement and M. Valko, Eur. J. Inorg. Chem., 2005, 1459 CrossRef CAS.
- J. Yang, P. Li, X. Li, L. Xie, N. Wang, H. Lei, C. Zhang, W. Zhang, Y.-M. Lee, W. Zhang, R. Cao, S. Fukuzumi and W. Nam, Angew. Chem., Int. Ed., 2022, 61, e202208143 CrossRef CAS PubMed.
- Y. Lin, H. Hinrika Cramer, M. van Gastel, Y. Tsai, C. Chu, T. Kuo, I. Lee, S. Ye, E. Bill and W. Lee, Inorg. Chem., 2019, 58, 9756 CrossRef CAS PubMed.
- H. Pan, H. Chen, Z. Wu, P. Ge, S. Ye, G. Lee and H. Hsu, JACS Au, 2021, 1, 1389 CrossRef CAS PubMed.
- E. G. Kovaleva, M. B. Neibergall, S. Chakrabarty and J. D. Lipscomb, Acc. Chem. Res., 2007, 40, 475 CrossRef CAS PubMed.
- S. M. Adam, G. B. Wijeratne, P. J. Rogler, D. E. Diaz, D. A. Quist, J. J. Liu and K. D. Karlin, Chem. Rev., 2018, 118, 10840 CrossRef CAS PubMed.
- E. G. Kovaleva and J. D. Lipscomb, Science, 2007, 316, 453.201 CrossRef PubMed.
- M. M. Mbughuni, K. K. Meier, E. Munck and J. D. Lipscomb, Biochemistry, 2012, 51, 8743 CrossRef CAS PubMed.
- M. Radon and K. Pierloot, J. Phys. Chem. A, 2008, 112, 11824 CrossRef CAS PubMed.
- H. Chen, M. Ikeda-Saito and S. Shaik, J. Am. Chem. Soc., 2008, 130, 14778 CrossRef CAS PubMed.
- S. Shaik and H. Chen, J. Biol. Inorg. Chem., 2011, 16, 841 CrossRef CAS PubMed.
- H. Chen, K. Cho, W. Lai, W. Nam and S. Shaik, J. Chem. Theory Comput., 2012, 8, 915 CrossRef CAS PubMed.
- G. J. Christian, S. Ye and F. Neese, Chem. Sci., 2012, 3, 1600 RSC.
- S. Ye, C. Riplinger, A. Hansen, C. Krebs, J. M. Bollinger, Jr. and F. Neese, Chem. – Eur. J., 2012, 18, 6555 CrossRef CAS PubMed.
- K. P. Jensen, B. O. Roos and U. Ryde, J. Inorg. Biochem., 2005, 99, 45 CrossRef CAS PubMed.
- K. P. Kepp, ChemPhysChem, 2013, 14, 3551 CrossRef CAS PubMed.
- Q. M. Phung and K. Pierloot, Phys. Chem. Chem. Phys., 2018, 20, 17009 RSC.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS.
- J. Ribas-Arino and J. J. Novoa, Chem. Commun., 2007, 3160 RSC.
- P. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS.
- M. E. Rose, Elementary theory of angular momentum, Dover Publications Inc., New York, 1957 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- S. Kossmann and F. Neese, J. Chem. Theory Comput., 2010, 6, 2325 CrossRef CAS PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463 CrossRef CAS PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- H. Chen, P. Zhang and S. Ye, Encyclopedia of Inorganic and Bioinorganic Chemistry, 2024 DOI:10.1002/9781119951438.eibc2883.
- C. Angeli, C. J. Calzado, C. de Graafcd and R. Caballol, Phys. Chem. Chem. Phys., 2011, 13, 14617 RSC.
- C. Angelia, R. Cimiragliaa and J. Malrieu, Mol. Phys., 2013, 111, 1069 CrossRef.
- L. Blancafort, P. Celani, M. J. Bearpark and M. A. Robb, Theor. Chem. Acc., 2003, 110, 92 Search PubMed.
- J. Malrieu, C. Angeli and R. Cimiraglia, J. Chem. Educ., 2008, 85, 150 CrossRef.
- H. Chen, M. Ikeda-Saito and S. Shaik, J. Am. Chem. Soc., 2008, 130, 14778 CrossRef CAS PubMed.
- D. Maiti, H. C. Fry, J. S. Woertink, M. A. Vance, E. I. Solomon and K. D. Karlin, J. Am. Chem. Soc., 2007, 129, 26 CrossRef PubMed.
- C. Wrtele, E. Gaoutchenova, K. Harms, M. C. Holthausen, J. Sundermeyer and S. Schindler, Angew. Chem., Int. Ed., 2006, 45, 3867 CrossRef PubMed.
- S. Y. Quek, S. Debnath, S. Laxmi, M. van Gastel, T. Krämer and J. England, J. Am. Chem. Soc., 2021, 143(47), 19731 CrossRef CAS PubMed.
- R. Trammell, K. Rajabimoghadam and I. Garcia-Bosch, Chem. Rev., 2019, 119, 2954 CrossRef CAS PubMed.
- C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Chem. Rev., 2017, 117, 2059 CrossRef CAS PubMed.
- S. Fukuzumi and K. D. Karlin, Coord. Chem. Rev., 2013, 257, 187 CrossRef CAS PubMed.
- S. Hong, Y. Lee, K. Ray and W. Nam, Coord. Chem. Rev., 2017, 334, 25 CrossRef CAS.
- H. Noh and J. Cho, Coord. Chem. Rev., 2019, 382, 126 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02915a |
| This journal is © the Owner Societies 2024 |