Open Access Article
Open Access ArticleSimulating transient X-ray photoelectron spectra of Fe(CO)5 and its photodissociation products with multireference algebraic diagrammatic construction theory†
Nicholas P.
Gaba
,
Carlos E. V.
de Moura
 ,
Rajat
Majumder
,
Rajat
Majumder
 and
Alexander Yu.
Sokolov
and
Alexander Yu.
Sokolov
 *
*
Department of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA. E-mail: vieirademoura.2@osu.edu; sokolov.8@osu.edu
First published on 21st May 2024
Abstract
Accurate simulations of transient X-ray photoelectron spectra (XPS) provide unique opportunities to bridge the gap between theory and experiment in understanding the photoactivated dynamics in molecules and materials. However, simulating X-ray photoelectron spectra along a photochemical reaction pathway is challenging as it requires accurate description of electronic structure incorporating core-hole screening, orbital relaxation, electron correlation, and spin–orbit coupling in excited states or at nonequilibrium ground-state geometries. In this work, we employ the recently developed multireference algebraic diagrammatic construction theory (MR-ADC) to investigate the core-ionized states and X-ray photoelectron spectra of Fe(CO)5 and its photodissociation products (Fe(CO)4, Fe(CO)3) following excitation with 266 nm light. The simulated transient Fe 3p and CO 3σ XPS spectra incorporating spin–orbit coupling and high-order electron correlation effects are shown to be in a good agreement with the experimental measurements by Leitner et al. [J. Chem. Phys., 2018, 149, 044307]. Our calculations suggest that core-hole screening, spin–orbit coupling, and ligand-field splitting effects are similarly important in reproducing the experimentally observed chemical shifts in transient Fe 3p XPS spectra of iron carbonyl complexes. Our results also demonstrate that the MR-ADC methods can be very useful in interpreting the transient XPS spectra of transition metal compounds.
1 Introduction
Time-resolved X-ray photoelectron spectroscopy (TR-XPS) is a versatile and highly sensitive experimental technique for probing electron and nuclear dynamics in molecules and materials.1–5 In the TR-XPS experiment, the chemical system is sequentially irradiated with two photons: an ultraviolet (UV) or visible pump, which excites the system and initiates the dynamics, and an X-ray or extreme UV (XUV) probe that ionizes an electron out of a core orbital. Changing the time delay between the two photons and measuring the electron count at a particular probe frequency yields the TR-XPS spectra that provide information about the electronic structure and dynamics near the localized core orbital being probed. Advances in X-ray radiation sources and enhancements in laser technology6–9 have made it possible to apply TR-XPS to a wide range of problems, including investigating the charge dynamics in semiconductor interfaces,10–12 tracking bond dissociation processes,13–16 and monitoring the excited-state dynamics of molecules.17–19As the utilization of TR-XPS continues to grow, there is an increasing demand for theoretical methodology that can help interpreting its transient spectral features. In contrast to conventional XPS that measures the response of a chemical system in the ground electronic state near equilibrium geometries,20–22 TR-XPS probes the energies of core electrons in excited states or at nonequilibrium ground-state geometries where electronic structure may exhibit significant multiconfigurational character. In these situations, standard single-reference methods such as ground-state and time-dependent density functional theory,23–26 linear-response and equation-of-motion coupled cluster theory,27–31 and the GW32,33 family of methods may prove to be unreliable, and one may need to use multireference approaches.34
However, most of the available multireference methods are designed to simulate electronic excitations in frontier molecular orbitals, called the active space, and are not well-suited to describe core excitation or ionization processes. Incorporating the core orbitals into the active space and restricting excitations in the reference wavefunction allows to overcome this problem but introduces approximations that can be difficult to control.35–49 Alternatively, core excitations can be described using linear-response or equation-of-motion multireference theories,50–56 which in addition to the excitations in the active space incorporate all single excitations from non-active molecular orbitals. Unfortunately, many of these methods are based on non-Hermitian operators or eigenvalue problems, which complicate the evaluation of excited-state properties and can produce unphysical (complex-valued) excitation energies.
Recently, we developed multireference algebraic diagrammatic construction theory (MR-ADC) for simulating excited states and electronic spectra of molecules.57–61 In addition to excited states in the active space, MR-ADC incorporates all single and double excitations involving non-active molecular orbitals starting with its second-order approximation (MR-ADC(2)). The MR-ADC methods are intruder-state-free, have computational cost similar to that of conventional low-order multireference perturbation theories, are guaranteed to yield real-valued excitation energies, and can be straightforwardly adapted for the simulations of XPS spectra by utilizing the core–valence separation (CVS) technique.62–66 The CVS-MR-ADC methods have been used to calculate the potential energy surfaces of core-excited states in diatomic nitrogen and the ground-state XPS spectra of ozone molecule and benzyne biradicals with significant multiconfigurational character.64–66
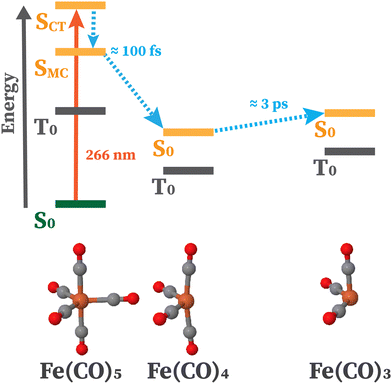
In this work, we present the first CVS-MR-ADC study of transient XPS spectra by applying these methods to iron pentacarbonyl (Fe(CO)5) and its photodissociation products following the excitation with 266 nm light (Fe(CO)x, x = 3, 4). The photodissociation of Fe(CO)5 has been studied using a variety of time-resolved experimental techniques in solution and gas phase. The solution phase dissociation has long been identified to involve triplet states of the photoproducts,67 and a femtosecond-resolution resonant inelastic X-ray scattering study has confirmed the production of Fe(CO)4 in its triplet ground state or coordinated with solvent molecules.68 The gas phase dissociation, however, has been the subject of debate over the specific pathway followed. An early study using transient infrared spectroscopy showed that photoexcitation causes Fe(CO)5 to lose several of its CO ligands, which number depends on the wavelength of excitation.69
A particular attention has been devoted to investigating the gas-phase photodissociation dynamics of Fe(CO)5 following the excitation at 266 nm, which causes the loss of two CO ligands to form Fe(CO)3.70,71 Starting with Fe(CO)5 in its 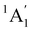 (D3h symmetry) ground state,72–74 absorption at 266 nm can populate several closely lying states,72,75 of which singlet excited E′ and
(D3h symmetry) ground state,72–74 absorption at 266 nm can populate several closely lying states,72,75 of which singlet excited E′ and 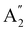 have been identified as potentially participating in the dissociation pathway.70,71,73,76,77 Trushin et al.70 proposed a completely singlet dissociation pathway proceeding through the C2v-symmetric 1A1 state of Fe(CO)4 on a timescale of less than 100 fs,78 followed by subsequent dissociation into singlet Fe(CO)3 within the next 3.3 ps. This singlet pathway, illustrated in Fig. 1, has been supported by studies utilizing ultrafast electron diffraction,73 TR-XPS,15,79 and time-resolved XUV absorption in conjunction with quantum chemical calculations.80 In particular, the gas-phase TR-XPS spectra measured by Wernet et al. and Leitner et al. provide us with the opportunity to benchmark the accuracy of CVS-MR-ADC in simulating transient spectra of transition metal complexes such as Fe(CO)5.
have been identified as potentially participating in the dissociation pathway.70,71,73,76,77 Trushin et al.70 proposed a completely singlet dissociation pathway proceeding through the C2v-symmetric 1A1 state of Fe(CO)4 on a timescale of less than 100 fs,78 followed by subsequent dissociation into singlet Fe(CO)3 within the next 3.3 ps. This singlet pathway, illustrated in Fig. 1, has been supported by studies utilizing ultrafast electron diffraction,73 TR-XPS,15,79 and time-resolved XUV absorption in conjunction with quantum chemical calculations.80 In particular, the gas-phase TR-XPS spectra measured by Wernet et al. and Leitner et al. provide us with the opportunity to benchmark the accuracy of CVS-MR-ADC in simulating transient spectra of transition metal complexes such as Fe(CO)5.
This paper is organized as follows. We first briefly describe the theory behind CVS-MR-ADC (Section 2) and outline computational details (Section 3). In Sections 4.1 and 4.2, we present the simulated transient XPS spectra for the core-level Fe 3p and inner-valence CO 3σ ionizations, respectively, and compare them to the experimental measurements in the XUV region of electromagnetic spectrum from Leitner et al.15 We analyze the results of our calculations in Section 4.3 where we investigate the effect of molecular geometries, spin–orbit coupling effects, active space, and basis set on the simulated XPS spectra. We present our conclusions in Section 5.
2 Theory
2.1 Multireference algebraic diagrammatic construction theory
We start with a brief overview of MR-ADC for ionization energies. A more detailed presentation of the theory can be found elsewhere.57–59,61,64,65The principal information about ionization of valence and core orbitals is contained in the one-particle Green's function (Gpq(ω))81,82 that describes the linear response of a chemical system in the electronic state |Ψ〉 with energy E to the ionizing radiation with frequency ω:
| Gpq(ω) = 〈Ψ|a†p(ω − H − E)−1aq|Ψ〉, | (1) |
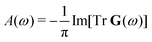 | (2) |
MR-ADC simulates the photoelectron spectra by computing efficient multireference approximations to Gpq(ω) that are constructed by (i) selecting a subset of frontier molecular orbitals, which give rise to the multiconfigurational character of |Ψ〉, as an active space, (ii) computing a complete active space self-consistent field (CASSCF) wavefunction83–85 for the selected active space (|Ψ0〉), and (iii) expanding Gpq(ω) in the multireference perturbation series starting with |Ψ0〉 as the zeroth-order wavefunction and dividing the Hamiltonian H into the zeroth-order (H(0)) and perturbation (V = H − H(0)) contributions. Choosing H(0) to be the Dyall Hamiltonian,86,87 the nth-order approximation to Gpq(ω) (termed as MR-ADC(n)) is constructed by representing this function in the nondiagonal matrix form
| G(ω) = T(ωS − M)−1T† | (3) |
The energies of ionized states (Ω) are computed by solving the generalized eigenvalue problem for the effective Hamiltonian matrix M
| MY = SYΩ | (4) |
| X = TS−1/2Y | (5) |
Two MR-ADC approximations are employed in this work: the strict second-order (MR-ADC(2)) and extended second-order (MR-ADC(2)-X) methods. Both MR-ADC(2) and MR-ADC(2)-X incorporate all electronic excitations in active orbitals and up to double excitations involving at least one non-active orbital. The MR-ADC(2) method approximates each matrix in eqn (3) up to the second order in multireference perturbation theory. The MR-ADC(2)-X approach improves the description of orbital relaxation effects by incorporating the third-order contributions to M and T in the treatment of double excitations.59,61,64,65,87 The ability to describe excitations in non-active orbitals contrasts MR-ADC with conventional multireference perturbation theories that are restricted to exciting electrons only in the active space.
2.2 Core–valence separation
The core-ionized states probed in X-ray photoelectron spectroscopy (XPS) correspond to the high-energy excited states that are deeply embedded in the eigenspectrum of MR-ADC effective Hamiltonian matrix M (eqn (4)) and are difficult to extract using conventional eigenvalue solvers. Fortunately, due to their high localization in space and energy spectrum, the coupling of core-ionized wavefunctions with other electronic states is usually rather weak and can be neglected, which is known as the core–valence separation (CVS) approximation.62,63 The CVS approximation has been shown to produce small (often negligible) systematic errors in excitation energies and transition intensities28,54,92–94 while preventing issues with the discretization of continuum states when using incomplete atom-centered basis sets.28,95Here, we employ our CVS implementation of MR-ADC(2) and MR-ADC(2)-X to efficiently simulate core-ionized states and XPS spectra of Fe(CO)5 and its photodissociation products.64,65 Introducing CVS in MR-ADC(2) and MR-ADC(2)-X leads to a significant reduction in computational cost as only the excitations involving at least one core orbital are included in the representation of MR-ADC matrices. In addition to core-ionized states, the utility of CVS technique has been demonstrated in the MR-ADC calculations of core-excited states and X-ray absorption spectra.60
2.3 Relativistic effects
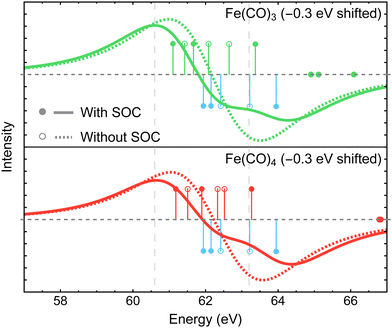
In addition to electron correlation, core-hole screening, and orbital relaxation, simulating core-excited and core-ionized states requires accurate treatment of relativistic effects.56,96–99 Among the two major relativistic interactions are (i) scalar relativistic effects due to the contraction or expansion of atomic orbitals that shift the energies of transitions in XPS spectra and (ii) spin–orbit coupling that alters the densities of states and photoelectron spectra when exciting electrons from core orbitals with non-zero angular momentum (e.g., 2p, 3p, 3d).100In this work, we use the spin-free X2C Hamiltonian101,102 to accurately and efficiently treat scalar relativistic effects in the CASSCF and MR-ADC calculations. To incorporate spin–orbit coupling, we employ a composite approach where the spin–orbit corrections to the MR-ADC(2) and MR-ADC(2)-X core ionization energies are computed at the MR-ADC(1) level of theory using the Breit–Pauli spin–orbit mean-field Hamiltonian. The details of our spin–orbit MR-ADC(1) implementation are provided in the ESI.†
3 Computational details
The molecular geometries of Fe(CO)x (x = 3–5) were optimized using second-order N-electron valence perturbation theory (NEVPT2)103,104 starting with complete active space self-consistent field (CASSCF) reference wavefunctions that included 10 electrons in 10 active orbitals (CAS(10e,10o)). These geometry optimizations were performed for the lowest-energy singlet state of each complex. For Fe(CO)5, the active space included five Fe 3d and five CO orbitals as shown in Fig. 2, in agreement with the previous multireference studies of this molecule.74,75,105 For Fe(CO)4 and Fe(CO)3, CAS(10e,10o) incorporated five Fe 3d and five CO-based orbitals. To simulate experimental conditions with free CO present,15 uncoordinated CO molecules were incorporated into the Fe(CO)4 and Fe(CO)3 calculations. All geometry optimizations were performed with the Molpro program106–108 using the def2-QZVPP basis set.109 Structures with free CO were optimized by constraining the Fe–C distance at 10.0 Å and allowing all other structural parameters to relax. Additionally, two-electron integrals were approximated using density fitting110–113 with the def2-QZVPP-JKFIT and def2-QZVPP-RI auxiliary basis sets employed for CASSCF and NEVPT2, respectively.114–117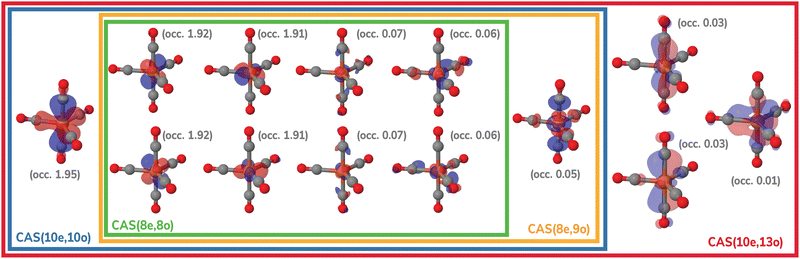 | ||
| Fig. 2 Active spaces of the Fe(CO)5 complex used for the multireference calculations in this work. For each orbital, natural occupations from the CAS(10e,13o) calculation are shown in parentheses. | ||
The XPS spectra of singlet Fe(CO)x (x = 3–5) for the core-level Fe 3p and inner-valence CO 3σ ionization were computed using the CVS-MR-ADC(2) and CVS-MR-ADC(2)-X implementations in the Prism program.118 The Prism code was interfaced with the Pyscf package,119 which provided the one- and two-electron integrals and CASSCF reference wavefunctions. For brevity, we refer to CVS-MR-ADC(2) and CVS-MR-ADC(2)-X as MR-ADC(2) and MR-ADC(2)-X henceforth.
The MR-ADC calculations were performed at the NEVPT2 singlet optimized geometries using the CASSCF reference wavefunctions with the CAS(10e,13o) active space (Fig. 2) and fully uncontracted def2-TZVPP basis set (unc-def2-TZVPP). The ηs = 10−5 and ηd = 10−10 parameters were specified to remove linearly dependent semiinternal and double excitations, respectively. We also considered alternative selections of equilibrium geometries, active spaces, and basis sets in Sections 4.3.1, 4.3.3 and 4.3.4. For the planar (D3h) geometry of Fe(CO)3, a smaller CAS(8e,12o) was used, due to a weaker interaction between the ligand σ orbitals and Fe dz2.
The MR-ADC simulations of XPS spectra were performed using density fitting where for each main basis set we employed the corresponding JKFIT and RI auxiliary basis sets in the CASSCF and MR-ADC calculations, respectively.114–117 Additionally, relativistic effects were incorporated using the spin-free X2C Hamiltonian101,102 and spin–orbit coupling calculations as described in Section 2.3 and ESI.† The XPS spectra were simulated by plotting the density of states
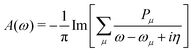 | (6) |
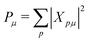 | (7) |
4 Results and discussion
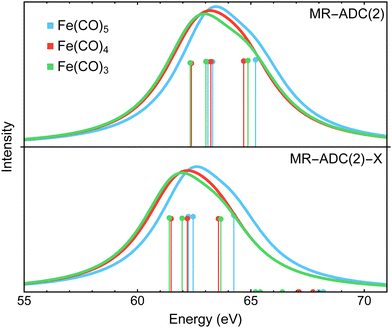
4.1 X-ray photoelectron spectra at the Fe 3p edge
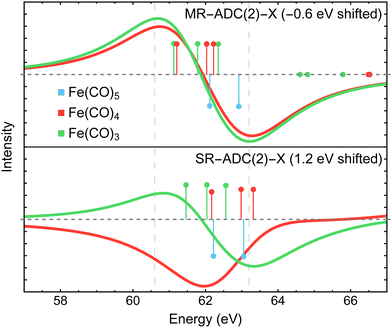
Fig. 3 compares the transient XPS spectra of Fe(CO)4 and Fe(CO)3 simulated using MR-ADC(2) and MR-ADC(2)-X with the experimental difference spectra15 for the core-level Fe 3p ionization. The experimental spectrum of Fe(CO)4 shows two broad features, a negative peak at 63.2 eV and a positive peak at 60.6 eV, indicating a significant redshift in the energy of Fe 3p core-ionized states (Fe 3p−1) upon the loss of the first CO ligand. The dissociation of second CO ligand resulting in Fe(CO)3 does not noticeably change the positions of both features but increases their intensities by ∼15 to 20%.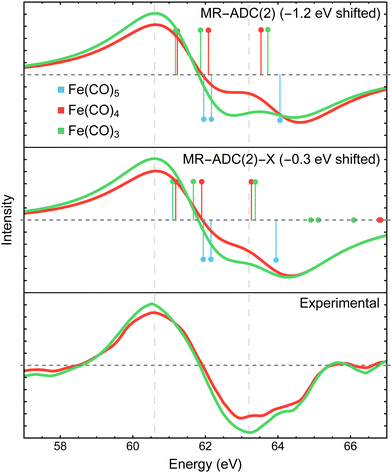 | ||
| Fig. 3 Difference Fe 3p X-ray photoelectron spectra of Fe(CO)4 and Fe(CO)3 relative to Fe(CO)5 measured experimentally15 and simulated using MR-ADC(2) and MR-ADC(2)-X. Vertical lines represent the computed core ionization energies and the corresponding photoelectron intensities. The simulated spectra were shifted to align the position of zero-intensity intercept with the experimental spectrum. Calculations employed the CAS(10e,13o) active space and uncontracted def2-TZVPP basis set. See Section 3 for more computational details. | ||
The MR-ADC(2) and MR-ADC(2)-X simulated Fe 3p difference spectra show a good agreement with the experimental results, reproducing the magnitude of observed spectral changes. Using the unc-def2-TZVPP basis set, the CAS(10e,13o) active space, and a broadening parameter of 1.8 eV, the MR-ADC(2) and MR-ADC(2)-X spectra are systematically shifted by ∼1.2 and 0.3 eV, respectively, relative to experiment. Aside from the systematic shift and the shape of negative feature, the MR-ADC(2) and MR-ADC(2)-X spectra are similar to each other and the experimental measurements. Both methods reveal structure in the negative feature observed in the experiment, but do not correctly describe its shape. As shown in Fig. 3, the structure of the negative feature in the simulated spectra can be attributed to a significant overlap of Fe 3p−1 density of states between Fe(CO)5 and its photodissociation products, which can be sensitive to small changes in molecular geometry and approximations in simulations.
Careful analysis of Fig. 3 reveals that the changes in the energies of individual Fe 3p−1 eigenstates upon photodissociation are significantly smaller (≲1 eV) than the separation between the maxima of positive and negative features observed in the experimental and simulated difference XPS spectra (>2 eV). Indeed, the simulated Fe 3p XPS spectra of each iron carbonyl complex shown in Fig. 4 exhibit at most 1 eV redshift, suggesting that the energetic stabilization of Fe 3p−1 states due to the enhanced core-hole screening upon the loss of CO ligands is significantly smaller than what can be inferred from the analysis of transient spectra. Similar redshift (≲1 eV) in the energies of Fe 3p−1 states has been observed in the results of multiconfigurational self-consistent field (MCSCF) calculations carried out by Leitner et al.15 who suggested that neglecting excited-state structural relaxation may be responsible for the smaller-than-expected redshift in the simulations.
Although our calculations did not incorporate vibrational dynamics and excited-state structural relaxation effects, Fig. 3 indicates that, in addition to ≲1 eV stabilization of Fe 3p−1 states upon photodissociation, at least two more electronic factors need to be considered to explain the >2 eV separation between the features in the difference spectra: (i) strong spin–orbit coupling that splits the Fe 3p−1 energy levels by ∼1.0 to 1.2 eV (see Section 4.3.2) and (ii) increase in ligand-field splitting of Fe 3p orbitals in Fe(CO)4 and Fe(CO)3 compared to higher symmetry Fe(CO)5 that separates the 3p−1 states further apart. The small ≲1 eV redshift in Fe 3p−1 states is also consistent with zero net change in the formal oxidation state of the Fe atom during the photodissociation, which is further supported by the results of Mulliken charge analysis that shows a marginal decrease in the Fe atom charge from +0.52 in Fe(CO)5 to +0.49 in Fe(CO)4 and Fe(CO)3 at the CASSCF(10e,10o) level of theory.
In addition to the energies of Fe 3p−1 eigenstates, the MR-ADC calculations provide access to transition intensities, which incorporate electron correlation effects. Fig. 3 demonstrates that MR-ADC(2) and MR-ADC(2)-X accurately capture the ∼15 to 20% increase in spectral intensities observed in experiment during the loss of second CO ligand. In our simulations, this intensity enhancement can be traced back to the difference in spread of Fe 3p−1 states, which is larger in Fe(CO)3 compared to Fe(CO)4 by ∼0.2 eV. In addition, the photoelectron transitions in Fe(CO)3 exhibit a small increase in computed spectroscopic intensities (∼1%), which provides a minor contribution to the observed intensity enhancement.
4.2 X-ray photoelectron spectra at the CO 3σ edge
The XPS difference spectra for the CO 3σ inner-valence ionization measured in experiment15 and simulated with MR-ADC are shown in Fig. 5. The experimental spectra exhibit a negative peak at ∼36.5 eV and a positive feature at ∼40 eV, which were assigned to the loss of coordinated CO in Fe(CO)5 and the generation of free CO in the reaction environment, respectively. In addition, the analysis of experimental data suggested that the CO ligands bound in Fe(CO)4 and Fe(CO)3 show a redshift in 3σ binding energy, but the precise value of the redshift could not be established due to poor resolution.15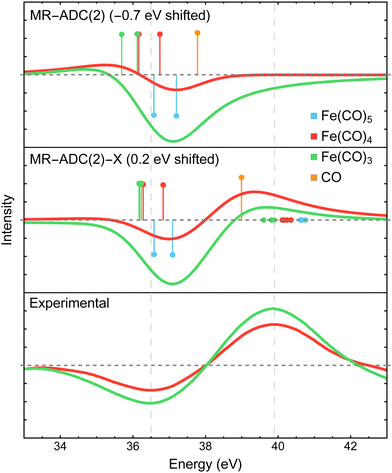 | ||
| Fig. 5 Difference CO 3σ−1 X-ray photoelectron spectra of Fe(CO)4 and Fe(CO)3 relative to Fe(CO)5 measured experimentally15 and simulated using MR-ADC(2) and MR-ADC(2)-X. Vertical lines represent the computed core ionization energies and the corresponding photoelectron intensities. The positive feature in experimental spectrum corresponds to free CO. To simulate free CO being present, one uncoordinated CO ligand was included in the Fe(CO)4 and Fe(CO)3 computations. The simulated spectra were shifted as indicated on each plot. Calculations employed the CAS(10e,13o) active space and uncontracted def2-TZVPP basis set. See Section 3 for more computational details. | ||
The MR-ADC calculations for Fe(CO)4 and Fe(CO)3 were performed with one uncoordinated CO molecule to simulate the presence of free CO. In agreement with experiment, the free CO molecule has a higher 3σ binding energy relative to CO in Fe(CO)5, with a ∼2.3 eV blueshift calculated at the MR-ADC(2)-X level of theory. Dissociating CO ligands results in a small (∼0.5 eV) redshift in the 3σ binding energy of coordinated CO, which is not sufficiently large to produce a positive feature with significant intensity when using the broadening parameter of 1.8 eV. These results are consistent with experimental data where a positive feature due to coordinated CO was not observed within the instrument resolution.15
4.3 Analysis of computational results
In the following, we will investigate how various parameters affect the result of MR-ADC simulations performed in this work, including the effect of equilibrium geometries, spin–orbit coupling, selection of active space and basis set, and the role of multireference treatment. In our analysis, we will focus on the Fe 3p edge, which was studied with a higher resolution in the experiment.15 The results for CO 3σ edge can be found in the ESI.†| Complex | D e, kcal mol−1 |
|---|---|
| Fe(CO)5 | 0.0 |
| Fe(CO)4 (C2v) + CO | 52.2 |
| Fe(CO)4 (C3v) + CO | 58.6 |
| Fe(CO)3 (Cs) + 2CO | 99.8 |
| Fe(CO)3 (D3h) + 2CO | 137.3 |
Two conformations of singlet Fe(CO)4 can be produced following the dissociation of either the equatorial or axial CO ligands in Fe(CO)5, resulting in the C2v or C3v structures, respectively. The two isomers have similar energies, with the C2v structure being favored by only 6.4 kcal mol−1 at the NEVPT2 level of theory (Table 1). Recent density functional theory study by Tross et al.80 suggested that Fe(CO)4 may spontaneously interconvert between the C2v and C3v structures during the course of photodissociation dynamics. The simulated difference spectra for the C2v and C3v isomers are shown in Fig. 6(b) and are compared to the experimental results. When convoluted with the 1.8 eV broadening, the C3v spectrum exhibits a smaller redshift of the Fe 3p feature compared to that for the C2v isomer. Adding the two difference spectra together with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio provides a better agreement with the experimental results than the spectrum of each isomer alone, which may support the findings of Tross et al. that both structures are similarly important during the course of photodissociation, and warrants further investigations that incorporate nuclear dynamics effects.
1 ratio provides a better agreement with the experimental results than the spectrum of each isomer alone, which may support the findings of Tross et al. that both structures are similarly important during the course of photodissociation, and warrants further investigations that incorporate nuclear dynamics effects.
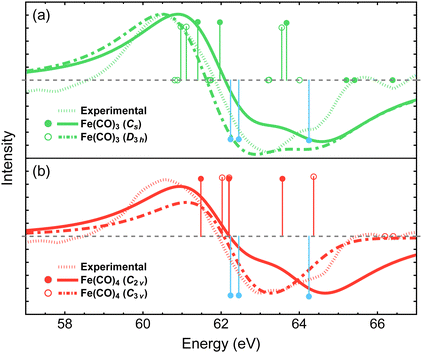 | ||
| Fig. 6 Difference Fe 3p X-ray photoelectron spectra for the two lowest-energy structures of Fe(CO)3 (a) and Fe(CO)4 (b) simulated using MR-ADC(2)-X and compared to the experimental spectrum from ref. 15. Vertical lines represent the computed core ionization energies and the corresponding photoelectron intensities. Blue lines correspond to Fe(CO)5. No shift was applied to the simulated spectra. See Section 3 for computational details. | ||
The dissociation of second CO ligand can result in two Fe(CO)3 structures with the Cs and D3h symmetries. As shown in Table 1, the Cs structure is lower in energy by 37.5 kcal mol−1 and is therefore expected to be energetically preferred. Fig. 6(a) shows that both structures exhibit similar redshifts of Fe 3p band. The spectrum of D3h isomer has a slightly broader negative feature, which is less consistent with the experiment compared to that of Cs structure, given our simulation parameters. However, overall, these results suggest that distinguishing spectral features of the Cs and D3h isomers would require achieving a higher resolution of experimental measurements if both structures participated in the photodissociation dynamics.
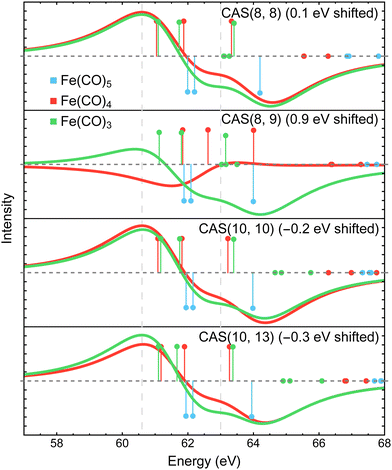
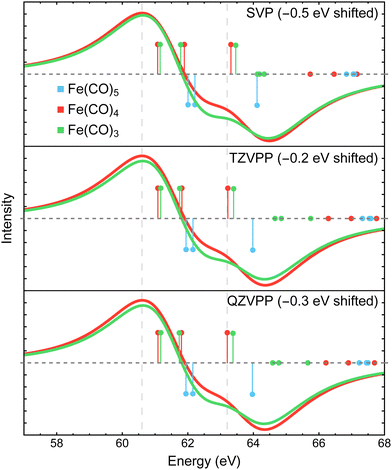
Fig. 8 shows the Fe 3p difference XPS spectra simulated using MR-ADC(2)-X with four active spaces ranging from CAS(8e,8o) to CAS(10e,13o). For Fe(CO)5, these active spaces are shown in Fig. 2, with more details provided in the ESI.† The smallest CAS(8e,8o) active space incorporated four Fe 3d-orbitals and four ligand-based orbitals. In CAS(8e,9o), an additional virtual orbital was added to the active space with the antibonding character between Fe dz2 and axial CO σ-orbital. The bonding counterpart of this orbital was added in CAS(10e,10o). Finally, three virtual orbitals describing the interaction between π-antibonding orbitals of CO and Fe 3d orbitals were added in CAS(10e,13o).
The MR-ADC(2)-X calculations with CAS(8e,8o), CAS(10e,10o), and CAS(10e,13o) yield similar spectra that show small differences in relative intensities and peak spacing of features in the transient XPS spectra. Including the bonding and antibonding combinations of Fe dz2 – axial CO σ orbitals from CAS(8e,8o) to CAS(10e,10o) reduces the spacing between the positive and negative features by ∼0.5 eV, resulting in a closer agreement with the experiment. Incorporating the CO π-antibonding orbitals in CAS(10e,13o) enhances the intensity of Fe(CO)3 peaks relative to that of Fe(CO)4, which further improves the agreement with the experimental results. The CAS(8e,9o) calculations result in qualitatively incorrect difference spectrum for Fe(CO)4 and significant (∼0.9 eV) underestimation in core ionization energies for other complexes. These results indicate that both bonding and antibonding Fe dz2 – axial CO σ orbitals are required to properly describe the screening of Fe 3p−1 states. This finding is supported by Fig. 2 where significant deviations from 2 and 0 are observed in the natural populations of Fe dz2 – axial CO σ orbitals.
To demonstrate the importance of high-order electron correlation effects, we performed the simulations of Fe 3p difference XPS spectra using single-reference ADC(2)-X method (SR-ADC(2)-X)61,93,121,122 without incorporating SOC effects. As shown in Fig. 9, SR-ADC(2)-X correctly predicts the spacing between core-ionized states of individual molecules but does not accurately reproduce the changes in ionization energies between them, predicting almost no redshift in Fe 3p edge between Fe(CO)4 and Fe(CO)5. In addition, the SR-ADC(2)-X calculations require a larger shift of the difference spectra compared to that of MR-ADC(2)-X in order to reproduce the negative feature relative to the experiment.
5 Conclusions
In this paper, we presented a computational study of transient X-ray photoelectron spectra (XPS) of Fe(CO)5, Fe(CO)4, and Fe(CO)3 for Fe 3p core-level and CO 3σ inner-valence ionization using multireference algebraic diagrammatic construction theory (MR-ADC). Although our calculations did not incorporate nuclear dynamics effects, the difference XPS spectra simulated using strict and extended second-order MR-ADC methods (MR-ADC(2) and MR-ADC(2)-X) were found to be in a good agreement with experimental results from time-resolved XPS measurements by Leitner et al.15 where singlet Fe(CO)4 and Fe(CO)3 appear as the photodissociation products of Fe(CO)5 following its excitation with 266 nm light.Our calculations reveal that the changes in the core-hole screening of Fe 3p−1 states due to the loss of CO ligands are not solely responsible for the large (>2 eV) redshift in the position of Fe 3p feature in the transient XPS spectra. The observed spectral changes are likely due to a combination of factors that determine the relative energies of the Fe 3p−1 states, including strong spin–orbit coupling and significant ligand-field splitting in the core-ionized photodissociated products. We estimate that the changes in core-hole screening effects amount to only ∼1 eV redshift in the difference spectra, which is significantly smaller than the splitting of Fe 3p−1 states due to spin–orbit coupling and ligand-field interactions. This analysis suggests that the chemical shifts observed in the transient M-edge XPS spectra of transition metal complexes may originate from several electronic structure effects as opposed to changes in the core-hole screening alone. In particular, the role of spin–orbit coupling and ligand-field environment must be considered and accurately quantified. Our results also indicate that, while all three iron carbonyl complexes studied in this work exhibit single-reference electronic structure, high-order theoretical methods must be used to properly account for significant dynamic correlation when simulating their XPS spectra.
The computational study presented in this work is the first of its kind performed using MR-ADC, which allows to incorporate strong electron correlation in a small subset of frontier molecular orbitals and weaker correlation for the remaining electrons while being able to simulate spectroscopic properties with large one-electron basis sets. Our results indicate that, in agreement with previous benchmarks,64,65 the MR-ADC(2)-X method provides highly accurate results that can be improved systematically by increasing the active space employed in the calculations. We also demonstrate that a first-order scheme for treating spin–orbit coupling effects in MR-ADC is highly effective in predicting the splitting of Fe 3p−1 energy levels and achieving better agreement with the experimental results. Further improvements to MR-ADC are underway in our group, including higher-order treatment of spin–orbit coupling and incorporating vibrational effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (NSF), under grant no. CHE-2044648. Additionally, N. P. G. was supported through the NSF REU grant no. CHE-2150102. Computations were performed at the Ohio Supercomputer Center under project no. PAS1583.123Notes and references
- A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758 CrossRef CAS PubMed.
- T. J. Penfold, C. J. Milne and M. Chergui, Advances in Chemical Physics, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2013, vol. 153, pp. 1–41 Search PubMed.
- M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065 CrossRef CAS PubMed.
- E. S. Ryland, M.-F. Lin, M. A. Verkamp, K. Zhang, K. Benke, M. Carlson and J. Vura-Weis, J. Am. Chem. Soc., 2018, 140, 4691–4696 CrossRef CAS PubMed.
- A. Bhattacherjee and S. R. Leone, Acc. Chem. Res., 2018, 51, 3203–3211 CrossRef CAS PubMed.
- E. Allaria, R. Appio, L. Badano, W. A. Barletta, S. Bassanese, S. G. Biedron, A. Borga, E. Busetto, D. Castronovo, P. Cinquegrana, S. Cleva, D. Cocco, M. Cornacchia, P. Craievich, I. Cudin, G. D'Auria, M. Dal Forno, M. B. Danailov, R. De Monte, G. De Ninno, P. Delgiusto, A. Demidovich, S. Di Mitri, B. Diviacco, A. Fabris, R. Fabris, W. Fawley, M. Ferianis, E. Ferrari, S. Ferry, L. Froehlich, P. Furlan, G. Gaio, F. Gelmetti, L. Giannessi, M. Giannini, R. Gobessi, R. Ivanov, E. Karantzoulis, M. Lonza, A. Lutman, B. Mahieu, M. Milloch, S. V. Milton, M. Musardo, I. Nikolov, S. Noe, F. Parmigiani, G. Penco, M. Petronio, L. Pivetta, M. Predonzani, F. Rossi, L. Rumiz, A. Salom, C. Scafuri, C. Serpico, P. Sigalotti, S. Spampinati, C. Spezzani, M. Svandrlik, C. Svetina, S. Tazzari, M. Trovo, R. Umer, A. Vascotto, M. Veronese, R. Visintini, M. Zaccaria, D. Zangrando and M. Zangrando, Nat. Photonics, 2012, 6, 699–704 CrossRef CAS.
- S. Hellmann, C. Sohrt, M. Beye, T. Rohwer, F. Sorgenfrei, M. Marczynski-Bühlow, M. Kalläne, H. Redlin, F. Hennies, M. Bauer, A. Föhlisch, L. Kipp, W. Wurth and K. Rossnagel, New J. Phys., 2012, 14, 013062 CrossRef.
- C. Pellegrini, A. Marinelli and S. Reiche, Rev. Mod. Phys., 2016, 88, 015006 CrossRef.
- J. Rossbach, J. R. Schneider and W. Wurth, Phys. Rep., 2019, 808, 1–74 CrossRef CAS.
- S. Neppl and O. Gessner, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 64–77 CrossRef CAS.
- O. Gessner and M. Guhr, Acc. Chem. Res., 2016, 49, 138–145 CrossRef CAS PubMed.
- M. Borgwardt, J. Mahl, F. Roth, L. Wenthaus, F. Brauße, M. Blum, K. Schwarzburg, G. Liu, F. M. Toma and O. Gessner, J. Phys. Chem. Lett., 2020, 11, 5476–5481 CrossRef CAS PubMed.
- L. Nugent-Glandorf, M. Scheer, D. A. Samuels, A. M. Mulhisen, E. R. Grant, X. Yang, V. M. Bierbaum and S. R. Leone, Phys. Rev. Lett., 2001, 87, 193002 CrossRef CAS PubMed.
- Z.-H. Loh and S. R. Leone, J. Chem. Phys., 2008, 128, 204302 CrossRef PubMed.
- T. Leitner, I. Josefsson, T. Mazza, P. S. Miedema, H. Schröder, M. Beye, K. Kunnus, S. Schreck, S. Düsterer, A. Föhlisch, M. Meyer, M. Odelius and P. Wernet, J. Chem. Phys., 2018, 149, 044307 CrossRef CAS PubMed.
- I. Gabalski, F. Allum, I. Seidu, M. Britton, G. Brenner, H. Bromberger, M. Brouard, P. H. Bucksbaum, M. Burt, J. P. Cryan, T. Driver, N. Ekanayake, B. Erk, D. Garg, E. Gougoula, D. Heathcote, P. Hockett, D. M. P. Holland, A. J. Howard, S. Kumar, J. W. L. Lee, S. Li, J. McManus, J. Mikosch, D. Milesevic, R. S. Minns, S. Neville, A. T. Noor, C. C. Papadopoulou, C. Passow, W. O. Razmus, A. Rooder, A. Rouzee, A. Simao, J. Unwin, C. Vallance, T. Walmsley, J. Wang, D. Rolles, A. Stolow, M. S. Schuurman and R. Forbes, J. Phys. Chem. Lett., 2023, 14, 7126–7133 CrossRef CAS PubMed.
- A. Stolow, J. Phys. Chem. B, 2003, 54, 89–119 CAS.
- Y. Liu, S. L. Horton, J. Yang, J. P. F. Nunes, X. Shen, T. J. A. Wolf, R. Forbes, C. Cheng, B. Moore, M. Centurion, K. Hegazy, R. Li, M.-F. Lin, A. Stolow, P. Hockett, T. Rozgonyi, P. Marquetand, X. Wang and T. Weinacht, Phys. Rev. X, 2020, 10, 021016 CAS.
- D. Mayer, F. Lever, D. Picconi, J. Metje, S. Alisauskas, F. Calegari, S. Düsterer, C. Ehlert, R. Feifel, M. Niebuhr, B. Manschwetus, M. Kuhlmann, T. Mazza, M. S. Robinson, R. J. Squibb, A. Trabattoni, M. Wallner, P. Saalfrank, T. J. A. Wolf and M. Gühr, Nat. Commun., 2022, 13, 198 CrossRef CAS PubMed.
- X. Chen, X. Wang and D. Fang, Fullerenes, Nanotubes, Carbon Nanostruct., 2020, 28, 1048–1058 CrossRef CAS.
- F. A. Stevie and C. L. Donley, J. Vac. Sci. Technol., A, 2020, 38, 063204 CrossRef CAS.
- C. Kalha, N. K. Fernando, P. Bhatt, F. O. L. Johansson, A. Lindblad, H. Rensmo, L. Z. Medina, R. Lindblad, S. Siol, L. P. H. Jeurgens, C. Cancellieri, K. Rossnagel, K. Medjanik, G. Schönhense, M. Simon, A. X. Gray, S. Nemšák, P. Lömker, C. Schlueter and A. Regoutz, J. Phys.: Condens. Matter, 2021, 33, 233001 CrossRef CAS PubMed.
- N. A. Besley, Acc. Chem. Res., 2020, 53, 1306–1315 CrossRef CAS PubMed.
- W. Hua, G. Tian and Y. Luo, Phys. Chem. Chem. Phys., 2020, 22, 20014–20026 RSC.
- D. Prendergast and G. Galli, Phys. Rev. Lett., 2006, 96, 215502 CrossRef PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103 CrossRef PubMed.
- J. Liu, D. A. Matthews, S. Coriani and L. Cheng, J. Chem. Theory Comput., 2019, 15, 1642–1651 CrossRef CAS PubMed.
- J. Liu and L. Cheng, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1536 Search PubMed.
- L. Halbert, M. L. Vidal, A. Shee, S. Coriani and A. S. P. Gomes, J. Chem. Theory Comput., 2021, 7(6), 3583–3598 CrossRef PubMed.
- F. D. Vila, J. J. Kas, J. J. Rehr, K. Kowalski and B. Peng, Front. Chem., 2021, 9, 734945 CrossRef CAS PubMed.
- D. Golze, J. Wilhelm, M. J. V. Setten and P. Rinke, J. Chem. Theory Comput., 2018, 14, 4856–4869 CrossRef CAS PubMed.
- L. Keller, V. Blum, P. Rinke and D. Golze, J. Chem. Phys., 2020, 153, 114110 CrossRef CAS PubMed.
- C. D. Rankine and T. J. Penfold, J. Phys. Chem. A, 2021, 125, 4276–4293 CrossRef CAS PubMed.
- H. Ågren and H. J. A. Jensen, Chem. Phys., 1993, 172, 45–57 CrossRef.
- A. B. Rocha, J. Chem. Phys., 2011, 134, 024107 CrossRef PubMed.
- A. B. Rocha and C. E. V. de Moura, J. Chem. Phys., 2011, 135, 224112 CrossRef PubMed.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- C. E. V. D. Moura, R. R. Oliveira and A. B. Rocha, J. Mol. Model., 2013, 19, 2027–2033 CrossRef CAS PubMed.
- G. Grell, S. I. Bokarev, B. Winter, R. Seidel, E. F. Aziz, S. G. Aziz and O. Kühn, J. Chem. Phys., 2015, 143, 074104 CrossRef PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Comput. Chem., 2016, 37, 477–486 CrossRef CAS PubMed.
- M. Guo, L. K. Sørensen, M. G. Delcey, R. V. Pinjari and M. Lundberg, Phys. Chem. Chem. Phys., 2016, 18, 3250–3259 RSC.
- F. Montorsi, F. Segatta, A. Nenov, S. Mukamel and M. Garavelli, J. Chem. Theory Comput., 2022, 18, 1003–1016 CrossRef CAS PubMed.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- I. Corral, J. González-Vázquez and F. Martín, J. Chem. Theory Comput., 2017, 13, 1723–1736 CrossRef CAS PubMed.
- D. Bhattacharya, K. R. Shamasundar and A. Emmanouilidou, J. Phys. Chem. A, 2021, 125, 7778–7787 CrossRef CAS PubMed.
- J. Brabec, K. Bhaskaran-Nair, N. Govind, J. Pittner and K. Kowalski, J. Chem. Phys., 2012, 137, 171101 CrossRef PubMed.
- M. Huang, C. Li and F. A. Evangelista, J. Chem. Theory Comput., 2022, 18, 219–233 CrossRef CAS PubMed.
- M. Huang and F. A. Evangelista, J. Chem. Phys., 2023, 158, 124112 CrossRef CAS PubMed.
- D. L. Yeager and P. Jørgensen, Chem. Phys. Lett., 1979, 65, 77–80 CrossRef CAS.
- D. L. Yeager, Applied Many-Body Methods in Spectroscopy and Electronic Structure, 1992, pp. 133–161 Search PubMed.
- J. A. Nichols, D. L. Yeager and P. Jørgensen, J. Chem. Phys., 1984, 80, 293–314 CrossRef CAS.
- B. Helmich-Paris, J. Chem. Phys., 2019, 150, 174121 CrossRef PubMed.
- B. Helmich-Paris, Int. J. Quantum Chem., 2021, 121, e26559 CrossRef CAS.
- A. Köhn and A. Bargholz, J. Chem. Phys., 2019, 151, 041106 CrossRef PubMed.
- D. Maganas, J. K. Kowalska, M. Nooijen, S. DeBeer and F. Neese, J. Chem. Phys., 2019, 150, 104106 CrossRef PubMed.
- A. Y. Sokolov, J. Chem. Phys., 2018, 149, 204113 CrossRef PubMed.
- K. Chatterjee and A. Y. Sokolov, J. Chem. Theory Comput., 2019, 15, 5908–5924 CrossRef CAS PubMed.
- K. Chatterjee and A. Y. Sokolov, J. Chem. Theory Comput., 2020, 16, 6343–6357 CrossRef CAS PubMed.
- I. M. Mazin and A. Y. Sokolov, J. Chem. Theory Comput., 2021, 17, 6152–6165 CrossRef CAS PubMed.
- S. Banerjee and A. Y. Sokolov, J. Chem. Theory Comput., 2023, 19, 3037–3053 CrossRef CAS PubMed.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206–222 CrossRef CAS.
- A. Barth and L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 23, 1038–1061 CrossRef CAS.
- C. E. V. D. Moura and A. Y. Sokolov, Phys. Chem. Chem. Phys., 2022, 24, 8041–8046 RSC.
- C. E. V. de Moura and A. Y. Sokolov, Phys. Chem. Chem. Phys., 2022, 24, 4769–4784 RSC.
- I. M. Mazin and A. Y. Sokolov, J. Chem. Theory Comput., 2023, 19, 4991–5006 CrossRef CAS PubMed.
- P. Portius, J. Yang, X.-Z. Sun, D. C. Grills, P. Matousek, A. W. Parker, M. Towrie and M. W. George, J. Am. Chem. Soc., 2004, 126, 10713–10720 CrossRef CAS PubMed.
- P. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- T. A. Seder, A. J. Ouderkirk and E. Weitz, J. Chem. Phys., 1986, 85, 1977–1986 CrossRef CAS.
- S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, J. Phys. Chem. A, 2000, 104, 1997–2006 CrossRef CAS.
- N. C. Cole-Filipiak, J. Troß, P. Schrader, L. M. McCaslin and K. Ramasesha, J. Chem. Phys., 2021, 154, 134308 CrossRef CAS PubMed.
- C. Daniel, M. Benard, A. Dedieu, R. Wiest and A. Veillard, J. Phys. Chem., 1984, 88, 4805–4811 CrossRef CAS.
- H. Ihee, J. Cao and A. H. Zewail, Angew. Chem., Int. Ed., 2001, 40, 1532–1536 CrossRef CAS PubMed.
- K. Pierloot, Mol. Phys., 2003, 101, 2083–2094 CrossRef CAS.
- B. J. Persson, B. O. Roos and K. Pierloot, J. Chem. Phys., 1994, 101, 6810–6821 CrossRef.
- O. Rubner, V. Engel, M. R. Hachey and C. Daniel, Chem. Phys. Lett., 1999, 302, 489–494 CrossRef CAS.
- T. Malcomson, R. G. McKinlay and M. J. Paterson, ChemPhotoChem, 2019, 3, 825–832 CrossRef CAS.
- M. Poliakoff and J. J. Turner, Angew. Chem., Int. Ed., 2001, 40, 2809–2812 CrossRef CAS PubMed.
- P. Wernet, T. Leitner, I. Josefsson, T. Mazza, P. S. Miedema, H. Schröder, M. Beye, K. Kunnus, S. Schreck, P. Radcliffe, S. Düsterer, M. Meyer, M. Odelius and A. Föhlisch, J. Chem. Phys., 2017, 146, 211103 CrossRef PubMed.
- J. Tross, J. Arias-Martinez, K. Carter-Fenk, N. Cole-Filipiak, P. Schrader, L. McCaslin, M. Head-Gordon and K. Ramasesha, Femtosecond core-level spectroscopy reveals signatures of transient excited states in the photodissociation of Fe(CO)5, ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-m1ggn-v2.
- W. Dickhoff and D. V. Neck, Many-body Theory Exposed! Propagator Description Of Quantum Mechanics In Many-body Systems, World Scientific Publishing Company, 2nd edn, 2008 Search PubMed.
- A. Fetter and J. Walecka, Quantum Theory of Many-Particle Systems, Dover Publications, 2012 Search PubMed.
- H. Werner and W. Meyer, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- H. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5794–5801 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- K. G. Dyall, J. Chem. Phys., 1995, 102, 4909–4918 CrossRef CAS.
- A. Y. Sokolov, Multireference Perturbation Theories Based on the Dyall Hamiltonian, arXiv, 2024, preprint, arXiv:2401.11262 DOI:10.48550/arXiv.2401.11262.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P. A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223 CrossRef CAS.
- J. P. Finley, P. A. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- R. Peng, A. V. Copan and A. Y. Sokolov, J. Phys. Chem. A, 2019, 123, 1840–1850 CrossRef CAS PubMed.
- S. Banerjee and A. Y. Sokolov, J. Chem. Phys., 2019, 151, 224112 CrossRef PubMed.
- M. F. Herbst and T. Fransson, J. Chem. Phys., 2020, 153, 054114 CrossRef CAS PubMed.
- K. D. Nanda and A. I. Krylov, J. Chem. Phys., 2020, 153, 141104 CrossRef CAS PubMed.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. DeBeer, J. Am. Chem. Soc., 2010, 132, 9715–9727 CrossRef CAS PubMed.
- J. M. Kasper, P. J. Lestrange, T. F. Stetina and X. Li, J. Chem. Theory Comput., 2018, 14, 1998–2006 CrossRef CAS PubMed.
- T. F. Stetina, J. M. Kasper and X. Li, J. Chem. Phys., 2019, 150, 234103 CrossRef PubMed.
- M. L. Vidal, P. Pokhilko, A. I. Krylov and S. Coriani, J. Phys. Chem. Lett., 2020, 11, 8314–8321 CrossRef CAS PubMed.
- P. Pyykkö, Ann. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef PubMed.
- K. G. Dyall, J. Chem. Phys., 2001, 115, 9136–9143 CrossRef CAS.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- T. Tsuchiya and B. O. Roos, Mol. Phys., 2006, 104, 1123–1131 CrossRef CAS.
- H. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pfluger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, 2021.1, a package of ab initio programs, see https://www.molpro.net.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. L. Whitten, J. Chem. Phys., 1973, 58, 4496–4501 CrossRef CAS.
- B. I. Dunlap, J. W. D. Connolly and J. R. Sabin, J. Chem. Phys., 1979, 71, 3396–3402 CrossRef CAS.
- O. Vahtras, J. Almlof and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359–363 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- C. Hattig, Phys. Chem. Chem. Phys., 2004, 7, 59–66 RSC.
- A. Hellweg, C. Hattig, S. Hofener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- C. E. V. de Moura and A. Y. Sokolov, Prism, an implementation of electronic structure theories for simulating spectroscopic properties, for current version see https://github.com/sokolov-group/prism.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. F. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- A. Rohatgi, Webplotdigitizer: Version 4.6, 2022, https://automeris.io/WebPlotDigitizer Search PubMed.
- J. Schirmer, A. B. Trofimov and G. Stelter, J. Chem. Phys., 1998, 109, 4734 CrossRef CAS.
- A. L. Dempwolff, M. Schneider, M. Hodecker and A. Dreuw, J. Chem. Phys., 2019, 150, 064108 CrossRef PubMed.
- O. S. Center, Ohio Supercomputer Center, https://osc.edu/ark:/19495/f5s1ph73.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized geometries of iron carbonyl complexes, selection of active spaces, total energies for optimized geometries, summary of numerical results and spin–orbit coupling implementation. See DOI: https://doi.org/10.1039/d4cp00801d |
| This journal is © the Owner Societies 2024 |