Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reverse intersystem crossing mechanisms in doped triangulenes†
Asier E.
Izu
 ab,
Jon M.
Matxain
ab,
Jon M.
Matxain
 ab and
David
Casanova
ab and
David
Casanova
 *ac
*ac
aDonostia International Physics Center (DIPC), 20018 Donostia, Euskadi, Spain. E-mail: david.casanova@dipc.org
bPolimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila, Kimika Fakultatea, Euskal Herriko Unibertsitatea (UPV/EHU), PK 1072, 20080 Donostia, Euskadi, Spain
cIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Euskadi, Spain
First published on 25th March 2024
Abstract
Thermally activated delayed fluorescence (TADF) has emerged as one of the most promising strategies in the quest for organic light emitting diodes with optimal performance. This computational study dissects the mechanistic intricacies of the central photophysical step, reverse intersystem crossing (rISC) in N and B doped triangulenes as potential multi-resonance TADF compounds. Optimal molecular patterns conducive to efficient rISC, encompassing dopant atom size, number, and distribution, are identified. Additionally, we assess various electronic structure methods for characterizing TADF-relevant molecular systems. The findings identify the distinct role of the direct and mediated mechanisms in rISC, and provide insights into the design of advanced TADF chromophores for next-generation OLED technology.
1 Introduction
Organic light emitting diodes (OLEDs) have revolutionized the technological market, finding ubiquitous application as luminescent displays in devices such as televisions and smartphones.1–3 The pursuit of better performing OLED devices has therefore garnered significant attention.In OLEDs, the recombination of charges leads to the formation of singlet and triplet states in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, imposing a stringent limitation on internal quantum efficiency. To mitigate non-radiative losses from the population of the (dark) triplet state manifold, two primary strategies have been proposed, each with the potential to achieve 100% internal quantum efficiency: doping with phosphorescent emitters4–6 and thermally activated delayed fluorescence (TADF).7–10 The former employs organometallic complexes to attain the necessary high spin–orbit coupling (SOC), allowing triplet states to undergo (phosphorescent) radiative decay. In contrast, TADF relies on organic molecules that recycle their non-radiative triplet excited states to fluorescence emissive singlets via reverse intersystem crossing (rISC) and thermal ambient energy, eliminating the need for expensive and toxic transition metals, e.g., Ir or Pt, used in phosphorescent OLEDs.
3 ratio, imposing a stringent limitation on internal quantum efficiency. To mitigate non-radiative losses from the population of the (dark) triplet state manifold, two primary strategies have been proposed, each with the potential to achieve 100% internal quantum efficiency: doping with phosphorescent emitters4–6 and thermally activated delayed fluorescence (TADF).7–10 The former employs organometallic complexes to attain the necessary high spin–orbit coupling (SOC), allowing triplet states to undergo (phosphorescent) radiative decay. In contrast, TADF relies on organic molecules that recycle their non-radiative triplet excited states to fluorescence emissive singlets via reverse intersystem crossing (rISC) and thermal ambient energy, eliminating the need for expensive and toxic transition metals, e.g., Ir or Pt, used in phosphorescent OLEDs.
The TADF phenomenon can be broken down into two main steps: triplet-to-singlet rISC and fluorescence from the lowest excited singlet state (S1). Efficient population of S1 through rISC necessitates a small energy difference between the excited singlet and triplet states (ΔEST = E(S1) − E(T1)), i.e., in the order of the thermal energy, and a strong coupling between the initial (spin triplet) and final (spin singlet) states, with SOC being the most common relativistic interaction connecting the two spin manifolds in organic compounds.11 Additionally, a good TADF chromophore must exhibit strong luminescence from S1, which can be quantified by the area of the emission band (oscillator strength).
The most commonly utilized strategy for designing systems with narrow T1/S1 energy gaps relies on the correlation between ΔEST and the exchange interaction among the frontier molecular orbitals (MOs). Vanishing orbital exchange can be achieved in molecules featuring weakly coupled and spatially separated donor and acceptor units. This situation typically involves T1 and S1 states holding strong charge transfer (CT) character.12–16 However, this strategy suffers from a number of drawbacks, primarily small photoluminescence quantum yields (PLQY) and poor color purity. The extensive structural reorganization of CT-character molecular architecture leads to broad emission spectra. Furthermore, CT-character excitations often exhibit small oscillator strengths, resulting in weak radiative emission.17
A notable departure from the usual donor–acceptor architecture was proposed by Hatakeyama et al., who designed TADF emitters with triangulene cores incorporating ortho-substituted B and N atoms, forming DABNA molecules.17 These molecules, often referred to as multi-resonance TADF (MR-TADF) compounds, feature a chemical structure that promotes the localization of the highest occupied and lowest unoccupied MOs (HOMO and LUMO) in different atomic sites. This leads to disjoint HOMO and LUMO, triggering small exchange interactions (small ΔEST), while still allowing for sizeable S0 ← S1 transition dipole moments. Furthermore, the backbone rigidity induces narrow emission bands. These properties have been associated with singlet and triplet states exhibiting a “short-range/local” CT character and long-range π-conjugation,17,18 motivating the ongoing search for new and improved MR-TADF chromophores.19–23
The main objective of this study is to elucidate the mechanistic intricacies of rISC in N and B doped triangulenes, which are potential candidates as MR-TADF compounds, through the application of quantum chemistry calculations. Furthermore, we endeavor to pinpoint optimal molecular patterns conducive to efficient rISC, including considerations of size, number, and distribution of dopant atoms. Additionally, our investigation assesses the suitability of various electronic structure methods for computationally characterizing molecular systems relevant to TADF.
The paper is organized as follows. In the first section, we delve into the theoretical expressions employed to characterize the rates of rISC mechanisms and provide an overview of the electronic structure methods investigated for the study of doped triangulenes. The subsequent section presents the results of our exploration into the capabilities of both density functional (DFT) and wave function approaches for the study of 16 triangulene derivatives. We carefully select the optimal methodology and conduct the computational analysis. Finally, in the Conclusions section, we thoroughly discuss the main findings of our investigations.
2 Theory and methodology
2.1 Reverse intersystem crossing rates
The rate of rISC from a triplet state to an excited singlet can be expressed using Fermi's golden rule: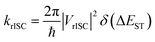 | (1) |
| V(d)rISC = 〈S1|ĤSO|T1〉 | (2) |
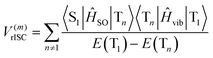 | (3) |
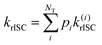 | (4) |
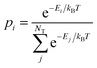 | (5) |
Finally, to evaluate rISC in eqn (1), we approximate the Franck–Condon weighted density of states using the Marcus approximation for the high temperature limit:37
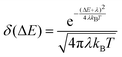 | (6) |
2.2 Molecular systems and nomenclature
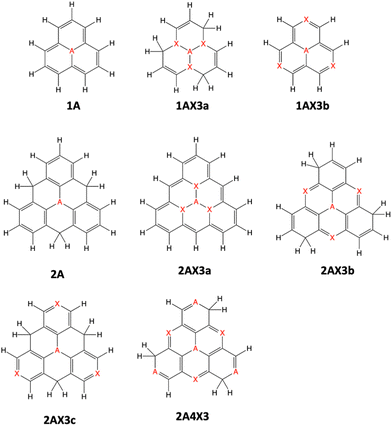
In this study, we examine a series of 16 triangulene nanographene molecules doped with nitrogen and/or boron atoms (Fig. 1). The selection of these compounds is deliberate, aimed at comprehending the influence of molecular size (phenalene or triangulene scaffold), doping quantity, type of doping atoms (B or N), and the distribution of dopants on their potential as MR-TADF molecules.2.3 Electronic structure calculations
Geometry optimization of the 16 studied molecules has been performed with the M06-2X exchange–correlation functional38 and the 6-31G(d) basis set, as it has shown good performance in the study of planar conjugated compounds.39–43 Transition energies to the low-lying excited singlet and triplet states have been computed at the time-dependent DFT (TDDFT) level with the Tamm–Dancoff approximation (TDA)44 in combination with three exchange–correlation functionals: M06-2X,38 B3LYP,45–47 and CAM-B3LYP.48 Excitation energies have been also computed at the spin–flip TDDFT (SF-TDDFT)49 level (within the TDA) from the Kohn–Sham triplet state configuration with the PBE50 functional,50 as previously recommended.51 Several post Hartree–Fock (HF) approaches have been employed: configuration interaction singles with perturbative doubles (CIS(D))52,53 with the resolution-of-the-identity (RI),54 equation-of-motion coupled-cluster singles and doubles (EOM-CCSD),55 and similarity transformed EOM domain-based local pair natural orbital CCSD (STEOM-DLPNO-CCSD).56–58 Vertical excitation energies have been computed with the def2-TZVP basis set except for those at the SF-PBE50 level that were obtained with the 6-31G(d) basis set. SOCs have been computed at the STEOM-DLPNO-CCSD/def2-TZVP level within the mean-field approach for the two-electron part as implemented in ORCA.59 Geometry optimizations, TDDFT and SF-TDDFT (TDA), CIS(D), and EOM-CCSD calculations have been done with the Q-Chem program.60 STEOM-DLPNO-CCSD results were obtained with the use of the RI approach for Coulomb integrals (RI-J)61 and the numerical chain-of-sphere integration for the HF exchange integrals (COSX)62 with ORCA.Along the manuscript, we consider three constant values for the triplet–triplet vibronic couplings in eqn (3): 1 meV (weak coupling), 10 meV (medium coupling), and 100 meV (strong coupling). The reorganization energy factor λ within the Marcus approximation (eqn (6)) has been fixed to 0.1 eV for all cases, as it is a common value in organic chromophores.63,64 State populations of (nearly) degenerated triplets have been obtained according to the Boltzmann distribution at T = 298.15 K.
3 Results and discussion
3.1 Method assessment
The singlet–triplet energy difference is a key parameter determining the kinetics of rISC. Therefore, the computational design and characterization of molecules with efficient rISC requires the use of electronic structure methods able to accurately predict singlet and triplet excitation energies. Accordingly, we firstly evaluate the performance of DFT-based and post-HF wave function methods in the calculation of S1 and T1 energies of the doped phenalenes and triangulenes in Fig. 1.Singlet–triplet energy gaps computed with different methods are shown in Fig. 2. Overall, the ΔEST values indicate small (or even negative) gaps for several doped compounds, particularly for structures: 1A, 1AX3b, 2AX3a, 2AX3b, 2NB3c and 2A4X3. On the other hand, the large energy differences (ΔEST > 0.5 eV) obtained for 1AX3a, 2A and 2BN3c seem to prevent their rISC capabilities.
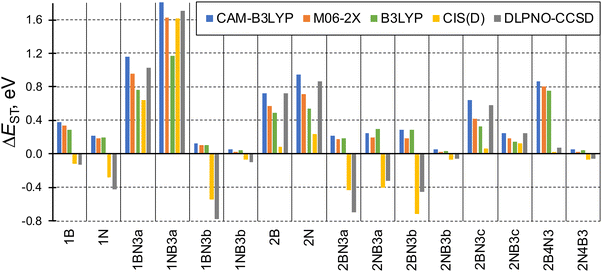 | ||
| Fig. 2 Computed energy gaps between the lowest excited singlet and triplet states (ΔEST = E(S1) − E(T1), in eV) of the studied molecules. Note: DLPNO-CCSD refers to STEOM-DLPNO-CCSD. | ||
Although the general trend for ΔEST computed along the studied family of compounds is qualitatively the same for the different approaches, some values present large quantitative disagreements. TDDFT gaps computed with the hybrid GGA (B3LYP), LRC (CAM-B3LYP) and hybrid meta-GGA (M06-2X) functionals are rather close to STEOM-DLPNO-CCSD for large (and positive) ΔEST values, especially with CAM-B3LYP. On the other hand, none of the functionals is able to produce inverted gaps, and exhibit large discrepancies with respect to post-HF energies with ΔEST < 0. Such behavior can be anticipated by the limitation of (linear response) TDDFT within the adiabatic approximation to account for the contribution of double excitations, which are known to stabilize the lowest excited singlet65 and might be necessary in order to accurately provide relative energies between low-lying states,66 as it has been recently reported for organic molecules with small or inverted singlet–triplet gaps.19,67,68 To further corroborate the importance of double excitations in some of these molecules, in Table S4 (ESI†) we compare CIS vs. CIS(D) singlet and triplet energies for molecule 2B4N3 (large overestimation of singlet–triplet gap by TDDFT) and 1NB3a (similar performance of TDDFT and post-HF).
In addition, we have also performed SF-TDDFT calculations. A priory, one advantage of employing the spin–flip excitation operator in TDDFT, as opposed to the standard linear-response approach, lies in its explicit incorporation of double excitations.51 However, the high symmetry of the studied molecules (D3h or C3h, Table S1, ESI†) induces orbital degeneracies at the frontier between occupied and unoccupied levels. Consequently, in many cases, the lowest triplet state lacks a well-defined single configuration. This results in a rather pronounced singlet–triplet mixed character, i.e., spin contamination, in both the reference triplet and the states computed using the SF-TDDFT approach. As a consequence, the results obtained with SF-TDDFT can be found in Table S2 (ESI†), but will not be further discussed here.
Amongst the different employed methods, only the two post-HF approaches are able to produce inverted singlet–triplet gaps (ΔEST < 0), which we relate (again) to the larger impact of double excitations in S1. On the other hand, CIS(D) energies in general follow the same trend as those obtained with STEOM-DLPNO-CCSD, although in some cases the differences are notably large, e.g., in 2BN3c.
These results make us to discard DFT-based methods (TDDFT and SF-TDDFT) for the study of rISC in B,N-doped triangulenes, as they seem to systematically overestimate ΔEST as compared to correlated wave function methods. Moreover, the variability between the post-HF methods motivates us to explore their accuracy in more detail. For that, we compare singlet and triplet excitation energies in compound 1B at the CIS(D) and STEOM-DLPNO-CCSD levels with respect to highly accurate calculations, i.e., EOM-CCSD and ADC(3) (Table 1).
The energy gap between the lowest singlet and triplet states in 1B remains small across all post-HF approaches. EOM-CCSD predicts S1 to be higher in energy than T1, while the singlet–triplet gap is inverted in ADC(3). Notably, EOM-CCSD excels in calculating excitation energies for states predominantly governed by single electron excitations,70 but its accuracy diminishes when double excitations are involved. Consequently, in cases like this, the inclusion of triple excitations, as in ADC(3), may yield a more balanced evaluation of ΔEST.
Interestingly, CIS(D) and STEOM-DLPNO-CCSD gaps are in very good agreement with ADC(3), with STEOM-DLPNO-CCSD displaying S1 and T1 energies closer to those from ADC(3). The accuracy in computing higher triplet states is also crucial for our study, as they can serve as mediators in the rISC process (eqn (3)). CIS(D) and STEOM-DLPNO-CCSD T2 energies exhibit a 0.3 eV discrepancy compared to EOM-CCSD.
Based on the analysis of energies presented in Table 1, we conclude that STEOM-DLPNO-CCSD provides the most reliable excitation energies among the two considered post-HF methods with low computational demands. Furthermore, while CIS(D) incorporates effects of doubly excited configurations perturbatively, STEOM-DLPNO-CCSD explicitly accounts for (coupled-cluster) double excitations, all while maintaining an affordable computational expense. Consequently, we conduct our computational study of rISC in doped triangulenes using the STEOM-DLPNO-CCSD level of theory. For consistency, singlet–triplet SOCs have been computed at the same level.
3.2 Direct vs. mediated rISC mechanisms
The conditions necessary for populating the excited singlet state via thermally activated rISC include a small singlet–triplet energy difference (ΔEST), typically on the order of kBT, and a non-vanishing coupling between the initial and final states. Fig. 3a displays the computed ΔEST for the 16 doped phenalenes and triangulenes. Most of these molecules exhibit relatively modest gaps between the lowest excited singlet and triplet states, as calculated using the STEOM-DLPNO-CCSD method. While small and positive gaps can be overcome with thermal energy, rISC becomes energetically prohibitive in molecules with a large S1/T1 energy separation, such as 1BN3a and 1NB3a. Notably, several of them feature an inverted gap (ΔEST < 0), which may serve as a driving force for rISC. However, excessively negative ΔEST values could impede fast rISC, as predicted by eqn (6).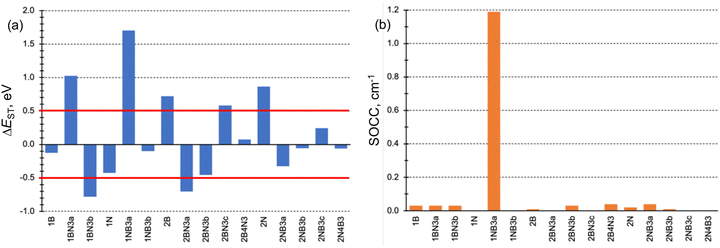 | ||
| Fig. 3 (a) Excited singlet–triplet energy gaps (ΔEST in eV) and (b) SOC constants (SOCC in cm−1) for the studied B and N doped phenalene and triangulene molecules. | ||
The SOC constants (SOCCs) between S1 and T1 are generally quite small (SOCC < 0.1 cm−1) in almost all molecules (Fig. 3b). This observation aligns with expectations for organic π-conjugated molecules.71 The exception to this behavior is 1NB3a compound, which exhibits a considerably stronger coupling (SOCC ≈ 1.2 cm−1) due to the different electronic character of S1 (nπ*) and T1 (ππ*) states, in agreement with the El-Sayed's rule.72
In the following, we investigate the rISC rates and analyze the main mechanisms in place. These include the direct population of S1via SOC (eqn (2)), as well as the mediation through auxiliary triplet states via the spin–vibronic mechanism (eqn (3)). We focus on molecules with not too large singlet–triplet gaps, |ΔEST| < 0.5 eV (Fig. 4). Instead of explicitly computing triplet–triplet vibronic interactions (〈Tn|Ĥvib|T1〉), we consider three distinct coupling regimes: weak (1 meV), medium (10 meV), and strong (100 meV). Changes in the strength of vibronic couplings may arise from various factors, including different chemical substitutions or varying environmental conditions, such as solvent polarity or molecular aggregation.
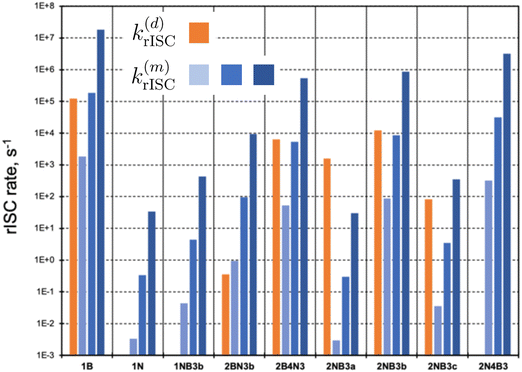 | ||
| Fig. 4 Direct (d) and mediated (m) rate constants (in s−1) for molecules with |ΔEST| < 0.5 eV. k(m)rISC has been computed for weak (1 meV, light blue), medium (10 meV, blue), and strong (100 meV, dark blue) vibronic couplings, respectively. Intermediate values to compute direct and mediated rates can be found in Table S5 (ESI†). | ||
Representation of direct rISC rates (orange bars in Fig. 4) clearly highlights compounds with small ΔEST and nonzero S1/T1 SOCs. Notably, 1B, 2NB3b, 2B4N3, and 2NB3a exhibit the highest k(d)rISC values. In contrast, molecules 1N, 1NB3b, and 2N4B3 possess vanishing SOC between S1 and T1 states, completely impeding the direct T1 → S1 transition. Alternatively, rISC mediated by higher triplet states can be rather efficient. Specifically, in addition to those molecules with 〈S1|ĤSOC|T1〉 = 0, the spin–vibronic mechanism dominates in 2BN3b, even in the weak vibronic regime.
Remarkably, the excited triplet state predominantly contributing to k(m)rISC is not necessarily T2. In most cases, these correspond to T4–T6, as they exhibit rather strong SOC with S1, while not being too high in energy. These findings underscore the importance of considering multiple triplets beyond T1 to thoroughly evaluate the role of the spin–vibronic mechanism.
Interestingly, in many instances, the direct and spin–vibronic mechanisms may have similar magnitudes, contingent on the vibronic coupling strength. It is crucial to note that our approach does not account for quantum interference effects between both paths, which could result in a synergistic increase or decrease of rISC rates.
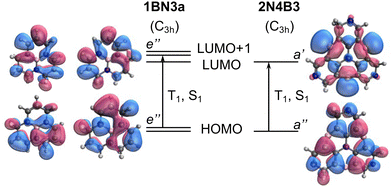
The impact of the orbital overlap is nicely illustrated by the comparison between the ΔEST values in 1BN3a and 2N4B3 compounds. The lowest singlet and triplet excited states in 1BN3a have a ππ* character mainly corresponding to the excitation between doubly degenerated (e′′) HOMO and LUMO+1 (Fig. 5). Both e′′-orbital pairs are delocalized over the entire molecule with major participation of 2p orbitals from the same atomic centers, i.e., non-disjoint orbitals, resulting in a rather large singlet–triplet gap (ΔEST = 1.02 eV, Fig. 3a). On the other hand, excitation to T1 and S1 in 2N4B3 arise from the electron promotion from the π-HOMO mostly localized on the C atoms bonded to the three B atoms, to the n-LUMO with major participation of the empty lone-pairs of the borons. Hence, the overlap in this case is much weaker, which explains the very small gap computed between T1 and S1 (ΔEST = −0.06 eV, Fig. 3a).
To exemplify the role of molecular symmetry in rISC, in the following, we analyze singlet–triplet computed SOCs in 1N (D3h structure) and 1B (C3h structure). The lowest singlet and triplet states in 1N are obtained as the single electron promotion from one of the doubly degenerated HOMOs (e′′) to the LUMO 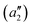 , resulting in E′ irrep for both states (Fig. 6). Since S1 and T1 belong to the same component of the twofold E′ irrep, their product contain E′ and
, resulting in E′ irrep for both states (Fig. 6). Since S1 and T1 belong to the same component of the twofold E′ irrep, their product contain E′ and 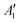 , but not
, but not 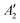 , while the componets of {Lq} belong to the (E′′,
, while the componets of {Lq} belong to the (E′′, 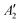 ) irreps. As a consequence, Γ(S1) × Γ(Lq) × Γ(T1) does not contain the totally symmetric irrep
) irreps. As a consequence, Γ(S1) × Γ(Lq) × Γ(T1) does not contain the totally symmetric irrep 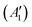 , resulting in zero T1/S1 SOC and forbidden rISC through the direct mechanism (k(d)rISC = 0 in Fig. 4). On the other hand, the molecular symmetry in 1B reduces to C3h with the HOMO and LUMO exhibiting the same symmetry (a′′). Therefore, S1 and T1 (both corresponding to the HOMO → LUMO excitation) belong to the A′ irrep, with angular momentum components with (E′′, A′) symmetries, and Γ(S1) × Γ(Lq) × Γ(T1) = (E′′, A′), allowing for non-zero SOC and efficient direct rISC.
, resulting in zero T1/S1 SOC and forbidden rISC through the direct mechanism (k(d)rISC = 0 in Fig. 4). On the other hand, the molecular symmetry in 1B reduces to C3h with the HOMO and LUMO exhibiting the same symmetry (a′′). Therefore, S1 and T1 (both corresponding to the HOMO → LUMO excitation) belong to the A′ irrep, with angular momentum components with (E′′, A′) symmetries, and Γ(S1) × Γ(Lq) × Γ(T1) = (E′′, A′), allowing for non-zero SOC and efficient direct rISC.
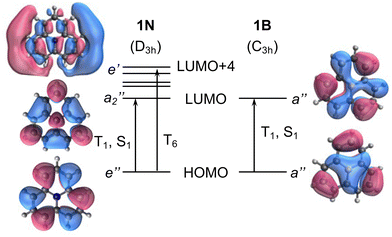 | ||
| Fig. 6 Frontier molecular orbital diagram of molecules 1N (left) and 1B (right). Vertical arrows indicate orbital transition to low-lying excited states. | ||
As discussed in the previous section, the mediated (spin–vibronic) mechanism might be crucial in some of these doped triangulenes, in which the relevant spin–orbit interaction takes place between the lowest singlet and some higher triplet state (Tn). This is the situation in molecule 1N, for which we have seen how the SOC between S1 and T1 is symmetry forbidden, while the S1/T6 coupling is quite strong (3.5 cm−1). This behavior can be understood by the πn* nature of T6 (Fig. 6), in accordance to El Sayed rule, opening the possibility for spin–vibronic rISC (k(m)rISC > 0 in Fig. 4).
3.3 Promising doped triangulenes
The results depicted in Fig. 3 and 4 provide valuable insights into the molecular structures with the most promising rISC capabilities.Within a given molecular scaffold and doping pattern (Fig. 1), those structures with a greater number of B atoms than N dopants generally exhibit more efficient rISC. An exception to this trend is observed in the 2A4X3 structure, which deviates from the expected behavior among compounds with a relatively small singlet–triplet gap (|ΔEST| < 0.5 eV). In this case, 2B4N3 and 2N4B3 present rates of similar magnitude.
The dependence of rISC efficiency on molecular size is strongly linked to the degree of π-conjugation within the molecule. Typically in these systems, larger conjugation tends to stabilize the S1 state more than the T1 state, resulting in a decrease of the ΔEST value and effecting the rISC capabilities. For example, 2AX3a molecules exhibit smaller energy gaps compared to their 1AX3a counterparts. Consequently, while 1NB3a exhibits a prohibitively large ΔEST, 2NB3a is predicted to have efficient rISC. Conversely, the increase in molecular size from 1A to 2A results in a loss of effective conjugation, leading to overly large energy gaps in the latter compounds (2B and 2N). The substitution of the phenalene scaffold with triangulene between 1AX3b and 2AX3b structures implies a moderate increase in conjugation, causing not very large changes in ΔEST, yet having a significant impact on their rISC efficiencies, as observed between 1NB3b and 2NB3b.
The distribution of dopant atoms in the molecule also significantly influences the photophysical properties, as evidenced in the 2AX3a, 2AX3b, and 2AX3c series of compounds. Specifically, larger separations between dopant atoms A and X (N and B or B and N) result in larger singlet–triplet gaps, making the 2AX3b structure optimal for efficient rISC. This behavior can be rationalized in terms of molecular conjugation, which decreases as 2AX3a > 2AX3b > 2AX3c.
While it is not entirely clear to establish a direct correlation between ΔEST or rISC rate and the amount of doping, overall, a larger number of dopants appears to be beneficial in promoting rISC, as exemplified in the 2A, 2AX3b, and 2A4X3 series of compounds.
4 Conclusions
In summary, our study of 16 nitrogen and/or boron-doped triangulene nanographene molecules has provided crucial insights into the appropriateness of electronic structure methods for unraveling the intricacies of rISC mechanisms and assessing their efficiencies.Comparison between singlet and triplet energies of the studied systems advises the use of post-HF methods accounting for double excitations. These contributions have a larger impact on the excited singlet energy, reducing the singlet–triplet gap, which for some molecules appears to be inverted (ΔEST < 0). Comparison with reference calculations including triplet excitations, that is at the ADC(3) level, makes us to conclude that STEOM-DLPNO-CCSD with the def2-TZVP basis set is a suitable method for the present study. Moreover, we believe that this approach should be rather accurate for the study of MR-TADF organic molecules in general. On the other hand, TDDFT calculations with different families of exchange–correlation functionals produce systematically larger and always positive ΔEST values. Although SF-TDDFT explicitly contains double excitations, it cannot be used to describe the doped phenalenes and triangulenes studied here due to the large spin-mixed character of the computed states, which we attribute to the high symmetry (D3h or C3h) of the compounds. Hence, despite the advantageous computational cost of DFT-based methods, we cannot consider them as appropriate for the accurate calculation of singlet–triplet energies.
Symmetry selection rules in many cases hinders SOC from T1 to S1, inactivating direct rISC. Contrarily, the spin–vibronic (mediated) mechanism, computed as a second order perturbation term, is extremely relevant for the population of the triplet manifold in all doped nanographenes with small to moderate singlet–triplet gaps. Notably, in many molecules, the triplet state mediator is not the energetically closest one to T1 (or S1), which imposes the need to take into account several highly excited triplets, i.e., beyond T2, in computational studies.
While a clear correlation between ΔEST or rISC rate and doping amount is not established, a larger number of dopants generally promotes efficient rISC. Our calculations also indicate that triangulenes with more B atoms than N atoms generally exhibit more efficient rISC, with dopant atom distribution also impacting the performance. Moreover, the degree of π-conjugation is a very important factor for rISC, as it tunes the singlet–triplet energy gap, with larger conjugation stabilizing S1 over T1.
In summary, our comprehensive analysis sheds light on the factors influencing rISC in doped triangulene molecules, providing valuable guidance for the design of efficient MR-TADF compounds.
Data availability
The data that supports the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors thank Gaetano Ricci for very insightful and helpful discussions. The authors acknowledge the Spanish Government MICINN (projects PID2022-136231NB-I00 and RED2022-134939-T) and the Eusko Jaurlaritza (Basque Government, project IT1584-22). D. C. is thankful for financial support from IKERBASQUE (Basque Foundation for Science). The authors are thankful for the technical and human support provided by the Donostia International Physics Center (DIPC) Computer Center.References
- A. Bernanose, M. Comte and P. Vouaux, Sur un nouveau mode d’émission lumineuse chez certains composés organiques, J. Chim. Phys., 1953, 50, 64–68 CrossRef CAS.
- C. W. Tang and S. A. VanSlyke, Organic electroluminescent diodes, Appl. Phys. Lett., 1987, 51, 913–915 CrossRef CAS.
- H.-W. Chen, J.-H. Lee, B.-Y. Lin, S. Chen and S.-T. Wu, Liquid crystal display and organic light-emitting diode display: present status and future perspectives, Light Sci. Appl., 2018, 7, 17168 CrossRef CAS PubMed.
- M. A. Baldo, D. F. O’Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Highly efficient phosphorescent emission from organic electroluminescent devices, Nature, 1998, 395, 151–154 CrossRef CAS.
- M. Baldo, S. Lamansky, P. Burrows, M. Thompson and S. Forrest, Very high-efficiency green organic light-emitting devices based on electrophosphorescence, Appl. Phys. Lett., 1999, 75, 4–6 CrossRef CAS.
- M. Thompson; P. Djurovich; S. Barlow and S. Marder, Organometallic Complexes for optoelectronic applications, 2007 Search PubMed.
- R. Kepler, J. Caris, P. Avakian and E. Abramson, Triplet excitons and delayed fluorescence in anthracene crystals, Phys. Rev. Lett., 1963, 10, 400 CrossRef CAS.
- B. Valeur and M. N. Berberan-Santos, Molecular fluorescence: principles and applications, John Wiley & Sons, 2012 Search PubMed.
- T. Nakagawa, S.-Y. Ku, K.-T. Wong and C. Adachi, Electroluminescence based on thermally activated delayed fluorescence generated by a spirobifluorene donor–acceptor structure, Chem. Commun., 2012, 48, 9580–9582 RSC.
- D. S. M. Ravinson and M. E. Thompson, Thermally assisted delayed fluorescence (TADF): Fluorescence delayed is fluorescence denied, Mater. Horiz., 2020, 7, 1210–1217 RSC.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Recent advances in organic thermally activated delayed fluorescence materials, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Thermally activated delayed fluorescence materials towards the breakthrough of organoelectronics, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Revealing the spin–vibronic coupling mechanism of thermally activated delayed fluorescence, Nat. Commun., 2016, 7, 1–7 Search PubMed.
- Y. Olivier, B. Yurash, L. Muccioli, G. D’Avino, O. Mikhnenko, J.-C. Sancho-Garcia, C. Adachi, T.-Q. Nguyen and D. Beljonne, Nature of the singlet and triplet excitations mediating thermally activated delayed fluorescence, Phys. Rev. Mater., 2017, 1, 075602 CrossRef.
- J. Gibson, A. P. Monkman and T. J. Penfold, The importance of vibronic coupling for efficient reverse intersystem crossing in thermally activated delayed fluorescence molecules, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS PubMed.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Ultrapure blue thermally activated delayed fluorescence molecules: efficient HOMO–LUMO separation by the multiple resonance effect, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS PubMed.
- A. Pershin, D. Hall, V. Lemaur, J.-C. Sancho-Garcia, L. Muccioli, E. Zysman-Colman, D. Beljonne and Y. Olivier, Highly emissive excitons with reduced exchange energy in thermally activated delayed fluorescent molecules, Nat. Commun., 2019, 10, 1–5 CrossRef PubMed.
- N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-I. Nakayama and S. Maeda, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nature, 2022, 609, 502–506 CrossRef CAS PubMed.
- A. L. Sobolewski and W. Domcke, Are heptazine-based organic light-emitting diode chromophores thermally activated delayed fluorescence or inverted singlet–triplet systems?, J. Phys. Chem. Lett., 2021, 12, 6852–6860 CrossRef CAS PubMed.
- X. Lv, J. Miao, M. Liu, Q. Peng, C. Zhong, Y. Hu, X. Cao, H. Wu, Y. Yang and C. Zhou, et al., Extending the p-Skeleton of Multi-Resonance TADF Materials towards High-Efficiency Narrowband Deep-Blue Emission, Angew. Chem., Int. Ed., 2022, 134, e202201588 CrossRef.
- P. Jiang, J. Miao, X. Cao, H. Xia, K. Pan, T. Hua, X. Lv, Z. Huang, Y. Zou and C. Yang, Quenching-resistant multiresonance TADF emitter realizes 40% external quantum efficiency in narrowband electroluminescence at high doping level, Adv. Mater., 2022, 34, 2106954 CrossRef CAS PubMed.
- S. Kohata, H. Nakanotani, Y. Chitose, T. Yasuda, Y. Tsuchiya and C. Adachi, Anti-Stokes Luminescence in Multi-Resonance-Type Thermally-Activated Delayed Fluorescence Molecules, Angew. Chem., Int. Ed., 2023, 62, e202312326 CrossRef CAS PubMed.
- A. Carreras and D. Casanova, Theory of Exciton Dynamics in Thermally Activated Delayed Fluorescence, ChemPhotoChem, 2022, 6, e202200066 CrossRef CAS.
- T. Ogiwara, Y. Wakikawa and T. Ikoma, Mechanism of intersystem crossing of thermally activated delayed fluorescence molecules, J. Phys. Chem. A, 2015, 119, 3415–3418 CrossRef CAS PubMed.
- Y. Zhao, Y. Wu, W. Chen, R. Zhang, G. Hong, J. Tian, H. Wang, D. Zheng, C. Wu and X. Jiang, et al., The Second Excited Triplet-State Facilitates TADF and Triplet–Triplet Annihilation Photon Upconversion via a Thermally Activated Reverse Internal Conversion, Adv. Opt. Mater., 2022, 10, 2102275 CrossRef CAS.
- P. L. Santos, J. S. Ward, P. Data, A. S. Batsanov, M. R. Bryce, F. B. Dias and A. P. Monkman, Engineering the singlet–triplet energy splitting in a TADF molecule, J. Mater. Chem. C, 2016, 4, 3815–3824 RSC.
- T. Förster, Excitation transfer and internal conversion, Chem. Phys. Lett., 1971, 12, 422–424 CrossRef.
- Z. Wang, C. Wu and W. Liu, NAC-TDDFT: Time-Dependent Density Functional Theory for Nonadiabatic Couplings, Acc. Chem. Res., 2021, 54, 3288–3297 CrossRef CAS PubMed.
- E. G. Hohenstein, Analytic formulation of derivative coupling vectors for complete active space configuration interaction wavefunctions with floating occupation molecular orbitals, J. Chem. Phys., 2016, 145, 174110 CrossRef PubMed.
- H. Lischka, M. Dallos, P. G. Szalay, D. R. Yarkony and R. Shepard, Analytic evaluation of nonadiabatic coupling terms at the MR-CI level. I. Formalism, J. Chem. Phys., 2004, 120, 7322–7329 CrossRef CAS PubMed.
- I. Lengsfield, H. Byron, P. Saxe and D. R. Yarkony, On the evaluation of nonadiabatic coupling matrix elements using SA-MCSCF/CI wave functions and analytic gradient methods. I, J. Chem. Phys., 1984, 81, 4549–4553 CrossRef.
- P. Saxe, B. H. Lengsfield and D. R. Yarkony, On the evaluation of non-adiabatic coupling matrix elements for large scale CI wavefunctions, Chem. Phys. Lett., 1985, 113, 159–164 CrossRef CAS.
- S. Faraji, S. Matsika and A. I. Krylov, Calculations of non-adiabatic couplings within equation-of-motion coupled-cluster framework: Theory, implementation, and validation against multi-reference methods, J. Chem. Phys., 2018, 148, 044103 CrossRef PubMed.
- X. Zhang and J. M. Herbert, Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory, J. Chem. Phys., 2014, 141, 064104 CrossRef PubMed.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, Correlation Function Formalism for Triplet Excited State Decay: Combined Spin–Orbit and Nonadiabatic Couplings, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef CAS PubMed.
- R. A. Marcus, Electron transfer reactions in chemistry. Theory and experiment, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying p⋯p interactions, Chem. Phys. Lett., 2013, 557, 170–175 CrossRef CAS.
- A. Pérez-Guardiola, M. E. Sandoval-Salinas, D. Casanova, E. San-Fabián, A. J. Pérez-Jiménez and J. C. Sancho-García, The role of topology in organic molecules: origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers, Phys. Chem. Chem. Phys., 2018, 20, 7112–7124 RSC.
- T. Wang, A. Berdonces-Layunta, N. Friedrich, M. Vilas-Varela, J. P. Calupitan, J. I. Pascual, D. Peña, D. Casanova, M. Corso and D. G. de Oteyza, Aza-Triangulene: On-Surface Synthesis and Electronic and Magnetic Properties, J. Am. Chem. Soc., 2022, 144, 4522–4529 CrossRef CAS PubMed.
- M. Vilas-Varela, et al., On-Surface Synthesis and Characterization of a High-Spin Aza-[5]-Triangulene, Angew. Chem., Int. Ed., 2023, 62, e202307884 CrossRef CAS PubMed.
- T. Wang, P. Angulo-Portugal, A. Berdonces-Layunta, A. Jancarik, A. Gourdon, J. Holec, M. Kumar, D. Soler, P. Jelinek, D. Casanova, M. Corso, D. G. de Oteyza and J. P. Calupitan, Tuning the Diradical Character of Pentacene Derivatives via Non-Benzenoid Coupling Motifs, J. Am. Chem. Soc., 2023, 145, 10333–10341 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- K. Kim and K. Jordan, Comparison of density functional and MP2 calculations on the water monomer and dimer, J. Phys. Chem., 1994, 98, 10089–10094 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. J. Cramer, Computational Chemistry, Theories and Models, 2004 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Shao, M. Head-Gordon and A. I. Krylov, The spin–flip approach within timedependent density functional theory: Theory and applications to diradicals, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- Y. A. Bernard, Y. Shao and A. I. Krylov, General formulation of spin-flip time-dependent density functional theory using non-collinear kernels: Theory, implementation, and benchmarks, J. Chem. Phys., 2012, 136, 204103 CrossRef PubMed.
- D. Casanova and A. I. Krylov, Spin-flip methods in quantum chemistry, Phys. Chem. Chem. Phys., 2020, 22, 4326–4342 RSC.
- M. Head-Gordon, D. Maurice and M. Oumi, A perturbative correction to restricted open shell configuration interaction with single substitutions for excited states of radicals, Chem. Phys. Lett., 1995, 246, 114–121 CrossRef CAS.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Lett., 1994, 219, 21–29 CrossRef CAS.
- Y. M. Rhee and M. Head-Gordon, Scaled second-order perturbation corrections to configuration interaction singles: Efficient and reliable excitation energy methods, J. Phys. Chem. A, 2007, 111, 5314–5326 CrossRef CAS PubMed.
- A. I. Krylov, Size-consistent wave functions for bond-breaking: The equation-ofmotion spin-flip model, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, A new method for excited states: Similarity transformed equation-of-motion coupled-cluster theory, J. Chem. Phys., 1997, 106, 6441–6448 CrossRef CAS.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- R. Izsák, A local similarity transformed equation of motion approach for calculating excited states, Int. J. Quantum Chem., 2021, 121, e26327 CrossRef.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- E. Epifanovsky, et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- F. Neese, An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- X. Amashukeli, J. R. Winkler, H. B. Gray, N. E. Gruhn and D. L. Lichtenberger, Electron-transfer reorganization energies of isolated organic molecules, J. Phys. Chem. A, 2002, 106, 7593–7598 CrossRef CAS.
- K. Chen, C. Kunkel, K. Reuter and J. T. Margraf, Reorganization energies of flexible organic molecules as a challenging target for machine learning enhanced virtual screening, Digital Discovery, 2022, 1, 147–157 RSC.
- M. E. Sandoval-Salinas, G. Ricci, A. Pérez-Jiménez, D. Casanova, Y. Olivier and J.-C. Sancho-Garcia, Correlation vs. exchange competition drives the singlet–triplet excited-state inversion in non-alternant hydrocarbons, Phys. Chem. Chem. Phys., 2023, 25, 26417–26428 RSC.
- P.-F. Loos, A. Scemama and D. Jacquemin, The quest for highly accurate excitation energies: A computational perspective, J. Phys. Chem. Lett., 2020, 11, 2374–2383 CrossRef CAS PubMed.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4, 1654–1682 CrossRef CAS.
- P. de Silva, Inverted singlet–triplet gaps and their relevance to thermally activated delayed fluorescence, J. Phys. Chem. Lett., 2019, 10, 5674–5679 CrossRef CAS PubMed.
- A. Dreuw and M. Hoffmann, The inverted singlet–triplet gap: a vanishing myth?, Front. Chem., 2023, 11, 1239604 CrossRef CAS PubMed.
- A. I. Krylov, Equation-of-Motion Coupled-Cluster Methods for Open-Shell and Electronically Excited Species: The Hitchhiker's Guide to Fock Space, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- C. M. Marian, Understanding and Controlling Intersystem Crossing in Molecules, Annu. Rev. Phys. Chem., 2021, 72, 617–640 CrossRef CAS PubMed.
- M. A. El-Sayed, Spin—Orbit Coupling and the Radiationless Processes in Nitrogen Heterocyclics, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- D. G. Fedorov and M. S. Gordon, Low-Lying Potential Energy Surfaces, 2002, ch. 13, pp. 276–297.
Footnote |
| † Electronic supplementary information (ESI) available: Symmetry point group for the ground state of studied molecules. Singlet and triplet energies computed with different methods. See DOI: https://doi.org/10.1039/d4cp00304g |
| This journal is © the Owner Societies 2024 |