Open Access Article
Open Access ArticleImproving the potential of paraCEST through magnetic-coupling induced line sharpening†
Xin
Guo
a,
Lei
Zhang
bc,
Jiesheng
Hu
a,
Balázs
Szilágyi
de,
Meng
Yu
 *a,
Shizhen
Chen
*bc,
Gyula
Tircsó
*a,
Shizhen
Chen
*bc,
Gyula
Tircsó
 d,
Xin
Zhou
d,
Xin
Zhou
 bc and
Jun
Tao
bc and
Jun
Tao
 *a
*a
aKey Laboratory of Cluster Science of Ministry of Education, School of Chemistry and Chemical Engineering, Liangxiang Campus, Beijing Institute of Technology, Beijing 102488, China. E-mail: mengyu@bit.edu.cn; taojun@bit.edu.cn
bState Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, National Center for Magnetic Resonance in Wuhan, Wuhan Institute of Physics and Mathematics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan National Laboratory for Optoelectronics, Wuhan 430071, China. E-mail: chenshizhen@wipm.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
dDepartment of Physical Chemistry, Faculty of Science and Technology, University of Debrecen, Egyetem tér 1, H-4032 Debrecen, Hungary
eDoctoral School of Chemistry, University of Debrecen, Egyetem tér 1, H-4032 Debrecen, Hungary
First published on 21st November 2023
Abstract
Magnetic coupling between paramagnetic centers is a crucial phenomenon in the design of efficient MRI contrast agents. In this study, we investigate the paraCEST properties and magnetic coupling effects of a novel homodinuclear Ni(II) complex, 1, containing a Robson type macrocyclic ligand. A thorough analysis of the complex's electronic and magnetic properties revealed that the magnetic coupling effect reduces the transverse relaxation rate and enhances the sharpness of the proton resonances, leading to enhanced CEST efficiency. This novel mechanism, which we coined “magnetic-coupling induced line sharpening” (MILS), can be crucial for optimizing the performance of paramagnetic metal complexes in paraCEST imaging. Moreover, magnetic coupling plays a critical role in the relaxation properties of homodinuclear complexes. Our study not only paves the way for the creation of advanced paraCEST agents with enhanced CEST capabilities and sensitivity but also provides valuable guidance for the design of other MRI contrast agents utilizing dinuclear metal complexes.
Introduction
Paramagnetic chemical exchange saturation transfer (paraCEST) agents are a crucial subclass of CEST magnetic resonance imaging (MRI) agents that have undergone significant progress over the last few decades.1,2 Compared to traditional Gd(III)-based proton relaxation agents, paraCEST agents utilize the paramagnetic shift effect of paramagnetic metals to create a substantial chemical shift difference (Δω) between labile or exchangeable protons and bulk water protons. The selective irradiation of the exchangeable proton's resonance frequency, in conjunction with chemical exchange (kex) with bulk water protons, results in the suppression of the bulk water signal, thereby generating negative image contrast.3 It is noteworthy that the unique imaging mechanism of CEST confers several salient benefits, such as the ease of on/off switching of image contrast, multicolor imaging through frequency encoding (by using different metal ions), temperature-sensitive contrast signals, and responsive paraCEST agents for sensing applications.4–8 Importantly, as Δω ≥ kex is the prerequisite for CEST,9 the intrinsic large Δω associated with paraCEST agents naturally expand the scope of exchangeable protons due to higher kex tolerance, while concurrently greatly reducing the unwanted off-resonance saturation and background interference. However, it should be noted that kex is also limited by the maximum permissible saturation pulse power for in vivo applications.A fundamental challenge in the use of paraCEST agents is the trade-off between the advantage of large Δω and the detrimental line broadening arising from paramagnetic relaxation enhancement (PRE).1 To mitigate PRE, transition metal ions with short electronic relaxation time (τs) are preferred. In this context, high-spin Co2+(Oh), high-spin Fe2+(Oh), and low-spin Fe3+(Oh) with degenerate ground states and low-lying excited energy levels can exhibit short τs ranging from 10−11 to 10−12 s due to efficient Orbach-type relaxation mechanisms.10 Conversely, Ni2+(Oh) is associated with a longer τs (∼10−10 s) as its dominant relaxation mechanism is the modulation of the zero-field splitting (ZFS) through reorientation or collisions due to its orbitally nondegenerate ground state (3A).10 Moreover, the magnitude of the proton hyperfine shift (Δω) depends on both magnetic moment and magnetic anisotropy that encompasses through-bond contact and through-space pseudocontact shift (PCS) contributions.11,12 These stringent requirements restrict the options available in terms of paramagnetic metal ions when designing paraCEST agents, leading the majority of research efforts to focus on the optimization of ligand structures to enhance the sensitivity of paraCEST agents. The necessity for a strategy to tune the magnetic properties of metal ions cannot be overstated.
Magnetic exchange coupling is a promising approach to modulate the magnetic properties of metal ions. This exchange interaction involves the electronic spin magnetic moments of metal ions, resulting in the formation of new spin energy levels and altering the spin quantum number. Magnetic exchange coupling can be further classified into ferromagnetic and antiferromagnetic couplings depending on the ground state preference. The impact of magnetic exchange coupling on the proton relaxation rate and linewidth is significant. For instance, the decrease in relaxivity observed in an antiferromagnetically coupled μ-oxo-bridged Fe(III) dimeric complex has been exploited to probe pH changes and enzymatic activity by Gale's group.13,14 The relaxation properties of a series of heterodinuclear transition metal Gd(III) complexes have also been investigated by Meade and coworkers.15 Magnetic exchange coupling also affects the electronic relaxation time (τs) of metal ions. In heterodimers, the presence of a paramagnetic metal ion with shorter τs can effectively reduce the τs of the slower relaxing metal ion. In the case of homodimers, it can be proven theoretically that τs remains constant as in principle no further relaxation pathway is introduced. Nonetheless, a two-fold decrease should be expected in proton relaxation assuming a nucleus senses one metal ion, which is particularly beneficial for paraCEST. However, the presence of new relaxation pathways and a consequent decrease in τs arising from new spin energy levels cannot be ruled out, i.e., the presence of large ZFS of the new S = 1 level is responsible for the sharp NMR linewidths of some copper(II) dimers.16 Among these lines, Harris' group has carried out some pioneering studies where the paraCEST properties of dimeric copper(II), cobalt(II), and mixed-valent iron(II)/(III) complexes were investigated.7,17,18 The utilization of magnetic coupling as a means of manipulating magnetic properties in the development of paraCEST agents has shown promising potential. However, there is a scarcity of examples of paraCEST complexes based on this strategy, and much remains to be understood in order to fully exploit the concept of magnetic coupling.
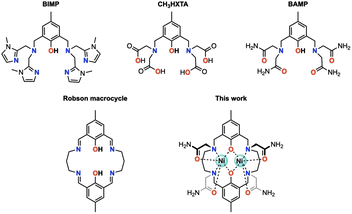
Octahedral nickel(II) complexes, with a borderline τs value of Ni2+(Oh), are typically not optimal for paraCEST applications due to their broad proton resonances. One innovative approach proposed by Morrow and colleagues utilizes a mixed aza–oxa 4,10-diaza-15-crown-5 macrocycle, resulting in sharp 1H NMR resonances and a strong paraCEST signal, possibly attributed to the pentagonal bipyramidal coordination geometry of the complex in solution endowed with a short τs value of Ni2+ (in the order of 10−12 s).19–21 Magnetic exchange coupling may also be a viable strategy for improving the paraCEST properties, with dinuclear Ni(II) complexes serving as a potential test subject. In this respect, we seek a reliable ligand platform that can support the simultaneous accommodation of two metal ions and promote magnetic coupling. Acyclic compartmental ligands such as BIMP, CH3HXTA, and BAMP (Fig. 1) have been considered potential candidates due to their ease of synthesis and literature precedent.17,22,23 Notably, the p orbitals on phenolate oxygen atoms provide superexchange pathways for magnetic interactions between the metal centers. However, their unsaturated coordination scaffold requires the incorporation of exogenous ligands (phosphate, acetate, azide, etc.) to complete the coordination sphere of the metal ion, which can compromise the biological stability of the resulting metal complexes. To this end, we have designed and synthesized a Robson macrocyclic ligand that is appended with carboxamide side arms (Fig. 1). The pre-organized binding cavities of the Robson macrocycle make it an attractive option for forming stable dinuclear complexes.24,25 Additionally, the versatility of the Robson macrocycle enables fine-tuning of its ring size and further modifications. Comprehensive studies have been conducted on the solution stability, magnetic properties, and paraCEST properties of the resulting dinuclear Ni(II) complex, unveiling the pivotal role of magnetic coupling in modulating the CEST efficiency. Specifically, in this magnetically coupled dinuclear system, the enhanced efficacy of CEST is attributed to the effect we refer to as “magnetic-coupling induced line sharpening” (MILS), which arises from the population of newly generated magnetic states according to Boltzmann distribution. To our knowledge, this is the first demonstration of a paraCEST agent based on a dinuclear Ni(II) complex.
Results and discussion
Syntheses and structural characterization
The metal-free Robson macrocycle was synthesized by reacting 2-hydroxy-5-methylisophthalaldehyde with 1,3-diaminopropane in the presence of NaClO4 that acts as a template. Reduction of the imine with NaBH4 followed by SN2 substitution with 2-bromoacetamide produced the target ligand (L). Refluxing L with two equiv of Ni(OAc)2·4H2O in MeOH, followed by reversed-phase chromatography, afforded [Ni2L](OAc)2·H2O·2CH3OH (1) as a blue powder. For comparison, a magnetically uncoupled heterodinuclear compound was synthesized by first reacting L with one equivalent of Ga(NO3)3·xH2O, followed by another equivalent of Ni(OAc)2·4H2O, to form [GaNiL]Br·CH3OH (2). Trivalent Ga(III) was selected here over divalent Zn(II) due to its better synthetic feasibility. The complete synthesis procedure can be found in the ESI.†Single crystals of 1 were obtained through slow diffusion of diisopropyl ether into a methanolic solution, resulting in blue, block-shaped crystals. The crystal structure of 1 was determined using single-crystal X-ray diffraction, revealing that it crystallizes in the monoclinic space group C2/c. The asymmetric unit consists of half a cationic Ni2 complex, one methanol, half a water molecule, and one acetate ion. Each Ni(II) ion is hexacoordinated with two μ-phenolate oxygen atoms, two trans-oriented carboxamide oxygen atoms, and two nitrogen atoms from the macrocycle. The coordination geometry was evaluated using the continuous shape measure (CShM) approach, which yielded a CShM value of 1.231 (OC-6), indicating a slight distortion from octahedral symmetry parameters determined to be 64.61° (Σ) and 207.14° (Θ).26,27 The coordination bond distances range from 2.01–2.12 Å with Ni–O (carboxamide) bond lengths being slightly longer than the rest. The Ni⋯Ni distance is 3.02 Å with a Ni–O–Ni bridge angle (θ) of 97.2°. The phenolate-rings exhibit a dihedral angle (ϕ) of 17.47°, forming a bend up and down from the Ni2O2 basal plane defined by the two Ni atoms and two phenolate O atoms (Fig. S1†). Both bridge and plane angles have important implications in determining the magnetic coupling interactions (vide infra). Interestingly, one of the propane backbone carbons was found to be disordered in two positions, indicating its highly flexible nature. Single crystals of [Ni2L]Cl2·3H2O (1′) were also obtained through slow evaporation of a 50 mM HEPES solution (pH = 7.2, 0.1 M NaCl) of 1, with a crystal structure closely resembling that of 1 (Fig. S2† and 2).
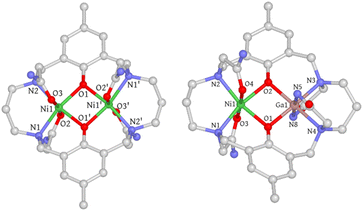 | ||
| Fig. 2 Crystal structures of 1 and 2. Hydrogen atoms, solvent molecules, disordered atoms, and counter-ions are omitted for clarity. C, gray; N, blue; O, red; Ni, green; Ga, pink. | ||
Single crystals of 2 were obtained using a method similar to that used for 1. However, the coordination geometry of 2 was found to be drastically different from that of 1 and 1′. Firstly, the Ga(III) metal center is axially coordinated to the deprotonated amide nitrogen atoms (N5 and N8) instead of the carboxamide oxygen atoms, which can be rationalized by the strong Lewis acidity of the trivalent Ga(III) ion that promotes amide deprotonation and prefers negatively charged nitrogen donors. A similar phenomenon has been previously observed in Ga(III), Co(III), and Cr(III) complexes.28–30 Secondly, the orientation of the carboxamide arms connected to N2 and N3 nitrogen atoms is in an “anti” conformation, whereas in 1 and 1′, a “syn” conformation is adopted. As a result, the phenolate rings are no longer parallel and form a dihedral angle of 23.48° (Fig. S5†). The electrostatic potential map indicates that this significant conformational change may be due to the need to minimize the steric/electrostatic repulsion between the amide pendant arms (Fig. S6†). Thirdly, the axial Ga–Ncarboxamide bond distances (1.96 and 1.97 Å) are noticeably shorter than their Ni(II) counterparts (2.07 and 2.09 Å). Surprisingly, the Ga–Ophenolate bond lengths are only slightly shorter than those of Ni(II) (Table S2†), which is likely due to the Coulomb repulsion between the metal centers that counteracts the bond contraction. Additionally, the equatorial Ga–Nmacrocycle bond lengths are elongated compared to Ni–Nmacrocycle bonds (Table S2†), which is attributed to the longer C–N bond than the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the amide groups, causing a size expansion of the five-membered chelate ring and concomitant Ga–Nmacrocycle bond elongation. In conclusion, the difference in coordination mode leads to substantial structural changes in 2.
O bond of the amide groups, causing a size expansion of the five-membered chelate ring and concomitant Ga–Nmacrocycle bond elongation. In conclusion, the difference in coordination mode leads to substantial structural changes in 2.
Aqueous stability and speciation
The aqueous stability of 1 was assessed by probing it against ion substitution using UV-vis spectroscopy. In the presence of large excess amounts of Ca2+, Zn2+, CO32− and H2PO4−, the UV-vis spectra of 1 do not exhibit any noticeable change, demonstrating its excellent kinetic stability against adventitious ions (Fig. S9–S12†). More thorough stability analysis of 1 comes from pH potentiometric titration experiments. The protonation constants of the ligand were determined by the pH-potentiometric method using 0.15 M NaCl ionic strength at 25 °C. Precipitation was observed during titration at pH above 8.0; therefore the protonation processes of the ligand were investigated by UV-visible spectrophotometry in the alkaline pH range using significantly more diluted (0.162 mM) ligand samples. The determined protonation constants are summarized in Table S6.† Based on UV-visible spectrophotometric titration, the phenolic OH groups possess fairly basic pKa values (pKa1 = 13.40(6) and pKa2 = 12.39(8)) while all other constants can be assigned to the protonation of the nitrogen atoms of the macrocycle. The pKa values of the phenolic OH group are relatively higher than anticipated, a phenomenon potentially attributed to intramolecular hydrogen bonding with neighboring nitrogen atoms within the macrocycle.31 The stability of the Ni(II) complexes was determined by fitting titration curves measured at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand
2 ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal ratios (ESI†). The equilibrium involving the ligand is rather complicated, as the ligand has six protonation sites and ten donor atoms, which leads to the formation of several protonated complexes in an acidic/near to neutral pH region. Furthermore, the chelator has two nearly equivalent Ni(II) binding sites; therefore the formation of dinuclear complexes was also assumed (as confirmed by X-ray crystallographic studies). Finally, in the alkaline pH range, metal-induced deprotonation of the amide groups might also occur, both in the case of mono-(NiLH-1) and dinuclear Ni(II) complexes (Ni2LH-1 and Ni2LH-2 species).32 Taking these considerations into account, the measured titration curves were well fitted with an equilibrium model involving ten complex species (Table S6†). Notably, coordination of one Ni(II) decreases the phenolic pKa values significantly (pKa1 = 7.57(4) and pKa2 = 10.46(4)), which further decreases after coordinating with a second one (pKa1 = 5.88(2) and 7.04(2)). The stability constants log
metal ratios (ESI†). The equilibrium involving the ligand is rather complicated, as the ligand has six protonation sites and ten donor atoms, which leads to the formation of several protonated complexes in an acidic/near to neutral pH region. Furthermore, the chelator has two nearly equivalent Ni(II) binding sites; therefore the formation of dinuclear complexes was also assumed (as confirmed by X-ray crystallographic studies). Finally, in the alkaline pH range, metal-induced deprotonation of the amide groups might also occur, both in the case of mono-(NiLH-1) and dinuclear Ni(II) complexes (Ni2LH-1 and Ni2LH-2 species).32 Taking these considerations into account, the measured titration curves were well fitted with an equilibrium model involving ten complex species (Table S6†). Notably, coordination of one Ni(II) decreases the phenolic pKa values significantly (pKa1 = 7.57(4) and pKa2 = 10.46(4)), which further decreases after coordinating with a second one (pKa1 = 5.88(2) and 7.04(2)). The stability constants log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(NiL) and log
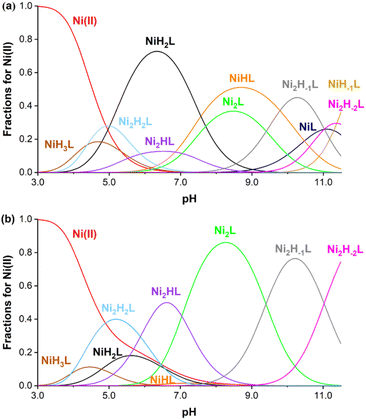
K(NiL) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(Ni2L) were determined to be 13.82(4) and 8.15(4), respectively, consistent with the excellent thermodynamic stability of the Ni(II) complex. Based on these data, concentration distribution curves were calculated (Fig. 3), which indicates the dominance of dinuclear complexes in the presence of two equivalents Ni(II) above pH = 5 (the CEST spectra were recorded at pH = 7.4 where Ni2L and Ni2HL dominate). Regardless of the fact that the ligand synthesized forms thermodynamically stable mono- and dinuclear complexes with Ni(II) ions, the kinetic inertness of the chelates suggested for in vivo applications is also critical. In order to test the performance of our Ni(II) chelate, we have studied a transmetalation reaction propagated by Cu(II) ions (available from a labile [Cu(Cit)]− complex c[Ni2L] = 0.25 mM and c[Cu(Cit)]− = 0.50 mM, Cit = citrate) at pH = 7.4 by UV-vis spectrophotometry. The preliminary study returned a half-life of 120 hours for the dissociation of the chelate, indicating a relatively high inertness of the dinuclear complex studied.
K(Ni2L) were determined to be 13.82(4) and 8.15(4), respectively, consistent with the excellent thermodynamic stability of the Ni(II) complex. Based on these data, concentration distribution curves were calculated (Fig. 3), which indicates the dominance of dinuclear complexes in the presence of two equivalents Ni(II) above pH = 5 (the CEST spectra were recorded at pH = 7.4 where Ni2L and Ni2HL dominate). Regardless of the fact that the ligand synthesized forms thermodynamically stable mono- and dinuclear complexes with Ni(II) ions, the kinetic inertness of the chelates suggested for in vivo applications is also critical. In order to test the performance of our Ni(II) chelate, we have studied a transmetalation reaction propagated by Cu(II) ions (available from a labile [Cu(Cit)]− complex c[Ni2L] = 0.25 mM and c[Cu(Cit)]− = 0.50 mM, Cit = citrate) at pH = 7.4 by UV-vis spectrophotometry. The preliminary study returned a half-life of 120 hours for the dissociation of the chelate, indicating a relatively high inertness of the dinuclear complex studied.
Magnetic properties
Magnetic susceptibility data for 1 were collected over a temperature range of 2–300 K at 5000 Oe (Fig. 4). The χMT value is 2.37 cm3 mol−1 K at 300 K, consistent with two non-interacting Ni(II) ions with spin orbit coupling contribution. The χMT decreases gradually upon cooling, reaching 1.68 cm3 mol−1 K at 50 K, after which the value drops abruptly to 0.14 cm3 mol−1 K at 2 K. This gradual decrease between 50 and 300 K indicates weak antiferromagnetic interaction between the Ni(II) centers, while the precipitous drop below 50 K arises from both zero-field splitting and weak intermolecular antiferromagnetic coupling. The PHI program was used to fit the magnetic susceptibility data of 1,33 based on the following spin-Hamiltonian (eqn (1)):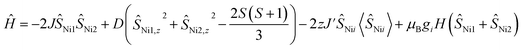 | (1) |
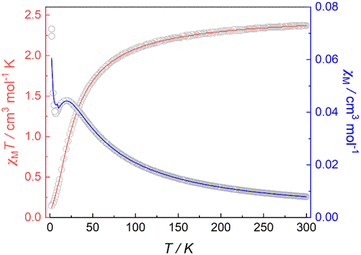 | ||
| Fig. 4 Variable-temperature magnetic susceptibility data for 1 collected at 5000 Oe. Red and blue lines correspond to fits of the magnetic data. | ||
Solution NMR studies
At 25 °C in aqueous buffer solution (pH 7.2), the magnetic moment (μeff) of 1 was determined to be 3.06 μB (per Ni2+ ion, assuming noninteracting metal centers) by the Evans method, consistent with a high-spin octahedral Ni(II) complex (S = 1) with contributions from orbital angular momentum. The magnetic moment was found to vary insignificantly from pH 6.6 to 8.2, indicating good aqueous stability and minimal change in the coordination environment around the metal center (Fig. S16†). At 310 K, the 1H NMR spectrum of 1 in D2O displayed seven paramagnetically shifted proton resonance signals at 186.2, 114.7, 63.8, 20.7, 9.4, 1.5, and −9.5 ppm, which is simpler than expected from the Ci molecular symmetry based on the crystal structure (Fig. S17†). This can be rationalized by the fluxional motion of the macrocyclic framework, giving rise to a pseudo C2h symmetry in solution, which is supported by the disorder of propane carbon in the crystal structure (vide supra). Moreover, the 1H NMR spectra of 1 exhibit minimal variation in the peak widths of the proton resonances between 25 °C and 37 °C (Fig. S18†), suggesting that dynamic processes involving structural fluctuations do not significantly contribute to the overall line widths. The Solomon equation suggests that the dipolar coupling-induced proton relaxation rate is inversely proportional to the sixth power of the proton-metal distance (r). Based on integration, T1 relaxation times, and line widths (full width at half-maximum, FWHM), the resonances at 1.5 and 20.7 ppm can be firmly attributed to phenolic methyl groups and aromatic protons. Assigning the remaining protons poses a challenge as they do not strictly adhere to the predictions of the Solomon equation, possibly owing to the influence of other relaxation mechanisms, such as Fermi contact coupling. Nevertheless, we attempted to assign all the protons by comparing them with similar complexes reported previously (Table S7†).42 Notably, a new peak at around 66 ppm was assigned to the exchangeable carboxamide protons based on the 1H NMR spectrum in HEPES buffer solution (Fig. S19†). In principle, one would anticipate the presence of two sets of magnetically equivalent carboxamide protons. The signal arising from the second set of exchangeable protons is likely concealed by the water signal.CEST properties
CEST spectra were obtained by collecting CEST data in an aqueous solution containing 10 mM of 1 with 50 mM HEPES and 100 mM NaCl buffered at pH 7.40 using a presaturation pulse of 24 μT for 4 s at 37 °C. The spectra were plotted by normalizing the intensity of the water 1H NMR signal (Mz/M0) against various presaturation frequencies ranging from 100 to −40 ppm referenced to the bulk water signal at 0 ppm. In accordance with the solution NMR results (Fig. S19†), a strong CEST peak was observed at 59 ppm from the bulk water signal (Fig. 6), corresponding to a 20% decrease in water signal intensity due to the exchangeable amide protons. At pH 7.15, the signal decreased to 13% (Fig. S20†), and the proton exchange rate (kex) at pH 7.40 was estimated to be 288 s−1 from the Omega plot, which drops to 240 s−1 at pH 7.15, indicating a base-catalyzed exchange mechanism (Fig. S23 and S24†), coherent with the observation that the fraction of Ni2HL species increases with decreasing pH (vide supra).43 The paraCEST properties of 1 were compared with those of other mononuclear Ni(II) complexes reported in the literature, as shown in Table S5.† While direct comparison is rendered challenging by variations in NMR instruments, sample conditions and the number of exchangeable protons contributing to the CEST signal, the paraCEST effect produced by 1 is comparable to or better than most of the Ni(II)-based paraCEST agents. In fact, it only falls short of the mixed dioxa-triaza macrocyclic systems developed by Morrow.6,19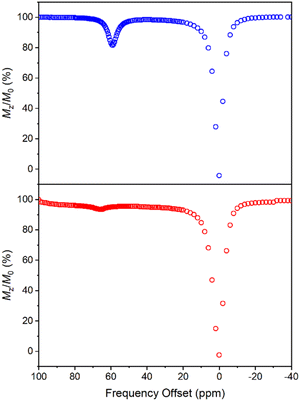 | ||
| Fig. 6 CEST spectra recorded at 9.4 T of 10 mM 1 (top) and 30 mM 2 (bottom) in 50 mM HEPES buffer solution at pH 7.40 and 37 °C, with a 4 s presaturation pulse of 24 μT. | ||
In contrast to 1, the CEST spectrum of 2 exhibits a peak at 66 ppm from the bulk water signal, indicating a relatively small reduction of only 6% in water intensity attributed to the CEST effect from the carboxamide protons coordinated to the Ni(II) center. Moreover, in our case, the CEST signal originating from the carboxamide protons coordinated to the diamagnetic Ga(III) center is not observed, possibly overshadowed by the water resonance. Notably, despite a much higher concentration, the CEST signal of 2 is significantly weaker than that of 1, although this could be partially attributed to its lower symmetry and fewer equivalent exchangeable protons. In hindsight, the hyperfine shift of amide protons in 1 is comparable to that of 2, which is somewhat underwhelming considering the dinuclear nature of 1. Both contact and pseudocontact shifts contribute to the observed hyperfine shift, with through-bond contact contribution maintaining relatively constant in both mononuclear and dinuclear systems due to the proximity of amide protons around the nickel center. In contrast, the dipolar, pseudocontact shift is additive to the effect of individual metal ions, provided they have similar unpaired electron density distribution.44 The underwhelming hyperfine shift of amide protons suggests that the dipolar effects of Ni(II) ions are probably opposite or more sophisticated than we expected.
Mechanistic implications
The significantly improved paraCEST properties of 1 compared to 2 require further clarification. Proton relaxation time measurements can provide valuable information about τs. In the absence of chemical exchange, the dipolar and contact contributions to proton longitudinal and transverse relaxation rates can be expressed using the Solomon equation:45Dipolar contribution:
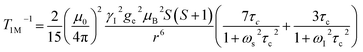 | (2) |
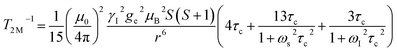 | (3) |
Contact contribution:
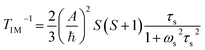 | (4) |
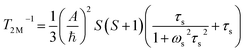 | (5) |
A is the hyperfine coupling constant, S is the spin quantum number, r is the metal–proton distance, and ωs and ωI are electron and nucleus transition frequencies, respectively. The correlation time τc in eqn (2)–(5) can be expressed as
| τc−1 = τs−1 + τr−1 | (6) |
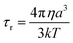 | (7) |
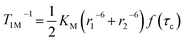 | (8) |
The longitudinal relaxation time (T1) of bulk water protons is another critical factor that can significantly impact the CEST effect. This relationship is described by the following equation:
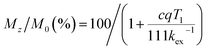 | (9) |
In summary, the enhanced paraCEST properties of 1 primarily stem from the Boltzmann population of newly generated energy levels resulting from magnetic coupling. As discussed above, in strongly coupled systems, this phenomenon leads to a multiplication coefficient of ½ in homodinuclear complexes, resulting in a reduction in the proton relaxation rate and sharpening of proton resonances. It is worth noting that this effect has been extensively investigated by Drago and Bertini.16,44,48 Furthermore, it is conceivable that this phenomenon may also influence the relaxation effects on bulk water in dinuclear systems. However, the exploration of this phenomenon remains limited within the paraCEST and contrast agent research communities. Finally, we also note that the above discussion does not take into account zero-field splitting factors within the newly generated magnetic states but the same trend should hold.
Conclusions
In conclusion, we have presented a comprehensive study on the design, synthesis, and characterization of a dinuclear Ni(II) complex that exhibits paraCEST properties. Through the utilization of various characterization techniques, we have identified the key factor contributing to the enhanced paraCEST efficiency of 1 as the “magnetic-coupling induced line sharpening” (MILS) effect, which mitigates the PRE effect on proton linewidth. This effect operates under the conditions of satisfying the “strong-coupling limit”, regardless of the intrinsic magnetic coupling nature (antiferromagnetic or ferromagnetic) as long as |J| ≪ kT. Nevertheless, we observe ambiguity in whether magnetic coupling results in a reduction of τs solely based on the value of τc. Our findings underscore the crucial role of magnetic coupling in addressing challenges and optimizing the performance of paramagnetic metal complexes in paraCEST imaging. Furthermore, the underlying concept can be potentially applied to all paraCEST agents employing first-row transition metals, and ongoing research in our lab aims to further explore this concept. In the context of in vivo applications, paraCEST agents encounter a notable challenge: their relatively low sensitivity compared to traditional MRI techniques. This sensitivity limitation primarily stems from constraints related to the maximum permissible saturation pulse power and the interference from exchanging proton species within biological tissues. The MILS strategy presented in our study provides valuable insights for enhancing paraCEST agent sensitivity at the single-molecule level. However, it is essential to acknowledge that addressing the sensitivity issue comprehensively requires further endeavors. This could involve optimizing local agent concentrations through meticulous chemical design and, complementarily, employing advanced material-based approaches. The latter may involve encapsulating paraCEST agents within diverse carrier systems such as micelles, polymers, and nanoparticles.Data availability
All data associated with this publication are provided in the main text and ESI.†Author contributions
M. Y., S. Z. C., and J. T. supervised the project. M. Y. conceived the idea, analyzed the data, and wrote the manuscript. X. G. synthesized the compounds, performed characterization, and analyzed the data. L. Z. performed all the CEST and relaxation time measurements. J. S. H. solved all the crystal structures. B. S. and G. T. conducted pH-potentiometric titrations, analyzed the data, and wrote part of the manuscript. M. Y., S. Z. C., G. T., X. Z., and J. T. provided resources and edited the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grants 22101021, 92061106, 22071009, U21A20392, 82127802, and 21921004) and Hungarian National Research, Development and Innovation Office (NKFIH K-128201 and K-134694 projects). B. S. was supported by the Doctoral School of Chemistry at the University of Debrecen, Hungary. S. Z. C. acknowledges the support from the Young Top-notch Talent Cultivation Program of Hubei Province. We also thank the Chemistry and Chemical Experiment Center and the Analysis & Testing Center of the Beijing Institute of Technology for technical support.Notes and references
- A. D. Sherry, D. D. Castelli and S. Aime, NMR Biomed., 2022, 36, e4698 CrossRef PubMed.
- J. Wahsner, E. M. Gale, A. Rodriguez-Rodriguez and P. Caravan, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- A. Gupta, P. Caravan, W. S. Price, C. Platas-Iglesias and E. M. Gale, Inorg. Chem., 2020, 59, 6648–6678 CrossRef CAS PubMed.
- R. Trokowski, J. Ren, F. K. Kálmán and A. D. Sherry, Angew. Chem., 2005, 117, 7080–7083 CrossRef.
- S. J. Dorazio, P. B. Tsitovich, K. E. Siters, J. A. Spernyak and J. R. Morrow, J. Am. Chem. Soc., 2011, 133, 14154–14156 CrossRef CAS PubMed.
- A. O. Olatunde, S. J. Dorazio, J. A. Spernyak and J. R. Morrow, J. Am. Chem. Soc., 2012, 134, 18503–18505 CrossRef CAS PubMed.
- A. E. Thorarinsdottir, K. Du, J. H. P. Collins and T. D. Harris, J. Am. Chem. Soc., 2017, 139, 15836–15847 CrossRef CAS PubMed.
- K. Du, A. E. Thorarinsdottir and T. D. Harris, J. Am. Chem. Soc., 2019, 141, 7163–7172 CrossRef CAS PubMed.
- P. C. van Zijl and N. N. Yadav, Magn. Reson. Med., 2011, 65, 927–948 CrossRef CAS PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, in NMR of Paramagnetic Molecules :Applications to Metallobiomolecules and Models, Elsevier, Amsterdam, Netherlands, 2016, pp. 175–253 Search PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, in NMR of Paramagnetic Molecules :Applications to Metallobiomolecules and Models, Elsevier, Amsterdam, Netherlands, 2016, pp. 25–60 Search PubMed.
- R. S. Drago, Physical Methods for Chemists, Saunders College Pub., Orlando, FL, 2nd edn, 1992 Search PubMed.
- H. Wang, A. Wong, L. C. Lewis, G. R. Nemeth, V. C. Jordan, J. W. Bacon, P. Caravan, H. S. Shafaat and E. M. Gale, Inorg. Chem., 2020, 59, 17712–17721 CrossRef CAS PubMed.
- H. Wang, M. B. Cleary, L. C. Lewis, J. W. Bacon, P. Caravan, H. S. Shafaat and E. M. Gale, Angew. Chem., Int. Ed., 2022, 61, e202114019 CrossRef CAS PubMed.
- L. M. Lilley, K. Du, M. D. Krzyaniak, G. Parigi, C. Luchinat, T. D. Harris and T. J. Meade, Inorg. Chem., 2018, 57, 5810–5819 CrossRef CAS PubMed.
- N. N. Murthy, K. D. Karlin, I. Bertini and C. Luchinat, J. Am. Chem. Soc., 1997, 119, 2156–2162 CrossRef CAS.
- K. Du and T. D. Harris, J. Am. Chem. Soc., 2016, 138, 7804–7807 CrossRef CAS PubMed.
- K. Du, E. A. Waters and T. D. Harris, Chem. Sci., 2017, 8, 4424–4430 RSC.
- P. J. Burns, J. M. Cox and J. R. Morrow, Inorg. Chem., 2017, 56, 4546–4555 CrossRef CAS PubMed.
- A. O. Olatunde, S. J. Dorazio, J. A. Spernyak and J. R. Morrow, J. Am. Chem. Soc., 2012, 134, 18503–18505 CrossRef CAS PubMed.
- R. N. Pradhan, S. Chakraborty, P. Bharti, J. Kumar, A. Ghosh and A. K. Singh, Dalton Trans., 2019, 48, 8899–8910 RSC.
- R. M. Buchanan, M. S. Mashuta, K. J. Oberhausen, J. F. Richardson, Q. Li and D. N. Hendrickson, J. Am. Chem. Soc., 1989, 111, 4497–4498 CrossRef CAS.
- R. C. Holz, B. Bennett, G. Chen and L.-J. Ming, J. Am. Chem. Soc., 1998, 120, 6329–6335 CrossRef CAS.
- M. T. Chaudhry, S. Akine and M. J. MacLachlan, Chem. Soc., 2021, 50, 10713–10732 CAS.
- P. A. Vigato, V. Peruzzo and S. Tamburini, Coord. Chem. Rev., 2012, 256, 953–1114 CrossRef CAS.
- R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, Dalton Trans., 2021, 50, 1086–1096 RSC.
- SHAPE 2.1; Electronic Structure Group, Universitat de Barcelona, Spain, 2013 Search PubMed.
- D. Shetty, S. Y. Choi, J. M. Jeong, L. Hoigebazar, Y. S. Lee, D. S. Lee, J. K. Chung, M. C. Lee and Y. K. Chung, Eur. J. Inorg. Chem., 2010, 34, 5432–5438 CrossRef.
- M. Yu, B. S. Bouley, D. Xie, J. S. Enriquez and E. L. Que, J. Am. Chem. Soc., 2018, 140, 10546–10552 CrossRef CAS PubMed.
- T. Weyhermüller, K. Weighardt and P. Chaudhuri, J. Chem. Soc., Dalton Trans., 1998, 3805–3814 RSC.
- I. Kenkel, A. Franke, M. Dürr, A. Zahl, C. Dücker-Benfer, J. Langer, M. R. Filipović, M. Yu, R. Puchta, S. R. Fiedler, M. P. Shores, C. R. Goldsmith and I. Ivanović-Burmazović, J. Am. Chem. Soc., 2017, 139, 1472–1484 CrossRef CAS PubMed.
- A. Jancsó, K. Selmeczi, P. Gizzi, N. V. Nagy, T. Gajda and B. Henry, J. Inorg. Biochem., 2011, 105, 92–101 CrossRef PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- K. K. Nanda, L. K. Thompson, J. N. Bridson and K. Nag, J. Chem. Soc., Chem. Commun., 1994, 1337–1338 RSC.
- K. K. Nanda, R. Das, L. K. Thompson, K. Venkatsubramanian, P. Paul and K. Nag, Inorg. Chem., 1994, 33, 1188–1193 CrossRef CAS.
- H. Sakiyama, Y. Chiba, K. Tone, M. Yamasaki, M. Mikuriya, J. Krzystek and A. Ozarowski, Inorg. Chem., 2017, 56, 138–146 CrossRef CAS PubMed.
- H. Sakiyama, K. Tone, M. Yamasaki and M. Mikuriya, Inorg. Chim. Acta, 2011, 365, 183–189 CrossRef CAS.
- S. Weissman, M. Antkowiak, B. Brzostowski, G. Kamieniarz and L. Kronik, J. Chem. Theory Comput., 2019, 15, 4885–4895 CrossRef CAS PubMed.
- D. A. Pantazis, J. Chem. Theory Comput., 2019, 15, 938–948 CrossRef CAS PubMed.
- M. J. Prushan, D. M. Tomezsko, S. Lofland, M. Zeller and A. D. Hunter, Inorg. Chim. Acta, 2007, 360, 2245–2254 CrossRef CAS.
- J. Cano, G. De Munno, J. Luis Sanz, R. Ruiz, J. Faus, F. Lloret, M. Julve and A. Caneschi, J. Chem. Soc., Dalton Trans., 1997, 1915–1924 RSC.
- J. Lisowski, Inorg. Chim. Acta, 1999, 285, 233–240 CrossRef CAS.
- W. T. Dixon, J. Ren, A. J. Lubag, J. Ratnakar, E. Vinogradov, I. Hancu, R. E. Lenkinski and A. D. Sherry, Magn. Reson. Med., 2010, 63, 625–632 CrossRef CAS PubMed.
- C. Owens, R. S. Drago, I. Bertini, C. Luchinat and L. Banci, J. Am. Chem. Soc., 1986, 108, 3298–3303 CrossRef CAS.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- R. A. Dwek, Nuclear magnetic resonance in biochemistry: applications to enzyme systems, Clarendon, Oxford, 1975 Search PubMed.
- I. Bertini, O. Galas, C. Luchinat, G. Parigi and G. Spina, J. Magn. Reson., 1998, 130, 33–44 CrossRef CAS PubMed.
- I. Bertini, C. Owens, C. Luchinat and R. S. Drago, J. Am. Chem. Soc., 1987, 109, 5208–5212 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2291721–2291723. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc04770a |
| This journal is © The Royal Society of Chemistry 2023 |