Open Access Article
Open Access ArticleStructural distortion by alkali metal cations modulates the redox and electronic properties of Ce3+ imidophosphorane complexes†
Andrew C.
Boggiano
 a,
Chad M.
Studvick
b,
Alexander
Steiner
c,
John
Bacsa
a,
Ivan A.
Popov
*b and
Henry S.
La Pierre
a,
Chad M.
Studvick
b,
Alexander
Steiner
c,
John
Bacsa
a,
Ivan A.
Popov
*b and
Henry S.
La Pierre
 *ad
*ad
aSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: hsl@gatech.edu
bDepartment of Chemistry, The University of Akron, Akron, Ohio 44325–3601, USA
cDepartment of Chemistry, University of Liverpool, Liverpool L69 7ZD, UK
dNuclear and Radiological Engineering and Medical Physics Program, School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
First published on 25th September 2023
Abstract
A series of Ce3+ complexes with counter cations ranging from Li to Cs are presented. Cyclic voltammetry data indicate a significant dependence of the oxidation potential on the alkali metal identity. Analysis of the single-crystal X-ray diffraction data indicates that the degree of structural distortion of the secondary coordination sphere is linearly correlated with the measured oxidation potential. Solution electronic absorption spectroscopy confirms that the structural distortion is reflected in the solution structure. Computational studies further validate this analysis, deciphering the impact of alkali metal cations on the Ce atomic orbital contributions, differences in energies of Ce-dominant molecular orbitals, energy shift of the 4f–5d electronic transitions, and degree of structural distortions. In sum, the structural impact of the alkali metal cation is demonstrated to modulate the redox and electronic properties of the Ce3+ complexes, and provides insight into the rational tuning of the Ce3+ imidophosphorane complex oxidation potential through alkali metal identity.
Introduction
The Ce3+/4+ redox potential is remarkably sensitive to the ligand coordination environment, spanning a uniquely large range of potentials for a single metal-based redox couple.1 This dependence on coordination chemistry and solvation is demonstrated by the range of redox properties exhibited in cerium systems. For example, Ce4+ ammonium nitrate (CAN) is among the strongest isolable chemical oxidants.2 At the other extreme, Ce3+ imidophosphorane (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR3, R = alkyl/amido) complexes exhibit redox potentials among those of the most potent chemical reductants.2–4
PR3, R = alkyl/amido) complexes exhibit redox potentials among those of the most potent chemical reductants.2–4
Over the past few decades, the molecular chemistry of lanthanides has seen a rapid expansion, with developments revealing that lanthanides exhibit a wider range of molecular oxidation states than previously thought possible.5–23 However, the number of ligand systems and synthetic pathways supporting tetravalent lanthanides, except for Ce4+, is very limited. Rational control of the Ln3+/4+ (Ln = lanthanide) redox potential through ligand design is a powerful tool for expanding Ln4+ chemistry. Seminal studies24–26 by Schelter and co-workers shed light on the critical role that ligand reorganization plays in Ce3+/4+ redox kinetics and thermodynamics. Identity of the cation results in divergent rates, potentials, and reactivity patterns among analogous complexes. In aggregate, this body of work demonstrated the critical role of structural aspects of the coordination sphere in Ce3+/4+ redox chemistry. Comprehensive studies of tuning the molecular Ln3+/4+ potential within a given ligand framework are limited to BINOLate (BINOLate = 1,1′-bi-2-naphtholate) complexes. Rationally leveraging characteristics of the outer coordination sphere to modulate metal redox properties of a metal center is noted as a challenging, but promising approach to control metal speciation.27
Imidophosphorane ligands dramatically shift the redox potentials of f-block complexes, and have demonstrated accessibility of molecular tetravalent Tb18 & Pr19 and the most reducing Ce3+ complexes reported.1,3,4,28 The factors that modulate the redox potentials of Ln imidophosphorane complexes have yet to be delineated, though the alkali metal is shown to be influential in the oxidation.3 The isolation of new tetravalent Ln complexes requires a thorough understanding of the factors that modulate the oxidation potential. Herein, an alkali metal series of Ce3+ imidophosphorane complexes is presented (Fig. 1). The comparison of cyclic voltammetry data and structural parameters derived from the solid-state structures demonstrate a positive, linear correlation between the degree of ligand sphere distortion and the measured oxidation potential (Epa). Lewis acidity of redox-inactive metals has previously shown to best describe the modulation of the redox potential in transition metal29–36 and uranyl37,38 systems, however, structural aspects of the coordination sphere and the size of the alkali metal cation display a better correlation in the imidophosphorane system reported here. Analysis of Ce3+ alkali metal series indicates that structural distortion can play a critical role in modulating the Ce3+/4+ potential across diverse ligand frameworks,1,24–26 however, in this imidophosphorane ligand system, Epc is relatively unperturbed and Epa spans 600 mV. The electronic effects of the structural perturbations on Epa are amplified by the unique binding of each alkali cation in the secondary coordination sphere of the zwitterionic imidophosphorane ligands.
Results
Synthesis
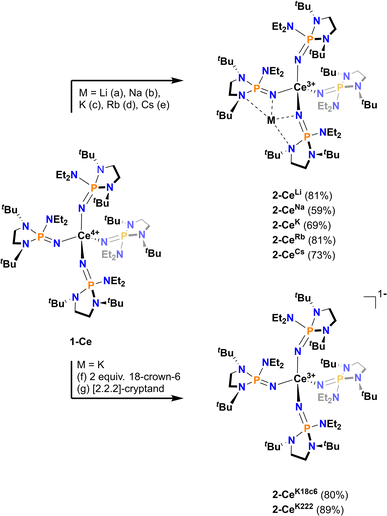
All Ce3+ alkali metal complexes were prepared via reduction of the previously reported4 tetravalent cerium complex, [Ce4+(NP(N,N′-di-tert-butylethylenediamide)(diethylamide))4] (1-Ce, [N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P(N,N′-di-tert-butylethylenediamide)(diethylamide)]− = NP*) (Scheme 1). The trivalent complexes, [M][Ce3+(NP(N,N′-di-tert-butylethylenediamide)(diethylamide))4] (M = Li+ (2-CeLi), Na+ (2-CeNa), K+ (2-CeK), Rb+ (2-CeRb), Cs+ (2-CeCs), K+([2.2.2]-cryptand) (2-CeK222), K+(18-crown-6)2 (2-CeK18c6)), span the alkali metal series (Li–Cs), with the outer-sphere potassium analogues (2-CeK222, 2-CeK18c6) serving as controls for minimal interaction with the counter cation. 2-CeLi and 2-CeNa were prepared via reduction of 1-Ce in the presence of excess Li or Na metal, respectively. An alternative method for the synthesis of the previously reported42-CeK using the potassium graphite intercalation compound, KC8, is reported here with improved yield (69%). The compounds 2-CeK18c6 and 2-CeK222 were prepared in an analogous manner to 2-CeK, with the addition of 2 equivalents of 18-crown-6 or 1 equivalent of [2.2.2]-cryptand, respectively. The rubidium and cesium congeners, 2-CeRb and 2-CeCs, were prepared using the corresponding alkali metal graphite intercalation compound. A new direct synthesis of 1-Ce is reported, providing an improved crystalline yield of 85%, compared to the 48% total yield in the previously reported, step-wise preparation (Scheme 1).4
P(N,N′-di-tert-butylethylenediamide)(diethylamide)]− = NP*) (Scheme 1). The trivalent complexes, [M][Ce3+(NP(N,N′-di-tert-butylethylenediamide)(diethylamide))4] (M = Li+ (2-CeLi), Na+ (2-CeNa), K+ (2-CeK), Rb+ (2-CeRb), Cs+ (2-CeCs), K+([2.2.2]-cryptand) (2-CeK222), K+(18-crown-6)2 (2-CeK18c6)), span the alkali metal series (Li–Cs), with the outer-sphere potassium analogues (2-CeK222, 2-CeK18c6) serving as controls for minimal interaction with the counter cation. 2-CeLi and 2-CeNa were prepared via reduction of 1-Ce in the presence of excess Li or Na metal, respectively. An alternative method for the synthesis of the previously reported42-CeK using the potassium graphite intercalation compound, KC8, is reported here with improved yield (69%). The compounds 2-CeK18c6 and 2-CeK222 were prepared in an analogous manner to 2-CeK, with the addition of 2 equivalents of 18-crown-6 or 1 equivalent of [2.2.2]-cryptand, respectively. The rubidium and cesium congeners, 2-CeRb and 2-CeCs, were prepared using the corresponding alkali metal graphite intercalation compound. A new direct synthesis of 1-Ce is reported, providing an improved crystalline yield of 85%, compared to the 48% total yield in the previously reported, step-wise preparation (Scheme 1).4
Cyclic voltammetry
Cyclic voltammograms were measured in tetrahydrofuran (THF) with either 50 mM [nBu4N][BPh4] or 100 mM [nBu4N][PF6] as the supporting electrolyte. Analyte concentration was generally 3 mM, except for 2-CeRb and 2-CeCs, which were measured at 1 mM concentration. 2-CeRb and 2-CeCs in solutions of 100 mM [nBu4N][BPh4] generated a colorless precipitate, so 50 mM electrolyte concentration was used in all experiments for consistency. Only [nBu4N][BPh4] allowed for measurement of all analytes in the series. The values measured in [nBu4N][PF6] solution are reported where possible (Table 1), though the following discussion is limited to values measured with [nBu4N][BPh4] as the supporting electrolyte.| 2-CeLi | 2-CeNa | 2-CeK | 2-CeRb | 2-CeCs | 1-Ce | 2-CeK18c6 | 2-CeK222 | |
|---|---|---|---|---|---|---|---|---|
| a Tabulated anodic (Epa) and cathodic (Epc) potentials measured by cyclic voltammetry in THF. Electrolyte cation is [nBu4N]+ in all experiments. Electrolyte concentrations = 50 mM for [nBu4N][BPh4] and 100 mM for [nBu4N][PF6]. All analyte concentrations = 3 mM, except for 2-CeRb and 2-CeCs, which were measured in 1 mM analyte concentration in 50 mM [nBu4N][BPh4]. b Features are not well defined, see Fig. S57. | ||||||||
| E pa [BPh4] | −1.37 | −1.45 | −1.71 | −1.87 | −1.98 | −1.83 | −1.92 | −1.94 |
| E pc [BPh4] | −1.74 | −2.71 | −2.76 | −2.82 | −2.73 | −2.87 | −2.78 | −2.74 |
| E pa [PF6] | −1.23 | −1.44 | −1.44 | −1.31b | −1.63 | −1.63 | −1.62 | |
| E pc [PF6] | −1.47 | −2.84 | −2.86 | −3.00b | −2.86 | −2.80 | −2.89 | |
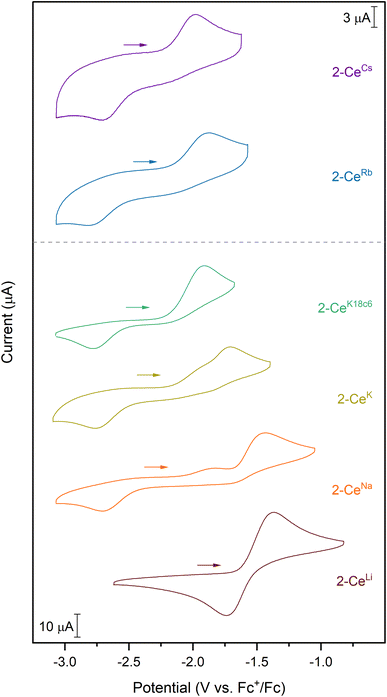
Except for 2-CeLi, the features in the cyclic voltammograms are electrochemically irreversible, with peak-to-peak separation (ΔEpp) ranging approximately 0.7–1.2 V. In 2-CeLi, ΔEpp is much smaller at ∼250 mV, indicating a quasi-reversible event. Epa is modulated across a range of ∼600 mV by the identity of the alkali metal. The electrochemical reduction (Epc) shows a smaller response to the alkali metal, occurring within a <200 mV range, excluding 2-CeLi. The anodic feature occurs at more positive potentials traversing the alkali metal series from Cs to Li. 2-CeLi is the least reducing compound, measured by Epa at −1.37 V vs. Fc+/Fc. The most reducing compound is 2-CeCs, with Epa = −1.98 V. The Na, K, and Rb congeners display intermediate Epa values, progressing to more negative values as the size of the cation increases. 2-CeNa and 2-CeK display secondary features around −1.9 V. The secondary feature is well resolved for 2-CeNa in both electrolytes, however, it is unresolved for 2-CeK with [nBu4N][PF6] as the supporting electrolyte. The ratio of the current response at the primary and secondary events varies with scan rate for both 2-CeNa and 2-CeK (Fig. S50–S52,† see Discussion for further analysis).
2-CeK18c6 and 2-CeK222 serve as controls in which structural distortion by the cation is minimized. 2-CeK18c6 and 2-CeK222 are among the stronger reductants of the series, with Epa values of −1.92 V and −1.94 V, respectively. Their oxidation potentials are close to that of the tetravalent complex, 1-Ce (Epa = −1.83 V), where no alkali metal counter cation is present. The similarity of the oxidation potentials of 2-CeK18c6, 2-CeK222, and 1-Ce validates 2-CeK18c6 and 2-CeK222 as models for studying redox processes with minimal interaction with the alkali metal.
Chemical oxidation
Chemical redox reactions were performed with both benzophenone (E°′ = −2.30 V in THF)2 and decamethylcobaltocenium hexafluorophosphate (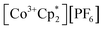 , E°′ = −1.91 V in MeCN)2 to probe the divergent Epc measured for 2-CeLi. The irreversibility of many of the redox features complicates estimating the chemical redox potential, but the potential was approximated to lie between Epa and Epc for each complex. Initially, benzophenone was chosen for its E°′ that is substantially more negative than the E1/2 of 2-CeLi (−1.56 V), and more positive than Epc of 2-CeK18c6 (−2.78 V), suggesting capability of being reduced by 2-CeK18c6, but not 2-CeLi. At room temperature, addition of a solution of 1 equiv. of benzophenone with 2-CeK18c6 in THF-d8 results in an immediate color change from light yellow to dark green. The corresponding reaction with 2-CeLi does not effect a color change. Nuclear magnetic resonance (NMR) analysis indicates complete consumption of benzophenone in the case of 2-CeK18c6, while benzophenone signals in the aryl region of the 1H NMR are present with 2-CeLi (Fig. S69 and S73†). Heating the reaction mixtures for 1 h at 60 °C led to complex degradation, however, the major species in the reaction of 2-CeLi was the trivalent starting material (Fig. S73 and S74†).
, E°′ = −1.91 V in MeCN)2 to probe the divergent Epc measured for 2-CeLi. The irreversibility of many of the redox features complicates estimating the chemical redox potential, but the potential was approximated to lie between Epa and Epc for each complex. Initially, benzophenone was chosen for its E°′ that is substantially more negative than the E1/2 of 2-CeLi (−1.56 V), and more positive than Epc of 2-CeK18c6 (−2.78 V), suggesting capability of being reduced by 2-CeK18c6, but not 2-CeLi. At room temperature, addition of a solution of 1 equiv. of benzophenone with 2-CeK18c6 in THF-d8 results in an immediate color change from light yellow to dark green. The corresponding reaction with 2-CeLi does not effect a color change. Nuclear magnetic resonance (NMR) analysis indicates complete consumption of benzophenone in the case of 2-CeK18c6, while benzophenone signals in the aryl region of the 1H NMR are present with 2-CeLi (Fig. S69 and S73†). Heating the reaction mixtures for 1 h at 60 °C led to complex degradation, however, the major species in the reaction of 2-CeLi was the trivalent starting material (Fig. S73 and S74†).
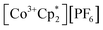 (E°′ = −1.91 V in MeCN)2 was identified as a more chemically inert reagent with E°′ in the targeted range. At room temperature, addition of
(E°′ = −1.91 V in MeCN)2 was identified as a more chemically inert reagent with E°′ in the targeted range. At room temperature, addition of 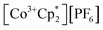 to a solution of 2-CeK18c6 in THF-d8 results in an immediate color change to a red/orange color characteristic of 1-Ce. The corresponding reaction with 2-CeLi does not produce a visually apparent change at room temperature. Both reactions were subjected to heating at 60 °C and analyzed via NMR, demonstrating the production of
to a solution of 2-CeK18c6 in THF-d8 results in an immediate color change to a red/orange color characteristic of 1-Ce. The corresponding reaction with 2-CeLi does not produce a visually apparent change at room temperature. Both reactions were subjected to heating at 60 °C and analyzed via NMR, demonstrating the production of 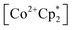 by oxidation of 2-CeK18c6, but not 2-CeLi (Fig. S63–S68, see ESI† for further analysis). Reactions with both benzophenone and
by oxidation of 2-CeK18c6, but not 2-CeLi (Fig. S63–S68, see ESI† for further analysis). Reactions with both benzophenone and 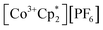 indicate that the reducing power of 2-CeLi is significantly less than 2-CeK18c6, in agreement with the CV data. Divergent behavior in the Li analogue is consistent with the Ce3+ BIONLate complexes reported by Schelter and co-workers.25 The steric bulk of the imidophosphorane ligand differentiates the series presented here compared to the Ce3+ BINOLate complexes, as inner-sphere functionalization is unlikely due to the inaccessibility of the Ce center. Density functional theory (DFT) analysis of the molecular orbital (MO) composition and energy levels of the metal-dominant MOs in the 2-CeM series (vide infra) supports the result that 2-CeLi is a much less-potent reductant compared to the rest of the series.
indicate that the reducing power of 2-CeLi is significantly less than 2-CeK18c6, in agreement with the CV data. Divergent behavior in the Li analogue is consistent with the Ce3+ BIONLate complexes reported by Schelter and co-workers.25 The steric bulk of the imidophosphorane ligand differentiates the series presented here compared to the Ce3+ BINOLate complexes, as inner-sphere functionalization is unlikely due to the inaccessibility of the Ce center. Density functional theory (DFT) analysis of the molecular orbital (MO) composition and energy levels of the metal-dominant MOs in the 2-CeM series (vide infra) supports the result that 2-CeLi is a much less-potent reductant compared to the rest of the series.
Structural analysis
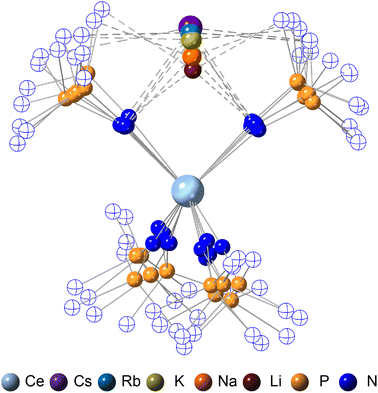
The crystallographically characterized complexes (2-CeLi, 2-CeNa, 2-CeK, 2-CeK18c6, 2-CeRb, and 2-CeCs) exhibit pseudo-tetrahedral geometry in the primary coordination sphere (Fig. 1). Two adjacent ligands form a pocket in which the alkali metal is bound (except for 2-CeK18c6 where the alkali cation is the outer sphere). There are two distinct types of Ce–N bonds, those binding the alkali metal (Ce–Ncapped) and those only bound to the metal center (Ce–Nterminal). The differences in bond lengths between Ce–Ncapped and Ce–Nterminal are about 0.1 Å, measuring approximately 2.3 and 2.4 Å, respectively, across the series. The contraction to about 2.2 Å in the structure of 1-Ce is consistent with the ∼0.14 Å contraction39 of the Ce ionic radius upon oxidation. The P–Nimido distance is, on average, 1.53(3) Å across all trivalent complexes. 2-CeLi exhibits notable deviations, with P–Nimido bond lengths ranging from 1.495(8) to 1.59(1) Å, with an average of 1.54(4) Å. 2-CeK18c6 exhibits shorter P–Nimido bonds, including the shortest P–Nimido bond among the Ce3+ complexes at 1.44(1) Å.The structures were examined for connections between the degree of distortion and the redox potentials measured by cyclic voltammetry (Table 2). The τ4 index40 was calculated as a measure of structural distortion present, defined as (360° − (α + β))/141° (where α and β are the two largest angles in the coordination tetrahedron). The parameter ΣΔ109.5 was also considered and is defined as the sum of the absolute difference between the ideal 109.5° and each of the six angles that compose the tetrahedral coordination sphere. ΣΔ109.5 is a component to an equation41 previously used to describe distortion of the geometry around boron in complexes with N → B moieties and has been implemented for similar Ln imidophosphorane complexes.42 The τ4 and ΣΔ109.5 values were calculated with the terminal N atoms constructing the primary coordination sphere, as well as the P atoms of the ligands. In the case of τ4, the values using the N coordination sphere show a linear correlation with Epa, however, 2-CeCs breaks the trend with an anomalously low τ4 value (Fig. S79A†). Calculating τ4 using the secondary P coordination sphere results in a linear correlation with Epa, and 2-CeCs does not return an anomalous value (Fig. 3A). When using the primary N coordination sphere, ΣΔ109.5 displays a linear correlation with Epa (Fig. S79C†). When calculating ΣΔ109.5 using the secondary P coordination sphere, a remarkable linear correlation is observed with Epa (R2 = 0.981 excluding 2-CeK18c6, R2 = 0.958 including 2-CeK18c6, Fig. 3B). See Discussion for further analysis.
| 2-CeLi | 2-CeNa | 2-CeK | 2-CeRb | 2-CeCs | 2-CeK18c6 | |
|---|---|---|---|---|---|---|
| a Numbers in parentheses are estimated standard deviations of the last digit. b More than one crystallographically unique molecule is present in the asymmetric unit, metrics for each molecule are presented. | ||||||
| Ce⋯M+ distance (Å) | 3.02(1) | 3.367(6) | 3.785(7) | 3.947(1) | 4.131(2) | 9.56(15) |
| 2.97(2) | 4.061(2) | |||||
| τ 4 Θ N–Ce–N | 0.928 | 0.915 | 0.929 | 0.945 | 0.941 | 0.948 |
| 0.889 | 0.903 | |||||
| τ 4 Θ P–Ce–P | 0.906 | 0.957 | 0.923 | 0.935 | 0.956 | 0.970 |
| 0.919 | 0.980 | |||||
| Σ Δ109.5 Θ N–Ce–N (°) | 49.4 | 37.3 | 34.0 | 29.5 | 28.5 | 15.7 |
| 53.4 | 30.9 | |||||
| Σ Δ109.5 Θ P–Ce–P (°) | 43.6 | 25.9 | 23.0 | 18.4 | 13.4 | 8.71 |
| 31.2 | 6.1 | |||||
 | ||
| Fig. 3 E pa measured by cyclic voltammetry (50 mM [nBu4N][BPh4] in THF) plotted vs. (A) τ4 calculated using P–Ce–P angles. (B) ΣΔ109.5 calculated using P–Ce–P angles. (C) Ionic volume (4/3·πr3, r = Shannon ionic radius39), 2-CeK18c6 data excluded from linear regression analysis. (D) Computed HOMO energy levels. | ||
Electronic absorption spectroscopy
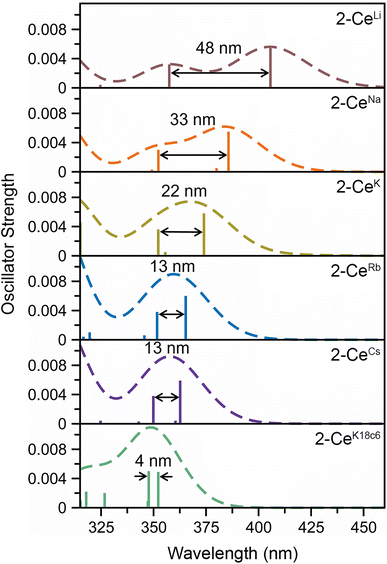
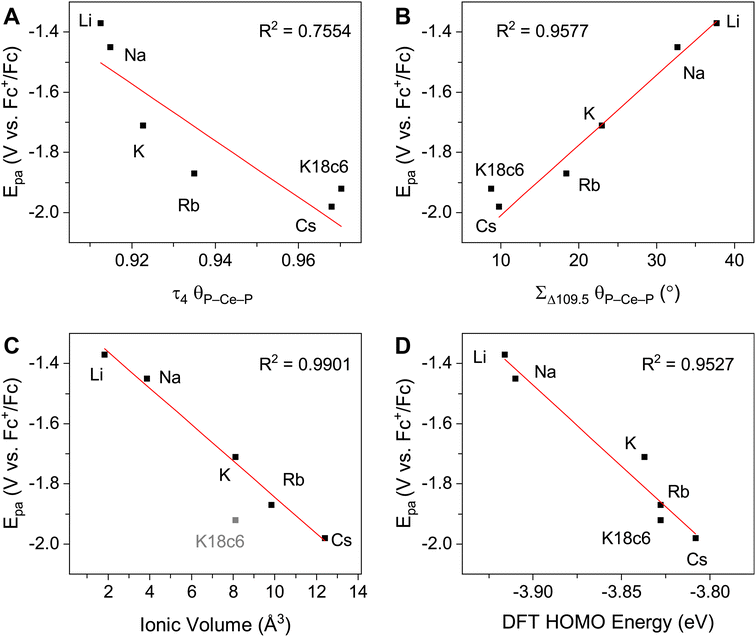
The UV-vis spectra are consistent with previously reported3,4,43 Ce3+ imidophosphorane complexes, featuring 4f–5d transitions at the edge of the UV-visible spectral window. The position of λmax for the 4f–5d transitions varies over a 53 nm (0.43 eV) range, from 361 nm in 2-CeK18c6 to 414 nm in the lower-energy feature in the spectrum of 2-CeLi. The molar extinction coefficients are generally 500–1000 M−1 cm−1 (Table S1†), consistent with those of similar complexes.3,4,43 The spectra of 2-CeLi and 2-CeNa diverge from the rest of the series, with two distinguishable features (Fig. 4A). The spectrum of the previously reported 2-CeK displays one feature, identified as a 4f–5d transition.4 The spectra of 2-CeK, 2-CeRb, and 2-CeCs appear remarkably similar. Computational studies (vide infra) predict subtle differences between the K, Rb, and Cs congeners, however, they are not visually identifiable given the resolution of the measurement. The observation of two 4f–5d transitions in the spectra of 2-CeLi and 2-CeNa is due to crystal field splitting of the 5d orbitals due to lower molecular symmetry.44–46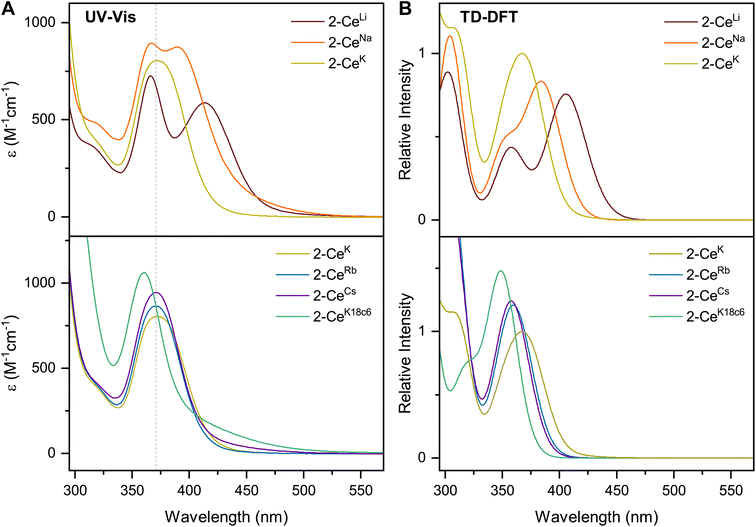 | ||
| Fig. 4 (A) Experimental UV-vis spectra measured in toluene, except for 2-CeK18c6, which was measured in THF. (B) Calculated spectra from TD-DFT, with half width at half height at 0.15 eV. Direct comparison of TD-DFT and UV-vis spectra for each complex is shown separately in Fig. S92–S99.† | ||
Density functional theory (DFT)
DFT calculations were employed to assess the effects of incorporating alkali metal cations, M+ (M = Li, Na, K, Rb, Cs, K(18c6)2), in the Ce3+ imidophosphorane complex. Specifically, changes in the metal–ligand bonding as a function of structural distortion induced by M+ were evaluated, the nature of electronic excitations was assigned, the energy shift of the 4f–5d transitions in this series was examined, and the degree of structural rearrangement occurring upon oxidation was assessed (see ESI† for computational details). Overall, the optimized structures show good agreement with the bond metrics from the XRD data (Table S2†), with the average Ce⋯M+ distances, Ce–N bond lengths, and the average Ce–N–P angles deviating less than 2.4%, 2.9%, and 3.7%, respectively, validating the theoretical models.In all complexes where M+ occupies a binding pocket in between the ligands, the Ce–Ncapped distances are distinct from Ce–Nterminal, e.g., 2.405 Å vs. 2.294 Å in 2-CeNa, respectively. This result agrees with the smaller total participation of Ce atomic orbitals (AOs) in the Ce–Ncapped bonds relative to Ce–Nterminal in the entire series from Li+ to Cs+: 7.7–7.9% vs. 11.0–12.0%, respectively (Table S3†). In both types of Ce–N bonds, there is little variation in the Ce AOs contribution throughout the series, in accordance with the minimal bond length changes: within 0.011 Å exp./0.006 Å theor. for Ce–Ncapped and 0.030 Å exp./0.030 Å theor. for Ce–Nterminal. Despite this, there is a recognizable trend, showing that, as the degree of structural distortion from the approximate tetrahedral symmetry decreases, there is a commensurate decrease in the disparity of bond lengths between Ce–Ncapped and Ce–Nterminal (Table S4†). This trend is also supported by the decreasing difference of the %Ce AOs participating in the Ce–Ncapped and Ce–Nterminal bonds, e.g., from 4.1% in 2-CeLi to 3.2% in 2-CeCs.
Adaptive Natural Density Partitioning (AdNDP47,48) analysis of the alkali metal-coordinated complexes revealed a chemical bonding pattern (Fig. S80, S81, Tables S3 and S5†) which is qualitatively similar to the one previously reported for [Ce(NP(NMe2)3)4]−.3 The Ce contribution in the Ce–N σ bonding is comparable between Ce–Ncapped (7.0–7.2%) and Ce–Nterminal (8.0–8.2%), and is appreciably larger than in the Ce–N–P π bonding, where it is smaller for the Ce–Ncapped–P π bonds (0.6–0.7%) compared to Ce–Nterminal–P π bonds (3.0–3.7%). The difference in the %Ce AOs in the bonding with Ncappedvs. Nterminal is due to the presence of M+, where the π electron clouds of two N 2p lone pairs extending to Ce and P are appreciably disrupted at the Ncapped atom compared to Nterminal, resulting in longer Ce–Ncapped bonds.
The average %Ce AOs, considering all Ce–N σ + π bonds in the M+-stabilized Ce3+ imidophosphorane complexes (9.4–9.8%), is slightly higher than in the bare 2-Ce− (9.0%). The overall stabilizing effect of coordinating M+ cations is also tracked in their MO energy levels relative to that of 2-Ce− (Fig. S82†). The decreasing contribution of the Ce AOs in the averaged Ce–N bonds goes in tandem with the increasing energy level of the Ce 4f-dominant highest occupied molecular orbital (HOMO) through the series: from −3.92 eV in 2-CeLi to −3.81 eV in 2-CeCs, increasing to −3.40 eV in 2-CeK18c6, and reaching the most positive value of −3.32 eV in 2-Ce− (Fig. S82–S89†).
The increasing HOMO energy levels linearly correlate with increasing Ce⋯M+ distances in the series from Li+ to [K(18c6)2]+, with R2 = 0.985 (Fig. S90†). The close proximity of Li+ to the Ce3+ center enables the strongest Ce⋯M+ interactions, substantially stabilizing the HOMO level in 2-CeLi. On the other hand, the significantly increased Ce⋯M+ charge separation in 2-CeK18c6 brings about the smallest changes in the geometric and electronic structure, with its HOMO energy deviating by only ∼0.09 eV from the “bare” 2-Ce−. The appreciably distinct MO energy levels of the complexes with the least (2-CeK18c6) and most (2-CeLi) distorted tetrahedral structures support their chemical reactivity patterns (vide supra). The higher HOMO energy level (Δ = 0.51 eV) as well as the larger energy gap between the 4f-dominant HOMO and ligand-dominant HOMO−1 (Δ = 0.20 eV) in 2-CeK18c6vs.2-CeLi explains a greater likelihood of the 4f unpaired electron in 2-CeK18c6 to participate in reactions, in accordance with its observed reactivity in reactions with benzophenone and  .
.
The stepwise trends in the MO energy levels that appear as a result of decreasing structural distortion from Li+ to [K(18c6)2]+ also manifest as a series of changes in the computed absorption spectra. The time-dependent DFT (TD-DFT) spectra show an excellent agreement with the UV-vis features (Fig. 4 and S91–S99†), very well reproducing the absorption peak positions of the expected 4f–5d transitions and splitting between them, where they are experimentally observed (Table S6†). The two distinct UV-vis absorption features of 2-CeLi and 2-CeNa found at 360–363 nm and 393–414 nm are identified as the most predominant 4f–5d transitions by natural transition orbital (NTO) analysis, with 84–87% probability for a single electron excitation from one orbital to another for each peak (Table S7 and Fig. S100–S102†). The splitting between the lower and higher energy 4f–5d transitions is slightly smaller in 2-CeNa than in 2-CeLi, i.e., 31 nm exp./33 nm theor. vs. 51 nm exp./48–54 nm theor., respectively (Fig. 5). This manifold of two 4f–5d transitions is maintained for the complexes with larger M+ (M = K, Rb, Cs) and 2-CeK18c6 as well, albeit, with decreased splitting as the distortion in the complexes lessens, i.e., dropping to 22 nm in 2-CeK, then to 13–16 nm in 2-CeRb and 2-CeCs, and further to 4 nm in 2-CeK18c6 (Tables S6–S7 and Fig. S103–S107†).
Vertical and adiabatic detachment energies (further referred to as VDE and ADE, respectively) were calculated to assess the degree of structural rearrangement (VDE, none; ADE, total) and probability of the retention/ejection of M+ upon oxidation in the series (Table S8†). Comparing VDE values for the M+ ejected (2-CeM → 1-Ce) and M+ retained (2-CeM → 1-CeM) redox reactions, two qualitatively different pictures are noted. For 2-CeLi, the more negative VDE value corresponding to the M+ retained reaction relative to the M+ ejected reaction (−0.69 V vs. −0.35 V) suggests that the retention of Li+ is favored upon oxidation. In contrast, for all other inner-sphere M+ counterparts (M = Na, K, Rb, Cs), the VDE for the ejection of M+ is appreciably more negative than for its retention (ranging from −1.30 V to −1.83 V vs. −0.76 V to −0.80 V). The difference between VDE values corresponding to the retention/ejection of M+ abruptly increases from 0.54 V/0.63 V in 2-CeNa/2-CeK to 1.00 V/1.05 V in 2-CeRb/2-CeCs. This gap indicates that 2-CeRb/2-CeCs are much more likely to eject the alkali metal cation upon oxidation than 2-CeNa/2-CeK.
The VDE values of the M+ ejected reactions of 2-CeRb/2-CeCs are very close to their experimental Epa values with [nBu4N4][BPh4] as the supporting electrolyte (−1.79 V theor./−1.87 V exp. for Rb+ and −1.83 V theor./−1.98 V exp. for Cs+), indicating minimal structural changes occurring upon oxidation. Conversely, the VDE for the retention of M+ in 2-CeLi (−0.69 V) is substantially different from the experimental oxidation potential of −1.37 V. The corresponding ADE value of −1.33 V matches the Epa value implying large structural rearrangement upon oxidation, in agreement with the largest deviation from the tetrahedral symmetry of 2-CeLi in the series. The VDE values for the M+ ejected redox reactions of 2-CeNa/2-CeK (−1.30 V/−1.40 V) suggest less structural rearrangement than 2-CeLi, but appreciably more than 2-CeRb, 2-CeCs, and 2-CeK18c6. Furthermore, the ADE values for the 2-CeM → 1-CeM redox reaction of 2-CeNa (−1.38 V) and 2-CeK (−1.43 V), which are close to their respective Epa values, imply that the M+-retained oxidation is also possible. However, this would require a larger structural rearrangement than for the 2-CeM → 1-Ce redox reaction as the VDE values for the M+-retained redox reactions (ca. −0.76 V) are significantly more positive than their experimental Epa values. This suggests a possibility of both inner- and outer-sphere complexes in solution for 2-CeNa/2-CeK.
Discussion
Quantification of structural distortion for 4-coordinate metal complexes is often quantified by the τ4 index.40 Given the flexibility of the imidophosphorane coordination sphere, the absence of consideration of the smallest angles renders τ4 less reliable in describing structural distortion. ΣΔ109.5 provides a more complete description of the ligand sphere by including all six tetrahedral angles. Based on size of the alkali metal and proximity to the Ce center, structural distortion could be predicted to increase as follows: 2-CeK18c6 < 2-CeCs < 2-CeRb < 2-CeK < 2-CeNa < 2-CeLi. P–Ce–P angles were used to quantify distortion, as N–Ce–N angles returned an anomalously low τ4 value for 2-CeCs because it fails to capture the distortion of the secondary coordination sphere. The improved performance of using P–Ce–P angles could be expected, due to the distortion largely affecting the secondary coordination sphere, rather than the primary Ce–N coordination sphere. Using P–Ce–P angles, the amount of structural distortion is proportional to the size of the alkali metal cation in the inner-sphere complexes (Fig. 3B). Structural metrics of 2-CeK18c6 are similar to those of 2-CeCs (Table 2), indicating minimal structural influence of the alkali metal cation in 2-CeCs.The modulation of Epa by the alkali metal cation spans a range of about 600 mV, which is comparable to the reported series of Ce BINOLate complexes.24,25 The electrochemical reduction (Epc) is less sensitive to alkali metal identity spanning less than 200 mV, except for 2-CeLi (Epc = −1.74 V), which is about 1 V more positive than the rest of the series. The more positive Epc and quasi-reversibility of 2-CeLi suggest that the electrochemically oxidized product diverges from the rest of the series. NMR experiments demonstrate that the geometry of 2-CeLi is constrained and intramolecular Li+ mobility is relatively slow at room temperature by the presence of two 31P{1H} signals (Fig. S4 and S5†). Computational studies support the retention of Li+ in the electrochemical oxidation of 2-CeLi. The VDE for 2-CeLi was calculated for the case of alkali metal ejection and retention upon oxidation. In contrast to the rest of the series, the VDE for retention of the Li+ ion is more negative than that considering ejection (−0.69 V vs. −0.35 V, Table S8†). The VDE for ejection of the alkali metal for the rest of the series (where applicable) was calculated to be much more negative than that of retention. For example, the VDE of 2-CeCs is calculated to be −1.83 V in the case of ejection vs. −0.80 V for retention of the Cs+ ion. The VDE for the ejection of Cs+ is much closer to the experimentally measured value (−1.98 V), suggesting 2-CeCs → 1-Ce redox reaction with minimal structural rearrangement upon oxidation.
Within this framework, the larger alkali metal cations exert less influence on the ligand coordination sphere as they lie toward the outer edge of the secondary coordination sphere. The similarities between the cyclic voltammograms of 2-CeRb and 2-CeCs compared to 2-CeK222 and 2-CeK18c6 suggest that less interaction with the secondary coordination sphere facilitates Ce3+ oxidation, i.e., results in more negative Epa values. The Lewis acidity of the alkali metal cation unequivocally influences the Ce3+ oxidation potential, however, the relationship between M+(H2O)x pKa (as a measure of M+ Lewis acidity) and Epa is not well correlated compared to examples of transition metal and uranyl complexes (Fig. S79E†).29–32,37,38,49–51
A secondary feature is observed at ca. −1.9 V in the cyclic voltammograms of 2-CeNa and 2-CeK (Fig. 2). Differential pulse voltammetry (DPV) demonstrates that two features are indeed present for the anodic event of 2-CeK (Fig. S60†). This behavior is attributable to an equilibrium between the inner- and outer-sphere complexes in solution. The potential of the secondary features is close to those of the outer sphere congeners 2-CeK18c6 and 2-CeK222, as well as the predicted potential for the hypothetical 2-Ce− (Table S8†). The similarity between the potentials of the secondary features and the outer-sphere congeners supports that some of 2-CeNa and 2-CeK may dissociate into the corresponding charge-separated, outer sphere complexes in electrolyte solution. NMR studies in cyclic voltammetry conditions in THF-d8 display a broadened 31P{1H} signal for 2-CeK (FWHM = 80 Hz, Fig. S78†) and a small secondary signal for 2-CeNa (Fig. S77†), supporting exchange between inner- and outer-sphere complexes in solution. These data suggest that the alkali metals of intermediate size (Na, K) can dissociate from the coordination sphere without Ce3+ oxidation in THF electrolyte solutions. Evidence for such a process does not present itself for 2-CeRb and 2-CeCs, which is likely due to the larger ionic radii of Rb+ and Cs+ precluding significant perturbation of the coordination sphere that is observed for smaller cations.
The NMR spectra of all complexes, except for 2-CeLi, indicate that the cation is mobile within the secondary coordination sphere on the NMR timescale, and a single 31P{1H} signal is observed in these systems at room temperature. Solution state UV-vis data demonstrate that the structural distortion of the coordination sphere is indeed present in the solution state, despite intramolecular mobility of the cation. The UV-vis spectra of 2-CeLi and 2-CeNa display two features, which are assigned as 4f–5d transitions through NTO analysis. The observation of two 4f–5d transitions in the solution-state measurements is an important piece of evidence supporting the presence of structural distortion in solution. The splitting of the 5d orbitals can be rationalized through crystal field theory as a splitting of the E state in the reduction of the symmetry of the complex from tetrahedral. This splitting would not be observed if the structural distortion is not maintained in solution. That is, if the solution structure was not distorted by the alkali metal cation due to exchange or diffusion of the alkali metal from the coordination sphere, the UV-vis spectra should resemble that of 2-CeK18c6. A good linear relationship (R2 = 0.953, Fig. 3D) between measured Epa and the calculated HOMO energies of the geometry-optimized complexes further supports that the electronic structure of Ce3+ is modulated by the alkali metal cation in solution.
While variable-temperature NMR (VT-NMR) data indicate that the cations have intra-molecular mobility in solution at temperatures >−60 °C, the room temperature UV-vis, CV, as well as computational results support that the structural effect of the alkali metal is present, despite exchange of the cation between different pairs of ligands. A clear relationship between the coalescence temperature (Tc) and structural metrics and/or Epa is not readily identifiable. This result suggests intramolecular mobility is a related, but distinct, phenomenon to structural distortion. The match in size between the secondary coordination sphere and the alkali metal is likely important, with K+ uniquely exhibiting mobility down to −80 °C in 2-CeK (Fig. S32 and S35†). The reader is directed to the ESI† for VT-NMR spectra and further discussion.
Cyclic voltammetry studies in solution reveal the modulation of the Ce3+ oxidation potential by the identity of the alkali metal cation. Distortion parameters from SC-XRD data provide a good linear correlation with Epa, demonstrating that structural aspects of the coordination sphere and size of the alkali metal cation influence the oxidation potential. Solution-state UV-vis data further demonstrate that the structural distortion measured in the solid-state is reflected in solution spectroscopic data. This effect is indicated by the presence of two 4f–5d transitions in 2-CeLi and 2-CeNa. This splitting of the f–d transition is due to 5d crystal field splitting caused by reduction of symmetry at the Ce center. TD-DFT results and NTO analysis support this assignment of the UV-vis spectra, and a good correlation between Epa and the calculated HOMO energies (Fig. 3D) provides additional evidence that the distortion by the alkali metal modulates the Ce3+ oxidation potential.
Conclusions
The correlation between the shift in Epa and electrostatic/Lewis acidic properties of the redox-inactive metal cation is well established in the literature across multiple classes of transition metal and uranyl complexes.29–38,49–51 The data presented herein demonstrate the impact of structural distortion by alkali metal bound in the secondary coordination sphere on the Ce3+ oxidation potential within an imidophosphorane framework. Quantification of the distortion of the ligand sphere by means of ΣΔ109.5 elucidates a linear, positive relationship between structural distortion and oxidation potential. Specifically, structural distortion by the alkali metal cation modulates the electronic structure of the ligand and Ce3+ ion, making oxidation more difficult as the coordination geometry deviates from the ideal pseudo-tetrahedral geometry. This distortion observed in the solid-state is reflected in solution electronic absorption spectroscopy, which reveals the reduced molecular symmetry at Ce3+ as a function of the alkali metal. The effect of alkali metal binding on the donation properties of the zwitterionic ligand and electronic structure of the trivalent lanthanide establishes a new ligand design consideration. Similar effects of zwitterionic ligands have been reported on Cu redox properties and small molecule activation chemistry.52–55 In this imidophosphorane system, optimization of alkali metal binding can be used to tune the potential of anionic metal complexes through the counter cation. This approach could be implemented across the periodic table, and potentially be applied to expand the range of molecular tetravalent lanthanides.Data availability
The data that support the findings of this study are available in the ESI† of this article and the crystallographic data are available in the CCDC database (2248373–2248375, 2248368, and 2248365).Author contributions
H. S. L and A. C. B. conceived the project. A. C. B. performed all syntheses and collected the experimental data. C. M. S. and I. A. P. designed and performed theoretical calculations and analyzed their outputs. J. B. and A. S. modelled and refined SC-XRD data. The manuscript was drafted by A. C. B. and C. M. S., and revised and edited by H. S. L. and I. A. P., and the final version was approved by all authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Science Foundation (NSF) through the Faculty Early Career Development Program (CAREER) under award no. 1943452. I. A. P. acknowledges computational resources at the Ohio Supercomputer Center and the ARCC HPC cluster at the University of Akron. SC-XRD experiments were performed at the GT SC-XRD facility.Notes and references
- N. A. Piro, J. R. Robinson, P. J. Walsh and E. J. Schelter, Coord. Chem. Rev., 2014, 260, 21–36 CrossRef CAS.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910 CrossRef CAS PubMed.
- N. T. Rice, J. Su, T. P. Gompa, D. R. Russo, J. Telser, L. Palatinus, J. Bacsa, P. Yang, E. R. Batista and H. S. La Pierre, Inorg. Chem., 2019, 58, 5289–5304 CrossRef CAS PubMed.
- N. T. Rice, I. A. Popov, D. R. Russo, T. P. Gompa, A. Ramanathan, J. Bacsa, E. R. Batista, P. Yang and H. S. La Pierre, Chem. Sci., 2020, 11, 6149–6159 RSC.
- M. R. MacDonald, J. E. Bates, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2012, 134, 8420–8423 CrossRef CAS PubMed.
- M. R. MacDonald, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2013, 135, 9857–9868 CrossRef CAS PubMed.
- C. M. Kotyk, M. E. Fieser, C. T. Palumbo, J. W. Ziller, L. E. Darago, J. R. Long, F. Furche and W. J. Evans, Chem. Sci., 2015, 6, 7267–7273 RSC.
- D. N. Huh, L. E. Darago, J. W. Ziller and W. J. Evans, Inorg. Chem., 2018, 57, 2096–2102 CrossRef CAS PubMed.
- C. T. Palumbo, L. E. Darago, M. T. Dumas, J. W. Ziller, J. R. Long and W. J. Evans, Organometallics, 2018, 37, 3322–3331 CrossRef CAS.
- D. N. Huh, S. R. Ciccone, S. Bekoe, S. Roy, J. W. Ziller, F. Furche and W. J. Evans, Angew. Chem., Int. Ed., 2020, 59, 16141–16146 CrossRef CAS PubMed.
- L. M. Anderson-Sanchez, J. M. Yu, J. W. Ziller, F. Furche and W. J. Evans, Inorg. Chem., 2023, 62, 706–714 CrossRef CAS PubMed.
- F. Jaroschik, F. Nief, X.-F. Le Goff and L. Ricard, Organometallics, 2007, 26, 1123–1125 CrossRef CAS.
- R. P. Kelly, L. Maron, R. Scopelliti and M. Mazzanti, Angew. Chem., Int. Ed., 2017, 56, 15663–15666 CrossRef CAS PubMed.
- C. T. Palumbo, I. Zivkovic, R. Scopelliti and M. Mazzanti, J. Am. Chem. Soc., 2019, 141, 9827–9831 CrossRef CAS PubMed.
- A. R. Willauer, C. T. Palumbo, R. Scopelliti, I. Zivkovic, I. Douair, L. Maron and M. Mazzanti, Angew. Chem., Int. Ed., 2020, 59, 3549–3553 CrossRef CAS PubMed.
- A. R. Willauer, C. T. Palumbo, F. Fadaei-Tirani, I. Zivkovic, I. Douair, L. Maron and M. Mazzanti, J. Am. Chem. Soc., 2020, 142, 5538–5542 CrossRef CAS PubMed.
- A. R. Willauer, I. Douair, A.-S. Chauvin, F. Fadaei-Tirani, J.-C. G. Bünzli, L. Maron and M. Mazzanti, Chem. Sci., 2022, 13, 681–691 RSC.
- N. T. Rice, I. A. Popov, D. R. Russo, J. Bacsa, E. R. Batista, P. Yang, J. Telser and H. S. La Pierre, J. Am. Chem. Soc., 2019, 141, 13222–13233 CrossRef CAS PubMed.
- N. T. Rice, I. A. Popov, R. K. Carlson, S. M. Greer, A. C. Boggiano, B. W. Stein, J. Bacsa, E. R. Batista, P. Yang and H. S. La Pierre, Dalton Trans., 2022, 51, 6696–6706 RSC.
- A.-M. Ariciu, D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Nat. Commun., 2019, 10, 3330 CrossRef PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- K. Kundu, J. R. K. White, S. A. Moehring, J. M. Yu, J. W. Ziller, F. Furche, W. J. Evans and S. Hill, Nat. Chem., 2022, 14, 392–397 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, D. A. Marchiori, H. Kwon, T. T. Nguyen, K. E. Rosenkoetter, D. Kuzmina, F. Tuna, R. D. Britt, J. R. Long and B. G. Harvey, J. Am. Chem. Soc., 2022, 144, 22193–22201 CrossRef CAS PubMed.
- J. R. Robinson, P. J. Carroll, P. J. Walsh and E. J. Schelter, Angew. Chem., Int. Ed., 2012, 51, 10159–10163 CrossRef CAS PubMed.
- J. R. Robinson, Z. Gordon, C. H. Booth, P. J. Carroll, P. J. Walsh and E. J. Schelter, J. Am. Chem. Soc., 2013, 135, 19016–19024 CrossRef CAS PubMed.
- J. R. Levin, W. L. Dorfner, P. J. Carroll and E. J. Schelter, Chem. Sci., 2015, 6, 6925–6934 RSC.
- M. M. MacInnes, Z. R. Jones, B. Li, N. H. Anderson, E. R. Batista, I. M. DiMucci, C. Eiroa-Lledo, K. E. Knope, M. Y. Livshits, S. A. Kozimor, V. Mocko, K. A. Pace, F. R. Rocha, B. W. Stein, J. N. Wacker and P. Yang, Dalton Trans., 2021, 50, 15696–15710 RSC.
- T. P. Gompa, A. Ramanathan, N. T. Rice and H. S. La Pierre, Dalton Trans., 2020, 49, 15945–15987 RSC.
- P.-H. Lin, M. K. Takase and T. Agapie, Inorg. Chem., 2015, 54, 59–64 CrossRef CAS PubMed.
- D. E. Herbert, D. Lionetti, J. Rittle and T. Agapie, J. Am. Chem. Soc., 2013, 135, 19075–19078 CrossRef CAS PubMed.
- E. Y. Tsui, R. Tran, J. Yano and T. Agapie, Nat. Chem., 2013, 5, 293–299 CrossRef CAS PubMed.
- E. Y. Tsui and T. Agapie, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10084–10088 CrossRef CAS PubMed.
- T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574 RSC.
- A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718 CrossRef CAS PubMed.
- N. G. Léonard, T. Chantarojsiri, J. W. Ziller and J. Y. Yang, J. Am. Chem. Soc., 2022, 144, 1503–1508 CrossRef PubMed.
- N. S. Idris, J. M. Barlow, S. A. Chabolla, J. W. Ziller and J. Y. Yang, Polyhedron, 2021, 208, 115385 CrossRef CAS.
- A. Kumar, D. Lionetti, V. W. Day and J. D. Blakemore, J. Am. Chem. Soc., 2020, 142, 3032–3041 CrossRef CAS PubMed.
- T. K. Ghosh, S. Maity, S. Ghosh, R. M. Gomila, A. Frontera and A. Ghosh, Inorg. Chem., 2022, 61, 7130–7142 CrossRef CAS PubMed.
- R. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC.
- H. Höpfl, J. Organomet. Chem., 1999, 581, 129–149 CrossRef.
- T. P. Gompa, S. M. Greer, N. T. Rice, N. Jiang, J. Telser, A. Ozarowski, B. W. Stein and H. S. La Pierre, Inorg. Chem., 2021, 60, 9064–9073 CrossRef CAS PubMed.
- K. S. Otte, J. E. Niklas, C. M. Studvick, A. C. Boggiano, J. Bacsa, I. A. Popov and H. S. La Pierre, Angew. Chem., Int. Ed., 2023, 62, e202306580 CrossRef CAS PubMed.
- H. Yin, P. J. Carroll, J. M. Anna and E. J. Schelter, J. Am. Chem. Soc., 2015, 137, 9234–9237 CrossRef CAS PubMed.
- H. Yin, P. J. Carroll, B. C. Manor, J. M. Anna and E. J. Schelter, J. Am. Chem. Soc., 2016, 138, 5984–5993 CrossRef CAS PubMed.
- M. K. Assefa, G. Wu and T. W. Hayton, Chem. Sci., 2017, 8, 7873–7878 RSC.
- N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590–9596 RSC.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- R. R. Golwankar, A. Kumar, V. W. Day and J. D. Blakemore, Chem. – Eur. J., 2022, 28, e202200344 CrossRef CAS PubMed.
- A. Kumar, D. Lionetti, V. W. Day and J. D. Blakemore, Chem. – Eur. J., 2018, 24, 141–149 CrossRef CAS PubMed.
- M. Sundararajan, ACS Omega, 2023, 8, 18041–18046 CrossRef CAS PubMed.
- A. B. Weberg, S. P. McCollom, L. M. Thierer, M. R. Gau, P. J. Carroll and N. C. Tomson, Chem. Sci., 2021, 12, 4395–4404 RSC.
- A. B. Weberg, R. P. Murphy and N. C. Tomson, Chem. Sci., 2022, 13, 5432–5446 RSC.
- A. B. Weberg, S. P. McCollom, R. P. Murphy and N. C. Tomson, Inorganic Chemistry, ChemRxiv, 2022, preprint, DOI:10.26434/chemrxiv-2022-lcb1w.
- A. B. Weberg, S. P. McCollom and N. C. Tomson, Inorganic Chemistry, ChemRxiv, 2022, preprint, DOI:10.26434/chemrxiv-2022-63pfg.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental procedures, spectra, cyclic voltammograms, analytical data, and computational details. CCDC 2248373–2248375, 2248368, and 2248365. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc04262f |
| This journal is © The Royal Society of Chemistry 2023 |