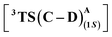Role of mutations in a chemoenzymatic enantiodivergent C(sp³)–H insertion: exploring the mechanism and origin of stereoselectivity

Abstract

New-to-nature enzymes have emerged as powerful catalysts in recent years for streamlining various stereoselective organic transformations. While synthetic strategies employing engineered enzymes have witnessed proliferating success, there is limited clarity on the mechanistic front and more so when considering molecular-level insights into the role of selected mutations, dramatically escalating catalytic competency and selectivity. We have investigated the mechanism and correlation between mutations and exquisite stereoselectivity of a lactone carbene insertion into the C(sp³)–H bond of substituted aniline, catalyzed by two mutants of a cytochrome P450 variant, “P411” (engineered through directed evolution) in which the axial cysteine has been mutated to serine, utilizing various computational tools. The pivotal role of S264 and L/R328 mutations in the active site has been delineated computationally using two cluster models, thus rationalizing the enantiodivergence. This report provides much-needed insights into the origin of enantiodivergence, furnishing a mechanistic framework for understanding the anchoring effects of H-bond donor residues with the lactone ring. This study is expected to have important implications in the rational design of stereodivergent enzymes and toward successful in silico enzyme designing.

---

Introduction

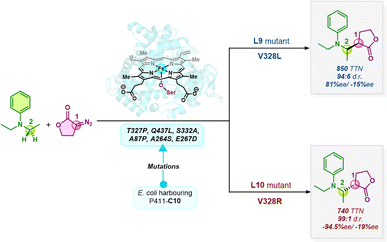
The field of asymmetric synthesis has seen remarkable success over the past three decades, providing numerous biologically active chiral compounds with exceptional levels of selectivity. Despite these advancements, relatively fewer methods have been identified that provide a unified route to access all stereoisomers in a stereodivergent manner. Carreira and co-workers have developed a fully stereodivergent dual catalyst system using chiral iridium and chiral amine co-catalysts for synthesizing γ,δ-unsaturated aldehydes via allylation of α-hydroxy and α-amino acetaldehydes.^1,2 This procedure controls the two stereogenic centers independently during the course of the reaction. Using another strategy, Buchwald and co-workers have demonstrated the synthesis of amino alcohols possessing two to three contiguous stereocenters using enal and enone substrates in a highly selective copper-catalyzed hydrosilylation/hydroamination sequence.³ Despite these promising reports in small molecule catalysis, stereodivergent methods still face unmet synthetic challenges, thus calling for alternative approaches.

An alternative is to turn to nature's privileged catalysts, enzymes. Enzymes are known to operate under mild conditions, remarkably promote rate enhancements, and exquisitely control the stereochemical outcome of reactions. However, the inherent chiral nature of enzymes and the specificity and selectivity provided by their active sites is quite detrimental to their use in achieving stereodivergent synthesis. Since enzymes do not exist as enantiomers, except for a few enantiocomplementary enzymes in nature,⁴ there is a significant limitation in achieving enantiodivergence. A breakthrough in this field was the advent of DE (directed evolution) to improve protein function, which has been widely used in designing novel proteins with significantly enhanced catalytic activity, thermostability, etc.^5,6 Aptly tuning the protein scaffold may create stereocomplementary enzymes to access all possible stereoisomers. For instance, Hilvert and co-workers have developed variants of promiscuous de novo retro-aldolases, RA95.0, catalyzing the asymmetric synthesis of γ-nitroketones via enantiocomplementary Michael-type reactions.^7,8 In another interesting study, the same group has engineered the promiscuous enzyme into four stereocomplementary carboligases for Michael addition of a tertiary carbanion to an unsaturated ketone.⁹ Xu et al. have engineered four stereocomplementary variants of (CALB) Candida antarctica lipase B to access all the stereoisomers in a transesterification reaction between racemic acids and racemic alcohols.¹⁰ Fasan and co-workers have developed engineered myoglobins for asymmetric intramolecular cyclopropanation resulting in stereodivergent preparation of cyclopropane fused γ- and δ-lactones from allyl diazoacetates.^11,12 Continuing efforts have ensued in stereodivergent intermolecular cyclopropanation reactions using diverse olefins and carbene precursors.^13–15 Arnold and co-workers have developed a serine-ligated variant of cytochrome P450 – “P411”, catalyzing stereodivergent cyclopropanation of unactivated alkenes to obtain all four stereoisomers with reasonable de (diastereomeric excess) and ee (enantiomeric excess).^16,17 Variants of P411 have been intensively engineered in recent years to achieve diverse stereodivergent syntheses.^18,19 In a recent study, the same group reported an enantiodivergent synthesis of β-amino lactone products via carbene insertion into secondary C(sp³)–H bonds of aniline derivatives catalyzed by P411 variants (P411-C10).²⁰ Two mutants were identified, differing by a single mutation at site 328 which showed consistently opposite stereopreference (Scheme 1).

Scheme 1 Enzymatic enantiodivergent C(sp³)–H insertion catalyzed by ‘P411’ mutants. Further mutations resulted in two mutants, L9 and L10, differing by a single point mutation (V328L/R), showing opposite stereopreference for this C–H insertion reaction (1 and 2 denote the two chiral centers on the carbene C and the secondary C center of aniline, respectively).

Although DE has magnificently unfolded in recent years to furnish enzymes that catalyze various stereodivergent reactions, the precise role of mutations remains cryptic. It is largely unclear how a select few mutations in the active site efficiently control the stereochemical outcome. This substantially restricts the development of novel catalysts for improved stereodivergent transformations. To address the inherent difficulties currently associated with such engineered enzymatic stereodivergent catalysis, we envision that computational studies could be the cornerstone in understanding the mechanism and gaining precise molecular-level insights into the role of mutations in dictating the stereoselectivity. Previous studies on an asymmetric C–H amination catalyzed by a similar enzymatic system, proceeding via an ionic pathway, have mainly focused on only a small model system for establishing the reaction mechanism, followed by “in-enzyme” MD (molecular dynamics) simulations.^21–24 Here, we report a thorough analysis by means of TS (transition state) modeling which is imperative to gain a qualitative and quantitative understanding of asymmetric induction. We have undertaken a comprehensive computational study, using a combination of different methods to understand the mechanism, stereoselectivity, and enantiodivergence of C(sp³)–H functionalization of a disubstituted aniline derivative employing a diazo lactone, as shown in Scheme 1. We initially used a truncated model containing the porphyrin pyrrole core, Fe center, and an –OMe ligand to mimic serine as the Fe-axial ligand of the enzyme. Different mechanistic proposals, including the concerted and radical pathways (vide infra), are explored using DFT (density functional theory). Subsequently, we implement MD simulations, conformational screening using GFN-xTB (geometry, frequency, noncovalent, extended tight binding), and the QM cluster approach to gain quantitative insights into the origin of the stereoselectivity of this enzyme-catalyzed asymmetric C(sp³)–H insertion reaction. Our goal is to discern the stereodetermining step and the role of mutations in enantiodivergence.

Results and discussion

Metallocarbene formation

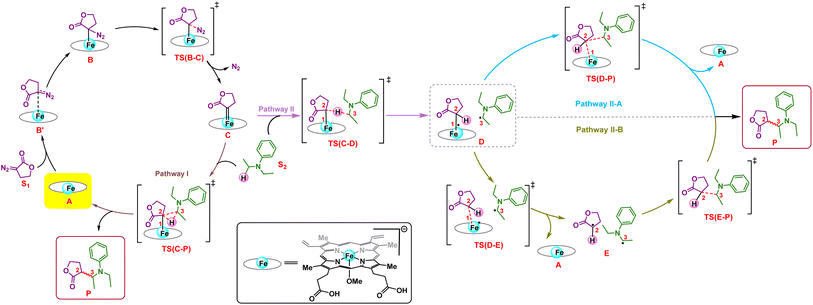
We first explore the reaction mechanism of C(sp³)–H insertion by taking a truncated model containing the porphyrin pyrrole core, Fe^II center, and an –OMe ligand (methoxy anion) to mimic serine as the Fe-axial ligand of the enzyme. This results in an overall negatively charged system. An investigation of all the possible spin states that the initial Fe^II complex A can adopt: OSS (open-shell singlet), CSS (closed-shell singlet), triplet, and quintet indicates that the quintet state of A is the most stable, in line with previous computational and experimental results.^25,26 The general mechanism is shown in Scheme 2.

Scheme 2 The general mechanism for the formation of the LAC (lactone carbene) (C) via different pathways; concerted pathway (Pathway I) and radical pathway (Pathway II), which is further followed by two plausible radical rebound pathways (II-A and II-B) leading to product formation.

The initial mechanism of metallocarbene C formation upon N₂ extrusion viaTS(B–C) is well established.^27,28 The first step is the formation of the far intermediate B′, which brings the diazo substrate and the complex A in proximity to each other. The OSS and triplet states have an additional higher energy reactant complex B with a meaningful Fe–C distance of 2.31 Å, as shown in Fig. 1 for ³B. The overall barrier for N₂ extrusion leading to the formation of C is 27.0 kcal mol⁻¹. Considering that the reaction occurs at room temperature, the activation energy value of 27.0 kcal mol⁻¹ is relatively high, and this aligns with the fact that there is no reaction in the absence of the enzyme (which helps bring down the activation energy barrier). The OSS state of C is found to be the most stable.²⁹ Our overall results for the formation of C are in line with previous computational studies of related reactions.^30–32

Fig. 1 Gibbs free energy profile (kcal mol⁻¹) of N₂ extrusion and subsequent C–H insertion at different spin states of Fe. Distances are in Å. The H atoms are omitted for clarity.

C–H insertion

Following the formation of C, the insertion can take place via two pathways: (I) involving a concerted hydride transfer viaTS(C–P) (Scheme 2, Pathway I) from the substrate to the carbene, (II) involving a stepwise mechanism with a HAT (hydrogen atom transfer) viaTS(C–D) followed by a C–C bond formation via radical rebound (Scheme 2, Pathway II). Despite recent advancements, the precise mechanistic understanding of this step is still fuzzy, and the enduring issue of enantioselectivity remains unresolved. A clear mechanistic understanding of the insertion step is imperative in providing chemists with unprecedented proficiency in the development of new catalysts for C–H insertion with elevated stereoselectivity.

In the current study, CSS undergoes a concerted yet highly asynchronous process via^CSSTS(C–P), with a relative free energy barrier of 27.1 kcal mol⁻¹, directly leading to product formation (Fig. 1). The other spin states follow a HAT process instead of a hydride-transfer process, where the relative free energy barrier is 18.1 kcal mol⁻¹via^OSSTS(C–D), consistent with previous studies by our group.^33,34 Thus, the HAT process is favorable over the concerted hydride transfer by 9.0 kcal mol⁻¹. This contrasts with the previous study by Zhang and coworkers, where a concerted hydride transfer was found to be more favorable, which highlights the sensitivity of the mechanism with respect to the substrate and catalyst.³⁵

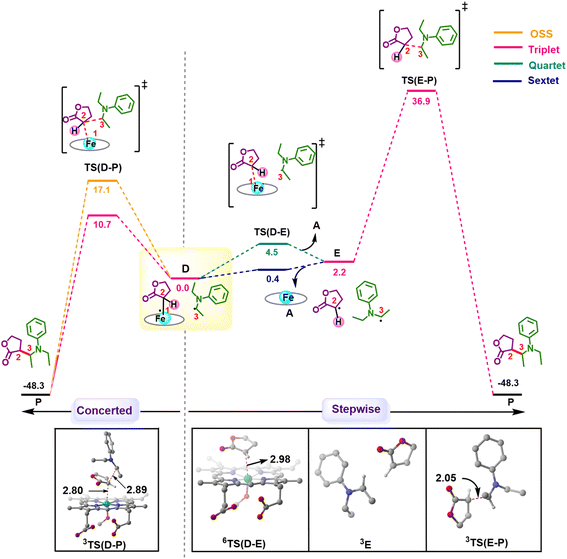
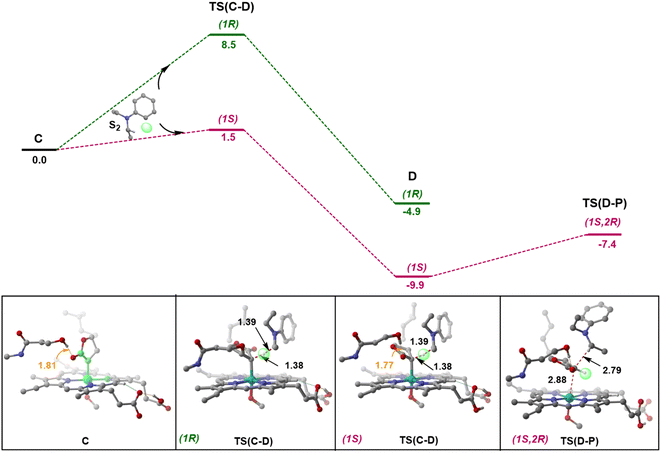
C–C radical rebound

After the HAT process, a radical rebound occurs to regenerate the catalyst and yield the final product. The rebound process can again be either concerted or stepwise. For the stepwise approach, the carbene substrate homolytically dissociates from the Fe–porphyrin complex viaTS(D–E) to yield a C-centered radical followed by the coupling of the two C-radicals (C(2)˙ and C(3)˙) resulting in C–C bond formation viaTS(E–P). If these two steps occur concomitantly, the C–C bond forms viaTS(D–P). The radical rebound TS on the OSS surface ^OSSTS(D–P) is disfavored by 6.4 kcal mol⁻¹ over the lowest lying TS on the triplet surface ³TS(D–P) (Fig. 2). Several attempts to obtain the ⁵TS(D–P) consistently resulted only in dissociation. This is likely due to a longer Fe–C(2) bond in the quintet state that favors a homolytic cleavage of this bond. It is found that ⁶TS(D–E) is preferred over ³TS(D–P) by 10.3 kcal mol⁻¹, in line with Arnold's recent report on a related enzymatic S–H insertion.³⁶ However, the formation of the final product via³TS(E–P) requires an activation free energy barrier of 36.9 kcal mol⁻¹ (Fig. 1), which makes the overall stepwise process unfavorable by 26.2 kcal mol⁻¹.

Fig. 2 Gibbs free energy profile (kcal mol⁻¹) for comparison of concerted and stepwise pathways for C–H insertion at different spin states of Fe. Distances are in Å. The H atoms are omitted for clarity.

This exploratory study on the reaction mechanism gives us an incisive idea at the molecular level. The N₂ extrusion is the RDS (rate-determining step) with an overall activation free energy barrier of 27.0 kcal mol⁻¹, occurring over a triplet surface. The C–H insertion proceeds via a HAT pathway on the OSS surface, again with the triplet surface lying close by in energy. A comparison of two possible pathways, concerted and stepwise, following the HAT step reveals that the Fe–C homolytic dissociation and subsequent radical rebound occur in a concerted manner with an overall activation barrier of 10.7 kcal mol⁻¹ on the triplet surface. However, at this point, the enantioselectivity-determining step in this reaction remains unresolved. Both HAT and radical rebound could account for enantioinduction. Unlike P450-catalyzed C–H hydroxylation^37–40 and engineered P411-catalyzed C–H amination,^41,42 where Fe^IV–OH or Fe^III–NHR intermediates undergo barrierless radical rebound, here, both low and intermediate spin radical intermediates (^OSSD and ³D) require substantial barrier (17.1 kcal mol⁻¹ and 10.7 kcal mol⁻¹) to undergo radical rebound viaTS(D–P). This is congruous with Liu and Yang's recent study, where the Fe^III–nitrene intermediate requires a considerable barrier for the radical rebound.⁴³ However, the group suggested an interesting result wherein the quintet spin state was found to be most favorable in the radical rebound TS, indicating a spin-crossover event in the radical intermediates prior to radical rebound. This inevitably indicates relatively long lifetimes of the radicals, which may lead to stereoablation prior to radical rebound. Thus, the origin of enantioinduction is still a puzzle at this stage – if the interconversion between the two prochiral carbene carbon-based radicals proceeds with a barrier lower than 10.7 kcal mol⁻¹, then the HAT step would fail to induce enantioselectivity, and the latter would only be affected by the energy difference between the radical rebound TSs (analogous to a Curtin–Hammett scenario).⁴⁴ Furthermore, the impact of critical active site residues on these individual steps in the catalytic cycle and the origin of stereodivergence remain unaddressed. To gain crucial insights into the origin of exquisite stereocontrol by the enzyme active site, we employed MD simulation followed by the QM cluster methodology. Since the electronic energy gap between the singlet and triplet is relatively low, and the final C–C coupling is the most stable in the triplet state we have looked at the triplet spin state for all our QM cluster studies.

Classical MD simulations

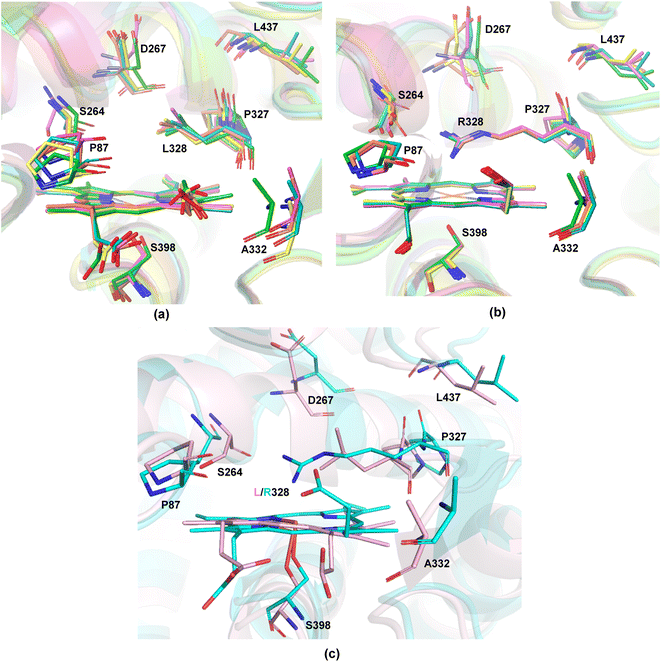
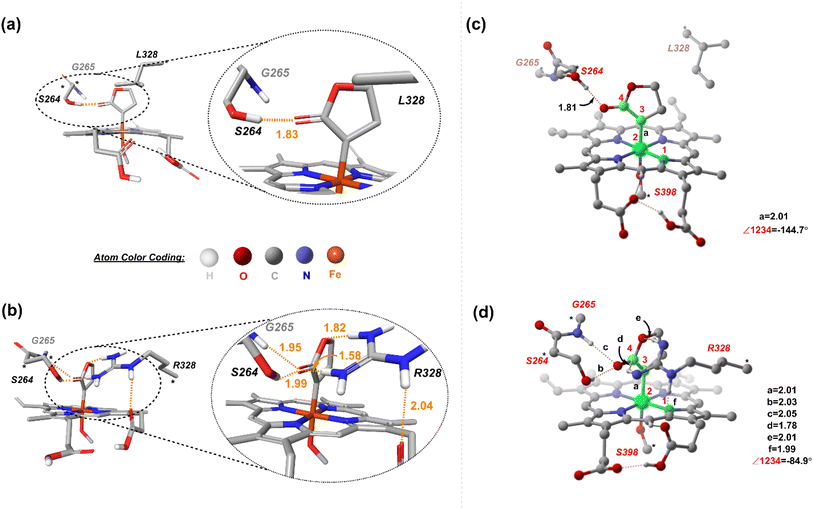
The available and related PDB structure (P411-E10 enzyme variant) was used as the initiation point to prepare two variants, P411-L9 and P411-L10, which Arnold and coworkers have hitherto reported.²⁰ Seven amino acids, namely A87, A264, E267, A332, T327, V328, and Q437, were mutated using the mutagenesis tool from Chimera.⁴⁵ Classical MD simulations were performed on the two key mutants, L9 (V328L) and L10 (V328R) for a total time of 500 ns taking five independent replicas of 100 ns each (see the ESI† for details). The average structure from each independent simulation was extracted based on RMSD clustering (Fig. 3(a) and (b)) and these were not seen to deviate appreciably from each other.

Fig. 3 Overlay of the average structures obtained from five independent replicas of 100 ns classical MD based on protein backbone RMSD of (a) L9 and (b) L10 showing the heme unit along with the mutated residues, (c) overlay of one of the 100 ns MD simulation snapshot (accepted final structure for carrying out further calculations) of L9 (pink) and L10 (cyan) showing the heme unit along with the mutated residues. The H atoms are omitted for clarity.

We thus took one of these average structures which was taken as a reference for RMSD-based clustering as our final accepted structure for carrying out further QM calculations. An overlay of one of the 100 ns MD simulation structures for L9 and L10 reveals that the protein backbone does not change appreciably except for the orientation of one of the propionate groups of the heme unit (Fig. 3(c)). This is intuitively logical owing to the presence of R328 in L10, which can effectively form hydrogen bonding interactions with the propionate carbonyl groups, thus pushing it upwards. Such an interaction is absent in L9, and the propionate units tend to stay away from the nonpolar L328 residue. The initial cluster models for L9 and L10 were prepared from one of the average structures obtained from classical 100 ns MD simulations.

Understanding the origin of stereoselectivity employing the QM cluster method

Multiple methods have been developed in the past few decades to tackle various questions on enzyme catalysis. Some of the prevalent ones are MD simulations, molecular docking, FEP (free energy perturbation), EVB (empirical valence bond), hybrid QM/MM (quantum mechanics/molecular mechanics), and the QM cluster or the QM-only approach.⁴⁶ Modeling enzymatic enantioselectivity poses a challenge as this requires high accuracy. The quantitative study of the former requires a thorough investigation of the reaction mechanisms, including the location of all stationary points along the reaction path. In recent years, QM/MM, EVB, and the QM cluster approaches have been successfully used in studying enzymatic enantioselectivity, each with its own advantages and disadvantages.⁴⁷ Here, we have employed the QM cluster methodology to discern the origin of enantioselectivity. Tracing reaction pathways with the QM cluster method has been widely used in recent years especially by mechanistically oriented chemists, to identify the structural changes in the model during a simulated reaction.^48–50 A particular advantage of the QM cluster method is the relatively smaller size of the considered system, which allows for accurate DFT methods and makes it easier to ensure that all states in the reaction path remain in a similar local minimum and offers a good trade-off between computational cost and accuracy. Two cluster models were carefully prepared, encompassing a few key residues which could affect the stereoselectivity.

QM cluster 1

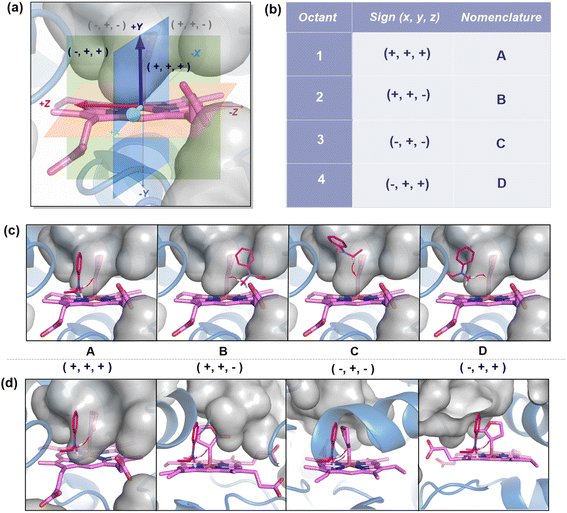
Two cluster models, corresponding to L9 and L10, were selected that include the heme cofactor, axial serine residue (S398), and three other amino acid residues; S264, G265, L328 (R328, for L10) (ESI Fig. S3†). The protonation state of the Arg residue (R328) was chosen based on computational and experimental reports, which unambiguously indicates that the Arg side chain is rarely deprotonated and retains its charge even in the hydrophobic interior of globular proteins.^51,52 The propionate groups of the heme are taken in the protonated form to avoid any artificial interactions owing to the presence of negative charges and to circumvent any perturbations to the active site. The models for L9 and L10 have 149 and 154 atoms, respectively. Prior studies on a related system highlight the crucial role of the mutation of Ala at position 264 to Ser. S264 provides an H-bonding interaction between its side chain and the lactone ester, stabilizing the LAC to explore a major conformation and playing a decisive role in the stereocontrol.²¹ We proceeded with an initial conformational screening of the metallocarbene intermediates using GFN-xTB, a semi-empirical tight-binding model,⁵³ a well-suited method to explore the conformational space of large systems. This evidently reduces the computational cost and is efficient. This conformational sampling lays out the relative orientation of LAC with respect to the heme in the active site (described by the dihedral ∠N₁–Fe₂–C₃–C₄). Sampling on C^L9 (ESI Table S6†) reveals that the low energy conformations correspond to ∠N₁–Fe₂–C₃–C₄ = 144.7°. This conformation allows an H-bonding interaction between the ester group of LAC and the side chain of S264 (Fig. 4(a) and ESI Fig. S4†).

Fig. 4 Lowest-energy structures of the metallocarbene intermediate of the H-bonding pattern seen in the lowest energy structures of (a) C^L9 and (b) C^L10. DFT optimized structures of (c) C^L9 and (d) C^L10. The H atoms (except the ones taking part in H-bonding) are omitted for clarity. The dashed orange lines represent H-bonding. Distances are in Å.

In contrast, sampling on C^L10 (ESI Table S6†) reveals that the lowest energy conformations correspond to one in which the ∠N₁–Fe₂–C₃–C₄ = 84.9°. This conformation exhibits an extensive H-bond network between the ester group of LAC and both S264 and R328 residues, with the latter residue forming an H-bond with the propionate group of heme (both figures have the protonated forms) (Fig. 4(b)). Further reorientations lead to a few slightly higher energy conformations with the LAC ester exhibiting H-bonding with R328. Notably, conformations with the ester group facing the side of S264 (such that H-bonding is only present with the serine residue) have comparatively higher energies (ESI Fig. S6†). The resulting low-energy stationary points (within an energy cut-off of 2 kcal mol⁻¹) were evaluated using DFT, and the high-energy ones were not further considered (Fig. 4(c) and (d)). It should be noted that DFT optimization always converges into one single conformation, irrespective of the starting conformation (taken from xTB scans). We next consider the approach of substrate S₂. Fig. 5 demonstrates the four possible modes via which S₂ can bind.

Fig. 5 (a) Coordinate diagram of the metallocarbene showing the different regions cut by the three planes, XY (green), YZ (blue), and XZ (red). (b) Nomenclature of the faces. (c) In all the poses, the heme-bound carbene unit has been fixed with S₂ approaching the four likely faces: A, B, C, and D. (d) The catalyst's (heme-bound carbene) orientation has been varied with S₂ approaching perpendicular to the plane of the paper. The red arrows indicate the HAT from S₂ to carbene carbon. The gray surface represents the free space/cavity.

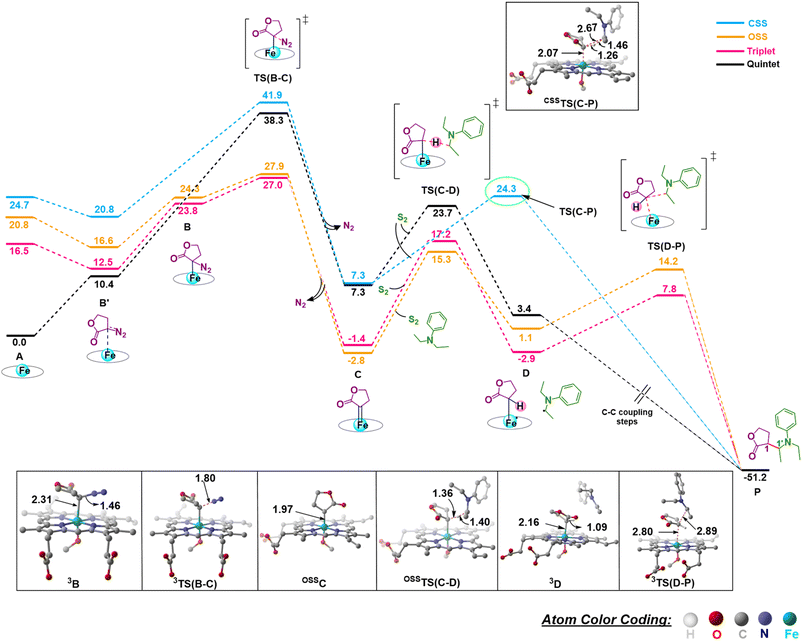
We first consider the porphyrin ring in the XZ plane (red) and the lactone ring in the YZ plane (blue) (Fig. 5(a)). Now, considering only the regions defined by the positive Y axis (the top face of the XZ plane), we look at the four octants intersected by the XY and YZ planes (steric hindrances prevent the approach of S₂ from regions defined by the negative Y-axis, as can be seen from the cavity surfaces in Fig. 5(c) and (d)). For convenience, we have adopted the nomenclature in the text as described in Fig. 5(b). Out of the four possible faces of the substrate approach, face A is the most accessible owing to the presence of the empty space, i.e., the cavity (shown by the gray surface in Fig. 5 and Section 2.2 of ESI†). All other faces are much more sterically demanding and, thus, were not considered while modeling the QM clusters. The nomenclature adopted in the subsequent text is as follows: 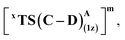where superscript x denotes the spin state taken for study, superscript y denotes the face from which S₂ approaches, subscript (1z) denotes the absolute stereochemistry at the carbene C of the HAT intermediate (D), and superscript m denotes the mutant (L9/L10). Since no crystal structures on the C(sp³)–H insertion products could be obtained, the absolute stereochemistry has been assigned based on a similar enzymatic reaction on C(sp³)–H amination reported by Arnold and co-workers.²¹ Their work on the same enzyme lineage yielded the (1S)-selective aminated product when the penta-mutant L6 (T327V, Q437L, S332A, A87P, & A264S) was used. The reaction proceeded with a nucleophilic attack by the amine substrate followed by rapid stereoselective proton transfer. (As a benchmark, we performed optimization of the LAC and subsequent TS modeling of L9 in OSS surfaces and found the triplet to be more stable than the former (ESI Table S8†).)

Revisiting the origin of enantioinduction

Owing to the anchoring of the LAC by H-bonding, HAT guides the preferential formation of one stereocenter at the carbene carbon. For instance, in the case of L9, the lowest energy transition structure for HAT corresponds to one where the ester group faces the side of S264, with the other side facing the hydrophobic L328 residue (Fig. 6).

Fig. 6 Total electronic energy profile of L9 (kcal mol⁻¹) for HAT and the lowest-energy radical rebound TSs with S₂ approaching from face A are shown. The H atoms (except the ones taking part in H-bonding) are omitted for clarity.

This seems viable owing to the favorable dispersion interactions between the nonpolar face of LAC and the hydrophobic L328 residue, in conjunction with stabilizing H-bonding interactions between the polar face of LAC and the hydrophilic S264 residue of the enzyme. Even upon the formation of the radical intermediates (D) following HAT, the H-bonding between the LAC and active site residues remains intact. The barrier for the radical rebound is significantly lowered in the presence of the enzyme (2.6 kcal mol⁻¹), as shown previously by various groups.^37–42 A PES (potential energy surface) scan along the ∠N₁–Fe₂–C₃–C₄ dihedral (similar to the one which has been defined while performing conformational sampling) reveals that the interconversion between (1S) and (1R) radicals requires a minimum free energy barrier of 6.7 kcal mol⁻¹ (ESI Fig. S2†). This unambiguously indicates that the formed radicals would recombine viaTS(D–P) before undergoing interconversion.‡ However, the radical formed at S₂ can easily undergo rapid conformational changes prior to radical rebound. Thus, it is safe to assume that the HAT determines the enantioselectivity of the product, with the diastereoselectivity being determined by the subsequent radical rebound step. It should be noted that we do not explicitly analyze and quantify the stereopreference obtained with L9 or L10 mutants from this small cluster model. Instead, we have primarily attempted to probe into the conformational flexibility of the metallocarbene intermediate and apprehend the debatable and underappreciated enantioinduction mechanism.

QM cluster 2

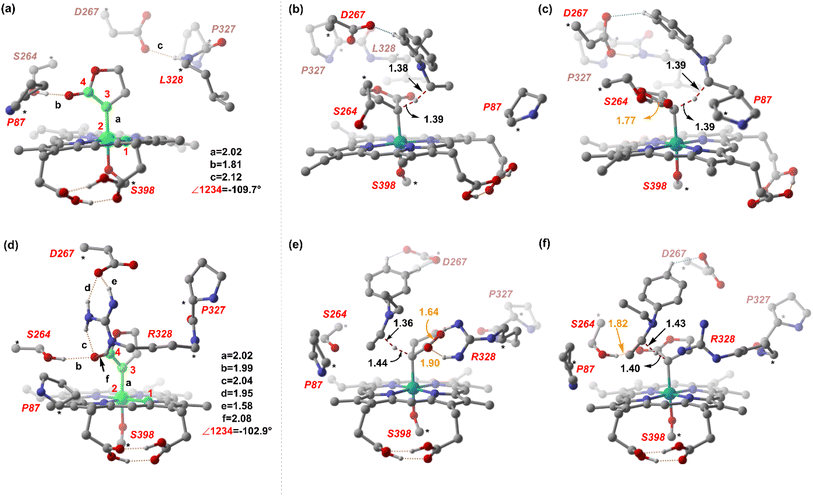
From our preliminary studies of the small cluster system, we extend our analysis to a more extensive cluster system to quantify and rationalize the enantiodivergence. QM cluster 2 comprises all the mutated residues within a 10 Å radius from the Fe center (ESI Fig. S9†). Two cluster models corresponding to L9 and L10 are selected, including the heme cofactor, axial serine residue (S398), and five other amino acid residues; P87, S264, D267, P327, L328 (R328, for L10). Asp267 is taken in its deprotonated state. The models for L9 and L10 have 180 and 185 atoms, respectively. Conformations of the metallocarbene species for both L9 and L10 are chosen based on QM cluster 1, and the H-bond patterns are seen to be identical (Fig. 7(a) and (d)).

Fig. 7 DFT optimized structures of (a) C^L9 and HAT TSs (b) and (c). (d) C^L10 and HAT TSs (e) and (f). Distances are in Å. Numbers in orange refer to the H-bond distances. The H atoms (except the ones taking part in H-bonding) are omitted for clarity.

The substrate approaches in a catalytic relevant mode for HAT, inducing a slight reorientation of the LAC while keeping the H-bonding intact. We look at the two diastereomeric HAT TSs corresponding to the approach of S₂ from face A for both L9 and L10. In L9, the binding mode where the LAC undergoes prominent H-bond interactions with S264 is clearly more reactive than the alternative one lacking it, resulting in the (1S)-selective TS, 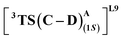to be 6.4 kcal mol⁻¹ more stable than the (1R)-selective one, 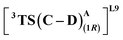(Fig. 7(b) and (c)). This is in line with Arnold's reports on C(sp³)–H amination reaction catalyzed by the same enzyme lineage, where the similar binding mode yields the (1S)-selective product.²¹ On the other hand, L10 complements L9 in product selectivity owing to the alternative anchoring of LAC by R328. This orientation corresponds to the (1R)-selective TS, 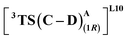where the R328 side chain efficiently H-bonds with the ester group of LAC, making it 3.6 kcal mol⁻¹ more stable than the (1S)-selective TS, 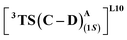(Fig. 7(e) and (f)). Although in 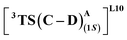H-bonding exists between LAC and the side chain of S264, it is less stabilizing than the former. This alternative anchoring via H-bonds by the key residues, i.e., S264 and R328 leads to an enantiodivergent synthesis with high ee (we further did single-point energy calculations using various levels of theory and found the selectivity to be persistently the same (ESI Table S10†)). To check the reliability of our calculations, we also studied the barriers for N₂ extrusion (the RDS) using our cluster model 2 for L9 and L10 and found them to be 0.3 kcal mol⁻¹ and 4.8 kcal mol⁻¹, respectively, with respect to the enzyme–substrate complexes. This distinctly highlights the crucial role of enzymes in lowering the activation barriers of the reaction it catalyzes.

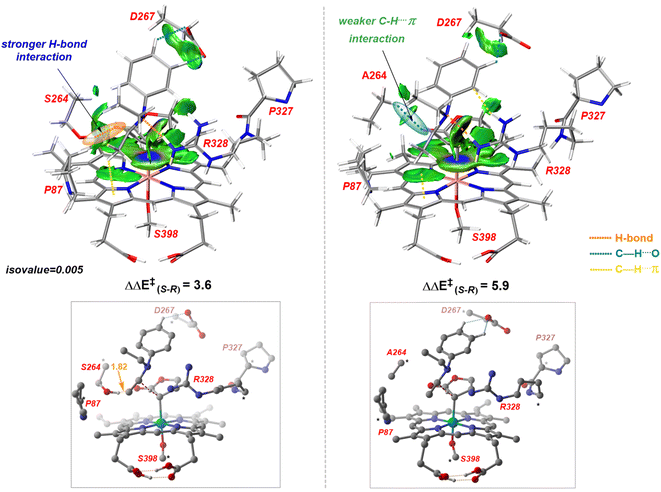
Our study shows that the dramatic reversal in ee from L9 to L10 arises from the initial conformation explored by the LAC. The binding mode of substrate S₂, i.e., the face of the metallocarbene, which is to be exposed for the transfer of the H atom, is seen to be independent of the mutant and is purely based on the shape of the cavity present in the active site. The residues S264 and R328 play a crucial role in the enantioselective formation of the radical intermediates D following the HAT, which then undergoes spontaneous diastereoselective radical rebound to yield the product. We look at the radical rebound TS in the case of L9, starting from the lower-energy (1S)-radical 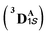that requires an overall activation barrier of 3.6 kcal mol⁻¹. A possible reason for the lower activation barrier in the enzyme active site compared to the model system (ΔG^‡ = 10.7 kcal mol⁻¹, ΔE^‡ = 16.5 kcal mol⁻¹) can be the stabilizing effects provided by the active site residues favoring the closer approach of the S₂ radical, concurrently facilitating Fe–C dissociation (ESI Fig. S11†). It is worth noting that, in the L9 mutant, in addition to stabilizing H-bonding interactions of the ester group of LAC with the side chain of S264, the LAC also exhibits hydrophobic interactions with the L328 residue, which further stabilizes the (1S)-selective TS. (ESI Fig. S12†). Analysis of NCIs (non-covalent interactions) by means of the IGMH (independent gradient model based on Hirshfeld partition)^54–56 on the diastereomeric TSs of the two mutants L9 and L10 shows that weaker NCIs, including C–H⋯O and C–H⋯π interactions between the substrates (S₁ + S₂) and the enzyme environment (defined by QM cluster atoms), are present in both the diastereomeric TSs, while stronger H-bonding interactions are present for the preferred TS – (1S)-selective for L9 and (1R)-selective for L10. The latter reveals an H-bond pattern similar to an “arginine fork” (ESI Fig. S13†).⁵⁷ Although reports on similar systems using MD simulations corroborate the importance and presence of H-bonding interactions in enzymes, a lack of clear mechanistic insights exists. For instance, Arnold's work on enzymatic C–H amination with different penta-mutants L5-FL (T327V, Q437L, S332A, A87P, & V328X) revealed that the mutants V328N and V328Q gave almost 90% ee toward the (1R)-selective aminated product. In contrast, the mutant V328R showed almost a racemic mixture. To this end, we performed an additional S264A mutation and performed a similar TS modeling (ESI Fig. S14†). Our calculations show that this mutant is also highly (1R)-selective and, in fact, expected to be more selective than L10 due to the absence of any strong H-bond in the (1S)-selective TS, 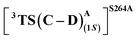compared to that of L10, 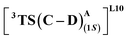(Fig. 8). This evidently highlights the significance of understanding the mechanism and TS modeling while addressing the origins of selectivity.

Fig. 8 IGMH analysis and optimized structures of (1S)-selective HAT TSs – for L10 (left) and S264A mutant (right). Energies are in kcal mol⁻¹, and distances are in Å. Numbers in orange refer to the H-bond distances. The H atoms (except the ones taking part in H-bonding) are omitted for clarity.

Conclusions

In summary, we have investigated the mechanism and origin of stereoselectivity of the recently developed enzymatic system for an enantiodivergent C(sp³)–H insertion to furnish a set of biologically relevant α-amino lactone products. We have examined multiple mechanistic pathways for C(sp³)–H insertion by employing a model system. The lowest-energy path constitutes a HAT followed by a concerted radical rebound pathway. After the primary establishment of the reaction mechanism, we used a combination of MD and QM cluster approach to rationalize the stereoselectivity acquired by two mutants, L9 and L10. Our calculations suggest that the HAT step is enantioselectivity-determining, leading to the formation of radical intermediates, which undergo spontaneous radical rebound to furnish the product. The relatively lower barrier for the radical rebound indicates that stereoablation at the carbene carbon center after HAT is unlikely, and the radical rebound, which dictates the stereochemistry at the S₂ carbon, is diastereoselectivity-determining. We have demonstrated and quantified the roles of key active site residues (including S264 and L/R-328) computationally, confining the LAC's orientation and thereby manifesting enantioinduction via H-bond interactions. We have shown that mutant L9 furnishes the (1S)-selective product, which complements the (1R)-selective L10 variant. It is worth noting that the orientation of the carbene and, consequently, the stereoselective outcome of the reaction can be precisely controlled just by introducing H-bond donor residues at precise locations at the active site. This strategy can be exploited as a design principle in the DE domain to achieve stereodivergent synthesis. Together, our study provides an improved understanding of the mechanism and the precise role of mutations at the molecular level for biocatalytic asymmetric transformations involving radical intermediates. It cannot be stressed enough that controlling key biocatalytic intermediates is the crux of enhancing activity and selectivity in these reactions. We believe that this study will serve rational and mechanism-driven protein engineering in the future to develop novel stereodivergent new-to-nature biocatalytic systems.

Methods

Computational details

All QM calculations were carried out with the DFT method implemented in the Gaussian 16 program.⁵⁸ The (U)B3LYP functional along with the SDD basis set with an effective core potential (ECP) for Fe and standard split valence Pople's basis set 6-31G** for all other atoms were used for gas-phase geometry optimizations.^59–64 Various benchmark studies by Shaik demonstrated the utility of the (U)B3LYP functional for studying iron porphyrin carbenes. (U)B3LYP has also been extensively proven to perform accurately in the computational modeling of iron-oxo chemistry.^65,66 Single-point calculations were performed for all stationary points to refine the energies further using a higher basis set, 6-311++G**, along with the D3 version of Grimme's dispersion correction.⁶⁷ To include the effect of the reaction medium, single-point calculations also included the solvent effect using the polarization continuum model (PCM) with diethyl ether (ε = 4.3) as solvent.^68,69 To check the reliability of the chosen level of theory, we performed benchmark studies using different DFT methods, and the results indicate that the choice of the (U)B3LYP functional is indeed well suited for studying these iron-porphyrin systems (see the ESI† for further details). A total of 500 ns MD simulations (five replica MD simulations of 100 ns each) were performed on the two mutants, L9 and L10, using the GPU code (pmemd) of the Amber18 package.⁷⁰ Subsequently, QM cluster models were prepared, where DFT is used to treat a well-chosen region around the enzymatic active site while the rest of the enzyme is approximated as a homogeneous polarizable medium.^71–74 To avoid any conformational changes, the C(α) atoms are frozen at their crystallographic positions. For the QM cluster approach, we only add the ZPE and thermal corrections since entropy calculations with frozen atoms are unreliable. The free/electronic (for QM cluster) energies reported are at the PCM_(ε=4.3)/(U)B3LYP-D3/6-311++G**,SDD(Fe)//(U)B3LYP/6-31G**,SDD(Fe) unless mentioned otherwise. Complete details on the MD simulations and GFN-xTB approach are given in the ESI.†

Data availability

The authors declare that all supporting data are available in the ESI† and from the corresponding author upon reasonable request.

Author contributions

G. J. and R. C. conceptualized the work. R. C. performed all calculations. G. J. and R. C. analyzed the data and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

G. J. thanks IISc and SERC (Supercomputer Education and Research Centre) for computing resources. R. C. thanks the Ministry of Education, Government of India, for the doctoral fellowship through the PMRF (Prime Minister's Research Fellowship). G. J. acknowledges the YSRA (Young Scientist Research Award) from BRNS (Board of Research in Nuclear Science), DAE (Department of Atomic Energy) (Grant number: 58/20/01/2023-BRNS/37023).

References

1. S. Krautwald, D. Sarlah, M. A. Schafroth and E. M. Carreira, Synfacts, 2013, 9, 0893.
2. T. Sandmeier, S. Krautwald, H. F. Zipfel and E. M. Carreira, Angew. Chem., Int. Ed., 2015, 54, 14363–14367.
3. S. L. Shi, Z. L. Wong and S. L. Buchwald, Nature, 2016, 532, 353–356.
4. P. F. Mugford, U. G. Wagner, Y. Jiang, K. Faber and R. J. Kazlauskas, Angew. Chem., Int. Ed., 2008, 47, 8782–8793.
5. N. J. Turner, Nat. Chem. Biol., 2009, 5, 567–573.
6. C. Zeymer and D. Hilvert, Annu. Rev. Biochem., 2018, 87, 131–157.
7. E. A. Althoff, L. Wang, L. Jiang, L. Giger, J. K. Lassila, Z. Wang, M. Smith, S. Hari, P. Kast, D. Herschlag, D. Hilvert and D. Baker, Protein Sci., 2012, 21, 717–726.
8. C. Zeymer, R. Zschoche and D. Hilvert, J. Am. Chem. Soc., 2017, 139, 12541–12549.
9. X. Garrabou, D. S. Macdonald, B. I. M. Wicky and D. Hilvert, Angew. Chem., Int. Ed., 2018, 57, 5288–5291.
10. J. Xu, Y. Cen, W. Singh, J. Fan, L. Wu, X. Lin, J. Zhou, M. Huang, M. T. Reetz and Q. Wu, J. Am. Chem. Soc., 2019, 141, 7934–7945.
11. X. Ren, A. L. Chandgude and R. Fasan, ACS Catal., 2020, 10, 2308–2313.
12. X. Ren, N. Liu, A. L. Chandgude and R. Fasan, Angew. Chem., Int. Ed., 2020, 59, 21634–21639.
13. A. L. Chandgude and R. Fasan, Angew. Chem., Int. Ed., 2018, 57, 15852–15856.
14. A. Tinoco, V. Steck, V. Tyagi and R. Fasan, J. Am. Chem. Soc., 2017, 139, 5293–5296.
15. D. M. Carminati, J. Decaens, S. Couve-Bonnaire, P. Jubault and R. Fasan, Angew. Chem., 2021, 133, 7148–7152.
16. P. S. Coelho, E. M. Brustad, A. Kannan and F. H. Arnold, Science, 2013, 339, 307–310.
17. A. M. Knight, S. B. J. Kan, R. D. Lewis, O. F. Brandenberg, K. Chen and F. H. Arnold, ACS Cent. Sci., 2018, 4, 372–377.
18. Z. Liu and F. H. Arnold, Curr. Opin. Biotechnol., 2021, 69, 43–51.
19. R. K. Zhang, K. Chen, X. Huang, L. Wohlschlager, H. Renata and F. H. Arnold, Nature, 2019, 565, 67–72.
20. A. Z. Zhou, K. Chen and F. H. Arnold, ACS Catal., 2020, 10, 5393–5398.
21. Z. Liu, C. Calvó-Tusell, A. Z. Zhou, K. Chen, M. Garcia-Borràs and F. H. Arnold, Nat. Chem., 2021, 13, 1166–1172.
22. M. Garcia-Borràs, S. B. J. Kan, R. D. Lewis, A. Tang, G. Jimenez-Osés, F. H. Arnold and K. N. Houk, J. Am. Chem. Soc., 2021, 143, 7114–7123.
23. R. D. Lewis, M. Garcia-Borràs, M. J. Chalkley, A. R. Buller, K. N. Houk, S. B. Jennifer Kan and F. H. Arnold, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7308–7313.
24. C. Calvó-Tusell, Z. Liu, K. Chen, F. H. Arnold and M. Garcia-Borràs, Angew. Chem., Int. Ed., 2023, e202303879.
25. D. A. Sharon, D. Mallick, B. Wang and S. Shaik, J. Am. Chem. Soc., 2016, 138, 9597–9610.
26. H. Su, G. Ma and Y. Liu, Inorg. Chem., 2018, 57, 11738–11745.
27. G. D. Stroscio, M. Srnec and R. G. Hadt, Inorg. Chem., 2020, 59, 8707–8715.
28. R. L. Khade, W. Fan, Y. Ling, L. Yang, E. Oldfield and Y. Zhang, Angew. Chem., Int. Ed., 2014, 53, 7574–7578.
29. E. Casali, E. Gallo and L. Toma, Inorg. Chem., 2020, 59, 11329–11336.
30. R. L. Khade and Y. Zhang, Chem.–Eur. J., 2017, 23, 17654–17658.
31. Y. Wei, A. Tinoco, V. Steck, R. Fasan and Y. Zhang, J. Am. Chem. Soc., 2018, 140, 1649–1662.
32. R. Balhara and G. Jindal, J. Org. Chem., 2022, 87, 7919–7933.
33. R. Balhara, R. Chatterjee and G. Jindal, Phys. Chem. Chem. Phys., 2021, 23, 9500–9511.
34. N. Manoj and G. Jindal, Chem. Commun., 2021, 57, 11370–11373.
35. Y. Zhang, Chem.–Eur. J., 2019, 25, 13231–13247.
36. K. Chen, S. Q. Zhang, O. F. Brandenberg, X. Hong and F. H. Arnold, J. Am. Chem. Soc., 2018, 140, 16402–16407.
37. S. Shaik, D. Kumar and S. P. De Visser, J. Am. Chem. Soc., 2008, 130, 14016.
38. F. Ogliaro, N. Harris, S. Cohen, M. Filatov, S. P. De Visser and S. Shaik, J. Am. Chem. Soc., 2000, 122, 8977–8989.
39. K. C. Haatveit, M. Garcia-Borràs and K. N. Houk, Front. Chem., 2019, 6, 663.
40. X. Wu, Y. Chen, X. Wang, W. Wei and Y. Liang, J. Org. Chem., 2021, 86, 13768–13773.
41. S. Kalita, S. Shaik and K. D. Dubey, Chem. Sci., 2021, 12, 14507–14518.
42. J. Wang, H. Gao, L. Yang and Y. Q. Gao, ACS Catal., 2020, 10, 5318–5327.
43. B. K. Mai, N. M. Neris, Y. Yang and P. Liu, J. Am. Chem. Soc., 2022, 144, 11215–11225.
44. J. Burés, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2012, 134, 6741–6750.
45. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
46. S. Ahmadi, L. B. Herrera, M. Chehelamirani, J. Hostaš, S. Jalife and D. R. Salahub, Int. J. Quantum Chem., 2018, 118, 1–34.
47. X. Sheng, M. Kazemi, F. Planas and F. Himo, ACS Catal., 2020, 10, 6430–6449.
48. P. E. M. Siegbahn and F. Himo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336.
49. F. Himo, J. Am. Chem. Soc., 2017, 139, 6780–6786.
50. F. Himo and S. P. de Visser, Commun. Chem., 2022, 5, 20–23.
51. C. A. Fitch, G. Platzer, M. Okon, B. E. Garcia-Moreno and L. P. McIntosh, Protein Sci., 2015, 24, 752–761.
52. M. J. Harms, J. L. Schlessman, G. R. Sue and E. B. García-Moreno, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 18954–18959.
53. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
54. C. Lefebvre, G. Rubez, H. Khartabil, J. C. Boisson, J. Contreras-García and E. Hénon, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936.
55. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
56. T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555.
57. S. S. Chavali, C. E. Cavender, D. H. Mathews and J. E. Wedekind, J. Am. Chem. Soc., 2020, 142, 19835–19839.
58. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016.
59. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
60. A. D. Beck, J. Chem. Phys., 1993, 98, 5648–5656.
61. W. J. Hehre, K. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
62. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
63. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
64. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
65. H. Chen, W. Lai and S. Shaik, J. Phys. Chem. Lett., 2010, 1, 1533–1540.
66. S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110(2), 949–1017.
67. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
68. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
69. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
70. A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2012, 8, 1542–1555.
71. P. E. M. Siegbahn and R. H. Crabtree, J. Am. Chem. Soc., 1997, 119, 3103–3113.
72. S. Ghafoor, A. Mansha and S. P. De Visser, J. Am. Chem. Soc., 2019, 141, 20278–20292.
73. F. Planas, M. J. McLeish and F. Himo, ACS Catal., 2019, 9, 5657–5667.
74. M. Prejanò, J. Škerlová, P. Stenmark and F. Himo, J. Am. Chem. Soc., 2022, 144, 14258–14268.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc02788k

‡ Following this argument, we have not looked at the radical-rebound TSs with the (1R)-selective radical as their energies will not affect the enantioinduction scenario.

---