Origin of the superior oxygen reduction activity of zirconium nitride in alkaline media

Abstract

The anion exchange membrane fuel cell (AEMFC), which can operate in alkaline media, paves a promising avenue for the broad application of earth-abundant element based catalysts. Recent pioneering studies found that zirconium nitride (ZrN) with low upfront capital cost can exhibit high activity, even surpassing that of Pt in alkaline oxygen reduction reaction (ORR). However, the origin of its superior ORR activity was not well understood. Herein, we propose a new theoretical framework to uncover the ORR mechanism of ZrN by integrating surface state analysis, electric field effect simulations, and pH-dependent microkinetic modelling. The ZrN surface was found to be covered by ∼1 monolayer (ML) HO* under ORR operating conditions, which can accommodate the adsorbates in a bridge-site configuration for the ORR. Electric field effect simulations demonstrate that O* adsorption on a 1 ML HO* covered surface only induces a consistently small dipole moment change, resulting in a moderate bonding strength that can account for the superior activity. Based on the identified surface state of ZrN and electric field simulations, pH-dependent microkinetic modelling found that ZrN reaches the Sabatier optimum of the kinetic ORR volcano model in alkaline media, with the simulated polarization curves being in excellent agreement with the experimental data of ZrN and Pt/C. Finally, we show that this theoretical framework can lead to a good explanation for the alkaline oxygen electrocatalysis of other transition metal nitrites such as Fe₃N, TiN, and HfN. In summary, this study proposes a new framework to rationalize and design transition metal nitrides for alkaline ORR.

---

Introduction

The fuel cell is a promising technology that has the potential to revolutionize energy generation and realize anthroposocial decarbonization.^1–4 Among various types of fuel cells, hydrogen fuel cells⁴ have gained significant attention due to their unique merits such as excellent energy efficiency, operational feasibility, and environment-friendliness. Hydrogen fuel cells use hydrogen gas as the fuel and oxygen from the air piped into the cathode as the oxidant to generate electricity. This process refers to two separate reactions which are the hydrogen oxidation reaction (HOR) and oxygen reduction reaction (ORR). Both reactions produce water and heat as byproducts, making hydrogen fuel cells a near zero-emission technology. Unfortunately, the broad application of this unique energy technology is plagued by the large overpotential of cathodic ORR which remains the bottleneck for the overall efficiency.^5,6

Currently, the most efficient and commonly applied catalysts for the ORR are still Pt-group metals (PGMs).^7,8 Nevertheless, their high cost still remains a key challenge. Hence, screening low-cost, stable, but still efficient alternatives is a sought-after goal. In this respect, earth-abundant transition metal X-ides (TMXs, X = O, N, C, etc.), a class of materials proven to be active and stable in some electrocatalyses,^9–14 have received considerable attention. Spontaneously, recent advances in anion exchange membrane fuel cells (AEMFCs)^15,16 have paved the way for a broader application of TMXs due to their ability to operate under alkaline conditions. Despite ongoing research on TMXs, although certain materials have indeed demonstrated potential for catalyzing the ORR,^17,18 their performance still falls short in comparison to commercial PGMs and their instability under strict working conditions poses a significant hurdle for their broader implementation. In particular, recent studies found that in addition to the large bandgap, an intrinsic limitation of transition metal oxides (TMOs) is the induced large dipole moment upon O*-adsorption, which in turn leads to weak O*-bonding under electrocatalytic conditions that results in the sluggish rate-determining step of O–O bond breaking during the ORR.¹⁹ This conclusion is in good agreement with the experimental high-throughput screening of ∼7800 identical TMOs for alkaline ORR.¹⁸ Given TMXs generally have pristine surfaces similar to TMOs, it can be simply expected that many TMXs could have the same bottlenecks for the ORR.²⁰

Interestingly, pioneering work by Yuan et al.²¹ reported a zirconium nitride (ZrN) catalyst that showed a high 4-electron (4e-) ORR performance, with the activity surpassing that of commercial Pt in alkaline media. This work is significant given the low-cost and versatile nature (i.e., ∼zero bandgap and considerable electrical conductivity) of ZrN,^22,23 which offers promising potential for its widespread application in energy conversion technology.^24–29 Similar ORR performance of ZrN was also found by some subsequent studies (e.g., ref. 15). However, despite the exciting nature of ZrN, the ORR mechanism and the activity origin of ZrN were not well understood. Missing this key insight would hamper the rational search and design of promising TMXs for the ORR. Therefore, a comprehensive analysis of its ORR activity origin, particularly coupling with state-of-the-art modelling methods, is urgently needed at the present stage.

Furthermore, when analyzing the underlying mechanism of TMXs, one must take into account the surface states of TMXs under operational conditions. These can significantly differ from those of the stoichiometric pristine form due to the existing equilibrium between water and O/H-containing adsorbates,³⁰ which may account for the stability of TMXs as the coverage layer could suppress the leaching of cations.³¹ Similar conclusions were drawn by the series of studies of the Mullins group³² regarding the concept of “pre-catalyst”, calling for a better understanding of the nature of a TMX surface under electrochemical reaction conditions. Although experiments have also revealed analogous trends in the surface oxidation phenomenon,^15,21 the attention given to this issue is still insufficient. Currently, most theoretical studies continue to be based on a pristine surface for reaction energy calculations,^33,34 which contradict with some experimentally observed performances. Underestimating the effect of a realistic coverage under electrochemical conditions could mislead the mechanism understanding. Additionally, when evaluating a catalyst under specific electrochemical conditions, one can never overlook the impact of pH as it may exert significant effects on the performance of a catalyst. In this context, it is essential to consider the effects of electric field since the changes in dipole moment can induce variations in the pH effect which changes the reaction energetics.^19,35,36

Herein, we posit that integrating surface state analysis and pH effects is indispensable to elucidating the origin of ZrN's ORR activity. Therefore, based on surface state analysis via surface Pourbaix diagrams and dipole moment analysis based on electric field simulations, we propose a new framework to analyze the ORR performance of ZrN, which effectively incorporates the pH effects. According to surface Pourbaix diagram calculations, the ZrN surface was found to be further oxidized under ORR operating conditions, with an additional ∼1 monolayer (ML) HO* covered on the surface. Electric field simulations revealed that this electrochemically oxidized surface can accommodate ORR adsorbates in a bridge-site adsorption configuration, particularly for O* which can be “buried” in the HO*-covered surface. This will lead to a small dipole change upon adsorption and a moderate O*-bonding strength that takes ZrN close to the theoretical optimum of the derived pH-dependent ORR volcano based on microkinetic modelling. The simulated polarization curve of the 1 ML HO*-covered surface obtained from the pH-dependent microkinetic model exhibits excellent agreement with experimental observations. To end with, this study proposes a new framework to describe the mechanism of the superior ORR activity of ZrN in alkaline media. We found that this framework can also describe the promising activity and stability of oxygen electrocatalysis of other transition metal nitrides such as Fe₃N, TiN, and HfN.

Results and discussion

Probing the surface states

First, by implementing surface energy calculations among various typical surfaces and terminations of a cubic ZrN (i.e., the most stable crystal structure of ZrN³⁷), (100) was found to be the most energetically favorable (Table S1†), consistent with previous experimental observations^15,21,38 and theoretical calculations.^9,29 With respect to unraveling the surface states of ZrN(100) at the potential and pH of interest, surface Pourbaix diagram (i.e., electrochemical phase diagram) calculations were employed. According to the operating conditions of alkaline ORR,²¹ the pH and potential were respectively considered at pH = 13 and 0.8 V vs. the reversible hydrogen electrode (RHE) (∼0.046 V vs. the standard hydrogen electrode, SHE). Interestingly, as shown in Fig. 1, ZrN(100) is found to be covered by ∼1 ML HO* in 0.1 M KOH under 0.8 V_RHE, which differs considerably from the stoichiometric pristine surface cleaved directly from bulk ZrN. The corresponding optimized structures can be found in Fig. S1.† This finding is consistent with the X-ray photoelectron spectroscopy (XPS) results reported by previous experiments,²¹ revealing the presence of an oxide/hydroxyl layer above ZrN. However, although comparable trends were observed in experimental studies,¹⁵ little attention has been paid to this distinct surface state during the ORR at TMXs, and subsequent computational work has continued to be based on the pristine surface which could inevitably mislead research outcomes. Meanwhile, recent studies^30,31 have shown that the surface coverage can effectively prevent the cation from leaching out from a surface, increasing the stability under relevant working conditions. Therefore, the 1 ML HO* on ZrN(100) can provide valuable insights into the stability of ZrN in alkaline ORR as reported by experiments.^15,21

Fig. 1 (a) Calculated 1D surface Pourbaix diagram as a function of potential (vs. SHE) (pH = 13; T = 298.15 K). (b) 2D surface Pourbaix diagram as a function of potential (vs. SHE) and pH (T = 298.15 K). (c) Optimized structures of the ZrN(100) surface before and after HO* coverage under ORR conditions. Insets are the corresponding top views. Green, blue, red, and white spheres denote Zr, N, O, and H, respectively.

Fig. 2 shows the calculated free energy diagrams of the 4e-ORR on Pt(111), ZrO₂(111), pristine ZrN(100), and ZrN(100) covered by 1 ML HO*. On Pt(111), 4e-ORR proceeds with relatively exothermic energetics, having the HO* removal as the rate-limiting step. ZrO₂(111) has a high barrier in the O–O bond activation that makes it not suitable for 4e-ORR. All of this is in good agreement with experimental measurements in that though Pt and ZrO₂ are relatively stable under ORR conditions, ZrO₂ generally show poor activities.^10,19,39 In terms of ZrN, a significant discrepancy in the ORR performance was observed on the ZrN(100) surface before and after the coverage of 1 ML HO*. The pristine surface demonstrates poor theoretical activity, with the rate-limiting step located at the removal of HO* on the surface. In contrast, the 1 ML HO*-covered ZrN(100) shows activity comparable to that of Pt(111). This observation can qualitatively explain the high activity of ZrN, which originates in the electrochemically oxidized surface under ORR conditions. Besides, these results highlight the importance of determining the surface state beforehand, as any subsequent activity analysis should be conducted based on a more realistic surface state under electrocatalytic operating conditions.

Fig. 2 Calculated free energy diagrams of the ORR at pristine ZrN(100) and ZrN(100) covered by 1 ML HO*, Pt(111),⁴⁰ and ZrO₂(111).¹⁹ The energy barriers of the elementary steps were estimated based on the method by Dickens et al.⁴¹ The potential was set to 0.8 V vs. RHE.

Interestingly, it can be seen that the binding energies of the key ORR adsorbates (i.e., HO*, O*, and HOO*) on the 1 ML HO* covered ZrN(100) fit well into the linear scaling relations for the low-index TMXs constructed from >200 available data points from ref. 19 and 41–44 (Fig. 3). This suggests that the bonding of ORR adsorbates at ZrN(100) can be described by the universal oxygen electrocatalysis scaling relations for TMXs, and thus it can be further analyzed by pH-dependent microkinetic modelling more quantitively.

Fig. 3 Linear scaling relations that determine the ORR activities on TMXs. (a) The identified scaling relations of E_HO*vs. E_HOO* and (b) E_HO*vs. E_O* constructed for low-index (defined as h² + k² + l² < 1) TMXs based on >200 TMX data points. Insets are the corresponding optimized structures. The slopes are fixed to 1 and 2 for E_HO*vs. E_HOO* and E_HO*vs. E_O*, respectively. Green, blue, red, and white spheres represent Zr, N, O, and H, respectively.

Modelling pH with an electric field

When performing a comprehensive analysis of an electrocatalyst's activity, the effects of pH are indispensable. Relevant mechanisms can exhibit substantial variability under different pH values. Likewise, the effects of pH may differ across various surface states due to the alterations in the adsorption-induced dipole moment change on distinct surfaces. Therefore, it is essential to consider pH when rationally analyzing the origin of ORR activity. Recent studies^35,45 demonstrated the feasibility to model pH-dependencies of the ORR by considering electric field effects, showing quantitative agreement with experimental measurements, especially on transition metals. The ORR process involves various intermediates and transition states which are all O-containing species with positive dipole moments. Consequently, electric fields will have a considerable impact on these oxygen species with stabilization under negative fields and destabilization under positive fields. As this electric field intensity is approximately linear to the SHE while the SHE scale is pH-dependent on the RHE,^35,46,47 the variations in the reaction energetics caused by different electric fields will be pH-dependent when scaled with the RHE. Fig. 4a and b show how these intermediates interact with different electric fields on the 1 ML HO*-covered and pristine ZrN(100) surfaces. Note that the dipole information of O* can be used exclusively as a descriptor of the ORR activity, where considerable dipole moment and polarizability are not expected for an ideal ORR catalyst. The reason is that a larger O*-adsorption dipole moment will lead to a weaker O*-bonding under electrocatalytic conditions that results in the sluggish O–O bond activation.¹⁹ Obviously, the intrinsic dipole moment (μ) and polarizability (α) of O* are substantially small at the ZrN(100) surface covered by 1 ML HO* (Fig. 4b), compared to the much larger μ and α at its pristine surface (Fig. 4a). The same trend is found in the calculated dipole moment (note: the absolute value is adopted here to denote the magnitude) of O* on these two surfaces, which are 0.26 and 0.76 e·Å for 1 ML HO*-covered ZrN(100) and the pristine surface, respectively. Moreover, as observed from the insets in the bottom of Fig. 4b, O* typically adopts an upright orientation on the metal-site via an atop adsorption configuration, resembling a “tall tree standing solely on the ground”. This configuration will form a lower coordination environment^19,48 and a weaker O*-bonding. When it comes to the fully oxidized surface, all the top sites are already occupied by the covering species (1 ML HO*), thus the additional O* will be adsorbed in a bridge-site (like a “growing tree in a forest of HO*”) with a higher coordination number. This configuration exhibits an optimal O*-bonding which is similar to the behavior observed in transition metals.¹⁹ Because the adsorbed O* is “buried” among the pre-covered HO*, it is shielded from a strong electric field effect, resulting in a small dipole moment upon adsorption. Moreover, as the adsorbate on a bridge site is closer to the surface in comparison to the atop site, a smaller adsorption-induced dipole moment and a more spatial overlap between O* and the site electron density are predictable (as shown in the insets of Fig. 4a and b). This observation also provides insights into the activity origin of the ORR. Overall, the superior activity of this self-oxidized (i.e., 1 ML HO*-covered) surface can be attributed primarily to its distinctive behavior. This behavior enables the surface to accommodate the O* adsorbate in a bridge site which is a coordinatively saturated adsorption configuration, leading to a small O* dipole moment and a moderate O* bonding strength.

Fig. 4 Electric field effects and pH-dependent microkinetic modelling. (a) Electric field effects on ORR adsorbates with fitted values for μ (e) and α (e² V⁻¹) for 1 ML HO*-covered ZrN(100) and (b) pristine ZrN(100). Insets show the calculated charge density difference induced by O* adsorption, where yellow and cyan represent charge accumulation and loss, respectively. (c) Derived pH-dependent volcano activity model for the ORR as a function of HO* adsorption (at 0.8 V vs. RHE). (d) Simulated ORR polarization curves on 1 ML HO*-covered ZrN(100) and Pt(111), plotted along with the experimental polarization curves for ZrN and Pt/C.²¹ Insets are the optimized structures with O* adsorption under different electric fields (−0.6, 0, and 0.6 V Å⁻¹). Green, blue, red, and white spheres represent Zr, N, O, and H, respectively. The adsorbed O for structures in (a) is marked in yellow.

pH-dependent microkinetic modelling

The results identified above were further incorporated into the pH-dependent microkinetic modelling coupled with the effects of electric fields.³⁵ Based on the microkinetic model (i.e., the volcano activity model) shown in Fig. 4c (where a more negative electric field corresponds to a more basic condition), it can be observed that the activity of the 1 ML HO*-covered ZrN(100) is near the peak of the volcano (i.e., the theoretical maximum activity), representing an optimal ORR performance. Besides, the shift of volcano plots in response to different electric fields is relatively minor. This is consistent with the results of the electric field analysis that indicates the stability of the O*-induced dipole moment on the covered surface under varying electric fields. Meanwhile, the ORR polarization curves of Pt(111) and 1 ML HO*-covered ZrN(100) were also simulated based on microkinetic modelling (Fig. 4d), showing excellent agreement with the experiments on Pt/C and ZrN.²¹ These results provide further evidence that the 1 ML HO*-covered surface is a more realistic surface state that also endows ZrN with superior alkaline ORR performance.

Herein, a new framework to elucidate the activity origin of ZrN for alkaline ORR has been outlined in Fig. 5a with the derived mechanism in Fig. 5b. Generally, we start from the surface state verification by surface Pourbaix diagram calculations and then compare the relevant free energy diagrams to draw the initial conclusion about the ORR energetics. Subsequently, electric field effects are considered to obtain the dipole moment and polarizability information which enables a thorough illustration of the activity origin. Finally, pH-dependent microkinetic modelling coupled with the electric fields is introduced. By the excellent matching with experimental observations, this microkinetic model further corroborates the actual surface state revealed by the preliminary Pourbaix diagram analysis.

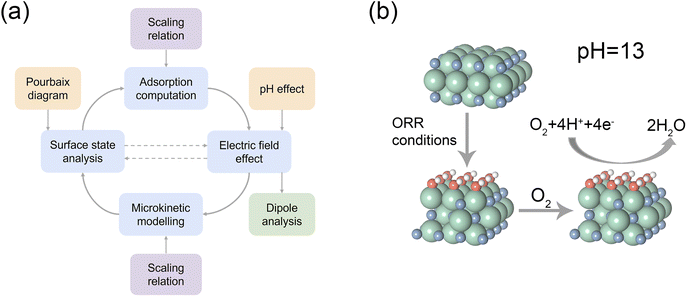Fig. 5 (a) An illustration of the proposed analytical framework. (b) The alkaline ORR mechanism on ZrN. Green, blue, red, and white spheres denote Zr, N, O, and H, respectively.

Lastly, considering the consistency observed from theory and experiments, we postulate that this new analytical framework can be extended to other systems to investigate the underlying mechanism responsible for the activity and stability under electrochemical operating conditions. Accordingly, we further analyzed the surface states of Fe₃N, TiN, and HfN as a function of pH and potential. The reason for choosing these three transition metal nitrides is that they were also proven to be active and relatively stable for the ORR^49–54 or OER^55,56 under alkaline conditions. TiN and HfN share a similar stable crystal structure with ZrN while Fe₃N has a hexagonal structure. The 2D and 1D surface Pourbaix diagrams of Fe₃N(111), TiN(100), and HfN(100) were computed (Fig. 6 and S2†). Notably, electrochemical oxidation is also observed on these three surfaces, consistent with recent experimental findings.^49,55,57 Furthermore, the dipole moment changes induced by O* adsorption on the oxidized surfaces were calculated (0.09, 0.02, and 0.21 e·Å for Fe₃N, TiN, and HfN under their electrochemical surface states, respectively) which are substantially minor. HO* adsorption energies on the pre-oxidized surfaces of Fe₃N(111) and TiN(100) together with the data on ZrO₂(111) and HfO₂(111) were fitted into the pH-dependent volcano plot (Fig. 6e) derived from the microkinetic models of 1 ML HO*-ZrN(100). It is obvious that 4/6 ML O* covered Fe₃N(111) and 1 ML O* covered TiN(100) locate near the top of the volcano, indicating a theoretical optimal activity that aligns with their experimental ORR activities.^49,53,54 Herein, we have provided examples to illustrate the universality of this framework as we believe that many TMX materials, especially transition metal nitrides, will undergo surface state transformation under electrochemical operating conditions,^30,32 which will significantly impact the dipole moment of the adsorbates.

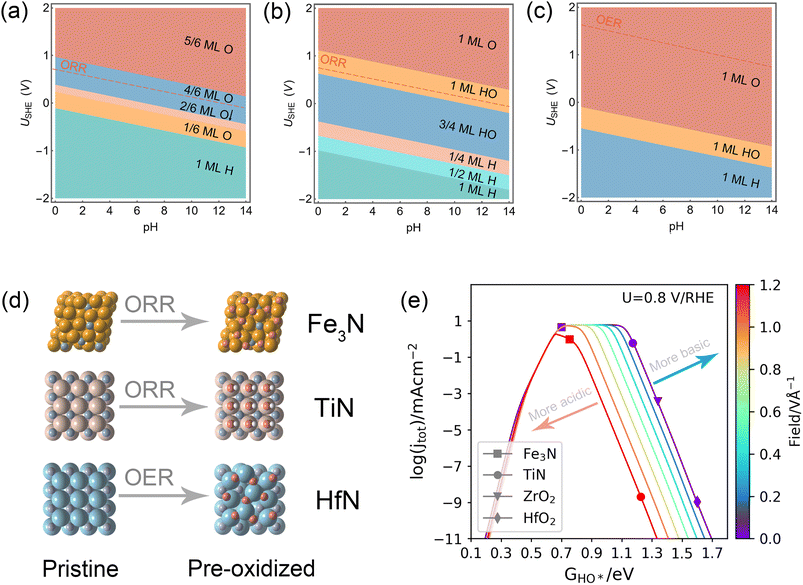Fig. 6 Calculated 2D surface Pourbaix diagrams as a function of potential (vs. SHE) and pH (T = 298.15 K) for (a) Fe₃N(111), (b) TiN(100), and (c) HfN(100). (d) Corresponding atomic structures before and after surface state changes. Yellow, brown, cyan, blue, red, and white spheres denote Fe, Ti, Hf, N, O, and H atoms, respectively. (e) Derived pH-dependent volcano activity model for the ORR as a function of HO* adsorption (at 0.8 V vs. RHE) plotted with the Fe₃N(111), TiN(100), ZrO₂(111), and HfO₂(111) under their identified surface states under ORR conditions. Note: the pristine surfaces were previously identified to be favorable under ORR conditions for ZrO₂ and HfO₂(111).¹⁹

Conclusion

In summary, we have proposed a framework to reveal the origin of the high ORR activity of ZrN in alkaline media, which combines surface state analysis, electric field effect simulations, and microkinetic modelling. First, an electrochemically oxidized surface comprising 1 ML HO* under ORR working conditions was revealed by surface Pourbaix analysis. The calculated free energy diagrams suggest that this oxidized surface is a more realistic active surface responsible for the superior activity of ZrN in alkaline ORR, instead of a pristine ZrN surface. The 1 ML HO* coverage standing initially upon the pristine surface provides a sanctuary for the adsorbates, akin to a “forest” where the O* can remain stable under varying electric fields. Within this 1 ML HO* coverage, the adsorbed O* can be “buried” in a bridge site, which results in a moderate O*-bonding strength and a small dipole moment change upon adsorption, ultimately leading to the superior ORR activity. When applying the fully oxidized surface to the advanced pH-dependent microkinetic modelling, ZrN is found to be located at the theoretical optimum of the pH-dependent ORR volcano. Its simulated polarization curve for the ORR exhibits excellent agreement with the experimental data. Furthermore, we demonstrated that the proposed framework can be applied to other systems such as Fe₃N, TiN, and HfN. Overall, this work highlights the significance of preliminary surface state determination and the use of O* dipole moment as an activity descriptor in oxygen electrocatalysis research. The proposed framework is expected to enable a comprehensive understanding of the underlying mechanisms and promote the development of PGM-free catalysts.

Computational and modelling details

The Vienna ab initio simulation package (VASP)⁵⁸ employing the projector augmented wave (PAW) method^59,60 was used for the spin-polarized density functional theory (DFT) calculations. Valence electrons were described by the Kohn–Sham wavefunctions⁶¹ which are expanded in a plane-wave basis set⁶⁰ with a kinetic energy cutoff of 520 eV. The convergence criterion for geometric relaxation was that the forces acting on each atom should be less than 0.03 eV Å⁻¹. Electron exchange and correlation interactions were calculated using the generalized gradient approximation (GGA)⁶² method parametrized by the revised Perdew–Burke–Ernzerhof (RPBE) functional.⁶³ A (3 × 3 × 1) k-point mesh was used to sample the Brillouin zone⁶⁴ and a vacuum slab of 15 Å was chosen in the z-direction to separate two periodic surfaces. The computational parameters for bulk structures were referenced to the Materials Project database.³⁷ The surface Pourbaix diagrams' energetics were computed using the computational hydrogen electrode (CHE) method proposed by Nørskov et al.⁶⁵ as a function of pH and potential. The zero-point energy (ZPE) and entropic corrections were obtained from a previous study⁶⁶ at 298.15 K. Solvation corrections were implemented for the HO* species, as the strong hydrogen bonding effects result in additional stabilization of bonding strengths. The values for these corrections were obtained from ref. 66 and 67. Electric fields (EF) were introduced based on the methods proposed by Kelly et al.35 using a saw-tooth potential corresponding to fields between −0.8 and 0.8 V⁻¹. Calculations concerning the electric field were performed using the Quantum Espresso code.⁶⁸ Comprehensive computational and modelling details, including the electric field simulation and microkinetic modelling, are given in the ESI.†

Data availability

Data are available from the corresponding authors upon reasonable request.

Author contributions

H. Liu and H. Li conceived the idea and designed the research framework. H. Liu, D. Z., S. H., C. D., and H. Li wrote the manuscript. H. Li supervised the project. H. Liu carried out the calculations and analysed the results. H. Liu and D. Z. performed microkinetic modelling. All authors discussed and analyzed the results during manuscript preparation.

Conflicts of interest

There is no conflict of interest to declare.

Acknowledgements

This work was supported by JSPS KAKENHI (Grant No. JP23K13703) and the Iwatani Naoji Foundation. We acknowledge the Center for Computational Materials Science, Institute for Materials Research, Tohoku University for the use of MASAMUNE-IMR (Project No. 202212-SCKXX-0204), the Institute for Solid State Physics (ISSP) at the University of Tokyo for the use of their supercomputers, and the assistance given by Research IT and the use of the Computational Shared Facility at The University of Manchester. H. Liu acknowledges the China Scholarship Council (CSC, No. 202006370085) and the University of Manchester for the joint PhD studentship to support his research. C. D'Agostino acknowledges the EPSRC (No. EP/V026089/1) for funding his research activities. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) license (where permitted by UKRI, ‘Open Government License’ or ‘Creative Commons Attribution No-derivatives (CC BY-ND) license may be stated instead) to any Author Accepted Manuscript version arising.

References

1. H. Guo, S. G. Kang and S. G. Lee, Exploring two-dimensional carbides as highly active catalysts for the oxygen reduction reaction: A density functional theory approach, Appl. Surf. Sci., 2022, 599, 153907–153914.
2. X. Gao, S. Kan, Y. Zhang, Y. Li, G. He and H. Liu, Cu-N_x active sites derived from copper phthalocyanine in porous carbon promoting oxygen reduction reaction, Synth. Met., 2022, 291, 117204–117210.
3. S. Chu and A. Majumdar, Opportunities and challenges for a sustainable energy future, Nature, 2012, 488, 294–303.
4. M. K. Debe, Electrocatalyst approaches and challenges for automotive fuel cells, Nature, 2012, 486, 43–51.
5. V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, The oxygen reduction reaction mechanism on Pt(111) from density functional theory calculations, Electrochim. Acta, 2010, 55, 7975–7981.
6. D. F. Abbott, S. Mukerjee, V. Petrykin, Z. Bastl, N. B. Halck, J. Rossmeisl and P. Krtil, Oxygen reduction on nanocrystalline ruthenia – local structure effects, RSC Adv., 2015, 5, 1235–1243.
7. C. Wang, N. M. Markovic and V. R. Stamenkovic, Advanced Platinum Alloy Electrocatalysts for the Oxygen Reduction Reaction, ACS Catal., 2012, 2, 891–898.
8. M. H. Shao, Q. W. Chang, J. P. Dodelet and R. Chenitz, Recent Advances in Electrocatalysts for Oxygen Reduction Reaction, Chem. Rev., 2016, 116, 3594–3657.
9. Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, Electroreduction of N2 to Ammonia at Ambient Conditions on Mononitrides of Zr, Nb, Cr, and V: A DFT Guide for Experiments, ACS Catal., 2015, 6, 635–646.
10. L. Zhou, H. Li, Y. Lai, M. Richter, K. Kan, J. A. Haber, S. Kelly, Z. Wang, Y. Lu, R. S. Kim, X. Li, J. Yano, J. K. Nørskov and J. M. Gregoire, Stability and Activity of Cobalt Antimonate for Oxygen Reduction in Strong Acid, ACS Energy Lett., 2022, 7, 993–1000.
11. J. Gao, H. Tao and B. Liu, Progress of Nonprecious-Metal-Based Electrocatalysts for Oxygen Evolution in Acidic Media, Adv. Mater., 2021, 33, e2003786.
12. Y. Wang, X. Li, M. Zhang, J. Zhang, Z. Chen, X. Zheng, Z. Tian, N. Zhao, X. Han, K. Zaghib, Y. Wang, Y. Deng and W. Hu, Highly Active and Durable Single-Atom Tungsten-Doped NiS(0.5) Se(0.5) Nanosheet @ NiS(0.5) Se(0.5) Nanorod Heterostructures for Water Splitting, Adv. Mater., 2022, 34, e2107053.
13. W. Yang, B. Zhou, Z. Jia, C. Wu, L. Wei, Z. Gao and H. Li, Coordination Engineering of Single-Atom Iron Catalysts for Oxygen Evolution Reaction, ChemCatChem, 2022, 14, e202201016.
14. W. Xiong, H. Yin, T. Wu and H. Li, Challenges and Opportunities of Transition Metal Oxides as Electrocatalysts, Chemistry, 2023, 29, e202202872.
15. X. L. Zhang, S. J. Hu, Y. H. Wang, L. Shi, Y. Yang and M. R. Gao, Plasma-Assisted Synthesis of Metal Nitrides for an Efficient Platinum-Group-Metal-Free Anion-Exchange-Membrane Fuel Cell, Nano Lett., 2023, 23, 107–115.
16. G. Gunasooriya, M. E. Kreider, Y. Liu, J. A. Zamora Zeledon, Z. Wang, E. Valle, A. C. Yang, A. Gallo, R. Sinclair, M. B. Stevens, T. F. Jaramillo and J. K. Norskov, First-Row Transition Metal Antimonates for the Oxygen Reduction Reaction, ACS Nano, 2022, 16, 6334–6348.
17. Y. Wang, J. Li and Z. Wei, Transition-metal-oxide-based catalysts for the oxygen reduction reaction, J. Mater. Chem. A, 2018, 6, 8194–8209.
18. D. Guevarra, J. A. Haber, Y. Wang, L. Zhou, K. Kan, M. H. Richter and J. M. Gregoire, High Throughput Discovery of Complex Metal Oxide Electrocatalysts for the Oxygen Reduction Reaction, Electrocatalysis, 2022, 13, 1–10.
19. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Analysis of the limitations in the oxygen reduction activity of transition metal oxide surfaces, Nat. Catal., 2021, 4, 463–468.
20. M. B. Stevens, M. Anand, M. E. Kreider, E. K. Price, J. Z. Zeledón, L. Wang, J. Peng, H. Li, J. M. Gregoire, J. Hummelshøj, T. F. Jaramillo, H. Jia, J. K. Nørskov, Y. Roman-Leshkov, Y. Shao-Horn, B. D. Storey, S. K. Suram, S. B. Torrisi and J. H. Montoya, New challenges in oxygen reduction catalysis: a consortium retrospective to inform future research, Energy Environ. Sci., 2022, 15, 3775–3794.
21. Y. Yuan, J. Wang, S. Adimi, H. Shen, T. Thomas, R. Ma, J. P. Attfield and M. Yang, Zirconium nitride catalysts surpass platinum for oxygen reduction, Nat. Mater., 2020, 19, 282–286.
22. N. Haberkorn, J. Basbus, S. Suárez and M. Sirena, Nanoscale electronic inhomogeneity in ZrNx thin films growth by reactive sputtering at room temperature, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 769.
23. J. Adachi, K. Kurosaki, M. Uno and S. Yamanaka, Thermal and electrical properties of zirconium nitride, J. Alloys Compd., 2005, 399, 242–244.
24. S. Guo, J. Hu, S. Luo, Y. Zhang, Z. Zhang, P. Dong, X. Zeng, M. Xu, L. Han, J. Yuan, C. Zhang and Y. Zhang, Zr enhanced Fe, N, S co-doped carbon-based catalyst for high-efficiency oxygen reduction reaction, Int. J. Hydrogen Energy, 2022, 47, 8348–8358.
25. S. Zhao, J. Ma, R. Xu, X. Lin, X. Cheng, S. Hao, X. Zhao, C. Deng and B. Liu, Synthesis and Characterization of Zirconium Nitride Nanopowders by Internal Gelation and Carbothermic Nitridation, Sci. Rep., 2019, 9, 19199.
26. C. Lu, C. Cui and F. Peng, Stress–Strain Relations and Deformation Mechanisms of ZrN and HfN Superconductors, Cryst. Growth Des., 2022, 22, 1104–1109.
27. Y. Ohgi, A. Ishihara, K. Matsuzawa, S. Mitsushima, K. Ota, M. Matsumoto and H. Imai, Catalytic activity of zirconium based cathode without platinum for oxygen reduction reaction, 10th Polymer Electrolyte Fuel Cells Symposium (PEFC) Conducted Under the Auspices of the 218th Meeting of the Electrochemical-Society (ECS), Las Vegas, NV, 2010, p. 609-+.
28. M. Chisaka, A. Ishihara, H. Morioka, T. Nagai, S. Yin, Y. Ohgi, K. Matsuzawa, S. Mitsushima and K. I. Ota, Zirconium Oxynitride-Catalyzed Oxygen Reduction Reaction at Polymer Electrolyte Fuel Cell Cathodes, ACS Omega, 2017, 2, 678–684.
29. A. Banerjee, B. M. Ceballos, C. Kreller, R. Mukundan and G. Pilania, A first-principles investigation of nitrogen reduction to ammonia on zirconium nitride and oxynitride surfaces, J. Mater. Sci., 2022, 57, 10213–10224.
30. H. Liu, X. Jia, A. Cao, L. Wei, C. D’agostino and H. Li, The Surface States of Transition Metal X-ides under Electrocatalytic Conditions, J. Chem. Phys., 2023, 158, 124705.
31. S. Pan, H. Li, D. Liu, R. Huang, X. Pan, D. Ren, J. Li, M. Shakouri, Q. Zhang, M. Wang, C. Wei, L. Mai, B. Zhang, Y. Zhao, Z. Wang, M. Graetzel and X. Zhang, Efficient and stable noble-metal-free catalyst for acidic water oxidation, Nat. Commun., 2022, 13, 2294.
32. B. R. Wygant, K. Kawashima and C. B. Mullins, Catalyst or Precatalyst? The Effect of Oxidation on Transition Metal Carbide, Pnictide, and Chalcogenide Oxygen Evolution Catalysts, ACS Energy Lett., 2018, 3, 2956–2966.
33. S. D. Young, B. M. Ceballos, A. Banerjee, R. Mukundan, G. Pilania and B. R. Goldsmith, Metal Oxynitrides for the Electrocatalytic Reduction of Nitrogen to Ammonia, J. Phys. Chem. C, 2022, 126, 12980–12993.
34. B. Saha, A. Shakouri and T. D. Sands, Rocksalt nitride metal/semiconductor superlattices: A new class of artificially structured materials, Appl. Phys. Rev., 2018, 5, 021101.
35. S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, Electric Field Effects in Oxygen Reduction Kinetics: Rationalizing pH Dependence at the Pt(111), Au(111), and Au(100) Electrodes, J. Phys. Chem. C, 2020, 124, 14581–14591.
36. H. Li, J. Long, H. Jing and J. Xiao, Steering from electrochemical denitrification to ammonia synthesis, Nat. Commun., 2023, 14, 112.
37. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002.
38. D. F. Arias, Y. C. Arango and A. Devia, Study of TiN and ZrN thin films grown by cathodic arc technique, Appl. Surf. Sci., 2006, 253, 1683–1690.
39. P. Madkikar, D. Menga, G. S. Harzer, T. Mittermeier, A. Siebel, F. E. Wagner, M. Merz, S. Schuppler, P. Nagel, A. B. Muñoz-García, M. Pavone, H. A. Gasteiger and M. Piana, Nanometric Fe-Substituted ZrO2on Carbon Black as PGM-Free ORR Catalyst for PEMFCs, J. Electrochem. Soc., 2019, 166, F3032–F3043.
40. A. Kulkarni, S. Siahrostami, A. Patel and J. K. Norskov, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction, Chem. Rev., 2018, 118, 2302–2312.
41. C. F. Dickens, C. Kirk and J. K. Nørskov, Insights into the Electrochemical Oxygen Evolution Reaction with ab Initio Calculations and Microkinetic Modeling: Beyond the Limiting Potential Volcano, J. Phys. Chem. C, 2019, 123, 18960–18977.
42. M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H.-Y. Su, J. Rossmeisl and J. K. Nørskov, Tailoring the Activity for Oxygen Evolution Electrocatalysis on Rutile TiO2(110) by Transition-Metal Substitution, ChemCatChem, 2011, 3, 1607–1611.
43. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165.
44. M. Bajdich, M. Garcia-Mota, A. Vojvodic, J. K. Norskov and A. T. Bell, Theoretical investigation of the activity of cobalt oxides for the electrochemical oxidation of water, J. Am. Chem. Soc., 2013, 135, 13521–13530.
45. Z. Duan and G. Henkelman, Theoretical Resolution of the Exceptional Oxygen Reduction Activity of Au(100) in Alkaline Media, ACS Catal., 2019, 9, 5567–5573.
46. P. S. Lamoureux, A. R. Singh and K. Chan, pH Effects on Hydrogen Evolution and Oxidation over Pt(111): Insights from First-Principles, ACS Catal., 2019, 9, 6194–6201.
47. L. D. Chen, M. Urushihara, K. Chan and J. K. Nørskov, Electric Field Effects in Electrochemical CO2 Reduction, ACS Catal., 2016, 6, 7133–7139.
48. H. Wan, A. W. Jensen, M. Escudero-Escribano and J. Rossmeisl, Insights in the Oxygen Reduction Reaction: From Metallic Electrocatalysts to Diporphyrins, ACS Catal., 2020, 10, 5979–5989.
49. R. Ohnishi, M. Katayama, D. Cha, K. Takanabe, J. Kubota and K. Domen, Titanium Nitride Nanoparticle Electrocatalysts for Oxygen Reduction Reaction in Alkaline Solution, J. Electrochem. Soc., 2013, 160, F501–F506.
50. A. Seifitokaldani, O. Savadogo and M. Perrier, Density Functional Theory (DFT) Computation of the Oxygen Reduction Reaction (ORR) on Titanium Nitride (TiN) Surface, Electrochim. Acta, 2014, 141, 25–32.
51. J. Chen, K. Takanabe, R. Ohnishi, D. Lu, S. Okada, H. Hatasawa, H. Morioka, M. Antonietti, J. Kubota and K. Domen, Nano-sized TiN on carbon black as an efficient electrocatalyst for the oxygen reduction reaction prepared using an mpg-C3N4 template, Chem. Commun., 2010, 46, 7492–7494.
52. M. Tang, Y. Wang, L. Luo, S. Lu, X. Liu and J. Zhang, Synergistic effect of carbon-decorated hollow TiN architecture for boosting oxygen reduction reaction activity and durability, Appl. Surf. Sci., 2023, 612, 155846–155856.
53. T. Li, M. Li, M. Zhang, X. Li, K. Liu, M. Zhang, X. Liu, D. Sun, L. Xu, Y. Zhang and Y. Tang, Immobilization of Fe3N nanoparticles within N-doped carbon nanosheet frameworks as a high-efficiency electrocatalyst for oxygen reduction reaction in Zn-air batteries, Carbon, 2019, 153, 364–371.
54. N. Xue, J. Liu, P. Wang, C. Wang, S. Li, H. Zhu and J. Yin, Scalable synthesis of Fe(3)N nanoparticles within N-doped carbon frameworks as efficient electrocatalysts for oxygen reduction reaction, J. Colloid Interface Sci., 2020, 580, 460–469.
55. C. Defilippi, D. V. Shinde, Z. Dang, L. Manna, C. Hardacre, A. J. Greer, C. D'Agostino and C. Giordano, HfN Nanoparticles: An Unexplored Catalyst for the Electrocatalytic Oxygen Evolution Reaction, Angew. Chem., Int. Ed. Engl., 2019, 58, 15464–15470.
56. F. Pei, M. Chen, F. Kong, Y. Huang and X. Cui, In-situ coupling FeN nanocrystals with Fe/Fe3C nanoparticles to N-doped carbon nanosheets for efficient oxygen electrocatalysis, Appl. Surf. Sci., 2022, 587, 152922–152931.
57. W. Wang, L. Liu, W. C. Leng, L. L. Cui and Y. Gong, Coordination Polymer-Derived Fe(3)N Nanoparticles for Efficient Electrocatalytic Oxygen Evolution, Inorg. Chem., 2021, 60, 12136–12150.
58. J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29, 2044–2078.
59. P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
60. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
61. W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, 1133.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
63. B. Hammer, L. B. Hansen and J. K. Norskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
64. H. J. Monkhorst and J. D. Pack, Special points for brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
65. J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
66. M. Bajdich, M. Garcia-Mota, A. Vojvodic, J. K. Norskov and A. T. Bell, Theoretical Investigation of the Activity of Cobalt Oxides for the Electrochemical Oxidation of Water, J. Am. Chem. Soc., 2013, 135, 13521–13530.
67. J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Norskov, Solvation Effects for Oxygen Evolution Reaction Catalysis on IrO2(110), J. Phys. Chem. C, 2017, 121, 11455–11463.
68. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc01827j

---