Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Network dynamics: a computational framework for the simulation of the glassy state
Georgios G.
Vogiatzis
 *abc,
Lambèrt C. A.
van Breemen
*abc,
Lambèrt C. A.
van Breemen
 b,
Markus
Hütter
b,
Markus
Hütter
 b and
Doros N.
Theodorou
b and
Doros N.
Theodorou
 a
a
aSchool of Chemical Engineering, National Technical University of Athens, 9 Iroon Polytechniou, 15780 Zografou, Greece. E-mail: gvog@chemeng.ntua.gr
bProcessing and Performance of Materials, Department of Mechanical Engineering, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
cDutch Polymer Institute (DPI), P.O. Box 902, 5600 AX Eindhoven, The Netherlands
First published on 27th February 2023
Abstract
An out-of-equilibrium simulation method for tracking the time evolution of glassy systems (or any other systems that can be described by hopping dynamics over a network of discrete states) is presented. Graph theory and complexity concepts are utilised, alongside the method of the dynamical integration of a Markovian web (G. C. Boulougouris and D. N. Theodorou, J. Chem. Phys., 2007, 127, 084903) in order to provide a unified framework for dealing with the long time-scales of non-ergodic systems. Within the developed formalism, the network of states accessible to the system is considered a finite part of the overall universe, communicating with it through well-defined boundary states. The analytical solution of the probability balance equation proceeds without the need for assuming the existence of an equilibrium distribution among the states of the network and the corresponding survival and escape probabilities (as functions of time) are defined. More importantly, the study of the probability flux through the dividing surface separating the system and its environment reveals the relaxation mechanisms of the system. We apply our approach to the network of states obtained by exploring the energy landscape of an atomistically detailed glassy specimen of atactic polystyrene. The rate constants connecting different basins of the landscape are evaluated by multi-dimensional transition-state-theory. We are able to accurately probe the appearance of the δ- and γ-subglass relaxation mechanisms and their relevant time-scales, out of atomistic simulations. The proposed approach can fill a gap in the rational molecular design toolbox, by providing an alternative to molecular dynamics for structural relaxation in glasses and/or other slow molecular processes (e.g., adsorption or desorption) that involve very distant time-scales.
Design, System, ApplicationWe report on the development of a rigorous out-of-equilibrium framework for simulating, at a molecular level, the time evolution of glassy systems (or any other systems that can be described by hopping dynamics in a network of discrete states). Network dynamics offers a computationally efficient alternative to standard molecular dynamics for simulating systems evolving through infrequent transitions, thus extending the molecular design toolbox. A system represented by a finite set of explored states communicates with its environment in state space through a well-defined dividing surface consisting of boundary states; this communication, in the form of the probability efflux, reveals the relaxation mechanisms of the system. As a proof of concept, we study the elementary structural relaxation events of long-chain glassy atactic polystyrene below its glass transition temperature. The appearance of the δ- and γ-subglass relaxation mechanisms and their relevant time-scales are probed at three different temperatures based on atomistic calculations and compared to experimental data obtained by dielectric spectroscopy and NMR experiments. The methodology developed can serve as a starting point for the molecular engineering design of materials (e.g., glassy polymers) with tailored relaxation processes in the frequency–temperature domain, hence with controlled plasticity, toughness and permeability to small molecules. |
1 Introduction
Simulating the slow dynamics of the glassy state at an atomistic scale remains a mostly unsolved problem; the time-scales of structural relaxation processes in the glassy state are out of reach (and will continue to be) for the modern computer hardware and software. The glassy state is not in thermodynamic equilibrium, unlike the two states between which it is often considered intermediate: the crystalline (if it exists) and the liquid. It is often speculated in the literature that there exists an ideal glassy state.1,2 The existence of an ideal glassy state, if that were to be under true thermodynamic equilibrium, would probably alleviate part of the methodological and computational burden to simulate the time-evolution of a glassy system. However, the fact that many physical properties of glasses depend on their history of formation and change (slowly) with time cannot fit into the picture of an ideal glassy state. Thus, a molecular simulation approach for studying (organic/inorganic; low/high molecular-weight) glasses should eventually deal with the out-of-equilibrium evolution of the system.While the lack of fundamental understanding has not hindered the technological exploitation of glassy polymers (most engineering plastics are amorphous solids), a bottom-up understanding of the ageing and relaxation mechanisms in the glassy state will enable the rational design of materials for extreme applications based on thoughtful molecular modelling. Molecular dynamics (MD) is widely employed as the standard method of molecular simulations of liquids. Nevertheless, it is of limited assistance in the amorphous glassy state,3 where the times of e.g. volume or enthalpy relaxation are comparable to or exceed the universally accepted 100 s-mark for the relaxation time close to the glass transition temperature.4,5 In order to keep the atomistic description of the system, within the framework of classical mechanics, its time evolution should be coarse-grained at the level of infrequent hopping events between different microscopic states, i.e., one should be able to discern between fast equilibration of the system within a constrained neighbourhood of its configuration space and slower diffusion to different neighbourhoods.
As postulated long ago by Goldstein,6 and observed by MD simulations,7 glassy polymer systems evolve by discrete transitions among basins of their potential energy landscape (PEL). This view provides a convenient framework for developing a method that will track the infrequent transitions governing the long time-scale evolution of the system. According to Stillinger and Weber,8,9 the glassy system spends most of its time fluctuating in the vicinity of local potential energy minima (i.e., “inherent structures”, ISs). For an ergodic system at equilibrium, a macroscopic observable could be rigorously cast as the sum of the Boltzmann-weighted properties calculated at the individual basins of the PEL. For an out-of-equilibrium system, such as a polymer glass, the occupancy probability of every basin becomes time-dependent. Moreover, there is a well-defined formation history that led a glassy specimen to get trapped in a single initial basin (e.g., by quenching from the melt state). Thus, the physical ageing process is envisioned as the time-dependent progression of traversing several basins.
Within the PEL framework, the dynamics (at long time-scales) is governed by hops from one basin to another. Transitions between basins, defined by individual ISs on the PEL, are hindered by energy barriers separating the basins. We assume that the elementary structural relaxation events (from basin to basin) are governed by the first-order saddle points of the energy with respect to atomic coordinates, i.e., transition states as defined by Munro and Wales.10 Starting out of the basin in which the system found itself after quenching into the glassy state, we can discover transition states in its vicinity by a combination of eigenmode-following and activation relaxation techniques, either on its potential energy surface,11 or on a free energy surface dictated by any combination of external stress/strain conditions.12 Full transition paths are constructed off of the saddle points by probing the steepest descent trajectories leading to the connected basins, and rate constants for the elementary structural transitions are obtained using multidimensional transition-state theory. All relevant thermodynamic properties, e.g., the free energy of the system at the minima and saddle points, are calculated from the potential energy and the vibrational frequencies, invoking a quasi-harmonic approximation (with analytical derivatives of the potential energy).13 The complete knowledge of the (potential or free) energy landscape is clearly out of reach. There will always be concerns that estimates of the out-of-equilibrium time-dependent properties are inadequate. By employing a random sampling procedure for exploring the energy landscape,11 we mitigated the problem and managed to achieve sampling of a very wide range of barrier heights and the corresponding transition rate constants.
A particularly attractive method for addressing the long time-scales of the glassy state is a variant of the metadynamics framework14,15 developed by Yip and his co-workers.16,17 Within metadynamics the system is repelled by the minimum in which it resides by adding a smooth energy penalty function. Its free energy is then minimised until a new minimum is found which is not directly affected by the penalty function. By repeating the combination of “lifting” (i.e., repulsion out of an energy minimum) and “relaxation” steps, a random walk on the PEL is effectively created. In essence, the memory of all previous penalties should be conserved during the simulation, but the complexity of the landscape is such that even a memory of a few steps is sufficient for an efficient sampling.
The tessellation of the PEL into basins of attraction, each one represented by the relevant IS located at its bottom, provides a rigorous way of coarse-graining the time evolution of the system as a hopping process over a network of discrete states. This idea was brought forward by Boulougouris and Theodorou,18 who devised a procedure for analytically solving the master equation over a Markovian network of states. Their method starts from a single state and progressively augments the network of states on-the-fly, invoking concepts of mean first-passage time (MFPT). Later, Boulougouris and Theodorou19 developed an elegant geometric approach for analysing the observables in terms of eigenvectors of the rate constant matrix. More recently, Boulougouris20 extended this approach to mapping the equilibrium thermodynamic states on Euclidean vectors, thus providing a geometric representation of equilibrium (and near equilibrium) classical statistical mechanics.
Mathematical techniques for dealing with processes involving mean first passage times were developed several decades ago within the framework of non-equilibrium physical chemistry and chemical physics.21–23 These concepts have since flourished in a very diverse spectrum of applications, ranging from reactions involving fluorescent trap states24–26 to cellular response out of biochemical reaction networks.27,28 Since the MFPT expresses an average timescale for a stochastic event to occur for the first time, it provides a rigorous coarse-graining scheme for mapping a multi-step (multi-stage) kinetic process to a single timescale, i.e., the time needed for the system to arrive at a final state, having started at some other state of the network.
We have been building a framework for understanding and predicting the glassy dynamics which gets unified by the present work. In the process, we first studied the networks of states visited by an ageing specimen by means of MD simulation in the glassy state,7 revealing the topological features of the network that we should reproduce by a systematic exploration of the energy landscape. We then developed efficient algorithms for locating minima and saddle points on the free energy landscape of a classical system described by molecular forcefields.11–13
In this work, we present an out-of-equilibrium molecular simulation approach capable of accessing the long-timescales of the glassy state by coarse-graining the time evolution of glassy systems as a traversal of a network of discrete states. First, we present the fundamental aspects of our formulation in a thorough and pedagogical way. The solution of the master equation is a well-known procedure. However, our formulation improves aspects of previous attempts and unveils new facets of the solution of the master equation in a network where absorbing states are present. Then, we discuss the significance of studying and analysing the probability flux towards the boundary states, which, to the best of our knowledge, has not been studied earlier. Finally, we introduce a measure of the ability of the developed network to faithfully represent the long-time dynamics of the simulated system, allowing us to judge the quality of the finite-sized network representation developed. By combining the exploration of the energy landscape around local minima with the description of dynamics by means of a master equation over an expanding network of states, we have managed to simulate ageing atactic polystyrene (aPS) specimens for times up to ms under realistic conditions of temperature and pressure. We can then identify the time-scales of the δ- and γ-subglass relaxations of atactic polystyrene by studying the boundary enclosing our finite-sized networks of states. Our findings complement the long-held, but somewhat neglected belief that structural relaxation in glasses can occur via secondary relaxation processes.29,30
2 Method
2.1 Coarse-graining dynamics in a network of transitions
In this work we consider the example of a polymer glass formed by quenching an equilibrium melt configuration. By subjecting the melt configuration to a prescribed cooling protocol, T(t) at constant pressure, we progressively lock (at temperatures lower than the glass transition temperature) the configuration in a specific basin of its potential-energy hypersurface. The tessellation of the energy hypersurface in basins surrounding its local minima, as proposed by Stillinger and Weber,8 provides a rigorous way of introducing the idea of discrete states, which is central to our formulation. By repeating the vitrification procedure with a different initial configuration, we may end up in a different basin, simply because the melt was in a different configuration at the beginning of the process. From an experimental point of view, changing the quenching rate (e.g. by cooling with liquid nitrogen) dramatically changes the dynamical behaviour of the glass. The properties of glasses depend on their formation history; the memory of the processes involved in the formation of the glass fades slowly with time. The effect of the history of formation on the dynamical properties of the produced glasses has been extensively studied by Grigoriadi et al.31,32 who have employed different quenching and ageing protocols, exploiting a state-of-the-art liquid-nitrogen cooling device for vitrifying polystyrene specimens before subjecting them to dielectric spectroscopy measurements.We can define a probability PformI = PI (t = 0) that the considered formation history leads to the basin around a specific inherent structure that has been labelled with I. Calculation of the exact formation probability is a tedious task. In lieu of the exact, process-dependent, PformI, we will use PI(0) = 1 as the initial condition for the time evolution of the specimen in the glassy state.
Despite the fact that the initial basin (where we arrived by quenching) is surrounded by energy barriers, the specimen will slowly move out of it to other parts of its configuration space. In order to emulate this process we explore the energy landscape by forcing the system to discover first-order saddle points in the vicinity of the initial basin. Detailed discussions of the methods developed for scanning the potential and the free energy landscape of aPS can be found in ref. 11 and 12, respectively.
While our approach is not limited to ageing glassy polymer specimens, we have to restrict ourselves to processes for which the transition rates depend only on the instantaneous state of the system, and not on the entirety of its history. Such memory-less processes are known as Markovian and are applicable to a wide range of systems. MD trajectories of the same glassy system7 have shown that a separation of time-scales holds, i.e., the system equilibrates within a basin quickly, while going out of that to a neighbouring one is an infrequent event. Moreover, a hierarchy of topological organisation of the basins of the PEL has been observed, with fast-communicating basins forming local neighbourhoods (i.e., “metabasins”) over longer time-scales. When the rate constant distribution for elementary transition events is very broad,11 a kinetic Monte Carlo (kMC) simulation may become trapped within clusters of states communicating via fast transitions, prohibiting the sampling of the more infrequent transitions out of the clusters, which govern the long-time evolution of the system (e.g., a glass or biomolecule27).
2.2 Graph representation of the network of transitions
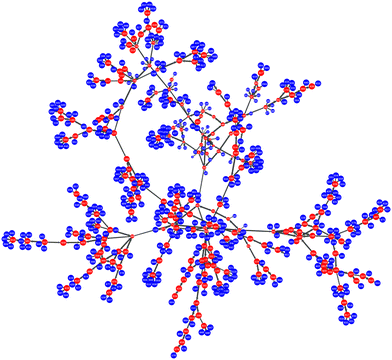
As elaborated in ref. 7, we envision the network of basins (and corresponding ISs) as a directed graph, whose vertices are the ISs and whose edges are the transitions between ISs (probed by exploring the PEL11). Our edges are directed: the edge eij ≡ ei→j is inherently different from the reverse edge, eji (different free energy barrier and therefore different rate constants for the pair of transitions). A two-dimensional view of an indicative network (graph) is presented in Fig. 1. Laying down the graph of the network on a plane allows for easy visual inspection and provides immediate insight into the basic features of its topology. However, the effectiveness of the visual representation strongly depends on the artistic taste of the drawing. An insightful planar view should contain as little edge crossing as possible and should evenly fill the available area with vertices. This problem has been addressed in the literature33 and many approaches have been proposed. We choose the solution suggested by Hu,34i.e., producing the layout by modelling the graph-drawing problem through a physical system of bodies with forces (harmonic springs) acting between them on the plane (“force-directed” algorithm). The algorithm finds a good placement of the bodies in two dimensions by minimising the energy of the system and is equivalent to our approach to a completely different problem, that of randomly dispersing grafting points for polymer chains on the surface of a nanoparticle.35 Our graph-theoretic calculations rely on the LEMON C++ library36 and the “graph-tool” python library developed by Tiago P. Peixoto.372.3 Analytical solution of the master equation
We consider the solution of the master equation in a finite network of states. The network, which can be built up by following any procedure, is considered as an exact representation of the “universe” within which the system can find itself. The representation becomes increasingly accurate by considering more states. It is divided into two subsets, the first one being the set of explored states, E, for which there is enough knowledge of their local environment, and the subset of boundary states, B, for which there is no knowledge of their surroundings (see Fig. 1). In other words, following the concept of thermodynamics, universe = system + surroundings, if the system would escape out of the set E, it could only visit one of the states belonging in B. Thus, the set B represents the immediate environment of the set E. We will denote with |E| and |B| the cardinalities (numbers of elements) of sets E and B, respectively.Our starting point is to restrict the original master equation to the subset E of states, where the states on its boundary, B, are turned into artificial absorbing states in order to keep track of the probability that flows out of E.
Following Boulougouris and Theodorou,18 we consider the conditional probability Qi(t; B) of observing the system visiting one of the explored states, viz., state i at time t starting from an initial distribution, given the additional constraint that the system has not visited any state out of the set B of predefined states (which does not contain i). Once states and inter-state rate constants are known, the system evolution at the state level can be tracked by solving the following master equation for Qi(t; B), where the boundary states are treated as absorbing:
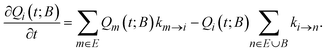 | (1) |
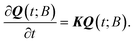 | (2) |
Assuming that time-scale separation renders the transitions infrequent events,38 the transition rate constants ki→j are independent of time and the evolution of the system is a Poisson process. Qi(t; B) is the probability of occupancy of state i at time t, under the constraint that the system gets absorbed by any of the states of its current boundary, B. The time-dependent Q(t; B) in the matrix representation of eqn (2) has all the Qi(t; B) as elements (the dimensionality of the probability vector Q is equal to the number of explored states, |E|). According to eqn (1) this changes as a result of influx of probability from all other explored states, and efflux of probability to both explored and boundary states.
The off-diagonal elements of K contain contributions from transitions connecting explored states, i.e., Kji = ki→j with i, j ∈ E. The diagonal elements, 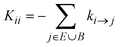 , contain contributions from within the set of explored states as well as outgoing (from E to B) contributions that cross the boundaries of the system, i ∈ E, j ∈ E ∪ B. There is no influx from B to E. In other words, the use of absorbing boundary conditions implies that all kj→i need not be considered for all j ∈ B and i ∈ E; they are calculated during the exploration of the energy landscape but they are not needed in the definition of K. The rate constant matrix K, as defined by eqn (1), is not symmetric, nor stochastic. Our formulation differs from the one of Wei and Prater39 because our network is not finite; the diagonal of K contains “leakage” terms out of the explored set E and into the boundary set B.
, contain contributions from within the set of explored states as well as outgoing (from E to B) contributions that cross the boundaries of the system, i ∈ E, j ∈ E ∪ B. There is no influx from B to E. In other words, the use of absorbing boundary conditions implies that all kj→i need not be considered for all j ∈ B and i ∈ E; they are calculated during the exploration of the energy landscape but they are not needed in the definition of K. The rate constant matrix K, as defined by eqn (1), is not symmetric, nor stochastic. Our formulation differs from the one of Wei and Prater39 because our network is not finite; the diagonal of K contains “leakage” terms out of the explored set E and into the boundary set B.
We can construct a negative definite matrix, ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) , out of K with the same eigenvalues, by following the standard procedure of scaling the rate constants with equilibrium probabilities.40 This is usually done by assuming the existence of an equilibrium distribution, i.e., the existence of a single zero eigenvalue for K. Then, by the application of the detailed balance condition, i.e., Pi(∞) ki→j = Pj(∞) kj→i, a symmetric reduced rate constant matrix,
, out of K with the same eigenvalues, by following the standard procedure of scaling the rate constants with equilibrium probabilities.40 This is usually done by assuming the existence of an equilibrium distribution, i.e., the existence of a single zero eigenvalue for K. Then, by the application of the detailed balance condition, i.e., Pi(∞) ki→j = Pj(∞) kj→i, a symmetric reduced rate constant matrix, ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) , is obtained. The diagonalization of a symmetric matrix is faster and more robust, since its symmetry ensures that eigenvalues are real and there is no need to perform computations involving complex numbers.41 However, in our formulation, there is no equilibrium distribution for the conditional probabilities Q; the system is continuously leaking to its boundary. Within our non-equilibrium framework, in order to make K symmetric, we consider the evolution of the system within the set of explored states E only, ignoring any connections to the boundaries. If the description of the system were complete within the current set of explored states, the solution below would fully describe the dynamics of the network. Let us consider the probabilities, PEi(t), of occupancy of every explored state, i ∈ E, as a function of time. Within the set E, the detailed balance condition holds, leading to an equilibrium distribution among states at infinite time:
, is obtained. The diagonalization of a symmetric matrix is faster and more robust, since its symmetry ensures that eigenvalues are real and there is no need to perform computations involving complex numbers.41 However, in our formulation, there is no equilibrium distribution for the conditional probabilities Q; the system is continuously leaking to its boundary. Within our non-equilibrium framework, in order to make K symmetric, we consider the evolution of the system within the set of explored states E only, ignoring any connections to the boundaries. If the description of the system were complete within the current set of explored states, the solution below would fully describe the dynamics of the network. Let us consider the probabilities, PEi(t), of occupancy of every explored state, i ∈ E, as a function of time. Within the set E, the detailed balance condition holds, leading to an equilibrium distribution among states at infinite time:
| PiE(∞)ki→j = PiE(∞)kj→i | (3) |
Given the equilibrium probabilities of the explored states, PEi(∞), the solution of eqn (1) can be developed analytically, with inspiration from the early work of Wei and Prater on the kinetics of a network of reversible chemical reactions.39 First, we transform the state probability vector Q(t; B) into a reduced state probability vector ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0051_0303.gif) (t; B) with elements:
(t; B) with elements:
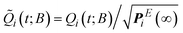 | (4) |
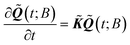 | (5) |
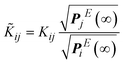 | (6) |
![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) is symmetric by virtue of the microscopic reversibility condition, eqn (3). The matrix is negative definite; it is proven that all eigenvalues of K, λm, with 1 ≤ m ≤ |E| are real negative numbers (see Appendix B).
is symmetric by virtue of the microscopic reversibility condition, eqn (3). The matrix is negative definite; it is proven that all eigenvalues of K, λm, with 1 ≤ m ≤ |E| are real negative numbers (see Appendix B). ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) has the same eigenvalues as K, i.e., all eigenvalues of K are negative, indicating that all conditional probabilities decay to zero for long times, i.e., Qi(∞; B) = 0. The conditional probability of the system occupying any i in the explored set (without having hit any boundary state) fades to zero at infinite time, since the set E is an open system.
has the same eigenvalues as K, i.e., all eigenvalues of K are negative, indicating that all conditional probabilities decay to zero for long times, i.e., Qi(∞; B) = 0. The conditional probability of the system occupying any i in the explored set (without having hit any boundary state) fades to zero at infinite time, since the set E is an open system.
Finally, the solution to the reduced master equation can be written as:39,40
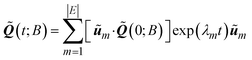 | (7) |
![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) , respectively. Once
, respectively. Once ![[Q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0051_0303.gif) (t) has been determined, the state probabilities Q(t) can be calculated via
(t) has been determined, the state probabilities Q(t) can be calculated via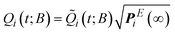 .
.
2.4 Probability flux towards the boundary states
A key ingredient of our formulation is the probability flux out of the set of explored states, E towards the set of boundary states B. We define the rate of reaching a specific boundary state j ∈ B between t and t + dt as:27,40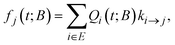 | (8) |
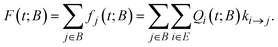 | (9) |
2.5 Escape and survival probabilities
Since by definition, the rate of reaching an absorbing state j ∈ B in a time interval [τ, τ + dτ] is fj(τ)dτ, the probability of having reached j ∈ B by time t is: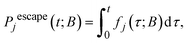 | (10) |
There are many escape routes from E to B, each one going via a particular state j ∈ B. Thus, we can define the total escape probability, i.e., the probability that the system has escaped to B by time t:
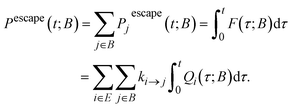 | (11) |
Apart from the escape probability, there is the complementary probability of the system having survived (“being alive”) after time t, i.e., that the system has not reached any of the boundary states (of B) up to time t,
| Palive(t; B) = 1 − Pescape(t; B). | (12) |
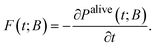 | (13) |
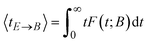 | (14) |
In the limit of t → ∞, the escape probability defined by eqn (11) takes the form:
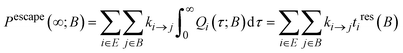 | (15) |
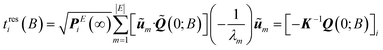 | (16) |
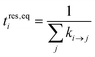 | (17) |
The summation of the residence times defines a mean exit time in the spirit of van Kampen40
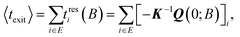 | (18) |
An intriguing feature of eqn (15) is that Pescape approaches unity as t → ∞, but it can have a limiting value that is smaller than one. By focusing on the boundary states, rather than on explored states, eqn (15) takes the following form:
 | (19) |
Please note that the sum of the conditional probabilities Qi(t; B) at time t does not provide an estimate of the probability of the system being “alive” at time t. By construction, if there is at least one state in B, all Qis decay to zero, irrespective of the size of the set of explored states (since K in eqn (2) is negative definite). Instead, the survival probability introduced by eqn (12) has an asymptotic finite value Palive(∞; B) for the system trapped within the set of explored states at long time-scales, even for finite-sized sets E, as seen by analysing Pescape(∞; B).
2.6 Expanding the network of states
The key to our approach is to build up the network of explored states by adding each time a new as yet unexplored state, i.e., a state jselect ∈ B is chosen to be included in E by means of dynamical sampling, aiming at increasing the probability of finding the system trapped within the network of explored states, E. The basin of this state is then explored in order to find neighbouring transition states (saddle point search) and the local minima at the other end of the transition are added as B-states. To this end we follow the selection proposed by Boulougouris and Theodorou18 which we briefly describe below.A time tselect is selected from the distribution of first passage times:
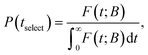 | (20) |
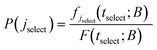 | (21) |
To summarise, in order to calculate the probability density of the first passage times (FPT) to the set B, from a state i ∈ E, one needs to solve the master equation for the evolution of the system with the absorbing boundary conditions at every j ∈ B, to obtain the probability current fj(t; B) into the absorbing state j, which then provides the FPT distribution through the aforementioned relations. Once jselect is selected, all states connected to it must be determined. The determination of all neighbours is performed by locating transition states in its vicinity which are then linked to new local minima through the creation of reaction paths.11
For a realistic description of the dynamics of the system, it is crucial that the full range of the relevant energy barriers is sampled, since the relevant rate constants will be included in the rate constant matrix of the network of states. As we pointed out and thoroughly discussed in our previous work11 the sampling of the transition states on the energy landscape (by directing the search along randomly chosen eigenvectors of the Hessian) is as unbiased as possible. The combination of methods employed therein allows for a very wide spectrum of possible transitions to be sampled. The signatures of the relaxation mechanisms are already present in the distributions of transition rate constants. The peaks of the distributions, indicating elementary structural relaxation events, are then translated, through the dynamic importance sampling, eqn (20) and (21) to distinct peaks of the efflux current, as we will see in the following section. Thus, accumulating realistic distributions of rate constants for the elementary structural transitions is of ultimate importance for reproducing the actual dynamics of the system under consideration.
3 Systems studied
The results presented in the following have been obtained from networks of states of a single 300-mer atactic PS system generated at temperatures of 300, 250 and 200 K. The generation of the initial configurations in the glassy state followed the same procedure as described in ref. 11 and 12: proper equilibration through coarse-grained connectivity altering Monte Carlo in the melt state, reverse mapping of the equilibrated configuration to the united-atom representation43 and finally molecular dynamics simulation in the melt state and quenching to the glassy state. Five independent melt configurations were used for obtaining an equal number of glassy configurations at each of the three temperatures of interest. The relevant results have been averaged by arithmetic (not equilibrium-Boltzmann) averaging.13,44 We have extensively employed the molecular model of Lyulin and Michels45 in the past and we use it for the present study, too.Rate constants for basin-to-basin transitions are calculated under the imposition of atmospheric pressure, as elaborated in ref. 12, i.e., by locating stationary points on the Gibbs energy landscape (restricted thermodynamic equilibrium imposed on both local minima and transition states). Under the imposition of the Gibbs energy, the i → j transition is inhibited by the barrier:
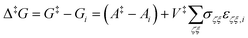 | (22) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) term included in the definition of the Gibbs energy in our previous studies (cf. Lempesis et al.46 and Vogiatzis et al.12) vanishes since for both states i and j one should employ the volume of the reference configuration (
term included in the definition of the Gibbs energy in our previous studies (cf. Lempesis et al.46 and Vogiatzis et al.12) vanishes since for both states i and j one should employ the volume of the reference configuration (![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) = ‡) that is shared by all states of the triplet. The relevant discussion can be found in ref. 12. Finally, we should note that by using the configuration at the saddle point as the reference configuration for defining the strain tensor, the last term on the right-hand side of eqn (22) appears with a positive sign. The interested reader is referred to ref. 12 and 13 for the details of the thermodynamic derivation. Eventually, the transition rate constant from state i to state j, through the transition state ‡ becomes
= ‡) that is shared by all states of the triplet. The relevant discussion can be found in ref. 12. Finally, we should note that by using the configuration at the saddle point as the reference configuration for defining the strain tensor, the last term on the right-hand side of eqn (22) appears with a positive sign. The interested reader is referred to ref. 12 and 13 for the details of the thermodynamic derivation. Eventually, the transition rate constant from state i to state j, through the transition state ‡ becomes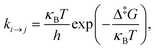 | (23) |
4 Results
4.1 Topological features of the generated networks
Before studying the dynamics of the system over the network of discrete states, we characterise its topology, that is, the connectivity between PEL basins at different scales of the underlying network of inherent structures. In our previous work7 we showed that the time trajectories of an ageing glassy polymer specimen of the same characteristics (atactic polystyrene of 30 kg mol−1 at T = 300 K), simulated by molecular dynamics, generate a structured walk on its PEL landscape. The network of states visited in the course of the time resembled the class of “small-world” (SW) networks that are frequently encountered in real-life problems and ignited the revolution of complexity science. Watts and Strogatz47,48 discovered that many networks behave like “small worlds” (SW), i.e., the neighbours of a specific vertex are very likely to be neighbours themselves, like in social networks (the common saying of “six degrees of separation”). The observation takes into account the mere connectivity of the network, without referring to the existence of any kind of physical distance between the vertices. The SW networks are in many ways different from randomly-connected networks, where no emerging patterns can be identified.In Table 1 we report the global and local clustering coefficients for networks of different sizes (in terms of the count of total states), generated by our network dynamics approach. Watts, Newman and Strogatz48–50 defined a clustering coefficient, which in the present study we are going to call “global” as:
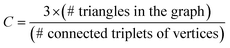 | (24) |
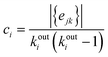 | (25) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eij is an edge of the graph}. For a directed graph, ejk is distinct from ekj, and the degree of outgoing connections is used in the denominator (in our network dynamics approach both ejk and ekj are present in the network by construction). Both clustering coefficients are normalised by definition.50 They become unity for a fully connected graph (every vertex is connected to any other vertex) and have typical values ranging from 0.1 to 0.5 in many small-world real-life networks.52
eij is an edge of the graph}. For a directed graph, ejk is distinct from ekj, and the degree of outgoing connections is used in the denominator (in our network dynamics approach both ejk and ekj are present in the network by construction). Both clustering coefficients are normalised by definition.50 They become unity for a fully connected graph (every vertex is connected to any other vertex) and have typical values ranging from 0.1 to 0.5 in many small-world real-life networks.52
| Size of the network (states) | Global clustering coefficient | Local clustering coefficient | Equivalent random network (global clustering coefficient) |
|---|---|---|---|
| 100 | 0.158983 | 0.333333 | 0.0286007 |
| 1000 | 0.1466336 | 0.1614005 | 0.00302781 |
| 2000 | 0.1429022 | 0.152981 | 0.00236507 |
All networks considered in Table 1 exhibit the clustering characteristics of small-world networks, i.e., clustering coefficients on the order of 0.1. We have studied the clustering at several stages of the expansion of the network (from 100 to 2000 states). In all cases both clustering coefficients are at least an order of magnitude higher than the average clustering coefficient of a random network, which can be analytically estimated48 as C ≃ 〈ci〉 ≃ k/n where k is the average vertex degree of the network and n the number of vertices. Initially, the local clustering coefficient deviates from the global one since it is very sensitive to the environment encompassing every state (vertex) of the network. We have already seen that the local clustering coefficient exhibits fluctuations for small networks.7 As the network expands they both converge to the same value. The asymptotic value obtained by the larger networks is close to 0.15 that is remarkably close to the value calculated for networks formed by tracking the states visited in the course of a MD trajectory in the glassy state, of the same system under the same conditions (temperature and pressure).7 The connectivity of the network has an inherent fractal nature, i.e., despite the fact that the MD trajectories could not go over many of the higher-lying transitions (which we are able to probe by saddle point search), the relative number of connections with respect to the total number of possible connections follows the same scaling rule. Finally, the topological features of the network of states do not depend on the temperature applied for the exploration. The temperature does not affect the underlying connectivity of the energy landscape; it only affects the magnitude of the rate constants.
4.2 Rate constants of the transitions of the network
We have thoroughly analysed the distribution of rate constants of elementary relaxation events on the (free) energy landscape of glassy atactic polystyrene in our previous studies.11,12 In this work we are interested in elucidating the connection between the spectrum of individual rate constants of elementary relaxation events on the Gibbs energy landscape and the appearance of ageing phenomena as the result of collective relaxation, i.e., involving all individual elementary relaxation events.The application of the saddle-point searching algorithms developed in our earlier studies11,12 allowed us to sample 4280 transitions on the energy landscape of our aPS system. The relevant distribution of transition-rate constants is depicted in Fig. 2. It is very broad, spanning thirty orders of magnitude on the inverse-time scale, necessitating the use of bins of equal width in a logarithmic scale, with the proper mapping for the density distribution. For the system studied, whose mean first-passage time is on the order of 10−5 s, we can split the distribution into additive contributions emanating from connections within the set of explored states, i.e., ki→j with i, j ∈ E, presented in subfigure (a), outgoing connections from the set of explored states and into the set of boundary states, ki→j with i ∈ E and j ∈ B, included in subfigure (b), and incoming connections from the set of the boundary states, i.e., ki→j with i ∈ B and j ∈ E. We should note that the latter class of transitions is not utilised during the exploration and augmentation of the network, since the boundary states are treated as absorbing (i.e., no connections from the B set to the E set of states). The overall distribution, marked in a dashed black line in all figures, can be compared with Fig. 10 of ref. 11 where we have thoroughly analysed its main features. In that work, it has been shown that the peaks of the distribution are located close to the macroscopically estimated (inverse) time-scales of the relaxation processes of aPS. However, the distribution is fuzzy and discerning its peaks is not easy.
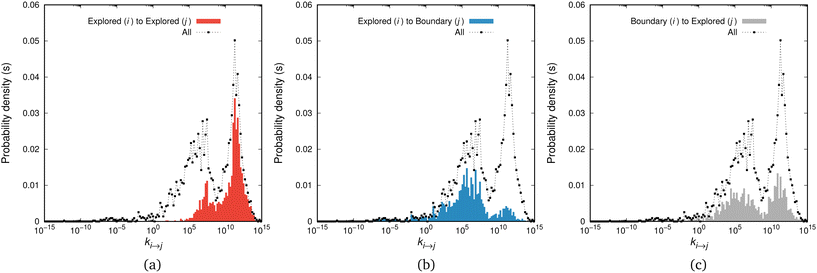 | ||
Fig. 2 Rate constant distributions, p(ki→j), for transitions connecting (a) explored to explored states, (b) explored to boundary states, and (c) boundary to explored states. The bins are equally spaced on the logarithmic axis and the distributions are normalised such that ∫p(ki→j)d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ki→j/s−1)= 1 is ensured for all transitions, i.e., the integral under the common black dashed line in all figures is unity, while the integrals of the coloured bars in (a), (b) and (c) yield the fraction of the relevant transitions (namely, 0.38 for the explored-to-explored transitions, 0.31 for the explored-to-boundary and 0.31 for the boundary-to-explored transitions). For a thorough analysis of the rate constant distribution the interested reader is referred to ref. 11. (ki→j/s−1)= 1 is ensured for all transitions, i.e., the integral under the common black dashed line in all figures is unity, while the integrals of the coloured bars in (a), (b) and (c) yield the fraction of the relevant transitions (namely, 0.38 for the explored-to-explored transitions, 0.31 for the explored-to-boundary and 0.31 for the boundary-to-explored transitions). For a thorough analysis of the rate constant distribution the interested reader is referred to ref. 11. | ||
The removal of a boundary state from the set B and its addition to the set of explored states is a time-dependent process. At the beginning of the augmentation of the network, states that can be reached via fast connections with their neighbours in the set of explored states are preferred for the expansion of the network. As the network grows larger, progressively slower connections are explored. This is evident in Fig. 2, where most transitions in the range [1010, 1015] s−1 have been explored by the system. The blue bars in Fig. 2(b) in this range are significantly lower than the overall distribution, almost exhausted. These connections are now present in Fig. 2(a), i.e., they are now found in the set of explored states. As the augmentation of the network proceeds, more connections (independent of their time-scale) are added to the network, but only those whose time-scale is commensurate to the mean first passage time of the network are preferred to be explored at later steps, e.g., a connection with 1/ki→j ∼ 104 s will be more probable to be chosen for exploration by a network with a mean first-passage time of 103 s, compared to a faster transition with ki→j ≃ 1012 s−1. Moreover, extremely slow connections (e.g., ki→j ∼ 10−15 s−1) are included in the network but they will most likely not be sampled.
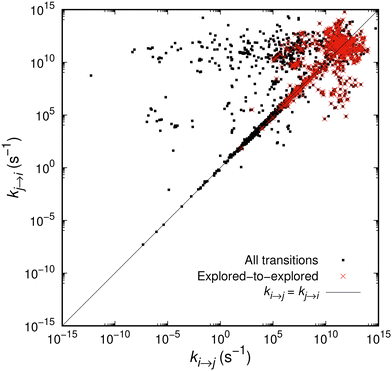
In Fig. 3 we plot the rate constant kj→iversus the rate constant ki→j, where i and j are ordered in such way that i corresponds to the state closer to the initial state (where the system arrived by quenching) of the network. In other words, if the explored state at t = 0 is found in the middle of our planar graph representation, an arrow i → j will always point outwards, towards the set of boundary states, B. The black points, corresponding to all transitions sampled during the expansion of the network, are clearly arranged on two horizontal bands, one around 1012 s−1 and another one around 105 s−1. This is consistent with the positions of the peaks in Fig. 2 and reflects the physical processes of relaxation. A peculiar pattern is observed consisting of two discrete groups of data points. The first one of them represents the “symmetric” transitions, where the barrier faced by the system in its forward and backward moves is comparable, i.e., ki→j ≃ kj→i; this is the straight line running along the diagonal of the figure. Then, there is a second but less pronounced group of transitions, where kj→i > ki→j mostly and is manifested by the cloud of points which are concentrated in the upper left triangle defined by the diagonal. These transitions have a backward rate constant on the order of 105 and 1012 s−1, while the forward rate constants are up to 15 orders of magnitude smaller.
The red points in Fig. 3 correspond to the rate constants of the transitions incorporated in the network of the explored states E. They form a remarkably symmetric sub-pattern, i.e., there is no bias in our calculations within the explored set depending on closeness of the initial state. On the contrary, there seem to be many explored-to-boundary and boundary-to-explored connections that are slower on the way out (away from the initial state) than on the way in. This probably means that our exploration accesses basins of higher free energy, from which the system would tend to go quickly back to the explored set. A boundary formed by slow outgoing transitions (and fast incoming) was anticipated by the distribution of rate constants in Fig. 2(b) and (c). It is a desirable feature indicating that the system is allowed to climb steep slopes surrounding it, from where it can easily fall back to the explored set. Moreover, slower transitions to the outside world increase the probability of the system remaining alive as t → ∞ (see eqn (15)); this is also desirable, since it provides a faithful description of long-time dynamics.
4.3 Rate constant matrix of the network
Diagonalization of the rate constant matrix of eqn (2) at a sufficiently large expansion of the network (i.e., long enough time-scales) provides a set of (inverse) time-scales that correspond to the collective redistribution of the system among states. While the distribution of the rate constants of individual transitions, Fig. 2, provides insight into the spectrum of time-scales for elementary transitions to occur, the eigenvalues of the rate constant matrix provide insight into the spectrum of time-scales governing the collective “flow” of the system within a specific network of states (both within E and its flow through B). According to eqn (16), the inverse of the eigenvalues of K (for given set of boundary states B and initial conditions, Q(0; B)) provides estimates of the residence time spent by the system at every state. The residence time is the result of the incoming and outgoing fluxes in that state, and thus an observable of the collective re-distribution in the network.The spectrum of eigenvalues, λm, with 1 ≤ m ≤ |E|, of K for a network of mean first passage time on the order of 10−6 s is presented in Fig. 4. As elaborated above, all eigenvalues of the K matrix are negative, by virtue of the “openness” of the system, since there is a continuous efflux of probability towards the set of the boundary states (cf. proof in Appendix B). They are ordered such that λ1 ≥ λ2 ≥ … ≥ λ|E|, i.e., the absolutely smallest is denoted by λ1 while the absolutely largest by λ|E|. We choose to make the histogram of their additive inverse, −λm, that will yield a distribution similar in form to the one depicted in Fig. 2(a). We can see that the (inverse) eigenvalues of the matrix governing the dynamical evolution of the network (for times commensurate to the mean first-passage time) extend from −1/λ|E| = 10−15 s up to −1/λ1 = 3.5 × 10−6 s. The system presented in Fig. 4 is a specimen at T = 300 K whose time evolution has been tracked up to a mean first passage time of 〈tE→B〉 = 3.18 × 10−6 s. It is observed that the MFP time is nearly identical to the negative inverse of the absolutely smallest eigenvalue of the rate constant matrix. This is not at all surprising. The MPFT is close to the exit time, 〈tE→B〉 ≃ 〈texit〉 = 3.21 × 10−6 s, and slightly smaller as expected based on the discussion in the Methodology section. In the calculation of the 〈texit〉, the absolutely smallest eigenvalue, λ1, of the rate constant matrix K becomes the dominant term in the summation of the right-hand side of eqn (18), since the matrix −K−1 is employed.
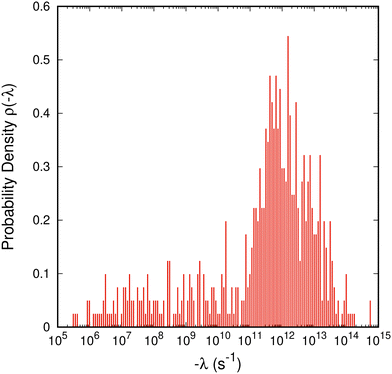 | ||
Fig. 4 Histogram of the characteristic rates (negative eigenvalues) of the rate constant matrix, K, governing the dynamical evolution of a network of states (eqn (2)) of aPS at T = 300 K. The bins are equally spaced on the logarithmic axis and the distribution is normalised such that ∫ρ(−λ)d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(−λ/s−1) = 1 holds. log10(−λ/s−1) = 1 holds. | ||
The eigenvalues of the rate constant matrix provide the full knowledge of the time evolution of the system, under given sets of explored, E, and boundary, B, states. However, they do not suffice to provide us with a direct connection with the macroscopically observed relaxation processes. Boulougouris and Theodorou18 speculated that the inverted eigenvalues of the rate constant matrix K (that drives the system to escape from the set of explored states at infinite time) are connected to the set of first-order relaxation processes of the system under consideration. We should note here again that the matrix K has only negative eigenvalues; there is no equilibrium distribution. While there should be some relation between the eigenvalues of the rate constant matrix and the time-scales of the macroscopically observed relaxation processes, there is no direct connection between them. We have already seen that the MFP time appears as the negative inverse of the absolutely smallest eigenvalue of K, and by assigning one relaxation mechanism for every eigenvalue of K we end up with |E| different relaxation processes, i.e., by considering a larger network more first-order relaxations emerge. Intuitively, this cannot hold and we provide a method to translate the dynamics through the boundary of the system to discrete relaxation processes in the following section.
4.4 Significance of the flux to the boundary states
Having seen that not all elementary processes (eigenvalues of the rate constant matrix) translate to macroscopic relaxations, we can identify time-signatures of the latter in a different way. As the system explores its phase space (and the corresponding network of states grows), it is always surrounded by boundary states, that form its “local environment”. By studying the efflux of probability from the current set of explored states, E, to the current set of boundary states, B, relaxation mechanisms will appear as peaks of the efflux current, i.e., as modes of exiting the set E. We can imagine the escaping process of the system as an ensemble of travellers departing from the initial state and facing a multitude of different routes. The diffusion of the system out and away of its initial state is governed by the structure of the network of the explored states. For extremely short times, all travellers will commute within the set of the set of explored states without touching its bounding edge. When our travellers reach the boundaries between E and B they are presented with a spectrum of different “exit highways”, each one characterised by a speed limit proportional to the rate constant of the corresponding transition. Escaping through fast exit lanes will be manifested at short time-scales, whereas escaping through slower exit lanes will manifest itself at longer time-scales. If the exploration of the energy landscape has not introduced any bias in the discovery of (free) energy barriers (as elaborated in our previous studies11,12), the distribution of rate constants, whose part is the distribution of rate constants connecting the sets E and B, is an inherent characteristic of the energy landscape. Eventually, at infinite time, some of the travellers will still wander within the network of explored states (we will elaborate on that below).The total efflux out of the set of explored states as a function of time for networks of different sizes is presented in Fig. 5. For a single explored state (red curve), the efflux to the set of boundary states initially exhibits a plateau. During that time the system escapes from its initial state utilising the available connections to B; the mixture of exit options is weighted by the rate constants of the individual connections and a dynamic equilibrium between the states in E and the states in B is established. Once the observation time exceeds the time-scale of the slowest connection out of the initial state, the system cannot be contained within E and the efflux drops to zero (i.e., the system has already escaped). By augmenting the set of explored states, specific patterns emerge in the total efflux profile. Collective escape phenomena manifest their existence as peaks in the total efflux; in the case of Fig. 5, a first peak appears at a timescale of 10−10 s, and a second peak at the time-scale of 10−6 s. The position of the peaks stabilises for larger networks; their height changes as a result of the probability efflux distribution extending to longer time-scales. The position of the peaks in the time axis is crucial; they correspond to macroscopically observed transitions, i.e., they mark the modes by which the system escapes collectively its current extent. That was the missing link in the previous attempts to extract the relaxation time-scales from network dynamics simulations. The escape pattern of the system is a combination of two different aspects: redistribution within the current set of explored states (governed by the explored-to-explored transitions) and escaping out of the set of explored states (governed by the explored-to-boundary transitions). All possible combinations of routes within E and exits from E to B are considered; their relative contributions and significance depend on time. For a sufficiently large set E, the form of the probability efflux converges into a certain form with well-defined maxima, which reflect specific molecular processes occurring within the glassy specimen. Remarkably, the asymptotic positions of the peaks observed in Fig. 5, one peak around 10−10 s and another one at 10−6 s, are comparable with the time-scales of the δ- and the γ-relaxations of atactic PS at T = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K (cf.Fig. 7 below).
K (cf.Fig. 7 below).
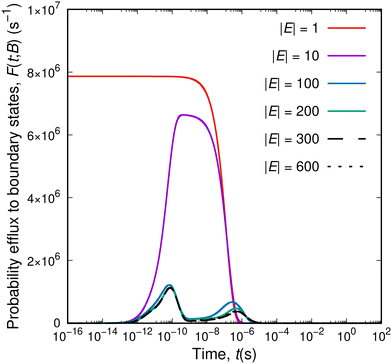 | ||
| Fig. 5 Probability efflux to the set of boundary states, F(t; B), as a function of time for different sizes of the network of explored states. The aPS system is simulated at T = 300 K. | ||
It is interesting that structural evolution deep into the glassy state takes place by means of well-defined relaxation processes, whose relevant timescales are associated with distinct ranges of barrier heights. Initially Greiner and Schwarzl29 and later Eulate and Cangialosi30 brought up the discussion on the existence of a fast mechanism of equilibrium recovery, beyond the standard (slow) one in the proximity of Tg identified as the α-relaxation. Their observations lie in contrast to the standard picture of physical ageing which is based on a continuous evolution of the thermodynamic state of the material towards equilibrium governed by the single timescale of the α-relaxation; the latter is usually adequate to describe physical ageing in the proximity of Tg. Based on our observations, and the previous work by Boulougouris and Theodorou18 we can support the hypothesis that the system is driven to lower free-energy states by means of secondary processes. However, the connection of the microscopic observations to the macroscopic long-term (one year and beyond) enthalpy loss measurements is still elusive. The interested reader is referred to a recent study by Jin and McKenna53 on the interpretation of the different experimental findings concerning the long-term relaxation of glasses below their Tg.
Monitoring the efflux to the boundary states is an integral part of analysing the networks generated by the method. The analysis of the dividing surface enclosing the system can reveal the way it interacts with its environment, i.e., the way of relaxing towards equilibrium. This behaviour takes an asymptotic form, with well-defined peaks at stationary values of t, even when the size of the set of explored states, |E|, is increasing. This is a result of the application of the dynamic importance sampling. We are preferentially sampling different parts of the spectrum of elementary transition rate constants at every stage of the expansion of the network, i.e., at short mean first passage times we are mostly sampling the fastest transitions (removing the relevant states from B and adding them to E), while at later stages we are sampling progressively slower transitions. The dynamic importance sampling ensures that there is no need for eliminating all fast transitions before exploring slower ones; that being the reason that the distribution of individual rate constants in Fig. 2(c) still contains very fast relaxations. The exploration of states is prioritised by the moving timescale observation set by tselect. At times comparable to the mean-first passage time to escape the network, the relative importance of fast and slow transitions at faster time-scales has already been incorporated in the explored networks and does not change by the addition of more slower transitions. In principle, there can be other ways to probe relaxation mechanisms based on a suitable manipulation of the rate constant matrix, but we strongly believe that the analysis of the efflux current is the most intuitive.
By expanding a network of states, the probability of entrapping the studied system within it, i.e., its survival probability Palive(t; B) at the same time t, becomes larger. The dependence of the survival probability on time is depicted in Fig. 6 for an aPS specimen at T = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. The survival probability exhibits a plateau (Palive = 1) at short times; the set of explored states provides the full description of the dynamics of the system for the corresponding time-scales. For a very small network of a single state (red curve in Fig. 6) the system cannot be trapped within the set of explored states. Once the longest timescale corresponding to the slowest transition out of the single state is exceeded, the system will escape. The larger the set of the explored states becomes, the more extended the plateau is. This is clearly seen in Fig. 6 for increasing the size of the network of explored states. At the time-scale of the mean first passage time, the survival probability rapidly decays before stabilising to a new plateau. Having defined the escape probability as the integral of the efflux current (eqn (11)), the system can be considered as trapped within a finite-sized network at long times. In other words, we allow for a finite, albeit small, probability that the constructed network is a sufficient description of the dynamics of the system even as t → ∞. Following the picture of the travellers adopted before, there is a finite fraction of these travellers that will still wander within the set E even at very long times. This is a fundamental difference with respect to the earlier formulation by Boulougouris and Theodorou,18 where the definition of the survival probability as the sum of the conditional probabilities, i.e.,
K. The survival probability exhibits a plateau (Palive = 1) at short times; the set of explored states provides the full description of the dynamics of the system for the corresponding time-scales. For a very small network of a single state (red curve in Fig. 6) the system cannot be trapped within the set of explored states. Once the longest timescale corresponding to the slowest transition out of the single state is exceeded, the system will escape. The larger the set of the explored states becomes, the more extended the plateau is. This is clearly seen in Fig. 6 for increasing the size of the network of explored states. At the time-scale of the mean first passage time, the survival probability rapidly decays before stabilising to a new plateau. Having defined the escape probability as the integral of the efflux current (eqn (11)), the system can be considered as trapped within a finite-sized network at long times. In other words, we allow for a finite, albeit small, probability that the constructed network is a sufficient description of the dynamics of the system even as t → ∞. Following the picture of the travellers adopted before, there is a finite fraction of these travellers that will still wander within the set E even at very long times. This is a fundamental difference with respect to the earlier formulation by Boulougouris and Theodorou,18 where the definition of the survival probability as the sum of the conditional probabilities, i.e., 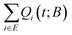 , fades to zero at t → ∞ by definition. This alternative definition of the survival probability is depicted by the solid lines in Fig. 6. Both metrics behave similarly with the exception of the long-time plateau that is missing from the earlier definition.
, fades to zero at t → ∞ by definition. This alternative definition of the survival probability is depicted by the solid lines in Fig. 6. Both metrics behave similarly with the exception of the long-time plateau that is missing from the earlier definition.
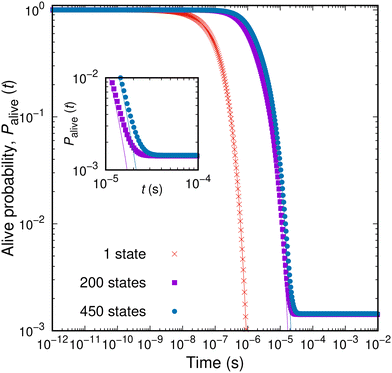 | ||
Fig. 6 Survival probability, Palive(t; B), as a function of time for different sizes of the network of explored states. Points represent the estimates defined by eqn (12), while solid lines the sum of the conditional probabilities over all states, i.e., 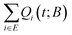 . In the inset to the figure the long-time behaviour of the two measures is depicted. . In the inset to the figure the long-time behaviour of the two measures is depicted. | ||
4.5 Comparison with experiments
The subglass relaxation processes of (polymer) glasses have been experimentally probed by a multitude of different (spectroscopic) techniques. The observed dynamical, mechanical or dielectric properties depend on the formation history of the specimens. Grigoriadi et al.31,32 have conducted systematic measurements of the dielectric response of atactic PS specimens of different formation histories. Within the range of the conditions those authors studied was the case of a freshly quenched aPS specimen, that fully resembles our simulation setup. In our case, the first state of the network in the glassy state is the one where the specimen landed after quenching from the melt state, i.e., at t = 0 we have a “fresh” glass with no thermal history (e.g., ageing or rejuvenation). Their measurements of a freshly quenched glassy specimen indicated three distinct relaxation processes, namely the α-relaxation of the glass transition, a β*-relaxation that was present only in the case of freshly quenched glasses and disappeared after ageing of the samples, and a γ-relaxation that was always measured irrespective of the thermal history of the sample. The experimental measurements by Grigoriadi et al. are depicted by the down-facing red triangles in the Arrhenius plot of Fig. 7. Going from left to right (higher to lower temperatures) the first transition to be observed is the α-relaxation which is clearly non-Arrhenius, the next one (that consists of three data-points at around τ ≃ 102 at 1000/T ≃ 2.8) is the β*-relaxation that is not present in aged specimens, and finally the Arrhenius-like γ-relaxation located at the rightmost part of the figure. In the same Arrhenius plot we include measurements of the relaxation times associated with the δ-relaxation process obtained by neutron scattering experiments,54 marked with the green dotted circles.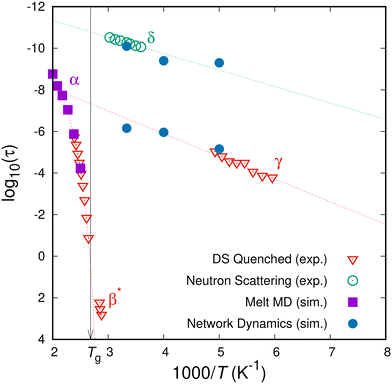 | ||
| Fig. 7 Relaxation map of atactic PS. Experimental measurements (by dielectric spectroscopy31 and neutron scattering54) and molecular simulation results (MD in the melt state and network dynamics in the glassy state) are presented. The dotted lines are the best-fit Arrhenius equations to the computationally and experimentally obtained relaxation times of the δ- and γ-relaxations; the corresponding activation energies are 12 kJ mol−1 and 20 kJ mol−1, respectively. | ||
Relaxation times obtained by molecular simulations are also included in Fig. 7. Analysing the orientational relaxation of characteristic vectors in the course of a molecular dynamics trajectory in the melt state can provide indicative relaxation times, e.g., the decorrelation of the orientation of the phenyl stem for the α-relaxation process, which are depicted by the purple squares in the leftmost (T > Tg) part of Fig. 7.43 The peaks from the probability efflux, Fig. 5, are included as the blue filled circles in Fig. 7. The results obtained from the position of the peaks of the efflux current to the boundary states are remarkably close to the experimentally observed relaxation time-scales for the δ and γ subglass relaxations. At the higher temperature (T = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K), we can reliably probe the characteristic time of the δ relaxation. While there is a lack of measurements for the lower temperature, our estimate lies close to the extrapolation by means of an Arrhenius equation of the neutron scattering measurements. The slope, which is the activation energy, is also in good agreement with ref. 54. As far as the γ relaxation is concerned, our simulation framework matches the experimental measurements at T = 200
K), we can reliably probe the characteristic time of the δ relaxation. While there is a lack of measurements for the lower temperature, our estimate lies close to the extrapolation by means of an Arrhenius equation of the neutron scattering measurements. The slope, which is the activation energy, is also in good agreement with ref. 54. As far as the γ relaxation is concerned, our simulation framework matches the experimental measurements at T = 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K and provides a reasonable estimate of the characteristic time of the γ relaxation at the elevated temperature of T = 300
K and provides a reasonable estimate of the characteristic time of the γ relaxation at the elevated temperature of T = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. Experimental measurements of the γ relaxation are not available at elevated temperatures, so we are using an Arrhenius extrapolation of the experimental measurements to judge the simulation results.
K. Experimental measurements of the γ relaxation are not available at elevated temperatures, so we are using an Arrhenius extrapolation of the experimental measurements to judge the simulation results.
5 Conclusions
The physical ageing of a polymer glass has been studied by the application of an out-of-equilibrium framework for the treatment of the master equation. The exploration of the (free) energy landscape of an atomistically detailed polymer specimen, together with the quasi-harmonic approximation for its vibrational motion, provides a suitable network of states (with well-defined transition rates for moving from one state to the other) that can serve as a basis for tracking the dynamical evolution of the system (under given external stress state). Moving along the lines of the pioneering work of Boulougouris and Theodorou,18 a Markovian time-integration scheme has been reimplemented for a finite network of states exposed to an unknown larger world through a dividing surface of boundary states. The distinction between “explored” and “boundary” (where the system gets absorbed) states is crucial. No equilibrium probability distribution is assumed; we show that our formalism reduces to the well-known equilibrium dynamics if there are no boundary states present in the network. By defining the appropriate conditional probabilities for the system to be trapped within the set of explored states, we manage to express the escape and survival probabilities for the finite-sized network, and eventually unveil the relaxation processes of the system by monitoring its time-dependent efflux from the explored network to the boundary states.Networks generated by the exploration of the (potential or free) energy landscape actually resemble the network of states visited by the system during a time trajectory as that was obtained by MD. The topological features, e.g., the clustering metrics of the networks, are found in perfect agreement with the previous MD studies. Since the energy exploration cannot be exhaustive, replicating the topology of the actual network is re-assuring for our efforts. Having the full knowledge of the network of states is far superior to studying a single MD trajectory, since we, in principle, can weight all trajectories within the given network. Even better, the method becomes more effective as the temperature is lowered, since the transition rate constants become lower and the transitions less frequent. Summarising, we have presented a viable alternative to brute force MD simulations with all ingredients of the method systematically exposed during the last years. Initially, MD simulations of the same system provided the benchmark data for its topological features.7 Then, analytical expressions of the first and higher-order derivatives of any classical molecular forcefield were derived,13 and methods for obtaining transition states (first-order saddle points) on the potential energy landscape,11 and an arbitrary free energy landscape12 were formulated. This work brings every piece of the puzzle together in a rigorous, general and unified framework.
There are more facets of the simulation of (polymer) glasses to be studied. We have not discussed the dependence of the time evolution on the formation history. This is an unresolved issue, even for experimental studies, where competing processes, e.g. thermal rejuvenation and quenching, seem to disturb the appearance of specific relaxation processes.31,32 The effect of the stereo-chemistry is also pronounced in polystyrene, with atactic, isotactic and syndiotactic polystyrenes behaving in a completely different way during ageing.55 Confinement of the specimen in one direction, i.e., creating a thin film can also have pronounced effects on ageing dynamics.56 Finally, from a computational point of view, solving the master equation by diagonalizing the rate constant matrix for a huge network of states may become impractical; lumping the fast-communicating states might be a way out of the problem,57 allowing us to access the time-scales relevant for the beta-relaxation and the transition from secondary to alpha process-assisted ageing.
Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A. Estimation of the equilibrium state probabilities by graph construction
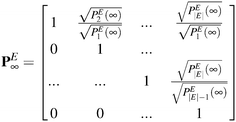
Implementation of the analytical solution scheme for the master equation for Q, eqn (1), requires that the equilibrium probabilities, PEi(∞) for i ∈ E, be available at the beginning of the calculation. These probabilities serve as a convenient change of basis for K, yielding![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) , which is symmetric (cf. Appendix B). An easy strategy for accomplishing this without diagonalizing matrix K is by considering the network of states as a directed graph.7 In the directed graph representation, the edges of the graph represent the states, while the vertices represent the transitions between them.
, which is symmetric (cf. Appendix B). An easy strategy for accomplishing this without diagonalizing matrix K is by considering the network of states as a directed graph.7 In the directed graph representation, the edges of the graph represent the states, while the vertices represent the transitions between them.
Having the graph layout at hand, the equilibrium probability of state i can be related to the equilibrium probability of state 1, by considering the shortest path (obtained by breadth first search, BFS) connecting these two states. Along the path of transitions, the ratio of the relevant rate constants is accumulated:
 | (A1) |
The method proposed here provides an analytical estimate of the equilibrium probabilities without resorting to the numerical solution of the stationary master equation. In order to solve the master equation,
| KPE = 0, | (A2) |
Appendix B. Negative definiteness of the rate constant matrix of a network of explored and boundary states
The matrix![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) as defined by eqn (6) is symmetric by virtue of the microscopic reversibility condition imposed on the rate constants of states in E. It has the same eigenvalues as K, since they are similar matrices, i.e.,
as defined by eqn (6) is symmetric by virtue of the microscopic reversibility condition imposed on the rate constants of states in E. It has the same eigenvalues as K, since they are similar matrices, i.e.,![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) = (PE∞)−1KPE∞ = (PE∞)−1KPE∞ | (B1) |
 | (B2) |
The eigenvalues of ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) (and those of K) are real, since
(and those of K) are real, since ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) is symmetric. All eigenvalues of
is symmetric. All eigenvalues of ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) are negative, if there is at least one boundary state present in the network, i.e., |B| > 0. The latter statement can be proved as follows: let a be an arbitrary |E|-dimensional vector of real elements. Then,
are negative, if there is at least one boundary state present in the network, i.e., |B| > 0. The latter statement can be proved as follows: let a be an arbitrary |E|-dimensional vector of real elements. Then,
 | (B3) |
Thus,
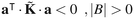 | (B4a) |
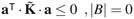 | (B4b) |
![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) as a negative definite matrix, if there exists at least one boundary state in the network. Otherwise, eqn (B4b) establishes
as a negative definite matrix, if there exists at least one boundary state in the network. Otherwise, eqn (B4b) establishes ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) as a negative semidefinite matrix, as in the standard theory of networks of chemical reactions, as first shown by Schuler.58
as a negative semidefinite matrix, as in the standard theory of networks of chemical reactions, as first shown by Schuler.58
It is easy to see that if λ is one of the real eigenvalues of ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) with corresponding real eigenvector ũ, then
with corresponding real eigenvector ũ, then ![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) ·ũ = λũ and therefore
·ũ = λũ and therefore
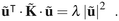 | (B5) |
![[K with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004b_0303.gif) is either negative definite, or negative semidefinite, the left-hand side of the latter equation is either
is either negative definite, or negative semidefinite, the left-hand side of the latter equation is either| λ < 0 |B| > 0 | (B6a) |
| λ ≤ 0 |B| = 0, | (B6b) |
Appendix C. Computational considerations
A major point of consideration is the scaling of the computational cost with the size of the system. MD simulation codes scale almost linearly with the size of the system, since the rate determining step is the evaluation of energy and forces. In the case of our network dynamics method, however, the lion's share of the wall-clock time spent by the code is devoted to diagonalizing the Hessian matrix, which is a relatively dense, symmetric real-valued matrix. The diagonalization of a dense matrix scales with the cube of the number of degrees of freedom, becoming prohibitive for large systems. GPU (graphics processing unit) computing provides a way out of the problem. Since GPUs provide an order of magnitude more processing elements than a CPU, dealing with linear algebra tasks is extremely efficient. Moreover, the method remains robust by employing diagonalization in single precision for intermediate steps and saving the more memory (and time) consuming diagonalization procedure for the stationary points.By considering a setup of a single CPU with eight processing cores running at 2.3 GHz and a system size of roughly one thousand atoms, MD and network dynamics spend comparable wall-clock time in order to simulate the same physical time. As far as the MD simulation is concerned, the LAMMPS MD engine59 achieves integration of the equations of motion for an aPS system consisting of a thousand atoms at the pace of 3.6 × 10−12 s of physical time per 1 s of wall-clock time. On the other hand, our network dynamics code for the same system and interactions would create a network of 10−5 s mean-first-passage time at 2.5 × 106 s, i.e., at a rate of 3.9 × 10−12 s of physical time per 1 s of wall-clock time. The comparison is performed at T = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. For lower temperatures, where the spectrum of TST-derived rate constants shifts to lower values, the network dynamics method will produce a longer mean-first-passage time for the same size of the network. Interestingly, the method becomes more efficient as the temperature is lowered. The reader is reminded that, whereas MD contributes a single trajectory to an out-of-equilibrium average, network dynamics contributes all possible trajectories within a given network of states; therein lies the main power of the network dynamics approach.
K. For lower temperatures, where the spectrum of TST-derived rate constants shifts to lower values, the network dynamics method will produce a longer mean-first-passage time for the same size of the network. Interestingly, the method becomes more efficient as the temperature is lowered. The reader is reminded that, whereas MD contributes a single trajectory to an out-of-equilibrium average, network dynamics contributes all possible trajectories within a given network of states; therein lies the main power of the network dynamics approach.
Acknowledgements
This research forms part of the research program of the Dutch Polymer Institute (DPI), projects #745ft14, #820 and #829.Notes and references
- V. M. Boucher, D. Cangialosi, A. Alegría and J. Colmenero, Phys. Chem. Chem. Phys., 2017, 19, 961–965 RSC.
- X. Monnier, J. Colmenero, M. Wolf and D. Cangialosi, Phys. Rev. Lett., 2021, 126, 118004 CrossRef CAS PubMed.
- J.-L. Barrat, J. Baschnagel and A. Lyulin, Soft Matter, 2010, 6, 3430–3446 RSC.
- C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, J. Appl. Phys., 2000, 88, 3113–3157 CrossRef CAS.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- M. Goldstein, J. Chem. Phys., 1969, 51, 3728–3739 CrossRef CAS.
- G. G. Vogiatzis, L. C. A. van Breemen and M. Hütter, Macromol. Theory Simul., 2019, 28, 1900036 CrossRef CAS.
- F. H. Stillinger and T. A. Weber, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 978–989 CrossRef CAS.
- F. H. Stillinger and T. A. Weber, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 2408–2416 CrossRef CAS.
- L. J. Munro and D. J. Wales, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3969–3980 CrossRef CAS.
- G. G. Vogiatzis, L. C. A. van Breemen and M. Hütter, J. Phys. Chem. B, 2021, 125, 7273–7289 CrossRef CAS PubMed.
- G. G. Vogiatzis, L. C. van Breemen and M. Hütter, J. Phys. Chem. B, 2022, 126, 7731–7744 CrossRef CAS PubMed.
- G. G. Vogiatzis, L. C. van Breemen, D. N. Theodorou and M. Hütter, Comput. Phys. Commun., 2020, 249, 107008 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- R. Martoňák, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 075503 CrossRef PubMed.
- A. Kushima, X. Lin, J. Li, J. Eapen, J. C. Mauro, X. Qian, P. Diep and S. Yip, J. Chem. Phys., 2009, 130, 224504 CrossRef PubMed.
- P. Cao, M. P. Short and S. Yip, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13631–13636 CrossRef CAS PubMed.
- G. C. Boulougouris and D. N. Theodorou, J. Chem. Phys., 2007, 127, 084903 CrossRef PubMed.
- G. C. Boulougouris and D. N. Theodorou, J. Chem. Phys., 2009, 130, 044905 CrossRef PubMed.
- G. C. Boulougouris, J. Stat. Mech.: Theory Exp., 2021, 2021, 023207 CrossRef.
- A. J. F. Siegert, Phys. Rev., 1951, 81, 617–623 CrossRef.
- S. K. Kim, J. Chem. Phys., 1958, 28, 1057–1067 CrossRef CAS.
- E. W. Montroll and G. H. Weiss, J. Math. Phys., 1965, 6, 167–181 CrossRef.
- A. Bar-Haim, J. Klafter and R. Kopelman, J. Am. Chem. Soc., 1997, 119, 6197–6198 CrossRef CAS.
- A. Bar-Haim and J. Klafter, J. Phys. Chem. B, 1998, 102, 1662–1664 CrossRef CAS.
- T. Ritz, S. Park and K. Schulten, J. Phys. Chem. B, 2001, 105, 8259–8267 CrossRef CAS.
- S. Iyer-Biswas and A. Zilman, Adv. Chem. Phys., 2016, 160, 261–306 CrossRef CAS.
- N. F. Polizzi, M. J. Therien and D. N. Beratan, Isr. J. Chem., 2016, 56, 816–824 CrossRef CAS PubMed.
- R. Greiner and F. R. Schwarzl, Rheol. Acta, 1984, 23, 378–395 CrossRef CAS.
- N. G. Perez-De Eulate and D. Cangialosi, Phys. Chem. Chem. Phys., 2018, 20, 12356–12361 RSC.
- K. Grigoriadi, T. Putzeys, M. Wübbenhorst, L. C. A. van Breemen, P. D. Anderson and M. Hütter, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1394–1401 CrossRef CAS.
- K. Grigoriadi, M. Wübbenhorst, L. C. A. van Breemen, T. Putzeys, A. Gennaro, P. D. Anderson and M. Hütter, J. Polym. Sci., 2020, 58, 1998–2009 CrossRef CAS.
- G. Di Battista, P. Eades, R. Tamassia and I. Tollis, Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, 1999 Search PubMed.
- Y. Hu, Math. J., 2005, 10, 137 Search PubMed.
- G. G. Vogiatzis and D. N. Theodorou, Macromolecules, 2013, 46, 4670–4683 CrossRef CAS.
- B. Dezső, A. Jüttner and P. Kovács, Electron. Notes Theor. Comput. Sci., 2011, 264, 23–45 CrossRef.
- T. P. Peixoto, figshare, 2014 Search PubMed.
- D. Chandler, J. Chem. Phys., 1978, 68, 2959–2970 CrossRef CAS.
- J. Wei and C. D. Prater, Adv. Catal., 1962, 13, 203–392 CAS.
- N. van Kampen, Stochastic Processes in Physics and Chemistry, Elsevier Science, 3rd edn, 2007 Search PubMed.
- G. H. Golub and H. A. van der Vorst, J. Comput. Appl. Math., 2000, 123, 35–65 CrossRef.
- D. N. Theodorou, in Principles of Molecular Simulation of Gas Transport in Polymers, John Wiley & Sons, Ltd, 2006, ch. 2, pp. 49–94 Search PubMed.
- G. G. Vogiatzis and D. N. Theodorou, Macromolecules, 2014, 47, 387–404 CrossRef CAS.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1986, 19, 139–154 CrossRef CAS.
- A. V. Lyulin and M. A. J. Michels, Macromolecules, 2002, 35, 1463–1472 CrossRef CAS.
- N. Lempesis, G. G. Vogiatzis, G. C. Boulougouris, L. C. van Breemen, M. Hütter and D. N. Theodorou, Mol. Phys., 2013, 111, 3430–3441 CrossRef CAS.
- S. H. Strogatz, Nature, 2001, 410, 268–276 CrossRef CAS PubMed.
- D. J. Watts and S. H. Strogatz, Nature, 1998, 393, 440–442 CrossRef CAS PubMed.
- M. E. J. Newman, SIAM Rev., 2003, 45, 167–256 CrossRef.
- M. E. J. Newman, S. H. Strogatz and D. J. Watts, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 026118 CrossRef CAS PubMed.
- E. Bullmore and O. Sporns, Nat. Rev. Neurosci., 2009, 10, 186 CrossRef CAS PubMed.
- M. Girvan and M. E. J. Newman, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7821–7826 CrossRef CAS PubMed.
- S. Jin and G. B. McKenna, Polym. Eng. Sci., 2022, 62, 1124–1136 CrossRef CAS.
- S. Arrese-Igor, A. Arbe, B. Frick and J. Colmenero, Macromolecules, 2011, 44, 3161–3168 CrossRef CAS.
- K. Grigoriadi, J. B. H. M. Westrik, G. G. Vogiatzis, L. C. A. van Breemen, P. D. Anderson and M. Hütter, Macromolecules, 2019, 52, 5948–5954 CrossRef CAS PubMed.
- I. McKenzie, D. Fujimoto, V. L. Karner, R. Li, W. A. MacFarlane, R. M. L. McFadden, G. D. Morris, M. R. Pearson, A. N. Raegen, M. Stachura, J. O. Ticknor and J. A. Forrest, J. Chem. Phys., 2022, 156, 084903 CrossRef CAS PubMed.
- N. Lempesis, D. G. Tsalikis, G. C. Boulougouris and D. N. Theodorou, J. Chem. Phys., 2011, 135, 204507 CrossRef PubMed.
- K. E. Shuler, Phys. Fluids, 1959, 2, 442–448 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |