Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Uncovering the role of non-covalent interactions in solid-state photoswitches by non-spherical structure refinements with NoSpherA2†
Lauren E.
Hatcher
 *a,
Lucy K.
Saunders
*a,
Lucy K.
Saunders
 b and
Ben A.
Coulson
b and
Ben A.
Coulson
 a
a
aSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 AT, UK. E-mail: HatcherL1@cardiff.ac.uk
bDiamond Light Source, Harwell Science and Innovation Campus, Fermi Ave, Didcot, OX11 0DE, UK
First published on 23rd December 2022
Abstract
We present a charge density study of two linkage isomer photoswitches, [Pd(Bu4dien)(NO2)]BPh4·THF (1) and [Ni(Et4dien)(NO2)2] (2) using Hirshfeld Atom Refinement (HAR) methods implemented via the NoSpherA2 interface in Olex2. HAR is used to explore the electron density distribution in the photoswitchable molecules of 1 and 2, to gain an in-depth understanding of key bonding features and their influence on the single-crystal-to-single-crystal reaction. HAR analysis is also combined with ab initio calculations to explore the non-covalent interactions that influence physical properties of the photoswitches, such as the stability of the excited state nitrito-(η1-ONO) isomer. This insight can be fed back into the crystal engineering process to develop new and improved photoswitches that can be optimised towards specific applications.
Introduction
Photoswitchable materials, that can be reversibly converted between at least two different (meta)stable states on exposure to light, are applicable in a variety of technologies including optoelectronics, data-storage media, solar energy and photocatalysis.1–3 Typically, bulk switching of the macroscopic physical property is accompanied by structural changes at the atomic scale and, by studying these structure–property correlations via in situ analytical techniques, researchers can obtain insight into the fundamental mechanisms responsible for switchability. For crystalline materials in which the structure changes occur in a single-crystal-to-single-crystal manner, the switching process can be followed by photocrystallographic methods.4 Even in crystals that can readily accommodate the movement of whole atoms or molecules, non-covalent interactions (NCIs) control various aspects of switching, including the most likely reaction pathways, photo-product and intermediate species or the excited-state populations achieved. This is particularly true of intermolecular interactions, e.g. hydrogen bonds, that must be disrupted throughout the solid to facilitate photoswitching in the bulk.5 Thus, NCIs are often key to explain important structure–property correlations.While single-crystal X-ray diffraction (SCXRD) refinements using the traditional Independent Atom Model (IAM) provide atomic-scale information before, after, and even during photo-switching, often information on NCIs is, at best, only inferred from the refined parameters (e.g. bond lengths and angles). Experimental charge density refinements can directly refine the electron density based on more accurate, non-spherical models e.g. multipolar refinements, providing unique understanding of the fine electron density.6–8 However, such experiments ideally require very high-resolution data (<0.5 Å). As many issues typical for photocrystallographic studies (e.g. radiation damage from light and/or X-rays, stimuli-induced phase transitions, or significant disorder resulting from partial conversion to the excited-state) can significantly limit the diffraction data quality obtained, these studies present a significant challenge for accurate experimental charge density analysis.
More recently, semi-empirical approaches have been proposed that sit between experimental charge density refinements and ab initio calculations.9 These include multipole-based databank approaches, e.g. the Invarioms10 or ELMAM11 methods, although these methods are typically limited to organic and bioorganic compounds where fewer atom types are required. The NoSpherA2 (Non-Spherical Atoms in Olex2) approach, implemented in the crystal structure refinement software Olex2,12 has already been applied to several interesting crystallographic problems, including those involving metal atoms.13–15 The software utilises Hirshfeld atom refinement (HAR) to calculate non-spherical atomic form factors, then refines these non-spherical atom shapes against the experimental electron density obtained by SCXRD.9 Through this combination of quantum mechanical calculations and experimental electron density refinement, a greatly improved crystallographic model is obtained that can provide new insight into the intra- and intermolecular bonding. The NoSpherA2 approach has some advantages over fully-experimental charge density analysis as it can be applied to materials that do not diffract to such high resolution as needed for multipolar refinements, and more readily to materials that contain disorder.
We herein present an application of NoSpherA2 to photo-switchable linkage isomer crystals. Using HAR, we investigate the electron density distribution (EDD) and NCIs present in the ground-state (GS) and excited-state (ES) isomers of two known systems: [Pd(Bu4dien)(NO2)]BPh4·THF (1),16 and [Ni(Et4dien)(NO2)2] (2),17,18 which can both be fully-converted between their nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) GS and photoinduced endo-nitrito-(η1-
O2) GS and photoinduced endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ES at 100 K. As well as dealing with the limited resolution imposed by in situ irradiation of the crystals, 1 and 2 present different challenges for HAR analysis: while 1 has a large asymmetric unit containing 130 atoms, including a heavy PdII metal centre, 2 contains fewer atoms but its d8 octahedral NiII centre requires an open-shell wavefunction calculation. By understanding the EDD and NCIs present in these systems we can explore the nature of the bonding between the isomerisable ligand and the metal. This insight is used to rationalise properties, e.g. the stability of the photoexcited state, knowledge that can be applied to rationally-design new materials for particular applications. The results show the applicability of HAR for photocrystallographic refinements and recommend its future application to other photoswitchable and photocatalytic materials.
NO) ES at 100 K. As well as dealing with the limited resolution imposed by in situ irradiation of the crystals, 1 and 2 present different challenges for HAR analysis: while 1 has a large asymmetric unit containing 130 atoms, including a heavy PdII metal centre, 2 contains fewer atoms but its d8 octahedral NiII centre requires an open-shell wavefunction calculation. By understanding the EDD and NCIs present in these systems we can explore the nature of the bonding between the isomerisable ligand and the metal. This insight is used to rationalise properties, e.g. the stability of the photoexcited state, knowledge that can be applied to rationally-design new materials for particular applications. The results show the applicability of HAR for photocrystallographic refinements and recommend its future application to other photoswitchable and photocatalytic materials.
Experimental
Synthetic procedures
All synthetic manipulations were carried out in air. Palladium(II) chloride, N,N,N′,N′-tetrabutyldiethylenetriamine (Bu4dien), nickel(II) chloride hexahydrate, N,N,N′,N′-tetraethyl-diethylenetriamine (Et4dien) and sodium tetraphenylborate were purchased from Merck (Sigma Aldrich), while potassium nitrite was purchased from Acros Organics. All solvents were purchased from Fisher Scientific. All starting materials and solvents were used as received, without the need for further purification.Single-crystal X-ray diffraction (SCXRD)
SCXRD data collection and processing were completed as described above. For both 1 and 2, diffraction data could be obtained to a resolution of d = 0.6 Å in both the GS and ES.
Results
Complex 1: [Pd(Bu4dien)(NO2)]BPh4·THF
![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) GS to the endo-nitrito-(η1-
O2) GS to the endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ES using near-UV LED light (400/405 nm), with full conversion to 100% ES population throughout the crystal bulk occurring very quickly (over a period of minutes) in comparison to other previously reported linkage isomer crystals.28 The ES lifetime is heavily temperature-dependent, being effectively metastable on the timescale of a standard SCXRD experiment below 240 K.16 Above this critical temperature, often defined as the “metastable limit” in photocrystallographic studies, ES → GS decay occurs on an observable timescale, with the rate of decay dictated by the temperature. This ES → GS process has been followed by time-resolved SCXRD studies.27,28
NO) ES using near-UV LED light (400/405 nm), with full conversion to 100% ES population throughout the crystal bulk occurring very quickly (over a period of minutes) in comparison to other previously reported linkage isomer crystals.28 The ES lifetime is heavily temperature-dependent, being effectively metastable on the timescale of a standard SCXRD experiment below 240 K.16 Above this critical temperature, often defined as the “metastable limit” in photocrystallographic studies, ES → GS decay occurs on an observable timescale, with the rate of decay dictated by the temperature. This ES → GS process has been followed by time-resolved SCXRD studies.27,28
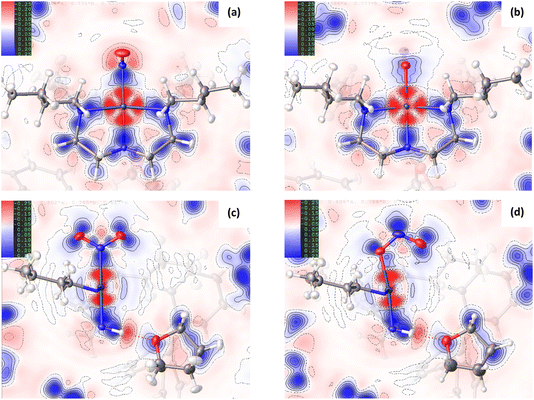
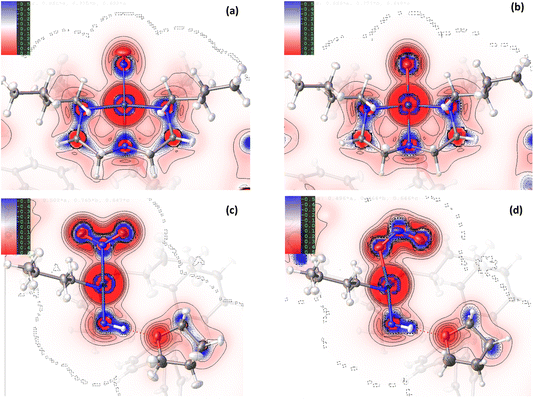
Comparison of the GS and ES maps for both the deformation density and Laplacian show differences in charge distribution in the Pd–N bonds to Bu4dien following excitation, with the valence shell charge concentrations (VSCCs) more localised in the GS compared to the ES (see Fig. 2(c) vs (d)), which is indicative of a change in the electronegativity of the ligand. These differences indicate a stronger Pd-to-Bu4dien interaction in the ES isomer and likely reflect the change in electronic structure at Pd(1) following conversion between nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) to nitrito-(η1-
O2) to nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomers. This is supported by a comparison of the experimental bond lengths from the crystal structure data (Tables S1.2/S1.3†). The Pd–N bonds to Bu4dien all shorten on excitation, with small but significant changes of ΔPd(1)–N(2) = −0.0119(12) Å and ΔPd(1)–N(4) = −0.0051(11) Å for the cis-coordinated donors and ΔPd(1)–N(3) = −0.0105(13) Å for the donor trans- to the nitrite group. These changes also remain consistent in the geometry-optimised structures.
NO) isomers. This is supported by a comparison of the experimental bond lengths from the crystal structure data (Tables S1.2/S1.3†). The Pd–N bonds to Bu4dien all shorten on excitation, with small but significant changes of ΔPd(1)–N(2) = −0.0119(12) Å and ΔPd(1)–N(4) = −0.0051(11) Å for the cis-coordinated donors and ΔPd(1)–N(3) = −0.0105(13) Å for the donor trans- to the nitrite group. These changes also remain consistent in the geometry-optimised structures.
Fig. 1(c)/(d) and 2(c)/2(d) provide a good visual analysis of the difference in electron density distribution within the nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and nitrito-(η1-
O2) and nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) groups. The Laplacian maps are particularly informative, with clear delocalisation evident across the N–O bonds of the GS isomer that is markedly reduced in the ES. Similarly, the GS deformation density (Fig. 1(c)) clearly shows both CC in the O(1) and O(2) lone pairs and a fairly high level of CC in the N–O bonds (strong blue features), while the ES map (Fig. 1(d)) shows much lower CC in the N–O bonds of nitrito-(η1-
NO) groups. The Laplacian maps are particularly informative, with clear delocalisation evident across the N–O bonds of the GS isomer that is markedly reduced in the ES. Similarly, the GS deformation density (Fig. 1(c)) clearly shows both CC in the O(1) and O(2) lone pairs and a fairly high level of CC in the N–O bonds (strong blue features), while the ES map (Fig. 1(d)) shows much lower CC in the N–O bonds of nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO). Instead, there appears to be a very strong localisation of charge in the N(1A) lone pair, a feature also backed up by the theoretical results. From topological analysis, there is a shift in the relative positions of the (3,−1) bond critical points (BCPs) between the GS and ES isomers, with BCPs equally positioned at 47% along both N → O directions in nitro-(η1-
NO). Instead, there appears to be a very strong localisation of charge in the N(1A) lone pair, a feature also backed up by the theoretical results. From topological analysis, there is a shift in the relative positions of the (3,−1) bond critical points (BCPs) between the GS and ES isomers, with BCPs equally positioned at 47% along both N → O directions in nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2), but moving 2% closer to the central N(1A) atom in the nitrito-(η1-ONO) ES (see Fig. S1.2 and Tables S1.4/1.5†). Theoretical Natural Bond Orbital (NBO) analysis also agrees with this bonding picture. In the GS nitro-(η1-
O2), but moving 2% closer to the central N(1A) atom in the nitrito-(η1-ONO) ES (see Fig. S1.2 and Tables S1.4/1.5†). Theoretical Natural Bond Orbital (NBO) analysis also agrees with this bonding picture. In the GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2), the σ(N–O) bonds are almost completely delocalised with 51.4% localisation on N(1) in N(1) → O(1) and 50.3% in N(1) → O(2) (Table S1.6†) and bond orders of 1.44 and 1.45 respectively (Table S1.7†). Conversely, for ES nitrito-(η1-ONO) the σ(N–O) bonds are more polar and the electron density more localised, with 60.4% localisation on N(1A) in N(1A) → O(1A) and 55.8% in N(1A) → O(2A), and unequal bond orders of 1.18 and 1.78. These results confirm that, while the electron density in nitro-(η1-
O2), the σ(N–O) bonds are almost completely delocalised with 51.4% localisation on N(1) in N(1) → O(1) and 50.3% in N(1) → O(2) (Table S1.6†) and bond orders of 1.44 and 1.45 respectively (Table S1.7†). Conversely, for ES nitrito-(η1-ONO) the σ(N–O) bonds are more polar and the electron density more localised, with 60.4% localisation on N(1A) in N(1A) → O(1A) and 55.8% in N(1A) → O(2A), and unequal bond orders of 1.18 and 1.78. These results confirm that, while the electron density in nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) is considerably delocalised across both N–O bonds, suggesting a partial double bond character in each, in the ES this delocalisation is much reduced. This is in line with the experimental bond lengths (Tables S1.2/S1.3†), and with other theoretical studies in the literature investigating the electron density distribution in related metal-nitrite complexes.30
O2) is considerably delocalised across both N–O bonds, suggesting a partial double bond character in each, in the ES this delocalisation is much reduced. This is in line with the experimental bond lengths (Tables S1.2/S1.3†), and with other theoretical studies in the literature investigating the electron density distribution in related metal-nitrite complexes.30
The change in EDD within the Bu4dien and nitrite ligands between GS and ES structures clearly reflects the NO2 → ONO switching. Comparing the GS and ES geometries about Pd(1) in the experimental crystal structures, the bond between Pd(1) and the nitrite ligand elongates by +0.0248(13) Å on excitation (Tables S1.2/1.3†). This indicates poorer overlap between O(1A) and Pd(1) in the ES, compared to that of N(1A) and Pd(1) in the GS, and is reflected in the deformation density (Fig. 1(c)/(d)). In the GS, the nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) ligand is well-placed to provide good σ-donation to Pd(1) via its N(1) lone pair, which is clearly aligned along the N(1)–Pd(1) bonding direction to match with the acceptor lobe of the PdII4dx2−y2 orbital. Conversely, the ES map shows that nitrito-(η1-
O2) ligand is well-placed to provide good σ-donation to Pd(1) via its N(1) lone pair, which is clearly aligned along the N(1)–Pd(1) bonding direction to match with the acceptor lobe of the PdII4dx2−y2 orbital. Conversely, the ES map shows that nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is less well-matched for donor–acceptor bonding, as the lone pairs on O(1A) do not align as well with the 4dx2−y2 orbital. It is clear there is less electron density available for n → 4d* donation, with a much lighter blue region aligned with the red sigma hole at the metal in Fig. 1(d). The majority of electron density on O(1A) is instead localised in the lone pair on the other side of the atom, which is not involved in metal–ligand bonding. Indeed, in the 3D representation (ESI Movie 2†) only this non-bonding lone pair is readily observed, which compares well to theoretical analysis of similar complexes in the literature.30 The fact that nitrito-(η1-
NO) is less well-matched for donor–acceptor bonding, as the lone pairs on O(1A) do not align as well with the 4dx2−y2 orbital. It is clear there is less electron density available for n → 4d* donation, with a much lighter blue region aligned with the red sigma hole at the metal in Fig. 1(d). The majority of electron density on O(1A) is instead localised in the lone pair on the other side of the atom, which is not involved in metal–ligand bonding. Indeed, in the 3D representation (ESI Movie 2†) only this non-bonding lone pair is readily observed, which compares well to theoretical analysis of similar complexes in the literature.30 The fact that nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is a less delocalised system, as argued above, likely explains the lack of an obvious donor lone pair for the Pd(1)–O(1A) interaction. The localisation of charge within the nitrito ligand itself provides less density for dative bonding to PdII, making nitrito-(η1-
NO) is a less delocalised system, as argued above, likely explains the lack of an obvious donor lone pair for the Pd(1)–O(1A) interaction. The localisation of charge within the nitrito ligand itself provides less density for dative bonding to PdII, making nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) the poorer σ-donor. This could also explain why nitro-(η1-NO2) is the thermodynamically-favoured isomer at ambient conditions, while the weaker bound nitrito-(η1-
NO) the poorer σ-donor. This could also explain why nitro-(η1-NO2) is the thermodynamically-favoured isomer at ambient conditions, while the weaker bound nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is a metastable state. However, despite these visual observations, topological analysis does confirm that a bond path exists between Pd(1) and O(1A), with a (3,−1) BCP located along this path (Fig. S1.2 and Table S1.5†).
NO) is a metastable state. However, despite these visual observations, topological analysis does confirm that a bond path exists between Pd(1) and O(1A), with a (3,−1) BCP located along this path (Fig. S1.2 and Table S1.5†).
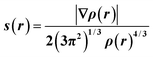 | (1) |
In regions of both covalent bonding and NCIs, s will have very small, near-zero values. Thus, it is a useful indicator to identify intra- and intermolecular bonding features. NCI analysis extends this by using density derivatives (specifically the second eigenvalue of the Laplacian, λ2) to distinguish between different types of NCIs. Specifically, the value of the function sign(λ2ρ) determines whether an NCI is non-bonding (sign(λ2ρ) > 0, for e.g. a close-contact steric interaction, or bonding (sign(λ2ρ) < 0), for e.g. a hydrogen bond.31
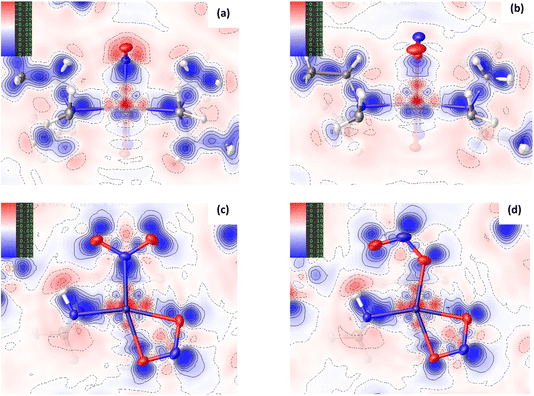
Fig. 3(a) and (b) show scatterplots of s vs sign(λ2ρ), computed for the GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and ES nitrito-(η1-
O2) and ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) photoactive cations respectively. In these plots, sharp features at low values of s correspond to NCIs, with the red-green-blue colour-coding highlighting the value of sign(λ2ρ), and thus the type of NCI represented (red = non-bonding, green = van der Waals and blue = bonding NCIs). The scatterplots essentially provide a fingerprint of the unique combination of NCIs for the GS and ES, respectively, and a quick visual comparison between them immediately highlights the similarities and differences between isomers. Fig. 3(c) and (d) show 3D representations of the same information, superimposed onto the molecules as isosurfaces of s = 0.5 that are colour-coded according to the same red-green-blue scale.
NO) photoactive cations respectively. In these plots, sharp features at low values of s correspond to NCIs, with the red-green-blue colour-coding highlighting the value of sign(λ2ρ), and thus the type of NCI represented (red = non-bonding, green = van der Waals and blue = bonding NCIs). The scatterplots essentially provide a fingerprint of the unique combination of NCIs for the GS and ES, respectively, and a quick visual comparison between them immediately highlights the similarities and differences between isomers. Fig. 3(c) and (d) show 3D representations of the same information, superimposed onto the molecules as isosurfaces of s = 0.5 that are colour-coded according to the same red-green-blue scale.
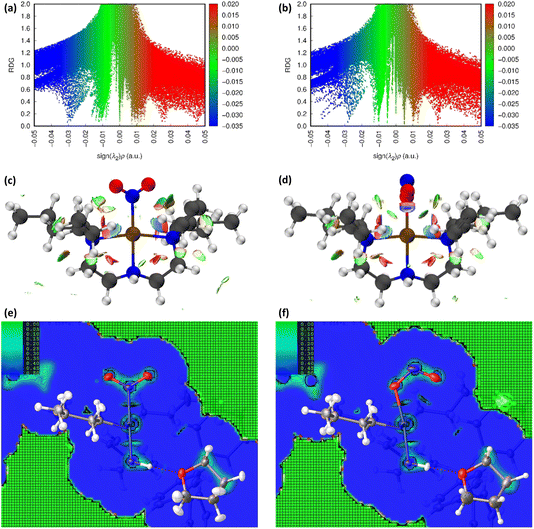 | ||
Fig. 3 Non-covalent interaction (NCI) analysis for GS and ES isomers of 1, using the reduced density gradient (RDG, s). Theoretical analysis: (a) plot of s vs sign(λ2ρ) for the GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) cation and (b) plot of s vs sign(λ2ρ) for the ES nitrito-(η1- O2) cation and (b) plot of s vs sign(λ2ρ) for the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) cation, providing a fingerprint of the NCIs in each isomer [generated in Multiwfn25 and visualised in Gnuplot33]. (c) 3D plot of s isosurfaces (s = 0.5 a.u.) for the GS nitro-(η1- NO) cation, providing a fingerprint of the NCIs in each isomer [generated in Multiwfn25 and visualised in Gnuplot33]. (c) 3D plot of s isosurfaces (s = 0.5 a.u.) for the GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) cation and (d) the ES nitrito-(η1- O2) cation and (d) the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) cation, highlighting the key NCIs in each isomer: colour-coding links to (a)/(b) plots with red = regions of sign(λ2ρ) > 0 i.e. steric interactions, green = regions of sign(λ2ρ) ≈ 0 and blue = regions of sign(λ2ρ) < 0 i.e. bonding interactions e.g. hydrogen bonds [generated in Multiwfn and visualised in VMD26]. HAR analysis: (e) 2D s (RDG) map for the GS structure of 1 in the Pd(1), N(1), O(1), O(2) plane and (f) 2D s (RDG) map for the ES structure of 1 in the Pd(1), O(1A), N(1A), O(2A) plane, showing key NCIs in the asymmetric unit [generated by HAR in NoSpherA2 NO) cation, highlighting the key NCIs in each isomer: colour-coding links to (a)/(b) plots with red = regions of sign(λ2ρ) > 0 i.e. steric interactions, green = regions of sign(λ2ρ) ≈ 0 and blue = regions of sign(λ2ρ) < 0 i.e. bonding interactions e.g. hydrogen bonds [generated in Multiwfn and visualised in VMD26]. HAR analysis: (e) 2D s (RDG) map for the GS structure of 1 in the Pd(1), N(1), O(1), O(2) plane and (f) 2D s (RDG) map for the ES structure of 1 in the Pd(1), O(1A), N(1A), O(2A) plane, showing key NCIs in the asymmetric unit [generated by HAR in NoSpherA2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9]. 9]. | ||
Common features of GS and ES plots are steric repulsions (red regions) at the positions of ring critical points (RCPs) in the chelating Bu4dien ligands and other steric repulsions between the butyl moieties and Pd(1). The scatterplots show that these steric interactions change only marginally on excitation. There are also two bonding-type intermolecular interactions from butyl hydrogens H(6B) and H(14A) to Pd(1) (light blue surfaces) in both the GS and ES molecules, which match with (3,−1) BCPs identified in the topological analysis (Tables S1.4/1.5†).
Key differences include changes in van der Waals interactions (green regions, sign(λ2ρ) ≈ 0), i.e. weak intramolecular C–H⋯O contacts between the butyl hydrogens and the nitrite group, which are clear in the 3D surface plots and the scatterplots. The sharper and longer green “spikes” in the ES plot indicate a decrease in s and so shorter, stronger contacts on excitation, which is supported by a comparison of the H(6A)⋯O(2)/O(2A) and H(14A)⋯O(2)/O(2A) short contact distances between the GS and ES structures. However, the biggest change in NCIs between the GS and ES isomers involves a new interaction between Pd(1) and the terminal O(2A) atom in the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ligand. This is highlighted by the dark blue region along the O(2A) → Pd(1) direction in Fig. 3(d), and new blue features at ca. −0.043 sign(λ2ρ) in Fig. 3(b) that are absent in Fig. 3(a). These results indicate that there is a stabilising contact between O(2A) and the metal centre, which can be classified as a bonding NCI. This conclusion is backed up by the bond path identified between Pd(1) and O(2A) in the topological analysis, with a (3,−1) BCP 37% along the O(2A) → Pd(1) direction (Fig. S1.2(c) and Table S1.5†).
NO) ligand. This is highlighted by the dark blue region along the O(2A) → Pd(1) direction in Fig. 3(d), and new blue features at ca. −0.043 sign(λ2ρ) in Fig. 3(b) that are absent in Fig. 3(a). These results indicate that there is a stabilising contact between O(2A) and the metal centre, which can be classified as a bonding NCI. This conclusion is backed up by the bond path identified between Pd(1) and O(2A) in the topological analysis, with a (3,−1) BCP 37% along the O(2A) → Pd(1) direction (Fig. S1.2(c) and Table S1.5†).
Fig. 3(e), (f) and S1.3† show 2D plots of s, that have been generated by HAR in NoSpherA2 and so additionally take into account intermolecular interactions within the asymmetric unit between cation, anion and THF solvent molecules. The HAR analysis confirms similar features to those in the theoretical NCI plots, with the key Pd(1)⋯O(2A) interaction in the ES clearly evident in Fig. 3(f). The ES deformation density also provides additional evidence of an interaction (Fig. 1(d)). The depletion of density at PdII (red lobe) has some extension towards O(2A), while the orientation of the O(2A) lone pair also aligns with this depletion, suggesting a degree of orbital overlap that supports a bonding interaction.
Complex 2: [Ni(Et4dien)(NO2)2]
![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and endo-nitrito-(η1-
O2) and endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomers due to thermal occupation of nitrito-(η1-
NO) isomers due to thermal occupation of nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) at higher temperatures, slowly cooling a crystal in the dark produces a clean nitro-(η1-
NO) at higher temperatures, slowly cooling a crystal in the dark produces a clean nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) isomer by 100 K, which is used as the GS for photocrystallography studies. Irradiation with 500 nm LED light promotes 100% conversion to a photoinduced nitrito-(η1-
O2) isomer by 100 K, which is used as the GS for photocrystallography studies. Irradiation with 500 nm LED light promotes 100% conversion to a photoinduced nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ES, which is metastable on the timescale of a standard SCXRD experiment up to 140 K. Above this temperature, the system dynamically decays back to its GS arrangement, with the ES decay lifetime dependent on temperature. Under continuous illumination (“pseudo-steady-state” conditions) conversion to a second exo-nitrito-(η1-
NO) ES, which is metastable on the timescale of a standard SCXRD experiment up to 140 K. Above this temperature, the system dynamically decays back to its GS arrangement, with the ES decay lifetime dependent on temperature. Under continuous illumination (“pseudo-steady-state” conditions) conversion to a second exo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ES linkage isomer is observed at small occupancy levels, indicating a short-lived ES,18 however little evidence of this exo form is seen under the steady-state photocrystallographic conditions used in the current study.
NO) ES linkage isomer is observed at small occupancy levels, indicating a short-lived ES,18 however little evidence of this exo form is seen under the steady-state photocrystallographic conditions used in the current study.
For complex 2, the EDD is seen to change between the GS and ES structures, although the changes are generally more subtle than those observed for 1. As for the Pd-complex, the deformation density maps clearly show dative covalent bonding from all ligands to NiII. For the equatorially-coordinated Et4dien ligand, n → 3d* donation from the N(3), N(4) and N(5) lone pairs is clearly observed, with strong alignment between these blue (+ve) density accumulation regions and the red (−ve) density depletion for the 3dx2−y2 antibonding acceptor orbital on Ni(1). It is evident in comparing GS and ES Laplacian maps in Fig. 5 that the VSCCs are more diffuse, albeit slightly, and have more extension along the N → Ni bonding direction for the GS than for the ES, indicating a stronger Ni-to-Et4dien interaction prior to excitation. Theoretical topology analysis neither supports nor contradicts these visual observations, showing no significant change in the positions of the BCPs in the Ni(1)–N(3), Ni(1)–N(4) or Ni(1)–N(5) bonds, as a percentage of the overall bond length, between the GS and ES structures (Fig. S2.3†). However, a comparison of the experimental bond lengths confirms an expansion of the Et4dien coordination sphere on excitation, with all 3 Ni–N bond distances undergoing a small but significant increase (ΔNi(1)–N(3) = +0.0049(15) Å, ΔNi(1)–N(4) = +0.0061(14) Å and ΔNi(1)–N(5) = +0.0098(14) Å, Tables S2.2/S2.3†). These observations are in direct contrast to analysis of 1, although the changes again likely reflect the change in the EDD that occurs on excitation.
Fig. 4(c)/(d) and 5(c)/5(d) again support visual analysis of the density changes within the nitrite ligands and, in the case of 2, the 2D contour plots are useful to study the EDD in both the isomerising η1-NO2 and photoinert η2-O,ON groups. The deformation density plots in Fig. 4(c)/(d) again clearly show the dative donor–acceptor bonding between the spectator nitrito-(η2-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,
,![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) N) ligand and NiII, with evidence of good orbital overlap of the O(3) lone pair with 3dx2−y2, and the O(4) lone pair with the (also antibonding) 3dz2 orbital in the GS and ES. As for Et4dien, the Laplacian plots (Fig. 5(c)/(d)) indicate slightly more extension of the O(3) and O(4) VSCCs towards Ni(1) in the GS, which is supported by a slight increase in the Ni–O bond distances after excitation (ΔNi(1)–O(3) = +0.0080(14) Å and ΔNi(1)–O(4) = +0.0109(14) Å) indicating a weakened interaction. The Laplacian plots (Fig. 5(c)/(d)) clearly show the delocalisation of charge across N(2), O(3) and O(4), which is supported by very similar theoretical bond orders for N(2)–O(3) and N(2)–O(4) (Table S2.7†). Finally, comparison of the isomerising η1-nitrite ligands completes the picture of how the EDD changes as a result of photoswitching. Within both the GS and ES ligands there is again clear delocalisation across the GS N(1), O(1) and O(2) and the ES N(1A), O(1A), O(2A) atoms, respectively, although it is evident that the VSCCs are more localised for the ES nitrito-(η1-
N) ligand and NiII, with evidence of good orbital overlap of the O(3) lone pair with 3dx2−y2, and the O(4) lone pair with the (also antibonding) 3dz2 orbital in the GS and ES. As for Et4dien, the Laplacian plots (Fig. 5(c)/(d)) indicate slightly more extension of the O(3) and O(4) VSCCs towards Ni(1) in the GS, which is supported by a slight increase in the Ni–O bond distances after excitation (ΔNi(1)–O(3) = +0.0080(14) Å and ΔNi(1)–O(4) = +0.0109(14) Å) indicating a weakened interaction. The Laplacian plots (Fig. 5(c)/(d)) clearly show the delocalisation of charge across N(2), O(3) and O(4), which is supported by very similar theoretical bond orders for N(2)–O(3) and N(2)–O(4) (Table S2.7†). Finally, comparison of the isomerising η1-nitrite ligands completes the picture of how the EDD changes as a result of photoswitching. Within both the GS and ES ligands there is again clear delocalisation across the GS N(1), O(1) and O(2) and the ES N(1A), O(1A), O(2A) atoms, respectively, although it is evident that the VSCCs are more localised for the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ligand than for GS nitro-(η1-
NO) ligand than for GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2), in line with, though less pronounced than, the differences seen for 1. This increased localisation in the ES is also broadly supported by the results from theoretical NBO analysis. The σ(N–O) bond in the GS is 55.5% localised on O in N(1)–O(1) and 51.3% in N(1)–O(2), as an average over the α and β spin orbitals, with bond orders of 1.30 and 1.21 respectively (Table S2.7†). This transforms to an average of 54.4% localisation on O in N(1A)–O(1A) and 56.3% in N(1A)–O(2A) in the ES, with less equal bond orders of 1.16 and 1.34, indicating that, overall, the σ(N–O) bonds are slightly more polar in the ES. For the ES nitrito-(η1-
O2), in line with, though less pronounced than, the differences seen for 1. This increased localisation in the ES is also broadly supported by the results from theoretical NBO analysis. The σ(N–O) bond in the GS is 55.5% localised on O in N(1)–O(1) and 51.3% in N(1)–O(2), as an average over the α and β spin orbitals, with bond orders of 1.30 and 1.21 respectively (Table S2.7†). This transforms to an average of 54.4% localisation on O in N(1A)–O(1A) and 56.3% in N(1A)–O(2A) in the ES, with less equal bond orders of 1.16 and 1.34, indicating that, overall, the σ(N–O) bonds are slightly more polar in the ES. For the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ligand, as in 1, charge is primarily concentrated into the N(1A) lone pair, which is evident in the deformation density (Fig. 4(d)) and in the positions of the calculated N–O BCPs, which both move symmetrically 1% closer to the central nitrogen atom in the ES (Fig. S2.3†).
NO) ligand, as in 1, charge is primarily concentrated into the N(1A) lone pair, which is evident in the deformation density (Fig. 4(d)) and in the positions of the calculated N–O BCPs, which both move symmetrically 1% closer to the central nitrogen atom in the ES (Fig. S2.3†).
Despite the similarities in the EDD within the isomerising ligands, experimental bond lengths show that the NiII–nitrite bond distance actually decreases by −0.0221(14) Å on excitation of 2, which is again the opposite change to that seen in 1. This decrease in the bond length is not particularly well evidenced in the deformation density (Fig. 4(c) vs (d)) where there appears to be stronger matching of the GS N(1) lone pair with the 3dz2 acceptor orbital compared to the corresponding O(1A) → Ni(1) donation in the ES. Similarly, comparison of the Laplacian plots (Fig. 5(c) vs (d)) shows a larger, more diffuse region of −∇2ρ(r) at N(1) that has greater extension towards the metal than the corresponding ES feature, which would typically indicate better n → 3d* donation in the GS.
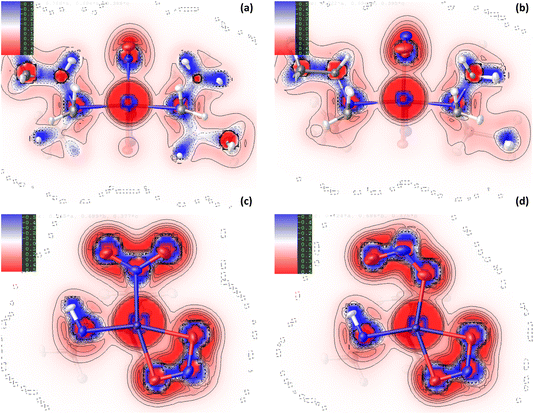
![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) maintained in the ES isomer. However, the key change in NCIs highlighted by Fig. 6 is the intramolecular N(4)–H(4)⋯O(2) hydrogen bond, which is necessarily disrupted by photoswitching in the nitrite group. Topological analysis confirms the presence of a bond path between O(2) and H(4) in the GS and O(2A) and H(4) in the ES, with BCPs identified at 63% and 62% along the O → H direction, respectively. In Fig. 6(a)/(d), this interaction is captured by the blue/green “spike” at ca. −0.026 sign(λ2ρ) in the GS scatterplot, which shifts to ca. −0.028 sign(λ2ρ) in the ES and a very slightly lower value of s. These changes suggest that the N–H⋯O interaction becomes slightly shorter and stronger on excitation, a fact supported by the experimental D⋯A hydrogen bond distances (ΔO(2/2A)⋯N(4) = −0.032(1) Å). Isosurface plots of s from HAR analysis (Fig. 6(e)/(f) and S2.4†) support the ab initio NCI analysis, highlighting the same intramolecular N–H⋯O and weaker C–H⋯O hydrogen bonding interactions to the nitrite ligand, as well as the steric repulsions involving the Et4dien co-ligand. Interestingly, however, the HAR s plots suggest there may be some evidence of a weak O(2A)⋯Ni(1) interaction, c.f. the O(2A)⋯Pd(1) NCI found for complex 1. In Fig. 6(f) there is clearly an additional NCI feature along the O(2A) → Ni(1) direction in the ES, which is not evident in the GS (Fig. 6(e)). The theoretical analysis does not find a bond path or BCP along O(2A) → Ni(1), which may suggest that any NCI here is weak, at best. However, it is interesting that the HAR finds evidence of similar nitrito → metal NCIs in both the Pd and Ni complexes.
O2) maintained in the ES isomer. However, the key change in NCIs highlighted by Fig. 6 is the intramolecular N(4)–H(4)⋯O(2) hydrogen bond, which is necessarily disrupted by photoswitching in the nitrite group. Topological analysis confirms the presence of a bond path between O(2) and H(4) in the GS and O(2A) and H(4) in the ES, with BCPs identified at 63% and 62% along the O → H direction, respectively. In Fig. 6(a)/(d), this interaction is captured by the blue/green “spike” at ca. −0.026 sign(λ2ρ) in the GS scatterplot, which shifts to ca. −0.028 sign(λ2ρ) in the ES and a very slightly lower value of s. These changes suggest that the N–H⋯O interaction becomes slightly shorter and stronger on excitation, a fact supported by the experimental D⋯A hydrogen bond distances (ΔO(2/2A)⋯N(4) = −0.032(1) Å). Isosurface plots of s from HAR analysis (Fig. 6(e)/(f) and S2.4†) support the ab initio NCI analysis, highlighting the same intramolecular N–H⋯O and weaker C–H⋯O hydrogen bonding interactions to the nitrite ligand, as well as the steric repulsions involving the Et4dien co-ligand. Interestingly, however, the HAR s plots suggest there may be some evidence of a weak O(2A)⋯Ni(1) interaction, c.f. the O(2A)⋯Pd(1) NCI found for complex 1. In Fig. 6(f) there is clearly an additional NCI feature along the O(2A) → Ni(1) direction in the ES, which is not evident in the GS (Fig. 6(e)). The theoretical analysis does not find a bond path or BCP along O(2A) → Ni(1), which may suggest that any NCI here is weak, at best. However, it is interesting that the HAR finds evidence of similar nitrito → metal NCIs in both the Pd and Ni complexes.
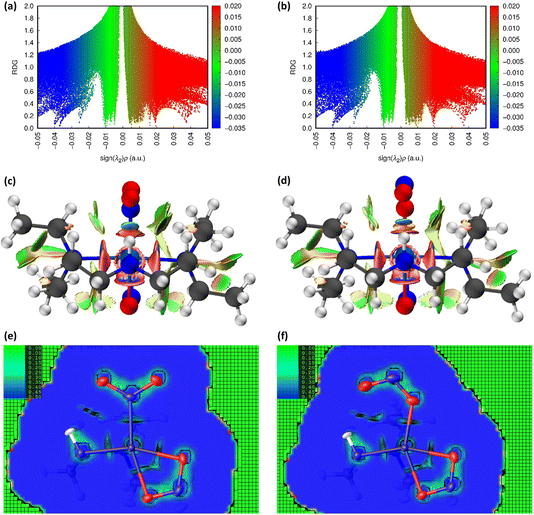 | ||
Fig. 6 Non-covalent interaction (NCI) analysis for the GS and ES isomers of 2, using the reduced density gradient (RDG, s). Theoretical analysis: (a) plot of s vs sign(λ2ρ) for GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and (b) plot of s vs sign(λ2ρ) for ES nitro-(η1- O2) and (b) plot of s vs sign(λ2ρ) for ES nitro-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO), providing a fingerprint of the NCIs in each isomer [generated in Multiwfn25 and visualised in Gnuplot33]. (c) 3D plot of s isosurfaces (s = 0.5 a.u.) for GS nitro-(η1- NO), providing a fingerprint of the NCIs in each isomer [generated in Multiwfn25 and visualised in Gnuplot33]. (c) 3D plot of s isosurfaces (s = 0.5 a.u.) for GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and (d) 3D plot of s isosurfaces (s = 0.5 a.u.) for ES nitrito-(η1- O2) and (d) 3D plot of s isosurfaces (s = 0.5 a.u.) for ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO), highlighting the key NCIs in each isomer: colour-coding links to (a)/(b) plots with red = regions of sign(λ2ρ) > 0 i.e. steric interactions, green = regions of sign(λ2ρ) ≈ 0 and blue = regions of sign(λ2ρ) < 0 i.e. bonding interactions e.g. hydrogen bonds [generated in Multiwfn and visualised in VMD26]. HAR analysis: (e) 2D s (RDG) map for the GS structure of 2 in the Ni(1), N(1), O(1), O(2) plane and (f) 2D s (RDG) map for the ES structure of 2 in the Ni(1), O(1A), N(1A), O(2A) plane, showing key NCIs in the asymmetric unit [generated by HAR in NoSpherA2 NO), highlighting the key NCIs in each isomer: colour-coding links to (a)/(b) plots with red = regions of sign(λ2ρ) > 0 i.e. steric interactions, green = regions of sign(λ2ρ) ≈ 0 and blue = regions of sign(λ2ρ) < 0 i.e. bonding interactions e.g. hydrogen bonds [generated in Multiwfn and visualised in VMD26]. HAR analysis: (e) 2D s (RDG) map for the GS structure of 2 in the Ni(1), N(1), O(1), O(2) plane and (f) 2D s (RDG) map for the ES structure of 2 in the Ni(1), O(1A), N(1A), O(2A) plane, showing key NCIs in the asymmetric unit [generated by HAR in NoSpherA2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9. 9. | ||
Discussion
Enhanced understanding of the key intra- and intermolecular interactions in 1 and 2, provided by the charge density analyses, allow us to equate the key bonding features with physical properties of the crystals, which can be used in the future design of new and improved photoswitches. The EDD and NCI analyses outlined in the Results highlight some common themes between the two photoactive linkage isomer crystals that are interesting to compare and contrast.Bonding and stability of the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/h3_char_004f_0332.gif) NO) isomer
NO) isomer
An important result for both 1 and 2 is that the O(2A) atom in the ES endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ligand appears to make a stabilising intramolecular NCI with the metal in both systems. This is an interesting feature that is not immediately apparent on first-glance at the ES crystal structures obtained by traditional IAM refinement, as the atom–atom distances and angles indicate that O(2A) does not create any formal bonding interaction in either system.16,17 The presence of such a stabilising interaction in both structures suggests that it is preferential for the endo-nitrito-(η1-
NO) ligand appears to make a stabilising intramolecular NCI with the metal in both systems. This is an interesting feature that is not immediately apparent on first-glance at the ES crystal structures obtained by traditional IAM refinement, as the atom–atom distances and angles indicate that O(2A) does not create any formal bonding interaction in either system.16,17 The presence of such a stabilising interaction in both structures suggests that it is preferential for the endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) arrangement to seek out some stabilising influence, and the fact this happens in two systems that are capable of very high ES population levels is notable.
NO) arrangement to seek out some stabilising influence, and the fact this happens in two systems that are capable of very high ES population levels is notable.
It is less surprising that in 2 the nitrite ligand forms a stabilising hydrogen bonding NCI with the available N–H donor on Et4dien. This intramolecular N–H⋯O bond can be classified as moderately-strong34 and it is clear that it is the most important NCI to the nitrite ligand for complex 2. A comparison of the NCI analyses (for 1 and 2) indicate that the N(4)–H(4)⋯O(2A) in 2 is a stronger and more stabilising contact than the Pd(1)⋯O(2A) interaction, which is the only key stabilising NCI to the nitrite in 1. This is evident in a comparison of the EDDs, where for 2 there is clear matching of regions of electron accumulation on O(2A) and depletion at H(4) for the formation of the bonding NCI (Fig. 4(d)), compared with poorer overlap in 1 between the available O(2A) lone pair with the 4dx2−y2 acceptor orbital in Fig. 1(d). The NCI analysis also supports this comparison. Contrasting the ES scatterplots for 1 (Fig. 3(b)) and 2 (Fig. 6(b)), we can see that the hydrogen bond interaction in 2 is associated with a smaller reduced density gradient of s ≈ 0.05, indicating a more strongly bonding NCI, compared with a value of s ≈ 0.10 for the Pd(1)⋯O(2A) interaction. Theoretical studies on related metal-nitrite systems in the literature predict similar stabilising interactions between endo-nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) and suitable donor groups within the molecule, where available,30 however a broader investigation of other linkage isomer switches, capable of achieving different final ES population levels, is required to make a thorough assessment of how necessary such NCIs are to facilitate good nitro → nitrito photoswitching. Another key comparison is that the formal metal–nitrite bonding interaction Pd(1)–N(1)/O(1A) in 1 is lengthened and weakened on excitation, while conversely the analogous Ni(1)–N(1)/O(1A) bond in 2 appears to strengthen with irradiation. It is possible that this difference reflects HSAB theory, as it might be expected that the “hard” O-donor in the ES nitrito-(η1-
NO) and suitable donor groups within the molecule, where available,30 however a broader investigation of other linkage isomer switches, capable of achieving different final ES population levels, is required to make a thorough assessment of how necessary such NCIs are to facilitate good nitro → nitrito photoswitching. Another key comparison is that the formal metal–nitrite bonding interaction Pd(1)–N(1)/O(1A) in 1 is lengthened and weakened on excitation, while conversely the analogous Ni(1)–N(1)/O(1A) bond in 2 appears to strengthen with irradiation. It is possible that this difference reflects HSAB theory, as it might be expected that the “hard” O-donor in the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) should have better affinity for NiII than for PdII, as the 3d8 metal is also expected to be the Lewis acid.
NO) should have better affinity for NiII than for PdII, as the 3d8 metal is also expected to be the Lewis acid.
All of the above results indicate that the nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomer should be a more stable ES for complex 2 relative to complex 1, which should have some manifestation in the physical properties of each system. For 2, we note that the nitrito-(η1-
NO) isomer should be a more stable ES for complex 2 relative to complex 1, which should have some manifestation in the physical properties of each system. For 2, we note that the nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomer can be thermally-occupied and is present at room temperature,17 while conversely, in 1 the ES nitrito-(η1-
NO) isomer can be thermally-occupied and is present at room temperature,17 while conversely, in 1 the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomer has only ever been observed as a light-induced metastable state. This fits with the conclusion from charge density analysis that nitrito-(η1-
NO) isomer has only ever been observed as a light-induced metastable state. This fits with the conclusion from charge density analysis that nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is better stabilised in 2 than in 1, and potentially explains the thermal accessibility of endo-nitrito in complex 2 under ambient conditions.
NO) is better stabilised in 2 than in 1, and potentially explains the thermal accessibility of endo-nitrito in complex 2 under ambient conditions.
It should also be noted that the nitrite ligands in 1 and 2 are involved in van der Waals NCIs (green in the NCO analyses) with alkyl moieties on the ethylenetriamine co-ligands, which are found to shorten quite significantly in the ES of 1, but do not change significantly for 2. However, as the NCI analysis clearly shows that these C–H⋯O contacts have a less bonding character than the Pd(1)⋯O(2A) and N(4)–H(4)⋯O(2A) interactions, this indicates that they are less likely to be as influential.
In terms of the photostability of the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) arrangements, the HAR and NCI analyses do not provide any significant new understanding. For both 1 and 2, nitrito-(η1-
NO) arrangements, the HAR and NCI analyses do not provide any significant new understanding. For both 1 and 2, nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is the photoinduced metastable state, which suggests that it should be less stable than nitro-(η1-
NO) is the photoinduced metastable state, which suggests that it should be less stable than nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2). Additionally, comparison of the photoreaction rates and metastable limits indicates that the ES isomer is more favourable in 1, as it can be accessed more quickly (>15 min irradiation for 100% population in 1, vs ∼1 h for 2) and remains metastable to a higher critical temperature (240 K in 1vs 140 K in 2).16,18 It is therefore evident that the photoexcited state stability must be influenced by other factors than the EDD. These likely include the absorption properties and photophysics of the material, kinetic factors e.g. the relative kinetic lability of the differing metal centres, and steric influences from the surrounding crystal lattice. Many of these factors have been discussed by us5,28,35,36 and others37–43 previously, and this conclusion highlights the complexity of rationally-designing solid-state photoswitchable crystals and the importance of considering the many, and often competing, influential factors that govern the photoreaction.
O2). Additionally, comparison of the photoreaction rates and metastable limits indicates that the ES isomer is more favourable in 1, as it can be accessed more quickly (>15 min irradiation for 100% population in 1, vs ∼1 h for 2) and remains metastable to a higher critical temperature (240 K in 1vs 140 K in 2).16,18 It is therefore evident that the photoexcited state stability must be influenced by other factors than the EDD. These likely include the absorption properties and photophysics of the material, kinetic factors e.g. the relative kinetic lability of the differing metal centres, and steric influences from the surrounding crystal lattice. Many of these factors have been discussed by us5,28,35,36 and others37–43 previously, and this conclusion highlights the complexity of rationally-designing solid-state photoswitchable crystals and the importance of considering the many, and often competing, influential factors that govern the photoreaction.
Competing influence of auxiliary ligands
Both complexes contain auxiliary ligands that are photoinert and thus are not observed to change significantly on excitation. 1 and 2 both contain chelating diethylenetriamine co-ligands, though with differing alkyl substitutions and, owing to the differing crystal fields of the 3d and 4d Group 10 metal centres, display differing coordination geometries at the metal. Despite this variety, it is possible to draw some comparisons as to the influence of the co-ligands on the photoswitchable nitrite ligand, and vice versa.The analysis of the EDD in 1 and 2 agrees that there is a more pronounced localisation of charge in the ES nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) ligands than in GS nitro-(η1-
NO) ligands than in GS nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2). The results for complex 1 highlight that this indicates a reduction in the σ-donor ability of nitrito-(η1-
O2). The results for complex 1 highlight that this indicates a reduction in the σ-donor ability of nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO), as the greater degree of localisation provides less density for dative bonding to the metal centre. It follows from this observed change in σ-donor ability that nitro-(η1-
NO), as the greater degree of localisation provides less density for dative bonding to the metal centre. It follows from this observed change in σ-donor ability that nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) is a stronger-field ligand than nitrito-(η1-
O2) is a stronger-field ligand than nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO), reflecting the fact that nitro-(η1-
NO), reflecting the fact that nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) is typically reported to be higher in the spectrochemical series.44 Given this, it might be expected that some evidence of a change in trans-influence can be found in the bond lengths, CCs and BCP positions between Pd(1)/Ni(1) and the auxiliary ligands in 1 and 2, respectively.
O2) is typically reported to be higher in the spectrochemical series.44 Given this, it might be expected that some evidence of a change in trans-influence can be found in the bond lengths, CCs and BCP positions between Pd(1)/Ni(1) and the auxiliary ligands in 1 and 2, respectively.
As discussed earlier, for complex 1 while the Pd–nitrite bond distance increases on excitation, the experimental and theoretical Pd–Bu4dien bond lengths all shorten in the ES, including the Pd(1)–N(3) distance directly trans- to the isomerising group. Thus, at first glance there does appear to be a shift in trans-influence on excitation of 1, based on bond length changes alone, as the switch to the weaker-field nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) donor is expected to correlate with a shortening, and thus strengthening, of the metal–ligand bond length trans- to itself (i.e. the Pd(1)–N(3) distance). Conversely, comparison of the calculated Pd–N bond orders for the GS and ES structures tends not to support this observation. Table S1.7† shows that the Pd(1)–N(3) bond order actually decreases from 0.63 in the GS to 0.59 in the ES, despite the observed (and calculated) bond shortening, although the cis-coordinated Pd(1)–N(2) and Pd(1)–N(4) bonds do show the expected bond order increase. The topological analysis does not provide strong evidence for either interpretation, with no significant shift in the positions of (3,−1) BCPs, as a percentage along their bond paths (Fig. S1.3†). However, a visual comparison of Fig. 1(a) and (b) reveals that the N(3) lone pair is more diffuse along the Pd → N direction in the ES than in the GS, which would indicate a strengthening of the Pd(1)–N(3) bond and therefore support the interpretation of some trans-influence evident in complex 1. A similar analysis can be completed for complex 2 to try and assess the validity of significant trans-influence. In contrast to 1, the Ni–nitrite bond distance actually decreases on excitation, which is at odds with the visual assessment of the EDD in the GS and ES and does not support the idea that nitrito-(η1-
NO) donor is expected to correlate with a shortening, and thus strengthening, of the metal–ligand bond length trans- to itself (i.e. the Pd(1)–N(3) distance). Conversely, comparison of the calculated Pd–N bond orders for the GS and ES structures tends not to support this observation. Table S1.7† shows that the Pd(1)–N(3) bond order actually decreases from 0.63 in the GS to 0.59 in the ES, despite the observed (and calculated) bond shortening, although the cis-coordinated Pd(1)–N(2) and Pd(1)–N(4) bonds do show the expected bond order increase. The topological analysis does not provide strong evidence for either interpretation, with no significant shift in the positions of (3,−1) BCPs, as a percentage along their bond paths (Fig. S1.3†). However, a visual comparison of Fig. 1(a) and (b) reveals that the N(3) lone pair is more diffuse along the Pd → N direction in the ES than in the GS, which would indicate a strengthening of the Pd(1)–N(3) bond and therefore support the interpretation of some trans-influence evident in complex 1. A similar analysis can be completed for complex 2 to try and assess the validity of significant trans-influence. In contrast to 1, the Ni–nitrite bond distance actually decreases on excitation, which is at odds with the visual assessment of the EDD in the GS and ES and does not support the idea that nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is the weaker-field ligand in this case. All metal–ligand distances to the auxiliary Et4dien and nitrito-(η2-
NO) is the weaker-field ligand in this case. All metal–ligand distances to the auxiliary Et4dien and nitrito-(η2-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,
,![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) N) ligands are found to increase in the ES isomer, with the largest change in the Ni(1)–O(4) bond (trans- to the isomerising group and so competing for the 3dz2 acceptor orbital). The theoretical bond orders agree with the experimental bond length changes (Table S2.7†), indicating a strengthening of the Ni–nitrite interaction on excitation and a corresponding weakening in the bonding interactions to the auxiliary ligands. Topological analysis again provides only limited information, with very little change observed on excitation excepting that while the Ni(1)–O(4) BCP moves 1% closer to NiII in the ES isomer on excitation, the Ni(1)–N(1)/O(1A) BCP mirrors this change, moving 1% closer to the nitrite ligand (Fig. S2.3†). In summary, though the changes for complex 2 are the reverse of those seen in complex 1, in both systems there appears to be some synergistic changes in the EDD of the isomerising nitrite group and the ligands trans- to them, which must compete for the same d-orbitals on the metal. As such, there appears to be some evidence of trans-influence in the EDD for both 1 and 2, although the question of whether nitro-(η1-
N) ligands are found to increase in the ES isomer, with the largest change in the Ni(1)–O(4) bond (trans- to the isomerising group and so competing for the 3dz2 acceptor orbital). The theoretical bond orders agree with the experimental bond length changes (Table S2.7†), indicating a strengthening of the Ni–nitrite interaction on excitation and a corresponding weakening in the bonding interactions to the auxiliary ligands. Topological analysis again provides only limited information, with very little change observed on excitation excepting that while the Ni(1)–O(4) BCP moves 1% closer to NiII in the ES isomer on excitation, the Ni(1)–N(1)/O(1A) BCP mirrors this change, moving 1% closer to the nitrite ligand (Fig. S2.3†). In summary, though the changes for complex 2 are the reverse of those seen in complex 1, in both systems there appears to be some synergistic changes in the EDD of the isomerising nitrite group and the ligands trans- to them, which must compete for the same d-orbitals on the metal. As such, there appears to be some evidence of trans-influence in the EDD for both 1 and 2, although the question of whether nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) or nitrito-(η1-
O2) or nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) is the weaker field ligand in both ligand fields is not clear.
NO) is the weaker field ligand in both ligand fields is not clear.
As well as the possible influence of HSAB rules, discussed above, another explanation for the apparently conflicting bond length changes between 1 and 2 is that there are competing steric and electronic effects that have a combined influence on the geometric parameters seen. For example, in complex 1 it is evident that in the ES the PdII 4dx2−y2 orbital is forced to tilt slightly to accommodate bonding to O(1A) (Fig. 1(c) vs (d)). This results in better overlap between 4dx2−y2 and donor lone pairs on Bu4dien, particularly for N(3), which can also account for the shortened Pd–N bond lengths. This is supported by more diffuse VSCCs for the ES isomer, indicating better donor–acceptor overlap (Fig. 2(d)) and by a reduction of the RMS deviation from the ideal square plane in the ES (GS RMSD for Pd(1), N(1), (N2), N(3) and (N4) = 0.0976, compared to ES RMSD for Pd(1), O(1A), N(2), N(3), N(4) = 0.0652). It is possible that, to accommodate the required geometry changes for best Pd–Bu4dien overlap, whilst also maintaining the Bu4dien’s chelating “bite” around PdII, the Pd(1)–N(3) bond is also forced to contract, regardless of any underlying trans-influence. For 2, though any reorientation of 3dz2 is less obvious in Fig. 4(c)/(d), any tilting would be less well accommodated by the bidentate nitrito-(η1-O,ON) ligand, which necessarily has a more restricted “bite” angle, leading to an overall lengthening of the Ni–η2-nitrito interaction. Steric crowding around each metal centre may also have an effect on the achievable metal–ligand overlap, which necessarily varies for the two different coordination environments. If steric and electronic influences are in competition, this clearly complicates the interpretation of simple geometric parameters, e.g. bond lengths and angles, which makes a stronger argument for the use of more involved analyses, such as HAR and charge density studies, to further investigate the complex variations in metal–ligand bonding between the GS and ES.
Interactions with the wider crystal structure
The benefit of HAR over the theoretical analyses presented here is that NoSpherA2 can incorporate interactions within the whole asymmetric unit of the crystal structure, whereas the ab initio calculations in this report are generated only for the isolated photoactive molecules. This is particularly useful in the case of 1, where additional components are present in the asymmetric unit. As such, we can make a limited assessment of the influence of intermolecular interactions by considering the NCIs between [Pd(Bu4dien)(NO2)]+, BPh4 and THF, using the HAR analysis already presented. There is no evidence of significant NCIs between the BPh4 anion and photoactive cation in either the deformation density or Laplacian plots. However, both the EDD and NCI analysis confirm the expected presence of an intermolecular N(3)–H(3)⋯O(3) hydrogen bond between the Bu4dien auxiliary ligand and the THF molecule. While this hydrogen bond does not directly involve any atoms of the isomerising nitrite ligand, its presence will affect the N(3)–H(3) group which, as discussed above, has the potential to exact some trans-influence on the η1-nitrite group. Comparison of the experimental N(3)⋯O(3) D⋯A and H(3)⋯O(3) H⋯A distances shows that the hydrogen bond lengthens by a small, but significant amount on excitation (ΔN(3)⋯O(3) = +0.024(2) Å, ΔH(3)⋯O(3) = +0.06(3) Å). This indicates a slightly stronger hydrogen bond in the GS, and concurrently slightly less electron density available in N(4)–H(4) for subsequent donation to Pd(1). This compares well to the EDDs shown in Fig. 1 and 2. As discussed in the Results, the N-donor VSCCs, including N(3), are more localised in the GS of 1 than the ES, providing reduced overlap for dative covalent bonding to Pd(1) and manifesting in a larger PdII–Bu4dien coordination sphere. There is also slightly more extension of the VSCCs along the H(3)⋯O(3) hydrogen bonding direction, and more diffuse CC within N(3)–H(3), for the GS (Fig. 1(c) vs (d)) which supports the observation of a shorter, stronger hydrogen bond in the GS. The results all indicate that the intermolecular hydrogen bond can influence the N(3)–Pd(1) bonding, and appears to act in synergy with any possible trans-influence on Pd(1)–NO2. This shows that it is important to consider the effects that all components, and potential components, could have on a photoactive crystal system at the design stage, which includes the choice of solvents both for synthesis and crystallisation.Finally, it should be noted that, while the HAR analysis presented allows some analysis of intermolecular interactions within the asymmetric unit, it does not account for interactions between adjacent asymmetric units and so provides no insight into the influence of the wider crystal structure. This is the key disadvantage for semi-empirical methods over experimental charge density studies, e.g. multipolar refinements, as some level of approximation must still be made in the wavefunction calculation. Previous studies have shown it is possible to take into account some of these wider interactions, for example by running HAR on dimers of the target unit across symmetry positions and assessing how the EDD changes in reference to the isolated unit.13 Unfortunately, this is beyond the scope of the current study as, due to the size and complexity of 1 and 2 this approach is too computationally intensive to be viable. For 1 and 2, intermolecular NCIs to the nitrite ligand are exclusively C–H⋯O and C–H⋯N short contacts that, while expected to be weaker in nature, may still have a combined effect in stabilising the nitro-(η1-![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) O2) and/or nitrito-(η1-
O2) and/or nitrito-(η1-![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) NO) isomers.16,18 As such, future work will look to improve on these limitations, aiming to incorporate nearest neighbours into the HAR analysis.
NO) isomers.16,18 As such, future work will look to improve on these limitations, aiming to incorporate nearest neighbours into the HAR analysis.
Conclusions
This study has shown that it is possible to use HAR to conduct charge density analyses on photoswitchable organometallic small molecule crystals of both medium and relatively large size, in both their ground and 100% photoexcited states. In combination with ab initio gas phase DFT calculations, these studies provide detailed insight into the EDDs and key NCIs that have some influence on the physical properties, most particularly on the thermal stability of the endo-nitrito isomer. Though there are some key limitations, e.g. an inability to take into account potentially important intermolecular interactions in the wider crystal structure, this initial study proves the validity of using NoSpherA2 to study photoactive linkage isomer crystals, and this method could easily be extended to other photoswitches of similar size and complexity, for e.g. photocatalytic systems. In future we plan to extend this approach to more complicated systems, e.g. crystals that only reach partial excitation at their maximum irradiation time,22,45 and whose diffraction power becomes considerably limited as a result of light damage on irradiation.46Author contributions
L. E. H. is responsible for the conceptualisation, methodology, data collection, formal analysis and visualisation of the data presented, writing (original draft), reviewing and editing the manuscript and for project administration and funding acquisition. L. K. S. contributed to the methodology and writing the manuscript (review and editing). B. A. C. is responsible for synthesis and crystallisation of the target materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. E. H. and B. A. C. are grateful for to the Royal Society for support (URF\R1\191104). In performing DFT calculations with Gaussian-09 we acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government. The authors are also grateful Florian Kleemiss for useful discussions on using the NoSpherA2 interface, particularly in the generation of ideal images for publication.Notes and references
- L. Zeng, X. Guo, C. He and C. Duan, ACS Catal., 2016, 6, 7935–7947 CrossRef CAS.
- H. Tsai, R. Asadpour, J.-C. Blancon, C. C. Stoumpos, O. Durand, J. W. Strzalka, B. Chen, R. Verduzco, P. M. Ajayan, S. Tretiak, J. Even, M. A. Alam, M. G. Kanatzidis, W. Nie and A. D. Mohite, Science, 2018, 360, 67 CrossRef CAS PubMed.
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- P. Coppens, Angew. Chem., Int. Ed., 2009, 48, 4280–4281 CrossRef CAS PubMed.
- L. E. Hatcher and P. R. Raithby, CrystEngComm, 2017, 19, 6297–6304 RSC.
- E. D. Stevens and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 536–539 CrossRef.
- P. Coppens, T. N. Gururow, P. Leung, E. D. Stevens, P. J. Becker and Y. W. Yang, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 63–72 CrossRef.
- N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921 CrossRef.
- F. Kleemiss, O. V. Dolomanov, M. Bodensteiner, N. Peyerimhoff, L. Midgley, L. J. Bourhis, A. Genoni, L. A. Malaspina, D. Jayatilaka, J. L. Spencer, F. White, B. Grundkötter-Stock, S. Steinhauer, D. Lentz, H. Puschmann and S. Grabowsky, Chem. Sci., 2021, 12, 1675–1692 RSC.
- B. Dittrich, C. B. Hubschle, K. Propper, F. Dietrich, T. Stolper and J. J. Holstein, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 91–104 CrossRef CAS PubMed.
- S. Domagala, B. Fournier, D. Liebschner, B. Guillot and C. Jelsch, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 337–351 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- L. K. Saunders, A. R. Pallipurath, M. J. Gutmann, H. Nowell, N. Zhang and D. R. Allan, CrystEngComm, 2021, 23, 6180–6190 RSC.
- G. Novelli, C. J. McMonagle, F. Kleemiss, M. Probert, H. Puschmann, S. Grabowsky, H. E. Maynard-Casely, G. J. McIntyre and S. Parsons, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2021, 77, 785–800 CrossRef CAS.
- M. Chocolatl Torres, S. Bernès and U. Salazar Kuri, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2021, 77, 681–685 CrossRef CAS PubMed.
- L. E. Hatcher, CrystEngComm, 2016, 18, 4180–4187 RSC.
- L. E. Hatcher, M. R. Warren, D. R. Allan, S. K. Brayshaw, A. L. Johnson, S. Fuertes, S. Schiffers, A. J. Stevenson, S. J. Teat, C. H. Woodall and P. R. Raithby, Angew. Chem., Int. Ed., 2011, 50, 8371–8374 CrossRef CAS PubMed.
- L. E. Hatcher, J. Christensen, M. L. Hamilton, J. Trincao, D. R. Allan, M. R. Warren, I. P. Clarke, M. Towrie, D. S. Fuertes, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem.–Eur. J., 2014, 20, 3128–3134 CrossRef CAS PubMed.
- CrysAlis Pro, Rigaku Oxford Diffraction Data Collection and Data Reduction GUI, Version 171.41.107a .
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- S. K. Brayshaw, J. W. Knight, P. R. Raithby, T. L. Savarese, S. Schiffers, S. J. Teat, J. E. Warren and M. R. Warren, J. Appl. Crystallogr., 2010, 43, 337–340 CrossRef CAS.
- L. E. Hatcher, CrystEngComm, 2018, 20, 5990–5997 RSC.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- L. E. Hatcher, M. R. Warren, J. M. Skelton, A. R. Pallipurath, L. K. Saunders, D. R. Allan, P. Hathaway, G. Crevatin, D. Omar, B. H. Williams, B. A. Coulson, C. C. Wilson and P. R. Raithby, Commun. Chem., 2022, 5, 102 CrossRef CAS PubMed.
- L. E. Hatcher, J. M. Skelton, M. R. Warren, C. Stubbs, E. L. da Silva and P. R. Raithby, Phys. Chem. Chem. Phys., 2018, 20, 5874–5886 RSC.
- F. Cortés-Guzmán and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef.
- J. T. Muya, H. Chung and S. U. Lee, RSC Adv., 2018, 8, 3328–3342 RSC.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. A. Boto, J.-P. Piquemal and J. Contreras-García, Theor. Chem. Acc., 2017, 136, 139 Search PubMed.
- Gnuplot v 5.4 (October 2022), Portable Graphing Utility, http://www.gnuplot.info/, accessed on 08/11/2022.
- G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxfor University Press, 1997 Search PubMed.
- L. E. Hatcher, J. M. Skelton, M. R. Warren and P. R. Raithby, Acc. Chem. Res., 2019, 52, 1079–1088 CrossRef CAS PubMed.
- M. R. Warren, S. K. Brayshaw, L. E. Hatcher, A. L. Johnson, S. Schiffers, A. J. Warren, S. J. Teat, J. E. Warren, C. H. Woodall and P. R. Raithby, Dalton Trans., 2012, 41, 13173–13179 RSC.
- A. A. Mikhailov, V. Y. Komarov, A. S. Sukhikh, D. P. Pishchur, D. Schaniel and G. A. Kostin, New J. Chem., 2020, 44, 18014–18024 RSC.
- B. Cormary, S. Ladeira, K. Jacob, P. G. Lacroix, T. Woike, D. Schaniel and I. Malfant, Inorg. Chem., 2012, 51, 7492–7501 CrossRef CAS PubMed.
- D. Schaniel and T. Woike, Phys. Chem. Chem. Phys., 2009, 11, 4391–4395 RSC.
- S. O. Sylvester and J. M. Cole, J. Phys. Chem. Lett., 2013, 4, 3221–3226 CrossRef CAS.
- J. M. Cole, K. F. Bowes, I. P. Clark, K. S. Low, A. Zeidler, A. W. Parker, I. R. Laskar and T.-M. Chen, Cryst. Growth Des., 2013, 13, 1826–1837 CrossRef CAS.
- A. Makal, J. Benedict, E. Trzop, J. Sokolow, B. Fournier, Y. Chen, J. A. Kalinowski, T. Graber, R. Henning and P. Coppens, J. Phys. Chem. A, 2012, 116, 3359–3365 CrossRef CAS PubMed.
- P. Coppens and S.-L. Zheng, in Supramolecular Photochemistry, John Wiley & Sons, Inc., 2011, pp. 155–174 Search PubMed.
- P. Atkins, P. W. Atkins and D. F. Shriver, Shriver & Atkins inorganic chemistry, W.H. Freeman, 2006 Search PubMed.
- B. A. Coulson and L. E. Hatcher, CrystEngComm, 2022, 24, 3701–3714 RSC.
- M. R. Warren, T. L. Easun, S. K. Brayshaw, R. J. Deeth, M. W. George, A. L. Johnson, S. Schiffers, S. J. Teat, A. J. Warren, J. E. Warren, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem.–Eur. J., 2014, 20, 5468–5477 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal structure data are not submitted to the CCDC as these structures are determined previously, CSD ref codes: WABGUE, WABHAL, WUZWIZ (1) and IYIPUC, IYIQIR, IYIRAK (2). See DOI: https://doi.org/10.1039/d2fd00158f |
| This journal is © The Royal Society of Chemistry 2023 |