Engineering of metal–organic frameworks (MOFs) for thermometry
Dashrathbhai B.
Kanzariya
 ,
Meetkumar Y.
Chaudhary
and
Tapan K.
Pal
,
Meetkumar Y.
Chaudhary
and
Tapan K.
Pal
 *
*
Department of Chemistry, Pandit Deendayal Energy University, Gandhinagar, Gujarat 382426, India. E-mail: tapan.pal@sot.pdpu.ac.in
First published on 3rd May 2023
Abstract
Metal–organic frameworks (MOFs ) are excellent candidates for use in chemistry, material sciences and engineering thanks to their interesting qualitative features and potential applications. Quite interestingly, the luminescence of MOFs can be engineered by regulation of the ligand design, metal ion selection and encapsulation of guest molecules within the MOF cavity. Temperature is a very crucial physical parameter and the market share of temperature sensors is rapidly expanding with technology and medicinal advancement. Among the wide variety of available temperature sensors, recently MOFs have emerged as potential temperature sensors with the capacity to precisely measure the temperature. Lanthanide-based thermometry has advantages because of its ratiometric response ability, high quantum yield and photostability, and therefore lanthanide-based MOFs were initially focused on to construct MOF thermometers. As science and technology have gradually changed, it has been observed that with the inclusion of dye, quantum dots, etc. within the MOF cavity, it is possible to develop MOF-based thermometry. This review consolidates the recent advances of MOF-based ratiometric thermometers and their mechanism of energy transfer for determining the temperature (thermal sensitivity and temperature uncertainty). In addition, some fundamental points are also discussed, such as concepts for guiding the design of MOF ratiometric thermometers, thermometric performance and tuning the properties of MOF thermometers.
1. Introduction
The importance of temperature and its sensing has been realized by many prodigious minds.1 Temperature plays an important role in numerous areas: the health sector, electronics systems, automobile parts, industrial environments, scientific experiments and biological phenomena.2–4 For precise monitoring of the temperature, we need to develop temperature sensors. The market share of temperature sensors in various sectors is presented in Fig. 1. The temperature sensor market was analysed by “Markets and Markets”, where it has been demonstrated that the market value for temperature sensors will be significantly enhanced from approximately 6 billion USD in 2020 to 8 billion USD by 2027.5 Therefore, the construction of suitable sensors that can measure the temperature gradient of any system or environment is imperative. In this regard, luminescence-based thermometers have recently been attracting the attention of researchers. Such luminescent sensors are normally prepared from quantum dots, organic dyes, polymers, ruthenium complexes or lanthanide-based materials with a suitable platform.6 Among them, lanthanide-based components and quantum dots are advantageous when considering the photostability of the fluorescence materials. Considering the platforms, diverse podiums such as mesoporous silica, coordination polymers, and inorganic materials are highly attractive.7,8 Recently, it has been noticed that luminescent metal–organic frameworks (MOFs) are excellent luminescent temperature sensors and particularly lanthanide-based luminescent MOFs are extremely appealing in this respect.9–15 | ||
| Fig. 1 Market share of temperature sensors in different sectors. These data obtained from ref. 5. | ||
MOFs are porous materials that are assembled from the connection between a metal ion (metal node or SBU) and an organic ligand. MOFs possess several crucial structural features, such as a regular organic–inorganic network,16,17 high crystallinity,18 porosity,19,20 flexibility,21,22 stability,23 host–guest interaction capability24 and easy functionalization25 with tuneable pore size.26 These features make them amenable to numerous potential applications, including sensing,27–30 catalysis,31,32 gas adsorption and sequestration,33–35 separation,36 and bio-application.37 Such structural features and potential applications can be finely modulated by judicial selection of the organic linker and metal ion.38
Regarding luminescent temperature sensing, the luminescence of MOFs is very important. The luminescence of MOFs can be induced by: (a) partitioning of the fluorophore moiety within the MOF channel, which prohibits aggregation-accelerated luminescence quenching, and (b) the PSM methodology of MOF allows the linker derivatization, ion (cation or anion) exchange, metal complexation and the inclusion of fluorophore molecules (dyes, quantum dots) to further assist in the regulation of the fluorescence property of MOFs. Such developments using MOFs have been nicely realized in many previous reports.39–41 Therefore, the fluorescence property of MOFs can be fine-tuned through the rational modulation of the various light emitting centres within the MOFs. Interestingly, lanthanide-based MOFs behave as multi-emissive and self-referencing sensors, where the ratiometric sensing property of the MOF would reveal the luminescence thermometry, allowing the construction of a temperature-sensing probe.42–46 Interestingly, the amalgamation of a fluorophore in the MOF network leads to the generations of thermometric probes.47,48 The diverse ligands that are employed for the construction of ratiometric MOF thermometers are listed in Scheme 1. These multi-emissive cum ratiometric-based temperature sensors are very accurate as the ratio of two distinct transitions leads to precise measurement of temperature.
In this review article, MOF-based thermometry is elaborated by first introducing fundamental concepts in optical thermometry. After that, some important concepts like the effects of the lanthanide and the organic chromophore, and enhancing the efficiency of the thermometer by chemical tuning, are also discussed. Finally, this review covers the applications along with the conclusions and future prospects.
2. Luminescence in MOFs and thermometry
The thermometry property of an MOF is related to its luminescence profile. As is quite well-known, emission occurs when the molecule comes down to the ground state from the excited state, which is accompanied with the release of a certain wavelength of light. This emission is divided into two categories: fluorescence and phosphorescence. The former is a quick process (10−15 s) and it occurs among energy levels of equal spin multiplicity. Conversely, phosphorescence is a delayed emission process and is associated with the emission between energy states with different spin multiplicity (T1 → S0). These two processes are known as radiative transitions. The famous Jablonski diagram is a very useful tool for understanding how the radiative and non-radiative transitions are connected with the luminescence process.49The luminescence profile of any probe can be evaluated based on a few factors and these are: (a) the changes in the luminescence intensity or the shifting of the emission maximum, (b) the quantum yield of the fluorophore and (c) the determination of the lifetime of the excited state, which can be obtained from the below equation:
 | (1) |
MOFs have a wide structural diversity that arises from the ligand, the guest molecules and the presence of inorganic ions or clusters.52,53 The photoluminescence of MOFs can arise from different approaches, such as LMCT, MLCT, MMCT, and LLCT, and also the included guest molecule within the network and the antenna effect (metal sensitization by linkers; particularly for lanthanides) control the fluorescence features of MOFs (Fig. 3).54 The charge transfer is generally from an area of higher charge density to one of lower charge density and has been used to explain the luminescence profile of molecules. The LMCT and MLCT concepts are used to explain the colour of the KMnO4 and tris(bipyridyl)iron(III) complex.55 The other two charge transfer transitions, MMCT and LLCT, are observed in many coordination complexes.56,57
 | ||
| Fig. 3 (a) Graphical presentation of the antenna effect (generally for the lanthanides) and (b) the different charge transfer approaches in MOFs. | ||
In MOFs, the linker and metal ions are assembled to construct a large network. Such connections engender a rigid and flexible architecture. Such structural flexibility can be fine-tuned with the judicious selection of the MOF-forming components. In addition, the formation of cavities in MOF scan also impact several of the potential features of MOFs. This porous space can capture a variety of fluorophore moieties. Consequently, the luminescence property of the MOF would be modified or changed. The above-mentioned charge transfers also occur within the MOF and virtually control the photo physical phenomena in the MOF. Pei and co-workers showed that the alternation of the LMCT process within the MOF network would result in fluoro-switching behaviour in the MOF.58 Two MOFs, Cu-ETTC and Gd-ETTC, were developed from the AIE ability ligand. The latter MOF is fluorescent, with an emission peak at 455 nm, while the former is almost non-emissive (Fig. 4). In the case of Cu-ETTC, with the occurrence of a strong LMCT process, Cu2+ is reduced to Cu1+, as confirmed from XPS analysis. This causes the luminescence quenching of Cu-ETTC.
 | ||
| Fig. 4 The construction of Gd-ETTC and Cu-ETTC from linker ETTC and the occurrence of the LMCT process. | ||
Feng and co-workers showed that the luminescent properties of an MOF can be tuned using structural variations.59 The authors derived two zinc-based MOFs: [Zn(PHTZ)(NIC)]2n and [Zn2(MTZ)(NIC)2(OH)]n·0.5nH2O by using linkers HMTZ, HPHTZ and HNIC with the Zn2+ ion. The former MOF is three-dimensional and the latter MOF is two-dimensional, and their structural variation arises from the diversity of the local environment. The 3D MOF showed the emission peak at 446 nm upon λex = 323 nm, which corresponds to the occurrence of LMCT and intraligand charge transfer, while the 2D framework displayed three distinct luminescence signals at 488, 454 and 393 nm upon λex = 313 nm.
Liu and co-workers described the synthesis of GDMU-4 from linker H4L5 and Zn2+ ions. The free linker and MOF exhibited luminescence signals at 435 and 415 nm upon excitation at 350 and 320 nm, respectively. The luminescence profile is ligand centred and the emission intensity of GDMU-4 is higher than that of the free linker. This is ascribed to the strong coordination of the linker to the Zn2+, which improves the rigidity of the system and thus reduces non-radiative transitions.60 Again, the same group functionalized the ligand H4L5 with a nitro group and a new linker H4DDN is formed, which formed another new zinc-based MOF. The emission peaks of the H4DDN and the new Zn-MOF were displayed at 438 and 430 nm upon λex at 320 and 290 nm, respectively.61 This is due to the MLCT process.
Li and co-workers constructed a Co-based framework, {[Co2(DIPT)4(PClA)2Cl2]·H2O}, which showed a blue shifted emission peak at 472 nm.62 This shift in wavelength is due to the MLCT process that is occurring within the MOF.
2.1. The origin of luminescence in MOFs is due to the presence of the linker
Organic linkers containing heterocyclic and/or carboxylic groups with π-conjugated backbones are generally favoured for the development of luminescent MOFs. Such a ligand architecture generally offers a stable network and the presence of available pi electrons travelling throughout the network reduces the HOMO–LUMO energy breach. Consequently, fascinating luminescence activity would ensue. It has been observed that the emission nature of the linker in an MOF is distinct from its free state with regard to peak position and peak intensity. The reason is the strong coordination action between the metal ion and the ligand, where the non-radiative decay rate is significantly reduced. Besides the role of the linker emission, the contribution from the metal ion towards the luminescence profile of MOFs has a great impact, particularly from lanthanide metal ions (vide infra).Cao and co-workers strategically altered the luminescence properties of MOFs through the linker exchange process.63 They initially synthesized UiO-66-(COOH)2, which underwent a post-synthetic linker exchange process with linker 1,4-naphthalene dicarboxylic acid to engender a new MOF UiO-66-hybrid. Interestingly, the MOFs UiO-66-(COOH)2 and UiO-66-hybrid exhibited emission peaks at 393 and 430 nm, respectively, upon λex at 365 nm. It has been noted that the emission peak of the hybrid MOF is blue-shifted by 50 nm in comparison to the linker H2NDC (λem = 480 nm).
The tuning of the luminescence property of MOF can be accomplished by metal exchange reaction in the metal nodes. For instance, Sun and co-workers utilized the linkers H3L6 and DABCO to synthesize a zinc-based MOF, {[Zn3(L6)2(DABCO)(H2O)]·9DMF}.64 They also derived an isostructural copper-based framework, {[Cu3(L6)2(DABCO)(H2O)]·15H2O·9DMF} (Cu-1), from the same linkers. The post-synthetic metal exchange reaction of {[Zn3(L6)2(DABCO)(H2O)]·9DMF} (Zn-1) leads to the construction of the MOF {[Zn2Cu(L6)2(DABCO)(H2O)]·11DMF·7H2O} (Zn-1′). However, under comparable experimental conditions, Cu-1 delivered Cu2Zn-MOF. These mixed metal MOFs could not be obtained through a de novo process. Remarkably, the luminescence intensities of these four frameworks are different. Specifically, the non-emissive Cu-1 showed good luminescence intensity compared with the post-synthetically obtained daughter frameworks Zn2Cu and ZnCu2 (Fig. 5).
 | ||
| Fig. 5 Crystal of Zn-1 before metal exchange reaction (a) and after copper metal exchange reaction (b). (c) The emission profiles of Cu-1′, Cu-1, Zn-1 and Zn-1′. Adapted from ref. 64. | ||
Chen and co-workers developed bio-MOF and bio-MOF-101-BCPPE through the SALE approach where the initial linker 2,6-NDC in bio-MOF-101 was substituted with H2BCPPE.65 Quite interestingly, no changes were observed in the crystallinity or network topology of both the mother and the daughter MOFs. The 1H NMR investigation revealed that 18.3 mol% of H2BCPPE is exchanged during the SALE process. This SALE process was also examined by naked eye under UV light (Fig. 6: inset). Upon excitation at 375 nm, the H2BCPPE exhibited green-yellow luminescence at 493 nm, whereas the pristine bio-MOF-101 and its daughter bio-MOF-101-BCPPE demonstrated emission peaks at 415 nm (blue emission) and 491 nm (green-yellow) under excitation at 340 nm and 375 nm, respectively. It has been noted that there is a 78 nm bathochromic shift between the pristine and the linker exchanged daughter framework (Fig. 6).
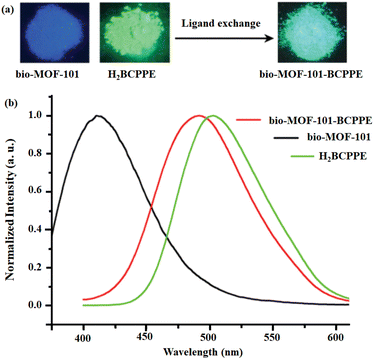 | ||
| Fig. 6 (a) The colorimetric response under UV of pristine MOF and its daughter framework after linker exchange experiment. (b) The luminescence profiles of H2BCPPE, bio-MOF-101 and bio-MOF-101-BCPPE. Adapted from ref. 65. | ||
Hong and co-workers developed a novel photoactive homochiral 3D MOF, [Cd(DTBA)(BPP)]3n by utilizing Cd2+ ions and a mixture of flexible linkers (H2DTBA and BPP).66 Single crystal structure study divulged that the MOF is composed of two types of helical chains: the three fold entities [Cd(DTBA)]n and [Cd(BPP)]n are the single and double-stranded helical chains correspondingly. The photoluminescence properties of the MOF at different temperatures were collected. At RT, upon excitation with 355 nm, it shows a blue emission band of 434 nm including a minor signal at 482 nm. This illustrates the metal-perturbed intraligand emissions of the BPP/DTBA linker.67 However, at 10 K, a single emission peak of the MOF is observed at 507 nm (Fig. 7). It has been noticed that there is a red-shift of the wavelength in the comparison of the room and low temperature that is due to LMCT.
 | ||
| Fig. 7 The luminescence profile of an MOF at two different temperatures. Adapted from ref. 66. | ||
Xu and co-workers described two luminescent MOFs, Zn-MOF and Cd-MOF, prepared from 2,3-PYDC and BPP linkers.68 Upon excitation at 372 and 370 nm, Zn-MOF and Cd-MOF showed strong luminescence at 436 and 438 nm, respectively. Upon λex at 370 nm, the ligand H2PYDC showed feeble luminescence intensity. The enhanced luminescence intensity for these two MOFs with respect to the organic linkers is due to the LMCT process and in addition, the chelation of the ligand with the metal ion effectively increases the rigidity of the network. Consequently, the rate of radiationless decay is declined.
2.2. Tuning MOF luminescence using guest molecules
Besides linkers and metal ions, the empty space of MOFs provides an important podium to induce interesting photophysical properties. The void can accommodate guest molecules like quantum dots,69,70 dyes,71 organic/inorganic molecules,72 and lanthanide metal ions73 to give fascinating luminescence phenomena. In addition, non-luminescent MOFs can be converted into luminescent entities by encapsulating these fluorophore molecules within the MOF matrix.74,75 Interestingly, owing to their good optical and electronic properties, the quantum yield of the derived MOF composite is enhanced. Thus, the sensing by the MOF can be manipulated and tuned by the encapsulation of a fluorophore molecule. For instance, Hu and co-workers fabricated a ratiometric QDs/CDs@ZIF-8 composite by incorporating QDs and CDs within ZIF-8.76 This luminescent composite exhibited the sensitive detection of Cu2+ metal ions (Fig. 8). This modified MOF composite showed good dispersibility in water, and displayed orange fluorescence. Upon excitation at 370 nm, the composite QDs/CDs@ZIF-8 emits at 430 nm and 620 nm, which signify the luminescence from the QDs and CDs, respectively. In the presence of Cu2+ ions, the emission intensity of the CDs (620 nm) is quenched, whereas the emission intensity of the QDs (430 nm) remains unchanged. The LOD for the recognition of Cu2+ ions is 1.53 nM. By using ZIF-8, Chi and co-workers encapsulated BPEI-CQDs to engender the strong fluorophore BPEI-CQDs/ZIF-8, which gave a luminescence peak at 440 nm (blue emission) under λex = 385 nm.77 | ||
| Fig. 8 The Cu2+ metal ion sensing by QDs/CDs@ZIF-8. Adapted from ref. 76. | ||
Su and co-workers reported the ratiometric MOF sensor Rh6@NENU-519 by incorporation of rhodamine 6G (Rh6) into the void of NENU-519.78 The excitation of Rh6@NENU-519 at 350 nm gave emission peaks at 565 and 406 nm, which are attributed to Rh6 and NENU-519, respectively. The detection of p/m/o-xylene by Rh6@NENU-519 was accomplished by comparison of the emission intensities at 406 and 565 nm.
Like QDs, the lanthanide ion can also be incorporated as a guest molecule within the MOF matrix to induce new luminescence features. In this regard, an interesting work was presented by Rosi and co-workers featuring the inclusion of lanthanide metal ions in bio-MOF-1 (Fig. 9). The lanthanide-doped MOFs Tb3+@bio-MOF-1, Sm3+@bio-MOF-1 and Eu3+@bio-MOF-1 depicted green, orange-pink and red colours, respectively, upon λex = 365 nm.79 Their results illustrated that bio-MOF-1 effectively transfers energy from the MOF to the lanthanide metal ions, i.e., strongly sensitizing the lanthanide metal ion.
 | ||
| Fig. 9 The inclusion of Tb3+, Sm3+, and Eu3+ in the network of bio-MOF-1 and their colour under UV light. Adapted from ref. 79. | ||
Wang and co-workers described the synthesis of a ratiometric MOF composite for the recognition of mercury ions by incorporating Ru(bpy)32+ inside UiO-66-NH2.80 The emission profile of the composite exhibited peaks at 604 and 437 nm, which are due to the Ru(bpy)32+ and UiO-66-NH2, respectively. Chen and co-workers prepared a photoswitchable framework by incorporating the diarylethene (DAE) molecule in the Eu-MOF.81 This DAE unit is sensitive to light and showed the ring closing and ring opening phenomena. As a result, the composite DAE@ Eu-MOF displayed different colours in the presence and absence of light.
2.3. Importance of lanthanides for thermometry
Lanthanide-based complexes or the doped lanthanide ions within the complexes play a great role in luminescence thermometry. The general electronic configuration of a lanthanide metal ion is [Xe]4fn (where, n = 0–14) and lanthanide metal ions contain diverse electronic energy levels. These energy levels show excellent photophysical properties.82 These 4f orbitals are covered by 5p and 5s orbitals and these orbitals lie far away from the nucleus compared to 4f orbitals. Consequently, their interaction with the ligand orbital is insensitive i.e., the spectroscopic and magnetic properties of lanthanide metal ions are hardly affected by the local environment. Thus, lanthanide metal ions have narrow, well defined and characteristic 4f–4f transitions. Further, lanthanide metal ions have a high quantum yield, long decay times and high photostability. Principally, the f–f transition is prohibited and hence the direct excitation of the f–f transition is unlikely, unless a high-power source is used. This problem can be avoided by using an organic ligand that can efficiently transfer the energy from the linker to the metal node and this method is called the “antenna effect” i.e., “luminescence sensitization” (Fig. 3a).83 Certain fundamental steps are associated with the antenna effect: (a) the first step is the absorption of light by the linker, resulting in the excitation of the linker from the GS to the ES, (b) then the energy movement occurs from the ES of the linker to the ES of the lanthanide metal ion, and (c) finally, the emission occurs from the excited lanthanide metal ion. These energy transfers are associated with changes in spin state along with some crucial features. In the first step, the linker is excited from the ground singlet state (S0) to the singlet excited state (S1) (Fig. 10), followed by changes of the spin state, which is known as intersystem crossing (ISC) i.e., from S1 of linker to the triplet excited state (T1). From the T1 state, the emission from the linker in the complex may occur (Fig. 10). In addition, the transfer of energy may happen from the T1 energy level of the ligand to the T1 energy level of the lanthanide metal ion and from there the lanthanide-based emission takes place (Fig. 10). It has been observed that, for the efficient transfer of energy from the T1 state of the ligand to the lanthanide ion, their energy levels should be comparable. The difference in energy between the T1 of the linker and the lanthanide accepting levels must be around 2000–4000 cm−1.84 However, the emission from the lanthanide metal ion is entirely dependent on the extent of energy transfer between the linker and the metal ion. If the energy allocation from the linker to the metal ion is very strong, then the luminescence (fluorescence or phosphorescence) from the ligand will not occur and we will get entirely lanthanide-based emission. If the energy transfer is partial, then luminescence from both the linker and metal ions would ensue. In this respect, the transfer of energy from the linker to the lanthanide metal ion generally happens at a higher energy level compared to the emitting level of the lanthanide-based emission, otherwise energy backflow will occur.Therefore, the designing of the ligand, the choice of lanthanide metal ion and suitable antennae (sensitization) effect are crucial to obtaining lanthanide-based emission. Since the lanthanide metal ion (+3 oxidation state) is a Lewis acid, as per Peerson's theory85 it will prefer to interact strongly with the hard Lewis bases. The O-donor and the N-donor atoms of the ligand are generally hard bases and they will prefer to from a strong bond with the lanthanide metal ion. In addition, the presence of chelating binding sites constructed from these donor atoms will enhance the luminescence intensity of the complexes. This is because the high rigidity of the system reduces the radiationless deactivation.86
As discussed earlier, thermometry based on a single transition is usually affected by environmental interference. To avoid this, double transition (ratiometric thermometer) is preferred because it nullifies the environmental interference through self-calibrating and self-standardising principles. The lanthanide-based emission is a very kind way to construct a ratiometric sensor, which can effectively work as a ratiometric thermometer. In this review, we will see the variety of lanthanide-based MOFs and lanthanide-doped metal ions within the MOF cavity used to develop ratiometric thermometers.
3. Luminescent thermometer and its performance
In general, luminescence thermometry based on signal transduction leading to the information about the temperature reading encompasses some crucial factors: (a) measuring the emission intensity, which involves either the measurement of the intensity of a single emission or a pair of emissions, (b) peak shifting in the emission maximum and (c) measuring the lifetime of the excited state of the emitting components.87,88 Usually, MOF thermometers based on measuring the emission intensity from a single transition can be affected by instrumental fluctuation and other environmental effects. These problems can be mitigated with the help of self-reference/self-calibrating ratiometric MOF-based thermometers. The working principle of this ratiometric thermometer is based on the ratio of the emission intensities of the two emissions. In this way, we can reduce the external influence, which helps to enhance the precise determination of the sensitivity of the sensor. Therefore, the precise determination of temperature by all MOF thermometers is generally assured through the measuring of the emission intensities arising from two different emissive centres (dual-centre thermometers). In the last section, we discussed the role of lanthanide ions, particularly Eu3+ and Tb3+, in the construction of MOF thermometers. Therefore, dual emitting centres leading to MOF thermometers can be accomplished by the fine tuning of the: (a) presence of lanthanide metal ions (Eu3+ or Tb3+), (b) linker and the lanthanide metal ions, (c) existence of two lanthanide metal ions (Eu3+ and Tb3+), and (d) the encapsulated fluorophore molecule inside the pore of the MOFs. The combinations of such moieties leading to the construction of MOF thermometers are listed in Table 1.| MOF thermometer | Sensitivity (% K−1) | Temperature range (K) | Maximum temperature (Tm) | Ref. |
|---|---|---|---|---|
| Eu0.001Tb0.999(BPDC-2N) | 1.92 | 100–300 | 175 | 115 |
| Eu0.001Tb0.999(BPDC-1N) | 1.86 | 143 | ||
| Eu0.001Tb0.999(BPDC-0N) | 1.10 | 188 | ||
| Eu0.15Tb0.85-1,3-BDC | 0.44 | 150–350 | 236 | 116 |
| Eu0.05Tb0.95-1,3-BDC | 0.20 | 333 | ||
| Eu0.1Tb0.9-1,3-BDC | 0.31 | 284 | ||
| Eu0.03Tb0.97-1,3-BDC | 0.19 | 338 | ||
| Eu0.125Tb0.875-1,3-BDC | 0.40 | 251 | ||
| Eu0.075Tb0.925-1,3-BDC | 0.24 | 314 | ||
| Eu0.0143Tb0.9857-BDC | 0.28 | 298–473 | 473 | 108 |
| Eu0.0143Tb0.9857-BPNDC | 1.85 | |||
| Eu0.0143Tb0.9857-OBA | 6.49 | 423–473 | 423 | |
| Eu0.37Tb0.63-BTC | 0.68 | 313–473 | 313 | 117 |
| Eu0.002Tb0.018-BDPO@PVA | 3.7 | 303–423 | 423 | 118 |
| [Eu0.08Tb0.92(HPIDC)(ox)0.5H2O]·3H2O | 0.6 | 303–473 | 473 | 119 |
| [Eu0.09Tb0.91L1](ClO4)3·H2O·2MeCN | 6.6 | 150–170 | 160 | 120 |
| Eu0.10Tb0.90-L2 | 1.75 | 303–423 | 423 | 121 |
| Eu0.0066Tb0.9934-L3 | 3.76 | 77–450 | 450 | 122 |
| MOF-5 doped by Eu,Tb | 1.8 | 303–473 | 473 | 123 |
| Eu0.19Tb0.81-PDDI | 0.19–0.37 | 313–473 | 473 | 124 |
| ZJU-88⊃perylene | 1.28 | 293–353 | 125 | |
| La0.95Tb0.05HL | 0.53 | 90–280 | 280 | 126 |
| [(CH3)2NH2]Eu0.036Tb0.964BPTC | 9.42 | 77–377 | 310 | 127 |
| 4-ANA⊂Gd4L4 | 0.92–1.58% °C−1 | 308–358 | — | 128 |
| Eu0.05Tb0.95bpydc | 2.59 | 25–300 | 179 | 129 |
| Eu0.05Tb0.95cpna | 2.55 | 25–300 | 131 | |
| Gd0.9995Eu0.0005TPTC | 4.67 | 313–473 | 313 | 130 |
| TbTPTC | 1.05 | 313–473 | 366 | |
| [Eu0.7Tb0.3(D-cam)(Himdc)2(H2O)2]3 | 0.079 | 100–450 | 450 | 131 |
| Nd0.577Yb0.423BDC-F4 | 0.816 | 293–313 | 313 | 132 |
| 10%RhB-90% FL@γ-CD-MOF | 4.03 | 253–353 | 343 | 133 |
| Nd0.95Yb0.05BPTC | 0.94 | 293–323 | 293 | 134 |
| [Cd2 (IMB)2 (mbix)2] 3H2O | 0.082 | 293–433 | 433 | 135 |
| POM@Tb-TATB (POM loading 9.1 wt%) | 2.68 | 293–323 | 300 | 136 |
| POM@Tb-TATB (POM loading 19.5 wt%) | 2.37 | |||
| DMASE⊂Zn-TCOMA | 1.1%–1.8% C−1 | 20–60 °C | — | 137 |
| Tb99.9/Eu0.1-MOF | 6.35 | 247–377 | 377 | 138 |
| Cdots&RB@ZIF-82-MMM | 0.74% C−1 | 293–353 | 293 | 139 |
| 0.52% C−1 | 353 | |||
| Nd0.5Yb0.5TPTC | 12.46 to 3.91 | 293–328 | 293 | 140 |
| 328 | ||||
| DyTPTC-2Me (thermally coupled) | 1.20% | 303–423 | 303 | 141 |
| DyTPTC-2Me (nonthermally coupled) | 8.46% | 423–503 | 503 | |
| [Sr(NH2-BDC)(DMF)]n | 7.5% | 100–300 | 13 | |
| Tb0.95Eu0.05BTCA | 31% | 4–50 | 4 | 96 |
| Tb0.957Eu0.043CPDA | 16% | 40–300 | 300 | 93 |
For dual-centre thermometers, the thermometric parameter (Δ) is equal to the ratio of the emission intensities of the two distinct transitions, as per eqn (2).40,89
 | (2) |
 | (3) |
 | (4) |
 | (5) |
Eqn (5) is based on two important facts: (a) if the intensity of one of the transitions (considering I2) shows a small temperature dependence with respect to the other transition, in this case the eqn (5) can be transformed as:
 | (6) |
(b) If the exponential term over-rules the intensity of the transition, in this case eqn (5) can be transformed as:
 | (7) |
These are the important equations which are use to determine the thermometric parameter for dual-centre thermometers. The efficacy and accuracy of the thermometer depend on some fundamental points. These vital points are: (i) relative thermal sensitivity (Sr), (ii) temperature uncertainty and (iii) reproducibility. The measurement of Sr (unit is %·K−1) can be accomplished with eqn (8) and it signifies the relative change of Δ with the change of temperature in degrees. The maximum value of Sr is recognised as the maximum relative sensitivity (Sm).
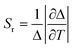 | (8) |
From this equation, if the value of the thermometric parameter decreases with increases in temperature, then the value of Sr will be negative, which is meaningless. Thus, Sr is greater than zero. With respect to absolute sensitivity (Sa, eqn (9)), the relative thermal sensitivity is more important because it does not depend on the nature of the thermometer and allows us to qualitatively compare different thermometric systems.
 | (9) |
For any thermometer, it is imperative to be able to precisely measure minute temperature changes. In this regard, the temperature uncertainty (δT) is another important feature, which is linked with the smallest temperature change and can be expressed as:
 | (10) |
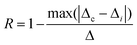 | (11) |
The term Δi is the thermometric parameter determined at each temperature and Δc is the average thermometric parameter.
4. Tuning the properties of thermometers
The beautiful coordination chemistry allows us the judicial selection of organic linker and metal ion by which we can engender numerous MOFs with their rational applications. It is possible that the efficiency of the thermometer can be advanced by changing the composition of the reacting solution, which involves the chemical makeup of the various reacting systems: (a) construction of a lanthanide-based MOF, (b) selecting linkers having diverse triplet energy levels, (c) introducing secondary linkers, (d) post-synthetic incorporation of linkers and lanthanide metal ions in the ligand back bone and SBU or metal node, respectively, (e) linker containing a binding site to incorporate lanthanide metal ions, and (f) encapsulation of a fluorophore molecule (dye, quantum dots etc.,) within the MOF framework.In the case of lanthanide -based MOFs, the energy levels of the linker and the lanthanide metal ion should be comparable to facilitate the flow of energy from the ES of the linker to the excited state of the lanthanide, which is energetically higher than the emission level. To achieve characteristic luminescence in Tb3+/Eu3+-MOF thermometers, the ligand should have a triplet excited energy state (TEES) of about 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–27
000–27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which is comparable to the receiving energy levels of Tb3+ (5D4, 20
000 cm−1, which is comparable to the receiving energy levels of Tb3+ (5D4, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) and Eu3+ (5D1, 19
500 cm−1) and Eu3+ (5D1, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 cm−1).90 This leads to the effective sensitization of Tb3+/Eu3+ and concomitantly their nice emission. In this regard, Qian, Chen and co-workers developed a mixed lanthanide MOF thermometer, Eu0.0069Tb0.9931-DMBDC, based on the emissions of Tb3+ and Eu3+ at 545 and 613 nm, respectively. The signature luminescence of both Tb3+ and Eu3+ are sensitized by the ligand DMBDC, which has a TEES of 23
030 cm−1).90 This leads to the effective sensitization of Tb3+/Eu3+ and concomitantly their nice emission. In this regard, Qian, Chen and co-workers developed a mixed lanthanide MOF thermometer, Eu0.0069Tb0.9931-DMBDC, based on the emissions of Tb3+ and Eu3+ at 545 and 613 nm, respectively. The signature luminescence of both Tb3+ and Eu3+ are sensitized by the ligand DMBDC, which has a TEES of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 cm−1 and allows the facile transfer of energy from the linker to the metal ion. Fascinatingly, the MOF network showed temperature sensing in the cryogenic temperature range and this is established from the linear association between the ratio of luminescence intensity and temperature from 50 to 200 K with a sensitivity is 0.38% K−1.91 The same group also reported a new lanthanide-based MOF thermometer, Tb0.9Eu0.1PIA, where the TEES of the linker PIA is 26
306 cm−1 and allows the facile transfer of energy from the linker to the metal ion. Fascinatingly, the MOF network showed temperature sensing in the cryogenic temperature range and this is established from the linear association between the ratio of luminescence intensity and temperature from 50 to 200 K with a sensitivity is 0.38% K−1.91 The same group also reported a new lanthanide-based MOF thermometer, Tb0.9Eu0.1PIA, where the TEES of the linker PIA is 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 cm−1, which makes the transfer of energy from the linker to the lanthanide metal ions feasible. Consequently, the MOF showed excellent temperature sensing in the range of 100–300 K with a sensitivity of 3.53% K−1.92 This MOF thermometer outperformed their previously reported lanthanide-based MOF thermometer. The thermal sensitivity of the thermometer depends on the triplet energy state (T1) of the organic linker, as it is responsible for the kinetics of the non-radiative transitions of Eu3+ and Tb3+, which ultimately affects the kinetics of the radiative transitions of Eu3+ (5D0 → 7FJ) and Tb3+ (5D4 → 7FJ). In the case of Tb0.9Eu0.1PIA, the T1 of H2PIA is about 26
455 cm−1, which makes the transfer of energy from the linker to the lanthanide metal ions feasible. Consequently, the MOF showed excellent temperature sensing in the range of 100–300 K with a sensitivity of 3.53% K−1.92 This MOF thermometer outperformed their previously reported lanthanide-based MOF thermometer. The thermal sensitivity of the thermometer depends on the triplet energy state (T1) of the organic linker, as it is responsible for the kinetics of the non-radiative transitions of Eu3+ and Tb3+, which ultimately affects the kinetics of the radiative transitions of Eu3+ (5D0 → 7FJ) and Tb3+ (5D4 → 7FJ). In the case of Tb0.9Eu0.1PIA, the T1 of H2PIA is about 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 cm−1, which is significantly higher than the 5D0 of Eu3+(17
455 cm−1, which is significantly higher than the 5D0 of Eu3+(17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) and the 5D4 of Tb3+(20
200 cm−1) and the 5D4 of Tb3+(20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1). The energy level difference between the ligand (H2PIA) and the Eu3+ ion is 9255 cm−1, which prohibits the thermally driven depopulation. Such an energy difference in DMBDC-based MOF is about 6106 cm−1. It is also noticed that by increasing the doping amounts of Tb/Eu/PIA, the thermal sensitivity can be tuned. The thermometer with higher doping of Tb3+ gives higher sensitivity (enhancing the Sr by about 20%), but simultaneously reduces the emission intensity of Eu3+ and this is due to the lower doping of Eu3+. In the last two examples, the temperature-sensing efficiency in terms of the working temperature range gradually increases. The temperature ranges of Eu0.0069Tb0.9931-DMBDC and Tb0.9Eu0.1PIA are 50 to 200 K and 100 to 300 K, respectively.
500 cm−1). The energy level difference between the ligand (H2PIA) and the Eu3+ ion is 9255 cm−1, which prohibits the thermally driven depopulation. Such an energy difference in DMBDC-based MOF is about 6106 cm−1. It is also noticed that by increasing the doping amounts of Tb/Eu/PIA, the thermal sensitivity can be tuned. The thermometer with higher doping of Tb3+ gives higher sensitivity (enhancing the Sr by about 20%), but simultaneously reduces the emission intensity of Eu3+ and this is due to the lower doping of Eu3+. In the last two examples, the temperature-sensing efficiency in terms of the working temperature range gradually increases. The temperature ranges of Eu0.0069Tb0.9931-DMBDC and Tb0.9Eu0.1PIA are 50 to 200 K and 100 to 300 K, respectively.
Qian, Cui and co-workers reported the synthesis of a mixed lanthanide-based MOF thermometer where the ligand CPDA showed a T1 of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 cm−1, which is higher TEES than the organic linkers in the last two examples.91,92 Subsequently, this thermometer (Tb0.957Eu0.043CPDA) showed better efficiency in terms of a wider temperature range (40–300 K).93 Interestingly, the determination of temperature by this thermometer is also associated with the colorimetric response. The temperature-sensing range is very good (cryogenic to room temperature; 40–300 K) and importantly, the cryogenic temperature-sensing efficacy is much better than the last two examples. Such sensing activity at cryogenic temperature is due to the high sensitization (TEES of CPDA is 27
027 cm−1, which is higher TEES than the organic linkers in the last two examples.91,92 Subsequently, this thermometer (Tb0.957Eu0.043CPDA) showed better efficiency in terms of a wider temperature range (40–300 K).93 Interestingly, the determination of temperature by this thermometer is also associated with the colorimetric response. The temperature-sensing range is very good (cryogenic to room temperature; 40–300 K) and importantly, the cryogenic temperature-sensing efficacy is much better than the last two examples. Such sensing activity at cryogenic temperature is due to the high sensitization (TEES of CPDA is 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 cm−1) of the ligand H3CPDA to the lanthanide metal ions. Further, the energy difference between the TEES of H3CPDA and the emitting level of Tb3+ (5D4, 20
027 cm−1) of the ligand H3CPDA to the lanthanide metal ions. Further, the energy difference between the TEES of H3CPDA and the emitting level of Tb3+ (5D4, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) is very large (6527 cm−1), which rules out the possibility of a back transfer of energy from Tb3+ to H3CPDA. This judgement is supported by the emission spectra of Tb3+ in TbDMBDC and TbCPDA. For TbCPDA, the emission of Tb3+ ions remains almost unchanged with increasing temperature, while the emission intensity of Tb3+ ions in TbDMBDC declines. Therefore, the energy transfer from the Tb3+ ion to the linker H3CPDA is restricted and the phonon-assisted energy transfer (PAET) Tb3+ → Eu3+ in Tb0.957Eu0.043CPDA is very effective with increasing temperature, resulting in higher temperature sensitivity than Eu0.0069Tb0.9931-DMBDC.
500 cm−1) is very large (6527 cm−1), which rules out the possibility of a back transfer of energy from Tb3+ to H3CPDA. This judgement is supported by the emission spectra of Tb3+ in TbDMBDC and TbCPDA. For TbCPDA, the emission of Tb3+ ions remains almost unchanged with increasing temperature, while the emission intensity of Tb3+ ions in TbDMBDC declines. Therefore, the energy transfer from the Tb3+ ion to the linker H3CPDA is restricted and the phonon-assisted energy transfer (PAET) Tb3+ → Eu3+ in Tb0.957Eu0.043CPDA is very effective with increasing temperature, resulting in higher temperature sensitivity than Eu0.0069Tb0.9931-DMBDC.
The same group further developed a Eu3+/Tb3+-MOF thermometer, Tb0.80Eu0.20BPDA, for the determination of temperature in the physiological range, 298–318 K.94 The ligand has a TEES of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 cm−1, which is sufficient to sensitize both the metal ions. The value of Sm is 1.19% K−1 at ∼313 K.
269 cm−1, which is sufficient to sensitize both the metal ions. The value of Sm is 1.19% K−1 at ∼313 K.
The development of a ratiometric MOF nanothermometer is very appealing for its high temperature sensitivity and reproducibility. In this context, Carlos and co-workers synthesized a mixed lanthanide-based MOF nanothermometer, Tb0.99Eu0.01(BDC)1.5(H2O)2 for the determination of physiological temperature. The Sr values of this nanothermometer in solid and water are found to be 0.14% and 0.31% K respectively.95
It has been observed that the Sr values of Tb0.80Eu0.20BPDA are almost 7.5 times higher than those of Tb0.99Eu0.01(BDC)1.5(H2O)2 at 313 K. The distribution of energy levels in the linker facilitates smooth energy transfer from the TEES of the linkers to the Eu3+ and Tb3+ ions. For effective energy transfer, the TEES of the linker should be energetically higher than the metal ions. In the case of H2BDC and H2BPDA, the TEES of H2BDC is above than that of H2BPDA. However, the immediate relaxation of the MOFs constructed from H2BDC is stronger than that of H2BPDA. So, the non-radiative decay and energy back transfers are not sufficient in Tb0.8Eu0.2BPDA to affect the sensitization process. Moreover, in Tb0.8Eu0.2BPDA the smooth transfer of energy to Eu3+ and Tb3+ ions occurs even at temperatures of 10 to 300 K. This is attributed to the proper arrangement of energy levels with suitable energy gaps among singlet and excited triplet energy levels of the H2BPDA linker and the energy backflow is insufficient to influence the sensitization of Tb0.8Eu0.2BPDA. The lifetime of Tb3+ (5D4) in mixed metal MOF is comparatively shorter than that of TbBPDA, but the lifetime of Eu3+ (5D0) is longer than that of EuBPDA in the temperature range of 293 to 328 K. Moreover, the lifetime of Tb3+ (5D4) in Tb0.8Eu0.2BPDA declines with temperature while the lifetime of Tb3+ (5D4) in TbBPDA is stable. This illustrates the facile energy transfer from Tb3+ → Eu3+ in Tb0.8Eu0.2BPDA. The energy transfer from the TEES of BPDA to the Tb3+ (5D4) and the occurrence of the Tb3+ → Eu3+ energy transfer result in the higher temperature sensitivity of Tb0.80Eu0.20BPDA.
Bouwman and co-workers synthesized a mixed lanthanide MOF thermometer, Tb0.95Eu0.05BTCA, for measurement of cryogenic temperature.96 The working capacity of the thermometer is in the low temperature range of 4–50 K with a relative maximum sensitivity up to 31% K−1 at 4 K. This may be due to the short Ln–Ln distances and the Ln chains available across the mixed metal MOF matrix to facilitate the smooth energy transfer from the excited state of Tb3+ to the neighbouring Eu3+ centre. The TEES value of the ligand is 26.6 × 103 cm−1 and this illustrates the occurrence of facile energy transfer from the linker to the metal ion without back transfer. Further, the occurrence of PAET from Tb3+ to Eu3+ and in addition the PAET among nearby Tb3+ resulted in excellent temperature sensitivity.
An additional linker in the MOF may also affect the temperature-sensing property. For instance, in an early report, Yan and co-workers developed a mixed lanthanide MOF thermometer, Ad/Tb0.999Eu0.001/BPDC, from mixed lanthanides (Tb3+/Eu3+) and mixed linkers (BPDC/adenine (AD)) under solvothermal condition.97 The measured lifetimes of Eu3+ and Tb3+ in AD/Eu/BPDC and AD/Tb/BPDC were found to be 1539 and 148.7 μs, respectively. Again, the lifetimes of Eu3+ and Tb3+ in the Tb0.999Eu0.001 system were calculated to be 1445 and 21 μs, respectively. These life time values indicate that the lifetime of the Tb3+ ion is decreasing and the energy achievement has occurred. Importantly, the mixed lanthanide MOF is established as a thermometric sensor. As the temperature increases, the emission intensities of Eu3+ and Tb3+ in Tb0.999Eu0.001 increase and decrease respectively. The increment of the emission intensity of Eu3+ is due to the transfer of energy from Tb3+ and this is weakened in the lower temperature range. The transfer of energy (ηTb→Eu) is calculated to be 85% at RT, which is very significant. The effect of the addition of an external linker (AD) was proved by comparing the temperature-sensing efficiencies of AD/Tb0.999Eu0.001/BPDC and Tb0.999Eu0.001/BPDC. The authors found that due to the inclusion of AD the sensitization efficiency and hence the flow of energy from Tb3+ → Eu3+ were greatly enhanced. Consequently, the working temperature range is increased to 100–300 K from 150–250 K. The thermal sensitivity of the thermometer Ad/Tb0.999Eu0.001/BPDC was found to be 1.23% °C−1. For Tb0.999Eu0.001/BPDC, the emission intensity of Tb0.999Eu0.001/BPDC decreases when the temperature is increased to 250 K and after this the emission intensity of Eu3+ is irregular.
Wu and co-workers used the linker DSTP and the secondary ligand oxalic acid (OA) to react with Tb3+/Eu3+ for the construction of a luminescent MOF thermometer, [Tb0.98Eu0.02(OA)0.5(DSTP)]·3H2O (Tb/Eu-1).98 Similarly, they constructed another luminescent MOF thermometer [Tb0.98Eu0.02(BDC)(DSTP)]·3H2O (Tb/Eu-2) by using another secondary ligand, BDC. Due to the presence of different ligands in these two MOF thermometers, their thermal stability is also varied. The decomposition temperatures of Tb/Eu-1 and Tb/Eu-2 are 653 and 788 K correspondingly. This is attributed to the three-dimensional polymeric network of Tb/Eu-2 whereas the Tb/Eu-1 has a layered architecture. The thermometer Tb/Eu-1 showed a linear relationship between the ratio of emission intensity (ITb/IEu) and the temperature in the range 77–275 K and displayed an Sm of 2.4% K−1 at 275 K. The other MOF thermometer, Tb/Eu-2, exhibited a linear relationship between the ratio of emission intensity (ITb/IEu) and the temperature in the range 125–250 K and displayed an Sm of 2.8% K−1 at 225 K. The high temperature sensitivity of Tb/Eu-2 is due to the proficient charge transfer from Tb3+ to Eu3+. Further investigation of the sensing mechanism revealed that the first TEES of the DSTP linker was calculated to be 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 cm−1, which is less than that of Tb3+ (20
050 cm−1, which is less than that of Tb3+ (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1, 5D4 state) and superior to that of Eu3+ (17
400 cm−1, 5D4 state) and superior to that of Eu3+ (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1, 5D0 state). Therefore, the ligand sensitization of Tb3+ effectively comes from the TEES of the auxiliary linkers (BDC/OA). The lower TEES of BDC with respect to linker OA promotes the back transfer, which in turn increases the energy transfer from Tb3+ to Eu3+.
200 cm−1, 5D0 state). Therefore, the ligand sensitization of Tb3+ effectively comes from the TEES of the auxiliary linkers (BDC/OA). The lower TEES of BDC with respect to linker OA promotes the back transfer, which in turn increases the energy transfer from Tb3+ to Eu3+.
Recently, Xia and co-workers described some remarkable work where they judiciously controlled the TEES of three isomorphic Eu3+/Tb3+-MOFs (Eu0.01Tb0.99X, where X = BDC-OH (A), BDC-NH2 (B) and NDC (C)) by wisely choosing three different linkers (Fig. 11).99 The substituents on these linkers have a large effect on their T1 state and hence the TEES of these linkers are quite diverse (Fig. 11). According to Latva's empirical rule, the best possible optimal energy transfer can be achieved if the energy gap (ΔE) between the sensitizer and the lanthanide excited state is between 2000 and 4000 cm−1. The ΔE values for ligand T1 of H2BDC-OH to 5D4 of Tb3+, H2BDC-NH2 to 5D0 of Eu3+ and H2NDC to 5D0 of Eu3+ are 3725, 3977 and 2861 cm−1, respectively. Therefore, effective energy transfer will happen in these systems. However, the transfer of energy from 1,4-H2NDC to the 5D4 of the Tb3+ centre will not take place because of the negative energy gap (Fig. 11). Thus, the energy transfer processes are quite different in these MOFs. For A, the energy transfer pathway is as follows: the light is absorbed by the linker H2BDC-OH, then ISC is followed by the maximum energy transfer from T1 of H2BDC-OH to 5D4 of Tb3+ and then the transfer of energy from 5D4 of Tb3+ to 5D0 of Eu3+, i.e., ligand → Tb → Eu. In the case of B, the transfer of energy occurs from T1 of H2BDC-NH2 to 5D0 of Eu3+ (ligand → Eu), as well as the trivial energy transfer from ligand → Tb → Eu. In C, the entire T1 energy of 1,4-H2NDC is relocated to 5D0 of Eu3+, i.e., ligand → Eu, and the fractional back energy relocation is observed from Eu3+ to NDC. The Δ values for A and B are based on the emission intensities of ITb/IEu with temperature, whereas the Δ value for C is based on the emission intensities of IEu/INDC. Therefore, to comprehend the high temperature sensitivity, a straightforward energy relocation chain is necessary, which can control the competition of diverse energy allocation processes and, as per the Latva rule, the suitable energy gap among acceptor and donor is imperative to have proficient energy relocation and back energy transfer processes. The Sm values for C, A and B were 7.32% °C−1, 2.49% °C−1, 2.24% °C−1 at temperatures of 48.2 °C, 152.8 °C and 151.5 °C, respectively. The diverse sensitivities of these MOF thermometers are ascribed to the energy transfer processes, which are quite different.
 | ||
| Fig. 11 The diverse TEES and transfer of energy are due to the presence of different linkers in Eu0.01Tb0.99X, X = NDC (C), BDC-NH2 (B) and BDC-OH (A). | ||
Yan and co-workers used the PSM process to establish an MOF thermometer.100 For this, they used the BPYDC linker to synthesize MOF-235 (consisting of Ga, Al and In). The linker contains N,N′-chelating sites for the guest metal ion, which undergoes the PSM process for the inclusion of lanthanide metal ions. Thus, the PSM process is nicely performed with synthesized MOFs for the inclusion of Eu3+ and Tb3+ ions at the chelating sites. The self-calibrating ratiometric thermometer is based on the ratio of two distinct transitions (I545/I613) of Tb3+ (5D4 → 7F5) and Eu3+ (5D0 → 7F2). This intensity ratio is linear in relation to the temperature range of 283–333 K. The thermal sensitivity of Eu3+/Tb3+@In-MOF-253 is 4.97% C−1 at 333 K and this sensitivity is much superior compared to the analogous Eu3+/Tb3+@Al-MOF-253 and Eu3+/Tb3+@Ga-MOF-253. It has been observed that, with an increase in temperature, the emission intensity of Tb3+ largely declines whereas the emission intensity of Eu3+ is partially augmented.
It is quite interesting to note that, apart from lanthanide-based MOFs, the development of an MOF thermometer can also be accomplished by integrating fluorophore moieties in the MOF matrix. In this regard, Cui, Qian and co-workers encapsulated two different dye molecules (4-Mu and Flu) within ZIF-8 to form ZIF-8⊃4-MU&Flu, which showed an excellent linear response to temperature (Fig. 12).101 The encapsulation of fluorophore moieties in the channel of the MOF restricts the free rotation, as well as avoiding the aggregation-induced luminescence quenching of fluorophore moieties. This leads to a 6.49% enhancement in the quantum yield of the MOF. This thermometer showed the distinct emission peak of the individual encapsulated dye molecules at λex = 360 nm. Upon increasing the temperature from 313 to 533 K, the emission intensities of both dye molecules gradually decrease. This indicates that as the temperature increases, the thermal activation of the radiationless processes is enhanced. Consequently, the lifetime of ZIF-8⊃4-MU&Flu is declined, which signifies the amplification of non-radiative decay. Further, Flu is more sensitive to temperature, i.e., its emission intensity quickly declines compared to that of 4-Mu with increasing temperature. Therefore, the diverse emission quenching rates of these dyes with temperature established the ZIF-8⊃4-MU&Flu as an efficient thermometer and the temperature sensitivity was derived based on the luminescence intensity ratio of IFlu/I4-MU. The Sm value for this thermometer was found to be 0.62% K−1 at 240 °C.
 | ||
| Fig. 12 3D image of dyes encapsulated in MOF, ZIF-8⊃4-MU&Flu, and its temperature-sensing property. Adapted from ref. 101. | ||
Xu and co-workers reported an MOF thermometer, CsPbBr3@Eu-BTC, based on the encapsulation of a CsPbBr3 quantum dot within the cavity of Eu-BTC.102 The composite displayed emission peaks at 618 nm (red emission) and 529 nm (green emission) upon excitation at 339 nm. These emission peaks correspond to the emissions from the Eu3+ ion (5D0–7F2) and quantum dots CsPbBr3, respectively. It has been noted that, with the increase in temperature from 20 to 100 °C, the emission intensity of CsPbBr3 at 528 nm decreases whereas the emission intensity of Eu-BTC at 618 nm increases (Fig. 13). This result is significant in comparison to the previous report, where the emission of Eu3+ ions is due to the electronic transition, which is associated with the “weak coupling” effect at lower temperature.103,104 Such a remarkable temperature response of the Eu3+ ion in CsPbBr3@Eu-BTC is possible owing to the strong luminescence nature of CsPbBr3 and the host matrix limiting the effect of the Eu-BTC.105 Thus, the two emitting centres in CsPbBr3@Eu-BTC seem to be independent and there is no energy transfer between them. Consequently, the opposite sensing activities of the Eu3+ ion and CsPbBr3 with temperature are beneficial to the fabrication of fluorescent thermometers. The thermometric sensor is based on the ratio of the emission intensities at 618 and 529 nm of Eu3+ ion and CsPbBr3 in CsPbBr3@Eu-BTC respectively. This ratiometric thermometric probe showed a sensitivity of 3.9% °C−1 at 20 °C. The temperature resolution of the composite is 0.004 °C.
 | ||
| Fig. 13 The diverse temperature-sensing behaviour of CsPbBr3 (529 nm) and Eu3+ ion (618 nm) in CsPbBr3@Eu-BTC upon excitation at 339 nm. Adapted from ref. 102. | ||
Recently, Jiao, Xu and co-workers developed three mixed lanthanide (Tb3+/Eu3+) MOFs, (Eu0.0143Tb0.9857-X, where X = H2BPNDC, H2OBA and H2BDC) for the determination of noncontact temperature.106 The lowest TEES of H2BDC, H2OBA and H2BPNDC are 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 cm−1, 25
385 cm−1, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 cm−1 and 23
575 cm−1 and 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 cm−1, respectively. These values suggest that the ligands in these frameworks are sufficient to sensitize the lanthanide metal ions. All of the MOFs are very effective at temperature sensing, and the sensitivities value of these lanthanide MOFs, Eu0.0143Tb0.9857-BDC, Eu0.0143Tb0.9857-OBA, and Eu0.0143Tb0.9857-BPNDC, are 0.28% K−1 (at 473 K), 6.49% K−1 (at 423 K) and 1.85% K−1 (at 473 K), respectively. The differences in their sensitivities are due to the diverse energy transfer from ligand to metal and, in addition, the flow of energy from Tb3+ → Eu3+, which are dictated by the variation of temperature.
310 cm−1, respectively. These values suggest that the ligands in these frameworks are sufficient to sensitize the lanthanide metal ions. All of the MOFs are very effective at temperature sensing, and the sensitivities value of these lanthanide MOFs, Eu0.0143Tb0.9857-BDC, Eu0.0143Tb0.9857-OBA, and Eu0.0143Tb0.9857-BPNDC, are 0.28% K−1 (at 473 K), 6.49% K−1 (at 423 K) and 1.85% K−1 (at 473 K), respectively. The differences in their sensitivities are due to the diverse energy transfer from ligand to metal and, in addition, the flow of energy from Tb3+ → Eu3+, which are dictated by the variation of temperature.
Li and co-workers synthesized two ratiometric MOF temperature sensors, Eu0.05Tb0.95TPTC-2Me and EuTPTC-2OMe, from ligands H4TPTC-2Me and H4TPTC-2OMe, respectively.107 For the EuTPTC-2OMe thermometer, the fluorescence intensity of the linker and Eu3+ at 418 and 614 nm decreases with the decline in temperature from 313 to 473 K. Shrinkage of the luminescence intensity in both cases is due to the occurrence of a non-radiative process. The rate of shrinkage of the luminescence intensity of Eu3+ is higher than that of the ligand. This illustrates the back transfer of energy from Eu3+ to the ligand. The luminescence intensity ratio of Iligand/IEu of EuTPTC-2OMe is considered to determine the temperature. Similarly, for Eu0.05Tb0.95TPTC-2Me, the ratio of the luminescence intensity of ITb/IEu is considered to measure the temperature. The temperature sensitivity of this MOF thermometer is due to the effective ligand sensitization and the transfer of energy from Tb3+ to Eu3+. The relative sensitivity values of EuTPTC-2OMe and Eu0.05Tb0.95TPTC-2Me at 473 K are 1.24% K−1 and 1.30% K−1, respectively.
Apart from lanthanide-based luminescence MOF thermometry, it is possible to demonstrate the thermometry behaviour through the incorporation of a dye or fluorophore moiety within the MOF void. Kaczmarek and co-workers developed nanocomposite MOF materials for the measurement of temperature during catalytic reactions.108 They synthesized three different MOF composites, NaYF4:Er,Yb@NaYF4@M, NaGdF4:Tm,Yb@M and NaGdF4:Er,Yb@M (where M = UiO-66-NH2), and the measurement of temperature is based on the room temperature upconversion (UC) fluorescence properties. The UC fluorescence study of the nanomaterial NaYF4:Er,Yb@NaYF4 was carried out in the temperature range 293.15–343.15 K under the irradiation of a CW laser. The emission peaks at 520 nm and 540 nm (green emission) are ascribed to the transitions of 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2, respectively. The emission at 650 nm (red emission) is attributed to the transition of 4F9/2 → 4I15/2 (Fig. 14a).
 | ||
| Fig. 14 (a) The normalized emission profile of NaYF4:Er,Yb@NaYF4 with temperature. (b) The normalized emission profile of NaYF4:Er,Yb@NaYF4@UiO-66-NH2 with temperature. Adapted from ref. 108. | ||
The UC thermometry based on Yb3+/Er3+ in the visible region depends on the emission intensity ratio of the thermally coupled excited levels 2H11/2 and 4S3/2. From the thermometric calibration curve, the maximum relative intensity of nanomaterial NaYF4:Er,Yb@NaYF4 was found at 0.742% K−1 at 293.15 K. Similarly, for NaYF4:Er,Yb@NaYF4@UiO-66-NH2, the emission profile was measured in the temperature range 293.15–343.15 K (Fig. 14b). Interestingly, the same electronic transition occurred as in the case of NaYF4:Er,Yb@NaYF4 and the ratio of green/red emission changes with the temperature. Moreover, as in NaYF4:Er,Yb@NaYF4, the green emission of NaYF4:Er,Yb@NaYF4@UiO-66-NH2 also prevails here and this is significant for thermometry. From the thermometric calibration curve, the obtained Sm is 0.937% K−1 at 293.15 K. Moreover, the thermometry showed reproducibility and uncertainty δT < 0.115 K.
Chen, Zhao and co-workers reported two NbO-type isostructural MOFs, ZnPZDDI and ZJU-56, from the ligands H4PZDDI and H4PDDI for the determination of temperature over a tuneable temperature range.109 To do this, they incorporated the red-emitting dye DSM and the lanthanide metal ion (Eu3+) into the pores of these two MOFs to produce four daughter MOFs, DSM@ZnPZDDI, Eu3+@ZnPZDDI, DSM@ZJU-56 and Eu3+@ZJU-56 (Fig. 15).
 | ||
| Fig. 15 The construction of various MOF composites as luminescent thermometers. Adapted from ref. 109. | ||
The maximum relative sensitivities of DSM@ZJU-56 and DSM@ZnPZDDI were found to be 1.11% K−1 and 0.44% K−1, respectively, at 298 K. Furthermore, the MOF composites Eu3+@ZJU-56 and Eu3+@ZnPZDDI demonstrated maximum relative sensitivities of about 14.56% K−1 (at 453 K) and 1.21% K−1 (at 436 K), respectively. These sensitivities illustrate that the thermometers Eu3+@ZJU-56 and DSM@ZJU-56 are effective with respect to their competitors. The higher sensitivity of Eu3+@ZJU-56 is ascribed to the ligand sensitization of Eu3+ by the linker PDDI at higher temperature, whereas the higher sensitivity of DSM@ZJU-56 is attributed to the strong interactions within the framework leading to the decrease of non-radiative decay. Based on a similar concept, the integration of a fluorophore (dye) moiety in the MOF network for the creation of MOF thermometers was also reported by Tan and co-workers.110 They incorporated rhodamine B (RhB dye) inside a zeolitic MOF (ZIF-71) to form an MOF thermometer, RhB@ZIF-71.
Apart from the crystalline MOF materials, the fabrication of MOF as a crystalline thin film or nanosheet film has been applied for thermometry.111 In this regard, Chen and co-workers described an excellent work where they fabricated a ratiometric thermometer by using a lanthanide-based MOF.112 The composite membrane, Eu0.0025Tb0.9975-BABDC-PBMA, is constructed by the copolymerization of Eu0.0025Tb0.9975-BABDC with BMA in the presence of UV light. Individual MOF membranes, M-BABDC-PBMA (where M = Tb and Eu) were also synthesized for better discussion. The emission intensity of both the individual membranes decreases with the rise in temperature. This is due to the non-radiative decay of these membranes. However, the mixed lanthanide membrane composite showed the increment of the fluorescence intensity of Eu3+ and the decline of the emission intensity of Tb3+ in the temperature range of 90–240 K. This diverse behaviour with temperature helps to establish the mixed lanthanide membrane as a self-calibrating thermometric probe. The Sr value of the mixed lanthanide membrane was calculated as 3.61% K−1 at 240 K.
Cao and co-workers reported three mixed metal MOF-based thin films (UiO-66(Zr&Eu)-X, where X = 1, 2 and 3) thermometers by tuning the composition of the constituent metal ions.113 Film 1 showed prominent luminescence peaks at 617 and 420 nm arising from the metal and linker under excitation at 360 nm. This fluorescence intensity gradually decreases with the increase of the temperature from 237 to 337 K (Fig. 16). This is ascribed to the non-radiative decay process. The ratio of I617/I420 showed a linear relationship over a wide range of temperature (237–337 K), which suggested the temperature sensitivity. The Sr values of UiO-66(Zr&Eu)-1, UiO-66(Zr&Eu)-2 and UiO-66(Zr&Eu)-3 were found to be 4.26%, 3.8% and 4.67% K−1, respectively. Interestingly, it has been noted that the sensitivity of the film also depends on the film thickness. The thermal sensitivity increases with decreasing film thickness. In addition, the film thermometer is recoverable for up to three cycles.
 | ||
| Fig. 16 The synthetic scheme for thin film and its thermometric property. Adapted from ref. 113. | ||
The same group (Cao and co-workers) also described the construction of hybrid thin films, Eu@UiO-66-hybrid film and Tb@UiO-hybrid film through electrophoretic deposition (EPD) techniques.114 These two hybrid films showed excellent thermal sensitivities of 4.26% K−1 and 2.76% K−1 for Eu@UiO-66-hybrid film and Tb@UiO-hybrid film, respectively.
Table 1 details the various MOF-based thermometers with their diverse crucial parameters to assess the efficiency of the thermometers. These thermometers show different relative sensitivities at different temperatures. There are a few fundamental aspects for a thermometer to behave as an efficient thermometer. The thermometers constructed with dyes, quantum dots, etc. within the MOF cavity, the thermal sensitivity of such thermometers can be determined by measuring the ratio of the emission intensities among the dyes i.e., Idye1/Idye2 or it may be possible by measuring Idye/IMOF or Idye/Iligand. Apart from the measurement of the emission intensities, the important eqn (2)–(10) are imperative for the measurement of Sr. For a thermometer involving a lanthanide-based MOF or lanthanide ions, then the mechanism of the working principle is a little different as the role of the antenna effect, i.e., the sensitization of the lanthanide metal ion by the linker, is extremely significant to obtain proper emission from the lanthanide ion. From, the energy profile diagram of the lanthanide emission, it is clear that the ligand absorbs suitable wavelength (or energy) and jumps from the ground level to the excited singlet level. Actually, the transfer of energy from the linker to the lanthanide ion generally occurs in the excited triplet state of the linker. Thus, the linker in the MOF has to change its spin state from the excited singlet state to the excited triplet state and this process is known as ISC. In this regard, Reinhoudt's empirical rule is very significant, which states that if the energy difference between the excited singlet and excited triplet states exceeds 5000 cm−1, then the ISC method becomes effective.142–144 After the ISC process, an appropriate energy difference between the acceptor (lanthanide metal ions) and donor (linker; sensitizer) is crucial for the effective transfer and back transfer of energy, and this process is predicted by the Latva rule.145 As per this rule, the energy gap between the sensitizer and the lanthanide metal ion should be between 2000 and 4000 cm−1 for optimum transfer of energy.146 It has been observed that most of the thermometers are lanthanide-based MOFs, and particularly Tb3+ and Eu3+ metal ions are largely used. The thermometric parameter of this kind of thermometer depends on the emission intensity ratio of Tb3+ (5D4 → 7F5) and Eu3+ (5D0 → 7F2) and the emission intensities of these two transitions are administered by the thermally activated transfer of energy among the linker and lanthanide metal ions and by back transfer of energy. In addition, the PAET from Tb3+ → Eu3+ is also responsible for the sensitivity of these two metal ions to temperature, which ultimately affects Sr. The schematic diagram of the PAET process is given in Fig. 17. The occurrence of PAET would be assessed by measuring the lifetime of the Tb3+ and Eu3+ ions. In general, if there is an occurrence of PAET from Tb3+ → Eu3+ then the lifetime of the Tb3+ ion decreases. The energy transfer efficiency (ηET) from Tb3+ → Eu3+ is calculated with the following equation:
 | (12) |
6. Conclusion and future prospects
Temperature is an essential physical parameter in many aspects, such as the automobile industry, scientific experiments, different electronic systems, and biological phenomena. For the precise determination of the temperature, we need to have efficient thermometric sensors. MOFs have the ability to measure the temperature in different ranges, like cryogenic (<100 K), medium (100–300 K), biological/physiological (298–323 K) and high temperature (>400 K). Lanthanides possess some crucial features: a ratiometric signal, high quantum yields, photostability and high decay times. Consequently, lanthanide-based MOFs are largely investigated for the construction of MOF thermometric sensors. Among the lanthanides, mostly Eu3+ and Tb3+ metal ions have been used for the construction of MOF thermometers. The other pairs of lanthanides, Yb3+/Tm3+, Yb3+/Nd3+, Nd3+/Tm3+, Yb3+/Nd3+, and Yb3+/Er3+, would be very interesting for medical and biological applications as these pairs sound promising for their NIR emission and upconversion luminescence properties. One of the pairs has been utilized by Kaczmarek and co-workers for MOF thermometry.108The aforementioned discussion conveyed that the thermometric property of MOFs is based on the development of a ratiometric MOF sensor that would be constructed on the following guidance: (i) lanthanide-based MOF, (ii) selecting linkers with the capability to sensitize the lanthanide metal ion, (iii) introducing secondary linkers, (iv) incorporation of a chromophore molecule within the MOF cavity, and (v) post-synthetic incorporation of lanthanide metal ions or linkers in the SBU or ligand backbone of the MOF. Concerning the linker sensitization (or antenna effect) for the most studied Tb3+/Eu3+-MOF thermometer, the TEES value of the linker is required to be in the region of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–27
000–27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. This energy level matches the accepting energy levels of Tb3+ (5D4, 20
000 cm−1. This energy level matches the accepting energy levels of Tb3+ (5D4, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) and Eu3+ (5D1, 19
500 cm−1) and Eu3+ (5D1, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 cm−1), and then the sensitization as well as the emission of lanthanides would be very efficient. Moreover, the transfer of energy between the host and guest molecules, and vice versa, and energy transfer between the ions, are very important for MOF thermometry. A few important parameters like relative sensitivity, temperature uncertainty and reproducibility are crucial to assess the effectiveness of MOF thermometers.
030 cm−1), and then the sensitization as well as the emission of lanthanides would be very efficient. Moreover, the transfer of energy between the host and guest molecules, and vice versa, and energy transfer between the ions, are very important for MOF thermometry. A few important parameters like relative sensitivity, temperature uncertainty and reproducibility are crucial to assess the effectiveness of MOF thermometers.
When constructing MOF thermometers, a few vital points need to be considered: (a) it is necessary to comprehend the energy transfer within MOFs. This will explain the effect of temperature on the thermal sensitivity and temperature uncertainty of the MOF materials. (b) The construction of bio compatible nanothermometers aimed at bio-applications is also very interesting. Such nanothermometers can be applied to measure the temperature in the intracellular region. (c) The construction of a multifunctional thermometer: in modern technology, it is recommended to have multi-functionalities in a single podium. In this regard, the amalgamation of MOF thermometry with other functionalities like the sensing of analytes, MRI, drug delivery etc., is very appealing. All these features combined with thermometry would be beneficial in biological applications. Zaworotko and co-workers described some excellent work where they developed Gd(III)-ZIF-MOF as a magnetic resonance thermometer.147 (d) The commercialisation of luminescence-based MOF thermometers. Therefore, suitable synthetic processes for scaling up MOF nanomaterials, MOF-polymer amalgams and the fabrication of the thin films are very important to the arrival of prototype MOF thermometers.
In summary, we have seen that MOFs can be easily fabricated into optical chemical platforms as ratiometric sensors for precise measurement of the temperature. Though significant progress has been made with MOF thermometry, much endeavour is required to decipher these MOF materials into real-time thermometers.
Abbreviations
| SBU | Secondary building unit |
| PSM | Post-synthetic modification |
| H2BDC | Terephthalic acid/1,4-benzene dicarboxylic acid |
| DMBDC | 2,5-Dimethoxy-1,4-benzenedicarboxylate |
| DSB | 3,5-Disulfobenzoic acid |
| PIA | 5-(Pyridin-4-yl)isophthalate |
| CPB | 4-Carboxyphenylboronic acid |
| PDA | 1,4-Phenylenediacetic acid |
| H3CPDA | 5-(4-Carboxyphenyl)-2,6-pyridinedicarboxylic acid |
| BPYDC | 2,2′-Bipyridine-5,5′-dicarboxylic acid |
| BPDC | Biphenyl-4,4-dicarboxylic acid |
| H2BPDC-0N | 4,4′-Biphenyldicarboxylic acid |
| H2BPDC-1N | 6-(4-Carboxyphenyl)nicotinic acid |
| H2BPDC-2N | [2,2′-Bipyridine]-5,5′-dicarboxylic acid |
| TPI | 4′-(1H-Tetrazol-5-yl)-[1,1′-biphenyl]-3,5-dicarboxylic acid |
| H2OBA | 4,4′-Dicarboxydiphenyl ether |
| H3PIDC | 4-Carboxy-2-(pyridinium-4-yl)-1H-imidazole-5-carboxylate monohydrate |
| QPTCA | [1,1′:4′,1′′:4′′,1′′′-Quaterphenyl]-4,4′′′-dicarboxylic acid |
| BPDA | Dimethyl 5-(4,4,5,5-tetramethyl1,3,2-dioxaborolan-2-yl) isophthalate |
| AD | Adenine |
| HIMC | 1H-Imidazole-4,5-dicarboxylic acid |
| D-CAM | 1,2,2-Trimethylcyclopentane-1,3-dicarboxylic acid |
| OA | Oxalic acid |
| HY | 5-Hydroxybenzene-1,2,4-tricarboxylic acid |
| BDC-OH | 2-Hydroxy benzene dicarboxylic acid |
| TCPTPY | 2-(2,6-Bis(4-carboxyphenyl)pyridin-4-yl)benzene-1,3,5-tricarboxylic acid |
| BTB | 5′-(4-Carboxyphenyl)-[1,1′:3′,1′′-terphenyl]-4,4′′-dicarboxylic acid |
| DSTP | 2,4-(2,2′:6′,2′′-Terpyridin-4′-yl)-benzenedisulfonic acid |
| H4PDDI | 5,5′-(Pyridine-2,5-diyl)diisophthalic acid |
| BCPI | 1,3-bis(4-carboxyphenyl)-1H-imidazole-3-ium |
| H2L−Cl | 1-(4-Carboxybenzyl)-4-(4-carboxyphenyl)pyridin-1-ium chloride |
| TPTC-2OMe | 2′,5′-Dimethoxy-[1,1′:4′,1′′-terphenyl]-3,3′′,5,5′′-tetracarboxylic acid |
| H4PZDDI | 5,5′-(Pyrazine-2,5-diyl)diisophthalic acid |
| H2BPNDC | Benzophenone-4,4′-dicarboxylic acid |
| H3BTC | Benzene tricarboxylic acid |
| BDC-NH2 | 2-Amino terephthalic acid |
| 1,4-H2NDC | 1,4-Naphthalene dicarboxylic acid |
| 2,6-H2NDC | 2,6-Naphthalene dicarboxylic acid |
| H3TATB | Triazine-1,3,5-tribenzoic acid |
| T1 | Triplet excited state |
| S0 | Ground singlet state |
| S1 | Singlet excited state |
| LMCT | Linker to metal charge transfer |
| MLCT | Metal to ligand charge transfer |
| LLCT | Linker to linker charge transfer |
| ETTC | 4,4,4,4-(Ethane-1,1,2,2-tetrayl)tetrabiphenyl-4-carboxylic acid |
| Hmtz | 5-Methyltetrazole |
| Hphtz | 5-Phenyltetrazole |
| Hnic | Nicotinic acid |
| H4L5 | [1,1′:3′,1′′-Terphenyl]-3,3′′,5,5′′-tetracarboxylic acid |
| H3L6 | [1,1′:3′,1′′-Terphenyl]-4,4′′,5′-tricarboxylic acid |
| H4ddn | 3,5-Di(3,5-dicarboxylphenyl)nitrobenzene |
| DIPT | 2-(2,4-Dichlorophenyl)-1H-imidazo [4,5-f]-[1,10]phenanthroline |
| PClA | 3-(2-Chlorophenyl)acrylate |
| HOMO | Highest occupied molecular orbital |
| LUMO | Lowest unoccupied molecular orbital |
| UiO | Universitetet i Oslo |
| DABCO | 1,4-Diazabicyclo[2.2.2]octane |
| DMF | N,N′-Dimethylformamide |
| SALE | Solvent assisted linker exchange |
| H2BCPPE | 1,2-Bis(4-(4-carboxyphenyl))-1,2-diphenylethene |
| H2dtba | 2,2-Dithiobisbenzoic acid |
| Bpp | 1,3-Bis(4-pyridyl)propane |
| 2,3-H2PYDC | 2,3-Pyridinedicarboxylic acid |
| QD s | Quantum dots |
| ZIF | Zeolite imidazolate framework |
| LOD | Limit of detection |
| BPEI | Branched poly(ethylenimine) |
| DAE | Diarylethene |
| GS | Ground state |
| ES | Excited state |
| ISC | Intersystem crossing |
| TEES | Triplet excited energy state |
| PAET | Phonon-assisted energy transfer |
| AIE | Aggregation induce emission |
| XPS | X-ray photoelectron spectroscopy |
| Ln | Lanthanide |
| RT | Room temperature |
| 4-Mu | Methylumbelliferone |
| Flu | Fluorescein |
| UC | Upconversion |
| DSM | 4-[p-(Dimethylamino)styryl]-1-methylpyridinium |
| EPD | Electrophoretic deposition |
| H4BTCA | 5-Hydroxy-1,2,4-benzenetricarboxylic acid |
| H2BABDC | 2,5-Bis(allyloxy)terephthalic acid |
| H2IMB | 4,4′-((1H-Imidazole-1-yl)methylene)dibenzoic acid |
| mbix | 1,3-Bis(imidazol-1-ylmethyl)benzene |
| POM | Polyoxometalate Na9[EuW10O36]·32H2O |
| DMASE | 4-(4-(Dimethylamino)styryl)-1-ethylpyridinium |
| H4TCOMA | Tetrakis[4-(carboxyphenyl)oxamethyl]methane acid |
| MMM | Mixed-matrix membranes |
| iBDPO | N,N′-Bis(3,5-dicarboxyphenyl)oxalamide |
| BMA | Butyl methacrylate |
| MRI | Magnetic resonance imaging |
| L1 | 2,6-Bis(1-methyl-imidazol-2-yl)pyridine |
| H2L2 | 3-Bis(3-carboxyphenyl)imidazolium |
| H4L3 | 2,6-Di(2′,4′-dicarboxylpheny)pyridine |
| H4L4 | 5,5′-(Carbonylbis(azanediyl))diisophthalic acid |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
DBK and MYC acknowledge PDEU for the institutional scholarship. TKP gratefully acknowledges financial support received from SERB, India (TAR/2021/000090) and R&D/SRP-2022-007, PDEU.References
- L. Michalski, K. Eckersdorf, J. Kucharski and J. McGhee, Temperature Measurement, Wiley, West Sussex, 2nd edn, 2002, pp. 471–478 Search PubMed.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326 RSC.
- A. H. Khalid and K. Kontis, Sensors, 2008, 8, 5673–5744 CrossRef CAS PubMed.
- R. P. Benedict, Wiley, New York, 1977 Search PubMed.
- Temperate sensor market, global forecast to 2027 (by product type, output, end-user industry, and geography); SE 2914; Markets and Markets: 2020.
- S. J. Cho, D. Maysinger, M. Jain, B. Rçder, S. Hackbarth and F. M. Winnik, Langmuir, 2007, 23, 1974–1980 CrossRef CAS PubMed.
- F. V. Bussche, A. M. Kaczmarek, V. V. Speybroeck, P. V. D. Voort and C. V. Stevens, Chem. – Eur. J., 2021, 27, 7214–7230 CrossRef PubMed.
- A. M. Kaczmarek and P. V. D. Voort, Materials, 2020, 13, 566 CrossRef CAS PubMed.
- J. K. Zaręba, M. Nyk, J. Janczak and M. Samoć, ACS Appl. Mater. Interfaces, 2019, 11, 10435–10441 CrossRef PubMed.
- Z. Wanga, S. Yua, H. Zhanga and H. Duan, Synth. Met., 2019, 255, 116104 CrossRef.
- D. A. Gálico, E. R. Souza, I. O. Mazali and F. A. Sigoli, J. Lumin., 2019, 210, 397–403 CrossRef.
- H. Yan, H. Ni, J. Jia, C. Shan, T. Zhang, Y. Gong, X. Li, J. Cao, W. Wu, W. Liu and Y. Tang, Anal. Chem., 2019, 91, 5225–5234 CrossRef CAS PubMed.
- P. Leo, D. Briones, J. A. García, J. Cepeda, G. Orcajo, G. Calleja, A. R. Diéguez and F. Martínez, Inorg. Chem., 2020, 59, 18432–18443 CrossRef CAS PubMed.
- S. Wang, B. Sun, J. Sun, X. Hao, X. Li, C. Zhou and Z. Su, Dyes Pigm., 2022, 202, 110256 CrossRef CAS.
- Y. Cui, F. Zhu, B. Chen and G. Qian, Chem. Commun., 2015, 51, 7420–7431 RSC.
- H.-R. Fu, N. Wang, J.-H. Qin, M.-L. Han, L.-F. Ma and F. Wang, Chem. Commun., 2018, 54, 11645–11648 RSC.
- T. K. Pal, R. Katoch, A. Garg and P. K. Bharadwaj, Cryst. Growth Des., 2015, 15, 4526–4535 CrossRef CAS.
- A. V. Artemev, M. P. Davydova, A. S. Berezin, D. G. Samsonenko, I. Y. Bagryanskaya, V. K. Brel, X. Hei, K. A. Brylev, O. I. Artyushin, L. E. Zelenkov, I. I. Shishkin and J. Li, ACS Appl. Mater. Interfaces, 2022, 14, 31000–31009 CrossRef CAS PubMed.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- P. Lama, A. Rawat, P. Sikiti and T. K. Pal, Inorg. Chem., 2022, 61, 939–943 CrossRef CAS PubMed.
- T. K. Pal, ChemistrySelect, 2019, 4, 536–542 CrossRef CAS.
- S. Pal, T. K. Pal and P. K. Bharadwaj, CrystEngComm, 2016, 18, 1825–1831 RSC.
- J.-S. Qin, S. Yuan, C. Lollar, J. Pang, A. Alsalme and H.-C. Zhou, Chem. Commun., 2018, 54, 4231–4249 RSC.
- N. Patel, P. Shukla, P. Lama, S. Das and T. K. Pal, Cryst. Growth Des., 2022, 22, 3518–3564 CrossRef CAS.
- U. Mondal, S. Bej, A. Hazra, S. Mandal, T. K. Pal and P. Banerjee, Dalton Trans., 2022, 51, 2083–2093 RSC.
- G. Li and Y. Han, ACS Cent. Sci., 2022, 8, 150–152 CrossRef CAS PubMed.
- D. B. Kanzariya, R. Goswami, D. Muthukumar, R. S. Pillai and T. K. Pal, ACS Appl. Mater. Interfaces, 2022, 14, 48658–48674 CrossRef CAS PubMed.
- B. Li, J. Coord. Chem., 2020, 73, 429–438 CrossRef CAS.
- H.-R. Fu, L.-B. Yan, N.-T. Wu, L.-F. Ma and S.-Q. Zang, J. Mater. Chem. A, 2018, 6, 9183–9191 RSC.
- Z.-F. Qiu, S.-M. Zhao, Z.-H. Xu, Y. Zhao, Z.-L. Wang and W.-Y. Sun, Cryst. Growth Des., 2021, 21, 5306–5316 CrossRef CAS.
- A. Bavykina, N. Kolobov, S. Khan, J. A. Bau, A. Ramirez and J. Gascon, Chem. Rev., 2020, 120, 8468–8535 CrossRef CAS PubMed.
- D. De, T. K. Pal and P. K. Bharadwaj, Inorg. Chem., 2016, 55, 6842–6844 CrossRef CAS PubMed.
- A. Rawat, S. Dhakla, P. Lama and T. K. Pal, J. CO2 Util., 2022, 59, 101939 CrossRef CAS.
- P. Lama, H. Aggarwal, C. X. Bezuidenhout and L. J. Barbour, Angew. Chem., Int. Ed., 2016, 55, 13271–13275 CrossRef CAS PubMed.
- T. K. Pal, D. De and P. K. Bharadwaj, Coord. Chem. Rev., 2020, 408, 213173 CrossRef CAS.
- Y. Deng, Y. Wu, G. Chen, X. Zheng and M. Dai, Chem. Eng. J., 2021, 405, 127004 CrossRef CAS.
- H. D. Lawson, S. P. Walton and C. Chan, ACS Appl. Mater. Interfaces, 2021, 13, 7004–7020 CrossRef CAS PubMed.
- S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS PubMed.
- A. Karmakar, P. Samanta, A. V. Desai and S. K. Ghosh, Acc. Chem. Res., 2017, 50, 2457–2469 CrossRef CAS PubMed.
- H.-Q. Yin and X.-B. Yin, Acc. Chem. Res., 2020, 53, 485–495 CrossRef CAS PubMed.
- M.-L. Hu, S. A. A. Razavi, M. Piroozzadeh and A. Morsali, Inorg. Chem. Front., 2020, 7, 1598–1632 RSC.
- J. Rocha, C. D. S. Brites and L. D. Carlos, Chem. – Eur. J., 2016, 22, 14782–14795 CrossRef CAS PubMed.
- Y. Zhang, S. Yuan, G. Day, X. Wang, X. Yang and H.-C. Zhou, Coord. Chem. Rev., 2018, 354, 28–45 CrossRef CAS.
- Z. Zhao, X. Shen, H. Li, K. Liu, H. Wu, X. Li and X. Gao, Angew. Chem., Int. Ed., 2022, 61, e202114340 CrossRef CAS PubMed.
- J.-W. Zhang, H. Li, J.-Q. Li, Y. Chen, P. Qu and Q.-G. Zhai, Dalton Trans., 2021, 50, 17482–17486 RSC.
- S. Bej, R. Das, D. Kundu, T. K. Pal and P. Banerjee, CrystEngComm, 2023, 25, 1626–1636 RSC.
- Y. Wan, L. Yu and T. Xi, Dyes Pigm., 2022, 202, 110234 CrossRef CAS.
- Y. Li, X. Xiao, Z. Wei and Y. Chen, ZAAC, 2022, 648, e202100323 CAS.
- D. Frackowiak, The Jablonski diagram, J. Photochem. Photobiol., B, 1988, 2, 399 CrossRef.
- J. Dong, D. Zhao, Y. Lu and W.-Y. Sun, J. Mater. Chem. A, 2019, 7, 22744–22767 RSC.
- T. K. Pal, Mater. Chem. Front., 2023, 7, 405–441 RSC.
- Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125 CrossRef CAS PubMed.
- Z. Hu, B. J. Deibert and J. Li, Chem. Soc. Rev., 2014, 43, 5815–5840 RSC.
- S. Záliš, C. Consani, E. Nahhas, A. Cannizzo, M. Chergui, F. artl and A. VlčekJr, Inorg. Chim. Acta, 2011, 374, 578–585 CrossRef.
- M. Robin, Inorg. Chem., 1962, 1, 337–342 CrossRef CAS.
- A. Vogler and H. Kunkely, Coord. Chem. Rev., 2017, 251, 577–583 CrossRef.
- Y. Zhao, J. Wang, W. Zhu, L. Liub and R. Pei, Nanoscale, 2021, 13, 4505–4511 RSC.
- D. S. Liu, Y. Sui, W. T. Chen and P. Feng, Cryst. Growth Des., 2015, 15, 4020–4025 CrossRef CAS.
- B.-H. Li, J. Wub, J.-Q. Liua, C.-Y. Gua, J.-W. Xua, M.-M. Luo, R. Yadav, A. Kumar and S. R. Batten, ChemPlusChem, 2016, 81, 885–892 CrossRef CAS PubMed.
- A. Ma, J. Wu, Y. Han, F. Chen, B. Li, S. Cai, H. Huanga, A. Singh, A. Kumar and J. Liu, Dalton Trans., 2018, 47, 9627–9633 RSC.
- H. Sun, Z. Wang, X. Li, S. Han, J. Wang and W. Li, Inorg. Chim. Acta, 2019, 486, 750–756 CrossRef CAS.
- J.-F. Feng, S.-y. Gao, T.-f. Liu, J. Shi and R. Cao, ACS Appl. Mater. Interfaces, 2018, 10, 6014–6023 CrossRef CAS PubMed.
- P.-P. Cui, X.-D. Zhang, P. Wang, Y. Zhao, M. Azam, S. I. Al-Resayes and W.-Y. Sun, Inorg. Chem., 2017, 56, 14157–14163 CrossRef CAS PubMed.
- S. S. Zhao, H. Zhang, L. Wang, L. Chen and Z. G. Xie, J. Mater. Chem. C, 2018, 6, 11701–11706 RSC.
- F. Rui, J. Fei-Long, C. Lian, Y. Chun-Feng, W. Ming-Yan and M.-C. Hong, Chem. Commun., 2009, 35, 5296–5298 Search PubMed.
- Z. Z. Lin, L. Chen, C. Y. Yue, C. F. Yan, F. L. Jiang and M. C. Hong, Inorg. Chim. Acta, 2008, 361, 2821–2827 CrossRef CAS.
- G.-H. Wang, Z.-G. Li, H.-Q. Jia, N.-H. Hu and J.-W. Xu, CrystEngComm, 2009, 11, 292–297 RSC.
- Y. Ma, G. Xu, F. Wei, Y. Cen, X. Xu, M. Shi, X. Cheng, Y. Chai, M. Sohail and Q. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 20801–20805 CrossRef CAS PubMed.
- X. Xu and B. Yan, J. Mater. Chem. C, 2016, 4, 1543–1549 RSC.
- X. Zheng, Y. Zhao, P. Jia, Q. Wang, Y. Liu, T. Bu, M. Zhang, F. Bai and L. Wang, Inorg. Chem., 2020, 59, 18205–18213 CrossRef CAS PubMed.
- R. Chen, J. Zhang, J. Chelora, Y. Xiong, S. Kershaw, K. Li, P. Lo, K. Cheah, A. Rogach, J. Zapien and C. Lee, ACS Appl. Mater. Interfaces, 2017, 9, 5699–5708 CrossRef CAS PubMed.
- Y. Yang, W. Liu, Q. Zhong, J. Zhang, B. Yao, X. Lian and H. Niu, ACS Appl. Nano Mater., 2021, 4, 4735–4745 CrossRef CAS.
- S. Saha, G. Das, J. Thote and R. Banerjee, J. Am. Chem. Soc., 2014, 136, 14845–14851 CrossRef CAS PubMed.
- S. Jin, H.-J. Son, O. K. Farha, G. P. Wiederrecht and J. T. Hupp, J. Am. Chem. Soc., 2013, 135, 955–958 CrossRef CAS PubMed.
- Y. Ma, G. Xu, F. Wei, Y. Cen, Y. Ma, Y. Song, X. Xu, M. Shi, S. Muhammad and Q. Hu, J. Mater. Chem. C, 2017, 5, 8566–8571 RSC.
- X. Lin, G. Gao, L. Zheng, Y. Chi and G. Chen, Anal. Chem., 2014, 86, 1223–1228 CrossRef CAS PubMed.
- W. Xie, W. He, S. Li, K. Shao, Z. Su and Y. Lan, Chem. – Eur. J., 2016, 22, 17298–17304 CrossRef CAS PubMed.
- J. An, C. Shade, D. Czegan, S. Petoud and N. Rosi, J. Am. Chem. Soc., 2011, 133, 1220–1223 CrossRef CAS PubMed.
- P. Jia, K. Yang, J. Hou, Y. Cao, X. Wang and L. Wang, J. Hazard. Mater., 2021, 408, 124469 CrossRef CAS PubMed.
- Z. Li, G. Wang, Y. Ye, B. Li, H. Li and B. Chen, Angew. Chem., Int. Ed., 2019, 58, 18025–18031 CrossRef CAS PubMed.
- K. Binnemans, Chem. Rev., 2009, 109, 4283–4374 CrossRef CAS PubMed.
- B. Yan, Acc. Chem. Res., 2017, 50, 2789–2798 CrossRef CAS PubMed.
- Y. Hasegawa and Y. Kitagawa, J. Mater. Chem. C, 2019, 7, 7494–7511 RSC.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- G. E. Khalil, K. Lau, G. D. Phelan, B. Carlson, M. Gouterman, J. B. Callis and L. R. Dalton, Rev. Sci. Instrum., 2004, 75, 192–206 CrossRef CAS.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326 RSC.
- X. D. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834–7869 RSC.
- C. D. S. Brites, P. P. Lima, N. J. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829 RSC.
- D. Parker, Coord. Chem. Rev., 2000, 205, 109–130 CrossRef CAS.
- Y. Cui, H. Xu, Y. Yue, Z. Guo, J. Yu, Z. Chen, J. Gao, Y. Yang, G. Qian and B. Chen, J. Am. Chem. Soc., 2012, 134, 3979–3982 CrossRef CAS PubMed.
- X. Rao, T. Song, J. Gao, Y. Cui, Y. Yang, C. Wu, B. Chen and G. Qian, J. Am. Chem. Soc., 2013, 135, 15559–15564 CrossRef CAS PubMed.
- Y. Cui, W. Zou, R. Song, J. Yu, W. Zhang, Y. Yang and G. Qian, Chem. Commun., 2014, 50, 719–721 RSC.
- D. Zhao, X. Rao, J. Yu, Y. Cui, Y. Yang and G. Qian, Inorg. Chem., 2015, 54, 11193–11199 CrossRef CAS PubMed.
- A. Cadiau, C. D. S. Brites, P. M. F. J. Costa, R. A. S. Ferreira, J. Rocha and L. D. Carlos, ACS Nano, 2013, 7, 7213–7218 CrossRef CAS PubMed.
- X. Liu, S. Akerboom, M. d. Jong, I. Mutikainen, S. Tanase, A. Meijerink and E. Bouwman, Inorg. Chem., 2015, 54, 11323–11329 CrossRef CAS PubMed.
- X. Shen, Y. Lu and B. Yan, Eur. J. Inorg. Chem., 2015, 916–919 CrossRef CAS.
- Y. Wei, R. Sa, Q. Li and K. Wu, Dalton Trans., 2015, 44, 3067–3074 RSC.
- T. Xia, Z. Shao, X. Yan, M. Liu, L. Yu, Y. Wan, D. Chang, J. Zhang and D. Zhao, Chem. Commun., 2021, 57, 3143–3146 RSC.
- Y. Zhou, B. Yan and F. Lei, Chem. Commun., 2014, 50, 15235–15238 RSC.
- W. Cao, Y. Cui, Y. Yang and G. Qian, ACS Mater. Lett., 2021, 3, 1426–1432 CrossRef CAS.
- J. Liu, Y. Zhao, X. Li, J. Wu, Y. Han, X. Zhang and Y. Xu, Cryst. Growth Des., 2020, 20, 454–459 CrossRef CAS.
- C. Wang, H. Lin, X. Xiang, Y. Cheng, Q. Huang, Y. Gao, X. Cui and Y. Wang, J. Mater. Chem. C, 2018, 6, 9964–9971 RSC.
- J. Liu, L. Pei, Z. Xia and Y. Xu, Cryst. Growth Des., 2019, 19, 6586–6591 CrossRef CAS.
- B. Wang, Y. Yu, H. Zhang, Y. Xuan, G. Chen, W. Ma, J. Li and J. Yu, Angew. Chem., Int. Ed., 2019, 58, 18443–18448 CrossRef CAS PubMed.
- W.-N. Miao, B. Liu, H. Li, S.-J. Zheng, H. Jiao and L. Xu, Inorg. Chem., 2022, 61, 14322–14332 CrossRef CAS PubMed.
- J. Liu, X. Han, Y. Lu, S. Wang, D. Zhao and C. Li, Inorg. Chem., 2021, 60, 4133–4143 CrossRef CAS PubMed.
- H. S. Jena, H. Rijckaert, C. Krishnaraj, I. V. Driessche, P. V. D. Voort and A. M. Kaczmarek, Chem. Mater., 2021, 33, 8007–8017 CrossRef CAS.
- R. S. Wang, M. Gong, X. Han, D. Zhao, J. Liu, Y. Lu, C. Li and B. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 11078–11088 CrossRef PubMed.
- Y. Zhang, M. Gutiérrez, A. K. Chaudhari and J.-C. Tan, ACS Appl. Mater. Interfaces, 2020, 12, 37477–37488 CrossRef CAS PubMed.
- G.-H. Wen, X.-M. Chen, K. Xu, X. Xie, S.-S. Bao and L.-M. Zheng, Dalton Trans., 2021, 50, 17129–17139 RSC.
- T. Feng, Y. Ye, X. Liu, H. Cui, Z. Li, Y. Zhang, B. Liang, H. Li and B. Chen, Angew. Chem., Int. Ed., 2020, 59, 21752–21757 CrossRef CAS PubMed.
- J.-f. Feng, T.-f. Liu, J. Shi, S.-y. Gao and R. Cao, ACS Appl. Mater. Interfaces, 2018, 10, 20854–20861 CrossRef CAS PubMed.
- J.-f. Feng, S.-y. Gao, T.-f. Liu, J. Shi and R. Cao, ACS Appl. Mater. Interfaces, 2018, 10, 6014–6023 CrossRef CAS PubMed.
- T. F. Xia, W. Q. Cao, L. L. Guan, J. Zhang, F. D. Jiang, L. B. Yu and Y. T. Wan, Dalton Trans., 2022, 51, 5426–5433 RSC.
- V. Trannoy, A. N. C. Neto, C. D. S. Brites, L. D. Carlos and H. Serier-Brault, Adv. Opt. Mater., 2021, 9, 2001938 CrossRef CAS.
- H. Z. Wang, D. Zhao, Y. J. Cui, Y. Yang and G. D. Qian, J. Solid State Chem., 2017, 246, 341–345 CrossRef CAS.
- S. B. Wang, B. Sun, Z. M. Su, G. H. Hong, X. Li, Y. L. Liu, Q. Q. Pan and J. Sun, Inorg. Chem. Front., 2022, 9, 3259–3266 RSC.
- Y. Yang, H. P. Huang, Y. Z. Wang, F. Z. Qiu, Y. Feng, X. R. Song, X. L. Tang, G. L. Zhang and W. S. Liu, Dalton Trans., 2018, 47, 13384–13390 RSC.
- D. M. Lyubov, A. N. C. Neto, A. Fayoumi, K. A. Lyssenko, V. M. Korshunov, I. V. Taydakov, F. Salles, Y. Guari, J. Larionova, L. D. Carlos, J. Long and A. A. Trifonov, J. Mater. Chem. C, 2022, 10, 7176–7188 RSC.
- Y. Yang, Y. Z. Wang, Y. Feng, X. R. Song, C. Cao, G. L. Zhang and W. S. Liu, Talanta, 2020, 208, 120354 CrossRef CAS PubMed.
- Y. Yang, L. Chen, F. L. Jiang, M. X. Yu, X. Y. Wan, B. Zhang and M. Hong, J. Mater. Chem. C, 2017, 5, 1981–1989 RSC.
- C. Xia, C. Y. Yu, M. M. Cao, J. F. Xia, D. Y. Jiang, G. H. Zhou, D. F. Zhang and H. L. Li, Ceram. Int., 2018, 44, 21040–21046 CrossRef CAS.
- D. Zhao, H. Z. Wang and G. D. Qian, CrystEngComm, 2018, 20, 7395–7400 RSC.
- Y. Cui, R. Song, J. Yu, M. Liu, Z. Wang, C. Wu, Y. Yang, Z. Wang, B. Chen and G. Qian, Adv. Mater., 2015, 27, 1420–1425 CrossRef CAS PubMed.
- X. Liu, M. A. Siegler and E. Bouwman, Eur. J. Inorg. Chem., 2016, 2016, 2984–2988 CrossRef CAS.
- Y. Pan, H.-Q. Su, E.-L. Zhou, H.-Z. Yin, K.-Z. Shao and Z.-M. Su, Dalton Trans., 2019, 48, 3723–3729 RSC.
- W. Liu, C. Chen, X. Huang, E. Xie and W. Liu, Chem. – Eur. J., 2019, 25, 10054–10058 CrossRef CAS PubMed.
- D. Zhao, D. Yue, K. Jiang, L. Zhang, C. Li and G. Qian, Inorg. Chem., 2019, 58, 2637–2644 CrossRef CAS PubMed.
- S. Wang, J. Jiang, Y. Lu, J. Liu, X. Han, D. Zhao and C. Li, J. Lumin., 2020, 226, 117418–117425 CrossRef CAS.
- Y. H. Han, C. B. Tian, Q. H. Li and S. W. Du, J. Mater. Chem. C, 2014, 2, 8065–8070 RSC.
- X. Lian, D. Zhao, Y. Cui, Y. Yang and G. Qian, Chem. Commun., 2015, 51, 17676–17679 RSC.
- M. Peng, A. M. Kaczmarek and K. V. Hecke, ACS Appl. Mater. Interfaces, 2022, 14, 14367–14379 CrossRef CAS PubMed.
- C. Gu, Y. Ding, X. Quan, M. Gong, J. Yu, D. Zhao and C. Li, J. Rare Earths, 2021, 39, 1024–1030 CrossRef CAS.
- E. Zhang, Y. He, L. Jiang, T. Cheng and P. Ju, J. Mol. Struct., 2021, 1229, 129800 CrossRef CAS.
- C. Viravaux, O. Oms, A. Dolbecq, E. Nassar, L. Busson, C. Mellot-Draznieks, R. Dessapt, H. Serier-Brault and P. Mialane, J. Mater. Chem. C, 2021, 9, 8323–8328 RSC.
- Y. Wan, Y. Cui, Y. Yang and G. Qian, Chin. Chem. Lett., 2021, 32, 1511–1514 CrossRef CAS.
- T. Zhou, S. Liu, S. Wang, S. Mi, P. Gao, X. Guo, Q. Su and H. Guo, Ind. Eng. Chem. Res., 2021, 60, 11760–11767 CrossRef CAS.
- Y. Ding, Y. Lu, K. Yu, S. Wang, D. Zhao and B. Chen, Adv. Opt. Mater., 2021, 9, 2100945 CrossRef CAS.
- D. Zhao, X. Han, S. Wang, J. Liu, Y. Lu and C. Li, Chem. – Eur. J., 2020, 26, 3145–3151 CrossRef CAS PubMed.
- Z. Li, Q. Wang, K. Yu, W. Cui, Y. He, B. Chen and D. Zhao, Inorg. Chem., 2023, 62, 5652–5659 CrossRef CAS PubMed.
- X. Mi, D. Sheng, Y. Yu, Y. Wang, L. Zhao, J. Lu, Y. Li, D. Li, J. Dou, J. Duan and S. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 7914–7926 CrossRef CAS PubMed.
- F. J. Steemers, W. Verboom, D. N. Reinhoudt, E. B. v. d. Tol and J. W. Verhoeven, J. Am. Chem. Soc., 1995, 117, 9408–9414 CrossRef CAS.
- A.-M. Badiane, S. Freslon, C. Daiguebonne, Y. Suffren, K. Bernot, G. Calvez, K. Costuas, M. Camara and O. Guillou, Inorg. Chem., 2018, 57, 3399–3410 CrossRef CAS PubMed.
- M. Latva, H. Takalob, V.-M. Mukkala, C. Matachescuc, J. C. Rodriguez-Ubisd and J. Kankarea, J. Lumin., 1997, 75, 149–169 CrossRef CAS.
- D. A. Hardy, R. A. Tigaa, R. E. Ortega, J. R. McBride and G. F. Strouse, J. Phys. Chem. C, 2019, 123, 31175–31182 CrossRef CAS.
- S.-Y. Zhang, Z.-Y. Wang, J. Gao, K. Wang, E. Gianolio, S. Aime, W. Shi, Z. Zhou, P. Cheng and M. J. Zaworotko, Chem, 2019, 5, 1609–1618 CAS.
| This journal is © The Royal Society of Chemistry 2023 |




