Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advancing energy storage through solubility prediction: leveraging the potential of deep learning†
Mesfin Diro
Chaka
 *ac,
Yedilfana Setarge
Mekonnen
b,
Qin
Wu
d and
Chernet Amente
Geffe
a
*ac,
Yedilfana Setarge
Mekonnen
b,
Qin
Wu
d and
Chernet Amente
Geffe
a
aDepartment of Physics, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia. E-mail: mesfin.diro@aau.edu.et
bCenter for Environmental Science, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia
cComputational Data Science Program, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia
dCenter for Functional Nanomaterials, Brookhaven National Laboratory, Upton, NY 11973, USA
First published on 15th November 2023
Abstract
Solubility prediction plays a crucial role in energy storage applications, such as redox flow batteries, because it directly affects the efficiency and reliability. Researchers have developed various methods that utilize quantum calculations and descriptors to predict the aqueous solubilities of organic molecules. Notably, machine learning models based on descriptors have shown promise for solubility prediction. As deep learning tools, graph neural networks (GNNs) have emerged to capture complex structure–property relationships for material property prediction. Specifically, MolGAT, a type of GNN model, was designed to incorporate n-dimensional edge attributes, enabling the modeling of intricacies in molecular graphs and enhancing the prediction capabilities. In a previous study, MolGAT successfully screened 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 promising redox-active molecules from a database of over 500
467 promising redox-active molecules from a database of over 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds, based on redox potential predictions. This study focused on applying the MolGAT model to predict the aqueous solubility (log
000 compounds, based on redox potential predictions. This study focused on applying the MolGAT model to predict the aqueous solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) of a broad range of organic compounds, including those previously screened for redox activity. The model was trained on a diverse sample of 8494 organic molecules from AqSolDB and benchmarked against literature data, demonstrating superior accuracy compared with other state of the art graph-based and descriptor-based models. Subsequently, the trained MolGAT model was employed to screen redox-active organic compounds identified in the first phase of high-throughput virtual screening, targeting favorable solubility in energy storage applications. The second round of screening, which considered solubility, yielded 12
S) of a broad range of organic compounds, including those previously screened for redox activity. The model was trained on a diverse sample of 8494 organic molecules from AqSolDB and benchmarked against literature data, demonstrating superior accuracy compared with other state of the art graph-based and descriptor-based models. Subsequently, the trained MolGAT model was employed to screen redox-active organic compounds identified in the first phase of high-throughput virtual screening, targeting favorable solubility in energy storage applications. The second round of screening, which considered solubility, yielded 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 promising redox-active and soluble organic molecules suitable for use in aqueous redox flow batteries. Thus, the two-phase high-throughput virtual screening approach utilizing MolGAT, specifically trained for redox potential and solubility, is an effective strategy for selecting suitable intrinsically soluble redox-active molecules from extensive databases, potentially advancing energy storage through reliable material development. This indicates that the model is reliable for predicting the solubility of various molecules and provides valuable insights for energy storage, pharmaceutical, environmental, and chemical applications.
332 promising redox-active and soluble organic molecules suitable for use in aqueous redox flow batteries. Thus, the two-phase high-throughput virtual screening approach utilizing MolGAT, specifically trained for redox potential and solubility, is an effective strategy for selecting suitable intrinsically soluble redox-active molecules from extensive databases, potentially advancing energy storage through reliable material development. This indicates that the model is reliable for predicting the solubility of various molecules and provides valuable insights for energy storage, pharmaceutical, environmental, and chemical applications.
1. Introduction
The continued use of fossil fuels has led to rising levels of carbon dioxide (CO2) in the atmosphere. As a result, renewable energy sources such as solar and wind power have been investigated as cleaner alternatives to fossil fuels.1 However, these renewable sources are intermittent for storing the energy produced to balance energy supply and demand. To address this challenge, researchers are developing low-cost and scalable energy storage systems (ESS) using rechargeable batteries that can enable large-scale storage of renewable energy.2,3 Lithium ions, redox flow, lead acid, sodium–sulfur (Na–S), and nickel–metal hydride (Ni–MH), systems are rechargeable battery systems that offer an efficient way to store energy. Although lithium-ion batteries are commonly used in applications, their ability to be utilized for grid-connected storage is limited because of factors such as the limited availability of raw materials, the concentration of resources in specific geographic locations, and safety issues.4 Many efforts are being made to improve the stability and cost-effectiveness of production and the environmental sustainability of materials used in lithium-ion batteries.5 Redox flow batteries (RFBs) are promising energy storage alternatives for grid scale applications due to their modular architecture, better scalability, low maintenance cost, and customizable operation.6Aqueous redox flow batteries (ARFBs) are a form of RFB that chemically store energy using two distinct redox-active species with variable reduction potentials.4 The negolyte and posolyte are pumped through an electrochemical cell composed of two electrodes (often carbon) isolated by an ion-selective membrane. The volume of the electrolyte storage tanks, quantities of redox-active chemicals, and variances in their reduction potentials affect the ARFB energy storage capacity. The power of an electrochemical cell stack is determined by its active species. This design allows the independent scaling of energy and power, which is not possible in enclosed batteries. ARFBs have been identified as highly potential grid-scale storage for energy alternatives owing to their scalability and unique design, which allows distinct control over power and energy output.7 The most important components of ARFBs are the redox-active species, and their redox potential and solubility determine their overall energy density.1,8 These redox-active organic compounds are integral to the functioning of redox flow batteries and serve as crucial components of electrolyte solutions. These compounds facilitate charge transfer between the electrodes, enabling the charge–discharge cycle of the cell. Unlike traditional metal-based electrodes, redox-active organic compounds offer several advantages, including higher energy density, a longer lifespan, and a lower cost.9,10 Consequently, they have emerged as key elements in advanced battery technologies, providing a viable alternative to conventional rechargeable batteries for grid-stabilization applications.11,12
Solubility prediction is essential in various fields, including ARFBs, because the poor solubility of organic molecules can lead to inefficient and unreliable system. Hence, an accurate prediction of the solubility of compounds is vital for the design of efficient and reliable energy storage application. Aqueous solubility of organic compound is an important attribute to explore since it has a direct impact on the power density, energy capacity, and energy density of aqueous redox flow batteries. The variables that influence the solubility of organic molecules in water include electrostatic interactions with water, solvent reorganization, delocalized charge density in aromatic rings, entropic contributions, and inter- and intramolecular hydrogen bonding. The thermodynamics of organic molecule aqueous solvation is a complex process involving many distinct sorts of interactions.7 Understanding and optimising organic compound aqueous solubility is therefore crucial for increasing the performance and efficiency of these next-generation energy storage devices.7 It also plays a significant role in chemical design processes, environmental studies, and drug development applications.13,14 In this context, the aqueous solubility of organic molecules has gained significant attention as a crucial property affecting various physical phenomena.15 Several methods can be used to predict the water solubility of organic compounds based on their chemical structure. Despite efforts to develop different models for precisely calculating water solubility, determining the solubility of organic compounds remains a challenging and time-consuming task.14,16 Scholars have investigated four approaches for solving this problem. First, empirical methods such as the generalized solubility equation (GSE) are used.17 Second, quantitative approaches based on structure–property relationships (QSPR) and cheminformatic descriptors were utilized.18 Third, physics-based methods, such as Monte Carlo simulations, molecular dynamics (MD), and first-principles simulations, have been used to reliably predict the reaction energy.19,20 Finally, data-driven techniques have been employed to address the challenges of solubility prediction.21,22
Machine learning (ML) has been recognized as an important data-driven method in a wide range of scientific domains, including materials science.23 ML has been successfully used to predict solubility using molecular property descriptors known as extended connectivity fingerprints (ECFP).18 Delaney24 developed a method for predicting solubility that utilized a dataset of organic compounds with known solubility values. This approach relies on molecular descriptors derived from the molecular structure, which is valuable when experimental data are limited. Delaney concluded that parameters such as the fraction of atoms in the ring, molecular weight, and number of rotatable bonds play crucial roles in predicting aqueous solubility. In another study by Delago,25 quantum chemical descriptors and statistical methods were employed to develop solubility prediction models. The results showed the effectiveness of the descriptors in predicting solubility, highlighting their significance in terms of health implications.
Deep learning approaches, such as graph neural networks (GNNs), have also gained popularity in the fields of physics and material science research because of their ability to solve complex problems.26–32 GNNs provide an approach to modelling molecules by representing them as graphical structures. In this representation, atoms act as nodes and bonds serve as edges, allowing GNNs to capture the connectivity and structural relationships within molecules. By harnessing this graph-based representation, GNNs have been shown to be able to predict the properties and characteristics of molecules. Several studies have demonstrated the potential of GNNs for tackling physical problems, including condensed matter physics and high-energy particle physics. For example, Thais et al.33 and Shlomi et al.32 employed GNNs to classify the particle interactions in high-energy particle physical. Additionally, Sanchez-Gonzalez et al.26 and Jaensch et al.34 demonstrated how GNNs can be used to simulate complex physics systems. Furthermore, GNNs excel in predicting material properties. Ward et al.35 demonstrated how machine learning algorithms accurately predict the characteristics of both crystalline and amorphous materials. Similarly, Dai et al.36 demonstrated the power of a GNN model across various microstructures. Recently, Zhang et al.37 proposed an approach using a GNN with a representation that outperformed traditional machine learning models for predicting material properties. The success stories of applying GNNs in various domains highlight their potential and effectiveness in advancing research and understanding in physics, material science, and other fields. Raissi et al.38 introduced an approach called physics-informed neural networks (ANNs), which combines deep learning techniques with equations known as partial differential equations (PDEs). This innovative method has been used to address various challenges, including fluid dynamics and electromagnetism.
GNNs are capable of learning and generalizing from molecular graph-structured data, making them well-suited for predicting molecular properties such as redox potential, as demonstrated by Chaka et al.39 This has important implications for using the GNN model for predicting the aqueous solubility of new materials for energy storage applications. Consequently, the application of GNNs to predict organic molecule solubility is crucial for the development of redox flow batteries with high efficiency and reliability, as well as numerous other uses in various industries. In this study, we used MolGAT39 together with a commonly used molecular graph format to train the model on the AqSolDB15 dataset to estimate the intrinsic water solubility of the organic molecules. The aim was not to develop a new modelling framework but rather to predict and classify compounds that could potentially be beneficial as redox-active materials that had already been screened in our previous work. We make several key contributions to this goal. To begin, we performed a thorough comparison of all commonly used atomic feature representations to identify the most appropriate one, and then excluded the atomic type from the feature list by performing a deep analysis of the model's flaws to better learn the underlying molecular structures. Second, we benchmarked the performance of the model against the experimental solubility data from the literature. Furthermore, virtual screening using the trained model was performed by predicting the intrinsic aqueous solubility of the promising redox-active compounds in our previous work. Hence, this effort will increase the usefulness of our screened compounds, which have redox-active characteristics and adequate solubility for energy storage applications, including redox flow batteries.
2. Methodology
In deep learning, fingerprint-based models provide a compact representation of material structures, thereby facilitating simpler training and data management. The extended connectivity fingerprint (ECFP) also referred to Morgan fingerprints(descriptors) is one of the commonly utilized representations, in this field.40 However, graph-based models are critical for predicting complex structure–property relationships for both condensed matter systems and molecules.42 Graphs are natural way to represent data in various problem areas. These graphs consist of sets of elements that have relationships and interactions, with each other. This natural representation proves to be powerful, in capturing the essence of the data. GNNs excel at learning functions that operate on graphs by including strong connection inductive biases. By incorporating domain knowledge concerning nodes (atoms) into the underlying topography of the artificial neural network model architecture, GNNs provide a considerable advantage.43 GNNs have shown exponential growth in recent years, with numerous applications in a wide range of scientific and technical disciplines.33,44,45 A critical component of the design of Graph Neural Networks (GNNs) is the message-passing system, which allows information to be sent along the graph's edges. This framework has been successfully applied to various graph types including molecular and crystal graphs. Notably, in the case of molecular graphs, message passing neural networks (MPNNs)46 with edge features that capture bond information are employed. Furthermore, the use of GNNs to crystal structures has been investigated, such as in the example of MEGNet,41 which combines geometric information and leverages global parameters, such as temperature, which is especially important for solid-state crystalline systems.The MolGAT model, introduced by Chaka et al.,39 is a type of GNN that learns molecular structures, bond attributes, and atomic properties using attention-based message passing techniques. When compared to other graph-based models, this model has demonstrated promising performance in predicting the redox potential of organic molecules.39 In this particular study, the MolGAT model was trained using the AqSolDB dataset to accurately predict the aqueous solubility of various organic molecules. The mathematical representation of this model is as follows:
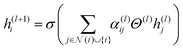 | (1) |
In eqn (1), the updated feature vector for node i in a particular layer of MolGAT is represented as h(l+1)i. To compute this updated feature, the feature vector h(l)i from the previous layer can be used. In this equation, we sum all the connected nodes j to node i in the graph, including node i itself, and the set of neighbours of node i is denoted as N(i). The weight matrix Θ(l) corresponds to the weight matrix of the layer in our model. This weight matrix was learned during training. Determine how the information from neighbouring nodes is combined to update the feature vectors for node i. Finally, we utilize an element nonlinear activation function such as the sigmoid or ReLU, denoted as σ(·). This activation function provides nonlinearity and allows the model to capture interactions between nodes in the molecular graph.
In eqn (1), the term αij(l) refers to a multi-head attention mechanism that is crucial for dynamically integrating inputs from neighboring nodes and edge characteristics. During the training process, the attention coefficients can be learned to allow the model to focus on the important edge attributes. This significantly enhances the capacity of the model to capture meaningful information from molecular graphs. This attention method works on the basis that each atom (node) does not have equal contributions, allowing it to simultaneously pay attention to many graph aspects. As a result, the MolGAT model provides a complete representation of the molecular graph, making it useful for predicting molecular properties. This attention mechanism can be mathematically represented as follows:
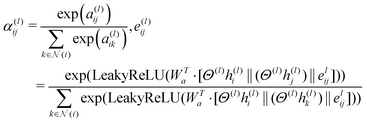 | (2) |
This attention mechanism (αij(l)) in eqn (2) provides weighting factors for calculating the attention coefficients of a particular edge (i,j) in the molecular graph of a specific layer (l) connecting atoms i and j. It compares the importance of the edge between atoms i and j with that of other edges connected to atom i. This comparison is based on scalar values a(l)ij and a(l)ik. The values were concatenated and combined using a weight matrix Wa. The resulting attention coefficient represents the relative significance of the edge between the atoms i and j. A learnable weight matrix Wa is used in this calculation, along with a Leaky Rectified Linear Unit (LeakyReLU) activation function. Attention scores are obtained by taking the dot product between the weight matrix (Wa) and the concatenation of the transformed node and edge feature vectors (Θ(l)h(l)i‖(Θ(l)h(l)j)‖e(l)ij and Θ(l)h(l)i‖(Θ(l)h(l)k)‖e(l)ij). The transformation process involves applying linear transformations to the diagonal matrix of learnable parameters (Θ(l)) at layer (l) to the initial node feature vectors (h(l)i and h(l)j) and the initial edge feature vector (e(l)ij). These transformed feature vectors are concatenated using the symbol ‖ and an exponential function (exp) is applied.
2.1 Dataset and preprocessing
To train our MolGAT model, we used the extensive and diverse AqSolDB dataset, which was referenced in ref. 15. AqSolDB is a valuable resource that is freely accessible to researchers, and encompasses 9982 distinct compound categories. To provide robustness in the aqueous solubility data, this dataset comprises a wide range of solubility values and 2D descriptors acquired from multiple sources. We did not use the offered 2D descriptor information because our deep learning model runs on graphs. Instead, we used the RDKit and PyTorch Geometric(PyG), tools to convert the SMILES string representations as indicated in Table S1 and Fig. S1 (ESI†) to a graph format.The data preprocessing of AqSolDB involved transforming the SMILES strings representing chemical structures into molecular graphs compatible with Pyg, which is a powerful library for deep learning on graphs. Initially, SMILES strings were parsed using RDKit to extract essential information such as atom types, bond types, and connectivity patterns. Subsequently, the extracted molecular representations were converted to a graphical format suitable for PyG. This involves mapping atoms to nodes and bonds between atoms and edges in the molecular graphs. Additionally, graph-level features, including edge attributes and node features, were incorporated to capture pertinent information about the molecular structure and properties, resulting in 30 atomic and 12 edge features, as shown in Table 1. With the construction of molecular graphs and the inclusion of relevant features, the data were prepared for further processing and model training using PyG. This comprehensive preprocessing pipeline enabled the application of graph neural networks and subsequent solubility predictions using the transformed molecular data.
| Graph-level | Attributes | Description | Size |
|---|---|---|---|
| Node | Atomic-number | Atomic number of atoms in a molecule(integer) | 1 |
| Charge | Formal charge (integer) | 1 | |
| Radicals | Number of radical electrons (integer) | 1 | |
| Chirality | Is S or R chirality type(one-hot encoding) | 2 | |
| Degree | Covalent bonds (one-hot encoding) | 8 | |
| Aromaticity | Part of atomic system (binary encoding) | 2 | |
| Number of Hs | Number of connected hydrogen | 5 | |
| Hybridization | Types of hybridization | 7 | |
| Atomic-mass | Atomic mass of each atom in a molecule | 1 | |
| Vdm-radius | van der Waals radius | 1 | |
| Subtotal | 30 | ||
| Edges | Bond-type | Single, double,triple,aromatic (one-hot encoding) | 4 |
| Conjugation | Is conjugated (binary encoding) | 1 | |
| Ring | Is a bond part of a ring (binary encoding) | 1 | |
| Stereo | Z, E, any,none,(one-hot encoding) | 6 | |
| Subtotal | 12 | ||
| Total | 42 |
2.2 Data splitting strategy and hyperparametrization
The AqSolDB dataset, which provides significant data for solubility prediction, is split into two subsets: training and testing. Partitioning was accomplished using a stratified random sampling procedure. The training subset consisted of 6795(80%) entries, and was used to train the MolGAT model. The testing subset received the remaining 1699(20%) of the dataset which was not used during the training. Instead, it was used to assess the performance and generalization capabilities of the trained model.In addition to splitting the AqSolDB dataset for training and testing, the hyperparameter setup of the solubility prediction model was optimized to improve its performance. This process involves fine-tuning the hyperparameters using Optuna, a hyperparameter optimization framework, and leveraging PyTorch Lightning to streamline the optimization procedure. By systematically adjusting the hyperparameters, we aimed to identify the optimal configuration that would yield the best results for solubility prediction. Various hyperparameters were explored, including the number of fully-connected layers (num_fc_layer), convolution layers (num_conv_layers), attention heads (num_heads), hidden dimensions (hidden_dim), batch size, dropout rate, and training epochs. The best hyperparameter configuration was determined after the hyperparameterisation process was conducted. The optimized configuration included setting the total number of fully-connected layers to four, the number of graph convolution layers to three, the number of attention heads to four, the number of hidden dimensions to 192, the batch size to 64, the dropout rate to 0.1, and training for 251 epochs. The test results were examined to assess the performance of the model with the best hyperparameter settings.
2.3 Model training workflow
The workflow of the proposed approach can be divided into four phases. First, the SMILES notation representing the molecular structure was processed to convert it into a graph representation suitable for the MolGAT model. This involves the extraction of relevant features and the encoding of molecular graphs. Second, the MolGAT model was trained using a training dataset in which predictions were made based on the input molecular features and corresponding experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values. During this step, the model parameters were optimized through iterative training. The prediction performance of the trained MolGAT model was benchmarked using an external dataset containing experimental log
S values. During this step, the model parameters were optimized through iterative training. The prediction performance of the trained MolGAT model was benchmarked using an external dataset containing experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values for molecules that were not used in the training phase. The model predicts log
S values for molecules that were not used in the training phase. The model predicts log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values for these compounds, which are then compared to the experimental values to assess the reliability and generalization capacity of the model. Finally, high-throughput screening was performed using the trained and optimized MolGAT model. This requires running the model on a large number of molecules to estimate their log
S values for these compounds, which are then compared to the experimental values to assess the reliability and generalization capacity of the model. Finally, high-throughput screening was performed using the trained and optimized MolGAT model. This requires running the model on a large number of molecules to estimate their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values. This approach can help effectively screen enormous chemical spaces and identify promising chemicals for further experimentation or drug discovery using the trained model.
S values. This approach can help effectively screen enormous chemical spaces and identify promising chemicals for further experimentation or drug discovery using the trained model.
To predict solubility using a graph-based approach, molecular graph attention networks (MolGAT) were employed to learn molecular embeddings and capture both local and global features of the molecules. This model consists of multiple graph attention convolution layers (MolGATConv1, MolGATConv2, and MolGATConv3) and three fully connected linear layers (Linear1, Linear2, and Linear3). The final linear layer (Linear3) outputs the final prediction of the aqueous solubility. The MolGAT model aggregates global attributes using a readout function, resulting in a comprehensive molecular representation. The final layer is used to predict the properties based on the learned molecular features. This enabled the model to make accurate predictions regarding the solubility of new organic molecules based on their molecular graph representations. In general, the model had 699![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 parameters and generates a scalar output from the final fully connected output(fc_out) layer as shown in Table 2. It also provides a concise summary of the graph neural network layers, layer names, layer output shapes, and their corresponding trainable parameters for predicting the aqueous solubility of organic molecules using the MolGAT model.
793 parameters and generates a scalar output from the final fully connected output(fc_out) layer as shown in Table 2. It also provides a concise summary of the graph neural network layers, layer names, layer output shapes, and their corresponding trainable parameters for predicting the aqueous solubility of organic molecules using the MolGAT model.
| Layer | Model shape | Attention weight | Node weights | Edge weights | Biases | Trainable parameters |
|---|---|---|---|---|---|---|
| MolGATConv1(heads = 4) | (30, 192,12, 4) | (1,4,396) | (30, 768) | (204, 192) | 192 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 984 |
| MolGATConv2(heads = 4) | (192, 192,12, 4) | (1,4,396) | (192, 768) | (204, 192) | 192 | 188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| MolGATConv3(heads = 4) | (192, 192,12, 4) | (1,4,396) | (192, 768) | (204, 192) | 192 | 188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| Linear1 | (384, 384) | — | (384, 384) | — | 384 | 147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
| Linear2 | (384, 192) | — | (192, 384) | — | 192 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
| Linear3 | (384, 192) | — | (192, 384) | — | 192 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
| Linear4(fc_out) | (192, 1) | — | (192, 1) | — | 1 | 193 |
| Total parms | — | — | — | 699![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 793 |
3. Results and discussion
3.1 Model training performance
Unlike other descriptor-based models, the MolGAT model is a graph-based neural network architecture that predicts molecular properties by considering molecular structures in addition to atomic and bond attributes. This MolGAT model was trained using the AqSolDB dataset to predict the aqueous solubility of organic compounds. The MolGAT model effectively managed the noisy optimization of the high-dimensional features of the graph neural network weights using the adam optimizer. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values were standardized to improve the performance of the MolGAT model by calculating the mean and standard deviation of the AqSolDB data. The transformation equation (data − mean)/std was applied to the target variable (log
S values were standardized to improve the performance of the MolGAT model by calculating the mean and standard deviation of the AqSolDB data. The transformation equation (data − mean)/std was applied to the target variable (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) to ensure that it has a mean of zero and standard deviation of one. After training, the predictions were rescaled back using the inverse transform equation: (data × standard) + mean.
S) to ensure that it has a mean of zero and standard deviation of one. After training, the predictions were rescaled back using the inverse transform equation: (data × standard) + mean.
The model achieved a mean absolute error (MAE) of 0.322, root mean squared error (RMSE) of 0.432, and R2 value of 0.98 on the training dataset. It also generalized reasonably well on the validation dataset, with an MAE of 0.393 and RMSE of 0.540 with R2 of 0.97, as shown in Fig. 1a and b as well as training and validation error plot in Fig. S6 (ESI†). This level of performance suggests that the MolGAT model effectively learns to map molecular graphs to the solubility values. The graph-based architecture allows it to leverage both the structural information (atoms and bonds) and properties of individual atoms. The attention mechanism helps the model to focus on the most relevant parts of the molecule for predicting solubility. MolGAT established its ability to effectively predict the aqueous solubility of organic compounds based on their molecular structures by obtaining low error and high R2 on both the training and validation sets. Generalization of the model on the test dataset as well as the experimental dataset from the literature suggests that it does not overfit the training data.
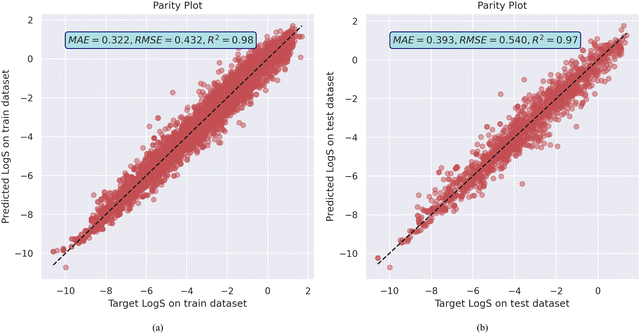 | ||
| Fig. 1 MolGAT model training and validation performance on AqSolDB (a) the parity plot of predicted against target aqueous solubility values, and (b) the model train and test losses. | ||
The saliency map plot in Fig. 2 shows the impact of the nodes and edges on a molecular graph during the training phase of the MolGAT model. This helps to understand the significance and reliability of atoms and bonds, providing insights into the input graph components that contribute the most to the model's predictions. The plot was generated by calculating the gradients of the model's output for the input graph elements, such as nodes and edges. These gradients capture how the output of the model changes when small perturbations are applied to input elements. By visualizing these gradients, the saliency map effectively highlights the elements that have the greatest impact on a model's predictions. This emphasizes the significance of incorporating molecular structures into GNN models, showing their superior ability to learn from the structure of a molecular graph when compared to other descriptor-based models.
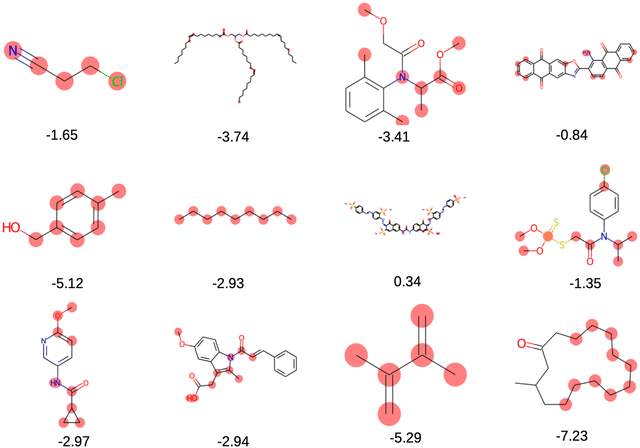 | ||
Fig. 2 A plot of the saliency map with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values, for the MolGAT model can show us which nodes and edges have an impact, on a molecular graph during training. S values, for the MolGAT model can show us which nodes and edges have an impact, on a molecular graph during training. | ||
We also evaluated the performance of the MolGAT model by quantifying its effectiveness relative to other models using three evaluation metrics: R2, MAE, and MSE. These metrics offer a comprehensive assessment of the predictive capabilities of the model and provide insights into the overall level of observed errors, as illustrated in Table 3. The parity plots of the the benchmarked models can be found in ESI† from Fig. S8–S12. The findings indicate that the MolGAT model achieves a superior R2 score and demonstrates lower values for both MAE and MSE, indicating a higher accuracy and reduced prediction errors. The Random Forest (RF) model is a type of descriptor-based model, whereas the rest of the models, such as MPNN (Message Passing Graph Neural Networks), GCM (Graph Convolution Model), Attentive FingerPrint(AttentiveFP), Graph-attention network (GAT), and MolGAT (Molecular Graph Attention Network), are all graph-based models. In RF, the descriptors were generated with a Morgan-figure print descriptor with a radius of four (4) and a length of 2048, just as the atomic and bond figures for the graph-based model were generated based on the nature of individual requirements.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S of organic molecules
S of organic molecules
| Loss | RF | MPNN | GCM | AttentiveFP | GAT | MolGAT (this study) |
|---|---|---|---|---|---|---|
| R 2 | 0.85 | 0.94 | 0.92 | 0.93 | 0.91 | 0.97 |
| MAE | 0.57 | 0.49 | 0.47 | 0.47 | 0.53 | 0.39 |
| MSE | 0.76 | 0.67 | 0.65 | 0.62 | 0.70 | 0.54 |
3.2 Benchmarking solubility prediction
The aqueous solubility prediction capabilities of the MolGAT model were validated by comparing the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values with experimental log
S values with experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values from the literature.47 For this validation, we utilized four solubility datasets based on different solvents: acetone, benzene, ethanol, and water. However, we only focused on the dataset specifically related to water solubility which consisted of 900 molecules in this benchmarking.
S values from the literature.47 For this validation, we utilized four solubility datasets based on different solvents: acetone, benzene, ethanol, and water. However, we only focused on the dataset specifically related to water solubility which consisted of 900 molecules in this benchmarking.
After encoding the molecules from this dataset in molecular form with the assistance of RDKit library tools, we obtained a set of non-overlapping molecules when compared against AqSolDB data. A set of randomly selected organic molecules from the external validation data with experimental water solubility was used for the comparison between the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S (mol L−1) values (log
S (mol L−1) values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt(mol L−1)) and the predicted log
Sexpt(mol L−1)) and the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values (log
S values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SPred) generated by the MolGAT model for each molecule is shown in Table 4. The results obtained by applying the MolGAT model to estimate water solubility exhibited remarkable similarity to values reported in relevant literature source47 with MAE: 0.50 and MSE: 0.42. By randomly selecting samples and their corresponding smile representations solely for water-soluble molecules, Table 4 illustrates both the experimental log
SPred) generated by the MolGAT model for each molecule is shown in Table 4. The results obtained by applying the MolGAT model to estimate water solubility exhibited remarkable similarity to values reported in relevant literature source47 with MAE: 0.50 and MSE: 0.42. By randomly selecting samples and their corresponding smile representations solely for water-soluble molecules, Table 4 illustrates both the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values (log
S values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt(mol L−1)) and predicted log
Sexpt(mol L−1)) and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values (log
S values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Spred(mol L−1)). The result of the Δ
Spred(mol L−1)). The result of the Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S (mol L−1) indicates that the MolGAT model has demonstrated a strong generalization ability when it comes to predicting aqueous solubility for organic compounds beyond those included within training datasets, which is an essential requirement for performing high-throughput screening tasks.
S (mol L−1) indicates that the MolGAT model has demonstrated a strong generalization ability when it comes to predicting aqueous solubility for organic compounds beyond those included within training datasets, which is an essential requirement for performing high-throughput screening tasks.
| Smiles | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt (mol L−1) Sexpt (mol L−1) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SPred (mol L−1) SPred (mol L−1) |
AE | SE |
|---|---|---|---|---|
Clc1c2C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c3c(C( O)c3c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c2ccc1)cccc3 O)c2ccc1)cccc3
|
−5.54 | −5.31 | 0.23 | 0.0529 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) [N+]([O−])c1c(C)c(C( [N+]([O−])c1c(C)c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)cc([N+]( O)O)cc([N+](![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)[O−])c1 O)[O−])c1
|
−2.60 | −2.06 | 0.54 | 0.2916 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)Cn1nnnc1 C(O)Cn1nnnc1
|
0.08 | 0.09 | 0.01 | 0.0001 |
Clc1c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)cc([N+]( O)O)cc([N+](![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)[O−])cc1 O)[O−])cc1
|
−1.75 | −2.41 | 0.66 | 0.4356 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC(C)(C)C)N[C@H](C( C(OC(C)(C)C)N[C@H](C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)C O)O)C
|
−0.74 | −0.93 | 0.19 | 0.0361 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)[C@@H](N)Cc1cc(O)c(O)cc1 C(O)[C@@H](N)Cc1cc(O)c(O)cc1
|
−1.53 | −1.25 | 0.28 | 0.0784 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) S1( S1(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)N(C)C( O)N(C)C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)Nc2ncccc2)/C( C(O)Nc2ncccc2)/C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c2sccc12 O)c2sccc12
|
−3.78 | −4.25 | 0.47 | 0.2209 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(N)Cc1ccc(O)cc1 C(N)Cc1ccc(O)cc1
|
−2.39 | −1.35 | 1.04 | 1.0816 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC(C)(C)C)N[C@H](C( C(OC(C)(C)C)N[C@H](C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)Cc1ccccc1 O)O)Cc1ccccc1
|
−2.15 | −2.24 | 0.08 | 0.0064 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC1CC2N(C)C(C1)CC2)[C@H](CO)c1ccccc1 C(OC1CC2N(C)C(C1)CC2)[C@H](CO)c1ccccc1
|
−1.72 | −1.93 | 0.21 | 0.0441 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) [N+]([O−])c1cc[n+]([O−])cc1 [N+]([O−])c1cc[n+]([O−])cc1
|
−0.69 | −1.82 | 1.13 | 1.2769 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) c1c2c(sc3c1cccc3)cccc2 c1c2c(sc3c1cccc3)cccc2
|
−5.54 | −4.19 | 1.35 | 1.8225 |
| Nc1c2c3c4c(cc2)cccc4ccc3cc1 | −6.61 | −6.92 | 0.31 | 0.0961 |
3.3 Solulibility prediction comparsion
To comprehensively assess the predictive capabilities of the MolGAT model, an analysis was conducted to compare its performance with those of other established prediction models. This evaluation involved examining and comparing the outcomes obtained from our model against validation data with experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S findings documented in the relevant literature.47 By conducting a comparative assessment of MolGAT with various descriptor- and graph-based machine learning models, we can accurately scrutinize and identify the optimal model based on their respective log
S findings documented in the relevant literature.47 By conducting a comparative assessment of MolGAT with various descriptor- and graph-based machine learning models, we can accurately scrutinize and identify the optimal model based on their respective log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SPred values. After careful analysis, it is evident that all of the models demonstrate reasonable predictions performance when compared to the experimental values (log
SPred values. After careful analysis, it is evident that all of the models demonstrate reasonable predictions performance when compared to the experimental values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt) as indicated in Table 5.
Sexpt) as indicated in Table 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) with the final external validation data47 with MolGAT, AttentiveFP, GAT,MPNN, and RF models
S) with the final external validation data47 with MolGAT, AttentiveFP, GAT,MPNN, and RF models
| Smiles | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt Sexpt |
MolGAT | AttFP | GAT | MPNN | RF |
|---|---|---|---|---|---|---|
Clc1c2C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c3c(C( O)c3c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c2ccc1)cccc3 O)c2ccc1)cccc3
|
−5.54 | −5.31 | −4.43 | −4.56 | −5.37 | −5.24 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) [N+]([O−])c1c(C)c(C( [N+]([O−])c1c(C)c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)cc([N+]( O)O)cc([N+](![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)[O−])c1 O)[O−])c1
|
−2.60 | −2.06 | −3.07 | −2.22 | −2.20 | −2.19 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)Cn1nnnc1 C(O)Cn1nnnc1
|
0.08 | 0.09 | −0.37 | −0.20 | −0.10 | −0.87 |
Clc1c(C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)cc([N+]( O)O)cc([N+](![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)[O−])cc1 O)[O−])cc1
|
−1.75 | −2.41 | −2.91 | −2.41 | −2.83 | −3.38 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC(C)(C)C)N[C@H](C( C(OC(C)(C)C)N[C@H](C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)C O)O)C
|
−0.74 | −0.93 | −1.28 | −0.92 | −0.78 | −1.07 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)[C@@H](N)Cc1cc(O)c(O)cc1 C(O)[C@@H](N)Cc1cc(O)c(O)cc1
|
−1.53 | −1.25 | −1.42 | −1.01 | −1.77 | −1.55 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) S1( S1(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)N(C)C( O)N(C)C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(O)Nc2ncccc2)/C( C(O)Nc2ncccc2)/C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)c2sccc12 O)c2sccc12
|
−3.78 | −4.25 | −3.34 | −2.72 | −4.42 | −2.75 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(N)Cc1ccc(O)cc1 C(N)Cc1ccc(O)cc1
|
−2.39 | −1.35 | −1.33 | −1.50 | −0.48 | −1.45 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC(C)(C)C)N[C@H](C( C(OC(C)(C)C)N[C@H](C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O)O)Cc1ccccc1 O)O)Cc1ccccc1
|
−2.15 | −2.24 | −3.01 | −2.51 | −2.91 | −3.84 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) C(OC1CC2N(C)C(C1)CC2)[C@H](CO)c1ccccc1 C(OC1CC2N(C)C(C1)CC2)[C@H](CO)c1ccccc1
|
−1.72 | −1.93 | −2.38 | −1.97 | −1.66 | −2.28 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) [N+]([O−])c1cc[n+]([O−])cc1 [N+]([O−])c1cc[n+]([O−])cc1
|
−0.69 | −1.82 | −1.70 | −1.81 | −0.89 | −2.26 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) c1c2c(sc3c1cccc3)cccc2 c1c2c(sc3c1cccc3)cccc2
|
−5.54 | −4.19 | −4.48 | −4.44 | −4.61 | −3.97 |
| Nc1c2c3c4c(cc2)cccc4ccc3cc1 | −6.61 | −6.92 | −5.23 | −4.93 | −6.64 | −7.10 |
| MAE | 0.50 | 0.79 | 0.72 | 0.51 | 0.88 | |
| MAE | 0.42 | 0.76 | 0.72 | 0.53 | 1.09 |
In the comparison provided in Table 5, the water solubility values of various compounds were evaluated using both the experimental data and predictions from the MolGAT, attentive fingerprint(AttentiveFP), message passing neural network(MPNN), and graph attention network(GAT) models. The compounds are identified by their SMILE notation, and the predicted values are presented in the models columns for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Spred, whereas the experimental water solubility values are displayed in the log
Spred, whereas the experimental water solubility values are displayed in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sexpt column. This comparative analysis has two primary objectives. First, we evaluated the predictive performance of our model. This involves assessing the ability to accurately predict outcomes based on the given data. Second, we investigated the influence of utilizing diverse datasets that differ from the training set. By doing so, we aimed to understand how our model performs when applied to different scenarios, specifically in the context of high-throughput screening. In general, the MolGAT model demonstrated a good agreement with the experimental results. In most cases, the predicted log
Sexpt column. This comparative analysis has two primary objectives. First, we evaluated the predictive performance of our model. This involves assessing the ability to accurately predict outcomes based on the given data. Second, we investigated the influence of utilizing diverse datasets that differ from the training set. By doing so, we aimed to understand how our model performs when applied to different scenarios, specifically in the context of high-throughput screening. In general, the MolGAT model demonstrated a good agreement with the experimental results. In most cases, the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values closely aligned with the observed log
S values closely aligned with the observed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values, indicating the reliability of the model in making accurate predictions. These findings provide confidence in the effectiveness of our model for filtering potential redox-active molecules with desirable aqueous solubility, as previously explored in our research.
S values, indicating the reliability of the model in making accurate predictions. These findings provide confidence in the effectiveness of our model for filtering potential redox-active molecules with desirable aqueous solubility, as previously explored in our research.
3.4 Funneling redox-active molecules with solubility prediction
To identify redox-active molecules suitable for energy storage applications, a two-step virtual screening process was implemented, resembling a funneling approach. The objective is to narrow down the vast chemical space to a select group of molecules that exhibit both redox activity and favorable solubility properties. The initial phase involved utilizing a MolGAT model trained on the RedDB48 dataset to screen 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 redox-active molecules. This model predicted the aqueous solubility of large organic compounds based on their molecular graph representations. The aim was to identify potential candidates for aqueous redox flow batteries, thereby refining the search space. Building on these results, the second phase focuses on refining the selection further.
467 redox-active molecules. This model predicted the aqueous solubility of large organic compounds based on their molecular graph representations. The aim was to identify potential candidates for aqueous redox flow batteries, thereby refining the search space. Building on these results, the second phase focuses on refining the selection further.
In the second phase, a MolGAT model specified in Section 2.3 was trained specifically for solubility prediction using the AqSolDB dataset with Section 2.1 in Table 1. This trained model was then applied to 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 redox-active molecules identified in the first phase to assess their solubility properties. As a result, approximately 12
467 redox-active molecules identified in the first phase to assess their solubility properties. As a result, approximately 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 promising molecules with both redox activity and favorable solubility characteristics have been identified. By employing this funnelling approach, the virtual screening process effectively filtered out a significant portion of the initial pool, leaving behind a smaller yet highly relevant subset of redox-active molecules with desirable solubility properties. The refined selection serves as a valuable starting point for further experimental investigations and potential utilization in energy storage devices such as redox flow batteries.
332 promising molecules with both redox activity and favorable solubility characteristics have been identified. By employing this funnelling approach, the virtual screening process effectively filtered out a significant portion of the initial pool, leaving behind a smaller yet highly relevant subset of redox-active molecules with desirable solubility properties. The refined selection serves as a valuable starting point for further experimental investigations and potential utilization in energy storage devices such as redox flow batteries.
Table 6 provides comprehensive information about a collection of screened molecules and their corresponding properties. The table includes columns for SMILES string notations, predicted redox potential, predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values derived from the MolGAT model prediction, and an indication of aqueous solubility (isSoluble) to determine if the molecule is soluble or insoluble. These findings are crucial in assessing the solubility characteristics of molecules and their relevance in various applications.
S values derived from the MolGAT model prediction, and an indication of aqueous solubility (isSoluble) to determine if the molecule is soluble or insoluble. These findings are crucial in assessing the solubility characteristics of molecules and their relevance in various applications.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values by MolGAT
S values by MolGAT
| Smiles | Redox potential | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SPred SPred |
isSoluble |
|---|---|---|---|
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1C(c2ccccc2) C1C(c2ccccc2)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Nc2cc( Nc2cc(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ON+[O−])c(O)cc21 ON+[O−])c(O)cc21 |
−2.881 | −4.262 | No |
| CCc1c(N)coc1C | 2.036 | −0.792 | Yes |
C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C C(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC NC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ON+[O−])C( ON+[O−])C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O O)O |
−1.003 | −1.665 | Yes |
C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC2 CC2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3C( C3C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1)NC( C1)NC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC3 NC3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2)C( C2)C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O O)O |
−1.782 | −3.048 | Yes |
OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)c1cc(Cl)cc2CC( O)c1cc(Cl)cc2CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Nc12)c3ccc(cc3)c4ccccc4 Nc12)c3ccc(cc3)c4ccccc4 |
−2.003 | −5.792 | No |
C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C C(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C2 C(C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC( NC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C( O)C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C21)C3 C21)C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(NC( C(NC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)N3)O)Br)Br S)N3)O)Br)Br |
−1.912 | −4.319 | No |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC1 CC1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCC( CCC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C1 O)C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
−1.020 | −0.779 | Yes |
Information about the number of compounds screened at stages of the virtual screening process using the MolGAT model is shown in Table 7. The first column, titled “Number of Compounds, reveals that 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds were initially considered for screening”. Moving on to the column, named “Promising Redox Active Compounds Screened” 23
000 compounds were initially considered for screening”. Moving on to the column, named “Promising Redox Active Compounds Screened” 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 were identified as promising redox-active molecules. This means that these compounds can undergo chemical reactions involving electron transfer, known as reactions. The third column, labeled “Promising Redox Active and Soluble Compounds Screened” indicates that further refinement resulted in the discovery of 12
467 were identified as promising redox-active molecules. This means that these compounds can undergo chemical reactions involving electron transfer, known as reactions. The third column, labeled “Promising Redox Active and Soluble Compounds Screened” indicates that further refinement resulted in the discovery of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 compounds that did not exhibit activity but also displayed favorable solubility characteristics. These findings highlight a screening approach aimed at narrowing down the pool of compounds by considering both activity and solubility factors.
332 compounds that did not exhibit activity but also displayed favorable solubility characteristics. These findings highlight a screening approach aimed at narrowing down the pool of compounds by considering both activity and solubility factors.
| Number of compounds | Promising redox-active compounds screened | Promising redox-active & soluble compounds screened |
|---|---|---|
| 500 K+ compounds used | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 467 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 332 |
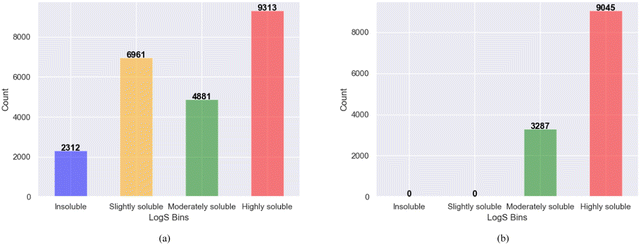
The bin edges of [−∞, −6, −4, −2, ∞] were employed to define distinct log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S categories for the screened molecules. Specifically, log
S categories for the screened molecules. Specifically, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values below −6 were categorized as “insoluble” values ranging from −6 to −4 were labeled as “slightly soluble” those falling between −4 and −2 were designated as “moderately soluble” and values exceeding −2 were classified as “highly soluble”. These categorized ranges effectively represent the different solubility levels of the screened molecules, as shown in Fig. 3a. After binning and removing duplicates, the examination of solubility (log
S values below −6 were categorized as “insoluble” values ranging from −6 to −4 were labeled as “slightly soluble” those falling between −4 and −2 were designated as “moderately soluble” and values exceeding −2 were classified as “highly soluble”. These categorized ranges effectively represent the different solubility levels of the screened molecules, as shown in Fig. 3a. After binning and removing duplicates, the examination of solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) categories revealed that among the 12
S) categories revealed that among the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 promising, soluble, and redox-active organic molecules obtained from the two phases of high-throughput screening, 3287 molecules were classified as moderately soluble, whereas 9045 molecules fell into the category of highly soluble compounds shown in Fig. 3b. These findings provide important information regarding the distribution and solubility of the screened compounds within the defined log
332 promising, soluble, and redox-active organic molecules obtained from the two phases of high-throughput screening, 3287 molecules were classified as moderately soluble, whereas 9045 molecules fell into the category of highly soluble compounds shown in Fig. 3b. These findings provide important information regarding the distribution and solubility of the screened compounds within the defined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S categories. Furthermore, the polar and non-polar functional groups also analyzed that may favor or hinder solubility of the screened promising redox-active molecules for further fine-tuning effects as shown in Fig. 4.
S categories. Furthermore, the polar and non-polar functional groups also analyzed that may favor or hinder solubility of the screened promising redox-active molecules for further fine-tuning effects as shown in Fig. 4.
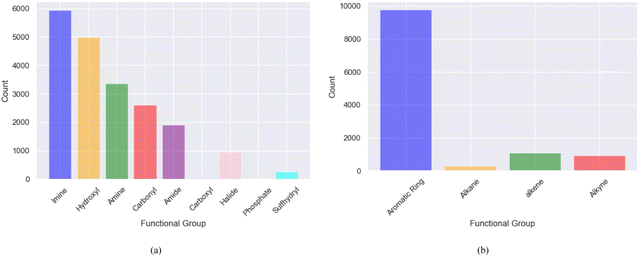 | ||
| Fig. 4 The distribution of dominant functional groups in promising soluble and redox-active molecules screened using MolGAT (a) polar functional groups (b) non-polar functional groups. | ||
The solubility of organic compounds depends on the balance between polar and nonpolar interactions. Polar functional groups generally enhance solubility by forming hydrogen bonds or undergoing ionization. However, nonpolar functional groups decrease solubility by limiting interactions with polar solvents such as water. In Fig. 4a, the prevalence of polar functional groups that enhance solubility in promising screened molecules that exhibit both solubility and redox activity is compared to the number of non-polar functional groups in Fig. 4b, which might hinder the solubility of the screened molecules which resemble the polar and non-polar functionals of AqSolDB in Fig. S5 (ESI†). Furthermore, Fig. 5 showcases randomly sampled screened molecules along with their corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values, providing additional insight into the solubility characteristics of the dataset.
S values, providing additional insight into the solubility characteristics of the dataset.
 | ||
Fig. 5 Randomly selected screened molecules with their corresponding predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values using MolGAT. S values using MolGAT. | ||
In this study, we developed a MolGAT solubility predictor, which is a web application based on the MolGAT model, to accurately predict the solubility of organic compounds. The application can be accessed at https://molgat.streamlit.app. Researchers can input a SMILES string representing the molecular structure and obtain rapid and reliable predictions of the aqueous solubility. The availability of the MolGAT Solubility Predictor facilitates easy access to solubility prediction capabilities and encourages collaboration among researchers in this field.
4. Conclusions
In this study, the MolGAT model was used to predict aqueous solubility, and its performance was compared with that of common models. The effectiveness of the model for solubility prediction was evaluated by comparing it to other GNN models, such as AttentiveFP, MPNNs, D-MPNN, GAT, and a descriptor-based model (Random Forest). The model, which was created for material property prediction, used the molecular representation learning of the GNN, which includes n-dimensional edge features, to obtain superior performance compared to other models. To confirm the reliability and generalizability of the model, its predictions were tested against experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S values from prior studies utilizing a vast collection of solubility data. Furthermore, we discovered that removing atom types from the atomic features had no effect on the performance of the MolGAT model predictions, which were considered during the redox-potential prediction in our previous study. This discovery not only shows the efficiency of the model but also streamlines the training process by lowering the computational complexity.
S values from prior studies utilizing a vast collection of solubility data. Furthermore, we discovered that removing atom types from the atomic features had no effect on the performance of the MolGAT model predictions, which were considered during the redox-potential prediction in our previous study. This discovery not only shows the efficiency of the model but also streamlines the training process by lowering the computational complexity.
Two-step virtual screening was used to identify redox-active molecules with favorable solubility properties for energy storage applications. This progressive screening approach allowed us to narrow the pool of compounds by considering both redox activity and solubility. Table 7 provided valuable information regarding the number of compounds screened at different stages using the MolGAT model. In the initial phase, the MolGAT model was trained on the RedDB48 dataset to screen 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 redox-active molecules from an initial pool of over 500
467 redox-active molecules from an initial pool of over 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds in our previous study. In this study, the screening of redox-active organic compounds was enhanced by considering their aqueous solubility (log
000 compounds in our previous study. In this study, the screening of redox-active organic compounds was enhanced by considering their aqueous solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S), which yielded 12
S), which yielded 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 promising molecules with favorable solubility for redox flow battery applications. This ensured that the MolGAT model could significantly reduce organic compound search spaces to screen promising organic molecules for energy storage applications by employing high throughput virtual screening. These carefully screened compounds lay the foundation for further investigation based on computational and experimental approaches.
332 promising molecules with favorable solubility for redox flow battery applications. This ensured that the MolGAT model could significantly reduce organic compound search spaces to screen promising organic molecules for energy storage applications by employing high throughput virtual screening. These carefully screened compounds lay the foundation for further investigation based on computational and experimental approaches.
In conclusion, the advantages of utilizing graph neural networks, particularly the MolGAT model, were demonstrated for predicting the molecular properties of organic compounds by leveraging their molecular graph representations with n-dimensional atomic and bond attributes. In addition, the two-step virtual screening process successfully identified redox-active organic molecules with desirable aqueous solubility, making them promising candidates for energy storage applications, particularly in redox flow batteries. Furthermore, this research may contribute to the advancement of energy storage systems for the development of efficient and reliable redox-active materials applicable to aqueous redox flow batteries. Finally, the trained model can predict the solubility of diverse compounds, providing useful insights into medicinal, environmental, and chemical applications.
Data availability
The AqSolDB15 solubility data used in this study were obtained from the Harvard Dataverse, an open data repository accessible to researchers. This thoroughly curated dataset collection provides significant information on the water solubility of numerous chemical compounds. Soluble and redox-active promising organic molecules were screened from large databases using the MolGAT model and made easily available for additional investigation and evaluation along with the original source code: https://github.com/mesfind/molgnn). Moreover, the availability of the MolGAT Solubility Predictor facilitates easy access to solubility prediction capabilities and encourages collaboration among researchers in this field.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a thematic research project (grant number TR/036/2020) sponsored by Addis Ababa University. This research used the computing facility of the Center for Functional Nanomaterials (CFN), which is a U.S. Department of Energy Office of Science User Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704 and Ethiopian Education and Research Network (EthERNet) at the Ethiopian Ministry of Education. Furthermore, Y. S. M. would like to to acknowledge the ICTP for their support through the Associates Programme (2020–2025).References
- J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed., 2017, 56(3), 686–711 CrossRef CAS PubMed.
- M. Ferrara, Y.-M. Chiang and J. M. Deutch, Joule, 2019, 3(11), 2585–2588 CrossRef.
- M. S. Ziegler, J. M. Mueller, G. D. Pereira, J. Song, M. Ferrara, Y.-M. Chiang and J. E. Trancik, Joule, 2019, 3(9), 2134–2153 CrossRef.
- D. G. Kwabi, Y. Ji and M. J. Aziz, Chem. Rev., 2020, 120(14), 6467–6489 CrossRef CAS PubMed.
- G. S. Gurmesa, N. E. Benti, M. D. Chaka, G. A. Tiruye, Q. Zhang, Y. S. Mekonnen and C. A. Geffe, RSC Adv., 2021, 11(16), 9721–9730 RSC.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158(8), R55 CrossRef CAS.
- A. Khetan, Batteries, 2022, 9(1), 24 CrossRef.
- F. Pan and Q. Wang, Molecules, 2015, 20(11), 20499–20517 CrossRef CAS PubMed.
- K. Wedege, E. Draževi’c, D. Konya and A. Bentien, Sci. Rep., 2016, 6(1), 39101 CrossRef CAS PubMed.
- L. Zhang, Y. Qian, R. Feng, Y. Ding, X. Zu, C. Zhang, X. Guo, W. Wang and G. Yu, Nat. Commun., 2020, 11(1), 3843 CrossRef CAS PubMed.
- S. Lee, J. Hong and K. Kang, Adv. Energy Mater., 2020, 10(30), 2001445 CrossRef CAS.
- C. M. Wong and C. S. Sevov, ACS Energy Lett., 2021, 1271–1279 CrossRef CAS.
- S. Boobier, D. R. J. Hose, A. J. Blacker and B. N. Nguyen, Nat. Commun., 2020, 11(1), 5753 CrossRef CAS PubMed.
- G. Panapitiya, M. Girard, A. Hollas, J. Sepulveda, M. Vijayakumar, V. Murugesan, W.-J. Wang, W. Wang and E. Saldanha, ACS Omega, 2022, 7(18), 15695–15710 CrossRef CAS PubMed.
- M. C. Sorkun, A. Khetan and S. Er, Sci. Data, 2019, 6(1), 143 CrossRef PubMed.
- L. J. Diorazio, D. R. J. Hose and N. K. Adlington, Org. Process Res. Dev., 2016, 20(4), 760–773 CrossRef CAS.
- J. Ali, P. Camilleri, M. B. Brown, A. J. Hutt and S. B. Kirton, J. Chem. Inf. Model., 2012, 52(2), 420–428 CrossRef CAS PubMed.
- N. Meftahi, M. L. Walker and B. J. Smith, J. Mol. Graphics Modell., 2021, 106, 107901 CrossRef CAS PubMed.
- S. Boothroyd, A. Kerridge, A. Broo, D. Buttar and J. Anwar, Phys. Chem. Chem. Phys., 2018, 20(32), 20981–20987 RSC.
- D. J. Fowles, D. S. Palmer, R. Guo, S. L. Price and J. B. O. Mitchell, J. Chem. Theory Comput., 2021, 17(6), 3700–3709 CrossRef CAS PubMed.
- M. C. Sorkun, J. M. V. A. Koelman and S. Er, iScience, 2021, 24(1), 101961 CrossRef CAS PubMed.
- Z. Ye and D. Ouyang, J. Cheminf., 2021, 13(1), 98 CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559(7715), 547–555 CrossRef CAS PubMed.
- J. S. Delaney, J. Chem. Inf. Comput. Sci., 2004, 44(3), 1000–1005 CrossRef CAS PubMed.
- E. J. Delgado, Fluid Phase Equilib., 2002, 199(1–2), 101–107 CrossRef CAS.
- A. Sanchez-Gonzalez, J. Godwin, T. Pfaff, R. Ying, J. Leskovec and P. W. Battaglia, arXiv, 2020, preprint, arXiv:2002.09405 DOI:10.48550/arXiv.2002.09405.
- A. Saeki and K. Kranthiraja, Jpn. J. Appl. Phys., 2020, 59, SD0801 CrossRef CAS.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys. Mater., 2019, 2(3), 032001 CrossRef CAS.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5(1), 1–36 CrossRef.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148(24), 241722 CrossRef PubMed.
- K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. J. Müller, Chem. Theory Comput., 2019, 15(1), 448–455 CrossRef PubMed.
- J. Shlomi, P. Battaglia and J.-R. Vlimant, Mach. Learn.: Sci. Technol., 2021, 2(2), 021001 Search PubMed.
- S. Thais, P. Calafiura, G. Chachamis, G. DeZoort, J. Duarte, S. Ganguly, M. Kagan, D. Murnane, M. S. Neubauer and K. Terao, arXiv, 2022, preprint, arXiv:2203.12852 DOI:10.48550/arXiv.2203.12852.
- F. Jaensch, K. Herburger, E. Bobe, A. Csiszar, A. Kienzlen and A. Verl, Proc. CIRP, 2023, 118, 50–55 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2(1), 16028 CrossRef.
- M. Dai, M. F. Demirel, Y. Liang and J.-M. Hu, npj Comput. Mater., 2021, 7(1), 103 CrossRef CAS.
- B. Zhang, M. Zhou, J. Wu and F. Gao, IEEE Access, 2022, 10, 62440–62449 Search PubMed.
- M. Raissi, P. Perdikaris and G. E. Karniadakis, J. Comput. Phys., 2019, 378, 686–707 CrossRef.
- M. D. Chaka, C. A. Geffe, A. Rodriguez, N. Seriani, Q. Wu and Y. S. Mekonnen, ACS Omega, 2023, 8(27), 24268–24278 CrossRef CAS PubMed.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput.-Aided Mol. Des., 2016, 30(8), 595–608 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31(9), 3564–3572 CrossRef CAS.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed.
- J. Allotey, K. T. Butler and J. Thiyagalingam, J. Chem. Phys., 2021, 155(17), 174116 CrossRef CAS PubMed.
- M. Dai, M. F. Demirel, Y. Liang and J.-M. Hu, npj Comput. Mater., 2021, 7(1), 103 CrossRef CAS.
- R. Mercado, T. Rastemo, E. Lindelöf, G. Klambauer, O. Engkvist, H. Chen and E. Jannik Bjerrum, Mach. Learn.: Sci. Technol., 2021, 2(2), 025023 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, arXiv, 2017, preprint, arXiv:1704.01212 DOI:10.48550/arXiv.1704.01212.
- BNNLab. BNNLab/solubility_data: Leeds solubility data, 2020.
- E. Sorkun, Q. Zhang, A. Khetan, M. C. Sorkun and S. Er, Sci. Data, 2022, 9(1), 718 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03992g |
| This journal is © the Owner Societies 2023 |