Hydrogen sharing between two nitroxyl radicals in the gas phase and other microsolvation effects on the infrared spectrum of a bulky hydroxylamine

Abstract

The sterically hindered nitroxyl radical TEMPO is co-expanded with its hydroxylamine TEMPO-H in a supersonic jet and probed by FTIR spectroscopy. One major and one minor conformation of the 1 : 1 complex are identified by their OH stretching signatures, the major one exhibiting a weaker hydrogen bond. The acidic hydrogen atom in these structures can switch between the two TEMPO units in a more or less symmetric double minimum potential with a high barrier. Both conformations are experimentally shown to have a self-exchange quantum tunnelling period longer than 15 ps or 1500 OH vibrational periods even when excited by 41 kJ mol⁻¹ along the OH stretching coordinate. The homodimer and more tentatively the monohydrate of TEMPO-H are also identified in the spectrum.

---

1 Introduction

XHX systems which share a hydrogen atom between two identical units X have been studied extensively due to their model character for the anharmonic quantum dynamics of the lightest nucleus and their vibrational bond contributions.¹ Often, they carry a negative overall charge and can be viewed as proton transfer systems XH⋯X⁻ ⇌ X⁻⋯HX. For the well-characterised bihalide anions, the proton actually prefers a mid-way position between the two halide ions and for X = Cl, the zero point energy strengthens the bond, instead of weakening it.² When X is an organic residue, one can subtly tune the symmetry and conformation of the resulting anionic complexes. This offers a playground for dynamical and kinetic studies.^3,4

Neutral radical complexes which share a hydrogen atom between two acceptors are less studied, with the exception of the paradigmatic H₃ system which is only (meta)stable in electronically excited states.⁵ The neutral FHF complex has remained elusive,⁶ whereas in the ClHCl case, helium nanodroplet experiments have shown the absence of a hydrogen bond.⁷ For BrHBr, isotope substitution controls the preferred structure in a particularly interesting way.⁸ It again appears desirable to extend the study of such neutral XHX species to organic radicals X, where conformational isomerism is expected to influence the energetics and dynamics of the shared hydrogen atom.⁹

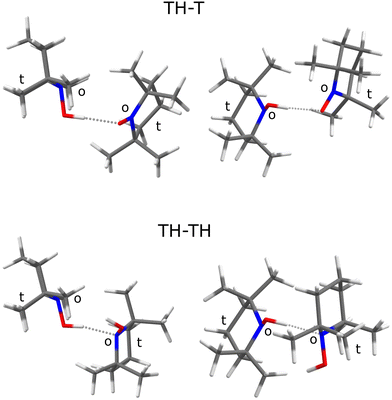
A natural choice for X is the persistent, sterically hindered TEMPO radical¹⁰ (T) or some of its derivatives,¹¹ which have shown to be relevant in many fields of molecular science such as controlled radical polymerisation,¹² spin labeling,¹³ and redox reactions.¹⁴ T can accept an OH⋯O hydrogen bond from its associated hydroxylamine TEMPO-H (TH). This complex TH–T (Fig. 1, top) undergoes hydrogen atom transfer to the formally equivalent T–HT structure through a barrier which is expected to be rather high¹⁵ due to the steric hindrance of T and TH.

Fig. 1 Most stable structures predicted at B3LYP/TZ level for the TH–T and the TH–TH complex from two perspectives, matching their sterically o(pen) faces of the >NO quasiplanes rather than the opposite t(ight) constellation of two methyl groups. Note that attaching a H to the T radical switches the acceptor preference from O to N.

The sterically hindered hydroxylamine TH is known as an anhydrous crystalline solid¹⁶ and as a crystal containing one water for every three TH units.¹⁷ In both cases, there are closed hydrogen bond networks, involving three TH units for the anhydrous structure and six for the trient- or 0.33-hydrate. In these structures, the hydroxylamine adopts a conformation where the hydrogen points to the open side (o) of the sterically hindered substituted nitroxyl unit and prefers to bind to the oxygen of a neighbouring hydroxylamine or water. To close the strained trimeric ring in the anhydrous crystal, the last TH binds to the N atom (instead of O) of the first unit. In the 0.33-hydrate, the N-binding is taken over by water molecules. There is thus a clear numerical preference for OH⋯O coordination and closed ring structures among TH units in the solid state. In this context, it is interesting to look at the structure of the TH–TH dimer, because calculations suggest an OH⋯N contact instead in the absence of further molecules (Fig. 1, bottom).

In this work, we investigate the FTIR spectra of vacuum-isolated, supersonically cooled, conformationally resolved 1 : 1 complexes of TH with itself and with water (w), which are better suited for a rigorous theory-experiment comparison than the infinite solids. A smaller hydroxylamine (N,N-diethylhydroxylamine) monohydrate has recently been structurally characterised in the gas phase¹⁸ and the parent hydroxylamine has also been investigated at high spectral resolution.¹⁹ Building on these experimental benchmark data for closed shell systems, we characterise the open shell 1 : 1 complexes of TH with T in the OH stretching region, to see whether there is evidence for degenerate hydrogen atom transfer (HAT) after OH stretching excitation.

Such degenerate self-exchange reactions^9,15 can be followed by stationary spectroscopy techniques. The most popular one is NMR line broadening in solution as a function of temperature, which can however have several origins beyond degenerate self exchange. Indeed, initial attempts to determine the self-exchange rate between TH and T in this way have reportedly been unsuccessful. Instead, pseudo self-exchange reactions between different TEMPO derivatives were studied and yielded empirical activation barriers on the order of 15 kJ mol⁻¹, but with large deuterium isotope effects.¹⁵ Therefore, the actual electronic transition states assuming classical nuclear motion should be considerably higher in energy. Indeed, early calculations in the gas phase suggest values on the order of 90 kJ mol⁻¹.¹⁵ Hydrogen tunnelling through these high but narrow barriers can explain the lower effective activation energy for the overall process in solution, where the binding partners have to meet by diffusion, bond to each other, transfer the hydrogen, and re-dissociate. The present work focuses on the actual HAT step in the pre-formed TH–T complex without significant thermal excitation or solvent influence and is thus particularly sensitive to the central barrier.

If T is coordinated on its o(pen) side¹⁰ (To), HAT from the preferred o(pen) conformation of TH (THo) in the THo–To complex can occur without major rearrangement of the molecular scaffolds. If another docking site of T is chosen by THo instead,¹⁰ HAT must be followed or preceded by torsion around the N–O bond to end up in an equivalent structure, thus widening the barrier. In the cold gas phase, fast HAT between degenerate structures manifests itself by spectral tunnelling splittings separating symmetric and antisymmetric wavefunctions for the H motion along the self-exchange reaction coordinate.^20,21 In the vibrational ground state, these splittings are exceedingly small due to the large barrier. However, when the OH stretching vibration is excited by one quantum, a significant fraction of the barrier can be overcome because the OH stretching motion resembles the reaction coordinate, at least for a THo–To structure which requires no large amplitude heavy atom motion. Therefore, it is conceivable that the infrared OH stretching spectrum of 1 : 1 complexes combining TEMPO-H with TEMPO exhibits tunnelling splittings Δν reflecting this periodic HAT, where the full period T in ps is given by the inverse of the splitting Δν in THz. In this work, we show that two conformations of the TH–T complex are very close in energy. It represents a considerable challenge for quantum theory to correctly predict their energy order. Despite supportive vibrational excitation by 41 kJ mol⁻¹, we find no evidence for HAT on a 15 ps time scale in the vibrational line profile, suggesting that the barrier between equivalent structures is either very high or rather broad.

2 Methods

The infrared spectra were obtained using a new supersonic jet gas recycling setup.²² The handling of the TEMPO radical (Sigma Aldrich, 98%), was described elsewhere.¹⁰ TEMPO-H was synthesised according to a one-step procedure.¹⁷ With the need for high purity solid samples of TEMPO-H, we modified a literature procedure as follows. Sodium ascorbate was reacted with TEMPO in deoxygenated water under vigorous stirring for 2 h. The resulting white precipitate was extracted with pentane and dried over anhydrous sodium sulfate. The pentane was removed in vacuo and sublimation of the white solid at −35 °C resulted in isolation of anhydrous white crystalline material in high purity and yield (91%). See the ESI† for details.

TEMPO-H and TEMPO (in some experiments also water) were evaporated into the evacuated stainless steel reservoir up to the indicated partial pressure and the carrier gas He (Nippon, 99.996%) was added up to 750 hPa. From there, about 5% of the gas mixture was expanded at room temperature in a 133 ms pulse through 7 magnetic valves into a pre-expansion chamber and guided through a 700 mm long, narrow slit nozzle into a large vacuum buffer. The size of the buffer ensures a large pressure gradient despite the high gas flow. This leads to adiabatic cooling and aggregation of the molecules within a few microseconds. Synchronisation of the mirror of a Bruker Vertex 70v FTIR interferometer to the gas pulses allowed to record cold, species-separated spectra in the OH/CH stretching range by a combination of a 150 W tungsten filament, CaF₂ optics, a suitable optical filter and a liquid-N₂-cooled 2 mm × 2 mm sandwich InSb/MCT detector. The vacuum buffer was permanently evacuated by a series of roots pumps. Their exhaust gas was recompressed by a screw pump to the original pressure, recovering the initial conditions in less than a minute. In this way, the gas could be circulated and reused about 50 times in 1000 pulses. During the circulation, the partial pressure of the water trace slowly accumulated from wall desorption, providing as a side effect an assignment aid for complexes including water. Furthermore, a small fraction of the TEMPO-H started to decompose into TEMPO during circulation, again providing an assignment aid from the time evolution of the spectra. By averaging the interferograms from 1000 pulses of the same gas filling, all spectra shown in Fig. 3 could be obtained from a total amount of about 0.25 g TEMPO and about 0.3 g TEMPO-H. See the ESI† for details.

The standard density functional approach used to obtain approximate structural and energetic predictions for the systems of interest in this work is three-body-inclusive D3-dispersion-corrected^23,24 B3LYP with the def2-TZVP basis set^25–27 in the harmonic approximation, in short B3LYP/TZ. The results were mainly obtained using ORCA 4.2.1,^28–30 with some interim ORCA 5.0.3^28,31 saddle point optimisation assistance (see the ESI† for small numerical differences), always after a CREST 2.10.2 structure search.^32,33 The employed keywords are listed in the ESI.† For selected structures, electronic energies with the def2-QZVP basis set were obtained (B3LYP/QZ). To interpolate between the spectral features of the different species, a uniform scaling factor is derived from a number of related closed-shell species (see ESI†). For the parent hydroxylamine,¹⁹ the OH stretching vibration (exp./theory = 3650/3789) and the two NH stretches (3359/3506, 3294/3428) point at a slightly smaller gas phase scaling factor (0.958–0.963) than the two isolated water stretches³⁴ (3756/3888, 3657/3782), which require multiplication by 0.966–0.967. The ratio for isolated TH (vide infra) is (3631/3794) = 0.957. Therefore, a rounded uniform scaling factor of 0.96 is used in all comparisons between DFT prediction and experiment. The rounding accounts for ±20 cm⁻¹ uncertainty, probably encompassing typical residual electronic structure and anharmonic errors for OH stretching fundamentals in weak to moderate strength hydrogen bonds. For the monohydrate of hydroxylamine, only matrix isolation data are available.³⁵ Due to the matrix-induced shifts, they are less useful to derive a gas phase scaling factor. For the hydrogen-bonded OH stretching fundamentals, the values range between 0.961 and 0.973 for Ar and N₂ matrices. Taking into account the scaling factor for matrix-embedded hydroxylamine itself,³⁶ which is 0.959 instead of 0.963 in the gas phase, 0.96–0.98 is the expected scaling factor range for the hydrogen-bonded OH groups of the monohydrate. The uncertainty of ±40 cm⁻¹ is too large to be useful for safe gas phase assignments.

3 Results and discussion

3.1 Predicted energy rankings of relevant species

The most stable TH–T complex is predicted to be quite strongly bound relative to its components, TH and T. At the B3LYP/TZ level employed primarily in this work, the radical hydrogen bond dissociation energy is 36.7 kJ mol⁻¹ with and 41.6 kJ mol⁻¹ without zero point vibrational (ZPV) correction. This is about twice the previous computational results in the literature,¹⁵ namely 18.4 and 21.3 kJ mol⁻¹, partly explainable by the superposition of London dispersion interaction on this hydrogen bond contact. Indeed, removing the D3(BJ,abc) correction at the B3LYP/TZ optimized structures reduces the attractive interaction by up to an order of magnitude. This suggests that London dispersion can promote the HAT process, by holding the two T radicals together when they share the hydrogen. More relevant for this work are relative energies, where some theory inaccuracies may partially cancel. On the other hand, already the size of the dispersion correction lowers the expectation on quantitative performance of the DFT calculations. Table 1 thus contains relative energies of molecules, molecular complexes and transition states discussed in this work with (ΔE⁰) and without (ΔE^e) zero-point vibrational energy at B3LYP/TZ level, also introducing their nomenclature. One can see that the OH group in TH has a strong preference to point towards the more o(pen) pair of flanking methyl groups (Fig. 1). It coordinates more or less equally well to the o(pen) and t(ight) faces of T, but the associated HAT transition state T–H–T which switches the roles of the nitroxyl radical and the hydroxylamine is significantly lower in the degenerate o–o case than in the conformation-changing o–t case. The absolute value of this barrier is seen¹⁵ to be sensitive to the quality of the theoretical treatment, underscoring the importance of the present experimental work in looking for evidence for barrier crossing. A third, somewhat less favourable complex of THo coordinating T closer to its molecular plane (Tp¹⁰) is an intermediate between the more stable o and t coordinations (see ESI†) and is believed to relax easily to either one or the other. This may explain its non-observation, but we leave an improbable re-assignment open (see Table 2).

Table 1 Relative energies of different conformations of monomer (X) and donor–acceptor (X–Y) species as well as transition states (X–H–Y) with (ΔE⁰) and without (ΔE^e in parentheses) inclusion of harmonic zero point energy for all non-imaginary modes at B3LYP/TZ level. The acceptor atom for hydrogen bonds is given in parentheses. Also included in brackets is a previous computational barrier at MPW1K/6-31 + G(d,p) level¹⁵

Species	Conf.	ΔE^0(ΔE^e)/kJ mol^−1	ΔE^0(ΔE^e)^15
TEMPO	T
TEMPO-H	TH
	THo	0.0 (0.0)
	THt	10.8 (12.0)
Water	w
TH–T (O)	THo–To	0.0 (0.0)
	To–H–To	45.6 (60.0)	[76.0 (90.6)]
	THo–Tt	0.5 (0.9)
	To−H−Tt	55.3 (69.0)
	THt–To	13.4 (14.7)
	THo–Tp	1.9 (1.8)
	THt–Tt	10.0 (11.6)
	THt–Tp	11.4 (12.7)
w–TH (N)	w–THo	0.0 (0.0)
	w–THt	11.7 (14.1)
TH–TH (N)	THo–THo	0.0 (0.0)
	THo–THt	12.8 (14.7)

---

Table 2 Experimentally observed OH stretching wavenumbers ṽ compared to harmonic B3LYP/TZ predictions ω uniformly scaled by 0.96 for TH and binary donor–acceptor complexes observed for the first time in this work. The value in parentheses refers to an unlikely alternative assignment of the strong transition to the predicted third-most stable THo–Tp isomer, see Table 1

Species	ṽ/cm^−1	0.96 ω/cm^−1
TH	3631	3642
TH–TH	3609	3624
w–TH	3534	3510
TH–T	3449	3429 (3444)
TH–T	3418	3412
TH–TH	≈3230	3237

---

The TH–TH coordination in the dimer is predicted to occur via the N atom (Fig. 1), in contrast to the main coordination found in the crystal structure.^16,17 If one of the TH units is replaced by w(ater), it assumes a donor role. These predictions set the stage for the experimental spectra of TH, T, and w co-expanded in different ratios and concentrations with helium to achieve low temperatures and promote complexation.

3.2 Spectral assignments

Fig. 2 shows the OH stretching region for a diluted (65 ppm) expansion of TH in helium (top spectrum). Besides traces of water, which grow with time due to the gas recycling in combination with wall desorption, there is a single sharp peak marked TH, which differs from the uniformly scaled prediction by 11 cm⁻¹. Doubling the TH concentration (middle spectrum) leads to three new signals. The two marked TH–TH match the scaled predictions for the most stable TH dimer within 15 cm⁻¹ and also have the correct qualitative intensity ratio, with the hydrogen-bonded OH being much stronger. Its broadening is indicative of fast intramolecular energy redistribution which is switched on by hydrogen bonding.³⁷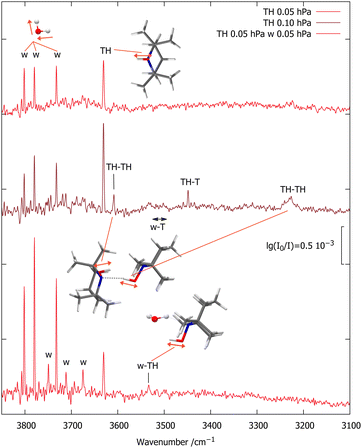

Fig. 2 FTIR spectra of TH with varying traces of T (<10%, based on CH signals, see ESI†) and w co-expanded in 750 hPa helium (darker red illustrates higher TH concentration). The OH stretching absorptions of TH, TH–TH and w–TH are marked, as are a few rotational transitions of the water monomer antisymmetric OH stretch (w) which become more visible with increasing water concentration.²²

The third new signal falls in between, in a spectral region where one would expect the TH–T self-exchange complex. Indeed, there is evidence that TH at higher concentration and longer gas recycling decomposes to form T radicals. Weak absorption in the region marked w–T also points at traces of the monohydrate of this radical, which was characterised before.¹⁰ To identify any monohydrate of TH in close vicinity, an expansion with high TH dilution and more water was investigated (bottom spectrum). It suppresses the w–T signals and enhances a band marked w–TH which is within 24 cm⁻¹ of the scaled harmonic prediction for this monohydrate with a cyclic OH⋯OH⋯N arrangement. In this complex, the more downshifted OH oscillator is expected to be centred on the water molecule.³⁴ A stronger band predicted at lower wavenumber due to this hydrogen bonded water OH vibration would be of interest in the context of the HyDRA challenge for monohydrates of organic molecules.³⁸ It cannot be detected, perhaps due to spectral overlap or anharmonic coupling, rendering the entire w–THo assignment quite uncertain.

Fig. 3 encodes these computational predictions and focuses on the TH–T complex by deliberately adding T to the expansion. Compared to the TH-only spectrum reproduced from Fig. 2 (upper trace), addition of 130 ppm T (second trace) gives rise to two strong signals marked TH–T with ≈3 : 1 intensity ratio, together with the already characterised T monohydrate.¹⁰ The higher-wavenumber signal of the TH–T pair is stronger and its relative strength increases slightly upon further dilution (third trace). This points at two isomers, with the higher-wavenumber isomer being more stable. The subtle inverse relationship between hydrogen bond shift and complex stability is another indication for the role of London dispersion interactions besides hydrogen bonding in holding the two units together. Roughly doubling the TH and w concentrations (bottom trace) doubles the TH–T and w–T signals and further increases the TH–TH and w–TH bands, as expected.

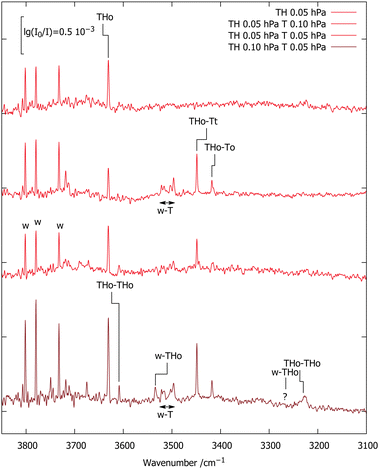Fig. 3 FTIR spectra of TH,T co-expansions in 750 hPa helium (darker red illustrates higher TH concentration). 0.96-scaled harmonic B3LYP/TZ predictions (see ESI† and Table 2) are connected with the experimental positions of selected transitions.

The two TH–T signals are split by 31 cm⁻¹. This should be compared to the two lowest, almost isoenergetic computed isomers which are split by 17 cm⁻¹. Their absolute prediction matches experiment within 6 and 20 cm⁻¹, respectively, if the higher wavenumber signal is assigned to THo–Tt and the lower wavenumber signal to THo–To, as assumed in Fig. 3. This is within the expected accuracy of the scaled harmonic estimate. An inverted assignment would introduce mismatches by 37 and 11 cm⁻¹ in opposite directions. However, theory forecasts the higher wavenumber isomer to be slightly less stable, which contradicts experimental intensities for these almost equally IR-active isomers and is likely due to the limited accuracy of the B3LYP/TZ approach in predicting sub-kJ mol⁻¹ energy differences. To check the robustness of the energy sequence of THo–Tt and THo–To, energy calculations at B3LYP/QZ level were carried out at the TZ-optimised structures. This shrinks the electronic energy gap from 0.9 to 0.7 kJ mol⁻¹ (see ESI†), moving in the right direction, but keeping the experimentally incompatible order. The third isomer remains at 1.8 kJ mol⁻¹. Therefore, the B3LYP functional appears to have a small deficiency in terms of ordering the two isomers, well within its expected accuracy. Both bands have a FWHM of 2.5–3 cm⁻¹ which is not much wider than the spectral resolution so that any tunnelling splittings due to periodic HAT are too small to be resolved. Higher spectral resolution may be limited by rovibrational structure, unless one moves to a colder and heavier helium nanodroplet environment.²⁷

3.3 Hydrogen atom transfer in the TH–T complexes

For the B3LYP/TZ method, the predicted wavenumber sequence of the two experimentally detected TH–T isomers is more trustworthy than a sub-kJ mol⁻¹ energy ranking. Therefore, the more intense signal is attributed to the THo–Tt isomer, where the hydroxylamine OH group points along the o(pen) direction and coordinates the radical from its t(ight) side. As Fig. 4 (upper part) shows, hydrogen transfer from this conformation initially leads to an energetically less favourable THt–To isomer. Assuming that relaxation to a lower isomer is hindered by a broad barrier involving large amplitude motion of the radical scaffolds, it is very unlikely that this isomer exhibits a tunnelling-split OH stretching vibration, although the OH stretching excitation effectively lowers the residual HAT barrier quite substantially. The process is likely to be in the ns or slower regime and therefore remains undetectable at the moderate resolution of the IR spectra.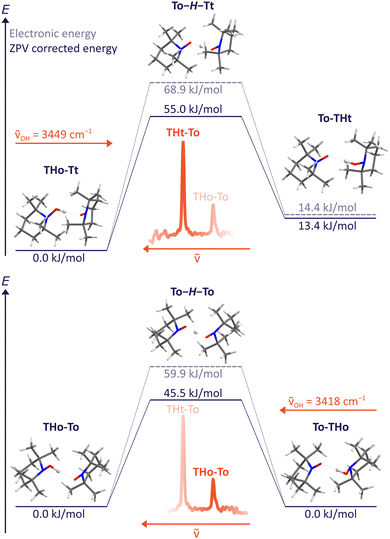

Fig. 4 HAT transition states T–H–T between different TH–T complex arrangements at B3LYP/TZ level, including and excluding zero point energy correction. The excitation wavenumber for OH stretching obtained from experiment is also indicated. A non-degenerate path segment for THo–Tt (upper) and the degenerate path for THo–To (lower panel) is explored. Slightly different values obtained with ORCA 5.0.3 can be found in the ESI.†

Dynamically more interesting is the THo–To isomer, which we attribute to the weaker, more downshifted signal. Here, HAT leads to a degenerate To–THo isomer and does not involve much heavy atom motion. Furthermore, the barrier is now predicted to be substantially lower than for the dominant THo–Tt species (bottom part of Fig. 4). We note that the electronic HAT barrier is still around 60 kJ mol⁻¹, but it is lowered by zero point motion to slightly more than 45 kJ mol⁻¹ in line with vibrational stabilisation in heavy-light-heavy systems.^1,8 Previous barrier values using a different density functional and smaller basis set for the purpose of HAT modelling in solution (Table 1) were considerably higher,¹⁵ underscoring the importance of the present experimental investigation in the gas phase. In view of the expected barrier height and narrowness, it is thus conceivable for the THo–To isomer that tunnelling is fast enough after OH stretch excitation to show up as a spectral doublet. The frequency splitting Δν corresponds to the inverse of the tunnelling period. Based on the observed resolution and the absence of such a resolved doublet, the period must be longer than 15 ps, equivalent to 1500 OH oscillations.

By lowering the barrier through suitable chemical substitution, it is conceivable that a tunnelling splitting may appear in the corresponding spectra of such derivatives.

4 Conclusions

The OH stretching vibrational spectra of bulky hydroxylamine complexes presented in this work are remarkably narrow under supersonic jet expansion conditions, in contrast to those of related oxime complexes.³⁹ This allows for the spectral resolution of subtle conformational isomerism and it provides upper bounds for the speed of degenerate hydrogen atom transfer from a hydroxylamine to its associated nitroxyl or aminoxyl radical. We believe that these are the largest neutral radical complexes which have been vibrationally characterised in the gas phase, so far⁴⁰ and they are clearly London dispersion stabilised.

Specifically, we have shown that TEMPO-H forms a hydrogen-bonded homodimer engaging nitrogen as the acceptor site, in contrast to the solid state, where oxygen is the predominant acceptor due to cooperative effects. We have also shown that there are two conformations of the complex of TEMPO-H with TEMPO, both engaging oxygen as the acceptor. The slightly less stable one based on experimental intensities leads to an equivalent structure after hydrogen atom transfer between the two oxygen atoms with rather little distortion of the organic scaffold. This should favour tunnelling, in particular when the complex is excited along the hydrogen transfer coordinate by OH stretching motion. Still, the complex can empirically undergo far more than 1000 vibrations before the hydrogen is transferred. The present results suggest that further lowering of the self-exchange barrier for hydrogen between two nitroxyl radicals may lead to the direct spectral manifestation of hydrogen atom tunnelling by a splitting of the OH stretching fundamental transition. This might be achieved by replacing the alkyl substitution present in TEMPO with aryl substitution.¹⁵ Phenoxy radicals²⁶ may also lead to lower barriers⁹ due to the aromatic conjugation. Self-exchange complexes based on phenoxy radicals are sterically less hindered and have already been characterised in the solid state,⁴¹ which is more challenging to model accurately by theory. Our gas phase approach promises to lift the contact between theory and experiment in the field of degenerate hydrogen atom transfer complexes to a higher level of accuracy.

For this purpose, higher level electronic structure calculations are now welcome, both for energies and for spectra. The latter may profit from inclusion of anharmonicity in reduced dimensionality. For the HAT process, semiclassical^42,43 and quantum dynamics⁴⁴ calculations would be particularly helpful to see whether the experimental constraint derived from the spectra is a tight or a loose one. This involves predictions for tunneling in vibrationally excited states of radical complexes^42,44,45 which are qualitatively expected to promote the process, but certainly challenging.

Author contributions

Investigation, writing – review & editing T. L. F. and M. A. T.; data curation, formal analysis, validation, visualisation T. L. F.; conceptualisation, funding acquisition, methodology, supervision, writing – original draft M. A. S.; All authors have read and agreed to the submitted version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455. We thank Inke Siewert, Sven Schneider and Ricardo Mata for valuable suggestions, support and discussions and Beppo Hartwig for computational support.

References

1. J. Manz, R. Meyer and H. H. R. Schor, J. Chem. Phys., 1984, 80, 1562–1568.
2. C. Stein, R. Ostwald, P. Botschwina and K. A. Peterson, J. Phys. Chem. A, 2015, 119, 5158–5164.
3. R. Böhmer, C. Gainaru and R. Richert, Phys. Rep., 2014, 545, 125–195.
4. K. Koszinowski and R. Rahrt, J. Am. Soc. Mass Spectrom., 2022, 33, 1411–1418.
5. G. Herzberg, J. Chem. Phys., 1979, 70, 4806–4807.
6. J. M. Merritt, J. Küpper and R. E. Miller, Phys. Chem. Chem. Phys., 2005, 7, 67–78.
7. C. P. Moradi and G. E. Douberly, J. Phys. Chem. A, 2015, 119, 12028–12035.
8. D. G. Fleming, J. Manz, K. Sato and T. Takayanagi, Angew. Chem., Int. Ed., 2014, 53, 13706–13709.
9. J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147.
10. E. M. Brás, T. L. Fischer and M. A. Suhm, Angew. Chem., Int. Ed., 2021, 60, 19013–19017.
11. F. Hecker, L. Fries, M. Hiller, M. Chiesa and M. Bennati, Angew. Chem., Int. Ed., 2023, 62, e202213700.
12. D. Greszta and K. Matyjaszewski, Macromolecules, 1996, 29, 7661–7670.
13. A. Meyer, S. Dechert, S. Dey, C. Höbartner and M. Bennati, Angew. Chem., Int. Ed., 2020, 59, 373–379.
14. M. Oelschlegel, S.-A. Hua, L. Schmid, P. Marquetand, A. Bäck, J.-H. Borter, J. Lücken, S. Dechert, O. S. Wenger, I. Siewert, D. Schwarzer, L. González and F. Meyer, Inorg. Chem., 2022, 61, 13944–13955.
15. A. Wu, E. A. Mader, A. Datta, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 11985–11997.
16. N. A. Giffin, M. Makramalla, A. D. Hendsbee, K. N. Robertson, C. Sherren, C. C. Pye, J. D. Masuda and J. A. C. Clyburne, Org. Biomol. Chem., 2011, 9, 3672–3680.
17. E. A. Mader, E. R. Davidson and J. M. Mayer, J. Am. Chem. Soc., 2007, 129, 5153–5166.
18. G. Salvitti, F. Baroncelli, C. Nicotri, L. Evangelisti, S. Melandri and A. Maris, Molecules, 2022, 27, 8190.
19. D. Luckhaus, J. Chem. Phys., 1997, 106, 8409–8426.
20. K. Giese, M. Petkovic, H. Naundorf and O. Kühn, Phys. Rep., 2006, 430, 211–276.
21. N. O. Lüttschwager, T. N. Wassermann, S. Coussan and M. A. Suhm, Mol. Phys., 2013, 111, 2211–2227.
22. H. C. Gottschalk, T. L. Fischer, V. Meyer, R. Hildebrandt, U. Schmitt and M. A. Suhm, Instruments, 2021, 5, 12.
23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
24. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
25. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
26. W. Sander, S. Roy, I. Polyak, J. M. Ramirez-Anguita and E. Sanchez-Garcia, J. Am. Chem. Soc., 2012, 134, 8222–8230.
27. D. Leicht, M. Kaufmann, R. Schwan, J. Schäfer, G. Schwaab and M. Havenith, J. Chem. Phys., 2016, 145, 204305.
28. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
29. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
30. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
31. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
32. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
33. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
34. M. Nedic, T. N. Wassermann, R. W. Larsen and M. A. Suhm, Phys. Chem. Chem. Phys., 2011, 13, 14050–14063.
35. G. Yeo and T. Ford, Vib. Spectrosc., 1991, 2, 173–181.
36. G. Yeo and T. Ford, J. Mol. Struct., 1990, 217, 307–323.
37. C. Emmeluth, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2003, 118, 2242–2255.
38. T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454.
39. M. Albrecht, P. Zielke, C. A. Rice and M. A. Suhm, J. Mol. Struct., 2008, 880, 2–13.
40. G. E. Douberly, in Infrared Spectroscopy of Molecular Radicals and Carbenes in Helium Droplets, ed. A. Slenczka and J. P. Toennies, Springer International Publishing, Cham, 2022, pp. 155–177.
41. Y. Hirao, T. Saito, H. Kurata and T. Kubo, Angew. Chem., Int. Ed., 2015, 54, 2402–2405.
42. G. V. Milnikov, O. Kühn and H. Nakamura, J. Chem. Phys., 2005, 123, 074308.
43. J. O. Richardson, Phys. Chem. Chem. Phys., 2017, 19, 966–970.
44. X.-G. Wang and T. Carrington, J. Chem. Phys., 2023, 158, 084107.
45. W. Fang, P. Winter and J. O. Richardson, J. Chem. Theory Comput., 2021, 17, 40–55.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic, computational and measurement details. See DOI: https://doi.org/10.1039/d3cp01156a

---