The bifunctional volcano plot: thermodynamic limits for single-atom catalysts for oxygen reduction and evolution

Abstract

Single-atom catalysts (SACs) are a promising route to create highly-efficient bifunctional catalysts for O₂ reduction and evolution. Here, we show how adsorption-energy scaling relations can be used to build a Sabatier-type bifunctional volcano plot. The plot helps establish thermodynamic limits to bifunctional SACs and suggests that high bifunctional activities are more easily reached by SACs containing several different species.

---

In view of the current climate crisis, cost-effective generation, temporary storage and utilization of renewable energies are of great interest.^1–3 While Li-ion batteries provide a valuable approach for storing energy for stationary (such as household buffer or grid-level storage)⁴ and automotive applications, energy density requirements for aviation and nautical applications cannot currently be met.⁵

An alternative to solve this problem would be the adoption of a “hydrogen economy”^6,7 mainly based on H₂/H₂O/O₂ interconversion. On the one hand, the electrolysis of water (2H₂O(l) → O₂(g) + 2H₂(g)), a widely available liquid, would produce hydrogen gas, which has a desirable energy density. On the other hand, H₂ would then be used in fuel cells to generate electrical energy when required while simultaneously producing water (O₂(g) + 2H₂(g) → 2H₂O(l)).

A more localized scheme is the so-called regenerative fuel cell, in which the forward direction uses stored hydrogen, while the reverse reaction enables the system to recharge and regenerate hydrogen. The implementation of this device, however, requires high-efficiency bifunctional catalysts, namely, materials that can catalyse the forward and backward reactions efficiently.^8,9 In particular, substantial overpotentials are found for half-reactions involving O₂, namely the oxygen evolution and reduction reactions (OER and ORR, respectively represented by the following forward and backward reactions: 2H₂O(l) ⇄ O₂(g) + 4H⁺ + 4e⁻). The analysis in this work is based on the well-established OER pathway shown in eqn (1)–(4),^10,11 the inverse of which is the associative ORR pathway.¹²

H₂O(l) → *OH + (H⁺ + e⁻) (1)

*OH → *O + (H⁺ + e⁻) (2)

*O + H₂O(l) → *OOH + (H⁺ + e⁻) (3)

*OOH → * + O₂(g) + (H⁺ + e⁻) (4)

Furthermore, if water and proton-electron pairs are used as the thermodynamic reference for the adsorption energies of the intermediates *O, *OH and *OOH, the energies of the electrochemical steps 1–4 are given by eqn (5)–(8):

ΔG₁ = ΔG_OH (5)

ΔG₂ = ΔG_O − ΔG_OH (6)

ΔG₃ = ΔG_OOH − ΔG_O (7)

ΔG₄ = ΔG_O2 − ΔG_OOH (8)

where ΔG_O2 is equivalent to four times the equilibrium potential, that is 4.92 eV in experiments, while other values are found through DFT calculations depending on the exchange-correlation functional used.¹³

In computational (electro)catalysis, scaling relations^14–16 describe the interconnected adsorption energies of reaction intermediates with similar surface-bond characteristics. Specifically, for the OER and the ORR catalytic pathways shown in eqn (1)–(4), they describe the direct, linear proportionality between ΔG_O, ΔG_OH and ΔG_OOH. Koper¹⁷ and Rossmeisl et al.¹⁰ pointed out that the scaling relation between *OOH and *OH has a (near) unity slope and an offset of ∼3.20 eV, which has been confirmed in numerous further studies.^10,18,19 Since the equilibrium potential of the OER and the ORR is 1.23 V vs. RHE and eqn (2) and (3) connect *OH and *OOH via two proton-electron transfers (*OH + H₂O(l) → *OOH + 2(H⁺ + e⁻)), ideally, *OOH and *OH should differ only by 1.23 V × 2e⁻ = 2.46 eV. This energy mismatch moves the top of the OER and ORR Sabatier-type activity plots far from the equilibrium potential, with a minimum overpotential of (3.20–2.46) eV/2e⁻ = 0.37 V.^10,11,17,20

This result, for the past ten years, led to a frantic search for catalysts that break the *OOH vs. *OH scaling relation.^20–23 Although ideal catalysts (i.e. those with null OER/ORR calculated overpotentials) break such a relation,^10,13,24 materials that do it are not necessarily efficient and inducing its breaking can actually worsen the activity.^25–27 In sum, with some caveats, the scaling relations between *O, *OH, and *OOH enable the making of Sabatier-type activity plots but might as well limit our ability to optimize OER and ORR catalysts.

In recent years, single-atom catalysts (SACs) have become a focus of intense study in view of their versatility, the wide number of reactions they catalyse,^28–30 such as the OER/ORR and HER, the water-gas-shift or the CO₂ electroreduction reaction, and also owing to the ability to tailor these catalysts by varying the surrounding (bonding) environment.³¹ For this reason, the application of SACs to the field of bifunctional catalysis is of great interest.^32–37 In the following sections, we will discuss the impact of scaling relations on the bifunctional performance of SACs.

To better quantify the performance of bifunctional catalysts, the bifunctional index (BI) was introduced.^38–40 The BI measures the simultaneous ability of a prospective catalyst to catalyse a redox couple, such as the OER/ORR, by subtracting the potentials needed to reach some given current densities for the forward and backward reactions. This directly implies that a lower BI would indicate a better bifunctional catalyst and a BI of 0 would indicate an ideal catalyst for the reaction couple. For the ORR/OER couple, it is defined in experiments as the difference between the potentials for which j_ORR = −1 mA cm⁻² and j_OER = 10 mA cm⁻².

BI = U_{jOER=10 mA cm⁻²} − U_{jORR=−1 mA cm⁻²} (9)

In practice, it has been shown that the trends in thermodynamic limiting potentials (calculated as: U_L,OER = max(ΔG₁, ΔG₂, ΔG₃, ΔG₄), U_L,ORR = max(ΔG₋₁, ΔG₋₂, ΔG₋₃, ΔG₋₄)) predicted from density functional theory (DFT) calculations are in close agreement with those obtained at such experimental current densities.^40–44 In addition, the associated overpotentials (η_OER = U_L,OER − 1.23 and η_ORR = 1.23 − U_L,ORR) can be directly compared under some assumptions.^41,45 This means that we can approximate eqn (9) as:

BI ≈ U_L,OER − U_L,ORR = η_OER + η_ORR (10)

For an ideal bifunctional catalyst, the DFT-calculated BI would be 0 V, which would signify no overpotential for the OER and ORR at the same time and indicate 100% round-trip efficiency. We note that because the BI is the sum of two overpotentials, it is not univocal and can sometimes be misleading. For instance, a promising value of BI can simultaneously correspond to a catalyst with a low ORR overpotential and a high OER overpotential (or vice versa), and a true bifunctional catalyst with good performance for both reactions.

To illustrate this, Fig. 1 contains the ORR and OER volcano plots as a function of ΔG_OH. Statistically, the most likely potential-limiting steps correspond to the reactions *O → *OOH and *OH → *O for the OER (eqn (2) and (3)), and the reactions *OH → H₂O and O₂ → *OOH for the ORR (the reverse of eqn (1) and (4), denoted as −1 and −4, respectively).^11,13 Since the minimum overpotential for the ORR is located at the intersection of the lines corresponding to steps −1 and −4, we invert this volcano plot to arrive at Fig. 1. For further details on the making of the plot in Fig. 1, see Fig. S1† in the ESI.

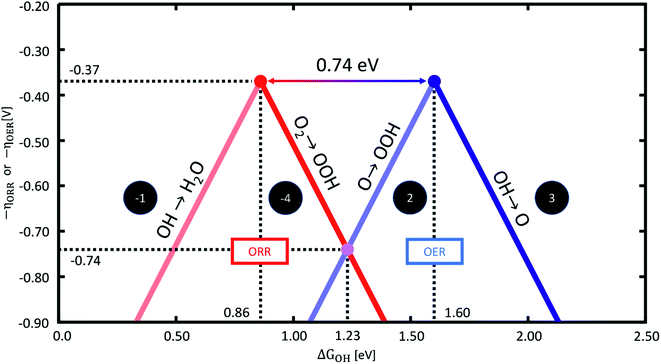Fig. 1 Sabatier-type activity plots based on scaling relations for the OER (right) and ORR (left) as a function of ΔG_OH. They are based on an energetic separation between *OOH and *OH of 3.20 eV, see Sections S1 and S2 in the ESI.† The most representative potential-limiting steps are noted in each case and have been determined statistically^13,18 from eqn (1)–(4) for the OER and the reverse equations for the ORR.

As mentioned before, the tops of the volcanoes are located at −η_OER = −η_ORR = −0.37 V, which can also be deduced by finding the intersection of the scaling lines, which we show explicitly in Section S2.† From this evaluation we can also conclude that the two tops of the volcanoes are located 0.74 eV apart in the scale of ΔG_OH.

Based on these considerations, we can evaluate two cases: (1) the bifunctional catalyst has (at least) two non-identical active sites for the OER and the ORR. Non-identical sites means that either the catalyst consists of e.g., two different materials that each catalyse one reaction, or that the active site undergoes a conformational transition in the range of U_L,ORR and U_L,OER. For instance, this can be an increase in the oxidation state of the metal centre of the SACs and/or the adsorption of an axial ligand, namely, –O or –OH, on one side of the active site. (2) The bifunctional catalyst has only one type of active site for the OER and ORR, and therefore needs to follow all scaling lines shown in Fig. 1 at the same time.

For case (1), there are two pairs of values for ΔG_O, ΔG_OH and ΔG_OOH, corresponding to the two different active centres. In such a case, one of the sites can be active for the ORR and the other for the OER. This means that the BI will be limited by the best possible onset potentials, each for the OER and the ORR volcanoes, namely, the two volcano apices in Fig. 1. Therefore, the minimum BI is BI_{min, case1} = 0.37 + 0.37 = 0.74 V. An extensive experimental and computational survey of ORR/OER bifunctional materials shows that 0.74 V is a good limit for composite materials with more than one type of active site, and BI values around 0.8–1.0 V typically correspond to good bifunctional catalysts.^38–40

For case (2), there is only one set of values for ΔG_O, ΔG_OH and ΔG_OOH, such that the BI is governed by the same scaling relations for steps 1–4 during the OER, and steps −4 to −1 during the ORR. This allows us to build a bifunctional ORR/OER activity plot. The functional shape of the BI is shown in Fig. 2. For a detailed analysis, including all equations for the separate regions of BI, see Section S3 in the ESI.†

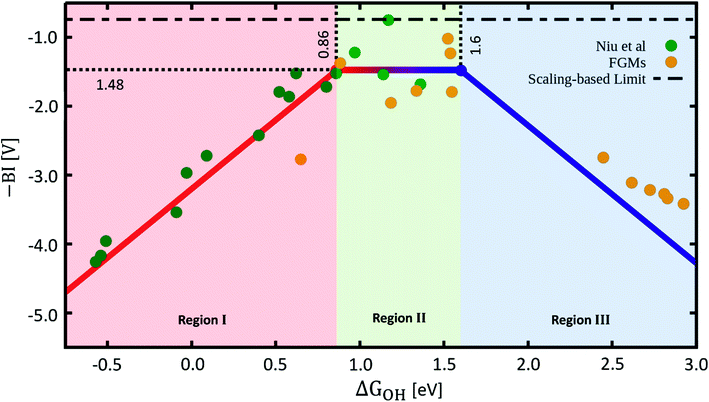Fig. 2 Sabatier-type bifunctional volcano plot for OER/ORR electrocatalysis with the additive inverse of the bifunctional index (−BI) plotted as a function of ΔG_OH. Datapoints labelled “Niu et al.” and “FGMs” were taken from the respective publications.^18,34,46 Further details on the making of this plot appear in Sections S3–S6 in the ESI.†

The plot has three main regions, shown in red, green, and blue in Fig. 2, for which the behaviour of BI is different. In the region of strong binding, shown in red in Fig. 2 (region I), where ΔG_OH < 0.86 eV, the overpotentials of the OER and ORR are governed by the steps −1 and 2, as can be seen in Fig. 1. This means that, since both functions have a positive slope in region I in Fig. 2, for increasing ΔG_OH, the BI will decrease.

Region II, shown in green in Fig. 2, where 0.86 eV < ΔG_OH < 1.6 eV, is characterized in Fig. 1 by a negative slope for the ORR (step −4), and a positive slope for the OER (step 2). The opposing slopes make the BI independent of ΔG_OH in this range and approximately equal to 1.48 V.

Lastly, in region III, shown in blue in Fig. 2, where ΔG_OH > 1.6 eV, both volcano lines for the OER (step 3) and ORR (step −4) have a negative slope in Fig. 1, i.e., are located on the weak-binding side of both volcanoes, which leads to a negative slope for −BI in Fig. 2.

In order to showcase this behaviour, we extracted datapoints from previous publications discussing the ORR and OER activities of SACs.^18,34,46 We corrected the datapoints, tabulated in Section S6,† for the differences that arise due to them being calculated using different exchange-correlation functionals (for more details, see Section S4†). We show them in Fig. 2 together with −BI as a function of ΔG_OH along the three regions mentioned before. As can be seen, the datapoints, with the exclusion of 4 anomalous points, which deviate beneficially from the *O vs. *OH scaling line (see Section S5†) and belong to group 9 of the periodic table (Co, Rh, Ir), all follow the general scaling-based predictions for −BI as a function of ΔG_OH. Interestingly, departures from the *O vs. *OH scaling relation have already been shown to enhance the OER activity of IrO₂(110)⁴⁷ and can be induced by modifying the electrolyte. In addition, Rh SACs have also been predicted to be highly active for other reactions.^37,48

In summary, the analysis of cases (1) and (2) suggests that for any bifunctional SAC catalyst with 0.74 V < BI < 1.48 V (bearing in mind the expected error bars from DFT): (i) there are two types of active sites, (ii) the active site undergoes a redox transition in the potential range between the calculated onsets of the ORR and the OER such that the active sites are different during the ORR and the OER, or (iii) there is a sizable departure from a scaling relation.

This suggests that SAC studies need to routinely take into account the in situ shape of the active sites under ORR and OER conditions, such as applied potentials and pH, mirroring the considerations based on surface Pourbaix diagrams applied for conventional metallic or metal-oxide catalysts.^49,50 In addition, errors inherited by the bifunctional volcano plot from scaling relations ought to be assessed, and a better descriptor (probably one involving a subtraction of adsorption energies) for the bifunctional activity plot which is less dependent on the exchange-correlation functional used could be found.⁵¹

Conclusions

Based on scaling relations, in this work we showed that the bifunctional index (BI), a metric for ORR/OER bifunctionality, can be as low as 0.74 V for SACs with several different types of active sites. We built a Sabatier-type bifunctional volcano plot, which unlike volcano plots for a single reaction, has a wide plateau at intermediate binding. The plot shows that SACs with a single type of active site are generally bound to have BIs of at least 1.48 V. For SACs with BIs lower than 1.48 V, there is likely to be sizable departures from the scaling relations between *O vs. *OH. We note, however, that these values may have wide associated error bars inherited from scaling relations, so they should be considered cautiously.

Going forward, further research could be devoted to applying the concepts in this study to non-SAC catalysts, such as dual-atom catalysts, transition metals and metal oxides. Furthermore, we would like to stress that modelling efforts should routinely consider conformational changes at the active sites caused by changes in potential and pH to accurately model the performance of bifunctional SACs. Interestingly, deviating from the *O vs. *OH scaling relation emerges as a means to obtain high bifunctional OER/ORR activities.

Author contributions

Manuel Kolb: formal analysis, investigation, visualization, and writing – original draft. Federico Calle-Vallejo: conceptualization, formal analysis, writing – review & editing, supervision, project administration, and funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The grants RTI2018-095460-B-I00, RYC-2015-18996, and MDM-2017-0767 were funded by MCIN/AEI/10.13039/501100011033 and by the European Union. This work was also partly supported by Generalitat de Catalunya via the grant 2017SGR13. The use of supercomputing facilities at SURFsara was sponsored by NWO Physical Sciences.

References

1. N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
2. R. E. Smalley, MRS Bull., 2005, 30, 412–417.
3. P. C. K. Vesborg and T. F. Jaramillo, RSC Adv., 2012, 2, 7933–7947.
4. J. Wüllner, N. Reiners, L. Millet, M. Salibi, F. Stortz and M. Vetter, Curr. Sustainable Energy Rep., 2021, 8, 263–273.
5. C. Wadia, P. Albertus and V. Srinivasan, J. Power Sources, 2011, 196, 1593–1598.
6. J. O. Bockris, Science, 1972, 176, 1323.
7. N. P. Brandon and Z. Kurban, Philos. Trans. R. Soc., A, 2017, 375, 20160400.
8. H.-Y. Su, Y. Gorlin, I. C. Man, F. Calle-Vallejo, J. K. Nørskov, T. F. Jaramillo and J. Rossmeisl, Phys. Chem. Chem. Phys., 2012, 14, 14010.
9. B. Paul and J. Andrews, Renewable Sustainable Energy Rev., 2017, 79, 585–599.
10. I. C. Man, H. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
11. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
12. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
13. E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, J. Electroanal. Chem., 2021, 896, 115178.
14. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 16105.
15. F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 116103.
16. M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4, 3748–3761.
17. M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260.
18. O. Piqué, F. Illas and F. Calle-Vallejo, Phys. Chem. Chem. Phys., 2020, 22, 6797–6803.
19. R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, J. Phys. Chem. C, 2016, 120, 24910–24916.
20. M. Busch, N. B. Halck, U. I. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Nano Energy, 2016, 29, 126–135.
21. Z.-F. Huang, J. Song, S. Dou, X. Li, J. Wang and X. Wang, Matter, 2019, 1, 1494–1518.
22. Y. Xie, Z.-W. Wang, T.-Y. Zhu, D.-J. Shu, Z.-F. Hou and K. Terakura, Carbon, 2018, 139, 129–136.
23. T. Sours, A. Patel, J. Nørskov, S. Siahrostami and A. Kulkarni, J. Phys. Chem. Lett., 2020, 11, 10029–10036.
24. C. H. Kjaergaard, J. Rossmeisl and J. K. Nørskov, Inorg. Chem., 2010, 49, 3567–3572.
25. N. Govindarajan, J. M. García-Lastra, E. J. Meijer and F. Calle-Vallejo, Curr. Opin. Electrochem., 2018, 8, 110–117.
26. N. Govindarajan, M. T. M. Koper, E. J. Meijer and F. Calle-Vallejo, ACS Catal., 2019, 9, 4218–4225.
27. K. S. Exner, Chem Catal., 2021, 1, 258–271.
28. Y. Chen, S. Ji, C. Chen, Q. Peng, D. Wang and Y. Li, Joule, 2018, 2, 1242–1264.
29. N. Cheng, L. Zhang, K. Doyle-Davis and X. Sun, Electrochem. Energy Rev., 2019, 2, 539–573.
30. F. Jaouen, E. Proietti, M. Lefèvre, R. Chenitz, J.-P. Dodelet, G. Wu, H. T. Chung, C. M. Johnston and P. Zelenay, Energy Environ. Sci., 2011, 4, 114–130.
31. X. Zhou, L. Chen, G. E. Sterbinsky, D. Mukherjee, R. R. Unocic and S. L. Tait, Catal. Sci. Technol., 2020, 10, 3353–3365.
32. Q. Deng, J. Zhao, T. Wu, G. Chen, H. A. Hansen and T. Vegge, J. Catal., 2019, 370, 378–384.
33. Q. Deng, J. Han, J. Zhao, G. Chen, T. Vegge and H. Anton Hansen, J. Catal., 2021, 393, 140–148.
34. H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2021, 9, 3590–3599.
35. C. Zhu, Q. Shi, S. Feng, D. Du and Y. Lin, ACS Energy Lett., 2018, 3, 1713–1721.
36. Q. Zhang and J. Guan, Adv. Funct. Mater., 2020, 30, 2000768.
37. S. Back, A. R. Kulkarni and S. Siahrostami, ChemCatChem, 2018, 10, 3034–3039.
38. A. Aijaz, J. Masa, C. Rösler, W. Xia, P. Weide, A. J. R. Botz, R. A. Fischer, W. Schuhmann and M. Muhler, Angew. Chem., Int. Ed., 2016, 55, 4087–4091.
39. J. Masa, W. Xia, I. Sinev, A. Zhao, Z. Sun, S. Grützke, P. Weide, M. Muhler and W. Schuhmann, Angew. Chem., Int. Ed., 2014, 53, 8508–8512.
40. M. Retuerto, F. Calle-Vallejo, L. Pascual, G. Lumbeeck, M. T. Fernandez-Diaz, M. Croft, J. Gopalakrishnan, M. A. Peña, J. Hadermann, M. Greenblatt and S. Rojas, ACS Appl. Mater. Interfaces, 2019, 11, 21454–21464.
41. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
42. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556.
43. F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189.
44. A. S. Bandarenka, H. A. Hansen, J. Rossmeisl and I. E. L. Stephens, Phys. Chem. Chem. Phys., 2014, 16, 13625.
45. M. Retuerto, L. Pascual, F. Calle-Vallejo, P. Ferrer, D. Gianolio, A. G. Pereira, Á. García, J. Torrero, M. T. Fernández-Díaz, P. Bencok, M. A. Peña, J. L. G. Fierro and S. Rojas, Nat. Commun., 2019, 10, 2041.
46. F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639.
47. D.-Y. Kuo, J. K. Kawasaki, J. N. Nelson, J. Kloppenburg, G. Hautier, K. M. Shen, D. G. Schlom and J. Suntivich, J. Am. Chem. Soc., 2017, 139, 3473–3479.
48. V. Tripkovic, M. Vanin, M. Karamad, M. E. Björketun, K. W. Jacobsen, K. S. Thygesen and J. Rossmeisl, J. Phys. Chem. C, 2013, 117, 9187–9195.
49. H. A. Hansen, I. C. Man, F. Studt, F. Abild-Pedersen, T. Bligaard and J. Rossmeisl, Phys. Chem. Chem. Phys., 2010, 12, 283–290.
50. H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722.
51. D. Krishnamurthy, V. Sumaria and V. Viswanathan, J. Phys. Chem. Lett., 2018, 9, 588–595.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08366j

---