Temperature-dependent reentrant phase transition of RNA–polycation mixtures

Abstract

Liquid–liquid phase separation (LLPS) of multivalent biopolymers is a ubiquitous process in biological systems and is of importance in bio-mimetic soft matter design. The phase behavior of biomolecules, such as proteins and nucleic acids, is typically encoded by the primary chain sequence and regulated by solvent properties. One of the most important physical modulators of LLPS is temperature. Solutions of proteins and/or nucleic acids have been shown to undergo liquid–liquid phase separation either upon cooling (with an upper critical solution temperature, UCST) or upon heating (with a lower critical solution temperature, LCST). However, many theoretical frameworks suggest the possibility of more complex temperature-dependent phase behaviors, such as an hourglass or a closed-loop phase diagram with concurrent UCST and LCST transitions. Here, we report that RNA–polyamine mixtures undergo a reentrant phase separation with temperature. Specifically, at low temperatures, RNA–polyamine mixtures form a homogenous phase. Increasing the temperature leads to the formation of RNA–polyamine condensates. A further increase in temperature leads to the dissolution of condensates, rendering a reentrant homogenous phase. This dual-response phase separation of RNA is not unique to polyamines but also observed with short cationic peptides. The immiscibility gap is controlled by the charge of the polycation, salt concentration, and mixture composition. Based on the existing theories of complex coacervation, our results point to a complex interplay between desolvation entropy, ion-pairing, and electrostatic interactions in dictating the closed-loop phase behavior of RNA–polycation mixtures.

---

Reversible liquid–liquid phase separation (LLPS) of multivalent biopolymers, such as signaling proteins and RNA, is a ubiquitous physical process underlying the formation of intracellular membrane-less compartments.^1,2 LLPS offers functionally distinct yet dynamic subcellular condensates and is thought to play central roles in RNA metabolism, stress response, nuclear organization, and many other intracellular processes.^3–6 Several proteins and nucleic acids have been shown to undergo LLPS in the cell, with various mechanisms that depend on the protein sequence, RNA sequence and secondary structure,^7–9 and environmental factors such as pH and temperature.¹⁰ This has led to a growing interest in understanding the molecular forces that drive biopolymer phase separation.

Earlier theories such as those by Flory and Huggins focused on enthalpy-driven LLPS.¹¹ Subsequent efforts pointed to the existence of other factors such as solvation energies that lead to an entropy-driven LLPS.^12–16 These two broad categories of LLPS have an orthogonal dependence on temperature. Enthalpy-driven LLPS is often manifested in an upper critical solution temperature (UCST) phase behavior, where increasing temperature leads to the suppression of LLPS.¹⁷ In contrast, entropy-driven LLPS often has a lower critical solution temperature (LCST) phase behavior, where LLPS is promoted at high temperatures and suppressed at low temperatures.¹⁷ It is worth noting that Flory and Huggins developed their theory for neutral polymer systems. For charged polymers, however, the existence of long-range electrostatic interactions, specific ion-mediated interactions, and solvation effects can give rise to more complex behaviors that are observed both in biology and in synthetic polymer systems. Therefore, mapping the temperature-dependent phase behavior of biopolymeric systems can give significant insights into the nature of thermodynamic driving forces underlying LLPS.

Many natural disordered proteins undergo liquid–liquid phase separation with a UCST phase behavior. For example, Molliex and coworkers reported that the ribonucleoprotein hnRNPA1 has a UCST phase behavior.¹⁸ Other proteins such as DDX4 and TIA1 were also shown to undergo UCST phase transitions.¹⁷ The roles of charged, polar, and aromatic residues in dictating the UCST phase behavior of proteins have been extensively discussed.^17,19–21 On the other hand, there are few protein systems found in the literature that can undergo an LCST phase transition. Amongst naturally occurring proteins, microtubule-associated protein tau has been shown to undergo either LCST or UCST transition depending on the salt conditions.^22–24 Another protein that has been shown to undergo an LCST transition is the proteasomal shuttle factor UBQLN2.²⁵ Among synthetic systems, a seminal work from Quiroz and Chilkoti showed that elastin-like polypeptides (ELPs) and resilin-like polypeptides (RPLs) can be programmed to undergo either an LCST or a UCST phase transition, respectively, depending on their primary sequence.²⁶ The authors identified distinct classes of amino acids that increase the tendency for LCST (charge depleted and hydrophobic amino acids) and UCST (polar and aromatic amino acids) transitions. Creating hybrid sequences with blocks of different amino acid compositions can lead to the coexistence of UCST and LCST in the same system, giving rise to an hourglass phase diagram with a miscibility gap at intermediate temperatures.^27,28 Further, the condensation and aggregation of synthetic systems such as charged polyelectrolytes have also been extensively studied against temperature and salt with UCST behavior being frequently observed.^29–33 However, a closed-loop phase diagram in the temperature-composition plane with T_LCST < T_UCST has been a rare trait for biologically relevant systems, although it is commonly discussed in theoretical classifications of phase diagrams and computational studies of polypeptides.^17,34

In this letter, we report that a homopolymeric RNA, poly(rU), displays a temperature-controlled dual-response phase behavior with concurrent UCST and LCST transitions in presence of small polycationic molecules such as polyamines and peptides. The LCST transition occurs at temperatures below the UCST transition, leading to a reentrant phase transition with an immiscibility gap that is close to the physiological temperature. Combined with the fact that RNA–polycation condensates undergo a reentrant phase separation as the mixture composition is varied, we reveal a closed-loop phase diagram of RNA–polycation mixtures in the temperature-composition plane. The immiscibility gap is controlled by the valence of the cation, the mixture composition, and the salt concentration. Our experiments indicate that the LCST transition is not strongly affected by the ionic strength of the mixture or the composition asymmetry while the UCST transition is strongly dependent on these factors. These results suggest that the UCST transition is a result of electrostatically driven inter-complex interactions³⁵ while the LCST transition is predominantly driven by solvation-mediated effects. Our results point to a unique system where the LCST and the UCST transitions are not encoded by the primary sequence pattern/composition, but rather by the collective properties of the RNA–polycation complexes.

Results

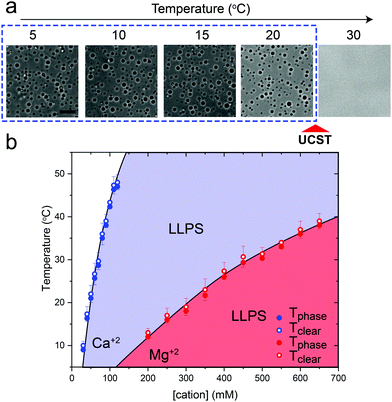
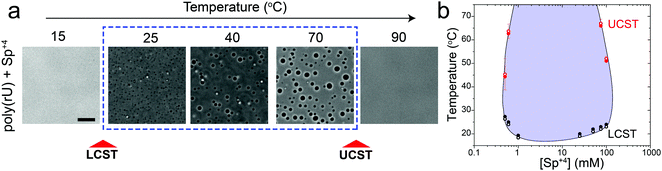
Previously, we have shown that homopolymeric poly(rU) RNA undergoes phase separation in presence of divalent cations such as Mg⁺² and Ca⁺².³⁶ In this work, we first used temperature-controlled microscopy to determine the phase behavior of poly(rU)–divalent cation mixtures as a function of temperature. We found that poly(rU)–Mg⁺² mixtures have a UCST transition where condensates are stabilized at low temperatures but dissolve at high temperatures (Fig. 1a). When subjected to multiple temperature cycling, the observed appearance of the RNA droplets during cooling (T_phase) and subsequent disappearance (T_clear) during heating were within ±1.0 °C, signifying no thermal hysteresis (Fig. 1b and Fig. S1, ESI†). We next probed the impact of varying Mg⁺² concentrations on the upper cloud-point temperature (UCPT) of the mixture. The UCPT increased monotonically with increasing Mg⁺² concentration in solution (Fig. 1b), suggesting more favorable conditions for LLPS. Repeating these measurements with Ca⁺² ions revealed that a ∼10-fold lower Ca⁺² concentration is sufficient to induce LLPS with a similar UCST phase behavior (Fig. 1c). This observed difference is consistent with previous reports on divalent cation effects on nucleic acid phase separation and can be attributed to a greater charge density and hence potency of Ca⁺² ions in backbone charge screening and engaging in interactions with RNA bases as compared to Mg⁺² ions.³⁶

Fig. 1 RNA–divalent cation mixtures display a UCST transition. (a) Bright-field microscopy images of poly(rU)–Mg⁺² mixtures at different temperatures showing a UCST transition. The Mg⁺² concentration is 400 mM, poly(rU) concentration is 1.5 mg ml⁻¹, and the buffer contains 25 mM Tris–HCl (pH 7.5). Scale bar represents 10 μm. (b) A plot showing the dependence of phase separation temperature (T_phase, solid symbols) during cooling and the temperature at which the system transitions back to a homogeneous mixture during heating (T_clear, open symbols) on the divalent cation concentration. Here, poly(rU) concentration was kept fixed at 1.5 mg ml⁻¹ in 25 mM Tris–HCl buffer (pH 7.5). Shaded regions indicate the conditions where phase separation occurs. Solid lines are drawn as guides to the eye.

In addition to divalent cations, poly(rU) RNA has previously been shown to undergo phase separation with multivalent cationic small molecules such as spermine and cationic polypeptides.^37–41 However, unlike divalent cations, spermine and cationic polypeptides mediate a reentrant LLPS of RNA as the polycation-to-RNA mixing ratio is varied isothermally.^39,41,42 This suggests that the complexation and phase behavior of RNA with polyamines and short cationic peptides is distinct from RNA–divalent cation mixtures. In fact, Keating and coworkers reported that poly(rU)–spermine mixtures undergo liquid–liquid phase separation with an LCST as opposed to the UCST behavior observed here for divalent cations.³⁷ However, the temperature range at which poly(rU)–spermine mixtures were tested was up to ∼37 °C. We hypothesized that since an LCST is present in poly(rU)–spermine mixtures, a UCST must be present as well since poly(rU)–spermine phase separation is likely driven by energetically-favored inter-complex interactions.^35,43 Accordingly, we prepared poly(rU)–spermine mixtures at variable compositions and inspected their phase behavior at different temperatures ranging from 4 °C to 90 °C. Remarkably, we observed that poly(rU)–spermine mixtures undergo a dual-response phase separation with both LCST and UCST transitions (Fig. 2a; Movie S1, ESI†). The LCST transition is observed at temperatures lower than the UCST transition, creating a closed-loop two-phase coexistence regime in the temperature-composition plane. Both the upper and lower cloud-point temperatures (UCPT and LCPT, respectively) of the mixture are dependent on the spermine-to-RNA ratio (Fig. 2b). At low spermine concentrations (<1 mM), the UCPT rapidly increases with the spermine concentration. Subsequently, we observe a sharp decrease in the UCPT at higher spermine concentrations (>50 mM, Fig. 2b). At intermediate spermine concentrations, the UCPT was >90 °C and therefore undetectable in our experimental setup. In contrast, the LCPT showed less sensitivity to mixture composition variation, indicating that the LCST transition might be driven by solvent-mediated interactions and not purely dependent on inter-complex interactions. We note that UCST phase transitions have been typically observed in complex coacervates where phase separation is driven by oppositely charged macromolecules.^44,45 More recently, experimental observations of an LCST transition have been documented for complex coacervates^37,46,47 and theoretically discussed by Muthukumar and colleagues.⁴⁸ However, to our knowledge, our results report the first experimental observation of a thermo-responsive closed-loop phase diagram in an RNA-based complex coacervate system.

Fig. 2 RNA–spermine mixtures have coexisting LCST and UCST phase transitions. (a) Bright-field images of poly(rU)–spermine mixtures at different temperatures showing an LCST and a subsequent UCST transition. The sample was prepared by mixing poly(rU) and spermine (Sp⁺⁴) at final concentrations of 1.5 mg ml⁻¹ and 60 mM, respectively, in a buffer containing 25 mM Tris–HCl (pH 7.5). Scale bar represents 10 μm. (b) Temperature phase diagram of poly(rU)–spermine mixtures at different spermine concentrations. Solid symbols indicate temperatures of droplet formation (T_phase) and open symbols indicate temperatures of droplet dissolution (T_clear). Here, poly(rU) concentration was kept fixed at 1.5 mg ml⁻¹ in 25 mM Tris–HCl buffer (pH 7.5). The shaded region indicates the conditions where phase separation occurs. The solid line is drawn as a guide to the eye.

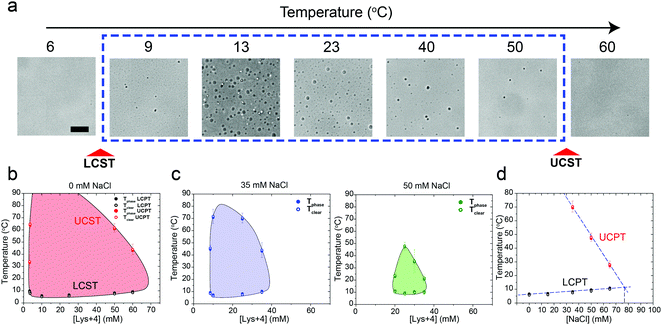
We next asked whether this temperature-controlled dual-response phase behavior is generic to other cationic macromolecules. To test that, we inspected the phase behavior of poly(rU) RNA with a tetra-amino acid peptide Lysine₄ (K₄) which carries the same formal charge (+4) as spermine. Indeed, a similar temperature-dependent dual-response phase behavior was observed for poly(rU)-K₄ mixtures as a function of mixture composition (Fig. 3a and b, Movie S2, ESI†). Previous work from our lab and others indicated that phase separation in oppositely charged polypeptide–RNA mixtures is tunable by the ionic strength of the medium.^36,39,41,49 Therefore, we next asked how increasing NaCl concentration in the medium impacts the two-phase coexistence region. We observed that increasing [NaCl] from 0 to 50 mM resulted in a substantial shrinkage of the two-phase regime. The UCPT in particular, but not the LCPT, was observed to rapidly decrease as the salt concentration increased (Fig. 3b–d). Finally, at ∼75 mM NaCl, LLPS was abrogated and the mixture remained soluble at all temperatures tested (90 °C ≥ T ≥ 5 °C). Overall, these data suggest that the electrostatic interactions, such as the dipolar interactions proposed by Muthukumar and colleagues, between the RNA–peptide complexes are likely to drive the UCST transition.³⁵

Fig. 3 The closed-loop phase behavior of RNA–polycation mixtures is sensitive to the ionic strength of the buffer. (a) bright field images of poly(rU)–Lys₄ mixtures showing both LCST and UCST transitions. The poly(rU) concentration was 1.5 mg ml⁻¹ and Lys₄ concentration was 50 mM in a 25 mM Tris–HCl (pH 7.5) buffer. The scale bar represents 10 μm. (b) State diagram of poly(rU)–Lys₄ mixtures at different Lys₄ concentrations and temperature conditions. Solid symbols indicate temperatures of droplet formation (T_phase) and open symbols indicate temperatures of droplet dissolution (T_clear). Here, poly(rU) was kept at 1.5 mg ml⁻¹ concentration in 25 mM Tris–HCl buffer (pH 7.5). (c) Same data as in (b) but with 35 mM NaCl (left) or 50 mM NaCl (right) added to the buffer. (d) The upper and lower cloud-point temperatures (UCPT and LCPT, respectively) were measured as a function of salt concentration. Samples were prepared at 1.5 mg ml⁻¹ poly(rU) and 25 mM Lys₄ in a buffer containing 25 mM Tris–HCl (pH 7.5) and variable salt conditions. Shaded regions in b and c indicate the conditions where phase separation occurs. Solid lines are drawn as guides to the eye.

In addition to salt and mixture composition variation, we measured the UCPTs and LCPTs as a function of total polymer concentration (at a fixed RNA/polycation ratio), at different pH values (pH 6–8.5), and in two independent buffers (HEPES and MOPS) which have substantially lower degree of pH variation as a function of temperature as compared to the Tris–HCl buffer.⁵⁰ These control measurements showed no substantial dependence of the cloud point temperatures (both UCPT and LCPT) on the aforementioned variables (Fig. S2, ESI†).

Several studies probed the phase behavior of RNA–peptide mixtures and analogous complex coacervates with temperature variation and did not report a temperature-controlled dual-response phase behavior.^{37,44–47,51} We hypothesized that the size of the closed-loop is strongly dependent on the charge/size of the cation molecule. To test this idea, we examined the phase behavior of poly(rU) mixtures with a smaller cationic molecule, spermidine (Sp⁺³), and with a larger cationic peptide, Lysine₁₀ (K₁₀). We observed that spermidine–poly(rU) mixtures show a narrower LLPS region as a function of temperature (Fig. 4a). Poly(rU) samples with K₁₀, on the other hand, remained phase-separated at all temperatures tested (4–90 °C; Fig. 4b). This observation is consistent with previous reports⁵² where the authors noted high temperature stability of complex coacervates. Although poly(rU)–K₁₀ mixtures displayed phase separation at all temperature tested, we found that poly(rU)–K₁₀ droplets became substantially smaller at 90 °C and 4 °C as compared to intermediate temperatures when K₁₀ concentration was increased (Fig. S3, ESI†). These data indicate the proximity of both LCST and UCST transitions in this case, albeit their occurrence is outside our experimentally accessible temperature (4–90 °C) window. In summary, our results suggest that small variations in the charge and/or size of the polycation strongly affect the dimensions of the closed-loop of RNA–polycation two-phase coexistence.

Fig. 4 Polycation charge and/or size strongly affect both LCST and UCST transitions. (a) Bright-field microscopy images of poly(rU)–spermidine mixtures (top) and poly(rU)–spermine mixtures (bottom) at different temperatures. Spermidine–poly(rU) sample showed both LCST and UCST transitions. The poly(rU) concentration was 1.5 mg ml⁻¹ and spermidine concentration was 25 mM in a 25 mM Tris–HCl (pH 7.5) buffer. The spermine concentration was chosen to be 18.75 mM to keep an identical charge concentration. The spermine–poly(rU) sample showed an LCST transition but did not show a UCST transition within the same temperature range. (b) Bright-field microscopy images of poly(rU)–K₄ mixtures (top; [K₄] = 50 mM) and poly(rU)–K₁₀ mixtures (bottom; [K₁₀] = 20 mM) at different temperatures. Both samples contain identical charge concentrations of the respective polycation. All scale bars represent 10 μm.

Discussion

Understanding the thermo-responsive phase behavior of proteins and nucleic acids can give direct insights into the molecular driving forces of liquid–liquid phase separation. Protein solutions commonly display a UCST behavior while LCST behavior has also been observed in some natural and synthetic systems.^22–26 In a recent review, Ruff and coworkers discussed temperature as an important stimulus for phase separation in biological systems and argued that protein sequence plays a primary role in dictating the temperature-dependent phase behavior.¹⁷ Experimental work by Quiroz and coworkers outlined the types of amino acid sequences that can undergo LCST versus UCST transitions and laid out design principles for controlling the temperature-responsive phase behavior of elastin-like polypeptides.²⁶ The coexistence of LCST and UCST in the form of an hourglass phase diagram (T_LCST > T_UCST) has been shown experimentally for elastin-like polypeptides and computationally for more generic IDPs.^27,28,34 However, a closed-loop phase diagram (with T_LCST lower than T_UCST) has not been experimentally observed for biological complex coacervates.

In this work, we show that both types of phase behaviors (LCST and UCST) can simultaneously occur in RNA mixtures with small cationic polypeptides and polyamines in the form of a closed-loop phase diagram. Both RNA and the peptides/polyamines used here are homopolymeric without any modular architecture or complex primary sequence features. This suggests that RNA–cation complexes have distinct solvation properties and inter-complex interactions depending on the identity and size of the polycation and the mixture composition. While our experiments with small divalent cations showed a UCST phase separation, larger polycations such as polyamines showed a reentrant phase separation with temperature, comprising both UCST and LCST transitions. Manipulating intermolecular interactions with salt led to the shrinkage of the immiscibility gap by lowering the UCST boundary and keeping the LCST transition almost unaffected. The effects of salt concentration and the mixture asymmetry on the UCST of the mixture that we observed in this study are consistent with a mean-field model that considers enthalpic interactions between polyelectrolyte complexes as a basis of LLPS.³⁵ Increasing the size of the polycation led to the extension of the immiscibility gap beyond our experimental temperature range, although, signs of the proximity of both UCST and LCST transitions were present at the extreme hot and cold temperatures tested, respectively (Fig. S3, ESI†). The increase in UCST as a function of the polycation valence is also consistent with the model proposed by Adhikari and colleagues.³⁵

What are the molecular parameters that drive LCST and UCST transitions of RNA solutions? Ruff and co-workers presented a conceptual framework for the thermo-responsive phase behavior of biomolecules.¹⁷ Although this review mainly focuses on the phase behavior of intrinsically disordered proteins (IDPs), the framework could be extended to nucleic acid phase separation. A UCST transition could be conceptualized utilizing simple Flory–Huggins formalism where the inter-polymer interactions along with the solvent–solvent and solvent–polymer interactions are considered in Flory's mean-field parameter, called χ.⁵³ To account for the temperature dependence of phase separation, χ can be empirically formalized as 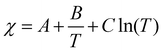where A (represents the entropic part), B, and C are constants.⁴⁶ Depending on the values and signs of the coefficients associated with the enthalpic part (B & C), various shapes of the phase diagram are possible including UCST behavior (B > 0; C = 0), LCST behavior (B < 0; C = 0), or a closed-loop (B < 0; C < 0). Although it is physically intuitive to conceptualize the UCST behavior based on the Flory–Huggins model by considering weakened polymer–polymer interactions as the temperature is increased, the LCST behavior is much more subtle and requires further attention. Extensive work by Vause and Walker, by Tanaka, and others in the 1980s and 1990s suggested that favorable hydrogen-bonding interactions between the polymer chain and the water molecules at lower temperatures underlie the occurrence of an LCST transition.^54,55 Subsequently, theoretical work integrating phase separation in the framework of the Flory–Huggins model and temperature-dependent solvation via H-bonding interactions successfully captured the closed-loop shape of the experimentally determined phase diagram of aqueous polymer mixtures.^55,56

In addition to the temperature dependence of the χ parameter, further considerations are needed for describing the thermo-responsive phase behavior of complex coacervates. Several theories have suggested that enthalpy-driven phase separation of oppositely charged polyelectrolytes is a two-step condensation process where the second step is the phase separation and it occurs through inter-complex interactions.^{35,48,57–60} In a recent work by Muthukumar and coworkers, the authors proposed the formation of polyelectrolyte complexes with dipolar trains upon mixing of oppositely charged polyelectrolytes.³⁵ These complexes undergo phase separation via dipole–dipole inter-complex attraction. This theory successfully recapitulates the known effects of salt and mixture composition on the phase separation behavior of oppositely charged polyelectrolytes, including the occurrence of reentrant phase transition upon varying mixture stoichiometry.^41,61,62 The extension of this theory suggested the possibility of both UCST, LCST, and the coexistence of UCST and LCST based on the interplay between polymer–solvent interactions and inter-complex dipolar attraction.⁴⁸ The authors argued that increasing temperature can increase the strength of dipolar inter-complex interactions due to the lowering of the dielectric constant and hence favor liquid–liquid phase separation at high temperatures (LCST behavior). This model is supported by the experimental observation of LCST behavior in the mixtures of oppositely charged strong polyelectrolytes (MW ∼150–200 kDa).⁴⁶ In another scenario where polymer–solvent interactions also increase with temperature, the model predicts the coexistence of UCST and LCST with LCST being higher than UCST due to the dominance of dipolar interactions at extremely high temperatures.⁴⁸ Interestingly, this theory does not discuss a closed-loop phase diagram since for that to occur, phase separation needs to be suppressed at high temperatures.

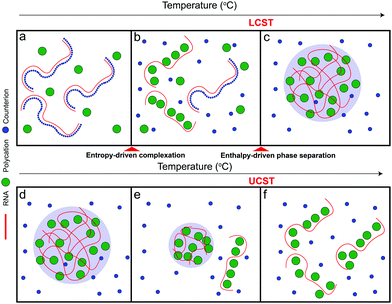
Based on the aforementioned discussion, we now describe a possible molecular mechanism that leads to the existence of a closed-loop phase diagram in the temperature-composition plane of a mixture of RNA and small polycations. We argue that phase separation in these systems is a two-step process that starts with the formation of polyelectrolyte complexes followed by the condensation of these complexes into mesoscopic condensates. The RNA–polycation complexes presumably form due to the entropic gain of counterion release.^63–65 The complexation occurs in the form of exchanging the counterions (which are small) with the oppositely charged polycations (which are larger) and hence the entropic gain of releasing counterions is larger than the entropic cost of constraining the polycations. Since this process is entropically driven, it is expected to be weakened at lower temperatures since the entropic contribution to the free energy of the system becomes less relevant at low temperatures⁵³ (Fig. 5a). It is also possible that such complexation is not favored at lower temperatures due to the enthalpic cost of reducing the polymer–water hydrogen bond interactions that oppose the entropy gain of counterion release.^54,55,63 As the temperature is increased, the entropic gain of exchanging counterions with the polycations becomes larger, dominating the enthalpic cost of breaking the polymer–water interactions, and hence more RNA–polycation complexes form (Fig. 5b). At the lower critical solution temperature (LCST), the population of complexes becomes sufficient to drive phase separation through inter-complex interactions (Fig. 5c) as proposed in the dipolar interaction model³⁵ or the electrostatic correlation energy model described by Zhang, Nguyen, and Shklovskii.^43,58–60 We note that, for stable dipolar trains to occur, the oppositely charged polyelectrolytes need to have symmetric or nearly symmetric lengths,³⁵ which is not the case for RNA–polycation mixtures since the polycations used in our study are significantly smaller than the RNA chain (average length of poly(rU) is ∼2200 nucleotides). Therefore, we argue that the correlation energy model is more appropriate to describe our system mainly due to the large asymmetry of size between the components. This condensation has an entropic cost due to the partitioning of the complexes into phase-separated liquid droplets as well as the differential partitioning of salt molecules within these two phases. At higher temperatures, the entropic cost of bringing the complexes together into condensates becomes higher than the enthalpic gain of inter-complex attractions and hence the droplets dissolve, leading to a homogenous solution of RNA–polycation complexes (Fig. 5d–f). Further, the valence of the polycations and the RNA may change at high temperatures due to different protonation states, which can also affect the enthalpic gain of complexation.⁶⁶ When the size of the polycation is increased (such as K₄-to-K₁₀ substitution), the entropic gain of forming complexes via counterion release becomes much larger than the entropic cost of constraining the polycations (due to the differences in size) leading to a lower temperature threshold of complex formation and subsequently a lower temperature threshold for phase separation (lowering of LCST). This may explain why mixtures of RNA with larger polycations (such as peptides) only show UCST transitions within the testable experimental temperatures.⁶⁷ At the same time, the increased size of the polycation leads to stronger electrostatic correlation energies (or the formation of more dipoles in the complexes) which subsequently leads to a higher UCST. These arguments are qualitatively consistent with the experimental results presented in this study (Fig. 2–4). Increasing salt concentration strongly affects the UCST since it affects the correlation attractions and may impact the complexation equilibrium.⁶³

Fig. 5 The interplay between entropy-driven complexation and enthalpy-driven phase separation may underlie the closed-loop phase behavior of RNA–polycation mixtures. A scheme summarizing the proposed mechanism for the closed-loop phase diagram exhibited by RNA–polycation mixtures. Panels (a–f) are the complexation and phase separation behaviors of the system with increasing temperatures. RNA is drawn as red chains, counter-ions are drawn as blue circles, and polycations are drawn as green circles.

In summary, we present RNA–polycation mixtures as suitable model systems to study the interplay between solvent-mediated interactions and intermolecular electrostatic interactions underlying the temperature-dependent dual-response phase behavior of the system. Our experimental results indicate that both types of interactions are significant and give rise to the coexistence of an LCST transition and a UCST transition within the experimentally accessible temperature range (4–90 °C). Together with previous studies,^35,37,41,48 our data provide experimental evidence of rich phase behavior of RNA–polycation mixtures that is profoundly modulated by the charge/size of the cation and the composition of the mixture. Further, our findings add to the rich literature of the phase behavior of oppositely charged polyelectrolytes and complement the above-mentioned seminal experimental and theoretical findings. Overall, these results provide new insights into the molecular driving forces that lead to temperature-dependent phase separation in multicomponent mixtures where phase separation is driven by heterotypic interactions. Further development of the theories of complex coacervates will provide a better and more general understanding of the molecular mechanisms underlying the UCST and LCST transitions in RNA–polycation mixtures.

Author contributions

P. R. B. conceived the idea. P. R. B. and I. A. designed the study. P. P. and I. A. performed the experiments and data analysis. P. R. B. and I. A. wrote the manuscript with input from P. P.

Conflicts of interest

Authors declare no competing interests.

Acknowledgements

P. R. B acknowledges the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health (R35 GM138186) and the College of Arts and Sciences at the University at Buffalo, SUNY for financial support. The authors acknowledge all the other members of the Banerjee laboratory for stimulating discussions and helpful suggestions at the various stages of the manuscript preparation.

References

1. Y. Shin and C. P. Brangwynne, Science, 2017, 357, eaaf4382.
2. S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298.
3. S. Alberti, Curr. Biol., 2017, 27, R1097–R1102.
4. A. S. Lyon, W. B. Peeples and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2020, 1–21.
5. J. A. Ditlev, L. B. Case and M. K. Rosen, J. Mol. Biol., 2018, 430, 4666–4684.
6. B. A. Gibson, L. K. Doolittle, M. W. Schneider, L. E. Jensen, N. Gamarra, L. Henry, D. W. Gerlich, S. Redding and M. K. Rosen, Cell, 2019, 179, 470–484 e421.
7. J. Guillén-Boixet, A. Kopach, A. S. Holehouse, S. Wittmann, M. Jahnel, R. Schlüssler, K. Kim, I. R. Trussina, J. Wang and D. Mateju, Cell, 2020, 181, 346–361 e317.
8. E. M. Langdon, Y. Qiu, A. G. Niaki, G. A. McLaughlin, C. A. Weidmann, T. M. Gerbich, J. A. Smith, J. M. Crutchley, C. M. Termini and K. M. Weeks, Science, 2018, 360, 922–927.
9. C. Roden and A. S. Gladfelter, Nat. Rev. Mol. Cell Biol., 2021, 22, 183–195.
10. H. Yoo, C. Triandafillou and D. A. Drummond, J. Biol. Chem., 2019, 294, 7151–7159.
11. P. J. Flory, J. Chem. Phys., 1942, 10, 51–61.
12. P. Flory, R. Orwoll and A. Vrij, J. Am. Chem. Soc., 1964, 86, 3507–3514.
13. P. J. Flory, R. Orwoll and A. Vrij, J. Am. Chem. Soc., 1964, 86, 3515–3520.
14. J. Barker and W. Fock, Discuss. Faraday Soc., 1953, 15, 188–195.
15. G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2003, 107, 3095–3097.
16. G. Ten Brinke and F. E. Karasz, Macromolecules, 1984, 17, 815–820.
17. K. M. Ruff, S. Roberts, A. Chilkoti and R. V. Pappu, J. Mol. Biol., 2018, 430, 4619–4635.
18. A. Molliex, J. Temirov, J. Lee, M. Coughlin, A. P. Kanagaraj, H. J. Kim, T. Mittag and J. P. Taylor, Cell, 2015, 163, 123–133.
19. E. W. Martin and T. Mittag, Biochemistry, 2018, 57, 2478–2487.
20. A. Bremer, M. Farag, W. M. Borcherds, I. Peran, E. W. Martin, R. V. Pappu and T. Mittag, Nat. Chem., 2021 DOI:10.1038/s41557-021-00840-w.
21. E. W. Martin, A. S. Holehouse, I. Peran, M. Farag, J. J. Incicco, A. Bremer, C. R. Grace, A. Soranno, R. V. Pappu and T. Mittag, Science, 2020, 367, 694–699.
22. S. Ambadipudi, J. Biernat, D. Riedel, E. Mandelkow and M. Zweckstetter, Nat. Commun., 2017, 8, 1–13.
23. S. Boyko, X. Qi, T.-H. Chen, K. Surewicz and W. K. Surewicz, J. Biol. Chem., 2019, 294, 11054–11059.
24. S. K. Rai, A. Savastano, P. Singh, S. Mukhopadhyay and M. Zweckstetter, Protein Sci., 2021, 30, 1294–1314.
25. T. P. Dao, R.-M. Kolaitis, H. J. Kim, K. O’Donovan, B. Martyniak, E. Colicino, H. Hehnly, J. P. Taylor and C. A. Castañeda, Mol. Cell, 2018, 69, 965–978 e966.
26. F. G. Quiroz and A. Chilkoti, Nat. Mater., 2015, 14, 1164–1171.
27. N. K. Dutta, M. Y. Truong, S. Mayavan, N. Roy Choudhury, C. M. Elvin, M. Kim, R. Knott, K. M. Nairn and A. J. Hill, Angew. Chem., 2011, 123, 4520–4523.
28. R. Balu, N. K. Dutta, N. R. Choudhury, C. M. Elvin, R. E. Lyons, R. Knott and A. J. Hill, Acta Biomater., 2014, 10, 4768–4777.
29. C. E. Sing and S. L. Perry, Soft Matter, 2020, 16, 2885–2914.
30. M. O. de La Cruz, L. Belloni, M. Delsanti, J. Dalbiez, O. Spalla and M. Drifford, J. Chem. Phys., 1995, 103, 5781–5791.
31. D. Priftis and M. Tirrell, Soft Matter, 2012, 8, 9396–9405.
32. N. Volk, D. Vollmer, M. Schmidt, W. Oppermann and K. Huber, Polyelectrolytes with Defined Molecular Architecture II, 2004, pp. 29–65.
33. S. Liu, K. Ghosh and M. Muthukumar, J. Chem. Phys., 2003, 119, 1813–1823.
34. G. L. Dignon, W. Zheng, Y. C. Kim and J. Mittal, ACS Cent. Sci., 2019, 5, 821–830.
35. S. Adhikari, M. A. Leaf and M. Muthukumar, J. Chem. Phys., 2018, 149, 163308.
36. P. L. Onuchic, A. N. Milin, I. Alshareedah, A. A. Deniz and P. R. Banerjee, Sci. Rep., 2019, 9, 12161.
37. W. M. Aumiller Jr, F. Pir Cakmak, B. W. Davis and C. D. Keating, Langmuir, 2016, 32, 10042–10053.
38. I. Alshareedah, G. M. Thurston and P. R. Banerjee, Biophys. J., 2021, 120, 1161–1169.
39. I. Alshareedah, T. Kaur, J. Ngo, H. Seppala, L.-A. D. Kounatse, W. Wang, M. M. Moosa and P. R. Banerjee, J. Am. Chem. Soc., 2019, 141, 14593–14602.
40. S. Boeynaems, A. S. Holehouse, V. Weinhardt, D. Kovacs, J. Van Lindt, C. Larabell, L. Van Den Bosch, R. Das, P. S. Tompa and R. V. Pappu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7889–7898.
41. P. R. Banerjee, A. N. Milin, M. M. Moosa, P. L. Onuchic and A. A. Deniz, Angew. Chem., Int. Ed., 2017, 56, 11354–11359.
42. T. Kaur, M. Raju, I. Alshareedah, R. B. Davis, D. A. Potoyan and P. R. Banerjee, Nat. Commun., 2021, 12, 1–16.
43. T. T. Nguyen and B. I. Shklovskii, J. Chem. Phys., 2001, 115, 7298–7308.
44. H. Kim, B.-j. Jeon, S. Kim, Y. Jho and D. S. Hwang, Polymers, 2019, 11, 691.
45. T. Lu, K. K. Nakashima and E. Spruijt, J. Phys. Chem. B, 2021, 125, 3080–3091.
46. S. Ali, M. Bleuel and V. M. Prabhu, ACS Macro Lett., 2019, 8, 289–293.
47. J. D. Tang, S. R. Caliari and K. J. Lampe, Biomacromolecules, 2018, 19, 3925–3935.
48. S. Adhikari, V. M. Prabhu and M. Muthukumar, Macromolecules, 2019, 52, 6998–7004.
49. E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 6476–6484.
50. K. J. Ellis and J. F. Morrison, Methods in enzymology, Elsevier, 1982, vol. 87, pp. 405–426.
51. Y. Lin, J. McCarty, J. N. Rauch, K. T. Delaney, K. S. Kosik, G. H. Fredrickson, J.-E. Shea and S. Han, eLife, 2019, 8, e42571.
52. H. M. Fares, A. E. Marras, J. M. Ting, M. V. Tirrell and C. D. Keating, Nat. Commun., 2020, 11, 1–13.
53. M. Rubinstein and R. H. Colby, Polymer physics, Oxford university press, New York, 2003.
54. J. S. Walker and C. A. Vause, Sci. Am., 1987, 256, 98–105.
55. A. Matsuyama and F. Tanaka, Phys. Rev. Lett., 1990, 65, 341.
56. E. E. Dormidontova, Macromolecules, 2002, 35, 987–1001.
57. A. Y. Grosberg, T. Nguyen and B. Shklovskii, Rev. Mod. Phys., 2002, 74, 329.
58. T. T. Nguyen, I. Rouzina and B. I. Shklovskii, J. Chem. Phys., 2000, 112, 2562–2568.
59. T. T. Nguyen and B. I. Shklovskii, J. Chem. Phys., 2001, 114, 5905–5916.
60. R. Zhang and B. Shklovskii, Phys. A, 2005, 352, 216–238.
61. W. C. Blocher and S. L. Perry, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1442.
62. S. L. Perry, Y. Li, D. Priftis, L. Leon and M. Tirrell, Polymers, 2014, 6, 1756–1772.
63. J. Fu and J. B. Schlenoff, J. Am. Chem. Soc., 2016, 138, 980–990.
64. A. N. Singh and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 1285–1292.
65. D. Priftis, N. Laugel and M. Tirrell, Langmuir, 2012, 28, 15947–15957.
66. P. Wang, J. L. Oscarson, S. E. Gillespie, R. M. Izatt and H. Cao, J. Solution Chem., 1996, 25, 243–266.
67. I. Alshareedah, M. M. Moosa, M. Pham, D. A. Potoyan and P. R. Banerjee, Nat. Commun., 2021, 12, 1–14.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01557e

‡ These authors contributed equally.

---