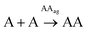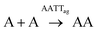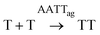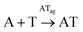Open Access Article
Open Access ArticleCollective adaptability in a replication network of minimal nucleobase sequences†
Sonia
Vela-Gallego
*a,
Zulay
Pardo-Botero
 b,
Cristian
Moya
b,
Cristian
Moya
 a and
Andrés
de la Escosura
a and
Andrés
de la Escosura
 *ac
*ac
aDepartment of Organic Chemistry, Universidad Autónoma de Madrid, Campus de Cantoblanco, 28049 Madrid, Spain. E-mail: andres.delaescosura@uam.es; sonia.vela@uam.es
bIMDEA Nanociencia, C/Faraday 7, 28049 Madrid, Spain
cInstitute for Advanced Research in Chemistry (IAdChem), Cantoblanco, 28049 Madrid, Spain
First published on 11th August 2022
Abstract
A major challenge for understanding the origins of life is to explore how replication networks can engage in an evolutionary process. Herein, we shed light on this problem by implementing a network constituted by two different types of extremely simple biological components: the amino acid cysteine and the canonical nucleobases adenine and thymine, connected through amide bonds to the cysteine amino group and oxidation of its thiol into three possible disulfides. Supramolecular and kinetic analyses revealed that both self- and mutual interactions between such dinucleobase compounds drive their assembly and replication pathways. Those pathways involving sequence complementarity led to enhanced replication rates, suggesting a potential bias for selection. The interplay of synergistic dynamics and competition between replicators was then simulated, under conditions that are not easily accessible with experiments, in an open reactor parametrized and constrained with the unprecedentedly complete experimental kinetic data obtained for our replicative network. Interestingly, the simulations show bistability, as a selective amplification of different species depending on the initial mixture composition. Overall, this network configuration can favor a collective adaptability to changes in the availability of feedstock molecules, with disulfide exchange reactions serving as 'wires' that connect the different individual auto- and cross-catalytic pathways.
Introduction
Research on life's origins constitutes a major multidisciplinary effort to unravel the physicochemical means by which living systems could emerge from non-living matter. Many questions remain open in the field, with implications that are both historical (how and where life originated), synthetic (how life can be synthesized from its basic molecular constituents), and conceptual (what essential features of living organisms allow characterization of their aliveness).1–5 Systems chemistry is proving to be useful in this respect, as it adopts a holistic view for the study of complex chemical systems, wherein dynamic out-of-equilibrium reaction and self-assembly processes govern the system's emergent behaviors.6–8 An important line in this area involves the development of chimeric systems that combine the properties of distinct biological building blocks, as a step towards replication, protometabolic networks and protocellular assemblies.9–13In the endeavour to mimic DNA's capacity for replication or, more generally, the capacity of living cells to self-reproduce, different forms of replication have been developed with both synthetic and biological molecules.14–18 The literature is rich in processes that display autocatalysis, either through the product's catalysis of its own formation,19cyclic autocatalysis,20,21 or in oscillatory reactions.22 Most of these autocatalytic transformations cannot be considered self-replication, since they lack the specificity required for information transfer at the molecular level.18 In the search for such specificity, template replication has been proven with different kinds of biopolymers and oligomers, including DNA,23,24 RNA,25,26 and oligopeptides,27,28 as well as with synthetic molecules not present in extant biology.29 However, this type of mechanism tends to halt the replication process due to an excessively strong binding (and therefore inhibition) of the template and product molecules, which handicaps efforts to achieve exponential product growth.
Network autocatalysis has been proposed as an alternative,30,31 with both theoretical and experimental models based on lipids,32,33 peptides,34,35 nucleic acids,36 and synthetic molecules.37 Autocatalysis in these networks is normally associated with self-assembly of the replicating species, most commonly into hybridized strands, fibers, micelles or vesicles, the latter being relevant to the formation of self-reproducing compartments.32,38 This type of replication was likely widespread in prebiotic scenarios, but, in order to favour the autonomy, robustness and evolutionary potential of replicator populations, they should have acquired additional capacities.39 For example, the possibility to perform out of equilibrium35,40–42 is critical for them to evolve. Acquiring catalytic properties could allow them to establish a supportive metabolism,43 while compartmentalization would benefit them at the population level, avoiding parasitic reactions and dilution effects.44 Finally, getting control on variability (through mutations) is a necessary capacity to evolve, with the mutations leading to traits that can be selected for. This can be achieved, among other possibilities, with nucleobase sequences.45 In this regard, herein we try to address the questions of how simple can be their constituent monomers, and what is the minimal sequence length that can drive the emergence of replication networks.23,45,46
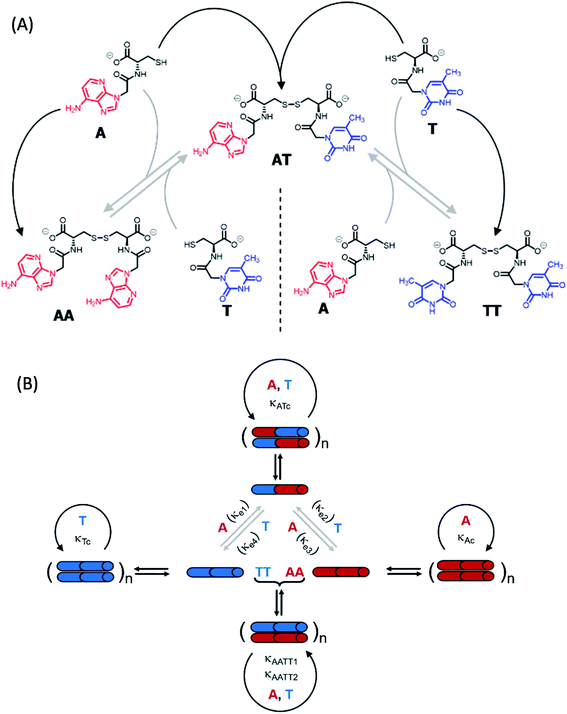
To shed light on those issues, we describe a new family of very simple exponential replicators emerging from monomers that display adenine or thymine (A and T), connected through amide bonds to the amino groups of cysteine (Fig. 1A). The role of the amino acid in these molecules is to link the nucleobases in a sequence, through oxidation of its reactive thiol into dynamic disulfide bonds. Supramolecular studies showed that such short nucleobase sequences are still capable of controlling the self-assembly of the three formed species (AA, TT and AT), thus determining their replication efficiency. In-depth kinetic experiments and simulations were used to study how the resulting aggregates affect the irreversible auto- and cross-catalytic oxidation pathways of A and T, and the concomitant reversible disulfide exchange reactions (Fig. 1B). In spite of the low complexity of the studied replicators, both in terms of the monomers structure (much simpler than that of ribonucleotides) and of the sequence length (dimers), complementarity of nucleobases enhances self-assembly and so the replication rate of the corresponding auto- and cross-catalytic pathways (AT and AA/TT, respectively), suggesting an adaptive potential that involves the interplay of different collective and competitive dynamic interactions between them.
Results and discussion
Synthesis and self-assembly of the network components
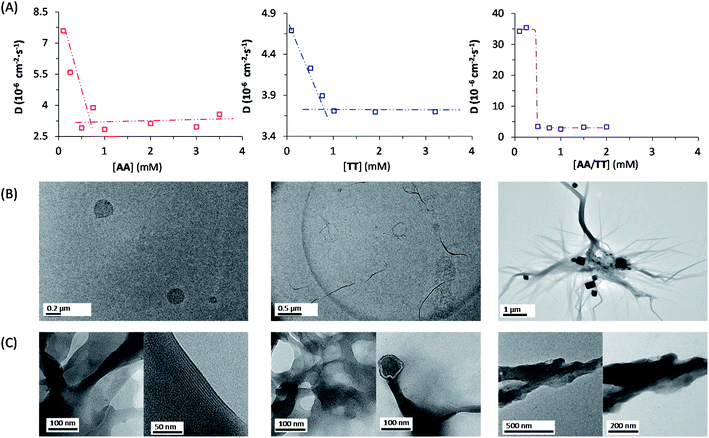
The network building blocks (A and T) and the corresponding disulfide homodimers were synthesized and characterized as described in the (ESI, Scheme S1†). 1HNMR revealed a slow oxidation into disulfides in DMSO (Fig. S1†), halted oxidation in acidic water (Fig. S2,† bottom), and fast oxidation in aqueous basic medium (pH 11; see Fig. S2,† top). One of the requisites to establish base pairing interactions between adenine and thymine, however, is that they stay non-ionized. In this respect, pH titrations monitored by 1H-NMR confirmed pKa values of 4.14 ± 0.02 for the protonated adenine moiety in AA (Fig. S3A†), and of 9.62 ± 0.03 for the dissociation of the thymine imide NH in TT (Fig. S3B†). It can be assumed that similar pKa values are applicable to AT, which is generated together with the homodimers when the oxidation reaction occurs from a mixture of A and T. On these bases, and considering that a slightly basic pH is optimum for disulfide formation/exchange,34 all the subsequent self-assembly and replication experiments were run in 50 mM borate buffer at pH 8.2. Under these conditions, atmospheric oxygen is the ultimate oxidant responsible for the transformation of thiol into disulfide derivatives.The existence of aggregation in such conditions was first demonstrated through diffusion-ordered spectroscopy (DOSY) for samples containing AA, TT or an equimolar mixture of AA/TT at different concentrations (from 0.1 to 4 mM). The diffusion coefficient (D) was calculated for all samples, through monitoring of the monoexponential attenuation of NMR signals during a pulsed field gradient experiment, followed by plotting the obtained D values versus concentration (Fig. 2A–C) to determine the critical aggregation concentration (cac). Datasets with two clearly differentiated linear regions were obtained for AA and TT, with the one above the cac showing a larger and constant D value, indicative of the presence of aggregates. The intersection between the two lines pointed to specific cac values of 0.51 and 0.9 mM, respectively. For the AA/TT mixture, a sharp transition between the aggregated and non-aggregated states was obtained. The high values of D observed at the low extreme of the concentrations range, in comparison to samples with an equivalent concentration of AA or TT, is likely related to the lower absolute concentration of each of the individual components in the mixture (half concentration with respect to the pure samples), which leaves them below their individual cac values. For the mixed assembly, in turn, a cac of 0.47 mM was obtained, by fitting the data with a Boltzmann equation (R2 = 0.9993) to detect the slope changing point (Section 3 in the ESI†). Overall, these supramolecular studies suggest that nucleobase sequence complementarity induces a stronger (as indicated by TEM, see below) and cooperative (as indicated by DOSY) self-assembly.
To assess the morphology of the aggregates, TEM studies were conducted at two different disulfide concentrations: 1 and 2 mM (Fig. 2B and C, respectively). At 1 mM, the low density of objects over the grid indicated minor aggregation of AA and TT, showing spherical assemblies for the former (Fig. 2B left/S5A†), yet they were very exceptional (impossible to be characterized by dynamic light scattering, DLS) and may not be representative of the main self-assembly pathway, and isolated fibrils for the latter (Fig. 2B middle/S6A†). Despite their low abundance, the presence of sulfur detected by energy dispersive X-ray spectroscopy (EDX) confirmed that all mentioned structures were formed by the corresponding disulfide compounds. For the AA/TT mixture, intertwined fiber assemblies were observed over the whole grid (Fig. 2B right/S7A†), in a significantly higher abundance than for AA or TT alone. This points to the importance of complementary nucleobase pairing to induce aggregation in the mixture. At the high concentration, aggregation was much more prominent (Fig. 2C) and resulted in lamellar structures for all cases, probably as a result of the hierarchical assembly of fibers into sheets, which could be enhanced by drying effects during the TEM samples preparation. The distance between adjacent sheets could be clearly determined in areas where the lamellar arrangement was perpendicular with respect to the grid surface, yielding similar values (∼4 nm) for AA and TT (Fig. S5B/S6B bottom†). For AA/TT, the stronger aggregation gave rise to thicker stacks of sheets (Fig. 2B right/S7B†) that did not permit estimation of the interlamellar distance. In any case, the formation of different assemblies for the three systems, including fibers and lamellar structures depending on concentration, points to a complex assembly landscape, with contribution from hydrogen bonding interactions, nucleobase π–π stacking and hydrophobic effects. The involved self-assembly mechanisms will be examined in-depth in subsequent studies but, since previous work has demonstrated the capacity of fibrillar and sheet assemblies to facilitate replication processes,34,47 we assume these to be the catalytically active ones also in the present case.
Replication experiments
The initial replication experiments were performed with only one monomer, either A or T at 4 mM concentration, in a reactor that is open to the air, which allows replenishing oxygen as the oxidant.‡ The reaction kinetics were monitored through reverse phase high-performance liquid chromatography (HPLC, see experimental section and Fig. S8–S11†), coupled to electrospray ionization mass spectrometry (ESI-MS) for identification of species. For this purpose, aliquots were taken at different reaction times and diluted into 1% aq. TFA, to quench both the thiols oxidation and disulfide exchange processes. Fig. S8/S9† show for instance the gradual decay of monomer and growth of dimer elution peak areas for the non-templated oxidation reactions. Calibration curves were performed for A, T, AA and TT in order to quantify their molar concentrations in each aliquot (Fig. S12–S15†). The kinetic profiles, plotted from the obtained concentrations at different reaction times, showed typical features of autocatalysis for both AA and TT (Fig. 3A and B): an initial slow growth of product (induction period) followed by a phase of faster growth (autocatalysis) until full conversion of monomer into dimer. This effect was not observed in control experiments where the oxidation of non-functionalized cysteine or N-acetylcysteine was monitored, for which the consumption of thiol was much slower (only 54% conversion after 500 h), and there was not the exponential acceleration of the reaction characteristic of autocatalysis (Fig. S16†). Importantly, for the nucleobase-containing systems, the change in curve slope was observed at a product concentration that matches its cac value, as determined by DOSY, proving that there is no autocatalysis in the absence of aggregates (i.e., below the cac). To confirm the products' autocatalytic nature, seeded experiments with 30% of AA or TT were conducted, maintaining the total concentration of starting materials in the same range as in the non-templated reactions. In both cases, a shortening of the induction period and an overall decrease in the reaction time was observed (Fig. 3C and D; while Fig. S17A and S17B† shows the direct comparison of seeded and non-seeded experiments), indicating that they actually contribute to increase the reaction rate. This effect was less prominent for TT, probably due to its lower tendency to aggregate (higher cac).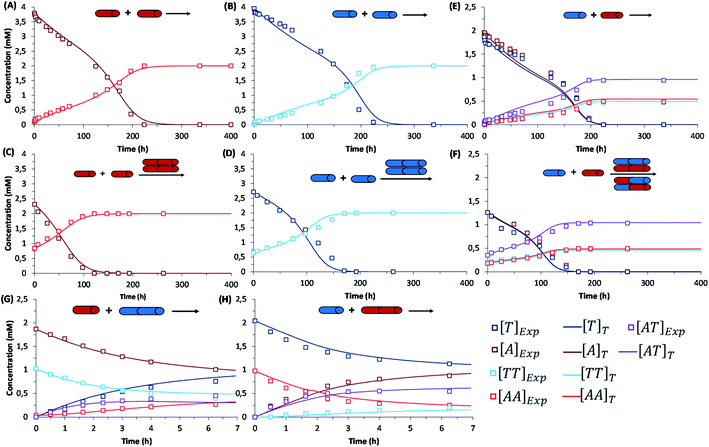 | ||
| Fig. 3 Kinetic profiles corresponding to: (first row) the autocatalytic formation of AA (A), TT (B), and the mixture of possible replicators AA/TT/AT (E); (second row) seeded experiments for the autocatalytic formation of AA (C), TT (D), and AA/TT/AT (F); (third row) disulfide exchange reactions (up to 7 h) between AA and T (G) or TT and A (H). Each panel shows the evolution of all involved species over time through experimental data (square data points) and fit curves (marked as []T in the figure legend), while the set of rate equations used for fitting are depicted in Table 1. In the templated reactions (C, D, F), the total concentration of starting materials was maintained in the same range as in the non-templated ones (A, B, E), with minor experimental deviations that are difficult to avoid but are considered in the mathematical analysis. Importantly, the non-seeded experiments were repeated three times, while seeded experiments and disulfide exchange reactions were repeated twice (Fig. S17–S20†). The treatment of fitting errors with such repeats is shown in Section 7 of the ESI.† | ||
Similar results were obtained when conducting the reactions from a mixture of A and T (2 mM each). Fig. 3E depicts the kinetic profiles obtained from HPLC monitoring over time (Fig. S10†), revealing the characteristic features of replication kinetics for both AA, TT and AT. Experiments seeded with 20% of a previously finished reaction resulted in a shortening of the induction period for the three replicating species (Fig. 3F, S17C and S17D†). However, the scenario becomes significantly more complex when the two nucleobases are present, as disulfide exchange reactions can also occur. To study the role of these exchange processes in the global network kinetics, two different reactions were performed (4 mM T + 2 mM AA and 4 mM A + 2 mM TT) with HPLC monitoring (Fig. S11†). In the obtained kinetic curves, two stages could be distinguished, the first one corresponding to a preeminent role of disulfide exchange during the first 7 h of reaction (Fig. 3G and H). After 7 h, the reaction stabilized for a short period and then continued the oxidation of thiol groups into disulfides, until complete consumption of free thiol monomers in the medium.
Kinetic analyses
The above replication data were used to analyse the contribution of all involved processes in the global network kinetics. Two different reactions were initially considered for the formation of each disulfide homodimer: the non-catalysed (R-A1 and R-T1) and the autocatalytic oxidation (R-A2 and R-T2) of the corresponding monomeric thiol (Table 1, boxes 1 and 2). In the reaction schemes, AAag and TTag refer to the self-assembled products, which emerge from the aggregation processes R-A3 and R-T3 and are in equilibrium with their constituent disulfide dimers, as it has been revealed by DOSY experiments. For kinetic calculations, hence, the concentration of aggregated replicator is needed at any given time. According to Chen et al.,48 the AAag and TTag concentrations are given by equation Eq-S1 (Section 6.1 in the ESI†), in which the total concentration of aggregating compound (CT) can be expressed as a function of C1 (the concentration of molecularly dissolved compound), ρ (a parameter related to the aggregation mechanism) and Keq (the equilibrium constant of the aggregation process). This equation can become complex to solve, but the problem is approachable considering that when CT is below 1/Keq, most molecules are in the monomeric form, whereas molecules aggregate rapidly if CT exceeds that value. In Fig. S21,† for example, when the analytical solutions of Eq-S1† for different values of ρ are compared to the proposed simplification, the outcome differences are negligible. Consequently, in the kinetic model below, Eq-S1† is simplified for all the different aggregation processes assuming that 1/Keq = cac (an assumption that is valid for any possible aggregation mechanism with ρ ≤ 1, see Fig. S21†), the cac being determined from the point of slope change in the kinetic curves (and compared with that obtained experimentally through DOSY).Despite calculating the equilibrium constants of the studied dinucleobase compounds, modelling the kinetics of the replication network constituted by AA, TT, AT and their thiol precursors, required addressing the rate equations for all the oxidation and thiol-disulfide exchange processes involved. The mechanistic and kinetic details of thiol oxidations and disulfide exchange are complex, however, as they depend on the employed oxidant, pH, the presence of metallic ion salts, etc. While the latter are always first-order on both thiol and disulfide, the former can vary with the conditions and mechanism, usually being first- or even lower-order with respect to the thiol.49,50 Since the mechanism of auto- and cross-catalysis exerted by the dinucleobase assemblies was not known, equations with different orders with respect to both the monomeric thiols and the disulfide aggregates were initially considered. Although in simpler systems, i.e., with reactions that occur in an isolated parallel fashion, the orders would be determined for each isolated process, the complexity of the network under study does not make plausible to probe the different rate equations individually, not even recommendable for predicting its collective behaviour, as there are at any moment various reactions occurring simultaneously. Instead, there are other approaches, involving fitting and simulating experimental data globally, which are being applied in systems chemistry for the study of complex autocatalytic networks.35,37,43,45 In the present case, a method for global kinetic analysis through fitting of the experimental data into different possible rate equations was developed (Sections 6 and 7 in the ESI†). This method is not only based on selecting the lowest mean absolute percentage errors and R2 values of the corresponding fittings (see Tables S1–S3†), but also on plotting dispersion graphs for the different fits that clearly point to specific rate equations and rule out the others (i.e., panel H in Fig. S22 and S23†). Moreover, it is strongly supported on an experimental basis, having employed data from up to five replication experiments (around 270 data points per dispersion graph) for each of the studied pathways (i.e., the autocatalysis of AA or TT, and the auto- and cross-catalytic amplification of AT and AA/TT, respectively), and enables addressing the complexity of the described replication network and other possible future systems.
That type of analysis was first applied to the case of the single-nucleobase replicators, that is, to the autocatalysis of AA or TT. The different rate equations for non-catalyzed (Eq-A1 and Eq-T1 represent the fittest ones according to the dispersion graphs in Fig. S22 and S23,† respectively) and autocatalytic regimes (Eq-A2 and Eq-T2, selected in the same manner) were defined in a MATLAB program (Table 1, boxes 1 and 2). The equilibrium constants of aggregate formation were considered through equations Eq-A3 and Eq-T3 (see above). The fitting curves can be seen in Fig. 3A–D (with R2 above 0.99 in all cases), and correspond to a global order of three for the autocatalytic stage (Eq-A2 and Eq-T2) and two with respect to the aggregated replicator. For a complete statistical treatment of fitting errors, see Section 7 of the ESI.† The fact that the best fittings were obtained for a reaction order of two with respect to the replicating species (therefore higher than one) points to an exponential growth.34,51 This was confirmed by plotting the reaction rate versus the replicator concentration, which shows the characteristic behaviour of exponential replicators (see an example for AA in Fig. S24†), as previously described by von Kiedrowski.51 The orders obtained in the rate equations Eq-A2 and Eq-T2 actually imply that in the ‘catalytic’ hybrid assemblies of monomeric thiol and disulfide dimer, the required ratio between both for the monomer to get activated towards oxidation is of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Importantly, in this replication model we are assuming that it occurs in a regime where aggregates break due to stirring, like others have shown before,34,40–42 therefore increasing the number of actives sites also in an exponential way. Further studies will be devoted to propose a solid mechanistic scheme of this replication process.
2. Importantly, in this replication model we are assuming that it occurs in a regime where aggregates break due to stirring, like others have shown before,34,40–42 therefore increasing the number of actives sites also in an exponential way. Further studies will be devoted to propose a solid mechanistic scheme of this replication process.
In any case, it is worth mentioning that the kinetic constants for the catalyzed reactions were about one order of magnitude greater than the non-catalyzed ones.§ The calculated equilibrium constants (KAAag = 1.9 mM−1 and KTTag = 1.25 mM−1), in turn, led to cac values of 0.53 and 0.8 mM, respectively, which are really close to those obtained from DOSY experiments, confirming the quality of the kinetic fits.
A similar procedure was applied for calculation of disulfide exchange kinetic constants, considering four possible reactions/equations (R-E1 to R-E4/Eq-E1 to Eq-E4 – Table 1, box 3; fitting curves in Fig. 3G and H). Importantly, the observed rates for disulfide exchange are about one order of magnitude slower than expected (they usually take place in the range from seconds to minutes).49 This fact can be attributed to the effect of aggregation, which reduces the amount of available disulfide for the reaction to take place. The constants resulting upon fitting (ke1, ke2, ke3, ke4) are one order of magnitude larger than those for the autocatalytic oxidation of monomeric thiols, which makes their reaction rates comparable.
Concerning the analysis of replication from mixtures of both nucleobase monomers, the landscape of non-covalent assembly pathways is more complex than for single replicators. In addition to the self-assembly of AA and TT, two other aggregate types must be considered, resulting from either the complementary interaction between AA and TT (AATTag) or from self-pairing of AT (i.e., ATag). The different aggregation of ATag, with respect to AAag, TTg or AATTag, is supported by previous findings for related nucleopeptide replicators, which show that homodinucleobase motifs behave differently as a minimal unit for recognition and replication, compared to heterodinucleobase ones.45 Consequently, these aggregates open the possibility to have auto- and cross-catalytic reactions, as AATTag can aid in reactions producing AA and TT (R-A4 and R-T4, respectively – Table 1, box 4), and ATag can assist in its own formation (R-AT2 – Table 1, box 5). For mathematical fitting of these processes (Fig. 3E and F), all constants concerning the non-catalyzed and autocatalytic formation of TT and AA, the disulfide exchange reactions, the aggregation constants of AA and TT and the order of those reactions with respect to aggregates in the autocatalytic regime were fixed as previously calculated. An additional requirement for the fitting was to assume that the two kinetic constants involved in the cross-catalysis of AA and TT (KAATT1 and KAATT2) must be identical.
This global analysis of the network kinetics revealed interesting aspects of its behaviour. While the uncatalyzed oxidation reactions have very similar values for the three possible disulfides, the auto- and cross-catalytic reactions were ∼4–5× faster when there is complementarity between nucleobase sequences (i.e. for AT and AA/TT) than when there is not (i.e., for AA or TT). Indeed, according to the calculated Keq values for the aggregation of both AATTag and ATag (∼2.1 mM−1), their cac would correspond to 0.47 mM (total concentration of disulfides), in agreement with the DOSY data. These minimal nucleobase sequences therefore seem to enhance their replication through complementary base pairing.
Interplay between synergistic/self-replication pathways
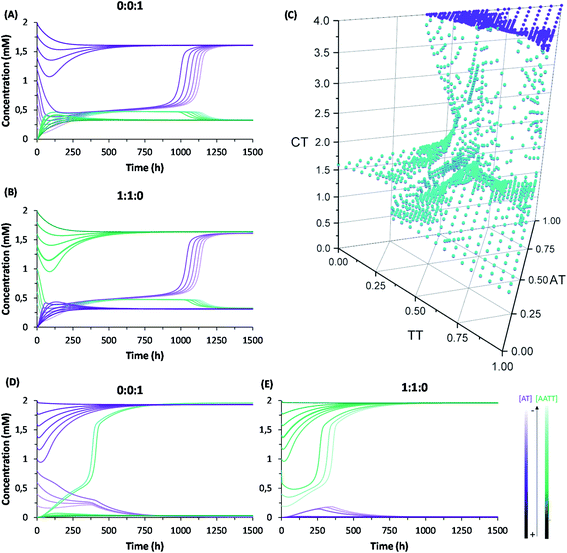
A complete kinetic assessment like the one presented herein, involving all the processes within a complex replication network with up to 4 different interconnected auto- and cross-catalytic pathways, is unprecedented in systems chemistry, and shall be crucial to predict the collective behaviour of this type of complex systems.52 For this purpose, it was decided to run model simulations, parametrized and constrained by the obtained experimental data, allowing to explore biological concepts (e.g., global adaptability, bistability, etc.) in conditions that are not easily accessible from an experimental point of view, which will be helpful to design new out-of-equilibrium experiments in future works. According to the above kinetic analysis, the network topology presents two dominant competing pathways: the autocatalytic replication of AT (Fig. 1B, top cycle); and the synergistic assembly of AA/TT, which results in cross-catalysis towards their common formation (Fig. 1B, bottom cycle). In a closed reactor, fast disulfide exchange contributes to balance both pathways, leading to a statistical mixture of the three replicating species (see Fig. 3E and F). In contrast, in an open reactor, the asymmetry between both competing pathways (see Table 1, kinetic constants in boxes 4 and 5), together with their possible interconversion through exchange reactions (Table 1, box 3), may lead to adaptive behaviors.53 To predict the evolutionary potential of this network topology in open environments, a continuous perfect mixing reactor (Section 6 in the ESI†) was modelled using the previously determined kinetic data. In the studied configuration, the 20 mL reactor could be initially loaded with any possible combination of the three species and continuously fed with monomers A and T (4 mM) through two different input streams of 1 μL min−1, while maintaining a constant reactor volume through the extraction of an equivalent output current. At these conditions the residence time of the replicating species in the reactor is 170 h, which ensures that a stationary state is reached and that they are not washed away by the continuous flow. Another advantage that this in silico reactor offered was the possibility to artificially freeze disulfide exchange reactions by drastically reducing their kinetic constants, allowing to assess the importance of disulfide exchange in the network collective dynamics (see below).When starting from an empty reactor ([replicators]o = 0), the system evolved as expected into a steady state dominated by AT (SSAT), where [AT] = 1.61 mM and [AA/TT] = 0.32 mM, the latter meaning total disulfide concentration (Fig. 4A, lightest colour curves). A significant decrease in the time needed to reach SSAT was observed when loading the reactor with increasing initial AT concentrations (Fig. 4A). SSAT was also obtained when the reactor was filled with AA/TT below a threshold concentration (see below). When [AA/TT]o was above that threshold, however, a new steady state appeared (SSAA/TT) where AA/TT were the dominant species ([AA/TT] = 1.63 mM) and AT decreased in concentration ([AT] = 0.31 mM) (Fig. 4B and S25†). A range of initial proportions of AA, TT and AT, and of total initial disulfide concentration (from 0 to 4 mM), was then tested to determine which steady state would be reached in each case. The result was a 3D surface (Fig. 4C), built from data points for which the resulting steady state changes, marking the boundary between initial conditions that favour SSAT (below the surface) or SSAA/TT (above the surface). In the graph, three main regions can be distinguished. First, AT always gets amplified far below a total initial concentration of 1.2 mM, and when the initial AT proportion is greater than 0.7. The amplification of AA/TT occurs, on the other hand, in points far above the surface, at total concentrations higher than 1.4 mM and initial proportions of AT under 0.6. Finally, in the middle region, close to the surface, small changes in the initial total concentration or in the ratios of the replicating sequences produce jumps from one steady state to another, which suggests a high network adaptability.
The capacity of a dynamic system to reach two different steady states depending on the initial conditions is called bistability, and in the present case it seems to be related to their possible interconversion through disulfide exchange. To test this possibility, the network behaviour was simulated in a hypothetical scenario where the exchange reactions were kinetically frozen, artificially reducing the values of their kinetic constants by six orders of magnitude compared to the experimental data (see Table S4†). In that situation, the dominant species in the reached steady state is AA/TT, unless the concentration of AT is initially much higher than that of the other sequences (Fig. 4D and E). In addition, the concentration of the ‘losing’ replicative system drops almost to extinction. The reason for this is that, in the absence of exchange reactions, the dominant catalytic species gets amplified sufficiently quickly to consume all the substrates fed into the reactor. This simulation thus proves the importance of disulfide exchange as wiring reactions that connect the different auto- and cross-catalytic pathways, endowing the whole replication network with a collectively better adaptive potential, as it can switch from one replicator to the other if the conditions are favourable.
Conclusions
The results of this work underscore the likelihood of replication networks emerging in conditions and from building blocks with reasonable prebiotic plausibility. The replicating species are built from the amino acid cysteine¶ and two canonical nucleobases, which have been reported in Miller-type experiments,54 Strecker-derived chemistry55 and HCN/cyanoacetylene oligomerization reactions.56 Although for practical reasons our synthesis of A and T was performed following standard organic synthesis techniques, the chemistry of amide and disulfide bond formation/exchange has been extensively studied in prebiotic contexts.2 More importantly, the molecular complexity of the replicators AA, TT and AT is significantly less than that of other different replicator families reported to date, suggesting that the structural requirements for chemical evolution to step into replicating species was probably not so high. The present cysteine-based derivatives do not need an oligopeptide or lipid chain to drive their self-assembly and replication processes. On the other hand, the smallest nucleic acid template replicators previously described required a minimum sequence of 6 nucleotides.15 Importantly, the self-assembly of AA, TT and AT is likely promoted by a combination of H-bond interactions between nucleobases, π–π stacking and hydrophobic effects. Building on such supramolecular capacities, the network described herein presents a collective behaviour that can provide significant adaptability between the individual synergistic and ‘selfish’ replication pathways, aided by exchange reactions that allow interconversion between the different replicating species.Data availability
All data are available in the manuscript and in the ESI.† The raw data directly saved from the instruments and simulations of this study are available from the corresponding authors upon reasonable request.Author contributions
S. V. G. performed the experiments, Z. P. B. contributed to the DOSY analyses, C. M. contributed to the computational kinetic analyses, A. d. l. E. conceived the project, S. V. G. and A. d. l. E. designed and analysed the experiments, and wrote and edited the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was supported by the H2020 FET-Open (A. d. l. E. and G. A.; CLASSY project, Grant Agreement No 862081) and the Spanish Ministry of Economy and Competitivity (A. d. l. E.; MINECO: CTQ-2017-89539-P, PID2020-119306GB-100 and EUIN2017-87022). We would like to acknowledge Dr Ana Pizarro for her advice in the NMR determination of the nucleobase pKa values in compounds AA and TT, and Dr Francisco Tato for initial tests on HPLC separations. The professional editing service NB Revisions was used for technical preparation of the text prior to submission.Notes and references
- L. Cronin and S. I. Walker, Science, 2016, 352, 1174 CrossRef CAS PubMed.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285 CrossRef CAS PubMed.
- J. W. Szostak, Angew. Chem., Int. Ed., 2017, 56, 11037 CrossRef CAS PubMed.
- J. D. Sutherland, Nat. Rev. Chem., 2017, 1, 0012 CrossRef CAS.
- R. Krishnamurthy and N. V. Hud, Chem. Rev., 2020, 120, 4613 CrossRef CAS PubMed.
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Chem. Soc. Rev., 2017, 46, 2543 RSC.
- Y. Ura, J. M. Beierle, L. J. Leman, L. E. Orgel and M. R. Ghadiri, Science, 2009, 325, 73 CrossRef CAS PubMed.
- D. Carbajo, Y. Pérez, J. Bujons and I. Alfonso, Angew. Chem., Int. Ed., 2020, 59, 17202 CrossRef CAS PubMed.
- S. Mann, Acc. Chem. Res., 2012, 45, 2131 CrossRef CAS PubMed.
- C. Gibard, S. Bhowmik, M. Karki, E. K. Kim and R. Krishnamurthy, Nat. Chem., 2018, 10, 212 CrossRef CAS PubMed.
- C. Bonfio, E. Godino, M. Corsini, F. Fabrizi de Biani, G. Guella and S. S. Mansy, Nat. Catal., 2018, 1, 616 CrossRef CAS.
- S. Morales-Reina, C. Giri, M. Leclercq, S. Vela-Gallego, I. de la Torre, J. R. Castón, M. Surin and A. de la Escosura, Chem.–Eur. J., 2020, 26, 1082 CrossRef CAS PubMed.
- M. Frenkel-Pinter, J. W. Haynes, A. M. Mohyeldin, M. C, A. B. Sargon, A. S. Petrov, R. Krishnamurthy, N. V. Hud, L. D. Williams and L. J. Leman, Nat. Commun., 2020, 11, 3137 CrossRef CAS PubMed.
- N. Paul and G. F. Joyce, Curr. Open Chem. Biol., 2004, 8, 634 CrossRef CAS PubMed.
- V. Patzke and G. v. Kiedrowski, Arkivoc, 2007, 2007, 293 Search PubMed.
- A. J. Bissette and S. P. Fletcher, Angew. Chem., Int. Ed., 2013, 52, 12800 CrossRef CAS PubMed.
- T. Kosikova and D. Philp, Chem. Soc. Rev., 2017, 46, 7274 RSC.
- P. Adamski, M. Eleveld, A. Sood, Á. Kun, A. Szilágyi, T. Czárán, E. Szathmáry and S. Otto, Nat. Rev. Chem., 2020, 4, 386 CrossRef.
- K. Soai, T. Shibata, H. Morioka and K. Choji, Nature, 1995, 378, 767 CrossRef CAS.
- R. Breslow, Tetrahedron Lett., 1959, 1, 22 CrossRef.
- J. E. Hein and D. G. Blackmond, Acc. Chem. Res., 2012, 45, 2045 CrossRef CAS PubMed.
- I. R. Epstein and K. Showalter, J. Phys. Chem., 1996, 100, 13132 CrossRef CAS.
- G. von Kiedrowski, Angew. Chem., Int. Ed., 1986, 25, 932 CrossRef.
- M. Kreysing, L. Keil, S. Lanzmich and D. Braun, Nat. Chem., 2015, 7, 203 CrossRef CAS PubMed.
- E. J. Hayden and N. Lehman, Chem. Biol., 2006, 13, 909 CrossRef CAS PubMed.
- T. A. Lincoln and G. F. Joyce, Science, 2009, 323, 1229 CrossRef CAS PubMed.
- D. H. Lee, J. R. Granja, J. A. Martinez, K. Severin and M. R. Ghadiri, Nature, 1996, 382, 525 CrossRef CAS PubMed.
- R. Mukherjee, R. Cohen-Luria, N. Wagner and G. Ashkenasy, Angew. Chem., Int. Ed., 2015, 54, 12452 CrossRef CAS PubMed.
- T. Tjivikua, P. Ballester and J. Rebek, J. Am. Chem. Soc., 1990, 112, 1249 CrossRef CAS.
- S. A. Kauffman, J. Theor. Biol., 1986, 119, 1 CrossRef CAS PubMed.
- V. Vasas, C. Fernando, M. Santos, S. Kauffman and E. Szathmáry, Biol. Direct, 2012, 7, 1 CrossRef PubMed.
- D. Segré, D. Ben-Eli, D. W. Deamer and D. Lancet, Orig. Life Evol. Biosph., 2001, 31, 119 CrossRef PubMed.
- I. Colomer, A. Borissov and S. P. Fletcher, Nat. Commun., 2020, 11, 176 CrossRef CAS PubMed.
- M. Colomb-Delsuc, E. Mattia, J. W. Sadownik and S. Otto, Nat. Commun., 2015, 6, 7427 CrossRef CAS PubMed.
- I. Maity, N. Wagner, R. Mukherjee, D. Dev, E. Peacock-Lopez, R. Cohen-Luria and G. Ashkenasy, Nat. Commun., 2019, 10, 4636 CrossRef PubMed.
- S. Arsène, S. Ameta, N. Lehman, A. D. Griffiths and P. Nghe, Nucleic Acids Res., 2018, 46, 9660 CrossRef PubMed.
- S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Nature, 2016, 537, 656 CrossRef CAS PubMed.
- P. Walde, R. Wick, M. Fresta, A. Mangone and P. L. Luisi, J. Am. Chem. Soc., 1994, 116, 11649 CrossRef CAS.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Open Biol., 2017, 7, 170050 CrossRef PubMed.
- B. Liu, J. Wu, M. Geerts, O. Markovitch, C. G. Pappas, K. Liu and S. Otto, Angew. Chem., Int. Ed., 2022, e202117605 CAS , early access..
- G. Monreal Santiago, K. Liu, W. R. Browne and S. Otto, Nat. Chem., 2020, 12, 603 CrossRef CAS PubMed.
- S. Yang, G. Schaeffer, E. Mattia, O. Markovitch, K. Liu, A. S. Hussain, J. Ottelé, A. Sood and S. Otto, Angew. Chem., Int. Ed., 2021, 60, 11344 CrossRef CAS PubMed.
- X. Miao, A. Paikar, B. Lerner, Y. Diskin-Posner, G. Shmul and S. N. Semenov, Angew. Chem., Int. Ed., 2021, 60, 20366 CrossRef CAS PubMed.
- S. Matsumura, Á. Kun, M. Ryckelynck, F. Coldren, A. Szilágyi, F. Jossinet, C. Rick, P. Nghe, E. Szathmáry and A. D. Griffiths, Science, 2016, 354, 1293 CrossRef CAS PubMed.
- A. K. Bandela, N. Wagner, H. Sadihov, S. Morales-Reina, A. Chotera-Ouda, K. Basu, R. Cohen-Luria, A. de la Escosura and G. Ashkenasy, Proc. Natl. Acad. Sci. U.S.A., 2021, 118, e2015285118 CrossRef CAS PubMed.
- B. Liu, C. G. Pappas, J. Ottele, G. Shaeffer, C. Jurissek, P. F. Pieters, M. Altay, N. Maric, M. C. A. Stuart and S. Otto, J. Am. Chem. Soc., 2020, 142, 4184 CrossRef CAS PubMed.
- B. Rubinov, N. Wagner, M. Matmor, O. Regev, N. Ashkenasy and G. Ashkenasy, ACS Nano, 2012, 6, 7893 CrossRef CAS PubMed.
- Z. Chen, A. Lohr, C. R. Saha-Möller and F. Würthner, Chem. Soc. Rev., 2009, 38, 564 RSC.
- M. Trujillo, B. Alvarez and R. Radi, Free Radic. Res., 2016, 50, 150 CrossRef CAS PubMed.
- P. Nagy, Antioxid. Redox Signaling, 2013, 18, 1623 CrossRef CAS PubMed.
- G. von Kiedrowski, in Minimal Replicator Theory I: Parabolic Versus Exponential Growth, 1993 Search PubMed.
- N. Lauber, C. Flamm and K. Ruiz-Mirazo, BioEssays, 2021, 43, 2100103 CrossRef CAS PubMed.
- N. Wagner and G. Ashkenasy, Nat. Chem., 2019, 11, 681 CrossRef CAS PubMed.
- E. T. Parker, H. J. Cleaves, J. P. Dworkin, D. P. Glavin, M. Callahan, A. Aubrey, A. Lazcano and J. L. Bada, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 5526 CrossRef CAS PubMed.
- C. S. Foden, S. Islam, C. Fernández-García, L. Maugeri, T. D. Sheppard and M. W. Powner, Science, 2020, 370, 865 CrossRef CAS PubMed.
- S. Islam and M. W. Powner, Chem, 2017, 2, 470 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Procedures for the synthesis and characterization of the network components, additional data, supramolecular studies and in depth discussion of the kinetic model and simulations. See https://doi.org/10.1039/d2sc02419e |
| ‡ Considering the solubility of oxygen at rt (8 mg L−1), a concentration of 0.25 mM is assumed. However, the oxidation reaction is slow, and the reactor is open to the air, which allows dissolving more oxygen while the reaction keeps progressing. |
| § All the kinetic constants obtained with this model are apparent constants, as they involve the oxygen concentration in solution. |
| ¶ It must be noticed that the prebiotic formation of cysteine probably occurred rather late in chemical evolution. |
| This journal is © The Royal Society of Chemistry 2022 |