Short and long-range electron transfer compete to determine free-charge yield in organic semiconductors†
Joshua M.
Carr
 a,
Taylor G.
Allen
a,
Taylor G.
Allen
 b,
Bryon W.
Larson
b,
Bryon W.
Larson
 b,
Iryna G.
Davydenko
c,
Raghunath R.
Dasari
b,
Iryna G.
Davydenko
c,
Raghunath R.
Dasari
 c,
Stephen
Barlow
c,
Stephen
Barlow
 bcd,
Seth R.
Marder
bcd,
Seth R.
Marder
 bcdef,
Obadiah G.
Reid
bcdef,
Obadiah G.
Reid
 *bd and
Garry
Rumbles
*bd and
Garry
Rumbles
 *bde
*bde
aUniversity of Colorado Boulder, Materials Science & Engineering Program, Boulder, CO 80303, USA
bNational Renewable Energy Laboratory, Chemistry and Nanoscience Center, Golden, CO 80401, USA. E-mail: Obadiah.reid@colorado.edu; Garry.rumbles@nrel.gov
cGeorgia Institute of Technology, School of Chemistry and Biochemistry, Atlanta, GA 30332, USA
dUniversity of Colorado Boulder, Renewable and Sustainable Energy Institute, Boulder, CO 80303, USA
eUniversity of Colorado Boulder, Department of Chemistry, Boulder, CO 80303, USA
fUniversity of Colorado Boulder, Department of Chemical and Biological Engineering, Boulder, CO 80303, USA
First published on 15th November 2021
Abstract
Understanding how Frenkel excitons efficiently split to form free-charges in low-dielectric constant organic semiconductors has proven challenging, with many different models proposed in recent years to explain this phenomenon. Here, we present evidence that a simple model invoking a modest amount of charge delocalization, a sum over the available microstates, and the Marcus rate constant for electron transfer can explain many seemingly contradictory phenomena reported in the literature. We use an electron-accepting fullerene host matrix dilutely sensitized with a series of electron donor molecules to test this hypothesis. The donor series enables us to tune the driving force for photoinduced electron transfer over a range of 0.7 eV, mapping out normal, optimal, and inverted regimes for free-charge generation efficiency, as measured by time-resolved microwave conductivity. However, the photoluminescence of the donor is rapidly quenched as the driving force increases, with no evidence for inverted behavior, nor the linear relationship between photoluminescence quenching and charge-generation efficiency one would expect in the absence of additional competing loss pathways. This behavior is self-consistently explained by competitive formation of bound charge-transfer states and long-range or delocalized free-charge states, where both rate constants are described by the Marcus rate equation. Moreover, the model predicts a suppression of the inverted regime for high-concentration blends and efficient ultrafast free-charge generation, providing a mechanistic explanation for why Marcus-inverted-behavior is rarely observed in device studies.
New conceptsIn this work we introduce the concept that free-charge generation in organic photovoltaic (OPV) materials may best be described by competition between long- and short-range electron transfer events, and that the distribution of rates as a function of distance follows the predictions of Marcus theory. Previous work, both from our group and others, has elucidated these individual concepts; none has put them together into a complete model that quantitatively describes novel experimental data and qualitatively agrees with a broad spectrum of past experimental results in the literature, as we do here. Our results reveal the fundamental connection between solution-phase electron transfer research that has been conducted in the chemistry community over many decades, and the younger materials science effort to develop efficient OPV materials. Our model provides insight into how the microstructure of OPV materials influences the electron transfer process via both entropic and quantum-mechanical mechanisms, and sets the stage for a fundamental understanding of how donor:acceptor energy-offsets interact with the coulomb binding energy to modulate the yield of free charges, and will inform estimates for the ultimate limit of open-circuit voltage in OPV materials. |
Introduction
Simple electrostatic arguments suggest that it should not be possible to make an efficient photovoltaic device from a material with a dielectric constant between 3 and 4. Yet single-junction organic photovoltaic (OPV) cells have now exceeded 18% power conversion efficiency, and progress continues apace.1 Many models have been proposed to describe photoinduced electron transfer (PET) between photoexcited donor and acceptor species in solid-state organic systems2–10 but a fully self-consistent, experimentally verifiable model has proved elusive. In particular, the disconnect between the solution-phase molecular PET community and the OPV world remains large. The description of electron transfer provided by Rudolf Marcus is the unquestioned foundation of work in the former field,11–13 while in the latter it has often been ignored or even explicitly discarded. It has been argued, for instance, that the Marcus formulation breaks down in OPV materials because of the high density of electronic states participating in electron transfer within extended molecular aggregates, such as when fullerene crystallites are present14 We seek to test this idea, exploring the limits of the Marcus rate equation (eqn (1)) in describing electron transfer in the presence of these extended molecular aggregates: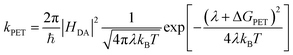 | (1) |
We have demonstrated this “inverted region” several times using free-charge carrier yield as a proxy for kPET, but usually in systems with modest charge carrier mobility, and in particular without large fullerene aggregates that might be expected to introduce a wide manifold of charge-transfer states that could lead to a weakening or absence of rate-constant/yield inversion.15–17 Here, we report charge yield and photoluminescence quenching (PLQ) as a function of the driving force for PET from a series of molecular donors at low concentration in a 6,6-phenyl C61-butyric acid methyl ester (PCBM) host matrix. Despite the fullerene host and its anticipated high density of states, we observe normal, optimal, and inverted regimes of free charge generation using time-resolved microwave conductivity (TRMC). However, PLQ experiments on the same samples reveal that the quenching efficiency rises much faster than the free charge yield, and quickly reaches 100% while the free-charge yield peaks at ∼80%. Moreover, there is no “inverted” regime observed for the PLQ, which remains at 100% even for the largest driving force (−0.69 eV) we were able to test.
These results can be self-consistently described by a Distributed Range Electron Transfer (DRET) model where localized charge-transfer (CT) states kinetically compete with free-charge (FC) states for the available exciton population. In each case, the rate-constant for electron transfer is described by the Marcus rate equation (eqn (1)), allowing for differing reorganization energies and driving forces for the FC and CT species. A sum over the rate constants for transfer to the available microstates for bound and free charge pairs over a wide range of distances allows FC states with larger electron–hole separation distances to compete effectively with shorter-range, more tightly bound, CT states when ΔGCT is near the optimum (ca. −0.4 eV). This process is enabled by a moderately long-range electron transfer process, described by an exponentially decaying electronic coupling element (HDA) at greater distances. These results unify our understanding of electron transfer in both solution and solid-state systems, and the model allows us to make experimentally testable predictions concerning the sub-gap FC and CT state spectra, the temperature-dependence of free-charge generation, and the behavior of the high concentration donor/acceptor blends used in OPV devices. Ultimately we predict that the high density of states available in high concentration donor:acceptor blends does indeed suppress the Marcus inverted regime in OPV devices; however the Marcus rate equation remains foundational to our understanding of electron transfer in these systems.
We first describe our experimental design and results, demonstrating the apparent discrepancy between photoluminescence quenching and free charge yield, as well as evidence for an inverted regime for free charge yield in our fullerene host. This is followed by a detailed description of the DRET model, the predictions it makes possible, and comparison with relevant literature.
Results and discussion
Testing eqn (1) requires two things: (1) an experimental observable that is controlled by kPET, and (2) the ability to tune ΔG across a useful range. Fig. 1 illustrates our approach. To satisfy the first criteria we choose to measure both photoluminescence quenching yield (φPLQ) and free-charge carrier yield (φFC) as this allows observation of both the reactants (excitons) and products (free charges) of the reaction. Each of these can be connected to kPETvia: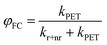 | (2) |
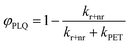 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole fraction film. Evidence for the isolation of our sensitizers comes from absorption spectroscopy (Fig. 1c and Fig. S1.1, ESI†). Fig. 1c shows, as examples, absorption spectra of a PCBM film sensitized with a phthalocyanine guest donor (red), the neat PCBM (brown), and the phthalocyanine in polystyrene and chlorobenzene solution (green and black, respectively). The extensive red-shifting and broadening typical of pure aggregated phthalocyanines18–21 is absent in these films, suggesting that we have indeed prepared samples that resemble a solid solution.
1 mole fraction film. Evidence for the isolation of our sensitizers comes from absorption spectroscopy (Fig. 1c and Fig. S1.1, ESI†). Fig. 1c shows, as examples, absorption spectra of a PCBM film sensitized with a phthalocyanine guest donor (red), the neat PCBM (brown), and the phthalocyanine in polystyrene and chlorobenzene solution (green and black, respectively). The extensive red-shifting and broadening typical of pure aggregated phthalocyanines18–21 is absent in these films, suggesting that we have indeed prepared samples that resemble a solid solution.
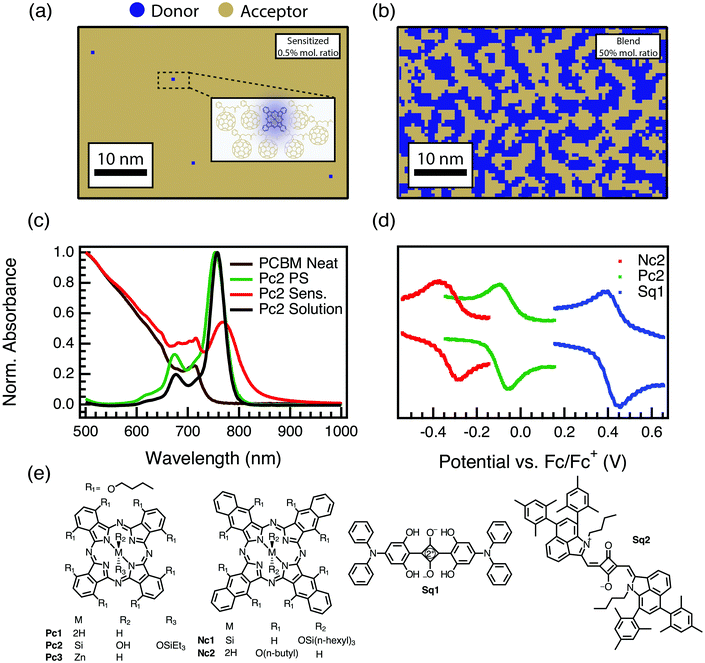 | ||
Fig. 1 (a) Quantitative illustration of a 0.5% mol fraction sensitized film with a random distribution of donors. Inset image shows a 5 nm scale zoomed in description of the microstructure with isolated donors in the PCBM host. (b) Illustration of a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mole fraction film. In both cases the tan color is used to represent PCBM while the blue is the sensitizer. (c) Normalized absorption spectra of Pc2 in 1 μM chlorobenzene solution (black), of Pc2 as sensitizer at 0.005 mol kg−1 in polystyrene (green), or PCBM (red), and of neat PCBM (brown) films. (d) Cyclic voltammograms showing ∼1 V range in oxidation potential achieved using our series of donor molecules. (e) Molecular sensitizer structures and abbreviations used in this work (see also Table 1). 50 mole fraction film. In both cases the tan color is used to represent PCBM while the blue is the sensitizer. (c) Normalized absorption spectra of Pc2 in 1 μM chlorobenzene solution (black), of Pc2 as sensitizer at 0.005 mol kg−1 in polystyrene (green), or PCBM (red), and of neat PCBM (brown) films. (d) Cyclic voltammograms showing ∼1 V range in oxidation potential achieved using our series of donor molecules. (e) Molecular sensitizer structures and abbreviations used in this work (see also Table 1). | ||
The symmetric broadening and slight red shift of the phthalocyanine spectrum in the PCBM host may be due to a combination of effects. First, we note that this phenomenon is universal for all our sensitizers, even those (Sq1 and Sq2) that we will show below do not exhibit strong PL quenching or free-charge generation. Raising the refractive index of the medium (from ∼1.5–1.6 in solution or polystyrene to ∼1.9–2 in the PCBM host22,23) would be expected to red-shift the absorption transition,24 and PCBM doping has been shown to produce just this effect, even at low weight percentages.25 It is also possible that there are contributions from the often observed charge-transfer absorption at the donor acceptor interface.26–28 The latter effect is deemed to be an unlikely explanation, however, as CT-absorption is usually confined to states far down the absorption tail with oscillator strengths at least two-orders of magnitude less than the primary excited state, and we do not observe charge-transfer emission bands in any of our PL data, nor is there any systematic dependence of the red-shift or broadening on ΔG, as would be expected.29,30
The second criteria above, tuning ΔG, was accomplished by choosing a series of donor derivatives with widely varying reversible oxidation potentials (characterized using cyclic voltammetry, Fig. 1d and e), which, along with a moderate variation in excited-state energies (Fig. S1.2 and Table S1.1, ESI†), afford a ∼0.7 eV range in ΔG (Fig. 1d, e and Table 1).
| Sensitizer | E ex (eV) | E ox,D (eV) | ΔGCT (eV) |
|---|---|---|---|
| a Assuming a one-electron redox reaction, these half-wave potentials can be expressed in units of eV instead of V. | |||
| Sq1 | 1.64 | 0.56 | −0.01 ± 0.03 |
| Sq2 | 1.24 | 0.12 | −0.05 ± 0.02 |
| Nc1 | 1.58 | 0.22 | −0.29 ± 0.01 |
| Pc2 | 1.62 | 0.13 | −0.42 ± 0.03 |
| Nc2 | 1.39 | −0.16 | −0.48 ± 0.05 |
| Pc1 | 1.59 | −0.06 | −0.58 ± 0.03 |
| Pc3 | 1.60 | −0.16 | −0.69 ± 0.03 |
The primary experimental result of this work is shown in Fig. 2, which displays φFC measured by TRMC and steady-state PLQ yield, φPLQ, as a function of the nominal Gibbs energy for PET to a localized charge-transfer state, ΔGCT (eqn (5)) within our dilutely sensitized films. Each data point represents one of the seven sensitizers (Fig. 1e and Table 1) at 0.005 mol kg−1 in a host matrix of PCBM. A Marcus-like trend in φFC with increasing ΔGCT is evident, with a distinct optimum of ca. −0.4 eV and a pronounced inverted regime at ΔGCT < −0.4 eV. The ΔGCT-dependence of the φPLQ, on the other hand, shows a rapid increase in quenching from ca. 0 to −0.3 eV, which then saturates at ∼100%. In all cases, selective excitation of our red-absorbing sensitizers beyond the absorption onset of PCBM eliminates the possibility of exciton diffusion and/or energy-transfer processes. Ordinarily TRMC experiments do not directly provide the yield of free-charges, but rather the product of free-charge carrier yield and the sum of the electron and hole mobilities (φΣμ)31,32
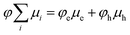 | (4) |
 | ||
| Fig. 2 Photoinduced free electron yield (φFC assuming μe = 0.056 cm2 V−1 s−1, red markers) and PLQ yield (φPLQ, blue markers). Data points are labeled with their corresponding sensitizer (Fig. 1e and Table 1). The dashed curves are the result of a global fit to both φPLQ and φFC using the DRET model, described by eqn (1), (6)–(12). Fit parameters are given in Table 2. Error bars are standard errors calculated from replicate measurements as described in the Experimental section. | ||
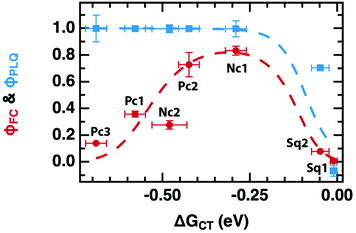
The driving-force axis of Fig. 2, ΔGCT, was created by choosing our series of donor molecules with appropriately varied oxidation potentials and exciton energies (Table 1) to act as guest sensitizers in the PCBM host (Fig. 1d and e). We calculate ΔGCT according to:
| ΔGCT = Eox,D − Ered,A − Eex | (5) |
| ΔGPET = Eox,D − Ered,A − Eex + ΔGS + W(D+/A−) | (6) |
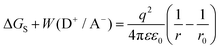 | (7) |
Taken by itself, the trend in φFC as a function of driving force in Fig. 2 may be readily explained by the Marcus formulation for the rate constant of PET (kPET, eqn (1)) if one makes the assumption that the only rate-constant in the system that changes as a function of driving force is kPET, as was done in eqn (2). However, the trend in φPLQ observed in Fig. 2 appears to contradict this simple hypothesis. φPLQ increases rapidly with ΔGCT, and there is no evidence of an inverted regime. Furthermore, we observe a maximum φFC at the optimum (ca. −0.3 to −0.4 eV) of only ∼80%, which is considerably lower than φPLQ, and lower than one would expect assuming values of kPET ∼1012 s−1 typically reported in OPV materials and observed in our TA experiments (see ESI,† Fig. S5.1-8). We can mostly rule out the possibility that the low apparent yield of charges is simply due to an incorrect mobility value, as the φFC curve remains reasonably bell-shaped without the flat-top one would expect if the free-carrier yield approached 100% over any considerable range (see Fig. 4b for an example). Similarly, the low free-charge yield and quenching efficiency cannot be accounted for by heterogeneity in the samples, where some sensitizers undergo ultrafast PET while others do not. Such a model would also predict a broad flat-topped shape in φFCvs. ΔGCT and would not explain why φPLQ = 100% across such a broad range. These observations are also consistent with our recent observations on donor films sensitized with indacenodithiophene nonfullerene acceptors, suggesting that this may be a very general phenomenon.37
We posit that the conflict observed above between the TRMC, PL, and TA measurements may be most simply explained through a competition between free-charge (FC), and localized charge-transfer (CT) states, partitioning kPET into two components: kPET = kFC + kCT, where CT states are a loss pathway, not an intermediate leading to FC. Fig. 3a conceptually illustrates this kinetic scheme with both the electrostatic potential and the Gibbs energy curve accounting for configurational entropy of the continuum of FC and CT states plotted.
 | ||
| Fig. 3 (a) Proposed kinetic model showing competing processes of charge transfer to localized CT states vs. FC states. The black trace is the coulomb work term from eqn (6) as a function of the separation distance between the electron and hole, r. The blue trace is a Gibbs energy curve including an entropic correction accounting for the number of sites available for charge transfer using eqn (12). The distinction between FC and CT states is defined by the point at which the Gibbs energy curve is within 1 kBT of its peak value, denoted rc. The kinetic process is as follows: (1) selective photoexcitation of the sensitizer (donor), (2) exciton dissociation into either FC or CT states with rate constants kFC and kCT, (3) ultimate recombination of FC states via the bimolecular rate constant γr. Both the exciton and the CT states may decay directly to the ground-state. (b) Illustration of the spherical shells of acceptor sites (grey) available to participate in electron transfer at any given radius, r, from the donor (blue); calculated according to eqn (12). (c) A microscopic cartoon depicting the influence of entropy after electron transfer, where there are more pathways that lead to separation (yellow) than those that lead to recombination or CT state formation (red). | ||
Upon photoexcitation a singlet exciton (S1) is formed on the donating sensitizer, and PET takes place across a wide distribution of distances, which we partition into FC states forming with the cumulative rate constant kFC, or CT states forming with cumulative rate constant kCT. The latter may decay to the ground state but do not dissociate to form free-charges due to their binding energy. Mobile charges in FC states may recombine with bimolecular rate constant (γr) through the localized CT states. The proposal of a delocalized charge-separated transition state, CS#, intermediate between the exciton and CT or FC states is not required by our present data, but it is consistent with the need for coupled donor or acceptor aggregates to produce free-charges.16,24–26 Whether this state is real or representative of a tunneling probability or wavefunction overlap between the donor and a distant acceptor is a matter of interpretation.
The kinetic scheme described above forms the basis of the analytical model with which we globally fit our φPLQ and φFC curves in Fig. 2. We refer to it as the Distributed Range Electron Transfer (DRET) model, as its key characteristic is a wide distribution in the range of PET and kinetic competition between free and trapped states.
Our derivation begins by re-defining FC and PLQ yields as a function of the partitioned rate constants, kFC, and kCT:
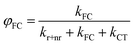 | (8) |
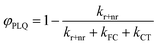 | (9) |
As the distinction between FC and CT states is purely one of charge-separation distance (r) within a continuous distribution, the full form of the Gibbs energy change for PET in eqn (6) and (7) combined with the Marcus rate equation (eqn (1)) can be used to describe this competition quantitatively, as different separation distances imply a different Gibbs energy change, and thus different rate constants. All that remains is to define the critical radius at which we partition this continuous distribution of states into “FC” and “CT” species, rc; a suitable probability distribution, P(r), that describes the likelihood of an electron tunneling any given distance, r, from the donor; and a description of the number of microstates available for charge-transfer as a function of distance, Ω(r). The product of these components is integrated over r in order to appropriately partition kPET:
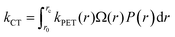 | (10) |
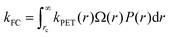 | (11) |
Recent literature has extensively discussed the potential role of configurational entropy (S = −kb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ω(r))),8,9,38–41 disorder,2,6,9,41 and charge-transfer state delocalization2,42–44 (related to P(r)) in understanding charge separation in OPV materials. These studies guide our choice of rc, the form of Ω(r), and that of P(r), drawing particular inspiration from the work of Ratner,11 Gregg,8 Kassal9 and Troisi.7
ln(Ω(r))),8,9,38–41 disorder,2,6,9,41 and charge-transfer state delocalization2,42–44 (related to P(r)) in understanding charge separation in OPV materials. These studies guide our choice of rc, the form of Ω(r), and that of P(r), drawing particular inspiration from the work of Ratner,11 Gregg,8 Kassal9 and Troisi.7
Our experiments yield a particularly simple form for Ω(r): isolated donor molecules in an electron accepting host. The hole is fixed in space on the isolated donor, and a spherical shell of acceptor molecules is available to accept an electron at any given radius as illustrated in Fig. 3b, thus:
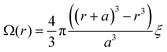 | (12) |
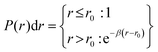 | (13) |
Eqn (1), (6)–(13) constitute a complete analytical model with which we globally fit our φPLQ and φFC data in Fig. 2 (global fit procedure in the ESI,† Section S7). The resulting fit parameters from the orthogonal distance regression we used are shown in Table 2. The only free fit parameters are β, λFC, and λCT. The fluorescence rate constant (kr+nr) was held constant at the average value we obtained from time-resolved PL measurements (Fig. S6.1, ESI†) conducted on each sensitizer; rc was assigned as 3.4 nm as described above, and HDA was set to 2.5 meV. Notably, this model results in a family of fitting solutions, not one unique parameter set, as shown in Fig. S7.1 (ESI†). It was thus necessary to constrain either HDA, β, or λCT in order to obtain a consistent solution. The value of 2.5 meV was chosen for HDA as it is qualitatively consistent with calculations,7 and allows all four of these parameters to assume physically reasonable values. However, this illustrates that the certainty of the exact parameter values is low even if the fit is very good.
| Fit parameter | Value |
|---|---|
| λ FC (eV) | 0.23 |
| λ CT (eV) | 1.3 |
| β (Å−1) | 0.35 |
| k r+nr (s−1) | 7.3 × 108 (held) |
| H DA (meV) | 2.5 (held) |
| r c (nm) | 3.4 (held) |
The fits we obtain to φFC, and φPLQ are both quite good. In particular, the DRET model successfully captures the divergence between φPLQ and φFC observed in Fig. 2. A key feature that makes this possible is that we allow the FC and CT states to take on different reorganization energies. While there is no quantitative physical basis for this assumption, we suggest that it may be connected with localization of these states. The far more localized CT states present a larger, more polarizing electric field to the local environment. Similarly, a more localized anion will experience greater intra-molecular bond distortions than one that shares the electron among several molecules. Both of these effects may contribute to the differing reorganization energies that the model allows, though we note that having artificially partitioned a continuum of states into the binary pair “FC” and “CT”, these reorganization energies can only represent the average value associated with these categories. Strikingly, the value of β that emerges from the fit is exactly in the range predicted by Troisi,7 and is well within previous experimental measurements for conjugated “bridge” molecules.47
We tested the unique ability of the DRET model to explain our data by comparing it to an equivalent formulation (described in ESI,† Section S10) that treats nearest-neighbor CT states as the intermediate between the exciton and the FC states. This sequential model cannot fit our data as well. In particular, such a model cannot reproduce the divergence between PL quenching and free charge yield (see Fig. S9.1, ESI†) at low driving force, because there is only one process responsible for quenching the PL in this case. However, it must be admitted that just the right systematic error in our charge yield measurements in just the right direction could lead to an adequate fit using both models. Here, the quality of the fit is less important than the physical principles upon which the model is based, and the broad consistency of its predictions with other data. As we describe thoroughly in our ESI,† Section S10, the DRET and sequential CT-State models are closely related: the only way CT states are able to dissociate in our sequential model is through integration over all possible charge-transfer rate-constants to distances beyond rc, combined with a slow CT-state recombination rate constant occasioned by Marcus-inverted behavior with respect to the ground-state. As such, the sequential CT-State model predicts rather slow primary charge-transfer from the exciton, with a rate-constant of ∼8 × 109 s−1 at ΔGCT = −0.3 eV, and very slow free charge generation with a rate constant of ∼1 × 107 s−1, neither of which are observed in our TRMC or TA kinetics. In contrast the DRET model predicts simultaneous FC and CT state generation with an overall rate constant of 5 × 1010 s−1 at the same driving force. Moreover, since the two mechanisms rely on the same physics, long-range charge transfer from the exciton to FC states will always out-compete delayed transfer from the CT-state to FC states unless the former is artificially prohibited as in our sequential model: any change in parameters that accelerates the latter (larger HDA or smaller β) will also accelerate the former.
A third possible model is that electron transfer produces FC states exclusively and that the variation in apparent free-charge yield with driving force is attributable to a change in the recombination rate constant, allowing for loss of the free-charge population back to CT states within our laser pulse. We deem this explanation to be unlikely, as we see no evidence that charge-carrier lifetime depends on ΔGCT (Fig. S4.9, ESI†) and we do not believe an ultrafast recombination mechanism could grow-in unobserved, as we vary ΔGCT in reasonably fine increments.
In addition to these models, there are at least two mechanisms that could quench the PL of our donor molecules in PCBM independent of integer electron transfer: energy transfer from the exciton to an optically-active band of CT states,26–28 or a fast internal conversion pathway via partial-CT states. At present, however, the DRET model remains the simplest, most self-consistent way to explain our data. Only future experiments testing its predictions will serve to distinguish these competing possibilities with greater certainty.
Comparing the values of kCT and kFC predicted by the DRET model as a function of ΔGCT provides insight into how it is able to reproduce our experimental observations in Fig. 2. Fig. 4a shows these individual rate constants calculated as a function of ΔGCT for the same fit parameters as in Table 2, using eqn (10) and (11). Notably, these are the primary quantities calculated in the DRET model, which underpin the yield calculations according to eqn (8) and (9). Here, kFC is observed to be sharply peaked while kCT continues to increase across this range of ΔGCT due to the difference in reorganization energy of the two species (0.23 vs. 1.3 eV, respectively). Thus, the observed “inverted region” in our FC yield, and the lack of one in the PLQ yield is explained: the high reorganization energy for the CT state, combined with the distance-dependence of ΔGPET in eqn (6), allows kCT to out-compete kFC at low driving force and at high driving force. Only in the intermediate regime does kFC win out, leading to a maximum FC yield around −0.4 eV despite a reorganization energy of 0.25 eV. Notably, the overall rate constant for charge transfer (black curve) is ultrafast at and above the optimal driving force, as we observe in TA (Fig. S5.9c, ESI†), and consistent with the literature. For any value of ΔGCT exceeding −0.35 eV the rate constant is 1011 s−1 or greater and exceeds 1012 s−1 for the −0.6 eV driving force typical of the polymer:fullerene solar cells where subpicosecond charge separation is nearly universally observed. However, we do not attribute great significance to the absolute values of these rate constants, as they scale with the square of HDA, the value of which is pinned in our fits, and no one unique fit exists for this data set.
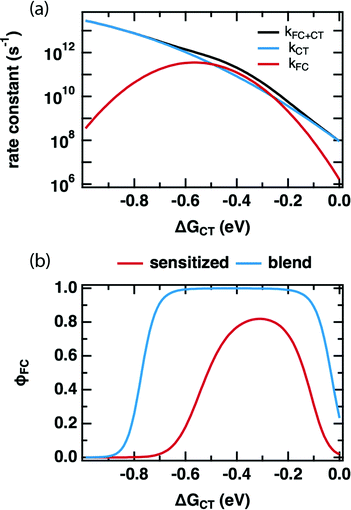 | ||
| Fig. 4 (a) PET rate constant(s) as a function of ΔGCT as predicted by the DRET model (eqn (1), (6)–(12)) using the fit parameters in Table 2. (b) FC yield (φFC) as a function of ΔGCT for the sensitized system studied in this work (red) and that of a predicted blend system as in Hood et al. (blue), which modifies the entropy through an increase in the number of available sites due to large aggregates of both donor and acceptor, rather than an isolated donor molecule in an accepting host.27 | ||
Up to this point, we have shown that a relatively simple model based on the Marcus rate equation (eqn (1)) can explain our experimental data if localized CT states compete with free-charge generation rather than being the intermediate between excitons and free charges, as is most often assumed. Here, we qualitatively reconcile these results with a broad spectrum of literature, showing that our model predictions are consistent with previous observations, not just our own experimental data.
The first key question: why do TRMC and other experiments on sensitized films so frequently result in inverted free-carrier yields and relatively low peak yields,15–17,48 whilst inverted behavior has only rarely been observed in organic photovoltaic devices,49–51 and free charge yield is often close to 100%? We posit that the difference lies in the number of microstates available to charge-separated species in high-concentration blends. Hood et al. have pointed out that the number of microstates is much higher for a quasi-planar interface between aggregated donors and acceptors than for an isolated donor in an accepting host.9Fig. 4b shows a comparison between our model, and an implementation that substitutes Hood's formulation for the number of microstates available in a high-concentration blend. In each case we use the same model parameters as in Table 2 but applied to these two different microenvironments. The red trace is the FC yield from an isolated donor in a homogenous mixture of acceptors, identical to our sensitized PCBM films, while the blue trace is for a planar interface between aggregated donors and acceptors. In the sensitized environment, the peak yield is ∼80% and includes both a slow turn-on in the normal region and slow turn-off in the inverted region, just as in our data. However, in the blend environment, the free-charge yield approaches 100%, producing a wide flat peak with rapid turn-on and turn-off in the normal and inverted regions. The latter does not begin in earnest until ΔGCT < −0.7 eV. We speculate that this behavior makes observation of an inverted region substantially more difficult in device studies, as much larger driving forces are required before it becomes evident. This is qualitatively consistent with the observations of Nakano et al., where a flat-topped curve was observed in photovoltaic devices and extremely exergonic reactions were required to observe inverted behavior.49
The second question concerns the nature and origin of the sub-gap “CT-state spectra” that have been widely observed in OPV materials.26–28 These data form the foundation from which localized CT-states were assigned as the intermediate between excitons and free charges, and have been broadly used as a method of characterizing the driving-force for PET.29,52 Intriguingly, very similar “CT-state” spectra are predicted by our DRET model. Given that HDA is an orbital overlap integral between the donor and the acceptor and P(r) describes its attenuation as a function of distance, it seems reasonable to use these to estimate the relative oscillator strength of CT states as a function of distance (where “CT” here is used broadly to encompass all charge transfer distances), noting that optically-excited long-range electron transfer is known to occur,53 and much more sophisticated calculations have already predicted its potential importance in OPV materials.54 Combined with the number of microstates, Ω(r), and the energy of those states with respect to the initial exciton, ΔGPET(r), it is possible to calculate CT-state spectra for both isolated donors and planar interfaces using our DRET model, as shown in Fig. S8.2 (ESI†). In the latter case many of these states have radii exceeding rc, and can thus be characterized as FC states that would give rise to exactly the same sort of efficient sub-gap carrier generation that is commonly observed.28,55 While these spectra do not predict completely excitation energy-independent quantum yield, we note that this has been a material-dependent observation, with some samples exhibiting a marked energy-dependence of the sub-gap quantum yield.55,56
Finally, we address the temperature-dependence of free-charge generation. An attentive reader will have noted that our model is likely to predict a strong temperature dependence: kPET, and more importantly the value of rc, are both explicitly temperature-dependent. This turns out to be true for isolated donors in an accepting host (Fig. S8.1a, ESI†). However, the DRET model predicts that for blends the temperature-dependence of free-charge generation will actually be quite weak down to ∼150 K, consistent with previous experiments.57,58 At lower temperatures, however, the free-charge yield is predicted to decline precipitously (Fig. S8.1b, ESI†). This may be due in part to our use of the simplest form of the Marcus rate equation, without the quantum-mechanical corrections that capture the existence of zero-point vibrational energy and tunneling through the barrier.11
Conclusions
We have demonstrated that the yield of free charges from PET in electron donor-sensitized PCBM films is dependent upon the driving force, exhibiting clear inverted behavior even in the presence of extended fullerene aggregates – consistent with an electron transfer model based on the Marcus rate equation for PET. However, excitations are quenched much more efficiently than would be expected based on the free-charge yield with no complementary inverted region. These results are self-consistently explained by a Distributed Range Electron Transfer (DRET) model that describes free-charge generation as a competition between the formation of short-range charge-transfer states and long-range free-charge states, each separately described using the Marcus rate equation. An equivalent model that employs the nearest-neighbor CT states as the intermediate between excitons and free charges cannot fit our data. Moreover, the model accurately predicts the electron transfer behavior of both dilutely sensitized and device-relevant concentration regimes through a simple change in how the number of available microstates for charge transfer is calculated, including the existence of sub-gap CT-state spectra and the temperature-dependence of free charge generation. Future work will explore this model in more detail, both the temperature dependence it predicts, and the donor concentration-dependence. These observations suggest a future unification of electron transfer theory in solution and solid-phase systems that will materially aid the advancement of science and technology based on electron transfer reactions in molecular systems.Experimental methods
Film fabrication
Phenyl C61 butyric acid methyl ester (PCBM) was acquired from Nano-C at 99.9% purity and used as received. 1,4,8,11,15,18,22,25-Octabutoxy-29H,31H-phthalocyanine (Pc1), zinc 1,4,8,11,15,18,22,25-octabutoxy phthalocyanine (Pc3), 5,9,14,18,23,27,32,36-octabutoxy-2,3-naphthalocyanine (Nc2), and 2,4-bis[4-(N,N-diphenylamino)-2,6-dihydroxyphenyl] cyclobutene-diylium-1,3-bis(olate) (Sq1) were all acquired from Sigma-Aldrich at >95% purity and used as received. Silicon 1,4,8,11,15,18,22,25-octabutoxyphthalocyanine triethylsiloxide hydroxide (Pc2) is from ref. 40 and used as synthesized. Silicon 2,3-naphthalocyanine bis(trihexylsilyloxide) (Nc2) was acquired from Alfa Chemistry at 98% purity and used as acquired. (2,4-Bis(1-butyl-6,8-dimesitylbenzo[cd]indol-2(1H)-ylidene)methyl)cyclobutene-diylium-1,3-bis(olate) (Sq2) was synthesized for this study and used as synthesized. This synthesis is given in the ESI,† Section S11.Sample films were fabricated by ultrasonic spray-coating host-sensitizer solutions onto 25 × 11 mm2 quartz substrates cleaned with acetone sonication for 10 min and 10 min of UV-ozone treatment. Stock solutions were prepared by dissolving each sensitizer in chlorobenzene at 1 mg mL−1, except for Pc3 which was dissolved in pyridine at 1 mg mL−1. PCBM and PS solutions were dissolved in chlorobenzene at 30 mg mL−1. Host-sensitizer solution mixtures were made by mixing sensitizer solution with PCBM or PS host solution at 0.005 mol kg−1 for a total volume of 1 mL. All films were spray coated in a nitrogen glovebox (<1 ppm O2). Spraying was accomplished by rastering the sample stage beneath the ultrasonic spray nozzle to coat a 50 × 60 mm2 area containing three 25 × 11 mm2 quartz substrates for making samples in triplicate under the same conditions. Atomized solution was delivered to the sample at a rate of 0.4 mL min−1 using a syringe pump and air-shaping was applied with a 6 L min−1 nitrogen stream to achieve fan-like jets for uniform spraying. The sample stage was heated to 100 °C to facilitate evaporation of high boiling solvents. Nozzle to substrate height was ca. 50 mm. 5 coats (repetitions of the raster routine) were done to achieve films ca. 1 μm in thickness. PS and PCBM host films are made from the same spray coating parameters.
Absorption measurements
Optical absorption is characterized using a Varian Cary 5000 UV-Visible spectrophotometer with the Diffuse Reflectance Accessory (DRA) and an angled center mount. Spectra are collected in the transmittance configuration, but because we collect with the center mount in the DRA, it is effectively a transreflectance (%TR) spectrum, as both the reflectance (%R) and transmittance (%T) are collected simultaneously. Excitation of the sample is with the full beam size which is centered on the film at an angle of incidence at 20°. The resolution of the instrument is 1 nm with grating changeovers at 800 nm and 350 nm. A baseline is collected by inserting a blank, cleaned quartz substrate into the center mount of the DRA under the same collection settings. Both a 100% transreflectance and a 0% transflectance, where the beam is blocked, is collected to baseline the instrument before collection. Absorptance (%A) is then calculated from the resulting spectrum by %A = 100% − %TR.Photoluminescence spectroscopy and PL quenching
Photoluminescence spectra were collected using a custom-built Princeton Instruments spectrometer. A liquid nitrogen-cooled, front-illuminated Si CCD (PyLoN) was used for collecting visible-NIR spectra (425–900 nm) and a 1D liquid-nitrogen cooled InGaAs array (PyLoN-IR) was used for SWIR measurements (850–1550 nm). Vis-NIR spectra were intensity calibrated using an IntelliCal USB-LSVN (9000-410) calibration lamp. SWIR spectra were calibrated using a SWIR quartz tungsten halogen lamp from Princeton Instruments. Dual monochromators (HRS 500) were used to achieve pseudo-monochromatic excitation from an Energetiq EQ99x laser driven light source, with typical FWHM bandwidths ∼16 nm using a 1200 g mm−1, 750 nm blaze grating. A single monochromator was used for detection (Princeton HRS-300) with 1200 g mm−1 (500 nm blaze) and 150 g mm−1 (800 nm blaze) gratings used for measuring vis-NIR and SWIR spectra, respectively. Typical exposures were 0.5–1 s with 0.25–1 mm detection slit widths. PL spectra for each sensitizer:PS film were excited at 380 nm. PL quenching experiments were accomplished by measuring PL of selectively excited sensitizers in inert polystyrene control samples and PCBM under identical conditions. PL quenching experiments were conducted by exciting the sensitizer:PCBM films at the same wavelengths used in the TRMC/TA experiments as denoted in Fig. S1.1 (ESI†). Three spots were measured on each film to obtain an average PL spectrum such that an average quenching ratio can be calculated. As shown in eqn (M1), the integrated counts for each spectrum were normalized by %A at the excitation wavelength (λex) and the ratio of %A-normalized, integrated counts between sensitizer:PS and sensitizer:PCBM films was used to calculate quenching. In practice, counts were divided by the power absorbed (counts W−1 absorbed) to account for power fluctuations.| PLQ ratio = 1 − (PLPCBM/APCBM)/(PLPS/APS) | (M1) |
Cyclic voltammetry (CV)
CV measurements were done in triplicate for each sensitizer and the PCBM against the Fc/Fc+ standard reference in an inert glovebox environment (<1 ppm O2). Experiments were performed on solutions of the sensitizer and PCBM in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ratio of dichlorobenzene to acetonitrile (Sigma-Aldrich 99.9% anhydrous grade) with 0.1 M Bu4N+PF6− (Sigma-Aldrich >99% electrochemical grade) in order to make sure that both the electrolyte and the analyte were dissolved entirely. Electrochemistry Power Suite software was used to control equipment and execute scans. Three cyclic scans were done prior to each cyclic voltammogram collection to ensure analyte equilibration with electrode surfaces. Scan rates varied from 100–200 mV s−1 and each solution was scanned in both directions to ensure symmetry and reversibility. A “compact voltammetry cell research kit” (Pine product # AKSPEKIT) was used to ensure the best repeatability of electrode placement from sample to sample. The cell includes a screen-printed three electrode system with a 2 mm Pt working electrode, a Pt counter electrode, and a silver wire pseudo-reference electrode. The electrodes and silver wire are rinsed and sanded between each measurement to prevent any contamination. Following scans, the E1/2 of the first oxidation potential for the sensitizer is used to approximate the energy level of the donor and the E1/2 of the first reduction for the PCBM is used to approximate the energy level of the acceptor, both with reference to the Fc/Fc+ standard E1/2. This procedure is inspired by work from Larson et al.41 While CV measurements are not entirely indicative of the solid-state energetics for these sensitizers, we argue that the solution-like nature of the sensitization for the Pcs/Ncs/Sqs combined with the self-consistent dataset that we are able to achieve through CV, that the relative shifts in the solid-state will be comparable so long as there is no aggregation. Furthermore, work done from Cardona et al. found that the conversion methods used for solution to solid-state energetics can vary greatly and use of a self-contained data set is more consistent.42 Errors for the CV measurements are determined from the standard deviation of the mean for the averaged triplicate solutions per sensitizer. Typical errors in this work are between ±10–50 mV for both the sensitizers and the PCBM.
1 v/v ratio of dichlorobenzene to acetonitrile (Sigma-Aldrich 99.9% anhydrous grade) with 0.1 M Bu4N+PF6− (Sigma-Aldrich >99% electrochemical grade) in order to make sure that both the electrolyte and the analyte were dissolved entirely. Electrochemistry Power Suite software was used to control equipment and execute scans. Three cyclic scans were done prior to each cyclic voltammogram collection to ensure analyte equilibration with electrode surfaces. Scan rates varied from 100–200 mV s−1 and each solution was scanned in both directions to ensure symmetry and reversibility. A “compact voltammetry cell research kit” (Pine product # AKSPEKIT) was used to ensure the best repeatability of electrode placement from sample to sample. The cell includes a screen-printed three electrode system with a 2 mm Pt working electrode, a Pt counter electrode, and a silver wire pseudo-reference electrode. The electrodes and silver wire are rinsed and sanded between each measurement to prevent any contamination. Following scans, the E1/2 of the first oxidation potential for the sensitizer is used to approximate the energy level of the donor and the E1/2 of the first reduction for the PCBM is used to approximate the energy level of the acceptor, both with reference to the Fc/Fc+ standard E1/2. This procedure is inspired by work from Larson et al.41 While CV measurements are not entirely indicative of the solid-state energetics for these sensitizers, we argue that the solution-like nature of the sensitization for the Pcs/Ncs/Sqs combined with the self-consistent dataset that we are able to achieve through CV, that the relative shifts in the solid-state will be comparable so long as there is no aggregation. Furthermore, work done from Cardona et al. found that the conversion methods used for solution to solid-state energetics can vary greatly and use of a self-contained data set is more consistent.42 Errors for the CV measurements are determined from the standard deviation of the mean for the averaged triplicate solutions per sensitizer. Typical errors in this work are between ±10–50 mV for both the sensitizers and the PCBM.
TRMC measurements
The TRMC technique has been described in detail in previous publications both in terms of the theory and the experimental setup.31,32 Film photoconductivity for this work is determined by the following: (1) TRMC transients are collected as a function of light intensity for each sample in the series to ensure that the response is linearly correlated. (2) Transients are fit with biexponential functions convoluted with the 7 ns cavity response. (3) The resulting peak value is normalized by the fraction of absorbed photons in the film. A Spectra-Physics PremiScan ULD/500 optical parametric oscillator pumped by a Spectra-Physics Quanta-Ray Nd:YAG laser was used to excite the samples with ca. 5 ns pulses in the peak absorption for each sensitizer as shown inset on the absorption figures in the ESI,† Fig. S1.1. TRMC transients with fits for each sample are shown in the ESI,† Fig. S4.1-8. TRMC measurement error is dominated by the error in measuring film absorption and errors associated with sample inconsistencies. The error shown for the yield data in Fig. 2 is estimated by taking an average yield for three replicate films for each sensitizer, then taking the standard deviation of the mean.Time-resolved photoluminescence (TRPL)
Optical excitation with ∼100 ps pulses at 700 nm was supplied by a NKT supercontinuum fiber laser (SuperK EXU-6-PP) with 2.69 MHz repetition rate. A 10 nm bandpass filter was used to reduce the spectral bandwidth of the excitation beam. A Hamamatsu 300–900 nm (C10910-04) streak camera was used to collect time-resolved PL spectra. Instrument response was captured by scattering some excitation light into the detector using ground glass in the sample position. Transients were analyzed at the wavelength of maximum PL intensity for each film.Standard errors
Standard errors reported in this paper are from averaged repeated measurements from each experiment. In doing so, we report the averaged value and the standard deviation of the mean from the repeated measurements as the experimental value and the error for those experiments. If a quantity is determined from multiple experimental values, such as ΔGCT, then the error reported is the propagated error from each experimental value, combined in quadrature.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by the Solar Photochemistry Program, Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. Work on squaraine synthesis and characterization was supported by the Office of Naval Research (N00014-21-1-2087 and N00014-21-1-2180). The U.S. Government retains (and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains) a nonexclusive, paid up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.References
- Y. Cui, H. Yao, J. Zhang, K. Xian, T. Zhang, L. Hong, Y. Wang, Y. Xu, K. Ma, C. An, C. He, Z. Wei, F. Gao and J. Hou, Single-Junction Organic Photovoltaic Cells with Approaching 18% Efficiency, Adv. Mater., 2020, 32(19), 1908205, DOI:10.1002/adma.201908205.
- S. Athanasopoulos, H. Bassler and A. Köhler, Disorder vs. Delocalization: Which Is More Advantageous for High-Efficiency Organic Solar Cells?, J. Phys. Chem. Lett., 2019, 10(22), 7107–7112, DOI:10.1021/acs.jpclett.9b02866.
- P. Peumans and S. R. Forrest, Separation of Geminate Charge-Pairs at Donor–Acceptor Interfaces in Disordered Solids, Chem. Phys. Lett., 2004, 398(1–3), 27–31, DOI:10.1016/j.cplett.2004.09.030.
- S. R. Yost and T. Van Voorhis, Electrostatic Effects at Organic Semiconductor Interfaces: A Mechanism for “Cold” Exciton Breakup, J. Phys. Chem. C, 2013, 117(11), 5617–5625, DOI:10.1021/jp3125186.
- T. M. Burke and M. D. McGehee, How High Local Charge Carrier Mobility and an Energy Cascade in a Three-Phase Bulk Heterojunction Enable >90% Quantum Efficiency, Adv. Mater., 2013, 26(12), 1923–1928, DOI:10.1002/adma.201304241.
- H. Eersel, R. A. J. van; Janssen and M. Kemerink, Mechanism for Efficient Photoinduced Charge Separation at Disordered Organic Heterointerfaces, Adv. Funct. Mater., 2012, 22(13), 2700–2708, DOI:10.1002/adfm.201200249.
- D. Caruso and A. Troisi, Long-Range Exciton Dissociation in Organic Solar Cells, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(34), 13498–13502, DOI:10.1073/pnas.1206172109.
- B. A. Gregg, Entropy of Charge Separation in Organic Photovoltaic Cells: The Benefit of Higher Dimensionality, J. Phys. Chem. Lett., 2011, 2(24), 3013–3015, DOI:10.1021/jz2012403.
- S. N. Hood and I. Kassal, Entropy and Disorder Enable Charge Separation in Organic Solar Cells, J. Phys. Chem. Lett., 2016, 7(22), 4495–4500, DOI:10.1021/acs.jpclett.6b02178.
- S. Athanasopoulos, S. Tscheuschner, H. Bässler and A. Köhler, Efficient Charge Separation of Cold Charge-Transfer States in Organic Solar Cells Through Incoherent Hopping, J. Phys. Chem. Lett., 2017, 8(9), 2093–2098, DOI:10.1021/acs.jpclett.7b00595.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, Contemporary Issues in Electron Transfer Research, J. Phys. Chem., 1996, 100(31), 13148–13168 CrossRef CAS.
- R. A. Marcus, On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I, J. Chem. Phys., 1956, 24(5), 966–978, DOI:10.1063/1.1742723.
- G. L. Closs and J. R. Miller, Intramolecular Long-Distance Electron Transfer in Organic Molecules, Science, 1988, 240(4851), 440–447, DOI:10.1126/science.240.4851.440.
- B. M. Savoie, A. Rao, A. A. Bakulin, S. Gélinas, B. Movaghar, R. H. Friend, T. J. Marks and M. A. Ratner, Unequal Partnership: Asymmetric Roles of Polymeric Donor and Fullerene Acceptor in Generating Free Charge, J. Am. Chem. Soc., 2014, 136(7), 2876–2884, DOI:10.1021/ja411859m.
- D. C. Coffey, B. W. Larson and A. W. Hains, An Optimal Driving Force for Converting Excitons into Free Carriers in Excitonic Solar Cells, J. Phys. Chem. C, 2012, 116(16), 8916–8923, DOI:10.1021/jp302275z.
- N. A. Pace, N. V. Korovina, T. T. Clikeman, S. Holliday, D. B. Granger, G. M. Carroll, S. U. Nanayakkara, J. E. Anthony, I. Mcculloch, S. H. Strauss, O. V. Boltalina, J. C. Johnson, G. Rumbles and O. G. Reid, Slow Charge Transfer from Pentacene Triplet States at the Marcus Optimum, Nat. Chem., 2020, 12(1), 63–70, DOI:10.1038/s41557-019-0367-x.
- R. Ihly, K. S. Mistry, A. J. Ferguson, T. T. Clikeman, B. W. Larson, O. G. Reid, O. V. Boltalina, S. H. Strauss, G. Rumbles and J. L. Blackburn, Tuning the Driving Force for Exciton Dissociation in Single-Walled Carbon Nanotube Heterojunctions, Nat. Chem., 2016, 8(6), 603–609, DOI:10.1038/nchem.2496.
- D. Placencia, W. Wang, J. Gantz, J. L. Jenkins and N. R. Armstrong, Highly Photoactive Titanyl Phthalocyanine Polymorphs as Textured Donor Layers in Organic Solar Cells, J. Phys. Chem. C, 2011, 115(38), 18873–18884, DOI:10.1021/jp2052085.
- B. W. Caplins, T. K. Mullenbach, R. J. Holmes and D. A. Blank, Femtosecond to Nanosecond Excited State Dynamics of Vapor Deposited Copper Phthalocyanine Thin Films, Phys. Chem. Chem. Phys., 2016, 18(16), 11454–11459, 10.1039/C6CP00958A.
- J. Park, O. G. Reid and G. Rumbles, Photoinduced Carrier Generation and Recombination Dynamics of a Trilayer Cascade Heterojunction Composed of Poly(3-Hexylthiophene), Titanyl Phthalocyanine, and C 60, J. Phys. Chem. B, 2014, 119(24), 7729–7739, DOI:10.1021/acs.jpcb.5b00110.
- G. J. Dutton and S. W. Robey, Exciton Dynamics at CuPc/C 60Interfaces: Energy Dependence of Exciton Dissociation, J. Phys. Chem. C, 2012, 116(36), 19173–19181, DOI:10.1021/jp305637r.
- M. Campoy-Quiles, C. Müller, M. Garriga, E. Wang, O. Inganäs and M. I. Alonso, On the Complex Refractive Index of Polymer:Fullerene Photovoltaic Blends, Thin Solid Films, 2014, 571, 371–376, DOI:10.1016/j.tsf.2014.02.096.
- A. J. Moulé and K. Meerholz, Interference Method for the Determination of the Complex Refractive Index of Thin Polymer Layers, Appl. Phys. Lett., 2007, 91(6), 061901, DOI:10.1063/1.2767232.
- T. Renger, B. Grundkötter, M. E.-A. Madjet and F. Müh, Theory of Solvatochromic Shifts in Nonpolar Solvents Reveals a New Spectroscopic Rule, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(36), 13235–13240, DOI:10.1073/pnas.0801025105.
- J. Wu, J. Luo, N. Cernetic, K. Chen, K.-S. Chiang and A. K.-Y. Jen, PCBM-Doped Electro-Optic Materials: Investigation of Dielectric, Optical and Electro-Optic Properties for Highly Efficient Poling, J. Mater. Chem. C, 2016, 4(43), 10286–10292, 10.1039/C6TC03932D.
- E. Buchaca-Domingo, K. Vandewal, Z. Fei, S. E. Watkins, F. H. Scholes, J. H. Bannock, J. C. de Mello, L. J. Richter, D. M. DeLongchamp, A. Amassian, M. Heeney, A. Salleo and N. Stingelin, Direct Correlation of Charge Transfer Absorption with Molecular Donor:Acceptor Interfacial Area via Photothermal Deflection Spectroscopy, J. Am. Chem. Soc., 2015, 137(16), 5256–5259, DOI:10.1021/ja512410f.
- J. J. Benson-Smith, L. Goris, K. Vandewal, K. Haenen, J. V. Manca, D. Vanderzande, D. D. C. Bradley and J. Nelson, Formation of a Ground-State Charge-Transfer Complex in Polyfluorene//[6,6]-Phenyl-C61 Butyric Acid Methyl Ester (PCBM) Blend Films and Its Role in the Function of Polymer/PCBM Solar Cells, Adv. Funct. Mater., 2007, 17(3), 451–457, DOI:10.1002/adfm.200600484.
- S. Albrecht, K. Vandewal, J. R. Tumbleston, F. S. U. Fischer, J. D. Douglas, J. M. J. Fréchet, S. Ludwigs, H. Ade, A. Salleo and D. Neher, On the Efficiency of Charge Transfer State Splitting in Polymer:Fullerene Solar Cells, Adv. Mater., 2014, 26(16), 2533–2539, DOI:10.1002/adma.201305283.
- Y. Zhong, M. Causa, G. J. Moore, P. Krauspe, B. Xiao, F. Günther, J. Kublitski, R. Shivhare, J. Benduhn, E. BarOr, S. Mukherjee, K. M. Yallum, J. Réhault, S. C. B. Mannsfeld, D. Neher, L. J. Richter, D. M. DeLongchamp, F. Ortmann, K. Vandewal, E. Zhou and N. Banerji, Sub-Picosecond Charge-Transfer at near-Zero Driving Force in Polymer:Non-Fullerene Acceptor Blends and Bilayers, Nat. Commun., 2020, 11, 833, DOI:10.1038/s41467-020-14549-w.
- K. Vandewal, A. Gadisa, W. D. Oosterbaan, S. Bertho, F. Banishoeib, I. Van Severen, L. Lutsen, T. J. Cleij, D. Vanderzande and J. V. Manca, The Relation Between Open-Circuit Voltage and the Onset of Photocurrent Generation by Charge-Transfer Absorption in Polymer: Fullerene Bulk Heterojunction Solar Cells, Adv. Funct. Mater., 2008, 18(14), 2064–2070, DOI:10.1002/adfm.200800056.
- O. G. Reid, D. T. Moore, Z. Li, D. Zhao, Y. Yan, K. Zhu and G. Rumbles, Quantitative Analysis of Time-Resolved Microwave Conductivity Data, J. Phys. D: Appl. Phys., 2017, 50(49), 493002, DOI:10.1088/1361-6463/aa9559.
- T. J. Savenije, A. J. Ferguson, N. Kopidakis and G. Rumbles, Revealing the Dynamics of Charge Carriers in Polymer:Fullerene Blends Using Photoinduced Time-Resolved Microwave Conductivity, J. Phys. Chem. C, 2013, 117(46), 24085–24103, DOI:10.1021/jp406706u.
- M. P. de Haas, J. M. Warman, T. D. Anthopoulos and D. M. de Leeuw, The Mobility and Decay Kinetics of Charge Carriers in Pulse-Ionized Microcrystalline PCBM Powder, 2006, 1617, 2274–2280 DOI:10.1002/adfm.200500882.
- A. J. Ferguson, N. Kopidakis, S. E. Shaheen and G. Rumbles, Dark Carriers, Trapping, and Activation Control of Carrier Recombination in Neat P3HT and P3HT: PCBM Blends, J. Phys. Chem. C, 2011, 115(46), 23134–23148, DOI:10.1021/jp208014v.
- D. Bao, B. Millare, W. Xia, B. G. Steyer, A. A. Gerasimenko, A. Ferreira, A. Contreras and V. I. Vullev, Electrochemical Oxidation of Ferrocene: A Strong Dependence on the Concentration of the Supporting Electrolyte for Nonpolar Solvents, J. Phys. Chem. A, 2009, 113(7), 1259–1267, DOI:10.1021/jp809105f.
- A. D. McNaught; A. Wilkinson and S. J. Chalk, IUPAC. Compendium of Chemical Terminology, (the “Gold Book”), Blackwell Scientific Publications, Oxford, 2nd edn, 2019 Search PubMed.
- T. G. Allen, P. Kafourou, B. W. Larson, M. Heeney, O. G. Reid and G. Rumbles, Reconciling the Driving Force and the Barrier to Charge Separation in Donor–Nonfullerene Acceptor Films, ACS Energy Lett., 2021, 3572–3581, DOI:10.1021/acsenergylett.1c01563.
- E. Kawashima, M. Fujii and K. Yamashita, Entropy Promotes Charge Separation in Bulk Heterojunction Organic Photovoltaics, J. Photochem. Photobiol., A, 2019, 382, 111875, DOI:10.1016/j.jphotochem.2019.111875.
- N. R. Monahan, K. W. Williams, B. Kumar, C. Nuckolls and X. Y. Zhu, Direct Observation of Entropy-Driven Electron-Hole Pair Separation at an Organic Semiconductor Interface, Phys. Rev. Lett., 2015, 114(24), 247003, DOI:10.1103/PhysRevLett.114.247003.
- W. Xue, Y. Tang, X. Zhou, Z. Tang, H. Zhao, T. Li, L. Zhang, S. Liu (frank), C. Zhao, W. Ma and H. Yan, Identifying the Electrostatic and Entropy-Related Mechanisms for Charge-Transfer Exciton Dissociation at Doped Organic Heterojunctions, Adv. Funct. Mater., 2021, 31(25), 2101892, DOI:10.1002/adfm.202101892.
- D. Liraz, P. Cheng, Y. Yang and N. Tessler, Translating Local Binding Energy to a Device Effective One, Sustainable Energy Fuels, 2020, 4(2), 760–771, 10.1039/C9SE01095E.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, The Role of Driving Energy and Delocalized States for Charge Separation in Organic Semiconductors, Science, 2012, 335(6074), 1340–1344, DOI:10.1126/science.1217745.
- N. A. Pace, O. G. Reid and G. Rumbles, Delocalization Drives Free Charge Generation in Conjugated Polymer Films, ACS Energy Lett., 2018, 3(3), 735–741, DOI:10.1021/acsenergylett.8b00108.
- H. M. Feier, O. G. Reid, N. A. Pace, J. Park, J. J. Bergkamp, A. Sellinger, D. Gust and G. Rumbles, Local Intermolecular Order Controls Photoinduced Charge Separation at Donor/Acceptor Interfaces in Organic Semiconductors, Adv. Energy Mater., 2016, 6(6), 1502176, DOI:10.1002/aenm.201502176.
- A. J. Barker, K. Chen and J. M. Hodgkiss, Distance Distributions of Photogenerated Charge Pairs in Organic Photovoltaic Cells, J. Am. Chem. Soc., 2014, 136(34), 12018–12026, DOI:10.1021/ja505380j.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Ultrafast Long-Range Charge Separation in Organic Semiconductor Photovoltaic Diodes, Science, 2014, 343(6170), 512–516, DOI:10.1126/science.1246249.
- B. Albinsson and J. Mårtensson, Long-Range Electron and Excitation Energy Transfer in Donor–Bridge–Acceptor Systems, J. Photochem. Photobiol., C, 2008, 9(3), 138–155, DOI:10.1016/j.jphotochemrev.2008.01.002.
- A. J. Ward, A. Ruseckas, M. M. Kareem, B. Ebenhoch, L. A. Serrano, M. Al-Eid, B. Fitzpatrick, V. M. Rotello, G. Cooke and I. D. W. Samuel, The Impact of Driving Force on Electron Transfer Rates in Photovoltaic Donor-Acceptor Blends, Adv. Mater., 2015, 27(15), 2496–2500, DOI:10.1002/adma.201405623.
- K. Nakano, Y. Chen, B. Xiao, W. Han, J. Huang, H. Yoshida, E. Zhou and K. Tajima, Anatomy of the Energetic Driving Force for Charge Generation in Organic Solar Cells, Nat. Commun., 2019, 10, 2520, DOI:10.1038/s41467-019-10434-3.
- G. Zhou, M. Zhang, Z. Chen, J. Zhang, L. Zhan, S. Li, L. Zhu, Z. Wang, X. Zhu, H. Chen, L. Wang, F. Liu and H. Zhu, Marcus Hole Transfer Governs Charge Generation and Device Operation in Nonfullerene Organic Solar Cells, ACS Energy Lett., 2021, 2971–2981, DOI:10.1021/acsenergylett.1c01154.
- S. Karuthedath, J. Gorenflot, Y. Firdaus, N. Chaturvedi, C. S. P. De Castro, G. T. Harrison, J. I. Khan, A. Markina, A. H. Balawi, T. A. D. Peña, W. Liu, R.-Z. Liang, A. Sharma, S. H. K. Paleti, W. Zhang, Y. Lin, E. Alarousu, D. H. Anjum, P. M. Beaujuge, S. De Wolf, I. McCulloch, T. D. Anthopoulos, D. Baran, D. Andrienko and F. Laquai, Intrinsic Efficiency Limits in Low-Bandgap Non-Fullerene Acceptor Organic Solar Cells, Nat. Mater., 2021, 20(3), 378–384, DOI:10.1038/s41563-020-00835-x.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Fast Charge Separation in a Non-Fullerene Organic Solar Cell with a Small Driving Force, Nat. Energy, 2016, 1, 16089, DOI:10.1038/nenergy.2016.89.
- J. Zhou, B. R. Findley, A. Teslja, C. L. Braun and N. Sutin, Ion Pairs from Photoexcited, “Random” Electron Donors and Acceptors: Alkylbenzenes and Tetracyanoethylene, J. Phys. Chem. A, 2000, 104(49), 11512–11521, DOI:10.1021/jp003005r.
- H. Ma and A. Troisi, Direct Optical Generation of Long-Range Charge-Transfer States in Organic Photovoltaics, Adv. Mater., 2014, 26(35), 6163–6167, DOI:10.1002/adma.201402294.
- D. H. K. Murthy, M. Gao, M. Vermeulen, L. D. A. Siebbeles and T. J. Savenije, Mechanism of Mobile Charge Carrier Generation in Blends of Conjugated Polymers and Fullerenes: Significance of Charge Delocalization and Excess Free Energy, J. Phys. Chem. C, 2012, 116(16), 9214–9220, DOI:10.1021/jp3007014.
- N. Felekidis, A. Melianas and M. Kemerink, The Role of Delocalization and Excess Energy in the Quantum Efficiency of Organic Solar Cells and the Validity of Optical Reciprocity Relations, J. Phys. Chem. Lett., 2020, 11(9), 3563–3570, DOI:10.1021/acs.jpclett.0c00945.
- W. J. Grzegorczyk, T. J. Savenije, T. E. Dykstra, J. Piris, J. M. Schins and L. D. A. Siebbeles, Temperature-Independent Charge Carrier Photogeneration in P3HT–PCBM Blends with Different Morphology, J. Phys. Chem. C, 2010, 114(11), 5182–5186, DOI:10.1021/jp9119364.
- F. Gao, W. Tress, J. Wang and O. Inganäs, Temperature Dependence of Charge Carrier Generation in Organic Photovoltaics, Phys. Rev. Lett., 2015, 114(12), 128701, DOI:10.1103/PhysRevLett.114.128701.
Footnote |
| † Electronic supplementary information (ESI) available: Absorption and emission characteristics of all samples and control samples, cyclic voltammograms for all sensitizer and host molecules, microwave conductivity transients for all samples and parameters from the global fits to each data set, femtosecond transient-absorption characterization of every sensitizer molecule including estimated triplet yields and ISC rate-constants, time-resolved photoluminescence characterization of every sensitizer molecule, temperature-dependence of FC yield and CT state spectra calculated using the DRET model, comparison of the DRET model with a sequential intermediate CT-state model, details of the sequential model implementation, synthesis and characterization of the squaraine donors. See DOI: 10.1039/d1mh01331a |
| This journal is © The Royal Society of Chemistry 2022 |
