Concluding remarks: Faraday Discussion on unimolecular reactions

Abstract

This Faraday Discussion, marking the centenary of Lindemann's explanation of the pressure-dependence of unimolecular reactions, presented recent advances in measuring and computing collisional energy transfer efficiencies, microcanonical rate coefficients, and pressure-dependent (phenomenological) rate coefficients, and the incorporation of these rate coefficients in kinetic models. Several of the presentations featured systems where breakdown of the Born–Oppenheimer approximation is key to understanding the measured rates/products. Many of the reaction systems presented were quite complex, which can make it difficult to go from “plausible proposed explanation” to “quantitative agreement between model and experiment”. This complexity highlights the need for better automation of the calculations, better documentation and benchmarking to catch any errors and to make the calculations more easily reproducible, and continued (and even closer) cooperation of experimentalists and modelers. In some situations the correct definition of a “species” is debatable, since the population distributions and time evolution are so distorted from the perfect-Boltzmann Lewis-structure zero-order concept of a chemical species. Despite all these challenges, the field has made tremendous advances, and several cases were presented which demonstrated both excellent understanding of very complicated reaction chemistry and quantitatively accurate predictions of complicated experiments. Some of the interesting contributions to this Discussion are highlighted here, with some comments and suggestions for next steps.

---

1 Introduction

About 100 years ago, in a world that was recovering from a devastating pandemic and scarred by war, Lindemann¹ proposed that collisions with bath gas provide the energy needed to overcome the activation energy of unimolecular reactions, and realized this implied that rate-coefficients are pressure-dependent. A few years later, Hinshelwood elaborated Lindemann's proposal into the well-known model for fall-off.⁴⁶ The current Faraday Discussion celebrates the centenary of Lindemann's presentation of his insight, and the many advances in our understanding of unimolecular and pressure-dependent reactions over the past century.

At the time Lindemann presented his hypothesis, many of the fundamental concepts and equations of theoretical chemical kinetics were unknown. Arrhenius's rate law was well-established (and Arrhenius was in the audience). The concept of quantized vibrational energy levels was already accepted, largely due to the work of Planck about ten years earlier. But Lindemann's model was developed about 4 years before Schroedinger proposed his equation and Heisenberg computed the energies of harmonic oscillators, showing that they have zero-point energy. It was several years later that Born and Oppenheimer showed how the Schroedinger equation leads to potential energy surfaces (PESs) and pointed out the non-adiabatic terms coupling PESs.

Hinshelwood, Rice, Ramsperger, and Kassel rapidly followed up on Lindemann's proposal in the 1920s, but all that work was done before Eyring and Polanyi invented Transition State Theory (TST) in 1935, and before Wigner wrote out his clear derivation and formulation of TST in 1938. For more on the many competing hypotheses about unimolecular reactions around the time of Lindemann's presentation, and the limited experimental data available then, see ref. 45.

It was not until 1952, about 30 years after Lindemann's famous presentation, that Marcus built on TST and the Rice–Ramsperger–Kassel model from the 1920s to formulate the famous RRKM equations.² In the second half of the 20^th century a variety of experiments tested the assumptions behind RRKM and other rate theories, and some k(E) and collisional energy transfer efficiencies were measured, usually indirectly but sometimes directly. It was not until 1983, more than 60 years after Lindemann first qualitatively explained fall-off, that Gilbert, Luther, and Troe derived an accurate form for the pressure-dependence of a rate coefficient k(T,P) by careful analysis of the master equation, and showed that it quantitatively matched experiment.³ As understanding of k(E) and k(T,P) solidified, several excellent textbooks on unimolecular reactions were written in the late 20^th century.^4–6

Throughout the 20^th century and continuing today, a large number of individual k(T,P) have been measured experimentally. This experimental work allowed the development of empirical methods for estimating collisional energy transfer efficiencies and k(E)’s. Due to advances in computer hardware and electronic structure theory, including the development of accurate density functionals, it started to become possible to quantitatively compute rate coefficients from first principles in the 1980s, and that capability has continued to dramatically improve until the present day.

Several methods were developed to handle systems with multiple wells (isomers) and multiple product channels, notably the chemically significant eigenvalue methods for extracting phenomenological k(T,P) from the master equation. Our improving ability to estimate or compute k(T,P)'s has led to their incorporation in multi-reaction kinetic models. Quite complicated kinetic models have been developed for many societally-important reaction systems involving pressure-dependent reactions (e.g. smog chemistry, stratospheric chemistry, combustion, pyrolysis), so in some respects this field is quite advanced. But there are still some important unresolved issues that were raised during this Discussion.

The present Faraday Discussion was organized around 4 key topics:

(1) Collisional energy transfer efficiencies

(2) Microcanonical rate coefficients k(E)

(3) Pressure-dependent rate coefficients k(T,P)

(4) Incorporating k(T,P) into kinetic models

Each of these topics are addressed in turn below, drawing a few examples from the many important and interesting papers presented, with a brief discussion of some unresolved issues and proposed next steps. For an excellent and more comprehensive overview of the current state of the field, particularly of the first 3 topics, see Stephen Klippenstein's paper associated with his Spiers Memorial Lecture, at the beginning of this volume (https://doi.org/10.1039/D2FD00125J).

2 Themes of this Discussion

Throughout this Faraday Discussion, several themes were addressed repeatedly:

(a) Beyond Born–Oppenheimer: non-adiabatic reactions

(b) Complexity (and the need for experimental–computational cooperation to address it)

(c) Correct explanation vs. quantitative agreement

(d) What is a chemical species?

2.1 Beyond Born–Oppenheimer

Our ability to deal with non-adiabatic reactions, e.g. where the entrance channel is on one electronic PES, but some of the products are formed on a different PES, has remarkably advanced in the last ∼20 years, and some of that progress was well-illustrated in papers presented at this Discussion. Some examples: Troe presented an interesting analysis of the OH + N reaction, where there are multiple electronic states in the entrance channel, and spin-flips and partial dissociation of the initially formed HON species are required to reach the lowest-lying PES (singlet HNO) (https://doi.org/10.1039/d2fd00018k). Cavallotti presented calculations on O + butadiene, where apparently dynamics on the initially-formed triplet PES, in competition with intersystem crossing, significantly affect the relative yields of products formed on the lower-lying singlet PES (https://doi.org/10.1039/d2fd00037g). And Hua Guo presented detailed calculations on how the J-dependent Renner–Teller coupling between ground and excited PESs of HCO explains experimental measurements of its photodissociation (https://doi.org/10.1039/d2fd00011c). The paper presented by Heathcote, on the electron-impact induced double ionization of neutrals, followed by the rapid dissociation of 2+ species into a pair of cations, highlighted some of the remaining challenges in dealing with systems where multiple electronic states are accessible (https://doi.org/10.1039/d2fd00033d).

2.2 Complexity

Many of the papers highlighted the complexity of the problems the community is addressing today, and the need for close cooperation between the experimentalists and the theoreticians/computationalists. More often than not, computers are required to compute the PESs, to compute the k(E)'s, to solve the master equations, to collect and analyze the experimental data, and to correctly compare the model with the data. This heavy reliance on computers is necessary, but it also raises many challenges: how to be sure the computer programs are correct, with no bugs? How can the computer program assist humans in understanding the system (rather than hiding the important details inside the black box)?

The complexity issues are of course quite severe for systems with hundreds of reactants (e.g. the pyrolysis model of Aerssens (https://doi.org/10.1039/d2fd00032f)), but even simple-looking systems like hexadiyne isomerization (presented by Osborn, https://doi.org/10.1039/d2fd00028h), dimethyloxetanyl (C₅H₉O) + O₂ (presented by Doner, https://doi.org/10.1039/d2fd00029f) and HC(O)OO + HOO (presented by Kuwata, https://doi.org/10.1039/d2fd00030j) are actually extremely complicated.

2.3 Correct explanation vs. quantitative agreement

We honor Lindemann because he correctly recognized the role of collision in chemical reactions.¹ However, his model, even after it was patched by Hinshelwood, did not quantitatively match the experimental data. Quantitative agreement with the shape of experimental fall-off curves was not achieved until about 60 years later, by Troe and co-workers,³ and only this century has the community been able to compute both the microcanonical rate coefficients and the collisional energy transfer efficiencies¹⁰ to obtain high-accuracy k(T,P) purely from first principles. Clearly we need both the correct physical picture and the experimentally-validated quantitative model. Lindemann's explanation was persuasive enough, and his model was close enough to the data, that the community accepted his explanation, long before there was a quantitative match between predictions and experiment. But as the systems get more complex, it can be harder and harder to convincingly demonstrate that a qualitative explanation is correct, and it of course gets much more challenging to build and to test a quantitative model. As a result, it sometimes takes many years between the time a hypothesis is proposed and when it is accepted as the explanation, and even more years after that before anyone can demonstrate that the proposed theory quantitatively matches experiment.

One relatively simple example is roaming radical reactions. The mechanism was proposed in 1993 by van Zee, Foltz, and Moore to explain their data,⁷ but that explanation was not widely accepted by the community until the work of Suits, Bowman, and coworkers in 2004.⁸ A convenient computational framework for quantitative predictions of roaming was presented in 2011 by Klippenstein, Georgievskii, and Harding.⁹ The new paper presented by Suits at this meeting (https://doi.org/10.1039/d2fd00050d), almost 30 years after the van Zee et al. experiments and hypothesis, suggests that further theoretical and experimental work may be needed to fully understand roaming, even in molecules as small as H₂CO. Roaming is just one example; there are many other kinetic phenomena which are currently in the gap between ‘qualitatively explained’ and ‘experimentally-validated quantitative model’.

The fourth theme of this Discussion, “What is a chemical species?”, is discussed in the section on phenomenological rate coefficients k(T,P) below.

3 Collisional energy transfer efficiencies

Lindemann¹ explained that pressure-dependence of rate coefficients is due to the competition between microcanonical reaction rates and collisional energy transfer, so the reaction rate is sensitive to both. However, reaction rates vary by many orders of magnitude, while collisional energy transfer efficiencies vary in a narrower range, so the error due to mis-estimating energy transfer efficiency is often smaller than the errors due to errors in estimates of k(E). Consequently, most researchers have focused on improving the calculation/estimation of k(E)'s, and most kinetic modelers have used rough models for energy transfer such as the exponential-down model, eqn (1), where E is the energy in the reactant, and the parameter α is an empirical estimate.

P(E → E − ΔE) ∼ exp(−αΔE) for ΔE > 0 (1)

α = 1/〈ΔE〉_down

This approximation is commonly made despite the fact that both experimental measurements and first-principles computations have shown that the exponential-down model is not very accurate. The paper presented by Mullin (https://doi.org/10.1039/d2fd00068g) at this Discussion provides additional experimental evidence that an improved model is needed, from experiments using an optical centrifuge to reach very high J states.

In recent years, our ability to compute k(E) has greatly improved, so in some systems the error in the computed k(T,P) might be more attributable to errors in the assumed collisional energy transfer efficiency than to errors in k(E). Jasper has developed methods for computing the energy transfer efficiency from first-principles (https://doi.org/10.1039/d2fd00038e).¹⁰ For several decades it has been possible to accurately compute intermolecular potentials, e.g. to predict the structures of van der Waals complexes. In this Discussion, both You (https://doi.org/10.1039/d2fd00058j) and Jasper (https://doi.org/10.1039/d2fd00038e) presented papers reporting a large number of these calculations. You's paper demonstrated that these ab initio potentials can be used to accurately predict some transport properties of gases a priori.

Jasper's paper (https://doi.org/10.1039/d2fd00038e) impressively demonstrated the ability to predict, ab initio, the change in reaction rates with bath gas near the low-pressure limit, for monoatomic, diatomic, and triatomic bath gases. Fig. 1 shows one example, comparing experimental data on the important reaction H + O₂ + M = HO₂ + M with Jasper's computed values for several different bath gases M.

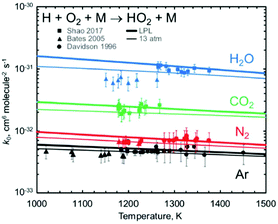Fig. 1 Predicted vs. experimental rate coefficients for H + O₂ + M → HO₂ + M near the low-pressure limit, showing how well Jasper's ab initio method works for predicting the dependence on bath gas composition (the identity of M). Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00038e) with permission from the Royal Society of Chemistry.

3.1 Collisional energy transfer efficiencies: next steps

As Jasper pointed out at this Discussion, the success shown in Fig. 1 suggests that it may now be time for the field to move on from using simplistic collisional energy transfer models such as exponential-down, and instead begin using more accurate energy transfer models, with parameters derived from ab initio calculations similar to what Jasper has done (https://doi.org/10.1039/d2fd00038e).¹⁰ However, there are several different issues that need to be addressed to make this transition:

(1) Are Jasper-type computational methods reliably accurate for all situations? How best to test this accuracy?

(2) Is there an even more accurate method we should be using?

(3) In the other direction: is there a fast approximation to the Jasper method, suitable for high-throughput calculations on a large number of reaction/bath combinations?

At this Discussion, Jasper also presented predictions of collisional energy transfer efficiency, F, as a function of the amount of energy transferred, ΔE, for the reverse reaction HO₂ + M → H + O₂ + M, see Fig. 2. The very large difference in F values for different bath gases at larger ΔE's, and the shape of the F(ΔE) curves for the triatomics, are both worthy of further investigation. These F's are consistent with experiment, see Fig. 1, suggesting that they are correct. On the other hand, the curves unexpectedly suggest that strong collisions, transferring more than 10 kJ mol⁻¹ of energy from the bath gas to the reactant, are quite important for triatomic bath gases, even though such strong collisions are unimportant for N₂ and completely negligible for Ar. It is not surprising that it is unlikely that Ar would donate 10 kJ mol⁻¹, since at the 1000 K condition simulated by Jasper, the average Ar atom only has about 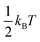∼ 4 kJ mol⁻¹ in the translational mode contributing to the HO₂ + Ar collision; only Ar atoms way out in the Boltzmann tail could donate 10 kJ mol⁻¹. The triatomic CO₂ has higher heat capacity and so has the possibility of donating much more energy in a collision than an Ar atom. At 1000 K, most of H₂O's vibrational states are inactive – its lowest fundamental is 1650 cm⁻¹, equivalent to T ∼ 2360 K, so at 1000 K most water molecules are in v = 0. So H₂O should have less energy available to donate than CO₂. But the simulations give similar F values for H₂O and CO₂. In the simulation, the vibrations were treated classically, so they are all active at all temperatures. Perhaps the classical simulations therefore over-estimate the probability that H₂O would transfer large ΔE? It would be helpful to test to see if this effect is large enough to be consequential for the kinetics.

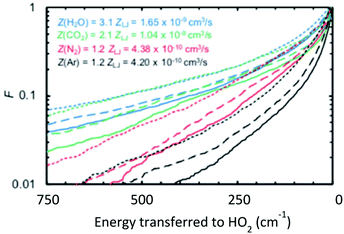Fig. 2 Computed fraction F of collisions that transferred energy ΔE from the bath gas to HO₂ causing reaction. The triatomics are much more likely to transfer large amounts of energy than Ar or N₂. Note these are upward not downward transitions, so even if the exponential-down model were accurate these semi-log plots would not be linear. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00038e) with permission from the Royal Society of Chemistry.

The shapes of the F(ΔE) curves in Fig. 2 are interesting, but perhaps a bit hard to interpret because this plot is for upward energy transfer from bath to reactant, but the common exponential-down model, eqn (1), is for downward (reactant/product to bath gas) energy transfers. It would be interesting to replot this information to display F(ΔE) for downward transitions. It is expected that this will remove some of the curvature (which is due to the energy dependence of the density of states), and making it clearer how differently the triatomic bath gases behave from the predictions of the ‘exponential-down’ simplistic model in eqn (1).

For systems like HO₂ + H₂O, it is plausible that the colliding molecules hydrogen bond and stay together long enough to transfer quite a lot of energy. It would be interesting to compare the actual F(ΔE) to that computed using the strong-collision limit. In the strong-collision limit one would expect a statistical distribution corresponding to perfect equipartition of the energy in the collision complex, constrained only by momentum and angular momentum conservation including some physical limit on the maximum impact parameter.

From this work and their prior work, Jasper and co-workers (https://doi.org/10.1039/d2fd00038e)¹⁰ have developed a detailed understanding of collisional energy transfer efficiencies, greatly superior to the models currently used in most master equation studies. One challenge for the community now is how to use this new capability to accurately predict collisional energy transfer efficiencies to improve both our understanding of individual reactions, and to devise methods to scale up from Jasper's simulations on individual reactions to improve the large kinetic models used for combustion and pyrolysis, that often involve hundreds of pressure-dependent reactions.

4 Microcanonical rate coefficients k(E)

A major focus of effort of this community over the past 40 years has been to measure and calculate microcanonical rate coefficients k(E), and related quantities such as k(E,J). Direct measurements of k(E) are very challenging. The rate k(E) must be in a narrow range: too slow and the energy resolution will be lost to collisions, but too fast and it will be hard to resolve the signal's time dependence. Also, high k(E), i.e. short lifetimes, correspond to significant energy uncertainty by the Heisenberg uncertainty principle, affecting the achievable energy resolution. Since k(E) varies rapidly with E, the reactant must be prepared in a narrow range of E. A convenient way to achieve that desired energy resolution is to use supersonic expansions to cool a reactant molecule to below 10 Kelvin at low pressure, and then add the desired energy E by laser techniques. Special spectroscopic characteristics of the reactant are needed to allow states with the desired E to be prepared. Usually a very sensitive but fast technique is needed to see if the reaction has occurred, e.g. laser induced fluorescence or selective photoionization of one of the products. Because of all these constraints and challenges, only a handful of direct energy-resolved time-resolved k(E) measurements have ever been reported.

One of the most impressive direct k(E) measurements, on the reaction ˙CH₂C(CH₃)₂OOH → OH + 1,1-dimethyl oxetane (C₄H₈O), was presented by Lester at this Discussion (https://doi.org/10.1039/d2fd00008c). The PES is shown in Fig. 3. The direct k(E) measurements are in very good accord with the k(E) calculations on a high-level PES, after accounting for complexities such as the internal rotors and heavy-atom tunneling, Fig. 4. This study is particularly interesting because this type of QOOH reaction is practically important, strongly affecting ignition of some fuels, and also important in the atmosphere.

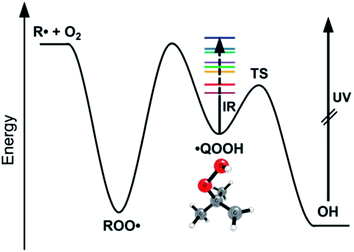Fig. 3 Bhagde et al. (https://doi.org/10.1039/d2fd00008c) used near IR excitation of the jet-cooled QOOH radical to prepare states of known energy E (colored stripes). After a variable time delay, the product OH was detected by laser-induced fluorescence. The dependence of the OH signal on the time delay gives k(E). Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00008c) with permission from the Royal Society of Chemistry.

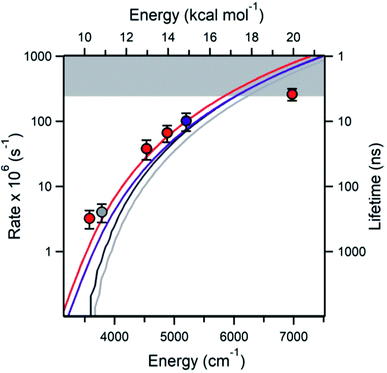Fig. 4 The measured (points) and various theoretically predicted k(E) (curves) for QOOH → OH + oxetane. The highest energy point is hitting the experimental time-resolution (gray band). Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00008c) with permission from the Royal Society of Chemistry.

Because of the challenges with direct rate measurements, often products are probed instead, to determine relative channel rates k₁(E)/k₂(E). The product ratio can change rapidly with energy in the vicinity of a reaction threshold, giving a strong signal and revealing rapid changes in at least one of the k's.^11,42 At this Discussion, Suits presented a very interesting case, where the different products measured were the same molecules, H₂ + CO, but the products had very different energy distributions indicative of the path taken on the PES (https://doi.org/10.1039/d2fd00050d). The experiment was done by exciting formaldehyde to different vibronic states of S₁; those states internally converted due to Born–Oppenheimer breakdown to highly energetic states of S₀, and then dissociated. Fig. 5 shows the PES. Suits and co-workers probed H₂ + CO, formed either via the simple tight transition state, or via a roaming pathway, where first a C–H bond breaks, and then the roaming H atom abstracts the second H from the HCO fragment. With very small changes in initial energy and rotational state, they observed huge changes in CO rotational energy distribution and in the translational energy distribution of the products, see Fig. 6. This strongly suggests that a new and quite important roaming reaction pathway is turning on in a specific energy range near the threshold for H + HCO dissociation.

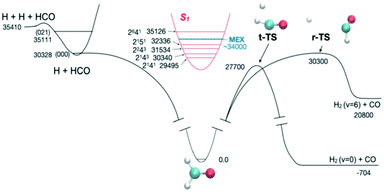Fig. 5 The experiments of Suits and co-workers probed the competition between reaction through the tight transition state (t-TS) and the roaming reaction channel (r-TS), by measuring changes in product energy distributions. The system was prepared in various energy states by exciting different rovibronic states of S₁. At energies near the H + HCO and some of the H + HCO(v₁,v₂,v₃) product channel thresholds the H₂ and CO product distributions change rapidly with energy, indicating dramatic changes in roaming yields. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00050d) with permission from the Royal Society of Chemistry.

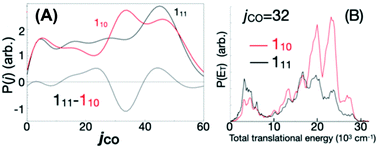Fig. 6 A tiny change in initial rovibronic state dramatically alters (A) the measured CO productrotational energy distribution, and (B) also the translational energy of the CO(j = 32). Apparently this is because small changes in initial energy dramatically affect the competition between the roaming reaction and the conventional tight-TS channel. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00050d) with permission from the Royal Society of Chemistry.

Something similar is seen in the H₂(v = 8) yield near certain H + HCO(v₁,v₂,v₃) product channels; the data indicates that the roaming channel remains competitive with the tight TS channel even 60 kJ mol⁻¹ above the H + HCO dissociation limit. Some peculiar behaviour of loose transition state channels near product vibrational state thresholds has been reported before in other systems, e.g. ref. 11, but the data presented by Suits is much more dramatic and interesting, and should lead to a better understanding of roaming radical reactions.

Cavallotti presented a paper (https://doi.org/10.1039/d2fd00037g) on the reaction O + butadiene that demonstrated how well modern quantum chemistry and rate calculation methods can handle even quite complicated systems with intersystem crossing and multiple product channels. The complicated intersecting triplet and singlet PESs are shown in Fig. 7. The initial triplet adduct isomers are formed with an energy slightly above some isomerization barriers on the triplet surface, at least 150 kJ mol⁻¹ above the minimum-energy crossing point between the triplet and singlet surfaces, and 100–300 kJ mol⁻¹ above several unimolecular reaction barriers on the singlet surface. This multitude of reactions leads to formation of many distinct products, several of which were measured using molecular beam techniques, Table 1.

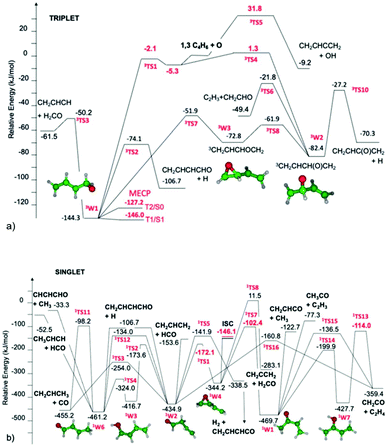Fig. 7 (a) Portion of the triplet C₄H₆O PES relevant to the O + butadiene reaction in a molecular beam. The minimum energy crossing points between singlet and triplet surfaces are denoted MECP. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00037g) with permission from the Royal Society of Chemistry. (b) Portion of the singlet C₄H₆O PES relevant to molecular beam experiments on O + C₄H₆. This connects with the triplet PES in (a) at the location marked ISC. Note the large number of possible products. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00037g) with permission from the Royal Society of Chemistry.

Table 1 Experimental vs. theoretical yields of nine different product channels formed in a crossed molecular beam of O(³P) + butadiene. The calculations were made using the PESs shown in Fig. 7. Most of the channels match as closely as one would expect given the experimental error bars, but there are some discrepancies. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00037g) with permission from the Royal Society of Chemistry

Product channels	CMB Expt. Ec = 32.6 kJ mol^−1	RRKM/ME Ec = 32.6 kJ mol^−1
	BF (%)	BF (%)
CH2CHCHCHO + H	6.2 ± 2.2	13.7 (T)
CH2CHCOCH2 + H		2.2 (T)
C4H4O + H2	1.8 ± 0.6	—
C3H6 + CO	20.2 ± 7.0	22.8 (S)
CH2CO + C2H4	6.9 ± 3.4	—
C3H5 + HCO	36.2 ± 12.0	44.4 (S)
CH2CHO + C2H3	9.5 ± 3.3	6.3 (T)
CH3CO + C2H3	0.4 ± 0.2	0.5 (T)
H2CO + C3H4	18.6 ± 9.3	9.2 (T)

---

The product distribution depends on the dynamics on the triplet PES before the intersystem crossing, indeed some of the products are apparently formed before intersystem crossing. The high level of agreement between the experiments and the model predictions, even in a case like this with close competition between multiple disparate reaction channels, indicates that many of the features of the PES must be accurate, (i.e. the quantum chemistry is quite good), and also that modern methods for computing microcanonical reaction rates (or at least the relative rates of competing channels) are quantitative, and that methods for computing intersystem crossing are at least semi-quantitative.

4.1 Microcanonical rate coefficients k(E): next steps

Although the Bhagde et al. (https://doi.org/10.1039/d2fd00008c) and Cavallotti et al. (https://doi.org/10.1039/d2fd00037g) papers, and many others, demonstrate the accuracy of current methods for predicting microcanonical rate coefficients for small polyatomics (in these cases molecules containing 4 carbon atoms) ab initio, there are significant challenges in extending these methods to a broader scope of reactions.

Current calculation methods rely heavily on accurate quantum chemistry calculations of the transition states. At present, the high-accuracy methods are affordable for reactions involving fewer than about 10 non-hydrogen atoms, but often are impractical for systems with more than about 20 non-hydrogen atoms. This is partially because of the N_electrons⁷ scaling of the CCSD(T)¹⁹ calculations that underlie most of these calculations, but also due to problems handling multiple large-amplitude motions and the associated exponential increase in the number of possible conformers discussed below.

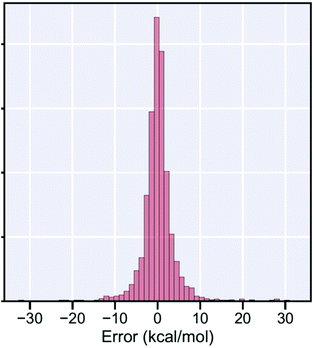
But fortunately many important reactions can be addressed using methods based on CCSD(T). With modern supercomputers, it is now possible to perform CCSD(T) calculations on thousands of reactions,¹² so many that one can use them as training data for machine learning,¹³ to construct fast estimators for barrier heights. These fast estimators are not 100% reliable, for a histogram of the deviations between our fast estimator and the actual CCSD(T) barrier heights see Fig. 8, but given enough training examples they can be more accurate than the much slower DFT calculations. These modern fast estimators for barrier heights can be combined with existing fast methods for estimating Arrhenius A factors (e.g. by Benson¹⁴) to quickly estimate high-pressure-limit rate coefficients. These fast fairly-accurate estimates are convenient for building kinetic models, and to identify which reactions in a system are likely to be important, and so require careful calculations.

Fig. 8 Histogram of the errors in our fast estimator of zpe-corrected reaction barrier height ΔE_o relative to high-accuracy CCSD(T)-F12a/cc-pVDZ-F12//wB97X-D3/def2-TZVP values for about 2000 reactions not included in the training set. The mean absolute error in the estimates is <3 kcal mol⁻¹, smaller than the average error in DFT calculations of these barriers.

Unfortunately, CCSD(T) and similar single-reference electronic structure methods do not work for all reactions. For reactions with species or transition states that are multi-reference in character, different electronic structure methods must be used, often requiring significantly more human effort and more computer power. So at present many of the reactions involving transition metals are impossible to compute accurately. There are also special difficulties computing reactions that involve heavy elements, where the non-relativistic Schroedinger equation is inaccurate. The shape of the PES at long bond-stretching distances (e.g. for roaming) can be difficult to compute, since multiple electronic states can have similar energies, one may need to use open-shell singlet methods rather than conventional closed-shell methods, and conventional basis sets may not be appropriate. Continued advances in quantum chemistry are needed to make quantitative predictions possible for a wider range of reactions, including reactions of larger species (e.g. the reactions nucleating particulate formation in combustion).

In this Discussion, Klippenstein pointed out that roaming-type reactions are very well-known in ion–molecule reactions, where they are often the dominant reaction channels over a broad range of conditions. One might expect roaming would also be important in any case where the two products have a strong interaction (e.g. hydrogen bond, van der Waals). The experiments reported by Suits suggest that roaming may continue to be important even well above the dissociation limit, even for small molecules, where presumably the interactions are weak. It would be interesting to explore if the understanding gained from ionic systems can be used to improve our ability to predict the behavior of neutral systems.

Several papers presented at this Discussion (e.g.https://doi.org/10.1039/d2fd00037g, https://doi.org/10.1039/d2fd00011c) demonstrated that it is now possible to compute microcanonical rate coefficients involving Born–Oppenheimer break-down, coupling more than one PES. Today these calculations are usually restricted to relatively small polyatomics, to reduce the computational expense, but the promising results shown at this Discussion suggest a broader range of systems are now coming within reach. But often these calculations will also require the use of multireference methods.

For all of the 20th century and into this century, the accuracy of k(E), k_∞(T), and K_eq(T) calculations was usually limited by errors in computed energies, particularly errors in barrier heights. Predicted Arrhenius A factors, entropies, and heat capacities were of course also imperfect, but their errors usually only made a minor contribution to the large total uncertainty. However, over the past ∼15 years quantum chemistry methods have greatly improved – I particularly highlight the F12 methods¹⁵ which have overcome many past problems with basis set convergence of CCSD(T) calculations – so now it is not uncommon to encounter situations where problems with identifying conformers and correctly handling large-amplitude motions noticeably affect the overall accuracy, and are more difficult than the high-level single-point energy calculations. This is not surprising: the number of conformers scales exponentially, roughly as 3^M, where M is the number of internal rotors. So doubling the size of a molecule or computing a TS for its self-reaction increases the CPU time required for the single-point CCSD(T) calculation by a factor of 2⁷ = 128, but doubling usually increases the number of conformers by about a factor of 3^M. If a DFT method that scales as N_electrons³ is used for the conformer search, and the size of the system is doubled, the cost of the conformer search scales up by 2³ × 3^M. If M = 5 for the original system, as in the 4-carbon QOOH molecule studied by Bhagde et al. (https://doi.org/10.1039/d2fd00008c), doubling the size of the system increases the CPU time required by almost a factor of 2000 (2³ × 3⁵ = 1944). That is, for many non-rigid molecules, conformer calculations have much worse scaling with molecule (or transition state) size than high-accuracy single-point calculations. Today we can do very good calculations on reactions involving fairly large rigid molecules and radicals (demonstrated e.g. by the paper presented by Mebel (https://doi.org/10.1039/d2fd00012a)), but systems of the same size with many floppy motions are often more challenging.

5 Pressure-dependent rate coefficients k(T,P)

The modern ability to accurately compute collisional energy transfer efficiencies and microcanonical rate coefficients ab initio allows us to construct the Master Equation (ME), and from it derive phenomenological pressure-dependent rate coefficients k(T,P). For situations where there is a significant gap between chemical reaction timescales and the collisional energy transfer timescales, and where the experimental timescale is much longer than the collisional energy transfer timescale, the Chemically Significant Eigenvalues (CSE) method^16–18 provides an excellent way to compute k(T,P).

At this Discussion, Osborn reported (https://doi.org/10.1039/d2fd00028h) recent re-measurements of the isomerization of 1,5-hexadiyne, one of the first complicated reaction systems studied using the CSE method.¹⁷ In combustion and pyrolysis, 1,5-hexadiyne is one of the initial adducts formed by propargyl recombination, a key reaction leading to aromatic ring formation. A model based on k(T,P) computed more than 15 years ago (and using exponential-down estimates of the collisional energy transfer efficiencies) gives predictions in good agreement with the new direct experimental measurements using the PEPICO technique, see Fig. 9.

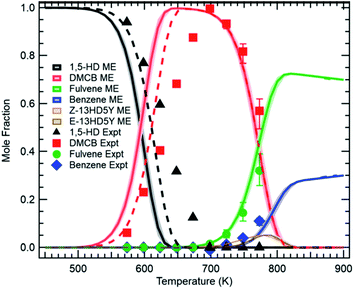Fig. 9 Direct measurements of C₆H₆ isomers formed from 1,5-hexadiyne pyrolysis (points) versus model predictions after ref. 17 (curves). Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00028h) with permission from the Royal Society of Chemistry.

There have now been many other experimental demonstrations of the accuracy of similar quantum chemistry + master equation predictions, including several at this Discussion (https://doi.org/10.1039/d2fd00030j, https://doi.org/10.1039/d2fd00024e, https://doi.org/10.1039/d2fd00045h, https://doi.org/10.1039/d2fd00031h, https://doi.org/10.1039/d2fd00039c), so these methods are now trusted to predict the behavior of pressure-dependent reaction systems before experimental data are available.

Doner presented such predictions at the Discussion, for the reactions of peroxy radicals formed from 2,4-dimethyl oxetane (https://doi.org/10.1039/d2fd00029f). Substituted oxetanes are known to be formed in partial oxidations of alkanes at pre-ignition temperatures, so these and analogous radicals are expected to be present in significant concentrations for some engine/fuel combinations.

A wide variety of products can be formed by these radicals, so Doner, Zádor, and Rotavera (https://doi.org/10.1039/d2fd00029f) used the automated KinBot program²⁰ to find many wells and transition states on the PES, and to help spawn the quantum chemistry and CSE calculations to obtain k(T,P) values for many reactions. The corresponding rate coefficients have complicated T (and P) dependence, see Fig. 10. The system shown in Fig. 10 is particularly interesting because it has more than one chiral center, and the consequent diastereomers have quite different reactivity and can form distinct products. To date, most kinetic models have ignored chirality, but that is clearly an inaccurate approximation.

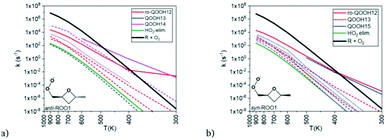Fig. 10 Predicted rate coefficients at 1 atm from the (a) anti and (b) syn peroxyl radicals shown to several different products as a function of time. The dashed lines are for well-skipping reactions. Notice how the change in the orientation of the methyl group significantly affects some of the k(T,P), favoring different products. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00029f) with permission from the Royal Society of Chemistry.

5.1 Pressure-dependent rate coefficients k(T,P): next steps

From one point of view, the field should be very pleased by the immense progress made in computing rate coefficients since the time of Lindemann, including several important advances in the last 20 years including accurate first principles k(E)'s and collisional energy transfer efficiencies, and the development of the CSE method for converting them into k(T,P). Can we build from this strong foundation to address a broader scope of problems?

One possible direction is to consider more complicated environmental effects on the rate coefficients, e.g. real rather than ideal gases. This direction of research would naturally lead towards how rate coefficients are affected if they occur in supercritical fluids, or even in normal fluids, i.e. solvent effects.

Reactions in the liquid phase may sound rather intimidating to an audience familiar with studying isolated small-molecule reactions occurring in a vacuum, but it is known that many reactions of neutrals have similar rate coefficients in solvent to those in the gas phase, suggesting the solvent effects may just be perturbations on the gas-phase reaction we understand well.

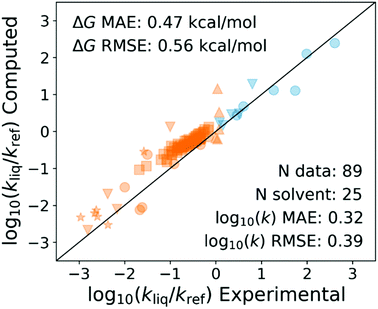
Recently my student Yunsie Chung computed the solvent effects on several free radical reactions (H-abstractions and radical additions to double bonds) from first principles using the COSMO-RS⁴⁷ method. The measured changes in rate coefficients in different solvents are compared with her predictions in Fig. 11. The predicted solvent effects are accurate enough (∼0.5 kcal mol⁻¹ errors, comparable to errors in careful calculations or measurements of gas phase E_a's) to give some hope that this may be the right approach. We have had excellent success predicting solvation of molecules,^21–24 even close to the critical point of the solvent,²¹ so it is perhaps not surprising that we can also compute the solvation energy of transition states.

Fig. 11 Predicted solvent effects vs. literature measurements on 9 different free-radical reactions in 25 different solvents, 295 K < T < 373 K, most at room temperature. The ratios are relative to the rates in gas phase, isooctane, or CCl₄, depending on data availability. The solvent effects change the rates by up to a factor of 1000× in either direction. The solvent effect predictions were made by Yunsie Chung, using COSMO-RS (TZVPD-FINE), based on DFT (ωB97X-D) calculations. The deviations correspond to errors in computed relative solvation free energies of about 0.5 kcal mol⁻¹.

Another interesting environmental effect is radiation. As discussed around the time of Lindemann's model, in most laboratory systems collisional energy transfer greatly dominates over radiative energy transfer, so radiation can be neglected. However, at very low pressures excited molecules may have a high probability of radiating before they suffer a collision, so radiative energy transfer cannot be ignored. At this Discussion, Plane presented (https://doi.org/10.1039/d2fd00025c) calculations showing that radiation puts a floor on the low-pressure-limit rate coefficient, Fig. 12. Interestingly, for the situation modeled, the low pressure limit appears to hit its floor around a pressure of 10⁻³ Torr, which is only a few orders of magnitude lower than the pressures used for many laboratory rate measurements. At a minimum the work by Plane and Robertson suggests we should modify our textbook discussions of the low-pressure-limit.

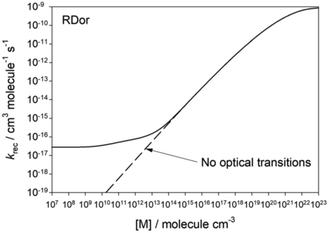Fig. 12 Predicted variation in the rate coefficient for SiO₂ + H₂O → OSi(OH)₂ as a function of pressure, at conditions relevant to the region near the star RDor. At low pressures the excited adduct is cooled primarily by radiation. Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00025c) with permission from the Royal Society of Chemistry.

Although there are many additional examples of interesting k(T,P) predictions such as Doner's and Plane's in the literature, with enough examples with good experimental validation to give the community confidence in the prediction methods, the Discussion highlighted that there are some reasons for concern about how phenomenological k(T,P) are computed, and even more questions about exactly what they mean.

To start with, there is a question about whether all the methods and software packages used to compute k(T,P) reliably give the same numerical values, and over what range of conditions reduced kinetic models made using these computed k(T,P) accurately replicate the solutions to the full master equations (and experiment). As Klippenstein pointed out, it is critical that all the inputs to the Master Equations (MEs) be clearly documented, including details such as symmetry numbers, how internal rotors were treated, and how densities of states were computed, to allow the calculations to be replicated. This proposal was strongly supported at the meeting; the next step would be to publish a clear statement of exactly what information should be archived with every ME calculation. Most current ME solvers use the exponential-down model for energy-transfer efficiencies, but the work of Jasper, Mullin, Burke, and others indicates more sophisticated energy-transfer models are needed. At this Discussion, Grinberg Dana, Robertson, and others advocated for the establishment of benchmark cases and round-robin comparisons to check that the different software packages for computing k(T,P) give the same results for the same inputs.

Johnson and Green (https://doi.org/10.1039/d2fd00040g) showed that various methods for computing k(T,P) from the ME give reduced models that sometimes deviate significantly from the full ME solution. This is sometimes due to fundamental failures of the methods, which are all based on approximations. But the largest errors are often due to numerical problems related to the extreme stiffness of the ME (or equivalently the very high condition number of the ME matrix). Sometimes both the numerical solution of the ME and the values of the derived k(T,P) are afflicted by numerical errors. Robertson pointed out that MESMER²⁵ can use octuple precision for its CSE implementation to try to ameliorate this. Most experiments do not validate all the k(T,P) over the full range. Slow experiments may only be sensitive to the slowest eigenvalue/eigenvector (this might be the case for the data shown in Fig. 9). Faster experiments such as shock-tube Schlieren measurements and some flash photolysis experiments can be sensitive to the fast chemical timescales and perhaps to some of the energy transfer timescales.

But there are also more fundamental problems with using a reduced phenomenological model based on a distinct-species Boltzmann zero-order picture to represent every system. Some years ago, Tsang noted that it is often possible to form some radicals with a nearly perfect-Boltzmann initial energy distribution, but it is not hard to find cases where more than half of those nascent Boltzmann-populated radicals have energies above the lowest reaction barrier. So very quickly about half of the initial population will be gone, and the population distribution will become very non-Boltzmann. Should the “species” be defined as the initial Boltzmann state, with extremely high reactivity and multi-exponential time-dependence, or the state achieved soon after, which is much more stable and kinetically well-behaved, but which represents less than half the concentration? This concept was pushed further by Labbe et al.²⁶ who developed the f_ne method to correct product branching ratios. At this Discussion, Burke (https://doi.org/10.1039/d2fd00054g) pointed out that for some species the populations of their higher energy states are so depleted that it can significantly affect their bimolecular reaction kinetics, i.e. the rates of elementary step reactions that do not ever form a complex could still be pressure-dependent.

This highlights the question “What is a chemical species?”, a major topic in the Discussion. One type of species definition is focused on chemical structure (geometry) or on spectroscopic signals that are sensitive to the atom positions. These definitions have the advantage of being tightly related to many common experimental measurements. IUPAC nomenclature, Lewis structures, and InChIs are all based on this sort of geometrical definition of a species. An alternative way of defining chemical species is based on time-dependence and chemical reactivity: the idea is that everything classified as a member of a single species in a kinetic model should have the same time evolution. Classifying A and B together as one species in a situation where B reacted away but A did not would not be sensible kinetically, even if A and B both gave exactly the same instrumental response in an experiment. And the reverse: as Georgievskii et al. have explained, at certain conditions it makes no sense to consider rapidly equilibrating isomers X and Y as distinct kinetic species even if they have very different geometries and spectra, since they will always have the same time evolution.¹⁸

In the high-pressure-limit, both types of definition are about the same: all the energy states of a molecule time-vary in unison because the Boltzmann energy distribution is maintained. In this perfect-Boltzmann limit many convenient relationships hold, e.g.eqn (2) is true even if the reaction is not equilibrated, providing a way to compute reverse rate coefficients from forward rate coefficients and thermochemistry:

K_eq(T) = k_forward(T)/k_reverse(T) (2)

It is challenging to find a species definition that works so well for isomers at low pressures and high temperatures. At those conditions the populations of different energy states of the same molecule can have very different time-dependencies, and react to form products in different ratios. In a low-P high-T condition, if one starts with a single isomer in a Boltzmann distribution, in a short time one will have a mixture of isomers, none of them in Boltzmann energy distributions, and the time-dependence of the decay of the initial molecule will be multi-exponential.

One could fall back to solving the full ME, since the energy-resolved species populations conform to our physical expectations of the behavior of a kinetic species. But that microcanonical representation includes an inconveniently large number of state variables, and the corresponding coupled differential equations are extremely stiff.

The eigenvectors of the ME matrix give sets of initial state populations that would uniformly decay as a single exponential, much as the Boltzmann populations of the energy states of a high-pressure-limit species all decay together as the species is consumed. This conforms to our idea of a chemical species, and is very convenient for mathematical treatment. But in a low pressure case, usually the eigenvectors include multiple isomer geometries, and most of the eigenvectors include negative numbers, so it is not clear that the eigenvectors provide a useful physical definition of a “species”. There are also an inconveniently large number of eigenvectors, one for each energy state of each molecule, so in practice one must truncate the representation. Commonly this is done by only explicitly considering the slower eigenvectors, and handling the effects of the many fast eigenvectors some other way, e.g. by Georgievskii et al.’s formula¹⁸ for bimolecular–bimolecular chemically-activated rate coefficients.

The CSE model starts from the fast–slow eigenvector separation, and then constructs a reduced kinetic model for the rate of change of the geometrically-defined isomers within the subspace defined by the slow eigenvectors. Within its limits of applicability, this approach gives accurate predictions for the time-evolution of the total population of each isomer, see Fig. 9 for an example. But note that the actual populations of the energy states of an isomer do not have a common time-evolution until all but the slowest mode are exhausted, and as a consequence the reactivity of the isomer (e.g. in bimolecular reactions) varies with time. This change in the populations of the high-energy states is related to the issue addressed by Burke's paper (https://doi.org/10.1039/d2fd00054g). Because of the time-variation of the energy distribution, some types of spectroscopy (e.g. of hot-bands) would give signals that are not proportional to the isomer concentration, which could cause confusion. All these effects are typically ignored in phenomenological models today, since in many cases the system is nearly-Boltzmannian on the time scale of bimolecular reactions or spectroscopic measurements.

It is not so clear how to define a useful analogue to eqn (2) for species whose population distributions are far from Boltzmann. In that case, one would not be safe assuming eqn (2) is accurate if K_eq was computed in the normal (perfect-Boltzmann) way. Further analyses and clear discussions about different useful definitions of species would be helpful, as would improved public software tools to help handle the complexity of the situation. At this Discussion, Klippenstein proposed the community try to build a more detailed kinetic model for the energy-resolved species populations, and carefully compare its predictions to the common phenomenological models, to check the accuracy of the conventional approach to kinetic modeling and identify what improvements are needed.

6 Incorporating k(T,P) into kinetic models

Despite the issues discussed above, with modern methods we appear to be able to calculate and/or measure k(T,P) which seem to be accurate enough for useful kinetic modeling. The next step is to incorporate these pressure-dependent rate coefficients into the kinetic models.

Usually, kinetic models have been constructed ignoring pressure-dependence initially, i.e. using rough estimates of k(T). These initial rough models can be constructed manually, though the process gets quite tedious, so use of automated approaches is increasingly popular.^27,44 Later, after the initial reaction network has been constructed, the model is gradually improved by replacing some of the roughly estimated k(T) with more realistic k(T,P) values, sometimes from experiment but more commonly computed using quantum chemistry and ME methods presented at this Faraday Discussion. This iterative model-construction procedure seems a bit risky: the pressure correction to a rate coefficient k(T) could be many orders of magnitude, so the initial model could be quite wrong, making it difficult to correctly assess if the reaction network is complete or which reactions are important. But in many cases only a few of the sensitive reactions in a kinetic model are strongly pressure-dependent, and often the person constructing the model is aware of most of them, so this procedure can work.

A nice example of this incremental ‘replace some k(T) by k(T,P)’ approach was presented at the Discussion by Aerssens, who applied it to a large complicated kinetic model for the pyrolysis of ethane and propane at reaction conditions typical of commercial steam crackers (large, high-temperature flow reactors used to produce alkenes and other basic chemicals). By replacing pressure-independent estimates of a dozen k(T) in the large model with more accurate k(T,P), Aerssens significantly improved the model (https://doi.org/10.1039/d2fd00032f). The final predictions closely match the yields of many of the most important components in the product stream, Fig. 13.

Fig. 13 Predictions of a large kinetic model for the outlet composition from steam cracking of propane vs. experimental measurements, after replacing 12 important rate coefficients in the model with high accuracy k(T,P). Reproduced from Faraday Discussions (https://doi.org/10.1039/d2fd00032f) with permission from the Royal Society of Chemistry.

6.1 Incorporating k(T,P) into kinetic models: next steps

This Discussion has highlighted the complexity of unimolecular reactions. Usually there are multiple isomerization and bimolecular product channels, and the system is time-evolving as a multi-exponential, making it challenging to experimentally measure all the processes. The rates and product distributions can change by many orders of magnitude with changes in temperature and pressure, but usually measurements are only feasible over a limited (T,P) range. As many papers presented at this Discussion demonstrated, computations can be very helpful in improving our understanding of the reacting system. But, unfortunately, calculating even a single rate coefficient k(T,P) often involves exploring a complicated PES involving many isomers and transition states, each with many conformers. Usually coupled-cluster or even more expensive quantum chemistry calculations are required to achieve useful accuracy. The collisional energy transfer efficiency calculations with different bath gases are also non-trivial, and they lead to complicated expressions described by several parameters. The last step, computing phenomenological k(T,P) using ME techniques takes less computer time, but has its own potential pitfalls, as discussed above.

Constructing an accurate kinetic model for a complicated reaction system, such as the pyrolysis system of Aerssens et al. (https://doi.org/10.1039/d2fd00032f), may require repeating that process for more than a thousand k(T,P)'s. Clearly, automation is needed. At present, many of the steps in the sequence of calculations have been automated, but there are still challenges and gaps.

Jasper and co-workers (https://doi.org/10.1039/d2fd00038e)¹⁰ have succeeded in computing collisional energy transfer efficiencies using well-established molecular dynamics software packages that automate many of the tasks. However, this workflow has not yet been used by many researchers, and the output of these calculations does not match the expected inputs for most existing ME codes, so there is considerable work to do to automate these calculations.

Very importantly, most of the steps in the electronic structure calculations have been automated, and are included in well-tested software packages, often with good documentation and user support. For many years one of the main challenges has been to provide very good guesses at transition state geometries, so the TS calculations would converge correctly. But in recent years a variety of methods have been developed that are making this less of a bottleneck, and some have been carefully validated.^20,28–30 There are still some steps in the quantum chemistry workflow that need to be better automated (e.g. multi-reference methods, methods for computing reactions involving Born–Oppenheimer breakdown, methods for conformers/rotors, error detection/correction).

Almost all of the ME software packages used to compute k(T,P) were designed to interface with a human user, not to be run automatically. There are several ongoing efforts to make these calculations more automatic. It is possible, using the Reaction Mechanism Generator (RMG),³¹ to automatically construct kinetic models including computations of all the k(T,P) during the construction process. However, this is quite computationally demanding, since with the RMG approach the computer decides what species and reactions belong in the model, and also what set of isomers and reactions belong in each Master Equation (ME), and estimates all the parameter values. So far this has only been done for a handful of systems, using fairly rough approximations for the inputs to the ME and for computing hundreds of thousands of k(T,P). For a recent work on automatically identifying which isomers and reactions should be included in the ME see ref. 32. At this meeting Doner discussed the screening method she used to avoid computing all the isomers (https://doi.org/10.1039/d2fd00029f).

A challenge for the near future is to make the end-to-end automation seamless, so it would be practical for a single researcher (with access to a supercomputer) to generate a fairly accurate prediction of the kinetics of his or her system of interest, including accurate estimates of all the important k(T,P). This could transform kinetics,³³ much as the development and dissemination of good software for DFT calculations at the end of the 20th century has transformed other subfields of chemistry. Achieving this goal will likely also require improved data management practices, since even at present both the experimental and computational data sets are becoming so large that they are difficult to manage, and very hard for someone not involved in the original work to replicate. And in addition to the technical challenges, there are a variety of social and economic challenges that will need to be addressed to make this vision a reality – who will fund and maintain such complicated software? How to set up the right incentives and provide the right tools to encourage good data management?

Here we have focused on the challenges of automating the calculations, which seems to be the clear next step. But after that work is completed, there will be perhaps even larger challenges in the future to design experiments to test very complicated models that make a huge number of predictions, and to automate the comparisons between complicated models and large experimental data sets, to make it easier to learn what the experiment is teaching us.

7 Conclusions

Looking backward over the past 100 years, the advances in our understanding and ability to predict unimolecular reactions have been astounding. Even in the past ∼30 years this field has advanced tremendously. About 30 years ago, many basic reaction concepts, and the algorithms and approximations leading to today's quantitative models were being solidified and disseminated,^5,6,34–39 roughly contemporaneously with important unambiguous direct^40,41 and indirect⁴²k(E) measurements. During the past 20 years computational methods and approximations (as well as computers) have significantly improved, so today many researchers routinely compute rather accurate k(T,P)'s, and have used them to achieve amazing understanding of rather complicated systems, as amply demonstrated at this Discussion (https://doi.org/10.1039/d2fd00037g, https://doi.org/10.1039/d2fd00032f, https://doi.org/10.1039/d2fd00028h, https://doi.org/10.1039/d2fd00030j, https://doi.org/10.1039/d2fd00024e, https://doi.org/10.1039/d2fd00045h, https://doi.org/10.1039/d2fd00031h, https://doi.org/10.1039/d2fd00039c). This is far beyond what could have been envisioned at the time of Lindemann's presentation;¹ indeed in the 1920's the expert view was that solving the equations to compute chemical reactions from first principles was impossible.⁴³

7.1 Looking forward

The current quality of model vs. experiment comparisons indicates that both the models and the experiments are in very good shape. But there are still many unimolecular reactions which we cannot predict reliably, reactions and reaction conditions that are not experimentally accessible, and reasons to suspect there might sometimes be issues in the theory/approximations/algorithms we are using. Can we get the calculations exactly right? Can we extend our computational methods to predict a much broader scope of systems, not just smallish molecules in the gas phase? Can we extend our experimental methods to match? More generally, can we build on the excellent work this community has done over the past 100 years, and bring what we have learned to advance other subfields of the chemical sciences?

So far, we are mostly working on small molecules, and already the complexity is such that many of our papers are written by fairly large teams of experimentalists and theoreticians, with associated organizational and financial challenges, not all of them resolved. Moving to much larger molecules will require extensive automation, and will make comparisons with experiment even more challenging. Good shared software, better data management, and continued good cooperation within our community will be needed to continue to make rapid progress.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I acknowledge Yunsie Chung for sharing her calculations and for making Fig. 11, and Kevin Spiekermann for making Fig. 8. I thank Struan Robertson for helpful conversations and for carefully reading a draft of this manuscript. I am grateful for funding from the Gas Phase Chemical Physics program of the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under Award DE-SC0014901. Additional funding from the MIT-Portugal Program is gratefully acknowledged.

Notes and references

1. F. A. Lindemann, Discussion on the Radiation Theory of Chemical Action, Trans. Faraday Soc., 1922, 17, 598–606.
2. R. A. Marcus, Unimolecular Dissociation and Free Radical Recombination Reactions, J. Chem. Phys., 1952, 20, 359–364.
3. R. G. Gilbert, K. Luther and J. Troe, Theory of Thermal Unimolecular Reactions in the Fall-off Range. II. Weak Collision Rate Constants, Ber. Bunsen-Ges. Phys. Chem., 1983, 87, 169–177.
4. W. Forst, Theory of Unimolecular Reactions, Academic Press, 1973.
5. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell, Oxford, 1990.
6. K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, 2nd edn, 1996.
7. R. D. van Zee, M. F. Foltz and C. B. Moore, Evidence for a second molecular channel in the fragmentation of formaldehyde, J. Chem. Phys., 1993, 99, 1664.
8. D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, The roaming atom: straying from the reaction path in formaldehyde decomposition, Science, 2004, 306(5699), 1158–1161.
9. S. J. Klippenstein, Y. Georgievskii and L. B. Harding, Statistical Theory for the Kinetics and Dynamics of Roaming Reactions, J. Phys. Chem. A, 2011, 115, 14370–14381.
10. A. W. Jasper, K. M. Pelzer, J. A. Miller, E. Kamarchik, L. B. Harding and S. J. Klippenstein, Predictive a priori pressure-dependent kinetics, Science, 2014, 346(6214), 1212–1215.
11. W. H. Green, A. J. Mahoney, Q.-K. Zheng and C. B. Moore, Bond-Breaking without Barriers II: Vibrationally Excited Products, J. Chem. Phys., 1991, 94, 1961.
12. K. A. Spiekermann, L. Pattanaik and W. H. Green, High Accuracy Barrier Heights, Enthalpies, and Rate Coefficients for Chemical Reactions, Sci. Data, 2022, 9, 417.
13. K. A. Spiekermann, L. Pattanaik and W. H. Green, Fast Predictions of Reaction Barrier Heights: Toward Coupled-Cluster Accuracy, J. Phys. Chem. A, 2022, 126, 3976–3986.
14. S. W. Benson, Thermochemical Kinetics. Methods for the Estimation of Thermochemical Data and Rate Parameters, Wiley & Sons, NY, 2nd edn, 1976.
15. T. B. Adler, G. Knizia and H.-J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127, 221106.
16. J. A. Miller and S. J. Klippenstein, The Recombination of Propargyl Radicals: Solving the Master Equation, J. Phys. Chem. A, 2001, 105, 7254–7266.
17. J. A. Miller and S. J. Klippenstein, The Recombination of Propargyl Radicals and Other Reactions on a C₆H₆ Potential, J. Phys. Chem. A, 2003, 107, 7783–7799.
18. Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, Reformulation and solution of the master equation for multiple-well chemical reactions, J. Phys. Chem. A, 2013, 117, 12146–12154.
19. J. F. Stanton, Why CCSD(T) works: a different perspective, Chem. Phys. Lett., 1997, 281, 130–134.
20. R. van de Vijver and J. Zador, KinBot: Automated Stationary Point Search on Potential Energy Surfaces, Comput. Phys. Commun., 2020, 248, 106947.
21. Y. Chung, R. J. Gillis and W. H. Green, Temperature-dependent solvation free energy estimation from minimal data, AIChE J., 2020, 66, e16976.
22. F. H. Vermeire and W. H. Green, Transfer learning for solvation free energies: from quantum chemistry to experiments, Chem. Eng. J., 2021, 418, 129307.
23. Y. Chung, F. H. Vermeire, H. Wu, P. J. Walker, M. H. Abraham and W. H. Green, Group Contribution and Machine Learning Approaches to Predict Abraham Solute Parameters, Solvation Free Energy, and Solvation Enthalpy, J. Chem. Inf. Model., 2022, 62, 433–446.
24. F. H. Vermeire, Y. Chung and W. H. Green, Predicting Solubility Limits of Organic Solutes for a Wide Range of Solvents and Temperatures, J. Am. Chem. Soc., 2022, 144, 10785–10797.
25. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER: An Open-Source Master Equation Solver for Multi-Energy Well Reactions, J. Phys. Chem. A, 2012, 116(38), 9545–9560.
26. N. J. Labbe, R. Sivaramakrishnan, C. F. Goldsmith, Y. Georgievskii, J. A. Miller and S. J. Klippenstein, Weakly-bound free radicals in combustion: “Prompt” dissociation of formyl radicals and its effect on laminar flame speeds, J. Phys. Chem. Lett., 2016, 7, 85–89.
27. S. Vernuccio and L. J. Broadbelt, Discerning complex reaction networks using automated generators, AIChE J., 2019, 65, e16663.
28. S. Maeda and Y. Harabuchi, On benchmarking of automated methods for exhaustive reaction path search, J. Chem. Theory Comput., 2019, 15, 2111–2115.
29. C. A. Grambow, A. Jamal, Y.-P. Li, W. H. Green, J. Zador and Y. V. Suleimanov, Unexpected Unimolecular Reaction Pathways of a gamma-Ketohydroperoxide from Combined Application of Automated Reaction Discovery Methods, J. Am. Chem. Soc., 2018, 140, 1035–1048.
30. L. Pattanaik, J. B. Ingraham, C. A. Grambow and W. H. Green, Generating Transition States with Deep Learning, Phys. Chem. Chem. Phys., 2020, 22, 23618–23626.
31. M. Liu, A. Grinberg Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee, E. J. Mazeau, K. Blondal, R. H. West, C. F. Goldsmith and W. H. Green, RMG 3.0: Advances in Automatic Mechanism Generation, J. Chem. Inf. Model., 2021, 61, 2686–2696.
32. M. S. Johnson, A. Grinberg Dana and W. H. Green, A Workflow for Automatic Generation and Efficient Refinement of Pressure Dependent Networks, Combust. Flame , submitted..
33. W. H. Green, Moving from Postdictive to Predictive Kinetics in Reaction Engineering, AIChE J., 2020, 66, e17059.
34. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, 1989.
35. D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current Status of Transition Theory, J. Phys. Chem., 1996, 100, 12771–12800.
36. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098.
37. C. Lee, W. Yang and R. G. Parr, Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
38. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
39. S. J. Klippenstein, A. L. L. East and W. D. Allen, A first-principles theoretical determination of the rate constant for the dissociation of singlet ketene, J. Chem. Phys., 1994, 101, 9198.
40. L. R. Khundkhar, J. L. Knee and A. H. Zewail, Picosecond photofragment spectroscopy. 1. Microcanonical state-to-state rates of the reaction NCNO = CN + NO, J. Chem. Phys., 1987, 87, 77.
41. E. R. Lovejoy, S. K. Kim and C. B. Moore, Observation of transition-state vibrational thresholds in the rate of dissociation of ketene, Science, 1992, 256(5063), 1541–1544.
42. W. H. Green, C. B. Moore and W. F. Polik, Unimolecular Reaction Rates and Transition States, Annu. Rev. Phys. Chem., 1992, 43, 591–626.
43. P. A. M. Dirac, Quantum Mechanics of Many-Electron Systems, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
44. C. Cavallotti, Automation of chemical kinetics: status and challenges, Proc. Combust. Inst., 2022 DOI:10.1016/j.proci.2022.06.002.
45. M. C. King and K. J. Laidler, Chemical kinetics and the radiation hypothesis, Arch. History Exact Sci., 1984, 30, 45–86.
46. C. Hinshelwood, The Kinetics of Chemical Change in Gaseous Systems, Clarendon Press, Oxford, 1926.
47. A. Klamt, V. Jonas, T. Buerger and J. C. W. Lorenz, Refinement and Parameterization of COSMO-RS, J. Phys. Chem. A, 1998, 102, 5074–5085.

---