 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The unimolecular decomposition of dimethoxymethane: channel switching as a function of temperature and pressure†
Tobias M.
Pazdera
,
Johannes
Wenz
and
Matthias
Olzmann
 *
*
Institut für Physikalische Chemie, Karlsruher Institut für Technologie (KIT), Kaiserstr. 12, 76131 Karlsruhe, Germany. E-mail: matthias.olzmann@kit.edu
First published on 31st March 2022
Abstract
Branching ratios of competing unimolecular reactions often exhibit a complicated temperature and pressure dependence that makes modelling of complex reaction systems in the gas phase difficult. In particular, the competition between steps proceeding via tight and loose transition states is known to present a problem. A recent example from the field of combustion chemistry is the unimolecular decomposition of CH3OCH2OCH3 (DMM), which is discussed as an alternative fuel accessible from sustainable sources. It is shown by a detailed master equation analysis with energy- and angular-momentum-resolved specific rate coefficients from RRKM theory and from the simplified statistical adiabatic channel model, how channel switching of DMM depends on temperature and pressure, and under which experimental conditions which channels prevail. The necessary molecular and energy data were obtained from quantum-chemical calculations at the CCSD(F12*)(T*)/cc-pVQZ-F12//B2PLYP-D3/def2-TZVPP level of theory. A parameterization describing the channel branching over extended ranges of temperature and pressure is derived, and the model is used to simulate shock tube experiments with detection by atomic resonance absorption spectroscopy and time-of-flight mass spectrometry. The agreement between the simulated and experimental concentration–time profiles is very good. The temperature and pressure dependence of the channel branching is rationalized, and the data are presented in a form that can be readily implemented into DMM combustion models.
1 Introduction
The kinetics of a unimolecular reaction in the gas phase is known to be governed by the competition between collisional energy transfer and the reactive steps of the energized reactant molecule.1 For competing unimolecular reactions of a given reactant, this often results in a complicated temperature and pressure dependence of the corresponding branching ratios, which can make modelling of complex reaction systems a difficult task. In particular, the competition between reactive steps proceeding via tight and loose transition states can cause problems (see e.g. ref. 2–5).A recent example from the field of combustion chemistry are the unimolecular decomposition reactions of oxymethylene ethers (OMEs) (see e.g. ref. 6). These compounds are discussed as additives or replacements for conventional diesel fuel7–9 because they possess diesel-compatible properties7,8 and may be produced sustainably.10–12 Moreover, due to their oxygen content and the lack of C–C bonds, OMEs lead to reduced soot formation and hence allow for combustion conditions where NOx emissions can be kept low.13–15 The smallest OME homologue, dimethoxymethane (DMM ≡ OME-1; where n in OME-n denotes the number of CH2O units in the CH3O(CH2O)nCH3 backbone), plays a particular role because, besides representing a fuel additive in itself,13 it can also serve as a model compound for the development of combustion mechanisms for higher OMEs.6
A key process for the autoignition of any fuel/O2 mixture is radical production from the closed-shell fuel molecule. This radical production can proceed via different pathways mainly depending on temperature. At low temperatures (T < 1000 K), bimolecular H abstraction reactions, initially by O2, are crucial whereas at higher temperatures also unimolecular decomposition reactions of the fuel molecule can become relevant (see e.g. ref. 16 and 17). If such radical-producing unimolecular decomposition channels compete with decomposition channels that yield closed-shell species, the kinetic branching ratio between these mechanistically different pathways is an influential quantity in combustion modelling. The complicated temperature and pressure dependence of this channel branching is, however, often difficult to quantify (see e.g. ref. 5 and the literature cited therein).
In the present work, we examine this problem of the competing unimolecular decomposition reactions of DMM, where the following molecular (R1)–(R6) and radical (R7)–(R10) decomposition channels are discussed:18–20
| CH3OCH2OCH3 → CH3OH + trans-CH3OCH | (R1) |
| CH3OCH2OCH3 → CH3OH + cis-CH3OCH | (R2) |
| CH3OCH2OCH3 → CH3OH + CH2OCH2 | (R3) |
| CH3OCH2OCH3 → H2CO + CH3OCH3 | (R4) |
| CH3OCH2OCH3 → H2CO + CH3CH2OH | (R5) |
| CH3OCH2OCH3 → CH4 + CH3OCHO | (R6) |
| CH3OCH2OCH3 → CH3 + OCH2OCH3 | (R7) |
| CH3OCH2OCH3 → CH3O + CH2OCH3 | (R8) |
| CH3OCH2OCH3 → CH3OCH2OCH2 + H | (R9) |
| CH3OCH2OCH3 → CH3OCHOCH3 + H | (R10) |
To trace back the origin of this set of reactions and to illustrate how the combustion chemistry of DMM can benefit from modern unimolecular rate theory, we briefly outline in the following the development of DMM pyrolysis and combustion mechanisms over the past two decades.
A first kinetic model for DMM oxidation was published in 2001 by Daly et al.21 to evaluate jet-stirred reactor experiments. In this model, the rate coefficients for the initial DMM decomposition reactions were taken from the corresponding reactions of dimethyl ether (DME) and diethyl ether (DEE). Nine years later, Dias et al.22 modelled DMM/O2/Ar flames, adopting the rate coefficients for the DMM-specific reactions from ref. 21. The same data were also used as a basis to model the results of a high-pressure flow tube study by Marrodán et al.23 in 2015. All these mechanisms21–23 have in common that for the unimolecular decomposition of DMM only the bond dissociation channels (R7)–(R10) were considered.
In 2017, Sun et al.24 in their modelling of OME-3 flames included both the radical channels (R7)–(R10) and the molecular elimination channel (R4), and parameterized its rate coefficient in analogy to the corresponding channel in DEE decomposition. In the same year, Hu et al.25 used a modified DMM model from Curran et al. (not readily available in the literature), which contained a channel CH3OCH2OCH3 → CH3OH + CH3 + CHO. In analogy to ref. 24, He et al.26 included in their model of OME-3 combustion, a molecular channel RH → R′H + CH2O as a general initiation step for OME-1 to OME-3. At about the same time, Vermeire et al.27 developed a model to describe DMM oxidation in jet-stirred reactor experiments but again considered only the two C–O bond fission steps. This restriction (accounting for C–O bond fission only) also applies to the models by Sun et al.,28 Peukert et al.,29 and Golka et al.30,31 (though in ref. 28, the elimination channel CH3OCH2OCH3 → CH3OH + CH3 + HCO is listed in the ESI).
For the first time, two molecular elimination channels, namely (R4) and CH3OCH2OCH3 → CH3OH + CH3 + HCO, were explicitly considered and discussed by Jacobs et al.32 but with rate coefficients again from analogy considerations of DME and DEE. With this model, the authors of ref. 32 were able to describe their ignition delay time experiments as well as other experimental studies from the literature. Only in 2020, Yu et al.,18 in a micro flow-tube/photoionization study, obtained experimental evidence for CH3OH as a direct thermal decomposition product of DMM. In accompanying quantum chemical calculations at CBS-QB3 level of theory,33 a total of 6 different molecular elimination channels, (R1)–(R6), were identified.18 In particular, it was found that the threshold energies of reactions (R1)–(R4) are well below the bond dissociation energies corresponding to (R7)–(R10). On the basis of microcanonical rate coefficients from Rice–Ramsperger–Kassel–Marcus (RRKM) theory,34,35 it was concluded that the latter bond dissociation reactions are unlikely as primary initial pyrolysis steps in comparison to the isomerization–elimination reactions.18
At about the same time, Sun et al.19 characterized 8 DMM decomposition channels (2 radical, 6 molecular) by quantum chemical calculations, to model their flow reactor pyrolysis experiments. These authors19 also found the low-lying molecular elimination reactions (R1)/(R2), (R3), and (R4) as well as three H2-eliminating reactions. But they concluded that under their experimental conditions (temperatures ranging from 783 to 1396 K at pressures of 30 and 760 torr), CH3OH elimination reactions are not competitive enough to notably influence fuel consumption. In a recent purely theoretical study, Al-Otaibi et al.20 characterized 11 DMM decomposition pathways (7 radical, 4 molecular) with density functional theory (DFT) and CBS-QB3 calculations. They also calculated canonical rate coefficients from RRKM theory and predicted a predominance of the bond dissociation reaction (R7) over the kinetically most favored complex decomposition reaction (R4) at p = 1 bar and T = 300–2000 K. Most recently, Li et al.36 modelled their high-temperature ignition delay time measurements (shock tube, T = 1050–1450 K, p = 1–10 atm) with an updated DMM mechanism, adopting the kinetic parameters of the radical DMM decomposition reactions from ref. 31. In this work,36 the molecular elimination channels were found to be unimportant.
So in total, a puzzling picture arises. On the one hand, there is striking theoretical evidence for molecular elimination channels in DMM with threshold energies well below the C–O bond dissociation energies. On the other hand, it appears as if almost all DMM pyrolysis experiments performed so far (with the exception of those from ref. 18) could be well described by taking into account the bond dissociation reactions only. It is the aim of the present work to contribute to the resolution of this apparent contradiction by applying quantum chemistry, statistical rate theory and kinetic-mechanistic modelling.
We use highly accurate quantum chemical methods and a multi-channel master equation approach to calculate thermal rate coefficients for the unimolecular decomposition pathways of DMM as a function of temperature and pressure. We discuss the varying contributions of radical and molecular channels to the overall kinetics of DMM pyrolysis at different temperatures and pressures. On the basis of our results, we propose an updated mechanism for DMM pyrolysis and use it to model earlier experimental data. We show that depending on the experimental conditions, either the molecular or the radical channels prevail, and we discuss the consequences for DMM pyrolysis under different experimental regimes.
2 Methodology
2.1 Quantum chemical calculations
Optimized geometries, the resulting rotational constants, and the harmonic vibrational wavenumbers of all stationary points on the potential energy surface that are relevant for reactions (R1)–(R10), were calculated with DFT at B2PLYP-D3/def2-TZVPP levels of theory.37–40 In a recent paper, Vuckovic and Burke41 demonstrated that this method is highly accurate in predicting geometries. It outperforms in many cases, other currently used density functionals and is of course more cost effective than ab initio methods of comparable accuracy. For the molecular reaction pathways (R1)–(R6), we additionally performed intrinsic reaction coordinate (IRC) calculations42 at the same level of theory to verify the transition states found and to provide potential energy profiles for tunneling corrections (see below). For all these geometry calculations, the Gaussian 16 software package43 was used.Single-point electronic energies of the stationary points were calculated with explicitly correlated coupled cluster theory at the CCSD(F12*)(T*)/cc-pVQZ-F12 level44–46 using the TURBOMOLE 7.4 software package.47 Results from benchmark studies for similar methods48 multiplied by a recommended correction factor of 2.5 for the 95% confidence limits,49 give estimated uncertainties for calculated reaction energies of ±2 kJ mol−1 for closed-shell systems and of ±3 kJ mol−1 for open-shell systems. While uncertainties of this magnitude may have a slight influence on the numerical values of the predicted branching ratios, they do not change the qualitative picture of the interplay between radical and molecular channels in the unimolecular decomposition of DMM.
2.2 Statistical rate theory and master equation calculations
Rate coefficients as a function of temperature and pressure for reactions (R1)–(R10) were obtained by solving a steady-state, one-dimensional (i.e. energy-resolved), ten-channel thermal master equation.50–52 We used a detailed balanced stepladder model for collisional energy transfer and calculated energy-specific rate coefficients from RRKM theory for reactions (R1)–(R6) and from the simplified statistical adiabatic channel model (s-SACM)53,54 for reactions (R7)–(R10). The anisotropy parameter of the s-SACM was set to its standard value of α/β = 0.5.55 Angular momentum conservation was accounted for in all reactions by calculating the energy-specific rate coefficients, ki(E,〈J〉T), for thermally averaged angular momentum quantum numbers, 〈J〉T, at the given temperature T in the master equation. Energy- and angular-momentum-dependent densities and sums of states were determined by direct counting procedures56,57 in the rigid rotor/harmonic oscillator approximation. Neither vibrational frequencies nor zero-point vibrational energies were scaled because no scaling factors are available for the dispersion-corrected double-hybrid functional. Moreover, scaling factors tend to cancel in rate coefficients calculated with statistical rate theory. For reactions (R1)–(R6), one-dimensional tunneling corrections58,59 of the Wentzel–Kramers–Brillouin type based on the IRC curves were applied. Tunneling through the centrifugal barriers for reactions (R7)–(R10) was neglected. The master equation was solved with the average energy transferred per down collision, 〈ΔE〉d (=ΔESL, the step size of the stepladder model51,60), as the only adjustable parameter; it was fitted to the sum of the temperature- and pressure-dependent rate coefficients of the C–O bond dissociation channels (R7) and (R8), which were determined in the earlier shock-tube experiments of this laboratory.31 The bath gas in these experiments was argon, and the Lennard–Jones parameters used in our calculations were taken from ref. 29. The channel-specific canonical rate coefficients ki(T,P) were obtained by averaging the microcanonical rate coefficients, ki(E,〈J〉T), over the normalized steady-state distribution of DMM, ñss(E; T,P), obtained as the solution of the ten-channel master equation: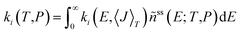 | (1) |
The details of our specific unimolecular rate theory implementations are given in ref. 61–63 and the literature cited therein. The master equation calculations were carried out over broad temperature and pressure ranges of T = 800–1800 K and p = 10−5 to 103 bar, respectively.
2.3 Kinetic modelling
The kinetic data calculated in the present work for the unimolecular decomposition steps (R1)–(R10) were incorporated in the DMM pyrolysis model from ref. 23 as modified in ref. 30. The entire mechanism is given in a machine-readable form (CHEMKIN format, see e.g. ref. 64 and 65) in the ESI.† For the simulations of the shock tube experiments, the program package OpenSMOKE++ was used.66 This program package, which is compatible with the CHEMKIN input format, numerically solves the system of coupled differential equations arising from a given reaction mechanism (elementary reactions, rate parameters and thermodynamic data) and provides, among other things, concentration–time profiles for all species. For the actual simulations of the present work, the option of a homogeneous batch reactor under adiabatic conditions in a constant volume regime was chosen. This approximation is justified for the conditions behind reflected shock waves with sufficiently short reaction times below 2 ms. At these conditions, heat loss and other non-ideal shock wave behavior can be neglected.3 Results and discussion
3.1 Quantum chemical calculations
A schematic potential energy diagram of reactions (R1)–(R10), summarizing the quantum chemical results of the present work, is shown in Fig. 1. The most important energetic quantities are collected and compared with values from the literature in Table 1, and the corresponding molecular structures are illustrated in Fig. S1 and listed in Table S1 of the ESI.† In agreement with ref. 18, we found for the four molecular elimination channels (R1)–(R4) threshold energies below the bond dissociation energies of (R7)–(R10) and for the two molecular elimination channels (R5) and (R6) threshold energies higher than those bond dissociation energies. This finding is in line with the results of ref. 19 and 20 though not all of these channels were discussed therein. On the other hand, in ref. 19 and 20 additional unimolecular reaction channels of DMM were mentioned but as the corresponding threshold energies are comparatively high, they appear to be of limited relevance for the pyrolysis kinetics. The agreement between the coupled cluster results of ref. 19 and this work is very good with the largest (unsigned) deviation being 2.3 kJ mol−1 and the average deviation being 0.9 kJ mol−1. The CBS-QB3 results of ref. 18 also reasonably agree (largest deviation: 12.3 kJ mol−1, average deviation: 4.3 kJ mol−1). The reason for the differences between the CBS-QB3 results from ref. 20 and those from ref. 18, which should be identical in principle, is unclear.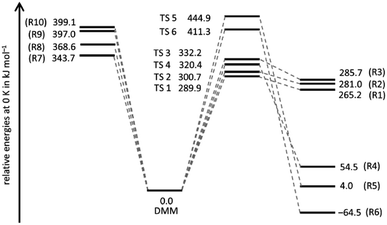 | ||
| Fig. 1 Energies relative to the energy of DMM of the products of reactions (R1)–(R10) and the transitions states (TS i) of the molecular channels (R1)–(R6). | ||
| Reaction (product pair) | This worka | Ref. 18b | Ref. 19c | Ref. 20d |
|---|---|---|---|---|
| a CCSD(F12*)(T*)/cc-pVQZ-F12//B2PLYP-D3/def2-TZVPP (T = 0 K). b CBS-QB3 (T unspecified). c CCSD(T)-F12/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ (T = 0 K). d CBS-QB3 (T = 0 K). e Toward oxirane + CH3OH. | ||||
| R1 (CH3OH + trans-CH3OCH) | 289.9 | 294 | 292.2 | — |
| R2 (CH3OH + cis-CH3OCH) | 300.7 | 305 | — | — |
| R3 (CH3OH + CH2OCH2) | 332.2 | 336 | 332.2 | 327.6e |
| R4 (H2CO + CH3OCH3) | 320.4 | 321 | 320.7 | 309.0 |
| R5 (H2CO + CH3CH2OH) | 444.9 | 443 | — | — |
| R6 (CH4 + CH3OCHO) | 411.3 | 409 | — | 398.9 |
| R7 (CH3 + OCH2OCH3) | 343.7 | 356 | 344 | 338.7 |
| R8 (CH3O + CH2OCH3) | 368.6 | 374 | 368 | 364.1 |
| R9 (CH3OCH2OCH2 + H) | 397.0 | 393 | 400 | 400.9 |
| R10 (CH3OCHOCH3 + H) | 399.1 | 403 | 401 | 402.5 |
In general, the absolute accuracy of quantum chemical calculations is difficult to assess, and statistical measures are frequently employed for characterization.49 In benchmark studies, uncertainties of ±(2–3) kJ mol−1 at the 95% confidence level are given for reaction energies from coupled cluster calculations similar to those of the present work (see Section 2.1).48 For CBS-QB3 calculations, larger uncertainties of ±(13–14) kJ mol−1 (again 95% confidence level) for enthalpies of formation were recommended in ref. 67. From the coupled cluster benchmark study, and by taking into account the fact that transition states are involved, it appears reasonable to assume that the uncertainties in the calculated threshold energies of the present work do probably not exceed ±5 kJ mol−1.
The rotational constants and harmonic wavenumbers necessary for the statistical rate theory calculations are given in Table S2 of the ESI.†
3.2 Statistical rate theory and master equation calculations
As already mentioned above, the master equation was solved with ΔESL, representing the average energy transferred per down collision, as the only adjustable parameter. The value was fitted to the temperature- and pressure-dependent rate coefficients reported in ref. 30 and 31 which were determined in shock tube experiments with time-resolved H atom detection using atom resonance absorption spectroscopy (H-ARAS). Note that in contrast to the approach in ref. 31, where only a two-channel master equation was used, the full ten-channel master equation was employed in the present work.In earlier studies,29–31 it was concluded from qualitative mechanistic considerations that under shock tube conditions mainly the C–O bond dissociation channels should contribute as rate-determining steps to hydrogen atom production. Following this assumption, we adjusted the value for ΔESL by fitting the calculated sum of the rate coefficients of the C–O bond dissociation reactions, k7 + k8, to the experimental values from ref. 30 and 31. The results for the optimum value of ΔESL = 400 cm−1 are shown in Fig. 2. With respect to sensitivity, we note that a variation of ΔESL by +/−200 cm−1 leads to an increase/decrease of the rate coefficients by about a factor of two with little variance over the entire temperature range but a slight increase of sensitivity for the lower pressures.
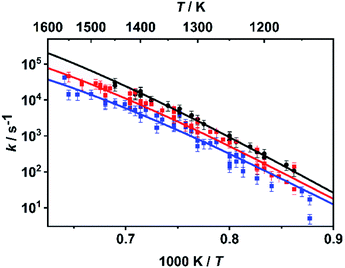 | ||
| Fig. 2 Rate coefficients k = k7 + k8 from the master equation calculations of the present work (lines) fitted to the rate coefficients from the shock tube experiments of ref. 30 and 31 (symbols) with ΔESL = 400 cm−1 at p ∼ 4.7 bar (black), p ∼ 1.1 bar (red), and p ∼ 0.4 bar (blue). | ||
To put the assumption that C–O bond dissociation channels dominate at high temperatures on a more quantitative basis, we consider in the following the calculated relative branching fractions of all ten channels for the fitted value of ΔESL. As is obvious from Fig. 3, the bond dissociation reaction (R7) increasingly dominates at temperatures above 900 K, which are typical for shock tube experiments. It is followed by the molecular elimination reaction (R1) and then by reactions (R8) and (R2). All other rate coefficients are lower by at least two orders of magnitude. Among the C–O bond dissociation channels, reaction (R7) clearly dominates over reaction (R8). For numerical evaluations of the rate coefficients ki(T,P), ‘log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p’ parameterizations (see e.g. ref. 65) are given in Table S3 of the ESI.† To enable a direct implementation of these results into combustion modelling, machine-readable files directly suitable for OpenSMOKE or CHEMKIN simulations are also given as ESI.†
p’ parameterizations (see e.g. ref. 65) are given in Table S3 of the ESI.† To enable a direct implementation of these results into combustion modelling, machine-readable files directly suitable for OpenSMOKE or CHEMKIN simulations are also given as ESI.†
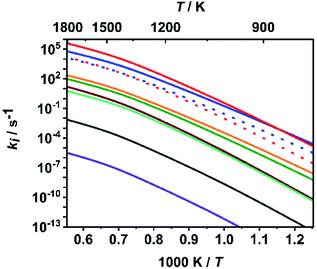 | ||
| Fig. 3 Calculated rate coefficients of reactions (R1)–(R10) at a pressure of p = 1 bar; top to bottom near left axis: (R7), (R1), (R8) (red dotted), (R2) (blue dotted), (R4), (R3), (R9), (R10), (R6) and (R5). | ||
To facilitate further discussion, Fig. 4 illustrates the pressure- and temperature-dependent switching between the combined radical and the combined molecular channels, (R7)–(R10) and (R1)–(R6), respectively. It is obvious that at the higher temperatures (1300 and 1800 K) the radical channels dominate at pressures above ca. 10 mbar whereas at the lower temperatures (800 K) the molecular channels prevail. This explains why in the low-temperature flow tube experiments of ref. 18 (T = 573–1243 K, pressure of a few tens of mbar), strong evidence for the molecular channels was found whereas these channels are much less important in the high-temperature shock tube studies of ref. 29 (T = 1100–1430 K, p = 1.2–2.5 bar) and ref. 30 and 31 (T = 1100–1600 K, p = 0.4, 1.1 and 4.7 bar). This is further illustrated in terms of relative branching fractions in Fig. 5. At lower temperatures near 800 K, the molecular channel (R1) dominates over the entire pressure range even though the radical channel (R7) gains some importance with increasing pressure; the relative branching fraction of the second molecular channel (R2) turns out to be nearly independent of pressure under these conditions. At higher temperatures near 1300 K, channel switching between reaction (R1), dominating at pressures below ca. 10 mbar, and reaction (R7), dominating at pressure above ca. 10 mbar, occurs. The predominance of the molecular channels in ref. 18 and the radical channel in ref. 29–31 becomes obvious.
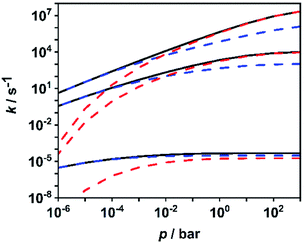 | ||
| Fig. 4 Calculated sums of the rate coefficients for the molecular channels (R1)–(R6) (blue dashed lines), for the radical channels (R7)–(R10) (red dashed lines), and total rate coefficient for all channels (R1)–(R10) (black solid line) at temperatures of 1800 K, 1300 K and 800 K (top to bottom). | ||
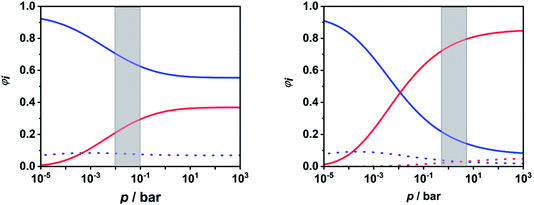 | ||
| Fig. 5 Calculated relative branching fractions of (R1) (blue solid line), (R2) (blue dotted line), (R7) (red solid line), and (R8) (red dotted line) at T = 800 K (left panel) and T = 1300 K (right panel). The pressure ranges of the flow tube experiments from ref. 18 (left panel) and the shock tube experiments from ref. 29–31 (right panel) are indicated as gray areas. | ||
In Fig. 6, the situation is illustrated in terms of microcanonical rate coefficients and molecular distribution functions. We show only the rate coefficients of the two most relevant molecular and radical channels. Note that a figure including all channels is given in the ESI (Fig. S2†). The most important feature reflecting the channel switching is the crossing of the specific rate constant curves of (R1) and (R7) near 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. At lower energies, the molecular channel (R1) dominates and at higher energies the radical channel (R2) dominates. The black dashed curves represents the molecular population of DMM at selected pressures from the high-pressure limit (right-hand curve) down to a pressure of 1 mbar (left-hand curve). With varying pressure, these populations move over this crossing range, sampling different ranges of energy contributing to the integrand of eqn (1). The switching of the dominating channel at pressures around p = 10 mbar for this temperature as shown in Fig. 5, right panel, is the necessary consequence. Such switching between lower lying channels with tight transition states and higher lying channels with loose transition structures is not uncommon in multi-channel unimolecular reactions, and in particular subtle angular momentum effects can occur (see e.g. ref. 2–5 and 68).
000 cm−1. At lower energies, the molecular channel (R1) dominates and at higher energies the radical channel (R2) dominates. The black dashed curves represents the molecular population of DMM at selected pressures from the high-pressure limit (right-hand curve) down to a pressure of 1 mbar (left-hand curve). With varying pressure, these populations move over this crossing range, sampling different ranges of energy contributing to the integrand of eqn (1). The switching of the dominating channel at pressures around p = 10 mbar for this temperature as shown in Fig. 5, right panel, is the necessary consequence. Such switching between lower lying channels with tight transition states and higher lying channels with loose transition structures is not uncommon in multi-channel unimolecular reactions, and in particular subtle angular momentum effects can occur (see e.g. ref. 2–5 and 68).
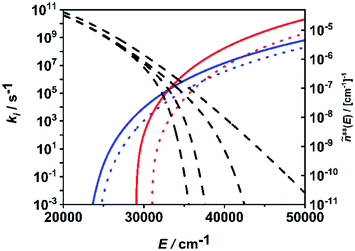 | ||
| Fig. 6 Microcanonical rate coefficients of the most important molecular (blue solid line: (R1), blue dotted line: (R2)) and radical (red solid line: (R7), red dotted line: (R8)) channels and normalized steady-state distributions of DMM at T = 1300 K and p = 1 mbar, p = 10 mbar, p = 1 bar and p → ∞ (dashed lines, left to right). | ||
The distinction between “tight” (sometimes referred to as “rigid”) and “loose” transition states was introduced by Marcus and Rice34 and quantified later in terms of activation entropy by Benson.69 Figuratively speaking, a tight transition state in a unimolecular decomposition reaction resembles the reactant configuration insofar as its internal states are characterized essentially by vibrational degrees of freedom. It is usually well localized and associated with a pronounced maximum of the potential energy along the reaction coordinate. In contrast, a loose transition state in a unimolecular decomposition reaction is more product-like, and its internal states are governed by the (hindered) internal rotations of the preformed fragments. It is typical for reactions with no localized maximum of the potential energy curve along the reaction coordinate but with an asymptotic approach toward the potential energy of the separated fragments. This makes the localization of a transition state structure difficult and strongly dependent on energy and total angular momentum. Due to the higher number of rotational states as compared to the number of vibrational states, a much steeper rise of the ki(E) curve arises for a loose transition state than for a tight transition state for a given reactant. This becomes obvious for the reaction system of the present work in Fig. 6 and S2.†
In terms of canonical rate coefficients, loose transition states correspond to higher activation entropies, ΔS‡i, and hence to larger preexponential factors in the high-pressure limit as compared to tight transition states. Illustrative numerical values for the DMM unimolecular reaction channels are given in Table 2. The expected very large values of ΔS‡i for the loose bond dissociation channels (R7)–(R10) are obvious, but it can also be realized that the well localized (that is, “tight”) transition states of reactions (R1)–(R6) can result in activation entropies distinctly above zero. Obviously, the use of ΔS‡i as a measure to formally distinguish between tight and loose transition states is limited.
| Reaction | log(A∞,i/s−1) | κ i | ΔS‡i/J K−1 mol−1 |
|---|---|---|---|
| R1 | 15.29 | 1.07 | 26.66 |
| R2 | 15.08 | 1.07 | 22.63 |
| R3 | 14.19 | 1.03 | 5.92 |
| R4 | 13.90 | 1.02 | 0.41 |
| R5 | 13.50 | 1.07 | −7.60 |
| R6 | 15.43 | 1.17 | 28.68 |
| R7 | 17.64 | — | 72.24 |
| R8 | 17.34 | — | 66.49 |
| R9 | 18.18 | — | 82.57 |
| R10 | 18.02 | — | 79.51 |
In the following, we briefly elucidate in a qualitative way, the relation between the activation entropies and the microscopic mechanisms of the molecular DMM decomposition channels (R1)–(R6). The corresponding transition state structures are displayed in Fig. S1.† In reactions (R1) and (R2), a CH3O–CH2 bond is broken, and simultaneously an H atom is shifted from the CH2 group to the departing CH3O moiety. Though this formally gives rise to structures resembling three-membered transition states, they are comparatively loose because the C–O bonds are already considerably stretched when the H atom is transferred to the O atom. Similar arguments apply to reaction (R6), where a CH3–O bond is broken, and an H atom is transferred from the CH2 group to the departing CH3 moiety. This explains the comparatively high values between 20 and 30 J K−1 mol−1 for ΔS‡1, ΔS‡2, and ΔS‡6. In reaction (R3), where also a CH3O–CH2 bond is broken, the transferred H atom stems from the opposite CH3 group. This obviously leads to a somewhat tighter transition state and a correspondingly lower value of ΔS‡3 = 5.92 J K−1 mol−1. Reactions (R4) and (R5) follow different microscopic mechanisms. In reaction (R4), also a CH3–O bond is broken, but the CH3 group is transferred to the other O atom, and simultaneously OCH2 is eliminated. That is, the formaldehyde molecule produced in (R4) contains the central CH2 group of DMM. The resulting transition state is tight, giving ΔS‡4 = 0.41 J K−1 mol−1. The reaction coordinate of (R5) is very complicated. An H atom from a CH3O group moves to the β-O atom, the remaining CH2O–CH2 bond is broken, and CH2O is eliminated. Simultaneously, in the other fragment a C–C bond is formed yielding HOCH2CH3. Due to this complex, sterically demanding rearrangement, the activation entropy is negative with a value of ΔS‡5 = −7.60 J K−1 mol−1. In terms of partition functions, the small values of ΔS‡4 and ΔS‡5 are essentially due to the absence of low-lying vibrational wavenumbers (<100 cm−1) in these very complex transition states. For a more detailed discussion of such general points, the reader is referred to standard monographs.50–52
Another aspect of the tight/loose distinction is the angular momentum dependence of the threshold energies, E0i(J). If the threshold energies are referenced to the rovibrational ground state of the reactant, that is to J = 0, they generally increase with increasing J approximately as E0i(J) ≈ E0i(J = 0) + B‡i(J) × J(J + 1).54 The weakly J-dependent centrifugal-corrected rotational constants, B‡i(J), are usually smaller for loose rather than for tight transitions states. Consequently, the differences between, or even the order of, the threshold energies, may change with increasing J. If for low J, the relation E0i(tight)(J) < E0j(loose)(J) holds, this may change into E0i(tight)(J) > E0j(loose)(J) for high J. Such behavior is sometimes called “rotational channel switching”3,5 and occurs in particular if the differences E0j(loose)(J) − E0i(tight)(J) > 0 for low J are small. For the reaction system of the present work, illustrative J-dependent threshold energies for the lowest molecular (tight) and radical (loose) channel are listed in Table S4.† It becomes obvious that the differences between these threshold energies become slightly smaller for increasing J, but rotational channel switching does not occur, even for the comparatively high temperatures between 800 and 1800 K and the correspondingly high thermal averages, 〈J〉T. The differences in the threshold energies for J = 0 are too large. Also the use of more realistic interfragment potentials instead of the Morse functions used in the s-SACM approach53–55 would not change this qualitative picture.
3.3 Kinetic modelling
In order to evaluate the validity of the kinetic data for DMM decomposition calculated in the present work and to verify the dominant role of the radical channels in the presence of low-lying molecular channels in shock tube experiments, the results from ref. 30 and 31 were modelled. As already mentioned in Section 2.3, the DMM pyrolysis model from ref. 23 and modified in ref. 30, was used, supplemented with the reactions and the kinetic data from the present work. This mechanism was then combined with AramcoMech3.0 as the hydrocarbon core mechanism.70 The complete mechanism along with the kinetic and thermodynamic data is given in the ESI.†Illustrative concentration–time profiles for well-separated temperatures, pressures and initial DMM concentrations are shown in Fig. 7 and 8. Here, the H atom concentration time profiles were measured with ARAS30,31 and the DMM concentration–time profiles with time-of-flight mass spectrometry (TOF-MS).30 The generally good agreement between the experimental and simulated profiles is obvious. We note that the experimental uncertainty of the concentration–time profiles including systematic errors is about ±10% for the H-ARAS71 and ±40% for the TOF-MS experiments.30
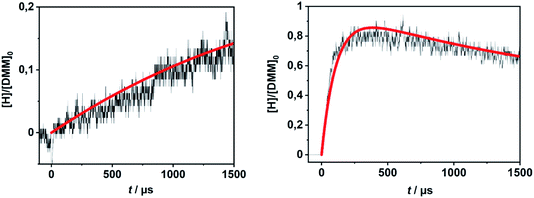 | ||
| Fig. 7 Hydrogen atom concentration–time profiles from DMM pyrolysis in a shock tube recorded with H-ARAS (black lines, see ref. 31) and calculated with the mechanism of the present work (red line); left panel: T = 1170 K, p = 1.1 bar, [DMM]0 = 4.1 × 10−11 mol cm−3, right panel: T = 1430 K, p = 0.4 bar, [DMM]0 = 8.9 × 10−11 mol cm−3. | ||
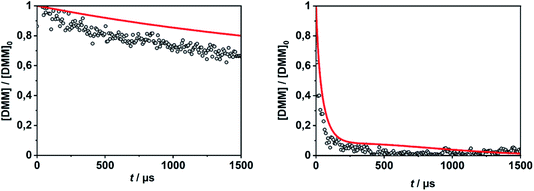 | ||
| Fig. 8 DMM concentration–time profiles from DMM pyrolysis in a shock tube recorded with TOF-MS (symbols, see ref. 30) and calculated with the mechanism of the present work (red line); left panel: T = 1150 K, p = 1.3 bar, [DMM]0 = 1.4 × 10−7 mol cm−3, right panel: T = 1430 K, p = 1.1 bar, [DMM]0 = 9.1 × 10−8 mol cm−3. | ||
4 Summary and conclusion
The kinetics of the parallel unimolecular decomposition reactions of DMM were characterized with high-level quantum chemical calculations and unimolecular rate theory. In agreement with recent findings from the literature,18–20 molecular elimination and radical-forming bond dissociation channels were identified, and kinetic data for each channel were derived. With these data, shock tube experiments of DMM pyrolysis with H-ARAS and TOF-MS detection could be adequately modelled. From the detailed master equation analysis, it could be shown that C–O bond dissociation channels in DMM dominate the decomposition kinetics in shock tube experiments despite the presence of energetically lower lying molecular elimination channels. The latter reactions may, however, significantly contribute at lower temperatures and pressures, which is in line with findings of a recent flow tube study.18 In this way, a consistent picture of the unimolecular decomposition kinetics of DMM seems to emerge. It provides an example for the capabilities and usefulness of modern unimolecular rate theory for both a fundamental understanding and a practical parameterization of important reactions in combustion chemistry.Whether such competition between molecular and radical decomposition channels of closed-shell species are significant for practical combustion processes is an open question. The answer certainly depends on the specific fuel and in particular on the relevant temperature range. While at low temperatures (T < 1000 K), mainly abstraction reactions from the fuel molecule are relevant for chain initiation, unimolecular decomposition reactions may contribute at higher temperatures. Many oxygenated fuels like alcohols, esters, ethers, and furanics are known to possess molecular decomposition channels. In contrast to simple bond fission reactions, such channels are sometimes difficult to identify by pure chemical intuition. In fact, this could be an important point, where the emerging combination of unimolecular rate theory and modern automatic mechanism generation may turn out to be useful in the future.72–74
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 237267381-TRR150. The authors also acknowledge the generous allocation of computer time by the state of Baden-Württemberg through bwHPC and the DFG through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).References
- F. A. Lindemann, Trans. Faraday Soc., 1922, 17, 598–606 RSC.
- Th. Just and J. Troe, J. Phys. Chem., 1980, 84, 3068–3072 CrossRef.
- J. Troe, J. Chem. Soc., Faraday Trans., 1994, 90, 2303–2317 RSC.
- G. Friedrichs, M. Colberg, J. Dammeier, T. Bentz and M. Olzmann, Phys. Chem. Chem. Phys., 2008, 10, 6520–6533 RSC.
- J. Troe, J. Phys. Chem. A, 2019, 123, 1007–1014 CrossRef CAS PubMed.
- Y. Fenard and G. Vanhove, Energy Fuels, 2021, 35, 14325–14342 CrossRef CAS.
- J. Burger, M. Siegert, E. Ströfer and H. Hasse, Fuel, 2010, 89, 3315–3319 CrossRef CAS.
- H. Liu, Z. Wang, J. Wang, X. He, Y. Zheng, Q. Tang and J. Wang, Energy, 2015, 88, 793–800 CrossRef CAS.
- Z. Wang, H. Liu, X. Ma, J. Wang, S. Shuai and R. D. Reitz, Fuel, 2016, 183, 206–213 CrossRef CAS.
- X. Zhang, A. O. Oyedun, A. Kumar, D. Oestreich, U. Arnold and J. Sauer, Biomass Bioenergy, 2016, 90, 7–14 CrossRef CAS.
- S. Deutz, D. Bongartz, B. Heuser, A. Käthelhön, L. S. Langenhorst, A. Omari, M. Walters, J. Klankermayer, W. Leitner, A. Mitsos, S. Pischinger and A. Bardow, Energy Environ. Sci., 2018, 11, 331–343 RSC.
- R. Sun, I. Delidovich and R. Palkovits, ACS Catal., 2019, 9, 1298–1318 CrossRef CAS.
- M. Härtl, P. Seidenspinner, E. Jacob and G. Wachtmeister, Fuel, 2015, 153, 328–335 CrossRef.
- H. Liu, Z. Wang, J. Wang and X. He, Energy, 2016, 97, 105–112 CrossRef CAS.
- A. Omari, B. Heuser and S. Pischinger, Fuel, 2017, 209, 232–237 CrossRef CAS.
- J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef.
- H. J. Curran, Proc. Combust. Inst., 2019, 37, 57–81 CrossRef CAS.
- T. Yu, X. Wu, X. Zhou, A. Bodi and P. Hemberger, Combust. Flame, 2020, 222, 123–132 CrossRef CAS.
- W. Sun, Z. Liu, Y. Zhang, Y. Zhai, C. Cao, J. Yang and B. Yang, Combust. Flame, 2021, 226, 260–273 CrossRef CAS.
- J. S. Al-Otaibi, M. A. Abdel-Rahman, A. H. Almuqrin, T. M. El-Gogary, M. A. M. Mahmoud and A. M. El-Nahas, Fuel, 2021, 290, 119970 CrossRef CAS.
- C. A. Daly, J. M. Simmie, P. Dagaut and M. Cathonnet, Combust. Flame, 2001, 125, 1106–1117 CrossRef CAS.
- V. Dias, X. Lories and J. Vandooren, Combust. Sci. Technol., 2010, 182, 350–364 CrossRef CAS.
- L. Marrodán, E. Royo, Á. Millera, R. Bilbao and M. U. Alzueta, Energy Fuels, 2015, 29, 3507–3517 CrossRef.
- W. Sun, G. Wang, S. Li, R. Zhang, B. Yang, J. Yang, Y. Li, C. K. Westbrook and C. K. Law, Proc. Combust. Inst., 2017, 36, 1269–1278 CrossRef CAS.
- E. Hu, Z. Gao, Y. Liu, G. Yin and Z. Huang, Fuel, 2017, 189, 350–357 CrossRef CAS.
- T. He, Z. Wang, X. You, H. Liu, Y. Wang, X. Li and X. He, Fuel, 2018, 212, 223–235 CrossRef CAS.
- F. H. Vermeire, H.-H. Carstensen, O. Herbinet, F. Battin-Leclerc, G. B. Marin and K. M. Van Geem, Combust. Flame, 2018, 190, 270–283 CrossRef CAS.
- W. Sun, T. Tao, M. Lailliau, N. Hansen, B. Yang and P. Dagaut, Combust. Flame, 2018, 193, 491–501 CrossRef CAS.
- S. Peukert, P. Sela, D. Nativel, J. Herzler, M. Fikri and C. Schulz, J. Phys. Chem. A, 2018, 122, 7559–7571 CrossRef CAS PubMed.
- L. Golka, I. Weber and M. Olzmann, Proc. Combust. Inst., 2019, 37, 179–187 CrossRef CAS.
- L. Golka, D. Gratzfeld, I. Weber and M. Olzmann, Phys. Chem. Chem. Phys., 2020, 22, 5523–5530 RSC.
- S. Jacobs, M. Döntgen, A. B. S. Alquaity, W. A. Kopp, L. C. Kröger, U. Burke, H. Pitsch, K. Leonhard, H. J. Curran and K. A. Heufer, Combust. Flame, 2019, 205, 522–533 CrossRef CAS.
- J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Peterson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef.
- R. A. Marcus and O. K. Rice, J. Phys. Colloid Chem., 1951, 55, 894–908 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS.
- N. Li, W. Sun, S. Liu, X. Qin, Y. Zhao, Y. Wei and Y. Zhang, Combust. Flame, 2021, 233, 111583 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Vuckovic and K. Burke, J. Phys. Chem. Lett., 2020, 11, 9957–9964 CrossRef CAS PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comput. Chem., 2011, 32, 2492–2513 CrossRef CAS PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- TURBOMOLE V7.4 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com Search PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097–1101 CrossRef CAS.
- R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell, Oxford, UK, 1990 Search PubMed.
- K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, 2nd edn, 1996 Search PubMed.
- W. Forst, Unimolecular Reactions, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- M. Quack and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1974, 78, 240–252 CrossRef CAS.
- J. Troe, J. Chem. Phys., 1983, 79, 6017–6029 CrossRef CAS.
- C. J. Cobos and J. Troe, J. Chem. Phys., 1985, 83, 1010–1015 CrossRef CAS.
- M. Olzmann and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1992, 96, 1327–1332 CrossRef CAS.
- M. Olzmann and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1994, 98, 1563–1574 CrossRef CAS.
- W. H. Miller, J. Am. Chem. Soc., 1979, 101, 6810–6814 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 2921–2926 CrossRef CAS.
- N. Snider, J. Phys. Chem., 1986, 90, 4366–4372 CrossRef CAS.
- M. Olzmann, Cleaner Combustion, ed. F. Battin-Leclerc, J. M. Simmie and E. Blurock, Springer-Verlag, London, 2013, pp. 549–576 Search PubMed.
- M. Pfeifle and M. Olzmann, Int. J. Chem. Kinet., 2014, 46, 231–244 CrossRef CAS.
- A. Busch, N. González-García, G. Lendvay and M. Olzmann, J. Phys. Chem. A, 2015, 119, 7838–7846 CrossRef CAS PubMed.
- K. Kuo, Principles of Combustion, Wiley, Hoboken, 2nd edn, 2005 Search PubMed.
- T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer, Berlin, 2014 Search PubMed.
- A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, Comput. Phys. Commun., 2015, 192, 237–264 CrossRef CAS.
- J. M. Simmie and K. P. Somers, J. Phys. Chem. A, 2015, 119, 7235–7246 CrossRef CAS PubMed.
- A. Matsugi, J. Phys. Chem. A, 2021, 125, 2532–2545 CrossRef CAS PubMed.
- S. W. Benson, Thermochemical Kinetics, Wiley, New York, 1968 Search PubMed.
- C.-W. Zhou, Y. Li, U. Burke, C. Banyon, K. P. Somers, S. Ding, S. Khan, J. W. Hargis, T. Sikes, O. Mathieu, E. L. Petersen, M. AlAbbad, A. Farooq, Y. Pan, Y. Zhang, Z. Huang, J. Lopez, Z. Loparo, S. S. Vasu and H. J. Curran, Combust. Flame, 2018, 197, 423–438 CrossRef CAS.
- I. Weber, P. Friese and M. Olzmann, J. Phys. Chem. A, 2018, 122, 6500–6508 CrossRef CAS PubMed.
- G. N. Simm, A. C. Vaucher and M. Reiher, J. Phys. Chem. A, 2019, 123, 385–399 CrossRef CAS PubMed.
- R. Van de Vijver and J. Zádor, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- J. A. Miller, R. Sivaramakrishnan, Y. Tao, C. F. Goldsmith, M. P. Burke, A. W. Jasper, N. Hansen, N. J. Labbe, P. Glarborg and J. Zádor, Prog. Energy Combust. Sci., 2021, 83, 100886 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2fd00039c |
| This journal is © The Royal Society of Chemistry 2022 |
