Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Speech-generated aerosol settling times and viral viability can improve COVID-19 transmission prediction†
Alan Y.
Gu‡
 ,
Yanzhe
Zhu‡
,
Yanzhe
Zhu‡
 ,
Jing
Li
,
Jing
Li
 and
Michael R.
Hoffmann
and
Michael R.
Hoffmann
 *
*
Linde Laboratories, California Institute of Technology, Pasadena, California 91125, USA. E-mail: mrh@caltech.edu; Tel: +1 626-395-4391
First published on 8th December 2021
Abstract
Droplets during human speech are found to remain suspended in the air for minutes, while studies suggest that the SARS-CoV-2 virus is infectious in experimentally produced aerosols for more than one hour. However, the absence of a large-scale association between regional outbreaks and weather-influenced virus-laden speech-generated aerosol characteristics such as settling time and viral viability makes it challenging for policy making on appropriate infection control measures. Here we investigate the correlation between the time series of daily infections and of settling times of virus-containing particles produced by speaking. Characteristic droplet settling times determined by the Stokes–Cunningham equation as influenced by daily weather conditions were estimated based on local meteorological data. Daily infection data were calibrated from local reported cases based on established infection timeframes. Linear regression, vector autoregression, simple recurrent neural network, and long short-term memory models predict transmission rates within one-sigma intervals using the settling times and viral viability over 5 days before the day of prediction. Corroborating with previous health science studies, from the perspective of meteorology-modulated transmission, our results strengthen that airborne aerosol transmission is an important pathway for the spread of SARS-CoV-2. Furthermore, historical weather data can improve the prediction accuracy of infection spreading rates.
Environmental significanceWeather effects on SARS-CoV-2 transmission have been long investigated, though the lack of first principles in making the association led to inconclusive findings. In addition, the role of the airborne transmission pathway in the spread of COVID has been under debate since the initial outbreak in early 2020. This work provides the first first-principle-based model to associate temperature and humidity with SARS-CoV-2 transmission via virus-laden aerosol settling time and viral viability, confirming the predictive power of weather on transmission. The predictive ability of these aerosol-relevant variables also supports indirect airborne transmission as an important pathway of SARS-CoV-2 spread. Similar methodology can predict flu and future epidemic transmission from weather forecast, as well as reveal their major transmission pathways. |
Introduction
The novel coronavirus (SARS-CoV-2) has caused more than 240 million infections and 4.8 million deaths globally from COVID-19 as of October 19, 2021.1 COVID-19 is known to cause considerable asymptomatic infections. Therefore, the ability to predict local COVID-19 outbreaks is imperative for effective public health management.2 Faster flu transmission during winter months is often linked to lower temperatures and relative humidity than occur during the summer.3 Virus-laden aerosols from infected human hosts evaporate into smaller aerosol particles at lower humidity and as a result, they take longer to settle out of the atmosphere. In addition, viruses in aerosols survive longer at lower ambient temperatures, and thus, they remain contagious for longer periods of time while airborne.4 Speech-generated aerosols may be suspended in air for 8 to 14 minutes,5 while viruses encapsulated in aerosol droplets could remain viable for 49 hours.6,7 Thus speech-generated aerosols are widely considered to have contributed to asymptomatic transmission of COVID-19.5,8,9 The fate and transport of these virus-laden aerosol droplets could be used for predicting the spread of COVID-19.Airborne transmission of COVID-19 has been studied extensively over the past year.10,11 Previous studies on predicting COVID-19 transmission and similar airborne transmission diseases were focused on using an infected population (SIR model)12 or meteorological observation13 directly as the input variables when predicting COVID transmission. Considering the non-linear relationships connecting weather to settling time and viral viability,7,14 using weather-derived settling times and viability as input variables may improve the goodness of fit as well as elucidating additional factors affecting airborne transmission.
Meteorological conditions such as temperature and humidity affect aerosol settling velocity by affecting the final size of aerosols after equilibration with ambient moisture through evaporation or condensation. The settling velocity of the equilibrated aerosols in the atmosphere is often calculated using Stokes' law,15 which has been traditionally used to estimate aerosol terminal velocity at ambient temperatures and pressures. Because it assumes no-slip boundary condition, it underestimates the terminal settling velocity for small particles of size < 1 μm. In air at 25 °C, the terminal velocity accounting for slip correction is 1.24 times faster than calculated from uncorrected Stokes' law for a 1 μm-diameter particle, and 2.2 times faster for a 200 nm-diameter particle. Stokes' law also assumes that aerodynamic stress is transferred primarily through viscous exchange, meaning it is valid for small Reynolds number Re < 1. Cunningham later introduces a correction factor to account for particle surface slippage and the resultant Stokes–Cunningham law applies for aerosols sizes as small as 100 nm at ambient temperature and pressure.16 Other models, such as the one proposed by Epstein17 and Millikan,18 are only applicable at Knudsen numbers Kn > 10, corresponding to nm-sized particles in the lower troposphere or micron-sized particles at millibar-level pressures.19
In addition to settling time, weather also affects the viability of viruses in suspended aerosols.20 In the case of SARS-CoV-2, high temperature, relative humidity (within 20–70% range) and ultraviolet B (UVB) light produce higher decay rates,7 which is in agreement with previous studies on an enveloped virus.21 In a study focused on the viability of SARS-CoV-2 on surfaces, investigators reported an extension of viability over longer times at low temperatures and humidities.22,23 Weather also affects influenza A virus viability, though the relationship depends on the specific solution medium.24
Given aerosol settling times and viral viability as the input variables, COVID-19 cases can be forecasted using regression analysis or machine learning models. Regression analyses such as linear regression and vector autoregression can identify key input variables among all the input variables but are limited to linear correlations only.25,26 Machine learning algorithms can find highly non-linear correlations but they do not reveal any intuitive relationship between the input and response variables. Machine leaning has been introduced as a promising alternative to existing forecasting models for influenza27 and SARS-CoV-2 (ref. 28) with temperature, humidity and sunlight intensity as input variables.
Herein, we test the model fitting and prediction performance of the transmission rate of COVID-19 in the US using the settling times of speech-generated aerosols coupled with viral viability data. In order to achieve this goal, weather information, evaporated speech aerosol settling times, and viral viability are processed in regression and recurrent neural network (RNN) models to forecast SARS-CoV-2 daily transmission rates. We compared linear regression, vector autoregression (VAR), simple RNN and long-/short-term memory (LSTM) RNN in terms of prediction performance of COVID-19 transmission. We expect that inclusion of first principles such as the Köhler equation for vapor pressure reduction on aquated aerosol size and settling velocity calculation improvements should removes some of the non-linearity that models need to accommodate in order to achieve better fitting and forecasting performance. A good model fitting and prediction performance would indicate that speech-generated airborne aerosols are a significant transmission route for COVID-19 and that the weather-affected speech-generated aerosol properties may be incorporated to assist further predictive model development.
Methods
Fig. 1a shows the data flow of the model from weather data to predicted SARS-CoV-2 transmission in this work. Each section of the model is elaborated in this section.Data mining
Five counties were selected for inclusion in our model development. They are Harris County, TX, King County, WA, Los Angeles County, CA, Maricopa County, AZ, and Santa Clara County, CA. The counties are representative of the top-20 most populated counties in the United States. Of the 5 counties selected none had zero-case days throughout April 2020. They also had moderately warm weather and no temperature below 0 °C. When temperatures are below 0 °C, additional data on water surface tension and sodium chloride solution partial molal volumes below normal melting point are needed. Constraining the predictive model to T > 0 °C avoids the complication of ice crystal formation within aquated aerosols.29 The daily local meteorological data, including daily average temperatures and relative humidities (RH) were obtained online from National Oceanic and Atmospheric Administration (NOAA) from 1 April to 29 August 2020. For counties with more than one station, the station with most data coverage for daily temperature and RH was chosen. The station numbers are 12960, 24233, 93134, 23183, and 23293 for Harris County, King County, Los Angeles County, Maricopa County, and Santa Clara County, respectively.The county-level COVID-19 confirmed case counts were obtained from USAFacts.org, who collected data from the Centers for Disease Control and Prevention (CDC), and the corresponding state- and local-level public health agencies. Data was acquired on 14 September 2020 and contained up-to-date daily confirmed cases. Given the extended asymptomatic period of COVID-19, the daily confirmed cases data was processed to reflect the daily active cases based on a disease progression timeline (Fig. 1b) that summarizes information provided by the CDC.30 The daily active cases of a certain day to study is therefore the sum of daily confirmed cases for the past 12 days and future 4 days.
Aerosol settling behavior
Given the fast kinetics of water evaporation from micron-sized aerosols (seconds)31,32 compared to their settling time from a typical human height (minutes),33 the Köhler equation (eqn (1)) is used to estimate the size of evaporated aerosols:14 | (1) |
 for sodium chloride solution,
for sodium chloride solution,  is the ratio of dry salt diameter to wet aerosol diameter,
is the ratio of dry salt diameter to wet aerosol diameter,  is the ratio of the characteristic length scale of Kelvin effect to dry salt diameter where the characteristic length scale is calculated as follows:
is the ratio of the characteristic length scale of Kelvin effect to dry salt diameter where the characteristic length scale is calculated as follows: | (2) |
 is the partial molal volume of water in the solution, σ is the surface tension of the solution–air interface, R is the gas constant and T the absolute temperature.
is the partial molal volume of water in the solution, σ is the surface tension of the solution–air interface, R is the gas constant and T the absolute temperature.
The speech-generated aerosols are modelled as sodium chloride solutions at physiological concentration of 80 mM, which is a typical salivary sodium concentration.34 The initial size of speech-generated aerosols before evaporation is taken as 6 μm, which is the most abundant size according to experimental measurements.35 The partial molal volume of water in a sodium chloride solution,36 water vapor pressure,37 water surface tension,38 and the binary diffusion constant of water vapor in air39 are taken from previous experimental data or semi-empirical relationships.
The settling velocity of the evaporated aerosol of a given size is calculated using the Stokes' law with the Cunningham correction factor shown in eqn (3)
 | (3) |
| Cc = 1 + 2.52Kn, | (4) |
 | (5) |
Assuming ideal gas law, the mean-free path, λ, for a given gas is
 is the molecular density of gas (2.46 × 1025 at 25 °C and 1 atm total pressure). λ = 95 nm for air at 25 °C.
is the molecular density of gas (2.46 × 1025 at 25 °C and 1 atm total pressure). λ = 95 nm for air at 25 °C.
From the aerosol settling velocity, the settling time is calculated assuming aerosols attain their terminal settling velocity immediately after release at a height of 1.5 meters. Because the settling time is used as an intermediate variable in the model depicted in Fig. 1 to check fitting and make predictions, the absolute height of release does not affect conclusions obtained.
Viral viability
Viral viability is calculated using empirical linear regression with interaction by Paul Dabisch.7 Because the regression equation is obtained from a limited range of temperature (10–30 °C) and humidity (20–70%), we focus on counties with moderate climate where the viability calculation is valid.Transmission model
The variable describing SARS-CoV-2 transmission is the “new case percentage increase (NCP),” which is calculated as the number of new positive tests on a particular day divided by the “total number of active cases (TNAC)” on that day. The TNAC on a day is estimated by summing all positive tests from 12 days before until 4 days after the day of interest as stated above.The time series data for each county are separated into a training set and a test set, with the test data set containing the last 4 days of data and the training set containing the remaining data. VAR and RNN models are developed using the training data. Subsequently, the predictive accuracy of the trained models is tested using the test data.
Linear regression analysis uses the settling times and viral viability between the day of interest and 5 days before as the input variables (total of 10). VAR uses the settling times, viral viability, and “new case percentage increase” between 1 day and n days prior to the day of interest as the input variables, where n is the order of VAR and selected by Akaike's Information Criterion. As an autoregressive algorithm, predictions of more than one day in the future are calculated using the predictions of previous days, not the actual data as in the linear regression or RNN models. Simple RNN uses the same input variables as the linear regression model, one hidden layer of 70 nodes, a max epoch of 105 and a learning rate of 10−4. LSTM uses the same input variables as RNN, one LSTM layer of 120 units, a max epoch of 106 and a batch size of 72. All models use the new case percentage increase on the day of interest as the response variable, which represents the transmission rate.
Results and discussion
In order to investigate the gravity settling of the speech-generated droplets, the settling velocity and dimensionless numbers of the Stokes–Cunningham modification were estimated for droplets of 6 μm size (Fig. S1†), which is used as the peak initial size of speech-generated droplets.35 It should be noted that this size is comparable to the average diameter of cough-generated droplet size of 5 μm.40 Thus, we use the size representing speech-generated droplets considering asymptomatic transmission of SARS-CoV-2,41 which is at its most contagious before symptom onset.42Fig. 2 shows the estimated terminal settling velocities of an evaporated aerosol as well as its associated Reynolds number and Knudsen number at that particular size and velocity in ambient air. The density of the aerosol is set to unity in this chart for illustration purposes; estimated sodium chloride solution density accounting for evaporation is used in producing all fitting and prediction results. Because the Stokes–Cunningham equation is only applicable to Re < 1 and particle size > 100 nm, the estimated terminal velocity is accurate up to approximately ∼10 μm and down to 0.1 μm in terms of aerosol size. Thus, the size spectrum is broad enough to encompass the entire range of sizes produced by equilibrating speech-generated aerosols with ambient moisture (vide infra). For the range of sizes shown in Fig. 2b, Kn ≪ 10. Thus, the Epstein or Millikan equations17,43 are not applicable in regard to the range covered (Fig. 2b). The decreasing trend of Kn as droplet size increases also confirms the importance of surface slippage at small droplet sizes.Droplets of an initial size of 6 μm equilibrate with atmospheric moisture and evaporate into smaller aerosols or condense into larger droplets as shown in Fig. 3a and b. Fig. 3a shows the temperature effect on the size of aerosol after evaporation or condensation, which is negligible within the temperature range seen in the counties investigated. Assuming that a few seconds are needed for droplets to evaporate to an equilibrium size,32 we further assume instantaneous kinetics, thus the temperature effects demonstrated in this work are expected to be smaller than in reality. Fig. 3b shows the relative humidity effect on the size of aerosol after evaporation (below 90% relative humidity) or condensation (at 100% relative humidity). A higher relative humidity corresponds to a larger equilibrium size of droplet or aerosol as expected. An initial size of 6 μm yields a droplet of size 1 to 10 μm in equilibrium with moisture, and this final droplet size is used to calculate its settling time from the height of 1.5 m shown in Fig. 3c. As expected from Fig. 3a, the temperature effects on the settling velocity are minimal. The relative humidity effect on settling time is significant, yielding as short as 1 min at 100% relative humidity and >20 min at <10% relative humidity. The evaporation and settling calculations agree with the classic Wells model.33,44 Similarly, the SARS-CoV-2 virus half-life is plotted as a function of ambient temperature and relative humidity in Fig. 3d. Lower temperatures and humidities yield longer viral half-lives. However, the relationship is highly nonlinear. The non-linearity poses a challenge to previous models13,45,46 using meteorological data directly as input variables. Current transmission models incorporating weather data as input variables have varying goodness of fits and correlation significances that may be due to how the meteorological variables were used.29 For example, humidity has been factored into models as relative humidity,47 absolute humidity,48 or dew point.49
The correlation between humidity and transmission may be related to the hydrophilic interactions between water and the proteins on the outer surface of SARS-CoV-2 virus via hydrogen bonding.50 The range of virus half-lives varies from several minutes to over an hour with typical ranges of temperature and humidity in April. These results underscore the potential effect of weather on airborne virus transmission. Results show that the weather affects the fate and transport of speech-generated, virus-laden droplets by changing the settling times and viral half-lives, and thus these intertwined effects may not be captured by a simple linear model.
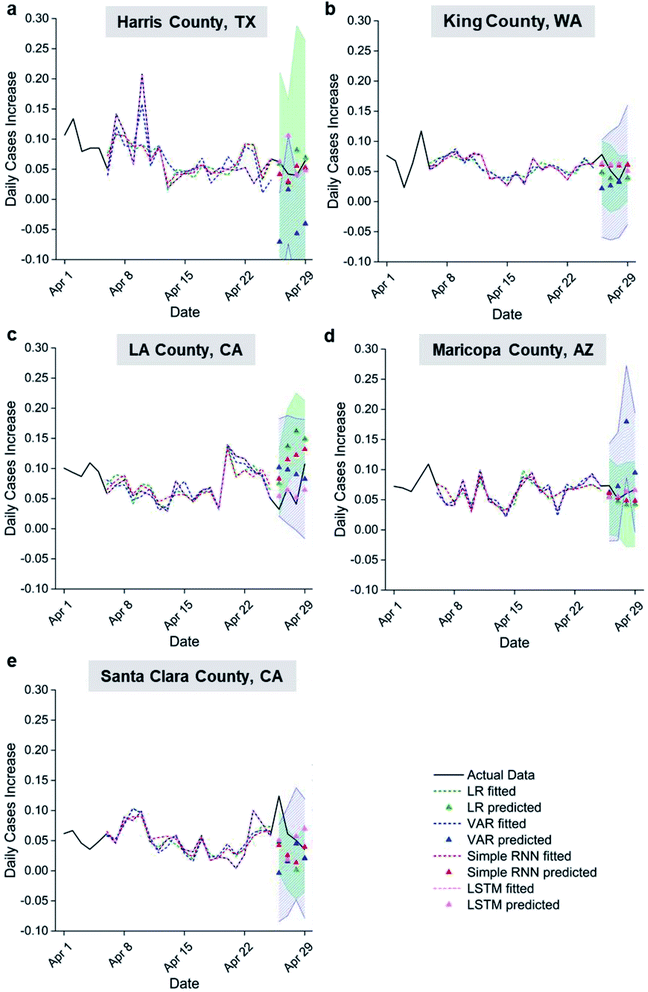
To establish an effective weather-based model for COVID-19 epidemic prediction, regression analyses (LR and VAR) and machine learning models (RNN and LSTM) were compared for 5 U.S. counties. Fig. 4 shows the time series of daily case percentage increase in the different US counties. The model fittings follow the major trends of the actual data and capture most of their peaks and troughs; the actual data of the last 4 days also fall inside the one-sigma prediction intervals despite simplicity of the models used. The goodness of fit and the prediction accuracy generally rank as follows: LSTM > simple RNN > LR > VAR (see r2 for fitting and residual sum of squares (RSS) for prediction in Table S1a and b†). Considering a key difference between VAR and the rest of the models are the use of auto-regressively predicted settling times and viral viability data versus actual data starting from the second day of prediction, the lowest fitting and prediction accuracy of VAR suggests inaccurate aerosol settling times and viral viability predictions from past data as expected. It is clear that accurate weather-originated data input is required to predict transmission rates accurately. VAR also includes past transmission rate data as an input, which is not included in the other models explored. This suggests that past transmission is not a significant input variable for predicting future transmission compared to the two weather-originated variables as normalized into a percentage increase. Improved fitting for LSTM over simple RNN suggests that weather beyond 5 days prior affects current transmission. Better fitting and prediction performance of neural network models compared to LR suggests nonlinearity in the correlation between settling time, viral viability, and transmission rate, even though reasonable linear correlations are observed. For example, the r2 values for the counties considered vary from 0.36 to 0.80 with an average of 0.59, achieved using input variables capturing two types of weather influences on transmission. Variability in goodness of fit among the counties may be explained by local residents, who have delay in time from the onset of symptom to getting a COVID test.
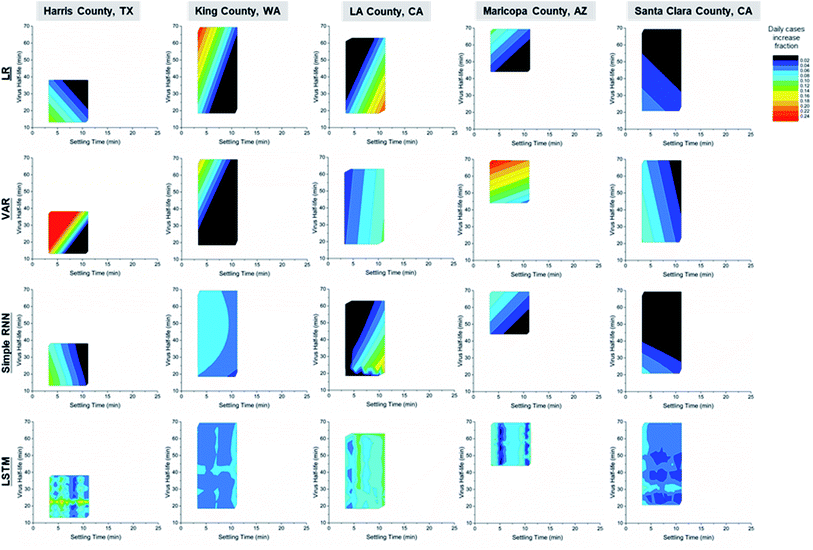
To better understand how weather-originated aerosol settling times and viral viability affect transmission, the contours of model predictions are shown in Fig. 5. The ranges of settling times and virus half-lives are determined in part by the local temperature and RH range during April, for each county of study. Note that the data points used to generate the contour plots are not uniformly distributed inside the contours, and the data to be predicted may not lie within the range of training data (see Fig. S2†). Although UV intensity is not a direct input variable in this model, it positively correlates with temperature51 and is, therefore, indirectly taken into account in this model.
Counties have faster transmission at longer aerosol settling times or longer virus half-lives. These results indicate that active-virus-laden aerosols are a major pathway for COVID transmission. The only exception to this claim was seen for Santa Clara County for which there appeared to be faster transmission at low viral viability and settling times leading to a less accurate prediction compared to the other counties that were analysed in Fig. 5. Harris, King and Maricopa counties show faster transmission with a longer virus half-life, while LA County had increased transmission rates at longer settling times. The LR, VAR and simple RNN predictions show clear trends, while the trend of LSTM predictions indicates hotspots for easy transmission in the 2D space of viral viability and aerosol settling times. This may be indicative of the small training data set used, considering the high accuracy of fitting and predictions by LSTM in Fig. 4. The different trends between LA County vs. Harris, King and Maricopa counties may be a result of their different policies and human behaviours not captured by the input variables in this work. Future work in the training of an LSTM model with sufficient data over a wide range of weather conditions from all seasons may reveal a clear trend of correlation similar to the LR, VAR and simple RNN models in this work.
The performance of transmission rate prediction based on aerosol settling times and viral viability was also studied with an extended dataset of Maricopa County from May to August 2020, as shown in Fig. 6. The r2 values are 0.172, 0.579, and 0.999![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956 for linear regression, simple RNN, and LSTM, respectively. Similar to the April data, LSTM has the closest fitting, followed by the simple RNN, and a linear regression. All three models have similar prediction accuracies, with RSS values of 0.0110, 0.0156, 0.0160 for linear regression, simple RNN, and LSTM, respectively. The matching performance of these 3 models are also observed in April Maricopa County data. The observed increase in new cases line falls within the one-sigma prediction interval for the last 21 days of available data.
956 for linear regression, simple RNN, and LSTM, respectively. Similar to the April data, LSTM has the closest fitting, followed by the simple RNN, and a linear regression. All three models have similar prediction accuracies, with RSS values of 0.0110, 0.0156, 0.0160 for linear regression, simple RNN, and LSTM, respectively. The matching performance of these 3 models are also observed in April Maricopa County data. The observed increase in new cases line falls within the one-sigma prediction interval for the last 21 days of available data.
The prediction from weather-driven settling times and viral viability to transmission rate in this work corroborates with previous findings that transmission is faster at low temperatures and humidities for COVID in major global cities from Nov 2019 to Feb 2020,52 in the US using state-level data over Jan–Apr 2020,53 and for Singapore using data from Jan–May 2020.13 Respiratory droplets travel can travel three times farther at lower temperatures and higher humidity compared to typical dry and hot environments.54
It should be noted that not all published work supports a link between weather and transmission. Linear machine learning models failed to establish the correlation between state-level (Italy and US) or country-level (rest of the world) transmission and meteorological data.47 This is most likely due to the non-linearity in linking temperature and humidity data to other variables that are important factors in transmission. For similar reasons, a recent multilinear regression model found no significant correlation between temperature, humidity and the basic reproductive number R0 of transmission.55 However, the lack of correlation between meteorological data and COVID transmission in China during early 2020 may be a result of strong policy changes overshadowing any weather effects.56
Other works have analysed the link between virus-laden aerosol settling and SARS-CoV-2 transmission from different perspectives.5,9,57 Smith et al., provided a useful model that assesses aerosol transmission of SARS-CoV-2 through respiratory droplet physics.57 Their study calculated the number of virus particles inhaled via indirect airborne transmission by calculating the persistence (settling time) of cough-generated aerosols, and concluded that aerosol transmission is a possible but not efficient route of transmission of SARS-CoV-2.57 This conclusion as well as evidence suggested by Stadnytskyi et al.5 and Anfinrud et al.9 agree with the conclusion of the present work to the extent that indirect airborne transmission is a possible route of transmission of SARS-CoV-2. The WHO, in the most recent update (Apr 30, 2021), has also acknowledged aerosol transmission as one of the major routes of transmission for SARS-CoV-2.58 Homogeneity of the aerosols in the space studied is often assumed in these approaches to translate aerosol persistence to aerosol inhaled, which can be far from reality.35 One advantage of this work is that by predicting transmission from aerosol persistence (and virus viability) via data analysis tools, homogeneity is not assumed. Because the infection risk assessment is embedded in the data analysis step connecting aerosol persistent and transmission, mathematical infection risk assessment models such as Wells–Riley and dose–response are also not required in this work. This approach reduces uncertainties introduced into the model as the infection threshold of SARS-CoV-2 is still unclear.59
A key assumption in the models presented is that the timeframes of virus transmission, disease progression, test-to-results, and hospitalizations are consistent across a studied population, their location, and time span. However, timeframes could actually be fluctuating and thus undermine the accuracy of our model predictions. For example, since COVID case data that is reported may have inherent time delays due, for example, to the shortage of test kits. Delays are an important parameter in this study, and thus model fitting residuals associated with this input variable cannot be eliminated. Another underlying assumption of this study is that the fraction of asymptomatic infections of total infections is constant. However, this is still unknown to the best of our knowledge. Our models also have simplifications that may be additional sources of error. These simplifications include that a sodium chloride solution, which is used as a surrogate model of physiological fluids, is a good proxy for virus-laden aerosols and that the surface tension of an aerosol droplet is only a function of its temperature and solute concentration. The neural network models use a random set of parameters initially for each neuron, and the optimized result can be dependent on this initial set of parameters, if they are actually too different from the optimal set.
Although the models in this work use the outdoor weather input variables and transmission can occur indoors, the outdoor temperature correlates positively with the indoor environment.60,61 The correlation coefficient (slope of linear regression), however, depends on the season and location. For example, Massachusetts has Toutdoor ∼ 0.04Tindoor at T < ∼10 °C, and Toutdoor ∼ 0.41Tindoor at T > ∼10 °C.62 South Korea has Toutdoor ∼ 0.13Tindoor at T < ∼15 °C, and Toutdoor ∼ 0.47Tindoor at T > ∼15 °C.63 The indoor absolute humidity also tracks the outdoor humidity across seasons and diverse locations.61,64,65 As a result, the outdoor transmission risk predicted in this work tracks with, and can be used as a surrogate for the indoor transmission risk.
Control measures such as mandatory mask-wearing and lockdowns are not accounted for by two input variables in this work. We limit our scope to April in Fig. 4 when nationwide lockdown was still in effect to minimize this variable in terms of its influence on transmission. The extended-time analysis on Maricopa County for May–August in Fig. 6 has lower fitting and prediction accuracy compared to the April results as shown in Table S1c.† The lower accuracy for longer time periods of analysis may be the result of encompassing more non-weather-related events, such as a significant increase in mask-wearing and the mass public protests of 2020. Although it is possible that the models presented in this work are not capable of handling data over longer times, the RNN models typically benefit from additional training data to improve prediction accuracy. They are expected to have improved prediction performance for longer study times, if non-weather-related events would be represented in the model.
Conclusions
Seasonality of airborne COVID transmission may be explained in part by weather-induced changes in the aerosol settling times and virus viability. We use Stokes' sedimentation model with a Cunningham correction factor for surface slippage in order to estimate the settling times of speech-produced aerosols after evaporation for Re < 1 and Kn ≪ 1. SARS-CoV-2 viral viability is estimated using an empirical relationship from local historical weather data. Linear regression, vector autoregression, and recurrent neural network models using the settling time, viral viability and past transmission rate successfully predict future transmission rates within one-sigma prediction interval. Airborne speech-generated aerosol transmission is a significant transmission route of SARS-CoV-2. Including aerosol settling time and viral viability from historical weather data as input variables can improve the accuracy of transmission rate prediction. Corroborating with publications and public actions over the past year, the findings of this study support implementation of control measures including social distancing, enforcing mask wearing, and systematic preventive measures such as improved ventilation in both community and healthcare settings.Overall, the evidence on weather influence of transmission has been contradictory and inconclusive. We note that the present work does not aim to prove that aerosol settling time and virus viability are exclusively important on predicting transmission rate. The fitting and prediction performance of the models presented suggests that weather plays a considerable role in transmission. Thus, the incorporation of weather-derived, transmission-mechanisms-based input variables, including aerosol settling times and virus viability, into epidemiological prediction model may worth further investigation. Future work in model development should also include additional variables that play a role in airborne or surface-based transmission such as wind speeds, turbulence (especially those created by speech which can lengthen the suspension time by 30–150 times66), and UVB intensity. Datasets should include more locations outside of the US where the weather system may be different. Furthermore, the study periods can be extended to allow for better machine learning algorithm training.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Bill & Melinda Gates Foundation Investment Grant INV-018569. The authors thank Paul Dabisch at National Biodefense Analysis and Countermeasures Center for sharing his insights on SARS-CoV-2 viability. The authors would like to acknowledge Richard Flagan for helpful discussions.References
- World Health Organization (WHO), COVID-19 weekly epidemiological update – 19 Oct 2021, 2021, https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19---19-october-2021, accessed Oct 25, 2021 Search PubMed.
- G. Qu, X. Li, L. Hu and G. Jiang, An Imperative Need for Research on the Role of Environmental Factors in Transmission of Novel Coronavirus (COVID-19), Environ. Sci. Technol., 2020, 54, 3730–3732 CrossRef CAS PubMed.
- A. Ianevski, E. Zusinaite, N. Shtaida, H. Kallio-Kokko, M. Valkonen, A. Kantele, K. Telling, I. Lutsar, P. Letjuka, N. Metelitsa, V. Oksenych, U. Dumpis, A. Vitkauskiene, K. Stasaitis, C. Ohrmalm, K. Bondeson, A. Bergqvist, R. J. Cox, T. Tenson, A. Merits and D. E. Kainov, Low Temperature and Low UV Indexes Correlated with Peaks of Influenza Virus Activity in Northern Europe during 2010–2018, Viruses, 2019, 11(3), 207 CrossRef CAS PubMed.
- J. Shaman and M. Kohn, Absolute humidity modulates influenza survival, transmission, and seasonality, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3243–3248 CrossRef CAS PubMed.
- V. Stadnytskyi, C. E. Bax, A. Bax and P. Anfinrud, The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11875–11877 CrossRef CAS PubMed.
- P. Dabisch, M. Schuit, A. Herzog, K. Beck, S. Wood, M. Krause, D. Miller, W. Weaver, D. Freeburger, I. Hooper, B. Green, G. Williams, B. Holland, J. Bohannon, V. Wahl, J. Yolitz, M. Hevey and S. Ratnesar-Shumate, The Influence of Temperature, Humidity, and Simulated Sunlight on the Infectivity of SARS-CoV-2 in Aerosols, Aerosol Sci. Technol., 2020, 1–15, DOI:10.1080/02786826.2020.1829536.
- M. Schuit, S. Ratnesar-Shumate, J. Yolitz, G. Williams, W. Weaver, B. Green, D. Miller, M. Krause, K. Beck, S. Wood, B. Holland, J. Bohannon, D. Freeburger, I. Hooper, J. Biryukov, L. A. Altamura, V. Wahl, M. Hevey and P. Dabisch, Airborne SARS-CoV-2 Is Rapidly Inactivated by Simulated Sunlight, J. Infect. Dis., 2020, 222, 564–571 CrossRef CAS PubMed.
- A. Rodriguez-Palacios, F. Cominelli, A. R. Basson, T. T. Pizarro and S. Ilic, Textile Masks and Surface Covers-A Spray Simulation Method and a “Universal Droplet Reduction Model” Against Respiratory Pandemics, Front. Med., 2020, 7, 260 CrossRef PubMed.
- P. Anfinrud, V. Stadnytskyi, C. E. Bax and A. Bax, Visualizing Speech-Generated Oral Fluid Droplets with Laser Light Scattering, N. Engl. J. Med., 2020, 382, 2061–2063 CrossRef PubMed.
- M. Z. Bazant and J. W. M. Bush, A guideline to limit indoor airborne transmission of COVID-19, Proc. Natl. Acad. Sci. U. S. A., 2021, 118 Search PubMed.
- K. A. Prather, L. C. Marr, R. T. Schooley, M. A. McDiarmid, M. E. Wilson and D. K. Milton, Airborne transmission of SARS-CoV-2, Science, 2020, 370, 303–304 CrossRef PubMed.
- A. J. Kucharski, T. W. Russell, C. Diamond, Y. Liu, J. Edmunds, S. Funk, R. M. Eggo, F. Sun, M. Jit, J. D. Munday, N. Davies, A. Gimma, K. van Zandvoort, H. Gibbs, J. Hellewell, C. I. Jarvis, S. Clifford, B. J. Quilty, N. I. Bosse, S. Abbott, P. Klepac and S. Flasche, Early dynamics of transmission and control of COVID-19: a mathematical modelling study, Lancet Infect. Dis., 2020, 20, 553–558 CrossRef CAS PubMed.
- S. K. Pani, N. H. Lin and S. RavindraBabu, Association of COVID-19 pandemic with meteorological parameters over Singapore, Sci. Total Environ., 2020, 740, 140112 CrossRef CAS PubMed.
- E. R. Lewis, An examination of Köhler theory resulting in an accurate expression for the equilibrium radius ratio of a hygroscopic aerosol particle valid up to and including relative humidity 100%, J. Geophys. Res., 2008, 113, D03205 CrossRef.
- G. G. Stokes, Mathematical and physical papers, Johnson Reprint Corp, 1850 Search PubMed.
- E. Cunningham, On the velocity of steady fall of spherical particles through fluid medium, Proc. R. Soc. London, Ser. A, 1997, 83, 357–365 Search PubMed.
- P. S. Epstein, On the Resistance Experienced by Spheres in their Motion through Gases, Phys. Rev., 1924, 23, 710–733 CrossRef CAS.
- R. A. Millikan, The General Law of Fall of a Small Spherical Body through a Gas, and its Bearing upon the Nature of Molecular Reflection from Surfaces, Phys. Rev., 1923, 22, 1–23 CrossRef.
- A. B. Jakobsen, J. Merrison and J. J. Iversen, Laboratory study of aerosol settling velocities using Laser Doppler velocimetry, J. Aerosol Sci., 2019, 135, 58–71 CrossRef CAS.
- K. Lin and L. C. Marr, Humidity-Dependent Decay of Viruses, but Not Bacteria, in Aerosols and Droplets Follows Disinfection Kinetics, Environ. Sci. Technol., 2020, 54, 1024–1032 CrossRef CAS PubMed.
- A. J. Prussin, 2nd, D. O. Schwake, K. Lin, D. L. Gallagher, L. Buttling and L. C. Marr, Survival of the Enveloped Virus Phi6 in Droplets as a Function of Relative Humidity, Absolute Humidity, and Temperature, Appl. Environ. Microbiol., 2018, 84, e00551–18 Search PubMed.
- K. H. Chan, J. S. Peiris, S. Y. Lam, L. L. Poon, K. Y. Yuen and W. H. Seto, The Effects of Temperature and Relative Humidity on the Viability of the SARS Coronavirus, Adv. Virol., 2011, 2011, 734690 CAS.
- N. Shimasaki and H. Morikawa, Prevention of COVID-19 Infection with Personal Protective Equipment, J. Disaster Res., 2021, 16, 61–69 CrossRef.
- W. Yang, S. Elankumaran and L. C. Marr, Relationship between humidity and influenza A viability in droplets and implications for influenza's seasonality, PLoS One, 2012, 7, e46789 CrossRef CAS PubMed.
- M. Dadar, Y. Fakhri, G. Bjorklund and Y. Shahali, The association between the incidence of COVID-19 and the distance from the virus epicenter in Iran, Arch. Virol., 2020, 165, 2555–2560 CrossRef CAS PubMed.
- N. F. Suhaimi, J. Jalaludin and M. T. Latif, Demystifying a Possible Relationship between COVID-19, Air Quality and Meteorological Factors: Evidence from Kuala Lumpur, Malaysia, Aerosol Air Qual. Res., 2020, 20, 1520–1529 CrossRef CAS.
- S. R. Venna, A. Tavanaei, R. N. Gottumukkala, V. V. Raghavan, A. S. Maida and S. Nichols, A Novel Data-Driven Model for Real-Time Influenza Forecasting, IEEE Access, 2019, 7, 7691–7701 Search PubMed.
- A. Tomar and N. Gupta, Prediction for the spread of COVID-19 in India and effectiveness of preventive measures, Sci. Total Environ., 2020, 728, 138762 CrossRef CAS PubMed.
- S. Babin, Use of Weather Variables in SARS-CoV-2 Transmission Studies, Int. J. Infect. Dis., 2020, 100, 333–336 CrossRef CAS PubMed.
- Centers for Disease Control and Prevention, Interim Clinical Guidance for Management of Patients with Confirmed Coronavirus Disease (COVID-19), https://www.cdc.gov/coronavirus/2019-ncov/hcp/clinical-guidance-management-patients.html, accessed October 06 Search PubMed.
- Y. Maruyama and K. Hasegawa, Evaporation and drying kinetics of water–NaCl droplets via acoustic levitation, RSC Adv., 2020, 10, 1870–1877 RSC.
- F. K. A. Gregson, J. F. Robinson, R. E. H. Miles, C. P. Royall and J. P. Reid, Drying Kinetics of Salt Solution Droplets: Water Evaporation Rates and Crystallization, J. Phys. Chem. B, 2019, 123, 266–276 CrossRef CAS PubMed.
- M. Rezaei and R. R. Netz, Airborne virus transmission via respiratory droplets: Effects of droplet evaporation and sedimentation, Curr. Opin. Colloid Interface Sci., 2021, 55, 101471 CrossRef CAS PubMed.
- B. Kallapur, K. Ramalingam, A. M. Bastian, A. Mujib, A. Sarkar and S. Sethuraman, Quantitative estimation of sodium, potassium and total protein in saliva of diabetic smokers and nonsmokers: A novel study, J. Nat. Sci., Biol. Med., 2013, 4, 341–345 CrossRef PubMed.
- L. Morawska, G. R. Johnson, Z. D. Ristovski, M. Hargreaves, K. Mengersen, S. Corbett, C. Y. H. Chao, Y. Li and D. Katoshevski, Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities, J. Aerosol Sci., 2009, 40, 256–269 CrossRef CAS.
- F. J. Millero, The apparent and partial molal volume of aqueous sodium chloride solutions at various temperatures, J. Phys. Chem., 1970, 74, 356–362 CrossRef CAS.
- D. R. Stull, Vapor Pressure of Pure Substances. Organic and Inorganic Compounds, Ind. Eng. Chem., 1947, 39, 517–540 CrossRef CAS.
- N. B. Vargaftik, B. N. Volkov and L. D. Voljak, International Tables of the Surface Tension of Water, J. Phys. Chem. Ref. Data, 1983, 12, 817–820 CrossRef CAS.
- R. E. Bolz, CRC Handbook of Tables for Applied Engineering Science, CRC Press, 1973 Search PubMed.
- G. A. Somsen, C. van Rijn, S. Kooij, R. A. Bem and D. Bonn, Small droplet aerosols in poorly ventilated spaces and SARS-CoV-2 transmission, Lancet Respir. Med., 2020, 8, 658–659 CrossRef CAS PubMed.
- H. Zhao, X. Lu, Y. Deng, Y. Tang and J. Lu, COVID-19: asymptomatic carrier transmission is an underestimated problem, Epidemiol. Infect., 2020, 148, e116 CrossRef PubMed.
- X. He, E. H. Y. Lau, P. Wu, X. Deng, J. Wang, X. Hao, Y. C. Lau, J. Y. Wong, Y. Guan, X. Tan, X. Mo, Y. Chen, B. Liao, W. Chen, F. Hu, Q. Zhang, M. Zhong, Y. Wu, L. Zhao, F. Zhang, B. J. Cowling, F. Li and G. M. Leung, Temporal dynamics in viral shedding and transmissibility of COVID-19, Nat. Med., 2020, 26, 672–675 CrossRef CAS PubMed.
- M. D. Allen and O. G. Raabe, Re-evaluation of Millikan's oil drop data for the motion of small particles in air, J. Aerosol Sci., 1982, 13, 537–547 CrossRef.
- R. R. Netz and W. A. Eaton, Physics of virus transmission by speaking droplets, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 25209–25211 CrossRef CAS PubMed.
- S. Jamshidi, M. Baniasad and D. Niyogi, Global to USA County Scale Analysis of Weather, Urban Density, Mobility, Homestay, and Mask Use on COVID-19, Int. J. Environ. Res. Public Health, 2020, 17 CAS.
- C. Ogaugwu, H. Mogaji, E. Ogaugwu, U. Nebo, H. Okoh, S. Agbo and A. Agbon, Effect of Weather on COVID-19 Transmission and Mortality in Lagos, Nigeria, Scientifica, 2020, 2020, 2562641 CrossRef PubMed.
- Z. Malki, E. S. Atlam, A. E. Hassanien, G. Dagnew, M. A. Elhosseini and I. Gad, Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches, Chaos, Solitons Fractals, 2020, 138, 110137 CrossRef PubMed.
- A. Chanda, COVID-19 in India: transmission dynamics, epidemiological characteristics, testing, recovery and effect of weather, Epidemiol. Infect., 2020, 148, e182 CrossRef CAS PubMed.
- V. C. Hughes, The Effect of Temperature, Dewpoint, and Population Density on COVID-19 Transmission in the United States: A Comparative Study, Am. J. Public Health Res., 2020, 8, 112–117 Search PubMed.
- E. Joonaki, A. Hassanpouryouzband, C. L. Heldt and O. Areo, Surface Chemistry Can Unlock Drivers of Surface Stability of SARS-CoV-2 in a Variety of Environmental Conditions, Chem, 2020, 6, 2135–2146 CAS.
- M. Beckmann, T. Václavík, A. M. Manceur, L. Šprtová, H. von Wehrden, E. Welk, A. F. Cord and A. Tatem, glUV: a global UV-B radiation data set for macroecological studies, Methods Ecol. Evol., 2014, 5, 372–383 CrossRef.
- M. M. Sajadi, P. Habibzadeh, A. Vintzileos, S. Shokouhi, F. Miralles-Wilhelm and A. Amoroso, Temperature, Humidity and Latitude Analysis to Predict Potential Spread and Seasonality for COVID-19, SSRN, 2020, 3550308, DOI:10.2139/ssrn.3550308.
- S. Gupta, G. S. Raghuwanshi and A. Chanda, Effect of weather on COVID-19 spread in the US: A prediction model for India in 2020, Sci. Total Environ., 2020, 728, 138860 CrossRef CAS PubMed.
- L. Zhao, Y. Qi, P. Luzzatto-Fegiz, Y. Cui and Y. Zhu, COVID-19: Effects of Environmental Conditions on the Propagation of Respiratory Droplets, Nano Lett., 2020, 20, 7744–7750 CrossRef CAS PubMed.
- J. Pan, Y. Yao, Z. Liu, X. Meng, J. S. Ji, Y. Qiu, W. Wang, L. Zhang, W. Wang and H. Kan, Warmer weather unlikely to reduce the COVID-19 transmission: An ecological study in 202 locations in 8 countries, Sci. Total Environ., 2021, 753, 142272 CrossRef CAS PubMed.
- Y. Yao, J. Pan, Z. Liu, X. Meng, W. Wang, H. Kan and W. Wang, No association of COVID-19 transmission with temperature or UV radiation in Chinese cities, Eur. Respir. J., 2020, 55, 5 Search PubMed.
- S. H. Smith, G. A. Somsen, C. van Rijn, S. Kooij, L. van der Hoek, R. A. Bem and D. Bonn, Aerosol persistence in relation to possible transmission of SARS-CoV-2, Phys. Fluids, 2020, 32, 107108 CrossRef CAS PubMed.
- World Health Organization, Coronavirus disease (COVID-19): How is it transmitted?, http://who.int/news-room/q-a-detail/coronavirus-disease-covid-19-how-is-it-transmitted, accessed 24 July 2021 Search PubMed.
- M. J. Evans, Avoiding COVID-19: Aerosol Guidelines, medRxiv, 2020 DOI:10.1101/2020.05.21.20108894.
- J. Pan, J. Tang, M. Caniza, J. M. Heraud, E. Koay, H. K. Lee, C. K. Lee, Y. Li, A. N. Ruiz, C. F. Santillan-Salas and L. C. Marr, Correlating Indoor and Outdoor Temperature and Humidity in a Sample of Buildings in Tropical Climates, Indoor Air, 2021, 31, 2281–2295 CrossRef CAS PubMed.
- J. L. Nguyen and D. W. Dockery, Daily indoor-to-outdoor temperature and humidity relationships: a sample across seasons and diverse climatic regions, Int. J. Biometeorol., 2016, 60, 221–229 CrossRef PubMed.
- J. L. Nguyen, J. Schwartz and D. W. Dockery, The relationship between indoor and outdoor temperature, apparent temperature, relative humidity, and absolute humidity, Indoor Air, 2014, 24, 103–112 CrossRef CAS PubMed.
- K. Lee and D. Lee, The Relationship Between Indoor and Outdoor Temperature in Two Types Of Residence, Energy Procedia, 2015, 78, 2851–2856 CrossRef.
- T. M. Habeebullah, I. H. A. Abd El-Rahim and E. A. Morsy, Impact of outdoor and indoor meteorological conditions on the COVID-19 transmission in the western region of Saudi Arabia, J. Environ. Manage., 2021, 288, 112392 CrossRef CAS PubMed.
- A. Ahlawat, A. Wiedensohler and S. K. Mishra, An Overview on the Role of Relative Humidity in Airborne Transmission of SARS-CoV-2 in Indoor Environments, Aerosol Air Qual. Res., 2020, 20, 1856–1861 CrossRef CAS.
- K. L. Chong, C. S. Ng, N. Hori, R. Yang, R. Verzicco and D. Lohse, Extended Lifetime of Respiratory Droplets in a Turbulent Vapor Puff and Its Implications on Airborne Disease Transmission, Phys. Rev. Lett., 2021, 126, 034502 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ea00013f |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2022 |