Accuracy of quantum chemistry structures of chiral tag complexes and the assignment of absolute configuration†
Kevin
Mayer
 a,
Channing
West
a,
Frank E.
Marshall
b,
Galen
Sedo
c,
Garry S.
Grubbs
II
a,
Channing
West
a,
Frank E.
Marshall
b,
Galen
Sedo
c,
Garry S.
Grubbs
II
 b,
Luca
Evangelisti
b,
Luca
Evangelisti
 *d and
Brooks H.
Pate
*d and
Brooks H.
Pate
 *a
*a
aDepartment of Chemistry, University of Virginia, 409 McCormick Rd., Charlottesville, VA 22904, USA. E-mail: bp2k@virginia.edu
bDepartment of Chemistry, Missouri University of Science and Technology, 142 Schrenk Hall, 400 W. 11th St., Rolla, MO 65409, USA
cDepartment of Natural Sciences, University of Virginia's College at Wise, 1 College Avenue, Wise, VA 24293, USA
dDepartment of Chemistry “G. Ciamician”, University of Bologna, via S. Alberto 163, Ravenna, 48123, Italy. E-mail: luca.evangelisti6@unibo.it
First published on 9th November 2022
Abstract
The absolute configuration of a molecule can be established by analysis of molecular rotational spectra of the analyte complexed with a small chiral molecule of known configuration. This approach of converting the analyte enantiomers, with identical rotational spectra, into diastereomers that can be distinguished spectroscopically is analogous to chiral derivatization in nuclear magnetic resonance (NMR) spectroscopy. For the rotational chiral tag method, the derivatization uses noncovalent interactions to install the new chiral center and avoids complications due to possible racemization of the analyte when covalent chemistry is used. The practical success of this method rests on the ability to attribute assigned rotational spectra to specific geometries of the diastereomeric homochiral and heterochiral tag complexes formed in the pulsed jet expansion that is used to introduce samples into the microwave spectrometer. The assignment of a molecular structure to an experimental rotational spectrum uses quantum chemistry equilibrium geometries to provide theoretical estimates of the spectrum parameters that characterize the rotational spectrum. This work reports the results of a high-sensitivity rotational spectroscopy study of the complexes formed between (3)-butyn-2-ol and verbenone. The rotational spectra of four homochiral and four heterochiral complexes are assigned. In addition, the 14 distinct, singly-substituted 13C isotopomer spectra of five of these species are assigned in natural abundance. Analysis of these spectra provides direct structural characterization of the complexes through determination of the carbon atom position coordinates. This data set is used to benchmark quantum chemistry calculations of candidate equilibrium geometries of the chiral tag complexes. The quantum chemistry calculations are limited to methods commonly used in the field of rotational spectroscopy. It is shown that the accuracy of the structures from quantum chemistry provides a high-confidence assignment of cluster geometries to the observed spectra. As a result, a high-confidence determination of the analyte (verbenone) absolute configuration is achieved.
Introduction
This work examines the ability to assign the absolute configuration of a molecule through identification of the structure of a complex formed between an analyte and a small, chiral molecule – called the “chiral tag.”1–8 The geometries of the chiral tag complexes, which are formed in a pulsed jet expansion where the analyte and tag molecule are added to the inert carrier gas, are analyzed using broadband molecular rotational spectroscopy. The goal of this approach is to develop a generally useful analytical chemistry methodology that can assign the absolute configuration of a molecule with high confidence and without the need of a reference sample of the analyte with known configuration. This application extends significant previous work on the structures of weakly bound complexes of chiral molecules in vibronic,9,10 vibrational,11,12 and rotational spectroscopy.13–15 The goal of developing an analytical chemistry methodology places additional demands on quantum chemistry structure determination. Specifically, there is a need for rapid quantum chemistry geometry optimizations so that the computational analysis does not lead to unacceptably long times to make the absolute configuration determination.The physical chemistry community continues to develop spectroscopy methods to assign the absolute configuration of molecules.16–21 Spectroscopy methods ultimately require quantum chemistry predictions of the spectrum for analysis. Perhaps the most successful technique is vibrational circular dichroism (VCD) and its related method of Raman optical activity.22,23 The keys to its success are an underlying spectroscopy method – vibrational spectroscopy – that has good chemical selectivity and the development of quantum chemistry methods to calculate the VCD spectroscopy with sufficient accuracy to make high-confidence determinations of the configuration.24,25 This spectroscopy technique has been validated in many experiments and has now been accepted as an analysis method in the U.S. Pharmacopeia (Chapters 〈782〉 and 〈1783〉). Photoelectron circular dichroism (PECD) has seen rapid development in the past few years from both the experimental and theoretical sides and continues to expand its scope of application.26–29 Nuclear magnetic resonance (NMR) spectroscopy has unrivaled chemical selectivity and generality and there are many applications of NMR in chiral analysis.30,31 However, the task of assigning absolute configuration still poses challenges. A common approach in NMR spectroscopy is to convert the enantiomers into diastereomers by adding an additional chiral center of known configuration and of high enantiopurity. This chiral center can be added through covalent chemistry – chiral derivatization – or through creation of long-lived complexes with the chiral discrimination agent in solution – chiral solvation. The challenge for assignment of absolute configuration is attributing the now distinguishable NMR resonances to a specific diastereomer structure. Methods to make this spectroscopic assignment using theoretical spectra from quantum chemistry, and to assess the confidence of the assignment, are under development.32,33
The application of rotational spectroscopy to chiral analysis is considered in this work.34–36 Rotational spectroscopy has important advantages as an analytical chemistry method. It has high chemical selectivity and the spectroscopy parameters – the rotational constants – are directly connected to the molecular geometry through the principal moments-of-inertia. As a result, the analysis only requires accurate geometries of the analyte from theory. Spectrometers for molecular rotational spectroscopy have unmatched spectral resolution.37–39 As a result, analysis can be performed on mixtures. In the case of chiral analysis, it is possible to analyze multiple species in a sample.1,40 In contrast, spectroscopy techniques with lower resolution, such as VCD, face difficulty in identifying low abundance species in a sample and generally require samples of high purity for analysis. Rotational spectroscopy also faces challenges as a general analytical chemistry method. These include the need to volatilize the sample to introduce it in the pulsed molecular beam, the physical requirement of a dipole moment, and decreasing sensitivity as molecular size increases due to the rapid increase in the rotational partition function.
Two approaches to chiral analysis using rotational spectroscopy have been developed recently. Interest in chiral analysis by rotational spectroscopy was sparked by the report of the microwave three-wave mixing techniques by Patterson, Schnell, and Doyle in 2013.41,42 The microwave three-wave mixing technique has similarities to chiroptical measurements. Two resonant microwave pulses are used to create a time-dependent quantum state that coherently emits at the sum or difference frequency of the preparation pulses.43–47 The phase of the emission signal is determined by the sign of the products of the dipole moment components in the principal axis system and these differ for the two enantiomers. The chiral signal, therefore, occurs at the same frequency, but with a different sign for the left- and right-handed version of the molecule as in other chiroptical spectroscopies. If the sample has an enantiomeric excess (EE), the absolute configuration of the dominant enantiomer can be assigned from the measured phase. However, despite an early claim that this phase could be measured in an absolute manner,35 there has been no subsequent report of an instrument design that can make absolute configuration determinations without the use of reference samples of known configuration. In its current state of development, microwave three-wave mixing cannot meet the challenge of assigning the absolute configuration of a new analyte.
The second approach to chiral analysis follows the strategy of NMR spectroscopy to convert enantiomers (with identical rotational spectra) into diastereomers (with distinguishable rotational spectra) by adding an additional chiral center of known configuration. In the rotational spectroscopy implementation, this additional chiral center is added using noncovalent interactions via cluster formation in a pulsed molecular beam.1–8 Noncovalent attachment of the “chiral tag” avoids any possible racemization of the analyte during the chiral derivatization process. One advantage of a chiral derivatization approach is that spectrometer signals associated with the two enantiomers now occur at different frequencies (i.e., the rotational transitions of the resulting diastereomers are fully resolved in the spectrometer). This contrasts with circular dichroism and three-wave mixing approaches where the transition frequencies are the same for the enantiomers and only differ in phase or sign. The practical result is that chiral tag rotational spectroscopy can also be used to make quantitative measurements of the enantiomeric excess of the analyte without the need of a reference sample of known EE to calibrate the instrument response.
The conceptual basis of chiral tag rotational spectroscopy is obvious, and the major challenges are to determine the practical limits of using this technique. The rotational spectroscopy community is just beginning to explore the scope of the method including the important issues of measurement sensitivity and the practical size limits for analytes. For the assignment of absolute configuration, there are important issues about the ability of quantum chemistry to guide the structural analysis of the rotational spectra of chiral tag complexes so that high-confidence enantiomer identification is possible. Quantum chemistry must be able to identify the lowest energy isomers of the chiral tag complexes that are likely to be present in the seeded pulsed jet expansion. Theoretical estimates of the molecular parameters used to predict a rotational spectrum must be accurate enough to assign specific isomers of the complexes to observed spectra. Finally, the theoretical calculations required to support the spectroscopic analysis need to be computationally efficient so that the absolute configuration can be determined on a reasonable time scale. These issues are explored in this work through an analysis of the rotational spectrum of verbenone complexed with butynol.
Experimental
The chiral tag complexes in this work are formed through the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation of verbenone with the small chiral molecule (3)-butyn-2-ol (butynol). A single (1S)-(−)-verbenone sample is used in all measurements and was obtained from Sigma-Aldrich (Product 218251 with a reported EE = 53.6 on the certificate of analysis). Three samples of the chiral tag were used: a racemic sample (CAS number: 2028-63-9), a high enantiopurity sample of (R)-butynol (CAS number: 42969-65-3), and a high enantiopurity sample of (S)-butynol (CAS number: 2914-69-4). The two enantioenriched samples have EE ∼ 98 as verified by chiral gas chromatography prior to the measurements. The rotational spectroscopy of both verbenone48 and butynol49 have been reported previously. Over the course of experiments using butynol as a tag, we have observed that butynal builds up in the sample even when refrigerated. To avoid this complication, freshly distilled butynol samples are used in the measurements.
1 complexation of verbenone with the small chiral molecule (3)-butyn-2-ol (butynol). A single (1S)-(−)-verbenone sample is used in all measurements and was obtained from Sigma-Aldrich (Product 218251 with a reported EE = 53.6 on the certificate of analysis). Three samples of the chiral tag were used: a racemic sample (CAS number: 2028-63-9), a high enantiopurity sample of (R)-butynol (CAS number: 42969-65-3), and a high enantiopurity sample of (S)-butynol (CAS number: 2914-69-4). The two enantioenriched samples have EE ∼ 98 as verified by chiral gas chromatography prior to the measurements. The rotational spectroscopy of both verbenone48 and butynol49 have been reported previously. Over the course of experiments using butynol as a tag, we have observed that butynal builds up in the sample even when refrigerated. To avoid this complication, freshly distilled butynol samples are used in the measurements.
Rotational spectra were recorded on a 2–8 GHz chirped-pulse Fourier transform microwave (CP-FTMW) spectrometer with the instrument design and technique previously described.50,51 The introduction of the analyte uses the reservoir nozzle design from NIST.52 The sample of verbenone was heated to 60 °C to achieve optimum sensitivity on the monomer spectrum. The butynol tag was introduced into the neon gas stream using an external reservoir system. A 50 mL beaker was loaded with 100 μL of butynol and placed into a stainless-steel reservoir with an inlet port for pure neon and a pressure regulated outlet for introduction of the butynol/neon mixture into the spectrometer. The neon input pressure was adjusted to produce an approximate 0.1% mixture of the butynol vapor pressure in neon (about 2.3 atm of neon in the external reservoir). The output pressure of the reservoir was set to about 1.5 atm.
Spectra were taken using enantiopure (R)-(+)-butynol, enantiopure (S)-(−)-butynol and racemic butynol with (1S)-(−)-verbenone. One goal for this study is to identify as many isomers of the chiral tag complex as possible. The deep average measurements used 2 million time-domain free induction decay (FID) traces for enantiopure tag samples and 1 million averages for the racemic sample. For the enantiopure measurements, this gave spectra with better than 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 signal-to-noise ratio for the strongest chiral tag complex spectra. Based on experience with the University of Virginia CP-FTMW spectrometer, an order-of-magnitude estimate of the analyte consumption is 1 nmol per FID. The 2 million average measurements with enantiopure butynol are, therefore, estimated to consume 300 mg of verbenone. The spectrometer acquires approximately 100
1 signal-to-noise ratio for the strongest chiral tag complex spectra. Based on experience with the University of Virginia CP-FTMW spectrometer, an order-of-magnitude estimate of the analyte consumption is 1 nmol per FID. The 2 million average measurements with enantiopure butynol are, therefore, estimated to consume 300 mg of verbenone. The spectrometer acquires approximately 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 FID per hour (8 FIDs collected on each sample injection cycle occurring at 3.3 Hz repetition rate) so that the enantiopure tag measurements require about 20 hours. The broadband rotational spectra were fit using JB95,53 Pickett's SPCAT/SPFIT,54–56 and Kisiel's PROSPE program package.57 The Kraitchman analysis28,58 of the 13C isotopomer spectra used Kisiel's program that includes Costain estimates of the coordinate errors.59
000 FID per hour (8 FIDs collected on each sample injection cycle occurring at 3.3 Hz repetition rate) so that the enantiopure tag measurements require about 20 hours. The broadband rotational spectra were fit using JB95,53 Pickett's SPCAT/SPFIT,54–56 and Kisiel's PROSPE program package.57 The Kraitchman analysis28,58 of the 13C isotopomer spectra used Kisiel's program that includes Costain estimates of the coordinate errors.59
The quantum chemistry calculations were performed using Gaussian 16.60 All geometry optimizations were performed using the keyword output = Pickett to calculate the rotational constants, electric dipole moment components, and atom positions in the principal axis system.
Results
A. Optimized chiral tag complex geometries from quantum chemistry
One challenge for chiral tag rotational spectroscopy is identifying candidate geometries for the tag complexes because there is the potential for a large number of isomers for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
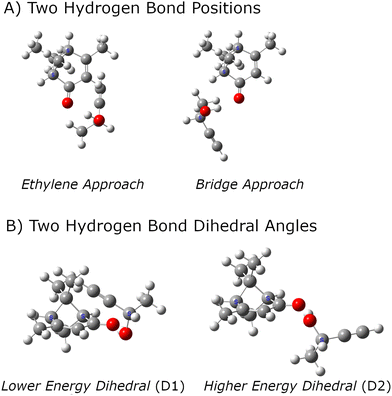
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between analyte and tag. Several computational chemistry tools for this search have been reported and used in rotational spectroscopy studies.61–64 However, the search for candidate structures in this work has used chemical intuition because there is a clear hydrogen bond formation position that is expected to dominate the noncovalent interactions. The general structural chemistry considerations are illustrated in Fig. 1. There are two distinct sites for hydrogen bond formation that are defined by the butynol –OH group attaching to positions where high electron density is expected for lone pairs in an sp2-hybridized oxygen atom. In the nomenclature used in this work, these two sites are designated as E – for approach from the ethylene side of carbonyl – or B when the butynol approaches from the side of the bridged structure of verbenone. It is found that there are generally two positions of butynol that are distinguished by the dihedral angle around the O⋯O axis of the hydrogen bond. These are simply designated as D1 and D2 where the D1 structure has lower energy in the quantum chemistry calculation. In all cases, the lower energy dihedral position, D1, places the acetylene group of butynol near the verbenone.
1 complexes between analyte and tag. Several computational chemistry tools for this search have been reported and used in rotational spectroscopy studies.61–64 However, the search for candidate structures in this work has used chemical intuition because there is a clear hydrogen bond formation position that is expected to dominate the noncovalent interactions. The general structural chemistry considerations are illustrated in Fig. 1. There are two distinct sites for hydrogen bond formation that are defined by the butynol –OH group attaching to positions where high electron density is expected for lone pairs in an sp2-hybridized oxygen atom. In the nomenclature used in this work, these two sites are designated as E – for approach from the ethylene side of carbonyl – or B when the butynol approaches from the side of the bridged structure of verbenone. It is found that there are generally two positions of butynol that are distinguished by the dihedral angle around the O⋯O axis of the hydrogen bond. These are simply designated as D1 and D2 where the D1 structure has lower energy in the quantum chemistry calculation. In all cases, the lower energy dihedral position, D1, places the acetylene group of butynol near the verbenone.
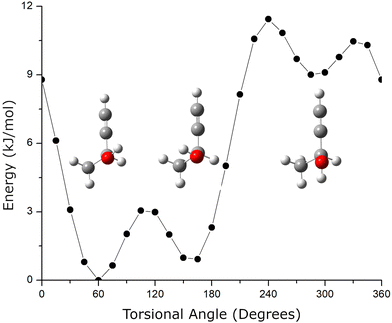
A second structural issue is that butynol has conformational flexibility. The relaxed potential energy surface for butynol is shown in Fig. 2. There are two low energy conformations. The lowest energy monomer conformation, denoted C1, has the OH anti to the methyl group. The conformation with the hydroxyl anti to the C–H bond is the second lowest energy conformer, C2. Both butynol conformations are found in low energy isomers of the chiral tag complexes identified by quantum chemistry and observed experimentally. The potential energy surface suggests the possibility for a third conformer with the –OH anti to the acetylene, but this conformation is expected to be high energy. This conformation is not observed in the reported gas phase rotational spectrum of butynol.42 Isomer searches starting from this butynol conformation were not considered.
With these structural features defined, an example of the naming convention for isomers in the quantum chemistry calculations is HOMEC1D2. This name would indicate that the complex is formed between (S)-verbenone and (S)-butynol, designated a homochiral complex. The butynol attaches from the ethylene side of the carbonyl with the lowest energy monomer conformation of butynol and with the second lowest energy dihedral orientation about the O⋯O hydrogen bond axis. Also note, the rotational spectrum would be identical for the enantiomer of this complex that is formed between (R)-verbenone and (R)-butynol.
Quantum chemistry results are only reported for a small set of quantum chemistry methods. The model chemistries used in this work are ones that are frequently used in the analysis of rotational spectra. These methods all include treatment of the dispersion interaction from correlated electron motion. Two methods are density functional approaches: B3LYP with Grimme's D3 dispersion corrections (with Becke–Johnson damping)65 and the higher-level B2PLYPD3 method.66 In a previous benchmarking study of quantum chemistry methods and rotational spectra of isolated compounds, these two approaches were shown to give good accuracy in the prediction of rotational constants.67 MP2 calculations are also reported. Finally, two basis sets of comparable size are used. The Pople basis set (6-311++G(d,p)) is a common basis set used in rotational spectroscopy analysis. The more recent def2TZVP basis is also evaluated in this work.68 The equilibrium geometry structures in the principal axis system, rotational constants derived from these structures, and dipole moment vector components in the principal axis system for the B3LYP GD3BJ def2TZVP model chemistry are reported in the ESI.† To reduce the manuscript length, figures that compare experimental and theoretical results are only shown for calculations with the def2TZVP basis set. The analogous figures using the Pople 6-311++G(d,p) basis set are available in the ESI.† The tables reporting computational results show results from both basis sets. A summary of the relative energies for the isomers identified in the geometry search for the quantum chemistry methods selected for this work is presented in Table 1.
| Isomer | def2TZVP | 6-311++G(d,p) | ||||
|---|---|---|---|---|---|---|
| B2PLYPD3 | B3LYP-GD3BJ | MP2 | B2PLYPD3 | B3LYP-GD3BJ | MP2 | |
| a For these calculations, the geometry optimized to the lower energy isomer in the dihedral angle about the O⋯O axis of the hydrogen bond (the associated D1 isomer). | ||||||
| HOMEC2D1 | 0 | 0 | 0 | 0.39 | 0 | 0.45 |
| HOMBC2D1 | 0.19 | 0.52 | 0.04 | 0 | 0.10 | 0 |
| HOMBC1D1 | 0.44 | 0.63 | 1.44 | 0.69 | 0.58 | 1.83 |
| HOMEC1D1 | 1.29 | 2.05 | 0.67 | 1.73 | 2.06 | 1.31 |
| HOMBC1D2 | 3.21 | |||||
| HOMEC1D2 | 5.57 | 6.24 | 4.75 | 5.64 | 6.35 | 4.24 |
| HOMBC2D2 | 6.44 | 6.62 | 7.83 | 6.69 | 6.48 | 8.96 |
| HOMEC2D2 | 7.33 | 8.02 | 8.39 | 9.98 | ||
| HETEC1D1 | 0 | 0 | 0 | 0.65 | 0.12 | 0.99 |
| HETBC1D1 | 0.10 | 0.29 | 0.07 | 0 | 0 | 0 |
| HETBC2D1 | 0.86 | 0.27 | 1.81 | 1.02 | 0.15 | 2.17 |
| HETEC2D1 | 1.56 | 1.55 | 0.65 | 1.78 | 1.54 | 1.42 |
| HETBC1D2 | 4.87 | 4.75 | 4.25 | 4.55 | 4.63 | 3.27 |
| HETEC2D2 | 6.65 | 6.78 | 7.62 | 7.18 | 6.68 | 8.96 |
| HETEC1D2 | 7.41 | 8.20 | ||||
| HETBC2D2 | 7.57 | 7.60 | 8.27 | 7.98 | 7.42 | 9.08 |
ΔElowest![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) energyHOM–HET energyHOM–HET |
0.14 | −0.26 | 0.08 | 0.14 | −0.26 | 0.11 |
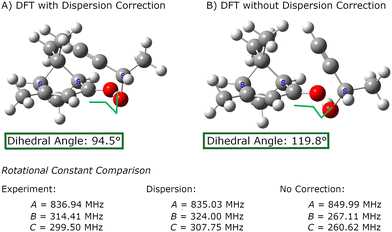
The importance of using methods that treat the dispersion interactions is illustrated in Fig. 3. Although the dispersion forces may be weak, they can produce large atom displacements when they act on a coordinate with a weak force constant. For verbenone–butynol complexes, the dispersion interactions can strongly affect the dihedral angle about the O⋯O hydrogen bond. Density functional calculations without dispersion correction produce equilibrium geometries that yield rotational constants with extremely poor agreement with experiment.
B. Assignment of rotational spectra for the chiral tag complexes
The analysis of the rotational spectra is guided by the quantum chemistry results. Assignments were performed using the theoretical estimates of the rotational constants and principal axis system dipole moment components starting from the lowest energy theoretical structure. The analysis is slightly complicated by the low enantiopurity of verbenone (EE = 54) which leads to significant amounts of both homochiral and heterochiral chiral tag complexes even when the high enantiopurity butynol samples are used. Two spectra were used to identify the complexes. One spectrum was acquired using (S)-butynol as the tag and this spectrum is dominated by homochiral tag complexes. The second spectrum used (R)-butynol so that the heterochiral complexes dominate. Rotational spectra for four isomers of the butynol–verbenone complex were identified for both the homochiral and heterochiral complexes. The rotational constants for these assigned spectra are compared to the rotational constants of the quantum chemistry equilibrium geometries in Table 2. The two experimental spectra are shown in Fig. 4. These spectra also show the residuals after the rotational transitions from all eight assigned spectra are cut from data set. Any other complexes present in the pulsed jet expansion are estimated to be less than 1% of the total number density of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes of the analyte and tag.
1 complexes of the analyte and tag.
| Isomer | Constant | Experimenta (MHz) | B2PLYPD3 def2TZVP | B3LYP GD3BJ def2TZVP | MP2 def2TZVP | B2PLYPD3 6-311++G(d,p) | B3LYP GD3BJ 6-311++G(d,p) | MP2 6-311++G(d,p) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Theory (MHz) | % error | Theory (MHz) | % error | Theory (MHz) | % error | Theory (MHz) | % error | Theory (MHz) | % error | Theory (MHz) | % error | |||
| a The values in parenthesis are the 1σ errors in the last two digit. | ||||||||||||||
| HOMBC1D1 | A | 948.88846(67) | 952.28 | −0.36 | 951.42 | −0.27 | 958.79 | −1.04 | 949.34 | −0.05 | 948.59 | 0.03 | 953.82 | −0.52 |
| B | 295.40012(29) | 299.72 | −1.46 | 301.22 | −1.97 | 302.90 | −2.54 | 297.94 | −0.86 | 300.30 | −1.66 | 299.58 | −1.42 | |
| C | 260.85724(28) | 265.02 | −1.60 | 265.94 | −1.95 | 267.82 | −2.67 | 263.84 | −1.14 | 264.89 | −1.55 | 266.73 | −2.25 | |
| HOMBC2D1 | A | 859.1653(14) | 863.35 | −0.49 | 861.45 | −0.27 | 869.77 | −1.23 | 858.99 | 0.02 | 858.43 | 0.09 | 861.86 | −0.31 |
| B | 306.20216(43) | 309.70 | −1.14 | 309.84 | −1.19 | 315.94 | −3.18 | 308.79 | −0.85 | 309.87 | −1.20 | 312.64 | −2.10 | |
| C | 291.24858(49) | 294.96 | −1.27 | 294.91 | −1.26 | 300.61 | −3.21 | 293.94 | −0.92 | 294.73 | −1.20 | 297.61 | −2.18 | |
| HOMEC2D1 | A | 836.9427(16) | 839.18 | −0.27 | 835.03 | 0.23 | 842.55 | −0.67 | 830.88 | 0.72 | 831.61 | 0.64 | 813.95 | 2.75 |
| B | 314.41418(43) | 320.14 | −1.82 | 324.00 | −3.05 | 328.48 | −4.47 | 322.13 | −2.45 | 324.04 | −3.06 | 341.11 | −8.49 | |
| C | 299.49708(44) | 304.93 | −1.81 | 307.75 | −2.75 | 310.84 | −3.79 | 305.79 | −2.10 | 307.22 | −2.58 | 319.39 | −6.64 | |
| HOMEC1D1 | A | 986.1931(10) | 992.43 | −0.63 | 994.36 | −0.83 | 994.34 | −0.83 | 987.11 | −0.09 | 991.19 | −0.51 | 983.24 | 0.30 |
| B | 276.80869(37) | 279.38 | −0.93 | 279.33 | −0.91 | 288.62 | −4.27 | 279.34 | −0.91 | 278.35 | −0.56 | 288.38 | −4.18 | |
| C | 261.96346(37) | 264.50 | −0.97 | 263.87 | −0.73 | 273.19 | −4.28 | 264.73 | −1.06 | 262.53 | −0.22 | 272.67 | −4.09 | |
| HETBC1D1 | A | 905.3497(13) | 906.31 | −0.11 | 905.49 | −0.02 | 912.40 | −0.78 | 903.26 | 0.23 | 903.57 | 0.20 | 905.61 | −0.03 |
| B | 286.52860(41) | 291.62 | −1.78 | 291.83 | −1.85 | 297.38 | −3.79 | 290.46 | −1.37 | 291.16 | −1.62 | 295.29 | −3.06 | |
| C | 276.45786(43) | 280.92 | −1.61 | 281.29 | −1.75 | 285.80 | −3.38 | 279.73 | −1.18 | 280.68 | −1.53 | 283.28 | −2.47 | |
| HETEC1D1 | A | 905.85816(81) | 911.96 | −0.67 | 912.05 | −0.68 | 914.10 | −0.91 | 906.64 | −0.09 | 909.39 | −0.39 | 888.73 | 1.89 |
| B | 286.90405(35) | 290.87 | −1.38 | 292.30 | −1.88 | 298.87 | −4.17 | 290.81 | −1.36 | 291.87 | −1.73 | 305.44 | −6.46 | |
| C | 278.45467(34) | 282.80 | −1.56 | 283.78 | −1.91 | 287.70 | −3.32 | 282.07 | −1.30 | 282.74 | −1.54 | 291.31 | −4.62 | |
| HETBC2D1 | A | 879.94543(84) | 881.39 | −0.16 | 876.62 | 0.38 | 890.50 | −1.20 | 878.09 | 0.21 | 873.07 | 0.78 | 887.28 | −0.83 |
| B | 320.34351(36) | 325.57 | −1.63 | 328.75 | −2.62 | 327.73 | −2.30 | 323.64 | −1.03 | 328.12 | −2.43 | 323.36 | −0.94 | |
| C | 279.56130(38) | 284.01 | −1.59 | 286.22 | −2.38 | 286.05 | −2.32 | 282.54 | −1.06 | 285.61 | −2.16 | 282.95 | −1.21 | |
| HETEC2D1 | A | 913.4767(27) | 919.95 | −0.71 | 918.12 | −0.51 | 921.38 | −0.87 | 912.71 | 0.08 | 917.20 | −0.41 | 907.26 | 0.38 |
| B | 300.39373(78) | 304.07 | −1.22 | 305.54 | −1.71 | 312.79 | −4.13 | 304.57 | −1.39 | 304.42 | −1.34 | 313.89 | −4.49 | |
| C | 278.01924(75) | 281.21 | −1.15 | 282.58 | −1.64 | 289.53 | −4.14 | 281.63 | −1.30 | 280.73 | −0.98 | 290.03 | −4.32 | |
In addition, the measurement sensitivity was sufficient to assign the 14 distinct singly-substituted 13C isotopomers in five of the eight complexes. These assignments are used to obtain direct structural information using Kraitchman's method.28,50 The carbon atom positions from Kraitchman analysis are reported in the ESI.† The full results of the spectroscopy fit using the S-reduction of the Watson Hamiltonian can also be found in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27,69 The ESI,† does not include the assigned transition frequencies. A major strength of rotational spectroscopy is that the Watson Hamiltonian provides a quantitative model with transition frequencies predicted to a fraction of the experimental line width. The full fit results and the dipole component information in Table 4 are sufficient to generate an accurate representation of the 78 assigned spectra in this work. Line lists are available on request.
27,69 The ESI,† does not include the assigned transition frequencies. A major strength of rotational spectroscopy is that the Watson Hamiltonian provides a quantitative model with transition frequencies predicted to a fraction of the experimental line width. The full fit results and the dipole component information in Table 4 are sufficient to generate an accurate representation of the 78 assigned spectra in this work. Line lists are available on request.
C. Isomer composition analysis
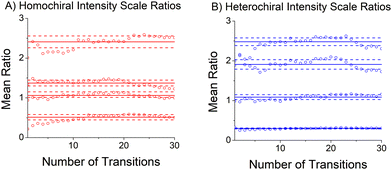
The relative abundances of the chiral tag complex isomers are estimated from the transition intensities in the broadband rotational spectrum. This analysis determines a scale factor between a theoretical spectrum and the experimental spectrum. The theoretical spectrum is calculated using SPFIT and uses the experimental rotational constants, the quantum chemistry estimates of the dipole moment components, and assumes thermodynamic equilibrium of the rotational energy levels at a temperature of 1 K. This temperature is chosen based on comparisons between observed and calculated spectra in many measurements in the CP-FTMW spectrometer. The average scale factor using the 25 strongest transitions in the spectrum is used to determine the fractional isomer composition. This process is illustrated in Fig. 5 which shows how the average transition intensity scale factor for the four chiral tag complex isomers varies as the number of transitions included in the average increases. As can be seen, the average scale factor shows approximately a 10% variation as the number of transitions increases up to 30. Based on this behavior, we estimate that the scale factors (and, therefore, the relative abundance of the isomers) have a measurement precision of 10% of the value. There is no way to determine the accuracy of the composition determination because there is no orthogonal, validated measurement method for determining the cluster composition. However, in a separate study this analysis approach was tested on the diastereomer content of menthone/isomenthone samples where the composition could be determined by GC/MS analysis.70 In that case, the accuracy of the diastereomer composition was better than 5% of value. The isomer composition of homochiral and heterochiral complexes in the three chiral tag measurements are reported in Table 3.| Isomer | (S)-Butynola (%) | (R)-Butynolb (%) | (RS)-Butynolc (%) |
|---|---|---|---|
a The measurement precision is estimated to be 10% of the value. The analyte, (S)-verbenone, was provided at EE = 54. Therefore, it has about 23% (R)-verbenone present and this makes it possible to analyze the heterochiral isomers even though the (S)-butynol tag is high enantiopurity (EE ∼ 98). The ratio of total homochiral to total heterochiral population is 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26, in good agreement with the expected 77 26, in good agreement with the expected 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 ratio from the manufacturer's EE determination for verbenone (77(S) 23 ratio from the manufacturer's EE determination for verbenone (77(S)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23(R)) given the estimated 10% precision.
b The measurement precision is estimated to be 10% of the value. As explained above, the homochiral sample composition analysis is possible due to the low enantiopurity of the analyte. The ratio of total homochiral to total heterochiral population is 19 23(R)) given the estimated 10% precision.
b The measurement precision is estimated to be 10% of the value. As explained above, the homochiral sample composition analysis is possible due to the low enantiopurity of the analyte. The ratio of total homochiral to total heterochiral population is 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 81, in good agreement with the expected 23 81, in good agreement with the expected 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77 ratio from the manufacturer's EE determination for verbenone (77(S) 77 ratio from the manufacturer's EE determination for verbenone (77(S)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23(R)) given the estimated 10% precision.
c The measurement precision is estimated to be 10% of the value. In this measurement, we can determine the relative total abundance of homochiral and heterochiral complexes. This ratio is 49 23(R)) given the estimated 10% precision.
c The measurement precision is estimated to be 10% of the value. In this measurement, we can determine the relative total abundance of homochiral and heterochiral complexes. This ratio is 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 (homochiral 51 (homochiral![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) heterochiral) – essentially equal in the precision limit of the measurement. heterochiral) – essentially equal in the precision limit of the measurement.
|
|||
| HOMBC1D1 | 47.7 | 46.4 | 48.5 |
| HOMBC2D1 | 24.2 | 25.0 | 24.4 |
| HOMEC2D1 | 20.4 | 20.5 | 19.8 |
| HOMEC1D1 | 7.8 | 8.1 | 7.3 |
| HETBC1D1 | 43.1 | 43.0 | 42.7 |
| HETEC1D1 | 31.8 | 31.9 | 31.9 |
| HETBC2D1 | 19.5 | 19.5 | 20.0 |
| HETEC2D1 | 5.7 | 5.6 | 5.4 |
| Isomer | Component | EXP intensity ratio | B2PLYPD3 def2TZVP | B3LYP GD3BJ def2TZVP | MP2 def2TZVP | B2PLYPD3 6-311++G(d,p) | B3LYP GD3BJ 6-311++G(d,p) | MP2 6-311++G(d,p) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAG dipole (D) | Intensity ratio | MAG dipole (D) | Intensity ratio | MAG dipole (D) | Intensity ratio | MAG dipole (D) | Intensity ratio | MAG dipole (D) | Intensity ratio | MAG dipole (D) | Intensity ratio | |||
| HOMBC1D1 | a | 1 | 4.61 | 1 | 4.73 | 1 | 4.35 | 1 | 4.61 | 1 | 4.79 | 1 | 4.15 | 1 |
| b | 0.21 | 2.24 | 0.24 | 2.25 | 0.23 | 2.22 | 0.26 | 2.40 | 0.27 | 2.40 | 0.25 | 2.37 | 0.33 | |
| c | 0.03 | 0.45 | 0.01 | 0.45 | 0.01 | 0.45 | 0.01 | 0.48 | 0.005 | 0.53 | 0.01 | 0.35 | 0.007 | |
| HOMBC2D1 | a | 1 | 4.62 | 1 | 4.73 | 1 | 4.43 | 1 | 4.65 | 1 | 4.79 | 1 | 4.35 | 1 |
| b | — | 0.31 | 0.005 | 0.22 | 0.002 | 0.60 | 0.02 | 0.34 | 0.005 | 0.26 | 0.003 | 0.58 | 0.02 | |
| c | 0.23 | 2.30 | 0.25 | 2.33 | 0.24 | 2.15 | 0.24 | 2.45 | 0.28 | 2.48 | 0.27 | 2.32 | 0.28 | |
| HOMEC2D1 | a | 1 | 4.66 | 1 | 4.74 | 1 | 4.44 | 1 | 4.77 | 1 | 4.89 | 1 | 4.50 | 1 |
| b | 0.15 | 1.32 | 0.08 | 1.41 | 0.09 | 1.33 | 0.09 | 1.35 | 0.08 | 1.41 | 0.08 | 1.45 | 0.10 | |
| c | 0.25 | 1.87 | 0.16 | 1.88 | 0.16 | 1.91 | 0.19 | 2.09 | 0.19 | 2.07 | 0.18 | 2.28 | 0.26 | |
| HOMEC1D1 | a | 1 | 4.27 | 1 | 4.35 | 1 | 4.08 | 1 | 4.28 | 1 | 4.42 | 1 | 4.05 | 1 |
| b | 0.37 | 2.57 | 0.36 | 2.65 | 0.37 | 2.40 | 0.35 | 2.66 | 0.39 | 2.76 | 0.39 | 2.47 | 0.37 | |
| c | 0.12 | 1.07 | 0.06 | 1.01 | 0.05 | 1.26 | 0.10 | 1.24 | 0.08 | 1.10 | 0.06 | 1.48 | 0.13 | |
| HETBC1D1 | a | 1 | 4.52 | 1 | 4.61 | 1 | 4.31 | 1 | 4.52 | 1 | 4.67 | 1 | 4.15 | 1 |
| b | — | 0.003 | 0.000 | 0.11 | 0.001 | 0.20 | 0.002 | 0.02 | 0.000 | 0.12 | 0.001 | 0.14 | 0.001 | |
| c | 0.24 | 2.43 | 0.29 | 2.45 | 0.28 | 2.35 | 0.30 | 2.59 | 0.33 | 2.60 | 0.31 | 2.51 | 0.37 | |
| HETEC1D1 | a | 1 | 4.43 | 1 | 4.50 | 1 | 4.27 | 1 | 4.48 | 1 | 4.59 | 1 | 4.31 | 1 |
| b | 0.26 | 2.37 | 0.29 | 2.44 | 0.29 | 2.31 | 0.29 | 2.48 | 0.31 | 2.55 | 0.31 | 2.41 | 0.31 | |
| c | 0.08 | 0.95 | 0.05 | 0.88 | 0.04 | 1.06 | 0.06 | 1.10 | 0.06 | 1.03 | 0.05 | 1.39 | 0.10 | |
| HETBC2D1 | a | 1 | 4.68 | 1 | 4.82 | 1 | 4.42 | 1 | 4.73 | 1 | 4.92 | 1 | 4.35 | 1 |
| b | 0.21 | 1.83 | 0.15 | 1.84 | 0.15 | 1.80 | 0.17 | 1.94 | 0.17 | 1.96 | 0.16 | 1.86 | 0.18 | |
| c | 0.11 | 1.27 | 0.08 | 1.33 | 0.08 | 1.24 | 0.08 | 1.38 | 0.09 | 1.46 | 0.09 | 1.29 | 0.09 | |
| HETEC2D1 | a | 1 | 4.49 | 1 | 4.59 | 1 | 4.28 | 1 | 4.54 | 1 | 4.65 | 1 | 4.25 | 1 |
| b | 0.16 | 1.79 | 0.16 | 1.80 | 0.15 | 1.61 | 0.14 | 1.80 | 0.16 | 1.92 | 0.17 | 1.63 | 0.15 | |
| c | 0.25 | 1.80 | 0.16 | 1.82 | 0.16 | 1.86 | 0.19 | 2.00 | 0.19 | 1.94 | 0.17 | 2.10 | 0.24 | |
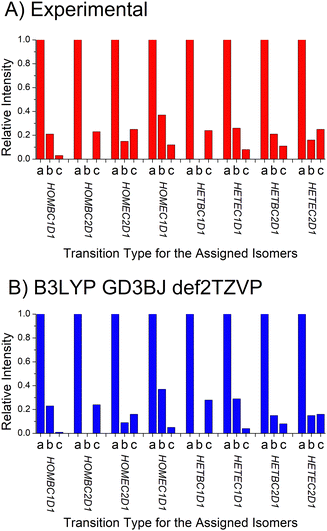
D. Dipole moment component analysis
The analysis approach described for determining the isomer composition of the chiral tag complexes is also used to determine the relative contributions of the a-, b-, and c-type contributions to the full rotational spectrum. In rotational spectroscopy, the relative intensities of these three spectrum components are proportional to the squares of the dipole moment vector components in the principal-axis system and provide another connection to the quantum chemistry calculations.29 In this analysis, three separate theoretical spectra are generated for each isomer that have only one nonzero dipole moment component (with the non-zero component set to 1D). The scale factors for these three spectra are then determined. A normalized ratio of the a-, b-, and c-type spectrum component intensities is reported in Table 4 where the largest scale factor (most intense spectrum) is set to 1. This table also reports the calculated dipole moments components and the relative intensities for the a-, b-, and c-type spectra expected based on the calculated dipole moment components.E. Benchmarking the quantum chemistry results
The practical implementation of chiral tag rotational spectroscopy for determination of the absolute configuration requires the ability of quantum chemistry to identify low-energy isomers of the chiral tag complexes and to make sufficiently accurate predictions of the rotational spectroscopy parameters (rotational constants for transition frequencies and components of the dipole moment vector for transition intensities) so that each observed spectrum can be confidently attributed to a chiral tag complex geometry.Assuming thermal equilibrium, the ratio of the population of a higher energy isomer, pn, to the population of the lowest energy isomer, p0, is related by a Boltzmann factor, eqn (1).
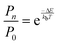 | (1) |
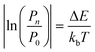 | (2) |
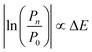 | (3) |
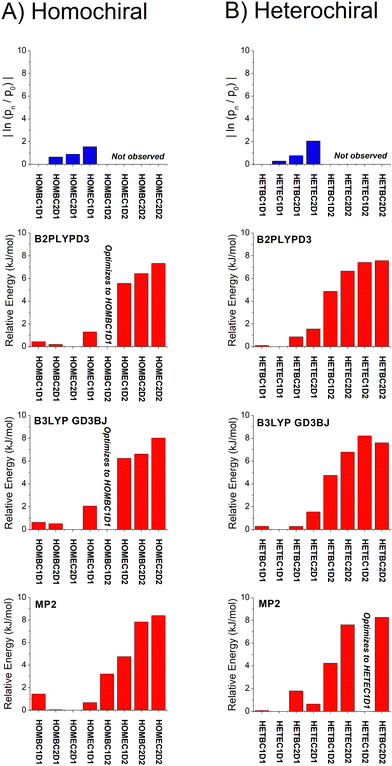 | ||
| Fig. 6 A graphical representation of the relative isomer energies reported in Table 1 for calculations with the def2TZVP basis set is shown. The three quantum chemistry methods are B2PPLYPD3, B3LYP GD3BJ, and MP2. In some cases, the geometry optimization collapsed into the lower energy geometry with different dihedral angle about the O⋯O axis of the hydrogen bond and these cases are indicated in the figure. An analogous figure using the 6-311++G(d,p) basis set is available in the ESI.† | ||
With these analysis caveats, the results shown in Fig. 6 show that all methods used in this work identify the four lowest energy isomers that dominate the rotational spectra (Fig. 4). The next set of structures, which correspond to higher energy isomers from the dihedral angle of the O⋯O hydrogen bond as illustrated in Fig. 1, are a significant energy increase relative to the four observed isomers. In all cases, there is little change to the relative energies of the isomers in the two DFT calculations despite the significant increase in computational time associated with the B2PLYPD3 method. There is the possible indication that the DFT methods provide a better characterization of the relative energies than MP2 in that these methods consistently identify the lowest abundance isomer in experiment with the highest energy isomer of the four low-energy geometries.
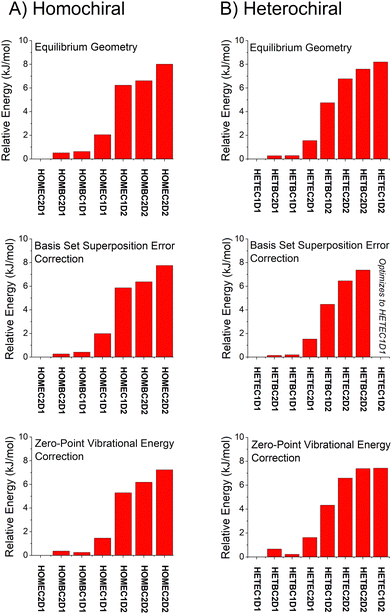
Overall, the B3LYP GD3BJ methods are successful at identifying the low-energy isomers observed in experiment with much shorter computational times. We have performed calculations to examine the effects of two issues know to affect relative energies using the B3LYP GD3BJ def2TZVP model chemistry. These calculations include a vibrational calculation to determine the zero-point vibrational energy contribution and a counterpoise calculation75,76 to account for basis set superposition errors. A summary of these results is shown in Fig. 7 for both the homochiral and heterochiral complexes. These corrections have little effect on the relative energies of the isomers. The minimal changes likely reflect the structural similarity of the isomers.
The current data set has the A, B, and C rotational constants for eight isomers of the verbenone–butynol hydrogen bond complex. The mean percent error and standard deviation of the error for the eight measurements are reported in Table 5. In this analysis, we separately report the statistics for the A, B, and C rotational constants. All isomers are near-prolate asymmetric tops (A ∼ 900 MHz, B ∼ 300 MHz, and C ∼ 300 MHz) and it is commonly observed that there are characteristically different error distributions for A and B/C in this case. Based on the mean percent error, the two DFT methods give improved performance over MP2 calculations and show very good accuracy with about 1% errors. The choice of basis set has minimal effect on the mean percent error. However, the better indication of performance for the quantum chemistry calculations could be the width of the error distribution that is characterized by the standard deviation of the percent errors in Table 5. For example, it might be possible through future additional benchmarking to gain a good understanding of the mean errors expected for chiral tag complexes and empirically correct for this effect – a similar approach to empirical scaling of vibrational frequencies from harmonic calculations. In that case, the distribution of errors becomes the key performance metric. The B2PLYPD3 method offers almost a factor of two improvement in the error distribution over B3LYP GD3BJ and this gain in accuracy might be important for identifying cluster geometries based on rotational constants. MP2 performance is poor relative to the DFT methods. We note that these conclusions for the rotational constant agreement in weakly bound complexes are the same as the ones reached by Grimme and Steinmetz for monomers.59 Finally, there is a slight reduction in the standard deviation of the percent error using the def2TZVP basis set perhaps giving it an advantage over the Pople basis set of comparable size.
| Constant | B2PLYPD3 def2TZVP | B3LYP GD3BJ def2TZVP | MP2 def2TZVP | B2PLYPD3 6-311++G(d,p) | B3LYP GD3BJ 6-311++G(d,p) | MP2 6-311++G(d,p) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean error | σ | Mean error | σ | Mean error | σ | Mean error | σ | Mean error | σ | Mean error | σ | |
| a The percent errors are [(experiment − theory)/experiment] × 100. | ||||||||||||
| A | −0.43 | 0.23 | −0.25 | 0.43 | −0.94 | 0.20 | 0.13 | 0.27 | 0.05 | 0.48 | 0.49 | 1.24 |
| B | −1.42 | 0.32 | −1.90 | 0.69 | −3.61 | 0.83 | −1.28 | 0.53 | −1.70 | 0.76 | −3.89 | 2.59 |
| C | −1.45 | 0.28 | −1.80 | 0.63 | −3.39 | 0.68 | −1.26 | 0.36 | −1.47 | 0.72 | −3.47 | 1.76 |
In the current study, the 14 distinct carbon atom positions in the chiral tag complex are determined from the natural abundance spectra of the singly-substituted 13C isotopomers for 5 of the eight identified isomers. The substitution structures for the highest abundance homochiral and heterochiral verbenone–butynol clusters are shown in Fig. 8 to illustrate the agreement between experimental carbon atom positions and the equilibrium geometries calculated with the B3LYP GD3BJ def2TZVP model (the substitution structures of the other three isomers are presented in the ESI†). The coordinate errors relative to the quantum chemistry equilibrium geometry are shown in Fig. 9. This analysis uses the absolute value of the coordinates for each carbon atom in the principal axis system of the “normal” isotopic species that has only 1H, 12C, and 16O atoms. Any coordinate where the experimental value of the square is negative due to inertial defects (which would lead to an imaginary value for the coordinate magnitude), is omitted. There were 12 out of 210 experimental coordinates excluded in this way. Note that the larger spread of errors at the small coordinate positions is also caused, in part, by the inertial defect issue. For the DFT methods, the distribution of coordinate error has a mean near zero showing good overall agreement for the carbon atom positions in theory and experiment. The distribution width is narrower for the B2PLYPD3 calculations and this smaller fluctuation in atom positions is consistent with the reduced percent error distribution observed for the rotational constants – the rotational constant error distribution is better because the structures are better. MP2 calculations have clearly poorer performance with a large mean error in the coordinate positions and a larger distribution of errors.
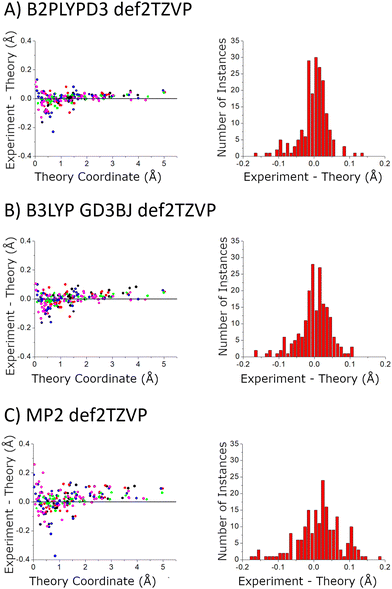 | ||
| Fig. 9 The accuracy of the quantum chemistry structures is benchmarked using the carbon atom coordinates – in the principal axis system for molecular rotation – obtained from the Kraitchman analysis. The scatter plot shows the difference in the absolute values of these coordinates (coordinate signs are unavailable from the spectroscopic analysis) as a function of the size of the coordinate. The coordinates come from the 5 structures that were measured with 13C-sensitivity: HOMEC2D1 (black), HOMBC2D1 (blue), HOMBC1D1 (magenta), HETEC1D1 (red), and HETBC1D1 (green). The figure for calculations with the 6-311++G(d,p) basis set is shown in the ESI.† | ||
The structural comparison is further examined in Fig. 10 using the distance of the carbon atom to the center-of-mass of the chiral tag complex geometry. In this comparison, the slopes of the error in the center-of-mass distance, R, are larger for the MP2 structures and indicates that these theoretical geometries are too compact (Rexp > Rtheory). Both DFT methods show similar linear trends in the distance error and have a positive slope indicating that the theoretical structures are also too compact, but with a significant improvement over the MP2 results. These conclusions support the ideas discussed by Grimme and Steinmetz in their rotational spectroscopy benchmark paper that the over-estimate of dispersion interactions in MP2 calculations produce geometries that are too compact.59 For the DFT methods, the choice of basis set does not show significant differences.
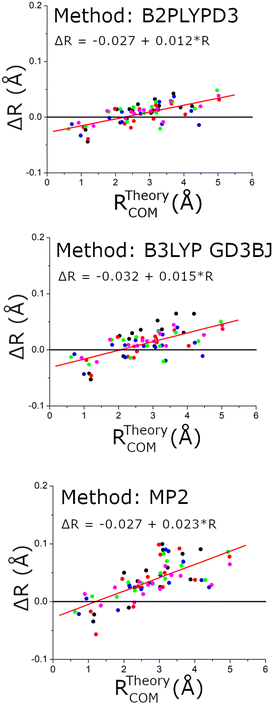 | ||
| Fig. 10 This figure shows the differences in the experimental and theoretical distance of each carbon atom from the center-of-mass of the chiral tag complex. The red line shows a linear regression analysis for each data set to help quantify the way these errors vary with the center-of-mass distance. The linear fit formulas are shown as insets in each figure. The coordinates come from the 5 structures that were measured with 13C-sensitivity: HOMEC2D1 (black), HOMBC2D1 (blue), HOMBC1D1 (magenta), HETEC1D1 (red), and HETBC1D1 (green). The figure for calculations with the 6-311++G(d,p) basis set is shown in the ESI.† | ||
Discussion
A. Complex formation
The results from this study highlight some important features of geometry relaxation in pulsed molecular beams.63–65 The basic model that has developed to explain isomer relaxation is that the internal energy in a collision complex undergoes intramolecular vibrational energy redistribution that makes it possible to overcome low barriers to isomerization. Subsequent collisions with the inert carrier gas remove the excess energy and vibrationally cool the complex. In the present work, both the analyte (verbenone) and tag (butynol) are dilute in the carrier gas with approximate molar concentrations of 0.1% each in neon. There are two types of collision complexes formed. When the analyte and tag encounter each other, the there is a strong noncovalent interaction, hydrogen bond formation for verbenone and butynol, and this energy would allow the chiral tag complex to broadly sample its isomer potential energy surface. The counterpoise calculations performed in this work estimate the analyte-tag complexation energy to be ∼40 kJ mol−1. The second type of encounter is between the chiral tag complex and the dominant neon carrier gas. These interactions involve the dispersion interaction of neon with the complex and provide less internal energy. However, as is observed for monomers, these interactions can be expected to efficiently relax conformational degrees of freedom.These ideas are supported by two observations of the chiral tag complex isomers populated in the pulsed jet expansion. First, only the lowest energy complexes identified by quantum chemistry are observed. The complex between butynol and verbenone could initially form with a wide range of structures since the dispersion interaction between the monomers is attractive in any orientation of the tag relative to the monomer. However, the final population shows only the butynol in a hydrogen bond position. Another interesting feature of the final cluster population is that butynol is found in both of its lowest energy conformations (with –OH anti to either the –CH3 or –CH groups). This contrasts with the behavior of the butynol monomer in the pulsed jet which undergoes conformational relaxation via collisions with neon. The monomer spectrum of the lowest energy isomer (–OH anti to –CH3) is the only one observed in the reported spectra. For the signal-to-noise ratio of the measurement, the population of the higher energy butynol that remains uncomplexed is less than 0.01% of the lowest energy isomer. This result shows that isomer searches for chiral tag complexes need to consider all low energy conformational forms of the analyte and tag not just those observed in the pulsed jet spectrum of the monomer. It is even possible that the lowest energy geometry of the complex will not resemble low energy conformations of the two monomers as was found for the chiral tag complex of alaninol with propylene oxide where the pulsed jet population is dominated by the lowest energy isomer identified in quantum chemistry where the propylene oxide inserts into an intramolecular hydrogen bond of alaninol.4
As the analyte-tag complex is stabilized and cooled by subsequent collisions with neon, conformational isomerization within the complex is possible. In the present study, quantum chemistry generally identifies two conformational minima for each isomer that correspond to two dihedral angles for conformational motion about the O⋯O axis of the hydrogen bond (as seen in Fig. 1). None of the higher energy conformations identified as equilibrium geometries in the quantum chemistry calculations are observed in the spectrum suggesting efficient conformational isomerization, although it is noted that these isomers are predicted to have significantly higher energies so that they might be present at number densities below the detection limit.
B. High-confidence assignment of the absolute configuration
The goal of this benchmarking study is to assess the ability of quantum chemistry to guide the spectrum analysis so that the absolute configuration of the analyte can be assigned with high confidence. The experimental methodology for determination of the absolute configuration of an analyte by chiral tag rotational spectroscopy is: (1) the spectrum is first acquired with a racemic tag sample so that both homochiral and heterochiral tag complexes are generated. The ability to observe both diastereomers increases the confidence in the final chiral analysis in an analogous way that has been described for NMR spectroscopy.25,26 (2) A second measurement is performed with a high enantiopurity sample of the tag with known absolute configuration. In this measurement, one set of observed rotational spectroscopy transitions will show a relative increase in intensity and the second set will decrease – as long as the analyte has an enantiomeric excess. Quantum chemistry is used to determine the different isomer structures in each set of transitions so that the sets can be identified as either homochiral or heterochiral complexes. At that point, the configuration of the analyte is determined if the absolute configuration of the tag is known with certainty.The spectroscopic information available for the structure analysis includes the rotational constants and the relative intensities of the a-, b-, and c-type spectrum components. High confidence is achieved when there is an exclusive “best match” between the experimental parameters and the theoretical estimates. This idea is shown in Fig. 12A where the spectroscopy parameters for the strongest spectrum observed when (S)-butynol is used is compared to the quantum chemistry predictions of the four lowest energy isomers in the homochiral and heterochiral family (B3LYP GD3BJ def2TZVP). The best match using the metrics of minimum to total percent error in the rotational constants and qualitative pattern match for the a-, b-, and c-type transition intensities is to the HOMBC1D1 theoretical structure. Since (S)-butynol is known to be tag, the dominant enantiomer of the analyte is determined to be (S)-verbenone since a homochiral complex is observed – a result consistent with the manufacturer's specification of the absolute configuration. The confidence of the analyte absolute configuration assignment is increased when the analysis of the whole family of observed spectra is performed. As shown in Fig. 12, when the four assigned spectra that dominate when high enantiopurity (S)-butynol is used as the tag are compared to the theoretical predictions, each is found to have an exclusive match and all four match to homochiral chiral tag complexes. The analogous figure for the spectra that dominate when (R)-butynol is used as the tag is included in the ESI.† In that case, all four spectra have exclusive matches to heterochiral structures increasing the confidence in the absolute configuration determination based on spectroscopic parameters.
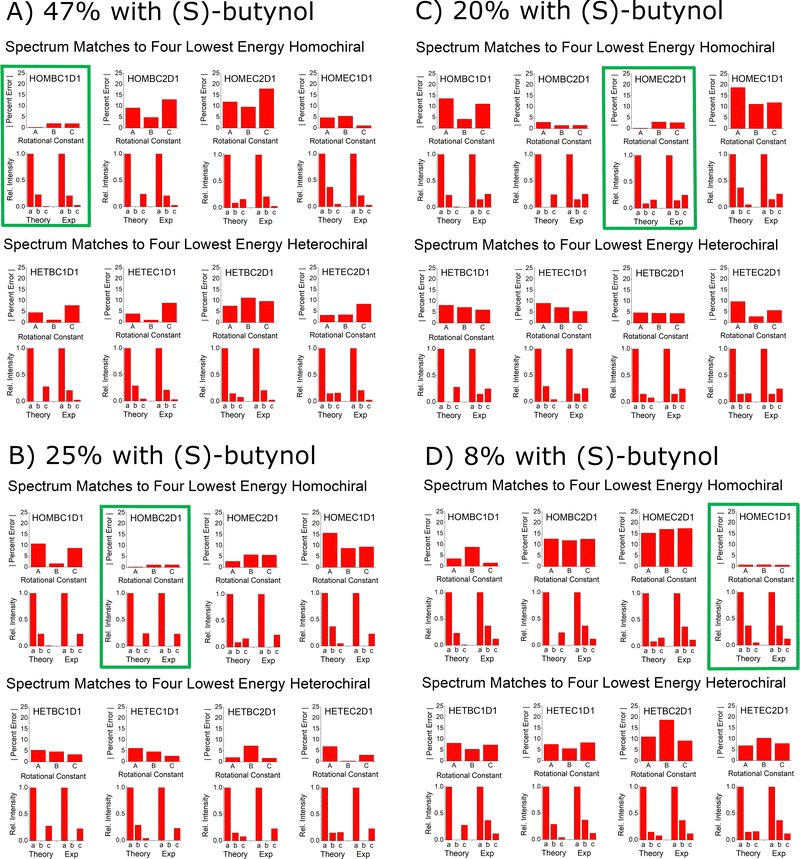 | ||
| Fig. 12 This figure illustrates the way that the spectral assignments guided by quantum chemistry are used to establish the absolute configuration of verbenone. Panel (A) shows the comparison between the experimental spectrum parameters for the highest abundance species observed when (S)-butynol is used as the tag and the lowest energy isomers of homochiral and heterochiral complexes identified in the quantum chemistry analysis using B3LYP GD3BJ def2TZVP. This comparison uses the percent error for the rotational constants and a comparison of the relative spectral intensities to the square of the dipole moment components. The best match for the spectrum is to the homochiral complex, HOMBC1D1 – outlined in green. Since the spectrum matches a homochiral geometry and the tag is known to be (S)-butynol, the absolute configuration is established as (S)-verbenone. The confidence in this determination is increased by the fact that the other three spectra observed in the (S)-butynol tag measurement also have exclusive matches to theoretical homochiral geometries. Furthermore, the other four spectra, which dominate when (R)-butynol is the tag, exclusively match the theoretical heterochiral geometries – as shown in the ESI.† | ||
The confidence in the assignment of the analyte absolute configuration can be significantly increased in favorable cases. Rotational spectroscopy, in principle, offers perhaps the highest confidence for absolute configuration determinations of any spectroscopy technique because it can yield direct structural information through the analysis of 13C isotopomers in natural abundance (and other isotopes, such as 15N and 18O, when the atom is present and there is sufficient measurement sensitivity). For example, Fig. 12 shows that the highest intensity spectrum observed when high enantiopurity (S)-butynol is employed as the tag is an exclusive match to a homochiral complex. In the current measurement, there is sufficient sensitivity to analyze the spectra of the singly-substituted 13C isotopomers in natural abundance yield the magnitude of their position coordinates in the principal axis system via Kraitchman analysis. Using the coordinate signs from the matching theoretical structure, the carbon atom framework geometry can be compared directly to the theory equilibrium geometry, as shown in Fig. 8A, and provides direct structural validation of the analyte absolute configuration. The practical limitation of verifying absolute configuration via the carbon atom framework geometry is that it requires significantly more sample to reach 13C sensitivity in natural abundance and for newly synthesized analytes this amount of sample may not be readily available.
C. Quantum chemistry recommendations for the analysis of chiral tag rotational spectra
For the application of assigning absolute configuration of an analyte by analysis of the diastereomeric structures formed upon complexation with a small, chiral tag molecule, the B3LYP GD3BJ def2TZVP model chemistry best meets the analysis needs of the verbenone–butynol system. Both DFT methods used in this work outperform MP2 calculations – a conclusion also reached in the previous benchmark work on monomers. The longer computational times of the B2PLYPD3 method do not appear to be justified, although the method does offer improved geometries that reduce the expected percent error distribution in rotational constant predictions. There is a less clear-cut choice in basis set for the two used in this study. Slightly lower fluctuations in rotational constant error and carbon atom positions are found for the def2TZVP basis set. Future tests of other methods, such as the use of other functionals,80 could potentially identify a better computational method for the identification of chiral tag complexes.Conclusions
As shown by the analysis of the verbenone–butynol complexes, chiral tag rotational spectroscopy is a practical method for assigning absolute configuration with high confidence. However, there are many issues that remain to be tested. Perhaps most important is to better understand the molecular size limits of the technique. The size limit depends on experimental issues such as the ability to volatilize the sample and the sensitivity of chiral tag rotational spectroscopy as the rotational partition function increases with increased analyte size. The accuracy of quantum chemistry is also crucial is setting the limits of this measurement approach. Understanding how the accuracy of the theoretical geometries changes with molecular size is key to the degradation in the confidence of the absolute configuration assignment as changes in the moments-of-inertia between diastereomer tag complex geometries become a smaller fraction of the total inertia.Another issue where quantum chemistry will be crucial to guiding the development of the method is the selection of tag molecule. In the current case, butynol is an obvious choice because it forms a hydrogen bond complex with verbenone which is expected to produce a large number density of complexes in the pulsed molecular beam. However, the metric of cluster number density might not produce the optimum measurement. For example, butynol complexation of verbenone produces four isomers with appreciable population in both the homochiral and heterochiral families and this both lowers the peak signal strength and adds spectral density. Perhaps a different tag with fewer low-energy isomers would yield improved spectra. This aspect of the tag performance could be screened by quantum chemistry. Similarly, the ultimate requirement is the production of homochiral and heterochiral tag complexes that have large and predictable differences in their rotational constant or dipole moment direction since the differences in these parameters determine the confidence in the absolute configuration assignment. Quantum chemistry screening for differentiability of the homochiral and heterochiral complexes is important to choosing the optimum measurement conditions.
As the rotational spectroscopy community explores the limits of the technique, the rotational spectroscopy data sets on noncovalent molecular complexes are expected to expand significantly. Although the focus of this work has been the evaluation of quantum chemistry methods that meet important requirements of analytical chemistry – mainly the need for low computational times – these emerging experimental data sets may be generally useful as benchmarks for new quantum chemistry methods with a focus on the role noncovalent interactions play in determining molecular structure.
Author contributions
All authors were involved in the conceptualization of the measurement and analysis. K. M. and C. W. performed measurements. K. M., B. H. P. and L. E. performed formal analysis through quantum chemistry, spectrum fitting, and data visualization. B. H. P., L. E., G. S. G., and G. S. were involved in writing, reviewing, and editing the manuscript.Conflicts of interest
B. H. Pate has a financial conflict of interest through founders’ equity in BrightSpec which offers commercial spectrometers for molecular rotational spectroscopy.Acknowledgements
The work at the University of Virginia was supported by National Science Foundation grant CHE-1904686. Quantum chemistry calculations performed at the University of Virginia were supported through a research allocation on Rivanna – the high-performance computing facility at the University of Virginia. The project was also supported by the National Science Foundation under grants CHE-1841346 and CHE-MRI-2019072 at Missouri University of Science and Technology.Notes and references
- B. H. Pate, L. Evangelisti, W. Caminati, Y. Xu, J. Thomas, D. Patterson, C. Perez and M. Schnell, in Chiral Analysis, ed. P. L. Polavarapu, Elsevier, 2018, 2nd edn, pp. 679–729 DOI:10.1016/B978-0-444-64027-7.00019-7.
- R. E. Sonstrom, J. L. Neill, A. V. Mikhonin, R. Doetzer and B. H. Pate, Chirality, 2022, 34, 114–125 CrossRef CAS PubMed.
- R. E. Sonstrom, D. M. Cannon and J. L. Neill, Symmetry, 2022, 14, 917 CrossRef CAS.
- J. L. Neill, A. V. Mikhonin, T. Chen, R. E. Sonstrom and B. H. Pate, J. Pharm. Biomed. Anal., 2020, 189, 113474 CrossRef CAS PubMed.
- F. Xie, N. A. Seifert, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 15703–15710 CrossRef CAS PubMed.
- F. Xie, N. A. Seifert, A. S. Hazrah, W. Jäger and Y. Xu, ChemPhysChem, 2021, 22, 455–460 CrossRef CAS PubMed.
- S. R. Domingos, C. Pérez, M. D. Marshall, H. O. Leung and M. Schnell, Chem. Sci., 2020, 11, 10863–10870 RSC.
- M. D. Mills, R. E. Sonstrom, Z. P. Vang, J. L. Neill, H. N. Scolati, C. T. West, B. H. Pate and J. R. Clark, Angew. Chem., Int. Ed., 2022, 61, e202207275 CrossRef CAS PubMed.
- M. Pierini, A. Troiani, M. Speranza, S. Piccirillo, C. Bosman, D. Toja and A. Giardini-Guidoni, Angew. Chem., Int. Ed. Engl., 1997, 36, 1729–1731 CrossRef.
- A. Latini, D. Toja, A. Giardini-Guidoni, A. Palleschi, S. Piccirillo and M. Speranza, Chirality, 1999, 11, 376–380 CrossRef CAS.
- A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992 CrossRef CAS PubMed.
- A. R. Al-Rabaa, E. Bréhéret, F. Lahmani and A. Zehnacker, Chem. Phys. Lett., 1995, 237, 480–484 CrossRef CAS.
- A. K. King and B. J. Howard, Chem. Phys. Lett., 2001, 348, 343–349 CrossRef CAS.
- Z. Su, N. Borho and Y. Xu, J. Am. Chem. Soc., 2006, 128, 17126–17131 CrossRef CAS PubMed.
- M. Becucci and S. Melandri, Chem. Rev., 2016, 116, 5014–5037 CrossRef CAS PubMed.
- H. D. Flack and G. Bernardinelli, Chirality, 2008, 20, 681–690 CrossRef CAS PubMed.
- P. Brázda, L. Palatinus and M. Babor, Science, 2019, 364, 667–669 CrossRef PubMed.
- S. Jang, H. Park, Q. H. Duong, E.-J. Kwahk and H. Kim, Anal. Chem., 2022, 94, 1441–1446 CrossRef CAS PubMed.
- C. Schlesinger, L. Tapmeyer, S. D. Gumbert, D. Prill, M. Bolte, M. U. Schmidt and C. Saal, Angew. Chem., Int. Ed., 2018, 57, 9150–9153 CrossRef CAS PubMed.
- B. Wang, J. F. Bruhn, A. Weldeab, T. S. Wilson, P. T. McGilvray, M. Mashore, Q. Song, G. Scapin and Y. Lin, Chem. Commun., 2022, 58, 4711–4714 RSC.
- P. Herwig, K. Zawatzky, M. Grieser, O. Heber, B. Jordon-Thaden, C. Krantz, O. Novotný, R. Repnow, V. Schurig, D. Schwalm, Z. Vager, A. Wolf, O. Trapp and H. Kreckel, Science, 2013, 342, 1084–1086 CrossRef CAS PubMed.
- L. A. Nafie, Vibrational Optical Activity: Principles and Applications, John Wiley & Sons Ltd., 2011 Search PubMed.
- P. J. Stephens, F. J. Devlin and J.-J. J. Pan, Chirality, 2008, 20, 643–663 CrossRef CAS PubMed.
- P. J. Stephens, J. Phys. Chem., 1985, 89, 748–752 CrossRef CAS.
- P. J. Stephens, D. M. McCann, J. R. Cheeseman and M. J. Frisch, Chirality, 2005, 17(Suppl.), 64 Search PubMed.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Geneaux and I. Powis, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- M. N. Pohl, S. Malerz, F. Trinter, C. Lee, C. Kolbeck, I. Wilkinson, S. Thürmer, D. M. Neumark, L. Nahon, I. Powis, G. Meijer, B. Winter and U. Hergenhahn, Phys. Chem. Chem. Phys., 2022, 24, 8081–8092 RSC.
- V. Svoboda, N. B. Ram, D. Baykusheva, D. Zindel, M. D. J. Waters, B. Spenger, M. Ochsner, H. Herburger, J. Stohner and H. J. Wörner, Sci. Adv., 2022, 8, eabq2811 CrossRef CAS PubMed.
- T. J. Wenzel and C. D. Chisholm, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 59, 1–63 CrossRef CAS PubMed.
- T. J. Wenzel, Differentiation of Chiral Compounds Using NMR Spectroscopy, John Wiley & Sons, Hoboken, NJ, 2nd edn, 2018 Search PubMed.
- S. G. Smith and J. M. Goodman, J. Am. Chem. Soc., 2010, 132, 12946–12959 CrossRef CAS PubMed.
- K. Ermanis, K. E. Parkes, T. Agback and J. M. Goodman, Org. Biomol. Chem., 2016, 14, 3943–3949 RSC.
- W. Gordy and R. L. Cook, The Distortable Rotor, Techniques of Chemistry, Microwave Molecular Spectra, 1984, ch. VIII, pp. 297–390 Search PubMed.
- W. Gordy and R. L. Cook, Derivation of Molecular Structures, Techniques of Chemistry, Microwave Molecular Spectra, Wiley (Knovel), 1984, ch. XIII, pp. 647–724 Search PubMed.
- W. Gordy and R. L. Cook, Asymmetric Top Molecules, Techniques of Chemistry, Microwave Molecular Spectra, Wiley (Knovel), 1984, ch. VII, pp. 227–296 Search PubMed.
- T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45 CrossRef CAS.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- J. P. Porterfield, L. Satterthwaite, S. Eibenberger, D. Patterson and M. C. McCarthy, Rev. Sci. Instrum., 2019, 90, 053104 CrossRef PubMed.
- V. A. Shubert, D. Schmitz, C. Pérez, C. Medcraft, A. Krin, S. R. Domingos, D. Patterson and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 341–350 CrossRef CAS PubMed.
- D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475–477 CrossRef CAS PubMed.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 023008 CrossRef PubMed.
- A. V. Shubert, D. Schmitz, C. Medcraft, A. Krin, D. Patterson, J. M. Doyle and M. Schnell, J. Chem. Phys., 2015, 142, 214201 CrossRef PubMed.
- J. U. Grabow, Angew. Chem., Int. Ed., 2013, 52, 11698–11700 CrossRef CAS PubMed.
- S. Lobsiger, C. Perez, L. Evangelisti, K. K. Lehmann and B. H. Pate, J. Phys. Chem. Lett., 2015, 6, 196–200 CrossRef CAS PubMed.
- N. T. Moon, K. Woelk and G. S. Grubbs, Symmetry, 2022, 14, 848 CrossRef CAS.
- K. K. Lehmann, J. Chem. Phys., 2018, 149, 094201 CrossRef PubMed.
- F. E. Marshall, G. Sedo, C. West, B. H. Pate, S. M. Allpress, C. J. Evans, P. D. Godfrey, D. McNaughton and G. S. Grubbs, J. Mol. Spectrosc., 2017, 342, 109–115 CrossRef CAS.
- K.-M. Marstokk and H. Mollendal, Acta Chem. Scand., Ser. A, 1985, 39, 639–649 CrossRef.
- J. L. Neill, S. T. Shipman, L. Alvarez-Valtierra, A. Lesarri, Z. Kisiel and B. H. Pate, J. Mol. Spectrosc., 2011, 269, 21–29 CrossRef CAS.
- C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15 CrossRef.
- R. D. Suenram, J. U. Grabow, A. Zuban and I. Leonov, Rev. Sci. Instrum., 1999, 70, 2127–2135 CrossRef CAS.
- D. Plusquellic, JB95 package, available from https://www.nist.gov/services-resources/software/jb95-spectral-fitting-program Search PubMed.
- B. J. Drouin, J. Mol. Spectrosc., 2017, 340, 1–15 CrossRef CAS.
- S. E. Novick, J. Mol. Spectrosc., 2016, 329, 1–7 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- Z. Kisiel, Programs for Rotational Spectroscopy (PROSPE), https://www.ifpan.edu.pl/~kisiel/prospe.htm Search PubMed.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- C. C. Costain, J. Chem. Phys., 1958, 29, 864–874 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Oswald, N. A. Seifert, F. Bohle, M. Gawrilow, S. Grimme, W. Jäger, Y. Xu and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 5080–5084 CrossRef CAS PubMed.
- A. L. Steber, W. Li, B. H. Pate, A. Lesarri and C. Pérez, J. Phys. Chem. Lett., 2022, 13, 3770–3775 CrossRef CAS PubMed.
- S. R. Domingos, C. Pérez, N. M. Kreienborg, C. Merten and M. Schnell, Commun. Chem., 2021, 4, 32 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- J. K. G. Watson, J. Chem. Phys., 1967, 46, 1935–1949 CrossRef CAS.
- R. E. Sonstrom, PhD thesis, University of Virginia, 2020.
- R. S. Ruoff, T. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- U. Erlekam, M. Frankowski, G. von Helden and G. Meijer, Phys. Chem. Chem. Phys., 2007, 9, 3786–3789 RSC.
- A. J. Minei and S. E. Novick, J. Chem. Phys., 2007, 126, 101101 CrossRef PubMed.
- N. A. Seifert, I. A. Finneran, C. Perez, D. P. Zaleski, J. L. Neill, A. L. Steber, R. D. Suenram, A. Lesarri, S. T. Shipman and B. H. Pate, J. Mol. Spectrosc., 2015, 312, 13–21 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031 CrossRef CAS.
- C. Puzzarini, J. F. Stanton and J. Gauss, Int. Rev. Phys. Chem., 2010, 29, 273–367 Search PubMed.
- C. Puzzarini, M. Heckert and J. Gauss, J. Chem. Phys., 2008, 128, 194108 CrossRef PubMed.
- M. Heckert, M. Kállay, D. P. Tew, W. Klopper and J. Gauss, J. Chem. Phys., 2006, 125, 044108 CrossRef PubMed.
- K. L. K. Lee and M. McCarthy, J. Phys. Chem. A, 2020, 124, 898–910 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Spectroscopy and structure analysis with quantum chemistry results. See DOI: https://doi.org/10.1039/d2cp04060c |
| This journal is © the Owner Societies 2022 |