The many forms of alpha-methoxy phenylacetic acid in the gas phase: flexibility, internal dynamics, and their intramolecular interactions†
Himanshi
Singh
 ab,
Pablo
Pinacho
ab,
Pablo
Pinacho
 *a,
Daniel A.
Obenchain
*a,
Daniel A.
Obenchain
 c,
María Mar
Quesada-Moreno
c,
María Mar
Quesada-Moreno
 d and
Melanie
Schnell
d and
Melanie
Schnell
 *ab
*ab
aDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany. E-mail: pablo.pinacho@desy.de; melanie.schnell@desy.de
bInstitute of Physical Chemistry, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Str. 1, 24118 Kiel, Germany
cInstitut fur Physikalische Chemie, Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany
dDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, Avda. Fuentenueva s/n, 18071 Granada, Spain
First published on 19th October 2022
Abstract
We present a rotational spectroscopy study of alpha-methoxy phenylacetic acid in the gas phase. This acid is a derivative of mandelic acid and is used in various organic reactions. The conformational landscape of alpha-methoxy phenylacetic acid was explored to gain insight into its intramolecular dynamics. A rich rotational spectrum was obtained using chirped-pulse Fourier transform microwave spectroscopy in the 2–8 GHz range. Five conformers out of six calculated low-energy forms were identified in the spectrum, and the assignment of the 13C singly substituted isotopologues for the lowest-energy conformer led to its accurate structure determination. Splitting patterns were analyzed and attributed to the internal rotation of a methyl top. The analysis of the non-covalent interactions within the molecule highlights the subtle balance in the stabilization of the different conformers. We thus provide high-level structural and intramolecular dynamics information that is also used to benchmark the performance of quantum-chemical calculations.
Introduction
Carboxylic acids are an important group of molecules in organic chemistry. Within this family of molecules, chiral carboxylic acids can be found in a myriad of molecules involved in biological processes.1 Mandelic acid (Fig. 1a) is an example of a chiral carboxylic acid used in the cosmetic industry, among other applications, to cure skin problems such as acne and pimples.2 The presence of a phenyl ring, a hydroxy group, and a carboxylic acid group attached to the chiral center provides different possibilities for intra- and intermolecular interactions. These functional groups offer great binding sites for solute and solvent interactions, which are also of crucial importance to understand their biological activities. Furthermore, the relative orientation of these groups also gives rise to a rich conformational landscape. It becomes important to study such molecules to identify the conformations that they can present, characterize their structures, analyze the interconversion pathways between the possible conformers, and evaluate their intra- and intermolecular interactions. Among different structurally sensitive experimental approaches, rotational spectroscopy is a valuable technique to address these challenges and perform the structural analysis of molecules. The study of such molecules in the gas phase provides detailed information about each conformation and allows us to characterize intramolecular interactions that stabilize the conformers.3–7 The accurate spectroscopic information on the structures and their interactions allows benchmarking quantum-chemical calculations that help improve their performance.8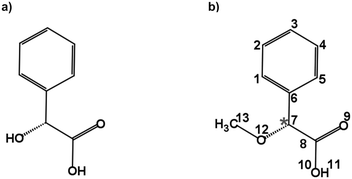 | ||
| Fig. 1 Schematic structures of (a) mandelic acid (C8H8O3) and (b) alpha-methoxy phenylacetic acid (AMPA; C9H10O3). The chiral centre is highlighted with an asterisk. | ||
Alpha-methoxy phenylacetic acid (AMPA, C9H10O3) is a derivative of mandelic acid (Fig. 1b) that serves as an NMR shift reagent and helps in the determination of enantiomeric purity.9 It presents two strong electron-withdrawing groups, namely a methoxy group and a carboxylic acid group together with a phenyl ring, making it highly flexible and giving rise to different kinds of intramolecular interactions. The complexation of the carboxylic acid group of AMPA with sulfoxide functional groups gives rise to strongly bound adducts, resulting in its use in the stereochemical analysis of sulfoxides.9 The phenylacetic acid group present in AMPA is an important moiety in many numerous pharmaceutical drugs such as atropine, camylofin, and phenacemide. Thus, the characterization of this group on the basis of AMPA can serve to model the internal dynamics of these kinds of drug molecules. Furthermore, studying AMPA helps in understanding the effect of solute–solvent interactions on the IR and VCD spectra in different solvents as reported by a recent study.10 In that study, six conformations of the AMPA monomer were predicted from quantum-chemical calculations. Although the monomeric conformers of AMPA could not be observed directly in experiments, dimers arising from the complexation with the non-polar solvents were observed.10 A detailed conformational analysis of AMPA is an important starting point to characterize its ability to interact with other molecules and predict the possible geometry changes. Here, we have investigated the monomer conformers of AMPA and unraveled its internal dynamics in the absence of further interactions in the gas phase using rotational spectroscopy.
Rotational spectroscopy is a powerful tool to obtain the structural information of molecules in the gas phase with high precision and resolution.11,12 The development of chirped-pulse instruments revolutionized the field of rotational spectroscopy.13 Using chirped-pulse Fourier-transform microwave (CP-FTMW) spectroscopy, it is possible to record the rotational spectra of complex, flexible molecular systems over a broad frequency range in a single experiment.14 The experiments are complemented by high-level quantum-chemical calculations and supported by spectral assignment programs. From a broadband rotational spectrum, it is possible to extract information about the structure and internal dynamics of isolated molecules and clusters. Some recent studies on biologically relevant molecules by CP-FTMW spectroscopy demonstrate its capabilities to investigate terpenes,3–7,15–18 monosaccharides,19 amino acids,20 drugs,21,22 and micro-solvated complexes.23–27 As a remarkable example, a study on citronellal5 highlights the rich conformational landscape of a flexible molecule evaluated by broadband rotational spectroscopy.
The results presented in this work discuss the observed conformations, their structural similarities, the stabilization interactions, and the conversion pathways that are of interest to better understand and benchmark systems with rich conformational space arising from high flexibility, using AMPA as a model system. This study can also serve as an important basis for future work on solute–solvent interactions of carboxylic acids with different solvents.
Methods
Computational methods
The conformational landscape of AMPA was explored in two stages. First, a conformational search was performed by a semi-empirical method using the GFN-xTB code.28 Several conformers were obtained, and their geometries were optimized using the B3LYP29–31 (Becke, three-parameter, Lee–Yang–Parr) exchange–correlation functional along with Grimme's D3 dispersion corrections,32 and Becke–Johnson (BJ) damping,33 combined with the def2-TZVP basis set,34 using the ORCA program.35,36Second, a complementary stepwise manual search for the orientation of the functional groups was performed. The chiral centre of AMPA has three functional groups, a phenyl ring, a carboxylic acid group (COOH), and a methoxy group (OCH3) (Fig. 1b). The individual orientations of these functional groups are responsible for the conformational flexibility of AMPA and characterize the naming scheme for different conformers as shown in Fig. 2.
In addition to the geometry optimizations at the B3LYP-D3(BJ)/def2-TZVP level of theory, single-point energy calculations at the DLPNO-CCSD/aug-cc-pVTZ level of theory were performed. Frequency calculations at the B3LYP-D3(BJ)/def2-TZVP level of theory were also performed to validate whether the equilibrium structures were real minima and to obtain the zero-point corrected relative energies. Systematic scans of some coordinates were carried out at the B3LYP-D3(BJ)/def2-TZVP level of theory to explore the relaxation pathways between the conformers, employing the ORCA35,36 and Gaussian program packages.37 Non-covalent interaction (NCI)38,39 analysis was performed to help identify the weak intramolecular interactions involved in the stabilization of the conformers and to characterize and visualize the forces.
Experimental methods
The rotational spectrum of AMPA was recorded using a broadband compact-passage acquired coherence technique (COMPACT) spectrometer in the 2–8 GHz frequency range.40 A sample of 99% purity purchased from Thermo Fischer Scientific was used for experiments without further purification. AMPA is a white crystalline solid at room temperature with a melting point of around 69–71 °C and a boiling point of around 165 °C according to the information of the supplier. The sample was heated in a reservoir at ca. 120 °C and mixed with neon as a carrier gas at a stagnation pressure of 2 bars. Additional experiments were performed under similar conditions using helium and argon as carrier gases to explore the conformational landscape of AMPA. The mixture was then supersonically expanded using a pulsed valve into a vacuum chamber at a repetition rate of 8 Hz. A microwave chirp pulse of 4 μs duration generated using an arbitrary waveform generator and amplified using a 300 W traveling wave tube amplifier was broadcast into a vacuum chamber using a horn antenna to polarize the molecular ensemble. The molecular signal was collected in the time domain as a free-induction decay (FID) of the macroscopic dipole moment of the molecular ensemble. The application of the fast Fourier transformation results in the rotational spectrum in the frequency domain. A detailed description of the experimental setup can be found elsewhere.40 A recent data acquisition scheme, the ‘fast frame setup’ option of a digital oscilloscope, was employed.41 Eight back-to-back excitation chirps were performed on each gas pulse, and the subsequent eight FID acquisitions were then co-added and averaged. The use of the fast frame setup decreases the measurement time and the sample consumption rate, resulting in an effective repetition rate of 64 Hz. The final spectrum with Ne as a carrier gas was obtained by coadding 4.3 million FIDs. For spectra with He and Ar, 3.8 and 3.5 million FIDs, respectively, were coadded. All the spectra recorded using a COMPACT spectrometer had a resolution of around 25 kHz and an accuracy in the frequency measurement better than 15 kHz.The initial assignment of experimental lines to rotational transitions was performed through a recurrent fit based on Watson's A-reduction Hamiltonian in the Ir representation as implemented in PGOPHER.42,43 These initially fitted rotational constants (A, B, and C) and quartic centrifugal distortion constants (ΔJ, ΔK, ΔJK, δJ, and δK) were then refined using the SPFIT/SPCAT programs developed by Pickett.44 The observed line splittings in two of the conformers due to a large amplitude motion of AMPA were analysed using the XIAM program.45 This applies the so-called ρ-axis method where ρ is a dimensionless vector that accounts for the interaction between the overall rotation and internal rotation.46 For experimental structure determination, we used the KRA, EVAL, and STRFIT programs as available on the PROSPE website.47
Results and discussion
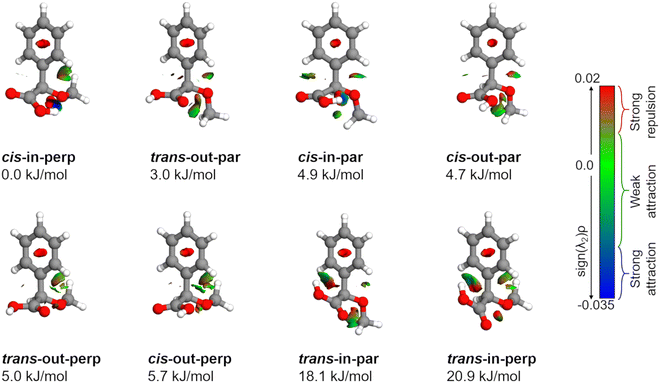
AMPA is a highly flexible molecule due to the possible configurations of the three functional groups and generates a rich conformational space (Fig. S1 and S2, ESI†). The spatial orientation of the methoxy group (dihedral angle τ, C13–O12–C7–C8) is observed to be either almost perpendicular or almost parallel with respect to the plane of the phenyl ring. The dihedral angle θ(O10–C8–C7–O12) can range from 0° to 360°, being either cis or trans with respect to the OCH3 group. Finally, the hydroxyl (OH) group of carboxylic acid, defined by the dihedral angle ϕ(H11–O10–C8–C7), can rotate to be pointing either towards (in) the OCH3 group or away from it (out). The combination of these possibilities produced eight minimum energy structures where the groups can be in perpendicular (perp) or parallel (par), cis or trans, and in or out configurations, respectively, as shown in Fig. 2. For example, the conformer cis-in-perp has the dihedral angle θ in cis, with the hydrogen of the OH group pointing towards the OCH3 group (in), and OCH3 is almost perpendicular to the phenyl ring. Table S1 of the ESI† lists the values of the three dihedral angles; τ, θ, and ϕ that characterize the different configurations for all eight conformers. The stepwise investigation revealed that one conformer, trans-in-perp, out of the eight possible structures was missed in the search by xTB. Six out of the eight conformations (Fig. 2) were found to be within a threshold of around 6 kJ mol−1 as listed in Table 1. Both the B3LYP and DLPNO-CCSD levels of theory predict a similar energy ordering of conformers, with the only exception of cis-in-par and cis-out-par. To obtain more accurate relative energies, we added the zero-point correction term from the B3LYP-D3(BJ)/def2-TZVP calculations to the single point energies obtained at the DLPNO-CCSD/aug-cc-pVTZ level of theory (Table 1). The structures of the eight different conformers of AMPA with their NCI analysis and zero-point corrected relative energies obtained at the B3LYP-D3(BJ)/def2-TZVP level are shown in Fig. 2.| Parameters | cis-in-perp | trans-out-par | cis-in-par | cis-out-par | trans-out-perp | cis-out-perp | trans-in-par | trans-in-perp |
|---|---|---|---|---|---|---|---|---|
| a A e, Be, and Ce are the equilibrium rotational constants in MHz. b μ α values (α = a, b, and c) are the values of the electric dipole-moment components in Debye. c ΔErel and ΔEZPE are the calculated (B3LYP-D3(BJ)/def2-TZVP) relative energies without and with the zero-point energy (ZPE) correction, respectively. d ΔErel-CC values are single point relative energies at the DLPNO-CCSD/aug-cc-pVTZ level of theory. e ΔEZPE-CC values are the single point relative energies (DLPNO-CCSD/aug-cc-pVTZ) corrected with the zero-point energy term from the frequency calculations at the B3LYP-D3(BJ)/def2-TZVP level of theory. | ||||||||
| A e/MHza | 1436.0 | 1615.7 | 1612.9 | 1632.5 | 1365.0 | 1373.8 | 1660.7 | 1450.3 |
| B e/MHz | 691.7 | 633.5 | 662.9 | 643.7 | 702.1 | 697.5 | 628.1 | 697.6 |
| C e/MHz | 582.8 | 571.3 | 540.3 | 562.8 | 605.9 | 605.8 | 562.2 | 580.1 |
| μ a/Db | −1.6 | 0.1 | −0.2 | 0.5 | −1.8 | 1.4 | −3.1 | −5.1 |
| μ b/D | 4.6 | 1.1 | 3.7 | −0.8 | 0.0 | 1.4 | −1.1 | 1.8 |
| μ c/D | −0.8 | 1.5 | −0.8 | −0.4 | −2.0 | 0.4 | −2.4 | −2.0 |
ΔErel/kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
0.0 | 3.9 | 4.5 | 5.4 | 5.8 | 6.3 | 19.5 | 22.2 |
| ΔEZPE/kJ mol−1 | 0.0 | 3.0 | 4.9 | 4.7 | 5.0 | 5.7 | 18.1 | 20.9 |
ΔErel-CC/kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.0 | 1.5 | 3.9 | 2.5 | 3.9 | 4.0 | 18.9 | 22.4 |
ΔEZPE-CC/kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
0.0 | 0.6 | 4.3 | 1.8 | 3.1 | 3.4 | 17.6 | 21.1 |
The upper black traces in Fig. 3 show two portions of the rotational spectrum (Ne-seeded) recorded using a COMPACT spectrometer. The experimental spectra are plotted against coloured traces, which represent the simulations of the observed conformers of AMPA using the experimentally fitted rotational constants. The typical energy threshold for observing conformers in our experiments is 6 kJ mol−1. For example, the fifteen conformations of citronellal were observed within this energy window.5 Each conformation has distinct rotational constants and dipole-moment components, giving rise to unique spectral signatures that allow differentiating them based on the rotational fingerprint and the type of spectrum observed. These distinct patterns of rotational transitions led to the identification of five conformers out of the six structures predicted in the above-mentioned energy window. All the experimentally determined sets of rotational constants can be assigned to a corresponding AMPA conformer as shown in Table 2.
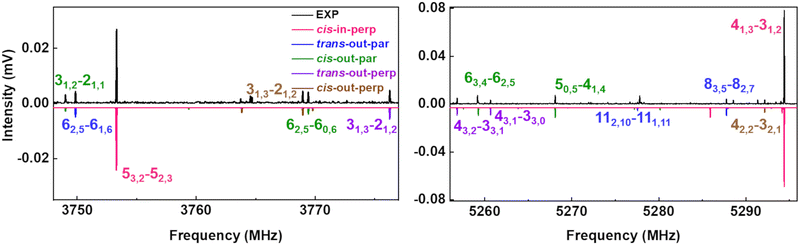 | ||
Fig. 3 Parts of the 2–8 GHz rotational spectrum of AMPA with the labelling scheme of the rotational transitions as 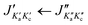 . The top part shows the experimental spectrum and the bottom part represents the simulations using the fitted rotational parameters for AMPA conformers (Table 2). The relative intensities are based on the predicted dipole moment components (Table 1). . The top part shows the experimental spectrum and the bottom part represents the simulations using the fitted rotational parameters for AMPA conformers (Table 2). The relative intensities are based on the predicted dipole moment components (Table 1). | ||
| Parameters | cis-in-perp | trans-out-par | cis-out-par |
|---|---|---|---|
| a A, B, and C are the rotational constants. ΔJ, ΔJK, ΔK, δJ and δK are the quartic centrifugal distortion constants. b Y and N indicate whether a, b, or c type of rotational transitions were observed or not, respectively. c N is the number of fitted transitions. σ is the root-mean-square deviation of the fit. d Standard error in parentheses in units of the last digit. | |||
| A/MHza | 1436.68000(29)d | 1619.14743(43) | 1636.37884(58) |
| B/MHz | 692.06967(12) | 635.06285(26) | 647.17771(31) |
| C/MHz | 583.21822(12) | 570.21890(26) | 560.19412(28) |
| Δ J /kHz | 0.07892(78) | 0.0723(20) | 0.1470(25) |
| Δ JK /kHz | 0.3036(19) | 0.1427(38) | — |
| Δ K /kHz | −0.0684(64) | — | — |
| δ J /kHz | 0.00462(13) | 0.00456(19) | — |
| δ K /kHz | −0.4362(24) | 0.867(10) | 2.977(36) |
| a/b/cb | Y/Y/Y | N/Y/Y | Y/Y/Y |
| V 3/kJ mol−1 | 8.263(9) | 7.552(2) | — |
| N | 248 | 167 | 54 |
| σ/kHz | 7.8 | 9.8 | 8.6 |
| Parameters | trans-out-perp | cis-out-perp |
|---|---|---|
| A/MHz | 1368.69142(41) | 1375.55303(71) |
| B/MHz | 703.73277(28) | 697.96749(45) |
| C/MHz | 605.92022(23) | 606.05148(44) |
| ΔJ/kHz | 0.0458(25) | 0.0468(79) |
| ΔJK/kHz | 0.4479(61) | 0.333(10) |
| ΔK/kHz | −0.323(16) | −0.0764() |
| δ J /kHz | 0.0059(11) | — |
| δ K /kHz | −0.532(17) | — |
| a/b/c | Y/N/Y | Y/Y/Y |
| V3/kJ mol−1 | — | — |
| N | 87 | 59 |
| σ/kHz | 7.9 | 8.3 |
The most intense transitions correspond to the low-energy conformers cis-in-perp and trans-out-par, due to their higher population. The rotational spectrum of the lowest energy conformer, cis-in-perp, shows all three a-, b- and c-type rotational transitions, while the second-lowest energy conformer, trans-out-par, presents only b- and c-type transitions, in good agreement with their predicted dipole-moment components as shown in Table 1. No transitions were observed for the third conformer, cis-in-par (vide infra). The rotational transitions of cis-out-par, the fourth most stable conformer, are in general weaker than those of the higher energy conformers, trans-out-perp and cis-out-perp. Based on the zero-point corrected relative energies, the fourth conformer should be more intense, so this effect could be explained by the relatively low values of the dipole-moment components for cis-out-par.
Conformational relaxation
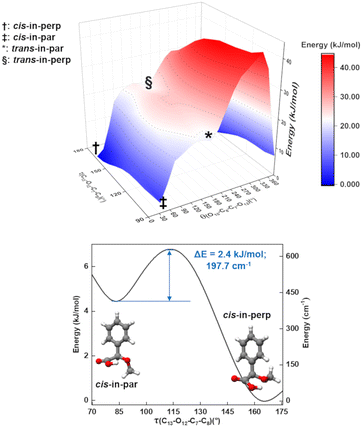
As mentioned, one of the predicted isomers, cis-in-par, could not be identified in the experimental spectrum. The explanation for the non-observation of the cis-in-par conformer could be its conversion to a lower energy structure in the course of the supersonic expansion (Fig. 4).Interestingly, each conformer of AMPA is connected to three other conformers by a change in the arrangement of one dihedral angle as shown in Fig. S3–S9 of the ESI.† These motions can be understood by performing systematic scans between the conformers, which give us the interconversion barriers for the conformer relaxation. In the case of the missing conformer (cis-in-par), the suggested relaxation pathway converts it into the lowest energy form by a change of the dihedral angle τ(C13–O12–C7–C8) (Fig. 4). This motion is predicted to be hindered by a barrier height of about 2.4 kJ mol−1 at the B3LYP-D3(BJ)/def2-TZVP level (3.6 kJ mol−1 at the DLPNO-CCSD/aug-cc-pVTZ level of theory), which is lower than the estimated barrier cut-off of 4.2 kJ mol−1 for conformer relaxation in a Ne-seeded supersonic expansion (Fig. 4).48,49 Thus, the non-observation of this conformer is consistent with its conversion into the lowest energy form.
A two-dimensional scan (Fig. 4) for the τ(C13–O12–C7–C8) and θ(O10–C8–C7–O12) coordinates shows the pathways and the relationships between several of the conformers. A second two-dimensional scan connecting the other four conformers is provided in Fig. S5 in the ESI.† The conformational relaxation pathways for the other detected conformers are hindered by potential barriers higher than 6 kJ mol−1 (Fig. S4–S9 of the ESI†), which prevent relaxation, in good agreement with the experimental observation of these conformers. Additional experiments were performed with He and Ar as carrier gases to explore their effect on the AMPA conformer relaxation pathways and are presented in Fig. S10 of the ESI.† In the experimental rotational spectra recorded using the three different carrier gases, the same five conformers were observed, and cis-in-par was always missing, even in the spectrum obtained with He as the carrier gas, where collisional relaxation processes are less efficient. The observation of the same five conformers regardless of the carrier gas demonstrates a selective relaxation of cis-in-par into cis-in-perp with all three different carrier gases and confirms the non-relaxation of the higher energy forms.
Internal rotation
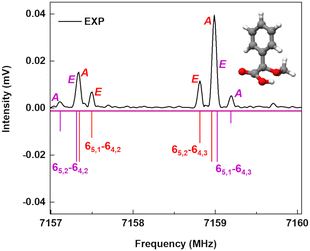
A spectral fine structure due to a large amplitude motion was observed: some of the transitions for cis-in-perp and trans-out-par were split into doublets (Fig. 5), which were attributed to the methyl top internal rotation. Here, the methyl group internal rotation gives rise to three-equivalent minima represented by a periodic function that describes how it varies with the coordinate for the motion. The expansion term arising due to the three-fold symmetry of the methyl group depends on the barrier height parameters V3 and V6 with a major contribution from V3,11 while the term V6 was not needed to obtain high-quality fits using XIAM, as presented in Table S3 of the ESI.† Each rotational energy level has two torsional sublevels denoted as the non-degenerate level A and a double degenerate level E, resulting in doublets in the rotational spectrum.Quantum-chemical calculations were performed to obtain an approximation for the theoretical barrier for the methyl top internal rotation. The V3 barrier depends on the position of the CH3 group and its neighboring environment as well as the bond characters. The V3 barriers for all observed AMPA conformers were calculated to be between 7 and 9 kJ mol−1 (B3LYP-D3(BJ)/def2-TZVP level of theory). The methyl internal rotation scans at the DLPNO-CCSD/aug-cc-pVTZ level of theory were also performed for the two lowest energy conformers cis-in-perp and trans-out-par, which predicted barrier heights of 8.1 and 7.7 kJ mol−1, respectively. The predicted internal rotation barriers at the B3LYP-D3(BJ)/def2-TZVP level of theory for the two lowest energy conformers are shown in Fig. 6, while the others are presented in Fig. S11 of the ESI.† The moderately high V3 barrier for the AMPA conformers makes most of the A and E state lines to appear blended in our spectrum. We could only resolve the splitting from transitions involving energy levels with Ka higher than 4, which are split into doublets spanning around 200–300 kHz. These components were analyzed and fitted using the XIAM program.45
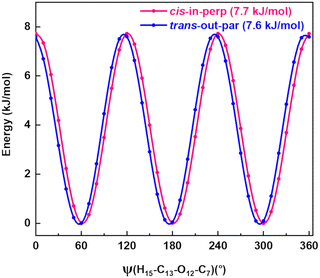 | ||
| Fig. 6 Methyl internal rotation scan for cis-in-perp and trans-out-par performed at the B3LYP-D3(BJ)/def2-TZVP level of theory. | ||
The internal rotation barrier obtained from the experimental splittings for cis-in-perp (8.263(9) kJ mol−1)) is higher compared to that for trans-out-par (7.552(2) kJ mol−1). This could be due to a CH⋯π interaction between the methyl group and the phenyl ring in cis-in-perp, which likely influences the rotation of the methyl top (vide infra). The computed barrier heights at the DLPNO-CCSD/aug-cc-pVTZ level for both conformers are in better agreement with the experimental values than those using B3LYP-D3(BJ)/def2-TZVP.
Experimental structure
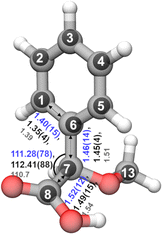
In the rotational spectrum with Ne as the carrier gas, we observed a signal-to-noise ratio of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the strongest transition, 60,6–51,5 of the most stable conformer, cis-in-perp, with an intensity of 780 μV. This allowed us to observe the rotational spectra of all of its singly-substituted 13C isotopologues in natural abundance (1.1%) and to derive its experimental structure. Table S2 in the ESI† summarizes the experimentally determined rotational parameters for the nine 13C isotopologues and those of the parent species. The atom coordinates of these carbon atoms with respect to the center of mass of the molecule were derived using Kraitchman's equations,50 allowing us to build the so-called substitution structure, rs, atom by atom. This method provides only the absolute values for the atomic coordinates, so the signs were taken from the calculations. A comparison between the equilibrium structure re obtained from quantum-chemical calculations at B3LYP-D3(BJ)/def2-TZVP and the experimental structure rs is displayed in Fig. 7, showing a remarkable agreement between them.
1 for the strongest transition, 60,6–51,5 of the most stable conformer, cis-in-perp, with an intensity of 780 μV. This allowed us to observe the rotational spectra of all of its singly-substituted 13C isotopologues in natural abundance (1.1%) and to derive its experimental structure. Table S2 in the ESI† summarizes the experimentally determined rotational parameters for the nine 13C isotopologues and those of the parent species. The atom coordinates of these carbon atoms with respect to the center of mass of the molecule were derived using Kraitchman's equations,50 allowing us to build the so-called substitution structure, rs, atom by atom. This method provides only the absolute values for the atomic coordinates, so the signs were taken from the calculations. A comparison between the equilibrium structure re obtained from quantum-chemical calculations at B3LYP-D3(BJ)/def2-TZVP and the experimental structure rs is displayed in Fig. 7, showing a remarkable agreement between them.
Alternative structural information was obtained by fitting the effective ground state structure, r0. The r0 structure was determined by performing a least-square fit of certain structural parameters using the rotational constants from all the observed species. The r0 parameters are shown in blue in Fig. 7. Table S4 in the ESI† summarizes the experimental structural r0 and rs parameters, such as the bond lengths and angles, in comparison with the re parameters. The signal-to-noise ratio was not sufficient to observe the rotational spectra of the 18O isotopologues in natural abundance (0.2%) or any rare isotopologue for the other isomers of AMPA.
Intramolecular interactions
The relative stability of the conformers can be further analyzed by investigating the intramolecular interactions present in AMPA. Fig. 2 shows the results of non-covalent interaction (NCI) plots, which help in visualizing and characterizing the different attractive and repulsive interactions present in the different AMPA conformers. The sign of the Laplacian of the density, ∇2ρ, is a widely used tool to distinguish between different types of interactions. This Laplacian has contributions from all the three principal axes of maximal variation, which have three eigenvalues λi of the electron density of the Hessian matrix. The second eigenvalue λ2 then helps in discerning between different types of non-covalent interactions such as hydrogen bonding, dispersion, and steric interactions. When λ2 < 0, it indicates the presence of strong attraction, while values around 0 reveal weak attraction. The positive values of λ2 imply repulsive interactions.38The cis-in-perp and cis-in-par conformers present the cis configuration together with the hydrogen atom from the carboxylic acid group pointing towards (in) the oxygen of the methoxy group. A moderately strong O–H⋯O intramolecular hydrogen bond is formed with bond lengths of 1.9 and 2.0 Å in cis-in-perp and cis-in-par, respectively. In the trans-in-par and trans-in-perp conformations, although the hydrogen atom from the carboxylic acid group is also pointing inwards, the intramolecular interaction is formed with the π-cloud of the benzene ring, O–H⋯π. In principle, that is also a stabilizing interaction based on the NCI plots, however, in order to form it, the carboxylic acid group is tilted from its preferred position, resulting in two high-energy conformations (Fig. 2).
Another stabilizing interaction is formed between one hydrogen atom of the phenyl ring and the lone pair of the oxygen atom of the OCH3 group. This CH⋯O interaction is present in the eight isomers of AMPA and seems to be of similar strength regardless of the par–perp configuration of the OCH3 group. There is another CH⋯O interaction, in this case between the hydrogen atom from the OCH3 group and the lone pair of the oxygen atom from the carboxylic acid group. This interaction also seems to be stabilizing, but is only possible in conformers that are in par configuration since only for those conformers the methoxy group is in the correct orientation to establish the contact. However, the conformers with the OCH3 group in the perp disposition have a possibility of an alternative interaction. This is a long-range CH⋯π interaction, bringing further stability to conformers in perp configuration. Finally, it is worth mentioning that a repulsive interaction is present in all the conformers of AMPA and occurs between two oxygen atoms opposed to each other. Regardless of the conformations, there is always a slight destabilization force between the oxygen from the methoxy group and one for the oxygen atoms from the carboxylic acid group.
As mentioned above, the interactions also influence the internal rotation barrier of the conformers. The experimental barrier height for cis-in-perp is slightly higher than that for trans-out-par due to the presence of the CH⋯π interaction between the methyl group and the phenyl ring. Fig. S11 in the ESI† shows the theoretical barrier heights for the cis-out-par, trans-out-perp, and cis-out-perp conformers. The theoretical calculations predict barriers to be slightly higher for the conformers in the perp configuration compared with those in par, in good agreement with the effect of the CH⋯π interaction. The presence of these interactions helps in explaining the energy ordering of the different conformers of AMPA and their internal dynamics.
Conclusions
We report new experimental and theoretical insights into the conformational landscape for the monomer of alpha-methoxy phenylacetic acid. We have successfully used broadband rotational spectroscopy and quantum-chemical calculations to probe its rich conformational space and internal dynamics. We experimentally identified and characterized five conformations out of six predicted low-energy structures, together with an accurate structure determination for the lowest energy conformer. The conformers are related to others via changes of the cis–trans, in-out, and perp-par configurations. The analysis of the interconversion pathways can explain why one conformer is not present in our experimental spectrum, regardless of the carrier gas used. The conformers are stabilized by non-covalent intramolecular interactions, and have been analysed to understand their energy order. Such intramolecular interactions govern the conformational landscape and influence the internal dynamics of AMPA, highlighting the importance of studying such interactions in detail. Both the DLPNO-CCSD/aug-cc-pVTZ and the B3LYP-D3(BJ)/def2-TZVP levels of theory seem to be good quantum-chemical methods to describe molecular systems such as AMPA, as is demonstrated by our detailed comparison with structural information from rotational spectroscopy. The present study forms the basis for future investigations about the micro-solvation of AMPA to understand solute–solvent interactions and to learn how solvation will affect the internal dynamics of similar molecules.Author contributions
Himanshi Singh: investigation, formal analysis, writing – original draft, and writing – review and editing. Pablo Pinacho: conceptualization, investigation, formal analysis, and writing – review and editing. Daniel A. Obenchain: formal analysis and writing – review and editing. María Mar Quesada-Moreno: investigation and writing – review and editing. Melanie Schnell: conceptualization, funding acquisition, project administration, and writing – review and editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Prof. Dr. Christian Merten for bringing this molecule to our attention. This work was supported by the collaborative linkage grant ‘‘Extreme light for sensing and driving molecular chirality (ELCH)’’, SFB1319, of the Deutsche Forschungsgemeinschaft. Parts of the computations were performed by using the European XFEL and DESY funded Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. The benchmarking aspect of this work was profited from the environment provided by the local research training group BENCH (DFG -389479699/GRK2455). P. P. would like to thank the Alexander von Humboldt Foundation for a postdoctoral fellowship. M. M. Q. M. thanks Fundación Alfonso Martín Escudero for a postdoctoral grant and Junta de Andalucía for a postdoctoral contract (DOC_01282).Notes and references
- C. Min and D. Seidel, Chem. Soc. Rev., 2017, 46, 5889–5902 RSC.
- S. Dayal, K. D. Kalra and P. Sahu, J. Cosmet. Dermatol., 2020, 19, 393–399 CrossRef PubMed.
- H. V. L. Nguyen, H. Mouhib, S. Klahm, W. Stahl and I. Kleiner, Phys. Chem. Chem. Phys., 2013, 15, 10012–10018 RSC.
- D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, Front. Chem., 2015, 3, 15 Search PubMed.
- S. R. Domingos, C. Pérez, C. Medcraft, P. Pinacho and M. Schnell, Phys. Chem. Chem. Phys., 2016, 18, 16682–16689 RSC.
- A. Krin, C. Pérez, P. Pinacho, M. M. Quesada-Moreno, J. J. López-González, J. R. Avilés-Moreno, S. Blanco, J. C. López and M. Schnell, Chem. – Eur. J., 2018, 24, 721–729 CrossRef CAS PubMed.
- M. M. Quesada-Moreno, A. Krin and M. Schnell, Phys. Chem. Chem. Phys., 2019, 21, 26569–26579 RSC.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- P. H. Buist and D. M. Marecak, J. Am. Chem. Soc., 1992, 114, 5073–5080 CrossRef CAS.
- K. Bünnemann and C. Merten, Phys. Chem. Chem. Phys., 2017, 19, 18948–18956 RSC.
- W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley, New York, 1984 Search PubMed.
- C. H. Townes and A. L. Schawlow, Microwave Spectroscopy, Dover, New York, 1975 Search PubMed.
- G. B. Park and R. W. Field, J. Chem. Phys., 2016, 144, 200901 CrossRef PubMed.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- V. A. Shubert, D. Schmitz, C. Medcraft, A. Krin, D. Patterson, J. M. Doyle and M. Schnell, J. Chem. Phys., 2015, 142, 214201 CrossRef PubMed.
- D. Schmitz, V. A. Shubert, B. M. Giuliano and M. Schnell, J. Chem. Phys., 2014, 141, 034304 CrossRef CAS PubMed.
- J. R. A. Moreno, T. R. Huet and J. J. L. González, Struct. Chem., 2013, 24, 1163–1170 CrossRef CAS.
- C. Medcraft and M. Schnell, Z. Phys. Chem., 2016, 230, 1–14 CrossRef CAS.
- E. J. Cocinero, A. Lesarri, P. Écija, Á. Cimas, B. G. Davis, F. J. Basterretxea, J. A. Fernández and F. Castaño, J. Am. Chem. Soc., 2013, 135, 2845–2852 CrossRef CAS PubMed.
- S. Blanco, A. Lesarri, J. C. López and J. L. Alonso, J. Am. Chem. Soc., 2004, 126, 11675–11683 CrossRef CAS PubMed.
- T. Betz, S. Zinn and M. Schnell, Phys. Chem. Chem. Phys., 2015, 17, 4538–4541 RSC.
- M. Varela, C. Cabezas, J. C. López and J. L. Alonso, J. Phys. Chem. A, 2013, 117, 13275–13278 CrossRef CAS PubMed.
- C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160 CrossRef PubMed.
- C. Pérez, J. L. Neill, M. T. Muckle, D. P. Zaleski, I. Peña, J. C. Lopez, J. L. Alonso and B. H. Pate, Angew. Chem., Int. Ed., 2015, 54, 979–982 CrossRef PubMed.
- P. Pinacho, A. Krin, C. Pérez, S. Zinn, J. C. López, S. Blanco and M. Schnell, Phys. Chem. Chem. Phys., 2018, 20, 15635–15640 RSC.
- S. Melandri, D. Consalvo, W. Caminati and P. G. Favero, J. Chem. Phys., 1999, 111, 3874–3879 CrossRef CAS.
- W. Li, M. M. Quesada-Moreno, P. Pinacho and M. Schnell, Angew. Chem., Int. Ed., 2021, 60, 5323–5330 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- S. Grimme, J. Antony and S. Ehrlich, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- M. J. Frisch, et al., Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84 CrossRef CAS.
- C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–5 CrossRef.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS.
- J. K. Watson, J. Mol. Spectrosc., 1977, 65, 123–133 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- H. Hartwig and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1996, 51, 923–932 CrossRef CAS.
- R. C. Woods, J. Mol. Spectrosc., 1967, 22, 49–59 CrossRef CAS.
- PROSPE – Programs for ROtational SPEctroscopy, https://www.ifpan.edu.pl/~kisiel/prospe.htm, (accessed July, 2022).
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- P. Pinacho, J. C. López, Z. Kisiel and S. Blanco, Phys. Chem. Chem. Phys., 2020, 22, 18351–18360 RSC.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures on conversion and internal rotation scans. Experimentally determined structures and line lists for the observed conformers. See DOI: https://doi.org/10.1039/d2cp03962a |
| This journal is © the Owner Societies 2022 |