Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A litmus test for the balanced description of dispersion interactions and coordination chemistry of lanthanoids†
Juana Vázquez
Quesada
 *a,
Jiří
Chmela
a,
Jean-François
Greisch
*a,
Jiří
Chmela
a,
Jean-François
Greisch
 b,
Wim
Klopper
b,
Wim
Klopper
 ab and
Michael E.
Harding
ab and
Michael E.
Harding
 *b
*b
aInstitut für Physikalische Chemie, Karlsruher Institut für Technologie (KIT), Campus Süd, Postfach 6980, D-76049 Karlsruhe, Germany. E-mail: juana.quesada@kit.edu
bInstitut für Nanotechnologie, Karlsruher Institut für Technologie (KIT), Campus Nord, Postfach 3640, D-76021 Karlsruhe, Germany. E-mail: michael.harding@kit.edu
First published on 3rd August 2022
Abstract
The influence of long-range interactions on the structure of complexes of Eu(III) with four 9-hydroxy-phenalen-1-one ligands (HPLN) and one alkaline earth metal dication [Eu(PLN)4AE]+ (AE: Mg, Ca, Sr, and Ba) is analyzed. Through the [Eu(PLN)4Ca]+ complex, which is a charged complex with two metals—one of them a lanthanoid—and with four relatively fluxional π-ligands, the difficulties of describing such systems are identified. The inclusion of the D3(BJ) or D4 corrections to different density functionals introduces significant changes in the structure, which are shown to stem from the interaction between pairs of PLN ligands. This interaction is studied further with a variety of density functionals, wave-function based methods, and by means of the random phase approximation. By comparing the computed results with those from experimental evidence of gas-phase photoluminescence and ion mobility measurements it is concluded that the inclusion of dispersion corrections does not always yield structures that are in agreement with the experimental findings.
1 Introduction
Due to its efficiency in comparison with correlated wave-function theories, Kohn–Sham density functional theory (KS-DFT) has become the most widely used quantum chemical method in chemistry and physics. Even though convergence in accuracy and predictability are not hierarchically defined as clearly as with correlated wave-function methods,1 efforts in this direction have for many years been graphically represented by what is called Jacob's ladder.2 Despite the endeavors made in the design and development of hierarchical enhancements of the KS-DFT methods, there are still certain intrinsic limitations in the exchange-correlation functionals such as the self-interaction error (SIE), deficiencies in describing strong correlation, and the lack of long-range dynamic correlation.3,4 This latter aspect becomes visible in the difficulties of KS-DFT to describe non-covalent interactions.Fortunately, during the past two decades, different approaches have been developed in order to overcome these drawbacks.5 Two of the most extended modi operandi have been the following: First, the attainment of dispersion interactions directly from the electron density by defining non-local correlation (NLC) functionals. This approach has brought about the so-called van der Waals functionals (vdW-DF) and represents a new conception within KS-DFT since it adds a description of the dispersion interactions directly to the DFT functionals by combining all kinds of correlations. Examples in this direction are the functionals vdW-DF1,6 and vdW-DF27,8 and the simpler and more efficient approaches of Vydrov and van Voorhis (VV9 and VV10).9–13 The second most used approximation, especially within the field of chemistry, is the so-called DFT-D methodology14–19 consisting in adjoining a semi-classical correction [see eqn (1)] to the known local functionals, which accounts for the long-range van der Waals interactions between particles in the gas phase described through the attractive correction −1/Rn (n = 6, 8,…), that is:
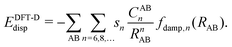 | (1) |
As mentioned above, the inclusion of dispersion interactions has enabled the use of DFT to describe non-covalent inter- and intra-molecular interactions23 which have been intensely studied primarily in unsaturated organic molecules, in so-called π–π-stacked structures, in biologically relevant molecules such as nucleic acids and proteins,24,25 and more scarcely also in complexes where metal–metal and metal–ligand interactions were analyzed (see, e.g., ref. 26–28). Challenges to be explored with all aforementioned approaches are those in which lanthanoids and actinoids are present and especially when different forms of long-range interactions concur simultaneously. Examples are charged systems in which partially flexible π-groups and diverse metals with a wide coordination sphere get together. In these cases, the dilemma between accuracy and computational feasibility becomes a decisive issue when it comes to finding a qualitatively correct answer.29
Some years ago, some of us worked on the characterization of Eu(III) complexes with different numbers of the 9-hydroxy-phenalen-1-one (HPNL) ligand.30–34 This ligand was chosen for its high absorption cross section, its long-lived phosphorescence, and its ability to coordinate and transfer energy to Eu atoms.35–37 In these studies, the structures of the complexes were always theoretically predicted making use of DFT by using the BP8638 functional in combination with the def2-SVP39,40 and def2-TZVPP39,40 basis sets. The computed values could confirm the experimental evidence obtained through mass selected gas-phase photoluminescence (PL) emission spectra as well as, in some cases, through ion mobility measurements. In the course of this research we came across a class of heterodimetallic complexes with four ligands, that is, Eu(III) 9-oxo-phenalen-1-one coordination complexes [Eu(PLN)4AE]+ with AE = Mg, Ca, Sr, and Ba (see Fig. 1),34 for which the BP86/def2-TZVPP approach predicted four different structural motifs.
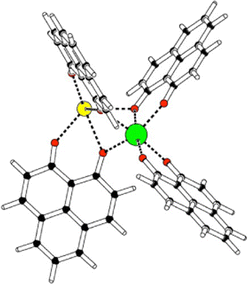 | ||
| Fig. 1 Schematic structure Eu(III)-9-oxo-phenalen-1-one [Eu(PLN)4AE]+ with AE = Mg, Ca, Sr, and Ba (europium: green; AE: yellow; oxygen: red). | ||
The two motifs lowest in energy, hereinafter called motif 1 and motif 2, were consistent with a six-fold coordinated Eu(III) ion and a five-fold coordinated alkaline earth ion. Motif 1 (M1) can be described as a complex where one PLN unit coordinates only with the Eu(III) ion while the other three are coordinated to both metal ions. In motif 2 (M2), on the contrary, one PLN unit coordinates only with the alkaline earth dication, whereas the other three form a propeller-like configuration in which the ligands are coordinated to the Eu(III) ion similar to leaf blades to a stem.31,41,42 For [Eu(PLN)4Ca]+ and [Eu(PLN)4Sr]+ motif 2 is only 7–9 kJ mol−1 more stable while for [Eu(PLN)4Mg]+ motif 1 is by 8 kJ mol−1 the lower conformation. The experimental evidence arising from the ion mobility analysis and the gas-phase photoluminescence (PL) measurements could not rule out at the time any of these energetically almost degenerate structures.43
The presence of the PLN ligands, typical π-systems, made us question if long-range correlation interactions in these systems might be relevant in distinguishing between motifs 1 and 2. Thus, the present work focuses on the investigation of dispersion effects in motif 1 (M1) and on the analysis of their influence on the molecular structure. For this purpose, the D3(BJ) and D4 models were primarily used and contrasted, when possible, with reference values obtained employing wave-function based methods, as well as with other approaches for evaluating dispersion effects within the framework of KS-DFT.
The remaining part of this manuscript is organized as follows: in Section 2 the theoretical and experimental methodology followed in this work is described. Section 3 is mainly focused on the structure of the [Eu(PLN)4Ca]+ complex. For this purpose, the effect of using different functionals, the inclusion of non-covalent interactions, and the influence of the starting structures in the geometry optimization process are first analyzed in Section 3.1. A comparison with the experimental data is carried out in Section 3.2. Section 4 elaborates on the results of Section 3 first by briefly discussing many-body dispersion effects (Section 4.1). A benchmark study of the π–π interactions between the PLN ligands is carried out in Section 4.2, the results are contrasted with values obtained using the random phase approximation (RPA) and with reference values obtained from wave-function-based CCSD(T)44 and CCSD(F12)(T)44,46,47 computations. In Section 4.3 the role of the alkaline earth and lanthanoid metals coordination sphere in the evaluation of the dispersion interactions by means of the D3(BJ) and D4 models is discussed. Finally, Section 5 summarizes the present work with the observation that the system studied here provides a litmus test for measuring the delicate balance between dispersion interactions and coordination chemistry of europium complexes.
2 Methods
2.1 Computations
All quantum chemical computations were performed using the Turbomole program package.48 DFT calculations were carried out using a spherical grid 5 for numerical integration as defined in the Turbomole program.49 Unless stated otherwise, the convergence thresholds were 10−8Eh and 10−5Eh/a0 for the self-consistent field (SCF) energy and for the Cartesian gradient, respectively. The resolution-of-the-identity approximation (also called density fitting) was applied in all cases.50–52 Using a Fermi-type expression dynamically determined, floating occupation numbers in the SCF computation were obtained in order to determine the number of unpaired electrons.In the present work, some of the most popular DFT functionals were employed. In increasing order of sophistication when describing the exchange–correlation contribution (Perdew's metaphorical Jacob's Ladder),2 the used functionals can be listed as follows: BP86,38 BLYP,53 and PBE54 functionals within the generalized gradient approximation (GGA), the TPSS,55 SCAN56 and M06-L57 functionals belonging to the meta-generalized gradient approximation (MGGA) functionals, the non-empirical PBE058 functional, the semi-empirical B3LYP59 and BHLYP53,59 functionals, and the meta-hybrid functionals TPSSh,60 M06,61 and M06-2X.61 The latter five belong to the class of hybrid functionals (HYB) with different percentages of exact Hartree–Fock exchange. Finally, two range-separated hybrid functionals including dispersion interactions, that is, ωB97M-V62 and ωB97X-D,63 were also tested. For those functionals that do not include long-range dynamic correlation (dispersion), the pairwise dispersion corrections D314–16 with Becke–Johnson damping function [D3(BJ)],17 and D418,19 as well as the nonlocal VV10 approach13,64 were incorporated to the already established local functionals. Moreover three van der Waals functionals, that is, optB88-vdW,65 BEEF-vdW66 and mBEEF-vdW67 based on a non-local electron density dependent correlation (NLC) were also added to the test set. Additional improvements beyond the pairwise additive description of the long-range electronic correlation were carried out by means of the use of the random phase approximation (RPA) within the framework of the adiabatic-connection fluctuation–dissipation theorem in the DFT formulation68–72 and as defined for ground-state energies and analytic first-order properties by Furche et al.73–76 The RPA approach is directly related to the post-Hartree–Fock methods sharing with them also a high computational demand.73,77–79 Combining DFT with a post-Hartree–Fock method, the double-hybrid functional B2PLYP80 with second order perturbation theory correlation energy was also used for energies. In the context of the wave-function theory, second-order Møller–Plesset perturbation theory (MP2)81 as well as explicitly correlated MP2 (MP2-F12)82 were considered, too, accounting for dynamic electron correlation effects. As reference values for the energies calculated in this work, the coupled-cluster singles and doubles with perturbational treatment of triple excitations [CCSD(T)] method44 and the CCSD(F12) method45–47 were employed. For all wave-function post-Hartree–Fock methods, the core electrons were not correlated (fc). Unless otherwise stated, the def2-TZVPP basis set39 was used in all computations.
As in previous works,31,33,34 the energy levels of the complexes were analyzed and simulated using an effective ligand-field Hamiltonian83–89 based on the theory of many-electron spectra first described by Racah.89–93 The computations with this effective Hamiltonian were carried out with the McPHASE package.94,95 In particular the Wybourne normalized ligand-field parameters, Lkp,94 were obtained with the pointc module employing the natural population analysis96 point charges calculated with different DFT functionals and the def2-TZVPP basis set. The Fk and ζ parameters were used as optimized for the nonanuclear [Eu9(PLN)16(OH)10+] complex.33
2.2 Experiment
In the gas-phase photoluminescence (PL) measurements, the desolvated ions were mass-selected, stored in an quadrupole ion trap, thermalized via collisions with a helium buffer gas at about 0.2 mbar and 85 K, and photoexcited by the 458 nm line of a continuous wave (cw) Ar+-laser with its beam orthogonal to the ion trap axis.31,32 Description of the experimental setup has been reported in detail elsewhere.34,97Structural information about gas-phase ions at room temperature was obtained using gas-phase ion mobility. Ion mobility mass spectrometry is a technique that spatially separates ions under the influence of an electric field by affecting their motion via collisions with a buffer gas.98,99Via the recording of the ions' arrival time at the detector, and calibrated against known references, their cross-sections can be determined accurately. Furthermore, distinguishing isomers with an identical mass-over-charge ratio was achieved at an ion mobility resolution of 150. As described in ref. 34, the N2 collision cross-sections inferred from trapped ion mobility spectrometry (TIMS) measurements on a timsTOF (Bruker, Bremen, Germany) at 300 K and a pressure of 0.923 mbar N2 (exit funnel) was compared to scaled He-collision cross-sections computed using both MOBCAL100–102 and IMOS.103–105 It is to be noted that the He-collision cross-sections computed using MOBCAL and IMOS are in perfect agreement. The scaling relationship, ΩN2 = 53.9 + 1.110ΩHe, was inferred from the comparison of the He and N2 cross sections reported for denatured polyalanine by Bush and coworkers.106 For the sake of simplicity, only He-collision cross-sections will be reported in this work.
3 Results
3.1 Investigation of the structure
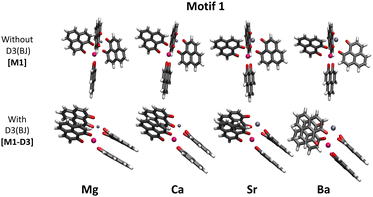
As already mentioned in the introduction, in our previous work,34 we aimed at finding the structures of a series of [Eu(PLN)4AE]+ complexes (Fig. 1). As in previous studies with Eu(III) compounds, the structures of these complexes were optimized at the BP86/def2-TZVPP level and in order to investigate more in detail motif 1, dispersion interactions were added. For this purpose, the D3(BJ) model was applied as a first approach to the problem. Fig. 2 shows the different optimized geometries obtained with and without dispersion corrections for motif 1 (M1-D3 and M1, respectively). [For Motif 2, for example, the geometrical changes are considerably less pronounced by including D3(BJ) dispersion interactions (see Section I of the ESI†).] With D3(BJ) corrections, the two-by-two π–π stacking of the PLN ligands apparently represents a key driving force resulting in a significant molecular reorganization for this motif (M1-D3).Energetically, for motif 1 the M1-D3 structures are considerably more stable than their M1 and their motif 2 [M2-D3] counterparts [see Table 1 of Section I of the ESI†] suggesting that the formation of the stacked PLN pair is associated with a significant attraction energy gain.
| Method | ΔE0 | ΔGTLIF | ΔGIM | Outcome | |||
|---|---|---|---|---|---|---|---|
| RR | FR | RR | FR | M1 | M1-D3 | ||
| BP86 | 0 | 0 | 0 | 0 | 0 | oo | oo |
| BP86-D3(BJ) | 1 | −1 | 0 | −1 | 0 | ss | ss |
| BP86-D4 | 0 | −1 | 0 | 0 | 0 | ss | ss |
| BLYP | 0 | 0 | 0 | 0 | 0 | oo | oo |
| BLYP-D3(BJ) | −24 | −15 | −18 | +2 | −8 | oo | ss |
| BLYP-D4 | −20 | −16 | −17 | −9 | −13 | hs | ss |
| BLYP-VV10 | −1 | −2 | −2 | +1 | 0 | hs | hs |
| PBE | 0 | −1 | 0 | 0 | 0 | oo | oo |
| PBE-D3(BJ) | −7 | −6 | −6 | −1 | −4 | oo | hs |
| PBE-D4 | −11 | −10 | −11 | −4 | −7 | oo | hs |
| PBE-VV10 | 0 | 0 | 0 | +1 | +1 | hs | hs |
| TPSS | −1 | 0 | 0 | +1 | 0 | oo | oo |
| TPSS-D3(BJ) | −8 | −4 | −5 | −11 | −3 | oo | ss |
| TPSS-D4 | 0 | +3 | +2 | +11 | +6 | hs | ss |
| TPSS-VV10 | +2 | −2 | −2 | 0 | 0 | hs | ss |
| B3LYP | 0 | 0 | 0 | 0 | 0 | oo | oo |
| B3LYP-D3(BJ) | −11 | −6 | −7 | +3 | +2 | oo | ss |
| B3LYP-D4 | −20 | −12 | −14 | +1 | −6 | oo | ss |
| BHLYP | 0 | 0 | 0 | 0 | 0 | oo | oo |
| BHLYP-D3(BJ) | −6 | −3 | −4 | +1 | −1 | oo | hs |
| BHLYP-D4 | −13 | −10 | −11 | −4 | −7 | oo | hs |
| TPSSh | 0 | 0 | 0 | 0 | 0 | oo | oo |
| TPSSh-D3(BJ) | −10 | −7 | −8 | 0 | −4 | oo | ss |
| TPSSh-D4 | 0 | +1 | +2 | +1 | +5 | hs | ss |
| PBE0 | 0 | 0 | 0 | 0 | 0 | oo | oo |
| PBE0-D3(BJ) | −7 | −6 | −7 | 0 | −3 | oo | hs |
| PBE0-D4 | −11 | −9 | −10 | −2 | −6 | oo | hs |
| M06-2X | −1 | oo | ss | ||||
| M06-2X-D4 | −8 | oo | ss | ||||
| optB88-vdW | 0 | 0 | 0 | 0 | 0 | oo | oo |
| BEEF-vdW | 0 | 0 | 0 | 0 | 0 | oo | oo |
| mBEEF-vdW | 0 | 0 | 0 | 0 | 0 | oo | oo |
As a major structural change occurs upon the inclusion of dispersion corrections resulting in the stacking of the PLN ligands in the M1-D3 structure, a more detailed analysis of the structure was accomplished for one of the complexes of the series, namely [Eu(PLN)4Ca]+. In this case the two structures obtained for this complex, that is, M1 (BP86/def2-TZVPP) and M1-D3 (BP86-D3(BJ)/def2-TZVPP) with open-open and stacked configurations, respectively (see Fig. 3), were taken as starting points for the optimization of the structure of this complex using a selection of DFT-functionals. Cartesian coordinates of M1 and M1-D3 are provided in Section II of the ESI.†
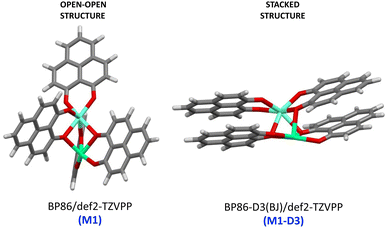 | ||
| Fig. 3 Starting-point configurations used for the geometry optimizations of the [Eu(PNL)4Ca]+ complex (europium: clear blue; calcium: green; oxygen: red). | ||
In particular, one or two functionals were chosen within each rung of Jacob's ladder, that is, GGA, MGGA, HYB, MHYB, and range-separated hybrid.107 For the double hybrid B2PLYP functional, gradient calculations and therefore geometry optimizations are currently not implemented in Turbomole. The inclusion of dispersion corrections by means of the DFT-D models D3(BJ) and D4 as well as by incorporation of the nonlocal functional VV10 was also investigated. Additionally, the van der Waals functionals optB88-vdW, BEEF-vdW and mBEEF-vdW, albeit especially suitable for solid-state calculations, were also tested.108 The results including energy differences and qualitative descriptions of the structures are given in Table 1.
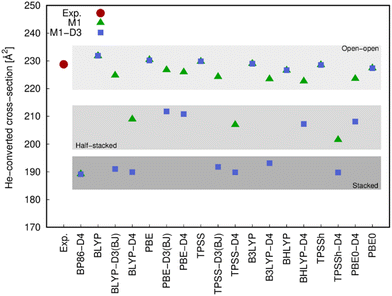
For all tested functionals without extra dispersion corrections, and regardless of the starting point geometry, open-open structures are obtained in all cases. Structures described as open–open are very similar so that the difference in energy is essentially zero. When dispersion interactions are taken into account using the D3(BJ), D4 and VV10 models the situation changes depending on the functional and the starting structure. Not only open-open structures but also a stacked configuration as well as a new type of structure (half-stacked) are obtained (see Fig. 4). With methods like TPSS-D4 and TPSSh-D4 the stacked and half-stacked structures are even practically isoenergetic (see Table 1). Although the electronic energy differences between the three structural configurations are of the order of a few kJ mol−1 (at most 24 kJ mol−1), the stability trend confirmed in all cases is, starting from the most stable, as follows: stacked > half-stacked > open–open.
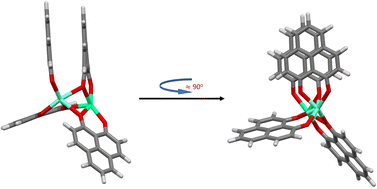 | ||
| Fig. 4 Half-stacked structure type for the [Eu(PNL)4Ca]+. (BLYP-D4/def2-TZVPP calculations resulting from using the M1 and M1-D3 structures as starting point for the geometry optimization, Table 1.) | ||
With the aim of identifying the nature of the critical points found in the geometry optimization using different methods, second derivatives of the potential energy were computed for all of the optimized geometries, verifying that all structures correspond to minima on the potential energy surface.109 Apart from the almost isoelectronic character of the three types of structures found, the zero-point vibrational energy (ZPE) of these three configurations did not differ by more than 2 cm−1 and the rotational constants, above all the B constant, depart by no more than 50 MHz within a particular functional and with and without dispersion corrections. The latter can clearly be observed in Table 1 where the different ground state energies are presented.
It is expected that Gibbs free energy contributions (ΔG) to the electronic energy using the conditions of the photoluminescence experiments (T = 85 K and P = 0.2 mbar) and the ion mobility measurements (T = 300 K and P = 0.923 mbar) will lead to relative stability results closer to what it would be expected experimentally. An estimate of ΔG was carried out via the module freeh of Turbomole. In a first approximation the harmonic approximation for vibrations and the rigid rotor model for the rotations were used in the calculation of the corresponding partition functions. The results obtained under the latter approach are presented in the column denoted as RR in Table 1. Additionally and considering that among the 264 vibrational frequencies of [Eu(PLN)4Ca]+, 12–17 have values below 100 cm−1 and 34–39 lie below 200 cm−1, a treatment of low-lying vibrational modes was carried out using the free-rotor approximation110 whose results are denoted as FR in Table 1.
In general, with the inclusion of the experimental conditions, the stability trend already observed continues to be confirmed, that is: stacked > half-stacked > open–open. The results obtained using the rigid-rotor model (RR) in comparison with those obtained using the free-rotor (FR) model seem to be slightly overestimated. Exceptions to the aforementioned bias are the results obtained with the TPSS-D4, and TPSSh-D4 methods where under the pressure and temperature conditions of both experiments the half-stacked structure is slightly more stable than the stacked structure, although only in the order of 5 kJ mol−1. Another exception is observed with the B3LYP-D3(BJ) method where under the experimental conditions of the ion mobility experiment the open–open structure is slightly more stable (only 2–3 kJ mol−1) than the stacked structure.
Regarding the uncertainties of the very small DFT energy differences presented, as well as the quality of the (harmonic) frequencies, the results from the the analysis of the Gibbs free energies at all conditions under consideration should be considered with caution. We therefore turn our attention in the next section to the comparison with the experimental evidence.
3.2 Comparison with the experimental information
The different structures resulting from most of the functionals (with and without dispersion corrections) employed in this work were compared with the experimental values arising from the ion mobility measurements (Fig. 5) and the photoluminescence spectrum (Fig. 6).The comparison of the He-converted cross-section of all structures obtained computationally with those obtained from the ion mobility measurement, suggest again (cf.Fig. 5) that only the open–open configuration is in agreement with the experimental information and both stacked and half-stacked structures can be clearly ruled out.
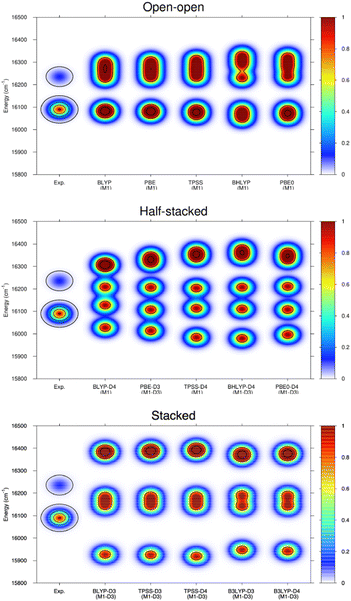
Ligand field theory is currently the only practical model to analyze and simulate the level structure of lanthanoid ions at an accuracy of about 50 cm−1. In the present work, the Stark splitting of the 7F2 level as well as the related transition energies (5D0 → 7F2 band) were computed to accomplish the comparison with experiment. The experimental broadening was simulated using Gaussian functions, whose widths are consistent with the experimental resolution and whose superposition provide the maxima displayed. As it can be observed in the few examples shown in Fig. 6, the open–open structure is consistently the one that is most in line with the experimental information both in energy range and number of splits, whereas the half-stacked and stacked structures progressively separate from the experimental profile regarding both features.
Thus, although the M1-D3 structures are energetically the most stable, they poorly agree with experiment, showing that at least in the present type of experimental conditions and resolution they are not present in the gas-phase measurements.
4 Discussion
4.1 Many-body dispersion effects
Being [Eu(PLN)4Ca]+ an open shell system with 458 electrons and requiring 2390 basis functions for calculations using the def2-TZVPP basis set, geometry optimizations using the RPA approach or wave-function-based methods such as MP2 or even CCSD(T) were not possible at this time. Therefore, in order to make an assessment of the performance of these two methods in this complex, the lanthanoid ion metal, Eu3+, was replaced by indium [In3+]. In3+ has a comparable size to Eu3+ with the advantage of having a closed-shell electronic structure with 444 electrons for the [In(PLN)4Ca]+ complex. In addition to the above mentioned computationally more demanding methods, a few DFT functionals were also tested for evaluating the comparability of the original complex with Eu3+ with that with In3+ (see Table 2 of ESI† and Section SIII). Regarding the results obtained with the RPA approach as well as with the MP2 wave-function-based method, the BP86/RPA calculations led to an open–open structure when the starting structure is M1. However, they result in a stacked structure when M1-D3 is the starting point in the optimization. Stacked or half-stacked configurations are obtained at the MP2 level.4.2 Benchmark study on the stacked PLN ligands
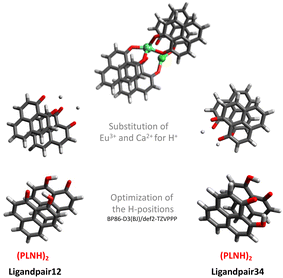
As the major structural change observed upon inclusion of dispersion corrections was the stacking of the PLN ligands in the M1-D3 structure, a more detailed analysis of the energy contributions in this configuration was accomplished (see Section IV of the ESI†). To investigate the problem more in depth, the first step was to select a model where dispersive interactions play a major role. Therefore, the Ca2+ and Eu3+ ions in the stacked M1-D3 structure obtained at the BP86-D3(BJ)/def2-TZVPP level were removed and a proton was added to each of the four ligand anions (PLN) resulting in two neutral dimers (PLNH)2, for which the positions of the added H atoms were optimized using the BP86-B3(BJ)/def2-TZVPP level of theory while leaving the rest of the structure fixed. Thus, two models were designed, which are denoted as Ligandpair12 and Ligandpair34 (see Fig. 7). The interaction energy of these model structures was based on the reaction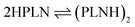 , and computed according to the following expressions:
, and computed according to the following expressions: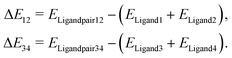 | (2) |
As is well known, the magnitude of the corrections due to dispersion effects depends on the functional used. Therefore, the next step to be considered was to contrast the dispersion interaction contributions obtained with different functionals corresponding to various rungs of Jacob's ladder.2 In addition, all results were compared with reference values obtained from wave-function based methods that cover electronic correlation in a more complete way. The most accurate method that could be used for this (still fairly large) molecular system is the CCSD(T) method. Moreover, the latter was corrected for the basis set incompleteness error via the F12 correction computed at the CCSD level of theory [CCSD(F12)].45,46 For consistency, in all cases the def2-TZVPP basis set was employed. However, in order to assess the adequacy of this basis set for the explicitly correlated calculations (F12), a comparative study between the def2-TZVPP and cc-pVTZ-F12111,112 basis sets employing various methods with and without F12 corrections was carried out on three different configurations of the benzene dimer [see Section V of the ESI]. In the case of Ligandpair12 and Ligandpair34, the tests carried out using second-order perturbation theory (MP2) with and without explicit F12 correlation show that the differences obtained with both basis sets amount to only 1 kJ mol−1, which is consistent with the results obtained for the benzene dimer. In addition, we compared MP2-F12 results obtained with the cc-pVTZ-F12 and cc-pVQZ-F12 basis sets111,112 to those obtained with the def2-TZVPP and found only a minor difference of 4–5 kJ mol−1. In view of these results, the use of the def2-TZVPP basis set was justified for the benchmark study on Ligandpair12 and Ligandpair34.
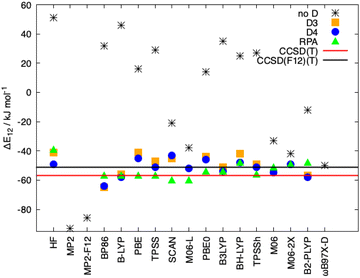
In Fig. 8, the interaction energies of the Ligandpair12 obtained with different functionals in comparison with the CCSD(T) and CCSD(F12)(T) reference values are displayed. (Similar results were obtained for Ligandpar34, see Fig. 6 of the ESI.†) The CCSD(F12)(T) reference values were obtained by adding to the CCSD(F12) energies the triples energy contribution from the CCSD(T) calculation. Without dispersion corrections, many interaction energies are fairly repulsive. Among all functionals without dispersion corrections, the highly parametrized Minnesota functionals, M06, M06-L and M06-2X,113 which show a certain ability to embrace medium-range electron correlation,114–116 as well as the SCAN functional and the double-hybrid B2PLYP achieve the best performance. As already mentioned in the literature,19,117 the inclusion of dispersion interactions using the atom-pairwise semi-classical models D3(BJ) and D4 remarkably improves the results for all of the functionals, yielding attractive overall interaction energies. It can be observed that precisely, and only, for the functional used as a starting point in the present work, that is, BP86, the D3(BJ) and D4 models overestimate (in an absolute sense) the dispersion interactions by about −14 kJ mol−1 and −8 kJ mol−1, respectively, in comparison with the CCSD(F12)(T) reference value. With the other functionals, the interaction energies for Ligandpair12 range between −41 and −57 kJ mol−1 while the CCSD(F12)(T) reference value is −51 kJ mol−1. As already mentioned, the atom-pairwise D3(BJ) model16 is based on the molecular geometry to estimate the intra- and intermolecular dispersion energies and therefore the changes in electron density are not considered in the dispersion coefficients. With the model termed D4,18,19,21,22 this last limitation is corrected with the incorporation of charge dependent dispersion coefficients. This improvement of the D4 model yields for the two cases studied here—two typical π–π-interaction systems—changes of only +2 to −7 kJ mol−1 for the dispersion energy, with the D4 energies slightly more attractive than those with D3(BJ). The good performance of the range-separated hybrid functional ωB97X-D63 that includes dispersion corrections following the DFT-D scheme is particular noteworthy, see Fig. 8.
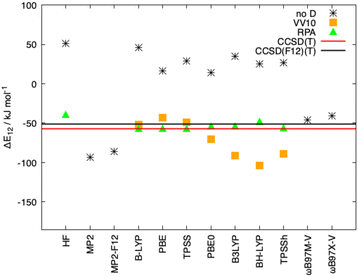
As mentioned in the introduction, the inclusion of long-range correlation effects can also be carried out through the incorporation of a fully nonlocal functional to the already established (exchange and correlation) functionals. The simpler and computationally cheaper nonlocal functional VV10 by Vydrov and van Voorhis was employed here, the results for Ligandpair12 using some of the functionals are: BLYP (−52 kJ mol−1), PBE (−43 kJ mol−1), and TPSS (−49 kJ mol−1). (see Fig. 9). These results are in agreement with previous studies in which it was found that, in general, nonlocal correlation functionals tend to overestimate the long-range dispersion interactions with errors ranging between 24% and 49%.118 Here we also stress the good performance of the range-separated hybrid functionals ωB97M-V and ωB97X-V of Head-Gordon et al.119 that include the non-local electron-density dependent correlation functional VV10. ωB97M-V and ωB97X-V show deviations of less than 5 kJ mol−1 from the CCSD(F12)(T) reference values. As it can be observed in Fig. 8 and 9, the wave-function based methods MP2 and MP2-F12 overestimate the interaction energy. Moreover, more complete accounts of electronic correlation in the framework of KS-DFT such as the random phase approximation (RPA) considerably improve, as expected, the predictions of the interaction energies in all cases.
4.3 Lanthanoid and alkaline earth metals coordination
Once the ligand–ligand interactions on the molecular configuration of [Eu(PLN)4Ca]+ had been analyzed, and in view of the structural results reported in the previous section, the next aspect to be considered is the coordination structure of the lanthanoid (Eu3+) and the alkaline earth metal (Ca2+) ions and their influence on the quantification of the London interaction energies. With its large coordination sphere, europium takes usually part in complexes with coordination numbers (CN) of 8, 9, or even higher, prompting coordination geometries of the dodecahedron, octahedron, square antiprism, cube, and bi- and tricapped trigonal prism types,120–127 and molecular point-group symmetries such as Oh, Td, D3d, D3h, and others. In the case of calcium the coordination number can significantly vary, from 9 to other much smaller, resulting in different coordination geometries.128 As mentioned in the previous sections, in case of the [Eu(PLN)4Ca]+ complex, the coordination number of the europium and calcium ions are 6 and 5, respectively, presenting consequently a certain distortion with respect to the ideal 6-coordination polyhedra129,130 and being close to an octahedral configuration.34 Having said this, in the framework of DFT-D, the concept of coordination numbers plays a significant role. In fact, the term “fractional coordination numbers” (fCN) was already introduced in the D3 model16 trying to differentiate between the diverse hybridization states of the atoms in a molecule and thus to account for different atom pair dispersion coefficients [CAB6, see eqn (1)], making them dependent on the “chemical” environment while remaining a purely geometric approximation. Just as this concept is defined,16 it leads to fCN values that are very similar to the conceptually defined CNs, as they are understood in coordination chemistry, in particular for molecules with atoms of the first and second rows. Typical values are 2, 3, and 4 for the carbon atom with sp, sp2 and sp3 hybridizations, respectively. However, the fCN tended to be very large and different from integer values in the case of metallic systems.19 With the D4 model, the calculation of the fCNs is slightly modified by including in their evaluation the atomic electronegativities of the two atoms involved in a bonding pair and by recasting the fCNs such that they roughly correspond to the Wiberg bond orders131 for single bonds. In addition to this, some adjustments are made in the Gaussian function weighting procedure. All this leads to a better description of the bonding environment and the hybridization type.18,19 Using the DFT-D316 and DFT-D418,19 programs, values for the fCN of europium and calcium in the [Eu(PLN)4Ca]+ complex were calculated for different DFT functionals and compared with the chemical coordination described in the first paragraph of this section (Table 4 of the ESI†). Values for the total dispersion energy of the complex as well as that between the Ca–Eu metal pair are also included in Table 4 of the ESI†. To point out that in the case of the DFT-D4 model, the electric charges are independent of the functional used and calculated following a classical model based on the electronegativity equilibration of Gaussian-type charge densities.19,132 In general, in the case of atoms of the first and second row and in comparison with the chemical coordination numbers, the D3(BJ) model tends to slightly overestimate the fCN values, whereas the D4 model slightly underestimates them. In the case of the two metals, the differences are quantitatively more relevant. For all the considered geometries, the D3(BJ) model estimates the fCN for europium close to 8 while that for calcium close to 7. In the case of the D4 model, the fCN is around 5 for the two metals, which is in good agreement with the chemical coordination number for calcium but somewhat small for europium. For the half-stacked and stacked structures, the fCN tends to be slightly larger than in the case of the open-open structures, especially in the case of calcium. As expected, with the model D3(BJ) the dispersion energy between the two metals is between 3 and 4 times larger than with the model D4, but in any case this energy does not represent more than about 1% of the total dispersion energy. The type of structure, open–open, half-stacked, or stacked, does not establish a difference in the dispersion interaction between metals. The total dispersion energy is in general greater in absolute terms with the D4 model except for the results obtained with the BP86 functional where |Edisp-D3(BJ)(Total)|>|Edisp-D4(Total)| in the case of stacked structures.Summarizing, it can be said that the D4 model quantifies the fCN values much more closely to the chemical CNs than the D3 model. However, this does not mean necessarily that the molecular structures resulting from the optimization, in view of the results, are more plausible with the D4 model than with the D3(BJ) model.
5 Conclusions and summary
The influence of non-bonded interactions on the structure of Eu3+ heterodimetallic complexes with four ligands, i.e., europium(III) 9-oxo-phenalen-1-one coordination complex [Eu(PLN)4Ca]+ was studied. The BP86-D3(BJ) and BP86-D4 methods were found to overestimate the energy of the π–π interaction between the PLN ligands in absolute terms. Although the D4 model takes into account not only the molecular geometry but also the atomic partial charges and provides values for the “fractional coordination numbers” closer to the conceptional coordination numbers of the metals, the optimized structures obtained with BP86-D4, BLYP-D4, TPSS-D4, and TPSSh-D4 are not in better agreement with the experimental evidence. For the cases analyzed, the nonlocal VV10 approximation leads to structural results (half-stacked or stacked configuration) that do not concur with the photoluminescence and ion mobility data. The three tested van der Waals functionals conclude with structures that are in agreement with the experimental findings. Explorations with the In(III)-model complex, that is, [In(PLN4Ca]+ indicate that the results with the RPA and MP2 can lead to qualitatively wrong results.In summary, in this work a molecular example was found where the evaluation of non-covalent interactions was not straightforward. Thus, a litmus test for the balanced description of dispersion interactions and coordination chemistry was revealed that may become a helpful benchmark system for future method developments in the framework of DFT as well as improvements in the context of computationally efficient wave-function based methods. Based on the findings of the comparison with the two experiments in Section 3.2, the following simple litmus test is proposed: for a given method two geometry optimizations are carried out starting from BP86/def2-TZVPP and BP86-D3(BJ)/def2-TZVPP optimized geometries (see ESI†). A method passes the test if at least one structure optimization yields an open–open structure. Of course the test cannot provide any information if a method passes or fails for the right reasons. Of the methods under study BP86-D3(BJ), BP86-D4, BLYP-D4, BLYP-VV10, PBE-VV10, TPSS-D4, TPSS-VV10, and TPSSh-D4 fail the test, because the dominant species found in two experiments cannot be reproduced even starting from a structure that is consistent with both experimental findings. The proposed litmus test is passed by all other methods employed in this work, of these BP86, BLYP, PBE, TPSS, B3LYP, BHLYP, TPSSh, PBE0, optB88-vdW, BEEF-vdW, and mBEEF-vdW yield only open-open structures.
The system under study represents a difficult balancing act between dispersion interactions and metal coordination in which pairwise semi-classical approaches like the D-models can lead to misleading results as previously observed, for example, in the study of cryogenic ion vibrational predissociation (CIVP),133 bond dissociation energies134 as well as energies,135 prediction of vibrational spectra136 and interconversion barriers.137
We finally note that as shown in this work the inclusion of dispersion corrections, at least via the D3(BJ), D4, and VV10 approaches, although decisive for the description of the interaction energy between the stacked ligandpairs, represents only a necessary but not sufficient condition for an unambiguous prediction of the molecular structures. Therefore, including dispersion corrections of this kind is not always the preferred option when optimizing geometries with DFT. Special attention must be paid to cases where the dispersion corrections influence results significantly.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
WK and JVQ gratefully acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) through Priority Program 1807 “Control of London dispersion interactions in molecular chemistry”, project KL 721/5-2. J.-F. G. acknowledges support from the Hector Fellow Academy (HFA) while part of the group of Professor Manfred M. Kappes. MEH acknowledges support by the Bundesministerium für Bildung und Forschung (BMBF) through the Helmholtz research program “Materials Systems Engineering” (MSE).References
- W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab initio molecular orbital Theory, John Wiley and Sons, New York, 1986, p. 5 Search PubMed.
- J. P. Perdew, A. Rizsinszky, J. Tao, V. N. Staroverov, G. E. Scuseria and G. I. Csonka, J. Chem. Phys., 2005, 123, 062201 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef CAS.
- A. J. Cohne, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289 CrossRef PubMed.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, Phys. Rev. Lett., 2009, 103, 063004 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2009, 130, 104105 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 062708 CrossRef.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 132, 164113 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- M. Bursch, A. Hansen, P. Pracht, J. T. Kohn and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 287 RSC.
- S. Spicher, E. Caldeweyher, A. Hansen and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 11635 RSC.
- E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499 RSC.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439 CrossRef CAS PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274 CrossRef CAS PubMed.
- S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741 RSC.
- T. Schwabe, S. Grimme and J.-P. Djukic, J. Am. Chem. Soc., 2009, 131, 14156 CrossRef CAS PubMed.
- S. Grimme and J.-P. Djukic, Inorg. Chem., 2011, 50, 2619 CrossRef CAS PubMed.
- M. Bursch, A. Hansen and S. Grimme, Inorg. Chem., 2017, 56, 12485 CrossRef CAS PubMed.
- M. Bogokeski, L. Vogt-Maranto, M. E. Tuckerman, K.-B. Müller and K. Burke, Nat. Commun., 2020, 11, 5223 CrossRef PubMed.
- J. Chmela, J.-F. Greisch, M. E. Harding, W. Klopper, M. M. Kappes and D. Schooss, J. Phys. Chem. A, 2018, 122, 2461 CrossRef CAS PubMed.
- J.-F. Greisch, M. E. Harding, B. Schafer, M. Rotter, M. Ruben, W. Klopper, M. M. Kappes and D. Schooss, J. Phys. Chem. A, 2014, 118, 94 CrossRef CAS PubMed.
- J.-F. Greisch, M. E. Harding, B. Schäfer, M. Ruben, W. Klopper, M. M. Kappes and D. Schooss, J. Phys. Chem. Lett., 2014, 5, 1727 CrossRef CAS PubMed.
- J.-F. Greisch, J. Chmela, M. E. Harding, W. Klopper, M. M. Kappes and D. Schooss, Inorg. Chem., 2016, 55, 3316 CrossRef CAS PubMed.
- J.-F. Greisch, J. Chmela, M. E. Harding, D. Wunderlich, B. Schäfer, M. Ruben, W. Klopper, D. Schooss and M. M. Kappes, Phys. Chem. Chem. Phys., 2017, 19, 6105 RSC.
- R. C. Haddon, R. Rayford and A. M. Hirani, J. Org. Chem., 1981, 46, 4587 CrossRef CAS.
- V. E. Bondybey, R. C. Haddon and J. H. English, J. Chem. Phys., 1984, 80, 5432 CrossRef CAS.
- R. Van Deun, P. Nockemann, P. Fias, K. Van Hecke, L. Van Meervelt and K. Binnemans, Chem. Commun., 2005, 590 RSC.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- R. Gulde, P. Pollak and F. Weigend, J. Chem. Theory Comput., 2012, 8, 4062 CrossRef CAS PubMed.
- M. Zhou, H. Tong, X. Wei and D. Liu, J. Organomet. Chem., 2007, 692, 5195 CrossRef CAS.
- R. Fernández-Galán, J. A. Navarro, F. Carrillo-Hermosilla, A. Antiñolo, I. López-Solera and E. Villaseñor, Aust. J. Chem., 2014, 67, 1063 CrossRef.
- J. Chmela, Theoretical optical spectroscopy of polynuclear transition metal and lanthanoid complexes, PhD Thesis, Karlsruher Insitut für Technologie (KIT), Karlsruhe, 2016, p. 56 Search PubMed.
- K. Raghavachari, G. Trucks, J. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- H. Fliegl, W. Klopper and C. Hättig, J. Chem. Phys., 2005, 122, 084107 CrossRef PubMed.
- W. Klopper, R. A. Bachorz, C. Hättig and D. P. Tew, Theor. Chem. Acc., 2010, 126, 289 Search PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4 CrossRef PubMed.
- TURBOMOLE V 7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866 CrossRef CAS PubMed.
- D. R. Klimeš, J. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- K. T. Lundgaard, J. Wellendorff, J. Voss, K. W. Jacobsen and T. Bligaard, e, 2016, 93, 235162 CrossRef.
- S. Kurth and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 10461 CrossRef CAS.
- Z. Yan, J. P. Perdew and S. Kurth, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 16430 CrossRef CAS.
- F. Furche, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195120 CrossRef.
- M. Fuchs and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235109 CrossRef.
- F. Furche and T. Van Voorhis, J. Chem. Phys., 2005, 12, 164106 CrossRef PubMed.
- H. Eshuis, J. Yarkony and F. Furche, J. Chem. Phys., 2010, 132, 234114 CrossRef PubMed.
- H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084 Search PubMed.
- A. M. Burow, J. E. Bates, F. Furche and H. Eshuis, J. Chem. Theory Comput., 2014, 10, 180 CrossRef CAS PubMed.
- G. P. Chen, V. K. Voora, M. M. Agee, S. G. Balasubramani and F. Furche, Annu. Rev. Phys. Chem., 2017, 68, 421 CrossRef CAS PubMed.
- G. E. Scuseria, T. M. Henderson and D. C. Sorensen, J. Chem. Phys., 2008, 129, 231101 CrossRef PubMed.
- G. Jansen, R.-F. Liu and J. G. Ángyán, J. Chem. Phys., 2010, 133, 154106 CrossRef PubMed.
- D. Lu, Y. Li, D. Rocca and G. Galli, Phys. Rev. Lett., 2009, 102, 206411 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 619 CrossRef.
- R. A. Bachorz, F. A. Bischoff, A. Glöβ, C. Hättig, S. Höfener, W. Klopper and D. P. Tew, J. Comput. Chem., 2011, 32, 2492 CrossRef CAS PubMed.
- C.-K. Duan and P. A. Tanner, J. Phys. Chem. A, 2010, 114, 6055 CrossRef CAS PubMed.
- C. Holzer, A. M. Wernbacher, J. M. Senekowitsch, K. Gatterer and A.-M. Kelterer, J. Phys. Chem. A, 2014, 118, 11499 CrossRef CAS PubMed.
- W. T. Carnall, G. L. Goodman, K. Rajnak and R. S. Rana, J. Chem. Phys., 1989, 90, 3443 CrossRef CAS.
- D. J. Newman, Adv. Phys., 1971, 20, 197 CrossRef CAS.
- K. Rajnak and B. G. Wybourne, Phys. Rev., 1963, 132, 280 CrossRef CAS.
- K. Rajnak and B. G. Wybourne, J. Chem. Phys., 1964, 41, 565 CrossRef CAS.
- G. Racah, Phys. Rev., 1949, 76, 1352 CrossRef CAS.
- G. Racah, Phys. Rev., 1942, 61, 186 CrossRef CAS.
- G. Racah, Phys. Rev., 1942, 62, 438 CrossRef CAS.
- G. Racah, Phys. Rev., 1943, 63, 367 CrossRef CAS.
- J. P. Elliott, B. R. Judd and W. A. Runciman, Proc. R. Soc. Lond. A, 1957, 240, 509 CAS.
- M. Rotter, J. Magn. Magn. Mater., 2004, 272–276, E481 CrossRef CAS.
- M. Rotter, M. D. Le, A. T. Boothroyd and J. A. Blanco, J. Phys.: Condens. Matter, 2012, 24, 213201 CrossRef PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- M. Kordel, D. Schooss, C. Neiss, L. Walter and M. M. Kappes, J. Phys. Chem., 2010, 114, 5509 CrossRef CAS PubMed.
- G. A. Eiceman and Z. Karpas, Ion mobility spectrometry, Taylor & Francis, Bocan Raton, 2005, p. 5 Search PubMed.
- H. Borsdorf and G. A. Eiceman, Appl. Spectrosc. Rev., 2006, 41, 323 CrossRef CAS.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082 CrossRef CAS.
- A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 1996, 261, 86 CrossRef CAS.
- I. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Anal. Chem., 2012, 84, 1026 CrossRef CAS PubMed.
- C. Larriba-Andaluz and C. J. Hogan, J. Chem. Phys., 2014, 141, 194107 CrossRef PubMed.
- C. Larriba and C. J. Hogan, J. Phys. Chem. A, 2013, 19, 3887 CrossRef PubMed.
- C. Larriba and C. J. Hogan, J. Comput. Phys., 2013, 251, 344 CrossRef CAS.
- M. F. Bush, I. D. G. Campuzano and C. V. Robinson, Anal. Chem., 2012, 84, 7124 CrossRef CAS PubMed.
- The geometry optimizations with the functional M06, for both starting geometries, as well as with the range-separated hybrid ωB97M-V and ωB97X-D, for the starting geometry M1-D3, did not converge. In the case of the highly parametrized Minnesota functional, after approximately 600 iteration cycles, only a convergence 10−3Eh/a0 was reached for the Cartesian gradient. Regarding the range-separated hybrid functionals ωb97M-V and ωB97X-D, for example the geometry optimization of the M1-D3 complex at the ωB97X-D/def2-TZVPP level reached convergence of only 10−3Eh/a0 for the Cartesian gradient norm after approximately 900 cycles. The 900 cycles required 10 months of computer time using 8 cores of an Intel(R) Xeon(R) Gold 6254@3.10GHz CPU. On the contrary, using the the starting geometry M1 the convergence behavior of these two functionals (ωb97M-V and ωB97X-D) is adequate resulting in a final open–open configuration.
- For these van der Waals functionals the convergence threshold for the Cartesian gradient was 10−4Eh/a0.
- Analytical first and second derivatives of the potential energy were used in all cases except for the BLYP-VV10, PBE-VV10, TPSS-VV10, optB88-vdW, BEEF-vdW and mBEEF-vdW functional for which a numerical differentiation was employed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955 CrossRef CAS PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- J. G. Hill and K. A. Peterson, Phys. Chem. Chem. Phys., 2010, 12, 10460 RSC.
- Y. Zhao and D. G. Truhlar, Chem. Phys. Lett., 2011, 502, 1 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289 CrossRef CAS PubMed.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105 CrossRef CAS PubMed.
- M. Shahbaz and K. Szalewicz, Theor. Chem. Acc., 2019, 138, 25 Search PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- M. G. B. Drew, Coord. Chem. Rev., 1977, 24, 179 CrossRef CAS.
- P. P. Gawryszewska, L. Jerzykiewicz, P. Sobota and J. Legendziewicz, J. Alloys Compd., 2000, 300, 275 CrossRef.
- R. Van Deun, P. Nockemann, P. Fias, K. Van Hecke, L. Van Meervelt and K. Binnemans, Chem. Commun., 2005, 590 RSC.
- J. G. Santos, J. D. L. Dutra, S. A. Junior, R. O. Freire and N. B. da Costa Junior, J. Phys. Chem. A, 2012, 116, 4318 CrossRef CAS PubMed.
- J. Xi, J.-H. Lan, G.-W. Lu, Y.-L. Zhao, Z.-F. Chai and W.-Q. Shi, Mol. Simul., 2014, 40, 379 CrossRef CAS.
- D. Xian, W. Zhou, J. Wang, D. Pan, X. Li, Y. Li, Y. Shi, W. Wu, Z. Tan and C. Liu, Dalton Trans., 2021, 50, 9388 RSC.
- K. Schnaars, M. Kaneko and K. Fujisawa, Inorg. Chem., 2021, 60, 2477 CrossRef CAS PubMed.
- D. L. Kepert, in Progress in inorganic chemistry, Vol. 24, ed. S. Lippard, John Wiley & Sons, New York, 1978, pp. 179–251 Search PubMed.
- N. S. Poonia and A. V. Bajaj, Chem. Rev., 1979, 79, 389 CrossRef CAS.
- E. L. Muetterties and L. J. Guggenberger, J. Am. Chem. Soc., 1974, 96, 1748 CrossRef CAS.
- J. Xu, E. Radkov, M. Ziegler and K. N. Raymond, Inorg. Chem., 2000, 39, 4156 CrossRef CAS PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083 CrossRef CAS.
- S. A. Ghasemi, A. Hofsteller, S. Saha and S. Goedecker, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045131 CrossRef.
- A. Tsybizova, L. Fritsche, V. Gorbachev, L. Miloglyadova and P. Chen, J. Chem. Phys., 2019, 151, 234304 CrossRef PubMed.
- M. Bot, V. Gorbachev, A. Tsybizova and P. Chen, J. Phys. Chem. A, 2020, 124, 8692 CrossRef CAS PubMed.
- D. Bernhard, F. Dietrich, M. Fatima, C. Pérez, H. C. Gottschalk, A. Wuttke, R. A. Mata, M. A. Suhm, M. Schnell and M. Gerhards, Beilstein J. Org. Chem., 2018, 14, 1642 CrossRef CAS PubMed.
- A. Nejad, E. Meyer and M. A. Suhm, J. Phys. Chem. Lett., 2020, 11, 5228 CrossRef CAS PubMed.
- C. Zimmermann, M. Lange and M. A. Suhm, Molecules, 2021, 26, 4883 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01414a |
| This journal is © the Owner Societies 2022 |