Solid solutions based on BaZn₂Si₂O₇ with thermal expansions from negative to highly positive – a review

Abstract

The compound BaZn₂Si₂O₇ shows a transition from a monoclinic low temperature phase to an orthorhombic high temperature phase at 280 °C which is accompanied by an increase in the volume of 3.3%. The temperature of the phase transition can be shifted to higher temperature by a replacement of Zn²⁺ by Mg²⁺ or the divalent transition metal cations, Mn²⁺, Co²⁺, Ni²⁺ or Cu²⁺ as well as by the replacement of Si⁴⁺ by Ge⁴⁺. By contrast, the replacement of Ba²⁺ by Sr²⁺ leads to the shift of the phase transition to lower temperatures. The coefficient of thermal expansion of the low temperature phase is exceptionally high and in the range from 10 to 15 10⁻⁶ K⁻¹, while that of the high temperature phase is small or even negative. The reason of the latter effect is a rotation of bridged ZnO₄ tetrahedra in opposite directions. This results in a strongly negative thermal expansion of the b-axis, while the expansion of the a- and c-axes are positive. Although melts of the stoichiometric compounds do not build a continuous network, glass formation can be achieved by the addition nucleation inhibitors, such as ZrO₂, Al₂O₃ or La₂O₃ or an excess of SiO₂. The quenched glasses crystallize at the surface while bulk crystallization is not observed. This changes if noble metals or higher concentrations of ZrO₂, WO₃ or P₂O₅ are added to the glass, then also bulk crystallization is possible. Homogeneously crystallized glass ceramics can also be obtained, by sinter crystallization of powdered glass or using sol–gel derived crystalline powders. Adjusting the composition of the respective solid solutions enables to tailor the coefficient of thermal expansion from negative to highly positive values.

---

1. Introduction

The compound BaZn₂Si₂O₇ shows a transition from a low to a high temperature phase at around 280 °C, accompanied by a steep increase in volume of 3.3%.¹ The low temperature phase shows a high coefficient of thermal expansion (CTE), which is in the range from 10–15 × 10⁻⁶ K⁻¹, while the CTE of the high temperature phase is very low or even negative.² The stoichiometric composition BaZn₂Si₂O₇ does not form a glass, however, the addition of some SiO₂ (or other oxides) leads to glass formation. From such a glass, the BaZn₂Si₂O₇ based phases can be crystallised by thermal treatment.^3,4

During the phase transformation, the crystal structure changes from monoclinic (<280 °C) to orthorhombic (>280 °C). The monoclinic low temperature phase (LT-phase) possesses a high (CTE) of 16 × 10⁻⁶ K⁻¹, while the CTE of the high temperature phase (HT-phase) is small or even negative.¹ In BaZn₂Si₂O₇, a total or partial replacement of Zn²⁺ by other divalent cations shifts the phase transition temperature to higher values.^2,5 This enables the preparation of materials with exceptionally high CTEs, also in the range from room temperature to 1000 °C, which are required for crystallizing glass seals to join metals, e.g. for high temperature solid oxide fuel cells (SOFC) or other high temperature reactors.^6–8

Otherwise, a partial substitution of Ba²⁺ by Sr²⁺ shifts the phase transition temperatures to lower values, even below room temperature.⁹ This enables the preparation of materials with a low thermal expansion.¹⁰ Such materials, however, based on lithium aluminosilicates and not on Ba_1−xSr_xZn₂Si₂O₇, are nowadays used for a large variety of applications, such as cook top panels, telescope mirrors, furnace windows and various optical devices.^11–13

Negative thermal expansion at room temperature and higher is an uncommon physical property, since most materials expand with increasing temperature. The most common materials with zero thermal expansion are silicates based on lithium aluminosilicates, such as beta-quartz and beta-eucryptite.¹⁴ These phases can be crystallized from glasses and enable the fabrication of large ceramic specimens, e.g. telescope mirror blanks with diameters of several meters.¹⁵ Other phases with negative thermal expansion which can be crystallized from glasses are MB₂Al₂O₇ with M = Ba, Ca, Sr.^16–18 Besides, ZrW₂O₈ and materials derived hereof are among the most commonly known negative thermal expansion phases.^19,20 However, they cannot be crystallized from glasses. ZrO₂ as well as WO₃ do not act as glass formers. To achieve glass formations, high quantities of other glass formers such as B₂O₃ or SiO₂ are necessary. If from such glasses, ZrW₂O₈ might be crystallized (although not described in the literature), the high quantities of residual glass phase cannot lead to zero thermal expansion.

In the following, the formation of solid solutions based on BaZn₂Si₂O₇ is described. The replacement of Ba²⁺, Zn²⁺ or Si⁴⁺ by other ions strongly affects the temperature attributed to the phase transition from the low to the high temperature phase and hence also the CTE. It is further described, how bulk materials based on these solid solutions can be prepared by sintering or by glass crystallization and how the CTE can be tailored.

2. Crystal structure and thermal expansion of pure BaZn₂Si₂O₇

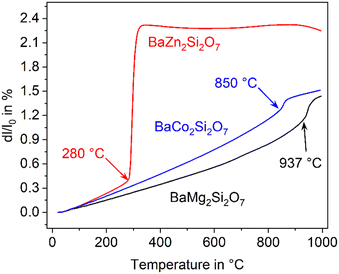
The compound BaZn₂Si₂O₇ has a high coefficient of thermal expansion up to a temperature of 280 °C. The attributed LT-phase is monoclinic with the space group C2/c.¹ Then, a transition to a high temperature phase, with the orthorhombic space group Ccm2₁, occurs. The thermal expansion behaviour is shown in Fig. 1. The coefficient of thermal expansion (CTE) of the LT-phase is exceptionally high and in the range of 10–15 × 10⁻⁶ K⁻¹. The phase transition is accompanied by a steep increase in volume of around 3.3%.¹ The HT-phase has a small or even negative CTE. Fig. 1 shows a comparison of results from dilatometry using a sintered powder compact and high-temperature X-ray powder diffraction (HT-XRD). To plot both data sets on one axis, the volumes from HT-XRD were converted to corresponding changes in length by taking the cube root. The thermal expansion measured by dilatometry and XRD are almost identical below as well as above the phase transition. The height of the volume jump, however, is different. In dilatometric measurements of compressed and sintered powders, the height of this jump cannot be exactly reproduced because the compact sample is damaged during phase transition.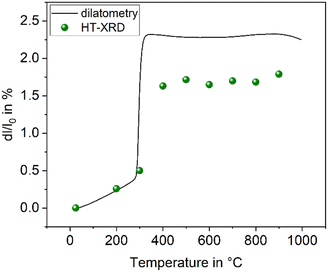

Fig. 1 Thermal expansion of BaZn₂Si₂O₇. Redrawn based on ref. 5.

Fig. 2 shows the crystal structures of LT- and HT-phase, respectively. Both structures are fairly similar: silicon and zinc are both fourfold coordinated and, in both cases, two silicon tetrahedra are bridged by oxygen. ZnO₄-tetrahedra form chains aligned along the crystallographic c-axis. The Ba²⁺ ions are located in channels and possess a quadratic pyramidal coordination where the Ba–O bond length of the apex is notably longer. Please note that the monoclinic and the orthorhombic unit cells are defined in a different manner and hence it is favourable to compare different planes and directions. For all subsequent descriptions, the crystallographic directions have been renamed. This facilitates to compare the HT- and LT-phases as well as their crystallographic directions. The directions were defined according to Fig. 2.

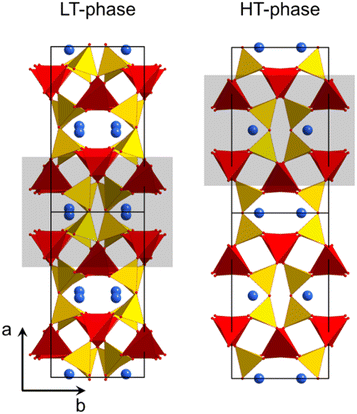Fig. 2 Crystal structure of LT- and HT-BaZn₂Si₂O₇.^1,21 The grey rectangles mark similar structural units, which convert into each other during phase transition.

In Fig. 3, the changes in the lattice constants of both the low and the high temperature phase are shown. From room temperature to 280 °C, the lengths of a- and b-axes increase strongly, while the CTE of the c-axis is smaller. The phase transition is clearly seen and accompanied by an increase of the a- and b-axes by 1.3 and 3.6%, respectively, while the c-axis contracts by around 1.4%. More notably is the behaviour above the phase transition temperature: while the lengths of a- and c-axes increase as expected, the b-axis contracts, i.e., the CTE in the direction of the b-axis is negative.

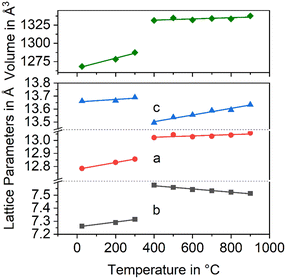Fig. 3 Lattice constants of BaZn₂Si₂O₇ as a function of temperature. Data taken from ref. 2.

3. Solid solutions based on BaZn₂Si₂O₇

3.1 Substitution of Zn²⁺ by divalent metal cations

In the literature, the total replacements of Zn²⁺ by Mg²⁺ or Co²⁺ and also, a partial replacement of Zn²⁺ by Ni²⁺ were reported.^2,5,22 In any case, a substitution of Zn²⁺ results in a shift of the phase transition to higher temperature. The thermal expansions of the end members of the solid solution series containing Zn²⁺, Co²⁺ and Mg²⁺ are displayed in Fig. 4. In the case of the dilatometry results presented in Fig. 4, the phase transition changes the microstructure of the specimens considerably and the data allow only a purely qualitative consideration. Especially in the case of BaZn₂Si₂O₇, very different dilatometric curves can be found in the literature (see ref. 2 and 5), which is due to the formation of cracks during phase transition. BaZn_2−yM_ySi₂O₇ solid solutions show qualitatively the same behaviour, however, the phase transition is continuously shifted to higher temperatures with decreasing Zn²⁺ concentration as shown in Fig. 5. Simultaneously, the volume effect, which runs parallel to the phase transition decreases and is by far not as high as for BaZn₂Si₂O₇.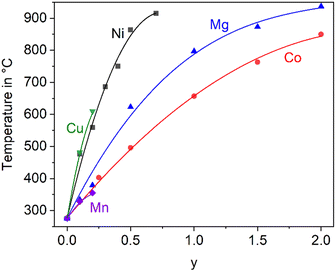

Fig. 4 Comparison of the dilatometric thermal expansion of BaZn₂Si₂O₇, BaCo₂Si₂O₇, and BaMg₂Si₂O₇.

Fig. 5 Temperature of the phase transition for solid solutions of BaZn_2−yM_ySi₂O₇ with M = Co, Cu, Mg, Mn, and Ni.^2,5,22,23 The lines are drawn as a guide for the eyes.

Mg²⁺ and Co²⁺ may totally replace Zn²⁺ without changing the crystal structure, while in the case of Cu²⁺ and Ni²⁺, a 100% substitution is not possible. In the literature, an end member BaCu₂Si₂O₇ is reported, however, the crystal structure is different from the BaZn₂Si₂O₇ phases.²⁴ A complete substitution of Zn²⁺ by Mn²⁺ is also reported in ref. 25, however, phase transition temperatures above room temperature are only given for a lower degree of substitution (compare Fig. 5).

3.2 Substitution of Ba²⁺ by Sr²⁺

The substitution of Ba²⁺ by Sr²⁺ has the opposite effect as the Zn²⁺ replacement. If only 5% of Ba²⁺ are replaced by Sr²⁺, the phase transition temperature decreases notably. This is shown in Fig. 6 for different replacements of Ba²⁺ against Sr²⁺. Already if 10% of Ba²⁺ are replaced by Sr²⁺, the phase transition temperature cannot be observed above room temperature. It is not exactly known whether the phase transitions occur at temperatures below room temperature, however, if 20% Ba²⁺ are substituted against Sr²⁺, the high temperature phase is still stable at 100 K.²⁶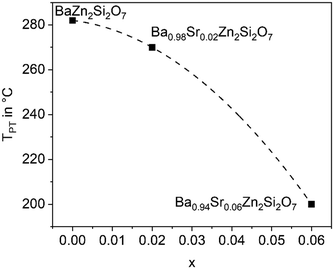

Fig. 6 Phase transition temperature (dilatometry) as a function of x in Ba_1−xSr_xZn₂Si₂O₇ solid solutions.

Fig. 7 presents the thermal expansion of Ba_1−xSr_xZn₂Si₂O₇ samples for various x-values. The CTEs are small up to a temperature of 400 °C and then increase. A smaller degree of substitution is favourable to achieve a negative CTE. Fig. 8 shows the lattice parameters of the Ba_0.6Sr_0.4Zn₂Si₂O₇ solid solution as a function of the temperature. It is shown that the a-axis as well as the c-axis expand during heating, while the b-axis strongly contracts. The volume of the unit cell decreases up to a temperature of 400 °C and then increases again.

Fig. 7 Thermal expansion of Ba_1−xSr_xZn₂Si₂O₇ as a function of the temperature for various x-values.

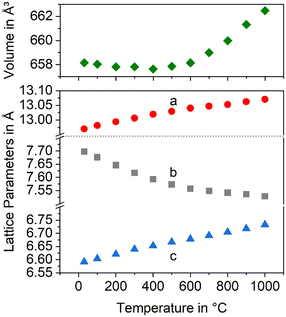Fig. 8 Lattice constants and unit cell volume of the Ba_0.6Sr_0.4Zn₂Si₂O₇ solid solutions as a function of temperature.

To study the origin of the negative CTE, single crystal X-ray diffraction was performed at temperatures of 220, 293 and 353 K. Fig. 9 shows a part of the network formed by ZnO₄ (red) and SiO₄ tetrahedra (yellow). The crystallographic c-axis is perpendicular to the drawing plane, while the b-axis is arranged vertically. With increasing temperature, two bridged ZnO₄ tetrahedra rotate in opposite directions. Simultaneously, the ZnO₄- and SiO₄-units, deform. This leads to a shortening of the crystallographic b-axis.²⁷ These experimental observations were confirmed by simulations using density functional theory.²⁷

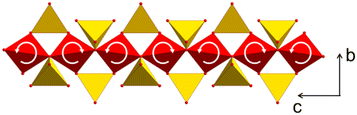Fig. 9 Part of the network formed by ZnO₄ (red) and SiO₄ tetrahedra (yellow). With increasing temperature, ZnO₄ tetrahedra rotate, which results in a stretching of the ZnO₄-chain in the direction of the c-axis and a shortening in the b-direction. Redrawn from ref. 9.

The phase transition temperatures as a function of the chemical compositions were calculated by density functional theory simulations.²⁸ In Table 1, the calculated phase transition temperatures as well as those determined by dilatometry or DSC are summarized. The differences in the phase transition temperatures can be explained by the higher inaccuracy of simulated phase transition temperatures.

Table 1 Experimentally determined and calculated phase transition temperatures of various phases in the system Ba_1−xSr_xZn_2−2yMg_2ySi₂O₇ (values taken from ref. 2 and 28)

Chemical composition (mol%)	T t experimental (°C)	T t calculated (°C)
a Determined by DSC. b Determined by dilatometry. c Calculated values.
BaZn2Si2O7	277^a	222^c
BaZn1.5Mg0.5Si2O7	623^a	567^c
BaZnMgSi2O7	797^a	775^c
BaZn0.5Mg1.5Si2O7	873^a	980^c
BaMg2Si2O7	937^a	869^c
Ba0.5Sr0.5ZnMgSi2O7	392^a	274^c
Ba0.75Sr0.25Zn0.5Mg1.5Si2O7	588^b	548^c

---

3.3 Substitution of Ba²⁺ by Sr²⁺ and Zn²⁺ by other divalent cations

In analogy to the replacement of Zn²⁺ in the BaZn₂Si₂O₇ lattice, also in the Ba_1−xSr_xZn₂Si₂O₇ lattice, Zn²⁺ can be substituted by other divalent cations. Generally, Zn²⁺ (ionic radius from ref. 29: 74 pm) can be substituted in the Ba_1−xSr_xZn₂Si₂O₇ lattice by cations with similar ionic radii. The latter should be in the range from 80 pm (Mn²⁺) to 92 pm (Co²⁺).

In Table 2, the mean CTEs from HT-XRD of different compositions are summarized. The pure Zn-compound has a CTE of 0.7 × 10⁻⁶ K⁻¹. This value decreases when Zn²⁺ is substituted. A higher degree of substitution with one and the same element leads to smaller CTEs. If the degree of substitution is kept constant, the lowest CTE is observed if Zn²⁺ is substituted by ions, which strongly shift the phase transition temperature. In Fig. 5, the effect of substitution on the phase transition temperature is shown. Ni²⁺ and Cu²⁺ have a larger effect than equimolar concentrations of the other ions and their incorporations lead to smallest CTEs. The CTE is lowest, if the degree of substitution is slightly below the limit which leads to the formation of the LT-phase with high thermal expansion.

Table 2 Mean CTEs for the temperature range from 30 to 300 °C for Ba_0.5Sr_0.5Zn_1.9M_0.1Si₂O₇ with different elements M (data taken from ref. 23)

Element M	CTE30–300°C in [10^−6 K^−1]
Mg	0.5
Co	0.1
Mn	−0.3
Ni	−1.6
Cu	−2.0

---

3.4 Substitution of Si⁴⁺ by Ge⁴⁺

In a BaZn₂Si₂O₇ lattice, up to 75% Si⁴⁺ can be replaced by Ge⁴⁺ without changing the phase while larger Ge⁴⁺-concentrations lead to the formation of secondary phases, such as Zn₂GeO₄.^30,31 As shown in Fig. 10, the temperature of the phase transition increases linearly with increasing Ge concentration from 280 °C for BaZn₂Si₂O₇ to around 700 °C for BaZn₂Si_0.5Ge_1.5O₇ an hence, in analogy to the substitution of Zn²⁺ by other divalent cations, the monoclinic low temperature phase is increasingly stabilized.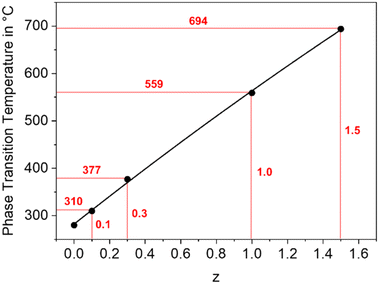

Fig. 10 Phase transition temperature of BaZn₂Si_2−zGe_zO₇ solid solutions as a function of the Ge concentration.

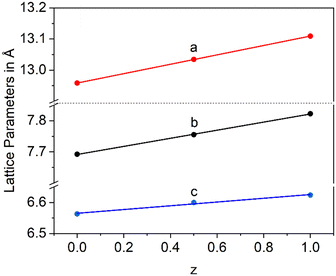
In a Ba_1−xSr_xZn₂Si₂O₇ solid solution, equimolar replacement of 50% of Si⁴⁺ by Ge⁴⁺, still results in the formation of the orthorhombic high temperature phase. As shown in Fig. 11, the unit cell parameters increase linearly with the degree of substitution.

Fig. 11 Lattice parameters of Ba_0.5Sr_0.5Zn₂Si_2−zGe_zO₇ solid solutions with z = 0, 0.5 and 1.

Fig. 12 shows lattice parameters of the orthorhombic high temperature phase with the composition Ba_0.5Sr_0.5Zn₂SiGeO₇. In analogy to Ba_0.5Sr_0.5Zn₂Si₂O₇, the a- and the c-axis expand during heating while the b-axis contracts. The volume of the unit cell decreases up to a temperature of 400 °C and then increases.

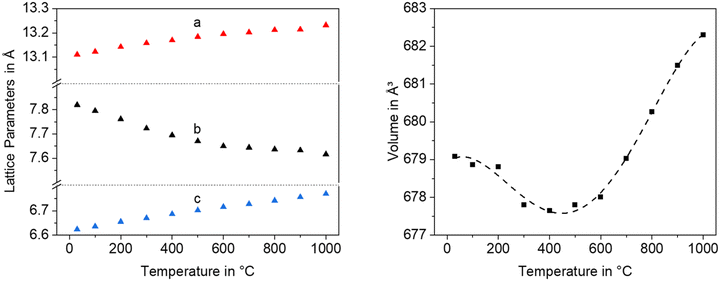Fig. 12 Lattice parameters and unit cell volume of Ba_0.5Sr_0.5Zn₂SiGeO₇ as a function of temperature.

3.5 Thermal expansion and its anisotropy of solid solutions based on Ba_1−xSr_xZn₂Si₂O₇

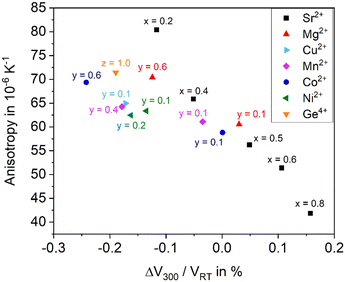
As shown above, the thermal expansion of solid solutions based on BaZn₂Si₂O₇ strongly depends on the substitution of Ba²⁺ by Sr²⁺, of Zn²⁺ by other bivalent elements and of Si⁴⁺ by Ge⁴⁺. Another important issue, however, is the degree of anisotropy of the thermal expansion. Generally, in all Ba_1−xSr_xZn₂Si₂O₇ solid solutions, the CTE of the crystallographic b-axis is strongly negative, while those of the a- and c-axes are positive. In the following, as a measure of the anisotropy, the difference of the CTEs of the axis with the highest and the smallest were taken (see Fig. 13). The data were all extracted from high temperature XRD. The “anisotropy” values were all in the range from 42 to 81 × 10⁻⁶ K⁻¹.

Fig. 13 Anisotropy versus the mean change of the volume of Ba_1−xSr_xZn_2−yM_ySi_2−zGe_zO₇ samples. If the Sr²⁺ concentration varies on the expense of Ba²⁺, Zn²⁺ is not substituted (y = 0, i.e., sample series Ba_1−xSr_xZn₂Si₂O₇). If Zn²⁺ or Si⁴⁺ are replaced, the x-value is kept constant with x = 0.5 (sample series Ba_0.5Sr_0.5Zn_2−yM_ySi_2−zGe_zO₇).

There is a general trend that samples with higher CTE possess a smaller anisotropy. For example, for the series Ba_1−xSr_xZn₂Si₂O₇ (without substitution of the Zn²⁺ position) the anisotropy decreases continuously from x = 0.2 to x = 0.8 (see black squares).

All other data are attributed to samples with the composition Ba_0.5Sr_0.5Zn_2−yM_ySi_2−zGe_zO₇. For a particular cation M²⁺ substituting y = 0.1 Zn²⁺, the CTE gets more negative, however, the anisotropy increases. This effect is most pronounced for Cu²⁺, followed by Ni²⁺, and Mn²⁺. Also, in the case of Co²⁺ and Mg²⁺, the effect is observed. Substitution of Si⁴⁺ by Ge⁴⁺ has a similar effect. Increasing y-values (i.e. increasing substitutions of Zn) lead to further increasing anisotropies and to further more negative CTEs in most cases. In summary, the maximum concentration of divalent cations substituting Zn²⁺, where still the high temperature phase occurs leads to the most negative CTEs, whereas a larger degree of substitution results in a decrease of the anisotropy.

4. Glass formation in the BaO/ZnO/SiO₂ and BaO/SrO/ZnO/SiO₂ systems

The stoichiometric compounds Ba_1−xSr_xZn₂Si₂O₇ and BaZn₂Si₂O₇ do not form glasses. That is due to the lack of a network structure. Assuming BaO and ZnO occur as network modifier, a continuous network is not formed and the mean network connectivity is equal to 1. That means, an Si₂O₇⁶⁻ structure should be predominant which charges are compensated in the average by one Ba²⁺ and two Zn²⁺ ions. This simple consideration fully explains that stoichiometric melts crystallize during cooling. The glass formation ranges of the systems BaO–ZnO–SiO₂ and SrO–ZnO–SiO₂ are given in ref. 32–34. To overcome the problem of spontaneous crystallization, the concentration of network formers has to be increased.

In the case of the system BaO/ZnO/SiO₂ from which mainly materials with high CTEs should be crystallized, the composition 18 BaO·27 ZnO·55 SiO₂ proved to be suitable for controlled precipitation of BaZn₂Si₂O₇. Here, the network connectivity is 2.36 which is just a little bit above the percolation threshold according to the percolation limit of 2.3.³⁵ At a lower network connectivity, the network is “floppy”, i.e. no more rigid and nucleation is facilitated. Therefore, the crystallization tendency should be comparatively low in comparison to a glass with the stoichiometry 20 BaO·40 ZnO·40 SiO₂. In the 18 BaO·27 ZnO·55 SiO₂ composition, the Ba/Zn ratio was chosen larger than 0.5 because an excess of barium should result in the additional crystallization of barium silicates, which also have high CTEs in the range from 12 to 15 × 10⁻⁶ K⁻¹, but the crystallization of Zn₂SiO₄ (willemite) with its exceptionally small CTE should be avoided.^36–38

In the system SrO–ZnO–SiO₂, a compound with very high thermal expansion does not precipitate. In a glass with the mol% composition 16 SrO·35 ZnO·45 SiO₂·1 ZrO₂·1 La₂O₃·2 B₂O₃, Sr₂ZnSi₂O₇ and Zn₂SiO₄ as major crystalline phases are described.³⁹ The crystallized glass has a CTE of around 7 × 10⁻⁶ K⁻¹. Higher SrO-concentrations may additionally lead to the precipitation of SrSiO₃.^40,41 The system BaO/SrO/ZnO/SiO₂ has a lower tendency towards crystallization than the system BaO/ZnO/SiO₂. This should be due to the occurrence of three different network modifying components which decreases the tendency towards crystallization. The glass with the composition 8 BaO·8 SrO·34 ZnO·50 SiO₂ can be obtained by melt quenching. It does not form a real network structure, however, the network connectivity (assuming again BaO and ZnO acting as network modifiers) is equal to two and hence something like a chain structure or a combined ring and chain structure should be formed. Another, more complex glass composition in this system is 8 BaO·8 SrO·35 ZnO·45 SiO₂·1 ZrO₂·1 La₂O₃·2 B₂O₃. Here, the concentration of ZnO was increased by 3 mol% (in comparison to that of the alkaline earths) to avoid the crystallization of high CTE barium silicates. Furthermore, the tendency towards crystallization was decreased by the addition of SiO₂, B₂O₃, ZrO₂ and La₂O₃. Minor concentrations of the latter two are well known nucleation inhibitors in melts of high basicity.^42,43 It should be noted, however, that higher concentrations of ZrO₂ have a nucleating effect in many systems.⁴⁴

If glasses containing both BaO and SrO together with ZnO and SiO₂ are crystallized, the stability range of the HT-phase is much smaller than of ceramics obtained via mixed oxide routes.^39,45 While in the case of ceramics, the HT-phase is stable for 0.2 < x < 0.8, in a glass with the same BaO/SrO ratio, both the LT- and the HT-phases are formed. The sole crystallization of the HT phase from glasses is observed for 0.5 < x < 0.8.³⁹ Higher SrO concentrations lead to the formation of Sr₂ZnSi₂O₇ and Zn₂SiO₄. The different phase formation of compact samples in comparison to powdered samples is supposedly due to the anisotropy of the thermal expansion which leads to notable internal stresses during cooling.

The phase transitions, observed in crystalline BaZn₂Si₂O₇ and isostructural compounds, can also be found in the respective crystallized glasses. In solid solutions precipitated from glasses, the phase transitions are shifted to higher values. In a glass with the molar composition 19 ZnO·27 BaO·54 SiO₂, from which BaZn₂Si₂O₇ was precipitated, the phase transition temperature occurs at 380 °C, i.e. around 100 K higher than in the stoichiometric crystalline phase.⁴⁶ Furthermore, the jump in volume is not observed; instead, a kink is visible.

5. Crystallization behaviour of glasses

Glasses in the system BaO/ZnO/SiO₂ show surface crystallization. Compounds, such as SrO, MgO, MnO, CoO, NiO, CuO, or GeO₂ used to crystallize solid solutions do not promote bulk nucleation. Nevertheless, the addition of nucleation agents, noble metals or oxidic compounds may lead to bulk nucleation. The latter are oxides of metals with high valency mostly in the range of four to six, such as TiO₂, ZrO₂ or a mixture hereof.^44,47–49

5.1 Surface crystallization

When thermally treated at temperatures not too far above T_g, glasses in the BaO/ZnO/SiO₂ and BaO/SrO/ZnO/SiO₂ systems show surface crystallization. In the BaO/SrO/ZnO/SiO₂ system, nucleation at the surface already leads to an orientation of the a- or b-axis parallel to the surface.⁵⁰ The highest growth velocity, however, is along the crystallographic c-axis (see Fig. 14). The crystals grow for some microns along the surface and then the growth direction changes continuously until the c-axis grows towards the bulk.⁵¹ A possible explanation might be oriented nucleation. However, this effect, which is described in a recent review, was not proven in detail for the glasses described here.⁵² The change in the growth direction is denoted as “crystal selection” or “survival of the fastest” and is due to the fact that crystals hinder each other during crystal growth and only crystals which are oriented with their fastest growing axis approximately perpendicular to the surface may survive.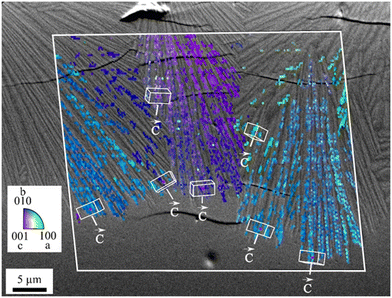

Fig. 14 Orientation of surface crystals with growing direction from the top to the bottom. The micrograph shows a cross section after crystallization for 1.5 h at 790 °C. The colour coded part of the micrograph is a superposition with an inverse pole figure map of an EBSD scan. (redrawn from ref. 50).

In the SEM micrograph (Fig. 14), a surface crystallized sample with the composition 8 BaO·8 SrO·34 ZnO·50 SiO₂ thermally treated 790 °C for 1.5 h is presented. The micrograph shows some cracks perpendicular to the long axis, the c-axis of the respective crystals which are supposedly formed during cooling of the sample. The thicknesses of the layers increase linearly with time (within the accuracy of the measurement). Hence, compounds which are not incorporated in the crystal, i.e. some excess SiO₂ are not increasingly enriched at the growth front and do not form a diffusion barrier which decelerates crystal growth with time.⁵³

5.2 Bulk nucleation, effect of nucleation agents

5.2.1 Metallic nucleation agents. Using metallic nucleation agents, solutions of noble metals salts such as PtCl₄, AuCl₃ and AgNO₃ are given to the raw materials from which the glass is to be melted. The concentrations necessary to achieve nucleation are 50 to 200 ppm for platinum compounds,^54–56 0.01 to 0.1 mol% for gold,^57,58 and at least 0.1 mol% for silver.^59,60 At high temperatures, the respective noble metal compounds are homogeneously dissolved as Pt²⁺, Au⁺ or Ag⁺. During subsequent cooling, these ions react with redox agents which have intentionally been added to the batch. The most commonly added component is antimony, however, also arsenic or tin can be used. At high temperatures, these compounds mainly occur as Sb³⁺, As³⁺ or Sn²⁺. During cooling a redox reaction of the following type (for the example antimony) takes place:

2Ag⁺ + Sb³⁺ → 2Ag + Sb⁵⁺ (1)

These redox reactions can be enhanced by a thermal treatment step at temperatures slightly above the glass transition temperature. The metals form clusters with sizes in the range from 5 to some hundred nanometres or even a few microns, which act as nucleation centres for a subsequent crystallization.

In principle, bulk nucleation can be achieved by the addition of platinum as well as of silver. In the case of silver, the Ba_0.5Sr_0.5Zn₂Si₂O₇ crystals do not directly grow on the silver nano crystals but an intermediate phase is formed, which seems to be an antimony doped willemite type (Zn₂SiO₄) phase.⁶¹ Only the formation of this core shell structure (see Fig. 15) initiates Ba_0.5Sr_0.5Zn₂Si₂O₇ crystallization. Fig. 16 shows micrographs of BaO/SrO/ZnO/SiO₂ based glass ceramics with different Ag₂O and Sb₂O₃ concentrations, crystallized under the same conditions (nucleation: 675 °C for 20 h, crystal growth; 760 °C for 5 h). Both samples show as main crystalline phase Ba_0.5Sr_0.5Zn₂Si₂O₇ as well as metallic silver (see small bright spots). The sample with Ag and Sb₂O₃ concentrations of 0.3 and 1.5 mol%, respectively shows a fairly coarse microstructure and numerous cracks. By contrast, the sample with 0.6 mol% Ag and 3 mol% Sb₂O₃ possesses a much finer microstructure. That is due to the occurrence of much more Ag particles. The twice as high silver concentration but also the higher Sb³⁺ concentration led to a much more effective nucleation and much smaller Ba_0.5Sr_0.5Zn₂Si₂O₇ crystals.

Fig. 15 STEM micrograph and elemental distribution of core–shell structures within a glass with the molar composition 9.5 BaO·9.5 SrO·38 ZnO·38 SiO₂·3.2 Ta₂O₅·1.5 Sb₂O₃·0.3 Ag after a two-step heat treatment at 675 °C for 10 h and 760 °C for 5 h and related EDX maps. The main crystal phase (denoted as “crystal”) is composed of Ba_0.5Sr_0.5Zn₂Si₂O₇.

Fig. 16 SEM micrographs of glasses from the system BaO–SrO–ZnO–SiO₂ nucleated with Ag + Sb₂O₃ in different concentrations after a two-step thermal treatment. Both micrographs show the same magnification.

5.2.2 Oxidic nucleation agents. As oxidic nucleation agents, comparatively high ZrO₂ concentrations of ≥6 mol% can be used.^62,63 Additionally, P₂O₅,⁶⁴ both P₂O₅ and Ce₂O₃,⁶⁵ WO₃ (ref. 66) and Ta₂O₅ (ref. 67) were reported to act as nucleation agents. It should be noted that the oxidic nucleation agents up to now reported in the literature for these glass systems are by far not as effective as the noble metals.

Fig. 17 shows the microstructure of a glass–ceramic with the composition 7.5 BaO·7.5 SrO·34 ZnO·43 SiO₂·7 ZrO₂·1 TiO₂ crystallized at 750 °C for 48 h and at 840 °C for 30 min.⁶³ Large crystals within the glass volume can be found, which seem to start growing from only one nucleus. Furthermore, crystal agglomerates of the Ba_0.5Sr_0.5Zn₂Si₂O₇ phase with diameters in the range from 40 to 60 μm are observed. The agglomerates consist of bundles of various crystals which all have similar orientations (see for example the crystal in the upper right corner of Fig. 17). The agglomerates are composed by 6 to 10 bundles with different orientations. The long dimension of the crystals is the crystallographic c-axis, as evidenced by electron backscatter diffraction. The nuclei themselves which possibly consist of ZrO₂ could not be detected.

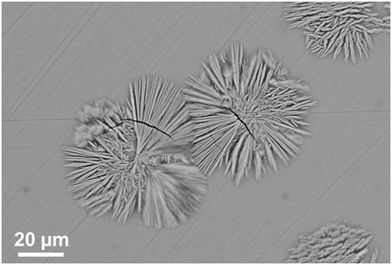Fig. 17 Microstructure of a sample with the composition 7.5 BaO·7.5 SrO·34 ZnO·43 SiO₂·7 ZrO₂·1 TiO₂ crystallized at 750 °C for 48 h and at 840 °C for 30 min.

Fig. 18 shows an SEM micrograph of a sample with the composition 9.4 BaO·9.4 SrO·37.6 ZnO·37.6 SiO₂·4 P₂O₅·2 Ce₂O₃ which is equal to 18.8 (Ba_0.5Sr_0.5Zn₂Si₂O₇)·4 P₂O₅·2 Ce₂O₃.⁶⁵ The addition of P₂O₅ and Ce₂O₃ to the stoichiometric compound obviously extends the glass forming range notably. During thermal treatment at 690 °C for 20 h and subsequently at 850 °C for 1 h, first surface crystallization of Ba_0.5Sr_0.5Zn₂Si₂O₇, Zn₂SiO₄, and CeO₂ can be observed. Furthermore, the crystallization of (Ba,Sr)₅(PO₄)₃Cl, a phase with the hexagonal apatite (Ca₅P₃O₁₂OH) structure (space group P6₃/m), occurred (see the bright crystals with hexagonal shape in Fig. 18). The c-axes of these crystals are oriented approximately perpendicular to the cut plane. The crystals growing around them are Ba_0.5Sr_0.5Zn₂Si₂O₇ which is also oriented with the c-axis in the same manner and hence epitaxial growth on the apatite crystal is assumed.

Fig. 18 SEM micrograph with the composition 9.4 BaO·9.4 SrO·37.6 ZnO·37.6 SiO₂·4 P₂O₅·2 Ce₂O₃, crystallized at 690 °C for 20 h and subsequently at 850 °C for 1 h.

6. Sintering of glass powders and sol–gel derived glasses

6.1 Sinter crystallization of glasses

If glasses are powdered, pressed into shape and subsequently sintered, the preparation procedure is denoted as “sinter crystallization”. It is assumed that first sintering due to viscous flow occurs and subsequently, nucleation at the inner surface of the sintering specimen. During the continuous heat treatment, complete densification takes place until all pores are eliminated and subsequently crystal growth occurs. The size of the crystals is usually in the same range as that of the powder particles. By contrast to the crystallization of bulk glasses, sinter crystallization leads to a homogeneous microstructure also if the corresponding bulk glass shows solely surface crystallization. Sinter crystallization of glasses in the system BaO/ZnO/SiO₂ is mostly applied to sealing applications and results in specimens with CTEs in the range from 10–15 × 10⁻⁶ K⁻¹. By contrast, sinter crystallized glass ceramics in the system BaO/SrO/ZnO/SiO₂ has its greatest potential in the preparation of materials with zero or negative CTE. Fig. 19 shows a microstructure of a sample with the composition 8 BaO·8 SrO·35 ZnO·45 SiO₂·1 ZrO₂·1 La₂O₃·2 B₂O₃ sinter crystallized at 800 °C for 1 h using a grain size <63 μm.⁴⁵ The dark areas in between the crystals mark the residual glassy phase, enriched in SiO₂ with a lower mean atomic number than the crystal phase. Although no EDX mapping is shown in Fig. 19, it has been confirmed experimentally on similar glass compositions by EDX that the dark phase is enriched in SiO₂.⁶⁸

Fig. 19 Microstructure of a sinter crystallized sample with the composition 8 BaO·8 SrO·35 ZnO·45 SiO₂·1 ZrO₂·1 La₂O₃·2 B₂O₃ sintered at 800 °C for 1 h. Redrawn from ref. 45.

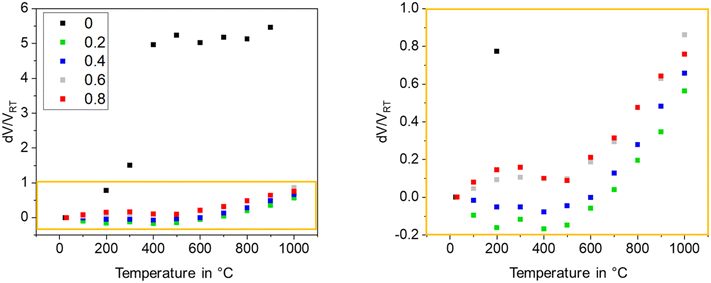
The thermal expansion is strongly affected by the grain size of the used glass powder. In general, the CTE is more negative, if the used grain size is larger. In Fig. 20, this effect is shown for sinter crystallized glass ceramics all prepared by thermal treatment at 950 °C for 1 h. The most negative CTE is obtained using the grain size fraction from 100 to 200 μm, while using the grain size fraction from 63 to 100 μm results in a material of positive CTE. Surprisingly, the CTE of some prepared materials determined by dilatometry is much more negative than that determined by high temperature XRD. This effect is due to the strong thermal expansion of the crystallographic b-axis and the contraction of the crystallographic a- and c-axis during cooling. This strongly anisotropic thermal expansion leads to stresses formed during cooling which result in microcracks. During heating, the microcracks will successively be closed while they are opened again during cooling.

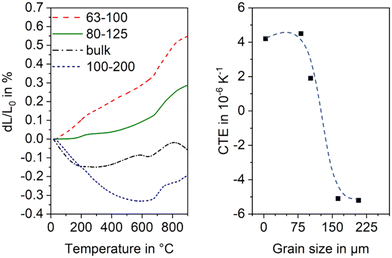Fig. 20 Thermal expansion of sinter crystallized glass powders with the composition 8 BaO·8 SrO·35 ZnO·45 SiO₂·1 ZrO₂·1 La₂O₃·2 B₂O₃ sintered at 950 °C for 1 h. Left: Dilatometric measurements. Right: CTE vs. grain size of sintered powders. The dashed line is just a guide for the eyes. Redrawn from ref. 45.

6.2 Sintering of sol–gel powders

Sol–gel derived powders generally possess small crystallites with sizes in the few to some 10 nm range which hence show high sinter activity.^69,70 In order to obtain Ba_1−xSr_xZn₂Si₂O₇, sol–gel powders were prepared as previously described.¹⁰ After hydrolysis, polycondensation and drying, the gel was milled and subsequently thermally treated at 530 °C. Then the calcined powder was hot pressed at 1100 °C for 10 min using a uniaxial pressure of 40 MPa which resulted in almost full densification. Dilatometry showed negative thermal expansion up to a temperature of 80 °C. At higher temperatures, the CTE increases steadily. Hence, the range of negative thermal expansion is shifted to lower temperatures than in the case of a stoichiometric crystalline compound. In analogy, a BaZn₂Si₂O₇ sample prepared via sol–gel route shows a lower phase transition temperature.

7. Remarks and outlook

The low temperature phase BaZn₂Si₂O₇ transfers to a high temperature phase at 280 °C which is accompanied by a volume increase of 3.3%. Substitution of Zn²⁺ against Mg²⁺, Mn²⁺, Ni²⁺, Co²⁺ or Cu²⁺ or of Si⁴⁺ by Ge⁴⁺ results in solid solutions and in a shift of the phase transition to higher temperatures. If Ba²⁺ is partially replaced against Sr²⁺, the phase transition temperature gets lower even below room temperature.

The most remarkable property of BaZn₂Si₂O₇ and solid solutions derived hereof are the CTEs. The low temperature phase has a high CTE in the range from 10 to 15 × 10⁻⁶ K⁻¹, which is approximately constant up to the phase transition temperature, for the case of a 100% replacement of Zn²⁺ against Co²⁺ up to 850 °C. The CTE of the high temperature phase is small or even negative. For a substitution of 10% Ba²⁺ against Sr²⁺, a negative CTE is observed from room temperature up to a temperature of 500 °C.

The addition of network forming compounds to the stoichiometric Ba_1−xSr_xZnSi₂O₇ and/or the addition of nucleation inhibitors enables the preparation of glasses by melt quenching. Controlled crystallization of such glasses results in surface nucleation. However, the addition of nucleating agents such as ZrO₂ or noble metals enables volume nucleation and the preparation of homogeneous glass ceramics. It should be mentioned that also the preparation of sintered ceramics from sol–gel derived powders with negative CTE is possible. Future developments should be focused on Ba_1−xSr_xZn_2−yM_ySi_2−zGe_zO₇ crystals with smaller crystallites, i.e., a more effective homogeneous nucleation. Another important issue are glass ceramics containing Ba_1−xSr_xZn_2−yM_ySi_2−zGe_zO₇ crystals of less pronounced anisotropy in the thermal expansion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the German Federal Ministry of Education and Research under the Grant Numbers 03VP01701 and 03VP01702 and by the German Research Foundation (DFG) under Grant Number TH 2241/1-1.

References

1. J. H. Lin, G. X. Lu, J. Du, M. Z. Su, C.-K. Loong and J. W. Richardson Jr, J. Phys. Chem. Solids, 1999, 60, 975–983.
2. M. Kerstan, M. Müller and C. Rüssel, J. Solid State Chem., 2012, 188, 84–91.
3. M. Kerstan, C. Thieme, A. Kobeisy and C. Rüssel, J. Mater. Sci., 2017, 52, 1789–1796.
4. D. Ehrt, A. Herrmann and M. Tiegel, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2011, 52, 68–76.
5. M. Kerstan, C. Thieme, M. Grosch, M. Müller and C. Rüssel, J. Solid State Chem., 2013, 207, 55–60.
6. S. S. Mitra and S. K. Joshi, J. Chem. Phys., 1961, 34, 1462–1463.
7. F. Tietz, Ionics, 1999, 5, 129–139.
8. M. K. Mahapatra and K. Lu, Mater. Sci. Eng., R, 2010, 67, 65–85.
9. C. Thieme, H. Görls and C. Rüssel, Sci. Rep., 2015, 5, 18040.
10. M. Kracker, C. Thieme, J. Häßler and C. Rüssel, J. Eur. Ceram. Soc., 2016, 36, 2097–2107.
11. B. Li, S. Wang and Y. Fang, J. Alloys Compd., 2017, 693, 9–15.
12. J. Liu, Q. Wang, Z. Zhang, Q. Zeng, H. Peng and Q. Chang, J. Non-Cryst. Solids, 2022, 576, 121226.
13. H. Bach and D. Krause, Low Thermal Expansion Glass Ceramics, Springer, Berlin, Heidelberg, 2nd edn, 2005.
14. G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, J. Phys.: Condens. Matter, 2005, 17, R217–R252.
15. E. D. Zanotto, Am. Ceram. Soc. Bull., 2010, 89, 19–27.
16. R. M. Hovhannisyan, Glass Technol., 2003, 44, 96–100.
17. J. F. MacDowell, J. Am. Ceram. Soc., 1990, 73, 2287–2292.
18. D. Tauch and C. Rüssel, J. Non-Cryst. Solids, 2005, 351, 2294–2298.
19. T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92.
20. J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8, 2809–2823.
21. R. D. Adams, R. Layland, C. Payen and T. Datta, Inorg. Chem., 1996, 35, 3492–3497.
22. C. Thieme and C. Rüssel, J. Mater. Sci., 2015, 50, 3416–3424.
23. C. Thieme, T. Waurischk, S. Heitmann and C. Rüssel, Inorg. Chem., 2016, 55, 4476–4484.
24. J. Janczak, R. Kubiak and T. Głowiak, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 1383–1385.
25. J. Ma, C. D. Dela Cruz, T. Hong, W. Tian, A. A. Aczel, S. Chi, J.-Q. Yan, Z. L. Dun, H. D. Zhou and M. Matsuda, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144405.
26. C. Thieme and C. Rüssel, Dalton Trans., 2016, 45, 4888–4895.
27. A. Erlebach, C. Thieme, C. Müller, S. Hoffmann, T. Höche, C. Rüssel and M. Sierka, Phys. Chem. Chem. Phys., 2020, 22, 18518–18525.
28. A. Erlebach, G. Belhadj Hassine, C. Thieme, K. Thieme, C. Rüssel and M. Sierka, Phys. Chem. Chem. Phys., 2021, 23, 25533–25541.
29. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
30. H. Koelmans and C. M. C. Verhagen, J. Electrochem. Soc., 1959, 106, 677–682.
31. C. Thieme and C. Rüssel, Materials, 2016, 9, 631.
32. C. Lara, M. J. Pascual and A. Durán, J. Non-Cryst. Solids, 2004, 348, 149–155.
33. M. Imaoka and T. Yamazaki, Rep. Inst. Ind. Sci., Univ. Tokyo, 1968, 8, 241–273.
34. G. W. Cleek and C. L. Babcock, NBS Monogr., 1973, 135, 1–39.
35. I. Avramov, R. Keding and C. Rüssel, J. Non-Cryst. Solids, 2000, 272, 147–153.
36. A. M. Hu, M. Li, D. L. M. Dali and K. M. Liang, Thermochim. Acta, 2005, 437, 110–113.
37. M. Kerstan and C. Rüssel, J. Power Sources, 2011, 196, 7578–7584.
38. M. Kerstan, M. Müller and C. Rüssel, Mater. Res. Bull., 2011, 46, 2456–2463.
39. C. Thieme, M. Schlesier, E. Oji Dike and C. Rüssel, Sci. Rep., 2017, 7, 3344.
40. B. Tiwari, A. Dixit and G. P. Kothiyal, Int. J. Hydrogen Energy, 2011, 36, 15002–15008.
41. B. Tiwari, A. Dixit, C. G. S. Pillai, S. C. Gadkari and G. P. Kothiyal, J. Am. Ceram. Soc., 2012, 95, 1290–1296.
42. K. Thieme and C. Rüssel, J. Eur. Ceram. Soc., 2014, 34, 3969–3979.
43. K. Thieme and C. Rüssel, J. Mater. Sci., 2015, 50, 1488–1499.
44. M. Dittmer, C. F. Yamamoto, C. Bocker and C. Rüssel, Solid State Sci., 2011, 13, 2146–2153.
45. C. Thieme, M. Schlesier, C. Bocker, G. Buzatto de Souza and C. Rüssel, ACS Appl. Mater. Interfaces, 2016, 8, 20212–20219.
46. C. Thieme and C. Rüssel, Ceram. Int., 2015, 41, 13310–13319.
47. E. Kleebusch, C. Patzig, M. Krause, Y. Hu, T. Höche and C. Rüssel, Sci. Rep., 2018, 8, 2929.
48. T. Höche, M. Mäder, S. Bhattacharyya, G. S. Henderson, T. Gemming, R. Wurth, C. Rüssel and I. Avramov, CrystEngComm, 2011, 13, 2550–2556.
49. C. Patzig, T. Höche, M. Dittmer and C. Rüssel, Cryst. Growth Des., 2012, 12, 2059–2067.
50. M. Kracker, L. Vladislavova, C. Thieme, T. Zscheckel, K. Thieme, T. Höche and C. Rüssel, RSC Adv., 2017, 7, 44834–44842.
51. M. Kracker, T. Zscheckel, C. Thieme, K. Thieme, T. Höche and C. Rüssel, CrystEngComm, 2019, 21, 1320–1328.
52. W. Wisniewski and C. Rüssel, Prog. Mater. Sci., 2021, 118, 100758.
53. T. Waurischk, C. Thieme and C. Rüssel, J. Mater. Sci., 2020, 55, 10364–10374.
54. L. Vladislavova, C. Thieme, T. Zscheckel, C. Patzig, T. Höche and C. Rüssel, J. Eur. Ceram. Soc., 2017, 37, 4801–4808.
55. L. Vladislavova, C. Thieme, T. Zscheckel, T. Höche and C. Rüssel, J. Alloys Compd., 2019, 793, 705–714.
56. L. Vladislavova, M. Kracker, T. Zscheckel, C. Thieme and C. Rüssel, J. Mater. Sci., 2018, 53, 11204–11215.
57. M. Kracker, C. Thieme, K. Thieme, C. Patzig, L. Berthold, T. Höche and C. Rüssel, RSC Adv., 2018, 8, 6267–6277.
58. C. Thieme, M. Kracker, C. Patzig, K. Thieme, C. Rüssel and T. Höche, J. Eur. Ceram. Soc., 2019, 39, 554–562.
59. M. Kracker, C. Thieme, K. Thieme, T. Höche and C. Rüssel, Ceram. Int., 2019, 45, 18760–18766.
60. C. Thieme, K. Thieme, M. Kracker, C. Patzig, L. Berthold, T. Höche and C. Rüssel, Ceram. Int., 2021, 47, 1126–1132.
61. C. Thieme, L. Vladislavova, K. Thieme, C. Patzig, T. Höche and C. Rüssel, J. Mater. Sci., 2022, 57, 6607–6618.
62. L. Vladislavova, C. Thieme and C. Rüssel, J. Mater. Sci., 2017, 52, 4052–4060.
63. L. Vladislavova, M. Kracker, T. Zscheckel, C. Thieme and C. Rüssel, Solid State Sci., 2018, 78, 107–115.
64. K. Thieme, T. Zscheckel, C. Thieme, T. Höche and C. Rüssel, J. Eur. Ceram. Soc., 2018, 38, 2017–2026.
65. K. Thieme, T. Zscheckel, C. Thieme, M. Kracker, C. Rüssel and T. Höche, Ceram. Int., 2018, 44, 19970–19980.
66. C. Thieme, A. Erlebach, C. Patzig, K. Thieme, M. Sierka, T. Höche and C. Rüssel, CrystEngComm, 2018, 20, 4565–4574.
67. S. Heitmann, K. Thieme, C. Thieme, M. Kracker, T. Höche and C. Rüssel, Ceram. Int., 2019, 45, 7580–7587.
68. C. Thieme, J. Am. Ceram. Soc., 2021, 105, 3544–3554.
69. C. J. Brinker and G. W. Scherer, Sol-gel science: the physics and chemistry of sol-gel processing, Academic Press, Boston, 1990.
70. S. Sakka, Handbook of sol-gel science and technology: processing, characterization, and applications, Kluwer Academic Publishers, Boston, 2005, vol. 3.

---