Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Engineering of a kinetically driven phase of phenoxazine by surface crystallisation†
Martin
Kaltenegger
 ab,
Sebastian
Hofer
a,
Roland
Resel
ab,
Sebastian
Hofer
a,
Roland
Resel
 *a,
Oliver
Werzer
*a,
Oliver
Werzer
 cd,
Hans
Riegler
c,
Josef
Simbrunner
cd,
Hans
Riegler
c,
Josef
Simbrunner
 e,
Christian
Winkler
e,
Christian
Winkler
 a,
Yves
Geerts
a,
Yves
Geerts
 bf and
Jie
Liu
bf and
Jie
Liu
 b
b
aInstitute of Solid State Physics, Graz University of Technology, Petersgasse 16, 8010 Graz, Austria. E-mail: roland.resel@tugraz.at
bLaboratoire de Chimie des Polymères, Faculté des Sciences, Université Libre de Bruxelles (ULB), CP 206/1, Boulevard du Triomphe, 1050 Bruxelles, Belgium
cDepartment for Pharmaceutical Technology and Biopharmacy, Institute of Pharmaceutical Sciences, Graz University, Universitätsplatz 1, 8010 Graz, Austria
dJOANNEUM RESEARCH Forschungsgesellschaft mbH, Institute for Surface Technologies and Photonics, Franz-Pichler-Straße 30, 8160 Weiz, Austria
eDivision of Neuroradiology, Vascular and Interventional Radiology, Medical University Graz, Auenbruggerplatz 9, Graz, 8036, Austria
fInternational Solvay Institutes of Physics and Chemistry, Brussels, Belgium
First published on 7th June 2022
Abstract
The appearance of different polymorphs at surfaces is a well-known phenomenon for organic molecules. Here the phenoxazine molecule, a small molecule with a rather rigid conformation whose bulk crystal structure (form 1) could be solved recently, is studied. The molecule was crystallized on silicon oxide surfaces from solution by drop casting and spin coating using five different solvents. Besides the concentration ranging from 0.8 g l−1 to 50 g l−1, the evaporation rate of the solvent was also controlled. By this process a new polymorph (form 2) was found which preferably forms at high solvent evaporation rates (e.g. by spin coating). The crystal structure was solved by combining grazing incidence X-ray diffraction with theoretical methods of packing determination based on molecular dynamics and density functional theory. Severe disorder is found within the structure of the new polymorph, similar to those known for form 1. Comparing the phases of phenoxazine with the results of the surface crystallization studies here reveals that the new phase is a kinetically driven phase of metastable character. This work shows that surface crystallization is a valuable tool to search for new polymorphs of organic molecules and to characterise them in terms of their kinetic appearance and thermodynamic stability.
Introduction
Polymorphism describes the ability of molecules to crystallize in various crystal forms. Those forms can differ in molecular conformation as well as in the packing of the molecules within the crystal structure. Variation of the polymorph phase usually impacts fundamental properties including mass density, melting temperature, mechanical and chemical stability, and mechanical or optical properties.1,2 In particular, for the applications of polymorph selection in pharmaceutics, solubility and dissolution behaviours further alter the bioavailability, i.e., the amount of active material in the body, and thus the therapeutic performance.3,4Polymorphism often appears in organic compounds because of weak intermolecular van der Waals interactions. Often the enthalpy difference between polymorphs lies in a range of 1 to 10 kJ mol−1 compared with the thermal energy of 2.5 kJ mol−1 at a temperature of 298 K.5,6 Polymorphs often differ by the space group of the crystal structure and by the molecular conformation that molecules adopt in crystals. Although crystal structure prediction is a well-established technique,7,8 the experimental access to specific polymorphs can be difficult. The crystallization process is dominated by kinetic effects which influence not only the formation of the initial crystal nuclei but also the subsequent crystal growth process.
There are many ways to tune the crystallization kinetics during solidification from solution. It was shown that organic molecules could crystallize in new and unknown polymorphs when thin film preparation technologies are used, since the crystallization kinetics can be varied on a large scale by thin film deposition techniques.9 Methods like drop casting, spin coating, dip coating or blade coating are used to deposit organic materials onto solid substrates.10–13 The evaporation rate of the solvent determines the characteristic relaxation times for conformational changes and molecular rearrangement so that the induction time can be strongly varied. The reasons for the polymorph selection within thin films are manifold. First, thin film deposition onto a solid surface is related to the phenomenon of heterogeneous nucleation.14–16 In such cases, the nucleation barrier is lower compared to bulk solution nucleation, resulting in favoured nucleation on surfaces.17–19 Second, the presence of a surface during the crystallization process decreases the system entropy at the interface, increasing the probability of the molecules to form crystal nuclei.20 As a consequence, specific polymorphs are exclusively generated in thin films. Besides the polymorph selection, hosting crystals at surfaces can protect less stable forms from transitioning towards a thermodynamically more stable polymorph.21
The compound of interest in this study is the small molecule phenoxazine used in pharmaceutics and organic electronics.22,23 Often, phenoxazine works as a parent molecule found in different biological organisms.22 Due to the widespread applications like antioxidants, antivirals, antibiotics, anticancer drugs and many more, phenoxazine and its derivatives are important compounds in medicine and as lead compounds in pharmaceutical research.24–29
In this work we show how the preparation of thin films can be used to form different polymorphs of phenoxazine. One form of phenoxazine is accessible in bulk crystals (form 1) and another form appears only in thin films at surfaces of silicon oxide (form 2). We investigate the differences in molecular packing of the crystal structure of the two forms and discuss the kinetic contribution to the selection of each.
Methods
Phenoxazine was purchased from Aldrich at a purity of 97%. Various solutions were prepared in spectroscopy grade chlorobenzene, toluene, cyclohexane, ethanol and tetrahydrofuran at a concentration of 5 g l−1. The solutions were stirred prior to deposition. In addition, phenoxazine solutions in tetrahydrofuran were prepared in concentrations ranging from 0.78 g l−1 to 50 g l−1. Drop casting and spin coating were performed on atomically flat silicon wafers (Siegert Wafers, Germany) hosting a thin native grown silicon oxide layer of about 2 nm checked by X-ray reflectivity. Prior to usage, the substrates were sonicated subsequently for 10 minutes in an acetone bath and in ethanol. The substrates were dried in a nitrogen stream and exposed to UV-ozone for 20 min. A final rinsing with distilled water and acetone was followed by drying in a nitrogen stream. The surface energies of the clean wafers were determined by the method of Owens and Wendt,30 obtaining 49 mN m−1 with a polar part of 24 mN m−1 and a dispersive part of 25 mN m−1.Drop casting was performed by depositing 90 μL or 50 μL solution onto 2 cm × 2 cm or 1 cm × 1 cm substrate pieces, respectively. The evaporation rate was varied by leaving the samples either uncovered in the fume hood or covered by one or two Petri dishes (diameter of 7 cm and 10 cm). The coverage reduces the evaporation rate from a few minutes (no cover) to about 20 minutes (one cover) up to one hour (two covers). The crystallization process was even extended up to several hours by sealing the crystallization environment using PARAFILM M. Spin coating was performed using a standard device; various spin velocities for different samples from 500 rpm to 4000 rpm were applied for 60 seconds. Dropping 90 μl solution and substrate spinning ended in homogenous flat films, but with differences in the appearance at the edges, typically for solutions not running off the substrate. Therefore, the material at the edges was removed prior to X-ray diffraction studies by using a cotton stick to investigate only relevant surface areas at the center of the substrate.
Optical microphotographs were taken using a NIKON Eclipse E200 microscope facilitating a reflection mode and crossed polarizers.
Specular X-ray diffraction experiments were performed using either an Empyrean system (PANalytical, the Netherlands) or an Ultima IV system (Rigaku Corporation, Japan). In both cases, sealed copper tubes were used in combination with parallel beam mirrors, beam masks and suitable detectors, a PixCel3D for the Empyrean system and a scintillation counter for Ultima IV. The scans were performed by θ/2θ scans providing information only along the surface normal. The angular scans are presented in the wave vector notation which is calculated from the specular scans viaq = 4π/sin(θ).
Grazing incidence X-ray diffraction (GIXD) experiments were performed at the beamlines XRD1 and SAXS both located at the synchrotron Elettra (Trieste, Italy). The incident wavelengths for these experiments were either 0.140 nm (XRD1) or 0.154 nm (SAXS). At both beamlines, Pilatus detectors collected the scattered intensities. Calibration was performed using LaB6 standards. Data processing was performed using the software GIDVis and are represented in wave vector notation which simplifies comparison of all X-ray diffraction from the various setups.31
The crystal structure of the thin film form is not accessible using standard crystal structure solution methods. The determination of molecular packing from a thin film requires a combination of the experimental GIXD and specular X-ray data with theoretical packing considerations. In a first step, indexation of the GIXD pattern reveals the lattice constants of the crystallographic unit cell by applying a self-developed strategy.32,33 The obtained unit cell was then used as the initial parameter for the molecular packing simulation using molecular dynamics (MD) based on the LAMMPS software package,34 the CHARMM general force field version 3.0.1,35 and the Dreiding generic force field.36 For each simulation run, two randomly oriented phenoxazine molecules were placed into an expanded volume of the found crystallographic unit cell. This procedure was repeated to generate several hundred trail structures. During a simulation run of a total runtime of 80 ps with 1 fs time steps, the dynamics are calculated while continuously shrinking to the experimentally determined unit cell size. The calculated structures are then filtered based on their final energies and clustered based on their similarity in packing. For each calculated structure, the squared structure factors |Fhkl|2 of individual diffraction peaks are calculated and compared to the experimentally determined ones from the GIXD investigations to identify the most likely packing. The structure factor Fhkl for a unit cell is calculated by:
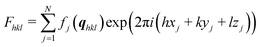 | (1) |
Density functional theory (DFT) as implemented in the FHI-aims code package (version 190906) is used for optimizing the geometric structure of the MD results.37 For this calculation the PBE functional38 was employed using a 4 × 4 × 4 k-point grid for sampling reciprocal space, and the Tkatchenko–Scheffler correction scheme39 for treating van der Waals interactions. Regarding the basis set, tight default settings for all included atomic species were used. Starting from the MD results, all atomic positions were allowed to relax until the largest force component on any atom was smaller than 0.01 eV Å−1. During this relaxation the unit cell parameters are held constant.
The Hirshfeld surface is calculated using the software CrystalExplorer 17.5.40 The contact distance (dnorm) is based on de (the distance from the point on the Hirshfeld surface to the nearest nucleus external to the surface) and di (the distance from the point on the surface to the nearest nucleus internal to the surface), normalizing by van der Waals radii for the particular atoms involved in close contact to the surface:
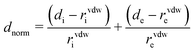 | (2) |
Results
Thin film investigations
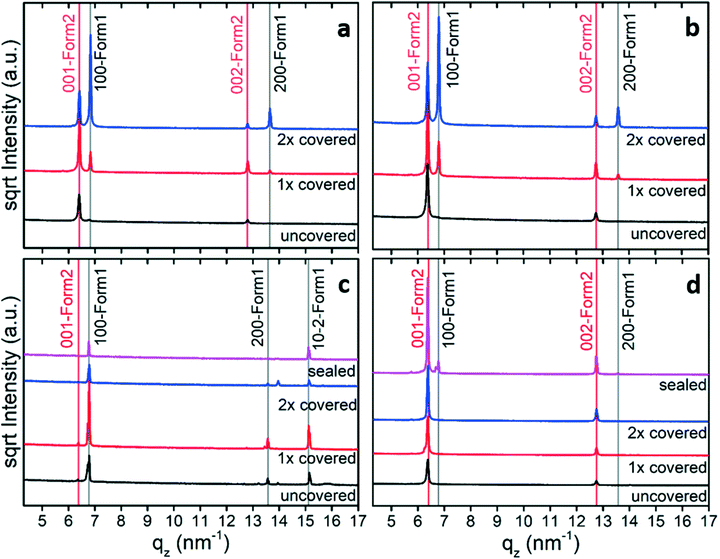
The impact of solvent choice and evaporation rate on the thin film formation and polymorph selection is tested by drop casting using different amounts of enclosures. Fast evaporation results when a drop of solution is placed on the substrate surface and left uncovered until full evaporation. The evaporation rate considerably reduces when the sample is enclosed by covering with one or two Petri dishes.The thin film samples were first investigated by specular X-ray diffraction to identify the appearance of polymorph phases and their preferred crystal orientations. Fig. 1 reveals the results from solutions of four different solvents. We compared the peaks with the expected peak positions of the known crystal structure of phenoxazine.41 This phase is denoted as form 1 or simply as bulk phase. This comparison reveals that the peak at 6.79 nm−1 corresponds to the (100) peak (100-form 1) and the peak at 13.56 nm−1 is the second-order reflection (200-form 1). In the case of cyclohexane (Fig. 1c), the peak at 15.11 nm−1 could also be assigned to the bulk phase of phenoxazine; it represents the (10–2) peak (10–2-form 1). The observation of exclusively (100) (and 200) peaks for most of the samples reveals that there is a strongly preferred orientation of the crystals relative to the substrate surface, i.e. the (100). For the cyclohexane sample another orientation also occurs. Further inspection of the patterns shows that the peaks located at 6.36 nm−1 and 12.81 nm−1 cannot be explained by the bulk phase and must result from another, yet unknown, polymorph (form 2). Calculating the d-spacing reveals that these peaks arise from one net plane distance and represent diffraction peaks of different order. As will be defined below, these peaks are indexed as (001) (001-form 2) and (002) (002-form 2). As there exist only peaks for one net-plane orientation, this means that the phenoxazine crystals in this phase are likely highly textured; the crystals are oriented with their (001) planes relative to the substrate surface, which is confirmed with the GIXD results later on.
Starting with samples without covers (black curves) reveals form 1 only in the case of cyclohexane (Fig. 1c). In the case of slower evaporation rate, both phases are found in films prepared from chlorobenzene and toluene (Fig. 1a and b, 2× covered), but the diffraction peaks of form 1 are significantly more intense. At elevated evaporation rates (Fig. 1a and b, 1× covered and uncovered) form 2 becomes dominant. From this observation it follows that using a low evaporation rate results in high amounts of form 1 crystals with respect to form 2. The higher intensities of form 2 peaks compared to that of form 1 might allow us at first glance to conclude the presence of a higher amount of the second form (form 2) compared to the bulk phase (form 1). But one needs to keep in mind that crystal extension42 or defects as well as differences in the structure factor are not taken into account here.
In the case of cyclohexane as solvent at low evaporation rate (Fig. 1c, 2× covered, sealing) the pure form 1 was obtained, but at high evaporation rate (Fig. 1c, 1× covered, uncovered) form 2 peaks are observed with small intensities, marked by red arrows. Preparing films from ethanol ended in the formation of mainly form 2 (Fig. 1d). Here, form 1 can merely be seen in the top pattern (grey arrow), which corresponds to the sealed sample.
The results depicted in Fig. 1 reveal that variation of the evaporation rate clearly influences the polymorphic phase formed at the substrate surface: slow evaporation rates induce crystallization towards form 1, while high evaporation rates shifts the tendency of crystallization towards form 2.
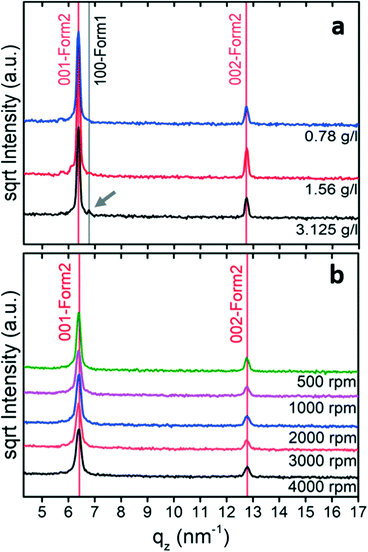
In the next step, the crystallization of phenoxazine from tetrahydrofuran solutions was investigated in detail. Drop casting experiments were performed using solution concentrations from 50 g l−1 down to 0.78 g l−1. Both phases appeared at high concentrations and the influence of the evaporation rate is similar to that in the previous drop casting experiments in that the amount of form 1 increases (and the fraction of form 2 decreases) by reducing the evaporation rate (Fig. S1a†). However, form 2 is formed at relatively low concentrations and only a small fraction of form 1 is observed in the samples obtained from the 3.125 g l−1 solution (Fig. 2a).
To increase the evaporation rate further, spin coating can be used. The specular X-ray diffraction patterns of such samples (10 g l−1) reveal that only one peak series is present and this belongs to form 2 with a (001) orientation (Fig. 2b). Changes in the spin velocity slightly affect the peak intensities. This results from the fact that the layer become thinner as the spin speed increases.
Optical micrographs (Fig. 3) show the influence of the evaporation rates on the thin film morphology. Beginning at high concentrations with fast evaporation and no cover (Fig. 3a) reveals spherulites. By decreasing the evaporation rate of the solvent (Fig. 3b and c), plate-like crystals appeared which are connected to morphologies of form 1.41Fig. 3d–f reveal the crystallization at low concentrations; the formation of extended dendrites is observed. Comparison with the corresponding X-ray diffraction pattern (Fig. 2a) confirms that form 2 at surfaces crystallizes in dendritic morphologies.
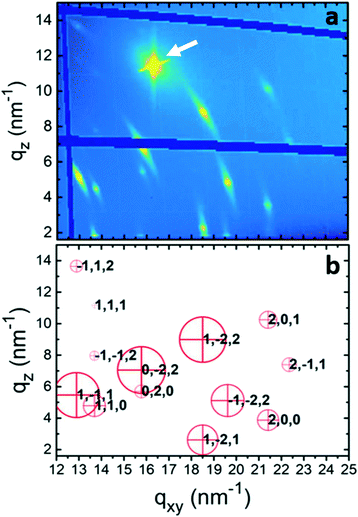
To gain further information about the crystal structure of form 2, grazing incidence X-ray diffraction experiments were performed. A spin-coated sample prepared from a 10 g l−1 tetrahydrofuran solution was investigated; the result is shown in Fig. 4a. The reciprocal space map reveals several diffraction peaks all over the map. The information along the qxy direction hosts information along the surface (in-plane), while that along qz (at qxy = 0) is the same information as the specular scan. The representation of the data is in logarithmic scale to identify peaks in a wide intensity range, and the dark blue areas result from blind regions of the detector. The isotropic nature of the substrate surface determines a 2D powder-like distribution of crystallites, i.e., random in-plane order exists, while having a single contact plane for all crystals.43 In this presented zoomed space map, there are 13 visible diffraction peaks. An entire GIXD reciprocal space map is presented in the ESI† (Fig. S2), which provides information on overall 20 diffraction peaks of phenoxazine crystals in form 2. The strong peak at around qz = 12 nm−1 and qxy = 16 nm−1 is from the silicon substrate.
The defined peak positions show that the sample is highly textured, i.e. a defined crystallographic plane is formed parallel to the substrate surface. Please note that the Bragg peaks appear within arcs, which result from some mosaicity of the phenoxazine crystals and appear more dominant due to the logarithmic scale. However, the centers of the arcs have a sharp character with a considerably higher intensity. The low mosaicity of the GIXD experiments are in good agreement with the results of specular X-ray diffraction, where the observed diffraction peaks are assigned to (001) and its higher-order reflections (Fig. 2b).
Crystal structure solution of form 2
Although a standard procedure does not exist for the solution of a crystal structure from a thin film, several examples are known from the literature.44–47 A combination of GIXD experiments with theoretical modelling is used. In a first step the crystallographic unit cell is determined by indexing of the observed diffraction peaks, taking into account for each peak two components of the scattering vector (qxy, qz). This indexation provides a triclinic unit cell with a = 5.88 Å, b = 7.98 Å, c = 10.6 Å, α = 109.1°, β = 98.48° and γ = 93.59° (Table 1). Each peak in the reciprocal space map could be explained by using this unit cell. The calculated peak positions are plotted in Fig. 4b by red crosses. It is worth noting that this indexing also explains all peaks in the specular X-ray diffraction scans of the spin-coated samples and the form 2 peaks of the drop-casted samples in Fig. 1. With this crystal setting the contact plane of the crystals at the silicon oxide surface is defined as the (001), or in other words, the phenoxazine crystals of form 2 possess a (001) texture.| Form 2 | Form 1 | Form 1 | |
|---|---|---|---|
| Thin film | Powder41 | Single crystal41 | |
| Formula | C12H9NO | C12H9NO | C12H9NO |
| Molar mass [g mol−1] | 183.21 | 183.21 | 183.21 |
| Temperature [K] | 293 | 293 | 100 |
| Crystal system | Triclinic | Monoclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c | |
| a [Å] | 5.88(2) | 9.51 | 9.335(2) |
| b [Å] | 7.98(2) | 5.805 | 5.768(1) |
| c [Å] | 10.60(2) | 8.522 | 8.261(2) |
| α [°] | 109.01(12) | 90 | 90 |
| β [°] | 98.48(12) | 103.8 | 103.17(3) |
| γ [°] | 93.59(21) | 90 | 90 |
| V [Å3] | 461.8 | 457.1 | 433.15 |
| Z | 2 | 2 | 2 |
| ρ [g cm−3] | 1.324 | 1.331 | 1.405 |
| Packing motif | Herringbone | Herringbone | |
| Crystal shape | Dendrites | Plates | Plates |
The unit cell gives information only on the available volume for the molecules in the crystal, but details about molecular packing are inaccessible. Here, molecular dynamics was used for molecular packing considerations; two phenoxazine molecules are placed into an expanded unit cell with subsequent shrinking of the unit cell size and energy optimization. A number of trails result in packings of reasonable low energy solutions which are compared with the experimental results on the basis of calculated structure factors of the individual peaks. The first series of calculations shows a good agreement between the experimentally observed intensities and the theoretical calculated ones. This first result showed that the molecular packing of phenoxazine molecules was found with reasonable accuracy.
A more detailed comparison reveals that there are some deviations of the calculation from the experimental results. The reasons for the differences can be caused by several features. First, there is no consideration for the statistical disorder of the oxygen/nitrogen as present in the bulk single crystal.41 Second, on inspection of the molecular packing, the low energy packing motifs found in the MD simulation always show a slight bending along the molecule's long axis which does not converge to a specific value, even during longer simulation runs. The angle is in the range of 9.5°, measured between the phenyl rings on each side of the O/N atoms (Fig. S3†). Such a bending is absent in the single-crystal solution.41 As the parametrization of the molecule in CHARMM-FF includes this bending, i.e. might be an inherent problem of the force field chosen, further optimization of the structure is employed via DFT calculations. Here the MD-optimized structure is taken as a starting geometry and all atomic positions are relaxed until the largest force component on any of the atoms is smaller than 0.01 eV Å−1. The resulting structure shows very little change in the packing motif, but the bending along the molecule's axis reduces significantly to 0.6°. The comparison to the experimental peak intensities with these DFT results shows some improvements in the resulting structure factors compared to those calculated from the initial MD simulation. A further, more detailed comparison is shown in the ESI† (Fig. S4).
To get rid of the molecular bending and thus obtain a more accurate solution, a new final MD simulation is implemented. This conformation of unbent molecules appears likewise in the single-crystal solution and makes the new approach plausible. As the bending is present in the used force field and the resulting minimized structures are showing an oscillating bending angle, the atoms are moved to their average positions after several runs. This average position coincides very nicely with the DFT-optimized phase as the bending is greatly reduced. The averaged structure is then minimized with the generic Dreiding-FF36 without any dynamics, resulting in straight molecules in their packing motif from the longer MD run. The occupational disorder is added to the atoms manually by mirroring the O/N atoms along the molecule's long axis and giving them an occupation factor of 0.5. The resulting structure is then checked with the software package Platon.48 Using the ADDSYM function, a missing P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry is detected and the structure is modified accordingly, incorporating the inversion center and reducing the asymmetric unit of the system in agreement with the new symmetry, resulting in the final presented structure. The CIF file of the final crystal structure is available in the ESI.†
symmetry is detected and the structure is modified accordingly, incorporating the inversion center and reducing the asymmetric unit of the system in agreement with the new symmetry, resulting in the final presented structure. The CIF file of the final crystal structure is available in the ESI.†
Fig. 4b reveals the calculated structure factors of our crystal structure solution depicted as red circles. The comparison with the square of the absolute value of the structure factors (Fhkl2) shows a reliable agreement with the experimental results. Thus, an acceptable crystal structure was found.
Discussion
Phenoxazine is an organic rod-like molecule which behaves in many aspects like rod-like conjugated molecules: the molecule crystallizes in a herringbone-motif structure49 and polymorphism is observed when crystallized at silicon oxide surfaces,50,51 but the herringbone arrangement of the molecules is preserved for the different phases.52,53 We will elucidate the crystallization properties of phenoxazine in two aspects. First, the two crystallographic phases are discussed in relation to each other, and second, the crystallization at substrate surfaces and the thin-film formation are discussed.Polymorphism of phenoxazine
Quite unexpected is that the first crystal structure solution of phenoxazine was obtained recently,41 although the molecule is rather small and the tendency of crystallization is high. This might be related to the disorder within the molecular packing: the herringbone pattern forms by partially reversed molecules with an occupation of 50%. Surprisingly, no contribution from hydrogen bonds between the oxygen atom and the nitrogen–hydrogen group is found. This phase is denoted as form 1 or bulk phase. The new phase of phenoxazine (noted as form 2) is presented within this work; it was found within thin films.The basic crystallographic parameters of both polymorphs are given in Table 1. The space group differs between the two phases: form 1 arises within the monoclinic space group P21/c, while the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) is found for form 2. In both cases, the lattice constants are comparable and there are two molecules within the unit cell (Z = 2). The bulk phase shows a slightly larger mass density, which suggests, according to the mass density rule,54 that the bulk phase is the thermodynamically stable phase. Both phases have the tendency to form rather thin flat crystals, with plate-like morphology for form 1 (ref. 41) (Fig. 3c) and dendrites for form 2 (Fig. 3d and e).
is found for form 2. In both cases, the lattice constants are comparable and there are two molecules within the unit cell (Z = 2). The bulk phase shows a slightly larger mass density, which suggests, according to the mass density rule,54 that the bulk phase is the thermodynamically stable phase. Both phases have the tendency to form rather thin flat crystals, with plate-like morphology for form 1 (ref. 41) (Fig. 3c) and dendrites for form 2 (Fig. 3d and e).
For both structures, the molecules arrange in a herringbone pattern with partially disordered molecules. However, subtle differences are present within the herringbone arrangement which can be described by a set of specific angles and the thickness of a single herringbone layer.55 These measurements are given for both structures in Table 2. Form 1 has a smaller thickness h (8.706 Å) of a single herringbone layer than that of form 2 (9.623 Å), which is a result of its larger tilt angles χ (1) and χ (2) of the long molecular axes relative to the herringbone plane. Since the long molecular axes of two neighbouring molecules are not absolutely parallel – they enclose a tilt angle δ relative to each other – two different angles χ (1) and χ (2) are given. The herringbone angle θ represents the tilt angle of the aromatic planes of the neighbouring molecules; for this angle only small differences are found.
| Form 1 | Form 2 | |
|---|---|---|
| Single crystal | Thin film | |
| h [Å] | 8.706 | 9.623 |
| χ (1) [°] | 23.9 | 20.7 |
| χ (2) [°] | 23.9 | 6.0 |
| δ [°] | 16 | 6 |
| θ [°] | 129.5 | 124.4 |
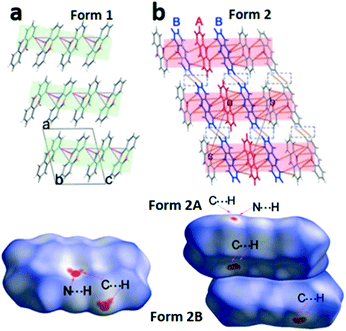
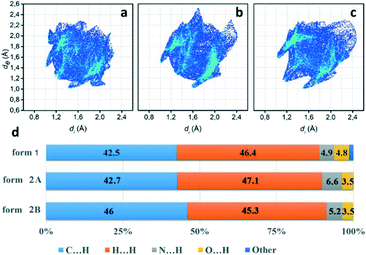
In the next step we analyse the molecular interplay within the herringbone arrangement (Fig. 5). The molecules in form 1 are connected with their closest neighbours through C–H⋯N, C–H⋯O and C–H⋯π short contacts to form a 2D network layer (marked in light green in Fig. 5a). The intermolecular interactions in form 2 differ from those in form 1, since two molecules in the asymmetric unit must be considered. Initially, molecules A of form 2 (denoted as form 2A) generate a chain through C–H⋯π short contacts, and these chains intersect with the adjacent molecule B of form 2 (form 2B) through C–H⋯N and C–H⋯π to form the herringbone sheet (displayed as red sheets in Fig. 5b). Additionally, neighbouring 2D sheets construct a 3D framework throughout the whole lattice by interactions of adjoining benzene rings from different form 2B molecules (highlighted by blue molecules in Fig. 5b).
To further investigate quantitatively and visually these intermolecular interactions in both phases, Hirshfeld surfaces are plotted in Fig. 5 and 2D fingerprints56,57 are given in Fig. 6. The individual contributions to the total binding energy are given in Fig. 6d. As shown in Fig. 5a, the big vivid red spots on the surface of form 1 belong to the short contacts of N⋯H, which are represented by two spikes in the 2D fingerprint plots (Fig. 6). The N⋯H short contacts occupy a contribution of 4.9% (Fig. 6d) to the total binding energy in form 1, which is smaller than that of form 2A (6.6%) and form 2B (5.2%). The smaller and less conspicuous red areas associated with the close C⋯H interaction (representing C–H⋯π short contacts) apparently reflects a longer distance than that of N⋯H contacts (Fig. 5a) in form 1; however, it is the dominant contact with an overwhelming contribution of 42.5% (Fig. 6d) to impact the bonding and to stabilize the interaction of the lattice. In the case of form 2, the C⋯H contacts are shorter in form 2A and 2B (see the two adjacent red spots labelled C⋯H in Fig. 5b) while longer (see the red area close to N⋯H, marked with C⋯H in Fig. 5b) than in form 1, exhibiting the denser and less conspicuous red regions on the surfaces, respectively.
It is noteworthy that, as shown in Fig. 6, the short distance of H⋯H contacts (which appear where de ≈ di or shorter than the H-atom van der Waals radius of 1.20 Å) is slightly closer (de + di < 2.4 Å, Fig. 6c) in form 2B than that in form 1 (de + di > 2.4 Å, Fig. 6a), corresponding to the molecular interplay between form 2B molecules from the neighbouring layers (highlighted by blue molecules in Fig. 5b). However, these close contacts which are shorter than the sum of H-atom van der Waals radii are usually thought to be repulsive in nature and contribute repulsion to their energy.
Visual inspection of the 2D fingerprints of form 2A (Fig. 6b) and form 2B (Fig. 6c) obviously identifies that they essentially have different fingerprints and differ from that of form 1 (Fig. 6a); therefore, the two forms are definitely different polymorphs of phenoxazine. A considerably greater range of values in de and di in form 2B and form 2A was evidently shown than that in form 1, which implies that the structure of form 2 is less dense than that of form 1. This is confirmed by comparing the mass density values, where the density of form 1 (1.331 g cm−3) is larger than that of form 2 (1.324 g cm−3) (Table 1).
The structure determination of form 1 was based on the single-crystal X-ray diffraction data.41 The structure suggests that the position of the N atom was substituted with the O atom and vice versa; therefore, half of the total sites were occupied by N atoms and half by O atoms within the entire volume of the crystal. This manifests that two different orientations of phenoxazine molecules were in its solid forms, i.e. half of them are oriented in one way while the rest will take the opposite orientation.58–62 This kind of static disorder in the structure was formed during the process of synthesis or crystallization and was affected by the conditions of the experiments.61,63 In form 2, the results are limited and do not allow one to decide on this behaviour. However, as the molecular interactions show similarities to form 1, this discordant behaviour might take place in form 2, i.e. the phenoxazine molecule can be rotated by a certain probability around the long molecular axis.
Surface crystallization of phenoxazine
The crystallization of phenoxazine on atomically flat silicon oxide surfaces with defined surface energy can be tuned in terms of polymorphism. Drop casting under environmental conditions from cyclohexane solutions results in pure form 1 which is assigned to the bulk phase or thermodynamically stable phase. Changing the solvent to ethanol reveals the formation of crystals of pure form 2. In the case of all five different types of solvents, a reduction of the evaporation rate, e.g. by covering or sealing of the substrate, results in a larger fraction of form 1 crystals. Changing to another surface crystallization method like spin coating (a method with an even larger evaporation rate of the solvent) also results in form 2 crystallites. These observations reveal that the formation of form 2 crystallites is associated with crystallization kinetics: a reduced relaxation time of the molecules due to enhanced solvent evaporation results in form 2. Please note that the boiling temperature of the used solvents (varying from 339 K for tetrahydrofuran up to 404 K for chlorobenzene) have a minor influence on the type of polymorph formed. Obviously, the variation of the evaporation rate varies less due to the differences in the boiling point than the reduced evaporation due to covering or sealing.An enhanced appearance of form 2 by increasing evaporation rates suggests that form 2 is a kinetic phase of phenoxazine, which is by definition of metastable character. This is in agreement with fundamental crystal structure considerations (discussed above) that form 1 is the thermodynamically stable phase.
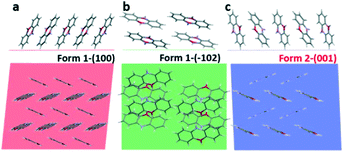
In the next step, we analyse the influence of the substrate on the crystallization of phenoxazine. For both phases a strong preferred orientation of the crystallites is observed. Combining the crystallographic information of our X-ray diffraction studies (preferred orientation) with the molecular packing within the crystal structure allows determining the orientation of the molecules relative to the substrate surface. Fig. 7 depicts the arrangement of molecules in side view (top) as well as in top view (bottom). In the case of form 1 we find the (100) plane as the contact plane (parallel to the substrate surface) and in the case of form 2 we find the (001) plane as the contact plane (Fig. 7a and c). In both cases, the herringbone layer is arranged parallel to the substrate surface and the molecules are close to standing upright. An additional orientation of the molecules is found by crystallization from cyclohexane solutions, the (−102) preferred orientation of form 1 (Fig. 7b).
Crystallisation of molecular materials at surfaces can show a variety of effects starting from different types of preferred orientation as well as the appearance of polymorphism.64,65
The formation of specific preferred orientations of crystallites relative to the substrate surface is frequently observed.66 At the molecular level, it is explained in terms of a competition of molecule/molecule interaction versus molecule/surface interaction.67 Dominant molecule/molecule interaction results in optimizing the aggregation of the molecules in terms of their strongest intermolecular interactions. Considering molecular assemblies of extended size, this can also be expressed in terms of surface energies. Low energy of the substrate surface results in the formation of a low-energy facet of the molecular crystals relative to the substrate surface. In fact, our surfaces show rather small surface energies of about 49 mN m−1, while characteristic surface energies of herringbone-packed molecules (with a rod-like shape) are considerably larger.68 The lowest surface energies are found for the herringbone layer arranged parallel to the substrate surface.68
The appearance of new polymorphs due to surface crystallisation is also a well-known phenomenon.69 Confinement to the substrate surface as well as variation of the crystallisation kinetics plays an important role.70–72 The question arises as to whether the found kinetic phase can be associated with a substrate-induced polymorph.46 Such polymorphs are frequently found when molecules crystallise at substrate surfaces and are assigned to be metastable phases, different from the thermodynamically stable phase.21 The appearance of a substrate-induced phase is associated with confinement of the molecular packing to the substrate surface.73,74 This suggests that the formation of the crystal nuclei starts at the substrate surface.75,76 For the two present cases of phenoxazine, we observe a confinement of the molecular packing to the substrate surface only in the case of form 1 (Fig. 7a), while in the case of form 2 the terminal ends of the phenoxazine molecules are not arranged within one plane (Fig. 7c). This observation indicates that the molecular packing of form 2 is not induced by the substrate surface. However, the optical microscopy images suggest that the formation of form 2 crystallites is associated with a process related to the substrate surface, since dendritic structures are found (Fig. 3d–f).
Conclusion
Crystallisation at surfaces provides a veritable tool for finding new polymorphs of molecular crystals. We studied the crystallization of the phenoxazine molecule from solution using five different solvents by varying the concentration and deposition technique. The solvent influences the formation of polymorphs, e.g., the recently characterized bulk phase (form 1) and an unknown polymorph (form 2) are found. A strong influence on polymorph formation is related to the evaporation rate of the solvent during the crystallization process. Enhanced evaporation rate induces or favors the formation of form 2. The crystal structure of form 2 is solved from thin-film samples using a combination of an experimental/theoretical approach, i.e., using grazing incidence X-ray diffraction and molecular dynamics simulations combined with density functional theory. It is found that the herringbone arrangement of the molecules is formed by 50% reversed molecules, a result already known for form 1 of phenoxazine. The molecular packing within both polymorphs is analysed by Hirshfeld surface analysis. Combining the crystal structure solution with the surface crystallization experiments reveals that form 2 is a kinetically driven metastable phase.Author contributions
M. Kaltenegger and H. Riegler prepared the thin films and performed grazing X-ray diffraction experiments; M. Kaltenegger and J. Simbrunner indexed the diffraction pattern; M. Kaltenegger and S. Hofer solved the crystal structure from experimental data; Ch. Winkler and S. Hofer were responsible for the theoretical calculations; J. Liu supervised the crystal structure solution and analysed the crystal structure and the Hirshfeld surface; M. Kaltenegger, O. Werzer, Y. Geerts, R. Resel and J. Liu prepared the first version of the manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. All authors contributed equally.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support of the Belgian National Fund for Scientific Research (FNRS) for the projects Phasetrans no. T.0058.14, Pi-Fast no. T.0072.18, and EOS 2Dto3D no. 30489208 is gratefully acknowledged. Financial support from ULB and the French Community of Belgium (ARC SADI) is also gratefully acknowledged. We thank the Elettra, Heinz Amenitsch (SAXS beamline) and Luisa Barba (XRD1 beamline) for their support. The work of C.W. was financially supported by the TU Graz Lead Project “Porous Materials at Work” (LP-03). The DFT results have been in part achieved using the Vienna Scientific Cluster (VSC3).References
- J. Bernstein, Cryst. Growth Des., 2011, 11, 632–650 CrossRef CAS.
- A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2014, 114, 2170–2191 CrossRef CAS PubMed.
- D. Singhal, Adv. Drug Delivery Rev., 2004, 56, 335–347 CrossRef CAS PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Pharm. Res., 2001, 18, 859–866 CrossRef CAS PubMed.
- L. Yu, Acc. Chem. Res., 2010, 43, 1257–1266 CrossRef CAS PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- N. L. Abraham and M. I. J. Probert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224104 CrossRef.
- S. L. Price, Phys. Chem. Chem. Phys., 2008, 10, 1996 RSC.
- B. Rodríguez-Spong, Adv. Drug Delivery Rev., 2004, 56, 241–274 CrossRef PubMed.
- P. Christian, C. Röthel, M. Tazreiter, A. Zimmer, I. Salzmann, R. Resel and O. Werzer, Cryst. Growth Des., 2016, 16, 2771–2778 CrossRef CAS PubMed.
- A. O. F. Jones, B. Chattopadhyay, Y. H. Geerts and R. Resel, Adv. Funct. Mater., 2016, 26, 2233–2255 CrossRef CAS.
- Chemical Solution Deposition of Functional Oxide Thin Films, ed. T. Schneller, R. Waser, M. Kosec and D. Payne, Springer Vienna, Vienna, 2013 Search PubMed.
- J. H. Kim, S. T. Williams, N. Cho, C.-C. Chueh and A. K.-Y. Jen, Adv. Energy Mater., 2015, 5, 1401229 CrossRef.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- M. L. Whittaker, P. M. Dove and D. Joester, MRS Bull., 2016, 41, 388–392 CrossRef CAS.
- D. Turnbull, J. Chem. Phys., 1950, 18, 198–203 CrossRef CAS.
- R. Sear, MRS Bull., 2016, 41, 363–368 CrossRef CAS.
- J. Anwar and D. Zahn, Angew. Chem., Int. Ed., 2011, 50, 1996–2013 CrossRef CAS PubMed.
- D. W. Oxtoby, J. Phys.: Condens. Matter, 1992, 25, 7627–7650 CrossRef.
- L.-W. Chen, J.-H. Chen and N. F. Zhou, J. Chem. Soc., Faraday Trans., 1995, 91, 3873 RSC.
- B. Wedl, R. Resel, G. Leising, B. Kunert, I. Salzmann, M. Oehzelt, N. Koch, A. Vollmer, S. Duhm, O. Werzer, G. Gbabode, M. Sferrazza and Y. Geerts, RSC Adv., 2012, 2, 4404 RSC.
- S. Katsamakas, A. L. Zografos and V. Sarli, Curr. Med. Chem., 2016, 23, 2972–2999 CrossRef CAS PubMed.
- E. A. Onoabedje, S. A. Egu, M. A. Ezeokonkwo and U. C. Okoro, J. Mol. Struct., 2019, 1175, 956–962 CrossRef CAS.
- A. Nowakowska-Oleksy, J. Sołoducho and J. Cabaj, J. Fluoresc., 2011, 21, 169–178 CrossRef CAS PubMed.
- R. A. AL-Okab and A. A. Syed, Spectrochim. Acta, Part A, 2007, 68, 739–746 CrossRef PubMed.
- K. M. Karlsson, X. Jiang, S. K. Eriksson, E. Gabrielsson, H. Rensmo, A. Hagfeldt and L. Sun, Chem. – Eur. J., 2011, 17, 6415–6424 CrossRef CAS PubMed.
- A. Iwata, T. Yamaguchi, K. Sato, R. Izumi and A. Tomoda, Tohoku J. Exp. Med., 2003, 200, 161–165 CrossRef CAS PubMed.
- M. A. Ezeokonkwo, S. N. Okafor, O. N. Ogbonna, E. A. Onoabedje, F. N. Ibeanu, E. U. Godwin-Nwakwasi and B. E. Ezema, Med. Chem. Res., 2020, 29, 63–74 CrossRef CAS.
- L. I. Kozlovskaya, G. Andrei, A. A. Orlov, E. V. Khvatov, A. A. Koruchekov, E. S. Belyaev, E. N. Nikolaev, V. A. Korshun, R. Snoeck, D. I. Osolodkin, E. S. Matyugina and A. V. Aralov, Antiviral Res., 2019, 163, 117–124 CrossRef CAS PubMed.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- B. Schrode, S. Pachmajer, M. Dohr, C. Röthel, J. Domke, T. Fritz, R. Resel and O. Werzer, J. Appl. Crystallogr., 2019, 52, 683–689 CrossRef CAS PubMed.
- J. Simbrunner, C. Simbrunner, B. Schrode, C. Röthel, N. Bedoya-Martinez, I. Salzmann and R. Resel, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 373–387 CrossRef CAS PubMed.
- M. P. Kainz, L. Legenstein, V. Holzer, S. Hofer, M. Kaltenegger, R. Resel and J. Simbrunner, J. Appl. Crystallogr., 2021, 54, 1256–1267 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2012 Search PubMed.
- M. Kaltenegger, L. Delaive, S. M. Gali, P. Brocorens, O. Werzer, H. Riegler, Y. H. Geerts, R. Lazzaroni, R. Resel and J. Liu, Cryst. Growth Des., 2022, 22, 1548–1553 CrossRef CAS.
- M. Birkholz, thin film analysis by X-ray scattering, John Wiley & Sons, 2006 Search PubMed.
- A. Moser, O. Werzer, H.-G. Flesch, M. Koini, D.-M. Smilgies, D. Nabok, P. Puschnig, C. Ambrosch-Draxl, M. Schiek, H.-G. Rubahn and R. Resel, Eur. Phys. J.: Spec. Top., 2009, 167, 59–65 Search PubMed.
- T. N. Krauss, E. Barrena, X. N. Zhang, D. G. de Oteyza, J. Major, V. Dehm, F. Würthner, L. P. Cavalcanti and H. Dosch, Langmuir, 2008, 24, 12742–12744 CrossRef CAS PubMed.
- S. C. B. Mannsfeld, M. L. Tang and Z. Bao, Adv. Mater., 2011, 23, 127–131 CrossRef CAS PubMed.
- A. O. F. Jones, C. Röthel, R. Lassnig, O. N. Bedoya-Martínez, P. Christian, I. Salzmann, B. Kunert, A. Winkler and R. Resel, CrystEngComm, 2017, 19, 1902–1911 RSC.
- R. Resel, A. Pichler, A. Neuhold, T. Dingemans, G. Schwabegger, C. Simbrunner, M. Moret and J. Simbrunner, Z. Kristallogr. - Cryst. Mater., 2014, 229, 385–393 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 473–482 CrossRef.
- T. Kakudate, N. Yoshimoto and Y. Saito, Appl. Phys. Lett., 2007, 90, 081903 CrossRef.
- A. Moser, I. Salzmann, M. Oehzelt, A. Neuhold, H.-G. Flesch, J. Ivanco, S. Pop, T. Toader, D. R. T. Zahn, D.-M. Smilgies and R. Resel, Chem. Phys. Lett., 2013, 574, 51–55 CrossRef CAS.
- R. Resel, N. Koch, F. Meghdadi, G. Leising, L. Athouel, G. Froyer and F. Hofer, Cryst. Res. Technol., 2001, 36, 47–54 CrossRef CAS.
- C. C. Mattheus, A. B. Dros, J. Baas, A. Meetsma, J. L. de Boer and T. T. M. Palstra, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 939–941 CrossRef CAS PubMed.
- A. Burger and R. Ramberger, Microchim. Acta, 1979, 72, 259–271 CrossRef.
- M. Oehzelt, G. Heimel, R. Resel, P. Puschnig, K. Hummer, C. Ambrosch-Draxl, K. Takemura and A. Nakayama, J. Chem. Phys., 2003, 119, 1078–1084 CrossRef CAS.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814 RSC.
- P. Müller, Crystallogr. Rev., 2009, 15, 57–83 CrossRef.
- C. C. Wilson, Crystallogr. Rev., 2009, 15, 3–56 CrossRef CAS.
- M. Habgood, R. Grau-Crespo and S. L. Price, Phys. Chem. Chem. Phys., 2011, 13, 9590 RSC.
- E. E. Rodriguez, A. Llobet, T. Proffen, B. C. Melot, R. Seshadri, P. B. Littlewood and A. K. Cheetham, J. Appl. Phys., 2009, 105, 114901 CrossRef.
- L. H. Thomas, T. R. Welberry, D. J. Goossens, A. P. Heerdegen, M. J. Gutmann, S. J. Teat, P. L. Lee, C. C. Wilson and J. M. Cole, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 663–673 CrossRef CAS PubMed.
- S. A. Barnett, A. T. Hulme and D. A. Tocher, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, o412–o415 CrossRef PubMed.
- H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933 RSC.
- A. M. Hiszpanski, R. M. Baur, B. Kim, N. J. Tremblay, C. Nuckolls, A. R. Woll and Y.-L. Loo, J. Am. Chem. Soc., 2014, 136, 15749–15756 CrossRef CAS PubMed.
- R. Resel, J. Phys.: Condens. Matter, 2008, 20, 184009 CrossRef.
- J. Taborski, P. Väterlein, H. Dietz, U. Zimmermann and E. Umbach, J. Electron Spectrosc. Relat. Phenom., 1995, 75, 129–147 CrossRef CAS.
- D. Nabok, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B, 2008, 77, 245316 CrossRef.
- D. Gentili, M. Gazzano, M. Melucci, D. Jones and M. Cavallini, Chem. Soc. Rev., 2019, 48, 2502–2517 RSC.
- D. Reischl, C. Röthel, P. Christian, E. Roblegg, H. M. A. Ehmann, I. Salzmann and O. Werzer, Cryst. Growth Des., 2015, 15, 4687–4693 CrossRef CAS PubMed.
- F. Paulus, B. D. Lindner, H. Reiß, F. Rominger, A. Leineweber, Y. Vaynzof, H. Sirringhaus and U. H. F. Bunz, J. Mater. Chem. C, 2015, 3, 1604–1609 RSC.
- J. Zablocki, O. Arteaga, F. Balzer, D. Hertel, J. J. Holstein, G. Clever, J. Anhäuser, R. Puttreddy, K. Rissanen, K. Meerholz, A. Lützen and M. Schiek, Chirality, 2020, 32, 619–631 CrossRef CAS PubMed.
- S. Schiefer, M. Huth, A. Dobrinevski and B. Nickel, J. Am. Chem. Soc., 2007, 129, 10316–10317 CrossRef CAS PubMed.
- R. Resel, A. O. F. Jones, G. Schweicher, R. Fischer, N. Demitri and Y. H. Geerts, IUCrJ, 2018, 5, 304–308 CrossRef CAS PubMed.
- R. Ruiz, D. Choudhary, B. Nickel, T. Toccoli, K.-C. Chang, A. C. Mayer, P. Clancy, J. M. Blakely, R. L. Headrick, S. Iannotta and G. G. Malliaras, Chem. Mater., 2004, 16, 4497–4508 CrossRef CAS.
- C. Lercher, C. Röthel, O. M. Roscioni, Y. H. Geerts, Q. Shen, C. Teichert, R. Fischer, G. Leising, M. Sferrazza, G. Gbabode and R. Resel, Chem. Phys. Lett., 2015, 630, 12–17 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2036900 (form 2). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00479h |
| This journal is © The Royal Society of Chemistry 2022 |