Three-state molecular potentiometer based on a non-symmetrically positioned in-backbone linker

Abstract

We report on the synthesis and single-molecule conductance of a para-oligo(phenylene)ethynylene (p-OPE) derivative with three well-defined conductance states. Employing theoretical models and comparing to reference compounds we show that this effect is due to the presence of the internal non-symmetrically placed pyrimidine ring, acting as an in-backbone anchor group. This is the first example in which the non-symmetric positioning of an internal binding site opens up two new conduction channels, giving rise, in a simple way, to a system that displays three conduction pathways which differ distinctively in both conductance and length.

---

Introduction

The knowledge gained thus far in the field of molecular electronics has demonstrated that molecules can emulate the function of different electronic components of macroscopic circuits. Many examples of molecular wires,^1–9 transistors,¹⁰ and two-state switches^11–15 have been demonstrated. Molecules able to act as multistate switches are particularly desirable as they may be envisaged in high-density data storage.¹⁶ In this context, some examples based on redox,^17–19 light-driven²⁰ and proton transfer²¹ processes have been proposed, but examples of molecules with more than two conductance values derived from different conduction pathways are scarce.^22–25 Kiguchi et al. proposed the concept of “switch-of-anchor” using a quaterthiophene-based (QT) molecular wire. This molecule displayed three different conductance signals, depending on the position of the thiophene groups interacting with the electrodes.²² A similar strategy was presented by Iwane et al. using a tripyridyl-triazine in which every heterocyclic ring behaved itself as an independent binding site.²³ All these studies agree in the use of several anchor points along the molecule backbone in order to create the target multichannel systems. Moreover, every conduction pathway is related with a particular length, so the switch between them can be controlled by modulating the distance between the electrodes in the junction. However, for this idea to be practical, it is essential to achieve well-defined conductance ranges together with well-separated path lengths. These requirements were not fulfilled in the previous examples, for which either the conductance or length values significantly overlap due to the typical junction-to-junction variations in molecular bridges. Molecules with multiple conduction pathways have the potential to encode information in their structure as function of their length, or even to act as molecular potentiometers under a mechanical stimulus.^26–33 Another important aspect in such systems is the ratio between the highest and the lowest conductance value, referred to as its switching factor. This parameter is key for quantifying the potential modulation of the total resistance performed by a potentiometer. Very recently, Li et al. reported that helical o-phenylenes could act as efficient potentiometers with switching factors of up to 150.³³ This value demonstrated by Li et al. greatly improves upon those obtained for linear molecules with two conductance pathways.^26–28,32 Among the few existing studies on compounds displaying three conductance pathways, the largest reported switching factor is about 1000 between the highest and lowest conductance paths.²³

Previously, we found that a symmetric pyrimidine-containing para-(phenylene)ethylene-type oligomer (p-OPE) displayed two well-spaced conductance pathways.³⁴ This behaviour was due to the unique binding properties of an in-backbone pyrimidine ring, whose ability to efficiently bind to the gold surface established a new and short conductance channel displaying a higher conductance value from that of the end-to-end configuration. This observation encouraged us to hypothesize that placement of a single heterocyclic ring at a specific position in this kind of linear backbone could result in three conductance pathways of different enough length to give rise to easily distinguishable conductance signals (Fig. 1).

Fig. 1 Working hypothesis: non-symmetric pyrimidine-based p-OPE with three different conductance pathways.

In this work, in order to demonstrate this hypothesis, we have designed and synthesised a new pyrimidine-based OPE derivative with the heterocycle placed in a non-symmetric position (Fig. 2, OPE4-pym) and also a series of analogous compounds to mimic the possible different conductance pathways (Fig. 2, OPE4-OMe, OPE3/S-pym and OPE2/S-pym). Thiomethyl (SMe) groups were used as terminal anchors for their efficient interaction with gold electrodes^35,36 without any specific deprotection step required as for other derivatives (e.g. acetyl protected thiols),³⁷ as well as their advantages against thiolate groups, such as lower reactivity and prevention of AuS oligomerization.³⁸ The single-molecule conductance of the compounds was studied using the scanning tunneling microscope (STM) break-junction technique³⁹ with a home-built STM. We show that our proposed molecular potentiometer, OPE4-pym, successfully produces three well-defined conductance signals separated by nearly 2 orders of magnitude, in molecular bridges with a length difference of around 0.6 nm. Comparison with theoretical calculations, as well as with the results of the reference compounds, allows us to assign these signals to one S-to-S pathway (where S is the sulphur in the SMe group) and two S-to-pyrimidine ones as schematized in Fig. 2.

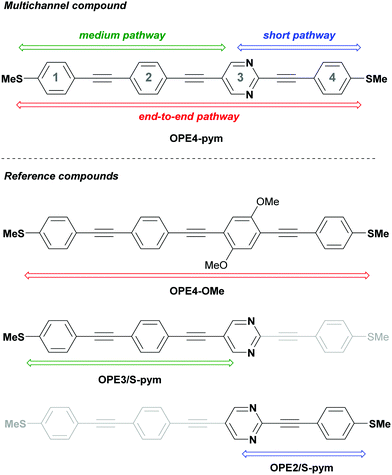Fig. 2 Structure of multichannel compound OPE4-pym and reference compounds for each possible conduction pathway.

Results and discussion

The single molecule conductance of all compounds was studied using the STM break-junction technique with an STM designed and built in house. The compounds were deposited onto gold-on-quartz substrates via a dip-coating procedure from CH₂Cl₂ solutions. The experiments were carried out in air, and we used mechanically cut gold wire as tips. Full details about the experiments are described in the experimental and theoretical methods section below.

Single-molecule experiments for pyrimidine-based OPE4-pym

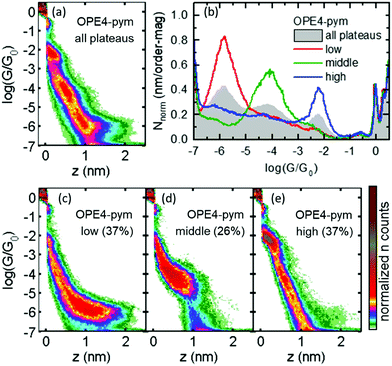
The 2D conductance histogram obtained for OPE4-pym is shown in Fig. 3a. This was built from thousands of individual conductance (G) versus distance (z) traces with molecular plateaus recorded during the retraction stage of the indentation cycles of the STM tip within the substrate (see ESI† for details). All histograms shown in Fig. 3 were built with traces from at least three different experimental runs using different tips and substrates, and after running an automatized routine that detects traces with plateaus (see ESI,† Fig. S1). It resulted in a complex histogram with three clear conductance groups of well-separated conductance and plateau length. For a better characterization of these three conductance states, we used a k-means clustering-based analysis⁴⁰ that allowed us to isolate the individual traces from each group. The independent 1D and 2D histograms for the three groups are presented in Fig. 3b and c–e respectively. Each group contains a very similar number of traces (37%, 26% and 37% of the total number of traces displaying plateaus recorded). In addition, the histograms of all the traces with and without plateaus of OPE4-pym are compared with the blank experiment with the substrate exposed to only solvent in Fig. S1 and S2 of the ESI.†

Fig. 3 (a) 2D histogram for OPE4-pym build from all traces displaying plateaus, (b) 1D histogram for all traces displaying plateaus of OPE4-pym (grey background) and those corresponding to low (red), middle (green) and high (blue) conductance after clustering analysis, (c), (d), and (e) 2D histograms of the three different groups of plateaus obtained after the clustering-based analysis method.

The average conductance value for each signal was determined by fitting a Gaussian curve to the corresponding 1D histograms and extracting the peak centre. This gave the following values: log (G/G₀) = −5.8 ± 0.37 for the low conductance group; log (G/G₀) = −4.1 ± 0.55 for the middle conductance group; and log (G/G₀) = −2.2 ± 0.21 for the high conductance group, where the error represents the half width at half maximum (HWHM) of the Gaussian fits. It is worth mentioning that the three molecular signals differ by almost two orders of magnitude in conductance between neighboring groups, close to the best values reported for two-path compounds, while the total variation in conductance is more than three orders of magnitude (highest to lowest group). Consequently, the switching factor for OPE-4-pym is ca. 4000. To the best of our knowledge, this value is one of the highest ever reported for single-molecule based potentiometers. Importantly, the plateau-length distributions further showed that each group contains junctions with well-separated distances. Typical mean plateau-length values are 1.7, 1.0 and 0.4 nm, for the low, middle and high conductance groups respectively (see Fig. 4b, d and f). The results of Fig. 3 show that generally only one of the conductance paths is observed per trace, although the green cloud of conductance around log (G/G₀) = −6 in Fig. 3e, highlights that the low-G configuration can sometimes form after the high-G state ruptures as the electrodes are further opened. Examples of typical single curves showing the latter are depicted in Fig. S5 of the ESI.†

Fig. 4 (a), (c) and (e) 1D histogram for the three different groups of OPE4-pym and their corresponding reference compounds. (b), (d) and (f) Plateau-length distributions for the three different groups of OPE4-pym and their corresponding reference compounds.

Comparison with reference compounds for each proposed pathway

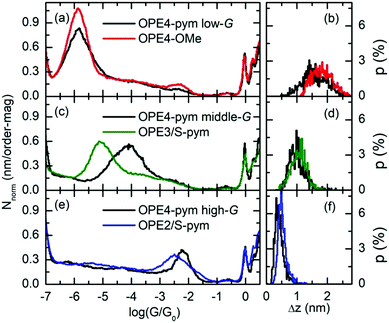
Fig. 4 summarizes the comparison of the 1D histograms and plateau-length distribution of the three groups of OPE4-pym with those of the reference compounds depicted in Fig. 2. OPE4-OMe is identical to OPE4-pym except we have exchanged the pyrimidine ring for a dimethoxyphenyl group which we do not expect to bind effectively to gold.^41,42 Firstly, in Fig. 4a the lack of any significant plateaus for OPE4-OMe leading to peaks in the histogram between log (G/G₀) = −2 and −5 shows that the features observed for OPE4-pym in this region can be ascribed to the presence of the pyrimidine ring in this compound while they cannot be formed for OPE4-OMe, without the pyrimidine ring. This proves that the pyrimidine ring is essential for a robust in-backbone linkage. Secondly, the main peak found for OPE4-OMe is in very good agreement with the low-G signal for OPE4-pym in both conductance (Fig. 4a) and plateau-length (Fig. 4b), proving that the low group corresponds to the S-to-S pathway. The results of OPE4-OMe revealed different main conductance values for experimental runs with high and low percentages of traces displaying plateaus, that could reflect the tendency for long OPE derivatives to group together via π-stacking (see ESI†). In any case, Fig. 4a shows the 1D histogram obtained for the flat-plateau group common to both regimes, attributed to just one molecule in the junction, being fully extended between the electrodes.

After showing that the two groups found between log (G/G₀) = −2 and −5 correspond to the presence of the pyrimidine ring, we next tested two further reference compounds which are analogues of shorter potential pathways through the molecule. Fig. 4c and 4d show the 1D histogram and the plateau-length distribution respectively for the molecular signals for OPE3/S-pym. This compound is equivalent to OPE4-pym except the 1-thiomethyl-4-ethynylphenylene group after the pyrimidine ring. Comparison with the results of OPE4-pym reveals this compound to have a very similar plateau length distribution to the middle conductance group, whereas the conductance peak sits below that for the full molecule. This points to OPE4-pym middle group arising from a situation in which one electrode binds to the S atom attached to ring 1 and the other electrode to the pyrimidine ring (ring 3 in Fig. 1), i.e. the ‘medium pathway’ depicted in Fig. 1. The conductance value of OPE3/S-pym is as expected, taking into account our previously reported value for a similar compound with one less phenyl group³⁴ and the general decay of one order of magnitude per phenyl ring reported for OPEs.⁴² On the other hand, the OPE4-pym middle group conductance is higher. We have also observed a similar difference in conductance between the in-backbone path and its reference model in our previous work based on OPE3 derivatives.³⁴ We believe that this is most probably caused by the direct interaction of one Au electrode with the remaining branch of the OPE4-pym on the other side of the pyrimidine ring. We will discuss this point in more detail in the next section.

Finally, Fig. 4e and 4f show the conductance histogram and plateau-length distribution for OPE2/S-pym, which models another potential pathway in OPE4-pym. Both agree well with those of the high-G group of OPE4-pym. The high conductance of these junctions is significant. Specifically, it is about one order of magnitude higher than that of thiol-OPE2-thiol, pyridine-OPE2-pyridine or thiol-OPE2-pyridine (nitrogen of pyridine either in para or ortho position), which are log (G/G₀) = −2.8, −3.2 and −3.6 respectively.^43,44 A further analysis of the data of OPE2/S-pym (see ESI†) shows that its main signal is composed of ‘sloping’ traces indeed finishing around log (G/G₀) = −3.3, suggesting that the coupling of the pyrimidine with the gold electrodes, which is initially very high, evolves as the electrodes are separated. Our results of Fig. 4e suggest that the remaining branch of OPE4-pym is stabilizing the bond of the pyrimidine, resulting in flatter plateaus of high conductance. This result highlights the double advantage of the pyrimidine versus the pyridine as an anchoring group. When placed within the backbone only the pyrimidine is able to establish a new stable conductance path, while, when placed at the end of the molecule, it enhances the molecular conductance either in meta³⁴ or in ortho position with respect to the anchor group when compared to its pyridine counterparts. This revealed as a key factor in our molecular potentiometer so as to achieve a high switching factor.

Overall, the comparison of the results for the reference compounds with those for the three signals of OPE4-pym support our initial hypothesis of the three conductance paths of our molecular potentiometer.

Theoretical modelling for junctions of OPE4-pym and their reference compounds

To gain further insight into the origin of the three conductance groups observed for OPE4-pym in the experiments, we carried out electron-transport calculations based on density functional theory (DFT) and non-equilibrium Green's function techniques (NEGF), following the procedure described in the “Theoretical Methods” subsection. We built four different geometries (displayed in Fig. 5) corresponding to plausible situations which can occur in the experiments. In what follows, we will refer to the “2-ring fragment” as the part of the molecule containing the heterocycle and the adjacent phenyl-SMe moiety (rings 3 and 4 in Fig. 2, equivalent to OPE2/S-pym), while we will refer to the “3-ring fragment” as the part of the molecule containing the heterocycle and the tolane-SMe moiety (rings 1, 2 and 3 in the same figure, equivalent to OPE3/S-pym). Geometry ‘a’ is the structure with the longest Au-Au distance (2.95 nm) and is obtained by connecting the molecule to gold through the SMe group on each side. As this group prefers binding to undercoordinated gold atoms,^28,45 only a top-binding geometry was considered. In geometry ‘b’ (with a shorter Au-Au distance of 1.69 nm), the 2-ring fragment is physisorbed on a lateral face of the lower gold electrode while the other end of the molecule is connected to the upper electrode via the SMe group. Thus, the shortest conductance pathway through the molecule is via the 3-ring fragment. In the reverse situation (geometry ‘d’) the 3-ring fragment is adsorbed on the lateral face of the lower electrode, leaving the shortest pathway through the molecule via the 2-ring fragment. The Au-Au distance is, in this case, 0.87 nm. It is worth stressing that, in both ‘b’ and ‘d’ cases, the lower terminal part of the molecule is also linked to gold via an S–Au coordination bond. Indeed, we observed that the final binding configuration at this side of the molecule was dictated by an interplay between the optimized C–S–Au angle and the physisorption interaction between the gold surface and the molecular branch. For geometry ‘c’, the heterocyclic ring is parallel to the side of the lower gold pyramid as in ‘b’ but, at the same time, also connected to gold via an N–Au bond. This geometry was obtained by relaxing the top gold atom (otherwise kept frozen), which consequently moved to the side of the pyramid, in a hollow position with respect to three surface atoms (see magnified detail in Fig. 5c) and bound to one of the two N atoms. Such a configuration would indeed be possible, given the roughness and high mobility of real gold electrodes. We were able to rule out a further potential geometry with the 3-ring fragment anchored to gold via an N–Au bond, see Fig. S12 of the ESI.†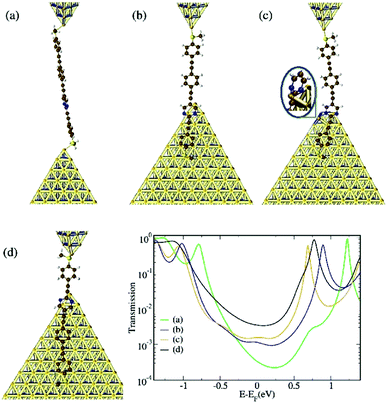

Fig. 5 (a–d) Binding geometries analyzed for OPE4-pym and the corresponding transmission curves (lower right panel).

Amongst all transmission curves displayed in the main panel of Fig. 5, the lowest conductance value (3.4 × 10⁻⁴G₀ determined by the transmission at the Fermi level) is given by geometry ‘a’ because of its longer Au–Au distance. The HOMO and LUMO in the corresponding curve are shifted to higher energy as a result of binding through S on both sides. For all the others, the LUMO sits at a lower energy as a result of the interaction between the heterocycle ring and gold. The conductance values for ‘b’ and ‘c’ are similar despite the aforementioned differences in the Au-heterocycle bond: only the energy alignment of the LUMO resonance seems to be affected (being shifted downwards in ‘c’ as a consequence of the direct N–Au bond), leaving the transmission in the region around the Fermi level relatively unmodified. Indeed, the transmission in the energy region immediately above the HOMO resonance is unaffected by the N–Au bond as the orbitals localized on the heterocycle lie further down in energy with respect to the HOMO. We believe that the experimental middle-G group could in principle be ascribed to either configuration ‘b’ or ‘c’, although the extra Au–N bond in ‘c’ is clearly expected to provide the junction with some extra mechanical stability. Due to the large width of the middle-G signal (with larger HWHM than the other groups, see Fig. 4), potentially both configurations are contributing. Finally, geometry ‘d’ yields the highest conductance values (3.5 × 10⁻³G₀), because of the very short Au–Au distance. We envisage that formation of an extra Au–N bond like in geometry ‘c’ should also be possible for this type of configuration. We also investigated the role of the physisorbed branches towards the electrical conductance by comparing geometry ‘b’ with OPE3/S-pym and ‘d’ with OPE2/S-pym (see ESI†). This analysis revealed that the direct interaction of the lower branch with the gold electrode (taking place via both the SMe anchoring and the gold–molecular π system interaction) not only ensures mechanical stability, but it also affects the size of the HOMO–LUMO gap of the system and, consequently, the conductance. This rationalizes the higher conductance of the middle-G group of OPE4-pym in relation to OPE3/S-pym found experimentally. For OPE2/S-pym, the difference found both experimentally and theoretically between this compound and the high-G group is less clear.

Overall, these theoretical results agree with the experimental findings well, despite the quantitative disagreement stemming from the well-known inaccuracies in DFT (and consequent HOMO–LUMO gap underestimation): the transmission curves of OPE4-pym in Fig. 5 show three main conductance groups, with a similar conductance variation from geometry ‘a’ to geometries ‘b’–‘c’, as from geometry ‘b’–‘c’ to geometry ‘d’, which we can relate to the also equivalent experimental changes in conductance from low- to middle- and from middle- to high-G groups. The agreement is also supported by the comparison of the experimental plateau-length values of Fig. 4b, d and f with those of the proposed configurations in Fig. 5. The typical values at the right end of the distributions (90th percentile of the total values) are 2.3, 1.4 and 0.6 nm, for the low, middle and high conductance groups of OPE4-pym respectively. These upper percentile values are expected to agree with the fully-stretched configuration, parallel to the direction of stretching, of each conductance path. Indeed, taking into account the gold relaxation after the breaking of the gold–gold contact (∼0.4 nm),⁴⁶ these values agree well with the aforementioned theoretical expected values of 2.95, 1.69 and 0.87 nm for configurations a, b and d in Fig. 5 respectively.

Conclusions

We have demonstrated a three-state multichannel system based on a simple p-OPE molecular backbone. Together with the primary end-to-end pathway, two extra conduction paths were observed, both shorter and of higher conductance. This is a result of the presence of the inner pyrimidine ring incorporated within the molecular backbone. The non-symmetric location of this group ensured a different length for the three conductance channels, giving rise to well-spaced signals. The conductance of each group is determined by an interplay between the gold–gold distance and the anchoring which, in the case of the middle- and high- conductance group, involves both the SMe and the gold–π interaction. The new conductance pathways increased the conductance by approximately two and four orders of magnitude respectively, compared to the original sulfur-to-sulfur pathway. These values constitute a switching factor of ca. 4000, one of the highest reported in literature. The key role of the pyrimidine ring in the generation of multiple conductance pathways in OPE4-pym was also confirmed by comparison with reference compounds and supported by electron-transport DFT-NEGF calculations. To our best knowledge, this is the first example whereby a non-symmetric molecule is used in a simple and direct strategy for generating three conduction paths of clearly differentiated conductance and length.

Experimental and theoretical methods

Synthesis and characterisation

Compound OPE4-pym and its reference compounds OPE4-OMe, OPE3/S-pym, OPE2/S-pym were prepared by Sonogashira cross-coupling reactions.⁴⁷ Experimental procedures are described in detail in the ESI.† The characterisation of intermediate compounds and copies of ¹H- and ¹³C-NMR spectra for every compound are provided in the ESI.† Characterisation of the studied molecules is shown below.

OPE4-pym . δ ¹H NMR (500 MHz; CD₂Cl₂) 8.84 (s, 2H), 7.56 (d, J = 3.2 Hz, 6H), 7.46 (d, J = 8.4 Hz, 2H), 7.26 (d, J = 8.5 Hz, 2H), 7.24 (d, J = 8.4 Hz, 2H), 2.52 (s, 3H), 2.51 (s, 3H). δ¹³C NMR (126 MHz; CD₂Cl₂) 159.5 (CH), 151.4 (C), 142.8 (C), 140.9 (C), 133.3 (CH), 132.4 (CH), 132.3 (CH), 132.1 (CH), 126.3 (CH), 126.1 (CH), 125.0 (C), 122.1 (C), 119.4 (C), 118.2 (C), 117.6 (C), 97.6 (C), 92.3 (C), 90.1 (C), 89.3 (C), 87.3 (C), 85.1 (C), 15.6 (CH₃), 15.4 (CH₃). HRMS (ES): m/z [M + H]⁺ calcd for C₃₀H₂₁N₂S₂: 473.1146; found: 473.1133.

OPE4-OMe . δ ¹H NMR (500 MHz; CDCl₃) δ 7.54 (d, J = 8.5 Hz, 2H), 7.51–7.46 (m, 4H), 7.44 (d, J = 8.5 Hz, 2H), 7.21 (dd, J = 8.5, 2.2 Hz, 4H), 7.03 (s, 2H), 3.91 (s, 3H), 3.91 (s, 3H), 2.51 (s, 6H). δ¹³C NMR (126 MHz; CDCl₃) δ 154.1 (C), 154.0 (C), 139.8 (C), 139.7 (C), 132.1 (CH), 132.0 (CH), 131.8 (CH), 131.6 (CH), 126.0 (CH), 125.9 (CH), 123.4 (C), 123.1 (C), 119.6 (C), 119.4 (C), 115.7 (CH), 113.8 (C), 113.2 (C), 95.2 (C), 94.9 (C), 91.4 (C), 89.4 (C), 87.7 (C), 85.9 (C), 56.6 (CH₃), 15.5 (CH₃). HRMS (ES): m/z [M + H]⁺ calcd for C₃₄H₂₇O₂S₂: 531.1452; found: 531.1442.

OPE3/S-pym . δ ¹H NMR (400 MHz; CD₂Cl₂) 9.12 (s, 1H), 8.86 (s, 2H), 7.55 (d, J = 2.0 Hz, 4H), 7.46 (d, J = 8.4 Hz, 2H), 7.24 (d, J = 8.4 Hz, 2H), 2.51 (s, 3H). δ¹³C NMR (101 MHz; CD₂Cl₂) 159.2 (CH), 157.4 (CH), 140.9 (C), 132.4 (CH), 132.3 (CH), 132.1 (CH), 126.3 (CH), 124.9 (C), 122.1 (C), 120.2 (C), 119.4 (C), 96.0 (C), 92.2 (C), 89.3 (C), 84.7 (C), 15.6 (CH₃). HRMS (ES): m/z [M + H]⁺ calcd for C₂₁H₁₅N₂S: 327.0956; found: 327.0950.

OPE2/S-pym . δ ¹H NMR (400 MHz, CD₂Cl₂) 8.72 (d, J = 5.0 Hz, 2H), 7.56 (d, J = 8.5 Hz, 2H), 7.27–7.21 (m, 3H), 2.51 (s, 3H). δ¹³C NMR (101 MHz, CD₂Cl₂) 157.8 (CH), 153.8 (C), 142.4 (C), 133.2 (CH), 126.1 (CH), 120.2 (CH), 117.7 (C), 88.9 (C), 87.6 (C), 15.4 (CH₃). HRMS (ES): m/z [M + H]⁺ calcd for C₁₃H₁₁N₂S: 227.0643; found: 227.0641.

Break-junction experiments

We created the molecular junctions using the break-junction technique with a home-built scanning tunneling microscope (STM) operating in ambient conditions (see ESI† for further information about this technique). We used commercial gold samples on quartz (Arrandee), and a freshly cut gold wire as tip. The samples were prepared by immersing the substrate in 10⁻⁴ M solutions of compounds of interest in CH₂Cl₂ for 5 min and drying them under a flow of nitrogen. A constant 160 mV bias voltage was applied between tip and substrate for the measurement. We used a linear current-to-voltage (I–V) converter with two amplification stages. The gains, of 10⁸ and 3.5 × 10¹⁰ V A⁻¹ respectively, were selected in order to obtain an appropriate range of conductance G = I/V for the compounds under study (8 orders of magnitude between 10G₀ and 10⁻⁷G₀ (G₀ = 2e²/h)). A protection resistor of 2 × 10⁶ Ω was placed in-series with the STM circuit.

Theoretical methods

Calculations based on density functional theory (DFT) were performed to determine the geometry and electronic structure of the molecular junctions. To this aim, the quantum chemistry code TURBOMOLE⁴⁸ was used, using a split-valence basis set with polarization functions⁴⁹ for all non-hydrogen atoms and the BP86 exchange–correlation functional.⁵⁰ The gold–molecule–gold junctions were built by placing the relaxed structures of the gas-phase molecules between two Au clusters of 35 and 242 atoms, respectively, and by performing a new optimization of the molecule, keeping the gold atoms frozen (if not stated otherwise). The DFT-D3 correction⁵¹ for the dispersive forces was included in the optimization of the geometries. The low-bias transmission of the junctions was then computed in the spirit of the Landauer formalism using Green's function techniques and following the previously described procedure.⁵² The conductance is given by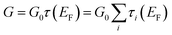 , where G₀ is the conductance quantum 2e²/h, E_F is the Fermi level, and {τ_i} are the transmission coefficients.

Authors contributions

Lucía Palomino-Ruiz: conceptualization, investigation, validation, formal analysis, writing – review & editing, visualization. Pablo Reiné: investigation, validation, formal analysis. Irene R. Márquez: investigation, validation, formal analysis. Luis Álvarez de Cienfuegos: conceptualization, investigation, formal analysis. Nicolás Agraït: methodology, formal analysis. Juan M. Cuerva: conceptualization, supervision, funding acquisition, writing – review & editing. Araceli G. Campaña: conceptualization, supervision, funding acquisition. Edmund Leary: formal analysis, writing – review & editing. Delia Miguel: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review & editing. Alba Millán: methodology, funding acquisition, supervision, writing – original draft, writing – review & editing. Linda A. Zotti: methodology, investigation, writing – original draft, writing – review & editing. M. Teresa González: conceptualization, formal analysis, funding acquisition, project administration, supervision, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the Secretaría de Estado de Investigación, Desarrollo e Innovación (Spain; CTQ2017-85454-C2-1-P), the Ministerio de Ciencia, Innovación y Universidades (MICINN, Spain; PGC2018-101181-B-I00; PGC2018-101873-A-I00) and the Comunidad de Madrid (project NanoMagCOST, CM S2018/NMT-4321). We also thank the Severo Ochoa Programme for Center of Excellence in R&D (SEV-2016-0686), the “María de Maeztu” Programme for Units of Excellence in R&D (grant No. CEX2018-000805-M) and the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (ERC-2015-STG-677023) for financial support. E. L. thanks the Comunidad de Madrid Atracción de Talento grant 2019-T1/IND-16384. P. R. thanks MINECO for a FPU contract and Universidad de Granada for a “Contrato-Puente”. I. R. M. thanks MICINN for a Personal Técnico de Apoyo contract (PTA2017-13681-I). L. A. Z. acknowledges the computer resources provided by the Centro de Computación Científica of the Universidad Autónoma de Madrid.

References

1. S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482.
2. Q. Lu, K. Liu, H. Zhang, Z. Du, X. Wang and F. Wang, ACS Nano, 2009, 3, 3861.
3. S. H. Choi, C. Risko, M. C. Ruiz Delgado, B. Kim, J.-L. Brédas and C. D. Frisbie, J. Am. Chem. Soc., 2010, 132, 4358.
4. L. Luo and C. D. Frisbie, J. Am. Chem. Soc., 2010, 132, 8854.
5. L. Luo, S. H. Choi and C. D. Frisbie, Chem. Mater., 2011, 23, 631.
6. K. H. Khoo, Y. Chen, S. Li and S. Y. Quek, Phys. Chem. Chem. Phys., 2015, 17, 77.
7. D. M. Guldi, H. Nishihara and L. Venkataraman, Chem. Soc. Rev., 2015, 44, 842.
8. Y. Zang, T. Fu, Q. Zou, F. Ng, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2020, 20, 8415.
9. F. G. Guijarro, S. Medina Rivero, S. Gunasekaran, I. Arretxea, R. Ponce Ortiz, R. Caballero, P. de la Cruz, F. Langa, L. Venkataraman and J. Casado, RSC Adv., 2020, 10, 41264.
10. M. L. Perrin, E. Burzuría and H. S. J. van der Zant, Chem. Soc. Rev., 2015, 44, 902.
11. N. Fuentes, A. Martín-Lasanta, L. Álvarez de Cienfuegos, M. Ribagorda, A. Parra and J. M. Cuerva, Nanoscale, 2011, 3, 4003.
12. M. Koole, J. M. Thijssen, H. Valkenier, J. C. Hummelen and H. S. J. van der Zant, Nano Lett., 2015, 15, 5569.
13. J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998.
14. Z. Liu, S. Ren and X. Guo, Top. Curr. Chem., 2017, 375, 56.
15. Y. Chen, L. Huang, H. Chen, Z. Chen, H. Zhang, Z. Xiao and W. Hong, Chin. J. Chem., 2021, 39, 421.
16. H. Li, Q. Xu, N. Li, R. Sun, J. Ge, J. Lu, H. Gu and F. Yan, J. Am. Chem. Soc., 2010, 132, 5542.
17. C. Simão, M. Mas-Torrent, J. Casado-Montenegro, F. Otón, J. Veciana and C. Rovira, J. Am. Chem. Soc., 2011, 133, 13256.
18. P.-Y. Gu, F. Zhou, J. Gao, G. Li, C. Wang, Q.-F. Xu, Q. Zhang and J.-M. Lu, J. Am. Chem. Soc., 2013, 135, 14086.
19. H. Chan, H.-L. Wong, M. Ng, C.-T. Poon and V. W.-W. Yam, J. Am. Chem. Soc., 2017, 139, 7256.
20. C. Ye, Q. Peng, M. Li, J. Luo, Z. Tang, J. Pei, J. Chen, Z. Shuai, L. Jiang and Y. Song, J. Am. Chem. Soc., 2012, 134, 20053.
21. W. Auwäter, K. Seufert, F. Bischoff, D. Ecija, S. Vijayaraghavan, S. Joshi, F. Klappenberger, N. Samudrala and J. V. Barth, Nat. Nanotechnol., 2012, 7, 41.
22. M. Kiguchi, T. Ohto, S. Fujii, K. Sugiyasu, S. Nakajima, M. Takeuchi and H. Nakamura, J. Am. Chem. Soc., 2014, 136, 7327.
23. M. Iwane, S. Fujii, T. Nishino and M. Kiguchi, J. Phys. Chem. C, 2016, 120, 8936.
24. M. El Abbassi, P. Zwick, A. Rates, D. Stefani, A. Prescimone, M. Mayor, H. S. J. van der Zant and D. Dulić, Chem. Sci., 2019, 10, 8299.
25. C. Seth, V. Kaliginedi, S. Suravarapu, D. Reber, W. Hong, T. Wandlowski, F. Lafolet, P. Broekmann, G. Royal and R. Venkatramani, Chem. Sci., 2017, 8, 1576.
26. J. S. Meisner, M. Kamenetska, M. Krikorian, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nano Lett., 2011, 11, 1575.
27. T. A. Su, J. R. Widawsky, H. Li, R. S. Klausen, J. L. Leighton, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, J. Am. Chem. Soc., 2013, 135, 18331.
28. T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7, 215.
29. P. Moreno-García, A. La Rosa, V. Kolivoška, D. Bermejo, W. Hong, K. Yoshida, M. Baghernejad, S. Filippone, P. Broekmann, T. Wandlowski and N. Martín, J. Am. Chem. Soc., 2015, 137, 2318.
30. L. Chen, Y.-H. Wang, B. He, H. Nie, R. Hu, F. Huang, A. Qin, X.-S. Zhou, Z. Zhao and B. Z. Tang, Angew. Chem., Int. Ed., 2015, 54, 4231.
31. Y. Komoto, Y. Yamazaki, Y. Tamaki, M. Iwane, T. Nishino, O. Ishitani, M. Kiguchi and S. Fujii, Chem. – Asian J., 2018, 13, 1297.
32. Z. Cai, N. Zhang, M. A. Awais, A. S. Filatov and L. Yu, Angew. Chem., Int. Ed., 2018, 57, 6442.
33. J. Li, P. Shen, S. Zhen, C. Tang, Y. Ye, D. Zhou, W. Hong, Z. Zhao and B. Z. Tang, Nat. Commun., 2021, 12, 167.
34. D. Miguel, L. Álvarez de Cienfuegos, A. Martín-Lasanta, S. P. Morcillo, L. A. Zotti, E. Leary, M. Bürkle, Y. Asai, R. Jurado, D. J. Cárdenas, G. Rubio-Bollinger, N. Agraït, J. M. Cuerva and M. T. González, J. Am. Chem. Soc., 2015, 137, 13818.
35. Y. S. Park, A. C. Whalley, M. Kamenetska, M. L. Steigerwald, M. S. Hybertsen, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2007, 129, 15768.
36. M. Frei, S. V. Aradhya, M. S. Hybertsen and L. Venkataraman, J. Am. Chem. Soc., 2012, 134, 4003.
37. H. Valkenier, E. H. Huisman, P. A. van Hal, D. M. de Leeuw, R. C. Chiechi and J. C. Hummelen, J. Am. Chem. Soc., 2011, 133, 4930.
38. E. Leary, L. A. Zotti, D. Miguel, I. R. Márquez, L. Palomino-Ruiz, J. M. Cuerva, G. Rubio-Bollinger, M. T. González and N. Agraït, J. Phys. Chem. C, 2018, 122, 3211.
39. B. Xu and J. N. Tao, Science, 2003, 301, 1221.
40. D. Cabosart, M. El Abassi, D. Stefani, R. Frisenda, M. Calame and H. S. J. van der Zant, Appl. Phys. Lett., 2019, 114, 143102.
41. Methoxy groups were incorporated to one of the phenyl rings in order to enhance solubility. It is well-known that this type of side chain do not significantly modify the conductance of the whole structure. See for instance: M. T. González, X. Zhao, D. Z. Manrique, D. Miguel, E. Leary, M. Gulcur, A. S. Batsanov, G. Rubio-Bollinger, C. J. Lambert, M. R. Bryce and N. Agraït, J. Phys. Chem. C, 2014, 118, 21655.
42. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262.
43. K. Yoshida, I. V. Pobelov, D. Z. Manrique, T. Pope, G. Mészáros, M. Gulcur, M. R. Bryce, C. J. Lambert and T. Wandlowski, Sci. Rep., 2015, 5, 9002.
44. X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173.
45. M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Phys. Rev. Lett., 2009, 102, 126803.
46. C. R. Arroyo, E. Leary, A. Castellanos-Gomez, G. Rubio Bollinger, M. T. Gonzalez and N. Agrait, J. Am. Chem. Soc., 2011, 133, 14313.
47. R. Chinchilla and C. Nájera, Chem. Rev., 2007, 107, 874.
48. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165.
49. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
50. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
51. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
52. F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis details. ¹H and ¹³C spectra of new compounds. Break-junction data analysis. Additional theoretical calculations. See DOI: 10.1039/d1tc02223g

‡ These authors contributed equally.

---