Open Access Article
Open Access ArticleInsight into the drastically different triplet lifetimes of BODIPY obtained by optical/magnetic spectroscopy and theoretical computations†
Zhijia
Wang‡
 a,
Antonio
Toffoletti‡
a,
Antonio
Toffoletti‡
 b,
Yuqi
Hou
b,
Yuqi
Hou
 a,
Jianzhang
Zhao
a,
Jianzhang
Zhao
 *a,
Antonio
Barbon
*a,
Antonio
Barbon
 *b and
Bernhard
Dick
*b and
Bernhard
Dick
 *c
*c
aState Key Laboratory of Fine Chemicals, School of Chemical Engineering, Dalian University of Technology, E-208 West Campus, 2 Ling Gong Rd., Dalian 116024, China. E-mail: zhaojzh@dlut.edu.cn
bDipartimento di Scienze Chimiche, Università degli Studi di Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: antonio.barbon@unipd.it
cLehrstuhl für Physikalische Chemie, Institut für Physikalische und Theoretische Chemie, Universität Regensburg, Universitätsstr. 31, D-93053 Regensburg, Germany. E-mail: Bernhard.Dick@chemie.uni-regensburg.de
First published on 22nd December 2020
Abstract
The triplet state lifetimes of organic chromophores are crucial for fundamental photochemistry studies as well as applications as photosensitizers in photocatalysis, photovoltaics, photodynamic therapy and photon upconversion. It is noteworthy that the triplet state lifetime of a chromophore can vary significantly for its analogues, while the exact reason was rarely studied. Herein with a few exemplars of typical BODIPY derivatives, which show triplet lifetimes varying up to 110-fold (1.4–160 μs), we found that for these derivatives with short triplet state lifetimes (ca. 1–3 μs), the electron spin polarization (ESP) pattern of the time-resolved electron paramagnetic resonance (TREPR) spectra of the triplet state is inverted at a longer delay time after laser pulse excitation, as a consequence of a strong anisotropy in the decay rates of the zero-field state sublevel of the triplet state. For the derivatives showing longer triplet state lifetimes (>50 μs), no such ESP inversion was observed. The observed fast decay of one sublevel is responsible for the short triplet state lifetime; theoretical computations indicate that it is due to a strong coupling between the Tz sublevel and the ground state mediated by the spin–orbit interaction. Another finding is that the heavy atom effect on the shortening of the triplet state lifetime is more significant for the T1 states with lower energy. To the best of our knowledge, this is the first systematic study to rationalize the short triplet state lifetime of visible-light-harvesting organic chromophores. Our results are useful for fundamental photochemistry and the design of photosensitizers showing long-lived triplet states.
Introduction
The excited state lifetimes of a chromophore are fundamental properties in photochemistry, for the description of the chromophore behaviour.1–3 They are also important for applications: for instance, for the design of luminescence materials, or for luminescence bioimaging (including time-resolved or time-gated luminescence imaging and fluorescence lifetime imaging microscopy)2 and photovoltaics,4,5 as well as for the study of the fundamental photophysical factors (energy transfer and electron transfer).6,7 Therefore, the understanding of the processes regulating this parameter and the ability to control excited state lifetimes are pivotal in these fields.The singlet excited state lifetimes of an organic chromophore can vary from ps to a few ns. The reason for the variation could be energy transfer, electron transfer, and vibration-induced non-radiative decay.1 The knowledge in this area is relatively mature, as such the variation of the singlet excited state lifetimes can be explained very well in general, and it has been implemented in the design of functional molecules, such as fluorescent molecular probes and luminescent materials.8–10
In stark contrast, investigations on the factors dictating the decay of triplet states are rare. Although the transition T1 → S0 is spin-forbidden, very often one may observe a short or a long triplet state lifetime, but the investigation on the variation of the triplet state lifetimes in a series of derivatives sharing the same chromophore is rare.11–13 The triplet state lifetime of a photosensitizer is pivotal for the application related to electron transfer or energy transfer, especially diffusion-controlled intermolecular processes, for which the efficiency directly depends on the triplet state lifetime of the photosensitizer.2,14,15 Longer triplet state lifetimes may enhance the intermolecular processes, and this has been confirmed by photodynamic therapy (PDT),16 photon upconversion,17–19 and photocatalysis (H2 evolution).20–23
The rules for the control of singlet excited state lifetimes cannot be simply extended to triplet states. For instance, the quenching of the fluorescence (singlet state) with the intramolecular free rotor effect is common, and it has been used to design fluorescent molecular probes for the detection of microenvironment viscosity.24,25 However, we found that even if the fluorescence was efficiently quenched by the rotor effect of some BODIPY derivatives (actually it is the torsion of the molecule in the S1 state), the triplet excited state of the same molecule was not quenched by the rotor effect at all.26 It seems also clear that the general intuition of the energy gap law cannot account for the difference: the T1 state of the BODIPY chromophore is 1.6 eV above S0 whereas the S1 state of the same chromophore is at 2.2 eV. Hence also the electron spin has to be considered to account for the different quenching effect, since it may play a major role in determining the relaxation kinetics of the triplet state.
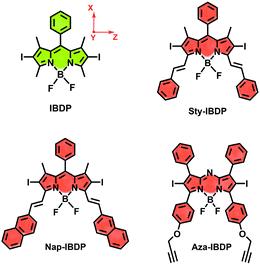
Moreover, we noted that for a specific chromophore, such as BODIPY, the triplet state lifetimes of its derivatives can vary up to 200-fold,27–30 and this property has been exploited extensively in luminescence bioimaging,31 photodynamic therapy,32 and photon upconversion.19 It has been confirmed that the excited state lifetimes of BODIPY compounds play an important role in all these applications. The molecular structure of the BODIPY chromophore can be feasibly modified and new fluorophores can be obtained in this way.27 For most of the fluorescent BODIPY derivatives with differently modified π-conjugation frameworks, the fluorescence lifetimes are in the range of a few ns. Instead, the lifetimes of the triplet state of the same chromophore can vary to a much larger extent.33 For instance, 2,6-diiodoBODIPY (IBDP) gives a triplet state lifetime of 160 μs, whereas the 2,6-diiododistyryl BODIPY analogue (Sty-IBDP) gives a surprisingly shorter triplet state lifetime (τT = 1–2 μs),34 although the un-iodinated distyryl analogues show similar singlet excited state lifetimes to native BODIPY.27 AzaBODIPY is also an intriguing fluorophore, which shows much red-shifted absorption compared to the parent BODIPY and superb stability.35,36 Interestingly, the triplet state lifetime of azaBODIPY (ca. 2 μs) is also much shorter than that of diiodoBODIPY.36,37 This is a mysterious phenomenon and it puzzled us for a long time.
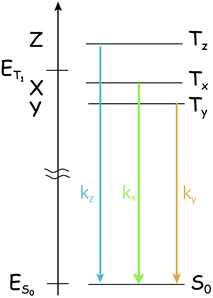
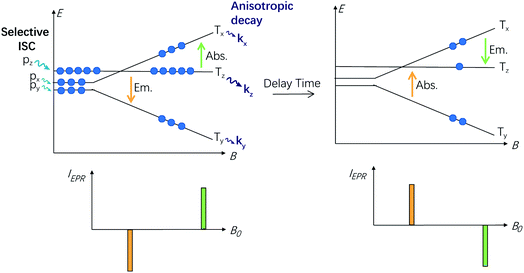
One point that marks a difference between the singlet state and the triplet states and might complicate the study of the photophysics of triplet states by optical methods is that the ‘triplet state’ is composed of three individual sublevels, even in the absence of a magnetic field. The three sublevels are not generally degenerate because of the dipole–dipole interaction between the two unpaired electrons,38 and spin/orbit terms also provide two Hamiltonian terms with the same form. The zero-field splitting (ZFS) Hamiltonian,
| HZFS = S × D × S | (1) |
acting on the spin variables, takes into account both dipole/dipole interaction and (minority) spin/orbit contributions. The eigenstates are named Tx, Ty, or Tz, and their energy displacement (eigenvalues) X, Y and Z (see Scheme 1) are the principal values (with an inverted sign) of the (traceless) D spin–spin dipolar tensor.
The lifting of the degeneracy of the three sublevels of the triplet state is rarely unveiled with the normal optical spectroscopy because the energy gaps between these sublevels normally lie in the range of 101 to 103 MHz (fraction of cm−1) for organic systems. For the normal optical spectroscopy of the compounds in fluid solution at room temperature (for instance, nanosecond transient absorption spectroscopy), the spectral resolution is not high enough to characterize the three sub-states of the T1 state, i.e. the three sublevels of the triplet state are observed as a whole. Hence some useful information is missing from the normal optical spectroscopy, such as the different population rates. In many cases this is not a real problem, due to the thermal equilibration of the substates (kinetically quantified by the electron spin-lattice relaxation time, or longitudinal relaxation time, T1; in the following, we'll use TSLR to avoid confusion with the triplet terminology), but in principle the three sublevels should be treated separately, as the intrinsic lifetime of the individual spin states Tx, Ty, and Tz is non-uniform.39–41
Several studies conducted by optical spectroscopy of transition metal complexes by the Shpol'skii matrix technique at liquid helium temperature have been published by the group of Yersin et al. These experiments can distinguish the three sublevels and yield the individual decay rate constants of the three substates (separated by large ZFS values of a few to dozens of cm−1). With the high resolution phosphorescence spectra recorded,42 the individual decay rate constants of the three sublevels can differ by one or two orders of magnitude. The advantage of high resolution luminescence spectroscopy is the direct detection of the ZFS and the energy gap between the sublevels of the triplet states.42 However, this method is only suitable for compounds showing phosphorescence, whereas many chromophores with triplet excited states populated upon photoexcitation do not give any phosphorescence. Moreover, the relative population rates of the three sublevels of the T1 state cannot be obtained with this method; therefore a more general method to study the decay of the individual substate of the T1 state is desired.
Time-resolved electron paramagnetic resonance (TREPR) is a powerful tool to study the triplet excited states, the formation of radical pairs and electron transfer processes.43–45 Concerning the study of triplet state properties, TREPR spectroscopy offers some advantages over time-resolved optical spectroscopy. Firstly, TREPR spectroscopy selectively detects the paramagnetic triplet species, not the singlet species. As a result, the spectra are without any complication from the evolution of the singlet states. Secondly, because of the high spectral resolution, TREPR can follow the evolution of the population of the single substate (in principle anisotropic).46,47 TREPR takes advantage of the ISC S1 → T1 which is electron spin selective for the zero-field states; consequently, the population rates of the three sublevels of the T1 state (both in a magnetic field and in zero-field) are different, leading to populations which are far from the Boltzmann distribution (electron spin polarization, ESP). Hence, the EPR signal will be either enhanced absorptive (A polarization) or emissive (E polarization), i.e. the EPR signal will be intensified greatly as compared to the normal steady-state EPR. Spin–orbit coupling ISC (SO-ISC) is not the only mechanism leading to the population of triplet states. Other mechanisms, for example, the radical pair (RP-ISC) and the spin orbit charge transfer ISC (SOCT-ISC), can also be studied by TREPR as they produce polarized states, with a specific ESP pattern that can be distinguished by TREPR.48,49 Moreover, the individual decay of the substates of the T1 state of a compound can be directly monitored by TREPR, often by measuring the peak magnitude evolution at different canonical orientations in the TREPR spectra of the triplet state; in some cases, anisotropic decay can manifest with a change of the sign of the ESP. However, the TREPR kinetics data must be analysed carefully as often the TREPR decay kinetics is not simply related to the triplet state lifetimes and the effect of the spin-lattice relaxation (SLR) has to be considered in the studies of the electron spin dynamics.50,51
Herein we used nanosecond pulsed laser excited TREPR and transient optical absorption spectroscopy to study the triplet state in a series of typical BODIPY derivatives, which are characterized by an anomalous short and multiexponential decay. For these derivatives we observed the inversion of the ESP pattern in TREPR spectra at longer delay times after a laser flash as a marker of anisotropy in the decay rate of the triplet sublevels. In fact, with the simulation of the kinetics, based on the model reported further, we attribute the inversion of the ESP to the initial overpopulation of the Tz substate and the subsequent much faster decay of this state than the other two sublevels of the T1 state. The individual decay rate constants were derived after a careful analysis of the TREPR based on a new approach to remedy the problem of overlapping signals, which might be present at the resonance fields of the principal components in isotropic solutions. The kinetic analysis (anisotropic SLR is not the major contribution to the ESP inversion in our case52) allowed the determination of the three decay rate constants of the sublevels of the T1 state, which can vary by a factor of 20. The reason for the difference of the decay rate constants was further studied with theoretical analysis, and it is attributed to the consequences of a near C2-symmetry for the T1 state of these molecules. These results are useful for the study of fundamental photochemistry of triplet photosensitizers, for the design of new triplet photosensitizers showing longer triplet state lifetimes, as well as for the improvement of the application of triplet photosensitizers.
Results and discussion
Selection of the compounds
Most iodinated BODIPY fluorophores show similar singlet excited state lifetimes (similar fluorescence lifetimes, τF).28 Examples are, for instance, the compounds IBDP (τF = 0.19 ns) and Aza-IBDP (τF = 0.46 ns), presented in Scheme 2. However, we noted that the triplet state lifetimes of the iodinated compounds, determined by nanosecond transient absorption spectroscopy, are significantly different (Table 1). The singlet state energies of the compounds (Scheme 2 and Table 1) vary in the range of 1.78–2.29 eV, the triplet state energies vary by a similar magnitude (1.13–1.53 eV).12,53 Therefore, the energy gap law itself will unlikely play a major direct role in the variation of the different triplet state lifetimes of these compounds.1| λ abs | ε | λ em | τ F /ns | Φ F | τ T /μs | Φ Δ | |
|---|---|---|---|---|---|---|---|
| a Maximal absorption wavelength, nm. b Molar absorption coefficient, in 104 M−1 cm−1. c Fluorescence emission wavelength, nm. d Luminescence lifetimes. e Fluorescence quantum yield, with IBDP (ΦF = 2.7% in acetonitrile), 1,7-dimethyl-3,5-dipheny-8-phenyl-4,4-difluoroboradiazaindacene (ΦF = 59% in toluene) and methylene blue (ΦF = 3% in methanol) as the standards. f Intrinsic triplet excited state lifetimes. g Singlet oxygen quantum yield (ΦΔ) with methylene blue as the standard (ΦΔ = 0.57 in DCM), λex = 603 nm. | |||||||
| IBDP | 532 | 8.5 | 551 | 0.19 | 4.0% | 160 | 0.85 |
| Sty-IBDP | 636 | 9.5 | 657 | 1.8 | 15.4% | 1.7 | 0.54 |
| Nap-IBDP | 656 | 10.3 | 680 | 2.0 | 12.5% | 1.4 | 0.45 |
| Aza-IBDP | 674 | 9.3 | 712 | 0.46 | 0.07% | 3.6 | 0.82 |
The chromophore in IBDP represents the most typical BODIPY skeleton (the emission band is centred at ca. 551 nm). Its analogue Sty-IBDP is also based on a popular chromophore, bearing aromatic groups to induce red-shifted absorption up to 636 nm (Fig. 1a).27 The fluorescence emission wavelengths of IBDP and Sty-IBDP are clearly different. The triplet state energy levels of IBDP (1.53 eV by TDDFT computation) and Sty-IBDP (1.13 eV) are also different. We selected Aza-IBDP because the azaBODIPY has intrinsic red-shifted absorption (Fig. 1a),35,36 and was widely used in photochemistry studies. In order to generalize our study, we selected another molecule with an extended π-conjugation framework, Nap-IBDP (Scheme 2), which shows similar absorption maxima to Sty-IBDP and Aza-IBDP.
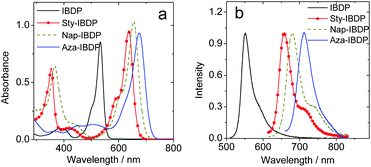 | ||
| Fig. 1 (a) UV-vis absorption spectra of the compounds. (b) Normalized fluorescence spectra of the compounds. c = 1.0 × 10−5 M in 2-methyltetrahydrofuran, 20 °C. | ||
Steady state and time-resolved optical spectroscopy
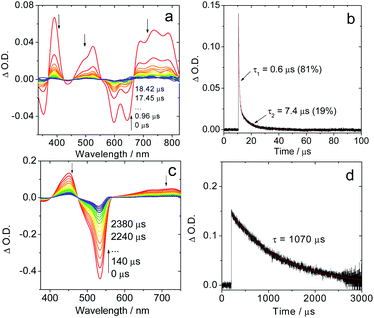
The fluorescence emission maximum is different for the various derivatives (Table 1); consequently, their respective singlet excited state energies (as approximately determined by the crossing point of the normalized UV-vis absorption and the fluorescence emission spectra) are different. Unfortunately, except for IBDP, the relative triplet state (T1) energy levels of the rest compounds are not readily available, because these compounds are not phosphorescent, even in frozen solution at 77 K (wavelength detection range of the spectrometer may also cause this problem. Fig. S17 and S18†). The lack of phosphorescence is likely due to the fact that the non-radiative decay rate constant is much larger than the radiative rate constant.11,54 For the above compounds, the triplet state was populated via ISC enhanced by the heavy atom effect.The nanosecond transient absorption spectra of the iodinated compounds were studied (Fig. 2). For IBDP, upon nanosecond pulsed laser excitation, the ground state bleaching band (GSB) centred at 530 nm was observed, and the excited state absorption bands (ESA) are centred at 450 nm and in the range of 600–750 nm (Fig. 2c). These features are in agreement with a previous report of the triplet state of 2,6-diiodoBODIPY.12,55 As the triplet lifetime of IBDP is long and the triplet quantum yield is high, there is a significant contribution to the decay from triplet–triplet annihilation (TTA). The decay traces of the triplet state of IBDP were analysed in three different solvents (2-MeTHF, toluene and acetonitrile) and a wide range of concentrations (range from 3 × 10−7 M to 2 × 10−5 M).
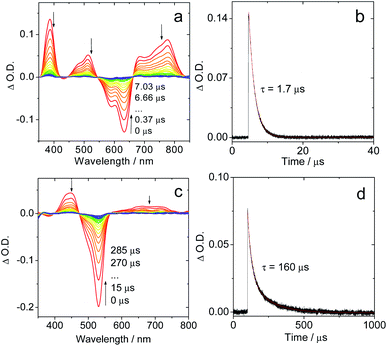 | ||
| Fig. 2 Nanosecond time-resolved transient absorption spectra of the compounds Sty-IBDP and IBDP. (a) Sty-IBDP upon ns pulsed laser excitation (λex = 600 nm) and (b) the decay trace of Sty-IBDP at 390 nm assigned to the excited state absorption of the triplet state. (c) IBDP upon ns pulsed laser excitation (λex = 533 nm) and (d) the decay trace of IBDP at 450 nm relative to the excited state absorption of the triplet state. The simulation of the decay trace was performed with a kinetic model with TTA considered (see the ESI† for details). c = 1.0 × 10−5 M in deaerated 2-methyltetrahydrofuran, 20 °C. | ||
The measurements of the triplet state lifetimes at different concentrations resulted in decay curves that apparently have different decay times; hence a contribution of TTA was considered in the analysis. At very low concentrations one might neglect the contribution of TTA, but data obtained at 3 × 10−7 M had a very weak signal (signal/noise ratio ca. 1). Nevertheless, those traces could be fitted with a monoexponential decay (Fig. S5†), resulting in decay times of 91 μs (acetonitrile), 226 μs (2-MeTHF), and 238 μs (toluene). Due to the high noise level we should expect a large uncertainty in the determination of these lifetimes. Therefore, we also made a global fit to 5 data sets for each solvent with concentrations up to 2 × 10−5 M. We used the kinetic model appropriate for a combination of intrinsic decay and TTA, setting the intrinsic lifetime equal for all data sets for a given solvent. This resulted in 85 μs (acetonitrile), 160 μs (2-MeTHF), and 172 μs (toluene) for the intrinsic lifetime (Fig. S6–S8†). These values are more reliable since they stem from data with a high signal/noise ratio.
For Sty-IBDP, the GSB and the ESA bands are in good agreement with a previous report (Fig. 2a).12 Interestingly, the triplet state lifetime of this compound is much shorter (1.7 μs) than that of IBDP. The short triplet state lifetime of Sty-IBDP is not due to the flexible molecular structure (i.e. the torsion about the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–C bonds of the stilbene moiety at excited states) because the triplet state lifetime of this compound in frozen solution (77 K) was determined to be 1.9 μs (average lifetime), similar to that at room temperature in fluid solution. The triplet state of Nap-IBDP was also studied with ns TA spectra, and a short triplet state lifetime of 1.4 μs was observed. Similar results were observed for Aza-IBDP (Fig. S1 and S3†). These directly measured triplet lifetimes of Sty-IBDP, Nap-IBDP and Aza-IBDP are intrinsic triplet lifetimes (for details, please refer to Fig. S9–S11†), because the TTA effect is negligible, as a result of the short triplet state lifetimes.
C/C–C bonds of the stilbene moiety at excited states) because the triplet state lifetime of this compound in frozen solution (77 K) was determined to be 1.9 μs (average lifetime), similar to that at room temperature in fluid solution. The triplet state of Nap-IBDP was also studied with ns TA spectra, and a short triplet state lifetime of 1.4 μs was observed. Similar results were observed for Aza-IBDP (Fig. S1 and S3†). These directly measured triplet lifetimes of Sty-IBDP, Nap-IBDP and Aza-IBDP are intrinsic triplet lifetimes (for details, please refer to Fig. S9–S11†), because the TTA effect is negligible, as a result of the short triplet state lifetimes.
In frozen solution the decay of IBDP (Fig. 3d) does not suffer from TTA, and hence the decay of nanosecond transient absorption at 77 K is monoexponential. All compounds with short triplet lifetimes show mono-exponentially decaying transient signals at room temperature. In stark contrast, multi-exponential decays of the transient signals were observed for these compounds at 77 K. For instance, the triplet state lifetimes of Sty-IBDP at 77 K were fitted as 0.6 μs (81%, population ratio) and 7.4 μs (19%, population ratio) (Fig. 3b). This result is consistent with the scenario that the individual sublevels of the compounds having different decay kinetics at 77 K.
For the compounds showing short-lived triplet states at room temperature, the mono-exponential decay of the transient signals indicates that the kinetics is an average over decay kinetics of the triplet sublevels that may differ drastically. At room temperature, the SLR is fast because Brownian motion in solution can induce the modulation of the electron–electron fine interaction.38,56 The modulation of both secular and pseudo-secular interactions produces electron spin TSLR relaxation,57 and, analogously, the modulation of the dipolar interaction with typical D-values of the order of 103 MHz (see next section) can induce an efficient re-equilibration of the three sublevels if TSLR is shorter than the electronic triplet excited state lifetime. In this case only mono-exponential decay kinetics (an averaged decay) can be detected by ns TA spectroscopy,42 whereas a different decay kinetics is detectable at 77 K in frozen solution. The fast decay channel of one sublevel, 0.6 μs (81%), should be responsible for the short triplet lifetime, which is in accordance with the TREPR spectral results.
The heavy-atom effect will enhance not only the S1 → T1 ISC, but also the T1 → S0 relaxation; thus it may shorten the triplet state lifetimes in the compounds presented in Scheme 2. The T1/S0 energy gap may play a role in the manifestation of the heavy atom effect in the triplet state lifetimes. The lifetime of an uniodinated styrylBODIPY chromophore is long (385 μs).58 This disagrees with the previously reported general rule for the fast decay of the T1 state given that the T1/S0 energy gap is small, for instance, chlorophyll.59
Time-resolved EPR: the different decay rate constants of the sublevels and their effect on the electron spin polarization (ESP) dynamics
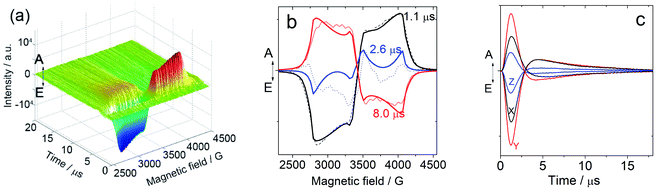
In order to study the ESP dynamics of the triplet excited state of the compounds and to unravel the reason for the drastically different triplet state lifetimes, two-dimensional time-resolved EPR spectra (2D TREPR) have been recorded for all the compounds studied in this work (IBDP, Sty-IBDP, Nap-IBDP, and Aza-IBDP). Fig. 4a shows the 2D TREPR spectrum of Sty-IBDP that is representative of the general spectral features shared by Aza-IBDP, Nap-IBDP and Sty-IBDP (the spectra are reported in Fig. S13 and S14†). For Sty-IBDP, the slices of the surface along the magnetic field at a delay time (td) of 1.1, 2.6 and 8.0 μs after the laser flash are shown in Fig. 4b. The TREPR spectrum at the shortest delay after the laser flash (∼1.1 μs) is taken near the maximum of the intensity, which is reached with a time delay of about 1 μs because of the response time of the EPR spectrometer cavity. The spectrum is typical of randomly oriented molecules with an excited triplet state ESP due to the anisotropic population of the sublevels from the first excited singlet state. The ESP pattern at early times for the three principal components (six canonical B0 positions) is eee/aaa (e: emission and a: enhanced absorption) and it is the same for all the compounds studied in this work. The other two spectra show a different pattern at longer delay times (td), i.e. aee/eaa and aaa/eee, see the spectra taken at td of 2.6 and 8.0 μs in Fig. 4b. This is the evidence of the so-called electron spin polarization inversion (the e or a feature of the canonical positions was inverted with increasing the delay time). The inversion is observable also from the slices of the 2D surface along the delay time (plane perpendicular to the magnetic field direction), as shown in Fig. 4c for the canonical positions.For the parent BODIPY molecule IBDP, this polarization inversion was not observed. The electron spin polarization pattern eee/aaa is persistent. The spectral profile does not change at a longer delay time after laser flash; up to 10 μs the pattern remains as eee/aaa and only a reduction of the signal intensity is observed (Fig. S15†).
For Sty-IBDP, Nap-IBDP, and Aza-IBDP, the initial pattern is the same as that for IBDP, and the ZFS parameters are smaller because the orbitals of the unpaired electrons are distributed over a larger molecular section (see Section 3 in the ESI†). This does not apply to Aza-IBDP, probably due to the presence of different side groups. Aza-IBDP has rather large ZFS values very close to those of IBDP, showing the confinement of the excited π-system to the BODIPY core. The shapes of the TREPR spectra at different delay times are different, i.e. the polarization depends on the delay time. For all three compounds Sty-IBDP, Nap-IBDP, and Aza-IBDP, the individual bands in the spectra evolve in a rather similar way and they show, at latest times, a complete inversion of the polarization of the main features (Fig. S13 and S14†). The unchanged D and E parameters for the TREPR spectra at different delay times indicate that the spectra are due to the same species, which evolve with time, and not due to other photo-produced species, or any impurities.39 The ESP inversion is not due to fast SLR; otherwise the final expected pattern of the principal components should be aaa/aaa (note that fast SLR will induce only an accelerated decay of the magnitude of the TREPR signal, but not an inversion of the ESP pattern).60 Moreover, the lineshape of the TREPR spectrum (Fig. 4) is Gaussian, meaning that the modulation of the spin–spin interaction is limited, and consequently the SLR is not very fast (in that case a Lorentzian lineshape should be found).61 Therefore, we attribute the inversion of the ESP polarity of the studied compounds to the difference in the decay rates of the sublevel of the T1 state.39,40
ESP inversion in the TREPR of triplet states was first reported for pyridazine at 3 K, which shows up to 10-fold different sublevel decay kinetics.39 ESP inversion was also observed for the TREPR spectra of the triplet state of C60 and C70, at 3 K.62 In both cases, at higher temperatures the SLR played a dominant role in the time evolution of the TREPR and ESP inversion is rarely observed (see for example ref. 63 and 64). It should be noted that ESP inversion can be observed only when the SLR is much slower than the decay of the sublevels of the T1 state, and the decay of the sublevels of the T1 state is strongly anisotropic.
The time evolution requires to be analysed in terms of the kinetic equations (supplied in the ESI†), based on the extension of Scheme 3, which can account qualitatively for the results.
We have modelled the time evolution of the experimental surfaces for the studied systems as due to processes that vary the population of the triplet states, namely the decay of the triplet sublevels to the ground state and the magnetic relaxation processes (SLR processes, i.e. the longitudinal relaxation time).
Then the total spectrum is calculated as:65
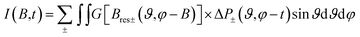 | (2) |
For the fitting of the 2D TREPR spectra with eqn (2), the input parameters were: the ZFS energies, the decay rates of the corresponding states (kx, ky and kz) and their initial population (px, py and pz), proportional to the population rates of the triplet from the excited singlet. The parameters are reported in Table 2.
| X | Y | Z | px | py | pz | k x (μs−1) | k y (μs−1) | k z (μs−1) | |
|---|---|---|---|---|---|---|---|---|---|
| a In MHz. Estimated errors are ±10 MHz. The ZFS principal value (X, Y and Z) is calculated (Table S6) and the orientation of ZFS principal directions is shown in Scheme 2. b Unable to be measured by TREPR because the lifetime is long (see optical measurements), and the decay of the TREPR signal, see Fig. S15, is mainly due to a fast spin relaxation (ca. 1 μs). | |||||||||
| IBDP | −330 | −1630 | 1960 | 0.12 | 0 | 1 | —b | —b | —b |
| Sty-IBDP | −140 | −1232 | 1372 | 0.07 | 0.05 | 1 | 0.11 | 0.04 | 2.3 |
| Nap-IBDP | −204 | −1243 | 1447 | 0.1 | 0.05 | 1 | 0.19 | 0.21 | 1.0 |
| Aza-IBDP | −518 | −1649 | 2167 | 0.35 | 0.36 | 1 | 0.19 | 0.17 | 0.41 |
The simulations of the 2D TREPR surfaces required a very long SLR time (≫ 10 μs). For this reason, we didn't include SLR in the kinetic model. We point out that TREPR measures intensities, proportional to population differences, which are related to the population of the ZFS states according to eqn (S1).† This implies that we can estimate the relative ratios of the populations px![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) py
py![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pz.
pz.
The polarization inversion (see Fig. 4b) was observed in our case because the largest populated state (Tz) is fast depopulated with respect to the other states, as depicted in Scheme 3. For instance, the kz value of Sty-IBDP is 37-times the kx value. Significantly different decay rate constants were observed for Nap-IBDP and Aza-IBDP as well (Table 2). It should be pointed out that in our simulation of the time dependency of the intensity at every field position of the TREPR spectra (Fig. 4c), the model takes into account the contribution of all molecules having resonance at that magnetic field. Previously, except for a few studies,66,67 the common approximation used was to consider mono-oriented distributions on resonance at the main features, which is a good approximation when the transition has a high intensity, but not when the transition has a small intensity, like along the Y-components.
From the data presented in Table 2, we find that, although the triplet population as a whole (sum of the three sublevels) evolves with a three-exponential function, likely the decay is well fitted by a bi-exponential function, with the fastest and dominant contribution due to the decay of the Tz state, and the slowest decay, with a smaller contribution, due to the sum of the decays of the Tx and of the Ty states. We therefore made a comparison between TREPR data and nanosecond transient absorption data taken at 77 K for Sty-IBDP. The agreement is remarkably good, if one takes into account a possible matrix effect due to non-identical solvents. From TREPR we have the triplet state of Sty-IBDP decays with a lifetime of 0.3 μs (89%, due to the decay of the Tz state), and a lifetime of 8.6 μs (11%, due to the decay of the Tx and Ty states, on average), whereas from nanosecond transient absorption spectral measurements (optical method), the lifetimes of Sty-IBDP were 0.6 μs (81%) and 7.4 μs (19%). Therefore, we have been able, by using the TREPR methods, to confirm the multi-exponential decay behaviour as determined by optical methods (nanosecond transient absorption spectroscopy), also in the absence of a spectral resolution of the single sublevels.
In general, SLR can play a role in the deactivation processes, by transferring the spin population between the three sublevels of the T1 state. In this case a monoexponential decay is expected, similar to the scenario for phosphorescent transition metal complexes at 77 K (e.g. Pt(II)/Ir(III) complexes), where the SLR is fast and the decay of the phosphorescence is mono-exponential.42 Our BODIPY molecules studied with TREPR are clearly different, and the slow SLR relaxation allows the observation of the inversion of the ESP and of the multi-exponential decay.
In optical spectroscopy, such differences are rarely taken into account: the triplet states of metal-free organic chromophores usually have small ZFS (ΔE < 10 cm−1) and the three substates are unresolved. Exceptions are phosphorescent transition metal complexes with 3MLCT states which show particularly large ZFS. In principle, the decay of the triplet state should be a multiexponential process, but often at ca. 77 K, a fast equilibrium might exist between the sublevels (SLR), and this results in a detection of a mono-exponential decay of the triplet population. In other words, the individual decay of the substates cannot be studied with the high-resolution phosphorescence method at 77 K. This is also true for some small organic molecules, and the SLR of the triplet state sublevels can only be slowed down at a cryogenic temperature of 3 K.40 However, our results show that at 77 K, TREPR spectroscopy is able to characterize the individual decay of the substates of the T1 states of organic compounds, exemplified by the BODIPY derivatives Sty-IBDP. The decay kinetics of Sty-IBDP, monitored with the nanosecond transient absorption spectra, show that the decay is biexponential below 118 K, and it becomes monoexponential above 118 K, indicating that the SLR is fast above 118 K and slow below this temperature.
Theoretical computation/consideration: explanation of the fast decay
According to the golden rule of Fermi, the rate constant for ISC from a triplet state T to a singlet state S is given by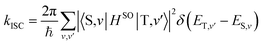 | (3) |
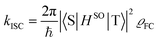 | (4) |
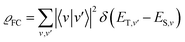 | (5) |
When the equilibrium geometries and vibrational frequencies of both electronic states do not differ too much, the Franck–Condon factors in the harmonic approximation decay exponentially with the difference in quantum numbers, which means also exponentially with the energy gap.
We calculated the SO coupling matrix elements 〈Tx,y,z|HSO|S0〉, related to the decay of the triplet state to the ground state by ISC, with wave functions from a single point CAS-CI(10|10) with the DH-cc-pVTZ atomic orbital basis at geometries optimized for the lowest triplet state with the DFT method. Conformers with different starting geometries and symmetries were tested, and Table 3 presents the results for conformers that differ in energy by less than 3 kcal mol−1. Taking the typical accuracy of the DFT method into account, these conformers might be thermally accessible. In the systems having C2 or C2v symmetry, the spatial wave functions of S0 and T1 belong to different irreducible representations, and hence all couplings are allowed by symmetry.
| Molecule | Sym. | ΔEb/kcal | S0–T1/cm−1 | SOC (S0/T1) | ||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| a In cm−1 units. b Energy difference with respect to the lower energy conformers. In kcal per mole units. CAS(10|10)-CI with the molecular orbitals from a RHF calculation at the triplet geometry optimized with the BP86 functional. c The addition of –H means that in the corresponding structures of Scheme 2, iodine atoms were substituted by hydrogen atoms. | ||||||
| IBDP | C 2v | 0.00 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 964 |
0.00 | −0.09 | 0.00 |
| Sty-IBDP | C 1 | 0.00 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
−0.01 | −0.21 | 0.06 |
| C 2 | 0.28 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218 218 |
0.00 | −0.50 | 4.37 | |
| Aza-IBDP | C 2 | 0.00 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
6.52 | 0.72 | −7.84 |
| C 1 | 2.60 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 724 |
1.55 | −11.3 | −2.70 | |
| Nap-IBDP | C 2 | 0.00 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017 |
0.00 | 0.93 | −8.21 |
| C 1 | 0.37 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 361 361 |
4.39 | 0.71 | 2.70 | |
| IBDP-H | C 2v | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 072 |
0.00 | 0.30 | 0.00 | |
| Sty-IBDP-H | C 1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 809 |
0.04 | 0.29 | −0.01 | |
| C 2 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903 903 |
0.00 | 0.32 | 0.26 | ||
| Aza-IBDP-H | C 2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438 438 |
0.33 | 0.01 | −0.72 | |
| C 1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 809 |
−0.27 | 0.32 | 0.12 | ||
| Nap-IBDP-H | C 2 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579 579 |
0.00 | 0.06 | 0.07 | |
| C 1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913 913 |
−0.22 | 0.19 | 0.26 | ||
SOC matrix elements are usually small in planar π-electron systems containing no heavy atoms. Our calculations show very small SOC matrix elements (<0.1 cm−1) for IBDP in spite of the presence of two iodine atoms, whereas for the compounds Sty-IBDP, Aza-IBDP, and Nap-IBDP rather large values up to >10 cm−1 were obtained. In order to test the origin of these large values, we repeated the corresponding calculations for all compounds after replacing the iodine atoms by hydrogens (with a C–H distance of 1.08 Å), keeping all other coordinates fixed. The corresponding values, collected in the lower part of Table 3, show that all SOC matrix elements are significantly smaller than 1 cm−1. Apparently, these small values are induced by the non-planarity of the π-electron system, due to the torsion of the substituents attached to the BODIPY chromophore, responsible for a symmetry reduction. However, we can expect a long triplet lifetime for the uniodinated styrylBODIPY chromophore as those SOC matrix element values are small. Obviously, the largest contributions to the SOC matrix elements are induced by the iodine atoms in Sty-IBDP, Aza-IBDP, and Nap-IBDP, but the symmetry also plays a role and makes a difference. This can explain the long triplet lifetime of IBDP and the uniodinated styrylBODIPY chromophore very well. With a high symmetry in IBDP (C2v), the coupling of the iodine atoms is inhibited, leading to a small SOC matrix element of S0/T1. For the uniodinated styrylBODIPY chromophore, there is no heavy atom effect and, as expected, a small SOC matrix element of S0/T1 was observed, which is of the same order as that for IBDP (Table 3). Hence both IBDP and the uniodinated styrylBODIPY chromophore have long triplet lifetimes.
These calculations yield a very good explanation of the observed lifetimes: the SOC matrix element of IBDP is rather small; therefore, for IBDP we expect a long triplet state lifetime. Also, the T1/S0 energy gap is large (ca. 13 000 cm−1 by phosphorescence, see Fig. S17†). We don't have a precise value for the Franck–Condon density of states, but we can assume that it decays exponentially with increasing energy gap. Since in IBDP this gap is ca. 4000 cm−1 larger than that for the other compounds, the Franck–Condon density of states will be much smaller in IBDP. Apparently, this term also plays a central role in determining the triplet state lifetime of IBDP.
The calculations predict in particular that the Tz state should decay fastest for Sty-IBDP, Aza-IBDP, and Nap-IBDP (except for the higher energy conformer of Aza-IBDP, where the Ty state has the largest SOC matrix element). These results are in accordance with TREPR, i.e., there is one sublevel (Tz) that decays much faster than the other two sublevels (see Tables 2 and 3). Therefore, the calculations fully support the observation that the ESP inversion is due to very anisotropic decay of the three triplet sublevels.
Previously the fast decay of one of the substates of the T1 state of ortho-diazaaromatics has been discussed in terms of the proximity of n–π* and π–π* states, but clearly this is not the case for our BODIPY derivative since all low-lying triplet states are π–π* states.40
The corresponding iodine-free molecules have much smaller SOC elements, making us to deduce that heavy atom effects play a major role in these structures. This argument is supported by experimental evidence for Sty-IBDP, if we compare the triplet lifetime with that of the styrylBODIPY unit without directly attaching iodine atoms. The long triplet state lifetime of the styryl-BODIPY unit (385 μs) with respect to the short triplet state of Sty-IBDP (a few μs) indicates that in Sty-IBDP the heavy atom effect determines the lifetime of the species.
Thus, we propose that the short triplet state lifetime of Sty-IBDP (also Nap-IBDP and Aza-IBDP) is due to the synergetic effect of the heavy atom effect and the small T1/S0 energy gap of these compounds. With a larger T1/S0 energy gap, the heavy atom effect in IBDP doesn't reduce the T1 state lifetime as significantly as that in Sty-IBDP, Nap-IBDP and Aza-IBDP, which have smaller T1/S0 energy gaps (ca. 1.06 eV) than IBDP (ca. 1.64 eV).
To conclude this section, we note that, at high temperature, the population is transferred between triplet substates by spin-lattice relaxation processes. Therefore, the depopulation of the single sublevel is a more complex process. For very fast spin relaxation, the depopulation of the three sublevels is the same, and the rate constant is the average of the three. Also, we expect other types of decay channels that might be activated, which make the decay homogeneous throughout the sublevels. Consequently, the conditions to observe polarization inversion are not always favourable, and the comparison with calculation might be difficult.
For interested readers, we also calculated the SOC elements related to the ISC process leading to the population of the triplet state from the excited singlet (Table S7†). This served as a further benchmark for the calculation. The results account for the polarization pattern found by TREPR for the studied molecules, and they are reported in the ESI.†
Conclusions
In summary, we revealed the reason for the drastically different triplet state lifetimes of a series of BODIPY derivatives. We found that the triplet state lifetimes of a few representative iodinated BODIPY derivatives are substantially different. 2,6-DiiodoBODIPY has a long-lived T1 state (lifetime τT = 160 μs), whereas diiodostyrylBODIPY shows a much shorter T1 state lifetime (1.4–3.6 μs). Optical transient spectroscopy can hardly offer any direct insight into the reason for the different triplet lifetimes (τT) of these derivatives. Herein we used pulsed laser excited time-resolved electron paramagnetic resonance (TREPR) spectroscopy to study the electron spin polarization (ESP) dynamics of the triplet states of these compounds. Interestingly, we found ESP inversion for the BODIPY derivatives showing short T1 state lifetimes, i.e. the polarization pattern of the triplet TREPR spectra (A or E. A stands for enhanced absorption and E stands for emission in the TREPR spectra) is inverted as the delay time is extended (in frozen solution at 80 K). This indicates strong anisotropy of the decay of the three sublevels of the T1 state, i.e. a faster decay of one sublevel of T1 (Tx, Ty or Tz) compared to the other two. With the simulation of the kinetics, we deduced that for Sty-IBDP, one sublevel (Tz) of the T1 state decays much faster (kz = 2.3 μs−1), 20-fold faster or more than the other two sublevels (kx = 0.11 μs−1 and ky = 0.04 μs−1 respectively), which causes the ESP inversion. The spin-lattice relaxation (SLR) of these organic molecules is slow (SLR ≫ 10 μs). SLR alone will only induce an accelerated decay of the TREPR signal, but not the inversion of ESP. For 2,6-diiodoBODIPY (IBDP), which has a long-lived T1 state (160 μs), no ESP inversion was observed.Theoretical computations indicate that the faster decay of one substate of T1 of the BODIPY derivatives correlates with the magnitude of the SOC matrix elements, which favors strong coupling between the Tz state and the ground state through the heavy atom effect. Without the heavy atom effect, the same chromophore demonstrates a much longer T1 state lifetime (385 μs). In the diiodoStyryIBDP derivatives the small T1/S0 state energy gap also contributes to the much shorter T1 state lifetimes. The nanosecond transient absorption spectra recorded at 77 K, which show a biexponential decay with decay times of 0.6 μs (81%) and 7.4 μs (19%), are in good agreement with the TREPR spectral analysis. To the best of our knowledge, this is the first systematic study to rationalize the short triplet state lifetime of visible light-harvesting chromophores, and the direct observation of the ESP inversion of an organic chromophore, i.e. the faster decay of one sublevel than the other two of the T1 state, at 80 K. Our results are useful for understanding the fundamental photochemistry concerning the decay kinetics of the T1 state of organic chromophores. They may be useful for the design of novel triplet photosensitizers with long triplet state lifetimes, and thus to improve the performance of these novel materials in applications such as photocatalysis, photodynamic therapy, photovoltaics, photon upconversion, etc.
Experimental section
General methods
All chemicals used in synthesis are analytically pure. UV-vis absorption spectra were recorded on a HP8453 UV-vis spectrophotometer (Agilent Ltd., USA). Fluorescence spectra were recorded on a RF-5301PC spectrofluorometer (Shimadzu Ltd., Japan). Luminescence lifetimes were measured on an OB920 fluorescence lifetime instrument (Edinburgh Instruments, U.K.), and an EPL picosecond pulsed laser was used for excitation.Nanosecond transient absorption spectroscopy
The nanosecond transient absorption spectra were recorded on an LP980 laser flash photolysis spectrometer (Edinburgh Instruments, UK) and the signals were digitized with a Tektronix TDS 3012B oscilloscope. The excitation was performed with a nanosecond pulsed laser (OpoletteTM 355II+UV nanosecond pulsed laser, OPOTEK, USA). Typical pulse length: 7 ns and pulse repetition used for measurement: 1 Hz. Typical laser energy: 5 mJ per pulse. The wavelength is tuneable in the range of 410–2200 nm. The apparent lifetime values (by monitoring the decay trace of the transients) were obtained with L900 software. The intrinsic triplet state lifetimes were obtained by fitting the decay traces with a kinetics model with the triplet–triplet annihilation quenching effect considered.26 All samples in flash photolysis and upconversion experiments were deaerated with N2 for 10 min before measurement.Time-resolved electron paramagnetic resonance spectroscopy
The TREPR spectra were recorded with two Bruker spectrometers with an extended detection bandwidth (6 MHz): an ER200D spectrometer equipped with a cylindrical cavity with optical access and cooled by a nitrogen flow for temperature control, and an ELEXSYS E580 spectrometer equipped with a dielectric cavity inside an Oxford CF900 cryostat cooled by liquid nitrogen. The time resolutions, depending on the cavity time response, was of the order of 200–300 ns for the cylindrical cavity, and 800–1000 ns for the dielectric cavity. Direct-detected signals (no modulation of the magnetic field was used) were recorded with LeCroy digital oscilloscopes with a GHz bandwidth. Photoexcitation was obtained from Nd:YAG pulsed lasers (Quantel Brilliant, pulse length = 5 ns) equipped with superior harmonic modules and eventually with an optical parametric oscillator (OPOTECH) for tunable irradiation in the visible region.During the acquisition, the samples were photoexcited with a nanosecond pulsed laser. The time-resolved EPR signals are acquired with a fast oscilloscope at 256 constant values of the static magnetic field B0, without the usual field modulation (direct detection mode). Each transient is averaged from 100 to 300 times, and then transferred to a PC and the data were stored. Then the different transients are collected and united in a plot producing a surface that shows the EPR signal intensity as a function of the field B0 and the time after the short laser pulse (duration ∼5 ns) which populates the excited triplet state. Cutting the surface with a plane perpendicular to the time axis at time t = td (μs), one obtains an EPR spectrum at a delay td after the light shot at tshot = 0 μs.
Quantum chemical computations
Calculations were performed with the ORCA program68,69 in the following sequence: first, the geometries of the triplet state were optimized with unrestricted density functional theory and the def2-SVP basis set. This basis uses effective core potentials (ECP) for iodine. We tested the functionals BP86, PBE0, and B3LYP (in the variant used by Gaussian). Although the latter two are hybrid functionals and use a much more computationally demanding method (coupled perturbed Hartree Fock) for the calculation of ZFS parameters, the results of all three functionals are rather similar. For the following calculations we used the geometries from the BP86 optimization. These geometries were transformed into the eigenframe of the ZFS tensor from the DFT calculation.In the next step, restricted Hartree–Fock orbitals were generated at these geometries with the cc-pVTZ-DK basis set and the linear relativistic Douglas–Kroll–Hess (DKH) Hamiltonian. This is a triple zeta basis set that includes the inner electrons explicitly and is optimized for use with this Hamiltonian. An active space of 10 orbitals with 10 electrons was chosen and full configuration interaction calculations were performed within this space. The wave functions for the lowest singlet and triplet states from this calculation were subsequently used to calculate ZFS parameters and spin–orbit coupling (SOC) matrix elements.
Author contributions
Dr Z. Wang carried out the synthesis of the compounds, the steady state/time-resolved optical spectroscopy studies and data analysis; Y. Hou did part of the nanosecond transient absorption and low temperature phosphorescence spectral study; Dr A. Barbon and Prof. A. Toffoletti performed the TREPR spectral measurements, while Dr A. Barbon implemented the model for the TREPR data analysis and wrote part of the manuscript; Prof. J. Zhao devised the project and wrote the manuscript; Prof. B. Dick carried out the quantum chemical calculations and the related data analysis and wrote part of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Z. W. thanks the Postdoctoral Research Foundation of China (2020M670108) for financial support. J. Z. thanks the Department of Chemical Science, University of Padua, Italy (Visiting Scientist Grant), the NSFC (U2001222, 21673031, 21761142005, 21911530095 and 21421005), the State Key Laboratory of Fine Chemicals (ZYTS201901) and the Fundamental Research Funds for the Central Universities (DUT19TD28) for financial support. B. D. thanks the Dalian University of Technology for the Haitian Professorship support.Notes and references
- N. J. Turro, V. Ramamurthy, V. Ramamurthy and J. C. Scaiano, Principles of molecular photochemistry: an introduction, University Science Books, 2009 Search PubMed.
- J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer Science & Business Media, 2013 Search PubMed.
- B. Valeur, Characteristics of fluorescence emission, Molecular Fluorescence: Principles and Applications, Wiley-VCH Verlag GmbH & Co. KGaA, 2012 Search PubMed.
- Y. Wu and W. Zhu, Chem. Soc. Rev., 2013, 42, 2039–2058 RSC.
- Z. Ning and H. Tian, Chem. Commun., 2009, 5483–5495 RSC.
- J. W. Verhoeven, J. Photochem. Photobiol., C, 2006, 7, 40–60 CAS.
- R. Ziessel and A. Harriman, Chem. Commun., 2011, 47, 611–631 RSC.
- A. P. De Silva, H. Q. N. Gunaratne, T. Gunnlaugsson, A. J. M. Huxley, C. P. McCoy, J. T. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515–1566 CrossRef CAS.
- M. Schäferling, Angew. Chem., Int. Ed., 2012, 51, 3532–3554 CrossRef.
- M. Wingen, J. Potzkei, S. Endres, G. Casini, C. Rupprecht, C. Fahlke, U. Krauss, K.-E. Jaeger, T. Drepper and T. Gensch, Photochem. Photobiol. Sci., 2014, 13, 875–883 CAS.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS.
- W. Wu, H. Guo, W. Wu, S. Ji and J. Zhao, J. Org. Chem., 2011, 76, 7056–7064 CrossRef CAS.
- J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323–5351 RSC.
- M. E. El-Khouly and S. Fukuzumi, J. Porphyrins Phthalocyanines, 2011, 15, 111–117 CrossRef CAS.
- Y. Lu, J. Wang, N. McGoldrick, X. Cui, J. Zhao, C. Caverly, B. Twamley, G. M. Ó Máille, B. Irwin, R. Conway-Kenny and S. M. Draper, Angew. Chem., Int. Ed., 2016, 55, 14688–14692 CrossRef CAS.
- R. Lincoln, L. Kohler, S. Monro, H. Yin, M. Stephenson, R. Zong, A. Chouai, C. Dorsey, R. Hennigar, R. P. Thummel and S. A. McFarland, J. Am. Chem. Soc., 2013, 135, 17161–17175 CrossRef CAS.
- T. N. Singh-Rachford and F. N. Castellano, Coordi. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332 RSC.
- J. Zhao, S. Ji and H. Guo, RSC Adv., 2011, 1, 937–950 RSC.
- D. P. Hari and B. Koenig, Angew. Chem., Int. Ed., 2013, 52, 4734–4743 CrossRef CAS.
- S. Fukuzumi and K. Ohkubo, Chem. Sci., 2013, 4, 561–574 RSC.
- D. Ravelli, M. Fagnoni and A. Albini, Chem. Soc. Rev., 2013, 42, 97–113 RSC.
- P. Wang, S. Guo, H.-J. Wang, K.-K. Chen, N. Zhang, Z.-M. Zhang and T.-B. Lu, Nat. Commun., 2019, 10, 1–12 CrossRef.
- M. A. Haidekker and E. A. Theodorakis, Org. Biomol. Chem., 2007, 5, 1669–1678 RSC.
- M. K. Kuimova, G. Yahioglu, J. A. Levitt and K. Suhling, J. Am. Chem. Soc., 2008, 130, 6672–6673 CrossRef CAS.
- Z. Lou, Y. Hou, K. Chen, J. Zhao, S. Ji, F. Zhong, Y. Dede and B. Dick, J. Phys. Chem. C, 2018, 122, 185–193 CrossRef CAS.
- G. Ulrich, R. Ziessel and A. Harriman, Angew. Chem., Int. Ed., 2008, 47, 1184–1201 CrossRef CAS.
- D. Frath, J. Massue, G. Ulrich and R. Ziessel, Angew. Chem., Int. Ed., 2014, 53, 2290–2310 CrossRef CAS.
- A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS.
- H. Lu, J. Mack, Y. Yang and Z. Shen, Chem. Soc. Rev., 2014, 43, 4778–4823 RSC.
- T. Kowada, H. Maeda and K. Kikuchi, Chem. Soc. Rev., 2015, 44, 4953–4972 RSC.
- A. Kamkaew, S. H. Lim, H. B. Lee, L. V. Kiew, L. Y. Chung and K. Burgess, Chem. Soc. Rev., 2013, 42, 77–88 RSC.
- J. Wang, Y. Lu, N. McGoldrick, C. Zhang, W. Yang, J. Zhao and S. M. Draper, J. Mater. Chem. C, 2016, 4, 6131–6139 RSC.
- J. Ma, X. Yuan, B. Küçüköz, S. Li, C. Zhang, P. Majumdar, A. Karatay, X. Li, H. Gul Yaglioglu, A. Elmali, J. Zhao and M. Hayvali, J. Mater. Chem. C, 2014, 2, 3900–3913 RSC.
- A. Gorman, J. Killoran, C. O'Shea, T. Kenna, W. M. Gallagher and D. F. O'Shea, J. Am. Chem. Soc., 2004, 126, 10619–10631 CrossRef CAS.
- N. Adarsh, M. Shanmugasundaram, R. R. Avirah and D. Ramaiah, Chem.–Eur. J., 2012, 18, 12655–12662 CrossRef CAS.
- S. Guo, L. Ma, J. Zhao, B. Küçüköz, A. Karatay, M. Hayvali, H. G. Yaglioglu and A. Elmali, Chem. Sci., 2014, 5, 489–500 RSC.
- A. Barbon, M. Bortolus, M. Brustolon, A. Comotti, A. L. Maniero, U. Segre and P. Sozzani, J. Phys. Chem. B, 2003, 107, 3325–3331 CrossRef CAS.
- M. Terazima, S. Yamauchi and N. Hirota, Chem. Phys. Lett., 1985, 120, 321–326 CrossRef CAS.
- M. Terazima, S. Yamauchi and N. Hirota, J. Chem. Phys., 1986, 84, 3679–3687 CrossRef CAS.
- M. R. Wasielewski, M. P. O'Neil, K. R. Lykke, M. J. Pellin and D. M. Gruen, J. Am. Chem. Soc., 1991, 113, 2774–2776 CrossRef CAS.
- A. F. Rausch, L. Murphy, J. G. Williams and H. Yersin, Inorg. Chem., 2009, 48, 11407–11414 CrossRef CAS.
- C. Hintze, P. Korf, F. Degen, F. Schütze, S. Mecking, U. E. Steiner and M. Drescher, J. Phys. Chem. Lett., 2017, 8, 690–695 CrossRef CAS.
- S. Richert, C. E. Tait and C. R. Timmel, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS.
- P. K. Poddutoori, Y. E. Kandrashkin, C. O. Obondi, F. D'Souza and A. van der Est, Phys. Chem. Chem. Phys., 2018, 20, 28223–28231 RSC.
- K. Möbius, W. Lubitz and A. Savitsky, Appl. Magn. Reson., 2011, 41, 113–143 CrossRef.
- A. Kawai and K. Shibuya, J. Photochem. Photobiol., C, 2006, 7, 89–103 CrossRef CAS.
- T. Miura, R. Carmieli and M. R. Wasielewski, J. Phys. Chem. A, 2010, 114, 5769–5778 CrossRef CAS.
- Z. E. X. Dance, S. M. Mickley, T. M. Wilson, A. B. Ricks, A. M. Scott, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2008, 112, 4194–4201 CrossRef CAS.
- K. Ishii, Y. Hirose, H. Fujitsuka, O. Ito and N. Kobayashi, J. Am. Chem. Soc., 2001, 123, 702–708 CrossRef CAS.
- Y. Teki, S. Miyamoto, M. Nakatsuji and Y. Miura, J. Am. Chem. Soc., 2001, 123, 294–305 CrossRef CAS.
- G. P. Wiederrecht, W. A. Svec, M. R. Wasielewski, T. Galili and H. Levanon, J. Am. Chem. Soc., 2000, 122, 9715–9722 CrossRef CAS.
- A. D. Quartarolo, N. Russo and E. Sicilia, Chem.–Eur. J., 2006, 12, 6797–6803 CrossRef CAS.
- D. Beljonne, Z. Shuai, G. Pourtois and J. Bredas, J. Phys. Chem. A, 2001, 105, 3899–3907 CrossRef CAS.
- R. P. Sabatini, T. M. McCormick, T. Lazarides, K. C. Wilson, R. Eisenberg and D. W. McCamant, J. Phys. Chem. Lett., 2011, 2, 223–227 CrossRef CAS.
- A. Barbon, M. Bortolus, A. L. Maniero and M. Brustolon, Phys. Chem. Chem. Phys., 2005, 7, 2894–2899 RSC.
- A. Collauto, A. Barbon and M. Brustolon, J. Magn. Reson., 2012, 223, 180–186 CrossRef CAS.
- Z. Wang, Y. Xie, K. Xu, J. Zhao and K. D. Glusac, J. Phys. Chem. A, 2015, 119, 6791–6806 CrossRef CAS.
- G. Robinson, Proc. Natl. Acad. Sci. U. S. A., 1963, 49, 521–529 CrossRef CAS.
- S. Ceola, L. Franco and C. Corvaja, J. Phys. Chem. B, 2004, 108, 9491–9497 CrossRef CAS.
- A. Barbon and M. Brustolon, Appl. Magn. Reson., 2012, 42, 197–210 CrossRef CAS.
- M. Terazima, N. Hirota, H. Shinohara and Y. Saito, Chem. Phys. Lett., 1992, 195, 333–338 CrossRef CAS.
- S. Yamauchi, N. Hirota and J. Higuchi, J. Phys. Chem., 1988, 92, 2129–2133 CrossRef CAS.
- T. Ikoma, K. Aklyama, S. Tero-Kubota and Y. Ikegami, J. Phys. Chem., 1991, 95, 7119–7121 CrossRef CAS.
- A. Toffoletti, Z. Wang, J. Zhao, M. Tommasini and A. Barbon, Phys. Chem. Chem. Phys., 2018, 20, 20497–20503 RSC.
- M. Di Valentin, S. Ceola, G. Agostini, G. M. Giacometti, A. Angerhofer, O. Crescenzi, V. Barone and D. Carbonera, Biochim. Biophys. Acta, Bioenerg., 2008, 1777, 295–307 CrossRef CAS.
- F. Ema, M. Tanabe, S. Saito, T. Yoneda, K. Sugisaki, T. Tachikawa, S. Akimoto, S. Yamauchi, K. Sato, A. Osuka, T. Takui and Y. Kobori, J. Phys. Chem. Lett., 2018, 9, 2685–2690 CrossRef CAS.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05494a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |