Aufbau vs. non-Aufbau ground states in two-coordinate d⁷ single-molecule magnets

Abstract

Single-molecule magnets (SMMs) with d⁷ electronic configurations often require designer ligands to satisfy the metals electronic conditions to achieve large angular momentum. Herein, the slow relaxation of the magnetization in two d⁷ metal complexes in near identical ligand fields is achieved from divergent origins. The two compounds, [Co^II{N(SiMePh₂)₂}₂] and [K(2,2,2-crypt)][Fe^I{N(SiMePh₂)₂}₂] (2,2,2-crypt = 2,2,2-cryptand), display unusual electronic configurations giving rise to SMM behavior originating either from 3d–4s orbital mixing or a non-Aufbau ground state. The chracteristics contributing to the rare non-Aufbau ground state configurations are illuminated by the use of a highly donating amido-ligand, which would be expected to significantly split the respective orbitals. Magnetic circular dichroism provides experimental support for ab initio determined electronic structures. Moreover, computational models reveal that the relative electronic configurations are largely retained independently of coordination geometry, provided that some degree of pseudo-linearity is retained. Thus, providing generalized design principles in the pursuit of linear d⁷ SMMs.

---

Introduction

Unusual electronic structures and increasing orbital angular momentum numbers, akin to those found in 4f chemistry, have reignited the interest in transition metal single-molecule magnets (SMMs),¹ whose predecessors relied on large spin clusters to facilitate slow relaxation of the magnetization. It has become evident through careful design considerations that orbital angular momenta as large as L = 3 may be achieved with transition metals (TMs).² Such staggering values are rare in TMs as the ligand field typically removes any orbital degeneracy, leading to quenching of the free ion orbital angular momentum (L = 0).³ Non-zero orbital angular momentum is possible to achieve when the ligand field is highly symmetric, preserving the degeneracy among two or more partially filled orbitals; or when the ligand field is sufficiently weak-enough that non-degenerate states remain close enough in energy to elicit angular momentum via excited state interactions. Although, in most cases the symmetry is low and the ligand field is sufficiently strong such that any degeneracy in the electronic terms is lifted, and anisotropy is a second order effect that arises from the mixing of excited states into the ground manifold by spin–orbit coupling.⁴ The magnitude of the anisotropy is therefore governed by the extent of spin–orbit coupling combined with the energy difference between these states. This energy difference is directly correlated with the anisotropy, where a smaller energy difference may elicit greater mixing, and subsequently greater anisotropy.

Thus, the most promising way to preserve the large L value of the free TM ion and induce magnetic anisotropy is to employ low coordinate molecular geometries resulting in weak ligand fields. Such environments (i.e., two-coordinate) are well suited for SMMs as they are mostly unaffected by Jahn–Teller distortions, which may yield non-zero orbital angular momentum (L ≠ 0).⁵ Despite this, linear geometries may be subject to Renner–Teller effects (i.e., bending) which lifts the orbital degeneracy, quenching the orbital moment.⁶ This effect has been demonstrated both experimentally and theoretically for linear Fe^II compounds containing N, C, and O donors,^7,8 and thus careful consideration of the ligand design must be taken into account to mitigate these effects. Two-coordinate metal complexes are of particular interest for their magnetic properties as the low-coordinate environment results in a narrow distribution of the d-orbital energies,⁹ creating a ratio between the ligand field strength and the spin–orbit coupling that more closely resembles that of lanthanides.¹⁰ As such, many linear transition metal complexes of the d¹–d⁹ series have been characterized electronically and/or magnetically.¹¹ Moreover, those of the d⁷ family are notable for their magnetic properties as the odd number of electrons in the d-manifold may afford the largest orbital angular momentum projection (M_L = 3).¹² However, achieving such staggering values with d⁷ metals is not trivial, as the first-order orbital angular momentum becomes partially quenched when even slight deviations to the idealized D_∞h symmetry occur.¹¹

Despite research on these low-coordinate systems having begun more than 50 years prior, the first report of a two-coordinate linear Fe^I SMM was only in 2013.^13,14 Demonstrating the impact of structural nuances, such as bending, on the observed orbital moment of these two-coordinate species. Since then, a number of two-coordinate d⁷ TM-based SMMs have been reported utilizing ligands such as N-heterocyclic carbenes,^15,16 cyclic alkyl(amino) carbenes,¹⁷ terphenyl phenoxides,¹⁸ amidos,¹⁹ and their combinations²⁰ to stabilize the d⁷ metal ion. Yet in 2018, a linear Co^II SMM was reported with the bulky alkyl ligand, ⁻C(SiMe₂ONaph)₃ (Naph = naphthalene),²¹ which showcased how significant anisotropy may be generated in linear compounds with sufficiently weak ligand fields, eliciting slow relaxation of the magnetization via a non-traditional ground state configuration. While several early studies have examined the origin of anisotropy in transition metal complexes of higher coordination numbers with respect to the ligand field strength and symmetry (i.e, molecular and crystalline),^22–24 the true tolerance of the orbital moment pertaining to the observed linearity of the ligand field is yet to be fully understood. Indeed, a difficulty in this undertaking is due in part to isolating air-sensitive, coordinatively unsaturated molecules.

To this end, we sought to explore alternative scaffolds from which to build low-coordinate metal complexes bearing unusual electronic configurations that may support large orbital moments beyond alkyl-based ligands, while simultaneously utilizing more versatile amido-based ligands to impose a strong magnetic axis.⁸ The differences in the magnetic and electronic properties of two commonly studied transition metal ions, with seemingly isoelectronic configurations, Fe^I and Co^II ions in a pseudolinear environment supported by the same bulky amido-based ligand were investigated. Herein, we describe the synthesis and magneto-optical characterization of [M{N(SiMePh₂)₂}₂] (M = Co^II; 1 and Fe^II; 2) and [K(2,2,2-crypt)][Fe{N(SiMePh₂)₂}₂] (3; 2,2,2-crypt = 2,2,2-cryptand), allowing a direct comparison of the ground state and spin–orbit coupling parameters that arise from structural nuances in the N–M–N angles, which ultimately govern the magnetic and electronic properties of d⁷ metals. By employing the same supporting ligand, magnetic anisotropy is generated in two differing ways from metal complexes of Co^II and Fe^I; (1) via 3d–4s orbital mixing in Fe^I; and (2) via a non-Aufbau ground state in Co^II supported for the first time by an amido-based ligand.

Results and discussion

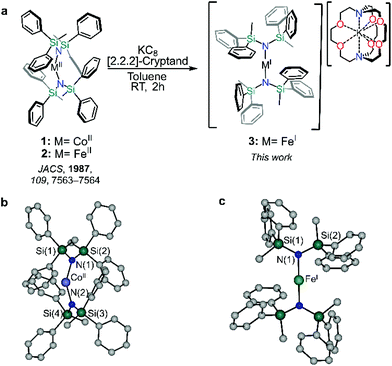
Synthesis and structure

Compounds 1 and 2 were prepared following a slightly modified literature procedure (see ESI† and Fig. 1). Under these conditions, crystallization of 1 consistently yielded a different structure than that reported by Powers and co-workers.²⁵ Notably, the rotation of the –SiMePh₂ groups differs between the crystal structures, ultimately templating the lattice in different fashions (Table S1†). Phase purity of 1 was confirmed via powder X-ray diffraction performed at room temperature (Fig. S1†) which confirmed the match to the new simulated powder pattern of 1, suggesting that the differences in the crystal lattice cannot simply be ascribed to different experimental temperatures at which the crystal structure was collected, but that the structure is likely controlled by the comparatively cooler crystallization temperature used in this study. Despite this, the structural parameters of compound 1 remain largely unaffected by the crystal lattice, leading only to a slightly more obtuse N–Co^II–N angle of 148.661(97)° vs. 147.0(2)°.

Fig. 1 Preparation of 1–3 and single crystal X-ray structure determinations of 1 and 3. (a) Reaction scheme for the synthesis of of [M{N(SiMePh₂)₂}₂] (1, M = Co^II; 2, M = Fe^II) and [K(2,2,2-crypt)][Fe{N(SiMePh₂)₂}₂] (3, M = Fe^I). Solid-state molecular structures of 1 (b) and 3 (c) H atoms and [K(2,2,2-cryptand)]⁺ were omitted for clarity.

Reduction of 2 with KC₈ in toluene in the presence 2,2,2-cryptand yielded 3 as deep red crystals, packing in the monoclinic C2/c space group as an anionic Fe^I metal complex supported by a [K(2,2,2-cryptand)] cation. The Fe–N bond length of 1.19135(13) Å is marginally shorter than 1.9219(17) Å for the previously reported [K(2,2,2-crypt)][Fe{N(SiMe₃)₂}₂].²⁶ The metal centre of compound 3 sits on a two-fold proper rotation axis, leading to a near linear N–Fe–N angle of 178.1°, marginally smaller than the idealized geometry as the metal ion does not sit on an inversion centre.^26,27 Yet, this N–M–N angle is significantly larger than both neutral metal complexes herein, 1 (148.6°) and 2 (169.0°). Such stark differences between the divalent and monovalent species are due in part to the greater degree of metal–(aryl-π) and π–π interactions of the divalent compound which promote the bent structure.^28,29 Conversely, in the case of 3, the interactions in the secondary sphere are dominated by short contacts between the aryl groups and 2,2,2-cryptand. Such a high degree of plasticity in the aparent bond angles and lengths has been observed in other TM two-coordinate metal complexes as a result of the complex interplay between the steric and dispersion forces within a crystal lattice.^18,30

Ab initio calculations and ligand field analysis

Given the propensity for such linearly coordinated TMs to exhibit interesting magnetic properties and sometimes unusual electronic structures, both compounds 1 and 3, were studied via ab initio methods. The effective ligand field orbitals and their energies are shown in Fig. 2. In all cases, the δ-symmetric orbitals (d_x²–y², d_xy) remain nearly degenerate (ΔE(1) > ΔE(3)), whereas the degeneracy of the π-symmetric orbitals (d_xz, d_yz) is partially removed due to the π-symmetric lone pair on the N-donor atoms of the ligands (Table S2†). This metal–ligand interaction raises the energy of the π-symmetric orbital which is perpendicular to the coordination plane for both 1 and 3. The ordering of the orbitals in 1 is what would be expected based on conventional crystal-field arguments; the δ-symmetric orbitals with the least amount of electrostatic interactions with the ligands lie lowest in energy, and the σ-symmetric orbital (d_z²) with the strongest interactions resides the highest. In the case of compound 3, the δ-symmetric orbitals are still more stable than the π-symmetric orbitals, while the σ orbital is the most stable. This drastic change compared to the energy of the σ orbital of 1, results from the mixing of the σ-symmetric 3d_z² orbital and the unoccupied 4s orbital of Fe^I resulting in a stabilizing effect (Table S3†). This phenomenon is a defining feature in the electronic structures of terminal iron nitride metal complexes leading to significant stabilization of the d_z² orbital owing to its interaction with the nitrogen p-orbitals,³¹ and has also been similarly observed in the solid state material Li₂(Li_1−xFe_x)N.³² In the case of 1, all five orbitals have more than 92% 3d character (based on reduced Löwdin orbital populations), while in 3, all the orbitals exceed 93%, with the exception of the σ-symmetric orbital which has only 80% 3d character.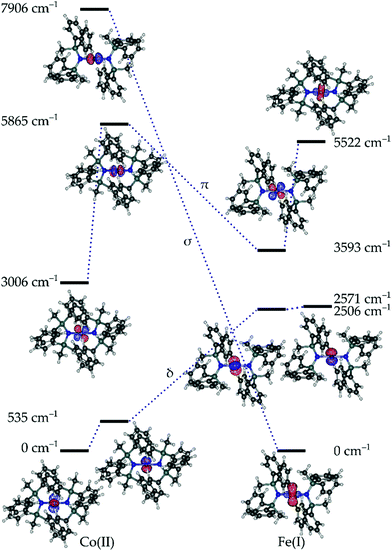

Fig. 2 Effective ligand field orbitals calculated for 1 and 3 using the AILFT framework. The dashed lines indicated the approximate σ, π, and δ symmetric orbitals.

The largest contribution to the σ-symmetric orbital of 3 after the 3d orbitals comes from the 4s orbital comprising 11%. Comparatively, the 3d–4s mixing in the alkyl analogue, [Fe{C(SiMe₃)₃}₂]⁻ is approximated at 8%,³³ and 14% for [Fe{N(SiMe₃)₂}₂]⁻.²⁷ The lack of strong 3d–4s mixing in 1 as opposed to 3 can be explained by the energy difference between the 3d and 4s orbitals in the respective free ions. The 3d–4s splitting in 1 and 3 are 18.4 eV and 6.1 eV respectively. The splitting in 1 is more than double that of its counterpart, explaining the lack of orbital mixing and the resulting energy of the σ-symmetric orbital.

Given the relative orbital energies, the resulting ground Aufbau configuration for 3 is σ²δ³π², which has a degeneracy in the δ orbitals giving rise to a degenerate ⁴Δ term. According to the calculations, the first excited state lies at 267 cm⁻¹ and the next state at 7720 cm⁻¹, which is consistent with a degenerate ground state (Tables S4 and S5†). Comparatively, the ground Aufbau configuration of 1 should be δ⁴π²σ¹, giving rise to a non-degenerate ⁴Σ term. However, the calculations for 1 show that the first excited state lies at 383 cm⁻¹, and the next resides at 3546 cm⁻¹. This may arise due to the low-lying π-orbital with respect to the δ-orbital,³⁴ or may indicate that the ground term is a doubly degenerate ⁴Π, ⁴Δ or ⁴Φ term. In a recent work, Long and co-workers showed that in a related quasi-linear compound, the Co^II ion adopts a non-Aufbau δ³π³σ¹ configuration with a ⁴Φ term.²¹ Comparatively, the strong splitting of the π-orbitals in 1 means that the angular momentum contribution is largely quenched, and the ground term is dominated by angular momentum arising from the nearly degenerate δ orbitals, this gives rise to an approximate ⁴Δ ground term (vide infra). This term is doubly degenerate in accordance with the calculated spin–orbit coupling constants of 507 cm⁻¹ for 1 and 342 cm⁻¹ for 3. This is sufficient to induce significant mixing with the two nearly degenerate states arising from the ⁴Δ ground term.

Thus, the calculations show that 1 and 3 will likely display significant magnetic anisotropy. In both cases, the doubly degenerate ground spin quartets are split into four Kramers doublets, M_J = ±7/2, ±5/2, ±3/2, and ±1/2. The splitting is sufficiently strong that the low temperature magnetic properties are best described in terms of S = ½ pseudospin Hamiltonian acting on the ground doublet. In the case of 1, the principal components of the g-tensor calculated for the ground doublet are g_x = 0.0732, g_y = 0.0758, and g_z = 10.9433. The g-tensor is sufficiently axial to support blocking of the ground-state QTM, giving an expected effective barrier of 369 cm⁻¹/590 K. Similarly, the calculated principal components of the g-tensor for the ground doublet of 3 are g_x = 0.0257, g_y = 0.0261 and g_z = 9.7282, which is again also sufficiently axial to block QTM and to allow relaxation via the first excited state doublet with an expected barrier of 190 cm⁻¹/273 K. Thus, both compounds 1 and 3 are expected to exhibit SMM properties as a result of these highly axial ground doublets, despite the inherent differences in the electronic structures of 1 and 3. In the case of 1, the magnetic properties arise as a result of a non-Aufbau ground configuration in an attempt to reduce interelectronic repulsions, whereas in 3 they are a result of a non-conventional orbital ordering due to 3d–4s mixing.

Static and dynamic magnetic susceptibility

In order to evaluate the magnetic anisotropy of compounds 1 and 3 as predicted via our computational study, both direct current (dc) and alternating current (ac) magnetic susceptibilities were evaluated. Variable temperature dc molar magnetic susceptibility (χ_M) measurements display room temperature χ_MT products of 3.72 cm³ K mol⁻¹ and 2.84 cm³ K mol⁻¹ for 1 and 3 respectively (Fig. S3†). Both compounds display susceptibilities larger than what is expected for the spin-only value (S = 3/2, χ_MT = 1.88 cm³ K mol⁻¹). However, given that the principal component of the g-tensor is g_z = 10.9433 and 9.7282 for 1 and 3, respectively; the expected room temperature χ_MT-value is ca. 3.12 cm³ K mol⁻¹ (assuming L_z = ±2). The larger experimental value measured for compound 1 indicates orbital contribution from the π-symmetric orbitals, despite the orbital moment being partially quenched by the ligand. Nevertheless, this partial contribution is significant enough to observe an increase in the room temperature susceptibility. Conversely, the smaller χ_MT-value obtained for compound 3 likely results from deviations from an ideal D_∞h symmetry. The same trend is similarly observed in the variable-field magnetization and reduced magnetization of compounds 1 and 3 (Fig. S3c, d and S4†).

The magnetic relaxation dynamics in these two closely related compounds were investigated in the absence of an external field (H_dc = 0 Oe), it is worth noting that any attempts to observe slow relaxation of the magnetization for compound 2 was not possible within the studied frequency range.³⁵ Previous work on d⁶, two-coordinate iron metal complexes provide both experimental and theoretical evidence of splitting being δ³σ¹π².³⁶ However, an (aryl-π)–Fe interaction that promotes the bent structure, assumed to be an extreme Renner–Teller distortion, effectively quenches the orbital angular momentum.⁶ Only in the presence of an applied magnetic field has slow relaxation been observed in other two-coordinate high-spin Fe^II metal complexes.³³ However, in the case of compounds 1 and 3, the in-phase (χ′_M(v); Fig. S6 and S8†) and out-of-phase (χ′′_M(v); (Fig. 3a and c) ac magnetic susceptibilities display distinct frequency dependent behaviour within the studied temperature ranges. The temperature dependent relaxation times (τ) were extracted by fitting the individual components of the χ′_M(v) and χ′′_M(v) susceptibilities to the generalized Debye model (Tables S6–S9 and Fig. S7 and S9†).³⁷ Due to the bimodal nature of the χ′′_M(v) susceptibilities for compounds 1 and 3 at zero-field (H_dc = 0 Oe), the magnetic relaxation of both compounds had to be fit using the sum of two Debye equations, which yielded two unique τ-values corresponding to a low frequency (LF) and high frequency (HF) region (Fig. S16 and S17†).³⁸ By plotting the τ⁻¹vs. T obtained from the χ′′_M(v), the temperature dependence of the magnetic susceptibility in the absence of an applied static field can be reproduced by considering the sum of the Orbach, Raman, Direct, and QTM relaxation pathways (eqn (S1)†). In both cases, the relaxation dynamics are dominated by through barrier mechanisms, where 1 and 3 could be effectively fit considering a combination of Raman, Orbach and QTM. Although, it should be noted that compounds 1 and 3 are accompanied by small U_eff-values at zero-field, which for 1, was necessary to include for the other parameters to remain physically reasonable (Table S16†). Fitting attempts with Raman relaxation as the sole contributor to the thermally activated region were unsuccessful and yielded unreasonable fit parameters.

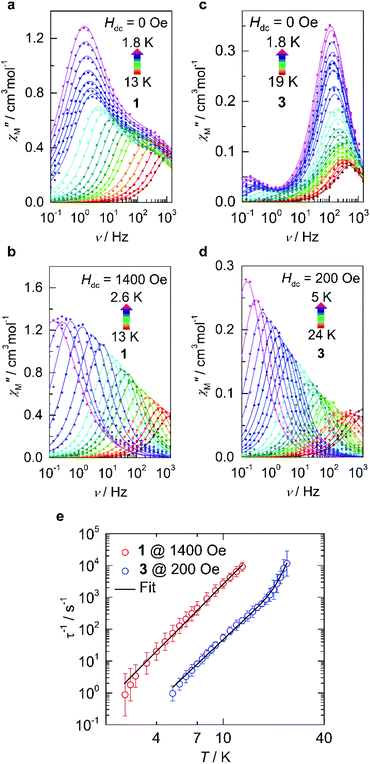Fig. 3 Dynamic magnetic data for 1 and 3. (a and b) Variable-temperature, variable-frequency out-of-phase (χ′′_M) components of the ac susceptibility data collected for 1 in the indicated temperature range in the absence of an applied static field (H_dc = 0 Oe; a) and in the presence of an applied field (H_dc = 1400 Oe; b). Solid lines represent fits to the generalized Debye model which are summarized in the ESI.† (c and d) The corresponding data are shown for 3 in the absence of an applied static field (H_dc = 0 Oe; c) and in the presence of an applied field (H_dc = 200 Oe; d). (e) Temperature dependence of the relaxation times (τ) in the presence of an applied static field for 1 (red) and 3 (blue). The solid line represents the sum of the Orbach and Raman relaxation mechanisms. Parameters and zero-field fits are summarized in Table S16 and Fig. S16 and S17.†

Given the limited frequency dependence of the relaxation times at low temperatures, investigation into the field dependence of the relaxation times was undertaken. The τ-values were extracted from the field-dependent χ′′_M(v) using a two-term generalized Debye model, from which we see a significant increase in τ upon increasing magnetic field strength and suppression of the second peak which has been shown to readily arise even in single-ion magnets.^39–41 In the case of compound 3, a well-defined peak shift towards lower frequencies (ca. 10 Hz) is observed upon application of a small external field, accompanied by rapid disappearance of the original process up to a field of 140 Oe (Fig. S10†), after which only a single Debye term is required to reproduce the data effectively (Table S11†). The relaxation times quickly reach saturation above 200 Oe (Fig. S11†) after which no appreciable increase in τ is observed. Similarly, the resulting behaviour of compound 1 required the sum of two generalized Debye terms to accurately reproduce the data up to fields of 1200 Oe (Table S10†), at which point τ tended towards zero, indicating complete suppression of the HF process while saturation is simultaneously reached in the LF region. Thus, optimal static fields of 1400 Oe and 200 Oe are obtained for 1 and 3, respectively.

Under these optimized conditions, QTM is effectively minimized, and the temperature dependent relaxation times for both 1 and 3 are longer and span the full frequency range (Fig. 3b, d, S12–S15, and Tables S12–S15†). The relaxation dynamics of 3 may be best described as a combination of Raman and Orbach mechanisms, eliciting best fit parameters of C = 2.67 × 10⁻⁵ s⁻¹ K⁻ⁿ, n = 4.97, τ₀ = 1.03 × 10⁻¹⁰ s, and U_eff = 334 K/232 cm⁻¹ (Fig. 3e, S17, and Table S16†). The obtained energy barrier is in excellent agreement with the theoretical model, conferring relaxation through the first excited state Kramers doublet (KD; 190 cm⁻¹) for 3. However, even at the optimal field of 1400 Oe, 1 does not show appreciable Orbach relaxation within the studied frequency and temperature range. Instead, the relaxation is effectively described as predominately Raman, meaning that if an Orbach mechanism were a possible pathway, the timescale to flip a spin over the anisotropy barrier would be much larger than what is experimentally attainable. Thus, the best-fit was obtained by considering only the Raman portion of eqn (S2),† yielding C = 1.31 × 10⁻³ s⁻¹ K⁻ⁿ and n = 5.29 (Fig. S16 and Table S16†).

Structural dependence on the electronic structure and anisotropy

Despite the stark difference in N–M–N angles of 1 and 3 (148.6° vs. 178.1°), both compounds exhibited slow relaxation of the magnetization under zero-field, indicative of ground states with non-zero orbital moments. This observation led us to examine the dependence of the local coordination geometry around the metal ion (i.e., the degree of bending) on the electronic configuration of linear Fe^I and Co^II metal complexes to gain a more thorough understanding of the tolerance of the pseudo-linearity towards enhancing anisotropy. To this end, a series of calculations were carried out on the two simplified model systems, [Fe{N(SiMe₃)₂}₂]⁺ (Fig. 4) and Co{N(SiMe₃)₂}₂ (Fig. 5), in which the aryl substituents have been replaced with –CH₃. The geometries were optimized using density functional theory while fixing the values of the N–M–N angle and the Si–N–N–Si dihedral angle. This was undertaken to prevent the aryl substituents from strongly distorting the immediate coordination sphere and invariably leading to inconsequential results between models, nevertheless, the model systems remain in good agreement with the experimental results. It is immediately clear that within the range of angles considered there is no strong qualitative change in the magnetic susceptibility in either of the studied model systems. In an idealized (180°) [Fe{N(SiMe₃)₂}₂]⁺, the ground state is described by a ⁴Δ term arising from a σ²δ³π² configuration stabilized by significant 3d–4s orbital mixing. The first excited term is ⁴Π, which lies considerably higher in energy due to the strong stabilization of the σ-symmetric orbital. For all geometries considered, the 4s-contribution to the σ-symmetric orbital varies between 12% and 20% based on the reduced Löwdin populations and the splitting between the terms remains large. With respect to Co{N(SiMe₃)₂}₂, in an ideal linear ligand field, the ground state is described by a ⁴Φ term arising from a non-Aufbau δ³π³σ¹ configuration with the excited ⁴Δ term, arising from a non-Aufbau δ³π²σ² configuration lying very close in energy. Significant mixing between the Φ and Δ manifolds takes place around the D_2h symmetry. The 3d–4s mixing is weaker in Co{N(SiMe₃)₂}₂ and varies between 4% and 10%. The pseudo-linearity of the electronic structure is retained upon decreasing the N–M–N angle to ca. 120° for Co{N(SiMe₃)₂}₂, and ca. 140° for [Fe{N(SiMe₃)₂}₂]⁺. Beyond these angles, the principal quantization axis of the AILFT orbitals no longer coincides with the N–M–N pseudoaxis, and the orbital order associated with the linear ligand field is lost. Thus, Co{N(SiMe₃)₂}₂ is somewhat more resistant to deviations from an ideal linear ligand field, which is reasonable considering the stronger spin–orbit coupling. Overall, within the range of geometries where the electronic structure retains resemblance of a linear system, the qualitative order of the electronic structure (Aufbau vs. non-Aufbau) remains the same. The ground state of [Fe{N(SiMe₃)₂}₂]⁺ is described by a ⁴Δ term due to the stabilization of the σ-symmetric orbital by 3d–4s orbital mixing, and the ground state of Co{N(SiMe₃)₂}₂ is described by a ⁴Φ term due to the non-Aufbau configuration. Around the D_2h symmetry, significant mixing between the ⁴Φ and ⁴Δ terms of Co{N(SiMe₃)₂}₂ occurs; however, both terms possess unquenched orbital contributions to the angular momentum, with both arising from non-Aufbau configurations.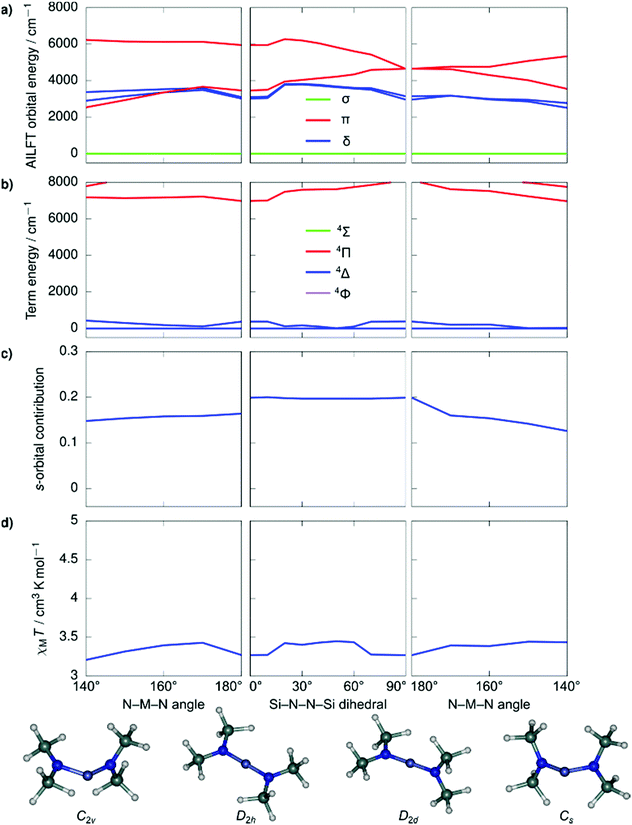

Fig. 4 Ab initio ligand field orbital energies (a); energies of low-lying terms (b); the 4s-orbital contribution to the σ-symmetric orbital based on the reduced Löwdin population (c); and magnetic susceptibility at 298 K (d) as calculated for the structural model Co{N(SiMe₃)₂}₂. The term energies are calculated at NEVPT2//SA-CASSCF(7,5) level before the inclusion of spin–orbit coupling and are labeled according to states in an idealized linear ligand field based on orbital occupations. The orbital symmetries have been determined by visual inspection. Full temperature-dependence of magnetic susceptibilities calculated for the various structures used in the bond angle scans is provided in Fig. S2.†

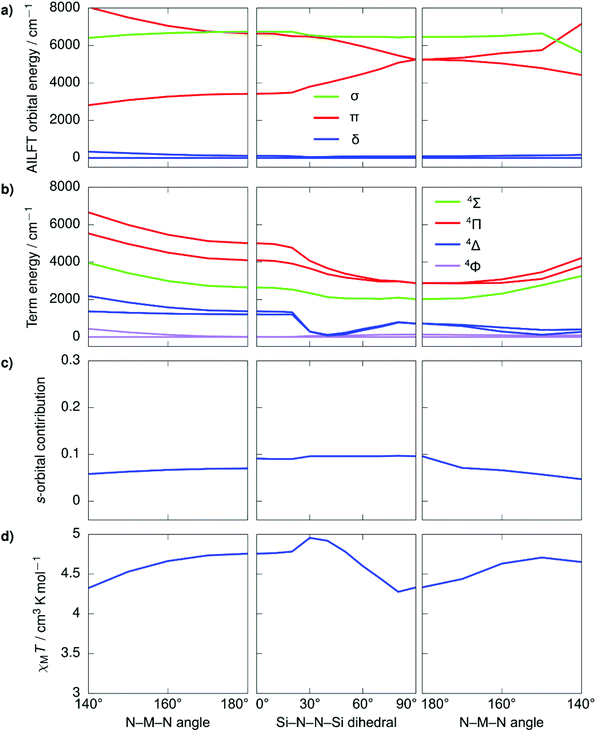Fig. 5 Ab initio ligand field orbital energies (a); energies of low-lying terms (b); the 4s-orbital contribution to the σ-symmetric orbital based on the reduced Löwdin population (c); and magnetic susceptibility at 298 K (d) as calculated for the structural model [Fe{N(SiMe₃)₂}₂]⁺. The term energies are calculated at NEVPT2//SA-CASSCF(7,5) level before the inclusion of spin–orbit coupling and are labeled according to states in an idealized linear ligand field based on orbital occupations. The orbital symmetries have been determined by visual inspection. Full temperature-dependence of magnetic susceptibilities calculated for the various structures used in the bond angle scans is provided in Fig. S2.†

Magnetic circular dichroism and magnetic hysteresis

Magnetic circular dichroism (MCD) is a powerful technique for the characterization of electronic levels.^42,43,63 The high-resolution endowed by the differential absorption of left and right circularly polarized light allow solving broad bands often observed in absorption spectra. The success of MCD for electronic levels characterization has been demonstrated for lanthanide,^44–47 actinide,^48–50 and transition metal^{51–55,61,62} compounds. Also, the technique is suitable for detection of magneto-optical hysteresis.^56–60

In order to corroborate the calculated energies and the inherent differences in the electronic structures of the experimentally obtained compounds 1 and 3, MCD experiments were conducted on mulls of the title compounds in Parabar 10 312 oil. The obtained MCD spectra for compounds 1 and 3 confirm that the expected allowed transitions are in good agreement with the computed quartets that lie in the visible region (Fig. 6 and S19†). These bands are consistent with the expected doubly degenerate ground spin quartets where only transitions with ΔS = 0 are formally allowed via selection rules. Resolution of the lower energy quartets are hindered by scattering effects at longer wavelengths, therefore the transitions located below ca. 15 000 cm⁻¹ (ca. 667 nm) could not be effectively determined under these conditions. Nonetheless, these results confirm that the computational model is suitable to explain the electronic structures of these compounds and consequently the predicted orbital occupancies are accurate. In addition to the obtained spectra, magnetization curves were collected for 1 and 3 by recording the MCD intensity at 613 nm (1) and 465 nm (3) as a function of applied field (Fig. S20†), this allows for a direct comparison with the analogous data obtained via SQUID magnetometry. M(H) curves with similar behaviour were obtained, indicating that the magneto-optical properties of the metal complexes are largely dictated by the ground state, as are the magnetic properties. Interestingly, for compound 3, at a sweep rate of 19 Oe s⁻¹ open hysteresis is observed between 1.55 and 3 K, with a coercive field of ca. 360 Oe for the transition centered at 465 nm (Fig. S21†). Comparatively, waist-restricted hysteresis is observed for compound 3 in the solid state via SQUID magnetometry up to a temperature of 4 K (Fig. S5†). At 1.8 K, the M(H) loop is open when H ≠ 0 Oe, the significant ground state QTM results in substantial reduction in the magnetization as the field approaches 0 Oe, while above 4 K, retention of the magnetization in the M(H) was not observable. The difference in the elicited magnetization response may be attributed to the polarization of the electronic transition,⁵⁶ consequently, only molecules with a specific orientation to both magnetic field and light propagation direction are excited in this method. I.e., the difference cannot be associated with a structural reorganization such as a change in the N–M–N angle arising from differing sample preparation techniques. For compound 1, we observed an open hysteresis only 1.55 K (Fig. S22†), which is sufficiently low that a coercive field of approximately 300 Oe, indicating that intermolecular interactions likely play a large role in the relaxation dynamics in solid-state.

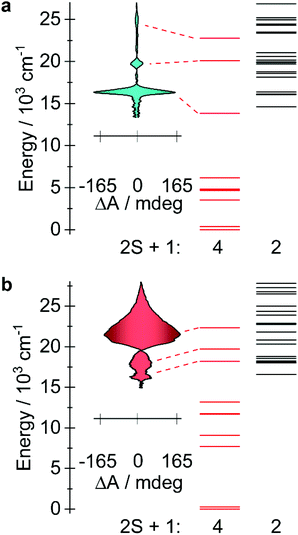Fig. 6 (a) MCD spectra of compound 1 obtained at 1.55 K with an applied field of +7 and −7 T (see Fig. S18†). The calculated doublet and quartet electronic state are represented by black and red lines, respectively. (b) The corresponding data are shown for compound 3.

Conclusions

Despite their seemingly isoelectronic configurations, compounds 1 and 3 exihibt slow relaxation of the magnetization of independent origin via either a rare example of non-Aufbau ground state configuration in the case of 1 or 3d–4s orbital mixing in 3. Even with unique electronic structures, the minimal energy difference between the δ orbitals of both molecules results in a doubly degenerate ground state for which our computational models were corroborated spectroscopically by MCD. By examining the dependence of the local coordination geometry around the metal ions, we find that the ligand field and the resulting order of electronic states are highly robust, remaining preserved even when the linearity of the N–M–N moiety is significantly altered (i.e., when the N–M–N angle is significantly bent). Thus, despite nearly a 30° difference in the N–M–N angle of compounds 1 and 3, the tolerance of the orbitals elicits ground states with non-zero orbital moments of differing origins. These findings expand the design and analytical criterion for highly sought-after d⁷ linear transition metal complexes, thus expanding our understanding of the ligand field and its formal limitation on the performance of transition metal SMMs. The ability to stabilize/destabilize the effective ligand field orbitals within the same ligand environment has great implications for magnetic anisotropy and its origin.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the University of Ottawa, Natural Sciences and Engineering Research Council of Canada, the Canadian Foundation for Innovation, the Magnus Ehrnrooth Foundation, as well as the University of Oulu (Kvantum Institute) for the funding of this work. We are grateful to Dr Thierry Maris and Mr Daniel Chartrand of the X-Ray Diffraction Laboratory at the Université de Montréal for the collection and analysis of diffraction data for 3. Computational resources have been provided by CSC-IT Center for Science in Finland and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533).

References

1. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
2. I. G. Rau, S. Baumann, S. Rusponi, F. Donati, S. Stepanow, L. Gragnaniello, J. Dreiser, C. Piamonteze, F. Nolting, S. Gangopadhyay, O. R. Albertini, R. M. Macfarlane, C. P. Lutz, B. Jones, P. Gambardella, A. J. Heinrich and H. Brune, Science, 2014, 344, 988–992.
3. B. N. Figgis, Nature, 1958, 182, 1568–1570.
4. P. S. Perlepe, D. Maniaki, E. Pilichos, E. Katsoulakou and S. P. Perlepes, Inorganics, 2020, 8, 39.
5. W. M. Reiff, A. M. LaPointe and E. H. Witten, J. Am. Chem. Soc., 2004, 126, 10206–10207.
6. W. A. Merrill, T. A. Stich, M. Brynda, G. J. Yeagle, J. C. Fettinger, R. De Hont, W. M. Reiff, C. E. Schulz, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2009, 131, 12693–12702.
7. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138.
8. M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156.
9. A. Sarkar, S. Dey and G. Rajaraman, Chem. – Eur. J., 2020, 26, 14036–14058.
10. J. T. Coutinho, B. Monteiro and L. C. J. Pereira, in Lanthanide-Based Multifunctional Materials, ed. P. Martín-Ramos and M. Ramos Silva, Elsevier, 2018, pp. 195–231.
11. P. P. Power, Chem. Rev., 2012, 112, 3482–3507.
12. M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214.
13. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581.
14. J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131.
15. X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380.
16. J. Du, L. Wang, M. Xie and L. Deng, Angew. Chem., Int. Ed., 2015, 54, 12640–12644.
17. P. P. Samuel, K. C. Mondal, N. A. Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer, L. Ungur, L. F. Chibotaru, J. Christian, V. Ramachandran, J. van Tol and N. S. Dalal, J. Am. Chem. Soc., 2014, 136, 11964–11971.
18. A. M. Bryan, G. J. Long, F. Grandjean and P. P. Power, Inorg. Chem., 2014, 53, 2692–2698.
19. C.-Y. Lin, J. C. Fettinger, F. Grandjean, G. J. Long and P. P. Power, Inorg. Chem., 2014, 53, 9400–9406.
20. A. A. Danopoulos, P. Braunstein, K. Y. Monakhov, J. van Leusen, P. Kögerler, M. Clémancey, J.-M. Latour, A. Benayad, M. Tromp, E. Rezabal and G. Frison, Dalton Trans., 2017, 46, 1163–1171.
21. P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 7319.
22. M. Gerloch and R. F. McMeeking, J. Chem. Soc., Dalton Trans., 1975, 2443–2451.
23. B. N. Figgis, J. Lewis, F. Mabbs and G. A. Webb, Nature, 1964, 203, 1138–1141.
24. B. N. Figgis, M. Gerloch, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1968, 2086–2093.
25. R. A. Bartlett and P. P. Power, J. Am. Chem. Soc., 1987, 24, 7563–7564.
26. C. G. Werncke, P. C. Bunting, C. Duhayon, J. R. Long, S. Bontemps and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2015, 54, 245–248.
27. C. G. Werncke, E. Suturina, P. C. Bunting, L. Vendier, J. R. Long, M. Atanasov, F. Neese, S. Sabo-Etienne and S. Bontemps, Chem. – Eur. J., 2016, 22, 1668–1674.
28. R. Weller, L. Ruppach, A. Shlyaykher, F. Tambornino and C. G. Werncke, Dalton Trans., 2021, 50, 10947–10963.
29. R. Weller, I. Müller, C. Duhayon, S. Sabo-Etienne, S. Bontemps and C. G. Werncke, Dalton Trans., 2021, 50, 4890–4903.
30. J. Pratt, A. M. Bryan, M. Faust, J. N. Boynton, P. Vasko, B. D. Rekken, A. Mansikkamäki, J. C. Fettinger, H. M. Tuononen and P. P. Power, Inorg. Chem., 2018, 57, 6491–6502.
31. J. M. Smith and D. Subedi, Dalton Trans., 2012, 41, 1423–1429.
32. M. S. Huzan, M. Fix, M. Aramini, P. Bencok, J. F. W. Mosselmans, S. Hayama, F. A. Breitner, L. B. Gee, C. J. Titus, M.-A. Arrio, A. Jesche and M. L. Baker, Chem. Sci., 2020, 11, 11801–11810.
33. M. K. Thomsen, A. Nyvang, J. P. S. Walsh, P. C. Bunting, J. R. Long, F. Neese, M. Atanasov, A. Genoni and J. Overgaard, Inorg. Chem., 2019, 58, 3211–3218.
34. R. Raumps, L. J. Batchelor, R. Maurice, N. Gogi, P. Jiménez-Lozano, N. Guihéry, C. de Graaf, A.-L. Barra, J.-P. Sutter and T. Mallah, Chem. – Eur. J., 2013, 19, 950–956.
35. E. Kuzmann, G. Zoppellaro, J. Pechousek, Z. Klencsár, L. Machala, J. Tucek, Z. Homonnay, J. Cuda, R. Szalay and M. Pápai, Struct. Chem., 2017, 28, 975–983.
36. N. F. Chilton, H. Lei, A. M. Bryan, F. Grandjean, G. J. Long and P. P. Power, Dalton Trans., 2015, 44, 11202–11211.
37. S. M. J. Aubin, Z. Sun, L. Pardi, J. Krzystek, K. Folting, L.-C. Brunel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329–5340.
38. R. Boča and C. Rajnák, Coord. Chem. Rev., 2021, 430, 213657.
39. L. T. A. Ho and L. F. Chibotaru, Phys. Rev. B, 2018, 98, 174418.
40. L. T. A. Ho and L. F. Chibotaru, Phys. Rev. B, 2016, 94, 104422.
41. J. Titiš, C. Rajnák, D. Valigura and R. Boča, Dalton Trans., 2018, 47, 7879–7882.
42. S. Piligkos, L. D. Slep, T. Weyhermüller, P. Chaudhuri, E. Bill and F. Neese, Coord. Chem. Rev., 2009, 253, 2352–2362.
43. N. J. Wolford, A. Radovic and M. L. Neidig, Dalton Trans., 2021, 50, 416–428.
44. M. Perfetti, M. Gysler, Y. Rechkemmer-Patalen, P. Zhang, H. Taştan, F. Fischer, J. Netz, W. Frey, L. W. Zimmermann, T. Schleid, M. Hakl, M. Orlita, L. Ungur, L. Chibotaru, T. Brock-Nannestad, S. Piligkos and J. van Slageren, Chem. Sci., 2019, 10, 2101–2110.
45. Y. Rechkemmer, J. E. Fischer, R. Marx, M. Dörfel, P. Neugebauer, S. Horvath, M. Gysler, T. Brock-Nannestad, W. Frey, M. F. Reid and J. van Slageren, J. Am. Chem. Soc., 2015, 137, 13114–13120.
46. P. Comba, L. J. Daumann, R. Klingeler, C. Koo, M. J. Riley, A. E. Roberts, H. Wadepohl and J. Werner, Chem. – Eur. J., 2018, 24, 5319–5330.
47. A. V. Malakhovskii, V. V. Sokolov and D. N. Karimov, Opt. Mater., 2021, 114, 110953.
48. D. J. Curran, G. Ganguly, Y. N. Heit, N. J. Wolford, S. G. Minasian, M. W. Löble, S. K. Cary, S. A. Kozimor, J. Autschbach and M. L. Neidig, Dalton Trans., 2021, 50, 5483–5492.
49. N. J. Wolford, D.-C. Sergentu, W. W. Brennessel, J. Autschbach and M. L. Neidig, Angew. Chem., Int. Ed., 2019, 58, 10266–10270.
50. N. J. Wolford, X. Yu, S. C. Bart, J. Autschbach and M. L. Neidig, Dalton Trans., 2020, 49, 14401–14410.
51. T. A. Kaden, B. Holmquist and B. L. Vallee, Inorg. Chem., 1974, 13, 2585–2590.
52. J. A. Larrabee, C. H. Leung, R. L. Moore, T. Thamrong-nawasawat and B. S. H. Wessler, J. Am. Chem. Soc., 2004, 126, 12316–12324.
53. K. L. Fillman, J. A. Przyojski, M. H. Al-Afyouni, Z. J. Tonzetich and M. L. Neidig, Chem. Sci., 2015, 6, 1178–1188.
54. S. Ye, G. Xue, I. Krivokapic, T. Petrenko, E. Bill, L. Que Jr. and F. Neese, Chem. Sci., 2015, 6, 2909–2921.
55. J. van Slageren, S. Piligkos and F. Neese, Dalton Trans., 2010, 39, 4999–5004.
56. J. C. Collingwood, P. Day and R. G. Denning, J. Chem. Soc., Faraday Trans., 1973, 269, 591–607.
57. P. A. Cox, D. J. Robbins and P. Day, Mol. Phys., 1975, 30, 405–411.
58. E. I. Solomon, E. G. Pavel, K. E. Loeb and C. Campochiaro, Coord. Chem. Rev., 1995, 144, 369–460.
59. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 1–8.
60. E. J. L. McInnes, E. Pidcock, V. S. Oganesyan, M. R. Cheesman, A. K. Powell and A. J. Thomson, J. Am. Chem. Soc., 2002, 124, 9219–9228.
61. N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Angew. Chem., 2021, 60 DOI:10.1002/anie.202110813.
62. M. Gonidec, E. S. Davies, J. McMaster, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2010, 132, 1756–1757.
63. T. T. da Cunha, J. Jung, M.-E. Boulon, G. Campo, F. Pointillart, C. L. M. Pereira, B. Le Guennic, O. Cador, K. Bernot, F. Pineider, S. Golhen and L. Ouahab, J. Am. Chem. Soc., 2013, 135, 16332–16335.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis and characterization; X-ray diffraction details including single crystal crystallography and powder (Fig. S1 and Table S1); ab initio details (Tables S2–S5); additional SQUID magnetometry (Fig. S2–S17 and Tables S6–S16) and additional MCD data (Fig. S18–S21). CCDC 2005381 and 2005382. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1qi00912e

‡ These authors contributed equally to this work.

---