 Open Access Article
Open Access ArticleRecent advances in understanding oxygen evolution reaction mechanisms over iridium oxide
Takahiro
Naito
 ,
Tatsuya
Shinagawa
,
Tatsuya
Shinagawa
 ,
Takeshi
Nishimoto
,
Takeshi
Nishimoto
 and
Kazuhiro
Takanabe
and
Kazuhiro
Takanabe
 *
*
Department of Chemical System Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, Japan. E-mail: takanabe@chemsys.t.u-tokyo.ac.jp
First published on 18th January 2021
Abstract
Water electrolysis driven by renewable energy can produce clean hydrogen, but its efficiency remains low, in part because of slow kinetics at the anode for the oxygen evolution reaction (OER). Learning from the most active catalysts for the OER, iridium oxides, would be the key to the development and establishment of design guidelines for active and stable OER catalysts. This article reviews in situ or operando spectroscopic and advanced computational studies in the past decade concerning the OER over iridium oxide for both the oxidation of water molecules and hydroxide ions. By collectively reviewing the reported findings, we illustrate the plausible OER catalytic cycles including the dissolution of iridium during the reaction, which at the same time disclosed discrepancies in the proposed mechanisms. Such discrepancies are thought to originate from variations in the experimental conditions employed in those studies, calling for comprehensive and systematic in situ or operando studies in the future. Toward the end, we discuss a recent approach for improving the activity and stability of OER catalysts.
1. Introduction
The transition to a sustainable society largely relies upon the utilization of renewable energy on a large scale. However, low energy density and intermittent availability hamper the widespread implementation of renewable energy, necessitating the development of systems that allow for its conversion to other forms of energy. The electrocatalytic process is a promising candidate for this purpose, which, using the electricity generated from renewable energy, can convert thermodynamically stable substances such as H2O and CO2 to energy-dense or value-added chemicals.1,2 Notwithstanding recent advances, the current technology of electrolysis fails to compete economically with fossil fuel-based counterparts,1 calling for research efforts on the development of efficient and cost-effective electrolysis systems.The oxygen evolution reaction (OER) is an anodic half-reaction that can be coupled with various cathodic counterparts, including the hydrogen evolution reaction (HER), the CO2 reduction reaction, and the N2 reduction reaction.3–8 The fundamental study on the OER can be traced back to 1955, when Rüetschi et al. first attempted to rationalize the OER performance over a variety of electrodes.9 Their study assessed the approximate bonding strength of M–OH (where M stands for metal) by analyzing the thermochemical and spectroscopic data,9 which were plotted with respect to the overpotential at 1 A cm−2 for the OER reported by Hickling and Hill in 1947.10 The plot revealed that the OER overpotential linearly scaled with the M–OH bonding energy, suggesting that M–OH bonding energy may serve as a descriptor for the OER activity.9 Later, this fundamental understanding was put forward by Trasatti in 1980,9 which revealed a correlation between the OER overpotential and the change of enthalpy from lower to higher oxide transition of transition metal oxides, e.g., from 3+ in Ir2O3 to 4+ in IrO2.11 The disclosed correlation is volcano-shaped; a metal oxide that requires a too large enthalpic change exhibits substantial overpotential, while another metal oxide that requires a too small enthalpic change also demands a large overpotential. This trend indicates that there exists an optimal enthalpy change that minimizes the overpotential for the OER, which was found for iridium oxide and ruthenium oxide having 79.5 and 83.4 kJ mol−1, respectively, for the transition from M2O3 to MO2.11 In fact, iridium oxide and ruthenium oxide are regarded even now as one of the most active OER electrocatalysts.12–14
These rationalizations of electrocatalysis rely on and are corroborated by experimental evidence. In the first place, the Tafel analysis might be used to elucidate the reaction mechanism and, in particular, to evaluate the rate-determining step (rds), which is the slowest elementary step of a multistep chemical reaction,15 of electrochemical reactions.16 In the case of the OER over iridium oxide, the Tafel slope values under acidic aqueous media were reported to be around 30–45 mV dec−1.17,18 These values, however, could not solely determine the rds because the multiple-step nature of the OER yields a variety of theoretically anticipated Tafel slope values when the electron transfer coefficient deviates from 0.5.16,19 This fact indicates the need for direct evidence by observing the catalyst surface via spectroscopic means to elucidate the surface state of the catalysts, the surface adsorbate on the catalysts, and in turn the reaction mechanism. Early reports in this line of study employed ex situ experiments. Typically, the as-made catalysts were characterized by techniques such as X-ray photoelectron spectroscopy (XPS) for the identification of the surface chemical state, electron microscopy for morphologies, and so on. The properties of the catalyst elucidated by these characterization studies were often attempted to be correlated with the catalytic performance. However, such analyses are not capable of providing a solid idea of catalysis because the catalyst material may undergo chemical and morphological changes by being placed in the actual electrolyte environment or during the catalytic reaction, which cannot be seen using characterization studies performed under a vacuum of pre-reaction samples.20–22 From this viewpoint, it is essential to investigate at least the catalyst of post-reaction. For instance, Kötz et al. studied the OER mechanism over iridium oxide using ex situ XPS at excitation around the O 1s and Ir 4f regions to track changes of its oxidic nature using post-reaction materials.21,23 They firstly placed the iridium sample in 1.0 M H2SO4 and applied potentials of 0.0 V, 0.6 V, or 1.25 V vs. saturated calomel electrode (SCE) (corresponding to 0.25 V, 0.85 V, or 1.5 V vs. reversible hydrogen electrode (RHE) at pH 0.14), before recording the XPS spectra. The obtained spectra captured a decrease in OH contribution and an increase in oxide intensity at increasing anodic potentials applied prior to the XPS measurements. These changes were ascribed to the transition from Ir(OH)3 to IrO(OH)2 at 0.22 V vs. RHE that is further oxidized to IrO3 at 1.5 V vs. RHE,21 leading to a proposal of a catalytic redox cycle involving Ir4+/5+/6+.21,23 This mechanistic understanding certainly helps in understanding the catalytic cycles. Nevertheless, nowadays, it is commonly considered that such ex situ measurements would not be satisfactory to fully rationalize the catalysis; e.g., the catalyst may attain a surface state different from its pristine state only during working conditions.23–25 This gap between the catalyst states under vacuum and working conditions hampered the establishment of a solid understanding of electrocatalysis.
From a different perspective, computational studies have advanced our understanding of OER electrocatalysis at a molecular level. A milestone report was published by Rossmeisl et al.5,26,27 Their framework of density functional theory (DFT) calculations considered the concerted proton–electron transfer (CPET) steps, where one H+ and one e− are transferred in a single kinetic step:28
| M + OH− ⇌ M–OH + e−, | (1) |
| M–OH + OH− ⇌ M–O + H2O + e−, | (2) |
| M–O + OH− ⇌ M–OOH + e−, | (3) |
| M–OOH + OH− ⇌ M + O2 + H2O + e−. | (4) |
Notwithstanding the success of the past computational approaches, the employed model omitted several considerations for the sake of simplicity and versatility. Firstly, those models did not compute kinetics. Analysis of the free energy of the reaction intermediates to elucidate the bottleneck was justified by the linear scaling relationship between the reaction energy and the activation energy, the so-called Brønsted–Evans–Polanyi (BEP) relationship.30 However, the BEP relationship is not always valid, and the pds and rds can differ from each other.31 Further complicating this kinetic aspect is the variation in the OER reactant. Depending on the electrolyte pH levels, the OER can proceed either as the oxidation of the hydroxide ion (OH−) or the water molecule (H2O), as shown in eqn (5) or eqn (6), respectively:32,33
| 4OH− ⇌ O2 + 2H2O + 4e−, | (5) |
| 2H2O ⇌ O2 + 4H+ + 4e−. | (6) |
| M + H+ ⇌ M–H+, | (7) |
| M + e− ⇌ M−. | (8) |
In this context, the recent decade has witnessed the development of spectroscopic techniques that enable the direct observation of the surface state in situ or operando14,40 and the advancement of computational calculations that can simulate and map the catalytic cycles in more detail.41 This review herein discusses the recent progress in understanding the OER mechanism based on in situ or operando experimental evidence as well as computational results. We limit ourselves to iridium oxide, one of the most active OER electrocatalysts. Readers interested in other catalysts can refer to other published studies.42–44 We illustrate plausible OER cycles via H2O oxidation in section 2 and review its spectroscopic and computational support, while section 3 deals with those for OH− oxidation. Section 4 discusses the dissolution mechanisms of iridium during the OER mechanism, corroborating the catalytic cycle.
2. OER mechanism via H2O oxidation over iridium oxide
Iridium oxide sits at or near the top of the volcano-shaped trend for the OER,11,29 and has been employed in commercial polymer electrolyte membrane (PEM) electrolyzers despite its high cost and scarcity.45 Developing active OER catalysts composed of Earth-abundant and cost-effective elements is the key to cost reduction and thus the introduction of hydrogen via electrolysis in the market. The rational design of such catalysts would require identification of the reaction mechanism and the working state of the best-performing iridium oxide catalysts. Accordingly, the recent decade has witnessed significant advancements in the understanding of OER electrocatalysis. Herein, this section collectively reviews the proposed mechanisms of H2O oxidation over iridium oxide based on spectroscopic evidence and advanced theoretical calculations. We firstly introduce an overall picture of plausible OER catalytic cycles, and subsequently review the spectroscopic and computational data supporting the scenarios in the later subsections.2.1. Proposed mechanism of H2O oxidation over iridium oxide
The existing literature allows for the elucidation of OER catalytic cycles over iridium oxide, illustrated in Fig. 1. There have been four reported cycles: (1) a cycle involving a surface adsorbate driven by the redox of the iridium centre (red colored in Fig. 1a), (2) a cycle involving a surface adsorbate driven by the redox of the adsorbed O species (blue colored in Fig. 1b), (3) a cycle involving the redox of the Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O state (green colored in Fig. 1c), and (4) the one that involves lattice oxygen (orange colored in Fig. 1d). Below we describe each cycle in more detail.
O state (green colored in Fig. 1c), and (4) the one that involves lattice oxygen (orange colored in Fig. 1d). Below we describe each cycle in more detail.
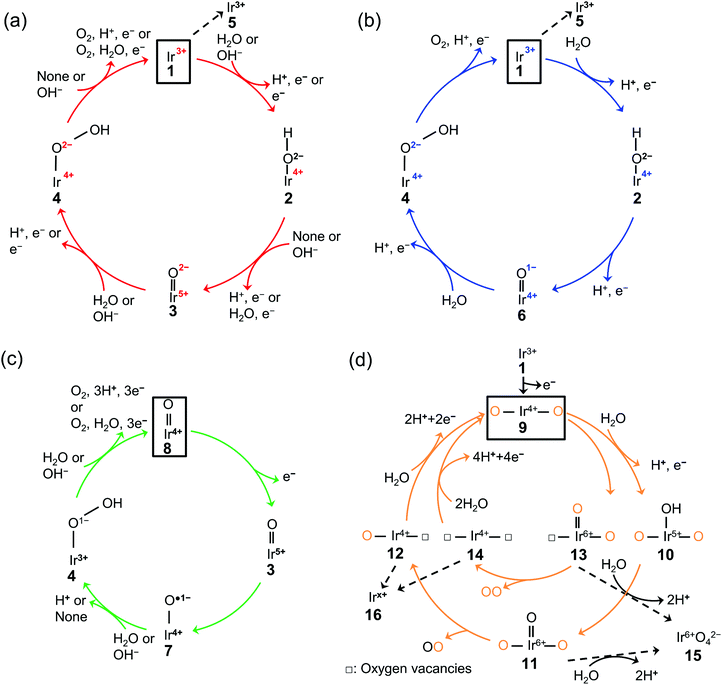 | ||
Fig. 1 Proposed mechanism of the oxygen evolution reaction (OER) over iridium oxide. Four different colors (red, blue, green, and orange) were used to illustrate four catalytic cycles. (a) The red-colored cycle is driven by the redox of the iridium center.17,29,46,47,66–68,95 (b) The blue-colored one proceeds via the redox of the adsorbed O species.17,29,46–51,68,95 (c) The green-colored cycle is characterized by the redox of the Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O state.17,58,67–69 (d) The orange-colored cycle involves the lattice oxygen, where the orange and black O represent the lattice oxygen and adsorbed oxygen species, respectively.63,65,71–74 The squares represent the initial state of each cycle, and the dashed lines indicate the dissolution path of iridium species. The (a) red, (b) blue, (c) green, and (d) orange cycles were reported for the H2O oxidation, while the (a) red and (c) green cycles were also reported for OH− oxidation as depicted in the figures. O state.17,58,67–69 (d) The orange-colored cycle involves the lattice oxygen, where the orange and black O represent the lattice oxygen and adsorbed oxygen species, respectively.63,65,71–74 The squares represent the initial state of each cycle, and the dashed lines indicate the dissolution path of iridium species. The (a) red, (b) blue, (c) green, and (d) orange cycles were reported for the H2O oxidation, while the (a) red and (c) green cycles were also reported for OH− oxidation as depicted in the figures. | ||
The scenario of the red-colored cycle in Fig. 1a starts with the oxidation of the initial state, Ir3+ (1 in the figure), with the H2O reactant, forming Ir4+–O2−H surface species (2) and H+via CPET. This species is oxidized to the Ir5+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O2− state (3) via a CPET step, which upon further oxidation is converted into Ir4+–O2−OH (4). By releasing O2, this state relaxes to Ir3+ (1). This cycle is consistent with the single-site mechanism commonly adopted for DFT calculations.16,50,54
O2− state (3) via a CPET step, which upon further oxidation is converted into Ir4+–O2−OH (4). By releasing O2, this state relaxes to Ir3+ (1). This cycle is consistent with the single-site mechanism commonly adopted for DFT calculations.16,50,54
The second scenario (blue colored in Fig. 1b) is similar to the first one except that the surface redox species is not only iridium but also oxygen. Firstly, the Ir3+ (1) is attacked by the H2O reactant, and forms Ir4+–O2−H surface species (2) releasing H+via CPET. This species is oxidized via a CPET step into the Ir4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1− state (6), which contains the electrophilic oxygen species (O1−) as a reactive intermediate.48–51 Ir4+
O1− state (6), which contains the electrophilic oxygen species (O1−) as a reactive intermediate.48–51 Ir4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1− experiences further oxidation with a H2O molecule to form Ir4+–O2−OH (4) via a CPET step. This state relaxes to Ir3+ (1) with releasing O2via CPET.
O1− experiences further oxidation with a H2O molecule to form Ir4+–O2−OH (4) via a CPET step. This state relaxes to Ir3+ (1) with releasing O2via CPET.
In contrast to the first two scenarios that involve the redox of either iridium or oxygen, the green-colored cycle in Fig. 1c proceeds by the redox of the Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O states. The initial Ir4+
O states. The initial Ir4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (8) changed the oxidation state to Ir5+
O (8) changed the oxidation state to Ir5+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (3) via ET. This Ir5+
O (3) via ET. This Ir5+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species (3) is the precursor to the reactive oxyl species31,52–57 of Ir4+–O˙1− (7) that reacts to form Ir3+–O1−OH (4) via PT. The formed Ir3+–O1−OH (4) releases O2 with H2O reactant and relaxes to Ir4+
O species (3) is the precursor to the reactive oxyl species31,52–57 of Ir4+–O˙1− (7) that reacts to form Ir3+–O1−OH (4) via PT. The formed Ir3+–O1−OH (4) releases O2 with H2O reactant and relaxes to Ir4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (8) via CPET. This route likely appears at a high overpotential (e.g., >2.4 V vs. RHE),58 where the accumulation of charge is considered to occur.59
O (8) via CPET. This route likely appears at a high overpotential (e.g., >2.4 V vs. RHE),58 where the accumulation of charge is considered to occur.59
The last cycle (orange-colored) shown in Fig. 1d proceeds via the releasing and filling of an oxygen vacancy at the iridium oxide surface, which was named the lattice oxygen evolving reaction (LOER) mechanism or lattice oxygen participated mechanism (LOM).60,61 This route likely appears at highly anodic potentials (e.g., >1.6 V vs. RHE for electrochemically prepared oxide from metallic iridium).62,63 In this scenario, two pathways are considered depending on the number of lattice oxygen atoms participating in the reaction. The first one depicted in the outer circle starts with the oxidation of Ir3+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (1) to form O–Ir4+–O (9) via ET. Lattice O bridging iridium sites of this O–Ir4+–O (9) are attacked by the H2O molecule to form O–Ir5+(–OH)–O (10) via PCET, which transforms into O–Ir6+(
O (1) to form O–Ir4+–O (9) via ET. Lattice O bridging iridium sites of this O–Ir4+–O (9) are attacked by the H2O molecule to form O–Ir5+(–OH)–O (10) via PCET, which transforms into O–Ir6+(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O (11) via CPET. This species releases oxygen to form O–Ir4+–□ species (12) where □ represents a vacant site, and this formed vacancy is subsequently filled by the attack of H2O to form O–Ir4+–O (9) via PCET. In the second pathway depicted in the orange-colored inner circle of Fig. 1d, evolved O2 consists of two lattice oxygens.64 In detail, the lattice O bridging the iridium sites (9) leaches out from the lattice to form □–Ir6+(
O)–O (11) via CPET. This species releases oxygen to form O–Ir4+–□ species (12) where □ represents a vacant site, and this formed vacancy is subsequently filled by the attack of H2O to form O–Ir4+–O (9) via PCET. In the second pathway depicted in the orange-colored inner circle of Fig. 1d, evolved O2 consists of two lattice oxygens.64 In detail, the lattice O bridging the iridium sites (9) leaches out from the lattice to form □–Ir6+(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O (13). Subsequently, this □–Ir6+(
O)–O (13). Subsequently, this □–Ir6+(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O state (13) releases O2 to form □–Ir4+–□ (14), where the two oxygen vacancies are filled by the attack of H2O to form O–Ir4+–O (9) via CPET.
O)–O state (13) releases O2 to form □–Ir4+–□ (14), where the two oxygen vacancies are filled by the attack of H2O to form O–Ir4+–O (9) via CPET.
2.2. Spectroscopic evidence to support the claimed catalytic cycle for H2O oxidation over iridium oxide
The OER catalytic cycles detailed in the previous section were obtained based on the recent in situ and operando characterization studies, which allowed for determining the working states of catalysts.65 The employed techniques include X-ray absorption near-edge structure (XANES), near-edge X-ray absorption fine structure (NEXAFS), X-ray absorption (XAS), XPS, and Raman spectroscopy. The key observations in the literature are highlighted and shown in Fig. 2 that elucidated OER electrocatalysis over iridium oxide.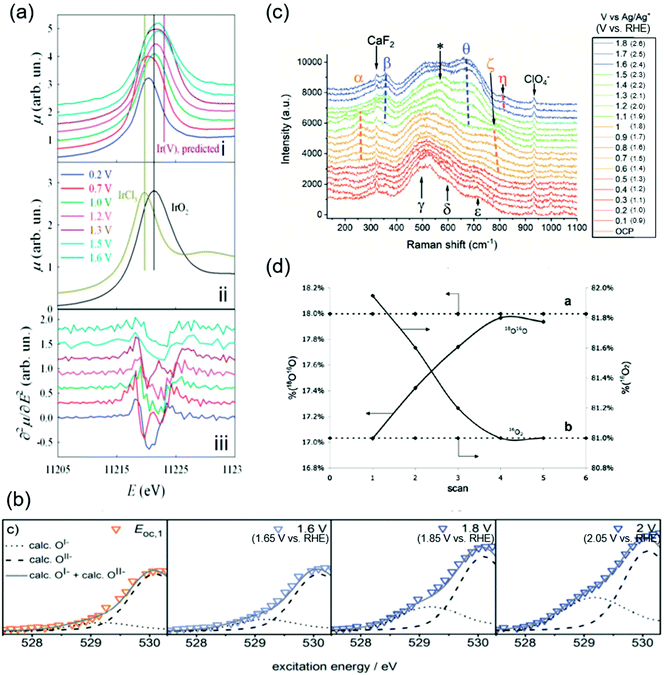 | ||
| Fig. 2 Spectroscopic data for H2O oxidation over iridium oxide. (a) In situ Ir-LIII X-ray absorption near-edge structure (XANES) spectra using hydrous iridium oxide with the applied potential from 0.2 to 1.6 V vs. reversible hydrogen electrode (RHE) in 0.5 M H2SO4 solution. White lines of the absorption in the Ir-LIII region are shown for iridium oxide at various potentials in the panel (i), and over the reference IrCl3 and IrO2 in panel (ii), and the second derivatives of the spectra shown in panel (i) are plotted in panel (iii). Reproduced from ref. 67 with permission from the Royal Society of Chemistry. (b) In situ near-edge X-ray absorption fine structure (NEXAFS) spectra in the O K-edge region in 0.1 M H2SO4 at 0.3 Pa at open circuit potential (OCP), 1.6, 1.8, and 2.0 V vs. standard hydrogen electrode (SHE) (corresponding to 1.66 V, 1.86 V, or 2.05 V vs. RHE at pH 0.97) using a sputtered iridium catalyst. Reproduced from ref. 48 with permission from the Royal Society of Chemistry. (c) In situ shell-isolated nanoparticle-enhanced Raman spectroscopy (SHINERS) spectra using electrochemically deposited iridium oxide in 0.1 M NaClO4 solutions at pH 10 at varying potentials from OCP to 1.8 V vs. Ag/Ag+ (corresponding to 2.6 V vs. RHE at pH 10). Reproduced from ref. 58 with permission from the Royal Society of Chemistry. (d) Differential electrochemical mass spectrometry (DEMS) results during a cyclic voltammogram in a potential window from ca. 0.05 V to 1.6 V vs. SHE (corresponding to ca. 0.05 V to 1.6 V vs. RHE at pH 0) in a 1 M HClO4 solution containing 10 wt% H218O over thermally prepared Ir16O2/Ti catalyst. Reprinted with permission from ref. 65. Copyright (2018) Elsevier. | ||
Initially, the spectroscopic evidence supporting the catalytic cycle in Fig. 1a was provided by an in situ XPS study in 2014.66 The group of Nilsson conducted in situ XPS measurements using IrO2 nanoparticles with the applied potential of 1.75 V vs. RHE in the presence of 10 Torr of H2O, i.e., neither acidic nor alkaline.66 By analyzing the XPS spectra in the Ir 4f region, they found that the IrO2 sample at open-circuit potential (OCP) retained the Ir4+ state upon exposure to H2O. Interestingly, the spectra exhibited a shoulder when an anodic potential of 1.75 V vs. RHE was applied, ascribed to the appearance of Ir+5. In the same study, they also examined the excitation around the O 1s region, and found that when the potential was switched from OCP to 1.75 V vs. RHE, the relative intensity of the peak ascribable to hydroxide species decreased while that of oxide increased.66 Taken together, their observation pointed to a deprotonation reaction during the course of the OER accompanying the oxidation of Ir4+ into Ir5+ states. This observation elucidates the change in the oxidation state of iridium during the catalytic cycle, corresponding to the transformation of Ir4+–O2−H+ (2) into Ir5+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O2− (3) in the red-colored cycle in Fig. 1a.
O2− (3) in the red-colored cycle in Fig. 1a.
In 2014 and 2015, Rondinini and co-workers reported in situ Ir-LIII XANES that also supports the red-colored catalytic cycle in Fig. 1a.67,68 The group investigated the XANES spectra over hydrous iridium oxide catalyst in the acidic solution of 0.5 M H2SO4 at varying potentials from 0.2 to 1.6 V vs. RHE, and their key result is shown in Fig. 2a.67Panel i of the figure displays white lines of the absorption in the Ir-LIII region at various potentials. When increasing the potential from 0.2 to 0.7 V vs. RHE, the white line position remained identical, being similar to that of the IrCl3 reference (the panel ii), which indicates the presence of the Ir3+ state. When the potential was further anodically shifted to 1.0 V vs. RHE, the white line position shifted toward higher energies. Because the resulting position at 1.0 V vs. RHE was identical to the IrO2 reference (the panel ii), the shift indicates the oxidation of Ir3+ into Ir4+ states. They further analyzed the second derivatives of the spectra as shown in panel iii of Fig. 2a. The figure displays double peak structures at 0.7 V and 1.3 V vs. RHE, which were ascribable to the transition from the Ir 2p levels to the split (t2g + eg) 5d states, indicating the presence of Ir4+ and Ir5+ at 0.7 V and 1.3 V vs. RHE, respectively.67 Collectively, their study proposed that iridium oxide changes its oxidation state from Ir3+ to Ir4+ at around 1.0 V vs. RHE and further to Ir5+ above 1.3 V vs. RHE (from 1 to 3 in Fig. 1), thus supporting the red- and green-colored cycles displayed in Fig. 1a.
In contrast, a study was reported in 2016 by Schlögl and co-workers that supports, based on NEXAFS, the anion redox mechanism shown as the blue-colored second scenario in Fig. 1b.48–51 The group recorded in situ NEXAFS spectra in the O K-edge region using a sputtered iridium catalyst at varying potentials of OCP, 1.6, 1.8, and 2.0 V vs. standard hydrogen electrode (SHE) (corresponding to 1.66 V, 1.86 V, and 2.05 V vs. RHE at pH 0.97, respectively) in 0.1 M H2SO4 solution at 0.3 Pa as shown in Fig. 2b.48 The spectra exhibited a broad peak, which was deconvoluted into two; one at the smaller energy was thought to originate from the electron-deficient oxygen species, and another one at the larger energy represents O2− species. The study labelled the former one as O1−, although it is still under debate whether the electron-deficient oxygen is electrophilic oxygen (O1−) or an oxyl radical (O˙1−).31,52–57 At more positive potentials, a hump appeared at the peak shoulder, indicating an increased contribution from the O1− state. In correlating to the OER activity, they found that the OER performance linearly scaled with the fraction of not O2− but O1−, and thus concluded that the electrophilic O1− species (6 in Fig. 1b) is the active species in catalysing the OER on iridium oxide.48 We note that these species were observed at potentials above 1.6 V in Fig. 2c higher than the potentials employed in other cases, implying that this route may become likely apparent in higher overpotential regions. This view is compatible with a recent study claiming the charging up of iridium species under highly anodic conditions.59
The experimental evidence supporting the green-colored third scenario depicted in Fig. 1c was provided using Raman spectroscopy.58,69 In 2020, Saeed et al. conducted in situ shell-isolated nanoparticle-enhanced Raman spectroscopy (SHINERS)58 using electrochemically deposited iridium oxide in 0.1 M NaClO4 solution at pH 10 at varying potentials from OCP to 1.8 V vs. Ag/Ag+ (corresponding to 2.6 V vs. RHE at pH 10).58 The measured spectra shown in Fig. 2c were divided into four distinct regions depending on the spectra features, (I) OCP to 0.5 V vs. Ag/Ag+ (corresponding to 1.3 V vs. RHE at pH 10), (II) 0.6 to 1.0 V vs. Ag/Ag+ (corresponding to 1.4 V to 1.8 V vs. RHE at pH 10), (III) 1.1 to 1.5 V vs. Ag/Ag+ (corresponding to 1.9 V to 2.3 V vs. RHE at pH 10), and (IV) 1.6 to 1.8 V vs. Ag/Ag+ (corresponding to 2.4 V to 2.6 V vs. RHE at pH 10), which are respectively red-, orange-, green-, and blue-colored spectra in the figure. The spectra exhibited multiple peaks, ascribed to the Ir–O–Ir twist, Ir–O–Ir stretch, or Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch based on the previous Raman studies.69,70 More specifically, the peaks labelled as α (252 cm−1) and β (357 cm−1) were both assigned to the Ir–O–Ir twist at different iridium oxidation states; the former contains Ir4+, and the latter contains Ir>4+.69,70 The five peaks of γ (504 cm−1), δ (608 cm−1), ε (719 cm−1), ζ (773 cm−1), and θ (672 cm−1) were all ascribed to the Ir–O–Ir stretch; δ was observed at the iridium oxidation state of +3, and γ, ε, and ζ were apparent for Ir+4, while θ indicates the higher oxidation state of Ir>+4.69,70 The one at η (813 cm−1) was thought to originate from the Ir
O stretch based on the previous Raman studies.69,70 More specifically, the peaks labelled as α (252 cm−1) and β (357 cm−1) were both assigned to the Ir–O–Ir twist at different iridium oxidation states; the former contains Ir4+, and the latter contains Ir>4+.69,70 The five peaks of γ (504 cm−1), δ (608 cm−1), ε (719 cm−1), ζ (773 cm−1), and θ (672 cm−1) were all ascribed to the Ir–O–Ir stretch; δ was observed at the iridium oxidation state of +3, and γ, ε, and ζ were apparent for Ir+4, while θ indicates the higher oxidation state of Ir>+4.69,70 The one at η (813 cm−1) was thought to originate from the Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch at Ir>4+.69,70 Regarding the assignment of this peak η in detail, previously the group of Schlögl investigated the influences of isotopes on the peak, and observed that this peak η was insensitive to the isotope H and D, indicative of the absence of H species in the vibration.69 In addition, in an experiment using solution containing 50
O stretch at Ir>4+.69,70 Regarding the assignment of this peak η in detail, previously the group of Schlögl investigated the influences of isotopes on the peak, and observed that this peak η was insensitive to the isotope H and D, indicative of the absence of H species in the vibration.69 In addition, in an experiment using solution containing 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (H2O16
50 (H2O16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O18), only two peaks of nearly equal intensity were observed as η, which suggests that this vibration contains a single O atom, or the absence of O–O.69 Furthermore, although the peak shift of single bonding Ir–O due to the substitution of O16 for O18 was calculated to be 45 cm−1, the observed shift was 59 cm−1. These observations led to a conclusion in the study that the peak η originated from Ir
H2O18), only two peaks of nearly equal intensity were observed as η, which suggests that this vibration contains a single O atom, or the absence of O–O.69 Furthermore, although the peak shift of single bonding Ir–O due to the substitution of O16 for O18 was calculated to be 45 cm−1, the observed shift was 59 cm−1. These observations led to a conclusion in the study that the peak η originated from Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O.69
O.69
In region (I) of Fig. 2c, the γ, δ, and ε peaks were apparent, indicative of the presence of the Ir4+ state. When entering region (II), an additional feature was observed in the spectra at α and ζ, which suggests that iridium species were still mostly composed of 4+ states. In region (III), the spectra exhibited contributions from β and θ, which implies the formation of >4+ states. These β and θ states persisted also in region (IV), where additionally the peak η appeared. Importantly, subsequent SHINERS spectroscopy combining the isotope labelling testing using D2O-based solutions (1 M NaClO4 at pD 10) demonstrated almost no change in the peak position of η from 813 cm−1 (in H2O) to 817 cm−1 (in D2O). Thus, they concluded that all peaks do not contain H elements such as hydroxides, peroxides, or the oxyl radical species, which are considered as the precursor for O–O bond formation.69 This study proposed that the OER catalytic cycle contains three intermediates, which all have an Ir–O bond, before rate-determining OOH formation, as shown in Fig. 1c.
The orange-colored last scenario of LOER in Fig. 1d was supported by studies using mass spectroscopy in conjunction with isotope labelling.65,71–74 In 2007, Fierro et al. conducted differential electrochemical mass spectrometry (DEMS) measurements during a cyclic voltammogram (CV) in a potential window from ca. 0.05 V to ca. 1.6 V vs. SHE (corresponding to ca. 0.05 V to ca. 1.6 V vs. RHE at pH 0) in a 1 M HClO4 solution containing 10 wt% H218O using thermally prepared Ir16O2/Ti catalyst, and their results are shown in Fig. 2d.65 Their study tracked the identity of evolved O2 (either 16O2 or 18O16O) while recording the CVs. Fig. 2d shows the composition of 18O16O and 16O2 at each CV scan, disclosing that the composition of 16O2 decreased with the cycle number while that of 16O18O increased from 17% to 18% until reaching a steady state after the third cycle. To corroborate this observation, they performed an additional CV-DEMS experiment using Ir18Ox in 1 M HClO4 containing ca. 10% H218O. Their results showed that the evolved O2 gas was initially composed of 18O16O at 0.9% in the first scan and was <0.5% after the fifth scan with a concomitant increase of 16O2 composition. These results allowed them to analyse the exchanging of lattice O of iridium oxide with O in the solution during the OER at steady state, and thus indicated the participation of lattice oxygen in the OER mechanism as depicted in the orange-colored cycle in Fig. 1d.
In addition to the spectroscopic study, morphological observations such as electron microscopy75–77 also shed light on the catalysis of iridium oxide. For instance, in 2017, Willinger et al. compared the structural features between the more active electrocatalyst, which was hydrothermally prepared and denoted as IrOx-(FHI), and the less active one, which was commercially available and denoted as IrOx-commercial.75 By analyzing the observed images of high-angle annular dark field scanning transmission electron microscopy (HAADF STEM), they found a larger amount of the tunnel-like motifs of hollandite structure in IrOx-FHI than that in IrOx-commercial,75 which was considered to be an active motif for the OER.78 Their subsequent electron pair distribution function (ePDF) analysis suggested that IrOx-FHI consisted of the hollandite structure, whereas IrOx-commercial consisted of 60% hollandite and 40% rutile unit cell.75 These observations allowed for proposing that the hollandite structure is the key for the highly active OER catalyst, iridium oxide.75 These studies demonstrate the significance of the morphological aspect on the OER activity.
Metal single-site catalysts have attracted increasing interest in recent years.79–82 In 2020, an in situ XAS study observing the oxidation state of atomically dispersed iridium oxide on indium tin oxide (ITO) in 0.1 M HClO4 during the OER was reported by Lebedev et al.79 They measured in situ XANES at Ir LIII-edge at 1.46 V vs. RHE and assigned an Ir–O distance of 1.83 ± 0.02 Å as an Ir+5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediate, which was the predominant species under OER conditions.79 Subsequently, the same authors further investigated the reaction mechanism by DFT calculation and suggested the formation of the Ir+6 dioxo intermediate after the formation of the Ir+5
O intermediate, which was the predominant species under OER conditions.79 Subsequently, the same authors further investigated the reaction mechanism by DFT calculation and suggested the formation of the Ir+6 dioxo intermediate after the formation of the Ir+5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O intermediate.79 This result of the formation of Ir+5
O intermediate.79 This result of the formation of Ir+5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is consistent with the observations on the heterogeneous solid states as discussed in this review.67 This type of study would cultivate a better understanding of OER catalysis from a comprehensive perspective, and furthermore would eventually bridge the gap between heterogeneous and homogeneous catalysis.83–85
O is consistent with the observations on the heterogeneous solid states as discussed in this review.67 This type of study would cultivate a better understanding of OER catalysis from a comprehensive perspective, and furthermore would eventually bridge the gap between heterogeneous and homogeneous catalysis.83–85
As described above, recent in situ and operando characterization studies captured the oxidation state of the active site and surface intermediate during the OER. The experimental evidence in Fig. 2 helps in reasoning the catalytic cycles, shaping the ones in Fig. 1. Notwithstanding the successful applications of these techniques to the electrocatalytic OER, there remains a discrepancy among studies about the oxidation state of iridium and oxygen as well as the surface intermediate, and thus the reaction mechanism. This discrepancy likely arises because of the non-unified catalyst and experimental conditions among reported studies, calling for further systematic investigations of the OER over iridium oxide with these sophisticated techniques.
2.3. Theoretical study corroborating the mechanism of H2O oxidation over iridium oxide
Theoretical studies help elucidate the reaction mechanism at molecular levels, and thus corroborate the experimental observations. Here in this subsection, we review selected theoretical studies on the OER over iridium oxide considering kinetics46,47,86 that were omitted in the previously established DFT models.5,26,27Ping et al. considered possible reaction pathways over the IrO2(110) surface, and computed reaction rates based on the microkinetic models at the constant potential of 1.36 V vs. normal hydrogen electrode (NHE) at pH 0 (corresponding to 1.36 V vs. RHE at pH 0).46Fig. 3a and b show the reaction intermediates and transition state (TS) structures as well as their free energy profile. In Fig. 3a, their considered model proceeds as follows: the initial state having Ir(OH)–O–Ir(OH) species (1′′) is partially deprotonated to form Ir(OH)–O–Ir(O) (1′). Then, two scenarios were considered after the formation of this species (1′). In the first scenario, the species (1′) experiences deprotonation to form Ir(O)–O–Ir(O) (1) that is then attacked by H2O (TS1) and forms Ir(OH)–O–Ir(OOH) (2). Alternatively, Ir(OH)–O–Ir(O) (1′) is attacked by H2O (TS1′) and is transformed into Ir(OH2)–O–Ir(OOH) (2′), which is then deprotonated to form Ir(OH)–O–Ir(OOH) (2). The thus-formed species (2) is deprotonated to form Ir(OH)–O–Ir(OO) (3) and subsequently Ir(O)–O–Ir(OO) (4). The species (4) releases O2 (TS2) and is protonated to Ir(O)–O–Ir(OH2) (5), which via internal PT transforms back to the initial state (1′′). To assess the feasibility of the pathways, they computed the reaction barrier at TS1 and TS1′, which amounted to 0.6 and 0.5 eV, respectively, as compiled in Fig. 3b. Notably, they thus proposed that a thermodynamically less favourable pathway (1′ → TS1′ → 2′ → 2) could be kinetically more favourable.46 This rationalization deepens the catalyst cycle in Fig. 1 with the proposal of rds being the formation of OOH (4 in Fig. 1a–c).
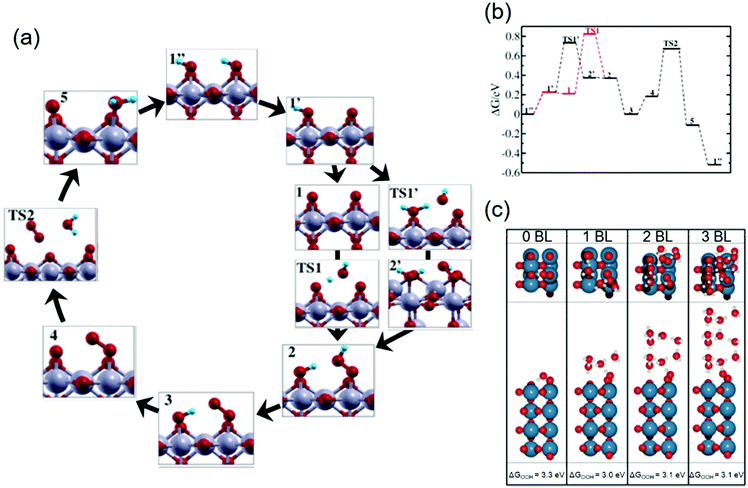 | ||
| Fig. 3 Theoretical studies for H2O oxidation over iridium oxide. (a) Considered reaction pathways for the OER over the IrO2(110) surface; red balls are O; blue balls are H; silver balls are Ir. (b) Computed reaction free energy diagram at the constant potential of 1.36 V vs. normalized hydrogen electrode (NHE) at pH 0 (corresponding to 1.36 V vs. RHE at pH 0) corresponding to the mechanism shown in the panel (a). Reprinted with permission from ref. 46. Copyright (2017) American Chemical Society. (c) The most stable structure for the IrO2(110) surface with adsorbed *OOH at the coordinatively unsaturated metal sites (CUS), *O on the neighboring CUS, and *O at the bridge, together with varying numbers of water bilayers (BL); blue balls are Ir; red balls are O; white balls are H. Reprinted with permission from ref. 47. Copyright (2017) American Chemical Society. | ||
To investigate the influence of solvent on the conformation of the reaction intermediate during the OER, Gauthier et al. studied the interface between rutile IrO2(110) and H2O.47Fig. 3c shows the most stable structures found for the IrO2(110) surface with adsorbed *OOH at the coordinatively unsaturated metal sites (CUS), *O on the neighbouring CUS, and *O at the bridge, together with varying numbers of water bilayers (BL).47 In the absence of an explicit solvent (0 BL), the geometry of adsorbed intermediates was determined by interaction among the surface species; the hydrogen of the *OOH species was the most stable when *OOH was directed to the bridging O with hydrogen bonds as illustrated in Fig. 3c (0 BL). The presence of the explicit solvent (1–3 BL) changed the dominant interaction of the H element in the adsorbed *OOH species from that with the surface to that with the BL. Fig. 3c (1–3 BL) illustrates the conformation in the presence of solvent: a more stable structure was found when a hydrogen bond was formed between the H of *OOH and the explicit solvent. Notably, as long as BL was taken into account, the number of BLs had little influence on the calculation results. Thus, the bond structure of the active adsorbate was likely determined by the explicit solvent rather than the neighbouring adsorbate. Although by the subsequent thermodynamic calculation with the solvent, they observed that the reaction pathway was relatively unchanged by the inclusion of the explicit solvent, the solvent was found to stabilize the OOH adsorbate by about 0.3 eV. This study was consistent with the reaction intermediates shown in Fig. 1a–c, and provided new insights into the conformation of surface species by considering the effect of the solvent that shall impact the kinetics.
These advanced theoretical calculations demonstrated quantitatively the significance of the kinetic barrier and solvent on the OER electrocatalysis. The insights provided in those studies help in picturing the transition state in the ideal scenario, and would shed light on the rational design of active catalysts. In addition, theoretical studies may be able to assess the feasibility of catalytic cycles proposed by experiments (the four scenarios in Fig. 1) and may refine our view on electrocatalysis in the near future.
3. OER mechanism via OH− oxidation over iridium oxide
There have been a limited number of studies on the OER over iridium oxide at alkaline pH levels, plausibly because of its lower OER stability than that under acidic conditions13,87 and the existence of alternative catalysts such as NiFeOx active toward the OER.13,87 Nonetheless, the investigation and elucidation of the OER over iridium oxide under alkaline pH conditions are of great significance because of two reasons. Firstly, the OER reactant varies with pH levels, H2O and OH− at acidic and alkaline pH levels, respectively, which corresponds to variation in the transition state and thus kinetics at different pH levels over iridium oxide. Understanding OER kinetics over iridium oxide under distinct conditions forms a generalized view into its catalysis, which would help rationally design OER catalysts. Secondly, increasing attention has recently been given to the OER at the near-neutral pH levels under buffered conditions,42,88–90 where the OER can proceed also as the oxidation of OH−. Insights into the OER at alkaline pH thus certainly help advance the electrocatalysis under near-neutral pH conditions. We in this section describe firstly the mechanism of OH− oxidation, before detailing spectroscopic evidence and theoretical calculations supporting the mechanism.3.1. Proposed mechanism of OH− oxidation over iridium oxide
There are two proposed OER mechanisms via OH− oxidation over iridium oxide that are essentially shared with those for the oxidation of H2O, depicted in Fig. 1: (1) a cycle involving surface adsorbate driven by the redox of the iridium centre (the red-colored cycle in Fig. 1a), and (2) a cycle involving the redox of the Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O state (the green-colored cycle in Fig. 1c). Notably, the difference between those cycles and the corresponding ones at acidic pH levels is that instead of the involvement of H2O, the cycles at alkaline pH consume the OH− reactant. In the next sections, we review reported studies supporting those scenarios.
O state (the green-colored cycle in Fig. 1c). Notably, the difference between those cycles and the corresponding ones at acidic pH levels is that instead of the involvement of H2O, the cycles at alkaline pH consume the OH− reactant. In the next sections, we review reported studies supporting those scenarios.
3.2. Spectroscopic evidence to support the claimed catalytic cycle for OH− oxidation over iridium oxide
In 2017, Ooka et al. reported the presence of Ir5+ at the rds using ultraviolet-visible light (UV-Vis) spectroscopy.17,91 They employed in situ evanescent wave (EW) spectroscopy at 1.2, 1.4, and 1.5 V vs. RHE in solutions at various pH levels from 2 to 12 over anodically deposited iridium oxide.17Fig. 4a shows the EW spectra measured at pH 12, in which two absorption peaks were apparent at approximately 410 and 580 nm at 1.2 V vs. RHE, assigned to Ir5+ and Ir4+, respectively, based on the previous UV-vis study.38 Interestingly, the former peak continuously shifted toward higher wavelengths at more positive potentials, ending at 456 nm at 1.5 V vs. RHE. Based on their previous time-dependent DFT (TDDFT) calculation result that theoretically elucidated spin states,91 they considered that this shift from 410 to 456 nm with the potential was due to the change of the spin of two adjacent oxygen ligands from symmetric to asymmetric ones, which they proposed as a state of iridium centre at the rds. Their study also examined the absorption at different pH levels, and the potential at which these absorptions appeared on the RHE scale is shown as a function of pH in Fig. 4b. In the figure, the absorptions at 410, 450 nm (as an approximate representative of 456 nm), and 580 nm are denoted as Abs 410 nm, Abs 450 nm, and Abs 580 nm, respectively, and Uonset,j stands for the onset potential of the OER. Interestingly, the potentials for Abs 580 nm and Abs 410 nm shifted with the pH value with a slope of 30 mV per pH on the RHE scale, implying that the redox reaction proceeds by transferring more than one proton per electron.92 In contrast, the potential for Abs 450 nm and OER onset was mostly insensitive to the pH values as shown in Fig. 4b. This consistent insensitivity implies that the rds of the OER over iridium oxide was not the valence change of the iridium centre, but the activation of the oxygen ligand, such as the activation of O2− to form O−.17,48,50 Overall, this study considered oxidation states consistent with the transition from Ir4+–O2−H+(2) to Ir5+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O2− (3) in the red-colored cycle of Fig. 1a, and proposed that the activation of the oxygen ligand would take place over Ir4+
O2− (3) in the red-colored cycle of Fig. 1a, and proposed that the activation of the oxygen ligand would take place over Ir4+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1− (6) as the rds.
O1− (6) as the rds.
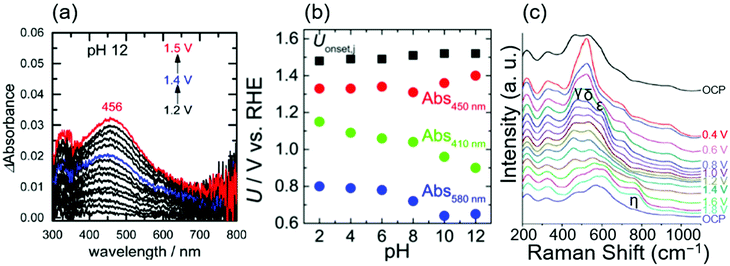 | ||
| Fig. 4 Spectroscopic data for OH− oxidation over iridium oxide. (a) In situ evanescent wave (EW) spectra in a mixed solution (NaOH, Britton–Robinson buffer and Na2SO4) at pH 12 over anodically deposited iridium oxide with varying potential from 1.2 to 1.5 V vs. RHE. (b) Potentials for the OER onset (black), absorption at 450 nm (red), 410 nm, (green), and 580 nm (blue) on the RHE scale compiled as a function of pH, recorded in mixed solutions (NaOH, Britton–Robinson buffer and Na2SO4) from pH 2 to 12 over anodically deposited iridium oxide. Reprinted with permission from ref. 17. Copyright (2017) American Chemical Society. (c) In situ surface-enhanced Raman spectroscopy (SERS) at varying potentials from OCP to 1.8 V vs. RHE in 0.1 M NaOH using iridium oxide on an Au substrate. Reproduced from ref. 69 with permission from the Royal Society of Chemistry. | ||
In 2017, Pavlovic et al. reported a result of in situ Raman spectroscopy that supports the green-colored catalytic cycle in Fig. 1.69 The group conducted in situ surface-enhanced Raman spectroscopy (SERS) at varying potentials from OCP to 1.8 V vs. RHE in 0.1 M NaOH using iridium oxide on an Au substrate, and the obtained spectra are shown in Fig. 4c.69 At OCP, they observed peaks at 465, 527, 600, and 702 cm−1, which were attributed to the Ir–O–Ir stretching vibrations of μ-oxo type oxygen linkages.70 Upon increasing the potential to 0.4 V, new peaks δ, ε, and γ appeared at 520, 595, and 476 cm−1, ascribable to the Ir–O stretch.70 The spectra remained unchanged until reaching >1.4 V, where an additional peak was observed at 771 cm−1 labelled as η. Their additional experiments employing the isotope D revealed that this peak η was insensitive to the isotopes H and D. In contrast, isotope labelling with 18O led to a shift of 59 cm−1, which differed from the expected shift of 45 cm−1 for the surface species containing single bonding of Ir–O. Based on these observations, they hypothesized that the peak η originated from Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration as opposed to any other species that contained O–O, or OH vibration,69 which would serve as a precursor to the reactive oxyl species.93,94 This Ir
O vibration as opposed to any other species that contained O–O, or OH vibration,69 which would serve as a precursor to the reactive oxyl species.93,94 This Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O corresponds the species 3 in Fig. 1a and c, and species 6 in Fig. 1b. The species 3 in Fig. 1c would transform into the reactive oxyl species 7 in Fig. 1c.
O corresponds the species 3 in Fig. 1a and c, and species 6 in Fig. 1b. The species 3 in Fig. 1c would transform into the reactive oxyl species 7 in Fig. 1c.
3.3. Theoretical study corroborating the mechanism of OH− oxidation over iridium oxide
A rigorous analysis for the OER mechanism concerning both the kinetics and thermodynamics was provided in 2019 by the group of Exner.95 Their approach relied on (1) DFT calculations to determine the free energy of the reaction intermediate and construct an ab initio Pourbaix diagram,96–100 and (2) Tafel plots46,47,96,101,102 to determine the electron transfer coefficient and free energies of the rate-determining transition state,95,103 under the assumption of the Ir, Ir–OH, Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and Ir–OOH intermediates. These considerations can be combined to construct a free energy diagram at a given overpotential, which allowed for pinning down the variation in the rds with applied overpotentials. Their ab initio Pourbaix diagram for IrO2(110) is shown in Fig. 5a, and a representative free energy diagram over IrO2(110) at an OER overpotential (ηOER) of 0.47 V in alkaline solution at pH 12.9 is presented in Fig. 5b. Interestingly, their analysis disclosed that at ηOER > 0.3 V, Ir–OOH is the thermodynamically most stable surface, and its conversion into Ir with releasing O2 is the rds at ηOER > 0.34 V,95 in contrast to the common understanding of the rds being the formation of O–O bonding.29,46,47,96,101,102 This study corroborated the cycle in Fig. 1a–c, with a new insight that not the formation but the decomposition of OOH determines the rate.
O and Ir–OOH intermediates. These considerations can be combined to construct a free energy diagram at a given overpotential, which allowed for pinning down the variation in the rds with applied overpotentials. Their ab initio Pourbaix diagram for IrO2(110) is shown in Fig. 5a, and a representative free energy diagram over IrO2(110) at an OER overpotential (ηOER) of 0.47 V in alkaline solution at pH 12.9 is presented in Fig. 5b. Interestingly, their analysis disclosed that at ηOER > 0.3 V, Ir–OOH is the thermodynamically most stable surface, and its conversion into Ir with releasing O2 is the rds at ηOER > 0.34 V,95 in contrast to the common understanding of the rds being the formation of O–O bonding.29,46,47,96,101,102 This study corroborated the cycle in Fig. 1a–c, with a new insight that not the formation but the decomposition of OOH determines the rate.
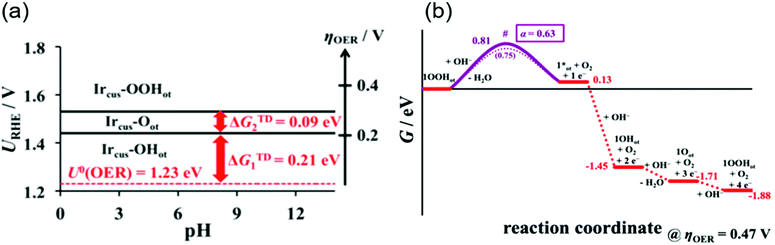 | ||
| Fig. 5 Theoretical studies for OH− oxidation over iridium oxide. (a) The ab initio Pourbaix diagram for a single-crystalline IrO2(110). (b) The free energy diagram over IrO2(110) in alkaline media (pH = 12.9) at an OER overpotential of 0.47 V. Reprinted with permission from ref. 95. Copyright (2019) American Chemical Society. | ||
4. Dissolution of iridium oxide during the OER
Although the degradation of OER activity over iridium oxide was observed in both acidic and alkaline solutions,13,101 mechanistic studies on the dissolution of iridium have been reported only in acidic solutions.62,71,72,104 Two types of dissolution pathways were proposed: (1) dissolving via redox of the iridium centre as Ir3+ (5) in Fig. 1a and b, (2) dissolving with releasing oxygen atom in iridium oxide as Ir6+ (15) or Irx+ (16) during the LOER in Fig. 1d. The measurements were basically performed by electrochemical testing using a scanning flow cell (SFC) with mass spectroscopy such as inductively coupled plasma mass spectrometry (ICP-MS) or with online electrochemical mass spectrometry (OLEMS),62,71,72 and key results are shown in Fig. 6.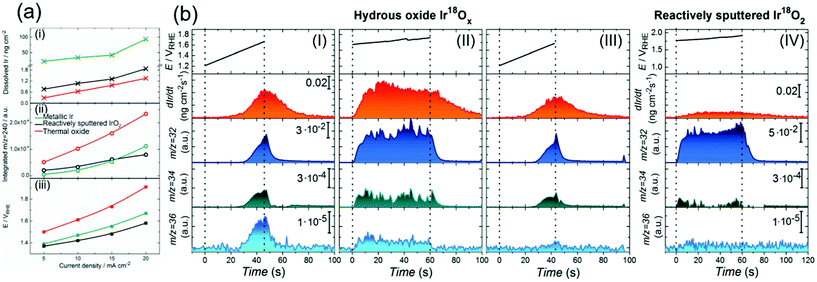 | ||
| Fig. 6 Experimental data on the dissolution of iridium oxides. (a) Results of a scanning flow cell (SFC) coupled with online electrochemical mass spectrometry (OLEMS) or inductively coupled plasma mass spectrometry (ICP-MS) in 0.1 M HClO4 solution at constant current densities of 5, 10, 15, or 20 mA cm−2 for 30 s using three types of iridium oxide: electrochemically prepared oxide from metallic iridium (denoted as metallic Ir, green), reactively sputtered IrO2 (black), and thermally prepared iridium oxide (red). (i) The amount of dissolved Ir, (ii) the amount of dissolved IrO3 (m/z = 240), and (iii) potential at the end of polarization on the current density. Reprinted with permission from ref. 62. Copyright (2018) Wiley-VCH. (b) Results for the dissolution amount of iridium species and evolved O2 gas (16O16O, 16O18O, and 18O18O at m/z = 32, 34, and 36, respectively) using a SFC coupled with OLEMS and ICP-MS in 0.1 M HCl16O4 solutions: (I) using hydrous Ir18Ox with sweeping the potential from 1.2 V vs. RHE to the potential where the current density reached a value of 20 mA cm−2; (II) using hydrous Ir18Ox at potentials where the current density reached 15 mA cm−2 for 60 s after the experiment in panel (I); (III) using hydrous Ir18Ox with sweeping the potential from 1.2 V vs. RHE to the potential where the current density reached a value of 20 mA cm−2 after the experiment in panel (II); and (IV) using reactively sputtered Ir18O2 at potentials where the current density reached 15 mA cm−2 for 60 s. Reproduced from ref. 71 with permission from the Royal Society of Chemistry. | ||
In 2018, Kasian et al. reported the dissolution reaction of iridium oxide under acidic conditions using a SFC coupled with OLEMS or ICP-MS.62 Their measurements were conducted in 0.1 M HClO4 solution at a constant current density of 5, 10, 15, or 20 mA cm−2 for 30 s, using three types of iridium oxide, namely electrochemically prepared oxide from metallic iridium (denoted as metallic Ir), reactively sputtered IrO2, and thermally prepared iridium oxide. Fig. 6a shows, as a function of the applied current density, the amount of dissolved iridium species in panel i, integrated signals of mass spectra at mass-to-charge ratios (m/z) of 240 as the representative of dissolved IrO3 in panel ii, and the corresponding potential on the scale of RHE (panel iii). The reactively sputtered IrO2 exhibited a lower dissolution rate than the metallic iridium similar to thermal oxide according to panel i, and the highest activity as in panel iii. Its superior activity with a slower dissolution rate was consistent with the previous study,105 and the lower dissolution rate of the thermal one likely originated from its thermodynamic stability.106 Notably, metallic Ir exhibited the largest amount of dissolved iridium as shown in panel i, and its dissolution rate as IrO3 exponentially increased with the current density unlike the other iridium oxides (panel ii). They proposed that this increase was due to two dissolution-pathways prevailing at distinct potentials: below 1.6 V vs. RHE, the iridium species likely formed HIr3+O2 and dissolved as Ir3+via the OER catalytic cycles involving Ir3+/4+/5+ as previously reported,72 and above 1.6 V vs. RHE, the IrO3 species react with water and are dissolved in the form of Ir6+O42−, which would not be able to be re-deposited on the catalyst surface, via the Ir4+/5+/6+ pathway.63 This reasoning is reflected in Fig. 1: (1) dissolution of Ir3+ (5 in Fig. 1a and b) for the pathway of 1 → 2 → 3 (or 6) → 4 → 5, and (2) dissolution of Ir6+ (15 in Fig. 1d) for the pathway through 9 → 10 → 11 → 15 or 9 → 13 → 15.
Recently, the dissolution of iridium oxide is thought to be related to the LOER mechanism71,73 based on previous observations over various oxide surfaces.64,107,108 Kasian et al. investigated a degradation mechanism using a SFC coupled with OLEMS and ICP-MS in 0.1 M HCl16O4 solution.71 They used two types of iridium oxide: electrochemically formed hydrous Ir18O2 catalysts, and reactively sputtered Ir18O2. The detected signals of evolved O2 gas were composed of three distinct species; 16O16O, 16O18O, and 18O18O at m/z = 32, 34, and 36, respectively.71Fig. 6b shows the detected concentration of dissolved iridium species and evolved oxygen gas. Their experimental protocol for hydrous Ir18O2 was (1) sweeping the potential from 1.2 V vs. RHE to the potential where the current density reached a value of 20 mA cm−2 in panel I, then (2) applying potential where the current density reached 15 mA cm−2 for 60 s in panel II, and finally (3) sweeping the potential again from 1.2 V vs. RHE to the potential reaching 20 mA cm−2 in panel III. Critically, the dissolution of iridium species was observed in every scan. The concentration of dissolved iridium species increased with increasing applied potential in protocol (1) and (3), and the concentration almost remained constant throughout protocol (2). Furthermore, comparison of step (1) shown in panel I with step (3) shown in panel III revealed that the signals of both 16O18O and 18O18O in pane III were smaller than those in panel I, implying that oxygen atoms in IrO2 participated in the OER. In contrast, their experiment using the sputtered IrO2 provided a distinct picture. Their experimental protocol was to apply a potential reaching 15 mA cm−2 for 60 s, the same as step (2) of the protocol for the hydrous ones, and the obtained result is provided in panel IV. Interestingly, the figure disclosed a lesser signal of iridium dissolution than the hydrous one, and negligible signals of 16O18O and 18O18O.71
In their study, Kasian et al. detailed the dissolution mechanism and lattice oxygen participation during the OER.71 Analysing the data in Fig. 6b disclosed that the ratio of the iridium dissolution rate and the 18O18O formation rate was the same for both hydrous and sputtered IrO2, suggesting a link between the participation of lattice oxygen and the dissolution of iridium. They subsequently studied the surface species and morphology of both samples using XPS and atom probe tomography (ATP) in conjunction with reported near ambient pressure XPS (NAP-XPS).24,49,109 It was observed that hydrous iridium oxide possessed nanopores and –Ir3+OOH– species, while the reactively sputtered one did not. They reasoned that the opened spaces provided by the nanopores would allow for frequent attacks by H2O molecules, facilitating the dissolution of iridium species as Irx+ (16) with the leaching of lattice oxygen atoms. Additionally, the Ir3+–OOH species would form HIr3+O2 that dissolves into the solutions as Ir3+.62,72 Taken together, the dissolution was faster for the hydrous one due to its morphological and chemical state, which accompanies the removal of lattice oxygen detected as the formation of 16O18O and 18O2, while such an event was less pronounced for the sputtered one due to the distinct surface state. These findings are reflected in the catalytic cycles described in the orange-colored cycle in Fig. 1d.
5. Summary and future outlook
This article reviewed the recent reports on the in situ or operando spectroscopic studies as well as advanced computational work for the OER over one of the most active catalysts, iridium oxide. By collectively summarizing the literature, we illustrated the OER catalytic cycles on iridium oxide for the oxidation of both H2O and OH− occurring mainly at acidic and alkaline pH levels, respectively. In situ or operando spectroscopic studies such as XPS and XANES captured the oxidation state and chemical environment of the catalysts at work, while the studies employing IR and Raman have elucidated the surface binding species in operando. The advanced calculations addressed the kinetic aspects of the OER catalysis, refining our view at the molecular level. Notably, while shaping the scheme of the catalytic cycles, we noticed that there exists some discrepancy regarding the active site, oxidation states, surface intermediates and rds. The discrepancy likely arose from distinct experimental conditions in the literature, e.g., the synthesis protocol for the iridium sample, electrolyte, applied potential, and so on. Therefore, it would be critical in future studies to comprehensively and systematically perform spectroscopic studies that can provide us with a more solid understanding of OER catalysis. In addition, a recent study claimed that the amount of accumulated oxidative charge of electrocatalysts dictates the activation energy of the reaction, which has not been taken into account in the previous studies on the mechanism.58 This novel concept may link the studies, which can further refine our view on OER catalysis.The established view on the reaction mechanism helps develop design principles of active and stable OER catalysts. The spectroscopic observation of the Ir5+ state in situ or operando49,66,67 implies that the rds occurs on this Ir5+ site, plausibly Ir![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, which is thought to convert into Ir–OOH in one of the cycles.29,46,47,69,110 This rationale suggests that stabilizing the Ir–OOH state by introducing a second component as a proton acceptor would accelerate this rds.111 Such an approach was theoretically supported with recent DFT calculations by Busch112 and has recently been demonstrated experimentally in the case of Mn-based catalysts.113
O, which is thought to convert into Ir–OOH in one of the cycles.29,46,47,69,110 This rationale suggests that stabilizing the Ir–OOH state by introducing a second component as a proton acceptor would accelerate this rds.111 Such an approach was theoretically supported with recent DFT calculations by Busch112 and has recently been demonstrated experimentally in the case of Mn-based catalysts.113
Another rational approach for improving the OER performance based on the rational understanding is the stabilization of the high-valence state of iridium by introducing a second component. It was reviewed in this article that iridium oxide dissolves into the solutions with oxidation states of 3+ or 6+.62,72 This finding suggests that stabilizing these oxidation states of iridium by introducing a second component would prevent the dissolution, which can prolong the lifetime of catalysts. In fact, improved stability was reported for IrOx/SrIrO3 in 2016,114 and IrOx–TiO2 in 2017.115 Thus, the rational design of catalysts based on the understanding of the reaction mechanisms would be an effective approach to improve the performance of iridium-based OER catalysts. Moreover, in such discussions of introducing additional components, the OER activity also improved by leaching the second or third component from the complex such as Sr from the perovskite of SrIrO3,114 Y from the pyrochlore of Y2Ir2O7,116 Ba and Ln from the double perovskite of Ba2PrIrO6,117 Ni and Co from Ir-based nanowire,118 and Ni from the IrNiOx core–shell structure.119 The thus-derived surface would contribute to the improvement of the OER activity by constructing highly active iridium centers such as iridium hydroxide-dominant surfaces.51 This review provides the community with a generalized view on the state-of-the-art understanding of the OER mechanism over iridium and will stimulate further understanding and development of OER catalysts in the future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A part of this work was supported by JSPS KAKENHI Grant Number 19K23569 and UTokyo-KAUST collaborative research OSR #4191 “Towards Sustainable Production of H2”.Notes and references
- S. Satyapal, J. Petrovic, C. Read, G. Thomas and G. Ordaz, The U.S. Department of Energy's National Hydrogen Storage Project: Progress towards meeting hydrogen-powered vehicle requirements, Catal. Today, 2007, 120, 246–256 CrossRef CAS.
- J. Yang, A. Sudik, C. Wolverton and D. J. Siegel, High capacity hydrogen storage materials: attributes for automotive applications and techniques for materials discovery, Chem. Soc. Rev., 2010, 39, 656–675 RSC.
- Y. Chen, C. W. Li and M. W. Kanan, Aqueous CO2 Reduction at Very Low Overpotential on Oxide-Derived Au Nanoparticles, J. Am. Chem. Soc., 2012, 134, 19969–19972 CrossRef CAS.
- K. P. Kuhl, T. Hatsukade, E. R. Cave, D. N. Abram, J. Kibsgaard and T. F. Jaramillo, Electrocatalytic Conversion of Carbon Dioxide to Methane and Methanol on Transition Metal Surfaces, J. Am. Chem. Soc., 2014, 136, 14107–14113 CrossRef CAS.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces, Energy Environ. Sci., 2012, 5, 7050–7059 RSC.
- T. Li, Y. Cao, J. He and C. P. Berlinguette, Electrolytic CO2 Reduction in Tandem with Oxidative Organic Chemistry, ACS Cent. Sci., 2017, 3, 778–783 CrossRef CAS.
- Y. Wang, S. Gonell, U. R. Mathiyazhagan, Y. Liu, D. Wang, A. J. M. Miller and T. J. Meyer, Simultaneous Electrosynthesis of Syngas and an Aldehyde from CO2 and an Alcohol by Molecular Electrocatalysis, ACS Appl. Energy Mater., 2019, 2, 97–101 CrossRef CAS.
- S. Garg, M. Li, A. Z. Weber, L. Ge, L. Li, V. Rudolph, G. Wang and T. E. Rufford, Advances and challenges in electrochemical CO2 reduction processes: an engineering and design perspective looking beyond new catalyst materials, J. Mater. Chem. A, 2020, 8, 1511–1544 RSC.
- P. Rüetschi and P. Delahay, Influence of Electrode Material on Oxygen Overvoltage: A Theoretical Analysis, J. Chem. Phys., 1955, 23, 556–560 CrossRef.
- A. Hickling and S. Hill, Oxygen overvoltage. Part I. The influence of electrode material, current density, and time in aqueous solution, Discuss. Faraday Soc., 1947, 1, 236–246 RSC.
- S. Trasatti, Electrocatalysis by oxides—Attempt at a unifying approach, J. Electroanal. Chem., 1980, 111, 125–131 CrossRef CAS.
- Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Horn, Synthesis and Activities of Rutile IrO2 and RuO2 Nanoparticles for Oxygen Evolution in Acid and Alkaline Solutions, J. Phys. Chem. Lett., 2012, 3, 399–404 CrossRef CAS.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS.
- S. Jung, C. C. L. McCrory, I. M. Ferrer, J. C. Peters and T. F. Jaramillo, Benchmarking nanoparticulate metal oxide electrocatalysts for the alkaline water oxidation reaction, J. Mater. Chem. A, 2016, 4, 3068–3076 RSC.
- J. R. Murdoch, What is the rate-limiting step of a multistep reaction?, J. Chem. Educ., 1981, 58, 32–36 CrossRef CAS.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion, Sci. Rep., 2015, 5, 13801 CrossRef.
- H. Ooka, A. Yamaguchi, T. Takashima, K. Hashimoto and R. Nakamura, Efficiency of Oxygen Evolution on Iridium Oxide Determined from the pH Dependence of Charge Accumulation, J. Phys. Chem. C, 2017, 121, 17873–17881 CrossRef CAS.
- D. F. Abbott, D. Lebedev, K. Waltar, M. Povia, M. Nachtegaal, E. Fabbri, C. Copéret and T. J. Schmidt, Iridium Oxide for the Oxygen Evolution Reaction: Correlation between Particle Size, Morphology, and the Surface Hydroxo Layer from Operando XAS, Chem. Mater., 2016, 28, 6591–6604 CrossRef CAS.
- T. Nishimoto, T. Shinagawa, T. Naito and K. Takanabe, Microkinetic assessment of electrocatalytic oxygen evolution reaction over iridium oxide in unbuffered conditions, J. Catal., 2020, 391, 435–445 CrossRef CAS.
- Y. H. Hall and P. M. A. Sherwood, X-ray photoelectron spectroscopic studies of the iridium electrode system, J. Chem. Soc., Faraday Trans. 1, 1984, 80, 135–152 RSC.
- R. Kötz, H. Neff and S. Stucki, Anodic Iridium Oxide Films: XPS-Studies of Oxidation State Changes and O2-Evolution, J. Electrochem. Soc., 1984, 131, 72–77 CrossRef.
- S. E. Castillo-Blum, D. T. Richens and A. G. Sykes, Oxidation of hexaaquairidium(III) and related studies: preparation and properties of iridium(III), iridium(IV), and iridium(V) dimers as aqua ions, Inorg. Chem., 1989, 28, 954–960 CrossRef CAS.
- R. Kötz and H. Neff, Anodic iridium oxide films: An UPS study of emersed electrodes, Surf. Sci., 1985, 160, 517–530 CrossRef.
- T. Reier, D. Teschner, T. Lunkenbein, A. Bergmann, S. Selve, R. Kraehnert, R. Schlögl and P. Strasser, Electrocatalytic Oxygen Evolution on Iridium Oxide: Uncovering Catalyst-Substrate Interactions and Active Iridium Oxide Species, J. Electrochem. Soc., 2014, 161, F876–F882 CrossRef CAS.
- T. Reier, Z. Pawolek, S. Cherevko, M. Bruns, T. Jones, D. Teschner, S. Selve, A. Bergmann, H. N. Nong, R. Schlögl, K. J. J. Mayrhofer and P. Strasser, Molecular Insight in Structure and Activity of Highly Efficient, Low-Ir Ir–Ni Oxide Catalysts for Electrochemical Water Splitting (OER), J. Am. Chem. Soc., 2015, 137, 13031–13040 CrossRef CAS.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Electrolysis of water on (oxidized) metal surfaces, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Thermochemistry of Proton-Coupled Electron Transfer Reagents and Its Implications, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of water on oxide surfaces, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. K. Norskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, The nature of the active site in heterogeneous metal catalysis, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- M. T. M. Koper, Analysis of electrocatalytic reaction schemes: distinction between rate-determining and potential-determining steps, J. Solid State Electrochem., 2013, 17, 339–344 CrossRef CAS.
- M. Auinger, I. Katsounaros, J. C. Meier, S. O. Klemm, P. U. Biedermann, A. A. Topalov, M. Rohwerder and K. J. J. Mayrhofer, Near-surface ion distribution and buffer effects during electrochemical reactions, Phys. Chem. Chem. Phys., 2011, 13, 16384–16394 RSC.
- B. E. Conway and B. V. Tilak, Interfacial processes involving electrocatalytic evolution and oxidation of H2, and the role of chemisorbed H, Electrochim. Acta, 2002, 47, 3571–3594 CrossRef CAS.
- R. Subbaraman, D. Tripkovic, K.-C. Chang, D. Strmcnik, A. P. Paulikas, P. Hirunsit, M. Chan, J. Greeley, V. Stamenkovic and N. M. Markovic, Trends in activity for the water electrolyser reactions on 3d M(Ni,Co,Fe,Mn) hydr(oxy)oxide catalysts, Nat. Mater., 2012, 11, 550–557 CrossRef CAS.
- B. E. Conway and B. V. Tilak, Behavior and characterization of kinetically involved chemisorbed intermediates in electrocatalysis of gas evolution reactions, Adv. Catal., 1992, 38, 1–147 CAS.
- T. Shinagawa, M. T.-K. Ng and K. Takanabe, Electrolyte Engineering towards Efficient Water Splitting at Mild pH, ChemSusChem, 2017, 10, 4155–4162 CrossRef CAS.
- L. Giordano, B. Han, M. Risch, W. T. Hong, R. R. Rao, K. A. Stoerzinger and Y. Shao-Horn, pH dependence of OER activity of oxides: Current and future perspectives, Catal. Today, 2016, 262, 2–10 CrossRef CAS.
- S. Trasatti, Electrocatalysis in the anodic evolution of oxygen and chlorine, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS.
- M. T. M. Koper, Theory of multiple proton–electron transfer reactions and its implications for electrocatalysis, Chem. Sci., 2013, 4, 2710–2723 RSC.
- B. Lassalle-Kaiser, S. Gul, J. Kern, V. K. Yachandra and J. Yano, In situ/Operando studies of electrocatalysts using hard X-ray spectroscopy, J. Electron Spectrosc. Relat. Phenom., 2017, 221, 18–27 CrossRef CAS.
- Q. Li, Y. Ouyang, S. Lu, X. Bai, Y. Zhang, L. Shi, C. Ling and J. Wang, Perspective on theoretical methods and modeling relating to electro-catalysis processes, Chem. Commun., 2020, 56, 9937–9949 RSC.
- S. Park, Y. H. Lee, S. Choi, H. Seo, M. Y. Lee, M. Balamurugan and K. T. Nam, Manganese oxide-based heterogeneous electrocatalysts for water oxidation, Energy Environ. Sci., 2020, 13, 2310–2340 RSC.
- F. Dionigi and P. Strasser, NiFe-Based (Oxy)hydroxide Catalysts for Oxygen Evolution Reaction in Non-Acidic Electrolytes, Adv. Energy Mater., 2016, 6, 1600621 CrossRef.
- J. Yu, Q. He, G. Yang, W. Zhou, Z. Shao and M. Ni, Recent Advances and Prospective in Ruthenium-Based Materials for Electrochemical Water Splitting, ACS Catal., 2019, 9, 9973–10011 CrossRef CAS.
- U. Babic, M. Suermann, F. N. Büchi, L. Gubler and T. J. Schmidt, Critical Review—Identifying Critical Gaps for Polymer Electrolyte Water Electrolysis Development, J. Electrochem. Soc., 2017, 164, F387–F399 CrossRef CAS.
- Y. Ping, R. J. Nielsen and W. A. Goddard III, The Reaction Mechanism with Free Energy Barriers at Constant Potentials for the Oxygen Evolution Reaction at the IrO2 (110) Surface, J. Am. Chem. Soc., 2017, 139, 149–155 CrossRef CAS.
- J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, Solvation Effects for Oxygen Evolution Reaction Catalysis on IrO2(110), J. Phys. Chem. C, 2017, 121, 11455–11463 CrossRef CAS.
- V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, R. Arrigo, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, In situ observation of reactive oxygen species forming on oxygen-evolving iridium surfaces, Chem. Sci., 2017, 8, 2143–2149 RSC.
- V. A. Saveleva, L. Wang, D. Teschner, T. Jones, A. S. Gago, K. A. Friedrich, S. Zafeiratos, R. Schlögl and E. R. Savinova, Operando Evidence for a Universal Oxygen Evolution Mechanism on Thermal and Electrochemical Iridium Oxides, J. Phys. Chem. Lett., 2018, 9, 3154–3160 CrossRef CAS.
- V. Pfeifer, T. E. Jones, S. Wrabetz, C. Massué, J. J. V. Vélez, R. Arrigo, M. Scherzer, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Reactive oxygen species in iridium-based OER catalysts, Chem. Sci., 2016, 7, 6791–6795 RSC.
- V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massúe, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, M. T. Greiner, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, The electronic structure of iridium and its oxides, Surf. Interface Anal., 2016, 48, 261–273 CrossRef CAS.
- N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Electronic structure of the oxygen-evolving complex in photosystem II prior to O–O bond formation, Science, 2014, 345, 804–808 CrossRef CAS.
- P. E. Siegbahn, Water oxidation mechanism in photosystem II, including oxidations, proton release pathways, O–O bond formation and O2 release, Biochim. Biophys. Acta, 2013, 1827, 1003–1019 CrossRef CAS.
- W. Lubitz, E. J. Reijerse and J. Messinger, Solar water-splitting into H2 and O2: design principles of photosystem II and hydrogenases, Energy Environ. Sci., 2008, 1, 15–31 RSC.
- J. Messinger, Evaluation of different mechanistic proposals for water oxidation in photosynthesis on the basis of Mn4OxCa structures for the catalytic site and spectroscopic data, Phys. Chem. Chem. Phys., 2004, 6, 4764–4771 RSC.
- Y. Gao, T. Åkermark, J. Liu, L. Sun and B. Åkermark, Nucleophilic Attack of Hydroxide on a MnV Oxo Complex: A Model of the O–O Bond Formation in the Oxygen Evolving Complex of Photosystem II, J. Am. Chem. Soc., 2009, 131, 8726–8727 CrossRef CAS.
- J. Limburg, V. A. Szalai and G. W. Brudvig, A mechanistic and structural model for the formation and reactivity of a MnV[double bond, length half m-dash] O species in photosynthetic water oxidation, J. Chem. Soc., Dalton Trans., 1999, 1353–1362 RSC.
- K. H. Saeed, M. Forster, J.-F. Li, L. J. Hardwick and A. J. Cowan, Water oxidation intermediates on iridium oxide electrodes probed by in situ electrochemical SHINERS, Chem. Commun., 2020, 56, 1129–1132 RSC.
- H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Pérez-Ramírez, B. R. Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Key role of chemistry versus bias in electrocatalytic oxygen evolution, Nature, 2020, 587, 408–413 CrossRef CAS.
- T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kotz and T. J. Schmidt, Thermodynamic explanation of the universal correlation between oxygen evolution activity and corrosion of oxide catalysts, Sci. Rep., 2015, 5, 12167 CrossRef CAS.
- X. Rong, J. Parolin and A. M. Kolpak, A Fundamental Relationship between Reaction Mechanism and Stability in Metal Oxide Catalysts for Oxygen Evolution, ACS Catal., 2016, 6, 1153–1158 CrossRef CAS.
- O. Kasian, J.-P. Grote, S. Geiger, S. Cherevko and K. J. J. Mayrhofer, The Common Intermediates of Oxygen Evolution and Dissolution Reactions during Water Electrolysis on Iridium, Angew. Chem., Int. Ed., 2018, 57, 2488–2491 CrossRef CAS.
- A. Grimaud, A. DemortiHre, M. SaubanHre, W. Dachraoui, M. Duchamp, M.-L. Doublet and J.-M. Tarascon, Activation of surface oxygen sites on an iridium-based model catalyst for the oxygen evolution reaction, Nat. Energy, 2016, 2, 16189 CrossRef.
- A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y.-L. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Activating lattice oxygen redox reactions in metal oxides to catalyse oxygen evolution, Nat. Chem., 2017, 9, 457–465 CrossRef CAS.
- S. Fierro, T. Nagel, H. Baltruschat and C. Comninellis, Investigation of the oxygen evolution reaction on Ti/IrO2 electrodes using isotope labelling and on-line mass spectrometry, Electrochem. Commun., 2007, 9, 1969–1974 CrossRef CAS.
- H. G. Sanchez Casalongue, M. L. Ng, S. Kaya, D. Friebel, H. Ogasawara and A. Nilsson, In Situ Observation of Surface Species on Iridium Oxide Nanoparticles during the Oxygen Evolution Reaction, Angew. Chem., Int. Ed., 2014, 53, 7169–7172 CrossRef CAS.
- A. Minguzzi, O. Lugaresi, E. Achilli, C. Locatelli, A. Vertova, P. Ghigna and S. Rondinini, Observing the oxidation state turnover in heterogeneous iridium-based water oxidation catalysts, Chem. Sci., 2014, 5, 3591–3597 RSC.
- A. Minguzzi, C. Locatelli, O. Lugaresi, E. Achilli, G. Cappelletti, M. Scavini, M. Coduri, P. Masala, B. Sacchi, A. Vertova, P. Ghigna and S. Rondinini, Easy Accommodation of Different Oxidation States in Iridium Oxide Nanoparticles with Different Hydration Degree as Water Oxidation Electrocatalysts, ACS Catal., 2015, 5, 5104–5115 CrossRef CAS.
- Z. Pavlovic, C. Ranjan, M. Van Gastel and R. Schlögl, The active site for the water oxidising anodic iridium oxide probed through in situ Raman spectroscopy, Chem. Commun., 2017, 53, 12414–12417 RSC.
- Z. Pavlovic, C. Ranjan, Q. Gao, M. van Gastel and R. Schlögl, Probing the Structure of a Water-Oxidizing Anodic Iridium Oxide Catalyst using Raman Spectroscopy, ACS Catal., 2016, 6, 8098–8105 CrossRef CAS.
- O. Kasian, S. Geiger, T. Li, J.-P. Grote, K. Schweinar, S. Zhang, C. Scheu, D. Raabe, S. Cherevko, B. Gault and K. J. J. Mayrhofer, Degradation of iridium oxides via oxygen evolution from the lattice: correlating atomic scale structure with reaction mechanisms, Energy Environ. Sci., 2019, 12, 3548–3555 RSC.
- S. Cherevko, S. Geiger, O. Kasian, A. Mingers and K. J. J. Mayrhofer, Oxygen evolution activity and stability of iridium in acidic media. Part 2. – Electrochemically grown hydrous iridium oxide, J. Electroanal. Chem., 2016, 774, 102–110 CrossRef CAS.
- S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, The stability number as a metric for electrocatalyst stability benchmarking, Nat. Catal., 2018, 1, 508–515 CrossRef CAS.
- K. Schweinar, B. Gault, I. Mouton and O. Kasian, Lattice Oxygen Exchange in Rutile IrO2 during the Oxygen Evolution Reaction, J. Phys. Chem. Lett., 2020, 11, 5008–5014 CrossRef CAS.
- E. Willinger, C. Massué, R. Schlögl and M. G. Willinger, Identifying Key Structural Features of IrOx Water Splitting Catalysts, J. Am. Chem. Soc., 2017, 139, 12093–12101 CrossRef CAS.
- J. Gao, C.-Q. Xu, S.-F. Hung, W. Liu, W. Cai, Z. Zeng, C. Jia, H. M. Chen, H. Xiao, J. Li, Y. Huang and B. Liu, Breaking Long-Range Order in Iridium Oxide by Alkali Ion for Efficient Water Oxidation, J. Am. Chem. Soc., 2019, 141, 3014–3023 CrossRef CAS.
- T. Li, O. Kasian, S. Cherevko, S. Zhang, S. Geiger, C. Scheu, P. Felfer, D. Raabe, B. Gault and K. J. J. Mayrhofer, Atomic-scale insights into surface species of electrocatalysts in three dimensions, Nat. Catal., 2018, 1, 300–305 CrossRef.
- W. Sun, Y. Song, X. Q. Gong, L. M. Cao and J. Yang, Hollandite Structure Kx≈0.25IrO2 Catalyst with Highly Efficient Oxygen Evolution Reaction, ACS Appl. Mater. Interfaces, 2016, 8, 820–826 CrossRef CAS.
- D. Lebedev, R. Ezhov, J. Heras-Domingo, A. Comas-Vives, N. Kaeffer, M. Willinger, X. Solans-Monfort, X. Huang, Y. Pushkar and C. Copéret, Atomically Dispersed Iridium on Indium Tin Oxide Efficiently Catalyzes Water Oxidation, ACS Cent. Sci., 2020, 6, 1189–1198 CrossRef CAS.
- K. Jiang, M. Luo, M. Peng, Y. Yu, Y.-R. Lu, T.-S. Chan, P. Liu, F. M. F. de Groot and Y. Tan, Dynamic active-site generation of atomic iridium stabilized on nanoporous metal phosphides for water oxidation, Nat. Commun., 2020, 11, 2701 CrossRef CAS.
- Y. Zhang, C. Wu, H. Jiang, Y. Lin, H. Liu, Q. He, S. Chen, T. Duan and L. Song, Atomic Iridium Incorporated in Cobalt Hydroxide for Efficient Oxygen Evolution Catalysis in Neutral Electrolyte, Adv. Mater., 2018, 30, 1707522 CrossRef.
- Y. Zhao, K. R. Yang, Z. Wang, X. Yan, S. Cao, Y. Ye, Q. Dong, X. Zhang, J. E. Thorne, L. Jin, K. L. Materna, A. Trimpalis, H. Bai, S. C. Fakra, X. Zhong, P. Wang, X. Pan, J. Guo, M. Flytzani-Stephanopoulos, G. W. Brudvig, V. S. Batist and D. Wang, Stable iridium dinuclear heterogeneous catalysts supported on metal-oxide substrate for solar water oxidation, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2902–2907 CrossRef CAS.
- S. K. Kaiser, Z. Chen, D. F. Akl, S. Mitchell and J. Pérez-Ramírez, Single-Atom Catalysts across the Periodic Table, Chem. Rev., 2020, 120, 11703–11809 CrossRef CAS.
- S. Mitchell and J. Pérez-Ramírez, Single atom catalysis: a decade of stunning progress and the promise for a bright future, Nat. Commun., 2020, 11, 4302 CrossRef CAS.
- W.-H. Lai, L.-F. Zhang, W.-B. Hua, S. Indris, Z.-C. Yan, Z. Hu, B. Zhang, Y. Liu, L. Wang, M. Liu, R. Liu, Y.-X. Wang, J.-Z. Wang, Z. Hu, H.-K. Liu, S.-L. Chou and S.-X. Dou, General p-Electron-Assisted Strategy for Ir, Pt, Ru, Pd, Fe, Ni Single-Atom Electrocatalysts with Bifunctional Active Sites for Highly Efficient Water Splitting, Angew. Chem., Int. Ed., 2019, 58, 11868–11873 CrossRef CAS.
- C. F. Dickens, C. Kirk and J. K. Nørskov, Insights into the Electrochemical Oxygen Evolution Reaction with ab Initio Calculations and Microkinetic Modeling: Beyond the Limiting Potential Volcano, J. Phys. Chem. C, 2019, 123, 18960–18977 CrossRef CAS.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, Benchmarking Hydrogen Evolving Reaction and Oxygen Evolving Reaction Electrocatalysts for Solar Water Splitting Devices, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS.
- M. W. Kanan and D. G. Nocera, In Situ Formation of an Oxygen-Evolving Catalyst in Neutral Water Containing Phosphate and Co2+, Science, 2008, 321, 1072–1075 CrossRef CAS.
- C. Costentin and D. G. Nocera, Self-healing catalysis in water, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13380–13384 CrossRef CAS.
- T. Naito, T. Shinagawa, T. Nishimoto and K. Takanabe, Water Electrolysis in Saturated Phosphate Buffer at Neutral pH, ChemSusChem, 2020, 13, 5921–5933 CrossRef CAS.
- H. Ooka, Y. Wang, A. Yamaguchi, M. Hatakeyama, S. Nakamura, K. Hashimoto and R. Nakamura, Legitimate intermediates of oxygen evolution on iridium oxide revealed by in situ electrochemical evanescent wave spectroscopy, Phys. Chem. Chem. Phys., 2016, 18, 15199–15204 RSC.
- P. Steegstra and E. Ahlberg, Influence of oxidation state on the pH dependence of hydrous iridium oxide films, Electrochim. Acta, 2012, 76, 26–33 CrossRef CAS.
- B. K. Mai and Y. Kim, Is It Fe(III)-Oxyl Radical That Abstracts Hydrogen in the C–H Activation of TauD? A Theoretical Study Based on the DFT Potential Energy Surfaces, Inorg. Chem., 2016, 55, 3844–3852 CrossRef CAS.
- X. Yang and M.-H. Baik, cis,cis-[(bpy)2RuVO]2O4+ Catalyzes Water Oxidation Formally via in Situ Generation of Radicaloid RuIV–O˙, J. Am. Chem. Soc., 2006, 128, 7476–7485 CrossRef CAS.
- K. S. Exner and H. Over, Beyond the Rate-Determining Step in the Oxygen Evolution Reaction over a Single-Crystalline IrO2(110) Model Electrode: Kinetic Scaling Relations, ACS Catal., 2019, 9, 6755–6765 CrossRef CAS.
- H. A. Hansen, I. C. Man, F. Studt, F. Abild-Pedersen, T. Bligaard and J. Rossmeisl, Electrochemical chlorine evolution at rutile oxide (110) surfaces, Phys. Chem. Chem. Phys., 2010, 12, 283–290 RSC.
- D.-Y. Kuo, J. K. Kawasaki, J. N. Nelson, J. Kloppenburg, G. Hautier, K. M. Shen, D. G. Schlom and J. Suntivich, Influence of Surface Adsorption on the Oxygen Evolution Reaction on IrO2(110), J. Am. Chem. Soc., 2017, 139, 3473–3479 CrossRef CAS.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Surface Pourbaix diagrams and oxygenreduction activity of Pt, Ag and Ni(111) surfaces studied by DFT, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730 RSC.
- K. S. Exner, J. Anton, T. Jacob and H. Over, Chlorine Evolution Reaction on RuO2(110): Ab initio Atomistic Thermodynamics Study - Pourbaix Diagrams, Electrochim. Acta, 2014, 120, 460–466 CrossRef CAS.
- K. S. Exner, J. Anton, T. Jacob and H. Over, Controlling Selectivity in the Chlorine Evolution Reaction over RuO2-Based Catalysts, Angew. Chem., Int. Ed., 2014, 53, 11032–11035 CrossRef CAS.
- L. G. V. Briquet, M. Sarwar, J. Mugo, G. Jones and F. Calle-Vallejo, A New Type of Scaling Relations to Assess the Accuracy of Computational Predictions of Catalytic Activities Applied to the Oxygen Evolution Reaction, ChemCatChem, 2017, 9, 1261–1268 CrossRef CAS.
- V. Sumaria, D. Krishnamurthy and V. Viswanathan, Quantifying Confidence in DFT Predicted Surface Pourbaix Diagrams and Associated Reaction Pathways for Chlorine Evolution, ACS Catal., 2018, 8, 9034–9042 CrossRef CAS.
- K. S. Exner, I. Sohrabnejad-Eskan and H. Over, A Universal Approach To Determine the Free Energy Diagram of an Electrocatalytic Reaction, ACS Catal., 2018, 8, 1864–1879 CrossRef CAS.
- A. Damjanovic, A. Dey and J. O. M. Bockris, Electrode Kinetics of Oxygen Evolution and Dissolution on Rh, Ir, and Pt-Rh Alloy Electrodes, J. Electrochem. Soc., 1966, 113, 739–746 CrossRef CAS.
- G. Beni, L. M. Schiavone, J. L. Shay, W. C. Dautremont-Smith and B. S. Schneider, Electrocatalytic oxygen evolution on reactively sputtered electrochromic iridium oxide films, Nature, 1979, 282, 281–283 CrossRef CAS.
- S. Cherevko, S. Geiger, O. Kasian, N. Kulyk, J.-P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J. J. Mayrhofer, Oxygen and hydrogen evolution reactions on Ru, RuO2, Ir, and IrO2 thin film electrodes in acidic and alkaline electrolytes: A comparative study on activity and stability, Catal. Today, 2016, 262, 170–180 CrossRef CAS.
- J. Willsau, O. Wolter and J. Heitbaum, Does the oxide layer take part in the oxygen evolution reaction on platinum?: A DEMS study, J. Electroanal. Chem., 1985, 195, 299–306 CrossRef CAS.
- M. Wohlfahrt-Mehrens and J. Heitbaum, Oxygen evolution on Ru and RuO2 electrodes studied using isotope labelling and on-line mass spectrometry, J. Electroanal. Chem., 1987, 237, 251–260 CrossRef CAS.
- V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massúe, M. T. Greiner, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, The electronic structure of iridium oxide electrodes active in water splitting, Phys. Chem. Chem. Phys., 2016, 18, 2292–2296 RSC.
- J. F. Li, Y. F. Huang, Y. Ding, Z. L. Yang, S. B. Li, X. S. Zhou, F. R. Fan, W. Zhang, Z. Y. Zhou, D. Y. Wu, B. Ren, Z. L. Wang and Z. Q. Tian, Shell-isolated nanoparticle-enhanced Raman spectroscopy, Nature, 2010, 464, 392–395 CrossRef CAS.
- N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Beyond the volcano limitations in electrocatalysis – oxygen evolution reaction, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688 RSC.
- M. Busch, Water oxidation: From mechanisms to limitations, Curr. Opin. Electrochem., 2018, 9, 278–284 CrossRef CAS.
- Y. Gorlin, C.-J. Chung, J. D. Benck, D. Nordlund, L. Seitz, T.-C. Weng, D. Sokaras, B. M. Clemens and T. F. Jaramillo, Understanding Interactions between Manganese Oxide and Gold That Lead to Enhanced Activity for Electrocatalytic Water Oxidation, J. Am. Chem. Soc., 2014, 136, 4920–4926 CrossRef CAS.
- L. C. Seitz, C. F. Dickens, K. Nishio, Y. Hikita, J. Montoya, A. Doyle, C. Kirk, A. Vojvodic, H. Y. Hwang, J. K. Norskov and T. F. Jaramillo, A highly active and stable IrOx/SrIrO3 catalyst for the oxygen evolution reaction, Science, 2016, 353, 1011–1014 CrossRef CAS.
- E. Oakton, D. Lebedev, M. Povia, D. F. Abbott, E. Fabbri, A. Fedorov, M. Nachtegaal, C. Copéret and T. J. Schmidt, IrO2-TiO2: A High-Surface-Area, Active and Stable Electrocatalyst for the Oxygen Evolution Reaction, ACS Catal., 2017, 7, 2346–2352 CrossRef CAS.
- D. Lebedev, M. Povia, K. Waltar, P. M. Abdala, I. E. Castelli, E. Fabbri, M. V. Blanco, A. Fedorov, C. Copéret, N. Marzari and T. J. Schmidt, Highly Active and Stable Iridium Pyrochlores for Oxygen Evolution Reaction, Chem. Mater., 2017, 29, 5182–5191 CrossRef CAS.
- O. Diaz-Morales, S. Raaijman, R. Kortlever, P. J. Kooyman, T. Wezendonk, J. Gascon, W. T. Fu and M. T. M. Koper, Iridium-based double perovskites for efficient water oxidation in acid media, Nat. Commun., 2016, 7, 12363 CrossRef CAS.
- S. M. Alia, S. Shulda, C. Ngo, S. Pylypenko and B. S. Pivovar, Iridium-Based Nanowires as Highly Active, Oxygen Evolution Reaction Electrocatalysts, ACS Catal., 2018, 8, 2111–2120 CrossRef CAS.
- H. N. Nong, T. Reier, H.-S. Oh, M. Gliech, P. Paciok, T. H. T. Vu, D. Teschner, M. Heggen, V. Petkov, R. Schlögl, T. Jones and P. Strasser, A unique oxygen ligand environment facilitates water oxidation in hole-doped IrNiOx core–shell electrocatalysts, Nat. Catal., 2018, 1, 841–851 CrossRef CAS.
| This journal is © the Partner Organisations 2021 |




