Open Access Article
Open Access ArticleGas electron diffraction then and now: from trisilyl phosphine to iso-propyl(tert-butyl)(trichlorosilyl)phosphine†
Isabella
Wagner
a,
David W. H.
Rankin
 b and
Sarah L.
Masters
b and
Sarah L.
Masters
 *a
*a
aSchool of Physical and Chemical Sciences, University of Canterbury, Private Bag 4100, Christchurch 8140, New Zealand. E-mail: sarah.masters@canterbury.ac.nz
bSchool of Chemistry, The University of Edinburgh, Joseph Black Building, David Brewster Road, Edinburgh, EH9 3FJ, UK
First published on 12th October 2021
Abstract
The gas-phase molecular structure of iso-propyl(tert-butyl)(trichlorosilyl)phosphine has been determined using a combination of gas electron diffraction and computational methods. The structure presents a conformational challenge that required use of the SARACEN method to combine theoretical observations into the least-squares refinement process, a great advance on the techniques used to solve the structure of the parent trisilyl phosphine. Five conformers were found on the potential-energy surface for iso-propyl(tert-butyl)(trichlorosilyl)phosphine using the UCONGA program, and following a series of individual structure refinements a combined model with the two most abundant confirmers was evaluated. Key structural parameters (ra) include rP–Si [225.5(6) pm], rSi–Clmean [204.0(1) pm] and rP–Cmean [204.0(1) pm], ∠P–C–H 101.5(5)°, ∠C–C–C (iPr) 110.5(5)°, ∠C–C–C (tBu) 109.2(5)° and ∠C–P–C 105.4(5)°.
Gas electron diffraction 50 years ago (A personal perspective by David Rankin)
At the time when the inorganic Section A of The Journal of the Chemical Society was evolving into Dalton Transactions, gas electron diffraction (GED) was revealing the molecular structures of many main-group compounds. There were plenty of surprises. In 1955, Ken Hedberg (Oregon) had used GED to show that trisilylamine, N(SiH3)3, had a planar NSi3 skeleton.1 The rationalisation of this completely unexpected structure – delocalisation of the nitrogen lone pair of electrons from their 2p orbital into the vacant silicon 3d orbitals – was not correct, but the sp2 hybridisation of the nitrogen atom implied by the structure was consistent with the very low basicity of the amine. By 1970, the last year before the birth of Dalton Transactions, trigermylamine, N(GeH3)3, had also been shown to have a planar skeleton.2Analysis of the skeletal vibrational modes of trisilylamine showed them to be consistent with a planar structure with D3h local symmetry,3 so when the modes of trisilyl phosphine were similarly interpreted,4 determination of its gas-phase structure became a priority. The surprise this time was that the skeleton was not planar.5 Not by a long way: the SiPSi angles were 95(2)°.
Trisilyl phosphine was the first compound with an Si–P bond to be studied by GED. It has a vastly simpler structure than the subject of this paper, but it was typical of what could be studied at that time. Least-squares refinement methods existed, but the program was written in Titan Autocode, and was submitted, along with the data for each refinement, on half a mile of punched tape. Correcting a single error involved sitting for half an hour with a finger on the copy button, hoping to be awake at the point where the correction was to be made. Then on your bike down town, where the input tapes, in a polythene bag, were left hanging on a peg at the computer centre. Back again the next day, hoping that the job had been run, with a stack of paper as the output. Four cycles of refinement of a structure as simple as that of trisilyl phosphine took about 15 minutes on Cambridge University's only generally available computer, with its 256 kilobytes of RAM.
By 1972, when Dalton Transactions was launched, I had moved to the University of Edinburgh. The structures of many silyl and germyl derivatives of main-group elements were known, but rather little about phosphorus derivatives. Compounds with –PH2 groups were generally not stable, so the simplest molecules were those with –PF2 groups. These are much more complex for GED, with extra ‘heavy’ atoms and lower symmetry. Fortunately, computing had advanced. Programs had been rewritten in Fortran, and punched tapes had been replaced by punched cards. Even bicycles had been replaced! A box of cards was left during the day at a pick-up point in the Chemistry Department. It was then driven 100 miles to Newcastle in a van, and by next morning it had been returned, together with the printed output. In this way many structures were determined, including that of the carbodi-imide F2PNCNPF2, the subject of my first paper in Dalton Transactions.6
In 50 years, the GED method has advanced beyond our wildest dreams. It was said then that ‘everything that can be done has been done’. But now there is more than ever than can be done – but not everything that can be done should be done! The combination of experimental and computational methods has opened doors, and the silicon-phosphorus structure that is the subject of this current paper illustrates the potential. However, how do we know that computational methods give reliable data for tricky conformational mixtures? Only by the painstaking analysis of experimental data, making GED as relevant now as it was 50 years ago.
Gas electron diffraction now
The subject of this structural study, P(tBu)(iPr)(SiCl3), presents many challenges for GED. First, it has three different phosphorus substituents, so it has no symmetry, either overall or locally within the substituents. Secondly, the rotational asymmetry of the iso-propyl group multiplies the number of possible conformers, which must be accounted for in a gas-phase study. Thirdly, the three chlorine atoms of the trichlorosilyl group make the largest contribution to the total scattering, so information about the rest of the structure, including the conformations adopted, is correspondingly more difficult to extract. GED alone cannot provide sufficient information, but a combination of GED with computational methods allows the full structure to be determined, in the knowledge that the outcome will be consistent with experiment. This molecule thus provides an excellent example of what is possible, more than 50 years on from the first study of a silyl phosphine.Trihalosilyl compounds are important precursors for the synthesis of highly functionalised silicon compounds.7 In previous studies8 it was shown that the silylation reaction rates of P-chlorophosphaalkenes or halodialkylphosphanes with hexachlorodisilane under mild conditions and without solvent decrease with bulkier ligands, whereas these reactions progress very quickly, without heating, for trimethylsilylphosphane. The electron-withdrawing effect of chlorine atoms is believed to cause additional stabilisation of the P–Si bond, so that, in contrast to trimethylsilylphosphanes, trichlorosilylphosphanes do not interact with chlorotrimethylgermane and -stannane.9 To help to understand the observed reactivity, gas-phase structures of the silylphosphines P(SiMe3)3, P(tBu)2(SiCl3) and P(tBu)(SiCl3)2 were previously determined by GED.7,10,11
Phosphines have trigonal-pyramidal coordination at the phosphorus atom, so the simplest representatives, PH312 and PMe313 have C3v symmetry. The replacement of H and Me by bulky substituents, such as tert-butyl, shows the effect of steric strain on the geometry of the molecule and can be clearly demonstrated by comparing the structures of PMe313 and P(tBu)3.14 The P–C bond lengths increase significantly from 184.6(3) pm to 191.9(5) pm, whilst the C–P–C bond angles increase from 98.6(3)° in the less sterically hindered PMe3 to 109.9(7)° in P(tBu)3. Steric interactions between the tert-butyl groups in P(tBu)3 are reduced by twisting of the tert-butyl groups by approximately 14° away from the perfectly staggered conformation.14
Previous studies of P(tBu)(SiCl3)2 and P(tBu)2(SiCl3) showed that in each case the perfectly staggered Cs structure was a saddle point on the potential-energy surface, whereas twisting of the tert-butyl and trichlorosilyl groups in the same sense by 15–20° from the staggered conformation and an axial tilt towards the phosphorus lone pair, lowering the symmetry from Cs to C1, reduces the steric strain.11 In both structures attractive forces between Cl and H were observed, with one of the methyl groups of the tert-butyl group in closer contact with the SiCl3 group.11
These earlier studies involved compounds with tert-butyl groups as the only organic substituents. Now introduction of an iso-propyl group reduces the steric strain, but also leads to greater potential for multiple conformers to exist, due to lower symmetry of the iso-propyl group and the greater flexibility of the ligand. Together, these structural changes make our work much more difficult, but comparing the structures of the molecules studied earlier with that of iso-propyl(tert-butyl)(trichlorosilyl)phosphine (1) gives insight into the interesting steric interactions between the groups themselves and with the lone pair of electrons, which in turn influence the reactivity of the compound. However, we still want to study this molecule in the gas phase as this gives the structure free from the influences of intermolecular interactions.
Experimental section
Synthesis
A sample of iso-propyl(tert-butyl)(trichlorosilyl)phosphine (1) was synthesised by W.-W. du Mont (Braunschweig, Germany).7 The purity of the sample was checked by 1H NMR, 29Si NMR, and 31P NMR spectroscopy.Computational methods
The initial search for stable conformers of 1 used the UCONGA program,15 which generated six distinct conformers. For these conformers geometry optimisation and frequency calculations at the B3LYP-D3/Def2TZVP level were performed using the resources of the EPSRC UK National Service for Computational Chemistry Software and the Gaussian09 program.16 DFT–D317 is a useful method for including dispersion corrections in density functionals. It is an advance on DFT–D by the introduction of an atom-pairwise specific dispersion coefficient and a cut-off radius so that only structural data, such as Cartesian coordinates and the atomic numbers, are important.17 The structures of all conformers were fully optimised; no imaginary frequencies were returned.Analytical second derivatives of the energy with respect to the nuclear coordinates were calculated at the B3LYP-D3/Def2TZVP level. These determined the nature of the potential-energy surface and were used in the program SHRINK18 to provide estimates of the amplitudes of vibration (u) and perpendicular distance corrections (k) for use in the gas electron diffraction refinements.
The structure of 1 with the atom numbering scheme is shown in Fig. 1.
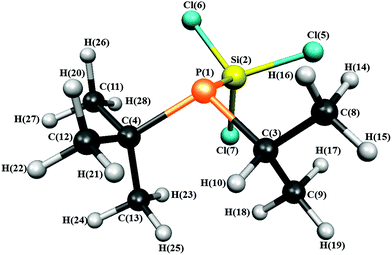 | ||
| Fig. 1 Molecular structure of iso-propyl(tert-butyl)(trichlorosilyl)phosphine in the gas phase showing the atom numbering. | ||
Gas electron diffraction
Electron scattering intensities were recorded using the Edinburgh gas electron diffraction apparatus.19 An accelerating voltage of ca. 40 keV (electron wavelength ca. 6.0 pm) was used, and sample and nozzle temperatures were 367 K and 381 K, respectively. Scattering intensities were recorded at nozzle-to-plate distances of 256.73 mm and 94.32 mm on Kodak Electron Image plates, three at each distance. The electron-scattering intensities were digitised using an Epson Expression 1680 Pro flatbed scanner and converted to mean optical densities as a function of the scattering variable, s, using an existing programme.20 The data-reduction and least-squares-refinement processes were carried out using the ed@ed program21 (Version 2.4) employing the scattering factors of Ross et al.22 The weighting points for the off-diagonal weight matrices for the two camera distances together with electron wavelengths, which were determined from the scattering patterns of benzene vapour, are given in ESI Table S1.† These were recorded immediately after patterns of 1 and analysed in exactly the same way, to minimise systematic errors in wavelengths and camera distances.Results
Quantum chemical calculations
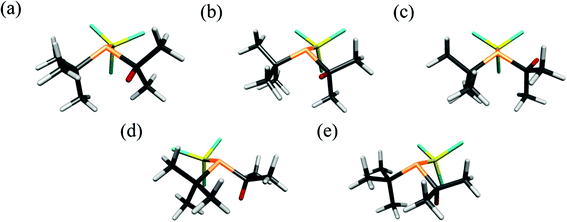
The UCONGA analysis initially yielded six structures. Geometry optimisations led to five distinct minima on the potential-energy surface.To aid understanding of the complex mix of conformers, each was given a name that roughly describes its structure. The chosen scheme labels each conformer with the torsion angle of the iso-propyl group, i.e. of the secondary hydrogen atom with respect to the lone pair on phosphorus, to the nearest degree, followed by either a “+” or “−” for the clockwise or counter-clockwise torsion of the tert-butyl and trichlorosilyl groups, respectively, with respect to the lone pair on the phosphorus atom when viewed along the P–X bond. If one of the bulky groups only deviates by a small amount (less than 10°) from the perfectly staggered position with respect to the lone pair, this is denoted by parentheses around the “+” or “−”. For example, +77++ indicates a clockwise torsion of the iso-propyl group of about 77° from the perfectly staggered position combined with clockwise torsions of the tert-butyl and trichlorosilyl groups. The structures of the optimised conformers are shown in Fig. 2, and calculated energies at the B3LYP-D3/Def2TZVP level relative to the most stable conformer (+77++) are shown in Table 1. The calculated molecular geometries of all conformers can be found in the ESI (Tables S2–S6†).
| Conformer | +77++ | +51−− | −91−(−) | +143−− | +165+− |
|---|---|---|---|---|---|
| a Energies are quoted relative to the lowest energy conformer, +77++, and include zero-point vibrational energy corrections. | |||||
| Relative energy/kJ mol−1 | 0.00 | 3.41 | 4.37 | 4.81 | 8.60 |
| Relative abundance at 367 K | 0.55 | 0.18 | 0.13 | 0.11 | 0.03 |
Gas electron diffraction refinements
Refinements were initially carried out for the lowest energy conformer as predicted by the quantum chemical calculations and then for each predicted conformer individually. Finally, a refinement modelling a mixture of the two lowest energy conformers was undertaken. The decision was taken not to include further conformers in the refinement as the dependency on the calculated values was so high at this point that the refinement would essentially return the calculated values. The combined refinement represents approximately 75% of the vapour composition and further meaningful experimental information was unlikely to be obtained from the refinement process due to the size and low symmetry of the molecule. The limit of what can be determined by gas electron diffraction has been reached, even using modern methods.The electron diffraction refinements for 1 were carried out using data given by the quantum chemical calculations described above, using the Structure Analysis Restrained by Ab initio Calculations for Electron diffractioN (SARACEN) method,23 with models of C1 symmetry. Given the large number of atoms in the molecule and the absence of any symmetry, some assumptions were made about the structure in order to reduce the number of geometric parameters required for a full structural description. They included local C3 symmetry of the Cl–Si–Cl angles in the trichlorosilyl group, as evidenced from the calculations, and of the methyl groups. The PSiCl3 group was allowed to deviate from C3v symmetry, as indicated by the calculations. The quantum chemical calculations also showed that all bond lengths of the same type were quite similar, and so they were assumed to be equal. Where possible groups of bond angles were represented by a refinable average angle. In this way the structure of 1 was defined by 31 independent geometric parameters: six bond lengths and differences, 17 bond angles and differences, and eight dihedral angles. A more detailed description of the model can be found in the ESI.†
Theoretical Cartesian force fields were generated at the B3LYP-D3/Def2TZVP level and converted into a set of force fields described by a set of symmetry coordinates, and root-mean-square (RMS) amplitudes were obtained using the SHRINK program.18
All independent geometric parameters were refined using a least-squares method. Restraints were applied, using the SARACEN method,23 to parameters that could otherwise not be sensibly refined. The starting values of the parameters were set at those given by the B3LYP-D3/Def2TZVP calculations, with weights derived from uncertainties, which were based on the changes in value of each parameter across the calculations at the B3LYP levels of theory. Selected groups of amplitudes of vibrations were also refined (ESI Tables S7–S8†). Uncertainties for these were set at 10% of the calculated values, as has been found to be suitable in previous studies.7,24 Final refined parameters for conformers +77++ and +51−− are given in Table 3.
| Conformer | +77++ | +51−− | −91−(−) | +143−− | +165+− |
|---|---|---|---|---|---|
| R D (%) | 6.88 | 7.01 | 8.90 | 7.81 | 7.81 |
| R G (%) | 9.76 | 9.83 | 12.03 | 10.78 | 10.74 |
| Parameter | +77++ | +51−− | ||||
|---|---|---|---|---|---|---|
| GED (ra) | B3LYP-D3/Def2TZVP | Restraint | GED (ra) | B3LYP-D3/Def2TZVP | Restraint | |
| a The P–C average and difference parameters define the P–C tBu (average − difference) and P–C iPr (average + difference) distances. See ESI† for full model description. | ||||||
| rSi–Cl | 204.0(1) | 206.7 | 203.8(2) | 206.7 | ||
| rP–Si | 225.5(6) | 224.9 | 224.2(7) | 225.4 | ||
| r P–C ava | 188.3(4) | 190.2 | 187.9(5) | 190.5 | ||
| rP–C diffa | 0.9(3) | 0.9 | 0.9(3) | 1.4(5) | 1.3 | 1.3(5) |
| rC–C | 153.1(2) | 153.4 | 153.2(3) | 153.5 | ||
| rC–H | 108.6(4) | 109.2 | 109.2(5) | 108.6(4) | 109.1 | 109.1(5) |
| ∠Cl–Si–Cl | 107.2(5) | 107.0 | 107.0(5) | 106.4(5) | 106.7 | 106.7(5) |
| ∠P–C(3)–H(10) | 101.5(5) | 101.5 | 101.5(5) | 100.5(5) | 100.5 | 100.5(5) |
| ∠C–C–H | 110.9(4) | 111.1 | 111.1(5) | 110.8(5) | 111.1 | 111.1(5) |
| ∠C–C–C iPr | 110.5(5) | 110.6 | 110.6(5) | 110.8(5) | 110.8 | 110.8(5) |
| ∠C–C–C tBu | 109.2(5) | 109.2 | 109.2(5) | 108.9(5) | 109.0 | 109.0(5) |
| ∠C–P–C | 105.4(5) | 105.2 | 105.2(5) | 106.4(5) | 107.3 | 107.3(5) |
| Φ Cl(6)–Si–P–C(3) | −170.0(14) | −170.5 | −170.5(20) | 174.3(15) | 172.0 | 172.0(15) |
| Φ Si–P–C(3)–C(9) | −32.3(19) | −30.6 | −30.6(20) | −59.3(20) | −57.1 | −57.1(20) |
| Φ Si–P–C(4)–C(12) | −168.7(16) | −169.5 | −169.5(20) | 157.8(14) | 156.3 | 156.3 |
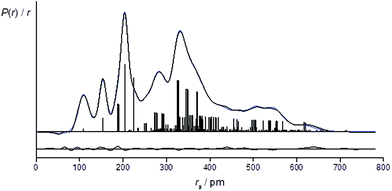
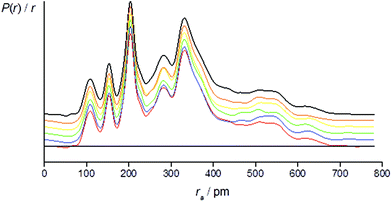
The success of the refinement of each conformer is shown by the R-factors (goodness-of-fit) (Table 2), and graphically by examining the radial distribution curves (RDCs) (Fig. 3) and difference curves and the molecular-scattering intensity curves (ESI Fig. S1–S6†).
R D is the R-factor assuming that no correlation is present in the experimental data. RG is the R-factor taking into account correlation. Correlation between adjacent experimental data points is reflected by RG being larger than RD, as is invariably observed for refinements in gas electron diffraction studies. A more in-depth explanation of the R-factors can be found in ref. (25) and references therein.
The least-squares correlation matrices for all refinements are given in ESI Tables S9–S14.†
Individual refinements of the conformers of 1 show that conformer +77++ gives the lowest RG value (0.0976) and agrees with the quantum chemical prediction of the most stable conformer at the B3LYP-D3/Def2TZVP level (see Tables 1 and 2). The next lowest RG value (0.0983) was given by conformer +51−−, which was also predicted by the quantum chemical calculations to be the second-most stable conformer, with an energy 3.4 kJ mol−1 higher than that of conformer +77++. The other conformers give RG values between 0.107 and 0.120, and clearly do not fit the experimental data so well, consistent with them contributing only small amounts to the total composition of the vapour.
A two-conformer refinement was performed using the two conformers (+77++ and +51−−) that had both the lowest computed energies and the best individual fits to the experimental GED data. The structure of each conformer was defined using a unique set of parameters as for the individual refinements, with the exception that both conformers shared common parameters for all bond lengths, with fixed differences from the theoretical values, as well as for selected bond angles. A more detailed description of the model can be found in the ESI.†
For the refinement using the combined model of conformers +77++ and +51−−, the computed distribution of these two conformers was used. The resulting goodness-of-fit was RG = 7.12% (RD = 5.79%), significantly better than for either conformer alone. The resulting RDC for the combined model is shown in Fig. 4. Selected final refined parameters for the combined model are given in Table 4.
| Parameter | GED (ra) | B3LYP-D3/Def2TZVP | Restraint |
|---|---|---|---|
| a The P–Si average and difference parameters define the P–Si distances in +77++ (average − difference) and +51−− (average + difference). b The P–C average is for all P–C distances in both conformers, the first difference describes the iso-propyl P–C bond length for both conformers. P–C diff +77++ is used to define the tert-butyl P–C bond length in +77++. P–C diff +51−− is used to define the tert-butyl P–C bond length in +51−−. c See ESI† for description of the averages and differences for angles. | |||
| rSi-Cl | 203.7(1) | 206.7 | |
| rP–Si ava | 224.8(7) | 225.2 | |
| rP–Si diffa | 0.2(1) | 0.2 | 0.2(05) |
| rP–C avb | 188.2(4) | 190.3 | |
| rP–C diffb | 1.1(3) | 1.1 | 1.1(3) |
| rP–C diff+77++b | 0.8(1) | 0.8 | 0.8(1) |
| rP–C diff+51−−b | 1.5(3) | 1.5 | 1.5(3) |
| rC–C | 153.5(2) | 153.5 | |
| rC–H | 108.8(3) | 109.2 | 109.2(5) |
| ∠Cl–Si–Cl | 107.1(5) | 107.0 | 107.0(5) |
| ∠P–C–H avc | 101.0(5) | 101.0 | 101.0(5) |
| ∠P–C–H diffc | 0.5(1) | 0.5 | 0.5(05) |
| ∠C–C–H | 110.9(5) | 111.1 | 111.1(5) |
| ∠C–C–C iso-Pr | 110.6(5) | 110.6 | 110.6(5) |
| ∠C–C–C tert-Bu | 108.9(5) | 109.2 | 109.2(5) |
| ∠C–P–Cc | 106.2(5) | 106.3 | 106.3(5) |
| ∠C–P–C diffc | 1.0(1) | 1.1 | 1.1(1) |
| Φ Cl(6)–Si–P–C(3) | −173.5(22) | −170.5 | −170.5(30) |
| Φ Si–P–C(3)–C(9) | −30.3(25) | −30.6 | −30.6(25) |
| Φ Si–P–C(4)–C(12) | −168.9(23) | −169.5 | −169.5(25) |
Discussion
The initial investigation of P(tBu)(iPr)(SiCl3) with the UCONGA program yielded six conformers, with geometry optimisation reducing this to five, each representing a minimum on the potential-energy surface. This demonstrates the impact the replacement of one methyl group by a hydrogen atom can have on the conformational composition of a molecule, as the closely related P(tBu)2SiCl3 has been previously found to exhibit only one stable conformer.7 This apparently minor chemical change makes the analysis of the structure profoundly more complicated. Without the use of the SARACEN method, in which gas electron diffraction data are supplemented with computational data, it would have been impossible to determine anything about the structure of the vapour.Conformer +77++ gives RG = 9.76% and conformer +51−− gives RG = 9.83%. The remaining three conformers give RG values of 10.7 to 12.0%. A mix of the first two conformers with a calculated distribution gives RG = 7.12, a much better overall fit to the data. Whilst it may have been possible to add a fixed amount of a third conformer, the dependency on the calculated structure was such that it was decided not to undertake this complicated refinement.
Good overall agreement between the theoretical and experimental structures is observed. For B3LYP-D3/Def2TZVP the calculated bond angles are within ∼0.6°, torsions within ∼2°, and bond lengths are within ∼2 pm of the experimentally determined values, with the exception of the Si–Cl bond length, which was overestimated by the theoretical methods [206.7 pm compared to the experimental value of 204.0(1) pm]. This is in line with discrepancies between experiment and theory in similar molecules. Other bond lengths calculated at the B3LYP-D3/Def2TZVP level are also slightly greater than the experimental values, except for Si–P, for which the experimental bond length, which was slightly, but not significantly, greater than calculated [(225.5(6) pm compared to 224.9 pm].
All five conformers found in this study exhibit structural similarities to those of sterically hindered phosphines studied previously.7,11,14 The GED refinement for the combined study yields rP–Ct = 189.2(4) pm. Corresponding P–C distances determined in previous studies of similar molecules are: P(tBu)3 [191.9(5) pm],14 P(tBu)(SiCl3)2 [190.6(6) pm],11 P(tBu)2SiCl3 [192.5(10) pm],7 P(tBu)H2 [189.6 pm],27 (determined by microwave spectroscopy), P(tBu)2Cl [189.4(5) pm],28 and P(tBu)2F [185.9(6) pm].14 The most striking variation in this group is the shortening correlated with the presence of electron-withdrawing substituents, countered by lengthening when there is steric crowding. rP–Ci was determined to be 187.4(4) pm, fitting with the P–C bond length in gauche-iso-propylphosphine P(iPr)H2 [187.7(1) pm].29 Even this P–C bond length shows no influence of the electron-withdrawing effect from the chlorine atoms on the silicon atom when compared with P(iPr)Cl2 [184.7(13) pm].28
It has been previously reported for P(tBu)2(SiCl3)7 and P(tBu)(SiCl3)211 that the angles at the phosphorus atom are all smaller than tetrahedral (∼109.5°), caused by the influence of the high p-orbital contribution to these bonds. This also applies in the present case. In this respect they are like all phosphines, despite the steric crowding of the ligands. Bond angles around a central phosphorus atom usually increase going from ∠Si–P–Si to ∠C–P–Si to ∠C–P–C.11 In the present study, it is seen that this is true for conformers −91−(−) and +51−−, while for conformers +165 +−, +143−− and +77++ one ∠C–P–Si is smaller than, and one bigger than, ∠C–P–C. The ∠C–P–Si that is smaller than ∠C–P–C involves the iso-propyl group. The smaller ∠C–P–Si of the iso-propyl group could be due to the its lower steric bulk, allowing it greater flexibility to move towards the trichlorosilyl group. It has also been suggested that in similar molecules there may be an attractive interaction between the chlorine atoms on the trichlorosilyl group and the hydrogen atoms on the iso-propyl group, which could be drawing the groups closer together.11 It is unclear from this study which is dominant.
If the position of the lone pair on phosphorus is defined as lying on the vector passing through the centroid of the three substituent atoms and the phosphorus atom, angles to the substituents can then be determined. It can be seen that ∠lp–P–Si is much larger than the two ∠lp–P–C, ∼125° compared to ∼107° (Table 5). This is a reflection of repulsions between the four electron pairs around the phosphorus atoms. The chlorine atoms on silicon withdraw electron density in the P–Si bond, resulting in the lp-P–Si angles being dramatically larger than the lp-P–C angles.
The P–C–H angles of conformers +165+− and +143 are ∼108°, whereas conformers −91−(−), +51−− and +77++ returned much smaller angles, between 100.5° and 101.5°. This was also observed in a previous study of iso-propyldichlorophosphine.26 Depending on the position of the tertiary hydrogen atom on the iso-propyl group and the lone electron pair of the phosphorus atom a gauche form (Fig. 5 left) or trans form (Fig. 5 right) exists. In the current study, the computational results for the gauche conformations of the tertiary hydrogen atom also show a smaller ∠P–C–H (∼101.4°) whereas the bond angle for the trans conformer is ∼108°. However, this could not be directly compared with iso-propyldichlorophosphine,26 due to the fact that we could not experimentally refine ∠P–C–H.
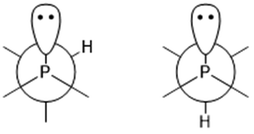 | ||
| Fig. 5 Newman projections of 1 along the P–C bond: left, gauche conformation; right, trans conformation. | ||
As mentioned previously, the replacement of a tert-butyl group by an iso-propyl group in 1 has resulted in a far more complicated structure, increasing from a single conformer for P(tBu)2(SiCl3)7 to five conformers for 1. A detailed discussion of the tilt angles is given in the supporting data with the analysis summarised here. The main tilts and torsions are given in Table 6. In the computed structures of the conformers, all three ligands are tilted more or less up towards the lone pair of the phosphorus atom, i.e. away from one another. This is also the case for the refined structure. The trichlorosilyl group returns a tilt of +1.7°, for the iso-propyl group the tilt is +3.4°, and the smallest tilt is for the tert-butyl group (+1.1°), according to the experimental data.
| Conformer | +77++ Ra | +77++ | +51−− |
|---|---|---|---|
| a +77++ R indicates data for the refined structure. b A positive tilt value indicates a movement towards the lone pair on the phosphorus atom. c V, W and X represent the centroids on the SiCl3, tert-butyl and iso-propyl groups respectively. | |||
| Tiltb | |||
| P–Si–Vc | 1.7 | 1.7 | 1.7 |
| P–C–Wc | 1.1 | 1.5 | 1.6 |
| P–C–Xc | 3.4 | 3.1 | 2.9 |
| Twist from perfectly staggered conformation | |||
| lp–P–Si–Cl | 10.5 | 11.5 | −7.7 |
| lp–P–C–C tBu | 27.0 | 24.7 | −12.0 |
| lp–P–C–H iPr | 12.7 | 15.6 | −11.2 |
Conclusions
The gas-phase structure of 1 has been determined using gas-phase electron diffraction. Quantum chemical calculations predicted a mixture of more than one conformer in the gaseous phase, which was confirmed by the experimental results. The structure refinement for the two-conformer model comprising the +77++ and +51−−conformers gave a significantly better goodness of fit compared to the individually refined conformers.Gas electron diffraction has come a long way since the inception of Dalton Transactions in 1972, and we believe there are many more insightful structural investigations to come such as determining structures of short-lived species or charged species, which in of itself is challenging to do with a charged beam probe. There are also many molecular investigations still to be done to help support and address efforts towards the UN Sustainable Development Goals, in particular around affordable and clean energy (UNSDG #7).30 The subject of this present study is an extreme example of what can now be done using GED. The combination of some relatively heavy substituents (chlorine) with low overall and local symmetry, leading to multiple conformers, would make a gas-phase structural determination by experimental methods alone impossible. However, when theoretical and experimental data are combined, the most significant geometrical parameters are determined experimentally. This also provides strong experimental evidence regarding the conformational composition of the vapour. Together, theory and experiment give key insights into the chemical properties of the compound.
Author contributions
SLM conceived the investigation, collected the data, supervised IW for the data analysis and co-wrote the manuscript. DWHR collected the data and co-wrote the manuscript. IW interpreted the electron diffraction data, ran the calculations and co-wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Wolf-Walther du Mont of the Technische University of Braunschweig for the synthesis of iso-propyl(tert-butyl)(trichlorosilyl)phosphine and acknowledge the use of the EPSRC UK National Service for Computational Chemistry Software (NSCCS) at Imperial College London in carrying out this work. IW thanks the German Academic Exchange Service (DAAD) for support with a PROMOs scholarship. SLM thanks the School of Physical and Chemical Sciences and the University of Canterbury for ongoing support of the electron diffraction apparatus and computational resources. SLM and DWHR thank the Engineering and Physical Sciences Research Council and its predecessors for continuous support of gas electron diffraction research in Edinburgh from its inception in 1977 until the end of 2010.References
- K. Hedberg, J. Am. Chem. Soc., 1955, 77, 6491–6492 CrossRef CAS.
- C. Glidewell, D. W. H. Rankin and A. G. Robiette, J. Chem. Soc. A, 1970, 2935–2937 RSC.
- E. A. V. Ebsworth, J. R. Hall, M. J. Mackillop, D. C. McKean, N. Sheppard and L. A. Woodward, Spectrochim. Acta, 1958, 13, 202–211 CrossRef CAS.
- G. Davidson, E. A. V. Ebsworth, G. M. Sheldrick and L. A. Woodward, Chem. Commun., 1965, 122–112 RSC.
- B. Beagley, A. G. Robiette and G. M. Sheldrick, Chem. Commun., 1967, 601–602 RSC.
- D. W. H. Rankin, J. Chem. Soc., Dalton Trans., 1972, 869–873 RSC.
- W. W. du Mont, L. Müller, R. Martens, P. M. Papathomas, B. A. Smart, H. E. Robertson and D. W. H. Rankin, Eur. J. Inorg. Chem., 1999, 8, 1381–1392 CrossRef.
- R. Martens and W. W. du Mont, Chem. Ber., 1992, 125(3), 657–658 CrossRef CAS.
- R. Martens and W. W. du Mont, Chem. Ber., 1993, 126(5), 1115–1117 CrossRef CAS.
- G. A. Forsyth, D. W. H. Rankin and H. E. Robertson, J. Mol. Struct., 1990, 239, 209–217 CrossRef CAS.
- S. L. Hinchley, H. E. Robertson, D. W. H. Rankin and W. W. du Mont, J. Chem. Soc., Dalton Trans., 2002, 20, 3787–3794 RSC.
- L. S. Bartell and R. C. Hirst, J. Chem. Phys., 1959, 31(2), 449–451 CrossRef CAS.
- L. S. Bartell and L. Brockway, J. Chem. Phys., 1960, 32(2), 512–515 CrossRef CAS.
- H. Oberhammer, R. Schmutzler and O. Stelzer, Inorg. Chem., 1978, 17(5), 1254–1258 CrossRef CAS.
- N. R. Gunby, S. L. Masters and D. L. Crittenden, J. Mol. Graphics Modell., 2017, 77, 286–294 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- V. Sipachev, J. Mol. Struct.: THEOCHEM, 1985, 121, 143–151 CrossRef; V. Sipachev, J. Mol. Struct., 2001, 567, 67–72 CrossRef.
- C. M. Huntley, G. S. Laurenson and D. W. H. Rankin, J. Chem. Soc., Dalton Trans., 1980, 6, 954–957 RSC.
- H. Fleischer, D. A. Wann, S. L. Hinchley, K. B. Borisenko, J. R. Lewis, R. J. Mawhorter, H. E. Robertson and D. W. H. Rankin, Dalton Trans., 2005, 19, 3221–3228 RSC.
- S. L. Hinchley, H. E. Robertson, K. B. Borisenko, A. R. Turner, B. F. Johnston, D. W. H. Rankin, M. Ahmadian, J. N. Jones and A. H. Cowley, Dalton Trans., 2004, 16, 2469–2476 RSC.
- A. Ross, M. Fink and R. Hilderbrandt, in International Tables for Crystallography, ed. A. J. C. Wilson, Kluwer Academic Publishers, Dordrecht, Netherlands, 1992, p. 245 Search PubMed.
- A. J. Blake, P. T. Brain, H. McNab, J. Miller, C. A. Morrison, S. Parsons, D. W. H. Rankin, H. E. Robertson and B. A. Smart, J. Phys. Chem., 1996, 100(30), 12280–12287 CrossRef CAS; P. T. Brain, C. A. Morrison, S. Parsons and D. W. H. Rankin, J. Chem. Soc., Dalton Trans., 1996, 24, 4589–4596 RSC; N. W. Mitzel and D. W. H. Rankin, Dalton Trans., 2003, 19, 3650–3662 RSC.
- R. Noble-Eddy, S. L. Masters, D. W. H. Rankin, H. E. Robertson and J.-C. Guillemin, J. Mol. Struct., 2010, 978(1–3), 26–34 CrossRef CAS.
- S. L. Masters, S. J. Atkinson, M. Hölbling and K. Hassler, Struct. Chem., 2013, 24(4), 1201–1206 CrossRef CAS.
- G. B. Soifer and S. N. Shurov, J. Struct. Chem., 2002, 43(5), 865–868 CrossRef CAS.
- Y. S. Li, A. W. Cox and J. R. Durig, J. Mol. Spectrosc., 1978, 70(1), 34–40 CrossRef CAS.
- V. A. Naumov and O. N. Kataeva, Struct. Chem., 1983, 24(5), 736–740 CrossRef.
- R. Noble-Eddy, S. L. Masters, D. W. H. Rankin, D. A. Wann, H. E. Robertson, B. Khater and J.-C. Guillemin, Inorg. Chem., 2009, 48(17), 8603–8612 CrossRef CAS PubMed.
- https://sdgs.un.org/goals .
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dt02888j |
| This journal is © The Royal Society of Chemistry 2021 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.0020
exp(−0.0020