Photoelectron circular dichroism of O 1s-photoelectrons of uniaxially oriented trifluoromethyloxirane: energy dependence and sensitivity to molecular configuration
Giammarco
Nalin
 a,
Kilian
Fehre
a,
Florian
Trinter
a,
Kilian
Fehre
a,
Florian
Trinter
 bc,
Nikolay M.
Novikovskiy
bc,
Nikolay M.
Novikovskiy
 de,
Nils
Anders
a,
Daniel
Trabert
a,
Sven
Grundmann
de,
Nils
Anders
a,
Daniel
Trabert
a,
Sven
Grundmann
 a,
Max
Kircher
a,
Arnab
Khan
a,
Raghu
Tomar
a,
Max
Hofmann
a,
Markus
Waitz
a,
Isabel
Vela-Pérez
a,
Gregor
Kastirke
a,
Juliane
Siebert
a,
Dimitrios
Tsitsonis
a,
Hironobu
Fukuzawa
a,
Max
Kircher
a,
Arnab
Khan
a,
Raghu
Tomar
a,
Max
Hofmann
a,
Markus
Waitz
a,
Isabel
Vela-Pérez
a,
Gregor
Kastirke
a,
Juliane
Siebert
a,
Dimitrios
Tsitsonis
a,
Hironobu
Fukuzawa
 f,
Kiyoshi
Ueda
f,
Joshua B.
Williams
g,
Denis
Kargin
h,
Martin
Maurer
h,
Catmarna
Küstner-Wetekam
d,
Lutz
Marder
d,
Johannes
Viehmann
d,
André
Knie
d,
Till
Jahnke
ai,
Markus
Ilchen
bdi,
Reinhard
Dörner
a,
Rudolf
Pietschnig
f,
Kiyoshi
Ueda
f,
Joshua B.
Williams
g,
Denis
Kargin
h,
Martin
Maurer
h,
Catmarna
Küstner-Wetekam
d,
Lutz
Marder
d,
Johannes
Viehmann
d,
André
Knie
d,
Till
Jahnke
ai,
Markus
Ilchen
bdi,
Reinhard
Dörner
a,
Rudolf
Pietschnig
 h,
Philipp V.
Demekhin
h,
Philipp V.
Demekhin
 *d and
Markus S.
Schöffler
a
*d and
Markus S.
Schöffler
a
aInstitut für Kernphysik, Goethe-Universität, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany. E-mail: nalin@atom.uni-frankfurt.de; fehre@atom.uni-frankfurt.de; schoeffler@atom.uni-frankfurt.de
bDeutsches Elektronen-Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany
cMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195, Berlin, Germany
dInstitut für Physik und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany. E-mail: demekhin@physik.uni-kassel.de
eInstitute of Physics, Southern Federal University, 344090 Rostov-on-Don, Russia
fInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai 980-8577, Japan
gDepartment of Physics, University of Nevada, Reno, Nevada 89557, USA
hInstitut für Chemie und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany. E-mail: pietschnig@uni-kassel.de
iEuropean XFEL GmbH, Holzkoppel 4, 22869 Schenefeld, Germany. E-mail: markus.ilchen@xfel.eu
First published on 15th July 2021
Abstract
The photoelectron circular dichroism (PECD) of the O 1s-photoelectrons of trifluoromethyloxirane (TFMOx) is studied experimentally and theoretically for different photoelectron kinetic energies. The experiments were performed employing circularly polarized synchrotron radiation and coincident electron and fragment ion detection using cold target recoil ion momentum spectroscopy. The corresponding calculations were performed by means of the single center method within the relaxed-core Hartree–Fock approximation. We concentrate on the energy dependence of the differential PECD of uniaxially oriented TFMOx molecules, which is accessible through the employed coincident detection. We also compare the results for the differential PECD of TFMOx to those obtained for the equivalent fragmentation channel and similar photoelectron kinetic energy of methyloxirane (MOx), studied in our previous work. Thereby, we investigate the influence of the substitution of the methyl group by the trifluoromethyl group at the chiral center on the molecular chiral response. Finally, the presently obtained angular distribution parameters are compared to those available in the literature.
1 Introduction
The interaction of circularly polarized light with chiral molecules leads to a range of chiroptical effects. One such effect, namely the photoelectron circular dichroism (PECD), has been demonstrated to have strong potential as a sensitive probe of this chiral light-molecule interaction. The effect manifests itself as a forward–backward asymmetry of the photoelectron angular emission distribution with respect to the light propagation direction, which inverts upon switching of the light's helicity or upon exchanging molecular enantiomers. After the first theoretical formulation provided by Ritchie in 19761 and the first experimental observation by Böwering et al. in 2001,2 PECD rapidly evolved into a well-established sensitive chiral recognition technique.3–6PECD is a universal chiroptical effect occurring in all regimes,7 from one-photon to multiphoton ionization8,9 and strong-field ionization,7,10,11 with a majority of experiments, so far, reporting on the ionization of valence electrons.12–16 PECD shows a complex dependence on the electronic17 and vibronic18 configuration, as well as the conformation,19,20 dimerization,21 clustering22 of molecules, and the energy of the emitted photoelectrons.23 The typical strength of PECD is on the order of a few percent. Its unique sensitivity has been exploited to study ultrafast molecular dynamics,24,25 especially time-resolved molecular relaxation,26 and it has been employed for real-time determination of the enantiomeric excess in racemic mixtures.27
Several experiments reported on PECD after core ionization of chiral molecules.13,23,28–36 In our recent work,32 we performed a differential study of PECD after O 1s-photoionization of uniaxially oriented methyloxirane molecules (MOx, C3H6O). To this end, the O 1s-photoelectrons were detected as coincident with two charged fragments. The molecular fragmentation axis was assumed to coincide with the emission direction of those ionic fragments relying on the validity of the so-called axial-recoil approximation.37 This assumption is often well justified for cases of rapid Auger decay of an inner-shell vacancy and subsequent Coulomb explosion of a molecular dication. Orientation of achiral molecules in space results in circular dichroism in the angular distribution (CDAD38,39) and in so-called apparent40 PECD. Such extrinsic angular asymmetries caused by the molecular orientation superimpose with the intrinsic asymmetries in the photoelectron emission from chiral molecules. It was found that a selection of certain fragmentation directions of MOx with respect to the light propagation direction yields an increase of the PECD by a factor of 10, as compared to randomly oriented molecules.
In the present work, we extend our previous study32 to a close relative of MOx, the trifluoromethyloxirane (TFMOx, C3H3F3O) molecule, in which all three hydrogen atoms of the methyl group are replaced by much heavier fluorine atoms. For further discussion, it is important to stress that by definition of the Cahn–Ingold–Prelog (CIP41) rules, this substitution exchanges the assigned handedness (S- to R-enantiomer and vice versa) despite the unchanged connectivity of the molecular backbone and the stereo-center in MOx and TFMOx (see Fig. 1). We investigate here the O 1s-photoelectrons of TFMOx for different kinetic energies. One of these energies coincides with that of the study on MOx presented in ref. 32. We selected, furthermore, for our investigation of TFMOx, one of the fragmentation channels which was studied previously for MOx.
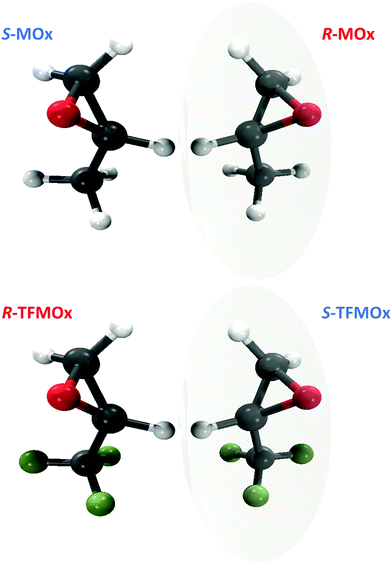 | ||
| Fig. 1 Top: Structure of S- and R-methyloxirane (C3H6O, MOx). Bottom: Structure of R- and S-trifluoromethyloxirane (C3H3F3O, TFMOx). Note that substitution of the methyl group (CH3) with the trifluoromethyl group (CF3) at the chiral center causes renaming of the respective R- and S-enantiomers according to the CIP rule.41 | ||
2 Research methods
2.1 Samples
An RS-mixture and samples of pure S- or R-TFMOx enantiomers were commercially obtained (SynQuest Laboratories) and used as received. Their chemical identity and purity were verified by nuclear magnetic resonance (NMR) spectroscopy. The 1H, 13C, and 19F NMR data were recorded on a Varian VNMRS-500 MHz or MR-400 MHz spectrometer at room temperature. Chemical shifts were referenced to residual protic impurities in the solvent (1H) or the deuterio solvent itself (13C) and reported relative to external Si(CH3)4 (1H, 13C) or C6H5CF3(19F). The chemical purity after integration of the fluorine NMR signal has been estimated to be higher than 96% for the RS-TFMOx mixture and higher than 96% or 98% for the S-TFMOx or R-TFMOx enantiomer, respectively. The NMR shifts were assigned based on the 2D-NMR (HSQC) spectra. The enantiomeric purity of the samples was investigated by high-performance liquid chromatography (HPLC) using a CHIRALPAK IG (4.6 mm × 250 mm) chiral analytical column. According to these measurements, the RS-TFMOx mixture is racemic within margins of error (S-TFMOx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R-TFMOX = 49%
R-TFMOX = 49%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51%), and the enantiopure S-TFMOx or R-TFMOx have an enantiomeric excess of approximately 95% (see Fig. 2 for details).
51%), and the enantiopure S-TFMOx or R-TFMOx have an enantiomeric excess of approximately 95% (see Fig. 2 for details).
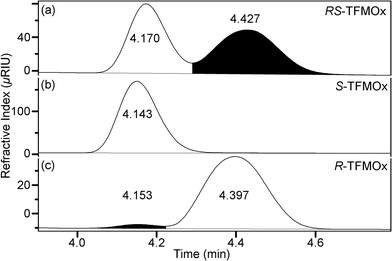 | ||
| Fig. 2 Ratio of enantiomers present in the samples of racemic RS-TFMOx (a) and its S- and R-enantiomers (b and c, respectively) as experimentally determined using HPLC. | ||
2.2 Experiments
The experiment was conducted in 8-bunch mode (pulsed operation) at synchrotron SOLEIL (Saint-Aubin, France) at beamline SEXTANTS using Cold Target Recoil Ion Momentum Spectroscopy (COLTRIMS42–44). The light's helicity was switched every two hours between circular left (CL) and circular right (CR). The samples were expanded through a nozzle of 60 μm diameter, and the expanding gas was skimmed two times, resulting in a free molecular gas jet of about 1 mm diameter. The jet was intersected at right angles to the synchrotron-radiation beam. A closed-loop recycling system was installed and used to reduce sample consumption.45 After photoionization, the ionic fragments and electrons were accelerated by the electric field of the COLTRIMS spectrometer in opposite directions towards time- and position-sensitive detectors. A mesh-free spectrometer with electrostatic lenses and field-free drift regions was employed in order to improve the analyzer's angle and mass resolutions, and to increase the overall detection efficiency. The electric field at the point of interaction was set to E = 116 V cm−1. The time- and space-focusing geometry of the COLTRIMS spectrometer46–48 resulted in a solid angle of acceptance of 4π for both, photoelectrons up to 15 eV and ions up to 10 eV kinetic energy.The electron energy calibration was carried out using a series of measurements on argon atoms, ionizing both, the 2p1/2 and 2p3/2 shells. From this series, a calibration function was created which links the measured electron positions-of-impact and times-of-flight with the photoelectron energy. The five photon energies for the TFMOx measurement (541.5, 542.5, 544.5, 546.5, and 550.1 eV) were chosen such that bands of the O 1s-photoelectrons peaked at kinetic energies of 3.1, 4.1, 6.1, 8.1, and 11.7 eV are created. The energy-calibration procedure covered this range of electron kinetic energies. The kinetic energy intervals of ±0.5 eV (within the FWHM = 1.0 eV of the photoelectron bands) were used in the subsequent analysis of the chiral asymmetry. The absolute and relative spatial orientation of the electron and ion detectors was checked comparing the molecular-frame photoelectron angular distributions of N2 K-shell electrons measured during the same beamtime to those reported in ref. 39. The impact positions and times-of-flight of the particles were measured using position- and time-sensitive microchannel plate (MCP) detectors, using delay-line anodes for position read-out (Roentdek GmbH). A HEX90 anode (∅ 90 mm) equipped with an 80 mm diameter MCP49 was used for the electron, and a HEX125L anode (∅ 125 mm) equipped with an efficiency-enhanced 75 mm diameter funnel MCP (Hamamatsu)50 for the ion detection. The momentum vector of each fragment at the instant of ionization is derived from their time-of-flight and impact position on the detector. Data were recorded with typical rates of 6 kHz on the ion and 10 kHz on the electron detector. The combined CF3+(m/z = 69)−C2Hi=1,2,3O+(m/z = 41, 42, 43) breakup channel contains roughly 2.5 × 105 valid events for each enantiomer, light helicity, and photon energy.
In order to cross-check the experimental results presented here, we performed a second short experiment at the permanent COLTRIMS end-station of the PIPE instrument, located at beamline P04 of the synchrotron PETRA III (DESY, Hamburg, Germany).51 In this case, hexagonal delay-line detectors with an active diameter of 80 mm (HEX90 anodes) were used for both, ion and electron detection. The ion arm of that spectrometer was a 17 cm long acceleration region without any meshes, while the electron arm was built in a time-focussing geometry.52 The dichroic parameter β1 was retrieved from the measured data by integrating over all possible fragmentation channels of TFMOx. Therefore, it was sufficient to record datasets for each polarization direction and photon energy for only 20 minutes. The data were recorded at detection rates of 15 kHz for the electron detector. The photoelectron-energy calibrations as well as detector-orientation calibrations were similarly performed as described above for the measurements at synchrotron SOLEIL.
2.3 Data analysis
Within the electric-dipole approximation, the laboratory-frame photoelectron angular emission distribution can be expanded in terms of Legendre polynomials PLvia the dichroic parameter β1 and the anisotropy parameter β2. For randomly oriented molecules and in the case of an ionization employing circularly polarized photons (with helicity ±1), the corresponding expansion reads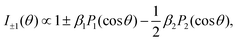 | (1) |
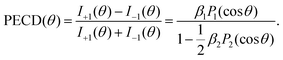 | (2) |
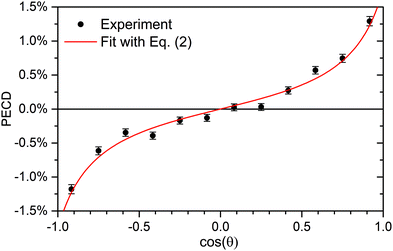 | ||
| Fig. 3 Retrieval of the anisotropy and dichroic parameters from the measured PECD of R-TFMOx recorded at the O 1s-photoelectron energy of 11.7 eV. A fit (red line) of the experimental data (circles with error bars) using eqn (2) yielded β1 = 0.76% ± 0.06% and β2 = 1.14 ± 0.15. | ||
In order to check for possible systematic experimental errors, various subsets of the experimental data were considered separately for this analysis. For example, the high electric fields of the spectrometer degraded the time-of-flight resolution and thus the resolution of the momentum component parallel to the spectrometer axis. As one cross-check, only the central part of the photoelectron time-of-flight distribution was examined and analyzed as a subset. Furthermore, in order to exclude possible influences of inhomogeneous detection probabilities, the electron detector was divided into its left and right half along the light propagation direction, and each subset was analyzed separately. The influence of possible ion feedback from the ion detector was investigated with the help of applying different conditions on the ion time-of-flight and by a selection of different ranges of sums of momenta for various fragmentation channels. All these subsets of the data yielded (within statistical errors) the same angular distribution parameters β1 and β2.
2.4 Theory
The O 1s-photoionization of TFMOx was described by the ab initio theoretical approach used in our previous angle-resolved studies on MOx32,34 and TFMOx33 molecules. The electronic structure and dynamics calculations were carried out by employing the Single Center (SC) method and code,54,55 which provide an accurate description of the partial angular momentum photoelectron continuum waves of ionized molecules. The calculations were performed for the equilibrium molecular geometry of the neutral ground electronic state of TFMOx. Details of the calculations can be found in our previous study of TFMOx.33 Therefore, only essential differences between the previous and present calculations are discussed below. While the calculations in ref. 33 were carried out within the frozen-core Hartree–Fock (FCHF) approximation, in the present work, the photoionization transition amplitudes were computed within the relaxed-core Hartree–Fock (RCHF) approximation, which accounts for the major effect of the monopole relaxation of molecular orbitals induced by the creation of the inner-shell vacancy. In addition, we increased here the SC expansions of the occupied orbitals by partial harmonics with![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c, |mc| ≤ 79 (as compared to
c, |mc| ≤ 79 (as compared to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c, |mc| ≤ 59 in ref. 33), while those for the partial photoelectron continuum waves were kept unchanged with
c, |mc| ≤ 59 in ref. 33), while those for the partial photoelectron continuum waves were kept unchanged with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ε, |mε| ≤ 29.
ε, |mε| ≤ 29.
The calculations were performed for different orientations of the molecular frame (MF) with respect to the laboratory frame (LF, ZLF is defined by the propagation direction of the circularly polarized light), which is given by the two Euler angles α and β. Note, that the third angle γ (which defines a rotation around the laboratory ZLF axis) is irrelevant in case circularly polarized light is used. In the experiment, a breakup into two molecular fragments was examined. Thus, only a single fragmentation axis was determined. Therefore, the corresponding differential PECD(θ, β) was obtained by numerical integration of the computational results over the orientation angle α. Here, the orientation interval α ∈ [0, 2π) was covered in steps of Δα = 0.025π. Since the fragmentation dynamics can be rather complicated (and not all of the particles are detected in coincidence), it is not straightforward to relate the fragmentation axis obtained in the experiment from the asymptotic momenta of the two detected ions to a given molecular orientation at the instant of ionization. Therefore, just as in our previous work on uniaxially oriented MOx,32 we used the molecular orientation axis at the instant of the photoionization process as a free parameter in the calculations and searched for the best visual correspondence between the computed and measured differential PECD. Details of this procedure can be found in the supplemental material document of our previous work.32
3 Results and discussion
3.1 Differential PECDs: MOx vs. TFMOx
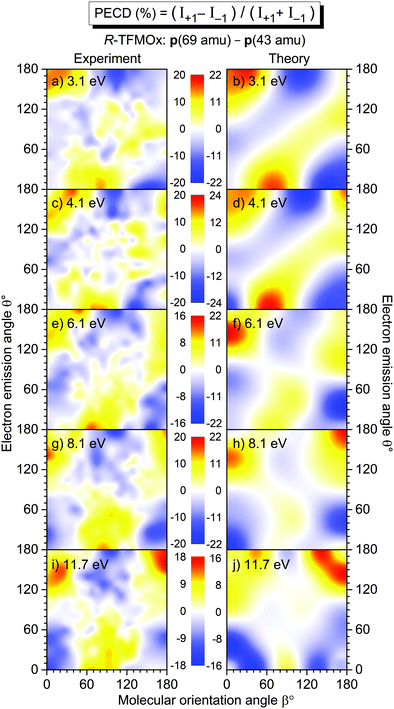
In our previous work on uniaxially oriented MOx,32 a differential PECD was studied for a photoelectron kinetic energy of 11.5 eV and two fragmentation channels. One of the channels represents a single-bond breakage with the loss of the methyl group, i.e., a breakup into CH3+(m/z = 15)−C2H2O+(m/z = 42). Therefore, in the present work, we decided to focus on a similar fragmentation channel of TFMOx, which represents a single-bond breaking with the loss of the trifluoromethyl group. We observed that additional losses of hydrogen atoms on the oxirane ring do not alter the measured electron emission distributions. Therefore, we examined here the differential PECD combining the datasets of the breakup channels CF3+(m/z = 69)−C2Hi=1,2,3O+(m/z = 41, 42, 43), which we designated as p(69 amu)−p(43 amu) for brevity. The relative momentum (i.e., the difference of the momentum vectors) of those two fragments defines a fragmentation axis of the molecule, and its orientation Euler angle β in the laboratory frame (with respect to the light propagation direction) is thus known. The molecule is that way, however, only uniaxially oriented which leaves one degree of freedom for its rotation around this axis.We first consider the photoelectron kinetic energy of 11.7 eV, which is very similar to that used in ref. 32 for MOx. The measured differential PECDs of uniaxially oriented enantiomers of TFMOx are depicted in the right column of Fig. 4 in panels (b) and (d). For some molecular orientations (i.e., some spatial orientations of the molecular fragmentation), the differential PECD reaches about 20%. Our measurements thus confirm the conclusion of ref. 32 that fixing already one axis of a chiral molecule in space enhances the chiral asymmetry by about an order of magnitude (as compared to about 1% observed for the randomly oriented molecules shown in Fig. 3). The asymmetry switches its sign upon exchanging of the enantiomers, which confirms the chiral origin of the observed effect. This normalized difference also obeys the analytically derived asymmetry equation:32 PECD(π − θ, π − β) = −PECD(θ, β), which implies a flip of its sign upon rotation of this two-dimensional map by 180° around the normal to the picture plane. Please note that this equivalence of changing the sign of the light helicity and exchanging the enantiomer holds only for enantiomeric pure samples and perfectly circularly polarized light (see ref. 10 for more details).
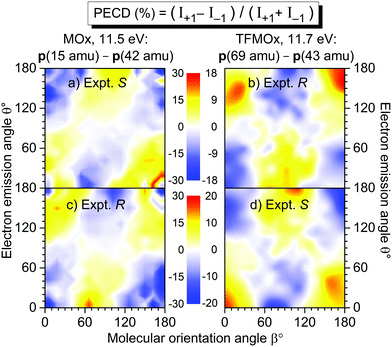 | ||
| Fig. 4 Measured differential PECD of the uniaxially oriented enantiomers of MOx (left column, data from ref. 32) and TFMOx (right column, present work) as a function of the photoelectron emission angle θ and the molecular orientation angle β. The PECD maps were obtained for O 1s-photoionization yielding similar electron kinetic energies (11.5 eV for MOx and 11.7 eV for TFMOx). Conceptually the same fragmentation channels are chosen, i.e., CH3+(m/z = 15)−C2H2O+ (m/z = 42) for MOx and CF3+ (m/z = 69)−C2Hi=1,2,3O+(m/z = 41, 42, 43) for TFMOx. According to the CIP rule, opposite enantiomers of these two chiral molecules with identical geometrical structure are compared in each row (see Fig. 1 for details). | ||
For comparison, panels (a) and (c) in the left column of Fig. 4 show the differential PECD of MOx from ref. 32. One can see that for equal fragmentation channels and similar photoelectron kinetic energies the differential PECDs observed for these two molecules are very similar in the strengths and structures. It is surprising that exchanging the three hydrogen atoms in the methyl group by the much heavier scatterers (fluorine atoms) does not significantly change the PECD landscape, observed at this photoelectron kinetic energy. A similar observation was made in a comparative study17 of the valence-shell PECD of MOx and TFMOx, where noticeable differences between the respective chiral asymmetries were found only for kinetic energies below 4 eV. In each row of this figure, we compare the data for MOx and TFMOx molecules of similar geometrical structures (therefore, opposite R- and S-enantiomers). One can see that the differential PECDs of the two molecules of similar geometrical structures have opposite-sign landscapes, whereas for identical R- or S-enantiomers of both molecules the measured sign landscapes are very similar. This fact confirms that the inner-shell PECD effect emerges as a result of a complex multiple scattering of the emitted photoelectron wave by the molecular potential. Indeed, similar stereo-descriptors of enantiomers assume a similar circular arrangement of the stronger-to-weaker scatterers, which couple the rotational motion of a photoelectron, driven by the electric field vector of circularly polarized light, with its translational motion (like a nut on a bolt23,32).
3.2 Energy dependence of PECD
A full account of the differential PECD of uniaxially oriented TFMOx, measured for the five aforementioned photoelectron kinetic energies, is depicted in the left column of Fig. 5. For all energies, there are molecular orientations at which the measured differential PECD reaches maximal values of about ±16% to ±20% [panels (a), (c), (e), (g), and (i) in the left column], which are at least larger by a factor of 10 than the respective orientation-averaged values β1 (see Section 3.3 and Fig. 6). Qualitatively, all measured differential PECDs depict similar landscapes including their signs. Nevertheless, a clear trend in the development of the measured differential PECDs with the increase of the photoelectron kinetic energy can be noticed. For the two lower kinetic energies of 3.1 eV in panel (a) and 4.1 eV in panel (c), as well as 6.1 eV in panel (e), we observe a sequence of positive–negative–positive–negative stripes (from top to bottom) which are about 45°-inclined. For the two higher kinetic energies of 8.1 eV in panel (g) and 11.7 eV in panel (i), it develops in a clear sequence of three horizontal positive–negative–positive islands at the top and an alternated sequence at the bottom.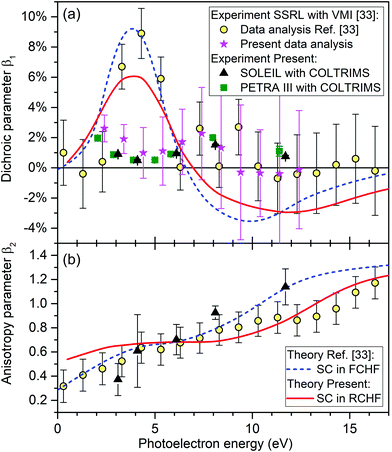 | ||
| Fig. 6 Dichroic parameter β1 (a) and the anisotropy parameter β2 (b) as given by eqn (1) for the O 1s-photoelectrons of R-TFMOx. Circles: experimental results recorded at the BL13-2 beamline of SSRL using a VMI setup, as reported in ref. 33. Stars: β1 obtained by the present reanalysis of the raw data underlying the values shown by circles from ref. 33 (see Section 3.3). Triangles: results of the present experiment performed at beamline SEXTANTS of SOLEIL using COLTRIMS. Squares: corresponding β1 values measured at beamline P04 of PETRA III. Dashed curve: frozen-core Hartree–Fock calculations performed with the SC method as reported in ref. 33. Solid curve: present relaxed-core Hartree–Fock calculations performed using the SC method. | ||
In order to calculate the differential PECD of uniaxially oriented TFMOx, we first assumed validity of the axial-recoil approximation,37 for which the momentum difference of two fragments represents an orientation of the molecular axis in space at the instant of ionization (i.e., the molecule does not rotate significantly during the Auger decay and subsequent fragmentation). This approximation worked well in our previous study.32 There, we found that—for the single-bond breaking with the loss of the methyl group—the optimal molecular axis, which provides the best description of the experiment, connects the oxygen atom with the carbon of the methyl group (see the ESI of ref. 32). Starting with this assumption, we searched for the optimal molecular fragmentation axis, which provides the best match between theory and experiment for the differential PECDs of uniaxially oriented TFMOx for all five electron energies.
As a result of our search, we find that the best visual correspondence between the measured and computed differential PECD is provided by a fragmentation axis which connects the oxygen atom with the CH2-group on the oxirane ring. It should be stressed that all five photoelectron energies yielded very similar optimal fragmentation axes which coincide within a solid angle of about 0.2 sr. The fact, that the axis obtained this way does not connect two charged fragments (the trifluoromethyl group and the oxirane ring) but lies almost in the plane of the oxirane ring, indicates a breakdown of the axial-recoil approximation for the TFMOx molecule. Indeed, a considerably larger mass of the trifluoromethyl group (as compared to the methyl group in MOx) and a much richer electronic structure of fluorine atoms (as compared to hydrogens) may lead to the fact that the centers of charge of the fragments do not coincide with their centers of mass. In this case, an intricate rotation of two fragments with respect to each other takes place in the course of a considerably slower dissociation of TFMOx (as compared to the same fragmentation channel of MOx with the much lighter methyl group), and, as a consequence, the differences of their asymptotic momenta do not represent the molecular orientation at the instant of photoionization.
The results of our calculations of the differential PECD of R-TFMOx, obtained for the optimal fragmentation axis, are depicted in the right column of Fig. 5. The calculations provide a semi-quantitative theoretical description of the measured differential PECD. Indeed, the overall landscapes and signs of the experimental differential PECDs, including the arrangement of stripes and islands discussed above, are reproduced by the theory. Detailed distributions of the experimental and theoretical asymmetries in their forms and strengths are, however, somewhat different. This leads to the fact that averaging the theoretical and experimental signals over molecular orientations yields different β1 values. This fact can be seen, e.g., for the photoelectron energies of 8.1 and 11.7 eV in the forward emission direction. In particular, in the experiment, molecular orientations yielding positive chiral asymmetries dominate over those which yield a negative PECD, while this situation is opposite in the theory [cf., in Fig. 5 panels (g) and (h), and separately panels (i) and (j), for the emission angles around θ = 0° and orientation angles around β = 90° with highest contribution weights]. This difference is reflected in the opposite signs of the computed and measured dichroic parameters at 8.1 and 11.7 eV [see panel (a) of Fig. 6 and its discussion in Section 3.3].
3.3 Anisotropy and dichroic parameters
The angular distribution parameters β1 and β2 of the O 1s-photoelectrons of TFMOx, measured at SOLEIL and defined by eqn (1), are depicted in Fig. 6 by black triangles. Panel (b) reveals that our experimental results for the anisotropy parameter β2 are in a good agreement with the experimental and theoretical results reported in ref. 33. The latter were computed by using the SC method within the FCHF approximation and are shown as a blue dashed curve. In contrast, however, our measured results for the dichroic parameter β1 disagree considerably with the experimental and theoretical results reported in ref. 33 in an energy range between 3 and 6 eV. As a cross-check, the dichroic parameter β1 obtained from a second experiment (see Section 2.2 for details) with a different setup at a different synchrotron-radiation facility is shown in panel (a) of Fig. 6 by green squares. It confirms the results from our main experiment (black triangles).In order to understand the considerable deviation between the presently and previously measured dichroic parameters β1 seen in panel (a) of Fig. 6 in the energy range of 3–6 eV, in a joint effort with the authors of ref. 33, we reanalyzed the original Stanford Synchrotron Radiation Lightsource (SSRL) raw data recorded at the BL13-2 beamline with a VMI setup. The reanalysis of raw images was performed independently for every run of a certain photon energy, helicity of the light, and enantiomer, using the following steps. The intensity in the surrounding of the momentum spheres was subtracted as the background. Then, the momentum sphere had to be centered. It turned out that the center varied from run to run on the level of a few percent of the radius of the momentum sphere giving rise to systematic errors if not corrected for. This shift had not been accurately corrected for in the original analysis in ref. 33. An Abel transformation was applied to the centered distributions followed by a transformation into polar coordinates. Finally, only those electrons, which have the proper kinetic energy, are selected for further analysis. This is done by gating on a certain thickness of the momentum sphere of the Abel-inversed data. The resulting subset of data (intensity as function of the emission angle with respect to the light propagation axis) is treated analogous to the COLTRIMS data (see Section 2.3). Results of this reanalysis of the SSRL data from ref. 33 are shown in panel (a) of Fig. 6 by pink stars (note that the reanalysis was performed only in the relevant energy range of the present experiment). The specified uncertainties correspond to the fit error from the extraction of the β1 parameter. A subdivision of each run from the SSRL measurement into two independent data sets confirmed both, the retrieved values of the β1 parameter and the respective uncertainties. As one can see from this figure, the dichroic parameters determined in all three experiments are now consistent.
In order to find a possible reason for the disagreement between the previously computed and all measured dichroic parameters in panel (a) of Fig. 6, we cross-checked the computational results of ref. 33. First of all, we reexamined the equilibrium geometry of the molecule obtained in ref. 33 on the (2,2)-CASSCF/6-31+G(d,p) level of theory and used there in the subsequent calculations. For this purpose, we now performed its optimization with DFT methods using the B3LYP hybrid functional with a 6-311+G(d,p) basis set. The minimal-energy structure was confirmed by the absence of imaginary frequencies. It turned out that both equilibrium structures differ only negligibly and the angular distribution parameters recomputed here in the FCHF approximation basically confirm those computational results of ref. 33 (not shown here for brevity). As a next step, we recomputed the angular distribution parameters of the O 1s-photoelectrons of TFMOx using the RCHF approximation. It is known to be more accurate for core ionization than the FCHF approximation used in the previous work.33 The results of these calculations are shown in Fig. 6 by red solid curves. As one can see, the effect of the core relaxation caused by the created inner-shell vacancy does not significantly change the energy dependence of the computed angular distribution parameters, and the presently computed β1 and β2 parameters agree well with the previously computed and measured data from ref. 33 (blue dashed curve and yellow circles). For the dichroic parameter β1, which is of primary interest here, relaxation of the core has just somewhat reduced its maximal and minimal values. Possible reasons for the remaining disagreement between the theoretical and experimental dichroic parameters are discussed in Section 4.
4 Conclusions and outlook
A joint experimental and theoretical study of the photoelectron circular dichroism (PECD) of the O 1s-photoelectrons of uniaxially oriented trifluoromethyloxirane (TFMOx) has been presented. We report the differential PECD for the combined single-bond breakup channels CF3+(m/z = 69)−C2Hi=1,2,3O+(m/z = 41, 42, 43) with the loss of the trifluoromethyl group at five photoelectron kinetic energies. The differential PECD of TFMOx, measured for a photoelectron kinetic energy of 11.7 eV, is very similar to that observed in our previous work32 for an almost equal (11.5 eV) photoelectron kinetic energy of the O 1s-photoelectrons and the (conceptually) same fragmentation channel (single-bond breaking with the loss of the methyl group) of methyloxirane (MOx). The measured PECD landscapes exhibit equal signs if one compares identical S- or R-enantiomers of those two molecules which possess similar hierarchical stereo arrangement of scatterers, and opposite signs for different enantiomers which have similar geometrical structures.The molecular fragmentation axis, found theoretically for this breakup channel, does not connect the CF3+ and C2H3O+ fragments, which is a clear indication that for larger molecules, the connection between the orientation of the molecule at the instant of photoionization and the asymptotic momenta of the detected fragments have a rather intricate interconnection. Such theoretically found optimal axes of molecular fragmentation might in principle be used to estimate times for a relative rotation of the fragments during the considered breakup. The computed differential PECDs reproduce the experimental results for all photoelectron kinetic energies on a semi-quantitative level. Having rather similar landscapes, the computed and measured differential PECDs differ in their forms and maximal asymmetry strengths. As a consequence, the averaging of those rather strong asymmetries over all molecular orientations yields different small values of the theoretical and experimental dichroic parameters β1. We performed a reanalysis of the raw data from the experiment published in ref. 33 leading to a revision of some of the data points previously reported. These corrected previous experimental results agree with new results from two different experiments performed at two light sources in the present work.
Being very similar in their geometrical structures, S/R-MOx and R/S-TFMOx molecules are very different in their chemical and, thus, electronic structures. This could be a reason for a very different degrees of agreement between theory and experiment in our earlier study of MOx32 and in the present and earlier studies of TFMOx.33 Because of considerably more electrons in TFMOx, the respective calculations seem to be much more sensitive to minor details of the molecular potential, especially for slow photoelectrons. Experimentally, very different masses of constituent parts in TFMOx make an unambiguous assignment of a molecular orientation axis to a certain fragmentation channel impossible. In order to clarify the remaining disagreement between the theoretical and experimental dichroic parameters β1, the O 1s-photoionization of TFMOx needs to be reinvestigated with alternative theoretical methods (e.g., TDDFT56 or CMS-Xα57). Ref. 28 reports a comprehensive theoretical study of the photoelectron angular distributions from chiral derivatives of oxirane by the former theoretical approach (note that TFMOx was not studied there). As one can learn from Fig. 8 of ref. 28, dichroic parameters computed for O 1s-photoelectrons of all considered oxirane derivatives exhibit a clear enhancement to about 5–8% within the photoelectron kinetic energy interval of 2–8 eV, supporting our theoretical findings on TFMOx. Taking also into account the robustness of the present and previous33 calculations performed by the SC method, a reason for the remaining disagreement between the theoretical and experimental dichroic parameters β1 can lie beyond the (fixed-nuclei one-particle approximation) electronic structure calculations performed here. For instance, a presence of a shape resonance in the O 1s-photoionization of TFMOx just above the ionization threshold may reduce the accuracy of the one-particle Hartree–Fock calculations performed here. In addition, slow photoelectrons may share their chiral asymmetry with the Auger electrons via post-collision interactions (PCI) neglected in the present one-particle approach.
Author contributions
The experiment was prepared and carried out by G. N., K. F., F. T., N. A., D. T., S. G., M. K., A. K., R. T., M. H., M. W., I. V.-P., G. K., J. S., D. T., H. F., K. U., J. B. W., C. K.-W., L. M., J. V., A. K., T. J., and M. S. S. Samples were analyzed by D. K., M. M., and R. P. Data analysis was performed by G. N., K. F., M. I., and M. S. S. Theoretical calculations were performed by N. M. N. and P. V. D. Initial draft was created by G. N., K. F., R. D., P. V. D., and M. S. S. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG)-Project No. 328961117-SFB 1319 ELCH (extreme light for sensing and driving molecular chirality). This research was also undertaken as part of the ASPIRE Innovative Training Network, which has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement No. 674960. H. F. and K. U. acknowledge the XFEL Priority Strategy Program of MEXT, the Research Program of ‘Dynamic Alliance for Open Innovations Bridging Human, Environment and Materials’ and the IMRAM project for support. K. F. acknowledges support from the German National Merit Foundation. M. I. acknowledges funding of a Peter-Paul-Ewald Fellowship by the Volkswagen foundation. M. S. S. thanks the Adolf-Messer Foundation for financial support. We thank the staff of SOLEIL for running the facility and providing beamtime under project 20180746 and beamline SEXTANTS for the excellent support. We also thank the staff of PETRA III for running the facility and providing beamtime under project H-20010092 and beamline P04 for the excellent support. The work at PETRA III was supported by BMBF.References
- B. Ritchie, Theory of the angular distribution of photoelectrons ejected from optically active molecules and molecular negative ions, Phys. Rev. A, 1976, 13, 1411–1415 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Asymmetry in photoelectron emission from chiral molecules induced by circularly polarized light, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- I. Powis, Photoelectron circular dichroism in chiral molecules, Adv. Chem. Phys., 2008, 138, 267–329 CrossRef CAS.
- L. Nahon, G. A. Garcia and I. Powis, Valence shell one-photon photoelectron circular dichroism in chiral system, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 322–334 CrossRef CAS.
- S. Turchini, Conformational effects in photoelectron circular dichroism, J. Phys.: Condens. Matter, 2017, 29, 503001 CrossRef CAS.
- R. Hadidi, D. K. Bozanic, G. A. Garcia and L. Nahon, Electron Asymmetries in the photoionization of chiral molecules: Possible astrophysical implications, Adv. Phys. X, 2018, 3, 1477530 Search PubMed.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, Universality of photoelectron circular dichroism in the photoionization of chiral molecules, New J. Phys., 2016, 18, 102002 CrossRef.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Circular dichroism in the photoelectron angular distributions of camphor and fenchone from multiphoton ionization with femtosecond laser pulses, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS.
- C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, Imaging photoelectron circular dichroism of chiral molecules by femtosecond multiphoton coincidence detection, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, M. Pitzer, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. S. Schöffler, Angular streaking in strong field ionization of chiral molecules, Phys. Rev. Res., 2019, 1, 033045 CrossRef CAS.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. Schöffler, Link between photoelectron circular dichroism and fragmentation channel in strong field ionization, J. Phys. Chem. A, 2019, 123, 6491–6495 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon, M. Lebech, J.-C. Houver, D. Dowek and I. Powis, Circular dichroism in the photoelectron angular distribution from randomly oriented enantiomers of camphor, J. Chem. Phys., 2003, 119, 8781–8784 CrossRef CAS.
- L. Nahon, G. A. Garcia, C. J. Harding, E. Mikajlo and I. Powis, Determination of chiral asymmetries in the valence photoionization of camphor enantiomers by photoelectron imaging using tunable circularly polarized light, J. Chem. Phys., 2006, 125, 114309 CrossRef PubMed.
- G. A. Garcia, L. Nahon, C. J. Harding and I. Powis, Chiral signatures in angle-resolved valence photoelectron spectroscopy of pure glycidol enantiomers, Phys. Chem. Chem. Phys., 2008, 10, 1628–1639 RSC.
- G. A. Garcia, H. Soldi-Lose, L. Nahon and I. Powis, Photoelectron circular dichroism spectroscopy in an orbitally congested system: The terpene endoborneol, J. Phys. Chem. A, 2010, 114, 847–853 CrossRef CAS PubMed.
- M. Tia, B. Cunha de Miranda, S. Daly, F. Gaie-Levrel, G. A. Garcia, I. Powis and L. Nahon, Chiral asymmetry in the photoionization of gas-phase amino-acid alanine at lyman-α radiation wavelength, J. Phys. Chem. Lett., 2013, 4, 2698–2704 CrossRef CAS.
- G. A. Garcia, H. Dossmann, L. Nahon, S. Daly and I. Powis, Photoelectron circular dichroism and spectroscopy of trifluoromethyl- and methyl-oxirane: A comparative study, Phys. Chem. Chem. Phys., 2014, 16, 16214–16224 RSC.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Vibrationally induced inversion of photoelectron forward-backward asymmetry in chiral molecule photoionization by circularly polarized light, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Geneaux and I. Powis, Determination of accurate electron chiral asymmetries in fenchone and camphor in the VUV range: Sensitivity to isomerism and enantiomeric purity, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- S. Turchini, D. Catone, N. Zema, G. Contini, T. Prosperi, P. Decleva, M. Stener, F. Rondino, S. Piccirillo, K. C. Prince and M. Speranza, Conformational sensitivity in photoelectron circular dichroism of 3-methylcyclopentanone, ChemPhysChem, 2013, 14, 1723–1732 CrossRef CAS PubMed.
- L. Nahon, G. A. Garcia, H. Soldi-Lose, S. Daly and I. Powis, Effects of dimerization on the photoelectron angular distribution parameters from chiral camphor enantiomers obtained with circularly polarized vacuum-ultraviolet radiation, Phys. Rev. A, 2010, 82, 032514 CrossRef.
- S. Daly, I. Powis, G. A. Garcia, H. Soldi-Lose and L. Nahon, Photoionization of epichlorohydrin enantiomers and clusters studied with circularly polarized vacuum ultraviolet radiation, J. Chem. Phys., 2011, 134, 064306 CrossRef.
- I. Powis, C. J. Harding, G. A. Garcia and L. Nahon, A valence photoelectron imaging investigation of chiral asymmetry in the photoionization of fenchone and camphor, ChemPhysChem, 2008, 9, 475–483 CrossRef CAS PubMed.
- S. Beaulieu, A. Comby, B. Fabre, D. Descamps, A. Ferré, G. Garcia, R. Géneaux, F. Légaré, L. Nahon, S. Petit, T. Ruchon, B. Pons, V. Blanchet and Y. Mairesse, Probing ultrafast dynamics of chiral molecules using time-resolved photoelectron circular dichroism, Faraday Discuss., 2016, 194, 325–348 RSC.
- M. Ilchen, P. Schmidt, N. M. Novikovskiy, G. Hartmann, P. Rupprecht, R. N. Coffee, A. Ehresmann, A. Galler, N. Hartmann, W. Helml, Z. Huang, L. Inhester, A. A. Lutman, J. P. MacArthur, T. Maxwell, M. Meyer, V. Music, H.-D. Nuhn, T. Osipov, D. Ray, T. J. A. Wolf, S. Bari, P. Walter, Z. Li, S. Moeller, A. Knie and P. V. Demekhin, Site-specific Interrogation of an Ionic Chiral Fragment During Photolysis Using an X-ray Free-Electron Laser, Commun. Chem., 2021 Search PubMed , https://arxiv.org/abs/2012.07100.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, Relaxation dynamics in photoexcited chiral molecules studied by time-resolved photoelectron circular dichroism: toward chiral femtochemistry, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS PubMed.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Real-time determination of enantiomeric and isomeric content using photoelectron elliptical dichroism, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni, D. Di Tommaso and P. Decleva, Density functional study on the circular dichroism of photoelectron angular distribution from chiral derivatives of oxirane, J. Chem. Phys., 2004, 120, 3284–3296 CrossRef CAS.
- U. Hergenhahn, E. E. Rennie, O. Kugeler, S. Marburger, T. Lischke, I. Powis and G. A. Garcia, Photoelectron circular dichroism in core level ionization of randomly oriented pure enantiomers of the chiral molecule camphor, J. Chem. Phys., 2004, 120, 4553–4556 CrossRef CAS PubMed.
- G. Alberti, S. Turchini, G. Contini, N. Zema, T. Prosperi, S. Stranges, V. Feyer, P. Bolognesi and L. Avaldi, Dichroism in core-excited and core-ionized methyloxirane, Phys. Scr., 2008, 78, 058120 CrossRef.
- V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. Mikajlo, C. J. Harding and I. Powis, Giant chiral asymmetry in the C 1s core level photoemission from randomly oriented fenchone enantiomers, J. Phys. Chem. A, 2008, 112, 3544–3549 CrossRef CAS PubMed.
- M. Tia, M. Pitzer, G. Kastirke, J. Gatzke, H.-K. Kim, F. Trinter, J. Rist, A. Hartung, D. Trabert, J. Siebert, K. Henrichs, J. Becht, S. Zeller, H. Gassert, F. Wiegandt, R. Wallauer, A. Kuhlins, C. Schober, T. Bauer, N. Wechselberger, P. Burzynski, J. Neff, M. Weller, D. Metz, M. Kircher, M. Waitz, J. B. Williams, L. P. H. Schmidt, A. D. Müller, A. Knie, A. Hans, L. Ben Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, R. Dörner, T. Jahnke, P. V. Demekhin and M. S. Schöffler, Observation of enhanced chiral asymmetries in the inner-shell photoionization of uniaxially oriented methyloxirane enantiomers, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- M. Ilchen, G. Hartmann, P. Rupprecht, A. N. Artemyev, R. N. Coffee, Z. Li, H. Ohldag, H. Ogasawara, T. Osipov, D. Ray, P. Schmidt, T. J. A. Wolf, A. Ehresmann, S. Moeller, A. Knie and P. V. Demekhin, Emitter-site-selective photoelectron circular dichroism of trifluoromethyloxirane, Phys. Rev. A, 2017, 95, 053423 CrossRef.
- G. Hartmann, M. Ilchen, P. Schmidt, C. Küstner-Wetekam, C. Ozga, F. Scholz, J. Buck, F. Trinter, J. Viefhaus, A. Ehresmann, M. S. Schöffler, A. Knie and P. V. Demekhin, Recovery of high-energy photoelectron circular dichroism through Fano interference, Phys. Rev. Lett., 2019, 123, 043202 CrossRef CAS.
- M. Pitzer, G. Kastirke, M. Kunitski, T. Jahnke, T. Bauer, C. Goihl, F. Trinter, C. Schober, K. Henrichs, J. Becht, S. Zeller, H. Gassert, M. Waitz, A. Kuhlins, H. Sann, F. Sturm, F. Wiegandt, R. Wallauer, L. P. H. Schmidt, A. S. Johnson, M. Mazenauer, B. Spenger, S. Marquardt, S. Marquardt, H. Schmidt-Böcking, J. Stohner, R. Dörner, M. Schöffler and R. Berger, Absolute configuration from different multifragmentation pathways in light-induced coulomb explosion imaging, ChemPhysChem, 2016, 17, 2465–2472 CrossRef CAS PubMed.
- M. Pitzer, G. Kastirke, P. Burzynski, M. Weller, D. Metz, J. Neff, M. Waitz, F. Trinter, L. P. H. Schmidt, J. B. Williams, T. Jahnke, H. Schmidt-Böcking, R. Berger, R. Dörner and M. Schöffler, Stereochemical configuration and selective excitation of the chiral molecule halothane, J. Phys. B, 2016, 49, 234001 CrossRef.
- R. N. Zare, Photoejection dynamics, Mol. Photochem., 1972, 4, 1–37 CAS.
- R. L. Dubs, S. N. Dixit and V. McKoy, Circular dichroism in photoelectron angular distributions from oriented linear molecules, Phys. Rev. Lett., 1985, 54, 1249–1251 CrossRef CAS PubMed.
- T. Jahnke, T. Weber, A. L. Landers, A. Knapp, S. Schössler, J. Nickles, S. Kammer, O. Jagutzki, L. Schmidt, A. Czasch, T. Osipov, E. Arenholz, A. T. Young, R. Diez Muino, D. Rolles, F. J. Garcia de Abajo, C. S. Fadley, M. A. Van Hove, S. K. Semenov, N. A. Cherepkov, J. Rösch, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Circular dichroism in K-shell ionization from fixed-in-space CO and N2 molecules, Phys. Rev. Lett., 2002, 88, 073002 CrossRef CAS PubMed.
- A. Pier, K. Fehre, S. Grundmann, I. Vela-Perez, N. Strenger, M. Kircher, D. Tsitsonis, J. B. Williams, A. Senftleben, T. Baumert, M. S. Schöffler, P. V. Demekhin, F. Trinter, T. Jahnke and R. Dörner, Chiral photoelectron angular distributions from ionization of achiral atomic and molecular species, Phys. Rev. Res., 2020, 2, 033209 CrossRef CAS.
- R. S. Cahn, C. Ingold and V. Prelog, Spezifikation der molekularen Chiralität, Angew. Chem., Int. Ed. Engl., 1966, 5, 385–415 ( Angew. Chem. , 1966 , 78 , 413–447 ) CrossRef CAS.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Cold target recoil ion momentum spectroscopy: A ‘momentum microscope’ to view atomic collision dynamics, Phys. Rep., 2000, 330, 95–192 CrossRef.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Recoil-ion and electron momentum spectroscopy: Reaction-microscopes, Rep. Prog. Phys., 2003, 66, 1463–1545 CrossRef CAS.
- T. Jahnke, T. Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. P. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, Multicoincidence studies of photo and Auger electrons from fixed-in-space molecules using the COLTRIMS technique, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS.
- K. Fehre, M. Pitzer, F. Trinter, R. Berger, A. Schießer, H. Schmidt-Böcking, R. Dörner and M. S. Schöffler, Closed-loop recycling of rare liquid samples for gas-phase experiments, Rev. Sci. Instrum., 2021, 92, 023205 CrossRef CAS.
- R. Dörner, V. Mergel, L. Spielberger, M. Achler, K. Khayyat, T. Vogt, H. Bräuning, O. Jagutzki, T. Weber, J. Ullrich, R. Moshammer, M. Unverzagt, W. Schmitt, H. Khemliche, M. H. Prior, C. L. Cocke, J. Feagin, R. E. Olson and H. Schmidt-Böcking, Kinematically complete experiments using cold target recoil ion momentum spectroscopy, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 124, 225–231 CrossRef.
- M. S. Schöffler, T. Jahnke, J. Titze, N. Petridis, K. Cole, L. P. H. Schmidt, A. Czasch, O. Jagutzki, J. B. Williams, C. L. Cocke, T. Osipov, S. Lee, M. H. Prior, A. Belkacem, A. L. Landers, H. Schmidt-Böcking, R. Dörner and T. Weber, Matter wave optics perspective at molecular photoionization: K-shell photoionization and Auger decay of N2, New J. Phys., 2011, 13, 095013 CrossRef.
- M. S. Schöffler, C. Stuck, M. Waitz, F. Trinter, T. Jahnke, U. Lenz, M. Jones, A. Belkacem, A. L. Landers, M. S. Pindzola, C. L. Cocke, J. Colgan, A. Kheifets, I. Bray, H. Schmidt-Böcking, R. Dörner and T. Weber, Ejection of quasi-free-electron pairs from the helium-atom ground state by single-photon absorption, Phys. Rev. Lett., 2013, 111, 013003 CrossRef.
- O. Jagutzki, A. Cerezo, A. Czasch, R. Dörner, M. Hattaß, M. Huang, V. Mergel, U. Spillmann, K. Ullmann-Pfleger, T. Weber, H. Schmidt-Böcking and G. D. W. Smith, Multiple hit readout of a microchannel plate detector with a three-layer delay-line anode, IEEE Trans. Nucl. Sci., 2002, 49, 2477–2483 Search PubMed.
- K. Fehre, D. Trojanowskaja, J. Gatzke, M. Kunitski, F. Trinter, S. Zeller, L. P. H. Schmidt, J. Stohner, R. Berger, A. Czasch, O. Jagutzki, T. Jahnke, R. Dörner and M. S. Schöffler, Absolute ion detection efficiencies of microchannel plates and funnel microchannel plates for multi-coincidence detection, Rev. Sci. Instrum., 2018, 89, 045112 CrossRef CAS.
- J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, The variable polarization XUV beamline P04 at PETRA III: Optics, mechanics and their performance, Nucl. Instrum. Methods Phys. Res. A, 2013, 710, 151–154 CrossRef CAS.
- W. C. Wiley and I. H. McLaren, Time-of-flight mass spectrometer with improved resolution, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- N. A. Cherepkov, Circular dichroism of molecules in the continuous absorption region, Chem. Phys. Lett., 1982, 87, 344–348 CrossRef CAS.
- P. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, Single center method: A computational tool for ionization and electronic excitation studies of molecules, J. Chem. Phys., 2011, 134, 024113 CrossRef.
- S. A. Galitskiy, A. N. Artemyev, K. Jänkälä, B. M. Lagutin and P. V. Demekhin, Hartree-Fock calculation of the differential photoionization cross sections of small Li clusters, J. Chem. Phys., 2015, 142, 034306 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni and P. Decleva, Time-dependent density-functional theory for molecular photoionization with noniterative algorithm and multicenter B-spline basis set: CS2 and C6H6 case studies, J. Chem. Phys., 2005, 122, 234301 CrossRef CAS.
- I. Powis, Photoelectron circular dichroism of the randomly oriented chiral molecules glyceraldehyde and lactic acid, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
| This journal is © the Owner Societies 2021 |