Probing anisotropic mechanical behaviour in carbamazepine form III

Abstract

Nanoindentation measurements of the mechanical properties of the (020), (002) and (101) crystal faces in carbamazepine (CBZ) form III revealed that the (020) face had a greater elastic modulus and hardness than the (002) and (101) faces, which had similar modulus and hardness values. Atomic force microscopy (AFM) imaging of the indents showed that whilst no surface plastic displacement was observed around the residual indents on the (020) face, indents on both (002) and (101) faces nucleated cracks in multiple orientations and showed slip bands parallel to (020). The computed compliance matrix of CBZ form III was in good agreement with the experimental results and predicted anisotropic stiffness, with E₍₀₂₀₎ > E₍₀₀₂₎ > E₍₁₀₁₎. Modelling also revealed that the molecular flexibility of CBZ results in a less stiff material than that of an equivalent rigid compound. Indentation in one direction results in the opening of the CBZ-butterfly wings whilst in the other two results in their closing. Molecular dynamics simulations confirmed the primary (020) slip plane, consistent with the AFM images of the indents. It was also found that shear on the primary (020) slip plane, requires the breaking and forming of CBZ hydrogen bonded dimers. The slip plane, (020), was identified as having the lowest structural rugosity and hydrogen bonding density but not the lowest attachment energy.

---

1. Introduction

Beyond their required biological activities, active pharmaceutical ingredients (APIs) need to have appropriate further physicochemical properties that enable their development into effective drug products. For example, APIs need to have suitable aqueous solubilities and kinetics of dissolution,¹ be able to grow from solution into adequately sized crystals with good filterability² and have the required mechanical properties for tabletting. If the physical properties of an API are poor, attempts to improve them are often sought through the design of alternative solid forms such as cocrystals,³ hydrates,^4–6 or polymorphs.⁷ This approach requires the development of new solid forms often involving different chemical compositions, which may require new and costly solid form screenings together with corresponding stability studies. Another route to modify properties is through the design, addition and fine tuning of various processes used for the production of the API. For example, sonocrystallisation,⁸ temperature cycling⁹ or appropriate use of milling¹⁰ are processes shown to enable modifications of particle size and shape distributions in crystalline powders which in turn can impact their filtration behaviour^11,12 or mechanical properties.⁸

Tablets contain a mixture of crystalline powders of the API and excipients. This mixture is referred to as the formulation and the exact proportion of the powder components is usually established on a trial-and-error basis working around the mechanical behaviour of the API powders so as to achieve a powder mixture that can be tabletted. Tablets formulated directly by compacting the API in isolation (without excipients) have the advantage of being smaller, not needing the formulation step and thus being cheaper to produce. Ultimately, the mechanical properties of the material API in powder form are primarily dictated by the mechanical properties of its single crystals. In that context, the study of the mechanical properties of single crystals directly using nanoindentation^13,14 offers the opportunity to determine an API's mechanical behaviour at early stages of drug development (when the material is only available in small quantities) and to probe a number of other solid-state phenomena upon exposing the material to tabletting (i.e. stressed induce phase transformations,¹⁵ dehydration^4,16…). The early acquisition of this information would provide extra tools to influence process design and control, allowing improvements to the drug's mechanical behaviour prior to its transition to formulation and tabletting.

Molecular crystals, particularly those with low symmetry forms, are well known to be highly anisotropic, with their properties varying along different crystal axes and faces. Growth rates,² dissolution¹⁷ and mechanical properties¹⁸ are, amongst others, properties known to be face and direction dependent. Of particular interest, nanoindentation enables the evaluation of anisotropy of mechanical properties in molecular crystals, when combined with basic face indexing pre-experiments. It can probe specific crystallographic surfaces over penetration depths <1 μm and requires an exposed area of a few μm². For this, however, large single crystals (hundreds of μm for at least two dimensions) are required so that repeated measurements on different {hkl} faces are possible. Most molecular crystals only expose one perhaps two {hkl} families of faces, hence it remains very challenging to perform nanoindentation experiments along different crystal directions. Despite these difficulties, the number of reports on anisotropic mechanical behaviour in molecular crystals measured with nanoindentation has increased considerably in recent years. Examples of these include works on saccharin,¹⁹L-alanine,²⁰ sucrose,²¹ difluoroboron avobenzone,²² piroxicam¹⁵ or a series of amino-acids²³ amongst others. Nanoindentation allows for the determination of a reduced modulus E_R (related to the modulus of elasticity E_(hkl) ≈ E_R,(hkl)(1 − ν),^24–26 with ν the Poisson's ratio) and hardness H of materials.

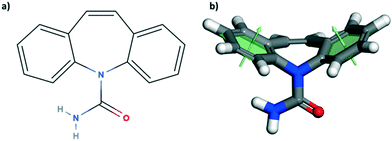
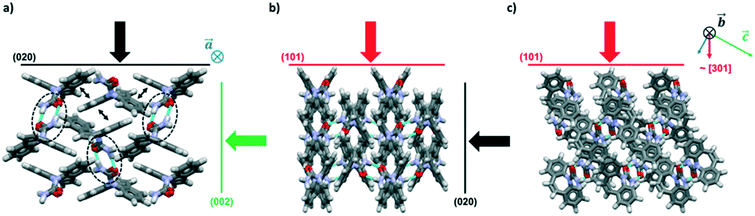
Here, we have studied the mechanical properties of carbamazepine (CBZ) form III (Fig. 1) along a number of crystallographic directions. CBZ, a drug used to treat epilepsy, has an interesting solid form landscape with five polymorphs^27–31 and a wide range of cocrystals.³² We have chosen the stable form III²⁸ for our nanoindentation studies since it readily crystallises as equant large crystals under various crystallisation conditions. Growth of appropriately sized crystals of CBZ-III from methanol allows for nanoindentation of three distinct faces: (020), (101) and (002). Nanoindentation combined with imaging analysis reveals distinct mechanical behaviour in the three directions. These experiments are supported by computer simulations to aid our understanding of plastic deformation of CBZ-III along the three directions studied. Overall, the study provides an enhanced understanding of the anisotropic mechanical behaviour in form III carbamazepine from a combined experimental and computational perspective.

Fig. 1 Molecular sketch of carbamazepine (a) and its corresponding 3-dimensional model representation (b). The two benzene rings form an angle of 130.7° (angle measured between the two green arrows, each orthogonal to the best fit plane of the corresponding ring).

2. Experimental section

Sample preparation

Slurries of carbamazepine in methanol (anhydrous, 99.8%, Sigma Aldrich) were heated to 40 °C. Solutions were then filtered and transferred into petri dishes which were left to cool (naturally from 40 °C to room temperature, ∼21 °C) and slowly evaporate under ambient conditions over 48 to 96 hours. The harvesting of the CBZ-III single crystals from their mother liquor was performed as follows. Due to the very high solubility of CBZ in methanol, a layer of hexane (HPLC, >95%, Fisher Chemical) was poured gently on top of the methanolic solution. The two solvents being immiscible, it allowed for the removal of the saturated solution from the crystals' surface while harvesting them with tweezers from solution, preventing secondary nucleation. Handling of crystals was always done with the aid of PEEK tweezers. Crystals retained for the nanoindentation experiments had dimensions of 0.5 × 0.5 × 0.25 mm, or larger. After face identifications, crystals were glued in the correct orientation using cyanoacrylate glue.

Face indexing

Representative single crystals of CBZ-III grown from methanol were face indexed by means of a goniometer mounted on a single crystal X-ray diffractometer (XCalibur-2, Rigaku Oxford Diffraction) with a MoKα X-ray source (λ = 0.71073 Å). Photographs of the single crystals were taken before each X-ray diffraction measurement (whilst rotating the crystals) and were used for subsequent face indexing. The unit cell parameters and the space group were determined and verified to match those of CBZ-III as reported in the Cambridge Structural Database³³ (CSD) refcode CBMZPN02.²⁸ Thus, the Miller indices used throughout the manuscript refer specifically to the unit cell parameters defined in this refcode. Indexing of the faces was carried out using the software CrysAlisPro (v. 171.40.14d, Rigaku Oxford Diffraction).³⁴

Nanoindentation

Experiments were carried out using a TI 950 Triboindenter (Bruker Nanomechanical Test Instruments, Minneapolis, USA) equipped with a diamond Berkovich probe. Indents were carried out on selected single crystals whose crystal shape clearly matched those identified during face indexing. Indentations were conducted under load-control mode using a unique trapezoid load function which is presented in the ESI.† Crystals of carbamazepine were large enough to allow for them to be firmly glued on a glass slide prior to the indentation experiments. 10 crystals were indented per crystal face tested, 9 indents were carried out per crystal and the distance between individual indents was set to 20 μm. Reduced modulus and hardness were extracted from the indentation curves as stated in ISO 14577.³⁵ Calibration of the tip was made using a PS-1 sheet sample (E_R = 2.91 GPa, VPG Micro-measurements, Malvern, USA), which was indented in between each single crystal tested to verify for possible tip contamination and calibration errors. As previously described in detail,¹⁴ prior to indentation we investigated the optimal maximum displacement, load rate and holding times which were fixed to 5 second load, 2 second hold and 5 seconds unload segments. The maximum load P_Max used was fixed to 3 mN as no further changes in the values of E_R and H were observed for higher loads.¹⁴

Imaging

Crossed polarised light was used to identify single crystals of good quality using an Axioplan2 Zeiss Microscope in transmission mode. Imaging of the indents was carried out using an atomic force microscope (AFM, Multimode8, Bruker), using PeakForce QNM in Air mode, with a TESP-V2 probe (k = 42 N m⁻¹).

Computation

All simulations were done with Materials Studio 2019 (ref. 36) using the COMPASS-II³⁷ forcefield with its own atomic charges, known to be a reliable forcefield for the simulation of molecular crystals.³⁸ Energy values of all simulations were converted to kJ mol⁻¹ and reported per molecule of CBZ.

Structure retrieval, geometry optimisation and attachment energy calculations. The crystal structure of CBZ form III (CBMZPN02) was retrieved from the CSD. Using the Forcite module, the crystal structure was geometry optimised allowing all atomic positions to relax while keeping the unit cell parameters constant to the observed room temperature unit cell parameters. The COMPASS-II optimised structure served as the initial model for the rest of the computations. Attachment energy calculations were then computed with the same model.

Simulation of compression. CBZ unit-cell parameters were compressed progressively in three different crystallographic directions. CBZ-III compressed cells were then geometry optimised with fixed unit cell parameters in two sets of simulations: treating the molecules as flexible and rigid. For the compressions, the required unit cell axis (or axes) was progressively reduced by 0.05 Å from its original experimental value whilst keeping the other cell axes constant, until the corresponding lattice energy became positive. The axes compressed were the b-axis, the c-axis and both the a and c-axis together to simulate compression upon indentation on the (020), (002) and (101) faces respectively.

Molecular dynamics (MD). Slip planes and slip directions of CBZ-III were studied by means of shearing MD simulations. Supercells of 96 molecules of CBZ-III were generated from the relaxed unit cell. A MD run at 298 K was first performed for 50 ps in the NVT ensemble to allow for the system to equilibrate. The system was then run for a further 50 ps in the NPT ensemble. Shearing simulations were then carried out in different directions (see ESI† and Results section) at 298 K using constant shearing rates of 5.10⁻⁴ ps⁻¹ for 1500 ps (NVT). Two simulations were done per shearing direction whereby the shear force was applied along one of the supercell axes, maintaining one of the two planes containing the sheared axis constant.

Mechanical properties. After the 50 ps-NVT and 50 ps-NPT MD equilibration runs, the resulting supercell was run for an additional 500 ps-NPT at 298 K. Every 5 ps, a series of strains were applied to the simulation cell. The stiffness and compliance matrices were then computed using the constant strain method. The components of the final stiffness and compliance matrices are averages of the entire simulation run. The Young's modulus was then computed in 3D and projected onto the (100), (010) and (001) planes using the ElAM computer program³⁹ and the values along the desired directions retrieved and presented in 2D plots in the Results section. Poisson ratios were also extracted from such simulations.

Surface rugosities. Surface rugosities were calculated for a number of (hkl) faces using the Bryant et al. method⁴⁰ as implemented in the CSD Python API.³³ Positive values indicate separation between planes in Å whilst negative values indicate layer intercalation.

3. Results

3.1. Experimental results

3.1.1. CBZ-III crystal habit, face indexing and crystal structure. Thick crystals of CBZ form III were obtained from methanol. Fig. 2 shows the face indexing of a representative single crystal. From methanol, CBZ-III exhibits a large dominant (020) face and, however less significant, still large (002) and (101) lateral faces. When viewed under the optical microscope, the shape of these two latter faces were identical. Hence to identify each face with certainty prior to sample mounting for indentation, the angle between the inclined top section of the crystal and the (002) and (101) faces were measured under the microscope and compared with the crystallographic data (Fig. 2, face indexing). The angles between the faces measured from the micrographs of 23 different crystals were 116.4° ± 0.8 and 123.4° ± 1.2, in excellent agreement with the theoretical crystallographic values. The dominance of the (020) face was further confirmed by preferential orientation powder-X-ray diffraction (PXRD, ESI†).

Fig. 2 Micrographs of a single crystal of CBZ form III grown from methanol, with its associated face indexing.

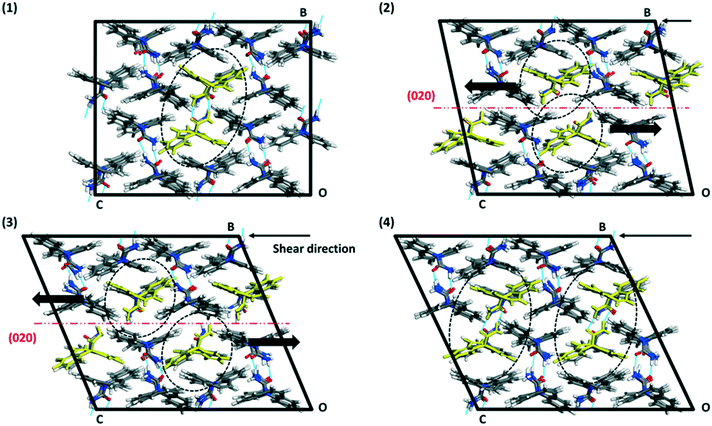
The crystal packing of CBZ-III along the three directions indented is presented in Fig. 3. Hydrogen bonded dimers (R²₂(8) amide⋯amide) and aromatic interactions are highlighted in Fig. 3a (black dashed circles and black arrows respectively). The lattice energy of CBZ-III U_LATT was calculated to be −145.6 kJ mol⁻¹ with contributions of around 20% of electrostatic interactions and 80% of van der Waals interactions (see ESI†). Dimers are oriented very closely along [010] (Fig. 3a) whilst van der Waals interactions are dominated mostly from the aromatic interactions between neighbouring aromatic rings of CBZ.

Fig. 3 Packing views of CBZ-III (CBMZPN02) along three directions (a–c) with indentation directions orthogonal to the three main indexed faces indicated as black, green and red arrows. Hydrogen bonded dimers are indicated in (a) with black dashed circles and aromatic interactions via small black double headed arrows.

3.1.2. Nanoindentation experiments. Crystals were mounted and indented on their three dominant faces (020), (002) and (101). Thirty crystals were mounted, ten on each of the faces. Fig. 4 shows one typical load-depth curve for each face indented. In all curves, multiple small bursts occurred upon loading (commonly referred to as “pop-ins”). The intensity of pop-ins observed on the loading section of nanoindentation experiments of molecular single crystals have been correlated with relevant crystallographic parameters such as specific d_hkl values or particular unit cell lengths by other groups.^19,41,42 We attempted to establish a similar correlation for carbamazepine, with no success (analysis presented in ESI†). The maximum depth of penetration h_Max reached is lower for the (020) faces compared to the (002) and (101) faces (Fig. 4).

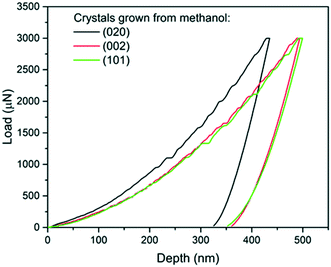Fig. 4 Load-depth curves from indentation carried out on a (020), a (101) and a (002) face of single crystals of carbamazepine form III crystals.

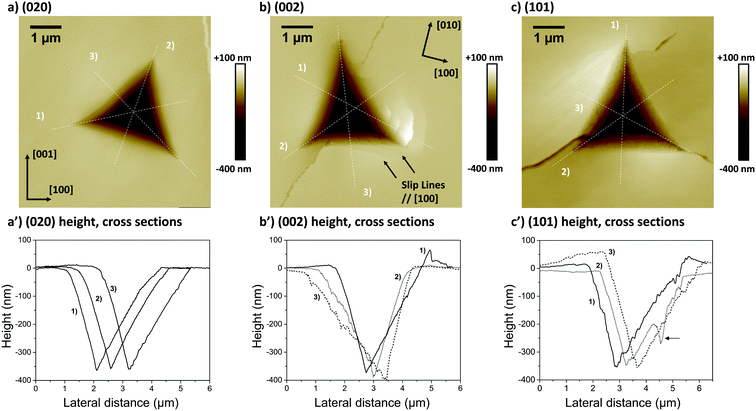
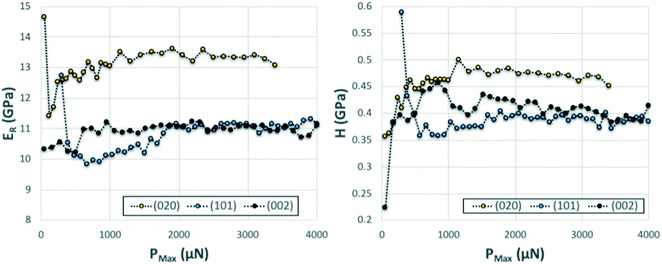
The associated averages and standard deviations of E_R and H obtained from these nanoindentation experiments are given in Table 1, whilst associated histograms of these datasets are presented in ESI.† The reduced modulus measured on the (020) faces is higher than those measured on the (002) and (101) by 26% and 29% respectively. Similarly, the hardness measured on the (020) face is higher than that of the two other faces, with an increase of approximately 20%. Differences between the (002) and (101) faces are less prominent and overall averages of both E_R and H on these faces are extremely similar.

Table 1 Absolute mechanical property values extracted from the indentation of three different faces of carbamazepine form III (crystals grown from methanol). Each value given is the mean value with the associated standard deviation of data acquired on 90 indents performed on 10 crystals (9 indents/crystal)

Face	E R ± stdv (GPa)	H ± stdv (MPa)
(020)	13.87 ± 0.26	470 ± 17
(002)	11.01 ± 0.22	396 ± 13
(101)	10.74 ± 0.28	394 ± 17

---

3.1.3. Imaging of indents. Atomic force microscopy (AFM) was carried out on a number of indents in order to assess the degree of plastic deformation around the indents. Images revealed that the three surfaces responded very differently upon indentation. A typical image of an indent on the hardest (020) surface in Fig. 5a shows the indent is well defined as a near-perfect equilateral triangle. No pile-ups, sink-ins or cracks were observed around indent edges. However, in Fig. 4, the load-depth trace of an indent carried out on the (020) face clearly contains pop-ins, which cannot be visually related to the formation of radial cracks because none were observed in Fig. 5a. These pop-ins are probably related to plastic deformation through dislocation nucleation, these dislocations propagate into the material to accommodate the volume displaced to generate the indent. Fig. 5a′ shows cross sections of the height map in Fig. 5a. Such sections are very smooth confirming the absence of surface pile up around an indent, often seen with the indentation of ductile materials.

Fig. 5 AFM height images of indents carried out on (a) a (020) face, (b) a (002) face and (c) a (101) face of distinct CBZ-III single crystals. Nanoscope analysis 1.8 was used to assess three height cross sections associated with each indent (a′–c′), with each cross section labelled 1 to 3. In (b) and (b′), cross section 1 was assessed slightly shifted off the centre of the indent to allow for better visualisation of the pile-up. The arrow in c′ indicates a crack.

The second and third AFM images (Fig. 5b and c) show indents carried out on the softer (002) and (101) faces respectively. Plastic deformations of several nature are observed in both cases with evidence of slips, radial cracks, small pile-ups and sink-ins. On the (002) face, slip lines run along [100] and individual cracks propagate along a direction close to (but not quite) [010] with cracks having a zig-zag shape. On the (101) face, similar deformation features are observed, however it was not possible to unequivocally determine the direction of the slip bands and radial cracks. We note that cracks on the (101) face also propagated alternatively along two directions, as seen in Fig. 5c. The presence of small pile-ups and sink-ins along some indent edges is visible in the cross-sections shown in Fig. 5b′ and c′. Such dramatic differences in the plastic response of CBZ crystals across different crystallographic faces are consistent with the differences in the values of E_R and H in Table 1.

We note that whilst indentation of the (002) and (101) faces resulted in cracks at the working P_Max of 3000 μN (which may result in an artificial reduction of the derived stiffness or hardness),^43,44 we did not observe a significant impact of these cracks on the resulting E_R or H values calculated at different maximum loads (Fig. 6). If cracks were to have a significant effect on these derived values, an increase in load should result in more cracks and thus a significant lowering of the calculated E_R and H values. As discussed previously,¹⁴ the maximum load P_Max used in nanoindentation measurements needs to be above a minimum value below which the data becomes inconsistent due to calibration issues. In this case, the plateau for acquisition of consistent data is reached in all three faces at around 2000 μN. At loads above 2000 μN, the derived values of E_R and H as a function of maximum load remain constant within the expected experimental variability for these measurements. For example at P_Max of 3000 μN, the derived mean E_R value for the (101) face on 90 independent indents on 9 different crystals is 10.74 GPa with a measured maximum and minimum values of 10.25 and 11.45 GPa respectively (ESI†). Similarly, the derived mean H value for the (101) face on 90 independent indents on 9 different crystals is 394 MPa with a measured maximum and minimum values of 359 and 428 MPa respectively. All measurements of E_R and H on P_Max values above 2000 μN (Fig. 6) lie within these ranges. This suggests that cracking, in this case, has little impact on the derived stiffness and hardness values. We also note that since the pile-ups and sink-ins observed in the (002) and (101) indents were small, no corrections were applied to the indentation area calculations.

Fig. 6 Series of nanoindentation measurements carried out with increasing P_Max on three single crystals of CBZ oriented along the three different crystal directions. The derived E_R (left) and H (right) as a function of P_Max appear fairly constant across the entire range tested.

3.2. Computational results

3.2.1. Elasticity. We calculated the elastic properties of CBZ-III using the COMPASS-II forcefield as implemented in Materials Studio. Calculations were made twice: 1) with the unit cell parameters set to room temperature values (embedded in the refcode CBMZPN02): RT-computed and 2) optimising them (≈ optimisation at 0 K): 0 K-computed. These results were obtained from the computed matrix of elastic compliance constants (presented in ESI†).³⁹ An average of both was also calculated and results along the indentation directions are shown in Table 2. We note that the RT-computed data are ≈20% below the experiment values whilst the 0 K-computed data are ≈20% above. The average computed values of Young's modulus E, however, match very well those measured experimentally. These were calculated from experimental reduced moduli E_R using the computed Poisson's ratio ν for each associated compressed direction (averaged in a similar way over both “0 K” and “RT” computed data). All values are given in Table 2.

Table 2 Experimental and computed Young's modulus as a function of the plane and hence direction of indentation of CBZ-III. Computed values are given for different set ups, including with (E_COMP-RT) and without (E_COMP-0K) optimising the unit cell parameters, as well as an average of both (E_COMP-AVG). Computed values of Poisson's ratios ν (0 K-RT averaged) for the corresponding compressed directions are also given

Plane indented	E EXP (GPa)	E COMP-RT (GPa)	E COMP-0K (GPa)	E COMP-AVG (GPa)	Poisson's ratio ν
(020)	13.16 ± 0.24	10.22	15.32	12.77	0.25
(002)	10.37 ± 0.20	7.42	12.35	9.89	0.26
(101)	9.59 ± 0.25	7.94	10.24	9.09	0.34

---

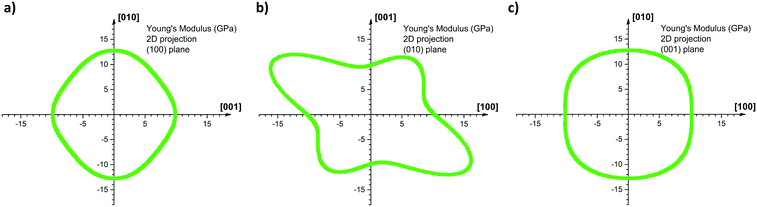
Fig. 7 shows the 2D projection of the “averaged-E” matrix on the (100), (010) and (001) planes, in which the distance of each data point from the centre of the graph corresponds to the absolute value of E computed for a given crystallographic direction. The highest computed value read is 19.0 GPa along [−302] and the lowest is 9.1 GPa along the [301] as shown in Fig. 7b. If we define here the anisotropy ratio (AR) as the ratio of the largest over the smallest value of a property, hence, for the Young's modulus, AR_COMP-AVG = 2.1. From Fig. 7a, we can extract E_Z = E₍₀₀₂₎ = 9.9 GPa and E_Y = E₍₀₂₀₎ = 12.8 GPa, thus the calculations confirm that E₍₀₀₂₎ < E₍₀₂₀₎ as observed experimentally. Moreover, the computed value for the direction normal to (101) (i.e. direction of indentation, ≈[301] as explained in ESI†) can be read in Fig. 7b as E₍₁₀₁₎ = 9.1 GPa. Again, E₍₁₀₁₎ < E₍₀₂₀₎ whilst E₍₁₀₁₎ is slightly lower in value than E₍₀₀₂₎ as observed experimentally. We note that the computed values for E are close to the measured values and predict the correct anisotropy of mechanical behaviour in CBZ-III, which is encouraging given the simplicity of the model (a classic COMPASS-II forcefield).

Fig. 7 2D projections of the computed Young's modulus onto the (a) (100) plane (b) (010) plane and (c) (001) plane. The intensity of the modulus is determined as the distance of the curve from the origin of the graph. For example, the computed Young's modulus along the c-axis is directly read E_Z = 9.9 GPa on the horizontal axis, graph (a), and on the vertical axis, graph (b), whereas along the b-axis E_Y = 12.8 GPa as read on vertical axis, graphs (a) and (c). Anisotropy is particularly marked on the (010) 2D projection, where the highest read Young's modulus is 19.0 GPa and the lowest is 9.1 GPa.

3.2.2. Molecular flexibility. As seen in Fig. 1b, CBZ molecules have a butterfly like shape with the two aromatic rings (butterfly wings) found in its form III at an angle θ₀ = 130.7°. Simulations of the deformation of the CBZ crystal structure along the three nanoindentation directions were carried out to study the influence of molecular shape on mechanical properties (Fig. 8a). Upon compression along [010], [001] or [301] directions (directions of indentation), intramolecular and intermolecular bonds will deform elastically prior to plastic deformation. Fig. 8b shows how the lattice energy U_LATT increases upon such compressions as a function of relative volume reduction (V/V₀ where V₀ is the volume of the uncompressed cell). The compression simulations were carried out in two ways: treating CBZ molecules either as rigid (dashed lines Fig. 8b) or flexible (solid lines Fig. 8b). For any value of relative volume V/V₀, U_LATT is seen to be lower for the compressions with the flexible molecule assumption, hence the system is more stable. In Fig. 8c, the deformation of the “wings” in the molecule is shown by displaying the change in angle between these two rings upon compression (using V/V₀ as the measure) along three indentation directions. The molecular deformation along the three directions is very different with compression along the [010] axis resulting in the opening of the butterfly wings (θ₁ > θ₀), whilst compression along the [001] and [301] directions resulting in their closing (θ₁ < θ₀).

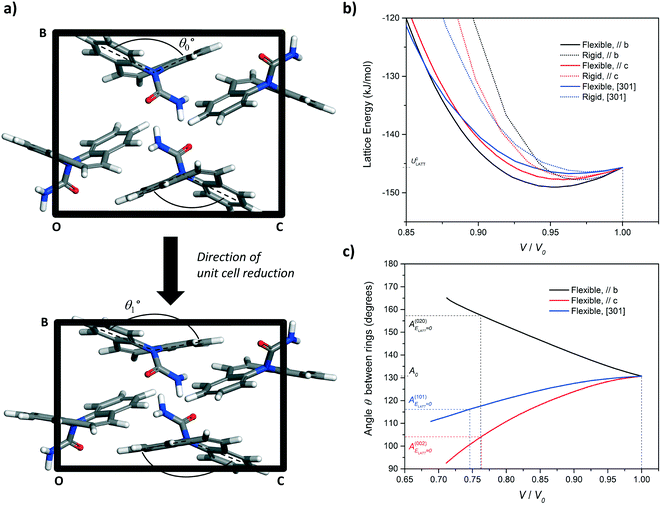Fig. 8 (a) Simulation of unit cell compression via a progressive reduction of the b-axis of CBZ-III. The evolution of the angle made by the two benzene rings of the CBZ molecule (Fig. 1) was monitored as a function of the unit-cell volume reduction. (b) Evolution of the lattice energy and (c) the butterfly wing angle as a function of unit cell compression along the [010], [001], and [301] directions for CBZ-III. Solid lines and dashed lines correspond to simulations treating the CBZ molecules as flexible and rigid respectively.

In Fig. 8b, the lattice energy functions can be conveniently fitted to a second order polynomial function. The modulus of elasticity along a crystal direction is theoretically proportional to the second derivative of the corresponding function, when assessed at U_LATT = U_LATT,MIN. Full details of the equation linking E and U_LATT, obtained for these derivatives, including numerical values and statistical measures of fit, are reported in ESI.† Here, we draw one simple conclusion: the second derivative is always lower for the potential energy functions of flexible molecules as compared to those for rigid molecules, which indicates that flexibility makes the material less stiff in CBZ-III.

3.2.3. Shear deformation. Given the difficulty in determining the (hkl) indices of the slip planes from analysis of the specimen surfaces after indentation of the faces, simulations of shear deformation of the crystals were performed to identify the influence of crystal structure on slip. The slip behaviour of planes in CBZ-III was computed by carrying out shearing simulations on supercells of 96 molecules. Extended details of the method are presented in the ESI.† For each indentation plane, two shearing simulations were performed, and for each simulation, pure shear was applied along the indentation direction, whilst keeping one plane fixed (which contains that direction) at one end of the simulation box whilst shearing it at the other end of the box. Thus, for example, for the indentation of the (002) plane, shearing along the [001] was studied in two simulations: i) fixing the (010) plane at one end of the box whilst shearing it at the other, and ii) fixing the (100) plane at one end of the box whilst shearing it at the other. The first of such simulations is shown in Fig. 9 which results in the shear of the (020) plane. Thus, the simulation reveals which plane will shear upon applying a shear force on the studied nanoindentation directions. An interesting result here is the sequential slip of the (020) plane, with slips occurring by a third of the c-unit cell length at a time (∼4.6 Å, this sequence is illustrated in Fig. 9). The first slip results in the breaking of CBZ⋯CBZ hydrogen bonded dimers (amide⋯amide R²₂(8) hydrogen bonds). Two further slipping bursts result in reformation of the dimers. This could possibly be interpreted as indicating that the slip mechanism occurs by a sequence of partial dislocations.

Fig. 9 Illustration of the (020) slip process from the [001] MD-shearing simulation of a 2 × 2 × 2 supercell keeping the (010) plane fix at one end of the box. The system was equilibrated at 298 K with MD prior to the shearing simulation. (1) Initial state simulation box. (2), (3) and (4) show the supercell at different simulation times (550 ps, 860 ps and 970 ps respectively), where two successive (020) planes are moving in opposite directions, here [001] and [00−1], in a stepped fashion. Intermolecular hydrogen bonds are shown as blue lines between molecules.

The results from the shearing simulations are presented in Table 3. At least one slip event occurred over the 1500 ps simulation time along the (020) plane in four simulations, which include all three indented faces. A single simulation showed slip along the (002) plane. One of the simulations showed no slip events prior to structural collapse (loss of long-range order in the supercell). Slip events are abrupt, occurring over a short time <10 ps. It is notable that only two simulations revealed repeating slip events (simulations 3 and 6, Table 3), indicating (020) is the most likely slip plane. These simulations only show repetitive crystal slips when indentation is carried out on the (002) or (101) face. We further note that the intensity of the shear (distance made by the (020)-molecules per slip event) is not an integer of a unit cell axis (1/3 of c-axis ∼4.6 Å, 1/4 of [301], indicating metastable intermediate states for a full slip to occur – partial dislocations).

Table 3 Results of molecular dynamics shearing simulations, including three shearing directions and two planes sheared per shearing direction, on the crystallographic planes indented. When slip was observed, the plane and the direction along which it was observed is reported

Indented face	Indenting/shear direction	Simulation number	Simulation static plane	Slip plane	Intensity × [direction] of slip	Comments
(020)	[010]	1	(100)	(020)	1 × [100]	One slip event, eventually collapse
		2	(001)	(020)	K × [001], K = 1/3	One slip event, eventually collapse
(002)	[001]	3	(010)	(020)	K × [001], K = 1/3	Repetition slip events over entire simulation
		4	(100)	(002)	[100]	One slip event, eventually collapse
(101)	[301]	5	(−103)	—	—	No slip, the system ends collapsing
		6	(010)	(020)	K × [301], K = 1/4	Repetitive slip events over entire simulation

---

3.2.4. Rugosity, attachment energy and periodic bond chains. There are, today, simple computational approaches available to predict mechanical behaviour of molecular crystals, and in particular to identify potential slip planes.⁴⁵ Initially, the energy of attachment U_ATT was used to predict weak planes along which slip systems can be most easily activated as it is proportional to the energy required to slice one (hkl) plane, but this hypothesis had limited success.⁴⁶ A second approach, developed by Bryant and co-workers,⁴⁰ is to compute the rugosity and the degree of interpenetration between the main crystallographic planes, assuming that slip is easier along low rugosity planes. Here the rugosity parameter is positive if the planes are not interlocked, thus indicating separation between the planes, and negative if the planes are interlocked. A third approach is to compute the energy between molecules in the crystals to reveal periodic bond chains (PBCs) also known as energy frameworks.^47,48 Bonds of different strengths are represented as tubes between the centroid of molecules within a supercell, revealing the strength and dimensionality of intermolecular interactions. Materials Studio with the forcefield COMPASS-II was used here to compute the three predictors in CBZ-III, the results are shown in Table 4 and Fig. 10.

Table 4 Family of planes in CBZ-III, their corresponding energy of attachment and their associated rugosity. We note that rugosity values reported here correspond to one (hkl) layer, whilst Bryant et al. report it for two consecutive layers⁴⁰

Family	U ATT (kJ mol^−1)	Rugosity (Å)
{020}	−83.4	+0.09
{200}	−122.9	−2.20
{002}	−71.2	−3.10
{011}	−64.2	−0.33
{101}	−87.2	−2.93
{101̄}	−78.1	+0.08

---

Fig. 10 PBCs defining the 3D energy framework of the crystal structure of CBZ-III (energy cut-off = −20 kJ mol⁻¹). Blue tubes indicate strongly stabilising, 0-dimensional hydrogen bonds (∼−47.4 kJ mol⁻¹) whilst purple and red tubes are mainly aromatic interactions, less stabilising but extending in 3D over the entire superlattice (purple tubes: ∼−39.3 kJ mol⁻¹, red tubes: ∼−26.2 kJ mol⁻¹, tubes parallel to the a-axis: ∼−20.6 kJ mol⁻¹).

One may state that the (011) plane is the most likely slip plane based on attachment energy computations or that the (020) and the (101̄) planes are the most likely slip planes based on the surface rugosities (these are the smoothest surfaces). Table 4 shows thus that the rugosity predictor seems to be in agreement with the experimental observations and the MD-shear simulations for the (020) face, however it shows that the attachment energy model fails.

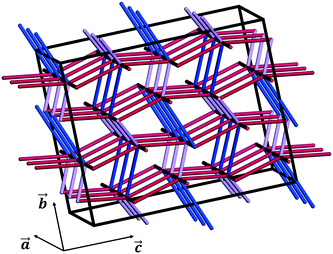
We note that these are simple predictive tools and should be used with care. In Fig. 10, PBCs in CBZ-III are shown in a 3 × 2 × 2 supercell (only interactions that are more stabilising than −20 kJ mol⁻¹ shown). This reveals a 3D network in CBZ-III, made up of hydrogen bonds (blue tubes) corrugated with aromatic interactions of various strengths (purple and red tubes). Such 3D-network materials have been reported to i) exhibit brittle mechanical responses⁴⁷ and ii) possess higher mechanical properties than their 2D counterparts.⁴⁹ Concerning this latter point, values reported in Table 1 are significantly higher than those reported for smaller 2D-network molecules such as in benzoic acid derivatives, even if systems with higher mean molecular volumes like carbamazepine should have reduced mechanical properties.⁴⁹

4. Discussion

We have studied CBZ-III experimentally with nanoindentation and have interpreted its mechanical behaviour using a number of simulation methods using the COMPASS-II forcefield. For the experimentation, we note that appropriate crystal growth is needed to obtain morphologies allowing nanoindentation of multiple crystal faces and thus assessment of the mechanical properties along independent directions for this system. Here, we found that growth from methanol provided a suitable chunky block morphology allowing indentation on three distinct faces.

For the computations, since calculations of mechanical properties (i.e. stiffness matrix) require the computation of the second derivatives of the system forces, the model describing the force/potential needs to be very accurate. A very accurate method based on DFT-d, however, would require of significant computational time and would not allow for MD or shearing simulations involving supercell models. It is thus challenging to find an accurate method that is also affordable computationally for the prediction of mechanical properties in molecular crystals.⁴⁵ Here the COMPASS-II model seemed to perform relatively well when both results – with and without unit cell parameter optimisation – of E were averaged. Further to this, the model allowed for the PBC calculations which revealed that CBZ-III is made of strong 3D continuous interactions (absolute values higher than 20 kJ mol⁻¹), so the material was expected to be harder than other comparable 2D or 1D interacting systems, and the identification of soft/slip planes was thus more complex. We also used this model to gain insights as to the mechanisms of inter and intra molecular deformations upon compression. Whilst there are a number of studies looking at the impact of intermolecular interactions on the mechanical properties of molecular crystals, to the best of our knowledge this is the first study which has studied the contribution of molecular flexibility.

Combining the simulation results and experimental data, we can assess the extent of anisotropy of the mechanical properties in CBZ-III in various ways. We extend here the definition of the anisotropy ratio (AR) as the ratio of the largest value of a property over the smallest for values measured/computed in a number of directions (i.e. E_MAX/E_MIN or H_MAX/H_MIN). A large AR would indicate a highly anisotropic behaviour whilst an AR = 1 would indicate a perfectly isotropic material. CBZ-III crystals had experimental AR values for E and H equal to 1.3 and 1.2 respectively (using data from Table 1). These AR values are in good agreement with typical AR results measured experimentally and reported in the literature. In molecular crystals, these ARs range from 1 to ∼2 for Young's modulus and from 1 to ∼1.6 for hardness.⁵⁰ From this, CBZ-III appears to be at the middle-lower end range of ARs for molecular crystals. For comparison, in crystalline metals ARs of the Young's modulus were reported to range from 1.12 (magnesium) to 3.42 (zinc).⁵¹

The anisotropy in mechanical behaviour was also manifest through the imaging of the indents on the three different crystal faces studied. This revealed that, upon indentation of the (020) face, neither significant surface displacement around the indent nor cracking was seen. However, indents on both the (002) and the (101) faces clearly displayed small material pile-up, slip traces and cracks. Our E_R values calculated at different P_Max and depth of penetrations (Fig. 6) show that for this system, the cracking seems to have no or little impact on the derived mechanical properties. This is also corroborated in the computations of E: the predicted stiffness for the studied faces match well the experimentally derived values. Interestingly, the faces that showed some degree of cracking, (002) and (101), were softer than the face that did not show cracking, (020). Normally, brittle faces are expected to be harder but we observed the opposite behaviour for CBZ-III.

It was difficult to accurately identify the slip planes from the images of the slip traces but, with the aid of simulations, these could unequivocally be assigned to the (020) planes. This result is surprising because i) the slip of (020) (Fig. 3a) requires of the breakage of hydrogen bonds and ii) (020) does not have the lowest energy of attachment (three other planes have a lower U_ATT). However, the associated rugosity of (020) predicts the highest probability of slip amongst the potential slip planes computed (Fig. 9). Hence, in this case it seems that interplanar rugosity is the most significant predictor of the primary slip plane.

To enable the slip of planes with negative rugosities, one can think of two alternatives. First, a large and local increase of the interplanar spacing d_hkl (repulsive intermolecular interactions) would make the rugosity positive, enabling a slip or possibly a crack. A second option would require the modification of molecular flexibility (angles between intramolecular bonds, for example θ₁ in Fig. 8) upon external stress in such a manner that a negative rugosity becomes positive. Both alternatives would probably require significantly more energy than that required to break the hydrogen bonds between two (020) planes. We note that the three options discussed (slicing and slip of planes with positive rugosity, local enlargement of d_hkl or modification of angles between intramolecular bonds) all require energy. To correctly identify slip planes in molecular systems, the challenge would be hence to quantify which one is the most favourable energetically. The shearing experiments do indeed predict easiest slip on the (020) plane even upon indentation of the (020) plane. This again confirms this plane contains the easiest/lowest energy deformation mechanism. However, upon indentation of (020), the (020) slip must be partly hindered because (020) is orthogonal to the indentation (shearing) direction, leading to higher values of hardness in this direction than in the other two. We note that the shearing simulations only afforded one slip event on the (020) simulations whilst several events occurred on the other faces for simulations of the same length of time.

Coming back to the rugosity calculations, planes with similar rugosities can indeed behave differently. For example, the rugosity calculations show that whilst (020) and (−101) faces have similar rugosities (+0.09 and +0.08 Å repectively), only the (020) plane serves as a slip plane as shown by the MD simulations. Here, the hydrogen bonds that need breaking for this slip to occur are important. In previous works, the breaking of hydrogen bonds has been acknowledged as playing an inhibitting role in slippage but it has not been quantified.⁴⁰ Here, we propose the calculation of what we define as the (hkl) plane hydrogen bond density (HB-density-(hkl)). For this, a 2D-unit cell on the plausible slip plane under consideration is calculated by identifying the shortest translations along two perpendicular directions to the plane direction. This is, crystallographically speaking, the 2D-unit cell on the plane of interest. The number of HBs that need breaking in this area for the plane to slip are then counted and the HB-density (number of bonds per unit of area) is calculated. Table 5 presents the rugosity data together with the HB-density for the most important planes. When seen together then, the combination of low rugosity (flat surface) and low HB-density-{hkl} (less energy required to break the HBs during slippage) does indeed unambigously reveal the (020) plane as the most likely slip plane in agreement with the MD simulations.

Table 5 Family of planes in CBZ-III, their corresponding rugosity, plane unit cell dimensions, number of hydrogen bonds in the plane unit cell and the resulting HB-density. We note that rugosity values reported here correspond to one (hkl) layer, whilst Bryant et al. report it for two consecutive layers⁴⁰

Slip plane family	Rugosity (Å)	Plane 2D unit cell dimensions (Å × Å)	Number of HBs in 2D unit cell	HB-density-{hkl} (−/Å^2)
{020}	+0.09	7.5 × 13.9	2	0.019
{−101}	+0.08	15.4 × 11.5	4	0.023
{011}	−0.33	7.5 × 17.8	4	0.029
(200)	−2.20	—	0	0.000
(101)	−2.93	—	0	0.000
(002)	−3.10	—	0	0.000

---

The simulation of unit cell compression also demonstrated that molecular deformation of CBZ is markedly different, depending on the deformation orientation. Compression of the hardest face, (020), leads to an opening of the CBZ butterfly wings whilst compression of the softer faces results in their closing. In both cases, this flexibility results in a softer material than that of an equivalent rigid molecule (Fig. 6b and ESI†).

Finally, we note that whilst this is the first study of mechanical behaviour in CBZ-III single crystals upon nanoindentation, previous works by Rowe and Roberts reported the mechanical properties of CBZ-III powder compacts with different levels of porosities. However measured on powder compacts, they reported a value of 13.2 GPa for the Young's modulus of CBZ-III.^52,53 Their reported value is close to those we obtained using nanoindentation on different faces.

5. Concluding remarks

The large size of crystals obtained by crystallising carbamazepine form III from methanol enabled nanoindentation testing along more than one crystal orientation. Nanoindentation showed that the (020) face of CBZ-III is stiffer and harder than the two other faces tested, (002) and (101). Imaging the indents using AFM revealed different plastic deformation processes between the (020) face and the (002) and (101) faces, with slip lines observed parallel to (020). On the surface around the indents performed on (020), there is no resolvable features or cracking that could be attributed to the nanoindentation experiment, whilst the latter two faces show indents around which nucleated slip bands and cracks as well as small pile up of the material.

Overall, whilst CBZ has a strong 3D network of interactions, the system deforms plastically through slip on the (020) plane, which requires the breaking (and reforming) of hydrogen bonds. The material also shows some brittleness and surface cracking was observed on indentation. MD-Shearing simulations showed results consistent with our experimental observations of the slip plane, whilst energy of attachment failed at predicting such a slip plane. Rugosity data combined with a new parameter we defined as the HB-density of the slip plane of interest, were able to reveal the (020) as the most likely slip plane in agreement with the experiments and the MD simulations. Computed Young's moduli gave a good picture of the anisotropy of mechanical behaviour in CBZ-III. Of particular interest, MD-shearing simulation add to a set of computable parameters such as attachment energy, planes rugosity, whose efficiency at predicting weak planes has often been challenged.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

AJCC thanks the Royal Society for an Industry Fellowship and a Research Grant. This work was supported by the Henry Royce Institute for Advanced Materials, funded through EPSRC grants EP/S009493/1, EP/R00661X/1, EP/P025021/1 and EP/P025498/1. BG thanks Roche and the University of Manchester for funding, and the staff in the Department of Chemistry XRD Facility in the School of Natural Sciences at the University of Manchester for their assistance. The authors thank Dr Pirmin Hidber for helpful discussions and Andrew Forrest for his help with the nanoindenter. The authors also thank the referees for their helpful comments.

References

1. M. L. Cheney, D. R. Weyna, N. Shan, M. Hanna, L. Wojtas and M. J. Zaworotko, Coformer Selection in Pharmaceutical Cocrystal Development: A Case Study of a Meloxicam Aspirin Cocrystal That Exhibits Enhanced Solubility and Pharmacokinetics, J. Pharm. Sci., 2011, 100, 2172–2181.
2. Y. Liu, J. Black, K. F. Boon, A. J. Cruz-Cabeza, R. J. Davey, R. Dowling, N. George, A. Hutchinson and R. Montis, When Crystals Don't Grow – the Growth Dead Zone, Cryst. Growth Des., 2019, 19, 4579–4587.
3. C. C. Sun and H. Hou, Improving Mechanical Properties of Caffeine and Methyl Gallate Crystals by Cocrystallization, Cryst. Growth Des., 2008, 8, 1575–1579.
4. F. Liu, D. E. Hooks, N. Li, N. A. Mara and J. A. Swift, Mechanical Properties of Anhydrous and Hydrated Uric Acid Crystals, Chem. Mater., 2018, 30, 3798–3805.
5. M. S. R. N. Kiran, S. Varughese, U. Ramamurty and G. R. Desiraju, Effect of Dehydration on the Mechanical Properties of Sodium Saccharin Dihydrate Probed with Nanoindentation, CrystEngComm, 2012, 14, 2489–2493.
6. S. Y. Chang and C. C. Sun, Superior Plasticity and Tabletability of Theophylline Monohydrate, Mol. Pharmaceutics, 2017, 14, 2047–2055.
7. P. Di Martino, A. M. Guyot-Hermann, P. Conflant, M. Drache and J. C. Guyot, A New Pure Paracetamol for Direct Compression: The Orthorhombic Form, Int. J. Pharm., 1996, 128, 1–8.
8. D. K. Bučar, J. A. Elliott, M. D. Eddleston, J. K. Cockcroft and W. Jones, Sonocrystallization Yields Monoclinic Paracetamol with Significantly Improved Compaction Behavior, Angew. Chem., Int. Ed., 2015, 54, 249–253.
9. H. Eisenschmidt, N. Bajcinca and K. Sundmacher, Optimal Control of Crystal Shapes in Batch Crystallization Experiments by Growth-Dissolution Cycles, Cryst. Growth Des., 2016, 16, 3297–3306.
10. F. Salvatori and M. Mazzotti, Manipulation of Particle Morphology by Crystallization, Milling, and Heating Cycles – A Mathematical Modeling Approach, Ind. Eng. Chem. Res., 2017, 56, 9188–9201.
11. R. Wakeman, The Influence of Particle Properties on Filtration, Sep. Purif. Technol., 2007, 58, 234–241.
12. G. Perini, F. Salvatori, D. R. Ochsenbein, M. Mazzotti and T. Vetter, Filterability Prediction of Needle-like Crystals Based on Particle Size and Shape Distribution Data, Sep. Purif. Technol., 2019, 211, 768–781.
13. U. Ramamurty and J. I. Jang, Nanoindentation for Probing the Mechanical Behavior of Molecular Crystals-a Review of the Technique and How to Use It, CrystEngComm, 2014, 16, 12–23.
14. B. P. A. Gabriele, C. J. Williams, M. E. Lauer, B. Derby and A. J. Cruz-Cabeza, Nanoindentation of Molecular Crystals: Lessons Learnt from Aspirin, Cryst. Growth Des., 2020, 20(9), 5956–5966.
15. P. Manimunda, E. Hintsala, S. Asif and M. K. Mishra, Mechanical Anisotropy and Pressure Induced Structural Changes in Piroxicam Crystals Probed by In Situ Indentation and Raman Spectroscopy, JOM, 2017, 69, 57–63.
16. S. Seethalekshmi, M. S. R. N. Kiran, U. Ramamurty and S. Varughese, Phase Transitions and Anisotropic Mechanical Response in a Water-Rich Trisaccharide Crystal, Cryst. Growth Des., 2020, 20, 442–448.
17. A. Danesh, S. D. Connell, M. C. Davies, C. J. Roberts, S. J. B. Tendler, P. M. Williams and M. J. Wilkins, An in Situ Dissolution Study of Aspirin Crystal Planes (100) and (001) by Atomic Force Microscopy, Pharm. Res., 2001, 18, 299–303.
18. D. Olusanmi, K. J. Roberts, M. Ghadiri and Y. Ding, The Breakage Behaviour of Aspirin under Quasi-Static Indentation and Single Particle Impact Loading: Effect of Crystallographic Anisotropy, Int. J. Pharm., 2011, 411, 49–63.
19. M. S. R. N. Kiran, S. Varughese, C. M. Reddy, U. Ramamurty and G. R. Desiraju, Mechanical Anisotropy in Crystalline Saccharin: Nanoindentation Studies, Cryst. Growth Des., 2010, 10, 4650–4655.
20. R. M. Mohamed, M. K. Mishra, L. M. Al-Harbi, M. S. Al-Ghamdi and U. Ramamurty, Anisotropy in the Mechanical Properties of Organic Crystals: Temperature Dependence, RSC Adv., 2015, 5, 64156–64162.
21. K. J. Ramos and D. F. Bahr, Mechanical Behavior Assessment of Sucrose Using Nanoindentation, J. Mater. Res., 2007, 22, 2037–2045.
22. G. R. Krishna, M. S. R. N. Kiran, C. L. Fraser, U. Ramamurty and C. M. Reddy, The Relationship of Solid-State Plasticity to Mechanochromic Luminescence in Difluoroboron Avobenzone Polymorphs, Adv. Funct. Mater., 2013, 23, 1422–1430.
23. I. Lubomirsky, I. Azuri, E. Meirzadeh, D. Ehre, S. R. Cohen, A. M. Rappe, M. Lahav and L. Kronik, Unusually Large Young's Moduli of Amino Acid Molecular Crystals, Angew. Chem., Int. Ed., 2015, 54, 13566–13570.
24. S. P. Timoshenko and J. Goodier, Theory of Elasticity, McGraw-Hill, New York, 2nd edn, 1951.
25. N. A. Stilwell and D. Tabor, Elastic Recovery of Conical Indentations, Proc. Phys. Soc., London, 1961, 78, 169–179.
26. A. C. Fischer-Cripps, Contact Mechanics, in Nanoindentation, 2011, pp. 1–19.
27. M. M. J. Lowes, M. R. Caira, A. P. Lotter and J. G. D. Van Watt, Physicochemical Properties and X-ray Structural Studies of the Trigonal Polymorph of Carbamazepine, J. Pharm. Sci., 1987, 76, 744–752.
28. J. N. Lisgarten, R. A. Palmer and J. W. Saldanha, Crystal and Molecular Structure of 5-Carbamyl-5H-Dibenzo[b,f] Azepine, J. Crystallogr. Spectrosc. Res., 1989, 19, 641–649.
29. M. Lang, J. W. Kampf and A. J. Matzger, Form IV of Carbamazepine, J. Pharm. Sci., 2002, 91, 1186–1190.
30. A. L. Grzesiak, M. Lang, K. Kim and A. J. Matzger, Comparison of the Four Anhydrous Polymorphs of Carbamazepine and the Crystal Structure of Form I, J. Pharm. Sci., 2003, 92, 2260–2271.
31. J. B. Arlin, L. S. Price, S. L. Price and A. J. Florence, A Strategy for Producing Predicted Polymorphs: Catemeric Carbamazepine Form V, Chem. Commun., 2011, 47, 7074–7076.
32. T. Gelbrich and M. B. Hursthouse, Systematic Investigation of the Relationships between 25 Crystal Structures Containing the Carbamazepine Molecule or a Close Analogue: A Case Study of the XPac Method, CrystEngComm, 2006, 8, 448–460.
33. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
34. P. R. O. CrysAlis, Version 171.40.14d, Oxford Diffraction/Agilent Technologies UK Ltd, England, Yarnton, 2018.
35. ISO 14577: Instrumented Indentation Test for Hardness and Materials Parameters, in Metallic Materials, Int. Organ. Stand. Geneva, Switz, 2015.
36. Dassault Systèmes BIOVIA, Materials Studio, Release 2019, Dassault Systèmes, San Diego, 2019.
37. H. Sun, Z. Jin, C. Yang, R. L. C. Akkermans, S. H. Robertson, N. A. Spenley, S. Miller and S. M. Todd, COMPASS II: Extended Coverage for Polymer and Drug-like Molecule Databases, J. Mol. Model., 2016, 22, 1–10.
38. R. L. M. Robinson, D. Geatches, C. Morris, R. MacKenzie, A. G. P. Maloney, K. J. Roberts, A. Moldovan, E. Chow, K. Pencheva and D. R. M. Vatvani, Evaluation of Force-Field Calculations of Lattice Energies on a Large Public Dataset, Assessment of Pharmaceutical Relevance, and Comparison to Density Functional Theory, J. Chem. Inf. Model., 2019, 59, 4778–4792.
39. A. Marmier, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, ElAM: A Computer Program for the Analysis and Representation of Anisotropic Elastic Properties, Comput. Phys. Commun., 2010, 181, 2102–2115.
40. M. J. Bryant, A. G. P. Maloney and R. A. Sykes, Predicting Mechanical Properties of Crystalline Materials through Topological Analysis, CrystEngComm, 2018, 20, 2698–2704.
41. S. Varughese, M. S. R. N. Kiran, K. A. Solanko, A. D. Bond, U. Ramamurty and G. R. Desiraju, Interaction Anisotropy and Shear Instability of Aspirin Polymorphs Established by Nanoindentation, Chem. Sci., 2011, 2, 2236–2242.
42. M. K. Mishra, U. Ramamurty and G. R. Desiraju, Solid Solution Hardening of Molecular Crystals: Tautomeric Polymorphs of Omeprazole, J. Am. Chem. Soc., 2015, 137, 1794–1797.
43. M. L. Oyen and R. F. Cook, A Practical Guide for Analysis of Nanoindentation Data, J. Mech. Behav. Biomed. Mater., 2009, 2, 396–407.
44. A. C. Burch, J. D. Yeager and D. F. Bahr, Indentation Fracture Behavior of Energetic and Inert Molecular Crystals, J. Mater. Res., 2019, 34, 3954–3963.
45. C. Wang and C. C. Sun, Computational Techniques for Predicting Mechanical Properties of Organic Crystals: A Systematic Evaluation, Mol. Pharmaceutics, 2019, 16, 1732–1741.
46. C. C. Sun and Y.-H. Kiang, On the Identification of Slip Planes in Organic Crystals Based on Attachment Energy Calculation, J. Pharm. Sci., 2008, 97, 3456–3461.
47. M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Energy Frameworks: Insights into Interaction Anisotropy and the Mechanical Properties of Molecular Crystals, Chem. Commun., 2015, 51, 3735–3738.
48. C. Wang and C. C. Sun, Identifying Slip Planes in Organic Polymorphs by Combined Energy Framework Calculations and Topology Analysis, Cryst. Growth Des., 2018, 18, 1909–1916.
49. B. Gabriele, C. Williams, M. Lauer, B. Derby and A. Cruz-Cabeza, Isomechanical Groups in Molecular Crystals and Role of Aromatic Interactions, Cryst. Growth Des., 2020, 20(11), 7516–7525.
50. C. Wang and C. C. Sun, The Landscape of Mechanical Properties of Molecular Crystals, CrystEngComm, 2020, 20, 1149–1153.
51. B. C. A. Hutchinson, 16: Anisotropy in Metals, Mater. Sci. Technol., 2015, 31, 1393–1401.
52. R. J. Roberts and R. C. Rowe, Influence of Polymorphism on the Young's Modulus and Yield Stress of Carbmazepine, Sulfathiazole and Sulfanilamide, Int. J. Pharm., 1996, 129, 79–94.
53. R. J. Roberts, R. S. Payne and R. C. Rowe, Mechanical Property Predictions for Polymorphs of Sulphathiazole and Carbamazepine, Eur. J. Pharm. Sci., 2000, 9, 277–283.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ce01659d

---